Energy efficiency optimization in MIMO heterogeneous wireless powered communication networks

Abstract

This paper studies the energy efficiency (EE) optimization problem in multiple-user multiple-input–multiple-output heterogeneous wireless powered communication network (HWPCN) in which the users in small cells can harvest energy from the small cell base stations in downlink and use harvested energy for uplink transmission. We consider the joint design problem of wireless energy transmission and wireless information transmission precoding matrices subject to the transmit power constraints at each BS and each user. Since the optimization problem under consideration is highly nonlinear non-convex fractional programming in design variables, it is mathematically challenging to obtain the optimal solutions. To tackle with this difficulty, we employ the difference of convex programming to obtain the concave lower bound of the achievable sum rates. Then, we apply the Dinkelbach approach to develop an efficient iterative algorithm in which the convex optimization problems are solved. Simulation results are provided to investigate the EE of the proposed algorithm in HWPCNs.

1 Introduction

In recent years, the novel standards and technologies in the fifth generation (5G) of wireless networks are expected to accommodate higher data rate for the excessively increasing demand of mobile data traffic. One of the key approaches is the deployment of heterogeneous networks (HetNets) where various types of base stations (BSs) are deployed to serve user equipments (UEs) [1, 23]. The HetNets can improve the coverage and throughput of wireless networks, especially for indoor environments [23]. However, the deployment of various types of BSs operating in the same frequency band can increase interference in HetNets which can limit the achievable spectral efficiency (SE). There have been considerable studies on how to tackle interference issues [8, 21]. In [21], a weighted minimum mean square error (WMMSE) method was proposed to cope with interference. The authors in [8] developed an interference alignment (IA) approach to handle with interference in the uplink transmission of HetNets. On the other hand, the dense deployment of BSs in the next generation of wireless commuications can cause the energy consumption issues.

In the last decade, the energy efficiency (EE) has become a crucial performance metric and has attracted great interest in wireless communication designs; see, e.g., [11, 19, 23] and references therein. Reference [11] considered EE optimization in HetNets by using the block coordinate ascent algorithm. The authors in [19] studied the EE optimization problem for spectrum-sharing HetNets. The issues of EE optimization for coordinated multi-point (CoMP)-simultaneous wireless information and power transfer (SWIPT) HetNet investigated in [23]. Towards green wireless communications, wireless energy transfer (WET) and energy harvesting techniques utilizing radio frequency (RF) signals have been received great attention as an important solution for prolonging battery lifetime of wireless devices without replacing their batteries. Thanks to WET technologies, the energy-limited wireless devices can harvest energy from radio frequency (RF) signals to supply power to their batteries and extend their lifetime. Two main research directions on energy harvesting, namely SWIPT [6, 9, 17, 18, 23] and wireless powered communication networks (WPCN) [3, 4, 14, 16] have been studied in various system configurations. However, the SWIPT systems are confined to downlink transmission, while the WPCNs consider not only downlink but also uplink transmission [16]. More specifically, the SWIPT systems accomplish both the WET and WIT operations at the same time and frequency while the WPCNs perform each progression separately over two sequential phases. Particularly, in the first WET phase, a BS broadcasts energy RF signals to the users over the downlink channels, and the users harvest the energy to charge their batteries. Then, in the consecutive uplink WIT phase, the users exploit harvested energy stored after the WET phase for transmitting their information signals to the BS. Thus, the WPCNs were called harvest-then-transmit (HTT) protocol introduced in [10]. Over the past few years, the WPCN configurations such as single-input–single-output (SISO) WPCNs in [10, 15], multiple-input single-output (MISO) WPCNs in [22, 25] and multiple-input–multiple-output (MIMO) WPCNs in [3, 4, 13, 14, 16] have been investigated in the literature. In [10, 15], the authors studied the dynamic time-division multiple access (TDMA) approach to optimize each time slot for maximizing the uplink sum achievable throughput. Also, by applying the dynamic TDMA method, the extended work to MISO WPCN in [22] was studied. In [22], the work jointly optimized the beamforming vectors and time allocation to maximize sum-rate. Moreover, in MIMO systems, the authors in [15] proposed an optimization algorithm that jointly optimizes the downlink energy and uplink information precoding matrices and time allocation for maximizing the uplink sum throughput of multi-user (MU). Similarly, the authors in [4] studied the max–min user uplink data rate optimization problem based on zero-forcing (ZF)-based approach in MU-MIMO WPCNs. The contributions of spectrum sharing in WPCNs were presented in [13, 15], which considered cognitive WPCNs (CWPCN). While the former studied a CWPCN system in the case of single-antenna users, the latter considered MU MIMO CWPCNs. In addition, the throughput optimization with imperfect channel state information (CSI) in MIMO WPCNs was considered in [3].

In this paper, we study jointly precoding designs in which the downlink WET precoding matrices at small BSs (SBSs), uplink WIT precoding matrices at UE and WIT at macro BS (MBS) are designed to maximize the EE of MU MIMO HWPCNs. Our major contributions are to develop an efficient iterative algorithm to maximize the EE MU MIMO HWPCNs. It is important to remark that the EE maximization in HetNets which is similar to our approach was investigated in [23]. However, there are several key differences between the work in [23] and our study. First, the work in [23] studied the MISO SWIPT model while our work focuses on the MIMO WPCN model. Different from the SWIPT scenario in which there exists only downlink transmission, the WPCN model involves both downlink and uplink transmission. Second, the work in [23] focused on using zero-forcing to design the beamformers for the MISO system. In contrast, our paper focuses on designing of precoding matrices for MU MIMO HWPCNs by developing the iterative algorithm based on the difference of two concave functions. It is also noted that the WPCN models were investigated in [4, 16]. However, both studies in [4, 16] considered the MU MIMO single-cell model whereas our work focuses on the multi-cell HetNet model. Noted that as compared to the single cell scenario in which there exists only inter-user interference, the received signals in multi-cell HetNet models suffer the additional inter-cell interference.

The present work will formulate the precoder design as an optimization problem which aims at maximizing the EE in MU MIMO HWPCNs subject to power constraints. It is shown that the resulting EE optimization problems are non-convex fractional programming and, thus, it is highly complicated to obtain the optimal solutions. Inspired by the works of [12], we derive the convave lower bound of the achievable rate by exploiting the concave property of the log-det function. Then, we apply the Dinkelbach method to develop an efficient iterative algorithm. The numerical simulations are provided to verify the convergence of our iterative algorithm, to evaluate the EE performance of the proposed EE optimization as compared to those of the SE optimization. In addition, we numerically investigate the impact of the energy harvesting duration on the EE and SE performance of HWPCNs. Our main contributions can be summarized as follows:

• We formulate the joint design of the precoders in the MU MIMO HWPCNs as an optimization problem in which the EE, defined as the ratio of the sum rates of the small cell users and macro cell users to the effective power consumption is maximized subject to transmit power constraints.

• To tackle the mathematical challenges in solving the non-convex fractional optimization, we develop the iterative algorithm by using the Dinkelbach method and optimization technique of difference of convex (D.C) functions.

• We provide the numerical results illustrating the convergence of the proposed algorithm and the effectiveness of the EE maximization as compared to the SE maximization.

The remainder of the paper is organized as follows. In Sect. 2, we introduce the system model of MU MIMO HWPCNs and, then, formulate the precoding design as an optimization problem. Then Sect. 3 presents an iterative algorithm to obtain the optimal precoding matrices. Section 4 provides numerical simulation results. Finally, the conclusions are presented in Sect. 5.

Notation

Matrices (vectors) are respectively represented by boldface upper (lower) case letters. $\mathbf{I}$ is an identity matrix with appropriate dimension. $\mathbf {X}^H, \left\langle \mathbf {X}\right\rangle$ and $\left| \mathbf {X}\right|$ represent the Hermitian transposition, trace and determinant of matrix $\mathbf {X}$. $\mathbf {X}\succeq 0$ stands for a positive semidefinite matrix. $\mathbf {x}\sim \mathcal {CN}\left( \overline{\mathbf {x}},\mathbf {R_x}\right)$ denotes a complex Gaussian random vector $\mathbf {x}$ with mean $\overline{\mathbf {x}}$ and covariance $\mathbf {R_x}$.

2 System model and problem formulation

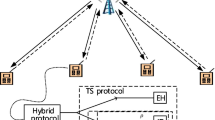
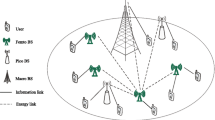
Consider a two-tier HetNet model which consists of L small cells deployed in the same coverage with a macro cell as depicted in Fig. 1. Each BS transmits its signals to its associated users, i.e., there are $L+1$ BSs transmitting in the same frequency band. The MBS denoted by $\text {BS}_0$ is equipped with $M_0$ antennas and serves $K_0$ users. UE k, ${\text {for}}\,k\in \mathcal {K}_0=\left\{ 1,\ldots ,K_0\right\}$, in the macro cell denoted by $\text {UE}_{k_0}$ is equipped $N_{k_0}$ antennas. SBS $\ell$ denoted by $\text {BS}_\ell$, for $\ell \in \mathcal {L}= \left\{ 1,\ldots ,L\right\}$, is equipped with $M_\ell$ antennas serving $K_\ell$ users in its coverage. User k in cell $\ell$ denoted by $\text {UE}_{k_\ell }$ is equipped with $N_{k_\ell }$ antennas for $k\in \mathcal {K}_\ell =\left\{ 1,\ldots ,K_\ell \right\}$. Note that $\mathcal {K}_0$ denotes the set of all users associated with the MBS while $\mathcal {K}_\ell$ for $\ell \ne 0$ represents the set of all users associated with SBS $\ell$. The notations for channels and precoding matrices are presented in Table 1 in which the channel coefficients encompass both small-scale fading and pathloss. We also assume that the ideal CSI is available at the BSs and users [20]. Assuming that the BSs and UEs are perfectly synchronized [20], we consider two phases of downlink WET and uplink WIT for the small-cell network while the MBS transmits the information signals to its macro-cell users. Without loss of generality, the durations of WET and WIT are normalized by $\tau$ and $(1-\tau )$, for $\tau \in [0,1]$, respectively. It is worth noting that both conditions of $\tau =0$ and $\tau =1$ are referred to as non-transmission of small cell users, e.g., when $\tau =0$, energy transmission time is zero and, thus, small cell users have no energy for uplink transmission, and when $\tau =1$, the uplink transmission duration of small cell users is zero.

Fig. 1

Model of two transmission phases in the MU MIMO HWPCN

Table 1 Notations

2.1 Downlink WET phase

In this phase, the SBSs convey the energy signals to recharge the power for the small-cell users while the MBS transmits the information signals to its macro-cell users. Let $\mathbf{s}_{0,k_0}^D\in \mathbb {C}^{d_{0,k_0}^I \times 1}$, $\mathbf{s}_{s,i_s}^E\in \mathbb {C}^{d_{s,i_s}^E \times 1}$ be $d_{0,k_0}^I$ and $d_{s,i_s}^E$ independent data and energy streams which are transmitted from $\text {BS}_0$ to $\text {UE}_{k_0}$ and $\text {BS}_s$ to $\text {UE}_{i_s}$, respectively. Without loss of generality, we assume that $\mathbb {E}\left( \mathbf{s}_{0,k_0}^D\left( \mathbf{s}_{0,k_0}^D\right) ^H\right) =\mathbf{I}_{d_{0,k_0}^I}$ and $\mathbb {E}\left( \mathbf{s}_{s,i_s}^E\left( \mathbf{s}_{s,i_s}^E\right) ^H\right) =\mathbf{I}_{d_{s,i_s}^E}$. $\text {BS}_0$ uses the linear precoding matrices $\mathbf{F}_{0,k_0}^D$ to beam the signals towards $\text {UE}_{k_0}$ while $\text {BS}_\ell$ uses the precoder matrix $\mathbf{F}_{\ell ,k_\ell }^E$ to beam the energy signals to $\text {UE}_{k_\ell }$. Apart from receiving the RF signals from its associated SBSs, each small cell user can also receive the RF signals from the other SBSs and MBS. By ignoring negligible noise power, the harvested energy at $\text {UE}_{k_\ell }$ can be given by

$$\begin{aligned} {\begin{matrix} Q_{k_\ell }\left( \mathbf{F}^E, \mathbf{F}^D \right) &{}= \tau \xi _{k_\ell }\left( \sum _{s=1}^L\sum _{i=1}^{K_s} \left\langle \mathbf{H}_{k_\ell ,s}^D\mathbf{F}_{s,i_s}^E\left( \mathbf{H}_{k_\ell ,s}^D\mathbf{F}_{s,i_s}^E\right) ^H\right\rangle \right. \\ &{}\quad \left. +\sum _{i=1}^{K_0}\left\langle \mathbf{H}_{k_\ell ,0}^D\mathbf{F}_{0,i_0}^D \left( \mathbf{H}_{k_\ell ,0}^D\mathbf{F}_{0,i_0}^D\right) ^H\right\rangle \right) ,\\ &{}\quad \ell \in \mathcal {L},k\in \mathcal {K}_\ell , \end{matrix}} \end{aligned}$$

(1)

where $\xi _{k_\ell }$ accounts for the loss of energy conversion and we have denoted the set of all energy precoding matrices by $\mathbf{F}^E=\left\{ \mathbf{F}_{\ell ,k_\ell }^E\right\} _{\ell \in \mathcal {L},k\in \mathcal {K}_\ell }$ for compact notation. Note that the energy at the small cell users only comes from the energy harvested in this WET phase and it will be utilized for uplink transmission in the second phase.

While the SBSs broadcast the energy signals to charge small-cell users in their coverage, the MBS transmits the information signals to its $\text {UE}_{k_0}$. The received signal at macro-user $\text {UE}_{k_0}$ is

$$\begin{aligned} \mathbf{y}_{k_0}&=\mathbf{H}_{k_0,0}^D\mathbf{F}_{0,k_0}^D\mathbf{s}_{0,k_0}^D + \sum _{i=1,i\ne k}^{K_0}\mathbf{H}_{k_0,0}^D\mathbf{F}_{0,i_0}^D\mathbf{s}_{0,i_0}^D\nonumber \\&\quad +\sum _{s=1}^L\sum _{i=1}^{K_s}\mathbf{H}_{k_0,s}^D\mathbf{F}_{s,i_s}^E\mathbf{s}_{s,i_s}^E + \mathbf{n}_{k_0},~~k\in \mathcal {K}_0 \end{aligned}$$

(2)

where $\mathbf{n}_{k_0}\sim \mathcal {CN}\left( 0,\sigma _{k_0}^2\mathbf{I}\right)$ is additive white Gaussian noise at $\text {UE}_{k_0}$. In this paper, it is assumed that interference at the receiver is treated as noise. Then, the achievable rate of $\text {UE}_{k_0}$ in the first phase from (2) is given by

$$\begin{aligned} R_{k_0}^{(1)}\left( \mathbf{F}^D,\mathbf{F}^E\right) =\tau \log \left| \mathbf{I}_{N_{k_0}}+\mathbf{H}_{k_0,0}^D\mathbf{F}_{0,k_0}^D \left( \mathbf{H}_{k_0,0}^D\mathbf{F}_{0,k_0}^D\right) ^H\mathbf{Z}_{k_0}^{-1}\right| \end{aligned}$$

(3)

where we have defined $\mathbf{F}^D=\left\{ \mathbf{F}_{0,k_0}^D\right\} _{k\in \mathcal {K}_0}$ and the covariance matrix of interference plus noise at $\text {UE}_{k_0}$

$$\begin{aligned} \mathbf{Z}_{k_0}\left( \mathbf{F}^D,\mathbf{F}^E\right)&= \sum _{i=1,i\ne k}^{K_0}\mathbf{H}_{k_0,0}^D\mathbf{F}_{0,i_0}^D\left( \mathbf{H}_{k_0,0}^D\mathbf{F}_{0,i_0}^D\right) ^H\nonumber \\&\quad +\sum _{s=1}^L\sum _{i=1}^{K_s}\mathbf{H}_{k_0,s}^D\mathbf{F}_{s,i_s}^E\left( \mathbf{H}_{k_0,s}^D\mathbf{F}_{s,i_s}^E\right) ^H\nonumber \\&\quad + \sigma ^2_{k_0}\mathbf{I}_{N_{k_0}}. \end{aligned}$$

(4)

2.2 Uplink WIT phase

In second phase, each $\text {UE}_{k_\ell }$ transmits $d_{k_\ell ,\ell }^I$ independent data streams denoted by the information signal vector $\mathbf{s}_{k_\ell ,\ell }^U$ to $\text {BS}_\ell$. We also assume that the covariance matrix $\mathbb {E}\left( \mathbf{s}_{k_\ell ,\ell }^U\left( \mathbf{s}_{k_\ell ,\ell }^U\right) ^H\right) =\mathbf{I}_{d_{k_\ell ,\ell }^I}$, meanwhile the MBS keeps transmitting the information signals to its users. $\text {UE}_{k_\ell }$ uses the precoding matrix $\mathbf{F}_{k_\ell ,\ell }^U$ to linearly process its signal before transmitting to its SBS. The received signal at $\text {BS}_\ell$ can be defined by

$$\begin{aligned} \mathbf{y}_\ell&= \sum _{k=1}^{K_\ell }\mathbf{H}_{\ell ,k_\ell }^U\mathbf{F}_{k_\ell ,\ell }^U\mathbf{s}_{k_\ell ,\ell }^U+\sum _{s=1,s\ne \ell }^L\sum _{k=1}^{K_s}\mathbf{H}_{\ell ,k_s}^U\mathbf{F}_{k_s,s}^U\mathbf{s}_{k_s,s}^U\nonumber \\&\quad +\sum _{k=1}^{K_0}\mathbf {G}_{\ell ,0}\mathbf{F}_{0,k_0}^D\mathbf{s}_{0,k_0}^D+\mathbf{n}_\ell ,~~\ell \in \mathcal {L} \end{aligned}$$

(5)

where $\mathbf{n}_\ell \sim \mathcal {CN}\left( 0,\sigma _{\ell }^2\mathbf{I}\right)$ is additive white Gaussian noise at $\text {BS}_\ell$. By treating interference as noise, the achievable rate of $\text {BS}_\ell$ is given by

$$\begin{aligned}&R_\ell \left( \mathbf{F}^D, \mathbf{F}^U \right) \nonumber \\&\quad =\left( 1-\tau \right) \log \left| \mathbf{I}_{M_\ell } +\sum _{k=1}^{K_\ell }\mathbf{H}_{\ell ,k_\ell }^U\mathbf{F}_{k_\ell ,\ell }^U \left( \mathbf{H}_{\ell ,k_\ell }^U\mathbf{F}_{k_\ell ,\ell }^U\right) ^H\mathbf{J}_\ell ^{-1}\right| \nonumber \\ \end{aligned}$$

(6)

where we have defined $\mathbf{F}^U=\left\{ \mathbf{F}_{k_\ell ,\ell }^U\right\} _{\ell \in \mathcal {L},k\in \mathcal {K}_\ell }$ and the covariance matrix of interference plus noise at $\text {BS}_\ell$ as

$$\begin{aligned} \mathbf{J}_\ell (\mathbf{F}^D, \mathbf{F}^U)&=\sum _{s=1,s\ne \ell }^L\sum _{k=1}^{K_s}\mathbf{H}_{\ell ,k_s}^U\mathbf{F}_{k_s,s}^U \left( \mathbf{H}_{\ell ,k_s}^U\mathbf{F}_{k_s,s}^U\right) ^H\nonumber \\&\quad +\sum _{k=1}^{K_0}\mathbf {G}_{\ell ,0}\mathbf{F}_{0,k_0}^D \left( \mathbf {G}_{\ell ,0}\mathbf{F}_{0,k_0}^D\right) ^H + \sigma ^2_\ell \mathbf{I}_{M_\ell }. \end{aligned}$$

(7)

With regard to macro-cell users, the received signals at the macro-cell users in this phase are distorted by interference from the uplink signals of small cell users. Thus, the received signal at $\text {UE}_{k_0}$ is

$$\begin{aligned} \mathbf{y}_{k_0}&=\mathbf{H}_{k_0,0}^D\mathbf{F}_{0,k_0}^D\mathbf{s}_{0,k_0}^D + \sum _{i=1,i\ne k}^{K_0}\mathbf{H}_{k_0,0}^D\mathbf{F}_{0,i_0}^D\mathbf{s}_{0,i_0}^D\nonumber \\&\quad +\sum _{\ell =1}^L\sum _{i=1}^{K_\ell }\mathbf {G}_{k_0,i_\ell }\mathbf{F}_{i_\ell ,\ell }^U\mathbf{s}_{i_\ell ,\ell }^U + \mathbf{n}_{k_0},~~k\in \mathcal {K}_0. \end{aligned}$$

(8)

Then the achievable rate of $\text {UE}_{k_0}$ in this second phase is given by

$$\begin{aligned}&R_{k_0}^{(2)}\left( \mathbf{F}^D,\mathbf{F}^U\right) \nonumber \\&\quad =\left( 1-\tau \right) \log \left| \mathbf{I}_{N_{k_0}}+\mathbf{H}_{k_0,0}^D\mathbf{F}_{0,k_0}^D \left( \mathbf{H}_{k_0,0}^D\mathbf{F}_{0,k_0}^D\right) ^H\mathbf{R}_{k_0}^{-1}\right| \nonumber \\ \end{aligned}$$

(9)

where the covariance matrix of interference plus noise at $\text {UE}_{k_0}$ has been defined as

$$\begin{aligned} \mathbf{R}_{k_0}\left( \tau ,\mathbf{F}^D,\mathbf{F}^U\right)&= \sum _{i=1,i\ne k}^{K_0}\mathbf{H}_{k_0,0}^D\mathbf{F}_{0,i_0}^D\left( \mathbf{H}_{k_0,0}^D\mathbf{F}_{0,i_0}^D\right) ^H\nonumber \\&\quad +\sum _{\ell =1}^L\sum _{i=1}^{K_\ell }\mathbf {G}_{k_0,i_\ell }\mathbf{F}_{i_\ell ,\ell }^U\left( \mathbf {G}_{k_0,i_\ell }\mathbf{F}_{i_\ell ,\ell }^U\right) ^H\nonumber \\&\quad + \sigma ^2_{k_0}\mathbf{I}_{N_{k_0}}. \end{aligned}$$

(10)

To investigate the system EE, it is relevant to compute the power consumption of the systems. The consumption power of $\text {BS}_0$, $\text {BS}_\ell$, $\text {UE}_{k_\ell }$ is respectively modeled as [23]

$$\begin{aligned} P_0\left( \mathbf{F}^D\right)= & {} \zeta _0\sum _{k=1}^{K_0}\left\langle \mathbf{F}_{0,k_0}^D \left( \mathbf{F}_{0,k_0}^D\right) ^H\right\rangle + P_{C_0},\end{aligned}$$

(11)

$$\begin{aligned} P_\ell \left( \mathbf{F}^E\right)= & {} \zeta _\ell \sum _{k=1}^{K_0}\left\langle \mathbf{F}_{\ell ,k_\ell }^E\left( \mathbf{F}_{\ell ,k_\ell }^E\right) ^H\right\rangle + P_{C_\ell }, \end{aligned}$$

(12)

and

$$\begin{aligned} P_{k_\ell }\left( \mathbf{F}^U\right) = \zeta _{k_\ell }\left\langle \mathbf{F}_{k_\ell ,\ell }^U \left( \mathbf{F}_{k_\ell ,\ell }^U\right) ^H\right\rangle + P_{C_{k_\ell }}, \end{aligned}$$

(13)

where $\zeta _0$, $\zeta _\ell$, and $\zeta _{k_\ell }$ represents the power amplifier drain inefficiency while $P_{C_0}$, $P_{C_\ell }$, $P_{C_{k_\ell }}$ are circuit power consumption which can be modeled as

$$\begin{aligned} P_{C_0}= & {} M_0P_{\text {ant}}^{\text {BS}}+P_0^{\text {fix}},\end{aligned}$$

(14)

$$\begin{aligned} P_{C_\ell }= & {} M_\ell P_{\text {ant}}^{\text {BS}}+P_\ell ^{\text {fix}}, \end{aligned}$$

(15)

and

$$\begin{aligned} P_{C_{k_\ell }}=N_{k_\ell }P_{\text {ant}}^{\text {UE}}+P_{k_\ell }^{\text {fix}} \end{aligned}$$

(16)

where $P_{\text {ant}}^{\text {BS}}$ and $P_{\text {ant}}^{\text {UE}}$ are respectively the transmit power of each antenna at the BS and UE transmitters while $P_0^{\text {fix}}$, $P_\ell ^{\text {fix}}$ and $P_{k_\ell }^{\text {fix}}$ are the fixed power consumption at the MBS, SBSs and UEs, respectively [18, 23].

2.3 Problem formulation for precoding designs

The design of interest is to find the optimal precoders to maximize the network EE subject to the transmit power constraints on the BSs and small cell users. The network EE is defined as the ratio of the achievable sum rate to overall power consumption [24] and can be formulated as

$$\begin{aligned}&\mathcal {EE}\left( \mathbf{F}^E,\mathbf{F}^D,\mathbf{F}^U\right) \nonumber \\&\quad =\dfrac{\sum _{k=1}^{K_0} R_{k_0}^{(1)}\left( \mathbf{F}^D,\mathbf{F}^E\right) +\sum _{k=1}^{K_0}R_{k_0}^{(2)}\left( \mathbf{F}^D,\mathbf{F}^U\right) +\sum _{\ell =1}^LR_\ell \left( \mathbf{F}^D, \mathbf{F}^U \right) }{\mathcal {P}\left( \mathbf{F}^E,\mathbf{F}^D,\mathbf{F}^U\right) }\nonumber \\ \end{aligned}$$

(17)

where $\mathcal {P}\left( \mathbf{F}^E,\mathbf{F}^D,\mathbf{F}^U\right) =\tau \sum _{\ell =1}^L P_\ell \left( \mathbf{F}^E\right) +P_0\left( \mathbf{F}^D\right) +\left( 1-\tau \right) \sum _{\ell =1}^L\sum _{k=1}^{K_\ell }P_{k_\ell }\left( \mathbf{F}^U\right) - \sum _{\ell =1}^L\sum _{k=1}^{K_\ell }Q_{k_\ell }\left( \tau ,\mathbf{F}^E,\right. \left. \mathbf{F}^D \right)$. Accordingly, the EE optimization problem is mathematically expressed as

$$\begin{aligned}&{\mathop {\max }\limits _{\{\mathbf{F}^E,\mathbf{F}^U,\mathbf{F}^D\}}}&\quad \mathcal {EE}\left( \mathbf{F}^E,\mathbf{F}^D,\mathbf{F}^U\right) \end{aligned}$$

(18a)

$$\begin{aligned}&\text {s.t.}&\quad \left( 1-\tau \right) \left\langle \mathbf{F}_{k_\ell ,\ell }^U(\mathbf{F}_{k_\ell ,\ell }^U)^H\right\rangle \le Q_{k_\ell }\left( \mathbf{F}^E, \mathbf{F}^D\right) , \nonumber \\&\quad \forall \ell \in \mathcal {L},~\forall k \in \mathcal {K_\ell },\end{aligned}$$

(18b)

$$\begin{aligned}&\quad \tau \sum _{k=1}^{K_\ell }\left\langle \mathbf{F}_{\ell ,k_\ell }^E\left( \mathbf{F}_{\ell ,k_\ell }^E\right) ^H\right\rangle \le P_{S_\ell },~\forall \ell \in \mathcal {L},\end{aligned}$$

(18c)

$$\begin{aligned}&\quad \left( 1-\tau \right) \sum _{k=1}^{K_0}\left\langle \mathbf{F}_{0,k_0}^D\left( \mathbf{F}_{0,k_0}^D\right) ^H \right\rangle \le P_{S_0}, \end{aligned}$$

(18d)

where $P_{S_0}$ and $P_{S_\ell }$ are the transmit power budget at $\text {BS}_0$, and $\text {BS}_\ell$, respectively. Thus, constraint (18b) guarantees that the small cell users cannot use energy in the WIT phase greater than energy harvested in the WET phase. Constraints (18c) and (18d) restrict the transmit power at BSs less than the maximum power budget. It is worth noting that the system EE will highly rely on the duration $\tau$, and, thus we will investigate the EE performance for different values of $\tau$ in numerical results.

It can be observed that the objective function (18a) is highly nonlinear and nonconvex fractional functions in coupling matrix variables. In addition, constraint (18b) is also nonconvex. Thus, the optimization problem () is nonconvex and mathematically challenging to solve. In the next section, we will introduce the approach to efficiently handle problem ().

3 Proposed algorithm derivation

To facilitate the nonlinearity of the optimization problem, we define $\mathbf{Q}_{\ell ,k_\ell }^E=\mathbf{F}_{\ell ,k_\ell }^E\left( \mathbf{F}_{\ell ,k_\ell }^E\right) ^H\succeq 0$, $\mathbf{Q}_{0,k_0}^D=\mathbf{F}_{0,k_0}^D\left( \mathbf{F}_{0,k_0}^D\right) ^H\succeq 0$, $\mathbf{Q}_{k_\ell ,\ell }^U=\mathbf{F}_{k_\ell ,\ell }^U\left( \mathbf{F}_{k_\ell ,\ell }^U\right) ^H\succeq 0$, we also denote $\mathbf{Q}^E=\left\{ \mathbf{Q}_{\ell ,k_\ell }^E\right\} _{\ell \in \mathcal {L},k\in \mathcal {K}_\ell }$, $\mathbf{Q}^D=\left\{ \mathbf{Q}_{0,k_0}^D\right\} _{k\in \mathcal {K}_0}$, $\mathbf{Q}^U=\left\{ \mathbf{Q}_{k_\ell ,\ell }^U\right\} _{\ell \in \mathcal {L},k\in \mathcal {K}_\ell }$. Then, the harvested energy in Eq. (1) can be rewritten as

$$\begin{aligned} {\begin{matrix} Q_{k_\ell }\left( \mathbf{Q}^E\right) &{}=\tau \xi _{k_\ell }\left( \sum _{s=1}^L \sum _{i=1}^{K_s}\left\langle \mathbf{H}_{k_\ell ,s}^D\mathbf{Q}_{s,i_s}^E \left( \mathbf{H}_{k_\ell ,s}^D\right) ^H\right\rangle \right. \\ &{}\quad \left. +\sum _{i=1}^{K_0}\left\langle \mathbf{H}_{k_\ell ,0}^D\mathbf{Q}_{0,i_0}^E \left( \mathbf{H}_{k_\ell ,0}^D\right) ^H\right\rangle \right) . \end{matrix}} \end{aligned}$$

(19)

The achievable rates of macro-cell users in the two phases of the downlink are respectively reformulated as

$$\begin{aligned} R_{k_0}^{(1)}\left( \mathbf{Q}^D, \mathbf{Q}^E\right) =\tau \log \left| \mathbf{I}_{N_{k_0}}+\mathbf{H}_{k_0,0}^D\mathbf{Q}_{0,k_0}^D \left( \mathbf{H}_{k_0,0}^D\right) ^H\mathbf{Z}_{k_0}^{-1}\right| \end{aligned}$$

(20)

where

$$\begin{aligned} \mathbf{Z}_{k_0}(\mathbf{Q}^D, \mathbf{Q}^E)= & {} \sum _{i=1,i\ne k}^{K_0}\mathbf{H}_{k_0,0}^D\mathbf{Q}_{0,i_0}^D\nonumber \\&+\sum _{s=1}^L\sum _{i=1}^{K_s}\mathbf{H}_{k_0,s}^D\mathbf{Q}_{s,i_s}^E\left( \mathbf{H}_{k_0,s}^D\right) ^H+ \sigma ^2_{k_0}\mathbf{I}_{N_{k_0}},\nonumber \\ \end{aligned}$$

(21)

and

$$\begin{aligned}&R_{k_0}^{(2)}\left( \mathbf{Q}^D, \mathbf{Q}^U\right) \nonumber \\&\quad =\left( 1-\tau \right) \log \left| \mathbf{I}_{N_{k_0}}+\mathbf{H}_{k_0,0}^D\mathbf{Q}_{0,k_0}^D\left( \mathbf{H}_{k_0,0}^D\right) ^H \mathbf{R}_{k_0}^{-1}\right| \end{aligned}$$

(22)

where

$$\begin{aligned} \mathbf{R}_{k_0}\left( \mathbf{Q}^D, \mathbf{Q}^U\right)= & {} \sum _{i=1,i\ne k}^{K_0}\mathbf{H}_{k_0,0}^D\mathbf{Q}_{0,i_0}^D \left( \mathbf{H}_{k_0,0}^D\right) ^H\nonumber \\&+\sum _{\ell =1}^L\sum _{i=1}^{K_\ell } \mathbf {G}_{k_0,i_\ell }\mathbf{Q}_{i_\ell ,\ell }^U\left( \mathbf {G}_{k_0,i_\ell }\right) ^H + \sigma ^2_{k_0}\mathbf{I}_{N_{k_0}}.\nonumber \\ \end{aligned}$$

(23)

The achievable rate of small-cell $\ell$ in the uplink is given by

$$\begin{aligned}&R_\ell \left( \mathbf{Q}^D,\mathbf{Q}^U\right) \nonumber \\&\quad =\left( 1-\tau \right) \log \left| \mathbf{I}_{M_\ell } +\sum _{k=1}^{K_\ell }\mathbf{H}_{\ell ,k_\ell }^U\mathbf{Q}_{k_\ell ,\ell }^U \left( \mathbf{H}_{\ell ,k_\ell }^U\right) ^H\mathbf{J}_\ell ^{-1}\right| \nonumber \\ \end{aligned}$$

(24)

where

$$\begin{aligned} \mathbf{J}_\ell \left( \mathbf{Q}^D,\mathbf{Q}^U\right)= & {} \sum _{s=1,s\ne \ell }^L\sum _{k=1}^{K_s}\mathbf{H}_{\ell ,k_s}^U\mathbf{Q}_{k_s,s}^U\left( \mathbf{H}_{\ell ,k_s}^U\right) ^H\nonumber \\&\quad +\sum _{k=1}^{K_0}\mathbf {G}_{\ell ,0}\mathbf{Q}_{0,k_0}^D\left( \mathbf {G}_{\ell ,0}\right) ^H + \sigma ^2_\ell \mathbf{I}_{M_\ell }.\nonumber \\ \end{aligned}$$

(25)

On the other hand, the consumption power of BSs and SUEs (11), (12), (13) also can be rewritten respectively as

$$\begin{aligned} P_0\left( \mathbf{Q}^D\right)= & {} \zeta _0\sum _{k=1}^{K_0}\left\langle \mathbf{Q}_{0,k_0}^D\right\rangle + P_{C_0},\end{aligned}$$

(26)

$$\begin{aligned} P_\ell \left( \mathbf{Q}^E\right)= & {} \zeta _\ell \sum _{k=1}^{K_0} \left\langle \mathbf{Q}_{\ell ,k_\ell }^E\right\rangle + P_{C_\ell },\end{aligned}$$

(27)

$$\begin{aligned} P_{k_\ell }\left( \mathbf{Q}^U\right)= & {} \zeta _{k_\ell } \left\langle \mathbf{Q}_{k_\ell ,\ell }^U\right\rangle + P_{C_{k_\ell }}. \end{aligned}$$

(28)

Accordingly, the design of EE maximization is recast as

$$\begin{aligned}&{\mathop {\max }\limits _{\{\mathbf{Q}^E,\mathbf{Q}^U,\mathbf{Q}^D\}}}&\quad \mathcal {EE}\left( \mathbf{Q}^E,\mathbf{Q}^D,\mathbf{Q}^U\right) \end{aligned}$$

(29a)

$$\begin{aligned}&\text {s.t.}&\quad \left( 1-\tau \right) \left\langle \mathbf{Q}_{k_\ell ,\ell }^U\right\rangle \le Q_{k_\ell }\left( \mathbf{Q}^E\right) ,\nonumber \\&\quad \forall \ell \in \mathcal {L},~\forall k \in \mathcal {K}_\ell ,\end{aligned}$$

(29b)

$$\begin{aligned}&\quad \tau \sum _{k=1}^{K_\ell }\left\langle \mathbf{Q}_{\ell ,k_\ell }^E\right\rangle \le P_{S_\ell },~\forall \ell \in \mathcal {L},\end{aligned}$$

(29c)

$$\begin{aligned}&\quad \left( 1-\tau \right) \sum _{k=1}^{K_0}\left\langle \mathbf{Q}_{0,k_0}^D\right\rangle \le P_{S_0},\end{aligned}$$

(29d)

$$\begin{aligned}&\quad \mathbf{Q}^U,\mathbf{Q}^E,\mathbf{Q}^D\succeq 0. \end{aligned}$$

(29e)

As can be observed that the constraints in () become convex however the objective function (29a) is not a concave–convex fractional one because the achievable sum rate is a nonconcave function. Thus, it cannot be straightforward to obtain the optimal solution to problem ().

Inspired by work [12], we exploit the D.C. procedure to handle the nonconvexity of the achievable rate function. Firstly, the achievable rate functions (20), (22), (24) can be rewritten respectively as the difference of two concave functions

$$\begin{aligned} R_{k_0}^{(1)}\left( \mathbf{Q}^D, \mathbf{Q}^E\right)= & {} \tau \left( \log \left| \mathbf{Z}_{k_0}+\mathbf{H}_{k_0,0}^D\mathbf{Q}_{0,k_0}^D \left( \mathbf{H}_{k_0,0}^D\right) ^H\right| -\log \left| \mathbf{Z}_{k_0}\right| \right) ,\end{aligned}$$

(30)

$$\begin{aligned} R_{k_0}^{(2)}\left( \mathbf{Q}^D, \mathbf{Q}^U\right)= & {} \left( 1-\tau \right) \left( \log \left| \mathbf{R}_{k_0}+\mathbf{H}_{k_0,0}^D\mathbf{Q}_{0,k_0}^D \left( \mathbf{H}_{k_0,0}^D\right) ^H\right| -\log \left| \mathbf{R}_{k_0}\right| \right) ,\nonumber \\ \end{aligned}$$

(31)

and

$$\begin{aligned} R_\ell \left( \mathbf{Q}^D,\mathbf{Q}^U\right) =\left( 1-\tau \right) \left( \log \left| \mathbf{J}_\ell +\sum _{k=1}^{K_\ell }\mathbf{H}_{\ell ,k_\ell }^U\mathbf{Q}_{k_\ell ,\ell }^U\left( \mathbf{H}_{\ell ,k_\ell }^U\right) ^H\right| -\log \left| \mathbf{J}_\ell \right| \right) . \end{aligned}$$

(32)

Then, given feasible points $\left( \bar{\mathbf{Q}}^{D(n)}, \bar{\mathbf{Q}}^{U(n)}, \bar{\mathbf{Q}}^{E(n)}\right)$ at iteration n, the rate functions $R_{k_0}^{(1)}\left( \mathbf{Q}^D, \mathbf{Q}^E\right)$, $R_{k_0}^{(2)}\left( \mathbf{Q}^D, \mathbf{Q}^U\right)$, and $R_\ell \left( \mathbf{Q}^D,\mathbf{Q}^U\right)$ are tightly lower bounded by the concave functions $\hat{R}_{k_0}^{(1)}\left( \mathbf{Q}^D, \mathbf{Q}^E\right)$, $\hat{R}_{k_0}^{(2)}\left( \mathbf{Q}^D, \mathbf{Q}^U\right)$, and $\hat{R}_\ell \left( \mathbf{Q}^D,\mathbf{Q}^U\right)$ respectively defined by

$$\begin{aligned} \widehat{R}_{k_0}^{(1)}\left( \mathbf{Q}^D,\mathbf{Q}^E\right)= & {} \tau \left( \log \left| \mathbf{Z}_{k_0}+\mathbf{H}_{k_0,0}^D\mathbf{Q}_{0,k_0}^D\left( \mathbf{H}_{k_0,0}^D\right) ^H\right| \right. \nonumber \\&\left. -\left( \log \left| \mathbf{Z}_{k_0}^{(n)}\right| +\left\langle \left( \mathbf{Z}_{k_0}^{(n)}\right) ^{-1}\left( \mathbf{Z}_{k_0}-\mathbf{Z}_{k_0}^{(n)}\right) \right\rangle \right) \right) ,\end{aligned}$$

(33)

$$\begin{aligned} \widehat{R}_{k_0}^{(2)}\left( \mathbf{Q}^D,\mathbf{Q}^U\right)= & {} \left( 1-\tau \right) \left( \log \left| \mathbf{R}_{k_0}+\mathbf{H}_{k_0,0}^D\mathbf{Q}_{0,k_0}^D\left( \mathbf{H}_{k_0,0}^D\right) ^H\right| \right. \nonumber \\&\left. -\left( \log \left| \mathbf{R}_{k_0}^{(n)}\right| +\left\langle \left( \mathbf{R}_{k_0}^{(n)}\right) ^{-1}\left( \mathbf{R}_{k_0}-\mathbf{R}_{k_0}^{(n)}\right) \right\rangle \right) \right) ,\nonumber \\ \end{aligned}$$

(34)

and

$$\begin{aligned} \widehat{R}_\ell \left( \mathbf{Q}^D,\mathbf{Q}^U\right)&=\left( 1-\tau \right) \left( \log \left| \mathbf{J}_\ell +\sum _{k=1}^{K_\ell }\mathbf{H}_{\ell ,k_\ell }^U\mathbf{Q}_{k_\ell ,\ell }^U\left( \mathbf{H}_{\ell ,k_\ell }^U\right) ^H\right| \right. \nonumber \\&\quad \left. -\left( \log \left| \mathbf{J}_\ell ^{(n)}\right| +\left\langle \left( \mathbf{J}_\ell ^{(n)}\right) ^{-1}\left( \mathbf{J}_\ell -\mathbf{J}_\ell ^{(n)}\right) \right\rangle \right) \right) . \end{aligned}$$

(35)

where $\mathbf{Z}_{k_0}^{(n)}{=}\mathbf{Z}_{k_0}(\bar{\mathbf{Q}}^{D(n)}, \bar{\mathbf{Q}}^{E(n)})$, $\mathbf{R}_{k_0}^{(n)}{=}R_{k_0}\left( \bar{\mathbf{Q}}^{D(n)}, \bar{\mathbf{Q}}^{U(n)}\right)$, and $\mathbf{J}_\ell ^{(n)}=\mathbf{J}_\ell \left( \bar{\mathbf{Q}}^{D(n)},\bar{\mathbf{Q}}^{U(n)}\right) .$ Then, the energy efficiency at iteration n can be rewritten as

$$\begin{aligned}&\widehat{\mathcal {EE}}\left( \mathbf{Q}^E,\mathbf{Q}^D,\mathbf{Q}^U\right) \nonumber \\&\quad =\dfrac{\displaystyle \sum _{k=1}^{K_0}\widehat{R}_{k_0}^{(1)}\left( \mathbf{Q}^D,\mathbf{Q}^E\right) +\sum _{k=1}^{K_0}R_{k_0}^{(2)}\left( \mathbf{Q}^D, \mathbf{Q}^U\right) +\sum _{\ell =1}^L \widehat{R}_\ell \left( \mathbf{Q}^D,\mathbf{Q}^U\right) }{\mathcal {P}\left( \mathbf{Q}^E,\mathbf{Q}^D,\mathbf{Q}^U\right) }.\nonumber \\ \end{aligned}$$

(36)

Thus, problem () can be recast as

$$\begin{aligned}&{\mathop {\max }\limits _{\{\mathbf{Q}^E,\mathbf{Q}^U,\mathbf{Q}^D\}}}&\quad \widehat{\mathcal {EE}}\left( \mathbf{Q}^E,\mathbf{Q}^D,\mathbf{Q}^U\right) \end{aligned}$$

(37a)

$$\begin{aligned}&\text {s.t.}&\quad (29b), (29c), (29d), (29e). \end{aligned}$$

(37b)

It is clear that the denominator of objective function in () is linear while the numerator is concave with respect to all positive semi-definite matrix variables $\left\{ \mathbf{Q}^E,\mathbf{Q}^D,\mathbf{Q}^U\right\}$. Thus, problem () is a concave–convex fractional programming and, then, the Dinkelbach approach can be applied to find optimal solution [5]. To this end, we introduce a parameter $\lambda$ and a parametric function $\mathcal {U}\left( \mathbf{Q}^E,\mathbf{Q}^D,\mathbf{Q}^U,\lambda \right) =\displaystyle \sum _{k=1}^{K_0}\widehat{R}_{k_0}^{(1)}\left( \mathbf{Q}^D,\mathbf{Q}^E\right) +\sum _{k=1}^{K_0}R_{k_0}^{(2)}\left( \mathbf{Q}^D, \mathbf{Q}^U\right) +\sum _{\ell =1}^L \widehat{R}_\ell \left( \mathbf{Q}^D,\mathbf{Q}^U\right) {-}\lambda \mathcal {P}\left( \mathbf{Q}^E,\mathbf{Q}^D,\mathbf{Q}^U\right)$. Then, problem () can be rewritten as

$$\begin{aligned}&{\mathop {\max }\limits _{\{\mathbf{Q}^E,\mathbf{Q}^U,\mathbf{Q}^D\}}}&\quad \mathcal {U}\left( \mathbf{Q}^E,\mathbf{Q}^D,\mathbf{Q}^U,\lambda \right) \end{aligned}$$

(38a)

$$\begin{aligned}&\text {s.t.}&\quad (29b), (29c), (29d), (29e). \end{aligned}$$

(38b)

By fixing $\lambda$, the optimization problem () is convex and it can be efficiently solved by the convex solver packages, for example, CVX [7]. For a given $\lambda ^{*}$, the optimal solution $\{\mathbf{Q}^{E*},\mathbf{Q}^{U*},\mathbf{Q}^{D*}\}$ to problem () is also the optimal solution to problem () if $\mathcal {U}\left( \mathbf{Q}^{E*},\mathbf{Q}^{D*},\mathbf{Q}^{U*},\lambda ^*\right) =0$ [5]. Thus, the step by step of the iterative algorithm to solve the problem () is summarized in Algorithm 1. It is worth noting that the objective function (37a37b) is a tight lower bound of that in (29a). Thus, the objective function (29a) is non-decreasing through iterations. In addition, due to transmit power constraints the objective function (29a) is upper bounded. Thus, the convergence of Algorithm 1 is guaranteed.

Table 2 List of simulation parameters

4 Simulation results

In this section, we evaluate the performance of our algorithm via numerical simulation results. In simulations, we consider the HetNet system consisting of four small cell deployed in the coverage of a macro cell. The macro BS is located at (0, 0) while 4 SBSs are located at positions (R/2, R/2), $(R/2,-R/2)$, $(-R/2,R/2)$, and $(-R/2,-R/2)$ where R is the radius of macro-cell. All system parameters and the path loss models are given in Table 2 [2, 17, 18, 23] in which the distance between the transmitter and the receiver in meters is denoted by D. The transmit power budget of all SBSs are assumed as $P_{S_\ell }=P_t$ and the transmit power budget of the MBS is $P_{S_0}=5P_t$. Unless specified otherwise, it is assumed $\tau =0.5$. The simulation results are averaged over 100 Monte Carlo runs with random locations of users.

Fig. 2

Convergence behavior of Algorithm 1 for different transmit power budgets

Example 1

In this example, we investigate the convergence characteristic of iterative Algorithm 1. We plot the convergence rate of the objective function over iterations under different values of $P_t$ in Fig. 2. It can be observed that the objective function of EE is not decreasing over iterations and it is converged in less than 50 iterations. The results from Fig. 2 also reveal that at the low transmit power region, the achievable EE tends to increase when the transmit power budget increases. However, the EE performance will not increase when the transmit power budget reaches to a certain level.

Example 2

This example examines the tradeoffs between the achievable EE and sum-rate (SR) in the considered HWPCNs. Figure 3 presents the average EE performance which is obtained by our EE maximization algorithm and those obtained by the SE maximization. Note that the optimal solution for maximizing the SE can be obtained by setting $\lambda =0$ in (). It can been seen from Fig. 3 that when the transmit power budget is higher than a certain level, the EE optimization algorithm offers higher EE than those of the counterpart of the SE optimization. These results can be explained that the EE optimization strategy only uses a portion of the transmit power budget which can offer the maximum EE rather than all transmit power budget when the transmit power budget increases to a certain level. In contrast, the SE optimization strategy tends to use all transmit power budget to maximum the system sum-rate, and the usage of all transmit power budget leads to a decrease in the achievable EE of the SE maximization method.

Fig. 3

The average achievable EE of Algorithm 1 and SE maximization versus different transmit power budgets

To investigate more insightful tradeoffs between the EE and SE, we plot the achievable sum-rate obtained by the EE maximization method and those obtained by the SE maximization approach in Fig. 4. As can be clearly seen from Fig. 4 that the average achievable sum-rate obtained from the SE optimization method increases with the transmit power budget. On the other hand, the average achievable sum-rate of the EE optimization strategy will not increase when the transmit power budge increases to a certain value. The reason is that when the transmit power reaches at a certain level, the power consumption causes energy inefficiency.

Fig. 4

Sum rate for EE maximization and sum-rate maximization

Example 3

This example studies the optimal EE and SE performance versus the duration $\tau$. We set the the transmit power budget is $P_t=30$ dBm. The average EE obtained from the EE maximization and sum-rate obtained from the SE maximization are depicted in Fig. 5. It can been seen that the achievable EE is reduced as $\tau$ increases. This is because an increase of $\tau$ means that the WET duration increases. The WET is not energy efficiency since the received power is significantly attenuated. On the other hand, the WET signals can also cause interference to the macro-cell users which results in a reduction of the macro-cell user sum-rate. This major observation can conclude that the WET can give a negative impact of the network EE. On the other hand, concerning the achievable sum-rate as can be seen in Fig. 5, there exists an optimal value of $\tau$ such that the achievable sum-rate is maximized.

Fig. 5

The EE and SE performance versus duration $\tau$

5 Conclusion

This paper has studied the precoding designs to maximize the EE in the multi-user HWPCNs in which precoding matrices in both WET and WIT phases have been jointly considered. To tackle the mathematical challenges of nonlinear fractional programming of the EE maximization problem, we have invoked the D.C. programming and Dinkelbach method to develop an efficiently iterative algorithm. The numerical simulation results have evaluated the EE performance of our approach.