1 Introduction

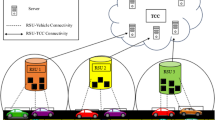
New generation of portable electronic devices and in-vehicle communication interfaces in vehicular networks enable lots of new Intelligent Transport System (ITS) applications. Examples of these applications consist of downloading multimedia contents [1], automatic collision warning [2], remote vehicle diagnostics [3], vehicle tracking [4], automobile high speed internet access [5], advertisements, infotainment [6] and also offloading cellular traffic to vehicular networks [7]. As a result, content downloading and data transmission via both Vehicle-to-Infrastructure (V2I) and Vehicle-to-Vehicle (V2V) have recently received significant attention from the research community. As Machine-tomachine communication (M2M) and Device-to-device communication (D2D) are envisioned to be the features of 5G cellular networks in an effort to realize Internet of Things (IoT), the number of machine-type devices (MTD) connected to a cellular base station in 2020 may be 10 times to 100 times more than the mobile phones. This issue is well investigated in the comprehensive report published by Cisco [8]. Based on its analysis, a 40-fold increase in the wireless network traffic volume is predicted in the next five years and it is estimated that the mobile network traffic volume will reach from 93 petabytes to 3600 petabytes by the end of 2020. To handle this large amount of data transmission, we need to enhance the throughput of vehicular networks.

One way to improve the throughput of vehicular networks is to equip the Road Side Units (RSUs) [9] with storage devices and use them as local caches for vehicles. This will help the vehicles to get access to a subset of files through these RSUs using the Dedicated Short-Range Communication (DSRC) technology [10, 11]. A vehicle interested in a file from the library has three options to download the file, (i) directly from the central server at the base station over cellular network, (ii) from the cache servers located at the RSUs over Vehicular Communication Networks (VCN), or (iii) from other vehicles using V2V communications. As reported in [12], the throughput of Vehicle-to-Vehicle communications is observed to be at most one-fifth of the throughput of Vehicle-to-Infrastructure communications. Consequently, the first two mentioned solutions attract more scientist’s attention to work on. Successful downloading of the enquired files by the vehicles from the local RSUs results in lower congestion and delay over the cellular network and the base station. Subsequently, the throughput of vehicular networks will be improved. However, the main question is how we should distribute the files in the caches of the RSUs to maximize the local hit ratio experienced by the vehicles. This is known as Cache Content Placement (CCP) problem and we will discuss about the research works related to this topic in Sect. 1.2.

In this paper, we develop two methods for solving the CCP in a distributed fashion. The main reason behind using this approach is that it will help the cache content placement to adapt faster to the dynamic situations (e.g., rapidly changing the traffic pattern of the vehicles in the streets or the popularity of files requested by the vehicles). Besides, the cost of communication and the network overhead are higher for the centralized approach. Additionally, the distributed approach prevents single point of failure. Accordingly, we formulate the CCP as the maximization of the expected hit ratio of the vehicles in downloading the enquired files, successfully from local RSUs instead of the base station. We propose solving CCP optimization problem by utilizing road side units.

We show that this problem is an NP-hard Integer Linear Programming (ILP). We model the problem using a game theoretic approach to optimize the objective function of the CCP distributively. The intuition behind using game theory is that it is a tool for decision making in the strategic situations and it is a powerful approach for designing distributed systems. Game theory has been previously applied in content dissemination problem for other types of networks [13, 14]. However, to the best of our knowledge, this is the first study on deploying game theory for improving content dissemination in networks with highly dynamic topology such as vehicular networks. We also design a distributed utility function for each RSU in our game theoretic model and show that our game is in the category of generalized covering games [15]. In addition, we provide a lemma presenting our proposed game as a potential game [15] with at least 50% efficiency of the optimum solution. Consequently, it will be guaranteed that there exist some local dynamics, such as best and better reply, which are convergent to an equilibrium. To continue, we propose a combinatorial optimization approach for CCP in order to find efficient solution at RSUs, using Markov approximation method [16]. The results show an improvement of 7.5% in the average hit ratio of the proposed method compared to other well-known cache content placement approaches.

1.1 Contributions

In summary, contributions of this paper are:

  • Presenting a new model for the centralized CCP and proving the interactability of this problem.

  • Proposing two approaches to solve CCP distributively. One is based on game theory and the other is based on combinatorial optimization approach.

  • A utility function is proposed for each RSU in order to find efficient content placement using RSUs’ local information.

  • Proposing a combinatorial optimization approach to find efficient solution for CCP at RSUs, using Markov approximation method.

  • Showing that the proposed content placement approach outperforms other cache content placement approaches such as MobiCacher, FemtoCacher and \(PopularityCacher\).

1.2 Related works

The idea of deploying caches for distributing contents in the networks has been investigated in [17,18,19]. The focus of these research works are on minimizing the delay experienced by the users during the hand-off between two access points in wireless networks. In [20], the authors use the combinatorial optimization approach to improve the quality of content dissemination in cellular networks. They attempt to solve the cache content placement problem for a network with fixed caches and fixed users and by considering the file popularity distribution and network topology as inputs to the problem. Our work is distinguished from [20], since we are considering the vehicular networks, where the mobility of the vehicles between RSUs plays a decisive role in solving CCP.

Simultaneously, several approaches were proposed to improve the performance of content distribution in vehicular networks. Some research works use network coding to reduce the download delays experienced by vehicles, e.g., Code Torrent [21], VANETCODE [22], CodeOn [23], and VCD [24]. These papers do not consider caching in their approaches, while here, we propose to store contents at the RSUs to enhance content-centric VANETs. Another related work is [25], where Luan et al. focus on improving the throughput of vehicular networks by considering some light-weight, low cost and easy to install buffers called Road Side Buffers (RSBs) as the local cache servers for the vehicles. They also consider a simple mobility model for vehicles in the streets based on an on-off Markov model. Here in our work, we consider a general and realistic mobility model for the vehicles and we let them to visit any sequence of RSUs along their traveling path.

In [26, 27], the authors investigate inter-vehicular communication for data dissemination in vehicular networks. Aser et al. in [26] propose a vehicle-to-vehicle based content distribution in the metropolitan area using the bus and metro networks. By exploring the stable bus schedule and predictable bus mobility pattern and by using temporary storage at bus stations, they suggest a routing protocol that takes the randomness of road traffic into account for delivering the content from source to destination. While making a collaboration between vehicles and using Vehicle-to-Vehicle communication can boost the network capacity, it is still insufficient to provide a reliable and high rate data service for vehicles due to the highly dynamic network topology and harsh channel condition. As reported in [12], the throughput of Vehicle-to-Vehicle communications is observed to be at most one-fifth of the throughput of Vehicle-to-Infrastructure communications.

PopularityCacher only considers the popularity of files and fills the caches only based on this parameter. This approach doesnt consider the geographical distribution of the RSUs and the mobility of the vehicles. Since RSUs store the most popular files in their caches, the diversity of files is low. As a result, vehicles visiting multiple RSUs in their paths cant take advantage of the RSUs storing the same set of files. Therefore PopularityCacher doesn’t show good performance compared to other content placement approaches.

FemtoCacher [20] considers the popularity of files and the geographical distribution of the RSUs and vehicles, but not the mobility of vehicles. Therefore, by changing the geographical distribution of vehicles in the map, this approach fails to adapt to the new situation. We discuss about this approach in details in Sect. 5.

Finally in [28], the authors consider a small base station scenario with mobile users. They consider application layer semantics of spatial and temporal locality and bring the mobility patterns of users into account to make caching decisions. Since this problem is NP-Complete, a polynomial-time heuristic solution called MobiCacher with bounded approximation ratio is proposed. The MobiCacher decomposes the original problem into subproblems, with one sub-problem for each small-BS, and every one of them is solved independently.

Compare to the mentioned research works, in this paper, we model the cache content placement problem in vehicular networks, where the highly mobile vehicles (requesters) play a decisive role in solving CCP. Also we formulate this problem using game theoretic approach and combinatorial optimization approach. By taking the mobility pattern of the vehicles in the streets into account, we also propose a utility function for each RSU, based on the average local hit ratio experienced by the vehicles, to solve the CCP problem distributively. In Sect. 5, we show that our approach outperforms other cache content placement approaches.

The rest of the paper is organized as follows. In Sect. 2, we discuss about the system model and the problem definition of our work. Section 3 presents a game theoretic approach and connect it to the class of games called covering games. In Sect. 4, we propose an approach to find an efficient solution for CCP using combinatorial optimization. In Sect. 5, we evaluate the performance of our proposed methods. Finally, in Sect. 6, we conclude our findings and outline directions of future researches.

Table 1 Semantics of notations used in this paper
Full size table

2 System model and problem formulation

We consider a vehicular network in an urban environment, where each vehicle may demand to download several files anytime along its route. The requested content can be related to the traffic pattern of the nearby streets, map of the local area, etc. We consider a collection of m RSUs indexed by set \({M}= \{1,2,\dots m\}\) and a library of n fixed files indexed by \(N=\left\{ {1,2,\dots ,n}\right\} \). The environment is homogeneous in terms of RSUs. For simplicity, we assume that all the files are of equal size.Footnote 1 We let the \(i{\mathrm{th}}\) RSU to have a storage capacity of up to \(L_i\) files. Vehicles in this setup can travel from any source to any destination. To model the mobility pattern of the vehicles, we consider a set of flows \({F} = \{f_1, f_2, \ldots , f_l\}\), where each \(f_i: 1 \le i \le l\) represents a stream of vehicles moving along a particular route. Hence, each flow is identified by a sequence of RSUs visited by the traffic stream and a real value that shows the traffic density of that flow. Therefore, a flow \(f \in F\) is represented as \(f = (M_f , \omega _{f})\), where \(M_f \subset M\) and \(\omega _{f}\) is the average number of vehicles in f in unit time. Flows can be easily learned by studying the traffic history of the streets over some periods of time (more details in Sect. 5). Let the relative popularity of a file \(k \in N\) in flow \(f \in F\) be \(\lambda _{f}^k,\) i.e., \(\sum _{k \in N} \lambda _f^k =1.\) Also, let the contents of RSU \(i \in M\) be \(X_i,\) i.e., \(X_i \subset N\), where \(|X_i| \le L_i\). Finally, we define \(X = \{ X_1, \ldots , X_m\},\) as the system state. Table 1 shows the semantics of the system parameters.

A vehicle interested in a file from the library has three options to download the file, (i) directly from the central server at the base station over cellular network, (ii) from the cache servers located at the RSUs over Vehicular Communication Networks (VCN), or (iii) from other vehicles using V2V communications. As we mentioned in Sect. 1, since the throughput of the V2V communication is poor [12], in this paper, we utilize the V2I communication. When interested in a file, a vehicle first send its request to the central server at the base station. The central server provides authorization for downloading from the RSUs along with the specifications of a search interval. The search interval may be chosen as a function of the delay tolerance of the requesting application. During the search period, the application requesting the file attempts to download the file from the cache servers that the end-user (vehicle) visits as it travels. When the attempts fail, the file will be downloaded directly from the central server at the end of the search interval. The success rate for downloading the files from local RSUs is called the hit ratio. For a given system state X, the average hit ratio is defined as,

$$\begin{aligned} Q(X)= \sum _{f=1}^{l} \sum _{k=1}^{n} q\left( |X|_{f,k}\right) \lambda _f^k\cdot \omega _f \end{aligned}$$
(2.1)

where \(q(\emptyset ) = 0\) and \(q(\bar{\emptyset }) =1\) and \(|X|_{f,k} = \{ m \in M : m \in f, k \in X_m\}\), the set of RSUs those belonging to flow f and has file k for a given system state X. Please note that we consider the cache capacity of the RSUs in the condition of the cache content placement optimization problem in 2.3.

It is easy to observe that the function in (2.1) is sub-modular. Let \(X_{\{s\}}\) represent an allocation of files in a set of RSUs \(s \subset M\). Suppose \(s \subset s'\) where \(s,s' \subset M\) and \(j \in M.\) Then,

$$\begin{aligned} Q(X_{\{s\} \cup j}) - Q(X_{\{s\}})&= \sum _{f: j \in f} \sum _{k \in X_j} \mathbf {1}_{|X_{\{s\}}|_{f,k} =\emptyset } \lambda _f^k \omega _f \nonumber \\&\ge \sum _{f: j \in f} \sum _{k \in X_j} \mathbf {1}_{|X_{\{s'\}}|_{f,k} =\emptyset } \lambda _f^k \omega _f\nonumber \\&= Q(X_{\{s'\} \cup j}) - Q(X_{\{s'\}}), \end{aligned}$$
(2.2)

where \(\mathbf {1}_A\) is the indicator function of statement A, that is, \(\mathbf {1}_A=1\) if A is true and \(\mathbf {1}_A=0\) otherwise. Also, the second inequality is due to the fact that \(|X_{\{s\}}|_{f,k} \subseteq |X_{\{s'\}}|_{f,k}.\)

Our goal is to find a state that maximizes the average hit ratio, that is solving the following optimization problem:

$$\begin{aligned} \begin{array}{llll} &{} {\text {max}} &{} &{} Q(X)\\ &{} \text {subject to} &{} &{} X_i = \{ S \subseteq N: |S| \le L_i\},\forall i \in M. \end{array} \end{aligned}$$
(2.3)

We refer this problem as Cache content placement (CCP) problem.

Next we discuss the computational complexity associated with solving the CCP.

2.1 Computational intractability

We show that CCP is NP- Hard by reducing the decision version of CCP to t-disjoint set cover problem which is known to be NP- complete [29]. First let us state the decision version of CCP.

CCP decision problem Does there exist a system state \(X = (X_i, \cdots , X_m)\) where \(X_i = \{S \subseteq N: |S| \le L_i \} \) for each \(i \in M\) such that \(Q(X) \ge r\) where \(r \in \mathbb {R}^{+}.\)

Next, we state t-disjoint set cover problem.

t-disjoint set cover problem Consider a bipartite graph \(G=(V_u,V_l,E)\) where the edges in E connect the upper vertex set \(V_u\) to the lower vertex set \(V_l\) (see Fig. 1). Let \(\mathscr {N}(v \in V_u) = \{v' \in V_l: (v,v') \in E\}\) be the set of neighbor vertices of v. The t-DSC(G) problem is to find t disjoint vertex set \(\{V_u^1,V_u^2,\dots ,V_u^t\}\), where \(V_u^i \subseteq V_u : \forall i \in \{1,2,\dots ,t\}\), such that \(\sum _{i=1}^{t}|V_u^i| = |V_u|\) and \(V_l = \cup _{v \in V_u^i} \mathscr {N}(v)\) for each \(i \in \{1,2,\dots ,t\}.\) For example, in Fig. 1, we categorize the upper vertex set into three disjoint cover sets in a way each of them covers all the vertices of the lower vertex set.

It is known that the t-DSC(G) problem is NP-complete [29]. In the following lemma, we formally prove the intractability of cache content placement problem.

Lemma 1

t-disjoint Set Cover Problem \(\le _L\) Cache Content placement Problem, where \(\le _L\) denotes the polynomial time reduction.

Fig. 1
figure 1

t-Disjoint set cover problem

Full size image

Proof

Consider the following instance of t-DSC(G) which we can map to a CCP decision problem: The set of caches correspond to the upper vertex set and the set of flows correspond to the lower vertex set, i.e., \(M = V_u\) and \(F = V_l.\) We connect \(f_i \in V_l\) to \(C_j \in V_u\) if \(C_j \in M_{f_i}\) which means, cache \(C_j\) is in the flow \(f_i\). Each flow \(f_i \in V_l,\) consists of several caches, that is, \(f_i = \{C_j \in V_u: (C_j, f_i) \in E\}.\) Let \(\omega _{f_i} =1, \forall i \in \{1,2,\dots ,l\}.\) Furthermore, we let the number of files to be equal to the number of disjoint sets, that is, \(n=t\). Also we let \(\lambda _f^k = 1/k\) for all \(f \in F\). Finally, we consider \(L_i=1, \forall i\). Having this parameter setup. now the question is how to divide the set of caches in \(V_u\) into t disjoint cover sets (and store each file in one of the cover sets) in order to make sure that all the flows in \(V_l\) have access to all the files in the library. This will map the t-DSC(G) to the CCP decision problem and therefore, solving CCP decision problem is harder than solving t-DSC(G). \(\square \)

3 Game theoretic model

In this section, we propose a game theoretic approach to optimize our objective function in 3 distributively. We model CCP as a strategic game with the following components:

  • A set of players \(M = \{1,2,\dots ,m\}\).

  • An action set \(X_i = \{S:S \subseteq N, |S|=L_i \}\) for each player i. In this section, the action set of each player is equivalent to the set of contents he chooses to store in its cache.

  • A utility function \(U_i : X_i \rightarrow \mathbb {R}^+\). where \(U_i(X_i,X_{-i})=\sum _{f:i \in f} \sum _{k \in X_i} \omega _f . \lambda _f^k . g(|X|_{f,k})\).

Here, \(X_i\) means that the content placement strategy of player or cache i is X and \(X_{-i}\) means that the content placement strategy of all the other caches except i is also X. We refer \(g:\mathbb {N} \rightarrow \mathbb {R}^+\) as resource sharing function. Now let \(g(k) = \frac{1}{k}\) for \(k > 0\) and \(g(k) = 0\) otherwise. We prove that our game is a valid utility game and as a result, the efficiency of equilibrium is guaranteed to be at least \(\frac{1}{2}\) [30]. To show that Cache Content Placement strategic game with the specified g function is a valid utility game, we consider the following definition. A game is said to be a valid utility game if it satisfies the following two properties:

  1. 1.

    \(U_i(X_i,X_{-i}) \ge Q(X) - Q(X_{-i})\).

  2. 2.

    \(\sum _i U_i(X_i,X_{-i}) \le Q(X)\).

where Q is the objective function defined in Sect. 2. Considering this definition, it can be shown that the agent utility function satisfies these two properties:

  1. 1.
    $$\begin{aligned} Q(X) - Q(X_{-i})&= \sum _{f:i \in f} \sum _{k \in X_i} (\mathbf {1}_{|X_{-i}|_{f,k}=\emptyset }) . \omega _f . \lambda _f^k \nonumber \\&\le \sum _{f:i \in f} \sum _{k \in X_i} \frac{1}{g(|X_{i}|_{f,k})} . \omega _f . \lambda _f^k \end{aligned}$$
    (3.1)
  2. 2.
    $$\begin{aligned} \sum _i U_i(X_i,X_{-i})&= \sum _i \sum _{f:i \in f} \sum _{k \in X_i} \frac{1}{g(|X_{i}|_{f,k})} . \omega _f . \lambda _f^k \nonumber \\&= \sum _f \sum _{k:|X_{i}|_{f,k}>0} g(|X_{i}|_{f,k}) . \frac{1}{g(|X_{i}|_{f,k})} . \omega _f . \lambda _f^k \nonumber \\&= Q(X). \end{aligned}$$
    (3.2)

Therefore, the mentioned game is a valid utility game and the efficiency of the equilibrium would be greater than \(\frac{1}{2}\). To make the distributed utility function of each player in this game theoretic model more readable, consider \(\gamma _f^k = \omega _f . \lambda _f^k\). Now we have:

$$\begin{aligned}&U_i(X) = \sum _{k=1}^N \left( X_i^k \sum _{f:i \in f} \frac{\gamma _f^k}{\sum _{j \in f} X_j^k} \right) , \end{aligned}$$
(3.3)

where \(X_i^k=1\) if file k exists in cache i and \(X_i^k=0\) otherwise. We designed this utility function in a way that all the RSUs in the same flow storing the same file in their caches will share the gain of storing that file proportionally. In Sect. 3.1, we connect this model to a collection of games called covering games.

figure a

3.1 Connection to the generalized covering problems

In the previous section, we discussed a game theoretic approach to solve the optimization problem in (2.3) distributively. In this section, we map the CCP problem to the set of problems, called generalized covering problems. We first recall the definition of generalized covering problem [31]:

  • Universal set U.

  • For each \(u \in U\), we have a weight \(w_u\).

  • Some sets \(A_1,A_2,\dots , A_m\) where \(A_i \subseteq 2^U\).

  • Pick \(a_i \in A_i\) such that \(\sum _{u \in \cup _{i=1}^m a_i} w_u\) is maximized.

Now we map the cache content placement problem to the generalized covering problems. We start by mentioning that in each RSU, by storing any single file, we can satisfy all the requests from the vehicles in the flows that pass through that RSU and request that file. Suppose \(U = \{(n,f):n \in N, f \in F\}\) is a collection of ordered pairs formed from a file \(n \in N\) and a flow \(f \in F\). In this representation, when a RSU stores some files, it will cover all the pairs of the global state space set where the first element is the stored files in that RSU and the second element is the set of all the flows that pass through that RSU. That is, RSU i covers the pairs \(\{(\alpha ,\beta ):\alpha \in N_i , \beta \in F_i\}\), where \(N_i\) is the set of all the files stored in the RSU i and \(F_i\) is the set of all the flows that pass through the RSU i. The weight associated with each element \(u \in U\) is \(w_u = \lambda _f^n . \omega _f\). Finally, for each \(i \in N\), we define \(A_i = \{f:i \in f\} \times \bar{x}\) where \(\bar{x} \in \mathscr {X} = \{s:s \subseteq N, |s| \le L_i\}\). Essentially, \(A_i\) is the collection of ordered pairs formed from the set of flows visiting RSU i and any set of files that can be stored in RSU i at a time. our goal is to choose the proper pairs for the RSUs to cover, that is the proper subset of file library for storing in each RSU, to maximize the total weight of the union of all the covered pairs in the global state space set.

By taking this model into account, we can say that our problem is in the class of covering game which is the general case of max-n-cover problem. The covering game is the subclass of congestion games [32], in which each player receives a payoff based on his utility sharing function. By taking a look at our definition for the players utility function in 3.3, we can find out that every RSU shares the payoff of storing a file with all the other RSUs that store that file and are in the same flow of that RSU.

In the following lemma, we will prove that cache content placement game is a potential game.

Lemma 2

Considering the potential function in (3.4), the class of games \(G=(M,\mathscr {X}_i,U_i)\) are potential games.

$$\begin{aligned}&\phi (X) = \sum _f \sum _k \sum _{j=1}^{\delta _{f,k}(X)} g(j) . \omega _f . \lambda _f^k. \end{aligned}$$
(3.4)

where function g is defined in Sect. 3 and \(\delta _{f,k}(X)\) is the number of RSUs in flow f that store file k in content placement X.

Proof

In order for our problem to be a potential game, we need to show that if a player changes his action set and increases his utility function by \(\varPsi \), then \(\phi (s)\) also increases by \(\varPsi \). We consider that player i changes his action set from \(s_i:\left( e_1,\dots ,e_L\right) \) to \({s_i}':\left( {e_1}',\dots ,{e_L}'\right) \). Therefore the difference between the new utility function and the old utility function would be as follows:

$$\begin{aligned}&\varPsi = \sum _{e \in s_i} \frac{1}{\delta _e\left( s_i,s_{-i}\right) } - \sum _{e \in {s_i}'} \frac{1}{\delta _e({s_i}',s_{-i})}. \end{aligned}$$
(3.5)

The difference between the new and old potential function would be:

$$\begin{aligned}&\phi ({s_i}',s_{-i}) - \phi \left( s_i,s_{-i}\right) \nonumber \\&= \sum _{e \in E} \sum _{i=1}^{\delta _e({s_i}',s_{-i})} f_e(i) - \sum _{e \in E} \sum _{i=1}^{\delta _e\left( s_i,s_{-i}\right) } f_e(i). \end{aligned}$$
(3.6)

for \(e \in {s_i}' and e \notin s_i\), we have \(\delta _e({s_i}',s_{-i}) = \delta _e\left( s_i,s_{-i}\right) +1\) and (3.6) will be simplified as follows:

$$\begin{aligned}&\sum _{e \in {s_i}',e \notin s_i} \left( \sum _{\delta _e\left( s_i,s_{-i}\right) +1}^{\delta _e({s_i}',s_{-i})} f_e(i)\right) = \sum _{e \in {s_i}',e \notin s_i} f_e\left( \delta _e({s_i}',s_{-i})\right) . \end{aligned}$$
(3.7)

for \(e \in s_i,e \notin {s_i}'\) we observe that \(\delta _e({s_i}',s_{-i})+1 = \delta _e\left( s_i,s_{-i}\right) \) and (3.6) will be simplified as follows:

$$\begin{aligned}&- \sum _{e \in s_i,e \notin {s_i}'} \left( \sum _{\delta _e({s_i}',s_{-i})+1}^{\delta _e\left( s_i,s_{-i}\right) } f_e(i)\right) \nonumber \\&= - \sum _{e \in s_i,e \notin {s_i}'} f_e\left( \delta _e(s_i,s_{-i})\right) . \end{aligned}$$
(3.8)

By summing up (3.7) and (3.8) we have:

$$\begin{aligned}&\sum _{e \in {s_i}',e \notin s_i} f_e\left( \delta _e({s_i}',s_{-i})\right) - \sum _{e \in s_i,e \notin {s_i}'} f_e\left( \delta _e(s_i,s_{-i})\right) \\&\quad = \left( \sum _{e \in {s_i}',e \notin s_i} f_e\left( \delta _e({s_i}',s_{-i})\right) + \sum _{e \in {{s_i}'\cap {s_i}}} f_e\left( \delta _e({s_i}',s_{-i})\right) \right) \\&\quad - \left( \sum _{e \in s_i,e \notin {s_i}'} f_e\left( \delta _e(s_i,s_{-i})\right) + \sum _{e \in {s_i\cap {s_i}'}} f_e\left( \delta _e(s_i,s_{-i})\right) \right) \\&\quad =U_i({s_i}',s_{-i}) - U_i(s_i,s_{-i}) = \varPsi . \end{aligned}$$

Therefore the game is a potential game. \(\square \)

Proving that the game is a potential game guarantees the existence of some local dynamics such as best response or better response which converges to an equilibrium. In the next section, we discuss about the performance of our proposed model.

4 Combinatorial optimization approach

In this section, for the sake of readability, we consider the cache placement matrix \(\mathbf {X}\) as a binary \(N \times M\) matrix, where the element \(X_{n,m}\) is equal to 1, if the file n is stored in the RSU m, and 0 otherwise. We also consider P(n) to be the average popularity of file n over all the flows, that is, \(P(n)=\frac{1}{|F|} \sum _{f=1}^{F} \lambda _f^n\). We also let \(I=\left\{ 1,2,\dots ,i\right\} \) to be the number of vehicles in the region of interest. Our objective is to find the optimum \(\mathbf {X}\) which maximizes the expected number of vehicles Q that download their requested files successfully from the local RSUs. Thus, first, we should find this expected number as a function of \(\mathbf {X}\), and then maximize it.

By considering the definition of flows in Sect. 2, and by studying the traffic history of the roads over time, we can extract a mobility pattern for the vehicles in the flows. That is, we can estimate that if a vehicle is in a specific flow, what is the probability for that vehicle to visit the nearby RSUs. We present this mobility pattern with a two dimensional matrix V. The element \(V_{i,m}\) shows the probability of visiting RSU m by the vehicle i. For example, if a vehicle reaching a junction may turn to each of the four possible directions with similar probability, then the elements of matrix V related to that vehicle and for the RSUs along each direction would be equal to \(\frac{1}{4}\). We let the probability of a vehicle visiting far away RSUs to be 0.

Now suppose that vehicle i needs file n. This vehicle can download his requested file from RSU m if he meets this RSU along his path, and also this RSU has stored file n, i.e., \(V_{i,m}=1\) and \(X_{n,m}=1\). Thus, the probability that this vehicle can download this file along his path from at least one RSU is equal to,

$$\begin{aligned} P_{suc} =1-\displaystyle \prod _{m=1}^{M} \left( 1-\big (V_{i,m} X_{n , m}\big ) \right) . \end{aligned}$$
(4.1)

By averaging over all the possible requests for this user, and summing over all the vehicles, the expected number of users satisfied by RSUs will be,

$$\begin{aligned} Q=\displaystyle \sum _{i=1}^{I} \sum _{n=1}^{N} \left[ 1- \prod _{m=1}^{M} \left( 1-\big (V_{i,m} X_{n , m}\big )\right) \right] P(n). \end{aligned}$$
(4.2)

Thus our optimization problem will be,

$$\begin{aligned} \begin{array}{cccc} &{} {\mathop {\text {max}}\limits _{\mathbf {X}}} &{} &{} Q \\ &{} \text {s.t.} &{}&{} \displaystyle \sum _{n=1}^{N} X_{n , m} \le L_m , \; \forall m, \\ &{} &{}&{} x_{n , m} \in \left\{ 0,1\right\} , \; \forall m , n.\\ \end{array} \end{aligned}$$
(4.3)

We can further simplify Q as follows:

$$\begin{aligned}&\nonumber \\ Q&=\displaystyle \sum _{i=1}^{I} \sum _{n=1}^{N} P(n) - \displaystyle \sum _{i=1}^{I} \sum _{n=1}^{N} \left( \prod _{m=1}^{M} \left( 1-\big (V_{i,m} X_{n , m}\big )\right) \right) P(n) \nonumber \\&= 1-\displaystyle \sum _{i=1}^{I} \sum _{n=1}^{N} \prod _{m=1}^{M} \left( \root M \of {P(n)} \right) \left( 1-\big (V_{i,m} X_{n , m}\big )\right) \nonumber \\&=1-\displaystyle \sum _{i=1}^{I} \sum _{n=1}^{N} \prod _{m=1}^{M} \left( \alpha _{n}-\big (\beta _{i,m,n} X_{n ,m}\big )\right) , \end{aligned}$$
(4.4)

where,

$$\begin{aligned} \alpha _{n}&= \root M \of {P(n) },\\ \nonumber \beta _{i,m,n}&= V_{i,m}\root M \of {P(n)}. \nonumber \end{aligned}$$

Thus, we can reformulate the optimization problem in (4.3) as:

$$\begin{aligned} \begin{array}{cccc} &{} \mathop {\text {min}}\limits _{\mathbf {X}}&{} &{} \displaystyle \sum _{i=1}^{I} \sum _{n=1}^{N} \prod _{m=1}^{M} \left( \alpha _{n}-\big (\beta _{i,m,n} X_{n ,m}\big )\right) \\ &{} \text {s.t.} &{}&{} \displaystyle \sum _{n=1}^{N} X_{n , m} \le L_m , \; \forall m, \\ &{} &{}&{} X_{n , m} \in \left\{ 0,1\right\} , \; \forall n , m. \\ \end{array} \end{aligned}$$
(4.5)

This optimization problem is an Integer Non Linear Problem (INLP), which is hard to solve in general. Also, our problem is similar to the optimization problem considered in [33], and since their problem is shown to be computationally intractable, we also look for non-exact solutions for our problem.

In order to do this, we consider different approaches which are as follow:

  • Random Placement In this approach, caches at all RSUs are randomly filled with the files of the library without taking into account file popularity distribution, RSUs range overlapping, and mobility patterns of vehicles. As we will see later in Sect. 5, these parameters are essential for improving our mentioned performance metric.

  • Heuristic Placement 1 In the first heuristic method we consider only the popularity of files. To do so, we first sort the files regarding to their popularity and then store the first \(L_m\) most popular files in RSU m for all the RSUs. Similar to the naive approach, this heuristic also doesn’t consider the mobility pattern of the vehicles and RSUs range overlapping. As we will discuss in Sect. 5, this heuristic would not show good results when the wireless range of the RSUs is high and the number of RSUs visited by each vehicle in his path increases.

  • Heuristic Placement 2 In the second heuristic method, we consider all the mentioned three essential parameters.We first sort the files regarding to their popularity. This will help us taking the files popularity into account. Also we sort the RSUs regarding to the number of visitation of each RSU by the vehicles and we show this by \(P = \left\{ P_1,P_2,\dots ,P_m\right\} \). For example, \(P_1\) is the most popular RSU. This parameter helps us taking the mobility pattern of the vehicles into account. We can do this because we have the vehicles paths as input to our problem and so we know that how many times each RSU will be visited by the vehicles during their trips. Now we store the first \(L_{P_1}\) most popular files in \(P_1\) and the next \(L_{P_2}\) most popular files in \(P_2\), etc. This will help us to take the RSU range overlapping into account.

  • Markov Approximation The next approach to solve our problem is to use a recently proposed method by Mingua et al. [34] called Markov approximation. The advantage of using this method is that the approximation gap is upper-bounded by \(\frac{1}{\gamma }\log |S|\), where \(\gamma \) is a positive constant and S is the set of all the feasible solutions of the optimization problem. That is, S is the set of all the matrices \(\mathbf {X}\) that meets the constraints in the optimization problem. In this approach, we first need to reformulate our objective function in (4.5) as follows:

    $$\begin{aligned} \begin{array}{llll} &{} {\mathop {\text {max}}\limits _{S}}&{} &{} \displaystyle \sum _{i=1}^{I} Q'_i(s) s \in S ,\\ \end{array} \end{aligned}$$
    (4.6)

    where,

    $$\begin{aligned} \begin{matrix} Q' = \displaystyle -\sum _{n=1}^{N} \prod _{m=1}^{M} \left( \alpha _{n}-\big (\beta _{i,m,n} X_{n ,m}\big )\right) ,\\ \end{matrix} \end{aligned}$$
    (4.7)

    and S would be the set of all the feasible solutions that meets the optimization problem’s constraints. The next step is to use the Log-Sum-Exp approximation function:

    $$\begin{aligned} g_{\gamma }(q') \triangleq \frac{1}{\gamma }\log \left( \displaystyle \sum _{\begin{array}{c} s \in S \end{array}} \exp \left( \gamma \sum _{\begin{array}{c} i \in I \end{array}} Q'_i(s) \right) \right) , \end{aligned}$$
    (4.8)

    where \(\gamma \) is a positive constant and \(q' = [\sum _{\begin{array}{c} i \in I \end{array}} Q'_i(s), s \in S] \). Finally by considering the objective function in (4.6) and by using the approximation in (4.8), we can solve the convex optimization problem in (4.9), instead of our original non-convex optimization problem:

    $$\begin{aligned} \begin{array}{cccc}&{\mathop {\text {max}}\limits _{\mathbf {p \ge 0}}}&\,&\displaystyle \sum _{\begin{array}{c} s \in S \end{array}} p_s \sum _{\begin{array}{c} i \in I \end{array}} Q'_i (s) - \frac{1}{\beta } \sum _{\begin{array}{c} s \in S \end{array}} p_s \log p_s \\ &{} \text {s.t.} &{}&{} \displaystyle \sum _{\begin{array}{c} s \in S \end{array}} p_s =1, \end{array} \end{aligned}$$
    (4.9)

    where \(p_s\) shows the time share of the content placement strategy s. Now we can solve this convex optimization problem with Karush–Kuhn–Tucker (KKT) [35] to obtain the \(p^*_{s} (q')\) [36]:

    $$\begin{aligned} \begin{matrix} p^*_{s} (q') =\frac{\exp (\gamma \sum _{\begin{array}{c} i \in I \end{array} } Q'_i (s) )}{\sum _{\begin{array}{c} s' \in S \end{array} } (\exp (\beta \sum _{\begin{array}{c} i \in I \end{array} } Q'_i (s')) },\quad \forall s \in S. \end{matrix} \end{aligned}$$
    (4.10)

    To proceed we need to design a Markov chain with state space X, which is the collection of all the feasible solutions to the problem and with the stationary state being \(p^*_{x} (q')\). In our problem, each state of the Markov chain will be a matrix S that satisfies our two optimization constraints. Each state in the Markov chain should be different from its neighbors only in one swap in the RSU’s contents. For example consider a part of the Markov chain shown in Fig. 2. In this example, we have three files and three RSUs, so each feasible solution X is a \(3 \times 3\) matrix that shows which file is stored in which RSU. As it is shown, each adjacent state should be different only in one file swap. That is, \(X_1\) stores the blue file in second RSU and the red file in third RSU, but its adjacent state \(X_2\) stores the blue file in the third RSU and the red file in second RSU. That means \(X_1\) and \(X_2\) are the same except that we swap the place of red and blue files in second and third RSU. Also \(X_2\) and \(X_3\) are the same except that we swap the blue and green files in first and third RSUs. Next, we need to choose a proper transition rate for the adjacent states. We use the suggested transition rates in [36]. For two adjacent x and \(x'\) that have direct transitions we have:

    $$\begin{aligned} \begin{matrix} R_{x , x'} =\alpha \exp \left( \beta \displaystyle \sum _{\begin{array}{c} i \in I \end{array}} \left( Q'_i (x') - Q'_i (x) \right) \right) , \end{matrix} \end{aligned}$$
    (4.11)

    where \(R_{x , x'}\) is the transition rate to go from state x to \(x'\). Now by having this Markov chain, we can start from one state and explore and visit other states by considering the transition rates and become closer to the optimum state.

Fig. 2
figure 2

Part of our Markov chain model. Each state is a feasible solution X for mentioned optimization problem

Full size image
Fig. 3
figure 3

Simulated map of the University of Colorado at Boulder, Main Campus

Full size image

5 Performance evaluation and discussion

We evaluated the performance of our two proposed content placement approaches by simulating a discrete-event urban environment using SUMO simulator [37]. As it is shown in Fig. 3, we simulated the 3 km \(\times \) 3 km map of the University of Colorado Boulder, Main Campus (which is completely similar to the real map of the environment, see Fig. 4). We randomly placed RSUs along the streets and set 100 vehicles to traverse the map with randomly selected destinations. The average velocity of each vehicle is considered to be 60km / h. Each vehicle may visit multiple RSUs along its path. Due to the existence of obstacles in the environment, such as building blocks or towers, we set the communication range of the RSUs uniformly within the range [200;500] m. Finally, we assumed to have 50 files in the library and the capacity of RSUs is set to be [5;10] files.

Fig. 4
figure 4

Real map of the University of Colorado at Boulder, Main Campus

Full size image
Fig. 5
figure 5

Comparison of the cache hit ratio different CCP approaches

Full size image

As depicted in Fig. 5, we compare different cache content placement approaches with the game theoritic approach mentioned in Sect. 3 and combinatorial approach mentioned in Sect. 4. In this regards, the random placement approach basically places the files randomly in the RSUs. The optimum approach places the files in the RSUs in a way that it maximizes the hit ratio experienced by the vehicles. The two heuristic based appraoches are already discussed in Sect. 4. For every number of RSUs, we simulate the network 100 times and we report the result with error bars. The confidence interval of the bars are 95%. The hit ratio of the caches has close relationship with the number of RSUs in the area of interest. The results in Fig. 5 show that for the number of RSUs less than 25 in the area, all the content placement approaches show poor performance, due to limited access of the vehicles to the local caches, and by increasing the number of RSUs, the performance will improve. As presented, both proposed methods shows better performance compared to other content placement approaches and also the results confirm the lower bound efficiency of half since the hit ratio of the game theory approach is greater than half of the hit ratio of the optimum approach. Note that the combinatorial approach shows better results compared to the game theory approach but with higher time complexity. We consider convergence rate as another performance metric to compare the complexity of the cache content placement approaches which we talk about it later in this section. Another point that we can derive from Fig. 5 is that the curves of the proposed approaches are concave. This will confirm that the objective function in (2.1) is sub-modular, as we mathematically proved it in (2.2).

We consider convergence rate as one over the number of iterations that each approach consumes to reach the equilibrium. As it is shown in Fig. 6, by increasing the number of RSUs in the environment, the convergence rate of both approaches will decrease.

In the rest of this section, we analyse the performance of the combinatorial approach (Markov approach) since it showed better hit ratio compared to the game theory appproach. Therefore, in the following, by proposed method, we mean the second approach that is the combinatorial approach.

Fig. 6
figure 6

Convergence rate of the game theory approach

Full size image
Fig. 7
figure 7

Comparing the cache hit ratio of four cache content placement approaches for different cache capacity at each sector

Full size image

5.1 Performance evaluation of the combinatorial approach

Figure 7 compares the hit ratio of the combinatorial content placement approach with three well-known cache content placement approaches (see Sect. 1.2 for more details about these approaches) and for different average cache capacity of RSUs. PopularityCacher only considers the popularity of files in each flow. This approach does not consider the geographical distribution of the RSUs and the mobility of the vehicles. Since RSUs store the most popular files in their caches, the diversity of files in each flow is low. As a result, vehicles visiting multiple RSUs in a flow can not fully benefit from the RSUs storing the same set of files. Therefore PopularityCacher produces the lowest hit ratio compared to other approaches. FemtoCacher [20] considers the popularity of files and the geographical distribution of the RSUs and vehicles, but not the mobility of vehicles. Therefore, by changing the geographical distribution of vehicles in the map, this approach fails to adapt to the new situation. MobiCacher [28] considers all the three mentioned parameters, that is, popularity of files in the sectors, geographical distribution of the RSUs in the map and the mobility of the vehicles. This is why this approach shows higher hit ratio compared to PopularityCacher and FemtoCacher. As we already discussed, deciding whether a content should be stored at each RSU or not is affected by what contents are stored in nearby RSUs. In MobiCacher, in order to simplify the proposed heuristic solution, the authors decompose the CCP problem into multiple sub-problems, one for each sector and solve each sub-problem independently. In contrast, in the two proposed approaches in our paper, we consider this dependency among RSUs. We design the utility function for each RSU in a way that if RSUs, which are in the same flow (geographically close to each other), store similar files, their utility decreases. In other words, RSUs in the same flow share the gain of storing similar files. This deduction of the utility function causes the contents of the RSUs in the same flow to diversify. As a result, the cache hit ratio experienced by the vehicles increases (see Fig. 7).

Next, we report the results of second approach, that is, combinatorial optimization or Markov approach for different vehicles’ mobility model. We compared the hit ratio of this methods with other content placement approaches discussed in section 4. The reported values for each method has the confidence interval of \(90\%\). As depicted in Fig. 8, we compared five different content placement approaches which we already discussed in Sect. 4. For every approach, we ran the simulation several times and report the hit ratio experienced by the vehicles with some box-plots. In every simulation run, the mobility pattern of the vehicles would be different. Since our content placement approach considers the mobility pattern of the vehicles, it can essentially adapt with every situation and make good decisions in various combinations of requesting contents from RSUs. In this regards, the Markov approximation method shows high hit ratio compared to two other proposed heuristics approaches. But as it is shown in Fig. 11, the time complexity of this method is higher than other approaches. Also the second heuristic method shows better performance due to the fact that it considers all the mentioned essential factors on the cache content placement problem. This heuristic took into account the mobility pattern of the vehicles, the popularity of the files and the overlapping of RSU ranges and therefore achieved better hit ratio compared to the first heuristic which only took into account the popularity of files.

Fig. 8
figure 8

Cache hit ratio of content placement methods, based on combinatorial optimization approach

Full size image
Fig. 9
figure 9

Hit ratio of the combinatorial optimization approach for various RSU communication ranges

Full size image
Fig. 10
figure 10

Cache hit ratio for different file library sizes

Full size image
Fig. 11
figure 11

Operational delay of the combinatorial optimization approach

Full size image

As it is shown in Fig. 9, generally, by increasing the RSU’s communication range, the hit ratio achieved by all the methods will increase except for the first heuristic. This is because, by increasing the range up to 200 m, the hit ratio of the first heuristic method increases due to the fact that the probability of visiting more RSUs for each vehicle along its path increases, But for the ranges more that 200 m, the hit ratio in this method decrease because this method doesn’t consider the RSU’s communication range. Therefore, by increasing the range, and by increasing the number of RSUs visited by vehicles along their paths, this method suggests to store redundant, and duplicate most popular files in the RSUs. This uniformity in storing files in multiple RSUs will cause the reduction of hit ratio in this method. But we don’t have this poor behavior in second heuristic, because we store the first C most popular files in the most popular RSU and the next C most popular files in the second most popular RSU, etc. This diversity in storing files in RSUs helps us to achieve high hit ratio even in the situations with large RSU communication ranges. In Fig. 10, we observed the effect of the cache sizes on the performance of the combinatorial content placement method. We simulated this approach for different file library sizes and for three different average cache sizes. First, it is obvious that by increasing the number of files in the library the hit ratio experienced by the vehicles will be decreased. Second, by increasing the average cache sizes, the availability of the vehicle requests in the local RSUs will be increased and the hit ratio of the caches will be also increased. For example, in the case where we have 20 files in the library and the average cache size is 10, the hit ratio of the caches would be \(100\%\) and vehicles can download all their requests from local RSUs. Overall, the results confirm the efficiency of this method. The combinatorial content placement approaches improves the throughput of vehicular networks by accepting reasonable operational delay for converging to an efficient equilibrium (see Figure 11). Finally, we should mention that to have better insight about the performance of the two proposed approaches, we need to evaluate them in more realistic and extensive environments. To complete this work, we should consider some parameters to make the model more similar to the realistic situations. For example we can take the network capacity of the RSUs into account. That is, when RSUs can only serve a certain number of requests at each time. Also we should consider the packet loss and other communication parameters of vehicular networks into account to have a more realistic model of the environment. Another way to extend this work is to utilize the V2V communication to improve the throughput of the vehicular networks even more. Additionally, we can extend our work to highway environments and observe the behavior of the proposed methods in those situations. Last but not least, we can consider a scenario in which the vehicles themselves can play the role of mobile RSU and be local caches for other vehicles in the nearby area.

6 Conclusion

In this paper, we proposed two approaches for improving the throughput of vehicular networks. Considering the RSUs to play the role of local cache servers for the vehicles, the requested files can now be satisfied locally which leads to have lower network congestion over the base station links.

In the first approach, we proposed a solution for the CCP problem using game theory that distributively suggests which file should be store in which RSU to maximize the local hit ratio experienced by the vehicles. In the second approach, we modeled this problem using combinatorial optimization. We formulated the problem as maximizing the expected number of users which can successfully download their requested files from RSUs, instead of downloading them from base station. We then proposed an optimization problem to find the best combination of files for storing in each RSU. The simulation results showed that these approaches improve the performance metric compared to other content placement approaches.