Causal reasoning from almost first principles

Abstract

A formal theory of causal reasoning is presented that encompasses both Pearl’s approach to causality and several key formalisms of nonmonotonic reasoning in Artificial Intelligence. This theory will be derived from a single rationality principle of causal acceptance for propositions. However, this principle will also set the theory of causal reasoning apart from common representational approaches to reasoning formalisms.

1 Introduction

The primary aim of this paper consists in providing both rational foundations and a principle-based description for a particular theory of causal reasoning. This theory, called the causal calculus, has been born as part of a general field of nonmonotonic reasoning in Artificial Intelligence,¹ where it has been shown to cover important areas and applications of AI, especially those that had persistently resisted feasible representation and modeling using standard logical methods. Moreover, an important advantage of the causal approach to problems of AI has always been the fact that, by its very nature, causal reasoning brings with it the promise of Explainable AI, an approach to artificial intelligence that is not only practically successful but is also susceptible to rational explanation and justification.

A new stage in the development of this theory has emerged with the realization that it can also provide a formal representation for Pearl’s approach to causality in the framework of structural equation models (see (Bochman & Lifschitz, 2015)). In addition, a number of applications of the causal calculus outside AI have been developed, such as problems of causal attribution (actual causality) in legal theory and causal representation of general dynamic reasoning. A detailed description of the causal calculus, as well as the range of its current applications in AI and beyond can be found in Bochman (2021). Given this ‘body of evidence’, a more ambitious aim of this study is to display the causal calculus as a formal basis for a general theory of causal reasoning, an important kind of reasoning that has deep historical roots and solid foundations. Hopefully, it should facilitate the return of causation to its proper and deserved place in the general picture of human reasoning.

Causation is a notoriously elusive and multifaceted notion, and its studies too often have fallen into the parable of the blind men and the elephant by choosing only one of its aspects as a key to the whole concept. This is the main reason why in this study we will apply, in some sense, a venerated Hilbert’s program to formalizing causal reasoning in that we will not define the meaning of its key notions, namely causation, proposition, and acceptance. Instead, we will assume that the content of these notions is determined globally by the postulates we will require them to satisfy (similar to the formalization of geometry in Hilbert’s program).² Any philosophical approach or a theory of causation that would do justice to these postulates could be appropriate for our purposes. Moreover, just as in geometry, this approach will allow us to investigate important variants of causal reasoning which are created by varying these postulates.

In accordance with this approach, even the philosophical terminology that we will occasionally use in this study, such as rationality, normativity, reasons, and explanations, could be viewed as indicative and explanatory rather than compulsory. Still, the natural and profound connections of causation with inference, reasons and explanations, though thoroughly ‘deconstructed’ by logical positivists and analytic philosophy,³ will play an important role in informal justifications of our formal constructions even though they will remain outside our formal theory. The existence of such connections should also augment the intended understanding of causation with features and dimensions that go beyond plain physical relations ‘out there’ in the world. In particular, we will often point out an inherently normative character of the principles and constructions of our theory.

At the beginning, the formalism of causal reasoning will be defined below according to the usual format in which logical systems of reasoning are defined. Namely, it will have a language that consists of a set of (causal) inference rules that are defined on an underlying set of propositions. And it will also have a semantics that will be defined in terms of valuations on propositions that are in accord with the causal rules. This semantics, however, will be based on a radically different, causal principle of acceptance for propositions that will set the corresponding reasoning system apart from traditional representational approaches to language and meaning. Moreover, our constructions and postulates will create immediate challenges for approaches that are based on the correspondence theory of truth. Thus, an important aspect of our general approach to causal reasoning will amount to the fact that, though a causal theory determines its associated rational semantics of acceptance, the latter does not and even cannot determine the original causal theory. This fact will create an entirely new reasoning situation that will have multiple consequences for the corresponding theory of causal reasoning. It will lead, in particular, to an entirely new agenda and desiderata for such a reasoning.

With a few exceptions, we will completely omit proofs of the results and theorems in this paper. All of them can be discerned, however, from the references provided in the bibliography. The exception will be made for proofs of some small key facts that could also illustrate how we can actually use causal reasoning in this setting. It should also be mentioned that the relevant terminology in this study has been significantly changed (compared with current and previous publications in this area) in order to make it more relevant, convenient and friendly for a broader audience.

2 Causal theories and their semantics

As it is common for reasoning formalisms, our system of causal reasoning will have a language and an associated semantics. Its language will be a set of causal rules defined on an underlying language of propositions, while its semantics will be a set of valuations on propositions that conform to the causal rules. At the first stage, our underlying language L will be defined simply as a set of (unstructured) propositions.

A causal rule is an inference rule of the form

$$\begin{aligned}a{{\,\mathrm{\Rightarrow }\,}}A,\end{aligned}$$

where a is a finite set of propositions and A a proposition. The rule says that a set a of propositions causes proposition A.⁴

By a causal theory we will mean an arbitrary set of causal rules. A causal theory will provide an ultimate basis of causal reasoning, mainly in the form of constraints it imposes on acceptance of propositions.

The basic principle of causal reasoning will be formulated as the following rationality postulate of acceptance for propositions:

• Causal Acceptance Principle A proposition A is accepted with respect to a causal theory $\Delta$ if and only if $\Delta$ contains a causal rule $a{{\,\mathrm{\Rightarrow }\,}}A$ such that all propositions in a are accepted.

If we take causes as something that provide reasons for their effects (answer the question why, using Aristotle’s phrase), then the above principle can be viewed as expressing a constitutive principle of rationality in our context, since it states that (acceptance of) propositions can both serve as and stand in need of reasons (see (Brandom, 2000)). In what follows, sets of accepted propositions that conform to the above principle will form the models of the corresponding causal theory.

There are two parts that constitute the above principle. These two parts could be expressed as two independent rationality postulates:

Preservation Principle:

If all propositions in a are accepted, and a causes A, then A should be accepted.

Principle of Sufficient Reason:

Any proposition should have a cause for its acceptance.

The Preservation Principle expresses a widely accepted claim that the very concept of an inference rule (however understood) presupposes that such a rule should preserve, or ‘transmit’, acceptance of the corresponding propositions. On a normative reading, it states that existence of (good) reason is sufficient for acceptance.

Leibniz’ Principle of Sufficient Reason is again a normative principle of reasoning stating that propositions require reasons for their acceptance, and such reasons are provided by establishing their causes. The origins of this principle can be found in the well-known law of causality, but also in Aristotle’s distinction between syllogisms and demonstrations.

Example 1

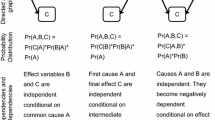
The following causal theory provides a causal description of some well-known example originated in Pearl (1987).⁵

$$\begin{aligned} Rained{{\,\mathrm{\Rightarrow }\,}}Grasswet\\ Sprinkler{{\,\mathrm{\Rightarrow }\,}}Grasswet\\ Rained{{\,\mathrm{\Rightarrow }\,}}Streetwet. \end{aligned}$$

Just as for ordinary deductive inference systems, if, for instance, Rained is accepted with respect to such a causal theory, then both Grasswet and Streetwet should also be accepted. However, in a causal reasoning with this causal theory, any acceptable set of propositions that contains Grasswet should contain either Rained or Sprinkler as its causes. Similarly, Streetwet implies in this sense acceptance of both its only possible cause Rained and a collateral effect Grasswet. Both derivations from causes to their effects and from effects to their possible causes constitute essential parts of causal reasoning.

In the framework of causal reasoning described in this study, the relation between the language (of causal rules) and its semantics (of acceptance) will always remain unidirectional. In particular, it can be made clear already at this stage that Preservation principle cannot be used as a sole principle of validity for the causal rules themselves. Namely, we cannot follow Tarski in defining causal rules as inference rules that preserve acceptance. This could be seen already from the fact that such a stipulation would immediately sanction the Reflexivity postulate of deductive inference (namely, all rules of the form $A{{\,\mathrm{\Rightarrow }\,}}A$) and this would trivialize in turn the second part of our rationality postulate, the principle of sufficient reason: on a causal reading, rules $A{{\,\mathrm{\Rightarrow }\,}}A$ will make all propositions self-justified (self-evident).⁶ Incidentally, this observation indicates also that (absence of) Reflexivity constitutes one of the key differences between causal inference and deductive consequence.

2.1 Rational semantics

The intended semantics of a causal theory that conforms to the above principles will be defined again along a standard route that employs valuations on propositions for describing semantics.

A valuation is a function $v\in \{0,1\}^L$ that assigns either 1 (‘truth’) or 0 (‘falsity’) to every proposition of the language. If $v(A)=1$, we will say that proposition A is accepted (‘taken-true’) in the valuation v. As usual, a valuation can be safely identified with its associated set of accepted propositions, and we will even abuse the above notation by viewing valuation v itself as a set of (accepted) propositions.

Remark

It should be mentioned already at this stage, however, that we will not identify non-acceptance of proposition A in a valuation (namely $v(A)=0$) with rejection of A. Moreover, our semantic constructions will become at some point openly asymmetric between acceptance and rejection;⁷ this asymmetry will play an important constructive role in our subsequent constructions. Still, we will invariably identify in what follows rejection of A with acceptance of its classical negation $\lnot A$.

For any set u of propositions and a causal theory $\Delta$, we will denote by $\Delta (u)$ the set of all propositions that are directly caused by u in $\Delta$, that is,

$$\begin{aligned} \Delta (u) = \{A\mid a{{\,\mathrm{\Rightarrow }\,}}A\in \Delta ,\ a\subseteq u\}. \end{aligned}$$

This notation will help us in formulating the following basic definition of semantics for our language.

Definition 1

• A causal model of a causal theory $\Delta$ is a valuation that satisfies the following condition:

  $$\begin{aligned} v=\Delta (v). \end{aligned}$$

• A rational semantics of a causal theory is the set of all its causal models.

The notion of a causal model provides precise formal expression of the Causal Acceptance principle since it determines that a proposition is accepted in a model if and only if it has a cause in this model.

$\Delta (u)$ is a monotonic operator on the set of propositions, while causal models correspond to fixed points of this operator. Consequently, any causal theory has at least one causal model, so it always has a rational semantics.

As an important special case, a causal theory always has the least model. This model can be obtained by applying the operator $\Delta ()$ iteratively, starting with the empty set $\emptyset$. This least model provides a faithful representation of the concept of (deductive) provability in our causal framework. However, this model expresses only a small part of the informational content embodied in the source causal theory. Moreover, this observation can actually be extended to the rational semantics itself.

A causal model, viewed just as a set of (accepted) propositions, and the rational semantics in general contain only purely categorical, factual information. In this respect, they provide only a possible factual output (a “factual shadow,” if you like) of the rich causal information embodied in the original causal theory. Unlike the case of an ordinary correspondence semantics, even the whole set of such possible outputs is insufficient for determining, or capturing back, the initial causal information, what causes what. We will see, in particular, that essentially different causal theories could ‘accidentally’ have the same rational semantics. Nevertheless, just as for ordinary reasoning formalisms, the rational semantics will play a crucial, indispensable role in evaluation and adjudication of causal theories. To begin with, we are going to show that it determines the underlying logic of causal reasoning.

3 Causal inference

It turns out that there are formal derivations (aka metainferences) among causal rules that always preserve the rational semantics. Such metainferences will be taken to constitute the underlying logic of causal reasoning. On our current maximal level of abstraction, this logic can be described as follows:⁸

Definition 2

A causal inference relation is a set of causal rules that is closed with respect to the following metainferences:

Monotonicity:

   If $a{{\,\mathrm{\Rightarrow }\,}}A$ and $a\subseteq b$, then $b{{\,\mathrm{\Rightarrow }\,}}A$;

Cut:

   If $a{{\,\mathrm{\Rightarrow }\,}}A$ and $a,A{{\,\mathrm{\Rightarrow }\,}}B$, then $a{{\,\mathrm{\Rightarrow }\,}}B$.

The above notion of causal inference incorporates two of the three basic postulates for ordinary Tarski consequence relations. It explicitly disavows, however, the first postulate of Tarski consequence, the Reflexivity postulate. As we will see, it is this ‘omission’ that creates the possibility of causal reasoning in this framework. Still, we will see that the remaining two postulates of causal inference are sufficient for a faithful characterization of a general notion of derivability among propositions that is determined by a given set of (causal) inference rules.

Remark

Causal inference need not be anti-reflexive. Reflexive rules $A{{\,\mathrm{\Rightarrow }\,}}A$ can belong to a causal theory, but in the framework of causal reasoning they already acquire a nontrivial content. More precisely, such a rule says that A is a self-evident proposition that does not require further justification for its acceptance. Propositions that satisfy such rules will be called causal assumptions in what follows.

We will extend causal rules to rules having arbitrary sets of propositions as premises using a familiar compactness recipe: for any set u of propositions, we define $u{{\,\mathrm{\Rightarrow }\,}}A$ as follows:

$$\begin{aligned}u{{\,\mathrm{\Rightarrow }\,}}A\ \equiv \ a{{\,\mathrm{\Rightarrow }\,}}A, \text { for some finite } a\subseteq u.\end{aligned}$$

For a set u of propositions, ${{\,\mathrm{\mathcal {C}}\,}}(u)$ will denote the set of propositions caused by u with respect to a causal inference relation ${{\,\mathrm{\Rightarrow }\,}}$, that is

$$\begin{aligned}{{\,\mathrm{\mathcal {C}}\,}}(u) = \{A\mid u{{\,\mathrm{\Rightarrow }\,}}A\}.\end{aligned}$$

As could be expected, the causal operator ${{\,\mathrm{\mathcal {C}}\,}}$ will play much the same role as the usual derivability operator for consequence relations. In particular, the above postulates of causal inference can be recast as the following properties of the causal operator:

Monotonicity:

   If $u\subseteq v$, then ${{\,\mathrm{\mathcal {C}}\,}}(u)\subseteq {{\,\mathrm{\mathcal {C}}\,}}(v)$.

Cut:

   ${{\,\mathrm{\mathcal {C}}\,}}(u\cup {{\,\mathrm{\mathcal {C}}\,}}(u))\subseteq {{\,\mathrm{\mathcal {C}}\,}}(u)$.

Thus, ${{\,\mathrm{\mathcal {C}}\,}}$ is a monotonic operator. Actually, due to compactness, ${{\,\mathrm{\mathcal {C}}\,}}$ is not only monotonic, but also a continuous operator. Still, ${{\,\mathrm{\mathcal {C}}\,}}$ is not inclusive, that is, $u\subseteq {{\,\mathrm{\mathcal {C}}\,}}(u)$ does not always hold. Also, it is not idempotent, that is, ${{\,\mathrm{\mathcal {C}}\,}}({{\,\mathrm{\mathcal {C}}\,}}(u))$ can be distinct from ${{\,\mathrm{\mathcal {C}}\,}}(u)$.⁹

On a positive side, causal inference preserves a number of familiar properties. Thus, any causal inference relation will already be transitive, that is, it will satisfy

(Transitivity):

   If $A{{\,\mathrm{\Rightarrow }\,}}B$ and $B{{\,\mathrm{\Rightarrow }\,}}C$, then $A{{\,\mathrm{\Rightarrow }\,}}C$.

Transitivity corresponds to the following property of the causal operator:

$$\begin{aligned}{{\,\mathrm{\mathcal {C}}\,}}({{\,\mathrm{\mathcal {C}}\,}}(u))\subseteq {{\,\mathrm{\mathcal {C}}\,}}(u).\end{aligned}$$

Note, however, that Transitivity is a weaker property than Cut, since it does not imply the latter (in the framework of causal inference).

For an arbitrary causal theory $\Delta$, we will denote by ${{\,\mathrm{\Rightarrow }\,}}_\Delta$ the least causal inference relation that includes $\Delta$, while ${{\,\mathrm{\mathcal {C}}\,}}_\Delta$ will denote the associated causal operator. By this definition, ${{\,\mathrm{\Rightarrow }\,}}_\Delta$ is precisely the set of all causal rules that are derivable from $\Delta$ by Monotonicity and Cut.

3.1 Causal inference vs. deductive consequence

A further insight into the properties of causal inference can be obtained by comparing it with associated consequence relations.

As already mentioned, the only formal difference between causal inference and ordinary Tarski consequence amounts to the Reflexivity postulate that holds for the latter, though not for the former. Note also that any causal theory, and hence any causal inference relation, can also be considered as an ordinary conditional theory (a set of inference rules), so it determines the corresponding consequence relation. The following construction provides a direct description of this consequence relation in terms of the source causal inference relation. Namely, for a causal inference relation ${{\,\mathrm{\Rightarrow }\,}}$, we can define the following consequence relation:

$$\begin{aligned}u\vdash _{{{\,\mathrm{\Rightarrow }\,}}}A\ \equiv \ A\in u\text { or } u{{\,\mathrm{\Rightarrow }\,}}A.\end{aligned}$$

Then the following fact can be easily verified.

Lemma 1

If ${{\,\mathrm{\Rightarrow }\,}}$ is a causal inference relation, then $\vdash _{{{\,\mathrm{\Rightarrow }\,}}}$ is the least consequence relation containing ${{\,\mathrm{\Rightarrow }\,}}$.

Let ${{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}$ denote the derivability operator corresponding to $\vdash _{{{\,\mathrm{\Rightarrow }\,}}}$. Then the above description can be reformulated as the following equality, for any set u of propositions:

$$\begin{aligned}{{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}(u)= u\cup {{\,\mathrm{\mathcal {C}}\,}}(u).\end{aligned}$$

The above equality shows, in effect, that ${{\,\mathrm{\mathcal {C}}\,}}(u)$ captures all nontrivial consequences included in ${{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}(u)$, except for u itself. Moreover, the Cut postulate immediately implies the following equality:

$$\begin{aligned}{{\,\mathrm{\mathcal {C}}\,}}(u)={{\,\mathrm{\mathcal {C}}\,}}({{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}(u)).\end{aligned}$$

Actually, the same Cut postulate implies also ${{\,\mathrm{\mathcal {C}}\,}}(u)={{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}({{\,\mathrm{\mathcal {C}}\,}}(u))$, so the causal operator absorbs ${{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}$ on both sides:

$$\begin{aligned}{{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}\circ {{\,\mathrm{\mathcal {C}}\,}}={{\,\mathrm{\mathcal {C}}\,}}\circ {{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}={{\,\mathrm{\mathcal {C}}\,}}.\end{aligned}$$

These equalities show that deductive consequences of a given causal theory can be safely used as intermediate premises and conclusions in causal inference. In a hindsight, this could explain why it has been so difficult to distinguish causal reasoning proper from general deductive reasoning. In particular, the above results allow us to see causal rules themselves as just a special kind of deductive rules. This vision naturally corresponds to Aristotle’s theory of reasoning in his Analytics where (causal) demonstrations were viewed as a species of syllogisms (deductions) (see (Bochman, 2021)). It should be kept in mind, however, that deductive inference alone is insufficient for determining the causal consequences of a set of propositions.

Our final result here provides an alternative description of the causal inference relation generated by a causal theory $\Delta$.

Corollary 2

$\quad {{\,\mathrm{\mathcal {C}}\,}}_\Delta (u)=\Delta ({{\,\textrm{Cn}\,}}_\Delta (u)).$

The above equation says, in particular, that in order to obtain all causal consequences of a given set of propositions, we can compute first all its deductive consequences (with respect to the original causal theory $\Delta$), and then find out only which propositions are directly caused by this derived set of consequences.

Just as for ordinary deductive reasoning, propositional theories, that is, sets of propositions that are closed with respect to inference rules still play an important role in describing causal inference (especially in proofs).

Definition 3

A set u of propositions is a propositional theory of a causal theory $\Delta$ if $\Delta (u)\subseteq u$.

Since causal inference relations can also be viewed as causal theories (sets of inference rules), we conclude that propositional theories of a causal inference relation are sets of propositions that satisfy the inclusion ${{\,\mathrm{\mathcal {C}}\,}}(u)\subseteq u$ for the associated causal operator ${{\,\mathrm{\mathcal {C}}\,}}$.

A propositional theory of a causal theory is a set of propositions that is closed with respect to its causal rules, namely, if $a\subseteq u$ and $a{{\,\mathrm{\Rightarrow }\,}}B$, then $B\in u$. Accordingly, such theories have much the same properties as ordinary theories (deductively closed sets) of consequence relations. Note, in particular, that the set of propositional theories is closed with respect to arbitrary intersections, and consequently any set of propositions is included in the least such theory.

As a consequence of the general correspondence between causal inference and deductive consequence, we obtain that any causal inference relation ${{\,\mathrm{\Rightarrow }\,}}$ has the same propositional theories as the corresponding consequence relation $\vdash _{{{\,\mathrm{\Rightarrow }\,}}}$. Moreover, it is well known that any consequence relation is uniquely determined by its propositional theories. A causal inference relation, however, is not fully determined by its propositional theories.

4 Causal vs. semantic equivalence

It will be shown now that causal inference provides an adequate and maximal logical framework for reasoning with causal models.

Definition 4

Two causal theories will be called semantically equivalent if they determine the same rational semantics.

Recall that a causal inference relation can also be considered as a causal theory. Moreover, if ${{\,\mathrm{\Rightarrow }\,}}_\Delta$ denotes the least causal inference relation that contains a causal theory $\Delta$, then we have:

Lemma 3

Any causal theory $\Delta$ is semantically equivalent to ${{\,\mathrm{\Rightarrow }\,}}_\Delta$.

Proof

If v is a propositional theory of $\Delta$, then $v={{\,\textrm{Cn}\,}}_{\Delta }(v)$, and hence $\Delta (v)=\Delta ({{\,\textrm{Cn}\,}}_\Delta (v))$. Consequently, $v=\Delta (v)$ iff $v=\Delta ({{\,\textrm{Cn}\,}}_\Delta (v))$. By Corollary 2, this implies that v is a model of $\Delta$ if and only if it is a model of ${{\,\mathrm{\Rightarrow }\,}}_\Delta$. $\square$

The above lemma implies that the postulates of causal inference, namely Monotonicity and Cut, are adequate for reasoning with causal models since they preserve the latter. This fact can be viewed as a primary justification for these postulates. Moreover, we will show that this notion of causal inference constitutes the maximal logic suitable for the rational semantics.

Definition 5

Two causal theories $\Delta$ and $\Gamma$ will be called logically equivalent, if each can be obtained from the other using the postulates of causal inference. Or, equivalently, when ${{\,\mathrm{\Rightarrow }\,}}_\Delta$ coincides with ${{\,\mathrm{\Rightarrow }\,}}_\Gamma$.

Now, as an immediate consequence of the previous lemma, we obtain:

Corollary 4

Logically equivalent causal theories are semantically equivalent.

The reverse implication in the above corollary does not hold, and a deep reason for this is that the rational semantics does not fully determine the content of the original causal theory. This means, in particular, that it may well happen that two essentially (i.e., informationally) different causal theories could determine the same rational semantics. This under-determination is closely related to a more general fact that both the rational semantics itself and semantic equivalence of causal theories are nonmonotonic notions; they are not preserved under extensions of causal theories with further causal rules. The following simple example illustrates this.

Example 2

Let us consider two causal theories: $\{A{{\,\mathrm{\Rightarrow }\,}}B\}$ and $\{A{{\,\mathrm{\Rightarrow }\,}}C\}$. These causal theories are obviously different, but they are semantically equivalent since they determine the same rational semantics, which contains a single model $\emptyset$ in which no proposition is accepted. Now let us add to these causal theories the same causal rule $A{{\,\mathrm{\Rightarrow }\,}}A$. Then the first causal theory will already have an additional model $\{A,B\}$, while the semantics of the second theory will acquire a different model $\{A,C\}$.

What we need, therefore, is a stronger, logical counterpart of the notion of semantic equivalence that would be preserved under addition of new causal rules. This immediately suggests the following definition.

Definition 6

Two causal theories $\Delta$ and $\Gamma$ will be said to be strongly semantically equivalent if, for any set $\Phi$ of causal rules, $\Delta \cup \Phi$ is semantically equivalent to $\Gamma \cup \Phi$.

Strongly equivalent causal theories are “equivalent forever”—that is, they are interchangeable in any larger causal theory without changing the associated rational semantics. This naturally suggests that strong equivalence could be a kind of logical equivalence with respect to some background logic of causal rules. And the next result will show that this logic is precisely the logic of causal inference.

Theorem 5

Two causal theories are strongly semantically equivalent if and only if they are logically equivalent.

Proof

The direction from right to left follows from the preceding corollary and the fact that, if $\Delta$ and $\Gamma$ are logically equivalent, then, for any $\Phi$, $\Delta \cup \Phi$ and $\Gamma \cup \Phi$ are also logically equivalent.

Assume now that $\Delta$ is not logically equivalent to $\Gamma$. Then we may assume for certainty that there are propositions a and B such that $a{{\,\mathrm{\Rightarrow }\,}}_\Delta B$ and $a{{\,\mathrm{\nRightarrow }\,}}_\Gamma B$. Let $u={{\,\textrm{Cn}\,}}_\Gamma (a)$ (that is, the least theory of $\Gamma$ that includes a). Then $u{{\,\mathrm{\Rightarrow }\,}}_\Delta B$ and $u{{\,\mathrm{\nRightarrow }\,}}_\Gamma B$. Let us consider two cases.

Suppose first that u is not a theory of $\Delta$. Then we choose $\Phi =\{A{{\,\mathrm{\Rightarrow }\,}}A\mid A\in u\}$ as a set of additional rules. Clearly, u will become a model of $\Gamma \cup \Phi$, though not of $\Delta \cup \Phi$, since u is still not a theory of $\Delta \cup \Phi$.

Suppose now that u is also a theory of $\Delta$. Since $u{{\,\mathrm{\Rightarrow }\,}}_\Delta B$, we have $B\in u$. Then we define $\Phi$ as $\{A{{\,\mathrm{\Rightarrow }\,}}A\mid A\in u{\setminus }{{\,\mathrm{\mathcal {C}}\,}}_\Delta (u)\}$. Note first that we still have $u{{\,\mathrm{\nRightarrow }\,}}_{\Gamma \cup \Phi }B$ (since ${{\,\mathrm{\mathcal {C}}\,}}_{\Gamma \cup \Phi }(u)$ coincides with ${{\,\mathrm{\mathcal {C}}\,}}_{\Gamma }(u)$), and hence u is not a model of $\Gamma \cup \Phi$. However, we have $u\subseteq {{\,\mathrm{\mathcal {C}}\,}}_{\Delta \cup \Phi }(u)$, and therefore u is a model of $\Delta \cup \Phi$. This shows that $\Delta$ and $\Gamma$ are not strongly equivalent. $\square$

The above result implies that causal inference relations are maximal inference relations that are adequate for causal reasoning with respect to the rational semantics: any derivation rule that is not valid for causal inference relations can be “falsified” by finding a suitable extension of two causal theories that would determine different rational semantics.

Note also that discriminating sets of causal rules $\Phi$ were restricted in the above proof to rules of the form $A{{\,\mathrm{\Rightarrow }\,}}A$. As we will see, such rules play an important general role in causal reasoning.

4.1 Axioms vs. assumptions

The rational semantics of causal theories is based on the law of causality, or Leibniz’s principle of sufficient reason, which requires that any accepted proposition should have an accepted cause. Accordingly, justification of accepted propositions (i.e., finding reasons for their acceptance) constitutes an essential part of this semantic framework. In fact, this is a common feature of many other formalisms of nonmonotonic reasoning in AI.¹⁰

The law of causality inevitably leads to a fundamental problem known already in antiquity as the Agrippan trilemma: if we do not want to accept infinite regress of causation, we should accept either uncaused or self-caused propositions. Now, in the framework of causal theories, there are two kinds of propositions that can play, respectively, these two roles:

Definition 7

• A proposition A will be called an axiom of a causal theory $\Delta$ if the rule $\emptyset {{\,\mathrm{\Rightarrow }\,}}A$ belongs to $\Delta$;

• A proposition A will be called a causal assumption of a causal theory if the rule $A{{\,\mathrm{\Rightarrow }\,}}A$ belongs to it.

Example 3

Let us return to Pearl’s example (Example 1):

$$\begin{aligned}Rained{{\,\mathrm{\Rightarrow }\,}}Grasswet\quad Sprinkler{{\,\mathrm{\Rightarrow }\,}}Grasswet\quad Rained{{\,\mathrm{\Rightarrow }\,}}Streetwet\end{aligned}$$

Note first that, taken by itself, this causal theory does not have causal models (more precisely, it has a single empty causal model), mainly because the causal status of Rained and Sprinkler are not determined. But now let’s make Rained and Sprinkler causal assumptions of our theory:

$$\begin{aligned}Rained{{\,\mathrm{\Rightarrow }\,}}Rained\qquad Sprinkler{{\,\mathrm{\Rightarrow }\,}}Sprinkler. \end{aligned}$$

As a result, the rational semantics of this causal theory will acquire three additional causal models:

$$\begin{aligned} \{Rained, Grasswet, Streetwet\}\quad \{Sprinkler, Grasswet\}\\ \{Rained, Sprinkler, Grasswet, Streetwet\} \end{aligned}$$

These models display already some correlations (or ‘regularities’) among the relevant propositions. For instance, that Rained is always accompanied by Grasswet and Streetwet in these models (deduction), but also that Streetwet is always accompanied by Rained (abduction).

In clear contrast with deductive reasoning, both axioms and causal assumptions provide reasonable end-points of the justification process in causal reasoning: axioms do not require justification, while causal assumptions naturally correspond in this sense to self-evident propositions. It is easy to show that for causal inference relations, any axiom will also be an assumption, though not vice versa. The difference between the two can be described as follows. Every axiom must be accepted in any reasonable model, and hence it should belong to every causal model. In contrast, any causal assumption can be incorporated into a causal model when it is consistent with the latter, but it does not have to be included into it. As a result, causal theories admit in general multiple causal models depending on the assumptions we actually accept. This functionality makes causal assumptions much similar to abducibles in a system of abductive reasoning. In fact, it has been shown in Bochman (2007) that causal inference relations allow us to provide a uniform and syntax-independent description of abductive reasoning. Moreover, it has been shown that in many regular cases (notably, in the finite case) the correspondence between causal and abductive theories is even bidirectional in the sense that the rational semantics of a causal theory coincides with the semantics of an associated abductive system.

5 Supraclassical causal reasoning

Now we are going to raise our abstract theory of causal reasoning to a full-fledged reasoning system that will subsume, in particular, both Pearl’s approach to causation and a number of prominent formalisms of nonmonotonic reasoning in Artificial Intelligence.

It turns out that the most basic desideratum, or prerequisite, for such a full-fledged system of reasoning amounts to the capability of using ordinary classical entailment as an integral part of causal reasoning.

Technically, a solution to the task of accommodating classical logical reasoning in our causal framework is quite straightforward. Recall that any causal theory has an associated (least) consequence relation, and this consequence relation can be safely used as intermediate steps in causal derivations. Accordingly, all we need is to require that this consequence relation should be supraclassical, that is, it should subsume classical entailment.

Even at this stage, however, we have to cope with the fact that in our construction of causal reasoning, the relation between the language of causal rules and its semantics is asymmetric: though a causal theory determines its associated rational semantics, the latter is insufficient for capturing back the (causal) content embodied in a causal theory. Applied to our present aim of incorporating classical logic into causal reasoning, the problem is that there seems to be no compositional (atomist) way of expressing the usual truth-tables of classical logical connectives ‘inferentially’ in terms of some derivation rules for causal theories. Moreover, the extension of our ‘vocabulary’ with classical logical connectives will actually extend our expressive capabilities beyond what is expressible in the causal language with propositional atoms only.¹¹ This expressive gain can even be considered as an advantage of the corresponding extended language, an advantage that will be exploited in what follows.

For all these reasons, the suggested definitions of supraclassical causal inference and its associated rational semantics below will be both minimalist and holist; they will require only that an appropriate causal reasoning system should respect (antecedently understood) classical entailment among propositions.

Remark

A more general picture of reasoning that naturally arises from the suggested construction is that causal reasoning is not a replacement or competitor of logical (deductive) reasoning, but its complement (or extension) for ubiquitous reasoning situations where we do not have logically sufficient knowledge – see (Bochman, 2021) for a more detailed discussion.

From now on, our underlying language L of propositions will be a classical propositional language with the usual classical connectives and constants $\{\wedge ,\vee ,\lnot ,\rightarrow ,\textbf{t},\textbf{f}\}$. The symbol $\vDash$ will stand for the classical entailment while ${{\,\textrm{Th}\,}}$ will denote the associated classical provability operator. In this and subsequent sections, $p,g,r,\dots$ will denote propositional atoms while $A,B,C,\dots$ will denote arbitrary classical propositions.

Definition 8

A causal inference relation in a classical language will be called supraclassical if it satisfies the following additional rules:

(Strengthening):

   If $b{{\,\mathrm{\Rightarrow }\,}}C$ and $a\vDash B$, for every $B\in b$, then $a{{\,\mathrm{\Rightarrow }\,}}C$;

(Weakening):

   If $a{{\,\mathrm{\Rightarrow }\,}}B$ and $B\vDash C$, then $a{{\,\mathrm{\Rightarrow }\,}}C$;

(And):

   If $a{{\,\mathrm{\Rightarrow }\,}}B$ and $a{{\,\mathrm{\Rightarrow }\,}}C$, then $a{{\,\mathrm{\Rightarrow }\,}}B\wedge C$;

(Truth):

   $\textbf{t}{{\,\mathrm{\Rightarrow }\,}}\textbf{t}$;

(Falsity):

   $\textbf{f}{{\,\mathrm{\Rightarrow }\,}}\textbf{f}$.

The origins of the above postulates can be found in Input/Output logics of Makinson and van der Torre (2000), the only difference being the last postulate, Falsity. Taken literally, the latter could be viewed as a causal version of the ancient principle ex nihilo nihil fit (‘Nothing comes from nothing"). However, given the other postulates (especially Weakening), it also implies ex falso quodlibet (“from falsehood, anything”), and its role consists, in effect, in excluding classically inconsistent causal models.

Due to Strengthening, a causal rule $a{{\,\mathrm{\Rightarrow }\,}}A$ becomes equivalent to a single-premise rule $\bigwedge a{{\,\mathrm{\Rightarrow }\,}}A$. In addition, a rule $\emptyset {{\,\mathrm{\Rightarrow }\,}}A$ with an empty set of premises becomes equivalent to the rule $\textbf{t}{{\,\mathrm{\Rightarrow }\,}}A$. Consequently, a supraclassical causal inference relation could already be viewed as a binary relation on the set of (classical) propositions.

The classical conjunction $\wedge$ can be given a fully modular description in this causal context (as the main connective in propositions) using the following double-line (bidirectional) derivation rules:

Note that these metainferences are valid for supraclassical causal inference. As a result, conjunctions of propositions can always be eliminated both in antecedents and consequents of causal rules. Moreover, let us say that a causal inference relation in a classical language is conjunctive if it is closed with respect to the rule $(\wedge R)$. Then we obtain that $A\wedge B$ is accepted with respect to such an inference relation if and only if both A and B are accepted with respect to it:

Lemma 6

If v is a causal model of a conjunctive causal inference relation, then

$A\wedge B\in v$ iff $A\in v$ and $B\in v$.

However, such a modular description is impossible for the classical negation in our causal context. Moreover, the fact that conjunction and negation form a functionally complete set of classical connectives makes the classical negation a culprit in the whole problem of (the absence of) a modular description for the supraclassical causal inference. We will see, however, that the problem of describing the behavior of negation in causal contexts is far from being trivial (see Sect. 10).

Causal reasoning with classical propositions requires also an appropriate ‘upgrade’ of the corresponding rational semantics. Namely, it requires that causal models should also be closed with respect to classical entailment.

Definition 9

• A classical causal model of a causal theory $\Delta$ is a classically consistent valuation (that is, $\textbf{f}\notin v$) that satisfies the following condition:

  $$\begin{aligned} v={{\,\textrm{Th}\,}}(\Delta (v)). \end{aligned}$$

• A rational supraclassical semantics of a causal theory is the set of all its classical causal models.

A classical causal model is a set of propositions that is closed both with respect to the causal rules and with respect to classical entailment. The principle of sufficient reason in such models is generalized, however, to the principle that any accepted proposition should (at least) be a classical logical consequence of accepted propositions that are caused in the model. In other words, a classical causal model is the least deductively closed model that is determined by its causal consequences.

Remark

Any classical causal model corresponds to a deductively closed set of classical propositions. Such models need not satisfy bivalence: it may well happen that neither proposition A nor its negation $\lnot A$ are accepted in such a model. Later we will consider a restriction of the supraclassical semantics to causal models that are (classical) worlds; it will be called a rational classical semantics (see Sect. 9). This latter semantics will sanction, however, a stronger logic of causal inference.

It turns out that supraclassical causal inference provides an adequate logical framework for reasoning with respect to the rational supraclassical semantics.

Definition 10

Two causal theories $\Delta$ and $\Gamma$ will be called semantically s-equivalent if they determine the same rational supraclassical semantics, and strongly s-equivalent if, for any set $\Phi$ of causal rules, $\Delta \cup \Phi$ is semantically s-equivalent to $\Gamma \cup \Phi$.

As before, if ${{\,\mathrm{\Rightarrow }\,}}^s_\Delta$ denotes the least supraclassical causal inference relation that contains a causal theory $\Delta$, then we have:

Lemma 7

Any causal theory $\Delta$ is strongly s-equivalent to ${{\,\mathrm{\Rightarrow }\,}}^s_\Delta$.

Thus, postulates of supraclassical causal inference are adequate for reasoning with respect to the rational supraclassical semantics since they preserve the latter. Note also that, for supraclassical causal inference relations, any causal model will already be a classical model (since it will be closed with respect to classical entailment), so their general rational semantics will coincide with the supraclassical semantics.

The following theorem shows that supraclassical causal inference constitutes a maximal logic suitable for the supraclassical semantics.

Theorem 8

Two causal theories are strongly s-equivalent if and only if they determine the same supraclassical causal inference relation.

Supraclassical causal inference preserves all the properties of general causal inference. Moreover, the correspondence between causal inference and deductive consequence can now be elevated to the correspondence between supraclassical causal inference and supraclassical consequence.

A consequence relation $\vdash$ in a classical language is called supraclassical if it subsumes classical inference, that is, $\vDash \ \subseteq \ \vdash$. Informally, supra-classicality means that the corresponding consequence relation includes classical entailment as part of its inference rules, though it can include also ‘material’ inference rules that are not reducible to classical entailment.

For any supraclassical causal inference relation there exists a least supraclassical consequence relation that includes it. This consequence relation can be described directly as follows:

$$\begin{aligned} A\vdash _{{{\,\mathrm{\Rightarrow }\,}}}B\ \equiv \ A{{\,\mathrm{\Rightarrow }\,}}(A{\rightarrow } B). \end{aligned}$$

Theorem 9

If ${{\,\mathrm{\Rightarrow }\,}}$ is a supraclassical causal inference relation, then $\vdash _{{{\,\mathrm{\Rightarrow }\,}}}$ is the least supraclassical consequence relation containing ${{\,\mathrm{\Rightarrow }\,}}$.

Let ${{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}$ denote the consequence operator corresponding to $\vdash _{{{\,\mathrm{\Rightarrow }\,}}}$. Then the above description can be extended to the following equality:

$$\begin{aligned} {{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}(u)={{\,\textrm{Th}\,}}(u\cup {{\,\mathrm{\mathcal {C}}\,}}(u)). \end{aligned}$$

The above equality shows again that causal inference captures all nontrivial consequences included in ${{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}(u)$, save for u itself. Moreover, as in the general case, we still have the following equalities:

$$\begin{aligned} {{\,\mathrm{\mathcal {C}}\,}}(u)={{\,\mathrm{\mathcal {C}}\,}}({{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}(u))={{\,\textrm{Cn}\,}}_{{{\,\mathrm{\Rightarrow }\,}}}({{\,\mathrm{\mathcal {C}}\,}}(u)). \end{aligned}$$

Accordingly, deductive consequences of a given causal theory (including now all classical entailments) can be safely used as intermediate premises and conclusions in supraclassical causal inference.

An important feature of supraclassical causal inference is that it already allows us to express the logical notion of causal equivalence among propositions of the underlying language.

Definition 11

Propositions A and B will be called causally equivalent with respect to a supraclassical causal inference relation if the latter contains the rule

$$\begin{aligned} \textbf{t}{{\,\mathrm{\Rightarrow }\,}}A\leftrightarrow B. \end{aligned}$$

Thus, A and B are causally equivalent if $A\leftrightarrow B$ is an axiom of the causal inference relation. The following result establishes precise sense in which this equivalence can be termed a logical one.

Theorem 10

Propositions A and B are causally equivalent in a supraclassical causal inference relation ${{\,\mathrm{\Rightarrow }\,}}$ if and only if any occurrence of A can be replaced by B in the rules of ${{\,\mathrm{\Rightarrow }\,}}$.

Proof

If A can be replaced by B in any rule of ${{\,\mathrm{\Rightarrow }\,}}$, then it can be replaced also in $\textbf{t}{{\,\mathrm{\Rightarrow }\,}}(A{\leftrightarrow } A)$, which holds by Truth. Hence, $\textbf{t}{{\,\mathrm{\Rightarrow }\,}}(A{\leftrightarrow } B)$ holds in ${{\,\mathrm{\Rightarrow }\,}}$.

We will denote by X(A/B) an arbitrary classical proposition obtained from a proposition X by replacing some of the occurrences of A in it by B. Clearly, $A{\leftrightarrow }B\vDash X{\leftrightarrow } X(A/B)$. Assume now that A and B are causally equivalent, and $X{{\,\mathrm{\Rightarrow }\,}}Y$. Then $X{{\,\mathrm{\Rightarrow }\,}}(A{\leftrightarrow }B)$ by Strengthening, and hence $X{{\,\mathrm{\Rightarrow }\,}}(Y{\leftrightarrow } Y(A/B))$ by Weakening. Consequently, $X{{\,\mathrm{\Rightarrow }\,}}Y(A/B)$ by And and Weakening. Thus, B can replace A in the heads of the rules from ${{\,\mathrm{\Rightarrow }\,}}$. In addition, we have $X(A/B),A{\leftrightarrow }B\vDash X$, and therefore $X(A/B)\wedge (A{\leftrightarrow } B){{\,\mathrm{\Rightarrow }\,}}Y$ by Strengthening. But we have also $X(A/B){{\,\mathrm{\Rightarrow }\,}}(A{\leftrightarrow } B)$, so we can apply Cut and obtain $X(A/B){{\,\mathrm{\Rightarrow }\,}}Y$. This shows that A can be replaced by B also in the bodies of the rules from ${{\,\mathrm{\Rightarrow }\,}}$. $\square$

Due to the above result, causal equivalence of propositions can be used, in particular, for describing definitional extensions of the underlying language with new propositions (cf. (Turner, 1999)).

6 Structural equation models

Pearl’s approach to causal reasoning in the framework of structural equation models (see (Pearl, 2009)) can be viewed as an important instantiation of our general theory.

A structural equation model¹² is a triple $M=\langle U,V,F\rangle$, where

• U is a set of exogenous variables,

• V is a finite set $\{V_1,V_2,\dots , V_n\}$ of endogenous variables that are determined by other variables in $U\cup V$, and

• F is a set of functions $\{f_1,f_2,\dots , f_n\}$ such that each $f_i$ is a mapping from $U\cup (V{\setminus } V_i)$ to $V_i$, and the entire set, F, forms a mapping from U to V.

Symbolically, F can be represented as a set of structural equations

$$\begin{aligned} V_i = f_i(PA_i,U_i)\quad i = 1,\dots ,n, \end{aligned}$$

where $PA_i$ is the minimal set of variables in $V{\setminus }\{V_i\}$ (parents of $V_i$) sufficient for representing $f_i$, and similarly for the relevant set of exogenous variables $U_i\subseteq U$. Each such equation stands for a set of “structural” equalities

$$\begin{aligned} v_i = f_i(pa_i,u_i)\quad i = 1,\dots ,n, \end{aligned}$$

where $v_i$, $pa_i$ and $u_i$ are, respectively, particular instantiations of $V_i$, $PA_i$ and $U_i$. Such an equality assigns a specific value $v_i$ to a variable $V_i$ depending on the values of its parents and relevant exogenous variables.

In Pearl’s account, every instantiation $U = u$ of the exogenous variables determines a particular “causal world” of the structural model. Such worlds stand in one-to-one correspondence with the solutions to the above equations in the ordinary mathematical sense. However, structural equations also encode causal information in their very syntax by treating every instantiation of the variable on the left-hand side of the $=$ as effect and treating the corresponding instantiations of the variables on the right as causes.¹³ Accordingly, the equality signs in structural equations convey the asymmetrical relation of “is determined by.” This causal reading does not affect the set of solutions of a structural model, but it plays a crucial role in determining the effect of external interventions and evaluation of counterfactual assertions with respect to such a model (see Sect. 8 below).

Since structural models are formulated in the language of structural equations, their comprehensive logical description could be achieved only in the first-order language. The corresponding generalization of the causal calculus to a first-order language has actually been described in Lifschitz (1997). Still, for our current purposes we can obviate this limitation of our (propositional) formalism by considering the Herbrand base of this first-order language as our propositional language in this section. This Herbrand base consists of all propositions of the form $X=x$, where X is some (exogenous or endogenous) variable while x is its particular admissible value. In other words, admissible value assignments to exogenous and endogenous variables of the structural equations can be viewed as propositional atoms of the corresponding propositional language. In particular, instantiations of exogenous and endogenous variables will be called, respectively, exogenous and endogenous atoms.

Using the above formulation, the representation of Pearl’s structural models in the causal calculus, suggested in Bochman and Lifschitz (2015), amounted in effect to viewing each structural equality $v_i = f_i(pa_i,u_i)$ for a particular instantiation of the relevant variables as a causal rule saying that the instantiation $pa_i$ of the parent endogenous variables $PA_i$ and the instantiation $u_i$ of exogenous variables $U_i$ causes the instantiation $f_i(pa_i,u_i)$ of $V_i$:

$$\begin{aligned} PA_i=pa_i, U_i=u_i\ {{\,\mathrm{\Rightarrow }\,}}\ V_i=f_i(pa_i,u_i). \end{aligned}$$

In the special case when all the relevant variables are Boolean, a Boolean structural equation $p=F$ (where F is classical logical formula) produces in this sense two causal rules

$$\begin{aligned} F{{\,\mathrm{\Rightarrow }\,}}p\quad \hbox {and} \quad \lnot F{{\,\mathrm{\Rightarrow }\,}}\lnot p. \end{aligned}$$

It should also be required that instantiations of exogenous variables (i.e., exogenous atoms) are causal assumptions of the corresponding causal theory. In other words, for any exogenus atom $U=u$, we should accept the rule

$$\begin{aligned} U=u\ {{\,\mathrm{\Rightarrow }\,}}\ U=u. \end{aligned}$$

For Boolean exogenous variables, this amounts to adding the following two rules for any such variable:

$$\begin{aligned} p{{\,\mathrm{\Rightarrow }\,}}p\quad \hbox {and} \quad \lnot p{{\,\mathrm{\Rightarrow }\,}}\lnot p. \end{aligned}$$

Given this translation, it has been shown that Pearl’s causal worlds correspond precisely to classical causal models of the associated causal theory that are worlds (maximal classically consistent sets of propositions).

Example 4

The following set of (Boolean) structural equations provides a representation of Pearl’s example (see Example 1) in structural models:

$$\begin{aligned} Grasswet = Rained \vee Sprinkler\qquad Streetwet = Rained. \end{aligned}$$

If Rained and Sprinkler are taken to be exogenous variables, while Grasswet and Streetwet are endogenous ones, then the corresponding Pearl’s structural model will have the same causal worlds as the following causal theory:

$$\begin{aligned} Rained{{\,\mathrm{\Rightarrow }\,}}Grasswet\quad Sprinkler{{\,\mathrm{\Rightarrow }\,}}Grasswet\quad Rained{{\,\mathrm{\Rightarrow }\,}}Streetwet\\ \lnot Rained, \lnot Sprinkler{{\,\mathrm{\Rightarrow }\,}}\lnot Grasswet\quad \lnot Rained{{\,\mathrm{\Rightarrow }\,}}\lnot Streetwet \end{aligned}$$

with an additional stipulation that Rained, $\lnot Rained$, Sprinkler and $\lnot Sprinkler$ are assumptions:

$$\begin{aligned} Rained{{\,\mathrm{\Rightarrow }\,}}Rained\quad \lnot Rained{{\,\mathrm{\Rightarrow }\,}}\lnot Rained\\ Sprincler{{\,\mathrm{\Rightarrow }\,}}Sprinkler\quad \lnot Sprinkler{{\,\mathrm{\Rightarrow }\,}}\lnot Sprinkler \end{aligned}$$

Compared with our previous causal description of this example (see Example 3), the above causal theory contains additional causal rules, namely causal rules for the corresponding negative literals. As we will see, however, these negative causal rules can be reproduced using a systematic procedure called negative causal completion—see Sect. 11 below.

7 Defaults in causal reasoning

The causal calculus is a significant part of a general field of nonmonotonic reasoning in Artificial Intelligence. As such, it has been shown to cover other important parts of nonmonotonic reasoning such as abduction and diagnosis, logic programming, and reasoning about action and change. As a further illustration of its expressive capabilities, we will describe in this section a ‘causal counterpart’ of one of the key, original formalisms of nonmonotonic reasoning, default logic of Raymond Reiter (see (Reiter, 1980)). Among other things, the corresponding causal representation will also allow us to clarify the meaning of the main notions associated with default logic and first of all of the concept of default itself. This concept will also be shown to play, in turn, an important general role in causal reasoning.

7.1 Defaults versus facts

Default logic is based on the notion of default as its basic concept, so the task of describing default reasoning in causal terms cannot be achieved without a proper formalization of this notion.

Recall that causal assumptions are propositions that satisfy rules of the form $A{{\,\mathrm{\Rightarrow }\,}}A$. Such propositions can be accepted in a causal model (without further justification) whenever they are consistent with the rest of accepted propositions.

Now, defaults can be viewed as a special kind of assumptions. Under this understanding, the difference between defaults and causal assumptions in general can be informally described as follows: defaults are assumptions that we must accept unless there are reasons to the contrary.

In order to formulate this (normative) requirement in causal terms, let as say that a proposition A is rejected in a causal model if the model contains a cause for the contrary proposition $\lnot A$. Then we can formulate the following (still informal) principle of Default Acceptance:

• Default Acceptance A default is a causal assumption that is accepted whenever it is not rejected.

The principle of Default Acceptance could be viewed as an ‘anti-Leibniz’ principle since it says, in effect, that a default assumption is not accepted only if we have reasons for its rejection. Note, however, that the original Leibniz principle of sufficient reason should still remain to hold in causal models. In particular, a proposition $\lnot A$ is accepted in such a model only if it has a cause in this model (that is, when A is rejected). Accordingly, the principle of Default Acceptance in causal models boils down to the principle of Default Bivalence:

• Default Bivalence For any causal model v and any default assumption A, either $A\in v$ or $\lnot A\in v$.

The above principle of default bivalence can be considered as a characteristic property of defaults (as a special kind of assumptions). Again, this is in contrast with classical logical reasoning where all propositions are required to satisfy bivalence. Note also that any axiom of a causal theory will also be a default on this understanding (namely a default that cannot be refuted). In this sense, defaults can be viewed as an intermediate concept between axioms and causal assumptions in general.

Default reasoning as it is formalized in default logic amounts to deriving justified conclusions from a default theory by using its inference rules and default assumptions. However, in the case when the set of all defaults is jointly incompatible with the background theory, we must make a reasoned choice among the default assumptions. At this point, default reasoning requires that a reasonable set of defaults that can be actually used in this context not only should be consistent and maximal but also should explain why the rest of the default assumptions should be rejected. An important prerequisite of such explanations is that the underlying inference system contains cancellation rules by which some sets of defaults refute others (given the known facts). The appropriate choices of default assumptions (called stable sets) will determine then extensions of a default theory which are taken to constitute the (nonmonotonic) semantics of the latter.

Bipolarity Turning to the justification status of the rest of propositions in default logic, the notion of an extension of a default theory presupposes, in effect, that any such proposition should be accepted only if it is grounded, ultimately, in the set of accepted defaults. In other words, once we choose an acceptable (“stable”) set of default assumptions, the rest of acceptable propositions should be derived from this set. This pertains, in particular, even to other causal assumptions that could belong to a (causal) theory; any such assumption becomes unacceptable unless it is derived from accepted default assumptions.

The above stringent, ‘puritan’ understanding of acceptance for defaults and the rest of propositions creates, in effect, a bipolar system of reasoning that divides all propositions into two classes with opposite principles of acceptance. The first class contains factual propositions that are viewed as unacceptable unless they are derived from other propositions (and ultimately from accepted defaults), while the second class contains defaults that are viewed as acceptable unless they are refuted by other propositions (and, again, ultimately by other accepted defaults). It is this understanding that also makes default logic a principal instantiation of (assumption-based) argumentation Bondarenko et al. (1997) where defaults play the role of arguments.

7.2 Default causal theories

A formal representation of default logic in the causal calculus can be described as follows.

Definition 12

A default causal theory is a pair $(\Delta ,\mathcal {D})$, where $\Delta$ is a causal theory, and $\mathcal {D}$ a distinguished subset of its causal assumptions, called defaults.

In the formal descriptions below, ${{\,\mathrm{\mathcal {C}}\,}}_{\Delta }$ will denote the causal operator corresponding to the least supraclassical causal inference relation that contains a causal theory $\Delta$. Our next definition describes the intended semantics of a default causal theory.

Definition 13

• A default model of a default causal theory $(\Delta ,\mathcal {D})$ is a classical causal model m of $\Delta$ that satisfies the following two conditions:

  • (Default Grounding) m is caused by the set of its defaults:

    $$\begin{aligned}m={{\,\mathrm{\mathcal {C}}\,}}_{\Delta }(m\cap \mathcal {D}).\end{aligned}$$

  • (Default Bivalence) For any default $D\in \mathcal {D}$, either $D\in m$ or $\lnot D\in m$.

• A default semantics of a default causal theory is the set of all its default models.

It can be verified that if an arbitrary set m of propositions satisfies the condition of Default Grounding, it will already be a causal model of the corresponding causal theory $\Delta$, that is, $m={{\,\mathrm{\mathcal {C}}\,}}_{\Delta }(m)$ will hold. Consequently, the default semantics can be viewed as a special case of the general rational semantics of causal theories. Still, there are two reasons why the reverse inclusion does not hold in general. First, a causal model can be generated not only by defaults, but also by other causal assumptions. Second, even when a causal model is caused (generated) by some set of defaults, it may still not satisfy the second condition of the above definition, the principle of default bivalence. This might happen, in particular, even when the relevant set of generating defaults is maximal in the sense that it is incompatible with every other default outside this set, but the background causal theory lacks appropriate cancellation rules that would allow us to refute these other defaults. As an extreme case, a default causal theory may even lack default models at all (though it always has causal models).

The above formalism can be shown to provide an adequate description of default logic in the sense that there are back and forth translations between default causal theories and their default semantics and ‘plain’ default theories in default logic with their semantics of extensions (see (Bochman, 2023)).

By the above representation, default logic can be viewed as a species of general causal reasoning. However, its specific features make default logic less suitable for some applications in AI, such as abductive reasoning (and diagnosis), or reasoning about actions that seem to require the use of assumptions that are not defaults in the sense of default logic. Still, in many important areas using defaults instead of general causal assumptions results in a more adequate representation. For instance, even Pearl’s original approach to causal reasoning (see the preceding section) can be viewed as an instantiation of a default causal theory where exogenous atoms play the role of defaults, while endogenous atoms play the role of factual propositions. Moreover, the whole approach to causal reasoning in Bochman (2021) was essentially based on viewing causal rules themselves as default assumptions in the above sense.

7.3 Causal rules as defaults

Already David Hume argued in Hume (1978) that causal reasoning cannot be viewed as a kind of logical inference, because even the full knowledge of the causes is insufficient for inferring effects a priori. Hume has suggested that the “source” of our causal assertions can be found in the habit, or custom, of inferences that we make on the basis of invariable regularities (‘constant conjunctions’) that we have observed in our past experience. However, John S. Mill has added to this two further observations (see (Mill, 1872)). First, that not every Humean regularity determines a causal relation (for instance, the succession of day and night does not). According to Mill, only those regularities could serve this causal role that both invariably occur and are unconditional of any further circumstances. Still, Mill’s second important observation was that “all laws of causation are liable to be counteracted or frustrated”. Nevertheless, Mill has thought that the idea of an invariable and unconditional regularity (viewed as an explication of causality) can still be preserved if we define the cause as the “sum total of the conditions positive and negative taken together; the whole of the contingencies of every description, which being realised, the consequent invariably follows.”

The idea of laws as invariable, exceptionless regularities has been a received understanding for most of the past century (see, e.g., (Hempel, 1965)), until it has been qualified in studies of nonmonotonic reasoning in AI. One of the central objectives of the latter has become a formalization of defeasible reasoning, a kind of reasoning in which inference rules and their conclusions can occasionally be canceled, or defeated, in presence of other rules.

The phenomenon of defeasibilty is actually well known also in the causal literature under the names prevention and preemption. These are causal situations in which some causal rules become disabled, or ‘canceled’ due to other active causal rules.

The simplest way of dealing with defeasibilty in nonmonotonic formalisms (that has been actually employed in such formalisms as default logic, logic programming, and circumscription) amounts to adding auxiliary ‘presumptions’ to an inference rule such that only their refutation could lead to cancellation of the rule. Applying this method to causal reasoning, we can represent defeasible causal rules as rules of the form

$$\begin{aligned} C,n{{\,\mathrm{\Rightarrow }\,}}E, \end{aligned}$$

where n is a new proposition that refers to the underlying causal mechanism or process that, given an “input” C, produces an “output” E. These auxiliary premises can be viewed, however, as default assumptions, so they are presumptively accepted unless they are explicitly refuted. Accordingly, if the cause C is accepted, we are entitled (justified) to infer the effect E, unless n is refuted, that is, unless $\lnot n$ is caused. In the latter case, a rule $C,n{{\,\mathrm{\Rightarrow }\,}}E$ will be actually defeated even though the cause C will still be accepted.¹⁴

Remark

The default representation of defeasibilty provides a feasible and working account of the latter while preserving monotonicity of (causal) inference rules themselves, in contrast to popular alternative approaches that are based on a total rejection of monotonicity as a way of solving this problem. These latter approaches usually encounter an opposite problem, namely why an inference rule will (normally) continue to hold even when new facts are added to the description.

The above more ‘articulated’ representation of causal rules has been called a deep representation in Bochman (2021), whereas a representation that does not explicitly mention the underlying mechanisms has been called a surface representation. This terminology has been justified by the fact that, in most cases of interest, the names of mechanisms can be systematically eliminated (“forgotten”) without affecting the associated rational semantics, and thereby a deep representation can be transformed into some surface representation.

Example 5

In our running example, let as suppose that the sprinkler can also wet the street unless our garden is fully fenced. We can represent this causal situation by adding the following two causal rules to our causal theory from Example 3:

$$\begin{aligned} Sprinkler,n{{\,\mathrm{\Rightarrow }\,}}Streetwet\qquad Fenced{{\,\mathrm{\Rightarrow }\,}}\lnot n, \end{aligned}$$

where Fenced is a new causal assumption, whereas n is a default assumption about a physical process by which the sprinkler waters the street (in the absence of obstructions). Then the associated rational semantics will obtain a number of new causal models, in particular,

$$\begin{aligned} \{Sprinkler, Grasswet, Streetwet, n\}\\ \{Sprinkler, Grasswet, Fenced, \lnot n\}\\ \{Rained, Sprinkler, Grasswet, Streetwet, Fenced, \lnot n\} \end{aligned}$$

Still, it can be shown that (given some auxiliary conditions) default assumption n can be eliminated from this causal theory by replacing the above two rules with the following rule:

$$\begin{aligned} Sprinkler,\lnot Fenced{{\,\mathrm{\Rightarrow }\,}}Streetwet. \end{aligned}$$

The default formulation of causal rules creates immediate advantages for the representation of causal laws that has been a problem for the logic-based accounts. Moreover, it makes the representation of causal claims much similar to their commonsense language descriptions. It is perfectly legitimate to say that A’s blow caused B’s nose to bleed and to feel confidence in this statement, though we would find it difficult to formulate a general law purporting to specify conditions under which blows are invariably, or unconditionally, followed by bleeding from the nose (see (Hart & Honore, 1985)). Moreover, even in this simple case, there is a logical possibility that just at the moment A struck, B independently ruptured a blood vessel! In other words, even here our causal claim is only a (defeasible) assumption, though a very plausible one.

8 Counterfactual equivalence and basic inference

In structural equation models, the relation between causal theories and their (rational) semantics surfaces as the relation between causal and purely mathematical understanding of structural equations. Thus, as in the general case of causal theories, two informationally different sets of structural equations may “accidentally” determine the same causal worlds. And at this point, a key feature of Pearl’s approach to causal reasoning amounts to the assumption that the relevant differences between causal theories can be revealed by performing the same interventions (“surgeries”) on them.

According to Pearl, in order to obtain answers to intervention (action) and counterfactual queries, we have to consider submodels of a given structural causal model. Given a particular instantiation x of a subset X of endogenous variables from V, a submodel $M_x$ of a structural model M is the model obtained from M by replacing its set of functions F by the following set:

$$\begin{aligned} F_x = \{f_i\mid V_i\notin X\}\cup \{X=x\}. \end{aligned}$$

In other words, $F_x$ is formed by deleting from F all functions $f_i$ corresponding to members of the set X and replacing them with the set of constant functions $X=x$. A submodel $M_x$ can be viewed as a result of performing an action $do(X=x)$ on M that produces a minimal change required to make $X=x$ hold true under any u. This submodel is used in Pearl’s theory for evaluating counterfactuals of the form, “Had X been x, whether $Y=y$ would hold?”

In order to simplify exposition, we will restrict the description below to the Boolean case. Then the corresponding transformation of causal theories can be described as follows:

Definition 14

For a causal theory $\Delta$ and a set L of literals, a revision $\Delta {*}L$ of $\Delta$ with L is a causal theory obtained from $\Delta$ by removing first all causal rules having either literals from L or their negations in heads, and then adding L as a set of new axioms (that is, adding rules $\textbf{t}{{\,\mathrm{\Rightarrow }\,}}l$ for each $l\in L$).

It can be verified that revisions of causal theories exactly correspond to submodels of Boolean structural models.

According to Pearl, every structural model stands not for just one but for a whole set of its submodels that embody interventional contingencies. These submodels determine the “causal content” of a given structural model in Pearl’s approach. In accordance with that, we can introduce the following definition:

Definition 15

Causal theories $\Gamma$ and $\Delta$ are intervention-equivalent if, for every set L of literals, the revision $\Gamma {*}L$ has the same causal worlds as the revision $\Delta {*}L$.

Now, at least in the finite case, it can be shown that intervention-equivalence of two causal theories amounts to coincidence of their associated causal counterfactuals (see (Bochman, 2021)).

The above considerations naturally suggest that Pearl’s approach is based on a particular account of causation according to which the content of a causal theory is fully determined by its ‘counterfactual profile’. In this sense, the approach can even be viewed as a further development of the counterfactual approach to causal reasoning initiated by David Lewis in Lewis (1973).

Recall that the connection between causal inference relations and a rational semantics of causal theories has been established via the notion of strong semantic equivalence, namely semantic equivalence that is preserved under addition of further rules to a causal theory. Taken in this perspective, the difference between our approach and that of Pearl amounts to taking intervention-equivalence instead of strong semantic equivalence as a basic information concept for causal theories. This alternative notion of equivalence sanctions, however, a somewhat different logic for causal reasoning.

8.1 Basic causal inference

It turns out that the Cut rule of causal inference does not preserve intervention-equivalence: there are causal theories that are equivalent with respect to supraclassical causal inference, but their revisions with the same literals determine different causal worlds (and different counterfactuals). In order to cope with this situation, we have to modify our postulates of causal inference.¹⁵

Definition 16

• A set of causal rules in a classical language will be called a causal production relation if it satisfies all the postulates of supraclassical causal inference except Cut.

• A causal production relation will be called basic if it satisfies the rule:

  (Or):

     If $A{{\,\mathrm{\Rightarrow }\,}}C$ and $B{{\,\mathrm{\Rightarrow }\,}}C$, then $A\vee B{{\,\mathrm{\Rightarrow }\,}}C$.

The postulate Or sanctions reasoning by cases for causal rules. Now, as follows from the above definition, basic inference is obtained from supraclassical causal inference by replacing the Cut postulate with Or. A detailed description of this kind of causal inference and its connections with other nonmonotonic formalisms in AI has been given in Bochman (2004, 2005). It has been shown, in particular, that this kind of inference can already be given a logical interpretation in possible worlds models; by this interpretation, a causal rule $A{{\,\mathrm{\Rightarrow }\,}}B$ is representable as a modal conditional

$$\begin{aligned}A\rightarrow \square B,\end{aligned}$$

where $\square$ is the usual necessity operator (see also (Turner, 1999)).

The above modal representation makes it a relatively easy task to study the properties of basic inference. It allows us to explain, in particular, why it does not satisfy Cut. In fact, basic inference is not even a transitive relation.

It has been shown in Bochman (2018) that basic inference constitutes, in effect, the internal logic of causal reasoning in Pearl’s causal models. More precisely, it has been shown that basically equivalent causal theories are intervention equivalent. Moreover, the reverse implication has been shown to hold for the special case of Pearl’s causal theories, that is, for causal theories obtained from structural equation models by the translation of Bochman and Lifschitz (2015). Some consequences of this correspondence have been discussed in Bochman (2021) in the context of analyzing different approaches to the notion of actual causality.

9 Classical causal inference and causal worlds

The differences between Pearl’s approach and our theory disappear, however, once we restrict our rational semantics to causal models that are worlds (in the usual classical meaning of the term). Note, however, that this move amounts to imposing Bivalence on the set of accepted propositions.

Definition 17

• A causal world of a causal theory $\Delta$ is a classical causal model of $\Delta$ which is also a world (maximal classically consistent set).

• A rational classical semantics of a causal theory is the set of all its causal worlds.

The above notion of rational classical semantics moves us one last step closer to the traditional correspondence semantics. Nevertheless, the distinction between rational and purely logical semantics remains, since even the rational classical semantics is still nonmonotonic with respect to the source causal theory, so the latter is not determined by the former.

It has been shown in Bochman (2004) that the postulate Or becomes an admissible derivation rule with respect to the world-based rational semantics.

Definition 18

A causal inference relation will be called classical if it is supraclassical and satisfies Or.

Classical causal inference combines the properties of both basic and supraclassical causal inference. In particular, the causal rules of such an inference inherit a logical semantics in the modal framework of possible worlds, in which they are interpreted as modal conditionals $A\rightarrow \square B$.

The following result will show that classical causal inference provides an adequate framework of reasoning with respect to the rational classical semantics. As before, we introduce first the following definitions:

Definition 19

Causal theories $\Gamma$ and $\Delta$ will be called

• (strongly) objectively equivalent if they are (strongly) semantically equivalent with respect to the rational classical semantics;

• c-equivalent if they determine the same classical causal inference relation.

Two causal theories are c-equivalent if each theory can be obtained from the other using derivation rules of classical causal inference relations. Then the following result demonstrates that classical causal inference is adequate for the rational classical semantics.

Theorem 11

Two causal theories are strongly objectively equivalent if and only if they are c-equivalent.

9.1 Factual and explanatory content of causal rules

In the framework of classical causal inference, the content of causal rules can be given a more fine-grained description.

Recall that causal rules serve two functional roles in a rational semantics. First, they propagate acceptance from their premises to their conclusions and thereby determine ordinary ‘deductive’ constraints on possible valuations. Their second function consists, however, in providing reasons, or explanations, for accepted propositions. Fortunately, these two roles can be separated in classical causal reasoning by decomposing any causal rule into a (factual) constraint and an explanation. More precisely, we have the following decomposition of causal rules:

Lemma 12

Any causal rule $A{{\,\mathrm{\Rightarrow }\,}}B$ is c-equivalent to a pair of rules

$A\wedge \lnot B{{\,\mathrm{\Rightarrow }\,}}\textbf{f}$ and $A\wedge B{{\,\mathrm{\Rightarrow }\,}}B$.

Proof

$A\wedge B\wedge \lnot B{{\,\mathrm{\Rightarrow }\,}}\textbf{f}$ by Falsity and Strengthening, and therefore $A{{\,\mathrm{\Rightarrow }\,}}B$ implies $A\wedge \lnot B{{\,\mathrm{\Rightarrow }\,}}\textbf{f}$ by Cut. In the other direction, if $A\wedge \lnot B{{\,\mathrm{\Rightarrow }\,}}\textbf{f}$ and $A\wedge B{{\,\mathrm{\Rightarrow }\,}}B$, then $A\wedge \lnot B{{\,\mathrm{\Rightarrow }\,}}B$ by Weakening, and hence $A{{\,\mathrm{\Rightarrow }\,}}B$ by Or. $\square$

A rule $A\wedge \lnot B{{\,\mathrm{\Rightarrow }\,}}\textbf{f}$ is a reductio ad absurdum constraint saying that proposition $A\wedge \lnot B$ is unacceptable. This implies, in particular, that classical implication $A\rightarrow B$ should hold in any causal world. Such a constraint provides, however, only purely factual information in causal reasoning that cannot be used, for instance, for deriving new causal rules in a causal theory. These constraints only restrict the set of models that are admissible (causally consistent) with respect to a causal theory. In this sense they play the role of ordinary classical formulas, namely they just express facts. However, they do not justify, or explain, anything, and hence they can be seen as devoid of explanatory content.

In contrast, causal rules of the form $A\wedge B{{\,\mathrm{\Rightarrow }\,}}B$ are deductively (‘factually’) trivial, since they do not impose restrictions on admissible models. Nevertheless, they play an important explanatory role in causal reasoning. Namely, such a rule says that, in any causal model in which A is already accepted, we can freely accept B, since it is self-explanatory in this context. Accordingly, such rules can be called (purely) explanatory rules.

Remark

Explanatory causal rules could also be viewed as weak causal claims by which the cause does not necessitate the effect, though it can explain why it occurred (cf. (Anscombe, 1981)). Using an old example from the causal literature, syphilis does not always cause paresis, though it is a reasonable explanation of why it happened.

Now the above lemma says that any causal rule can be decomposed into a factual constraint and an explanatory rule. This decomposition neatly delineates two kinds of information conveyed by causal rules. One is factual information that constraints the set of admissible models, while the other is explanatory information describing what propositions are caused (explainable) in such models. Moreover, the decomposition shows that these two kinds of content are actually independent of each other, so the full informational content of causal theories can be safely represented as a (disjoint) union of their factual and explanatory contents.

The interplay of the factual and explanatory contents determines, eventually, the properties of the associated rational semantics. It is responsible, in particular, for the nonmonotonic character of the latter. Namely, nonmonotonicity arises from the fact that these two kinds of content have opposite impacts on acceptance of propositions. Thus, addition of constraints leads, as expected, to reduction of the set of admissible causal models (and hence to increase of factual information). However, the addition of explanatory rules leads, in general, to increase of admissible causal models, and hence to decrease of derived factual information.

9.2 Propositional completion of causal theories

The overwhelming majority of applications of causal reasoning in AI and beyond make use of only a restricted form of causal rules, often called determinate rules, and there are deep reasons for this restriction that are grounded in the very notion of determinism.

Definition 20

• A causal rule is determinate if it has the form $A{{\,\mathrm{\Rightarrow }\,}}l$, where l is a literal or falsity $\textbf{f}$. A causal theory is called determinate if it contains only determinate rules.

• A causal theory is definite if it is determinate and any propositional atom appears in heads of no more than a finite number of its causal rules.

It has been established already in McCain and Turner (1997) that the rational classical semantics of a definite causal theory (being just a particular set of classical worlds) coincides with the fully classical semantics of a certain derived set of classical formulas called a propositional completion of this causal theory.

Given a definite causal theory $\Delta$, we can define its propositional completion $comp(\Delta )$, as the set of all classical formulas of the form

$$\begin{aligned}l\leftrightarrow \bigvee \{A\mid A{{\,\mathrm{\Rightarrow }\,}}l\in \Delta \},\end{aligned}$$

where l is either a literal or falsity $\textbf{f}$. Then the following result shows that the classical models of $comp(\Delta )$ precisely correspond to causal worlds of $\Delta$.

Theorem 13

Rational classical semantics of a definite causal theory coincides with classical logical semantics of its completion.

Example 6

Using once more our running Pearl’s example, the causal theory from Example 4 has the following propositional completion:

$$\begin{aligned} Grasswet\leftrightarrow (Rained\vee Sprinkler)\\ \lnot Grasswet\leftrightarrow (\lnot Rained\wedge \lnot Sprinkler)\\ Streetwet\leftrightarrow Rained\\ \lnot Streetwet\leftrightarrow \lnot Rained \end{aligned}$$

By the above theorem, the models of this classical propositional theory will coincide with the causal worlds of the original causal theory.

Yet another observation that could be made about the above propositional completion is that the conditions for the negative literals $\lnot Grasswet$ and $\lnot Streetwet$ are actually derivable from the conditions for the corresponding positive literals, so the above propositional theory is logically reducible to

$$\begin{aligned} Grasswet\leftrightarrow (Rained\vee Sprinkler)\qquad Streetwet\leftrightarrow Rained \end{aligned}$$

Actually, this is yet another consequence of a more general fact that the negative causal rules of the original causal theory can be derived from the corresponding positive rules using negative causal completion—see Sect. 11 below.

An important practical consequence of the above theorem is the possibility of using standard logical tools in computing the causal semantics. Still, it should be kept in mind that the above construction of propositional completion is global (holist) with respect to the original causal theory, so it could change nonmonotonically with addition of further causal rules. That is why even in the context of classical causal inference, deduction cannot replace causal reasoning.

10 Default negation and logic programming

The problem of representing negation has emerged as one of the main problems of nonmonotonic reasoning, and it has immediate implications for causal reasoning. Accordingly, a proper treatment of negation in causal contexts can be viewed as an important part of an adequate analysis of causal reasoning in general.

So far, we have largely ignored the distinction between positive and negative propositions and have treated both indiscriminately. This uniformity could even be viewed as a significant theoretical advantage, and adherents of many traditional approaches to reasoning in general and causality in particular have justly celebrated it.

A large group of philosophers has rejected, however, this generalization of causal relation to absences and negation, or at least its uniformity, though for varying reasons. Beside some general metaphysical and conceptual objections, the corresponding studies have pointed out some important differences between these two kinds of causal assertions, as well as specific difficulties that arise in interpreting and justifying negative causal claims.

It turns out that even the formalism of classical causal inference still has required ‘degrees of freedom’ that allow us to formalize an important alternative understanding of negation, namely the concept of default negation. The latter is based on the idea that a negative proposition can be accepted whenever we do not have reasons for accepting the corresponding positive proposition.¹⁶ In this respect, the rational semantics complements this idea in that it embodies a particular, causal closed world assumption, according to which the current causal theory provides an exhaustive description of all the causal factors that could be used as a reason for acceptance of propositions in a model.

The above notion of default negation allows us to provide a causal representation of yet another key formalism of nonmonotonic reasoning in AI - logic programming. On the causal interpretation described below, any general logic program can be seen as a causal theory satisfying the principle of negation as default (alias the closed world assumption). Moreover, given this principle, the correspondence between logic programs and causal theories will turn out to be bidirectional in the sense that any causal theory is reducible to some logic program. A more detailed description of this correspondence as well as corresponding proofs can be found in Bochman (2005).

Speaking generally, the causal interpretation of logic programs is based on a recurrent idea that logic program rules provide definitions for the literals in their heads. The declarative meaning of logic programs in modern logic programming involves, however, an additional component: namely, an asymmetric treatment of positive and negative information, which is reflected in viewing the corresponding negation operator ${{\,\mathrm{\textbf{not}}\,}}$ appearing in program rules as negation as failure (see, e.g., (Baral, 2003; Lifschitz, 2019)). It turns out that such an understanding can be uniformly captured in our theory by accepting the Default Negation postulate below that gives a formal expression to the closed world assumption.

Definition 21

A classical causal inference relation will be called negatively closed, if it satisfies

• (Default Negation)    $\lnot p{{\,\mathrm{\Rightarrow }\,}}\lnot p$, for any propositional atom p.

The above principle makes negations of atomic propositions causal assumptions in the corresponding causal inference relation. Moreover, given Bivalence (that holds for causal worlds), the Default Negation postulate stipulates, in effect, that negations of atomic propositions are defaults. As a result, the principle of sufficient reason is reduced in such systems to the necessity of explaining only positive facts. The postulate can be seen as giving a formal expression to Reiter’s closed world assumption from Reiter (1978) and reflects the main distinctive feature of reasoning behind logic programs and databases.

A logic program $\Pi$ (see (Baral, 2003)) is a set of program rules of the form

$$\begin{aligned} {{\,\mathrm{\textbf{not}}\,}}d,c\leftarrow a,{{\,\mathrm{\textbf{not}}\,}}b \end{aligned}$$

(*)

where a, b, c, d are finite sets of propositional atoms.

Now, a stable causal interpretation of logic programs amounts to interpreting every program rule (*) as the following causal rule:

$$\begin{aligned} d,\lnot b{{\,\mathrm{\Rightarrow }\,}}\bigwedge a\rightarrow \bigvee c. \end{aligned}$$

Then it can be shown that a stable semantics of a program $\Pi$ coincides with the classical causal semantics of its translation. In addition, it can be shown that negatively closed causal inference relations constitute precise causal logic behind stable logic programming. Moreover, any causal rule can be identified with some program rule under this interpretation. Accordingly, any causal theory in which negated atoms are defaults is reducible to a logic program, and vice versa.

11 Negative causal completion

The concept of negation as default (which is formalized in logic programming) covers a significant portion of our understanding and use of negation in local situations. Still, it does not fully reflect the behavior of negation in the context of causal reasoning. The difference can be roughly described as follows. When negation is viewed as default, negative propositions are exempted from the need of causal explanation; in other words, they do not need causes for their acceptance. The only thing we should care about is consistency of such negative propositions with other, positive assertions and known causal rules. Explanatory rules $\lnot p{{\,\mathrm{\Rightarrow }\,}}\lnot p$ provide precisely this functionality. Commonsense causal reasoning, however, tends to preserve the symmetry between positive and negative assertions and treat also the latter as something that can be caused and be causes themselves. For instance, a fully symmetric treatment of positive and negative propositions is implicit in Pearl’s approach to causality (at least in the Boolean case).

From now on, we will restrict our attention to determinate causal theories that involve only literals in the heads of their rules. For this case, a certain mix of the above two views of negation suggests itself.¹⁷ It will be called the principle of negative causation.

Definition 22

(Negative Causation Principle) A causal rule $B{{\,\mathrm{\Rightarrow }\,}}\lnot p$ is acceptable with respect to a determinate causal theory $\Delta$ if any causal rule of the form $A{{\,\mathrm{\Rightarrow }\,}}p$ that belongs to $\Delta$ is such that A is (classically) incompatible with B.

According to this principle, B causes $\lnot p$ when it undermines all potential causes of p in $\Delta$. In some sense, this principle could be viewed as a “positive” reformulation of the ancient principle ex nihilo nihil fit, namely,

Negation (absence) of effects follows from negation (absence) of causes.

Note that, like the concept of default negation itself, this principle is also nonmonotonic: an acceptable negative causal claim can become unacceptable with an addition of new positive causal rules to the causal theory.

The above principle of negative causation is actually directly encoded in Pearl’s structural approach to causality (when applied to Boolean endogenous variables). It is also compatible, however, with philosophical approaches to causality according to which positive causation (or causation between real events) is the only “genuine” causation, whereas negative causation is, at best, a derivative notion (see, e.g., (Armstrong, 1997) and (Dowe, 2000)).

Now, the following completion construction is based on an idea that default negation can be captured ‘causally’ (or inferentially) by adding to a positive causal theory all acceptable rules of negative causation.

Let $A_p$ denote the disjunction of all bodies of the rules from a causal theory $\Delta$ that have an atomic proposition p as its head, that is

$$\begin{aligned} A_p=\bigvee \{C\mid C{{\,\mathrm{\Rightarrow }\,}}p\in \Delta \}. \end{aligned}$$

Note that $B{{\,\mathrm{\Rightarrow }\,}}\lnot p$ is an acceptable rule if and only if B is incompatible with $A_p$. Accordingly, all acceptable negative causal rules are subsumed by rules of the form $\lnot A_p{{\,\mathrm{\Rightarrow }\,}}\lnot p$ for each atom p. This sanctions the following notion of negative completion:

Definition 23

A negative causal completion of a definite causal theory $\Delta$ is a causal theory $Nc(\Delta )$ obtained from $\Delta$ by adding rules of the form

$$\begin{aligned} \lnot A_p{{\,\mathrm{\Rightarrow }\,}}\lnot p, \end{aligned}$$

for all atoms p that appear in the heads of causal rules from $\Delta$.

Negative completion can be used for completing positive causal theories that do not contain negative literals in the heads of their rules.

Example 7

It can be verified that the ‘full’ causal theory for Pearl’s example (see Example 4) can be obtained as a negative causal completion of the positive causal theory from Example 3. Indeed, if we take the three rules

$$\begin{aligned} Rained{{\,\mathrm{\Rightarrow }\,}}Grasswet\quad Sprinkler{{\,\mathrm{\Rightarrow }\,}}Grasswet\quad Rained{{\,\mathrm{\Rightarrow }\,}}Streetwet \end{aligned}$$

and apply Definition 23 to them, we obtain the following negative causal rules:

$$\begin{aligned} \lnot Rained, \lnot Sprinkler{{\,\mathrm{\Rightarrow }\,}}\lnot Grasswet\quad \lnot Rained{{\,\mathrm{\Rightarrow }\,}}\lnot Streetwet. \end{aligned}$$

Moreover, the same construction makes $\lnot Sprinkler$ and $\lnot Rained$ causal assumptions on the basis of the fact that Sprinkler and Rained are assumptions of the original positive theory.

12 Conclusions

The causal calculus is a working theory of causal reasoning which has been shown to provide a formal basis for reasoning and problem-solving in many areas, especially in AI, but also in legal theory and dynamic reasoning. This theory provides also a formal representation for Pearl’s approach to causation and thereby suggests itself as a natural basis for a unified approach to causal reasoning.

The theory of causal reasoning described in this study poses, however, a lot of questions for a general theory of reasoning. The causal calculus is primarily an inferential, rule-based formalism in which the language determines its associated semantics, but the latter does not determine the original language. Already this asymmetry should force us to reconsider the basic notions associated with representational approaches such as the meaning/reference of language expressions in the context of causal reasoning. In this respect, our inferential theory shares many features as well as problems with the modern proof-theoretic approach to language and semantics (see, e.g., (Schroeder-Heister, 2012)). However, it is also an essentially nonmonotonic formalism, and this puts into question, for instance, the very possibility, or even desirability, of constructing a causal reasoning system or its semantics bottom up from propositional atoms. Thus, we have employed a global, holist approach to incorporating classical entailment into causal reasoning. Though this construction is obviously deviant from standard ways of describing logical reasoning formalisms, it nevertheless provides all that is needed for an efficient use of such a combined causal reasoning in applications, including derivations of conclusions and computation of the corresponding models. Actual work with this formalism could defuse the suspicion that it is somehow deficient or flawed in this respect. This construction distinguishes our theory, however, from standard proof-theoretic approaches that attempt to provide a reductionist inferential description of logical connectives in terms of associated introduction and elimination rules.

In a more general perspective, the miracle of resurrection of causal reasoning in artificial intelligence and other important fields of science confirms once again that causation should be viewed as an essential part of our reasoning, a kind of reasoning that has deep, though almost forgotten, roots in human history. Our inferential approach to causation largely endorses Elizabeth Anscombe’s claim that causality consists in the derivativeness of an effect from its causes (see (Anscombe, 1981)), and it goes back as far as to Aristotle’s theory of causal demonstrations as a special kind of syllogisms (deductions), to Leibniz’s obliteration of the distinction between reasons and causes, and even to Hume’s views of inference as an ‘impression source’ of causation. This view of causal reasoning provides also natural connections of our theory with a general approach of inferentialism (see, e.g., (Peregrin, 2014)), or at least with a version of it that (in contrast to Sellars and Brandom) does not put conceptual barriers between causal and inferential (normative). But all this should be a subject of an entirely different study.