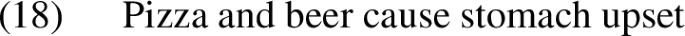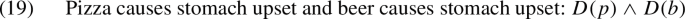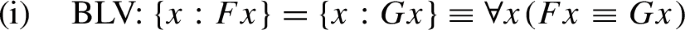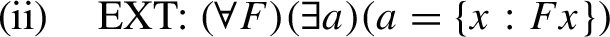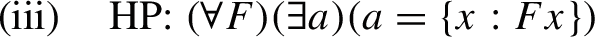Abstract
Although number sentences are ostensibly simple, familiar, and applicable, the justification for our arithmetical beliefs has been considered mysterious by the philosophical tradition. In this paper, I argue that such a mystery is due to a preconception of two realities, one mathematical and one nonmathematical, which are alien to each other. My proposal shows that the theory of numbers as properties entails a homogeneous domain in which arithmetical and nonmathematical truth occur. As a result, the possibility of arithmetical knowledge is simply a consequence of the possibility of ordinary knowledge.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
There are numerous reasons to affirm that mathematical knowledge is possible. Nonetheless, the feasibility of a satisfactory explanation of mathematical knowledge has been seriously questioned in the specialized literature. On the one hand, in contrast to other knowledge domains, mathematics enjoy a high applicability rate. On the other hand, our perceptual limitations concerning the content of mathematical statements have induced several difficulties in explaining arithmetical knowledge. An explanation of why the statement ‘2+2=4’ is true and the statement ‘2+2=5’ is false would justify our belief that two plus two equals four and not five. Without such an explanation, the question remains as to how we justify that belief. More generally speaking, what is the basis for our claim that mathematical knowledge is possible? This paper addresses this question for the particular case of arithmetic, accounting for the possibility of arithmetical knowledge.
The current work is organized into three stages. In \(\mathsection \)2, I present the problem of arithmetical truth in the framework of Benacerraf’s dilemma and show in what sense different theories have addressed it. As I argue, the main drawback of this dilemma is that it involves theoretical assumptions that can be easily challenged. Rejecting those assumptions has allowed several answers to appear satisfactory despite failing to show the possibility of arithmetical knowledge. In \(\mathsection \)3, I introduce two homogeneity conditions for truth and knowledge. These conditions result from getting rid of most of the theoretical preconceptions, preserving the fundamental concerns that underlie the problem raised by Benacerraf. Namely, the fact that the impossibility of arithmetical knowledge is a consequence of assuming two different and alien realities, one mathematical and the other nonmathematical, in which the nature of truth, and therefore, of knowledge would be irreconcilably different. To conclude, in \(\mathsection \)4, I outline my theory of numbers as properties and show that it lays the groundwork to meet the homogeneity conditions. In this sense, I offer a language of properties that reveals that arithmetic and nonmathematical number-sentences admit the same type of constructions. I argue that admitting the possibility of nonmathematical knowledge requires admitting the possibility of knowledge of properties. If numbers are properties similar to those regarded in nonmathematical discourse, the possibility of nonmathematical knowledge entails the possibility of arithmetical knowledge.
While the traditional theories fail to meet the homogeneity conditions, the theory of numbers as properties succeeds, showing that arithmetical knowledge is possible and explaining how it is possible.
2 Benacerraf and the traditional strategy
In his most influential work, Benacerraf (1973) claims that, on the one hand, if numbers exist, we are causally isolated from them. Since our most familiar knowledge acquisitions require causal interactions, the realist faces the challenge of accounting for the possibility of mathematical knowledge. This problem leads him to conclude that from a realist view, mathematical knowledge is impossible (p.671). On the other hand, an antirealist about numbers rejects that arithmetical sentences are true in virtue of facts about the denotations of their singular terms and predicates. Since there are no numbers, they cannot be the denotations of the arithmetical sentences’ singular terms. According to Benacerraf, this thesis differs from the explanation of the truth of most sentences. A satisfactory semantics for mathematical language must not be discordant with a satisfactory semantics for ordinary language. The conspicuous dilemma is that either numbers do not exist and the arithmetical semantics is unsatisfactory, or numbers exist and our epistemology is unsatisfactory for arithmetic. This argument has given rise to countless works favoring each of the positions involved in the debate. Nevertheless, as I argue, the theories provided do not address the more in-depth concerns that the dilemma embodies.
Benacerraf’s dilemma has not become obsolete because, in the face of a significant number of answers, the same difficulties arise repeatedly. Some widely accepted theories in the tradition are still a potential target of the original criticisms. For example, Shapiro’s structuralism describes natural numbers as a structure—the abstract form of a system (Shapiro 1983, p. 74). This idea conflicts with the intuition that knowledge in everyday life is not primarily about abstract structures of systems. The contrast suggests that arithmetical knowledge requires a singular epistemology, which guarantees access to entities that are not frequent (if any) in nonmathematical contexts. Unfortunately, the view does not address the critical problem underlying the dilemma—beyond the particular assumptions of the original formulation, the core of the problem is that a satisfactory epistemology must work for all knowable domains. In other words, the ontology of each of these domains must be in such a way that it appropriately admits the best accepted epistemological assessments in order to make the corresponding knowledge ascriptions. Ultimately, the nature of things determines how we know them. Admittedly, the structuralist may propose a comprehensive structuralist ontology, but this option does not seem to achieve the acceptance of the majority. On the other hand, fitting structuralism into a causal epistemology requires convoluted explanations that might not work with everyday knowledge.
The rejection of particular epistemological and semantic theories has become systemic in this debate. A realist may argue that Benacerraf’s argument entails that it would be impossible to know about anything causally isolated from us (p. 671). After all, there are many other counterexamples to reject a crude causal epistemology. The antirealist may perform the equivalent strategy from the other horn of the dilemma. Benacerraf suggests that Tarski’s semantics counts as satisfactory (p. 667), but this claim can easily be rejected.
The traditional strategy is based on theories of mathematical truth that reconcile a particular epistemology and semantics (consider, for example, (Maddy, 1980; Field, 1980; Maddy, 1981; Shapiro, 1983; Field, 1989; Balaguer, 1995, 1998), among others). Not surprisingly, as long as there are no conclusive accounts of general truth and our knowledge of it, traditional strategy theories continue to be discarded. These theories are usually developed by adopting one of the two conditions imposed by Benacerraf and rejecting the other. Either way, such explanations imply a commitment to specific theories of truth and knowledge.Footnote 1 The debate suggests that the solution to the problem for a theory of mathematical truth should be free of commitments to particular epistemic or semantic accounts. To this extent, my argument begins by clarifying the underlying concerns that give rise to the problem raised by Benacerraf. The analysis entails two conditions that specify a basis of minimum homogeneity grounded in one reality (which may well be populated by entities of a diverse nature). Once we consider numbers as attributive properties of multiplicity, the dilemma is not resolved but dissolved.
3 Homogeneity conditions
In order to capture Benacerraf’s substantial concerns, I present two homogeneity conditions that aim to eliminate as many theoretical assumptions as possible from the original formulation. The homogeneity conditions seek to smooth out the common ground to provide a satisfactory account of arithmetical truth. To this end, addressing the most relevant considerations of each competing position is imperative. On the one hand, the antirealist argues that a standard account posits unnecessary entities, thus sacrificing ontological parsimony. In contrast, the realist claims that a combinatorial theoryFootnote 2 introduces different theories of truth, sacrificing theoretical economy. Benacerraf’s argument reveals that the cost of the antirealist ontological parsimony plus the realist theoretical economy is unaffordable. In other words, the solution to the difficulty should go through a balance in which the explanatory power of each position is maximized, reducing its cost. A satisfactory explanation of numbers must meet the following homogeneity conditions. (As shown in different works, e.g., Clarke–Doane (2017) and Topey (2020), the tension discussed here arises in varied domains. My interest is in natural numbers but the homogeneity conditions can also be considered for other abstract entities.)
3.1 The semantic homogeneity condition
In discussing the example of an anti-Platonist view, Benacerraf addresses combinatorialism, whose main thesis is that truth-values are to be assigned to mathematical sentences on the basis of syntactic features about them (where these are usually proof theoretic). According to Benacerraf, assuming that we have a satisfactory semantics for nonmathematical sentences, the combinatorialist would have a problem due to the contrast between the two kinds of accounts. Compare for example:

with

In (1), the truth conditions are given in terms of the denotations of the singular terms and predicates. In contrast, (2) doesn’t seem to preserve the analysis of truth in terms of ‘referential’ concepts of naming, predication, satisfaction, and quantification. Admittedly, the combinatorialist might question whether this kind of explanation provides satisfactory semantics even for ordinary language. However, this question misses the point. An explanation in terms of ‘referential’ concepts of naming, predication, satisfaction, and quantification may be rejected, but the relationship between concrete objects and the true statements about them remains to be explained. An alternative semantic account must still be offered and the new theory envisioned for ordinary language would also have to fit the combinatorialist thesis.
The notion of truth is determined by conditions that may or may not be satisfied by sentences within a language. Suppose the truth conditions of mathematical sentences differ entirely from the truth conditions of ordinary sentences.Footnote 3 Here Benacerraf’s concern takes the whole place. In that case, we have that the interpretation of mathematical statements radically differs from that of nonmathematical statements for semantic or syntactic reasons. Given that the statements are of the same form in both contexts, the difference between both interpretations would reflect a more profound difference in their truth conditions. But what else, if not the truth conditions, determines the nature of truth itself? The concern arises about how discrepancies in truth conditions between mathematical and non-mathematical discourses may affect the very conception of mathematical truth.Footnote 4.
Intuitively we think that something (perhaps a very minimal aspect) is shared between what we consider to be true within mathematics and what we consider to be true outside of it. There may well be differences in our explanations across different contexts, but these differences should emerge at the level of the analyses of the denotations of the singular terms and predicates. Compare: how different can the truth conditions for sentences about Aristotle be from the truth conditions for sentences about the Moon? There is just one explanation of truth here, even though there are different explanations for the truth of ‘Aristotle was born in Stagira’ and ‘the Moon is 384,400 kms from the Earth’. Whatever these differences are, they emerge at the level of the analyses of ‘Aristotle’, ‘born in’, ‘Moon’, ‘kilometer’, etcetera. An equivalent contrast comes into place for the case of mathematical objects. An explanation of the mathematical sentences’ truth should tolerate differences in content only to the extent that it does not clash with our most basic intuitions about truth.
Accepting only one truth (that may well be highly tolerant to variations regarding particular contexts) sets a standard of minimal homogeneity, which has a cost lower than the commitments entailed by particular semantics. The following condition captures this idea:

Despite its particularities, semantics should preserve the intuition that the explanation of truth for the relevant fragment of language reflects (in some sense) that sentences contain terms whose function is to select what the sentence is about, setting conditions to specify how things have to be for the sentence to be true. Consider the following:

If I complain that (3) is false, I am doing so because I believe that what the sentence conveys does not correspond to the facts about the Jets and the 2021 Super Bowl (the Jets did not even make the playoffs),Footnote 5. Similarly, if I complain that

is false, I am doing so because I believe that what (4) says somehow does not correspond to some kind of facts about 126 and 5. A homogeneous semantics requires a language with no fundamental differences between the terms that occur in statements such as (3) and those in sentences such as (4).
3.2 The epistemic homogeneity condition
Consider the prominent realist position, Standard Platonism. According to this view, numbers exist. They are abstract, mind-independent objects, and these objects and their relations are the truthmakers of arithmetical sentences. In order to know whether arithmetical sentences are true, we need to know something about their truthmakers. Since we are not causally connected to abstract objects, our explanation of knowledge of sentences such as

differs from that of sentences such as

Intuitively, we can know that (6) is true because our causal connections with Pete Townshend and his family let us realize that the object (Pete) belongs to the class of things with the property the oldest son of Cliff Townshend. However, this causal avenue of knowledge is closed off if numbers are abstract objects. So we cannot know numbers if the Standard Platonist is right. This difference challenges the idea of a mathematical truth account that meshes with a reasonable epistemology. According to Benacerraf:
The concept of mathematical truth, as explicated, must fit into an over–all account of knowledge in a way that makes it intelligible how we have the mathematical knowledge that we have. [p. 667]
As many have argued,Footnote 6 there is no reason to assume that the causal avenue is the only avenue to knowledge. Still, the causal isolation of the standard Platonist’s numbers appears problematic even without a crude causal epistemology. For instance, according to Hartry Field, mathematicians are highly reliable about what they believe in mathematics. If the truths of mathematics were different, what mathematicians would believe would also be correspondingly different. Since abstract objects are causally isolated, the realist is unable to explain the reliability of our mathematical belief-forming processes. That is, if mathematicians are to be reliable, we must deny the existence of abstract mathematical objects.Footnote 7.
I do not endorse either Benacerraf’s or Field’s epistemological preferences, for that matter, any argument that relies on particular epistemologies. There is nonetheless something to be gained from Benacerraf’s and Field’s arguments, which can be presented in the following scheme:
- (\(P_{1}\)):
-
Nonmathematical knowledge requires condition Q
- (\(P_{2}\)):
-
Knowledge about numbers cannot meet condition Q
- (\(C_{\ }\)):
-
Arithmetical knowledge is impossible
Benacerraf and Field motivate a requirement Q on knowledge by considering certain instances of nonmathematical knowledge and treating these as paradigms. Nonetheless, there is a gap in the justification that (\(P_{1}\)) plus (\(P_{2}\)) entails (C). Paradigms such as the example (6) most clearly support (\(P_{1}\)) but do not provide elements to articulate (\(P_{1}\)) and (\(P_{2}\)) in such a way that (C) can be drawn as a conclusion. The missing element should guarantee that condition Q could be in principle applied to both kinds of knowledge, and the adequacy of the argument supports the conclusion. Thus, (\(P_{1}\)) plus (\(P_{2}\)) will only get us to (C), assuming an additional condition that homogenizes arithmetic and nonmathematical knowledge and thus adequately articulates the premises. I suggest the following principle:

That is, mathematical knowledge and nonmathematical knowledge must fall under the umbrella of a reasonable epistemology.
Suppose we add the epistemic homogeneity condition to the argument and assume that there is knowledge. In that case, there is a condition \(Q'\) that both nonmathematical and arithmetical knowledge could meet in principle. Benacerraf himself seems concerned with this sort of homogeneity:
An account of knowledge that seems to work for certain empirical propositions about medium-sized physical objects but which fails to account for more theoretical knowledge is unsatisfactory. Not only because it is incomplete, but because it may be incorrect as well, even as an account of the things it seems to cover quite adequately. [p. 162]
In the end, reality is described by sentences with both mathematical and nonmathematical contents. A satisfactory epistemology should homogeneously explain mathematical and nonmathematical knowledge.
In the following sections, I suggest a theory of numbers as plural properties of multiplicity. After drawing the numbers-as-properties account, I show that such a theory satisfies the homogeneity conditions. Undoubtedly, opponents of the theory of numbers as properties may reject this proposal as a solution to Benacerraf’s problem. If so, they must provide an alternative theory that meets the homogeneity conditions (which, as shown, set weaker conditions than those imposed by Benacerraf’s original formulation).
4 Numbers as properties
There is a wide variety of theories that regard numbers as properties (Hodes 1984; Hofweber 2005; Maddy 1981; Moltmann 2013; Yi 1999, among others). These theories usually explain number properties by traditional definitions. Such definitions are often introduced by identifying properties that impose additional requirements to instances of the number-properties in play. In contrast, my proposal does not need to identify any additional properties to numbers (or, for what matters, to the bearers). In my view, a number-property is uniquely determined by what can be instantiated by. Namely, the number n is the property that can be instantiated by arbitrary pluralities of n individuals as such. This kind of instantiation requires further specification.
The fact that this theory is not founded on defining properties implies that the requirements for a theory of properties to complement this account are minimal. For current purposes, it is sufficient to consider that properties exist and can be instantiated. The present proposal may indeed be challenged from a skeptical view of properties. In this case, the proponent of such a view is welcome to provide an alternative explanation as long as the theory satisfies the homogeneity conditions.
4.1 Plural properties
From a broad conception, properties differ from other entities by a potential relation with certain objects—properties are susceptible to be instantiated by objects. Referring to particular results from Yi (1999), I argue that plural properties are properties that many things can instantiate as such. That is, as being many things. This idea requires rejecting a common understanding of instantiation. According to a standard conception, properties are ruled by the following principle.

Consider the following example,

In (7), ‘are women’ is predicated of something that appears to be plural: Thelma and Louise. Nevertheless, the principle of singularity says that whatever appearance of plurality there is here, it is only superficial. Fact (7) can be analyzed as:

In (8), the apparent plurality has disappeared. Instead of predicating a single property that holds of a plurality, we have analyzed (7) by saying that the property be woman occurs twice, once for each individual.
Notwithstanding (8) may be an adequate analysis of (7), examples of properties that cannot be reduced to individual properties suggest extending our conception of properties so that facts are explained as the instantiation of properties by many things as such. Consider, for instance:

When Ann, Ben, Carlos, and Danna are performing No Exit, none of them performs the play separately, and none of them could be. Only pluralities can perform No Exit. (In No Exit there are never less than three characters on stage.) In contrast, while pluralities can be women, so too can an individual be a woman. The property performing No Exit admits only pluralities in its argument placeFootnote 8; be woman admits pluralities and also admits individuals in its argument place. This contrast suggest a difference in the plural nature of the properties predicated in (7) and (9). This difference is captured by the following definition.

According to this definition, Performing No Exit is strictly plural; be woman is not.
Plural properties are backed by multiple systems of plural logic, in which plural reference, plural quantification, and plural predication are recognized as primitive (see, for example, Oliver and Smiley (2013); Rayo (2006); Yi (2005)). The development of plural logic systems responds, among other things, to the limitations imposed by theories of properties that presuppose the principle of singularity.
4.2 Plural properties of multiplicity
Intuitively, when conveying arithmetical content, we naturally understand ourselves as using sentences about the denotations of their singular terms and predicates, just as we do when using ordinary nonmathematical language. Language reflects our attitudes towards what we speak about. The theory of numbers as properties requires a language of properties compatible with our attitudes toward ordinary true sentences. (For a discussion on the de re attitudes towards numbers, see Kripke (1992), (Gómez-Torrente, 2019, Chap. 4), Vivanco (2020).)
As argued, the non-strictly plural property predicated in (7) is just one property, which is instantiated by many things as such,

In particular, be woman is instantiated by two many things. Assuming that Thelma and Louise are different, we can infer from (7) that,

In (10), the property be two women is instantiated by Thelma and Louise. This property differs from the property predicated in (7) in the same sense as the property predicated in (9). Namely, be two women is a strictly plural property while be women is not. Moreover, the property be two women implies an element of multiplicity (this claim can be explained, for example, in virtue of the fact that ‘are two women’ is the predicate of felicitous answers to specific How-many questions (Vivanco, 2020, p. 7)). Indeed, it can be inferred from (10) that:

If there are plural properties, then multiplicity properties are among them. Furthermore, since the instantiation of multiplicity properties can’t be reduced to individuals (neither Thelma nor Louis separately instantiates the property be two womenFootnote 9), the multiplicity properties are strict plural properties.
The logic of plurals expresses the characteristic of strictly plural properties of being non-distributive. Once the language of plurals is regimented, properties can be analyzed so that strictly plural properties, such as be two women, can be decomposed and non-strictly plural properties can be dispensed Yi [p. 188]. A property such as the one predicated in (7) is parsed as follows:

where ‘\(\alpha s\)’ stands for the plurality of Thelma and Louise and the superscript P indicates that W (be women) is not strictly plural. On the right side of the definition, \(H(\beta ,\alpha s)\) expresses that \(\beta \) is an individual of the plurality \(\alpha s\). Since W is a non-strictly plural property, it can be reduced to a property instantiated by each individual of the plurality. From this definition, we have that be two women can be analyzed as follows:

Thus, a plural property such as be two woman can be decomposed into the strictly plural property be two and the non-strictly plural property be women. The idea is to show that Thelma and Louise’s being of the same kind is irrelevant to their being two. As a result of this analysis, Yi provides the following definitions framed in the language of plurals offered:
-
Be-one(\(\alpha s\))\(\equiv _{def}\exists \beta \forall \delta [H(\delta ,\alpha s)\leftrightarrow \delta =\beta ]\)
-
Be-two(\(\alpha s\))\(\equiv _{def} \exists \beta \exists \gamma (\beta \ne \gamma \wedge \forall \delta [H(\delta , \alpha s)\leftrightarrow \delta =\beta \wedge \delta =\gamma ])\)
On the right side of the definitions, H is the relation between an individual \(\delta \) and its plurality \(\alpha s\). The number one is identified with the property that the individual of the plurality is identical to itself. The number two is identified with the property that the individuals of the plurality are distinct from each other.
As shown by the examples, a strictly plural property differs from a non-strictly plural property in that the latter cannot be reduced to properties or relations on individual arguments. Nonetheless, since both are strictly plural, the difference between a plural property such as the one in (9) and the property be two remains to be determined.

Although individuals cannot instantiate the property be performing No Exit, this can be instantiated (in principle) by pluralities of m individuals with \(m=3\), \(m=4\), and \(m\ge 5\). In contrast, the property be two can be instantiated neither by individuals nor by pluralities of m individuals for \(m\ne 2\).
The property be two is a strictly plural property of multiplicity. Indeed, this claim calls for the current account to spell out multiplicity in terms of plural instantiation. I then argue that the number n is the property that is susceptible to be instantiated by arbitrary pluralities of n things as such and cannot be instantiated by pluralities of m things as such for \(m\ne n\).
Consider \(P_{1}, P_{2},\dots , P_{m}\), an arbitrary plurality of m individuals. Just as a strictly plural property is instantiated by many things as such, meaning that one thing cannot instantiate the property, the property be n is instantiated by n many things as such, meaning that be n cannot be instantiated by m things if \(m<n\). That is, be n is not distributive to any extent. Just as be two women does not admit of an individual as an argument; be three does not admit two things, nor one individual; be four does not admit of three things, nor two things, nor one individual, etcetera.
Grammar provides reasons in favor of the non-distributivity of be two:

Sentence (12) is not grammatical. However, if \(n\ne 1\), grammar does not provide any evidence in this respect:

Sentence (13) is grammatical, albeit false. Admittedly, the mere fact that (13) is false does not imply that be three does not admit Thelma and Louise as an argument. Nevertheless, it should be noted that the reduction of a multiplicity property to a plurality of a smaller multiplicity is a consequence of the standard theory, which is ruled by the principle of singularity. Once the principle of singularity is rejected, the instantiation of pluralities as such is allowed, thus limiting the scope of distributivity between properties. The rejection of such a principle precludes the indiscriminate distributivity of plural properties. The property be n is instantiated by n many things as such, therefore, it cannot be instantiated by pluralities of m things if \(m<n\).
Consider now \(m>n\). We can take \(\frac{m!}{n!(m-n)!}\) many pluralities of n individuals from the plurality \(P_1, P_2\dots , P_m\). The property be n admits all these pluralities because it is exemplified by their individuals as such. However, although the plurality \(P_1, P_2\dots , P_m\) shares individuals with its ‘subpluralities’ of n individuals, \(P_1, P_2\dots , P_m\) cannot instantiate be n. To illustrate this point, consider again:

and also:

From the truth of (10) and (14) it does not follow that

In the same way that the rejection of the principle of singularity opens the door to the instantiation of properties by many things as such, thus blocking the distributivity of plural properties to individuals, this new perspective allows for the instantiation of multiplicity properties by n many things as such.
Up to this point, my proposal is consistent with Yi’s. However, I object to his characterization of number-properties, and expand on the results of rejecting the principle of singular instantiation. The proposal of numbers as attributive properties of multiplicity requires taking the instantiation of pluralities as such with absolute seriousness. In my view, the natural number n is the multiplicity property that can be instantiated by n many things as such. As I argue later, searching for an internal property that characterizes number properties is problematic. The number n is just the property be n—the property whose argument places admit arbitrary pluralities strictly of n individuals.
4.3 Arithmetic properties
The path toward semantic homogeneity requires an analysis of the arithmetical statements compatible with the analysis provided up to this point. In this sense, it must be shown that arithmetic statements can be analyzed in the same language of properties as nonmathematical statements—just as the term ‘two’ in the sentence

stands for the property be two, the term ‘two’ in the sentence

stands for the property be two. So the term ‘plus’ stands for a relation between properties. Moreover, in the sentence

the corresponding Arabic numerals stand for the same number property as in (11) and (16); signs of sum and identity stand for relations among number properties. (For a comprehensive account of verbal and Arabic numerals referring to properties, see Gómez-Torrente (2019), pp. 108–139.) These claims must be supported by a translation of the primitive statements on which arithmetic is formalized.
The translation presented here borrows a fragment from Yi’s plural logic notation.Footnote 10 I do not provide the whole system but only certain relevant elements introduced to extend elementary logic to a logic of plurals. Later, I introduce additional notions to express the arithmetic principles.
-
1.
Primitive terms: In addition to singular constants and singular variables, such as ‘Thelma’ and ‘Louise’, and ‘\(\alpha \)’ and ‘\(\beta \)’, we have:
-
Plural variables. For instance ‘\(\alpha s\)’, ‘\(\beta s\)’. (Plural variables correspond to plural pronouns as used anaphorically in sentences like ‘There are some humans and they cooperate’.)
-
-
2.
Term connective: ‘@’ (‘and’) This operator has a collective reading. In this way, we can build a complex object on which the predication is not distributed as in the usual conjunction. Consider the following sentence as an illustration:
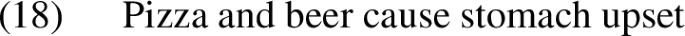
In a standard (non-collective) reading of the conjunction \(D(p\wedge c)\), sentence (18) amounts to:
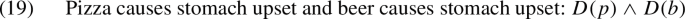
In a collective reading, pizza and beer constitute a complex object (pizza@beer) that is formed with a conjunction, but that only admits a collective reading. That is taking (18) as it is: \(D\left( p@b\right) \).
-
3.
In addition to singular predicates (logical, such as ‘Is-identical-with’, and nonlogical, such as ‘being-a-woman’, we have plural predicates:
-
Logical: ‘H’ (‘Is-one-of’)
-
Nonlogical: for example, ‘Play-together’, ‘Cooperate’
-
-
4.
In addition to the sentential connectives ‘\(\lnot \)’ and ‘\(\wedge \)’, and the singular existencial quantifier ‘\(\exists \)’, we have:
-
The plural existential quantifier: ‘\(\Sigma \)’ (‘There-are-somethings...such-that’)
The universal quantifiers ‘\(\forall \)’ and ‘\(\Pi \)’ (‘Any-thing...are-such-that’) are introduced via the usual definitions.
-
To provide a formal reconstruction to formulate arithmetic statements in a language that expresses numbers as properties, we need to add an extra plural predicate to express the instantiation relation and a nominalization operator that, when placed in front of a formula, produces a singular term:
-
2*.
Nominalization operator: ‘ \(\hat{}\) ’ Given a predicate F, the term \(\hat{}F\) denotes as a singular term the property referred by the predicate F. Thus, this operator allows us to convert complex formulas into expressions of the same kind as singular variables and constants. For example, formulas such as: \(x=x\)\(H(\beta ,\alpha s)\) are turned into the singular terms: \(\hat{}\ ( x=x)\)\(\hat{}\ (H(\beta ,\alpha s))\)
-
3*.
Plural predicate: ‘I’ (‘Is-instantiated-by’)
Now we can express the instantiation by pluralities as predication on properties: \(I(x,\alpha s)\) is the instantiation of x by the plurality \(\alpha s\) as such.
For the translation of first-order arithmetic sentences, we need to introduce additional notions:
-
1.
Nonlogical symbols: ‘0’ (as an individual constant whose intuitive meaning is ‘zero’); and S(x, y) (a dyadic individual predicate, with the intuitive meaning ‘y is the successor of x’).
-
The term that stands for the property that admits arbitrary pluralities of strictly zero elementsFootnote 11. That is, ‘0’, translates as ‘ \(\hat{}\ (\lnot \exists \beta [H(\beta ,\alpha s)])\) ’
-
The term that expresses the property that a numeric property has of being the successor of another, this is ‘S(x, y)’, translates as ‘\(y=\hat{}\ (\exists \beta \sum \gamma s(I(x,\gamma s)\wedge H(\beta , \alpha s)\wedge \forall \delta [H(\delta ,\gamma s)\leftrightarrow H(\delta ,\alpha s)\wedge \delta \ne \beta ]))\)’
-
That is, the successor of n is the multiplicity property instantiated by arbitrary \(n+1\)–pluralities, defined as the property such that there is \(\beta \) in \(\alpha s\), where \(\beta \) is different from the individuals of some plurality \(\gamma s\) that instantiates Be–n as such, and the individuals of \(\gamma s\) are individuals of \(\beta s\).
-
Let us introduce the abbreviation ‘N(x)’ for the expression
‘\(\prod \gamma \textrm{s}(H(0,\gamma \textrm{s})\wedge \forall \beta \forall \delta (H(\beta ,\gamma \textrm{s})\wedge S(\beta ,\delta )\rightarrow H(\delta ,\gamma \textrm{s}))\rightarrow H(x,\gamma \textrm{s}))\)’
The property identified as 0 intuitively satisfies ‘N(x)’—it cannot happen that if the antecedent of the main conditional in the previous expression is satisfied, the consequent is not satisfied (one of the conjuncts of the conditional is \(H(0,\gamma s)\)). Intuitively, we also see that ‘N(x)’ is satisfied by the number-property 1:
\(1=\hat{}\ (\exists \beta \sum \gamma s(I(0,\gamma s)\wedge H(\beta , \alpha s)\wedge \forall \delta [H(\delta ,\gamma s)\leftrightarrow H(\delta ,\alpha s)\wedge \delta \ne \beta ]))\)
The property be zero is one of the \(\gamma \)s, and for any number property \(\beta \) (that is part of the \(\gamma \)s), its successor is also part of the \(\gamma \)s. Since S(0, 1), then \(H(1,\gamma s)\). The same intuitive reasoning applies to each of the properties we identify with the natural numbers. The idea is the same as in the explanation of implicit recursive definitions: the plurality of the numerical properties is the smallest plurality that contains zero. This plurality is closed under the operation of adding the successor of the previously contained elements.
-
2.
Provided that we have an arithmetic formula \(\varphi \):
-
‘\(\forall x\varphi \)’ translates as ‘\(\forall x(N(x)\rightarrow )\)’ followed by the translation of \(\varphi \).
-
‘\(\lnot \varphi \)’ translates as ‘\(\lnot \)’ followed by the translation of \(\varphi \).
-
‘\(\varphi \wedge \psi \)’ translates as the translation of \(\varphi \) followed by ‘\(\wedge \)’ followed by the translation of \(\psi \).
Disjunctions, implications, and existential statements are translated into terms of the above in the usual way.
-
The current translation addresses the concern that this theory of numbers as properties might be incompatible with the uses of numerical terms in formal arithmetic. The statements taken as primitives in a standard construction of the natural numbers have an intuitive interpretation under this kind of translation. That is, the translations of the Peano axioms are intuitively true:
-
1.
N(0): The number–property be zero satisfies the formula ‘N(x)’.
-
2.
\(\forall x\forall y (N(x)\wedge S(x,y)\rightarrow N(y))\): A number–property be m (where S(n, m)) satisfies the formula ‘N(x)’ because the number–property be n satisfies the formula ‘N(x)’.
-
3.
\(\forall x\forall y\forall w\forall z (N(x)\wedge N(y)\wedge N(w)\wedge N(z)\wedge S(x,w)\wedge S(y,z)\rightarrow (x=y\leftrightarrow w=z))\): If given the properties be n and be m, then be x is the same number–property as be y, and S(n, x) and S(m, y), then the property be n and the property be m are the same property.
-
4.
\(\forall x\forall y (N(x)\wedge S(x,y)\rightarrow \lnot \ y = 0)\): For any number–property be m if there exists the property be n such that S(n, m), then the property be m cannot be the property be zero (since there is no numerical property x such that \(0=\hat{}\ (\exists \beta \sum \gamma s(I(x,\gamma s)\wedge H(\beta , \alpha s)\wedge \forall \delta [H(\delta ,\gamma s)\leftrightarrow H(\delta ,\alpha s)\wedge \delta \ne \beta ]))\)). This is because, as no plurality of \(-1\) individuals can be determined, there is no plural property that can be strictly instantiated by that pluralityFootnote 12.
-
5.
\((\varphi (0)\wedge \forall x\forall y(N(x)\wedge S(x,y)\wedge \varphi (x)\rightarrow \varphi (y)))\rightarrow \forall x(N(x)\rightarrow \varphi (x))\) (Induction schema): If the property be zero has a property \(\varphi \) and given any property be n such that \(\varphi (n)\), then the property be m (where S(n, m)) also has property \(\varphi \), then all properties that satisfy the formula ‘N(x)’ have property \(\varphi \).
Intuitively, the recursive definitions of sum, product, and exponentiation (where ‘\(+\)’, ‘\(\times \)’ and ‘e’ are triadic predicates) can be introduced by the translation in this language of properties.
-
1.
Sum: For all \(x, +(x,0,x)\) Given x, y, z, w and v, if S(y, z), \(+(x, y, w)\), and S(w, v), then \(+(x,z,v)\)
-
2.
Product: For all \(x, \times (x,0,0)\) Given x, y, z, w and v, if S(y, z), \(\times (x, y, w)\), and \(+(w,x,v)\), then \(\times (x, z, v)\)
-
3.
Exponentiation: Let \(\alpha \) be such that \(S(0,\alpha )\). Then for all \(x, e(x,0,\alpha )\) Given x, y, z, w and v, if S(y, z), e(x, y, w), and \(\times (x,w,v)\), then e(x, z, v)
4.4 Semantic homogeneity
Without straying too far from our pretheoretical intuitions, number discourse can be translated into a language of properties. This translation establishes a minimum basis that reveals that we speak of the same when we use everyday number sentences and when we use arithmetic sentences. I do not intend to provide any particular semantics here; instead, I lay the groundwork for a theory that meets the semantic homogeneity condition. From the analysis presented above, number-terms in sentences, such as

and

stand for properties regardless of their occurrences.
An account of numbers as properties does not necessarily determine that a position is realist, nor that it is antirealist. A contrast with paradigmatic realist views and with some antirealist positions illustrates this point.
4.5 Neo-logicism and numbers as properties
Consider Frege’s classic example:


In his Grundlagen, Frege (1884) argued that a substantial lesson can be drawn from the fact that, on the one hand, ‘four’ occurs as an adjective in (20), while in (21), ‘four’ occurs as a singular term. In Frege’s framework ‘The number of moons of Jupiter’ and ‘four’ are singular terms, referring to numbers, regarded as objects by Frege.
As is well known, Frege’s proposal relies on linguistic commitments posited by his ideas about language, which in turn depended on certain metaphysical prejudices. The difficulties faced by the Fregean ontology—consequently, by the formal systems accompanying it—have been widely discussed by both supporters and detractors. Indeed, different authors have considered that aside from the extensions of the concept be n-equinumerous, Frege’s theory was a theory of numbers as properties (Chateubriand, 2016; Rayo, 2002). Frege himself, after the exposure of Russell’s paradox, seems to have been open to that possibility:
Since a statement of number based on counting contains an assertion about a concept, in a logically perfect language a sentence used to make such a statement must contain two parts, first a sign for the concept about which the statement is made, and secondly a sign for a second-level concept. These concepts form a series and there is a rule in accordance with which, if one of these concepts is given, we can specify the next. But still we do not have in them the numbers of arithmetic; we do not have objects, but concepts. How can we get from these concepts to the numbers of arithmetic in a way that cannot be faulted? Or are there simply no numbers in arithmetic? Could the numbers help to form signs for these second-level concepts, and yet not be signs in their own right?Footnote 13
Considering the original project’s failure (relative to Frege’s objectives), it is fairer to contrast the current proposal to the contemporary theories that try to rescue Frege’s logicist program. In order to make the aforementioned analysis, let us consider neo-logicism in terms of three central theses: (1) neo-fregeanism—a general conception of the relation between language and reality; (2) the method of abstraction—a particular method for introducing concepts into language; (3) the scope of logic—second-order logic is logic (MacBride, 2003). One of the main advantages of the present proposal is that (2) is rejected in such a way that (1) is preserved and remains neutral concerning (3)Footnote 14.
The proposal of numbers as multiplicity properties that arbitrary pluralities can instantiate as such shows that complex identification principles for numbers are not needed. In particular, no abstraction principle of any kind is required; at least not in the sense that an account of numbers as objects does. The theory of numbers as properties does not affirm that the property be n is an individual in the Platonist’s strict sense. That is, it does not require introducing new objects. This is the substantial difference between traditional Platonism and the present explanation in epistemological terms. Even seemingly simple defining principles (for example, those suggested by Yi) are highly implausible when accounting for epistemic access to arithmetical truths. The epistemology suggested in the subsequent sections plainly marks the difference with any logicist-type program: the theory of numbers as properties admits an epistemic explanation in terms of empirical and linguistic capacities, ruling out the essential role of principles of logic in an account of arithmetic knowledge. This, of course, does not imply that determining rules cannot be established. These rules will ultimately be based on the way in which the number-properties can be instantiatedFootnote 15.
In addition to providing a more plausible solution to the epistemic problem, the numbers as properties proposal accounts for the relation between language and reality without facing metaphysical problems such as the so-called bad company. Bad company objections state that if the abstraction method for introducing the concept of numbers were legitimate, then it should be possible to use it in general. Nevertheless, the general application of the abstraction method allows for introducing concepts and associated objects of which we would otherwise be wary. Alternatively, the stipulation of abstraction principles conflicts with the commitments we have already made (for a more detailed description, see MacBride (2003)). The view defended here avoids this kind of objection, still accounting for a relation between reality and language. Although the conception of numbers as properties involves a notion of abstraction, identifying that different pluralities of the same multiplicity have the same number-property (Gómez-Torrente, 2019, p. 132), this abstraction does not imply postulating any object. Furthermore, the abstraction at stake concerns arbitrary pluralities of n individuals, which rules out the necessity of additional properties for the pluralities, particularly when those pluralities are individuals. This point solves the question of the distinction between a number and Julius Caesar; the number–property of arbitrary pluralities of multiplicity n is entirely independent of the existence of Julius Caesar or any other individual.
Leaving aside the imposition of a theory on names, if we assume that the number four is the property be four, statements such as (20) and (21) do not seem so mysterious. In both cases, numerals stand for a property. With this property, we predicate things about objects and we can also talk about it conveying the same instantiation with the instances at play.
There are still things to be said about the possible instantiations of number–properties and their relations with other existing things in the world. For example, it is interesting to ask whether these instantiations are also possible for pluralities of infinite multiplicity or what would happen if the concrete universe was finite. Regarding the first question, although this research focuses on the case of pluralities of finite cardinality, none of the commitments acquired here closes the door to an extended explanation that includes infinite cardinals.Footnote 16 Lastly, it is worth recalling that the property be n can be instantiated by arbitrary pluralities of multiplicity n, particularly by pluralities of properties. Following the rules presented in 4.3, it can be seen that the number of concrete objects in the universe is not a limitation for the existence of very large numbers.
A theory of numbers as properties does not have to commit to realist positions. Paradigmatic examples show that a theory that privileges the adjective uses of numerical terms (typically considered as those that stand for properties) fits into an antirealist conception. This is the case of the view advocated by Hofweber (2005). According to Hofweber, the term ‘four’ occurs as a determiner in both (21) and (20). What he calls plural arithmetical statements (for instance, (20)) are formulated with bare determiners, while in sentences such as (21), the determiner is concealed due to a syntactic abnormality. If numbers are properties, as I propose, the distinction between the forms of the determinant is superfluous. The term ‘four’ stands for the multiplicity property be four. In (21), we are talking about the property concerning the moons of Jupiter (where the relation is none other than that the moons of Jupiter have the property of being four). In (20), the property of being four is predicated on the plurality of Jupiter’s moons.
Another antirealist theory that fits with the present proposal is found in Yablo (2014). According to Yablo [pp. 177–198], sentences (20) and (21) have the same real content,Footnote 17 which states that the moons of Jupiter are four. Thus, the real content of (21) is about particular concrete objects—the moons of Jupiter—and not about the abstract object that the number four would be.
But regardless of our realist or antirealist inclinations, the truth is that the properties we attribute to an object are relevant to the ascriptions of knowledge about it. The property be four is relevant to the truth of (21) as well as to the truth of (20), even if the real content of both sentences is about Jupiter’s moons and not about the number four.
5 Arithmetical knowledge
Day-to-day knowledge of objects involves epistemic access to properties. In particular, it involves the instantiation relation between a property and its potential bearers. Ascriptions of knowledge about facts such as

depend on the correct attribution of properties such as be tall to objects such as John. For an epistemology to be satisfactory, the justification conditions for knowledge must account for our access to properties (which, in turn, determines our epistemic relationship to objects and vice versa). This work does not endorse any particular epistemology. This proposal aims to show the plausibility of explaining arithmetical knowledge from the view of numbers as properties.
If n is the plural property of multiplicity be n, knowledge ascriptions regarding n are founded on the ability of agents to attribute n to any plurality of n individuals. The fact that pluralities of n individuals strictly instantiate the multiplicity property be n makes it possible for an agent to correctly attribute the number n to a plurality without needing to know anything in particular about its individuals (other than that they are n). Access to the number n requires to be able to correctly attribute it to pluralities of n individuals. The development of this ability is the starting point to make arithmetical knowledge possible.
Children acquire basic arithmetical knowledge at an early age from contact with small pluralities of physical objects (or their representations). This knowledge is reflected in the assignment of exact measures of multiplicity to identifiable pluralities through the linguistic ability of counting, which improves by the management of numerical notation, such as Arabic or verbal numerals (for detailed linguistic analysis, see Wiese (2003) and Wiese (2020)). Several studies in cognitive sciences explain these arithmetic abilities as starting from the number sense, a pre-linguistic sense, which has to do with how human and non-human animals can respond automatically to the numerical features of the world (e. g. Baroody et al. (2003); Dehaene (1997); Levine et al. (1992); Canobi and Bethune (2008)). Empirical data show that at a very early age, there are two active representational systems related to the number sense. These are the approximate-number system and the object monitoring system. The first includes relations with the property of numerosity itself, and the second, relations with certain pluralities of physical objects (Gilmore & Spelke, 1992).
The object monitoring system is described as a mechanism for responding to small multiplicities (3–4 members) of sensory elements by encoding their members with other mental symbols stored in working memory (the phenomenon of subitization is a result of this mechanism). The approximate-number system responds to large multiplicities of sensory elements by representing them as segment-like magnitudes fluctuating on a mental number line. In this sense, the attribution of small numbers (the first with which we acquire competence) is strongly rooted in sensory contact with small pluralities of physical objects. Not so the attribution of greater numerical properties. This ability is founded on the identification of multiplicities through counting. The ability to attribute numbers to pluralities is implicitly reflected in using numerals as adjectives. The human cognition of numbers evolves significantly once the general concept of cardinality is acquired (Feigenson et al., 2004; Carey, 2009).
5.1 Epistemic homogeneity
Several studies in cognitive science support the thesis that the theory of numbers as properties entails the possibility of arithmetical knowledge. The evidence show that there is a strong relationship between arithmetical knowledge and the ability to attribute numerical properties to their corresponding pluralities. Furthermore, these abilities are explained in terms of mental numerical dispositions, direct interaction with small pluralities, and the generalization of concepts through linguistic resources.
Identifying a number property merely by how it can be instantiated endows the present theory with a significant advantage over other theories of numbers as properties. Typically, theories search for defining (constitutive) properties of numbers. However, multiple problems arise from those properties (often arbitrary or not sufficiently well defined). In particular, they do not contribute with a solution for the epistemic problem. As simple as the definitions may seem, once they are introduced, the strategy systematically fails to account for arithmetical knowledge, which is characterized by its simplicity and naturalness. As an illustration, Yi (1999) tries to weaken the defining conditions of a number by specifying only logical properties among the individuals of the pluralities that bear that number. The simplest example quickly faces the epistemic problem of identifying the number–properties. Recall the definition of be two:

From this definition, it follows that to know the number two is to know that the individuals of a plurality that instantiate the property be two are different from each other. It is unclear whether agents are always in a position to fulfill this condition. For example, imagine a child who thinks that two unicorns are identical. Her notion of being identical might not be too sophisticated. To this extent, she might not be able to specify that the unicorns are different from each other (apart from the fact that the unicorns are two). Nevertheless, this does not prevent her from correctly attributing the property be two to the plurality of those unicorns.
Whether the theory regards numbers as objects or properties, the identification problem is likely to be faced by any attempt to define numbers through more primitive properties. My proposal rests on the fact that attributions of the property be n can be made to arbitrary pluralities of n individuals. In this way, the identification of the number–properties does not depend on anything other than how they can be instantiated. If numbers are the properties described here, an epistemology for arithmetic will ultimately depend on access to the relations between properties and their potential bearers. The same access must be considered in ascriptions of knowledge about nonmathematical facts such as (22).
6 Concluding remarks
The theory of numbers as properties lays the groundwork for a theory of truth to satisfy the conditions of semantic and epistemic homogeneity. The arguments presented in this paper show that if numbers are properties, we have a homogeneous domain in which a semantic theory can account for the contents of number expressions (in both their adjectival and substantival forms) in the same way that it accounts for the contents of terms in ordinary discourse. The translation of ordinary and arithmetic statements into a language of properties establishes conditions of possibility for homogeneous semantics.
The above results imply that arithmetical knowledge is possible, starting from the bases of the Benacerrafian argument, whose original formulation entails the impossibility of arithmetic knowledge. As argued, traditional theories of arithmetical truth solved the Benacerraf’s problem. Nevertheless, the original theoretical assumptions allow for providing solutions to the dilemma without accounting for the possibility of arithmetical knowledge. In this paper, I argue that a satisfactory arithmetical truth theory must meet the semantic and epistemic homogeneity conditions. Furthermore, I have shown that meeting the homogeneity requirements is possible if numbers are properties. As a result, arithmetical knowledge is possible. Additionally, different results in cognitive science support the thesis that numbers are properties, providing evidence of a transparent relation between the ability to correctly attribute multiplicity properties to arbitrary pluralities of individuals and the acquisition of arithmetical concepts. All this together not only shows that arithmetical knowledge is possible but also enlightens how it is possible.
The present work focuses on arithmetic due to its theoretical, philosophical, and historical relevance. Some traditions, though, attempt to extend explanations on natural numbers to other numerical structures (see, for example, Hale (2000) on neo-logicism and Heyting (1959) on intuitionism). The theory of numbers as properties contributes to various arguments against the foundational role of set theory in arithmetic. However, since mathematics provides constructions of numerical structures from natural numbers, this proposal opens the door to frameworks in which properties can be constructive tools alternative to sets. Once the multiplicity properties are introduced in mathematical discourse, it makes sense to consider different relations and other related properties. The results presented here invite further investigation of numbers as properties.
Notes
According to (Field 1989, pp. 232–233), his reformulation of the Benacerraf’s problem does not depend on causal epistemology. However, this formulation seems to presuppose a reliabilist epistemology, which is nothing but the evolution of causal epistemology (with its own objections). In any case, without explaining how to determine such reliability, we can assume that Field is again imposing a causal requirement. [See Clarke–Doane 2017]
Benacerraf calls ‘combinatorial’ those theories of mathematical truth according to which “the truth conditions for arithmetic sentences are given as their [...] derivability from specified sets of axioms". [p. 665]
Undoubtedly, different discourses give rise to variations in truth conditions. An illustrative example is the case of empty names. However, these cases do not fall within the relevant fragment of language that concerns Benacerraf. Although the statement ‘Tom Sawyer was born in Missouri’ has the same form as ‘Aristotle was born in Stagira’, it is fairly clear that our epistemic relationship with the statements is different in the relevant sense.
Yablo (2014) considers different ways of being true for a sentence Note that the discussion here is different. Even if there are different ways of being true, that does not imply that there are different kinds of truth.
It might seem that, in this example, a correspondence theory of truth is presupposed. However, this use of ‘correspond’ is not linked to specific semantic theories but rather to speakers’ natural intuition about the relationship between language and its subject matter. While a correspondence theory of truth typically asserts that a statement’s truth or falsity is solely determined by its accuracy in describing the world, in everyday usage, speakers assume a more general connection between language and facts, which is related to their notions of truth falsehood, lying, misinforming, and so on, without delving too deeply into the specifics.
Burgess, for example, simply rejects Benacerraf’s problem as inapplicable to Quine’s program, on the grounds that our beliefs about abstract objects are justified as a whole as part of our best scientific theories, Burgess (1990).
Hartry Field. Realism, Mathematics, and Modality Blackwell, 1989.
The difficulties grounded in singular instantiation are not solved by distinguishing between relations and properties. The advocate of the principle of singularity assumes that places of arguments in relations are also singular. We may interpret (9) as a relation. Nevertheless, the relation also must be plurally instantiated. For example, (9) might be the relation between Ann, Ben, Carlos, and Danna (as such) and No Exit. On the other hand, it is unclear whether (9) is the relation performing No Exit occurring for some individuals. To begin with, the arity of the relation would be indeterminate, it depends on the individuals in it.
Yi’s technical apparatus allows properties to be described using a language of plurals. In this sense, he distinguishes between pure and impure plural properties—Impure plural properties are expansions of what he calls singular bases:
For example, the property that I call be human[s], indicated by ‘is-a-human\(^{P}\)’,is the plural expansion of be a human. Now, any plural expansion is distributive, that is, it is instantiated by some things as such if and only if it is instantiated by every one of them. [p. 187]
The reader interested in the exhaustive formalization can refer to Yi (1999).
The plurality of zero individuals is, as the definition indicates, that which has no elements (of course there are many concepts that determine this plurality. One of them, for example, is the concept of being different from itself).
Although the notion of property at stake is austere, it has been established that properties are identified by how they can be instantiated (regardless of whether they are actually instantiated). A plurality of minus one individuals cannot instantiate any plural property of multiplicity. Certainly, it may be argued that in the strict sense, there are no pluralities of zero individuals either, thus the property be zero is also not well defined. The assertion here is that the property be zero can be instantiated by any plurality that does not have individuals, and we can specify these pluralities. For example, if Be-zero(\(\alpha \)s), then \(\alpha \)s is the plurality such that if \(H(\beta ,\alpha s)\), then \(\beta \ne \beta \). This identification may be controversial under metaphysical considerations, but it succeeds specifying \(\alpha \)s. In contrast, it is unclear how this could be achieved for the property be \(-1\) (while still keeping the simplicity of the plural properties of multiplicity considered here).
Notes for Ludwig Darmstaedter, pp. 366–7
The neo-logicist program preserves logicism’s spirit of reducing the truths of arithmetic to logical statements that can be known without appealing to experience, thus solving the epistemic problem for arithmetical sentences. Frege’s concerns lead him to draw the axioms of arithmetic from the so-called Basic law V, which was supposed to achieve the ontology required by his metaphysical program:
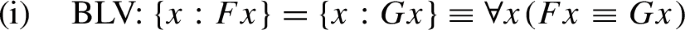
As Russell showed, this principle presupposes that:
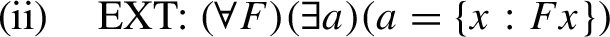
which is false. The neologicist proposal suggests adopting Hume’s Principle as the abstraction principle—since it does not presuppose (ii)—and deriving Peano axioms from it:
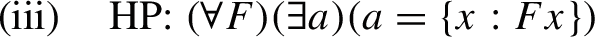
The contemporary debate addresses whether (iii) is a logical principle in such a way that it solves the epistemic problem for arithmetic.
Many thanks to the referee who suggested the contrast with neo-Fregeans to illuminate and specify the current proposal. Their comments have been quite insightful. I also thank them for the suggestion of the following abstraction-like rule:
‘The property ‘be n’ is identical to the property ‘be m’ if and only if for any plurality \(\alpha s\) and for any plurality \(\beta s\), the \(\alpha s\) are n and the \(\beta s\) are m if and only if the \(\alpha s\) and \(\beta s\) are equinumerous.
Note that pluralities do not constitute the equivalence class that number would be. The relevant relationship between equinumerous pluralities is that they both are plural instances of the same property of multiplicity. As the reviewer remarks, the statement above is true of properties; the process of going from predicate instantiation to properties is already reasonably widely accepted and at least only as contentious as the existence of properties is.
This question was discussed with Mario Gomez-Torrente during the Mathematics, Modality and Knowledge Symposium, at the CLMPST, 2023.
In Yablo’s framework, the literal content is what the statement would mean, if taken literally; the real content is what we in fact communicate with the statement. The literal content of “She has butterflies in her stomach” places various insects in her digestive tract; the real content only claims that she is nervous. The literal content of “The number of planets is even" says something about a relation between planets and a certain type of abstract object; the real content says only that the planets are evenly-numbered.
References
Balaguer, M. (1995). A Platonist epistemology. Synthese, 103(3), 303–325.
Balaguer, M. (1998). Platonism and anti-platonism in mathematics. Oxford University Press.
Baroody, A.J., Wilkins, J.L.M., Tiilikainen, S. (2003). The development of children’s understanding of additive commutativity: from protoquantitative concept to general concept? A.J. Baroody & A. Dowker (Eds.), The development of arithmetic concepts and skills: constructing adaptive expertise (pp. 127–160). Lawrence Erl–baum Associates.
Benacerraf, P. (1973). Mathematical truth. Journal of Philosophy, 70(19), 661–679.
Burgess, J. (1990). Epistemology & nominalism. A. Irvine (Ed.), Physicalism in mathematics (pp. 1–15). Dordrecht: Springer Netherlands.
Canobi, K. H., & Bethune, N. E. (2008). Number words in young children’s conceptual and procedural knowledge of addition, subtraction and inversion. Cognition, 108(3), 675–686.
Carey, S. (2009). The origin of concepts. Oxford University Press.
Chateubriand, O. (2016). Números como propiedades de segundo orden. J. Ferreirós (Ed.), El árbol de los números. cognición, lógica y práctica matemática (pp. 112–130). Sevilla: Universidad de Sevilla.
Clarke–Doane, J. (2017). What is the Benacerraf problem? F. Pataut (Ed.), New perspectives on the philosophy of paul benacerraf: Truth, objects, infinity. Springer Verlag.
Dehaene, S. (1997). The number sense: How the mind creates mathematics. Oxford University Press.
Feigenson, L., Dehaene, S., & Spelke, E. (2004). Core systems of number. Trends in Cognitive Sciences, 8(7), 307–314.
Field, H. (1980). Science without numbers. Princeton University Press.
Field, H. (1989). Realism, mathematics, and modality. Blackwell.
Frege, G. (1884). Foundations of arithmetic (J.L. Austin, Trans.). L. Nebert.
Gilmore, C. K., & Spelke, E. S. (1992). Children’s understanding of the relation between addition and subtraction. Cognition, 44(1), 43–74.
Gómez-Torrente, M. (2019). Roads to reference. Oxford University Press.
Hale, B. (2000). Reals by abstraction. The Proceedings of the Twentieth World Congress of Philosophy, 6, 197–207.
Heyting, A. (1959). Constructivity in mathematics. Amsterdam: North- Holland Pub. Co.
Hodes, H. T. (1984). Logicism and the ontological commitments of arithmetic. Journal of Philosophy, 81(3), 123–149.
Hofweber, T. (2005). Number determiners, numbers, and arithmetic. Philosophical Review, 114(2), 179–225.
Kripke, S.A. (1992). Logicism, wittgenstein, and de re beliefs about numbers. Unpublished transcript of the Whitehead Lectures delivered at Harvard University in May of 1992 .
Levine, S. C., Jordan, N. C., & Huttenlocher, J. (1992). Development of calculation abilities in young children. Journal of Experimental Child Psychology, 53(1), 72–103.
MacBride, F. (2003). Speaking with shadows: A study of neo-logicism. The British Journal for the Philosophy of Science, 54(1), 103–163.
Maddy, P. (1980). Perception and mathematical intuition. Philosophical Review, 89(2), 163–196.
Maddy, P. (1981). Sets and numbers. Noûs, 15(4), 495–511.
Moltmann, F. (2013). Reference to numbers in natural language. Philosophical Studies, 162(3), 499–536.
Oliver, A., & Smiley, T. (2013). Plural logic. Oxford University Press.
Rayo, A. (2002). Frege’s unofficial arithmetic. The Journal of Symbolic Logic, 67(4), 1623–1638.
Rayo, A. (2006). Beyond plurals. A. Rayo & G. Uzquiano (Eds.), Absolute generality (pp. 220–254). Oxford University Press.
Shapiro, S. (1983). Mathematics and reality. Philosophy of Science, 50(4), 523–548.
Topey, B. (2020). Realism, reliability, and epistemic possibility: On modally interpreting the benacerraf-field challenge. Synthese, 199(1–2), 4415–4436.
Vivanco, M. (2020). Referential uses of Arabic numerals. Manuscrito-International Journal of Philosophy, 43(4), 142–164.
Wiese, H. (2003). Numbers, language, and the human mind. Cambridge University Press.
Wiese, H. (2020). The co-evolution of number concepts and counting words. Lingua, 117(5), 758–772.
Yablo, S. (2014). Aboutness. Princeton University Press.
Yi, B. (1999). Is two a property? Journal of Philosophy, 96(4), 163–190.
Yi, B. (2005). The logic and meaning of plurals. part i. Journal of Philosophical Logic, 34, 459–506.
Acknowledgements
Versions of this material were presented at MIT, UNAM, University of Miami, Vienna (at the “What in the World(s)?!” conference), Prague (at the 16th CLMPST), and elsewhere. I owe thanks to Mario Gomez-Torrente, Carmen Curcó, Otávio Bueno, Max Fernandez, Simon Evnine, Stephen Yablo, Agustín Rayo, Milo Phillips-Brown, and Curtis Miller for their insightful comments and the fruitful discussions held throughout the process of this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
I declare that Dr. Otávio Bueno, one of Synthese’s editors, was my doctoral advisor at the University of Miami. However, I clarify that the research developed in this work was carried out entirely independently of the doctoral research developed under Dr. Bueno’s supervision, and the submission followed the rules to ensure a double-blinded review.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Vivanco, M. Numbers as properties. Synthese 202, 114 (2023). https://doi.org/10.1007/s11229-023-04330-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04330-z