Brownian motion from a deterministic system of particles

Abstract

Can Brownian motion arise from a deterministic system of particles? This paper addresses this question by analysing the derivation of Brownian motion as the limit of a deterministic hard-spheres gas with Lanford’s theorem. In particular, we examine the role of the Boltzmann-Grad limit in the loss of memory of the deterministic system and compare this derivation and the derivation of Brownian motion with the Langevin equation.

1 Introduction

The derivation of the laws of statistical and thermal physics from microscopic dynamics is a major challenge for the philosophy of science. There are longstanding discussions on whether the entropy law can be derived from a microscopic description of phenomena (e.g., Callender, 1999; Earman, 1986a; Uffink, 2001). In this context, particular attention has been paid to the derivation of the Boltzmann equation and the H-theorem (e.g., Brown et al., 2009), and Lanford’s theorem has notably renewed these discussions by raising the question of whether this major mathematical result for the kinetic theory of gases can explain “the emergence of irreversibility” (Uffink & Valente, 2015). By contrast, philosophers have not yet paid attention to the derivation of another important statistical and thermal physics law that uses Lanford’s theorem: this is the derivation of Brownian motion from a deterministic classical system of hard spheres.

Brownian motion has been extensively studied both in physics and mathematics. It was originally developed for studying the erratic movement of a dust particle or pollen grain in fluid induced by collisions with the fluid molecules. Given that a fluid can be modelled as a hard-spheres system, the derivation of this random motion has been identified as “a fundamental problem of statistical mechanics” (Beck, 1990, p. 324).¹ Indeed, at the microscopic scale, the laws of motion and the collisions in the hard-spheres system are deterministic. However, at a larger scale, the motion of the target particle, i.e., the Brownian particle, exhibits random behaviour. Accordingly, the derivation of Brownian motion raises the question of how random evolution might appear at the macroscopic scale, although all the dynamics at the microscopic scale are deterministic.

This paper tackles this problem by focusing on the recent derivation of Brownian motion from the dynamics of a hard-spheres gas provided by Bodineau et al. (2016), which comes from earlier ideas by van Beijeren et al. (1980). According to Bodineau et al., their derivation “is the very first result describing the Brownian motion as the limit of a deterministic classical system of interacting particles” (2016, p. 496). Accordingly, this derivation is worthy of investigation by the philosophy of science. First, it does not resort to a stochastic force for the dynamics of the Brownian particle. The micro-dynamics stems only from elastic collisions and deterministic dynamics. Secondly, this derivation requires different limiting regimes to obtain Brownian motion, such as the Boltzmann-Grad limit. These limits are essential for this derivation and have to be carefully investigated to account for the appearance of a memoryless behaviour from a deterministic system. Finally, as the authors claim, they “provide a rigorous derivation of the Brownian motion” (ibid., p. 493. My emphasis). This mathematical derivation is different from the usual physicists’ derivation of Brownian motion with the Langevin equation. Our analysis might interest philosophers of science concerning the respective aims of the two derivations and the specific idealizations required in both derivations.

The overall objective of the paper is to shed light on this mathematical derivation of Brownian motion based on Lanford’s theorem. For that purpose, we first recall the usual derivation of Brownian motion from the Langevin equation. We highlight that it makes use of a stochastic assumption for the dynamics of the Brownian particle, i.e., a random force that represents the effects of a huge number of collisions (Sect. 2). Section 3 then sketches the main steps of the rigorous derivation of Brownian motion and provides an overview of this derivation. In particular, we emphasize that Bodineau et al.’s derivation does not resort to a random force. It makes use of Lanford’s derivation of the Boltzmann equation from the Hamiltonian equations of motion of hard spheres. Furthermore, the derivation of Brownian motion requires two successive limiting regimes, i.e., the Boltzmann-Grad limit and the diffusive limit, which play a crucial role in the appearance of Brownian motion. Section 4 first analyses some salient upshots of Lanford’s theorem for Brownian motion. Section 5 then analyses the role of the limiting regimes. More precisely, we clarify the role of the Boltzmann-Grad limit in the loss of memory of the deterministic system. Finally, Sect. 6 compares the two derivations of Brownian motion, viz. with the Langevin equation and with Lanford’s theorem, and analyses their respective interests. In particular, we stress that both derivations rest on a common principle, i.e., memoryless behaviour appears with the loss of correlations of the deterministic system particles.

2 Brownian motion with the Langevin equation

This section first recalls a few features in the physical theory of Brownian motion. One of the main results, notably due to Einstein in 1905, is the equation of the mean-squared displacement.² In the one-dimensional case, because of the thermal fluctuations of molecules of the fluid, the position x of a Brownian particle satisfies the relation:

$$\left\langle {x^{2} } \right\rangle = 2D \, t$$

(1)

where D is the diffusion constant that equals k_BT/(6πµa), with k_B the Boltzmann constant, T the temperature of the fluid, µ its friction constant, and a the radius of the Brownian particle. This equation states that the mean-squared displacement of the Brownian particle is linear in time, which is valid, as we will see below, for a sufficiently long time.

This equation is generally obtained in physics textbooks from the Langevin equation, a stochastic version of Newton’s second law of dynamics (e.g., Mazenko, 2006, p. 6; Reif, 1965, p. 560; Wannier, 1987, p. 475). This equation involves two forces, a friction force and a random force, which represent the effects of collisions on the Brownian particle:

$$md^{2} x/dt^{2} = \, F_{f} + \, F_{s}$$

(2)

The frictional force is described by Stokes’s law F_f = ‒6πµa dx/dt. The stochastic force F_s is defined such as its mean value < F_s> equals zero and that < F_s (t₁) F_s (t₂) >  = B δ(t₁,t₂), with B the strength of the force and δ the Dirac distribution. In other words, the value of the random force at any time t₂ is uncorrelated to its value at any time t₁.

In order to obtain Eq. (1) from Eq. (2), we first multiply Eq. (2) by the position x, then take its mean value, apply the property < F_s x >  = 0 for the random force, and make use of the equipartition of the energy relation (see Genthon, 2020, p. 10). After some algebraic manipulations, we obtain the following equation for the time evolution of the mean-squared displacement:

$$d\left\langle {x^{2} } \right\rangle /dt = 2k_{B} T/\left( {6\pi \mu a} \right) + \, C{\text{ exp}}\left( { - \left( {6\pi \mu a/m} \right)t} \right)$$

(3)

with C the constant integration. The second term of the right hand side very quickly decreases to zero, with a time constant of around 10^‒8 s in real conditions. Only the first term rapidly becomes non-negligible. Accordingly, we integrate the equation with time and recover, for a sufficiently long time, the mean-squared displacement law of Brownian motion (Eq. 1). It has to be noticed that this Brownian motion is also defined and studied in a mathematical context as a Wiener process (see, e.g., Nelson, 2001; Pitman & Yor, 2018, Roger & Williams, 2000). Brownian motion B_t (as written below Ξ(t)) is defined as a random variable that is almost surely continuous, which has a Gaussian distribution and stationary independent increments. The discussions in mathematics and physics on Brownian motion address different kinds of questions but still pertain to the same memoryless behaviour.

We stress that the derivation of Brownian motion from the Langevin equation resorts to a crucial idealization for the dynamics, viz a random force representing the effect of a very large number of uncontrollable collisions. On this point, Luczak (2016, p. 406) provides insightful analysis and argues that this idealization is justified by reflecting a “collision assumption” at the micro-scale, viz. the assumption that the velocities of molecules are, at any time, independent of the velocity of the Brownian particle. Given that the mean-squared relation of Brownian motion (Eq. 1) is experimentally well confirmed, Luczak then raises the question: “why does the Langevin equation work?” This question is worthy of investigation and concerns what we call the representation problem, i.e., why Brownian motion and the Langevin equation adequately represent the behaviour of a pollen grain in water. By contrast, the present paper does not directly address this question. There is another problem regarding Brownian motion, which we call the derivation problem, to which this paper is dedicated. This is the problem of obtaining Brownian motion from a genuine deterministic classical system without resorting to a random force in the dynamics.

Before analysing the derivation problem, we stress a preliminary distinction between what we call empirical Brownian motion and mathematical Brownian motion. Empirical Brownian motion is the motion observed in nature, e.g., the erratic motion of a pollen grain in a glass of water. This phenomenon looks random, but we are agnostic about its real nature. Mathematical Brownian motion is the representation of this phenomenon by a memoryless process, as a Wiener process. This paper is mainly dedicated to this second notion and, to a lesser extent, to the relationship between these two notions. For the sake of readability, the ‘mathematical’ specification will remain implicit in the paper except where otherwise specified.

3 The rigorous derivation of Brownian motion

This section offers an overview of the rigorous derivation of Brownian motion provided by Bodineau et al. (2016) before investigating some salient features of this deviation in the remainder of the paper. This presentation is mainly based on Gallagher’s paper (2019).

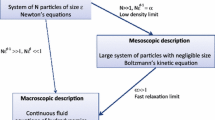
Let us consider a system of N hard spheres with a diameter d that evolve and collide according to the laws of classical mechanics. We describe the dynamics of the N particles with Hamiltonian equations of motion. In this system, let us focus on one particle. The other N‒1 hard spheres are assumed to be at thermal equilibrium. Under these circumstances, the main result of Bodineau et al.’s derivation is that, in the limit N → ∞, d → 0, and Nd² → ∞, the tagged particle converges to a Brownian motion. This derivation involves two main steps, each of them requiring a limiting regime (see Fig. 1). We sketch these two main steps without going into technical details.

Fig. 1

Overview of the derivation of Brownian motion. Step 1: The linear Boltzmann equation is derived from the Liouville equation within the Boltzmann-Grad limit. Step 2: The heat equation and Brownian motion are derived from the linear Boltzmann equation in the diffusive limit

Step 1 goes from a microscopic description of the gas to a mesoscopic one. More precisely, Step 1 derives a linear Boltzmann equation from the Liouville equation of the N hard-spheres system. The Liouville equation describes the evolution of the Hamiltonian system H in the phase space:

$${\textbf{Liouville equation}}: \partial \mu /\partial t \, = \, \{ H,\mu \}$$

(4)

This represents the time evolution of the probability density µ of the hard-spheres system in the phase space. The linear Boltzmann equation represents the time evolution of the probability density f that a hard sphere is located at the position x with a velocity v at the time t:

$${\mathbf{linear}} \, {\mathbf{Boltzmann}} \, {\mathbf{equation}}:\partial f/\partial t + \, v\partial f/\partial x \, + \, \alpha \, L\left[ f \right] \, = 0$$

(5)

This first step requires Lanford’s theorem, to which we will return in Sect. 4. This theorem proves that the solution µ of the Liouville equation tends to the solution f of the Boltzmann equation in a certain limiting regime, viz. the Boltzmann-Grad limit. This is the limit where N → ∞, d → 0 so that Nd² = α converges to a finite quantity (see, e.g., Earman, 1986a, p. 230; Valente, 2014; Uffink & Valente, 2015). This quantity α represents the inverse of the mean-free path of the microscopic particles. Moreover, since the number of particles per unit of volume Nd³ tends to zero, the Boltzmann-Grad limit is the limit of infinitely rarefied gas. We will discuss the role of this limit in more detail in Sect. 5.

For now, it is noteworthy that Bodineau et al.’s derivation involves a linear Boltzmann equation, where the collisional operator L[f] is an integral over all the collisions in the gas for which the N‒1 hard spheres are initially assumed to be at the thermal equilibrium. This is a distinctive feature of using Lanford’s theorem to derive the H-theorem (see Valente, 2014; Uffink & Valente, 2015). The Boltzmann equation involves a different collisional operation C[f] and describes how the gas approaches equilibrium. The linear Boltzmann equation is a particular case of the Boltzmann equation with respect to initial data. In the present case, we are interested in fluctuations of the gas molecules around thermal equilibrium that affect the tagged particle. Accordingly, the collisional operator L[f] describes a gas at the thermal equilibrium, and we study the motion of the tagged particle in this fluid.

After that, step 2 derives the Brownian motion from the previous linear Boltzmann equation (Eq. 5). First of all, the heat equation is derived from the linear Boltzmann equation:

$${\mathbf{heat}} \, {\mathbf{equation}}:\partial \rho /\partial t \, - \, \kappa \, \Delta_{x} \rho \, = \, 0$$

(6)

where ρ represents the probability density of particles, and κ the diffusivity constant. The heat Eq. (6) is derived from Eq. (5) by taking the diffusive limit. This is the limit where Nd² or α tends to infinity (Nd² = α). Indeed, in this diffusive limit, “the linear Boltzmann equation does have the heat equation as an asymptotic regime” (Gallagher, 2019, p. 79). This means that the solution of the linear Boltzmann equation tends to the solution of the heat equation in this limit. Furthermore, if we focus on the time evolution of the tagged particle within this limit, one recovers the Brownian motion. The process associated with the tagged particle indeed converges to Brownian motion: “In the same asymptotic regime, the process Ξ(τ) = x₁(ατ) associated with the tagged particle converges in law toward a Brownian motion” (ibid., p. 79; see also Bodineau et al., 2016, p. 503). More precisely, this Brownian motion has a variance κ. One thus recovers the relationship between the heat equation and Brownian motion since the solution of the heat equation is a gaussian distribution (with a gaussian distribution as initial condition. See, e.g., Duplantier, 2006, p. 223). To sum up, the fluctuations of the N‒1 hard spheres gas at the thermal equilibrium leads to the heat equation in this diffusive limit. Within this fluctuating gas of particles, it is shown that the tagged particle behaves as a Brownian particle.

4 Brownian motion with Lanford’s theorem

This rigorous derivation of Brownian motion is based on Lanford’s derivation of the Boltzmann equation involved in Step 1. Lanford’s theorem (1975, 1976) is a masterpiece for the kinetic theory of gases. It is “maybe the most important mathematical result of kinetic theory” (Villani, 2010, p. 100). However, Bodineau et al.’s derivation of Brownian motion is not a simple application of this theorem. To begin with, we clarify the relationship between Lanford’s theorem and Bodineau et al.’s derivation of Brownian motion. After that, we will discuss salient features of this derivation regarding some limitations of Lanford’s theorem.

First of all, we stress that Bodineau et al.’s derivation of Brownian motion stems from Lanford’s theorem. Bodineau et al. use several theoretical resources of Lanford’s theorem, such as the convergence of the BBGKY hierarchy to the Boltzmann hierarchy in the Boltzmann-Grad limit.³ According to the authors, ‘‘our proof is based on the fundamental ideas of Lanford’’(Bodineau et al., 2016, p. 493). However, the derivation of Brownian motion goes beyond Lanford’s theorem. It extends this work for some conditions: ‘‘the idea is to improve Lanford’s result by considering fluctuations around some global equilibrium’’(ibid., p. 499). This extension arises from studying a hard-spheres gas for which N‒1 particles are at thermal equilibrium. Without going into technical details, this approach allows them to extend the convergence of series expansions and, as we will discuss below in this section, extend the time validity of the derivation of the Boltzmann equation. Moreover, Bodineau et al.’s works involve the derivation of a particular case of the Boltzmann equation, i.e. the linear Boltzmann equation. On this point, Bodineau et al.’s derivation of Brownian motion also extends the works due to van Beijeren et al., (1980), who studied a hard-spheres system at the thermal equilibrium. ‘‘Using Lanford’s result about the convergence of the solutions of the BBGKY hierarchy to the solutions of the Boltzmann hierarchy’’(van Beijeren et al., 1980, p. 237), these authors obtained several results on the linear Boltzmann equation.⁴ Therefore, thank to the original Lanford’s results on the Boltzmann equation, but also to van Beijeren et al.’s works (1980) on the hard-spheres gas at thermal equilibrium, Bodineau et al. offer a technical tour de force by obtaining a rigorous derivation of Brownian motion.

Lanford’s theorem is mostly known for obtaining the H-theorem, which can be interpreted as the increasing entropy law. It states that a minus H-function, which is a function of the solution of the Boltzmann equation, increases monotonically with time, like the entropy of an ideal gas.⁵ Accordingly, for Uffink (2007), “the results obtained are the best efforts so far to show that a statistical reading of the Boltzmann equation or the H-theorem might hold for the hard spheres gas” (2007, p. 111). Moreover, for Earman (1986a, p. 231), it seems “the best way” and “the most fruitful approach” to tackle the problem of irreversibility. Lanford’s derivation has thus been mainly discussed concerning the problem of irreversibility (see also Valente, 2014; Uffink & Valente, 2015; Ardourel, 2017). However, despite its importance for the foundations of the kinetic theory of gases and the problem of irreversibility, several criticisms have been addressed to the epistemological consequences of this theorem, mostly because it involves some drastic limitations. We now discuss these objections and argue that the derivation of Brownian motion does not in fact suffer these limitations. The derivation of Brownian motion avoids these limitations because it extends Lanford’s results by studying hard-spheres gases close to thermal equilibrium.

First, a major objection pertains to the time validity of Lanford’s theorem. Sklar points out this limitation: “This derivation has the virtue of rigorously generating the Boltzmann equation, but at the cost of applying only to one severely idealized system and then only for a very short time” (Sklar, 2015, Sect. 4. Our emphasis). Lanford’s derivation of the Boltzmann equation is indeed valid for a very short time of the order of 1/Nd² (i.e., α^‒1). This allows only one fifth or so of the particles to collide: “for realistic gases in standard conditions, it amounts to a few milliseconds” (Valente, 2014, p. 318). Accordingly, it is argued that one should not pay too much attention to Lanford’s derivation for the problem of irreversibility because it does not provide us with information on what happens in real gases.⁶ Be this as it may, this time validity objection cannot be addressed to the derivation of Brownian motion, which turns out to be valid for any time. This point is a salient feature of the derivation of Brownian motion. The time-bound for the Boltzmann derivation comes from mathematical convergence constraints (Valente, 2014, p. 332). More precisely, Lanford’s derivation of the Boltzmann equation makes use of a formal series expansion for the solutions of the Boltzmann equation. However, this series expansion can be applied only on this short time interval of the order of α^‒1. Nevertheless, this restriction does not hold for the derivation of Brownian motion. This major difference comes from the fact that Brownian motion is derived from a linear Boltzmann equation instead of the usual Boltzmann equation. As Gallagher (2019) emphasizes, “the main achievement consists in deriving the linear Boltzmann equation for an arbitrarily long time (contrary to the Lanford theorem which only holds for times of the order α⁻¹)” (Gallagher, 2019, p. 79. Our emphasis. See also Bodineau et al., 2016, p. 509). Without entering into technical details, the point is that the restriction to the linear Boltzmann equation allows resorting to a mathematical property of the theory of differential equations, the “maximum principle”, thank to which the time-validity for the convergence of the formal series can be extended in time. This difference comes from the initial configurations of the hard-spheres gas in the case of the linear Boltzmann equation, where the N‒1 particles are assumed to be at the thermal equilibrium. Roughly speaking, the mathematical constraints that prevent a large time validity for the derivation of the Boltzmann equation can be overcome here thanks to the linear property of the Boltzmann equation at stake for the derivation of the heat equation.

Another related objection to the scope of Lanford’s theorem concerns the need for infinitely rarefied gases. As Valente (2014) points out: “A more serious limitation comes from the appeal to the Boltzmann-Grad limit. […] [D]espite the number of its particles growing to infinity, the gas becomes infinitely rarefied. This restricts the domain of applicability of Lanford’s result dramatically, in that it may only apply to very diluted gases” (Valente, 2014, p. 319). Lanford’s derivation of the Boltzmann equation indeed holds in the Boltzmann-Grad limit, which involves that the volume occupied by the hard spheres goes to zero. Again, this derivation might thus be viewed as non-informative regarding the appearance of irreversibility in real gases. We do not discuss this objection either, but rather stress that the derivation of Brownian motion does not straightforwardly face this objection.⁷ Although this derivation requires the Boltzmann-Grad limit in step 1 of the derivation, it then resorts to the diffusive limit in step 2. The use of this second limiting regime is essential to obtain Brownian motion, and is again a distinctive feature of the derivation of Brownian motion since it avoids the restriction to infinitely rarefied gases. In the Boltzmann-Grad limit, the quantity Nd² = α is constant, and thus the density of particles Nd³ tends to zero. By contrast, the diffusive limit α → ∞ involves that the gas is not rarefied at all. Since the quantity Nd² can be interpreted as the number of collisions per unit of time, the number of collisions tends to infinity. As Bodineau et al. claim, “one can think of α as a parameter tuning the density of the background particles” (2016, p. 503). This second limiting regime thus makes the derivation of Brownian motion meaningful regarding the huge number of incontrollable collisions involved in the empirical Brownian motion.

5 How is the memory of the deterministic system lost?

This section now investigates how a memoryless process appears in this derivation. Section 3 made clear that a random force is not assumed in the dynamics of the Brownian particle. The loss of memory of the deterministic system has to be found elsewhere. For that purpose, we argue that the Boltzmann-Grad limit used in step 1 of the derivation plays a crucial role on this point. Although the derivation of Brownian motion requires the diffusive limit, and thus that the number of collisions tends to infinity, the loss of memory for the deterministic system appears before the use of this limit. It occurs as soon as the Boltzmann-Grad limit is used. The authors of the derivation clearly raise this point: “In the Boltzmann-Grad limit, the memory of the system is lost” (Bodineau et al., 2016, p. 543). We thus make the distinction between the appearance of Brownian motion, which requires the diffusive limit, and the loss of memory of the deterministic system, which already occurs with the Boltzmann-Grad limit. This section further analyses this second point. We claim that two different concomitant reasons explain the loss of memory with the Boltzmann-Grad limit. This limiting regime indeed comprises two mathematical limits: the limit for which the diameter d of hard spheres tends to zero and the infinite limit for the number N of particles. Each of them, and perhaps the two, play a crucial role in the loss of the memory of the deterministic system.

5.1 Non-deterministic collisions

Let us start by examining the limit d → 0. It leads to an important property concerning the loss of memory of deterministic systems. More specifically, collisions between two hard spheres become indeterministic in the limit where the diameter d of hard spheres tends to zero. This property is claimed by Norton (2012) when he investigates the Boltzmann-Grad limit⁸:

If two points of the limit state collide (a measure zero event), we can no longer determine the collision outcome. We need to determine six quantities: three velocity components for each of the two outgoing points. We have only four equations: three for momentum conservation and one for energy conservation. Hence, any collision has become indeterministic. Until we reach this limit state, collision outcomes can be determined uniquely since we have the added condition that, when spheres collide, the momentum transfer is perpendicular to the plane of contact of the two sphere’s surfaces. (2012, p. 219)

The conservation laws completely determine a system of two hard spheres that are going to collide. As Lanford (1975) himself makes clear, “What happens in a binary collision is completely determined by the requirements of conservation of (kinetic) energy and linear momentum together with the condition that momentum transferred in collisions is orthogonal to the plane of contact” (Lanford, 1975, p. 8). By contrast, a system of two mass points is no longer determined because the extra constraint to define a plane of contact is missing.

Let us analyse this point further. For this purpose, let us call ω_ij the unit vector between the centres of the two hard spheres labelled by i and j. This vector ω_ij is uniquely determined as long as the diameter d of the two spheres i and j is greater than zero. However, by using the Boltzmann-Grad limit, and thus the limit d → 0, the unit vector ω_ij tends to a vector ω which is no longer uniquely determined and which loses the memory of the directions of the particles i and j after the collision. This point is clear when we pay attention to the passage from the vector ω_ij to the vector ω in the derivation of the Boltzmann equation. Before taking the Boltzmann-Grad limit, the description of collisions appeals to a collision integral defined as a function of ω_ij, namely C(ω_ij). This collision integral is involved in equations that contain all the information on the deterministic collisions of the hard spheres and are time-reversal invariant. However, in the Boltzmann-Grad limit, this collision integral tends to C(ω), for which the directions of particles after collisions become randomly defined. The mathematician Golse (2014) highlights this point (with our notations):

While d is greater than 0, laws of collisions are reversible because there is a unique vector ω_ij with respect to the position of particles i and j. Instead, when d → 0, the definition of the collision integral [C(ω][…] requires the vector ω, analogous to ω_ij, which is now randomly and uniformly distributed on the sphere. (Golse, 2014, p. 35)⁹

We find the same kind of analysis in other papers, such as in Degond, 2004 (p. 12).¹⁰ In the same vein, Valente (2014) emphasizes that when the diameter of spheres tends to zero, “the positions q_i and q_j of the centers of the two particles, and hence the vector ω_ij is no more defined. Therefore, the laws of collisions cannot apply in their standard form in the Boltzmann-Grad limit” (Valente, 2014, p. 319).

To sum up, we suggest that the loss of memory of the deterministic hard-spheres gas in the Boltzmann equation derivation might come from the fact that the vector ω_ij is no longer uniquely determined in the Boltzmann-Grad limit, because of the limit d → 0. Furthermore, this vector is randomly distributed in the Boltzmann-Grad limit when it is used to derive the Boltzmann equation, meaning that the directions of particles after collisions are random.

5.2 Vanishing recollisions

Let us now focus on the limit N → ∞ within the Boltzmann-Grad limit. We will see that it also involves a loss of memory for the deterministic system of hard spheres. To begin with, it is not very surprising that non-deterministic behaviour appear within a deterministic system by considering the infinite limit for the number of particles. The philosophical literature provides us with various examples of such cases in other contexts. For instance, there are infinite billiards systems (Lanford, 1975, p. 50; Earman, 1986b, p. 39), infinite masses and strings systems (Norton, 2012), or an infinite dominos cascade (Norton, 2017), which reveal that indeterministic behaviours can come from infinite deterministic systems. However, in the present case we are interested in a specific property, viz. the loss of memory of the deterministic system, which, as we will argue below, might arise for a specific reason compatible with the previous one discussed in Sect. 5.1.

The appearance of memoryless behaviour within the Boltzmann-Grad limit might be due to the loss of correlations between the hard spheres when one resorts to the limit N → ∞. Our point is that, in the Boltzmann-Grad limit, the number of recollisions tends to zero. A recollision occurs when two hard spheres that have collided in the past — even indirectly, ‘‘via collisions in chain with other particles’’ (Gallagher, 2019, p. 77) — collide again afterwards. The hard-spheres gas described by the Liouville equation has recollisions. These recollisions involve correlations between the hard spheres and thus keep the memory of the deterministic system. By contrast, the Boltzmann equation and the linear Boltzmann equation derived with Lanford’s theorem does not involve recollisions, which is of first importance in the mathematical works on the derivation of the Boltzmann equation (see, e.g., Gallagher, 2019, p. 77). By using the limit N → ∞, one eliminates the situations in which particles that have collided (directly or indirectly) in the past can collide again in the future. This property is made clear by the authors of the derivation: “for any fixed n [with n < N], the set of initial configurations with n particles leading to such recollisions is of vanishing measure in the N → ∞ limit” (Bodineau et al., 2018, p. 992). More precisely, a measure-theoretic argument ensures that, in the N → ∞ limit, the set of initial configurations for hard spheres that would lead to recollisions has a measure zero. This property is crucial from step 1 of the derivation, i.e., to prove that the Liouville equation tends to the Boltzmann equation. We leave the mathematical considerations aside, but we point out that, for the purpose of the present article, the loss of memory in the deterministic hard spheres system might thus come from vanishing recollisions in the infinite limit.

Let us take stock. We have analyzed two different reasons why a hard-spheres gas loses the memory of the deterministic system with the Boltzmann-Grad limit. First of all, the deterministic laws of collisions can no longer apply when the diameter d of the hard spheres goes to zero. We thus face indeterministic collisions. Moreover, the recollisions disappear when the number N of particles goes to infinity. Particles are thus uncorrelated. We do not see why one or the other reason should be ruled out. Moreover, nothing forces us to choose between the two limits since they are both required in the Boltzmann-Grad limit. Therefore, although we have clarified the role of the Boltzmann-Grad limit in the loss of memory of the deterministic system, we are not in a position to take a stance in favour of one option rather than the other one.

6 Two derivations of Brownian motion

Let us wrap up. We first introduced the derivation of Brownian motion with the Langevin equation and then discussed in more detail its derivation based on Lanford’s theorem. This section discusses certain salient upshots regarding these two derivations.

First, it is noteworthy that the two derivations have different goals and come from different scientific communities. The derivation with the Langevin equation stems from a physicist’s perspective. It consists of building a dynamical model that accounts for the mean-squared displacement formula of a particle in the fluid. The second derivation comes from a mathematician’s perspective. It aims to show how the deterministic dynamical equations at the microscopic scale, viz. Hamiltonian equations of a hard-spheres gas, are connected with differential equations at higher scales, viz. the equations of the kinetic theory of gases and the equation of diffusion of fluid dynamics. The mathematical techniques used in the two derivations are very specific for each of the two fields. Although elementary algebraic manipulations are required for the first one, Lanford’s theorem, series expansions and several convergence proofs techniques are used for the second one. All in all, the first derivation is framed within a physics modelling activity, whereas the second one is proof-oriented.

Relatedly, as we mentioned above, the two derivations raise different philosophical issues. The derivation of Brownian motion with the Langevin equation raises the representation problem, i.e., the problem of knowing why memoryless motion adequately describes the behaviour of a particle in a fluid. This answer to this question appeals to identifying physical ingredients, such as “microphysical facts” (Luczak, 2016, p. 407) that justify this representation. By contrast, the derivation of Brownian motion with Lanford’s theorem raises the question of how memoryless behaviour can be obtained from a deterministic system, which we called the derivation problem. The answer to this question appeals to clarifying the articulation between differential equations that describe a hard-spheres gas at different scales, which mostly requires deploying mathematical techniques, making use of different mathematical frameworks (e.g., the BBGKY hierarchy and the Boltzmann hierarchy), and providing convergence proofs, without invoking physical ingredients.

Secondly, the two derivations involve different idealizations according to their respective aims. The Langevin equation idealizes the effects of many incontrollable collisions of molecules as a random force in the dynamical model. By contrast, there is no random force assumed in Bodineau et al.’s derivation. However, the derivation requires other idealizations, and in particular, the Boltzmann-Grad limit and the diffusive limit, with which the number of particles tends to infinity, their diameter tends to zero, and the number of collisions per unit of time tends to infinity. These idealizations allow us to connect the microscopic description of the gas (with the Hamiltonian equations) to the mesoscopic one (with the linear Boltzmann equation), and finally, to the macroscopic one (with the heat equation).

Thirdly, despite their respective differences, we maintain that the two derivations support a common view regarding the appearance of memoryless behaviour. Luczak (2016, p. 407) argues for a “microphysical fact” that would justify using the idealized random force in the Langevin equation. It is the fact that “at all times (except perhaps initially), the velocity of any incoming colliding fluid molecule and the incoming velocity of the Brownian particle are approximately probabilistically independent” (2016, p. 406). For him, “it seems reasonable to think, as the microphysical fact intends to suggest, that any correlations that form between the velocities of colliding particles wash out incredibly quickly” (ibid., p. 407). The huge number of collisions in the fluid would make it very unlikely that correlations between molecules are maintained in time. As we have seen in Sect. 5, the derivation of Brownian motion from Lanford’s theorem supports this claim from another perspective. The correlations between the hard spheres of the gas are lost with the Boltzmann-Grad limit, either because the collisions in the gas become non-uniquely determined or because recollisions between particles vanish (or because of both reasons). Accordingly, the crucial idealization used in the Langevin equation can be connected to the crucial idealization used in the derivation of Brownian motion with Lanford’s theorem, which both stem from the loss of correlations between particles of the deterministic system. This is an interesting case for which mathematics and physics, resorting to very different techniques and following very different scientific aims, still offer, at some point, a common picture of physical phenomena.

7 Conclusion

A fundamental question for statistical and thermal physics is how Brownian motion can be derived from a deterministic classical system. This paper tackles this problem by examining its rigorous derivation from the dynamics of a hard-spheres gas, which is claimed to be “the very first result describing the Brownian motion as the limit of a deterministic classical system of interacting particles” (Bodineau et al., 2016, p. 496). We analysed this derivation, which is based on Lanford’s theorem and appeals to the mathematical tools used to rigorously derive the Boltzmann equation and the H-theorem. We first show that some limitations in this rigorous derivation of the Boltzmann equation (e.g., its short time validity) do not apply in the case of the derivation of Brownian motion. We then examined the role of the Boltzmann-Grad limit in the loss of memory of the deterministic system of a hard-spheres gas. In particular, in this limit, particles that have already collided do not collide again. We thus connected this property with the usual way to derive the Brownian motion with the Langevin equation by discussing the justifications for the idealized random force, which also appeal to the loss of correlations of the fluid molecules. We highlight that these two derivations are very different, both from the standpoint of the scientific communities (physics and mathematics) but also with respect to their scientific aims. However, these works show how such radically different approaches to Brownian motion can contribute to offering a common and complementary picture of it.