Abstract
Sentences about logic are often used to show that certain embedding expressions (attitude verbs, conditionals, etc.) are hyperintensional. Yet it is not clear how to regiment “logic talk” in the object language so that it can be compositionally embedded under such expressions. In this paper, I develop a formal system called hyperlogic that is designed to do just that. I provide a hyperintensional semantics for hyperlogic that doesn’t appeal to logically impossible worlds, as traditionally understood, but instead uses a shiftable parameter that determines the interpretation of the logical connectives. I argue this semantics compares favorably to the more common impossible worlds semantics, which faces difficulties interpreting propositionally quantified logic talk.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Philosophers talk about logic all the time. They debate which logic is correct (if any), which laws of logic hold, which inferences are valid, and so on. But philosophical debates are not the only place where such talk occurs. We can attribute beliefs about logic to people (“My colleague thinks intuitionistic logic is correct”), counterfactually reason about alternative logics (“Teaching logic would be way harder if the law of noncontradiction failed”), and more besides. Such “logic talk” seems continuous with the way we talk about non-logical matters. Yet relatively little has been done to situate such talk about logic within a broader semantic theory. My aim here is to make some initial steps toward such a theory—that is, to develop a semantics for logic talk.
By ‘logic talk’, I roughly mean any sentence that is, in some sense, about logic, i.e., a metalogical claim. Here are some simple examples:

These are stereotypical examples of the kinds of claims philosophers debate. But logic talk is not restricted just to these sorts of simple sentences. It includes, e.g., sentences that describe what holds according to other logics.

It also includes sentences that embed metalogical claims under, e.g., attitude verbs, conditionals, or modals.

Embedded examples such as (7)–(9) pose two challenges for the theory of logic talk. First, there is the familiar hyperintensionality problem. The standard intensional semantic theories for attitude verbs, conditionals, and modals predict that these expressions validate the replacement of necessary equivalents. Yet this prediction seems incorrect, as illustrated by (10)–(12).

These do not seem equivalent to (7)–(9), even though (assuming classical logic is correct) their constituents are necessarily false, and thus necessarily equivalent. One challenge, then, is to explain what’s going on here.
But these examples raise a second, more basic problem: it’s not even clear how to regiment metalogical claims in the first place. Normally, metalogical claims are stated in the metalanguage—we talk of axiomatic proofs, models, sequents, and so on. Examples like (7)–(9) require bringing such talk into the object language: we need to assign compositional semantic values to metalogical claims. But how? We cannot, for instance, regiment (8) as ‘ ’: the string ‘\(\vDash \mathop {\lnot }\nolimits (\phi \mathbin {\wedge }\mathop {\lnot }\nolimits \phi )\)’ is not a formula of the object language but rather an abbreviation in the metalanguage. What we need is an object-level regimentation of ‘\(\vDash \mathop {\lnot }\nolimits (\phi \mathbin {\wedge }\mathop {\lnot }\nolimits \phi )\)’ so that it can be given a compositional semantic value.
’: the string ‘\(\vDash \mathop {\lnot }\nolimits (\phi \mathbin {\wedge }\mathop {\lnot }\nolimits \phi )\)’ is not a formula of the object language but rather an abbreviation in the metalanguage. What we need is an object-level regimentation of ‘\(\vDash \mathop {\lnot }\nolimits (\phi \mathbin {\wedge }\mathop {\lnot }\nolimits \phi )\)’ so that it can be given a compositional semantic value.
My goal is to motivate and develop a formal system called hyperlogic that can help address these problems. Hyperlogic solves the regimentation problem using three ingredients. First, it introduces a multigrade operator  representing entailment. So where
representing entailment. So where  are formulas,
are formulas,  is a formula which, intuitively, represents the claim that
is a formula which, intuitively, represents the claim that  entail \(\beta \). Second, laws of logic are formalized with propositional quantifiers (Fine , 1970). Thus, we can regiment the law of excluded middle as
entail \(\beta \). Second, laws of logic are formalized with propositional quantifiers (Fine , 1970). Thus, we can regiment the law of excluded middle as  . Finally, claims about what laws hold according to a logic are formalized using an “according-to” operator \(\mathop {@}\nolimits \) borrowed from hybrid logic (Areces and ten Cate , 2006). So, we can regiment (4) as
. Finally, claims about what laws hold according to a logic are formalized using an “according-to” operator \(\mathop {@}\nolimits \) borrowed from hybrid logic (Areces and ten Cate , 2006). So, we can regiment (4) as  where \({il}\) stands for intuitionistic logic.
where \({il}\) stands for intuitionistic logic.
To solve the hyperintensionality problem, theorists standardly invoke “logically impossible worlds” as arbitrary sets of formulas. However, I argue that there are difficulties interpreting propositional quantifiers in an impossible worlds semantics for embedding expressions like counterfactuals. Instead, I build off Kocurek and Jerzak’s (2021) hyperintensional semantics, which introduces a shiftable parameter that provides the interpretation of the connectives (Muñoz , 2020; Muskens , 1991; Williamson , 2009). I will show how this theory can be expanded to a hyperintensional semantics with propositional quantifiers that fits more naturally with hyperlogic. As we will see, this semantics retains the flexibility of logically impossible worlds without the technical difficulties they bring.
Throughout, I will be working within a classical framework in the background. This is not because I think classical logic is the “one true” logic or that hyperlogic must be developed within a classical setting to be intelligible (Meyer and Routley , 1977).Footnote 1 The task of developing an adequate semantics for logic talk arises independently of which logic is actually correct (if any). My goal, rather, is to demonstrate one general strategy for developing such a semantics. The choice of a classical background logic is just a convenient starting point.
The plan is as follows. In Sect. 2, I examine the regimentation problem in more detail and present some desiderata that any adequate solution to it should satisfy. In Sect. 3, I propose the language of hyperlogic as a solution to the regimentation problem. In Sect. 4, I introduce the impossible worlds approach as a solution to the hyperintensionality problem and argue it faces difficulties interpreting propositional quantifiers. In Sect. 5, I show how to expand Kocurek and Jerzak’s (2021) hyperconvention semantics into a semantics for hyperlogic that can more adequately interpret propositional quantifiers. I conclude in Sect. 6 with some ways we might extend hyperlogic to cover a broader range of phenomena.
2 The regimentation problem
Let’s start with the regimentation question: how do we regiment metalogical claims so that they can be interpreted in the object language?
To illustrate the problem, consider again (7)–(9). To provide a semantics for these sentences, we first need to regiment them in a formal language—one with a belief operator \(\mathop {\textsf {B}}\nolimits \), a counterfactual  , or an epistemic modal
, or an epistemic modal  respectively. We can partly regiment these claims as follows:
respectively. We can partly regiment these claims as follows:

To assign these sentences truth conditions, however, we need to finish the regimentation: we need to formalize the embedded sentences as some formulas (e.g., \({il}\), lnc, and \({cl}\) respectively), and then write down a semantic clause for each. But how? What semantic clause do we give such formulas?
One way to avoid this problem is to formalize metalogical claims as distinct atomics \(p_{{il}}\), \(p_{lnc}\), and \(p_{cl}\). The formal interpretation of these atomics is simply determined by a valuation function provided by a model. Then (7)–(9) become:

This atomic regimentation works well enough for many purposes. But it has two main disadvantages. First, it ignores the internal logical structure of metalogical claims. For example, metalogical claims can have quantificational structure, as illustrated by (3):

The reasons why we can’t accurately regiment such quantificational structure with atomic formulas are familiar (e.g., they can’t distinguish de dicto from de re sentences). Similarly, the atomic regimentation is blind to the structure of according-to claims, as in (4):

This insensitivity to logical form is undesirable. It would be better if the syntax of our formal language at least somewhat matched (even if not perfectly) the actual syntactic structure of such talk.
Second, it does not capture differences in patterns of reasoning with metalogical claims. For example, consider the following argument:

This seems like impeccable reasoning regardless of what one thinks about the premises. By contrast, the following argument is bad:

Yet the difference between (13) and (14) cannot be captured on the current approach, as both arguments are represented as having the form:

For another example, contrast (15), which seems like good reasoning, and (16), which does not:

After all, given that there are contradictions, if all contradictions entail everything, then some do. So (15) seems like good reasoning. But there are logics on which everything is entailed by some contradiction or other (e.g., everything is entailed by the result of conjoining it with its negation) even though contradictions don’t entail everything. So (16) does not seem like good reasoning.
Let me be clear: I am not claiming that (14) and (16) are bad because they’re invalid. On a standard (classical) notion of validity, these arguments are all trivially valid since they have either an impossible premise or a necessary conclusion.Footnote 2 My point, rather, is that there is some good-making feature that (13) and (15) have and that (14) and (16) lack. Very roughly, (13) and (15) seem to be good forms of reasoning regardless of one’s views about which logic is correct, whereas (14) and (16) do not. Even if we do not call this feature “validity”, it demands explanation nonetheless.
3 The language of hyperlogic
I now develop a solution to the regimentation problem called hyperlogic. The purpose of this section is simply to introduce the language of hyperlogic and explain its intended interpretation. I’ll give a semantics in Sect. 5.
3.1 The language
To introduce the language of hyperlogic, we start with the language of propositional modal logic, which I’ll call \({\mathcal {L}}\). The language contains an infinite stock of propositional variables  , boolean connectives (\(\mathop {\lnot }\nolimits \), \(\mathbin {\wedge }\), \(\mathbin {\vee }\), \(\mathbin {\rightarrow }\)), and modal operators (\(\mathop {\Box }\nolimits \),
, boolean connectives (\(\mathop {\lnot }\nolimits \), \(\mathbin {\wedge }\), \(\mathbin {\vee }\), \(\mathbin {\rightarrow }\)), and modal operators (\(\mathop {\Box }\nolimits \),  ).Footnote 3 The syntax is given below in Backus-Naur form:
).Footnote 3 The syntax is given below in Backus-Naur form:

To get the language of hyperlogic, we make three additions to \({\mathcal {L}}\).
First, we add a left-multigrade operator \(\mathbin {\rhd }\) representing entailment. It is “left-multigrade” in that it takes a finite (possibly empty) list of formulas on the left and a formula on the right.Footnote 4 Informally, we can read  as “
as “ entail \(\psi \)”. Similarly, we can read \(\mathop {\rhd }\nolimits \phi \) as “\(\phi \) is valid”. The notion of entailment that \(\mathbin {\rhd }\) represents need not be solely logical per se. In principle, it can be interpreted as analytic, a priori, metaphysical, or whatever other notion of entailment one employs in characterizing validity for arguments. Thus, we can represent the claim that my shirt being red entails its being colored as \(r \mathbin {\rhd }c\). Like any other operator, the interpretation of \(\mathbin {\rhd }\) is something to be specified by a model.
entail \(\psi \)”. Similarly, we can read \(\mathop {\rhd }\nolimits \phi \) as “\(\phi \) is valid”. The notion of entailment that \(\mathbin {\rhd }\) represents need not be solely logical per se. In principle, it can be interpreted as analytic, a priori, metaphysical, or whatever other notion of entailment one employs in characterizing validity for arguments. Thus, we can represent the claim that my shirt being red entails its being colored as \(r \mathbin {\rhd }c\). Like any other operator, the interpretation of \(\mathbin {\rhd }\) is something to be specified by a model.
Second, we’ll introduce propositional quantifiers ( ,
,  ) that bind into sentence position.Footnote 5 This allows us to represent quantificational structure more faithfully. For example, here is how we can regiment (3):
) that bind into sentence position.Footnote 5 This allows us to represent quantificational structure more faithfully. For example, here is how we can regiment (3):

Furthermore, we can now regiment laws of logic as universally quantified sentences.Footnote 6 Thus, the law of excluded middle can be regimented as follows:

Third, we will introduce operators borrowed and modified from hybrid logic. Hybrid logic is an extension of modal logic with terms denoting individual worlds. These terms act both as special atomics that are true at exactly one world and as arguments for certain operators.Footnote 7 Specifically, hybrid logic adds the following to propositional modal logic:
-
(i)
two new kinds of atomic formulas, viz., state variables
 and state nominals
and state nominals  , which are true at exactly one world;
, which are true at exactly one world; -
(ii)
an operator \(\mathop {@}\nolimits _\sigma \) (‘according to \(\sigma \),...’) for each state term \(\sigma \), which resets the current world of evaluation to be the world denoted by \(\sigma \)
-
(iii)
an operator \(\mathop {\downarrow }\nolimits s\) (‘where s stands for the current world,...’) for each state variable s, which resets the value of s to be the current world of evaluation.
Hybrid logic is useful for, among other things, modeling temporal language, which often contains names for specific times, e.g., ‘It’s 3 pm’ or ‘At 3 pm, it’ll rain’ (Yanovich , 2015). The idea here is to extend our language with hybrid operators for interpretations of the base language, including the connectives (\(\mathop {\lnot }\nolimits \), \(\mathbin {\wedge }\), etc.), rather than for individual worlds.Footnote 8
Putting this all together, here is the full language of hyperlogic, which I’ll call \({\mathcal {H}}\). We introduce two new sets of atomic formulas:  (interpretation variables) and
(interpretation variables) and  (interpretation nominals). An interpretation term is a member of \({\textsf {ITerm}} :=\textsf {IVar}\cup \textsf {INom}\). We use
(interpretation nominals). An interpretation term is a member of \({\textsf {ITerm}} :=\textsf {IVar}\cup \textsf {INom}\). We use  for interpretation terms. The syntax of \({\mathcal {H}}\) is given as follows:
for interpretation terms. The syntax of \({\mathcal {H}}\) is given as follows:

For instance, let \({cl}\) stand for classical logic and let \({il}\) stand for intuitionistic logic. Then we can regiment (1) and (4) as follows:Footnote 9

In sum, here is how we can regiment logic talk in hyperlogic:
-
\(\ulcorner {l\hbox { is correct}}\urcorner \) is regimented using l as an interpretation nominal.
-
\(\ulcorner {\hbox {according to }l, \phi }\urcorner \) is regimented as \(\mathop {@}\nolimits _l\phi \).
-
 is regimented as
is regimented as  .
. -
\(\ulcorner {\hbox {it is a law that }\phi ({q}_{1},...,q_{n})}\urcorner \) is regimented as
 .
.
3.2 Solving the regimentation problem
Recall, there are two issues with the atomic regimentation: it does not faithfully represent the internal structure of metalogical claims, and it does not capture the relative goodness of patterns of reasoning with such claims. We are now in a position to see how hyperlogic addresses these concerns.
First, the language of hyperlogic clearly provides us with a more faithful representation of the internal syntactic structure of logic talk. We’ve already seen how propositional quantifiers allow us to represent quantificational structure and how hybrid operators allow us to represent the common structure in according-to sentences. This does not mean the language of hyperlogic matches perfectly with the syntactic structure of logic talk. But it does far better than the atomic regimentation.
Second, we can now explain the relative goodness of patterns of reasoning with logic talk. For example, consider (13) and (14) again:

Intuitively, the difference between (13) and (14) is that the former but not the latter has the form of a good inference regardless of one’s views about logic. Specifically, it has the following form, which seems to be impeccable reasoning even if the premises are false:

Similarly, (15) has the logical form of a good inference regardless of one’s views about logic, while (16) does not.

Up to this point, I’ve refrained from spelling out what “regardless of one’s views about logic” means. This will be made more precise later (Sect. 5.4). To foreshadow, we can define two notions of validity in hyperlogic: a classical notion and a “universal” notion. An argument is classically valid if it’s truth-preserving on a classical interpretation of the connectives. An argument is universally valid if it’s truth-preserving on any interpretation of the connectives. The sense in which (13) and (15) are “good”, then, is that both arguments are universally valid. By contrast, (14) and (16), though classically valid (for trivial reasons), are not universally valid.
With hybrid operators, we can move back and forth between classical validity and universal validity.
-
 is universally valid iff
is universally valid iff  is classically valid, where l does not occur in
is classically valid, where l does not occur in 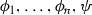 .
. -
 is classically valid iff
is classically valid iff  is universally valid, where \({cl}\) is a classical nominal.
is universally valid, where \({cl}\) is a classical nominal.
So there’s no need to settle which notion of validity is the “true” notion (though there can still be fruitful debate over which is better for which purpose). Both notions of validity can be seen as virtues of an argument.
4 Impossible worlds
Thus far, we’ve only focused on the regimentation problem. Now let’s return to the hyperintensionality problem. While one could try to explain away hyperintensionality by appeal to pragmatics, I will simply assume that hyperintensionality is generally a semantic phenomenon. The challenge, then, is to develop a hyperintensional semantics for the relevant embedding expressions (e.g., attitude verbs, counterfactuals, etc.), i.e., a semantics on which necessarily (even logically) equivalent sentences are not intersubstitutable salva veritate.
The standard semantic approach to dealing with hyperintensionality is what I’ll call the impossible worlds approach.Footnote 10 This approach modifies intensional semantic theories by introducing “impossible worlds” where necessarily equivalent sentences can be distinguished.
In this section, I will consider whether the impossible worlds semantics can provide us with a simple solution to the hyperintensionality problem. I argue that the standard implementation of this semantics runs into problems when we try to extend it with languages with propositional quantifiers, which we’ve seen are crucial to solving the regimentation problem.
4.1 Impossible worlds semantics
The impossible worlds approach starts by expanding the notion of a “world” so as to include both possible and impossible worlds. We can think of a world as an ersatz entity—say, a set of formulas (Nolan , 1997). Truth-at-a-world reduces to membership: \(\phi \) is true at an ersatz world w iff \(\phi \in w\). A “possible” world is just a maximal compossible set of formulas, whereas an “impossible” world is a set that is not both maximal and compossible. So to transform an intensional semantics into a hyperintensional one, we simply replace possible worlds with worlds in this broader sense.
To illustrate, let’s see how this approach applies to counterfactuals.Footnote 11 According to the standard “selection” semantics, a counterfactual is true iff at all the selected (“closest”) possible worlds where the antecedent is true, the consequent is true. This is implemented formally by introducing a selection function f, which takes a set of possible worlds X and a possible world w, and “selects” a set of possible worlds f(X, w) as the “closest” or “most similar” X-worlds to w (Stalnaker , 1968; Lewis , 1973). Thus, a counterfactual  is true at a possible world w iff
is true at a possible world w iff  (where
(where  ).
).
Applied to this semantics, the impossible worlds approach allows selection functions to select sets containing impossible worlds. More precisely, we start with an extension of \({\mathcal {L}}\) with counterfactuals:

An impossible worlds model is a quadruple \(\mathcal {I}= \left\langle W,P,f,V \right\rangle \), where W is a nonempty set of worlds, \(P \mathrel {\subseteq }W\) is a nonempty set of possible worlds,  is a selection function (perhaps satisfying certain constraints, e.g., \(f(X,w) \mathrel {\subseteq }X\)), and V is a valuation function where:
is a selection function (perhaps satisfying certain constraints, e.g., \(f(X,w) \mathrel {\subseteq }X\)), and V is a valuation function where:
-
(i)
 for each \(w \in P\) and each \(p \in {\textsf {Prop}}\)
for each \(w \in P\) and each \(p \in {\textsf {Prop}}\) -
(ii)
 for each \(w \in \overline{P}\) and each \(\phi \).Footnote 12
for each \(w \in \overline{P}\) and each \(\phi \).Footnote 12
Satisfaction (\(\Vdash \)) is defined as follows. If \(w \in \overline{P}\), then \(\mathcal {I},w \Vdash \phi \) iff \(V(\phi ,w) = 1\). If \(w \in P\), then \(\Vdash \) is defined recursively:

Consequence is defined as preservation of truth over possible worlds: \(\Gamma \vDash \phi \) if for all \(\mathcal {I}= \left\langle W,P,f,V \right\rangle \) and all \(w \in P\), if \(\mathcal {I},w \Vdash \Gamma \), then \(\mathcal {I},w \Vdash \phi \). Since possible worlds are all classical, this notion of consequence is an extension of classical \(\mathbf{S5 }\). But counterfactuals are hyperintensional: even if \(\phi \) and \(\psi \) are logically equivalent (i.e., true at all the same possible worlds in every model), there can still be impossible worlds in some models where \(\phi \) and \(\psi \) differ in truth value.
Note, there are no recursive clauses for how the truth of a complex formula at an impossible world is related to the truth of its constituents. This is because, in order to model logic talk, some impossible worlds need to be logically impossible.Footnote 13 And when it comes to the logically impossible, anything goes: there are impossible worlds where \(\mathbin {\wedge }\) and \(\mathbin {\vee }\) are equivalent, where \(\mathop {\lnot }\nolimits \) is a redundant operator, or even where everything is true. Such worlds are strange, to be sure, but nothing rules them out—in fact, such worlds are needed to fully model logic talk. So there simply is no single set of recursively defined truth conditions that applies to every logical impossibility. This means truth at impossible worlds must be determined by fiat via the valuation function. As we’ll now see, this feature of the impossible worlds semantics causes it difficulties.
4.2 Quantifier problems
To provide a full semantics for metalogical claims, the impossible worlds semantics needs to be capable of being extended to a language that’s capable of solving the regimentation problem, such as hyperlogic. I will now present a challenge to doing this. Specifically, I argue that the impossible worlds semantics, as stated, faces difficulties adequately interpreting propositional quantifiers.
The standard semantics for propositional quantifiers (\(\mathbf{S5 }\pi +\)) interprets them as quantifiers ranging over sets of worlds (Fine , 1970). So where \(\mathcal {M}= \left\langle W,V \right\rangle \) is a possible worlds model and where \(X \mathrel {\subseteq }W\), let \(V^p_X\) be like V except that \(V^p_X(p,w) = 1\) iff \(w \in X\) and let \(\mathcal {M}^p_X = \left\langle W,V^p_X \right\rangle \). Then here is the semantics for propositional quantifiers in \(\mathbf{S5 }\pi +\):

In words,  is true iff \(\phi \) is true on every interpretation of p, where “an interpretation of p” is just an assignment of p to some possible-worlds proposition (i.e., a set of possible worlds).
is true iff \(\phi \) is true on every interpretation of p, where “an interpretation of p” is just an assignment of p to some possible-worlds proposition (i.e., a set of possible worlds).
Importing this into the impossible worlds semantics, we get something like the following. Where \(\mathcal {I}= \left\langle W,P,f,V \right\rangle \), let \(V^p_X\) be like V except that \(V^p_X(p,w) = 1\) iff \(w \in X\), and let \(\mathcal {I}^p_X = \left\langle W,P,f,V^p_X \right\rangle \). Then:

Thus, propositional quantifiers have essentially the same meaning as in \(\mathbf{S5 }\pi +\), except now p can denote a more fine-grained proposition, viz., a set of worlds that may include some impossible worlds, too.Footnote 14
The problem with this proposal is that \(V^p_X\) only changes the truth of p at impossible worlds, not the truth of complex formulas involving p. To see why this is an issue, consider the following inference (where \(q \ne p\)):

Intuitively, this is invalid: just because one contradiction (e.g., \(q \mathbin {\wedge }\mathop {\lnot }\nolimits q\)) counterfactually implies q, it does not follow that all contradictions do (at least, not if we want counterfactuals to be hyperintensional). Yet, according to the semantics for propositional quantifiers above, it is valid precisely because changing the interpretation of p does not change the interpretation of \(p \mathbin {\wedge }\mathop {\lnot }\nolimits p\), i.e., \(V^p_X(p \mathbin {\wedge }\mathop {\lnot }\nolimits p,w) = V(p \mathbin {\wedge }\mathop {\lnot }\nolimits p,w)\).Footnote 15
This problem suggests we need to define \(V^p_X\) so that it differs from V not just on the interpretation p but also on the interpretation of complex formulas involving p. The trouble is that it is not clear how to do this. Again, when it comes to the logically impossible, anything goes. How do we know whether some arbitrary impossible world is supposed to be one that allows contradictions? And even if it does, how do we know which interpretations of p generate contradictions? Without further guidance, we simply have no way of knowing how we are allowed to interpret \(p \mathbin {\wedge }\mathop {\lnot }\nolimits p\) at an impossible world given an arbitrary interpretation of p.
We might try to solve this problem by simply quantifying over all the ways of interpreting complex formulas from interpretations of their constituents. More precisely, let \(V' \sim _p V\) iff \(V'\) is like V except for how it interprets formulas with p. Then the proposal is:

Unfortunately, this won’t work either. Consider the following argument (where p doesn’t occur free in \(\phi \)):

Clearly, this argument is not valid: there is no contradiction that would be true if intuitionistic logic were correct. But on these truth conditions for the quantifiers, it is valid: assuming \(\phi \) is impossible, our witness can be a \(V'\) like V in every way except \(V'(p \mathbin {\wedge }\mathop {\lnot }\nolimits p,u) = 1\) iff  .
.
The problem is that some impossible worlds are meant to be governed by specific nonclassical logics. Intuitively, we only want to quantify over propositions that conform to the logic of a world. On the current truth conditions, though, there are no constraints on which interpretations of complex formulas we can quantify over. So we can quantify over interpretations of formulas that violate those logics at those worlds.
To solve this problem, we need to equip worlds with something like a semantics for the connectives, i.e., a set of rules that tell us how to interpret complex formulas given an interpretation of their constituents. That way, when we reinterpret the atomics, the semantics will automatically give guidance for how that changes the interpretation of complex formulas. As we’ll see, that is exactly what the hyperconvention semantics provides.
5 The hyperconvention semantics
I now present an alternative semantics, the hyperconvention semantics, for hyperlogic. This semantics is based on Kocurek and Jerzak’s (2021) “logical expressivist” semantics for counterlogicals, which relativizes truth to a shiftable parameter (a “hyperconvention”) that provides the interpretation of the logical connectives (Muñoz , 2020; Muskens , 1991; Williamson , 2009). I build off this semantics to develop a semantics for hyperlogic. In Sect. 5.5, I’ll show how this semantics avoids the problems plaguing the impossible worlds semantics from Sect. 4.2.
5.1 Hyperconventions
Kocurek and Jerzak are primarily concerned with counterlogicals, i.e., counterfactuals with logically impossible antecedents. They argue that counterlogicals can only be semantically nonvacuous if we are allowed to shift the interpretation of the logical connectives. This because, they argue, if we hold fixed what words like ‘not’ and ‘or’ actually mean when evaluating (17), then we would expect (for the usual Kripkean reasons) that (17) is trivially true, whereas it clearly seems false.

To capture this thought, they introduce the notion of a hyperconvention (inspired by Gibbard’s (2003) notion of a hyperplan). Hyperconventions provide an interpretation of the modal language \({\mathcal {L}}\), including the logical connectives. They model the interpretation of a connective as an operation on sets of worlds—intuitively, an ordinary possible worlds proposition. For instance, a hyperconvention c will map \(\mathop {\lnot }\nolimits \) to a function \(c(\mathop {\lnot }\nolimits )\) from propositions to propositions. They then relativize truth to a world and a hyperconvention. So \(\mathop {\lnot }\nolimits \phi \) is true at w according to c iff \(w \in c(\mathop {\lnot }\nolimits )(X)\) where X is the proposition expressed by \(\phi \) according to c.
Kocurek and Jerzak motivate this semantics by situating it in a more general philosophy of logic (what they call “logical expressivism”) on which purely logical claims are expressions of commitments to logics. Expressions of logical commitments are meant to contrast with factual claims about “the one true logic” or descriptive claims about how speakers actually use logical vocabulary. Rather, their picture is that speakers have a range of factual beliefs as well as commitments to using language in a certain fashion. Such commitments are not automatically determined by the speaker’s factual beliefs, but can be informed by them (like an intention or a plan).Footnote 16
In what follows, I want to build off this idea to develop a semantics for hyperlogic. To be clear, we do not need to endorse Kocurek and Jerzak’s logical expressivism to do this. We can, if we wish, interpret the hyperconvention parameter as a purely factual one (e.g., determined by the way speakers at a world use logical vocabulary). In employing the hyperconvention semantics, we need not take a stand on these controversial issues. The crucial idea, for our purposes, is to separate out the semantic contributions of the interpretation of the connectives from the world parameter so that the two can be shifted independently.
Let’s define the notion of a hyperconvention more formally.Footnote 17
Definition 1
(Hyperconvention) Let \(\pi _{}\) be a new symbol not in the signature of \({\mathcal {H}}\). A hyperconvention over a set W is a function c with domain  such that:
such that:
-
(i)
\(c(\pi _{}) \mathrel {\subseteq }\mathop {\wp }W\) (the proposition space of c, written as \(\pi _{c}\))
-
(ii)
\(c(p) \in \pi _{c}\) for all \(p \in {\textsf {Prop}}\)
-
(iii)
 where
where 
-
(iv)
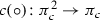 where
where 
-
(v)
 .
.
For readability, we may write \(\star _c\) (with infix notation) instead of \(c(\star )\). Let \(\mathbb {H}_{W}\) be the set of all hyperconventions over W.
A convention over W is a nonempty set of hyperconventions over W. Let \(\mathbb {C}_{W} = \mathop {\wp ^+}\mathbb {H}_{W}\) be the set of conventions over W.
Notice I have not placed any constraints on the possible interpretations of \(\mathbin {\rhd }\). We don’t require \(\mathbin {\rhd }\) obey any sort of structural rule (commutativity, contraction, etc.). We don’t even require \(\mathbin {\rhd }\) to be factive (so that \(\mathbin {\rhd }_c X \mathrel {\subseteq }X\)) or noncontingent (so that  is always either W or \(\emptyset \)).Footnote 18 This is mainly for the sake neutrality, as I do not want to take a stand on what entailment relations count as “genuine” logics. Ultimately, we will let the models determine which interpretations of \(\mathbin {\rhd }\), or any of the other connectives, are to be considered.
is always either W or \(\emptyset \)).Footnote 18 This is mainly for the sake neutrality, as I do not want to take a stand on what entailment relations count as “genuine” logics. Ultimately, we will let the models determine which interpretations of \(\mathbin {\rhd }\), or any of the other connectives, are to be considered.
Most logics can be represented by a convention, i.e., a set of hyperconventions. In fact, it can be shown that any (finitary, single-conclusion) logic over \({\mathcal {L}}\) can be represented by a convention assuming W is infinite (§A). One can often represent the most commonly discussed logics using a possible worlds semantics for that logic.
To illustrate, let’s consider a convention representing an intuitionistic propositional logic (I’ll ignore modal operators for now). Let \(\mathcal {K} = \left\langle W,\le \right\rangle \) be an intuitionistic Kripke frame. Let \(C_{\mathcal {K}}\) be the set of hyperconventions c satisfying the constraints below:

Then \(C_{\mathcal {K}}\) represents the logic of \(\mathcal {K}\): any propositional \(\phi \) is intuitionistically valid over \(\mathcal {K}\) iff  for each \(c \in C_{\mathcal {K}}\) (where
for each \(c \in C_{\mathcal {K}}\) (where  ; see Definition 5 in Sect. 5.3).
; see Definition 5 in Sect. 5.3).
It is essential to this example that \(\pi _{c}\) is not the full powerset. Otherwise, \(p \mathbin {\rhd }\mathop {\lnot }\nolimits \mathop {\lnot }\nolimits p\) would be falsifiable in \(C_{\mathcal {K}}\)—that is, \(c(p) \mathrel {\not \subseteq }\mathop {\lnot }\nolimits _c\mathop {\lnot }\nolimits _c c(p)\) for some \(c \in C_{\mathcal {K}}\)—and so \(C_{\mathcal {K}}\) would not represent intuitionistic logic.Footnote 19 It is crucial to the intuitionistic Kripke semantics that truth is persistent under \(\le \): if w satisfies \(\phi \) and \(w \le v\), then v satisfies \(\phi \). The “counterexamples” to double negation introduction involve sets that are not upward closed under \(\le \). Most nonclassical logics come equipped with a view about what counts as a proposition. In order to represent a logic, one must ensure the proposition space captures the relevant notion of a proposition for that logic.
5.2 Three notions of proposition
Again, the key idea behind the hyperconvention semantics is to evaluate truth relative to a world and a hyperconvention. That way, according-to operators can shift the interpretation of the connectives by shifting the hyperconvention parameter of points of evaluation or “indices”. Thus, indices need to be defined as world-hyperconvention pairs.
Definition 2
(Index) Given a set of hyperconventions H over W, an index over H is a pair \(\left\langle w,c \right\rangle \) where \(w \in W\) and \(c \in H\). Let \(\mathbb {I}_{H} = W \mathrel {\times }H\) be the set of indices over H. Where \(A \mathrel {\subseteq }\mathbb {I}_{H}\), let  .
.
Since truth is evaluated relative to worlds and hyperconventions, there are several notions of a “proposition” in this semantics, each of which play an important role. First, there is a coarse-grained notion of a proposition as a set of worlds. World propositions act as the interpretation of propositional variables relative to a hyperconvention; operations over world propositions act as the interpretation of the connectives relative to a hyperconvention. Second, there is a more fine-grained notion of a proposition as a set of indices. Index propositions act as the refined compositional semantic values of formulas assigned by our model.
There is also a third, intermediate notion of a proposition worth discussing: sets of indices A where, relative to any hyperconvention c, the set of worlds A(c) is in the proposition space of c.
Definition 3
(Visible proposition) Given a set of hyperconventions H over W, a visible proposition over H is a set of indices \(A \mathrel {\subseteq }\mathbb {I}_{W}\) such that \(A(c) \in \pi _{c}\) for all \(c \in \mathbb {H}_{W}\). Let \(\mathbb {P}_{H}\) be the set of visible propositions over H. I’ll use \(X,Y,\dots \) for world propositions, \(A,B,\dots \) for index propositions, and \(P,Q,\dots \) for visible propositions.
Observe that if H is nonempty, then \(\mathbb {P}_{H}\) is nonempty, since the proposition space of any hyperconvention is nonempty. In particular, c(p) is always a member of \(\pi _{c}\) by clause (ii) of Definition 1. Thus, the index proposition \(P_p\), where \(P_p(c) = c(p)\) for all c, is visible.
Visible index propositions are the kind of proposition that the propositional quantifiers range over. We do not want quantifiers to range over all index propositions. For if they did, it would be too easy to refute a law of logic according to a nonclassical logic. To illustrate, recall the example from Sect. 5.1 of the convention \(C_{\mathcal {K}}\) representing intuitionistic logic. We saw that if the proposition space of every \(c \in C_{\mathcal {K}}\) were unrestricted, we could find counterexamples to double negation introduction (\(p \mathbin {\rhd }\mathop {\lnot }\nolimits \mathop {\lnot }\nolimits p\)), which is intuitionistically valid. Similarly, if the domain of propositional quantification were to include every index proposition, we could find counterexamples to the quantified version of double negation introduction ( ).Footnote 20 By contrast, if we restrict the domain of propositional quantification to visible propositions, no such counterexample can be constructed.
).Footnote 20 By contrast, if we restrict the domain of propositional quantification to visible propositions, no such counterexample can be constructed.
5.3 Semantics
We are now ready to present the semantics more explicitly. The models of our semantics must specify (i) a set of states (or “worlds”), (ii) a domain of admissible conventions, (iii) a domain of admissible (visible) propositions, and (iv) a valuation function.Footnote 21
Definition 4
(Hypermodel) A hypermodel is a tuple of the form \(\mathcal {M}= \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},V \right\rangle \), where:
-
\(W \ne \emptyset \) is a state space
-
\(D_{\mathbb {C}}\mathrel {\subseteq }\mathbb {C}_{W}\) is a convention domain; we also define \(D_{\mathbb {H}}= \bigcup D_{\mathbb {C}}\) to be the hyperconvention domain
-
\(D_{\mathbb {P}}\mathrel {\subseteq }\mathbb {P}_{D_{\mathbb {H}}}\) is a proposition domain such that:
-
(i)
for all \(p \in {\textsf {Prop}}\), \(P_p \in D_{\mathbb {P}}\), where \(P_p(c) = c(p)\)
-
(ii)
for all \(c \in D_{\mathbb {H}}\) and \(X \in \pi _{c}\), there is a \(P \in D_{\mathbb {P}}\) where \(P(c) = X\)
-
(i)
-
V is a valuation such that:
-
(i)
\(V(p) \in D_{\mathbb {P}}\)
-
(ii)
\(V(l) \in D_{\mathbb {C}}\)
-
(iii)

-
(i)
where x is a variable and \(\nu \) is a possible value for that variable, we write \(V^x_\nu \) for the valuation like V except that \(V^x_\nu (x) = \nu \). We likewise write \(\mathcal {M}^x_\nu \) for \(\left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},V^x_\nu \right\rangle \).
I have imposed two very weak requirements on the domain of propositional quantification, largely for technical convenience. First, the index proposition that picks out the interpretation of p at each hyperconvention must be included in the domain. This ensures that hyperconventions that assign different world propositions to the atomics are not indiscernible.Footnote 22 Second, each world proposition in a hyperconvention’s proposition space must be picked out by some index proposition in the domain. This rules out “propositional impossibilia”, i.e., world propositions that from the model’s perspective do not exist.
Finally, here is the semantics:
Definition 5
(Semantics) Where  :
:

where  .
.
Here is an informal statement of the semantic clauses. Propositional variables denote visible index propositions; so p is true at \(\left\langle w,c \right\rangle \) iff w is a member of the world proposition assigned to p at c. Interpretation terms denote conventions, i.e., sets of hyperconventions; so \(\iota \) is true at \(\left\langle w,c \right\rangle \) iff c is a member of the convention denoted by \(\iota \), i.e., \(\iota \) denotes a “correct” convention from c’s perspective. Connectives denote intensional operations; so (e.g.) \(\mathop {\lnot }\nolimits \phi \) is true at \(\left\langle w,c \right\rangle \) iff (i)  denotes a world proposition that exists according to c, and (ii) the operation c assigns to \(\mathop {\lnot }\nolimits \), when applied to
denotes a world proposition that exists according to c, and (ii) the operation c assigns to \(\mathop {\lnot }\nolimits \), when applied to  , yields a world proposition that is true at w. Quantifiers range over interpretations of the propositional variables; so (e.g.)
, yields a world proposition that is true at w. Quantifiers range over interpretations of the propositional variables; so (e.g.)  is true at \(\left\langle w,c \right\rangle \) iff \(\phi \) is true at \(\left\langle w,c \right\rangle \) on any interpretation of p within the proposition domain. According-to operators quantify over the hyperconventions in a convention; so \(\mathop {@}\nolimits _\iota \phi \) is true at \(\left\langle w,c \right\rangle \) iff \(\phi \) is true at w on any maximally specific convention compatible with the convention denoted by \(\iota \). Finally, the binder is a device for keeping track of individual hyperconventions; so \(\mathop {\downarrow }\nolimits i.\phi \) is true at \(\left\langle w,c \right\rangle \) iff \(\phi \) is true at \(\left\langle w,c \right\rangle \) when we reassign i to denote
is true at \(\left\langle w,c \right\rangle \) iff \(\phi \) is true at \(\left\langle w,c \right\rangle \) on any interpretation of p within the proposition domain. According-to operators quantify over the hyperconventions in a convention; so \(\mathop {@}\nolimits _\iota \phi \) is true at \(\left\langle w,c \right\rangle \) iff \(\phi \) is true at w on any maximally specific convention compatible with the convention denoted by \(\iota \). Finally, the binder is a device for keeping track of individual hyperconventions; so \(\mathop {\downarrow }\nolimits i.\phi \) is true at \(\left\langle w,c \right\rangle \) iff \(\phi \) is true at \(\left\langle w,c \right\rangle \) when we reassign i to denote  .
.
Let me note one feature of the semantics that some may find questionable: iterated according-to operators are redundant in that \(\mathop {@}\nolimits _\iota \mathop {@}\nolimits _\kappa \phi \) is semantically equivalent to \(\mathop {@}\nolimits _\kappa \phi \). Thus, all logics agree on what holds according to all other logics. Just speaking for myself, I do not have clear intuitions about whether this is correct. In general, it is unclear how to interpret a sentence like (18).

In one sense, (18) seems false: intuitionistic logic doesn’t say anything about what laws hold according to classical logic. But in another sense, (18) seems true: according to intuitionistic logic, classical logic is incorrect precisely because the law of excluded middle holds according to it. In other words, if intuitionistic logic “says nothing” about what holds according to classical logic, then it “says nothing” about whether classical logic is correct.
I suspect there are simply two ways to hear (18). For simplicity, I’ve chosen to set this issue aside and treat iterated according-to operators as redundant. This is in line with how these operators standardly work in hybrid logic and it simplifies the formalism greatly. But I acknowledge one may want to generalize hyperlogic to allow for nonredundant iteration of according-to operators. There are ways of generalizing the framework to accomplish this, but I want to set this complication aside. I view this redundancy as an idealizing assumption that requires further investigation, rather than the final say on the logic of according-to operators.
5.4 Consequence
In the hyperconvention semantics, there are two notions of consequence we can define. There is a classical notion of consequence, i.e., truth-preservation relative to a classical interpretation of the connectives. There is also a universal notion of consequence, i.e., consequence no matter how we interpret the connectives.
To make this precise, I need to explain what a “classical” convention is. Throughout, I will use \({cl}\) as a designated classical interpretation nominal.
Definition 6
(Classical hyperconvention) A hyperconvention c over W is classical if for all \(X,Y \in \pi _{c}\):

and for all  :
:

A convention is classical if all of its member are classical. A hypermodel \(\mathcal {M}\) is classical if \(V({cl})\) is classical.
If c is classical, then the truth conditions for the connectives reduce to their classical ones and, moreover, \(\mathbin {\rhd }\) reduces to necessary implication:  .
.
Definition 7
(Consequence) Where \(\Gamma \mathrel {\subseteq }{\mathcal {H}}\) and \(\phi \in {\mathcal {H}}\):
-
\(\Gamma \) classically entails \(\phi \), written \(\Gamma \vDash \phi \), if for any classical hypermodel \(\mathcal {M}= \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},V \right\rangle \), any \(w \in W\), and any \(\underline{c \in V({cl})}\):

-
\(\Gamma \) universally entails \(\phi \), written
 , if for any classical hypermodel \(\mathcal {M}= \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},V \right\rangle \), any \(w \in W\), and any \(\underline{c \in D_{\mathbb {H}}}\):
, if for any classical hypermodel \(\mathcal {M}= \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},V \right\rangle \), any \(w \in W\), and any \(\underline{c \in D_{\mathbb {H}}}\): 
Note universal entailment is still restricted to classical hypermodels, even though it requires truth-preservation over any hyperconvention. This restriction is largely a matter of formal convenience, as it allows us to rigidly refer back to classical logic (or rather, a classical interpretation of the connectives) using \({cl}\). Universal entailment, however, still requires truth preservation over any hyperconvention, even nonclassical ones.
In Sect. 3, I noted that classical validity and universal validity can be defined in terms of one another. I now make this observation precise.
Theorem 8
(Embedding Validity). Let \(\Gamma \mathrel {\subseteq }{\mathcal {H}}\) and \(\phi \in {\mathcal {H}}\). Where l is an interpretation nominal, let  .
.
-
(a)
Assume \(l \ne {cl}\) does not occur anywhere in \(\Gamma \) or in \(\phi \). Then
 iff \(\mathop {@}\nolimits _l\Gamma \vDash \mathop {@}\nolimits _l\phi \).
iff \(\mathop {@}\nolimits _l\Gamma \vDash \mathop {@}\nolimits _l\phi \). -
(b)
\(\Gamma \vDash \phi \) iff
 .
.
Proof
The only interesting direction is the right-to-left direction of (a). Suppose \(\mathop {@}\nolimits _l\Gamma \vDash \mathop {@}\nolimits _l\phi \) and \(\mathcal {M},w,c \Vdash \Gamma \). Let \(\mathcal {M}^l_c = \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},V^l_c \right\rangle \), where \(V^l_c\) is exactly like V except that  . By a simple induction on formulas, if \(\chi \) does not contain l, then \(\mathcal {M},w,c \Vdash \chi \) iff \(\mathcal {M}^l_c,w,c \Vdash \chi \). Hence, \(\mathcal {M}^l_c,w,c \Vdash \Gamma \), and so \(\mathcal {M}^l_c,w,c' \Vdash \mathop {@}\nolimits _l\Gamma \) for each \(c' \in V^l_c({cl})\). By supposition, \(\mathcal {M}^l_c,w,c' \Vdash \mathop {@}\nolimits _l\phi \), in which case \(\mathcal {M}^l_c,w,c \Vdash \phi \). Therefore, \(\mathcal {M},w,c \Vdash \phi \).
. By a simple induction on formulas, if \(\chi \) does not contain l, then \(\mathcal {M},w,c \Vdash \chi \) iff \(\mathcal {M}^l_c,w,c \Vdash \chi \). Hence, \(\mathcal {M}^l_c,w,c \Vdash \Gamma \), and so \(\mathcal {M}^l_c,w,c' \Vdash \mathop {@}\nolimits _l\Gamma \) for each \(c' \in V^l_c({cl})\). By supposition, \(\mathcal {M}^l_c,w,c' \Vdash \mathop {@}\nolimits _l\phi \), in which case \(\mathcal {M}^l_c,w,c \Vdash \phi \). Therefore, \(\mathcal {M},w,c \Vdash \phi \).
In Sect. 3, I said we could explain the relative goodness of patterns of reasoning with logic talk by appealing to a notion of consequence where the premises entail the conclusion “regardless of one’s views about logic”. Universal consequence can capture this notion of relative goodness. For instance, \(\mathop {@}\nolimits _\iota \phi \) and \(\iota \) universally entail \(\phi \), which explains why inferences like (13) seem good. Thus, the logic of hyperlogic has the requisite features needed to fully resolve the regimentation problem.
5.5 Counterfactuals
Now let’s look at how the hyperconvention semantics would handle counterfactuals. One simple way to do this is to combine the hyperconvention semantics in Sect. 5.3 with Kocurek and Jerzak’s (2021) logical expressivist semantics for counterfactuals. On this approach, counterfactuals are allowed to shift hyperconventions, so that the antecedent and consequent may be evaluated relative to other logics.Footnote 23 Like with the standard selection semantics, we may assume that which hyperconventions the counterfactual may shift to will depend on the context (specifically, on which indices count as “closer” or “more similar” to the starting index in that context). Thus, even if two sentences are necessarily equivalent according to our actual conventions, the counterfactual may require taking us to a convention that distinguishes between those sentences.Footnote 24
We can flesh this out formally as follows. Again, just for illustration, I will adopt a selection semantics for counterfactuals.
Definition 9
(Selection hypermodel) A selection hypermodel is a tuple \(\mathcal {M}= \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},f,V \right\rangle \), where \(\left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},V \right\rangle \) is a hypermodel in the sense of Definition 4 and  is a selection function.
is a selection function.
Definition 10
(Selection semantics) Satisfaction is defined as in Definition 5 with the following additional clause:

where  .
.
Simply put:  is true at \(\left\langle w,c \right\rangle \) iff \(\psi \) is true at all the closest indices to \(\left\langle w,c \right\rangle \) where \(\phi \) is true. Again, we could place constraints on f (e.g., \(f(A,w,c) \mathrel {\subseteq }A\)) as desired.
is true at \(\left\langle w,c \right\rangle \) iff \(\psi \) is true at all the closest indices to \(\left\langle w,c \right\rangle \) where \(\phi \) is true. Again, we could place constraints on f (e.g., \(f(A,w,c) \mathrel {\subseteq }A\)) as desired.
Kocurek and Jerzak (2021) prove that their logical expressivist semantics generates the same logic as that of the impossible worlds semantics: \(\Gamma \) entails \(\phi \) in the impossible worlds semantics iff \(\Gamma \) classically entails \(\phi \) in the logical expressivist semantics semantics. Since the hyperconvention semantics is an extension of the logical expressivist semantics, the same holds for the hyperconvention semantics over the quantifier-free and hybrid-free fragment (i.e., over the language \({\mathcal {L}}\) extended with  ). Thus, (classical) consequence in the two semantic theories coincide. In particular, both do equally well at solving the hyperintensionality problem, at least over this restricted language.
). Thus, (classical) consequence in the two semantic theories coincide. In particular, both do equally well at solving the hyperintensionality problem, at least over this restricted language.
But there are two major differences between the semantic theories. First, in the hyperconvention semantics, truth is determined in a uniform, compositional manner: the semantic value of a complex formula is always a function of the semantic value of its parts. It’s just that the “semantic value” of a formula is a set of world-hyperconvention pairs, rather than a set of worlds. By contrast, the semantic value of a formula in the impossible worlds semantics is a set of possible and impossible worlds. In general, two formulas with the same semantic value relative to a model may make different contributions to the semantic value of complex formulas. Thus, even if  , it does not follow that
, it does not follow that  . This is not necessarily a decisive objection to the impossible worlds semantics, but it is a theoretical cost.
. This is not necessarily a decisive objection to the impossible worlds semantics, but it is a theoretical cost.
Second, when we expand the language to include propositional quantifiers, the hyperconvention semantics seems to fare much better than the impossible worlds semantics. Earlier in Sect. 4, we saw that the impossible worlds semantics faced problems interpreting propositional quantifiers in part because impossible worlds do not contain a set of rules for determining truth. This led to the awkward result that either  entails
entails  , or that
, or that  entails
entails  .
.
The hyperconvention semantics overcomes this problem. Hyperconventions are essentially rules for interpreting complex formulas from their constituents. So quantifiers range not only over interpretations of p but also interpretations of complex formulas involving p. As a result,  does not (classically or universally) entail
does not (classically or universally) entail  . But since quantifiers are restricted to visible propositions, they cannot quantify over every way of interpreting a formula. This is a restriction we saw was independently motivated even before we considered counterfactuals. As a result,
. But since quantifiers are restricted to visible propositions, they cannot quantify over every way of interpreting a formula. This is a restriction we saw was independently motivated even before we considered counterfactuals. As a result,  does not (classically or universally) entail that
does not (classically or universally) entail that  . Thus, the hyperconvention semantics enjoys a distinctive advantage over the impossible worlds approach.
. Thus, the hyperconvention semantics enjoys a distinctive advantage over the impossible worlds approach.
With that said, the hyperconvention semantics does not entirely jettison the notion of an impossible world. In a way, world-hyperconvention pairs can be seen as a different model of what an impossible world is. On the standard picture, impossible worlds are ersatz entities, e.g., sets of formulas. In the hyperconvention semantics, impossible worlds are more like worlds “under an alternative description” (i.e., paired with an alternative hyperconvention). The latter determines the former—indeed, every set of \({\mathcal {L}}\)-formulas is the truth set of some world-hyperconvention pair. But unlike the impossible worlds semantics, the hyperconvention semantics achieves this without appealings to separate truth conditions for possible and impossible cases. This allows us to capture the flexibility of impossible worlds as arbitrary sets of formulas while avoiding the challenges facing the impossible worlds semantics in Sect. 4.2.
6 Conclusion
We started with two challenges for developing a semantics for logic talk. First, there’s a regimentation problem: how do we regiment logic talk in the object language so as to be compositionally embeddable? To this question, I proposed hyperlogic as a solution. I argued that it was more satisfactory as a language for regimenting logic talk than the brute-force atomic regimentation.
Second, there’s a hyperintensionality problem: how do we interpret logic talk so that embedding expressions can discern classically equivalent sentences? To this question, I proposed the hyperconvention semantics as a solution. We saw that this semantics avoids the problems plaguing the more common impossible worlds semantics. Yet it does so in a way that still preserves the flexibility of impossible worlds.
In closing, I mention two ways in which hyperlogic can be fruitfully generalized that would be worth further investigation in future research. First, there’s the question of how to extend hyperlogic with attitude verbs, such as a belief operator \(\mathop {\textsf {B}}\nolimits \). A natural proposal would be to add an accessibility relation \(R_{\mathop {\textsf {B}}\nolimits }\) between indices to hypermodels and then interpret \(\mathop {\textsf {B}}\nolimits \) as follows:Footnote 25

This could be useful for addressing the problem of logical omniscience for agents who are perfect reasoners but endorse a nonclassical logic. For instance, while \((\mathop {\rhd }\nolimits \phi ) \mathbin {\rightarrow }\mathop {\textsf {B}}\nolimits \phi \) is not valid, \((\mathop {\textsf {B}}\nolimits \iota \mathbin {\wedge }\mathop {@}\nolimits _\iota (\mathop {\rhd }\nolimits \phi )) \mathbin {\rightarrow }\mathop {\textsf {B}}\nolimits \phi \) is valid (assuming \(\mathbin {\rhd }\) is factive and noncontingent).Footnote 26 In other words, if an agent accepts a (reasonable) logic, their beliefs are closed under that logic, though beliefs need not be closed under classical consequence generally.
However, this prediction may seem unwelcome if we want to model agents who are uncertain or mistaken about what holds according to a specific logic. As it stands, interpretation terms are rigid in the hyperconvention semantics, meaning their denotation does not shift. Thus,  entails
entails  , i.e., agents are always omniscient about what follows from what according to each logic. Similarly,
, i.e., agents are always omniscient about what follows from what according to each logic. Similarly,  entails
entails  for any \(\alpha \), i.e., claims about what follows from what according to a specific logic are counterfactually trivial.
for any \(\alpha \), i.e., claims about what follows from what according to a specific logic are counterfactually trivial.
To avoid this prediction, we would need to allow interpretation nominals to be nonrigid, so that belief operators (and counterfactuals) can shift their interpretation. That way, even if an agent nominally accepts a logic, they may be uncertain or mistaken about what follows according to that logic. Such a revision could also be employed to generalize the semantics so that iterated according-to operators are not redundant.
Second, given that counterfactuals can shift the interpretation of \(\mathop {\lnot }\nolimits \), \(\mathbin {\wedge }\), and so on, it would be natural to wonder whether counterfactuals can shift the interpretation of counterfactuals as well. Even if we accept that  is valid, we may want to consider logics where it is not, and even counterfactually entertain its failure (‘If
is valid, we may want to consider logics where it is not, and even counterfactually entertain its failure (‘If  weren’t valid,...’).
weren’t valid,...’).
Furthermore, though hyperconventions constrain the domain of propositional quantifiers, the basic meaning of the quantifiers is held fixed across hyperconventions. But different logics often provide different semantics for the propositional quantifiers, too. Thus, one may want hyperconventions to control the interpretation of propositional quantifiers.
As it stands, we cannot simply have hyperconventions interpret counterfactuals and quantifiers as with the other connectives. The problem is that the meanings of these expressions depend not just on the hyperconvention of evaluation but other hyperconventions as well. Thus, on pain of set-theoretic circularity, we could not have  since c itself occurs in \(D_{\mathbb {H}}\), and so appears in \(\mathbb {P}_{D_{\mathbb {H}}}\).
since c itself occurs in \(D_{\mathbb {H}}\), and so appears in \(\mathbb {P}_{D_{\mathbb {H}}}\).
One strategy for dealing with this is to introduce a set of “markers”, which act as pointers to operations on sets of indices. Then hyperconventions can map  to one of these markers, thereby indirectly specifying how to interpret
to one of these markers, thereby indirectly specifying how to interpret  . (A similar strategy can apply to propositional quantifiers.) More precisely, a hypermodel will now be a tuple of the form \(\mathcal {M}= \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},M,F,V \right\rangle \), where M is some nonempty set of “markers” and F maps each \(m \in M\) to an binary operation on sets of indices, i.e.,
. (A similar strategy can apply to propositional quantifiers.) More precisely, a hypermodel will now be a tuple of the form \(\mathcal {M}= \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},M,F,V \right\rangle \), where M is some nonempty set of “markers” and F maps each \(m \in M\) to an binary operation on sets of indices, i.e.,  . We revise the definition of hyperconventions so that
. We revise the definition of hyperconventions so that  , and revise the clause for counterfactuals:
, and revise the clause for counterfactuals:

A hyperconvention in this sense is classical if  is a selection function in the sense of Definition 9. Thus, in shifting the hyperconvention, we may also shift the interpretation of the counterfactual.
is a selection function in the sense of Definition 9. Thus, in shifting the hyperconvention, we may also shift the interpretation of the counterfactual.
Notes
Indeed, this project is in many ways connected to work in relevant logic (Dunn and Restall , 2002; Mares , 2004; Mares , 2020). I view hyperlogic as a step towards developing what Routley (2019) calls a “universal logic”: a logic that’s “applicable in every situation whether realised or not, possible or not” (see Nolan (2018) for a critical overview of Routley’s program). The approach taken here will be different from Routley’s in that I aim to develop a universal logic within a classical framework, rather than revise the base logic. Other choices of background logic may be equally (or even more) fruitful as starting points (Girard and Weber , 2015; Weber , 2014; Weber et al. , 2016). It would be also worth investigating how the hybrid aspects of hyperlogic change in nonclassical settings; see Braüner (2006, 2011); Braüner and de Paiva (2006); Chadha et al. (2006) for work on intuitionistic hybrid logic, as well as Standefer (2020) for work on relevant logics for ‘actually’.
Of course, (14) and (16) may be invalid on a stricter notion of validity. For example, these arguments could be deemed invalid in the sense of relevant logic (Anderson and Belnap , 1975; Dunn and Restall , 2002; Mares , 2004; Mares , 2020). Again, my assumption of a classical background logic is just a starting point. Alternative choices of background logic might lead to different views on what exactly is wrong with these arguments (see Weber (2014); Girard and Weber (2015); Weber et al. (2016) for semantical analyses within nonclassical metatheory). My claim is just that these arguments seem bad in some sense that is not accounted for by saying they’re invalid on a classical conception of validity.
We could add other connectives to the language, including those that arise in nonclassical logics such as “intensional” conjunction and disjunction operators from relevant logic (Dunn and Restall , 2002) or exponentials from linear logic (Di Cosmo and Miller , 2019). But I will stick with the standard “boolean” connectives for ease of exposition.
We could make \(\mathbin {\rhd }\) right-multigrade also to account for multiple-conclusion logics, but we’ll set this complication aside.
The idea to introduce hybrid operators of this sort comes from Kocurek and Jerzak (2021), though they introduce it for different reasons, viz., to distinguish between convention-shifting readings of counterlogicals from non-shifty readings. I’ll discuss Kocurek and Jerzak’s (2021) motivation in Sect. 5.1.
One complication with this regimentation of (4): it’s not entirely clear how we should regiment a law’s failure according to some logic. There are at least three ways a law \(\lambda \) can “fail” for a logic l. There’s an “external” notion: \(\lambda \) externally fails for l if it’s not the case that according to l, \(\lambda \) holds (\(\mathop {\lnot }\nolimits \mathop {@}\nolimits _l\lambda \)). There’s also an “internal” notion: \(\lambda \) internally fails for l if its negation holds according to l (\(\mathop {@}\nolimits _l\mathop {\lnot }\nolimits \lambda \)). Finally, there is a third, intermediate “classical” notion: \(\lambda \) classically fails for l if according to l, \(\lambda \) does not hold, where the ‘not’ here is interpreted as classical negation. This is the notion of failure we get by holding fixed what we actually mean by ‘fails’ or ‘does not hold’ (given our background logic is classical) within the scope of according-to operators. Thus, we can regiment this notion using the \(\mathop {\downarrow }\nolimits \) binder (\(\mathop {@}\nolimits _l\mathop {\downarrow }\nolimits i.\mathop {@}\nolimits _{cl}\mathop {\lnot }\nolimits \mathop {@}\nolimits _i\lambda \)). For concreteness, I have regimented (4) using the internal notion, but nothing in what follows hinges on this choice.
See Nolan (1997); Vander Laan (2004); Krakauer (2012); Brogaard and Salerno (2013); Jago (2014); Kment (2014); Berto et al. (2018); Berto and Jago (2019); French et al. (2020). There are other approaches to hyperintensionality that I do not have space to consider here. See Fine (2012); Schaffer (2016); Wilson (2018); Leitgeb (2019) for some prominent examples. For an overview of different approaches to hyperintensionality, see Berto and Nolan (2021).
My implementation of the impossible worlds approach to counterfactuals is largely in line with that of French et al. (2020). See also Mares (1997); Nolan (1997); Brogaard and Salerno (2013); Kment (2014); Berto et al. (2018) for other examples. This semantics is closely related to the Routley-Meyer semantics for relevant logics; see Mares (2004) for an overview.
Following Tanaka (2018), this clause could be generalized so that formulas can take multiple (or no) truth values at an impossible world. This additional complication does not affect the main arguments below, however, so I will set this aside.
As Tanaka (2018) and Sandgren and Tanaka (2020) note, there are two senses in which a world can be logically impossible: it can be logically different, in that the laws of logic differ from the actual laws, or it can contain a violation of a logical law (Kocurek and Jerzak, 2021: pp. 22–23 on actual vs. counterfactual logical impossibility). Here, by “logically impossible”, I mean to neutrally refer to either notion of logical impossibility. The semantics provided in Sect. 5 can represent either kind of logical impossibility.
Nolan (1997: p. 563) argues that not every set of impossible worlds counts as a proposition. Thus, we may want to include in our models a domain of sets of worlds the quantifiers can range over. (So the semantics would be closer to \(\mathbf{S5 }\pi \).) This won’t affect the substantive points in what follows, however.
Proof: suppose
 where \(\mathcal {I}= \left\langle W,P,f,V \right\rangle \) and \(w \in P\). Let \(X \mathrel {\subseteq }W\). Since possible worlds are classically consistent,
where \(\mathcal {I}= \left\langle W,P,f,V \right\rangle \) and \(w \in P\). Let \(X \mathrel {\subseteq }W\). Since possible worlds are classically consistent,  . But since \(V^p_X\) doesn’t reassign the truth of \(p \mathbin {\wedge }\mathop {\lnot }\nolimits p\), \(V^p_X(p \mathbin {\wedge }\mathop {\lnot }\nolimits p,v) = V(p \mathbin {\wedge }\mathop {\lnot }\nolimits p,v)\) for all \(v \in \overline{P}\). Hence,
. But since \(V^p_X\) doesn’t reassign the truth of \(p \mathbin {\wedge }\mathop {\lnot }\nolimits p\), \(V^p_X(p \mathbin {\wedge }\mathop {\lnot }\nolimits p,v) = V(p \mathbin {\wedge }\mathop {\lnot }\nolimits p,v)\) for all \(v \in \overline{P}\). Hence,  , and so
, and so  . Moreover, since \(q \ne p\), \(V^p_X(q,w) = V(q,w)\), and so
. Moreover, since \(q \ne p\), \(V^p_X(q,w) = V(q,w)\), and so  . Therefore, if
. Therefore, if  for any \(X \mathrel {\subseteq }W\), then it holds for all X. In other words,
for any \(X \mathrel {\subseteq }W\), then it holds for all X. In other words,  entails
entails  .
.This view can be seen as a species of logical pluralism (Beall and Restall , 2006), though the latter is a broader category. Kocurek and Jerzak (2021: p. 17) argue that logics are effectively semantic conventions governing logical vocabulary. According to logical expressivism, adopting a logic is akin to adopting a language: just as there is no such thing as “the one true” semantic convention, so too, there is no such thing as “the one true” logic.
Since Kocurek and Jerzak’s (2021) semantics does not include propositional quantifiers or an entailment operator, we need to generalize their notion of a hyperconvention.
One reason to allow \(\mathbin {\rhd }\) to be noncontingent is to model logics such as \(\mathbf{K3 }\) on which there are no logical validities. It would be natural to capture this fact about \(\mathbf{K3 }\) with the formula
 . But if entailment facts are necessary, then this formula will be falsifiable.
. But if entailment facts are necessary, then this formula will be falsifiable.Proof: let \(w \in W\) be such that there is a \(w' > w\) in W. Let
 . Then:
. Then: 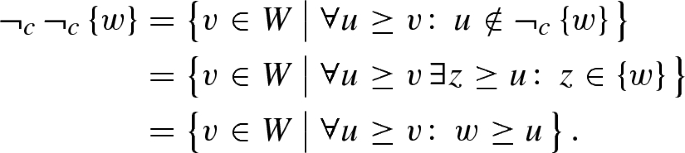
But
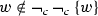 , since \(w' \ge w\) but \(w \ngeq w'\). Thus,
, since \(w' \ge w\) but \(w \ngeq w'\). Thus,  .
.Proof: just pick an index proposition whose restriction to some \(c \in C_{\mathcal {K}}\) is
 .
.While Kocurek and Jerzak (2021) model logics (which are the referents of interpretation terms) as hyperconventions, this proposal is too stringent for our purposes, as it would require logics to provide interpretations of every propositional variable. To avoid this concern, we can let the interpretation terms denote conventions, i.e., sets of hyperconventions (Kocurek and Jerzak, 2021, fn. 21).
Note, however, that V(p) need not be \(P_p\); this is essential, since quantifiers need to be capable of reinterpreting atomics.
Note, this does not mean that counterfactuals are “metalinguistic” in the sense of being about language or conventions. Rather, the semantics models hyperintensionality by allowing counterfactuals to shift the conventions used to interpret material in their scope. Compare: quantifiers shift variable assignments, but that doesn’t mean they’re “about” variable assignments.
We could remove relativization to c and say \(R_{\mathop {\textsf {B}}\nolimits }\) relates worlds to indices. Either approach would be fine for our purposes.
If an agent accepts a logic that is not factive (so a validity might be false) or is contingent (so a validity need not be necessarily valid), we should not expect their beliefs to be closed under that logic anyway.
References
Anderson, Alan R., & Belnap, Nuel D. (1975). Entailment: The logic of relevance and neccessity. Princeton University Press.
Areces, C., & ten Cate, B. (2006). Hybrid logics. In P. Blackburn, F. Wolter, & J. van Benthem (Eds.), Handbook of modal logic (pp. 821–868). Elsevier.
Bacon, A. (2020). Logical combinatorialism. The Philosophical Review, 129, 537–589.
Beall, J. C., & Restall, G. (2006). Logical pluralism. Oxford: Oxford University Press.
Berto, F., French, R., Priest, G., & Ripley, D. (2018). Williamson on counterpossibles. Journal of Philosophical Logic, 47, 693–713.
Berto, F., & Jago, M. (2019). Impossible worlds. Oxford University Press.
Berto, F., & Nolan, D. (2021). Hyperintensionality. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy. Metaphysics Research Lab, Stanford University.
Braüner, T. (2006). Axioms for classical, intuitionistic, and paraconsistent hybrid logic. Journal of Logic, Language, and Information, 15, 179–194.
Braüner, T. (2011). Intuitionistic hybrid logic: Introduction and survey. Information and Computation, 209, 1437–1446.
Braüner, T. (2017). Hybrid Logic. In E. N. Zalta (ed.), The stanford encyclopedia of philosophy. Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/sum2017/entries/logic-hybrid/
Braüner, T., & de Paiva, V. (2006). Intuitionistic hybrid logic. Journal of Applied Logic, 4, 231–255.
Brogaard, B., & Salerno, J. (2013). Remarks on counterpossibles. Synthese, 190, 639–660.
Bull, R. A. (1969). On modal logic with propositional quantifiers. The Journal of Symbolic Logic, 34, 257–263.
Chadha, R., Macedonio, D., & Sassone, V. (2006). A hybrid intuitionistic logic: Semantics and decidability. Journal of Logic and Computation, 16, 27–59.
Di C. R. & Miller, D. (2019). Linear Logic. In E. N. Zalta (ed.), The stanford encyclopedia of philosophy. Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/entries/logic-linear/
Dunn, J. M., & Restall, G. (2002). Relevance logics. In D. M. Gabbay & F. Guenthner (Eds.), Handbook of philosophical logic (Vol. 6, pp. 1–128). Springer.
Einheuser, I. (2006). Counterconventional conditionals. Philosophical Studies, 127, 459–482.
Fine, K. (1969). For some proposition and so many possible worlds. University of Warwick. Ph.D. thesis.
Fine, K. (1970). Propositional quantifiers in modal logic. Theoria, 36, 336–346.
Fine, K. (2012). Counterfactuals without possible worlds. Journal of Philosophy, 109, 221–246.
French, R., Girard, P., & Ripley, D. (2020). Classical counterpossibles. The Review of Symbolic Logic 1–20.
Fritz, P. (2020). Propositional quantification in bimodal S5. Erkenntnis, 2, 455–465.
Gibbard, A. (2003). Thinking how to live. Harvard University Press.
Girard, P., & Weber, Z. (2015). Bad worlds. Thought, 4, 93–101.
Holliday, W. H. (2017). A note on algebraic semantics for S5 with propositional quantifiers. Notre Dame Journal of Formal Logic, 60, 311–332.
Holliday, W. H., & Litak, T. (2018). One modal logic to rule them all? In G. Bezhanishvili, G. D’Agostino, G. Metcalfe, & T. Studer (Eds.), Advances in modal logic (Vol. 12, pp. 367–386). College Publications.
Jago, M. (2014). The impossible. Oxford University Press.
Kaminski, M., & Tiomkin, M. (1996). The expressive power of second-order propositional modal logic. Notre Dame Journal of Formal Logic, 37, 35–43.
Kaplan, D. (1970). S5 with quantifiable propositional variables. Journal of Symbolic Logic, 35, 355.
Kment, B. (2014). Modality and explanatory reasoning. Oxford University Press.
Kocurek, A. W. (2019). Hyperlogic: A system for talking about logics. In J. J. Schlöder, D. McHugh, and F. Roelofsen (Eds.), Proceedings for the 22nd Amsterdam colloquium (pp. 238–247).
Kocurek, A. W., & Jerzak, E. J. (2021). Counterlogicals as counterconventionals. Journal of Philosophical Logic, 50, 673–704.
Kocurek, A. W., Jerzak, E. J., & Rudolph, R. E. (2020). Against conventional wisdom. Philosophers’ Imprint 20, 1–27.
Krakauer, B. (2012). Counterpossibles. University of Massachusetts, Amherst Ph.D. thesis.
Leitgeb, H. (2019). HYPE: A system of hyperintensional logic (with an application to semantic paradoxes). Journal of Philosophical Logic, 48, 305–405.
Lewis, D. K. (1973). Counterfactuals. Harvard University Press.
Mares, E. D. (1997). Who’s afraid of impossible worlds? Notre Dame Journal of Formal Logic, 38, 516–526.
Mares, E. D. (2004). Relevant logic: A philosophical interpretation. Cambridge University Press.
Mares, E. D. (2020). Relevance logic. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy. Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/entries/logic-relevance/
Meyer, Robert K., & Routley, Richard. (1977). Extensional Reduction–I. The Monist, 60, 355–369.
Muñoz, P. (2020). Behavioral attitudes in hyperintensional grammar (pp. 1–41). (un published)
Muskens, Reinhard A. (1991). Hyperfine-grained meanings in classical logic. Logique et analyse, 34, 159–176.
Nolan, D. (1997). Impossible worlds: A modest approach. Notre Dame Journal of Formal Logic, 38, 535–572.
Nolan, D. (2018). Reflections on Routley’s ultralogic program. Australasian Journal of Logic, 15, 407–430.
Routley, R. (2019). Ultralogic as universal? Springer.
Sandgren, A., & Tanaka, K. (2020). Two kinds of logical impossibility. Noûs, 54, 795–806.
Schaffer, J. (2016). Grounding in the image of causation. Philosophical Studies, 173, 49–100.
Stalnaker, R. C. (1968). A theory of conditionals. In N. Rescher (Ed.), Studies in logical theory (American philosophical quarterly monographs 2) (pp. 98–112). Basil Blackwell Publishers.
Standefer, S. (2020). Actual issues for relevant logics. Ergo, 7, 241–276.
Tanaka, K. (2018). Logically impossible worlds. Australasian Journal of Logic, 15, 489–497.
Vander Laan, D. A. (2004). In F. Jackson & G. Priest (Eds.), Counterpossibles and similarity. Lewisian Themes.
Weber, Z. (2014). Naïve validity. The Philosophical Quarterly, 64, 99–114.
Weber, Z., Badia, G., & Girard, P. (2016). What is an inconsistent truth table? Australasian Journal of Philosophy, 94, 533–548.
Williamson, T. (2009). Probability and danger. The Amherst Lecture in Philosophy, 4, 1–35.
Williamson, T. (2013). Modal logic as metaphysics. Oxford University Press.
Wilson, A. (2018). Grounding entails counterpossible non-triviality. Philosophy and Phenomenological Research, 46, 716–728.
Yanovich, I. (2015). Expressive power of “now” and “then” operators. Journal of Logic, Language, and Information, 24, 65–93.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Thanks to Harold Hodes, Jens Kipper, Carlotta Pavese, Rachel Rudolph, Zeynep Soysal, Will Starr, James Walsh, and two anonymous reviewers, as well as the participants of the 11th Semantics and Philosophy in Europe conference, the 22nd Amsterdam Colloquium, and the Fall 2019 Cornell Semantics Reading Group for helpful comments and discussion. An early (albeit unrefined) version of the system I develop here can be found in Kocurek (2019).
Appendix
Appendix
1.1 A representability theorem
In this appendix, I establish that any finitary single-conclusion logic can be represented in the hyperconvention semantics. In fact, we can represent any logic using just a single hyperconvention. In addition, I show that this improves upon the semantics in Kocurek and Jerzak 2021, which can only represent a smaller set of logics.
First, we need to clarify what we mean by ‘logic’ and ‘represent’.
Definition 11
(Logic) A logic over \({\mathcal {L}}\) is a set \(\mathbf{L }\mathrel {\subseteq }{\mathcal {L}}^{<\omega } \mathrel {\times }{\mathcal {L}}\) of pairs of the form  . (We allow the lefthand side to be the empty tuple \(\diamondsuit \).) We may write
. (We allow the lefthand side to be the empty tuple \(\diamondsuit \).) We may write  in place of
in place of  . We use \(\vec {\phi }\) as shorthand for
. We use \(\vec {\phi }\) as shorthand for  , where the length is implicit (possibly zero).
, where the length is implicit (possibly zero).
Definition 12
(Representability) A logic \(\mathbf{L }\) is representable in \(\mathcal {M}= \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},V \right\rangle \) if there’s a \(c \in \mathbb {H}_{W}\) such that for all  :
:

Theorem 13
(Representation) Every logic is representable in an infinite hypermodel (i.e., \(\left| {W}\right| = \aleph _{0}\)).
Proof
Let  be an injection. Let
be an injection. Let  . Define c as follows.
. Define c as follows.

Let \(\mathcal {M}\) be a hypermodel over W with c in its hyperconvention domain such that \(V(p)(c) = [p]\) (e.g., we can let \(V(p) = P_p\)). By a simple induction,  for all \(\phi \in {\mathcal {L}}\).
for all \(\phi \in {\mathcal {L}}\).
Thus, if  , then \(([\phi _1],\dots ,[\phi _n] \mathbin {\rhd }_c [\psi ]) = W\), so
, then \(([\phi _1],\dots ,[\phi _n] \mathbin {\rhd }_c [\psi ]) = W\), so  . Conversely, if
. Conversely, if  , then \(([\phi _1],\dots ,[\phi _n] \mathbin {\rhd }_c [\psi ]) = [p_1]\), so
, then \(([\phi _1],\dots ,[\phi _n] \mathbin {\rhd }_c [\psi ]) = [p_1]\), so  .
.
Theorem 13 contrasts with the situation for the semantics developed in Kocurek and Jerzak 2021. There, they do not introduce an entailment operator \(\mathbin {\rhd }\) into the language, so there is no obvious way to represent logics in the usual sense. In a footnote, they suggest the following (rephrased in our notation): c represents \(\mathbf{L }\) in \(\mathcal {M}\) iff  iff for all w, if
iff for all w, if  , then \(\mathcal {M},w,c \Vdash \psi \). I will now show that on this understanding of representability, a strictly smaller class of logics are representable by a hyperconvention.
, then \(\mathcal {M},w,c \Vdash \psi \). I will now show that on this understanding of representability, a strictly smaller class of logics are representable by a hyperconvention.
Definition 14
(Properties of logics) A logic \(\mathbf{L }\) is intensional if it satisfies the following properties:
-
Reflexive: \(\phi \mathbin {\Rightarrow }_\mathbf{L }\phi \)
-
Transitive: if \(\vec {\psi } \mathbin {\Rightarrow }_\mathbf{L }\chi \) and \(\vec {\phi } \mathbin {\Rightarrow }_\mathbf{L }\psi _i\) for each \(\psi _i\), then \(\vec {\phi } \mathbin {\Rightarrow }_\mathbf{L }\chi \)
-
Commutative: if \(\vec {\phi },\vec {\psi } \mathbin {\Rightarrow }_\mathbf{L }\chi \), then \(\vec {\psi },\vec {\phi } \mathbin {\Rightarrow }_\mathbf{L }\chi \)
-
Monotonic: if \(\vec {\phi } \mathbin {\Rightarrow }_\mathbf{L }\psi \), then \(\vec {\phi },\chi \mathbin {\Rightarrow }_\mathbf{L }\psi \)
-
Congruential: it obeys replacement of logical equivalents:
-
for
 : if \(\phi \mathbin {\Leftrightarrow }_\mathbf{L }\phi '\), then \(\mathop {\bullet }\nolimits \phi \mathbin {\Leftrightarrow }_\mathbf{L }\mathop {\bullet }\nolimits \phi '\)
: if \(\phi \mathbin {\Leftrightarrow }_\mathbf{L }\phi '\), then \(\mathop {\bullet }\nolimits \phi \mathbin {\Leftrightarrow }_\mathbf{L }\mathop {\bullet }\nolimits \phi '\) -
for
 : if \(\phi \mathbin {\Leftrightarrow }_\mathbf{L }\phi '\) and \(\psi \mathbin {\Leftrightarrow }_\mathbf{L }\psi '\), then \(\phi \mathbin {\circ }\psi \mathbin {\Leftrightarrow }_\mathbf{L }\phi ' \mathbin {\circ }\psi '\).
: if \(\phi \mathbin {\Leftrightarrow }_\mathbf{L }\phi '\) and \(\psi \mathbin {\Leftrightarrow }_\mathbf{L }\psi '\), then \(\phi \mathbin {\circ }\psi \mathbin {\Leftrightarrow }_\mathbf{L }\phi ' \mathbin {\circ }\psi '\).
-
Observe that reflexivity, commutativity, and monotonicity entail (in fact, given transitivity, are equivalent to) the following property:
-
Reiterative: \(\vec {\phi } \mathbin {\Rightarrow }_\mathbf{L }\phi _i\) for each \(\phi _i\).
Definition 15
(Intensional representability) A logic \(\mathbf{L }\) is intensionally representable in \(\mathcal {M}= \left\langle W,D_{\mathbb {C}},D_{\mathbb {P}},V \right\rangle \) if there’s a \(c \in \mathbb {H}_{W}\) such that for all  :
:

Theorem 16
(Intensional Representation). A logic \(\mathbf{L }\) is intensionally representable in an infinite hypermodel \(\mathcal {M}\) iff \(\mathbf{L }\) is intensional. Regardless of \(\mathcal {M}\)’s size, \(\mathbf{L }\) is intensionally representable in \(\mathcal {M}\) iff \(\mathbf{L }\) is intensional and the number of nonequivalent finite sequences of formulas is no greater than \(\left| {W}\right| \).
Proof
The left-to-right direction is straightforward: one simply checks that necessary implication has all the features of an intensional logic.
For the right-to-left direction, we begin by defining the finite theory space of \(\mathbf{L }\), which is a generalization of the Lindenbaum-Tarski algebra. Where  , define:
, define:

The finite theory space of \(\mathbf{L }\) is the order \(\mathbb {F}_\mathbf{L }= \left\langle F_\mathbf{L },\le _\mathbf{L } \right\rangle \) where:
-

-
\([\vec {\phi }]_\mathbf{L }\le _\mathbf{L }[\vec {\psi }]_\mathbf{L }\) iff \(\vec {\phi } \mathbin {\Rightarrow }_\mathbf{L }\psi _i\) for each \(\psi _i \in \vec {\psi }\).
From now on, we’ll leave the \(\mathbf{L }\)-subscripts implicit. Recall that a meet-semilattice is a partial order where the meet (i.e., greatest lower bound) of any two elements exists.
Claim
\(\mathbb {F}\) is a meet-semilattice with a top element.
Proof
Since \(\mathbf{L }\) is reiterative,  for \(1 \le i \le n\). So \(\le \) is reflexive. The transitivity and antisymmetry of \(\le \) follow from the transitivity of \(\mathbf{L }\). The top element is simply \([\left\langle \right\rangle ]\). As for the existence of meets, define the meet \(\sqcap \) operation as follows:
for \(1 \le i \le n\). So \(\le \) is reflexive. The transitivity and antisymmetry of \(\le \) follow from the transitivity of \(\mathbf{L }\). The top element is simply \([\left\langle \right\rangle ]\). As for the existence of meets, define the meet \(\sqcap \) operation as follows:

That \([\vec {\phi },\vec {\psi }] \le [\vec {\phi }]\) and \([\vec {\phi },\vec {\psi }] \le [\vec {\psi }]\) follows from reiterativity. Moreover, if \([\vec {\chi }] \le [\vec {\phi }]\) and \([\vec {\chi }] \le [\vec {\psi }]\), then \([\vec {\chi }] \le [\vec {\phi },\vec {\psi }]\) by definition of \(\le \). So \(\sqcap \) really is a meet operation.
It is a well-known fact of order-theory that any partial order can be order-embedded into its powerset algebra in a meet-preserving manner. Since \(F_\mathbf{L }\) is at most the size of W, that means there’s an injective map  such that:
such that:
-
(i)
\([\vec {\phi }] \le [\vec {\psi }]\) iff \(f([\vec {\phi }]) \mathrel {\subseteq }f([\vec {\psi }])\)
-
(ii)
\(f([\vec {\phi },\vec {\psi }]) = f([\vec {\phi }]) \cap f([\vec {\psi }])\).
What’s more, we can take \(f([\left\langle \right\rangle ]) = W\). For if \(f([\left\langle \right\rangle ]) \ne W\), define \(f^*\) to be exactly like f except \(f^*([\left\langle \right\rangle ]) = W\). It is easy to then verify that \(f^*\) is still an order-embedding that preserves finite meets.
Define c as follows (where  and
and  ):
):

This is well-defined. For if \(f([\phi ]) = f([\psi ])\), then \([\phi ] = [\psi ]\) by injectivity. Thus, \(\phi \mathbin {\Leftrightarrow }_\mathbf{L }\psi \). So by congruentiality, \(\mathop {\bullet }\nolimits \phi \mathbin {\Leftrightarrow }_\mathbf{L }\mathop {\bullet }\nolimits \psi \), which means \([\mathop {\bullet }\nolimits \phi ] = [\mathop {\bullet }\nolimits \psi ]\). Hence, \(f([\mathop {\bullet }\nolimits \phi ]) = f([\mathop {\bullet }\nolimits \psi ])\). (And similarly for binary connectives.)
Throughout, let \(\mathcal {M}\) be a hypermodel of the relevant size with c in its hyperconvention domain where \(V(p)(c) = c(p)\). By induction:
Claim
For any \(\phi \in {\mathcal {L}}\),  .
.
Finally, we show that c intensionally represents \(\mathbf{L }\) in \(\mathcal {M}\).
- \(\mathbin {\Leftarrow }\):
-
Suppose
 . Thus,
. Thus,  . Since f is order-reflecting,
. Since f is order-reflecting,  . So there is a
. So there is a 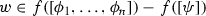 . Now observe:
. Now observe: 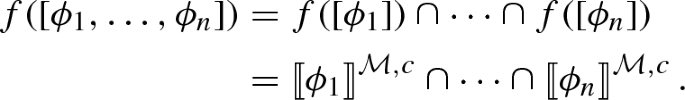
Hence,
 but \(\mathcal {M},w,c \nVdash \psi \).
but \(\mathcal {M},w,c \nVdash \psi \). - \(\mathbin {\Rightarrow }\):
-
Suppose
 . Then
. Then  . Since f is order-embedding:
. Since f is order-embedding: 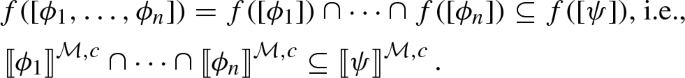
Therefore, c intensionally represents \(\mathbf{L }\) in \(\mathcal {M}\). \(\square \)
Rights and permissions
About this article
Cite this article
Kocurek, A.W. Logic talk. Synthese 199, 13661–13688 (2021). https://doi.org/10.1007/s11229-021-03394-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-021-03394-z





 and state nominals
and state nominals  , which are true at exactly one world;
, which are true at exactly one world; is regimented as
is regimented as  .
. .
. is universally valid iff
is universally valid iff  is classically valid, where l does not occur in
is classically valid, where l does not occur in  .
. is classically valid iff
is classically valid iff  is universally valid, where
is universally valid, where  for each
for each  for each
for each  where
where 
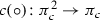 where
where 
 .
.

 , if for any classical hypermodel
, if for any classical hypermodel 
 iff
iff  .
. where
where  . But since
. But since  , and so
, and so  . Moreover, since
. Moreover, since  . Therefore, if
. Therefore, if  for any
for any  entails
entails  .
. . But if entailment facts are necessary, then this formula will be falsifiable.
. But if entailment facts are necessary, then this formula will be falsifiable. . Then:
. Then: 
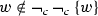 , since
, since  .
. .
. : if
: if  : if
: if 
 . Thus,
. Thus,  . Since f is order-reflecting,
. Since f is order-reflecting,  . So there is a
. So there is a 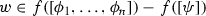 . Now observe:
. Now observe: 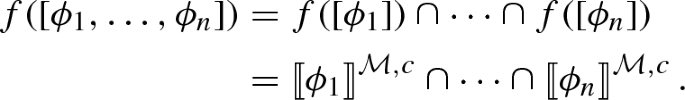
 but
but  . Then
. Then  . Since f is order-embedding:
. Since f is order-embedding: