Transitions in evolution: a formal analysis

Abstract

Evolutionary transitions in individuality (ETIs) are events during which individuals at a given level of organization (particles) interact to form higher-level entities (collectives) which are then recognized as new individuals at that level. ETIs are intimately related to levels of selection, which, following Okasha, can be approached from two different perspectives. One, referred to as ‘synchronic’, asks whether selection occurs at the collective level while the partitioning of particles into collectives is taken for granted. The other, referred to as ‘diachronic’, asks about the origins of the partitioning of particles into collectives. After having presented the two perspectives and a classical formalism used to deal with the levels-of-selection question in the literature, namely the multilevel version of the Price equation, I show that because this formalism treats the levels-of-selection question from a synchronic perspective, it is inadequate to explain ETIs. This is because a fundamental aspect of ETIs is the origin of collectives. From there, I develop a framework for levels of selection compatible with the diachronic perspective. This framework relies on the distinction between what I call, on the one hand, a ‘functional aggregative collective trait’, and on the other hand, a ‘functional non-aggregative collective trait’. After having presented this distinction, I implement it in the Price equation, leading to a new statistical partitioning of this equation which, I argue, represents a causal decomposition more relevant for ETIs. Finally, I exploit this partitioning to explain the critical stages of an ETI. In addition to its explanatory power, a measure of the degree of functional non-aggregativity could be used as a proxy for the degree of individuality of a collective.

1 Introduction: two ways to understand multilevel selection

The levels-of-selection problem, perhaps evolutionary biology’s most enduring problem (see Williams 1966; Sober and Wilson 1994, 1998; Keller 1999; Okasha 2006; West et al. 2007; Wilson 1975; Wilson and Wilson 2007), has traditionally been addressed in a synchronic rather than diachronic fashion (Okasha 2006, 2018; Griesemer 2000).¹ The synchronic perspective, taking a two-level scenario in which a population of lower-level entities (particles) are organized in higher-level entities (collectives), asks whether selection currently acts at the particle or the collective level, while a diachronic perspective asks about the evolutionary origins of new levels of selection.

There is a tradition to regard levels of selection, when asked synchronically,² as a matter of convention rather than facts (e.g., Dugatkin and Reeves 1994; Kerr and Godfrey-Smith 2002; West et al. 2007). Following this perspective, whether selection occurs solely at the level of particles, or as the result of a combination of different processes of selection occurring at the particle and the collective level, is just a matter of perspective and modeling choices.

This conventionalist answer to the levels-of-selection problem, which is not unrelated to Kim’s causal exclusion argument (Kim 2005, Chap. 1), proves nonetheless insufficient when the question of the levels of selection is asked in a diachronic rather than a synchronic fashion.³ In fact, asking this question synchronically assumes that collectives already exist, or at least that they have some plausibility of existence, while nothing is said about their origin(s). Yet, there is mounting evidence that modern organisms (collectives of cells), including ourselves, are the outcomes of a succession of evolutionary events, known as evolutionary transitions in individuality (ETIs),⁴ which have led particles to form collectives. These collectives have in turn entered into a new ETI which led to the formation of even higher-level entities, and so forth. In other words, life is hierarchically nested, and this nestedness is a product of evolutionary processes in which natural selection, in all likelihood, has played an important role (Maynard Smith and Szathmary 1995; Okasha 2006; Maynard Smith and Szathmary 1995; Calcott and Sterelny 2011; Bouchard and Huneman 2013; Michod 1999; Buss 1987; Bourke 2011; Clarke 2014, 2016; Godfrey-Smith and Kerr 2013; van Gestel and Tarnita 2017). Bourke (2011, pp. 11–15) distinguishes six major types of ETIs which have occurred in the tree of life. These are the transition from separate replicators to cells enclosing genomes, from separate unicells to symbiotic unicells (eukaryotic cells), from asexual unicells to sexual unicells, from unicells to multicellular organisms, from multicellular organisms to eusocial societies, and from separate species to interspecific mutualisms.⁵ If the conventionalist position about levels of selection is perfectly sound, it is still incomplete since it is unable to account for these six ETIs.

To fully account for ETIs, the levels-of-selection question one should thus also address the question of the origins of the levels of organization. There is, furthermore, something troubling in the claim that whether selection occurs at the particle or collective level is a matter of perspective, when it is taken for granted that the way particles and collectives are nested is the outcome of evolution. By answering the question of levels of selection, one should thus be able to tell why life is hierarchically organized, rather than not, and propose mechanisms underlying this organization, but also, at the same time, still be compatible with the conventionalist position.

Thus, the sound proposition that levels of selection are not factual but a matter of convention is in tension with the equally sound proposition that life is factually nested. One way to release this tension is to recognize that the diachronic and synchronic approaches to the levels of selection, although related, understand the notion of ‘level of selection’ in two different ways. In fact, one can maintain from a synchronic approach that talking about the strength of selection at different levels of organization is just one way to partition a single evolutionary process, among many other ways. At the same time, motivated by the diachronic approach, one can recognize that some ways of partitioning a population of particles into collectives are more (biologically) legitimate than others, because they say something factual about the world, something that a less legitimate partitioning or a description purely at the particle level would leave out. This part left out, I want to argue, is whether the partitioning corresponds to biological units or individuals (for an overview of the topic of biological individuality see Wilson and Barker 2019). If this is correct, an important question with respect to levels of selection becomes what the (evolutionary) mechanism(s) underlying the emergence of new units are. Answering this question will be the main focus of my paper.

To do so, it should first be noted that from a diachronic perspective one does not aim to know whether selection is currently acting differently at different levels of organization, but rather what relevant parameter(s) must evolve so that, at the beginning of an ETI, any partitioning of particles into collectives would represent arbitrary collectives, to a situation in which genuine collectives are present. To answer this question requires also identifying relevant criteria to delimit genuine collectives from arbitrary ones, a task I undertake in Sect. 3, by proposing non-aggregativity, a concept developed by Wimsatt (2007, Chap. 12), as a candidate for making this demarcation. Correctly answering this question will require a full articulation of the terms used at the different levels of organization. A purely verbal account, although possible, would make this task difficult. A more rigorous approach, which I will use here, is to start from the formalism of the Price equation (Price 1970, 1972). The Price equation has been used to deal with the levels-of-selection question from a synchronic perspective. In the next section, I review this approach and show why it cannot be used to answer the levels-of-selection question in a diachronic context. In Sect. 4, I develop an alternative form of the Price equation by formalizing the aggregativity criterion, proposed in Sect. 3 to demarcate genuine from arbitrary collectives, which permits us to approach the levels-of-selection question from a diachronic perspective. Finally, in Sect. 5, I propose an account of ETIs using the equation developed in Sect. 4, by changing the value of the parameter proposed in Sect. 3. I conclude by listing a number of limitations to my approach and ways to develop it.

2 The multilevel version of the price equation and (some of) its limitations

A classical framework within the synchronic approach to the levels-of-selection question is the use of the hierarchical or multilevel form of the Price equation (for details see Price 1972; Hamilton 1975; Okasha 2006; Frank 1998, Chap. 2). It is derived from its single-level form (Price 1970; Okasha 2006, Chap. 1), the latter of which expresses the total evolutionary change of a character (z), say of particles, between two times (typically, but not necessarily, generations, see Bourrat (2015a)) in a population of entities ($\varDelta \overline{z}$, where $\overline{z}$ is the average value of the character), as the sum of two terms, as follows:

$$\begin{aligned} \varDelta \overline{z}={\text {Cov}}(\omega _i,z_i)+{\text {E}}(\omega _i \varDelta z_i). \end{aligned}$$

(1)

The first term on the right-hand side (${\text {Cov}}(\omega _i,z_i)$) represents the covariance between the character z and the relative reproductive output $\omega$ of an entity i,⁶ the latter of which is defined as $\omega _i=\frac{w_i}{\overline{w}}$, where w is the absolute fitness of i. This term is often labeled as the ‘selection’ term. The second term on the right-hand side (${\text {E}}(\omega _i \varDelta z_i)$) measures the extent to which, on average, the character of offspring entities $\overline{z'}$—which might be measured on the same entities between two times—deviates from that of their parent. This term is often labeled the ‘transmission-bias’ term. If the entities reproduce perfectly or do not change over time, this term is nil.

One property of Eq. (1) is that it can be defined at any level of organization for any sorts of entities, so long as one can attribute them a character and a relative growth rate between two times. This means that, considering a population of collectives made of particles with a collective character $\textit{Z}$ and a collective relative reproductive output $\varOmega$, one can write a collective-level version of Eq. (1) as:

$$\begin{aligned} \varDelta \overline{Z}={\text {Cov}}(\varOmega _k,Z_k)+{\text {E}}(\varOmega _k \varDelta Z_k), \end{aligned}$$

(2)

where the index k refers to the collective k in the population of collectives.

Following Okasha (2006, pp. 64–65), provided the character $Z_k$ and collective relative reproductive output $\varOmega _k$ of collective k, respectively, can be expressed as a statistical aggregate (more on this notion to come)⁷ of the character z and relative fitness $\omega$, respectively, of its constituent particles, we can define these quantities as:

$$\begin{aligned} Z_k=\frac{1}{n}\sum \limits _{j=1}^{n}z_{jk}, \end{aligned}$$

(3)

where $z_{jk}$ represents the character attributed⁸ to the particle j in the collective k, and n is the number of particles in collective k; and:

$$\begin{aligned} \varOmega _k=\frac{1}{n}\sum \limits _{j=1}^{n}\mathop {}_{_k}\omega _{jk}, \end{aligned}$$

(4)

where $\omega _{jk}$ represents the relative fitness attributed to particle j in collective k. If $Z_k$ and $\varOmega _k$ are not statistical aggregates of particle character and fitness respectively—for instance the collective character is ‘density of particles’, or ‘level of particle differentiation’—the relationship between particle and collective character/fitness will be more complex. I will assume here only the simplest cases.

With this in place, Eq. (2) can be re-written into a multilevel form with two levels by considering that the selection term at the collective level (${\text {Cov}}(\varOmega _k,Z_k)$), represents ‘between-collective selection’, and the transmission-bias term (${\text {E}}(\varOmega _k \varDelta Z_k)$) represents ‘within-collective selection.’

The interpretation of the collective-level transmission-bias term as ‘within-collective selection’ is warranted by the fact that the transmission-bias term contains the single form of the Price equation within every single collective one level lower. Expressing it in terms of covariance between particle character z and particle fitness $\omega$ within each collective, that is, applying the single form of the Price equation recursively for each collective, the transmission-bias term can be expressed as an expected covariance between particle character and particle fitness within each collective. Assuming, for simplicity, that particle-level reproduction is asexual and perfect, that all collectives have the same size, that reproduction of particles and collectives occur in discrete generations and at the same time and that there is no migration of particles between collectives—I will keep these assumptions throughout—we can rewrite Eq. (2) as:⁹

$$\begin{aligned} \varDelta \overline{Z}={\text {Cov}}(\omega _i,z_i)={\text {Cov}}(\varOmega _k,Z_k)+{\text {E}}({\text {Cov}}_{\mathrm{k}}(\omega _{jk},z_{jk})), \end{aligned}$$

(5)

where ${\text {Cov}}_{\mathrm{k}}$ is a covariance measured within collective k.

Importantly, because one of our assumptions is that the collective character Z is a statistical aggregate of z, we have $\varDelta \overline{Z}=\varDelta \overline{z}$, which means that:

$$\begin{aligned} \varDelta \overline{z}={\text {Cov}}(\omega _i,z_i)={\text {Cov}}(\varOmega _k,Z_k)+{\text {E}}({\text {Cov}}_{\mathrm{k}}(\omega _{jk},z_{jk})). \end{aligned}$$

(6)

Assuming that the relationship between z and w is causal from z to $\omega$, so that changing the value of z of a particle by means of an ideal intervention (Woodward 2003; Pearl 2009) would lead to a change in the value of $\omega$ of this particle, the two-level version of the Price equation vindicates the conventionalist position about levels of selection. In fact, intervening on the character value of one particle, changing it from one value to another, assuming it is causally efficacious, will change the covariance value within the collective it belongs to, that is, the value of the second term on the right-hand side of Eqs. (5) and (6) (${\text {E}}({\text {Cov}}_{\mathrm{k}}(\omega _{jk},z_{jk}))$). Yet, since changing the value of a single particle within a collective also affects the value of one collective character and its fitness, this implies that the first term on the right-hand side of Eqs. (5) and (6) (${\text {Cov}}(\varOmega _k,Z_k)$) will necessarily change too. Thus, because it is impossible to change the value of selection at one level without at the same time changing the value at the other level, it is implausible to consider the two levels as being distinct or autonomous in any strong sense.¹⁰ Rather, my interpretation is that the two levels represent a way of partitioning selection that reveals a biological structure that the observer finds relevant for an explanation.

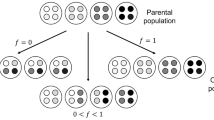
The conventionalist position is reinforced by noticing that in the multilevel version of the Price equation, the way collectives are formed can be totally arbitrary. This point has been noted many times in the literature (e.g., Nunney 1985; Heisler and Damuth 1987; Okasha 2006), but an illustrative example will drive the point home. Suppose a population of 16 particles of two phenotypes, ‘white’ and ‘black’, in equal proportions, with respective character values of $z=0$ and $z=1$. Assume that black particles deterministically produce two offspring while the white particles only produce one at each generation. Applying Eq. (1), we find $\varDelta \overline{z}=\frac{1}{6}$, which represents a measure of the average change, after one generation, of the particle character. Assume now that the 16 particles are distributed in 4 collectives in the way presented in Fig. 1a. In such a situation, applying Eq. (5) or (6), we also find that $\varDelta \overline{z}=\varDelta \overline{Z}=\frac{1}{6}$ with ${\text {Cov}}(\varOmega _k,Z_k)=\frac{1}{12}$ and ${\text {E}}({\text {Cov}}_{\mathrm{k}}(w_{jk},z_{jk}))=\frac{1}{12}$. A classical interpretation would, in this case, be that selection occurs in the same direction and with the same magnitude at the particle and collective level.

Yet, this way of partitioning the collectives is only one among many possible ways (both in terms of composition of the collectives and in terms of number of particles within a collective). For instance, if the particles are arranged in the ways presented in Fig. 1b–d, which are merely arbitrary rearrangements of the particles when compared to Fig. 1a, then each way leads to different answers for the magnitude of particle-level and collective-level selection, under a classical interpretation. What’s more, if we now change the size of collectives from 4 particles to say 2 (8 collectives), or 8 particles (2 collectives) as represented in Fig. 1e, or if we assume that collectives can have different sizes as represented in Fig. 1f, then, for each of these cases, Eq. (5) or (6) (or slightly modified versions of them to account for collectives of different sizes) will give different answers, under the classical interpretation, for the magnitude of selection at the two levels. The overall covariance will, nevertheless, keep the same value, namely $\frac{1}{6}$, regardless of how the particles are arranged.

Fig. 1

Population of 16 particles with the same frequency of two types (0.5 black and 0.5 white) organized in collectives in six different ways. Assuming that white particles each have 1 offspring, and black particles have 2 offspring, independently from the collective they are found in, then applying the multilevel version of the Price equation finds different values for particle-level and collective-level selection in each situation. In and of itself, the Price equation cannot be used to determine whether a collective has genuine or arbitrary boundaries

Importantly, note that in the preceding paragraph I have assumed no particular reason why the collectives should be organized the way they are. The fact that the multilevel version of the Price equation can be applied consistently in different ways (size and compositions of collectives), which lead to different interpretations in terms of levels of selection, demonstrates that it should only be applied for situations in which there are independent reasons to assume that the partitioning of the particles into collectives, chosen by the observer, represents a genuine feature of the world. This means that, in its classical form, the multilevel Price equation cannot account for the origins of the partitioning into collectives. Because of this, it is a bad candidate to account for ETIs in which the main question of interest is the origin of collectives. Although the classical version of the multilevel Price equation is not adequate to account for ETIs, I propose in Sect. 4 a modified version of it that points toward critical aspects of ETIs and permits a coherent description of ETIs using a single equation.

Before going further, I will briefly discuss Okasha’s (2006, Chap. 8) model for ETIs. Okasha’s starting point is the distinction between multilevel selection 1 (MLS1) and multilevel selection 2 (MLS2). The distinction was initially introduced by Damuth and Heisler (1988) as a way to understand two perspectives on multilevel selection which were often conflated in the literature. From an MLS1 perspective, the focus of analysis is the particle level and the fitness of a collective is measured in terms of particles produced. From an MLS2 perspective, the focus of analysis is both the collective and the particle level. Collective fitness is defined as the number of collectives produced without focusing on the number of particles contained in a collective. Based on Michod’s (2005) analysis that particle fitnesses during an ETI are progressively transferred to the collective level, so that collectives progressively gain individuality, Okasha’s proposal is that a shift from MLS1 to MLS2 takes place to the point that, at the end of the transition, “MLS2 [...] occurs autonomously of MLS1” (Okasha 2006, p. 238). This shift is thus seen as factual rather than as epistemic or conventional by Okasha. And, in fact, Okasha defended himself against the claim from Waters (2011) that the ‘shift’ from an MLS1 to an MLS2 approach can be regarded merely as a matter of perspective.

I regard Okasha’s account as problematic. First, it goes against the idea that collective fitness ultimately depends on particle fitness, a position I consider as hardly tenable for reasons I have developed elsewhere.¹¹ Second and related, it relies on the idea of fitness transfer, which, if it can be used metaphorically (Godfrey-Smith 2011; Bourrat 2015b), is hard to flesh out without relying on a strong version of emergence, although see the next section where I briefly discuss a way to interpret the notion of transfer of fitness. Considering these problems, the modified version of the Price equation I propose below will largely be independent from the Michod/Okasha view about fitness transfer. I want to acknowledge, however, that my approach has been motivated by the aim of solving the problems their account faces and for that reason it has been a very useful one. Note that Okasha (2006) did not attempt to formalize ETIs using the classical Price formalism, but merely gestured towards it. Michod and Roze (1999) and Clarke (2014, see also Clarke 2016) have, however, made such an attempt.

3 Aggregativity, genuine collective character and reproduction

We saw in the previous section that the main problem with the multilevel Price equation is that it is sensitive to the way collectives are partitioned in the population of particles. Fundamentally, the problem with this approach is that it cannot distinguish collectives that have a biological reality from collectives that do not and have been considered as collectives for arbitrary reasons or criteria that are irrelevant to the question at hand, namely ETIs.

From there, a natural starting point is to ask whether there is a criterion or set of criteria that could be the basis for distinguishing collectives that have some biological reality, from those that do not. A further desideratum is that such a criterion or criteria are implementable in some formalism (such as the Price equation). A classical answer to the question of what distinguishes a genuine collective from an arbitrary one is that the former interacts ‘as a whole’ with its environment or that selection acts ‘directly’ on the collective, while this is not the case in the former case, in which each particle interacts directly with the environment and selection acts on particles. This way of presenting the distinction is, for instance, the one given by Hull (1980) in his definition of an ‘interactor.’ The idea of an entity interacting as a whole is also underlying Williams’ (1966, pp. 16–17) classical distinction between a ‘herd of fleet deer’ and a ‘fleet herd of deer.’ The difference in word order conveys the idea that, in the former case, each individual deer interacts with its environment separately when escaping predators, while in the latter case, the whole herd interacts as a whole (for a discussion see Sober 1984, Introduction). Finally, Okasha (2006, p. 5) introduced the notion of a ‘cross-level by-product’ which he defines as a side-effect of a cause that can run up and down levels of organization. When explaining this idea, Okasha explicitly uses the language of ‘direct selection’: “[f]or example, direct selection on individuals living in a group-structured population may lead to a character-fitness covariance at the group level, and thus the appearance of a selection process acting directly on the groups.” (2006, p. 5, my emphasis. One can replace ‘group’ and ‘individual’ with ‘collective’ and ‘particle’, respectively).

Although all these notions make sense intuitively, because collective properties (including those associated with ‘fitness’) depend on that of particles, they all fall prey to a form of the conventionalist argument briefly presented in the Introduction, since properties or characters at the collective level, ceteris paribus, depend on the properties or characters at the particle level (see also footnote 10). In a population, talking about the properties of particles or of collectives just invokes different perspectives on the same population. If this is right, it implies that, to make sense, the idea of entities interacting as a ‘cohesive whole’ or ‘directly’ must refer to a concept that is compatible with the dependence of collective characters on particle characters,¹² yet captures the biological fact that collectives are not fully arbitrary entities, so that there can be reasons to define them in one way rather than another.

But even with such a concept at hand, it would still be insufficient to account for a collective in an evolutionary context. What makes a collective relevant for evolution is that it is able to participate in an evolutionary response to selection. I use here the language of quantitative geneticists (e.g., Falconer and Mackay 1996), for whom evolution by natural selection is the outcome of two components, a selection process that changes the average value of a character within one generation, and the ability to give traction to this change cross-generationally (the response).¹³ Although a response to selection, and more generally evolution, can occur for a limited amount of time when there is no multiplication, for these processes to occur indefinitely will involve the multiplication of the entities of this population (Bourrat 2014)—typically, but not necessarily, by reproduction (Bouchard 2008, 2011). The idea of a collective being able to reproduce in and of itself is a marker of transitions for some authors (see for instance Godfrey-Smith 2009, 2011, 2015; Griesemer 2000).

Like the idea of collective-level selection, the idea of collective-level multiplication is difficult to articulate because any notion of collective multiplication relies ultimately on the multiplication of at least some of the particles that compose it (often through some very complex function). Thus, with multiplication too, one must find a way to distinguish the idea of a collective multiplying from that of its particles multiplying based on criteria that are both consistent with the inescapable dependence of collective multiplication on particle multiplication, and at the same time provide some insights on the fact that collectives multiply in a way that captures the distinction between a particle multiplying somehow independently from and as part of a collective.

To capture the ideas of collective-level interaction with the environment (selection phase) and collective-level reproduction (evolutionary response phase),¹⁴ I propose that the concept of functional aggregativity from Wimsatt (2007, Chap. 12, see also Wimsatt 1986) is key to make this distinction. The idea underlying the notion of functional aggregativity is that a system’s properties are aggregative if operations of substitution, addition/subtraction, and decomposition and reaggregation of the parts of the system, do not change the relationship between the properties of the parts of the system taken independently and the properties of the system in its (biological) context. For a system’s property to be an aggregative property of its parts there should thus be no functionally relevant interactions between its parts in producing the system’s property.¹⁵ A system might be functionally aggregative for one property but not for another, and for some operations but not others. Finally it might be aggregative when the system is decomposed in one way but not another. In all these cases the system is partially aggregative. As shown by Wimsatt, complete aggregativity is very rare in nature, with mass being the only example of a fully aggregative property.¹⁶

Applied to our question at hand, I propose that the notions of genuine collective-level character(s) and reproduction correspond to the notions of non-aggregative collective character(s) and reproduction. The criterion of aggregativity fits neatly with the idea of an ETI, for which an archetypal ground zero is a situation in which all the particles of a ‘collective’ (which is not a unit, but delimited arbitrarily by an observer) are interacting with their environment and reproducing independently—or nearly so—from one another, to a situation in which collective-level characters are non-aggregative functions of particle characters.

To illustrate the idea of aggregativity versus non-aggregativity, suppose a modified version of Dawkins (1976) rowing metaphor (a metaphor also used by Maynard Smith and Szathmary (1995) with what they call the ‘sculling game’), which I borrow from Corning (2003, 2010, p. 65). The world champion for single sculling is able to cover a distance of 2000 m in about 6 min and 30 s (see Fig. 2a). If we now take the world champion team for double sculling, the time goes down to 6 min (see Fig. 2b), and the world champion team for quad sculls is able to cover the 2000 m in 5 min 38 s (see Fig. 2d). If the performance of a team of scullers was an aggregative property of the scullers that compose a boat, then, assuming each sculler of a boat would perform the same for single sculling, the time to cover the 2000 m would not vary whether the boat has one, two or four scullers (see blue line in Fig. 3 in which the distinction between aggregativity and some forms of non-aggregativity is represented graphically and abstractly).¹⁷ Yet, because the time to cover the 2000 m decreases as one adds scullers (the performance increases), there is a synergistic effect for performance at sculling (see red line in Fig. 3). The existence of a synergistic property for a system is an indication the system is at least partly a non-aggregative one.

Fig. 2

Time taken for the world champion of single sculling (a), the world champion team for double sculling (b), a team two individuals back-to-back (c), and the world champion team for quad sculling (d), to cover 2000 m

Fig. 3

Representation of the effect of increasing the size of a collective on the performance attributed to a single particle in the case of an aggregative trait (blue line), a linear non-aggregative trait (linear synergy of scale; red line), and a non-aggregative trait (synergy of scale) with a threshold effect (green line). (Color figure online)

In nature this type of synergy, which Corning (2003, pp. 17–19) calls ‘synergy of scale’, is very common. One example—many more can be found in Corning (2003, 2010)—is that of a bacterium in a biofilm. A biofilm is “an assemblage of microbial cells that is irreversibly associated (not removed by gentle rinsing) with a surface and enclosed in a matrix of primarily polysaccharide material” (Donlan 2002). When organized in a biofilm, bacteria are able to better resist an antimicrobial agent by a magnitude which is 10 to 1000 times larger than is the case for cells suspended in liquid (Mah and O’Toole 2001). A second biological example of synergy proposed by Corning (2003, p. 24) is the effect of huddling in emperor penguins. These birds have different strategies to resist the cold. One of them is to adopt a specific posture that reduces heat loss. Another is to huddle with other penguins. When this second strategy is used, it has been estimated that penguins lose between 20 and 50% less energy than a penguin in isolation loses (Prévost 1961). The reduction of heat loss achieved by many penguins is higher than that of single penguins taken independently.

A special case of synergy of scale proposed by Corning (2003, pp. 19–20) is what he calls ‘threshold effects.’ For some collective characters, a threshold effect exists in the sense that the character is not even exhibited when a particle is in isolation from other particles. This is the case for instance with the perception of luminescence in Vibrio fisheri, a species of bacteria which can live symbiotically in the light organ of the bobtail squid (Mcfall-Ngai 1994; McFall-Ngai 2014; Bouchard 2010, 2018). In a planktonic state, the bacteria do not express detectable bioluminescence. It is only in the presence of other Vibrio bacteria that they will do so, when a certain density of bacterial cells is reached in the light organ of the squid. The bacteria can sense when this density is reached by cell-to-cell communication (quorum sensing), and trigger the expression of genes that will induce the production of bioluminescence (Waters and Bassler 2005). More generally, quorum sensing systems permit a bacterium (together with other bacteria) to perform a range of activities that it would not be able to do in a planktonic state because of some synergy of scale including threshold effects. The idea of a threshold effect, as opposed to a synergy of scale with no threshold, is illustrated in Fig. 3 (green and red line respectively).

What might distinguish ‘simple’ synergies of scale from threshold effects, I propose, is that in the former cases, the principles that apply to a particle (taken independently) and to a collective are the same, but because the particles are organized into a collective one cannot consider anymore that they apply to the particles in the same way that they would if the particles were taken independently. For instance, in the case of the emperor penguins, although the same thermodynamic principles apply to a single penguin and to a group of penguins, when the group of penguins huddles, the fact that each penguin is not wholly surrounded by air, but only part of its surface is, becomes relevant. Effectively, a huddle of penguins can be considered as a single mass with a smaller surface area than that of the penguins taken separately. In the case of threshold effects things are different. In fact, the collective phenotype is not properly exhibited at the particle level.¹⁸ This might be the result of principles that only occur at a particular scale, but not others, even though the collective level depends on the particle level. In the case of Vibrio bioluminescence, although each bacterium is able in principle to produce some luciferase, the protein responsible for the bioluminescence (Miyashiro and Ruby 2012), a single bacterium would not be able to produce enough to be detectable. Light only becomes visible for an observer (or a possible predator) when a given density of luciferase is reached, one that can only be produced by a large number of bacteria (assuming everything is equal). The ability to detect light is governed by rules which mean that only a collective of bacteria can produce visible light.

I have illustrated the idea of non-aggregativity with synergistic effects involving scales. As briefly alluded to above, there are other criteria, beyond that of scale, to characterize a non-aggregative system. In fact, Wimsatt (2007, pp. 280–281, see also Wimsatt 1986) has proposed that a system is aggregative when the system exhibits four non-independent properties. The first one is ‘intersubstitution’: the parts of a system can be rearranged without changing the properties of the system. For instance, in the case of sculling, putting two scullers back-to-back will lead to a different outcome (the boat doesn’t move) than when they are put in the traditional position (see Fig. 2c). The second one is ‘size scaling’ which corresponds to a lack of synergy of scale discussed above. The third one is ‘decomposition and reaggregation’: the parts of a system can be decomposed and then recomposed without changing the property of the system. Finally, the last one is ‘linearity’, which according to Wimsatt corresponds to the idea that there is no interaction between the parts of the system. For instance, in the case of sculling, there are interactions between the scullers which permit them to go faster when they are more numerous.

In the remainder of the article, I will focus primarily on non-aggregativity qua size scaling which also relates to linearity, and leave aside the properties of intersubstitution, decomposition and reaggregation.¹⁹ This is not because I regard these as unimportant, but rather because they would be harder to formalize mathematically, which ultimately is my goal here. Furthermore, size scaling seems to be crucially involved in ETIs since during transitions the collective-level entity is typically larger than a particle-level one, and an evolutionary explanation must explain this phenomenon.

Before going further, two remarks should be made. First, for Wimsatt (2007), a failure in aggregativity is a condition for the system to exhibit emergent properties. As pointed out by Humphreys (2016, pp. 234–240), equating failure in non-aggregativity with emergence can be problematic in the following sense. If non-aggregativity is equated with emergence, emergence will turn out to be a very common phenomenon in nature. Although for Humphrey an account that sees emergence as a common phenomenon in nature should not be rejected too hastily, it might be considered by some that such an account does not capture well what is classically meant by emergence. That said, the conclusions I make here do not hinge on whether non-aggregativity can be equated with emergence since I regard the distinction between aggregative and non-aggregative properties as key to account for ETIs independently from the implications non-aggregativity may have for emergence.

Second, one interpretation of Michod’s notion of transfer of fitness (see Michod 2005) from the particle to the collective level mentioned at the end of the previous section could be that ‘transfer’ corresponds to the progressive change of the collective from an aggregative to an non-aggregative system with respect to fitness. This indeed seems to be what Michod has meant when, together with Shelton (see Shelton and Michod 2014), he proposed the notion of ‘counterfactual fitness’:²⁰ the fitness a particle would have in the absence of a collective, that is, if the fitness of a particle was measured in a non-social context. Although this is a move in the right direction, the notion of counterfactual fitness takes the collective in which it should be measured for granted. Furthermore, considering the difficulties surrounding the concept of fitness (Rosenberg and Bouchard 2010; Ariew and Lewontin 2004; Godfrey-Smith 2009), it is perhaps better not to attempt to start using fitness as a measurable property and rather use other properties causally influencing multiplication or growth. The formal approach I develop in the next section permits to avoid these difficulties.²¹

4 Formalization

In the previous section, I proposed that what makes a collective ‘genuine’ is that its characters and ability to reproduce are non-aggregative functions of the characters and reproduction of its particles. One way to implement the concepts of aggregativity and non-aggregativity (qua synergy of scale) mathematically is to use the notions of particle additive and non-additive contribution to the collective character, where non-additivity measures the amount of synergy for the collective character. Note however that ‘(non-)additivity’ and ‘(non-)aggregativity’ are not perfectly overlapping concepts. In fact, recall that size scaling and linearity (synonymous with additivity) are only two aspects of aggregativity. Additivity is just one way to measure imperfectly the degree of non-aggregativity in a system with respect to a property. Importantly, it should also be noted that the notion of additivity, as it is used in population biology (e.g., additive fitness), is a purely statistical one. As such a non-aggregative character could manifest as a statistical additive character at the population. In particular, this is because in this context ‘additivity’ refers to terms in a particular population, not to terms insensitive to population-level changes (e.g., change in frequency of an allele). For a brief yet more rigorous treatment of this point see Lewontin (1991). As such, ‘additivity’ in the context of population biology does not typically correspond to functional independence of the entities forming a population, which is to what I will refer by ‘functional additivity’ here (see also Footnote 26).

Before proceeding, I will introduce a different version of the Price equation from the one presented in Sect. 2 in which a term of heritability appears. This different version, which I label the ‘Lewontinized’ version of the Price equation, for reasons that will soon be obvious, can be derived from the classical form. The reason I use this version is that heritability can be indirectly associated with the notion of reproduction via the response to selection, something that is not possible with the classical version of the Price equation.²² Starting from Eq. (1), using the same assumptions we can rewrite it as:

$$\begin{aligned} \begin{aligned} \varDelta \overline{z}=\,&h^2 {\text {Cov}}(\omega _i,z_i)+{\text {E}}(\varDelta z_i)\\ =\,&h^2\beta _{wz}{\text {Var}}(z_i)+{\text {E}}(\varDelta z_i), \end{aligned} \end{aligned}$$

(7)

where $h^2$ represents the heritability of the character $\textit{z}$ (I will assume there is no correlation between the parental and offspring environment), and $\beta _{wz}$ is the slope of the regression of an entity fitness and the value of the character. It measures, assuming there is a relation of causality between a character and the reproductive output of the entity bearing this character, the strength of this relationship. Under these assumptions $h^2$ is defined as:

$$\begin{aligned} h^2=\frac{{\text {Cov}}(\overline{z'_i},z_i)}{{\text {Var}}(z_i)}, \end{aligned}$$

where $\overline{z'_{i}}$, is the average character of offspring particles coming from i. I refer to this version of the Price equation as ‘Lewontinized’, because as shown by Okasha (2006, Chap. 1), it almost vindicates Lewontin’s (1970) three conditions for evolution by natural selection, namely (1) phenotypic variation (2) that lead to differences in fitness, and (3) which are heritable.²³ Condition (1) is equivalent to ${\text {Var}}(z_i)>0$; condition (2) is equivalent to $\beta _{wz}\ne 0$ since the coefficient can only be positive if there is variation in the population and we supposed that there is a causal relationship between the character and its reproductive output;²⁴ and condition (3) is equivalent to $h\ne 0$. One difference between Lewontin’s three conditions and Eq. (7) is that the latter also describes evolutionary change due to other factors than natural selection, which are captured by the second term of the equation, namely ${\text {E}}(\varDelta z_i)$. Importantly, because of the similarities between Lewontin’s conditions and the Price equation, most problems associated with one approach will also be found in the other. This is a point which I believe has been under-appreciated in the literature.

One difference between Eqs. (7) and (1) is that the transmission-bias term of Eq. (1) is weighted by $\omega$ while it is not in Eq. (7). In Eq. (1), if an entity does not reproduce then its transmission bias is 0, while this does not affect the transmission-bias term in Eq. (7), so that one must assign a value for the average offspring character of entities that this entity would have if it was able to reproduce. Following Bourrat (2015a), I will assume by convention that this value, in such cases, is equal to that of the average offspring character in the population. This convention can be justified on the basis that an entity producing no offspring, or offspring with the average value of the offspring population, does not make any difference in terms of character change at the next generation.

Since the Price equation can be derived for a character at any level of organization, we can write a version of Eq. (7) at the collective level as:

$$\begin{aligned} \varDelta \overline{Z}=H^2 {\text {Cov}}(\varOmega _k,Z_k)+{\text {E}}(\varDelta Z_k), \end{aligned}$$

(8)

where $H^2$ is the collective-level heritability of Z and is defined as:

$$\begin{aligned} H^2=\frac{{\text {Cov}}(\overline{Z'_k},Z_k)}{{\text {Var}}(Z_k)}, \end{aligned}$$

(9)

where $\overline{Z'_k}$ is the average character of offspring collective coming from k.

With the Lewontinized version of the Price equation in place, I will now characterize the degree of functional (non-)aggregativity of a collective character $\textit{Z}$ in terms of particle character, in terms of functional additivity and non-additivity. To do so, let us define the character of a particle $\textit{j}$ belonging to collective k ($z_{jk}$), so that:

$$\begin{aligned} z_{jk}=\alpha _{jk}+ \gamma _{jk}. \end{aligned}$$

(10)

I refer to the first term on the right-hand side of Eq. (10), $\alpha _{jk}$, as the functional additive component of the character of particle j in collective k, that is, the character this particle (or a particle with the same intrinsic properties) would have if its character was measured independently from other particles. I refer to the second term on the right-hand side, $\gamma _{kj}$, as the non-additive or synergistic component of the character of particle j in collective k.

A pragmatic way to obtain the value of the functional additive and non-additive components of a particle’s character would involve developing an experimental design and measuring the value of the particle character taken independently. This value would correspond to the functional additive component of the particle ($\alpha _{jk}$). To obtain the non-additive component would involve first measuring the value of the collective character, then dividing this value by the number of particles it contains. We would have at hand the character attributed to the particle in the collective context ($z_{jk}$). To obtain the value of the non-additive component, one would then have to subtract the value of the character of the particle taken independently from the value of the character attributed to the particle, since $\gamma _{jk}=z_{jk}-\alpha _{jk}$.

Furthermore, to establish that this non-additive component corresponds to functional non-additivity, collectives composed of particles with the same character when taken independently (i.e., same composition for the aggregative component of particle character) should have the same collective character, everything else being equal. When this condition is established, this is evidence that the interactions between the particles of the two collectives are similar or, in other words, that the boundaries of the collectives chosen by the observer correspond to genuine boundaries. In cases where this condition is not verified, this is evidence that at least some particles with a given aggregative character interact differently in the two collectives carved up by the observer and having the same particle composition. In such situations it would be reasonable to assume that the boundaries drawn by the observer around the collectives do not correspond to genuine boundaries.

I have assumed here that no errors of measurement are made. In a real setting, such errors would exist and the value of each component could be determined only with some confidence using appropriate statistical tests after having eliminated environmental effects and the influence of other particle characters different from z on the collective character.²⁵ More concretely, this means that the level of non-aggregativity could be measured experimentally.

Substituting Eq. (10) into Eq. (3), we have:

$$\begin{aligned} Z_k= \frac{1}{n}\sum \limits _{j=1}^{n}\mathop {}_{_k} (\alpha _{jk}+ \gamma _{jk})= A_k+ \varGamma _k, \end{aligned}$$

(11)

where $A_k$ and $\varGamma _k$ are the average additive contribution and non-additive contribution, respectively, of the particles composing the collective k to its collective character.

Mutatis mutandis, we define $Z'$ as:

$$\begin{aligned} Z_k'= A'_k+ \varGamma '_k. \end{aligned}$$

(12)

Before going further, I should clarify the two notions of aggregativity I have used so far, namely statistical and functional aggregativity. These two notions correspond to the difference between the decomposition of the collective character ($\textit{Z}$) in terms of particle contributions in Eq. (3) and in Eq. (11), respectively. In Eq. (3), the decomposition of the character is statistical. That is to say, that even though the character might be at least partly the result of interactions between its particles, each particle will be considered as making a single (statistical) contribution to the collective character ($z_{jk}$). I referred to this as the character attributed to the particle, because it does not take into account the fact that one part of this character results from the interaction between the particles. The collective character is just an average of its particle statistical contributions and thus it is a statistical aggregate. This statistical way of partitioning the contribution of particles is compatible with any other partitioning, whether arbitrary or not, and thus with that of Eq. (12). But in this latter equation, aggregativity corresponds to (or aims at approximating) Wimsatt’s notion presented in Sect. 3. Aggregativity is here functional rather than statistical. It corresponds to the property a collective would exhibit if the property of each of its particles was taken independently (that is, it corresponds to $\alpha _{jk}$). Crucially, a functional-aggregate character will always be a statistical-aggregate character, but the converse is not true.²⁶

Importantly, contextual analysis, which is considered by some as a more causally faithful partitioning of the covariance particle character and particle fitness—one that takes into account the structure of a population (for more on contextual analysis see Heisler and Damuth 1987; Goodnight et al. 1992; Goodnight and Stevens 1997; Okasha 2006; Okasha and Paternotte 2012; Godfrey-Smith 2008; Earnshaw 2015; Jeler 2014; Bourrat 2016)—does not make the distinction between functional and statistical aggregates either, so that, like the classical version of the multilevel Price equation, it can be applied to units that are not functional ones, and thus falls prey to some of the problems associated with the multilevel form of the Price equation. Note, furthermore, that like the multilevel version of the Price equation, contextual analysis only accounts for the selection phase of a process, not the response to the selection phase. This point is made clear by one of the main architects of contextual analysis, Charles Goodnight, who together with colleagues writes that “[t]his model is based on phenotypic change in the traits of individuals and the group means of these traits but makes no assumptions about the inheritance of these traits” (Goodnight et al. 1992, pp. 759–760).

The distinction between statistical and functional aggregativity is important in the context of ETIs and more specifically with the use of the Price equation. In fact, if the functional interactions between particles is one of the drivers for ETIs, surely this phenomenon should appear in the formalism. Yet, using the Price equation, a functional non-aggregative collective character will appear as a statistical aggregate, so long as this character can be defined from the point of view of the particle character. As I show below, the functional decomposition provided in Eq. (12) becomes very useful to interpret ETIs when inserted into the Lewontinized version of the Price equation for collective character [Eq. (8)].

With $\textit{Z}$, $\overline{Z'}$, and $H^2$ being defined and the distinction between statistical and functional aggregativity drawn, we can now substitute Eqs. (9), (11), and (12) in Eq. (8). This leads to:

$$\begin{aligned} \begin{aligned} \varDelta \overline{Z}=&\frac{{\text {Cov}}(\overline{Z'_k},Z_k)}{{\text {Var}}(Z_k)} {\text {Cov}}(\varOmega _k,Z_k)+{\text {E}}(\varDelta Z_k)\\ =\,&\frac{{\text {Cov}}(\overline{A'_k} + \overline{\varGamma '_k},A_k+\varGamma _k)}{{\text {Var}}(A_k+ \varGamma _k)} {\text {Cov}}(\varOmega _k,A_k+ \varGamma _k)\\&+{\text {E}}(\varDelta Z_k). \end{aligned} \end{aligned}$$

(13)

Applying the distributive rule for variances and covariances, Eq. (13) can be rewritten as:

$$\begin{aligned} \begin{aligned} \varDelta \overline{Z} =&\frac{{\text {Cov}}(\overline{A'_{k}}, A_k)+{\text {Cov}}(\overline{A'_{k}},\varGamma _k)+{\text {Cov}}( \overline{\varGamma '_k},A_k)+{\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)}{{\text {Var}}(A_k+ \varGamma _k)} {\text {Cov}}(\varOmega _k,A_k+ \varGamma _k)\\&+{\text {E}}( \varDelta Z_k)\\ =\,&\frac{\mathrm{Cov}(\overline{A'_{k}}, A_k)+{\text {Cov}}(\overline{A'_{k}},\varGamma _k)+{\text {Cov}}( \overline{\varGamma '_k},A_k)+{\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)}{{\text {Var}}(A_k+ \varGamma _k)} {\text {Cov}}(\varOmega _k,A_k)\\&+\frac{{\text {Cov}}(A'_{\bar{k}}, A_k)+{\text {Cov}}(A'_{\bar{k}},\varGamma _k)+{\text {Cov}}( \overline{\varGamma '_k},A_k)+{\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)}{{\text {Var}}(A_k+ \varGamma _k)} {\text {Cov}}(\varOmega _k,\varGamma _k)\\&+{\text {E}}( \varDelta Z_k). \end{aligned} \end{aligned}$$

(14)

Assuming there is no covariance between the average offspring functional additive and the parental non-additive components of collective character (${\text {Cov}}(\overline{A'_{k}},\varGamma _k)=0$), as well as no covariance between the functional additive component of the parental collective character and the functional non-additive component of average offspring collective character (${\text {Cov}}(A_k,\overline{\varGamma '_k})=0$), so that they are independent (which are both reasonable assumptions as there is no particular reason why they should be correlated²⁷), Eq. (14) simplifies into:

$$\begin{aligned} \begin{aligned} \varDelta \overline{Z} =\,&\frac{{\text {Cov}}(\overline{A'_{k}}, A_k)+{\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)}{{\text {Var}}(A_k+ \varGamma _k)} {\text {Cov}}(\varOmega _k,A_k)\\&+\frac{{\text {Cov}}(\overline{A'_{k}}, A_k)+{\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)}{{\text {Var}}(A_k+ \varGamma _k)} {\text {Cov}}(\varOmega _k,\varGamma _k)+{\text {E}}(\varDelta \varGamma _k). \end{aligned} \end{aligned}$$

(15)

Finally, this equation can be developed into:

$$\begin{aligned} \begin{aligned} \varDelta \overline{Z} =\,&\frac{{\text {Cov}}(\overline{A'_{k}}, A_k)}{{\text {Var}}(A_k+ \varGamma _k)}{\text {Cov}}(\varOmega _k,A_k)+\frac{{\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)}{{\text {Var}}(A_k+ \varGamma _k)} {\text {Cov}}(\varOmega _k,A_k)\\&+\frac{{\text {Cov}}(\overline{A'_{k}}, A_k)}{{\text {Var}}(A_k+ Z)} {\text {Cov}}(\varOmega _k,\varGamma _k)+\frac{{\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)}{{\text {Var}}(A_k+ \varGamma _k)} {\text {Cov}}(\varOmega _k,\varGamma _k)\\&+{\text {E}}( \varDelta Z_k). \end{aligned} \end{aligned}$$

(16)

Let us now define collective heritability as:

$$\begin{aligned} H^2=H^2_A+H^2_\varGamma , \end{aligned}$$

(17)

where $H^2_A$ is the functional additive (aggregative) component of collective heritability, and is equal to:

$$\begin{aligned} H^2_A=\frac{{\text {Cov}}(\overline{A'_{k}}, A_k)}{{\text {Var}}(A_k+ \varGamma _k)}, \end{aligned}$$

(18)

and $H^2_\varGamma$ is the non-additive component of collective heritability which is equal to:

$$\begin{aligned} H^2_\varGamma =\frac{{\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)}{{\text {Var}}(A_k+ \varGamma _k)}. \end{aligned}$$

(19)

Inserting Eqs. (18) and (19) in Eq. (16), we get:

$$\begin{aligned} \begin{aligned} \varDelta \overline{Z} =\,&\overbrace{H^2_A\overbrace{{\text {Cov}}(\varOmega _{k},A_{k})}^{\text { Particle selection}}}^{\begin{array}{c} \text { Particle response}\\ \text { to particle selection} \end{array}}+\overbrace{H^2_\varGamma {\text {Cov}}(\varOmega _{k},A_{k})}^{\begin{array}{c} \text { Collective response}\\ \text { to particle selection} \end{array}}\\&+\underbrace{H^2_A{\text {Cov}}(\varOmega _k,\varGamma _k)}_{\begin{array}{c} \text { Particle response to}\\ \text { collective selection} \end{array}}+\underbrace{H^2_\varGamma \underbrace{{\text {Cov}}(\varOmega _k,\varGamma _k)}_{\text { Collective selection}}}_{\begin{array}{c} \text { Collective response to}\\ \text { collective selection} \end{array}}\\&+\underbrace{{\text {E}}(\varDelta Z_{k})}_{{\begin{array}{c} \text { Transmission bias of }\\ \text { collective character} \end{array}}}. \end{aligned} \end{aligned}$$

(20)

Inspired by the terminology used in quantitative genetics (Falconer and Mackay 1996), I propose to interpret the first term on the right-hand side ($H^2_A{\text {Cov}}(\varOmega _k,A_k$)) as the particle response to particle selection. In fact, both the component of the covariance between collective fitness and collective character, and the component of collective heritability, concern here the functional additive (aggregative) component of the collective character ($\textit{A}$).²⁸ I propose, following the same reasoning, that the second term on the right-hand side should be interpreted as the collective response to particle selection, since the covariance component between collective fitness and collective character concerns here the functional additive component of the collective character ($\textit{A}$), while the collective heritability component concerns the non-aggregative component of the collective character ($\varGamma$). Mutatis mutandis, I propose to interpret the third and fourth terms on the right-hand side ($H^2_A{\text {Cov}}(\varOmega _k,\varGamma _k)$, and $H^2_\varGamma {\text {Cov}}(\varOmega _k,\varGamma _k)$, respectively), as the particle response to collective selection, and the collective response to collective selection, respectively. The fifth term on the right hand side (${\text {E}}(\varDelta Z_k)$) is the transmission bias of the collective character.

However, it should be noted that strictly speaking all components of $H^2$ and $\textit{Z}$ (i.e., aggregative and non-aggregative) refer to the collective-level character. Yet, there is some ground to argue that the aggregative components represent outcomes that would occur if there was no group structure in the population.²⁹ For that reason, I assume that the aggregative components of selection and heritability refer in some legitimate sense, to the particle level in Eq. (20).

Before moving further, something should be said about the relationship between collective-level heritability and collective-level reproduction. Heritability and reproduction are obviously very different concepts. As shown in Bourrat (2015a), the concept of heritability extends to situations in which there is no reproduction. Yet, in a case in which one can distinguish discrete generations of particles and collectives, as I have assumed, for there to be a positive heritability across generations the collectives (and particles that constitute them) must reproduce. Thus, although the Lewontinized version of the Price equation, in and of itself, is silent about whether genuine collective-level reproduction occurs or whether it is only a functional aggregate of the activities of the particles that compose the collectives, one can nevertheless deduce some consequences about collective-level reproduction from the existence of a non-additive component of collective-level heritability ($H^2_\varGamma >0$) in particular situations.

Although $H^2$ can be $\mathrm{1}$ when there is no genuine collective character (functionally additive trait), $H^2_\varGamma$ will be nil. This implies that the positive collective-level heritability should be fully attributed to the aggregative activities of the particles that compose the collectives with respect to the character of particles that compose the collective. From there, since there would be no interaction between the particles for the collective trait, one might be tempted to argue that there could be no genuine collective-level reproduction. This last remark is, however, incorrect. In fact, it may well be the case that there is genuine collective-level reproduction due to the interaction of traits that are different from the focal trait Z. Thus, one possibility to make collective heritability a better proxy for the absence or presence of genuine collective-level reproduction, is to put forward the following two criteria, one that concerns the absence of collective-level reproduction, while the other concerns its presence:

Sure criterion for the absence of genuine collective-level reproduction: Collective-level reproduction is spurious, that is due to the functionally aggregative reproductive activities of the particles that compose it, when the non-aggregative contribution of particles to the collective character is nil for all possible collective traits.

I qualified this criterion as a ‘sure criterion,’ because if it is fulfilled, then for sure, there cannot be collective-level reproduction. In fact, for there to be genuine collective-level reproduction, particles should at least interact for one collective trait that would enable collective-level reproduction. Note that the converse of the sure criterion is not true. In fact, the existence of functional non-aggregativity for a collective trait is not enough for collective-level heritability and reproduction. To deal directly with the presence of collective-level reproduction, I propose the following criterion:

Criterion indicating genuine collective-level reproduction: When collective-level reproduction is genuine, that is not solely due to the functionally aggregative reproductive activities of the particles that compose it, there will exist a positive covariance between the parental and average offspring non-aggregative component of the collective character (${\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)\ne 0$).

This criterion can be justified as follows: if there is genuine collective-level reproduction, this implies that at least one collective-level character is the result of the interaction of the particles that compose a collective and lead to the emergence of collective-level reproduction, the latter of which I define as a higher than chance probability for two offspring particles from a single parent to form a collective offspring (i.e., positive assortment of particle offspring based on their parental origin). That such an interaction exists will impact any non-aggregative trait. Note that this is not a ‘sure’ criterion because ${\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)$ could be different from 0 without there being any collective-level reproduction. Thus, the converse of the criterion is not true. Nevertheless, the criterion is an indicator. Other criteria, such as the existence of a developmental phase (which I do not treat here) might permit us to define collective-level reproduction more precisely.

Another approach to detect collective-level reproduction is to move away from heritability, and rather focus on the variance of the average collective character for a given parent, without considering the aggregative and non-aggregative components of the collective character, as I have proposed elsewhere (Bourrat, in press). If the variance is high, this is evidence that the particles of a collective parent are not reproducing together, while if there is a low variance, they are, which indicates a genuine collective-level reproduction. That the offspring particles of a collective together form a new collective, could however be due to the environment and consequently not attributable to the interaction of particles (especially if the collective character is a functional aggregate of the particle character). One ‘test’ in such a case for knowing whether collective-level reproduction is genuine would be to see whether the variance in collective-offspring character from one parent remains low when the environment is changed. If it remains low, this would be evidence that the interaction between the particles that compose the collective are responsible for the collective-level reproduction rather than external conditions. Note, however, that a structured environment could very well be an important driver of ETIs and collective-level reproduction (by making the interaction between neighboring particles more likely than with remote particles). This is an idea I explore elsewhere with collaborators (Black et al. 2019). I will come back to the distinction between collective-level heritability and reproduction in the next section.

Having distinguished the four different ways in which particle and collective selection and particle and collective heritability can interplay using a partitioning of the Price equation [Eq. (20)] in which the collective character is defined as an outcome of the interactions of the particles rather than as a pure statistical contribution of them, we now have an ontologically sound conception of levels of selection, one which is immune to the problems to which the classical multilevel equation presented in Sect. 2 falls prey, and consequently we are in a good position for providing an analysis of the conditions required for an ETI to occur.

5 The different stages of an ETI

5.1 Stage 0

Before an ETI has started, as I argued earlier, it is reasonable to assume that there are no (or marginal) interactions between the particles of a collective. In fact, there is no biological reality of collectives. This implies that however the collectives are partitioned in the population of particles, taking Eq. (20), for any collective character thus delimited, we have $Z_k= A_k$ so that $\varGamma _k=0$ and $\overline{\varGamma '_k}=0$. As $H^2_\varGamma =0$, we have ${\text {Cov}}(\overline{\varGamma '_k},\varGamma _k)={\text {Cov}}(0,0)=0$. Similarly, because $\varGamma _k=0$ and, because a covariance with a constant is nil, we have ${\text {Cov}}(\varOmega _k,\varGamma _k)=0$.

Taking all this into consideration, Eq. (20) simplifies into:

$$\begin{aligned} \varDelta \overline{Z}=H^2_A {\text {Cov}}(\varOmega _k,A_k)+E(\varDelta Z_k ). \end{aligned}$$

(21)

Equation (21) is simply Eq. (8) where the collective character is not only a statistical aggregate, but also a functional aggregate of particle character.

Note that the fact that the particles reproduce perfectly guarantees neither that the aggregative component of colective-level heritability is 1, nor that the transmission bias is nil. Particles within each collectives reproducing differentially could and will typically lead collective-level heritability being lower than 1 and to a non-nil collective-level transmission bias.

Modern biological situations matching Stage 0 will be any case in which the individuals of a population interact in such a way that no non-aggregative components of character are produced one hierarchical level above. For instance, to take an example in the taxonomic group most studied in the context of ETIs, namely the family of volvocine green algae (see Herron 2016, for a discussion of the transition to multicellularity in this family). One might want to take a population of Chlamydomonas reinhardtii which are unicellular organisms belonging to this family, and carve it into different collectives. Yet, because the collective character exhibited at the collective level, in this case, would not be different from the aggregate of each cell taken independently, $\varGamma$ would be nil in each collective, vindicating no individuality at that level. Any other example of arbitrary collectives created by the observer will lead to the same outcome.

5.2 Stages 1 and 2

5.2.1 Genuine collective character

One first-stage candidate of an ETI is the formation of collectives with characters which are not merely the functional aggregate of the particle characters. Formally, this implies that the non-additive component of the collective character ($\varGamma$) is different from 0. However, that $\varGamma$ is different from 0 implies neither that the covariance between the collective character and the collective fitness is positive, nor that the covariance between the collective parental character and the average offspring character is positive, so that $H^2_\varGamma$ is positive. Suppose for now that ${\text {Cov}}(\varOmega _k,\varGamma _k)\ne 0$ and that $H^2_\varGamma =0$. This latter assumption could be justified on the grounds that, if a particular sort of interaction has a functional effect on the collective in a situation in which offspring particles are dispersed randomly in the offspring population (there is no mechanism of collective-level reproduction), then the probability that this interaction is reformed at the next generation is not higher than for any other interaction.³⁰ With these assumptions Eq. (20) simplifies into:

$$\begin{aligned} \begin{aligned} \!\varDelta \overline{Z} =\,&H^2_A {\text {Cov}}(\varOmega _k,A_k)+ {0}{\text {Cov}}(\varOmega _k,A_k)\!+H^2_A{\text {Cov}}(\varOmega _k,\varGamma _k)\!+0{\text {Cov}}(\varOmega _k,\varGamma _k)\!+{\text {E}}(\varDelta Z_k)\\ =\,&\underbrace{H^2_A{\text {Cov}}(\varOmega _k,A_k)}_{\begin{array}{c} \text { Particle response to}\\ \text { particle selection} \end{array}}+\underbrace{H^2_A{\text {Cov}}(\varOmega _k,\varGamma _k)}_{\begin{array}{c} \text { Particle response to}\\ \text { collective selection} \end{array}}+\underbrace{{\text {E}}(\varDelta Z_k)}_{{\begin{array}{c} \text { Transmission bias}\\ \text { of collective}\\ \text { character} \end{array}}}. \end{aligned}\!\! \end{aligned}$$

(22)

Under these assumptions, we thus have a response due to the particle contribution to collective heritability to both particle and collective selection (${\text {Cov}}(\varOmega _k,A_k)$ and ${\text {Cov}}(\varOmega _k,\varGamma _k)$, respectively). A possible interpretation of Eq. (22) is that during the first stage of an ETI, one component of the overall selection process is independent from the particles being organized in collectives, while the other component of selection is due to the particles being organized in collectives. Because there is no genuine collective reproduction and therefore a nil non-aggregative component of collective heritability, any change in collective-level character can only be the result of the reproductive activities of particles.

Modern biological examples matching this case could be the case of the biofilm or the squid-vibrio symbiosis mentioned in Sect. 3, in which there definitely is a non-aggregative component of collective-level character—which will vary depending on focal trait—but for which the pattern of reproduction at the collective level is not different from the pattern of reproduction of each cell (for example, composing the biofilm taken independently). Of course, due to the fact that the different partners of a biofilm do not, strictly speaking, disperse randomly—although we might imagine situations in which this might nearly be the case—the $H^2_\varGamma$ might not be nil. Yet this stage, like any of the stages presented in this section, is an idealized situation which will only partly describe the biological complexity. Furthermore, recall that the non-aggregative-component of collective-level heritability is only a proxy for collective-level reproduction.

5.2.2 Genuine collective reproduction and inheritance

A second first stage candidate for ETIs, which could occur independently of whether there is genuine collective-level selection (${\text {Cov}}(\varOmega _k,\varGamma _k)\ne 0$) (that is, independently from the previous candidate for the first stage), is that the reproduction of collectives becomes more than the mere aggregative reproduction of the particles forming each collective (I assume here that collective reproduction and inheritance go hand in hand).

As a result of the positive covariance between parental character and average offspring character, we have $H^2_\varGamma >0$. If we now assume, contrary to what we assumed in Sect. 5.2.1, that there is no collective selection since the non-aggregative component of collective-level character might be neutral so that ${\text {Cov}}(\varOmega _k,\varGamma _k)=0$, we can rewrite Eq. (20) as:

$$\begin{aligned} \begin{aligned} \varDelta \overline{Z} =\,&H^2_A{\text {Cov}}(\varOmega _k,A_k)+H^2_\varGamma {\text {Cov}}(\varOmega _k,A_k)+H^2_A0+H^2_\varGamma 0+{\text {E}}(\varDelta Z_k)\\ =\,&H^2_A{\text {Cov}}(\varOmega _k,A_k)+H^2_\varGamma {\text {Cov}}(\varOmega _k,A_k)+{\text {E}}(\varDelta Z_k). \end{aligned} \end{aligned}$$

(23)

Under the assumptions of no genuine collective-level selection, but where collective-level reproduction is present, the two terms of Eq. (23), $H^2_A{\text {Cov}}(\varOmega _k,A_k)$ and $H^2_\varGamma {\text {Cov}}(\varOmega _k,A_k)$ represent respectively, the particle-level and the collective-level components of the response to the particle-level component of selection. As mentioned earlier, this would imply a first stage of ETIs in which the non-aggregative component of a collective-level character is neutral.

A modern biological example matching this situation is harder to find than with the other first stage-candidate. We might nevertheless imagine a situation close to the wrinkly spreader model studied by Rainey and collaborators (Rainey and Rainey 2003; Rainey and Kerr 2010; Hammerschmidt et al. 2014; Rose et al. 2019). In this model, a strain of the bacteria Pseudomonas fluorescens produces a mutant that is able to secrete a sticky polymer. When this polymer is produced in large quantity, this leads to the formation of a mat at the air-liquid interface of a test tube which, in turn, gives a growth advantage to the bacteria trapped within the mat, since there is more oxygen—a limiting factor for growth—at the air-liquid interface than in the solution. The polymer is costly to produce but the advantage provided outweighs the cost. Of course, as studied by Rainey and collaborators, this situation leads ultimately to the evolution of individuals (cheaters) benefiting from the mat but without producing the costly polymer. We could, starting from this biological model, imagine a situation in which the production of a sticky polymer is a by-product of another trait that is strictly beneficial to the cell producing it and with no cost involved when cells are sticking to one another. After a certain size, which could be a function of the stickiness of the polymer, the collective would fragment into smaller collectives. In this situation, there would a number of collective-level traits having a neutral non-aggregative component and yet which are heritable due to the fact that fragmentation would not, by and large, mix the population of bacteria. Note that, in this situation, the assumption I made of the cells and collective reproducing at the same time would be violated. In fact, collective-level reproduction would occur by a means different from particle-level reproduction. In effect, collective-level reproduction by fragmentation does not require (in the short term), the reproduction of particles. This demonstrates one more time that the model I assume is an idealization from real biological situations. I discuss this type of limitation in the next section.

5.2.3 Genuine collective selection and reproduction

A likely scenario is that collective-level selection and collective-level reproduction occur jointly, rather than separately, during ETIs as assumed in the previous two subsections. Taking the insights of both Eqs. (22) and (23) presented earlier, this leads to a form of Eq. (20) in which all four response to selection terms are different from 0.

A modern biological situation matching this stage is cyanobacteria colonies of the genus Nostoc, which have non-aggregative components of collective-level properties, such as an extracellular polymeric substance which provides specific UV absorption properties to the colony (Potts 2002), the latter of which is certainly correlated with fitness (contrary to the hypothetical case mentioned in Sect. 5.2.2). Another point worth mentioning is that some cells of Nostoc colonies are differentiated cells which are able to fix nitrogen, a limiting factor for growth. These cells are called ‘heterocysts’. Which cell of the colony becomes a heterocyst is determined by a complex mechanism at the colony level (Wolk 1996) and is thus subject to selection at that level, since these cells would not have a heterocyst phenotype had their phenotype been measured independently from the colony. In many species of Nostoc the reproduction of the colony can occur by fragmentation of a colony filament—although for some species this represents only a minor mode of reproduction. As mentioned in Sect. 5.2.2, the fragmentation mode of reproduction leaves many of the cell-cell interactions intact and consequently permits the non-aggregative component of collective-level heritability to be potentially high.

5.3 Stage 3: elimination of particle-level selection and inheritance

At the end of an ETI, it is reasonable to assume that the collective-level character becomes a pure non-additive function (or nearly so) of the particle properties, which would imply that the functional additive component of the collective character is nil. Note that this phenomenon could occur in a single mutational step. We have:

$$\begin{aligned} Z_k= \varGamma _k, \end{aligned}$$

(24)

If we replace this in Eq. (20), assuming there is some collective-level heritability, we get:

$$\begin{aligned} \begin{aligned} \!\varDelta \overline{Z} =\,&0{\text {Cov}}(\varOmega _k,0)+H^2_\varGamma {\text {Cov}}(\varOmega _k,0)\!+0{\text {Cov}}(\varOmega _k,\varGamma _k)\!+H^2_\varGamma {\text {Cov}}(\varOmega _k,\varGamma _k)\!+{\text {E}}(\varDelta \varGamma _k)\\ =\,&\underbrace{H^2_\varGamma {\text {Cov}}(\varOmega _k,\varGamma _k)}_{\begin{array}{c} \text { collective response to}\\ \text { collective selection} \end{array}}+\underbrace{{\text {E}}(\varDelta Z_k)}_{{\begin{array}{c} \text { Transmission bias}\\ \text { of collective}\\ \text { character} \end{array}}}. \end{aligned}\!\!\!\!\! \end{aligned}$$

(25)

Equation (25) has the same form as Eq. (9). In fact we have $H^2_\varGamma =H^2$, and since $A=0$, we have ${\text {Cov}}(\varOmega _k,Z_k)={\text {Cov}}(\varOmega _k,\varGamma _k)$. Although an alternative equation to Eq. (25) from a particle-level perspective can be given since we assumed that Z is a statistical aggregate of particle character, Eq. (25) represents a better causal decomposition granted that the aggregative/non-aggregative distinction captures the distinction between a unit and an arbitrary collective.

There are a plethora of biological situations matching this stage at different levels of organization. Different models of the evolution of the eukaryotic cell are good examples of processes leading to a situation in which the aggregative component of the collective-level character (the collective here is the eukaryotic cell or its ancestors) becomes nil. For instance, a recent version of the endosymbiotic theory for the origin of the eukaryotic cell (for a history of the different endosymbiotic theories see Martin et al. 2015), called the ‘inside-out theory’ (Baum and Baum 2014), proposes that an archaea (the host) extruded its membrane over generations around ‘proto-mitocondria’ symbionts living on its surface in order to achieve a higher level of contact with the symbionts, increasing the performance of both partners. The progressively larger and larger extrusions, according to the theory, led to the formation of blebs that engulfed the symbionts. Finally the blebs fused and formed what was becoming a modern eukaryotic cell. Following such a scenario, the aggregative component of a trait such as ‘rate of nucleoside synthesis’³¹ decreased as the symbiosis became increasingly obligatory, to the point of vanishing when each partner is unable to survive without the other. This consequently left only the non-aggregative component of selection and response to selection as being different from 0.

6 Limitations and conclusions

The version of the Price equation I proposed in terms of functional additive (aggregative) and non-additive (non-aggregative) components of collective character and heritability should not be regarded as a full model for ETIs, but rather as an approach that gives some insights on the processes involved in ETIs. There are several reasons for that. The first and foremost is perhaps that the Price equation is primarily a visualization tool, not a model permitting us to predict the dynamics of a population of particles. Using the Price equation can give us snapshots at different stages of an ETI and point to some important differences at these stages.

A second type of limitation is that during an ETI, the generation time of the particles and that of the collective they compose typically become decoupled, as was mentioned above when presenting biological examples matching the different stages of an ETI. In other words, development comes into play. Yet, in my assumptions I have proposed that particle-level reproduction and collective-level reproduction coincide, an assumption which, even if it is legitimate at Stage 0 since any collective is just an aggregation of the particles that compose it, will typically not be at a later stage. Taking the example of a multicellular organism such as a zebra, between two events of zebra reproduction, there are a high number of cell divisions which constitute development, and which my equation does not account for. This is a significant limitation, of the model I proposed, to keep in mind, especially when referring to the fitness of a collective and that of a particle, which are typically measured over different periods of absolute time (generations of particles and collectives, respectively) (Bourrat 2015c). Related to this limitation is the fact that I have assumed no migration of particles between collectives—this is implicit with the assumption that generations of particles and collectives coincide perfectly. This is also a strong idealization. In most biological situations, migration between collectives with fuzzy boundaries might be the norm rather than the exception.³² That said, the general equation I proposed could be modified or qualified for these phenomena to be taken into consideration. I leave this for future work.

A third limitation is that the notions of aggregativity and non-aggregativity I have proposed are very abstract ones. Non-aggregativity does not point to a particular mechanism enabling collectives to be formed. This is not a problem in and of itself since it points towards the kind (albeit abstractly) of relationship one should look for to explain ETIs, but by no means does it represent a substitute for the precise mechanisms realizing those collective-level properties. If my analysis is correct, however, any mechanism of ETIs should be about the transformation from collectives which score low on aggregativity to collectives which score high for multiple traits.

A further limitation of my model is that collectives at all stages of the ETI are pure compositions of their particles. Yet, it is reasonable to suppose that at least in some cases of ETIs, the entities considered as collectives at the end of the ETI, are not purely made of the types of particles which started to interact at the beginning of the ETI. What was then their environment might be endogenized and become fully part of the collective entity. Here again, in principle this could be accounted for from a Pricean perspective, by considering the evolution of more than one trait using covariance matrices, instead of a single trait, following the method proposed by Lande (1979). This leads to a related limitation which I have already alluded to, namely that it is trait based, while individuals are collections of interacting traits. Here again moving to covariance matrices, where the aggregativity of multiple traits is taken into consideration (including any existing covariance between traits), as well as the aggregativity of their reproduction (via $H^2_\varGamma$), could mitigate the problem.

This last remark is also relevant for addressing yet another limitation of my analysis. Recall that I have distinguished functional aggregative traits from statistical aggregative traits. For a multilevel analysis of the Price equation to be carried, the collective trait must be a statistical aggregate trait of the particle traits. Yet, there are collective-level traits, as mentioned earlier, which are not a statistical aggregate of a particle-level trait. This is the case, for instance, with the collective trait ‘density of particles’ or the trait ‘degree of particle phenotypic differentiation.’³³ The reason these traits are not statistical aggregates of a particle-level trait is that they involve variables that are not properties of the particles but rather of their environment, such as the physical space or resources available. One way to address this issue would be to take into account all the variables and their relevant relationships for producing the collective-level trait (once again using covariance matrices), so that once this is taken into consideration the collective-level trait ends up as a collective-level statistical aggregate of the particles that compose the collective, and all other relevant variables.

Finally, an important limitation of my approach is that I have addressed collective-level reproduction only indirectly with the non-aggregative component of collective-level heritability. I regard the implementation of the concept of collective-level reproduction in a diachronic formal approach to levels of selection, as an urgent and important problem to be addressed. The sole focus on heritability in recent approaches (e.g., Herron et al. 2018; Bourrat in press), although a welcome improvement over approaches that completely neglect it, is nevertheless not enough, since the notion of collective-level heritability typically invoked takes collective-level reproduction for granted, rather than explains it as a result of evolution.

These different limitations—and others that I have not mentioned—mean that the formal analysis presented here will be limited in scope, so that not all ETIs will strictly fit it. Nevertheless, in spite of these limitations, I have set the stage for future work, both experimental and theoretical, in this area.