A theory of change for prioritised resilient and evolvable software systems

Abstract

The process of completing, correcting and prioritising specifications is an essential but very complex task for the maintenance and improvement of software systems. The preservation of functionalities and the ability to accommodate changes are main objectives of the software development cycle to guarantee system reliability. Logical theories able to fully model such processes are still insufficient. In this paper we propose a full formalisation of such operations on software systems inspired by the Alchourrón–Gärdenfors–Makinson (AGM) paradigm for belief revision of human epistemic states. We represent specifications as finite sets of formulas equipped with a priority relation that models functional entrenchment of properties. We propose to handle specification incompleteness through ordered expansion, inconsistency through ordered safe contraction and prioritisation through revision with reordering, and model all three in an algorithmic fashion. We show how the system satisfies basic properties of the AGM paradigm, including Levi’s and Harper’s identities. We offer a concrete example and complexity results for the inference and model checking problems on revision. We conclude by describing resilience and evolvability of software systems based on such revision operators.

1 Introduction

The process of designing software starts usually from a list of requirements, intended as properties expressing desires of a stakeholder concerning the software to be developed. Given a certain domain knowledge, the requirements are meant to be implemented and satisfied by corresponding specifications, intended as properties of the system.¹ The notion of reliability for software systems has been mainly formulated in terms of continuity of correct service and is an attribute of dependability along with availability, maintainability, safety and security. Software reliability is heavily complicated by change in the life-cycle of computing systems. The process of modifying or re-defining systems specifications is required by increasing architectural complexity of the actual implementations, or improving software quality. In either case, “software maintenance has been regarded as the most expensive phase of the software cycle”.² A considerable amount of research has already been dedicated to the understanding, planning and execution of software evolution, in particular for requirements evolution, see e.g. Ernst et al. (2009). Typically, this occurs as part of the late life-cycle of the system and it is dictated by

• Architectural degeneration, i.e. the violation or deviation of the architecture, increasing with changes being made to the original, see e.g. Eick et al. (2001) and Lindvall et al. (2002);

• Flexibility requirements, i.e. the system property that defines the extent to which the system allows for unplanned modifications, see e.g. Port and Liguo (2003);

• Requirements prioritisation, i.e. the design choice which defines the relevance of corresponding functionalities, and in turn their resilience in view of future changes, see e.g. Fellows (1998) and Firesmith (2004).

In this context, the persistence of service delivery when facing changes is referred to as resilience and it is combined with correct evolvability, as the ability to successfully accommodate changes, see Laprie (2008). They can be taken as building blocks for defining and proceduralising a notion of reliability for software systems. The laws of software evolution for computational systems linked to a real environment (Lehman 1980; Lehman et al. 1997) express the importance of an appropriate understanding of software change. Change classification schemes, assessing the impact and risk associated with software evolution, present challenges (Mens et al. 2005) which include integration in the conventional software development process model. This, in turn, means that a model of software change at design and implementation stages is essential to assess and anticipate errors and to determine system’s reliability in view of threats to functionalities. Late life-cycle misfunctions, where the system produces negative side-effects absent in other systems of the same type, require corrective changes after testing on the actual code (i.e. excluding model-based testing). Disfunctions, where the system is less reliable or effective than one expects in performing its function are more likely to be assessed at early stages, where perfective changes result from new or changed requirements, see Lientz and Swanson (1980) and Sommerville (2004).³ A third classification is that of adaptive changes, where the system or its environment are evolving.⁴ The understanding, modelling and development of a theory for software evolution are thus crucial tasks (Mens et al. 2005).

Let us consider a concrete example, extracted from Zowghi et al. (1996, sec. 2):

Consider the requirements engineering process involved in developing a wordprocessor. The initial problem statement only specifies that this wordprocessor is intended to be used by children. Two assumptions may be made immediately that are related to the domain knowledge and usability. Firstly, since all word processors by default have a spell check functionality, we may specify a requirement for existence of a spelling check function. Secondly, since it is intended for use by children, we may add a set of requirements for the ability to change the colour of screen and text etc. These assumptions are added to the initial statement to represent our current state of belief about the software we are to develop and are then presented to the problem owners for validation. They, in turn, confirm that spell check is indeed a requirement but since they will only have monochrome terminals available there is no need for colour change. So we need to revise our set of beliefs to contract those requirements related to colour.

Besides requirements evolution, such a revision may also be induced at a lower level of abstraction. Consider the formulation of a specification satisfying given requirements, and an implementation thereof. The specification can be seen as a model of the physical artefact. When the latter violates some of the properties expressed by the former, a revision of the examined system in one of the above mentioned ways becomes necessary. Consider the following variant of the above case:

The initial problem statement only specifies that this wordprocessor is intended to be used by children. Two assumptions may be made immediately that are related to the domain knowledge and useability. Firstly, since all word processors by default have a spell check functionality, we may specify a requirement for existence of a spelling check function. Secondly, since it is intended for use by children, we may add a set of requirements for the ability to change the colour of screen and text etc. These assumptions are added to the initial statement to represent our current state of belief about the software we are to develop. The system is then developed accordingly, but the functionality to change the colour of the screen is not implemented. We extract the specification of the current implementation and compare it with the intended one. We notice the two are not logically equivalent, hence we wish to modify the latter to accommodate the required change. We consider this a perfective change. In the new implementation, the developers add the ability to insert graphs and figures. Again, a specification may be extracted and compared to the intended one: as the product is intended for children, the new functionality is considered superfluous and we wish to remove it. We consider this a corrective change. In the next development cycle, the functionality to spellcheck is made dependent on the ability to switch languages: for each language, an appropriate spellcheck is developed. The comparison with the intended model shows the logical difference, but it also indicates the dependency of a required functionality from a non-required one. The model is changed to accommodate the latter, in order not to loose the former. We consider this an adaptive change.

Despite the triviality of the above example, it seems clear that the above operations, possibly automatically performed, would be a significant aid to the process of software evolution. Even more so, if the products under considerations are no longer word-processor, but safety-critical systems, where the removal operation might induce significant effects.⁵

One way to account for corrective, perfective and adaptive changes on an implementation diverging from the specification is to treat them similarly to change operations in scientific theories. In particular, in this paper we define formal operations inspired by the AGM belief change theory, see Alchourrón et al. (1985). This area at the intersection of software engineering and theory change has been only very little explored: the only approach explicitly based on AGM is to be found in Zowghi et al. (1996), offering a framework to reason about requirements evolution in terms of belief change operations. In Dam and Ghose (2014), belief revision is used to deal with change propagation in model evolution. In Mu et al. (2011) and Booth’s (2001) negotiation-style for belief revision is used to model change from current to to-be system requirements, aiming at some form of compromise based on prioritisation. AGM belief revision has been investigated for logic programming under answer set semantics in Delgrande et al. (2013a, b). While notoriously a number of methods in software engineering have focused on developing implementation from specifications (Spivey and Abrial 1992; Abrial 2005), our analysis concentrates on the modelling of perfective, corrective and adaptive changes to design new specifications from early (incorrect) implementations that are the object of change. Here the passage from model to implementation to new model is crucial.

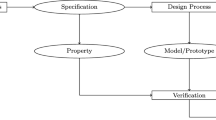
The case under consideration can be reformulated as follows in the process of software development. We start with $\mathcal {S}_{m}$, intended as a specification for a software system: translated in an abstract formal model, this is considered as a logical theory, i.e. a set of formulas closed under logical consequence, i.e. where all the properties implied by the formulas should be considered valid. An implementation of $\mathcal {S}_{m}$ will be denoted by $\mathcal {I}$. This actual artefact will have its own formal model, possibly automatically extracted, and it will be denoted by $S_{i}$. This new model cannot be treated as a logical theory, because it will verify only a finite number of formulas. Therefore, $S_{i}$ needs to be considered as a base. Assuming a discrepancy is found between the intended model $\mathcal {S}_{m}$ and $S_{i}$, some change is performed on the latter to obtain a new specification $\mathcal {S}'_{m}$.⁶ This dynamics, which can be labelled Specification Evolution, is illustrated in Fig. 1. To model this process concretely, we start with considering $\mathcal {S}_{m}$ as a software theory, i.e., the deductive closure of a (finite) set of formulas, each representing a property of our system. Our aim is to define some operation that allows the construction of a new theory from the previous one by performing some perfective, corrective or adaptive change. In order to manipulate such a theory in an algorithmic fashion and define concrete operations, we deal with a finite base $S_{i}$ representing the software system which offers a syntactic representation of the theory $\mathcal {S}_{m}$ and is not logically closed. In other words, we assume that the specification of any however large software and its manipulation should be accounted for in terms of a finite representation. This concrete formulation of the specification evolution is labelled System Change and it is illustrated in Fig. 2.

Fig. 1

Specification evolution

Fig. 2

System change

We consider the computational aspect of the operators introduced in this paper, i.e. the computational complexity of reasoning with the operators. In literature, there are mainly two questions assuming a finite propositional language as in this paper:

• Inference Given a knowledge base $S_{i}$, a new formula $\phi _{i}$ and a query $\psi _{j}$ (represented as propositional formulas), decide whether $\psi _{j}$ is a logical consequence of $S_{i}*\phi _{i}$, the revised knowledge base. (Here $*$ is interpreted as a revision operator.) The complexity of this problem was first studied by Eiter and Gottlob (1992).

• Model checking Given a knowledge base $S_{i}$, any such knowledge base can be equivalently represented by the set of its models, denoted as $\mathcal {M}(S_{i})$. A model M is supported by the knowledge base $S_{i}$ iff $M\in \mathcal {M}(S_{i})$, i.e., $M\models S_{i}$. The model checking problem is thus to decide whether a model is supported by the revised base. Formally, given a knowledge base $S_{i}$, a new formula $\phi _{i}$, and a model M (represented by a valuation of propositional letters), decide whether $M\in \mathcal {M}(S_{i}*\phi _{i})$.

In AI literature, the complexity of various belief revision and update operators has been extensively studied by Liberatore and Schaerf (2001). We show that for our revision operator with reordering, the inference problem is in co-NP, whereas the model checking problem is in the second level of the polynomial hierarchy, i.e., $\varSigma ^\mathrm{P}_2$.

The rest of this paper is structured as follows. In Sect. 2 we introduce our formal machinery. In Sect. 3 we formulate our definitions of expansion, safe contraction and revision for system evolution and offer their algorithmic translations. In Sect. 4 we present a notorious example of a broken algorithm and its redesign through the operators introduced in this paper. In Sect. 5 we present the complexity results. In Sect. 6 we offer resilience and evolvability properties on our theory. We conclude with remarks on future research.

2 Preliminaries

The alphabet of a propositional formula is the set of all propositional atoms occurring in it. A valuation of an alphabet X is a truth assignment to all the propositional letters in X. An interpretation of a formula is the truth assignment when the valuation to the atoms of its alphabet is given. A model M of a formula $\phi _{i}$ is an interpretation that satisfies $\phi _{i}$ (written $M\models \phi _{i}$). Interpretations and models of propositional formulas will usually be denoted as sets of atoms (those which are mapped into true). A theory T is a logically closed set of formulas. An interpretation is a model of a theory if it is a model of every formula of the theory. Given a theory T and a formula $\phi _{i}$ we say that T entails $\phi _{i}$, written $T\models \phi _{i}$, if $\phi _{i}$ is satisfied by every model of T.

We consider a software theory as the deductive closure of a finite set of formulas $\mathcal {S}_{m}=Cn(S_m)$ where $S_{m}=\{\phi _{1}, \dots , \phi _{n}\}$, i.e. $\mathcal {S}_{m}:=\{\phi _{i}\mid S_{m}\models \phi _{i}\}$, where each $\phi _{i}$ expresses a specific behaviour that the intended software system $\mathcal {S}_{m}$ should display. In the following we will use respectively theory and system to refer to these two distinct formal objects. The consequence relation $\vDash$ for $\mathcal {S}_{m}$ is classical with the following essential properties:⁷

• 1. $\mathcal {S}_{m} \vDash \top$.

• 2. $\mathcal {S}_{m} \vDash (\phi _{i}\rightarrow \phi _{j})$ and $\mathcal {S}_{m} \vDash \phi _{i}$, implies $\mathcal {S}_{m}\vDash \phi _{j}$.

• 3. $\mathcal {S}_{m}\vDash \phi _{i}$ implies $\mathcal {S}_{m}\nvDash \lnot \phi _{i}$.

$\vDash$ intuitively reflects property expressiveness: $\phi _{i}\vDash \phi _{j}$ says that a property specification $\phi _{i}$ holding for a system $S_{m}$ induces property specification $\phi _{j}$ in the corresponding theory $\mathcal {S}_{m}$.

We call functional entrenchment an ordering $\phi _{i}\le \phi _{j}$ which says that $\phi _{i}$ is at least as embedded as $\phi _{j}$ in view of the functionalities of the system. This means that the satisfiability of functionality $\phi _{j}$ might depend or be less essential than the satisfiability of functionality $\phi _{i}$. Another way to present the intuitive meaning of the entrenchment relation $\phi _{i}\le \phi _{j}$ in the context of software systems is to say that one would prefer to remove first $\phi _{j}$ than $\phi _{i}$. Functional entrenchment is defined by two properties:

• 1. Transitivity: if $\phi _{i}\le \phi _{j}$ and $\phi _{j}\le \phi _{k}$, then $\phi _{i}\le \phi _{k}$;

• 2. Dominance: if $\phi _{i}\vDash \phi _{j}$, then $\phi _{i}\le \phi _{j}$;

An argument about the utility of such an entrenchment is the following: assume we have a set $\{p,q\}$ where the two formulas are unrelated and not ordered by any preference; assume that for some reason we are required to remove from that set the formula $(p\vee q)$ and its consequences; in this situation we would be forced to obtain the empty set as a result of the contraction operation, as either formula in the current set implies $(p\vee q)$; on the other hand, obviously, it would be enough to remove either one of the two formulas p or q, if there was some priority order defined over them to allow us choosing.

We now refer to the system $S_{i}=\{\phi _{1}, \dots , \phi _{n}\}$ as a knowledge base, i.e. a set of formulas not closed under logical consequence. Recall that this is due to the need of representing a model of a physical implementation $\mathcal {I}$ in some concrete programming language of the corresponding theory $\mathcal {S}_{m}$. We say that $S_{i}$ is consistent if there exists a model for $S_i$. Let now $(S_{i},<)$ denote a finite set of formulas with a partial order. When referring to the model abstracted from $S_{i}$ we shall use $\mathcal {S}_{i}$ in order to denote $Cn(S_{i}, <)$. If $S_{i}$ is not a faithful translation of $S_{m}$ (and hence of its theory $\mathcal {S}_{m}$), in the sense of either not satisfying some property included in $S_{m}$, or satisfying some contradictory property or reflecting an undesired functional entrenchment, we then wish to perform changes.

For our complexity results we assume familiarity with basic concepts of computational complexity, and we use standard notations of complexity classes. In particular, the class P denotes the set of problems whose solution can be found in polynomial time by a deterministic Turing machine, while NP denotes the class of problems that can be solved in polynomial time by a nondeterministic Turing machine. The class co-NP denotes the set of decision problems whose complement is in NP. We also use higher complexity classes defined using oracles. In particular P$^A$ (NP$^A$) corresponds to the class of decision problems that are solved in polynomial time by deterministic (nondeterministic) Turing machines using an oracle for A in polynomial time.

3 Change operations

A change operation is triggered by some $\phi _{i}$ satisfying one of the following conditions:

• Incompleteness handling $S_{m}\vDash \phi _{i}$ and $S_{i}\nvDash \phi _{i}$, i.e. the implementation does not satisfy one of the intended functionalities;

• Inconsistency handling $S_{m}\nvDash \phi _{i}$ or $S_{m}\vDash \lnot \phi _{i}$ and $S_{i}\vDash \phi _{i}$, i.e. the implementation satisfies a functionality not intended by the model, or one whose negation was intended by the model;

• Priority handling $S_{m}\vDash \{\phi _{i}\le \phi _{j}\}$ and $S_{i}\vDash \{\phi _{j}\le \phi _{i}\}$, i.e. the implementation satisfies a different functional entrenchment than the one intended by the model.

Each of these three cases expresses a form of inconsistency between bases. Automatic techniques for inconsistency checking of systems are available both through theorem proving and model checking, also within the AGM paradigm, and widely reported in the literature (Kolyang and Wolff 1996; Buccafurri et al. 1999; Sousa and Wassermann 2007; Zhang and Ding 2008; Guerra and Wassermann 2010). Formal operations can be defined on $S_{i}$ so that either the current input in the implementation becomes valid for the model; or the specification that makes our current input invalid is removed; or the order of the base is changed, in combination with the other operations.

• In the first case, $S_{i}$ is changed to include $\phi _{i}$: we indicate the result of this change as expansion. This formal operation reflects the implementation of a new functionality and hence qualifies as a perfective change.

• In the second case, $S_{i}$ is changed to remove $\phi _{i}$ (under a complete system, which we do not assume, this implies inclusion of $\lnot \phi _i$ in $S_i$): we indicate the result of this revision as contraction. A contraction operation should aim at removing the least expressive properties to induce a minimal loss of functionalities; at each stage of the implementation consistency is preserved. This formal operation reflects the removal of an undesired functionality (error fixing) and hence qualifies as a corrective change. Such change operation in software design and system evolution should be defined in view of resilience, intended as the maximal preservation of functionalities not related to the removed property.

• We call instead adaptive change the category of modifications that result from a required novel priority ordering in the system so as to make one property safer from future corrective changes. This can be defined as a combination of corrective and re-ordered perfective changes and it is related to system evolution.

In all cases, a new model $\mathcal {S}'_{m}$ is obtained, from which a new implementation can be formulated.

We formalize perfective, corrective and adaptive changes respectively in terms of expansion, safe contraction and revision with a reordering operation: these operations are formally defined from the next subsection, and they modify existing well-known operation from the AGM paradigms to be adapted to prioritised bases. Expansion $+$ is rather easy to associate to functionality extension. Safe contraction − has had only little attention in the large literature in epistemic logic using the AGM paradigm, but it appears essential to the issue of property resilience in system evolution and it also satisfies the criteria of a minimal contraction operator, hence ensuring that as little as possible is lost. Finally, we consider an operator $\diamond$ which is defined to satisfy as much as possible the standard AGM revision $*$ postulates and additionally makes the property object of the operation safer from future contraction operations. This recalls operations of preference change, e.g. in Alechina et al. (2015) where preferences are treated as a special kind of theory, and minimal change contraction and revision operations are defined. Safe contraction defined over bases exists already from the literature (Fuhrmann 1991), where it is called minimal contraction and our postulates for ordered safe contraction match those offered there. An efficient form of AGM belief contraction (linear time) satisfying all but one of the AGM postulates is defined in Alechina et al. (2005) for a realistic rule-based agent which can be seen as a reasoner in a very weak logic (but still over deductively closed sets of beliefs). More importantly, we use such operations to define property and system resilience and offer a definition of system evolution.

In view of our application, some of the properties of the AGM paradigm need to be re-designed, in virtue of the fact that revision operations are not defined on theories but rather on finite bases. This has the advantage of being computationally far more appealing. Moreover, a relevant addition in our model is the use of an entrenchment relation to define a functional priority relation over the properties of the system and to dictate both removal and reordering. Notice that functionality prioritisation and its mapping to sub-characteristics (induced in our model by a relation between the inference relation and the ordering) is proposed and implemented also in structured methods for architectural evolvability in industrial setting, see e.g. Breivold et al. (2008).

3.1 Ordered expansion

The process of designing a piece of software can be seen as moving from an empty set of functionalities (the trivial system specification, i.e. one that implements no operations) to one that includes some property specifications. This process is akin to an expansion of the software model abstracted from the trivial implementation $S_{i}=\emptyset$ with respect to a new functionality $\phi _{i}$. This is denoted by $(S_{i})^{+}_{\phi _{i}}$. In general, the expansion operation is intended in the following as adding a new functionality that has the least entrenchment with respect to the existing ones. This can be informally justified by considering the new property as the weakest one, in view of the fact that its effect on the system is still unknown. This general rule is obliterated only in the case when the expansion formula validates a formula already in the base, in which case the functional entrenchment requires to insert it directly before that in the order. This means we need to compute such set in order to position our expansion formula.

Definition 1

(Ordered expansion) We first define

$$\begin{aligned} \varXi = S_i \cap Cn(\phi _i) \end{aligned}$$

where $Cn(\phi _i)=\{\psi \mid \phi _i\models \psi \}$. Our ordered expansion is denoted as

$$\begin{aligned}&S'_{m}= (S_{i})^{+}_{\phi _{i}}:= (S_{i} \cup \{\phi _{i}\},<') \hbox { where }\\&\quad<'= <\cup \{(\phi _k, \phi _i), (\phi _i, \phi _j)\mid \phi _j\in \varXi , \phi _k\in S_i{\setminus } \varXi \} \end{aligned}$$

In Fig. 3 we provide an explicit algorithm (in pseudocode) to compute the result of the safe ordered expansion operator.

Fig. 3

Algorithm for ordered expansion

Example 1

$$\begin{aligned} \{p<q\}^{+}_{(q\vee r)}=(p<q<(q\vee r)) \end{aligned}$$

(1)

Example 2

$$\begin{aligned} \{p<(q\vee r)\}^{+}_{q}=(p<q<(q\vee r)) \end{aligned}$$

(2)

Let us explain the Example 2 step by step: given a base with functionalities expressed by formulas p and $q\vee r$, where the latter is less entrenched than the former (e.g. because it depends from it), we wish to add a functionality expressed by formula q: then we simply add it to our specification, but its positioning in the functional entrenchment requires it comes between p and $q\vee r$, because $q \vDash q\vee r$.

Software system creation has then a starting point $S_{i}\nvDash \phi _{i}$, for any $\phi _{i}$. Any expansion operation after the first one should preserve consistency in $S_{i}$. Otherwise, each expansion by $\phi _{i}$ needs to be accompanied by the implicit elimination of the contradictory $\lnot \phi _{i}$ from the list of feasible property descriptions according to $S_{i}$. Hence, each non-consistent expansion requires a minimal set of contraction operations.

3.2 Ordered safe contraction

We now consider contracting $S_{i}$ in view of a system functionality $\phi _{i}$. We denote this by $(S_{i})^{-}_{\phi _{i}}$. In general, the contraction operation is intended in the following as removing the minimal number of functionalities that have the least entrenchment with respect to the existing functionalities in order to remove the property $\phi _{i}$ at hand. This can be informally justified by considering the contraction as removing the least entrenched or essential properties. In order to define a procedure for this, we require to compute both the set of properties that are implied by and that imply the contraction formula. This does not amount to compute the entire consequence set of $S_{i}$ (i.e. $\mathcal {S}_{i}$), but rather to perform a membership check for the contraction formula, to identify whether it implies or is implied by one of the formulas in the base. Then we identify among these the minimal ones in the entrenchment. The resulting operation is also expressive about the properties that are safe with respect to the contraction and the output of our procedure is still taken to be a (contracted) base.

Definition 2

(Ordered contraction) We first define

$$\begin{aligned} \varXi = S_i \cap (Cn(\phi _i) \cup \overline{Cn}(\phi _i)) \end{aligned}$$

where $Cn(\phi _i)=\{\psi \in S_{i}\mid \phi _i\models \psi \}$ and $\overline{Cn}(\phi _i)=\{\psi \in S_{i}\mid \psi \models \phi _i\}$. We then have a sequence of subsets of $\varXi$, i.e., $(\varXi _i)_{i\ge 0}$, inductively defined as follows:

$$\begin{aligned}&\varTheta _0=\varXi \\&\varXi _i=\{\psi \mid \psi \hbox { is a minimal element of }\varTheta _i\hbox { wrt. }<\}\\&\varTheta _{i+1}= \varTheta _i{\setminus } \varXi _i \end{aligned}$$

Note that as $\varXi$ is finite, we have that there is some n such that $\varXi =\bigcup _{i=0}^n \varXi _i$. We then define

$$\begin{aligned} k_0= \min \left\{ k\mid S_i{\setminus } \bigcup _{i=0}^k \varXi _i \not \models \phi _i\right\} \end{aligned}$$

and

$$\begin{aligned} (S_{i})^{-}_{\phi _{i}}:= \left( S_i{\setminus } \bigcup _{i=0}^{k_0} \varXi _i ,<'\right) \hbox { where }<'= \left( <\upharpoonright _{S_i{\setminus } \bigcup _{i=0}^{k_0} \varXi _i }\right) \end{aligned}$$

where $\upharpoonright$ indicates a projection function.

This definition expresses the content of the new system as obtained by a function from the current $S_{i}$ to a new base whose models do not imply $\phi _{i}$. In Fig. 4 we provide an explicit algorithm (in pseudocode) to compute the result of the safe contraction operator.

Fig. 4

Algorithm for ordered safe contraction

Example 3

$$\begin{aligned} \{p<q<r\}^{-}_{(q\vee r)}=\{p\} \end{aligned}$$

(3)

Example 4

$$\begin{aligned} \{p<(q\vee r)<r\}^{-}_{r}=\{p\} \end{aligned}$$

(4)

Example 5

$$\begin{aligned} \{p<(q\vee r)<r\}^{-}_{r\wedge p}=\{p<(q\vee r)\} \end{aligned}$$

(5)

Let us explain the Example 5 step by step: given a base with functionalities expressed by formulas p, $q\vee r$ and r, in this functional entrenchment order, we wish to remove the combination of functionalities p and r, i.e. their logical conjunction: in this case, we are not required to remove both functionalities, but just one of them (as we do not wish to eliminate both, but their combination); then we induce a contracted base with the minimal removal required, hence preserving as much as possible the functionalities. The result removes r, which is the least entrenched functionality.

Note that by our definition of ordered safe contraction the preference is always to remove formulas that express less entrenched functionalities. This might appear counter-intuitive, for example in the case where the less entrenched functionalities is the result of a combination of several components, and therefore its loss might potentially result more impactful than the removal of a more entrenched, but less complex functionality. Note that if to express the case of composed functionalities of a given degree we use logical conjunction, our ordered safe contraction will only require the removal of a component, rather than of the whole set of functionalities. The following is a variant of Example 5 which illustrates this case:

Example 6

$$\begin{aligned} \{p<(q\vee r)<(r\wedge s)\}^{-}_{r\wedge s \wedge p }=\{p<q< s\} \end{aligned}$$

(6)

Note that the choice of which component to preserve in this case is purely contextual and it might be dictated by applications, as it might affect other functionalities: here the choice of preserving s means we need to modify also $q\vee r$. Different is the case where a complex functionality is expressed by logical disjunction or implication:

Example 7

$$\begin{aligned} \{p<(q\vee r)<(r\vee s)\}^{-}_{(r\vee s) \wedge p }=\{p<q\} \end{aligned}$$

(7)

Example 8

$$\begin{aligned} \{p<(q\vee r)<(r\rightarrow s)\}^{-}_{(r\rightarrow s) \wedge p }=\{p<(q\vee r)\} \end{aligned}$$

(8)

Here the contraction operation is costly because we are forced to loose the whole complex functionality, and in the Example 7 even to weaken the additional functionality expressed by $q \vee r$. It is only with the more complex operation of revision with reordering introduced in the next subsection that this problem can be avoided.

From the definition of safe contraction and properties of the consequence relation over the contraction formula, the following can be proven about $\mathcal {S}_{i}$ (i.e. referring to the closure of $S_{i}$):

Lemma 1

[Alchourrón and Makinson (1985)] $(S_{i}\cap Cn(\lnot \phi _{i}))\subseteq (S_{i})^{-}_{\phi _{i}}$.

Proof

Suppose $\phi _{j}\in S_{i}$, $\lnot \phi _{i}\vDash \phi _{j}$ and $\phi _{j}\notin (S_{i})^{-}_{\phi _{i}}$. Then $(\lnot \phi _{i}<\phi _{j})$ and there is some minimal $S_{i}{\setminus }\varXi _{i}\vDash \phi _{i}$. Take $S_{i}{\setminus } \varXi _{j}=S_{i}{\setminus }\varXi _{i}{\setminus } \{\phi _{j}\}$ then $S_{i}{\setminus }\varXi _{i}=S_{i}{\setminus }\varXi _{j}\cup \{\phi _{j}\}$ and $S_{i}{\setminus }\varXi _{j}\cup \{\phi _{j}\}\vDash \phi _{i}$. Since by assumption $\lnot \phi _{i}\vDash \phi _{j}$, then $\lnot \phi _{j}\vDash \phi _{i}$ and so $S_{i}{\setminus }\varXi _{j}\cup \{\lnot \phi _{j}\}\vDash \phi _{i}$, but this contradicts the minimality of $\varXi _{i}$. $\square$

In the context of Software Engineering, a contraction operation should aim at removing the least expressive properties to induce a minimal loss of functionalities. We capture this formally by the functional entrenchment ordering < on properties, similarly to what is done with epistemic entrenchment (Gärdenfors and Makinson 1988). Hence, in a contraction process, one starts removing from the last element in the order to preserve as much as possible the operational properties of the system. Among the different (although in some ways related, see Alchourrón and Makinson 1986) contraction functions, safe contraction is a natural candidate for the contraction on a finite set of property specifications under this ordering preserving system functionalities:

Definition 3

(Safe contraction) A property $\phi _{j}$ is safe with respect to $(S_{i})^{-}_{\phi _{i}}$ if and only if $\phi _{i} \nvDash \phi _{j}$.

AGM revision is usually characterized by Gärdenfors postulates. These are modified as follows: the closure postulate is missing, provided the output of our procedure is again constrained to be a base; and the recovery postulate is missing, as the result of ordered contraction followed by ordered expansion does not necessarily returns the original order of the base. The resulting postulates match those in Fuhrmann (1991):

• 1. Inclusion $(S_{i})^{-}_{\phi _{i}} \subseteq S_{i}$

• 2. Vacuity $(\phi _{i} \notin Cn(S_{i})) \rightarrow ((S_{i})^{-}_{\phi _{i}} = S_{i})$

• 3. Success $(\phi _{i} \notin Cn(\emptyset )) \rightarrow \phi _{i} \notin Cn((S_{i})^{-}_{\phi _{i}})$

• 4. Extensionality $(\phi _{i} \equiv \phi _{j}) \rightarrow (S_{i})^{-}_{\phi _{i}} = (S_{i})^{-}_{\phi _{j}}$

Proposition 1

Safe contraction satisfies (1)–(4).

Proof

Similar to the one in Alchourrón and Makinson (1985), except for Success:

• 1. For Inclusion immediate from the definition of $(S_{i})^{-}_{\phi _{i}}$ from $S_{i}$ and $\varXi$.

• 2. For Vacuity if $\phi _{i}\notin Cn(S_{i})$, there is no $\varXi _{i}$ such that $\varXi _{i}\vDash \phi _{i}$, hence every $\phi _{j}\in S_{i}$ is safe in $(S_{i})^{-}_{\phi _{i}}$.

• 3. For Success Assume that $(\phi _{i} \notin Cn(\emptyset ))$ and $(S_{i})^{-}_{\phi _{i}}\vDash \phi _{i}$; then there is $(S_i{\setminus } \bigcup _{i=0}^{k_0} \varXi _i , <')\vDash \phi _{i}$ and because $\varXi _{i}$ is finite and < is non-circular, there is a minimal element $\varXi _{i}\vDash \phi _{j}$ for which one of the following holds:

  • $\phi _{j}=\phi _{i}$: then because $(S_i{\setminus } \bigcup _{i=0}^{k_0} \varXi _i , <')\vDash \phi _{j}$ it must be safe in $(S)^{-}_{\phi _{i}}$; but by construction $\phi _{j}$ cannot be safe in $(S_{i})^{-}_{\phi _{i}}$ because $\varXi _{i}\vDash \phi _{i}$ and $\phi _{j}=\phi _{i}$;

  • $\phi _{j}<\phi _{i}$: because $(S_i{\setminus } \bigcup _{i=0}^{k_0} \varXi _i , <')\vDash \phi _{j}$ it must be safe in $(S)^{-}_{\phi _{i}}$, but by Dominance $\phi _{j}\vDash \phi _{i}$ and so $\phi _{i}$ should be safe in $(S_{i})^{-}_{\phi _{i}}$, but cannot be;

  • $\phi _{i}<\phi _{j}$: because $(S_i{\setminus } \bigcup _{i=0}^{k_0} \varXi _i , <')\vDash \phi _{j}$ it must be safe in $(S)^{-}_{\phi _{i}}$, but by Dominance $\phi _{i}\vDash \phi _{j}$, and because $\phi _{i}$ cannot be safe in $(S_{i})^{-}_{\phi _{i}}$, so is not $\phi _{j}$.

• 4. For Extensionality if $Cn(\phi _{i})\equiv Cn(\phi _{j})$, then $(S_i{\setminus } \bigcup _{i=0}^{k_0} \varXi _i ,<')\equiv (S_i{\setminus } \bigcup _{i=0}^{k_0} \varXi _j , <')$, hence $(S_{i})^{-}_{\phi _{i}}=(S_{i})^{-}_{\phi _{j}}$ $\square$

Along the lines of the interpretation of < in terms of security and reliability in Alchourrón and Makinson (1985), if the consequence relation $\vDash$ for $S_{i}$ is intended to describe specification expressiveness, then the more it can be logically inferred from a property, the more expressive that property is. In turn, our safe contraction module < makes more expressive properties safer, removing first those with the least inferential impact. This justifies our Dominance axiom; with Transitivity, the following continuing conditions hold (Alchourrón and Makinson 1985):

Proposition 2

(Continuing down) If $\phi _{i}<\phi _{j}$, and $\phi _{k}\vDash \phi _{j}$, then $\phi _{i}\le \phi _{k}$, for all $\phi _{i,j,k}\in S_{i}$.

This is shown easily by Dominance and Transitivity. It means that if $\phi _{i}$ is more functionally entrenched than $\phi _{j}$ and $\phi _{k}$ induces $\phi _{j}$, then $\phi _{i}$ is also at least as functionally entrenched as $\phi _{k}$.

Proposition 3

(Continuing up) If $\phi _{i}\vDash \phi _{j}$, and $\phi _{i}<\phi _{k}$, then $\phi _{j}\le \phi _{k}$, for all $\phi _{i,j,k}\in S_{i}$.

Again shown by Dominance and Transitivity. This says that if a property $\phi _{i}$ induces $\phi _{j}$ and is also as functionally entrenched as $\phi _{k}$, then $\phi _{j}$ is also as functionally entrenched as $\phi _{k}$.

3.3 Revision with reordering

In the standard literature on belief revision, revision is understood as the operation of adding new information to a knowledge base because of new information received about the world. In the following we analyse a revision induced by a new formula that requires to be prioritised over the existing ones. Intuitively, this is the case of a new property that we want to maximally protect from any later contraction. We obtain this by an operator that satisfies all properties of the AGM revision, and additionally re-defines the partial order in the base.

Definition 4

(Revision with reordering)

$$\begin{aligned} (S_{i})^{\diamond }_{\phi _{i}}= (((S_{i})^{-}_{\lnot \phi _{i}})^{+}_{\phi _{i}},<') \hbox { where }<'= <\cup \{(\phi _{i}, \phi _{j}) \mid \phi _{j} \in ((S_{i})^{-}_{\lnot \phi _{i}})\}. \end{aligned}$$

Below we provide an explicit algorithm (in pseudocode) to compute the result of the revision operator. As expected, we shall call the expansion and safe contraction procedures defined in the previous algorithms.

This procedure defines an AGM revision operator $*$, in that it satisfies the Levi’s identity, with the additional property that the revised base has acquired a new priority relation $<'$. Note that while expansion only performs a reordering if the added functionality implies some functionality present in the older base, by placing the former before the latter, revision with reordering ensures this happens (because it is defined in terms of expansion) but additionally prioritise the new functionality over any other unrelated one. To see this, consider the following three examples, one for each possible position of the contracted formula relatively to <:

Example 9

$$\begin{aligned} \{p<q\}^{\diamond }_{\lnot p}=((\{p<q\}^{-}_{p})^{+}_{(\lnot p)})^{<'}=\{\lnot p<q\} \end{aligned}$$

(9)

Example 10

$$\begin{aligned} \{p<q\}^{\diamond }_{\lnot q}=((\{p<q\}^{-}_{q})^{+}_{(\lnot q)})^{<'}=\{\lnot q< p\} \end{aligned}$$

(10)

Example 11

$$\begin{aligned} \{p<q<r\}^{\diamond }_{\lnot q}=((\{p<q<r\}^{-}_{q})^{+}_{(\lnot q)})^{<'}=\{\lnot q<p<r\} \end{aligned}$$

(11)

Let us explain the Example 11 step by step: given a base with functionalities expressed by formulas p, qr and r, in this functional entrenchment order, we wish to perform ordered revision by $\lnot q$. The following is the ordered series of changes:

$$\begin{aligned}&\{p<q<r\}^{\diamond }_{\lnot q}=\\&(\{p<q<r\}^{-}_{q}=\{p<r\}\\&(\{p<r\})^{+}_{(\lnot q)}=\{p<r<\lnot q\}\\&(\{p<r<\lnot q\})^{<'}=\{\lnot q<p<r\} \end{aligned}$$

In the first step, we remove q from the base, which is conflicting with the desired new functionality; in the second step, we add the new desired functionality $\lnot q$; in the third step we reorder the base, bringing up the new functionality in the order over any other functionality p, r which has survived the initial removal operation (and preserving the order among them).

For the case illustrated above in Example 8 of a complex functionality expressed by logical implication, the operation of revision with reordering gives us the possibility to remove a higher ordered functionality and to preserve a lower ordered but more complex one:

Example 12

$$\begin{aligned} \{p<(q\vee r)<(r\rightarrow s)\}^{\diamond }_{\lnot ((r\rightarrow s) \wedge p)}=\{(r\rightarrow s)<(q\vee r)\} \end{aligned}$$

(12)

Ordered revision also satisfies the following:

Proposition 4

(Harper’s identity)

$$\begin{aligned} (S_{i})^{-}_{\phi _{i}}= S_{i}\cap (S_{i})^{\diamond }_{\lnot \phi _{i}} \end{aligned}$$

This equation identifies the contraction operation with the intersection of the original base with the revised one. To show this, we refer to the result of the identities above using their example number:

Example 13

$$\begin{aligned} (6)\cap \{p<q\}=\{q\}=\{p<q\}^{-}_{p} \end{aligned}$$

(13)

Example 14

$$\begin{aligned} (7) \cap \{p<q\}=\{p\}=\{p<q\}^{-}_{q} \end{aligned}$$

(14)

Example 15

$$\begin{aligned} (8) \cap \{p<q<r\}=\{p<r\}=\{p<q<r\}^{-}_{q} \end{aligned}$$

(15)

An informal way to justify this is as follows: a minimal revision $(S_{i},<)^{*}_{\lnot \phi _{i}}$ should keep the difference between the revised base and the original base minimal, i.e. keep as much as possible in common; hence, the contextual overlap among the two will be as large as it can be while conforming with $\lnot \phi$; this makes the intersection $(S_{i},<)\cap (S_{i},<)^{*}_{\lnot \phi _{i}}$ a plausible candidate for a minimal contraction of $S_{i}$ on $\phi _{i}$. In turn, this confirms that our contraction is indeed a minimal change operator. As $\diamond$ can be defined in terms of − and $+$, it preserves the Gärdenfords postulates.

4 Example

It has been recently shown that some implementations of the Mergesort algorithm are broken, including the Timsort hybrid algorithm (de Gouw et al. 2015). We present here briefly the specification evolution from the broken implementation to the fixed specification, with remarks adapted to our analysis. The main loop of Timsort is presented in Fig. 5.

Fig. 5

Main loop of Timsort

Consider this system specification as our $S_{m}$, whose theory is $\mathcal {S}_{m}$. This loop will satisfy an instance with stackSize$=4$, which we refer to as our formula $\phi _{i}$. We now consider a Java implementation $\mathcal {I}$ of the above theory and the resulting system $S_{i}$, which will have a corresponding formulation of $\phi _{i}$ above, namely of the loop with stackSize$=4$: $S_{i}$ will hence include a disjunctive formula (to mimic the while loop) where each element is an implication with the antecedent assigning a value size to the stack and to the length of the run, and the consequent executing the merge:

$$\begin{aligned} \begin{array}{c} \phi _{i}=\{(\mathtt {stackSize,runLen}==4 \rightarrow \mathtt {mergeCollapse()})\vee \\ (\mathtt {stackSize,runLen}==3 \rightarrow \mathtt {mergeCollapse()})\vee \\ (\mathtt {stackSize,runLen}==2 \rightarrow \mathtt {mergeCollapse()})\vee \\ (\mathtt {stackSize,runLen}=1 \rightarrow \mathtt {assert\ ts.stackSize} == 1)\} \end{array} \end{aligned}$$

The implementation is presented in Fig. 6. In this implementation, it is the case that $S_{i}\nvDash \phi _{i}$ after violation of the invariant ArrayIndexOutOfBoundsException in pushRun, see de Gouw et al. (2015).

Fig. 6

Java implementation of Timsort

In order not to loose generality, one does not want to just remove $\phi _{i}$. Hence one must individuate some $\phi _{j}<\phi _{i}$ and proceed to revise the model $S_{i}\mapsto S'_{i}$. We first proceed by contraction $S'_{i}=(S_{i})^{-}_{\phi _{j}}$ and then formulate some $\phi _{k}$ and proceed by expansion $S''_{i}=(S'_{i})^{+}_{\phi _{k}}$. Our $\phi _{j}$ is now identified as the mergeAT(n) commands obtained by the satisfied if clauses. This will match the mergeCollapse() commands on lines 10 and 17 of the Timsort loop.

$$\begin{aligned} \begin{array}{c} \phi _{j}=\{((\mathtt {stackSize}>0 \wedge \mathtt {stackSize[n]}--2) \rightarrow \\ (((\mathtt {runLen[n-1]}<= \mathtt {runLen[n]}+\mathtt {runLen[n+1]}) \wedge \\ (\mathtt {runLen[n-1]}< \mathtt {runLen[n+1]}))\rightarrow \\ \mathtt {[n-2]} \wedge \mathtt {mergeAT(n)} \vee \\ (\mathtt {runLen[n]}<= \mathtt {runLen[n+1]})\rightarrow \\ \mathtt {mergeAT(n)})) \} \end{array} \end{aligned}$$

We then proceed with formulating $\phi _{k}$ as OR clauses in the if else loops;

$$\begin{aligned} \begin{array}{c} \phi _{k}=\{ ((\lnot ((\mathtt {stackSize,runLen}>1)\vee (\mathtt {runLen[n]}<= \mathtt {runLen[n+1]})) \vee \\ ((\mathtt {runLen[n-1]}<= \mathtt {runLen[n]}+\mathtt {runLen[n+1]}) \wedge \mathtt {mergeCollapse()}) \vee \\ \mathtt {assert\ ts.stackSize} == 1)) \} \end{array} \end{aligned}$$

finally, $\phi _{j}$ is again added $S'''_{i}=(S'_{i})^{+}_{\phi _{j}}$. The resulting new implementation is shown in Fig. 7. Notice that with respect to $\phi _{j}$, a reordering in the functional entrenchment is also taking place.

Fig. 7

New Java implementation

5 Model checking

In this section, we consider the complexity of the model checking and inference problems for the change operations introduced in Sect. 3, along the line of Liberatore and Schaerf (2001) and Eiter and Gottlob (1992). We will mainly focus on the revision with reordering introduced in Sect. 3.3, as this is the most interesting one. Its definition subsumes the safe contraction, while the expansion is trivial.

We first examine the model checking problem. Recall that we are given a knowledge base $(S_i, <)$ where $S_i$ is given as a set of propositional formulas and < is the associated order over $S_i$, a model M which is given as a valuation, a formula $\phi _{i}$ which is to be updated with respect to $S_i$, the model checking problem determines whether $M\models (S_i)^\diamond _{\phi _{i}}$.

Proposition 5

The model checking problem is in co-NP.

Proof

We first check whether $M\models \phi _{i}$, which can be in done in polynomial time. (As a matter of fact, it is in ALOGTIME, which is a uniform version of NC$^1$, so probably much lower than P.) If the answer is negative, we conclude that the model is not supported by the revision. Otherwise we proceed to check whether $M\models \text {Safe Contraction}(S_i, \lnot \phi _{i})$. To this aim, we first compute $\varTheta =\{\psi _{i} \in S_i\mid M\models \psi _{i}\}$.

Recall that for the safe contraction, we order the formulas in $S_i$ in the way such that

• $S_i=\biguplus _{k=1}^i S_k$, i.e., a disjoint union of $S_k$’s for $k=1, \dots , i$, and

• for all $1\le j\le k$, $S_j$ is the set of minimal elements of $S_i{\setminus } \bigcup _{1\le k\le j-1}S_k$.

As a more succinct notation, we usually write $S_1<S_2<\cdots <S_m$. The partition can be obtained by standard topological sorting in polynomial time. Let

$$\begin{aligned} K=\min \left\{ \ell \mid \bigcup _{\ell \le k\le m}S_k \subseteq \varTheta \right\} . \end{aligned}$$

If $K=1$, then clearly $M\models \text {Safe Contraction}(S_i, \lnot \phi _{i})$ and we are done. We then assume that $K>1$. In this case we claim that

$$\begin{aligned} M\models \text {Safe Contraction}(S_i, \lnot \phi _{i})\ \text {iff}\ \bigcup _{K-1 \le k\le m}S_k\models \lnot \phi _{i}. \end{aligned}$$

To see this, suppose $M\models \text {Safe Contraction}(S_i, \lnot \phi _{i})$, i.e. $\text {Safe Contraction}(S_i, \lnot \phi _{i})\subseteq \varTheta$. Note that, according to the definition of K, $\bigcup _{K-1 \le k\le m}S_k\not \subseteq \varTheta$. It follows that

$$\begin{aligned} \text {Safe Contraction}(S_i, \lnot \phi _{i})\subsetneq \bigcup _{K-1 \le k\le m}S_k, \end{aligned}$$

and thus

$$\begin{aligned} \text {Safe Contraction}(S_i, \lnot \phi _{i})= \bigcup _{j\le k\le m}S_k\ \text {for some}\ j\ge k. \end{aligned}$$

According to the definition of safe contraction, we have that

$$\begin{aligned} \bigcup _{K-1 \le k\le m}S_k\models \lnot \phi _{i}. \end{aligned}$$

For the other direction, suppose that $\bigcup _{K-1 \le k\le m}S_k\models \lnot \phi _{i}$. According to the definition of K, it must be the case that

$$\begin{aligned} \text {Safe Contraction}(S_i, \lnot \phi _{i})\subseteq \bigcup _{K \le k\le m}S_k \subseteq \varTheta \end{aligned}$$

which implies that $M\models \text {Safe Contraction}(S_i, \lnot \phi _{i})$. We observe that checking $\bigcup _{K-1 \le k\le m}S_k\models \lnot \phi _{i}$ amounts to checking the validity of the formula

$$\begin{aligned} \bigwedge _{\xi \in \bigcup _{K-1 \le k\le m}S_k} \xi \implies \lnot \phi _{i}, \end{aligned}$$

which can be done in co-NP. This gives a co-NP algorithm for checking $M\models \text {Safe Contraction}(S_i, \lnot \phi _{i})$. Overall, we have a co-NP algorithm for checking $M\models (S)^\diamond _{\phi _{i}}$. This completes the proof. $\square$

Below we give an example to show that the order associated with the knowledge base has to be considered during model checking, because with different orders the results vary.

Example 1

(Order matters) Given $S_i=\{p,q\}$, $\phi _i=\lnot (p\wedge q)$ and $M(p)=1, M(q)=0$. Obviously $M\models \phi _{i}$. If we have $p<q$, then the revision would be $\{q, \phi _{i}\}$. If p and q are unordered, then the revision would be $\{\phi _{i}\}$. In the former case, $M\not \models \{q, \phi _{i}\}$ while in the latter case, $M\models \{ \phi _{i}\}$. $\square$

A decision algorithm for the model checking problem is presented in Fig. 8.

Fig. 8

Model checking algorithm

We now turn to the inference problem. Again we focus on the revision with reordering. Formally, we are given a knowledge base $(S_i, <)$, two formulas $\phi _{i}$ and $\phi _{j}$ where $\phi _{i}$ is to be updated wrt $S_i$, the inference problem determines whether $(S_i)^\diamond _\phi \models \phi _{j}$.

Proposition 6

The complexity of satisfiability checking is in $\varSigma ^\mathrm{p}_2$, i.e., $\mathrm{NP}^\mathrm{NP}$.

Proof

As in the proof of Proposition 5, we first compute $\varTheta =\{\psi _{i} \in S_i\mid M\models \psi _{i}\}$. Recall that for the safe contraction, we order the formulas in $S_i$ in the way such that

• $S_i=\biguplus _{k=1}^i S_k$, i.e., a disjoint union of $S_k$’s for $k=1, \dots , i$, and

• for all $1\le j\le k$, $S_j$ is the set of minimal elements of $S_i{\setminus } \bigcup _{1\le k\le j-1}S_k$.

We observe that $(S_i)^\diamond _{\phi _{i}}\models \phi {j}$ iff there exists some d such that

• (i) $\bigcup _{d\le k\le m} S_k \cup \{\phi _{i}\}\models \phi _{j}$, and

• (ii) $\bigcup _{d\le k\le m} S_k \not \models \lnot \phi _{i}$.

The “only if” direction is trivial, as according to the definition of safe contraction,

$$\begin{aligned} \text {Safe Contraction}(S_i, \lnot \phi _{i})= \bigcup _{K-1 \le k\le m}S_k \end{aligned}$$

such that $\text {Safe Contraction}(S_i, \lnot \phi _{i})\not \models \lnot \phi _{i}$ and $\text {Safe Contraction}(S_i, \lnot \phi _{i})\cup \{\phi _{i}\}\models \phi _{j}$.

For the “if” direction, assume such d exists, then it must be the case that

$$\begin{aligned} \bigcup _{d\le k\le m} S_k \cup \{\phi _{i}\}\subseteq \text {Safe Contraction}(S_i, \lnot \phi _{i}) \end{aligned}$$

because of (ii), and we must have that

$$\begin{aligned} \text {Safe Contraction}(S_i, \lnot \phi _{i})\cup \{\phi _{i}\}\models \phi _{j} \end{aligned}$$

because of (i). Now note that both (i) and (ii) can be checked in co-NP and NP respectively, we can easily obtain an $\mathrm{NP}^\mathrm{NP}$ algorithm, which completes the proof. $\square$

A decision algorithm for the inference checking problem is presented in Fig. 9.

Fig. 9

Inference algorithm

6 Remarks on resilience and evolvability

In the introduction we have suggested that the concept of reliability for software systems can be defined in terms of notions of resilience and evolvability.

Resilience for a computational system reflects its (graded) ability to preserve a working implementation under changed specifications. The above analysis of software theory change allows us to provide a precise definition of resilience in the presence of removal or failure of certain components. In the literature on software change, this process corresponds to preservation of behavioural safety by specification approximation, see e.g. the taxonomy offered in Buckley et al. (2005). Various attempts have been made to formalise perseverance of validity under change. The most common one encountered in this research area is that of system robustness (Bloem et al. 2010a, b). One (older) interpretation is given in terms of the inability of the system to distinguish between behaviours that are essentially the same, see Peled (1997). More recently, the term resilience has been used to refer to the ability of a system to retain functional and non-functional identity with the ability to perceive environmental changes; to understand their implications and to plan and enact adjustments intended to improve the system-environment fit (De Florio 2013).

Evolvability is the ability to successfully accommodate changes, the capacity to generate adaptive variability in tandem with continued persistence (Cook et al. 2005) and more generally the system’s ability to survive changes in its environment, requirements and implementation technologies (Ciraci and van den Broek 2006). The crucial need to accommodate changes in requirements and corresponding intended functionalities with the least possible cost while maintaining architectural integrity has been stressed since Rowe et al. (1998). Our analysis of resilience and evolvability has focused on functional entrenchment and the change in view of prioritised functionalities.

In view of the operation of ordered contraction, resilience of functionalities in a software system can be defined by functional entrenchment via logical consequence:

Definition 5

(Property resilience) Consider property specifications $\phi _{i},\phi _{j}\in \mathcal {S}_{m}$ and a relevant implementation $S_{i}$. Then $\phi _{i}$ is resilient in $(S_{i})^{-}_{\phi _{j}}$ iff $\phi _{j}\nvDash \phi _{i}$.

This holds immediately by Definition 3. Generalising, one can say that a software system specification $S_{i}$ is resilient with respect to a property specification $\phi _{i}$ if the latter is safe in any contracted subsystem that preserves minimal functionalities of $S_{i}$. System resilience as the resistance to change of property specifications (as in Definition 5) can be essential to determine system antifragility (De Florio 2014). Software antifragility has been characterized as self-healing (automatic run-time bug fixing) and adaptive fault-tolerance (tested e.g. by fault-injection in production) (Monperrus 2017). An inferential notion of resilience helps characterizing a certain degree of fault-tolerance; the latter is considered strictly intertwined with self-healing properties: while not all fault-tolerant systems are self-healing, one can argue that self-healing techniques are ultimately dependable computing techniques (Koopman 2003). Our resilient core, intended as the persistence of service delivery (Laprie 2008) in view of functionalities contraction, allows to determine the adaptation required by changes in terms of valid and invalid properties of its contractions and can anticipate results of its expansions. In particular, given the non-resilient part of the system, it is possible to establish which properties will still be instantiated in any subsystem. In this sense, resilience is a function of dependability between functionalities, expressed as an inferential relation.

Proposition 7

(Accountability) For any $\phi _{j}\in \varXi _{i}$ as per Definition 2 such that $\phi _{j}$ is minimal w.r.t $\phi _{i}<\phi _{j}$, then $(S_{i})^{-}_{\phi _{i}}\nvDash \phi _{j}$. For any $\phi _{j}\in \varXi _{i}$ as per Definition 2 such that $\phi _{j}$ is not minimal w.r.t $\phi _{j}<\phi _{i}$, then $(S_{i})^{-}_{\phi _{i}}\vDash \phi _{j}$.

This holds immediately by Definition 2, Dominance and Definition 3. Furthermore, we have qualified our ordered revision operator as a function of evolvable software systems. In the context of prioritised functionalities, we have more precisely formulated evolvability as the property of a software to be updated to fulfill a newly prioritised set of functionalities. This allows to deal explicitly with one of the main problem of architecture design (Breivold and Crnkovic 2010). The advantage of our analysis is again based on the relation between the priority order and the inferential relation, as expressed by the Dominance property. This can be useful to guarantee a prevision property on formulas affected negatively by a revision operation:

Proposition 8

(Prevision) For any properties $\phi _{i},\phi _{j}\in S_{i}$ such $\phi _{i}<\phi _{j}$, there is always a $S'_{i}=(S_{i})^{\diamond }_{\phi _{k}}$ such that $\phi _{i}$ becomes an element w.r.t. < exposed to a further contraction.

This holds by Dominance and Definition 4. In other words, revision with reordering (i.e. a novel prioritisation of evolvable sub-characteristics for a system) always implies the possibility of building a system with a module including a previously safe property which is no longer safe to future contractions.

In view of such prevision property, one can re-factor the impact of evolvability on sub-characteristics, in order to know how much a novel prioritisation will make the system exposed. To do so, it is sufficient to consider:

• 1. The cardinality of the consequence set of each property $\mid Cn(\phi _{i})\mid$;

• 2. An order on their sizes, denoted by $\prec$;

• 3. And a preference weighting on selected revisions, denoted by $\lessdot$.

Definition 6

(Preference on revision) Consider a system $S_{i}:=\{\phi _{i}<\phi _{j}<\phi _{k}<\dots <\phi _{n}\}$, such that $\phi _{i}\nvDash \phi _{j}$ and $\phi _{j}\nvDash \phi _{k}$. Then $(S_{i})^{\diamond }_{\lnot \phi _{j}}\lessdot (S_{i})^{\diamond }_{\lnot \phi _{k}}$ iff $\mid Cn(\phi _{j})\mid \prec \mid Cn(\phi _{k})\mid$.

In other words, if a reorder revision should be selected between two options which do not have a logical relation, the impact of the removed properties in the system should be taken into account in terms of the respective consequences on the models. Note that preference on revision requires to move our analysis from the specification base $S_{i}$ to the model $\mathcal {S}_{m}$.

Software tools based on either theorem proving or model checking techniques can implement this theory to several aims. In view of Property Resilience from Definition 5 and Proposition 7, it is possible to express direct and indirect dependency relations between software packages in the presence of uninstall operations. A similar task is performed proof-theoretically by a natural deduction calculus with an explicit notion of trust in Primiero and Boender (2018). More importantly, it will be possible to provide information as to the resulting state of the system after uninstall operation have been performed, anticipating possible resulting unstable conditions and the eventual impossibility of the system to perform critical operations. The utility of Proposition 8 in combination with Definition 6 is again in view of assessing the state of the system in the presence of uninstall operations, by anticipating which functionalities may result threatened and establishing removal options of minimal impact on the system among possible ones. Although the present work does not aim at the development of any such tool, we believe that a solid theoretical basis to this aim is a valuable contribution.

Different authors have quantified software maintenance between $40\%$ and $>90\%$ of build costs, depending on the software project considered, project development methodology used and best practices applied. A checklist used to explore the realism and accuracy of maintenance requirements (see for example Hunt et al. 2008) should include, among others, the following questions:

• 1. Which parts of the system will be preserved and allow incremental maintenance?

• 2. Are healthy chunks of the original code being rewritten or changed?

• 3. Which pieces of software will need (non-incremental) maintenance?

• 4. Can you assess which (non-incremental) maintenance operations are the least invasive on the current system?

We believe our formal model can be used to provide answers to such questions, and thus be of further help to the constraints of software maintenance costs.

7 Conclusion

We have presented a theory of software change inspired by techniques used in belief revision theory. We have highlighted how operators on contraction, expansion and revision with reordering over a base with functional entrenchment allow to identify resilience and evolvability properties for software systems. We have moreover identified the complexity of such operations and gave a real case scenario on a recent example of a broken algorithm. Future research will focus on enhancements of this model that can be of further interest to the software engineering community, e.g. by operations of multiple contraction and selective revision. From the conceptual point of view, the interest is in the modelling of anti-fragility properties for software systems in the light of revision and update operations.