Counterfactual reasoning within physical theories

Abstract

If one is interested in reasoning counterfactually within a physical theory, one cannot adequately use the standard possible world semantics. As developed by Lewis and others, this semantics depends on entertaining possible worlds with miracles, worlds in which laws of nature, as described by physical theory, are violated. Van Fraassen suggested instead to use the models of a theory as worlds, but gave up on determining the needed comparative similarity relation for the semantics objectively. I present a third way, in which this similarity relation is determined from properties of the models contextually relevant to the truth of the counterfactual under evaluation. After illustrating this with a simple example from thermodynamics, I draw some implications for future work, including a renewed possibility for a viable deflationary account of laws of nature.

1 Introduction: the importance of counterfactual reasoning

Reasoning with physical theories is replete with modal and, especially, counterfactal conditionals and inferences therewith. For example, Newtonian gravitation seems to warrant the claim that “if two bodies have different masses, and if they were brought near a third body in turn, they would exhibit different acceleration” (van Fraassen 1980, p. 60). Competent users of the theory endorse this conditional even if no masses were so brought. Moreover, they also ground claims for intervention and control:

Suppose the actual length of the pendulum on my grandfather clock is L. The model permits us to calculate the period, T. It also permits us to calculate a slightly greater period T’ corresponding to a slightly greater length L’. Suppose the clock is running slightly fast. I claim that turning the adjusting screw one turn counterclockwise would increase the length of the pendulum to L’, and this would increase the period to T’, so that the clock would run slightly slower. (Giere 1999, p. 96)

Although the example is simple, it exemplifies a pattern of reasoning that underlies most, if not all, successful applications of classical physics to applied problems and engineering tasks.

Such reasoning extends to modern physics as well, illuminating, for example, the role that the global phase of a quantum state plays in how (non-relativistic) quantum theory specifies its observables:

If in one possible world, an isolated system is in state $\psi$ and in another it is in state [$-\psi$], no amount of empirical information actually available can tell the observer which of these two worlds he is in. But ...if the system had interacted with another one in such and such a way, the results would have been different in the two cases. (van Fraassen 1980, p. 62)

According to the standard von Neumann-Dirac formulation of quantum theory, one represents a measurement on a system with a binary (“yes”/“no”) outcome as a projection operator P on the quantum state space, so that the probability of a positive outcome is given by $|P\psi |^2$—this is the so-called Born rule. Different global phases (such the factor of $+1$ or $-1$ described above) yield the same probability. But they also yield different patterns of constructive and destructive interference when the system interacts with another, or even with itself! Indeed, this latter case is the basis of the famously astounding double-slit inference experiments. Thus for both classical and modern physical theories, counterfactual claims underlie the observable, not merely observed, predictions of the theory.

Philosophers of science, meanwhile, have often taken patterns of counterfactual reasoning using a scientific theory as central to a proper understanding of how scientific theories explain (Woodward 2017), leading possibly through the definition of natural laws (Carroll 2016) and causation (Menzies 2017) to the application of induction and the confirmation of theories (Goodman 1983, Ch. 3) and definition of determinism (Earman 1986). The standard semantics for counterfactuals, known as variably strict conditionals, can be given in terms of a comparative similarity relation among possible worlds, and was developed (in various essentially equivalent versions) by Stalnaker (1968), Lewis (1973, 1981), and Kratzer (1981), But these semantics pose, however, at least two interconnected problems for their application to physical phenomena.

First, there is the issue of the scope of the worlds themselves. Although there is debate about how to understand the nature of possible worlds (Menzel 2017), the real problem here is that, whatever their nature, metaphysically possible worlds generally outstrip those nomically allowed by a physical theory. If there are possibilia incompatible with those that a physical theory of interest permits, yet those possibilia are the ones used to provide a semantics for counterfactual reasoning using the theory, in what sense is one really using the theory for reasoning? How does the theory constrain that reasoning at all?

In the same works quoted above, van Fraassen and Giere proposed a solution strategy to this problem: replace the use of possible worlds in the semantics with models of the theory being used. For instance, van Fraassen (1980, p. 199) advises that “If language use is guided by an accepted scientific theory, then we must look to that theory in order to construct models of the language in use,” enjoining us to try to “characterize (fragments of) scientific language by means of the concepts of formal semantics but in such a way that the model structures derive in an obvious way from the models of scientific theories.” For example, “if I say that it is impossible to observe a muon directly, or to melt gold at room temperature, this is because no counterpart to such events can be found in any model of the science I accept” (van Fraassen 1980, p. 218). Put another way, the original goal of the semantics for counterfactuals was to model their meaning in natural language, which may not be sufficiently regimented in comparison with scientific reasoning that uses them. By restricting attention to this more limited goal—i.e., implicitly prefacing reasoning with, “According to physical theory T,”—one can properly solve this first problem.¹

Modal and counterfactual reasoning using these models then warrants conclusions about the world in virtue of the models’ successful representational features. This is one of the basic features of representational modeling, to facilitate surrogative reasoning. Indeed, van Fraassen (1989, p. 214) writes that “reference or denotation is gained indirectly because certain parts of the model may correspond to elements of reality. The exploration of modal discourse may then draw largely on structure in the models, which outstrips their representation of reality.” For him, successful representation is a matter of isomorphism between the empirical (sub-)structure of a theory and appearances (van Fraassen 1980, p. 64), while Giere (1999, p. 95) states that “here ‘successful representation’ does not imply an exact fit, but at most a fit within the limits of what can be detected using existing experimental techniques.” Now, van Fraassen and Giere disagree about whether such reasoning warrants evidence in the reality of the possibilia (beyond their observable features) that a class of scientific models represents, but for present purposes, one can hold the realism debate in abeyance.

There is still a second problem that the standard semantics for counterfactual reasoning faces, one concerning the comparative similarity relation. Formally, this is a three-place relation $j \le _i k$ among worlds i, j, k that are accessible from i, interpreted as “j is at least as similar to world i as world k.” One requires that it satisfy the following properties:²

• Quasi-Reflexive For all j, if there is some k such that either $j \le _i k$ or $k \le _i j$, then $j \le _i j$.

• Transitive For all j, k, l, if $j \le _i k$ and $k \le _i l$, then $j \le _i l$.

Quasi-reflexivity requires that any world deemed comparatively similar to another is always at least as similar as itself is to that other. Transitivity just requires that comparative similarity orders its elements in the expected way.

These formal properties are not nearly stringent enough to determine a unique comparative similarity relation, which is needed to evaluate the truth of counterfactuals. So how is one to determine this? Lewis (1986a, pp. 47–48) famously suggested the following ranked desiderata:

• 1. It is of first importance to avoid big, widespread, diverse violations of law.

• 2. It is of second importance to maximize the spatio-temporal region throughout which perfect match of particular fact prevails.

• 3. It is of third importance to avoid even small, localized simple violations of law.

• 4. It is of little or no importance to secure approximate similarity of particular fact, even in matters that concern us greatly.

These desiderata have at least four undesirable features for present purposes. First, they are unhelpfully vague. Perhaps this vagueness is appropriate for a semantics concerned with reasoning in natural language, but one wonders whether one can achieve something more precise with regimented scientific reasoning, if only because it is a narrowed and more regimented domain of discourse. Second, the desiderata depend on an account of natural law—Lewis has in mind his own “systems” account—but debates about laws abound (Carroll 2016). A sophisticated and scientifically sensitive account of natural law may be apt here, but consensus on what this could be seems distant. Third, even provided such an account, the ranking depends on the countenance of possible worlds containing “miracles”—violations of scientific law—which recapitulates the first problem for the application of the standard semantics. Stated in the present terms, this was the seeming incompatibility of reasoning within a scientific theory while countenancing states of affairs that the theory forbids. If one solves this by restricting attention to models of the theory under consideration as proposed, however, the first and third desiderata are moot. Fourth, the second desideratum references spatio-temporal regions, but not all physical theories have models that represent spatio-temporal features—for example, models of thermodynamic systems at equilibrium.

This is where the present essay aims to contribute. Instead of trying to amend these problematic features, I abandon Lewis’s suggestion for a new way of determining a comparative similarity relation on a set of models representing a physical theory. In particular, I propose in Sects. 4 and 5 to encode the similarity of models through the similarity of their contextually relevant properties, which provides a structured model of the logic VWU (or VCU, as described there). In particular, I give an account of contextual relevance for a given counterfactual and how the properties (through the formal device of semi-pseudometrics) so relevant determine the comparative similarity of models. This overcomes the problems with Lewis’s account while making essentially no substantive assumptions about scientific realism or the metaphysics of laws of nature. Indeed, no assumptions about the existence of laws is needed.³ This shows that, contrary to widespread belief, an account of physical law is not indispensable for counterfactual reasoning in physics.

Part of what makes this possible is an important difference in goals from those mentioned working on natural laws: instead of formally reconstructing the grounds for or “saving the phenomena” of intuitive judgments of the truth of counterfactual statements in physics and the validity of patterns of reasoning using them, I aim to reform and make precise those informal judgments more systematically.⁴ The goal is to facilitate precise counterfactual reasoning with theories for which our intuitions are indefinite or muddled, rather than show how we could have the intuitive judgments that we do. In other words, it is Carnapian explication rather than non-transformative conceptual analysis.

To further motivate my account, I consider and criticize beforehand (in Sect. 2) a different proposal to understand counterfactuals in science as simpler strict conditionals (Muller 2005) before introducing the variably strict ones (in Sect. 3).⁵ Then, to illustrate, I compare my account (in Sect. 6) with one due to Maudlin (2007) that is at first glance unrelated, showing how mine in fact encompasses and extends it. Then I apply this semantics to a few simple examples from elementary equilibrium thermodynamics in Sect. 7. My goal is to provide evidence that my proposal not only makes contact with science, but is ineffectual without and inextricable from it. Finally, I outline in the concluding Sect. 8 some suggestions and challenges for extending the present ideas to other (non-physical) scientific theories and models, and to probabilistic models, as well as directions for further research regarding the logic described and its implications for the status of laws of nature within the metaphysics of science.

2 The poverty of strict conditionals

The idea to develop a formal semantics using models of theories as substitutes for possible worlds is not entirely new. In order to further develop the concept of observability for constructive empiricism in response to criticism by Ladyman (2000), Muller (2005, p. 70) states that, among others, his own

major aim is to provide a rigorous account of modal language in science, notably including subjunctive conditionals, without relying on Modal Realism, without even mentioning fictional worlds, and staying within the confines of the semantic view on scientific theories.

Muller proposes to use the standard relational semantics for modal languages, provided by a frame (W, R), where W is a set (of “nodes,” often—but not necessarily—interpreted as possible worlds,) and R is a binary relation (of “accessibility”) on W. The elements of the set in this case are simply the models of a theory, or a subclass thereof, and the definitions of the logical connectives and the modal operators is standard; regarding the latter, for any sentence $\phi$ of the theory, with Boolean valuation $v_\phi : W \rightarrow \{ \top , \bot \}$, $\Diamond \phi$ is true at $i \in W$ just when there is some $j \in W$ such that iRj and $v_\phi (j)=\top$. In other words, $\Diamond \phi$ is true at i just when $\phi$ is true at some $j \in W$ accessible from i; in fact, this gives an interpretation of the accessibility relation in terms of relative possibility. This is the “possibility” operator: “$\Diamond \phi$” is interpreted as “it is possible that $\phi$ (in the models W).” Muller (2005, p. 92) then defines

• Necessity $\Box \phi \leftrightarrow \lnot \Diamond \lnot \phi$,

• Subj. Conditional $(\phi \boxright \psi ) \leftrightarrow (\Box (\phi \rightarrow \psi ) \wedge \Diamond \phi )$.

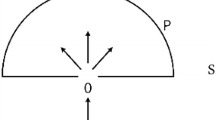
The definition of the modal necessity operator is standard; the second conjunct in the definition of the subjunctive conditional, $\Diamond \phi$, makes counterfactual conditionals with impossible antecedents false rather than, as they would be without it, true, but what’s important for present purposes is the first conjunct, $\Box (\phi \rightarrow \psi )$. This sentence, known as a strict conditional, is true at i just when the material conditional $\phi \rightarrow \psi$ is true at all j accessible from i. See, for example, Fig. 1 for a diagrammatic illustration.

Fig. 1

The models accessible from i are depicted as the interior of the circle S. Those models in which $\phi$ and $\psi$ are true are depicted by the interiors of the regions with the respectively labeled curved boundaries. The gray region indicates all those models in which $\phi$ is true which are also accessible from i. Because this region lies entirely within the set of models accessible from i in which $\psi$ is true, the strict conditional $\Box (\phi \rightarrow \psi )$ is true at i. [This figure is after Figure 1C of Lewis (1973, p. 6)]

What about the accessibility relation that the semantics requires? Here, Muller (2005, p. 94) writes that,

Generally speaking, we should and we can pick and choose a relevant accessibility relation at the level of the theory (all models), at the level of a sub-theory (a subset of models of T), or at the level of a single model. Not anything is possible, however, because the language of scientists in use puts constraints on what we can sensibly define. That use of language should be our guide in defining accessibility relations sensibly when we want to make sense of science.

So, different collections of models may have different accessibility relations, but those relations should be fixed once and for all so as to fit best what scientists seem to assert.

There are at least two problems for this proposal for present purposes. First, the interpretation of the accessibility relation as a notion of relative possibility seems to make its determination entirely dependent on the interpretation of and assent to given particular sentences from scientists. While that can be a noble goal in itself, it is not the present one, as I described in Sect. 1, which is to provide a formal framework that can be used to facilitate counterfactual reasoning—its title ought not be “Saving the Linguistic Phenomena” (Muller 2005, p. 94) but rather “Rational Reconstruction” to build a formal apparatus that, as a tool for reasoning, allows one to reason in complex situations where language proficiency is no guarantee of correctness.

The second, more general problem arises from the insistence on using the strict conditional in the definition of the subjunctive (hence, counterfactual) conditional, one that is in fact already well known. The nub is that the strict conditional satisfies the law of implicative weakening, i.e., whenever $\Box (\phi \rightarrow \psi )$ is true at i, so is $\Box ((\phi \wedge \phi ') \rightarrow \psi )$ for any $\phi '$. (This is also known at the law of antecedent strengthening.) This is just because the set of models for which $\phi \wedge \phi '$ holds is a subset of those for which $\phi$ holds, so the former models that are accessible from i are a subset of the latter models that are accessible from i.

While this a welcome feature in, e.g., the material conditional, it will not do for the subjunctive. Consider, as a toy example, a radioactive atom surrounded by sensitive radiation detectors, for which we would like to affirm that radiation would be detected if the atom were to decay, but not so if the atom were also in a lead box. No frame makes both of these statements true at any model. To see this, consider the following symbolization key:

$\phi$::

The atom decays.

$\phi '$::

The atom is in a lead box.

$\psi$::

Radiation is detected.

One would like to exhibit a frame that makes $\Box (\phi \rightarrow \psi )$ and $\Box ((\phi \wedge \phi ') \rightarrow \lnot \psi )$ true. However, because the strict conditional satisfies the law of weakening, whenever $\Box (\phi \rightarrow \psi )$ is made true at a model, the sentence $\Box ((\phi \wedge \phi ') \rightarrow \psi )$ is made true at that model, too. Since the truth of this sentence just means that all the accessible $\phi \wedge \phi '$ models are also $\psi$ models, none of them are $\lnot \psi$ models. Thus, any frame that makes $\Box (\phi \rightarrow \psi )$ true at a model makes $\Box ((\phi \wedge \phi ') \rightarrow \lnot \psi )$ false at that model.⁶ The fact that Muller allows for different accessibility relations when restricting attention to different sets of models does not help, for the set of models being considered—some crude caricature of the early radiation theory, say—is fixed in the vignette.

3 The viability of variably strict conditionals

The most important problem for strict conditionals—their general satisfaction of the law of implicative weakening, as discussed at the end of Sect. 2—is well known. Indeed, van Fraassen (1980, pp. 114–117) himself has been skeptical of an analysis of counterfactuals using the strict conditional for the same reasons.⁷ He also endorses the solution by Lewis and others adumbrated in Sect. 1.

In a bit more detail:⁸ Given a comparative similarity relation $\le _i$ on models W, as described in Sect. 1,

$\phi \boxright \psi$ is true at $i \in W$ (relative to $\le _i$) if and only if for every $\phi$-model h comparable to i by $\le _i$, there is some model j such that both

• 1. $j \le _i h$ and

• 2. every $\phi$-model k such that $k \le _i j$ is also a $\psi$-model.

In other words, for every accessible model h in which the antecedent holds, there is another model, j, at least as similar to i as h, such that all models k at least as similar to i as j are also models in which the consequent holds. Informally, one could gloss this as the condition that the counterfactual conditional is true at a model when in all sufficiently similar models in which the antecedent holds, the consequent holds, too.

These semantics are called “variably strict” because they are similar to those of the strict conditional, except the scope of the models considered is not fixed solely by the accessibility relation; rather, this scope varies by the nature of the antecedent, expanding or contracting according to the comparative similarity relation so as to find (or fail to find) the model j as described in the above definition. This variable scope precludes the variably strict conditional from satisfying the law of implicative weakening in general. For, it is no longer the case that scope of the models in which $\phi$ holds is a superset of those in which $\phi \wedge \phi '$ hold, when these are considered as antecedents to the conditional evaluated at i: the scope for the latter expands from just those sufficiently similar $\phi$-models to i to the sufficiently similar $(\phi \wedge \phi ')$-models to i. Indeed, it is simple to illustrate—see Fig. 2—how this works for the case described in Sect. 2 to make both $\phi \boxright \psi$ and $(\phi \wedge \phi ') \boxright \lnot \psi$ true at a model.

Fig. 2

In this diagram, points represent models of W for which an accessibility relation R and a comparative similarity relation $\le _i$ are assumed, the latter supposed, for simplicity of illustration, to be total on the models accessible from i. The accessible models at least as similar to i as j and $j'$ are, respectively, $S = \{k \in W : k \le _i j \}$ and $S' = \{k \in W : k \le _i j' \}$. Those models in which $\phi$, $\phi '$, and $\psi$ are true are depicted by the interiors of the respectively labeled regions with curved boundaries. The gray region in S indicates the subset of its models in which $\phi$ is true. Since these are all models at which $\psi$ is true, $\phi \boxright \psi$ is true. The other gray region indicates the subset of the models of $S'$ in which $\phi \wedge \phi '$ is true. Since these are all models at which $\psi$ is false, $(\phi \wedge \phi ') \boxright \lnot \psi$ is true. [This figure is after Figure 2 of Lewis (1973, p. 11), with some modifications]

Despite this success, van Fraassen (1980, p. 118) went on to conclude that it showed that “science does not imply the truth of any counterfactual” (except in special trivial cases). First, he noted the contextuality of the comparative similarity relation: depending on the context of assertion, certain properties are held fixed and others are let to be variable. Which are so held fixed in general makes a difference to the truth value of a counterfactual conditional. Second, he observed that “Science does not imply that the context is one way or another” (van Fraassen 1980, p. 118) so “scientific propositions are not context-dependent in any essential way” (van Fraassen 1980, p. 118). Together these imply the aforementioned conclusion, hence the non-objectivity of modal claims (van Fraassen 1989, p. 35–36). This is just a version of the second major problem for counterfactual reasoning in science described in Sect. 1, for which Lewis’s proposal described there will not do.

But Muller (2005, p. 90) has already responded that this conclusion follows only because van Fraassen has taken

context-independence as a necessary condition for objectivity .... We shall demonstrate that ‘context’ can be replaced with a model or a subset of models of an accepted theory, or with an accepted theory, which has little if anything to do with a loss of objectivity—on the contrary.

Recall from Sect. 1 that Muller sought to interpret counterfactual conditionals as strict conditionals (more or less), with the models and accessibility relations for the relational frames used in the conditionals’ semantics determined by the theory or theory fragment chosen. If successful, this would have blocked the argument against objectivity,⁹ and given scientific theories a claim to imply the truth of some counterfactual conditionals, all by denying van Fraassen’s second premise that science does not determine context—in particular, without adopting any assumptions about laws of nature. But, as I argued there, Muller’s proposal founders on the usual formal problems that the strict conditional faces, such as its undesirable satisfaction of the law of implicative weakening. This problem motivated interpreting counterfactuals as variably strict conditionals instead, but I shall argue that one can still implement Muller’s general strategy of determining the context for variably strict conditionals without adding anything to the scientific theory used. This shall be the goal of the next Section.

4 Similar Models through Similar Properties

Since instead of possible worlds I have already resolved to relativize the nodes of the formal semantics to be the models of a particular physical theory, what remains of the “context” of evaluation of a counterfactual conditional, construed as a variably strict conditional, is the comparative similarity relation on the models. In this Section, I describe the formal apparatus regarding properties of models that constructs this relation, then, in Sect. 5 how that apparatus is determined from a set of those properties minimally relevant to the truth value of a counterfactual under consideration.

Recall that the models W of a theory represent different states of affairs within the descriptive scope of the theory. In particular, each ascribes some definite properties to what they represent, and each such property can be represented by a valuation function. Given a property P, the valuation $v_P: W \rightarrow V$ assigns to each model a value in the valuation space V; for qualitative properties this is simply $\{ \top , \bot \}$ while for quantitative properties this may be the real line or some other structure. In any case, this valuation space is often equipped with additional structure. Of particular interest here is when that structure includes a semi-pseudometric:

Definition

A semi-pseudometric on a space X is a function $d: X \times X \rightarrow [0,\infty )$ satisfying the following conditions for all $x,y \in X$:

• 1. $d(x,x)=0$, and

• 2. $d(x,y)=d(y,x)$.

A semi-pseudometric is like a typical distance (“metric”) function, but more general in two ways. The first condition above states that the distance between a point and itself is always the minimum: zero. This is more general than a typical distance function (and what garners the “pseudo” moniker) because it allows non-identical points to be assigned zero by the function. The second condition, the same as a distance function, states that it is a symmetric function. What’s missing (and what garners the “semi” moniker) is the requirement that it satisfy the well-known triangle inequality, that $d(x,z) \le d(x,y) + d(y,z)$ for all $x,y,z \in X$. Of course, many semi-pseudometrics of interest are pseudometrics, semi-metrics, or metrics, but for present purposes these properties need not be assumed.

Here are three simple examples of semi-pseudometics for properties of models:

• Qualitative Property Consider a generic qualitative property Q, so that $v_Q: W \rightarrow \{ \top , \bot \}$. A natural metric, hence semi-pseudometric, on its valuation space is the identity function:

  $$\begin{aligned} d_Q(x,y) = {\left\{ \begin{array}{ll} 0 &{}\text { if } x=y,\\ 1 &{}\text { if } x \ne y. \end{array}\right. } \end{aligned}$$

  (1)

• Percentage Composition Suppose that the models are of boxes of gas of various compositions, and that A is the ratio of argon by volume to that of the pure component which has the highest proportion by volume. Then $v_A$ has a valuation space consisting of ratios of dimensional quantities, and one natural pseudometric, hence semi-pseudometric, on it is

  $$\begin{aligned} d_A(x,y) = |[x]\,{-}\,[y]|, \end{aligned}$$

  (2)

  where the square brackets indicate taking the dimensionless part. This satisfies the triangle inequality but different samples of gas with the same ratio of argon by volume to that of different pure components which have the highest proportion by volume in the box would be assigned a distance of zero, so it is a pseudometric.

• Lorentzian Distance Suppose that the models are of Minkowski spacetime $(M,\eta ),$ each with a distinguished point $p\in M$, and that D is the geodesic distance between those points. Then the valuation function for the distinguished point is $v_D: W \rightarrow M$, and one natural semi-pseudometric on its valuation space M is

  $$\begin{aligned} d_D(x,y) = D(x,y). \end{aligned}$$

  (3)

  If the distinguished points are null-related, the distance between them is zero, even if they are distinct. Since distinct timelike-related points in Minkowski spacetime are each null-related to a common point, the triangle inequality fails in general, and $d_D$ is only a semi-pseudometric.

Consider now any property P of models in W with valuation $v_P$ whose valuation space V is equipped with a semi-pseudometric $d_P^V: V \times V \rightarrow [0,\infty )$. $d_P^V$ induces another semi-pseudometric $d_P^W$ on W as follows:

$$\begin{aligned} d_P^W(x,y) = d_P^V(v_P(x),v_P(y)). \end{aligned}$$

(4)

Thus a collection of properties $\mathcal {P}$ of models in W with corresponding set of valuations ${\mathcal {V}}_{{\mathcal {P}}}$ induces a set of semi-pseudometrics $\mathcal {D}_{\mathcal {P}}^W$ on W. Such a set in turn determines a three-place relation $j \le _i k$ for $i,j,k \in W$ as follows:

$$\begin{aligned} j \le _i k \leftrightarrow \forall d_P^W \in {\mathcal {D}}_{{\mathcal {P}}}^W, d_P^W(i,j) \le d_P^W(i,k). \end{aligned}$$

(5)

The relation thus defined satisfies the constrains of a comparative similarity relation, described in Sect. 1, when the accessibility relation on models is taken to be the universal relation—i.e., all models are accessible from all others. According to it, j is at least as similar to i as k if and only if the differences between the relevant property valuations $v_P^W$ of i and j are each no larger than those between i and k.

Because any comparative similarity relation is a model for Lewis’s basic variably strict logic of counterfactual conditionals V, this demonstrates that natural or widely agreed-upon distances (from semi-pseudometrics) on the valuations spaces for a collection of properties of a set of models determine the truth conditions for counterfactual conditionals using those models as nodes. (In fact, the more general similarity structure on models, which is related formally to topological structure, determines these truth conditions (Fletcher 2019, §6.1), but that level of generality is not needed for present purposes.)

A bit more can be said, however. Stating the main semantic result of this section requires one more definition:

Definition

A collection of semi-pseudometrics $\mathcal {D}$ on a set X is said to be separating when, for each $x,y \in X$, there is some $d \in \mathcal {D}$ such that $d(x,y)=0$ implies $x=y$.

Furthermore, we may say that a collection of properties on models of W whose valuations have valuation spaces equipped with semi-pseudometrics is separating when its induced collection of semi-pseudometrics on W is separating. Separating collections of properties on a set of models are just those that allow one to distinguish one model from another solely from their distances according to at least one semi-pseudometric induced from a property.

Gathering the previous facts proves the following:

Theorem

Each space equipped by a (separating) collection of semi-pseudometrics induces a comparative similarity relation on that space that makes it a model for the logic VWU (VCU).

For, among the V-logics:

• The U-logics are exactly those with universal accessibility relations.

• The W-logics are exactly those whose models have their comparative similarity relation satisfying $i \le _i j$ for all nodes $i,j \in W$.

• The C-logics are exactly those whose models have their comparative similarity relation such that, for all nodes $i,j \in W$, if $j \le _i i$ then $i = j$.

These are said to satisfy uniformity, weak centering, and centering, respectively (Lewis 1973, p. 120). Thus the above theorem follows immediately from the definition of the semi-pseudometrics and their induced comparative similarity relation on a space. Notably, both VWU and VCU are among the four logics that Lewis (1973, p. 130) primarily endorses for counterfactual conditionals (although he ranks VC highest among them).

Although I have been focusing on semantic structures for logics for counterfactual reasoning, it may help to recall the syntactic characterization of the logics VWU (VCU). Let $\phi ,\psi ,$ and $\chi$ (possibly with subscripts) denote sentences formed by the usual recursive compounding of sentence letters, sentential constants $\top$ and $\bot$, logical connectives, and the modal operators $\boxright , \Box ,$ and $\Diamond$. Then the logics in question have the following inference rules (Lewis 1973, p. 132):

• 1. Modus Ponens;

• 2. “Deduction within Conditionals”: for any $n \ge 1$,

  $$\begin{aligned} \frac{\vdash (\chi _1 \wedge \cdots \wedge \chi _n) \rightarrow \psi }{\vdash ((\phi \boxright \chi _1) \wedge \cdots \wedge (\phi \boxright \chi _n)) \rightarrow (\phi \boxright \psi )}; \end{aligned}$$

• 3. and Interchange of Logical Equivalents.

They also have the following axioms (or really, axiom schemata), to be explained presently (Lewis 1973, pp. 22, 132):

• 1. Truth-functional tautologies

• 2. $\square \phi \leftrightarrow (\lnot \phi \boxright \phi )$, $\Diamond \phi \leftrightarrow \lnot \square \lnot \phi$

• 3. $\phi \boxright \phi$

• 4. $\square \phi \rightarrow (\psi \boxright \phi )$

• 5. $(\phi \boxright \lnot \psi ) \vee (((\phi \wedge \psi ) \boxright \chi ) \leftrightarrow (\phi \boxright (\psi \rightarrow \chi )))$

• 6. $(\phi \boxright \psi ) \rightarrow (\phi \rightarrow \psi )$

• U1. $\Diamond \phi \rightarrow \square \Diamond \phi$

• U2. $\square \phi \rightarrow \square \square \phi$

• C. $(\phi \wedge \psi ) \rightarrow (\phi \boxright \psi )$

The first and third are self-explanatory; the second effectively defines the usual modalities of necessity and possibility through the counterfactual conditional. The fourth is version of the truth of conditional with tautologous consequents, but expanded to include necessary antecedents. The fifth Lewis (1973, p. 133) apologetically denigrates as “long and obscure,” but it has a natural interpretation as a version of the equivalence of exportation, with the proviso that the exported sentence $\psi$ is not made false at the closest $\phi$ nodes. The sixth ensures that the counterfactual conditional is also in general a subjunctive conditional: when the conditional and the antecedent are true at a node, the consequent is also true at that node. The two U axioms are the syntactic expression of a universal accessibility relation: what’s possible and necessary doesn’t differ from node to node. These in total form the axioms for VWU. The C axiom, when added to these, yields VCU; it states that when any two propositions hold at a node, the counterfactual conditional linking them does, too, which would not be true in general if for one node, another is at least to similar to it as it is to itself.

5 Minimally relevant properties

In the previous Section, I showed how a set of properties whose corresponding valuation spaces are each equipped with a semi-pseudometric gives rise to a comparative similarity relation on the models to which they pertain. But how is this set of properties to be determined? Much can be said, but I shall suggest, roughly, that it is the properties which are relevant to the truth of the counterfactual being evaluated. How shall I understand relevance? Here I can only give a partial sketch instead of a complete answer. Not only do I expect that the details may vary significantly from theory to theory, but the analysis of relevant properties in each case may be subtle enough to merit its own treatment. But, vary as they may, these details are all grounded in the details of the theories from which they arise, not from subjective criteria outside of the theory’s scope. Thus my goal is to provide some plausibility for the idea that, even without a fully detailed account of relevance, any such account, once made precise and good, will be apt for providing a contextual semantics for counterfactual conditionals whose context is definite and does not depend on whim or fancy. Indeed, the sketch I give will bear on the examples in Sect. 7.

To set the stage for the issues involved it may be helpful to review briefly how the present goal differs from related goals in neighboring provinces of philosophical inquiry. In a word, most of these have focused, at least in part, on syntactic criteria for relevance, while the notion of relevance to be at hand should be semantic, a feature of the models of a theory, not depending on any special features of a language in which the theory is formulated. For instance, the long tradition of relevance logic (Mares 2014) has focused on describing a concept of relevant implication or entailment more circumspect than its well-known classical cousin, but its restriction is typically formulated in terms of the structure of the related sentences.

There is another tradition aimed at understanding the structure of relevance from the vantage of philosophy of language and metaphysics.¹⁰ Some of the programs within this tradition are also substantially syntactic, needfully so because of their goal to capture aspects of purported hyperintension in natural language. They aim to capture how even intensionally equivalent sentences of a language could be understood as being “about” different subject matters. Following Hawke (2018), we can distinguish at least three such: the atom-based, subject-predicate, and ways-based programs. According to the atom-based program, “the subject matter of [a formal sentence] $\phi$ can be identified, in some sense, with the set of atomic claims from which $\phi$ is composed” (Hawke 2018, p. 698), which requires distinguishing the atoms of the language used. By contrast, according to the subject-predicate program, “the subject matter of $\phi$ is the set of objects of which something is said by stating $\phi$” (Hawke 2018, p. 698). Although the archetypal version by Perry (1989) has syntactical elements in its formulation, they are mostly superficial. But the sort of relevance of present concern isn’t merely having the same subject matter, in the sense of making predications of the same objects: the properties predicated should be relevant because they potentially make a difference to the truth value of the counterfactual under examination.

So: how to make sense of the idea that some property’s values potentially make a difference for another’s? Lewis (1986b) famously suggested a difference-making principle in his account of causation, the schema for which has been expanded to truth-making (Lewis 2001), explanation (Strevens 2004, 2008), epistemology (Comesaña and Sartorio 2014), and mechanisms (Glennan 2017). But these principles have themselves typically (though not universally) contained counterfactual conditionals—e.g., “We think of a cause as something that makes a difference, and the difference it makes must be a difference from what would have happened without it” (Lewis 1986b, pp. 160–161)—invoking which would only obscure the identification of difference-making properties.¹¹ But Lewis (1988a, b) also initiated the ways-based program for understanding the structure of relevance, according to which a subject matter is a just a distinction among different ways the world could be, and relevance is construed (more or less) as overlapping subject matter. Lewis’s goal is different from the present one, however, pulling his development away from what is needed for propositional difference-making. Nevertheless, it is the closest to my present goals among the available options, so I shall adapt some of its semantic insights, along with some modifications very loosely inspired from the sophistications in the ways-based program of Yablo (2014).¹²

First, it will help to introduce some terminology. Any property P applicable to the models W of a theory comes with a valuation $v_P : W \rightarrow V$ for some valuation space V. For any $\theta \in V$, one can define the level set of $v_P$ at $\theta$ as $L(v_P,\theta ) = \{ w \in W : v_P(w) = \theta \}$. The level sets of a valuation $v_P$ partition the models W into classes each of whose elements shares a common value in V. Given two properties, P and $P'$, with valuations $v_P: W \rightarrow V$ and $v_{P'}: W \rightarrow V'$, their values $\theta \in V$ and $\theta ' \in V'$ are orthogonal in W when $L(v_P,\theta ) \cap L(v_{P'},\theta ') \ne \emptyset$.

A set of properties $\mathcal {P}$ is minimally relevant to a property P for models in W when it satisfies the following two conditions.

• Connection For each $P' \in \mathcal {P}$, there is some value $\theta ' \in v_{P'}[W]$ and some value $\theta \in v_P[W]$ that are not orthogonal in W.

• Quasi-Independence For any $P',P'' \in \mathcal {P}$, if $v_{P'}(w) = \theta '$ entails that $v_{P''}(w) = \theta ''$ for all $w \in W$, then $v_{P''}(w) = \theta ''$ entails that $v_{P'}(w) = \theta '$ for all $w \in W$ and $\{P'\}$ and $\{P''\}$ induce the same comparative similarity relation on W.

The connection condition ensures that some value of each $P' \in \mathcal {P}$ entails the negation of some value of P. If it entails many such, it can entail some unique value of P. Because of the symmetry of the definition, this provides that relevant properties $\mathcal {P}$ are ones whose values are necessary or sufficient for some value of P. The quasi-independence condition ensures a sort of minimality: any property valuations which are not logically independent are equivalent with respect to the comparative similarity relation they induce.¹³

For any given property P, in general there will be many sets of properties $\mathcal {P}$ minimally relevant to it. Some sets will not contain enough properties, while others too much. Say that such a set $\mathcal {P}$ is quasi-maximal if and only if whenever $\mathcal {P} \subset \mathcal {P}'$ and $\mathcal {P}'$ is minimally relevant to P, $\mathcal {P}$ and $\mathcal {P}'$ induce the same comparative similarity relation on W. So, whenever a property can be added to a quasi-maximal set $\mathcal {P}$ of properties while preserving its minimal relevance for P, that addition does not make a difference for the induced comparative similarity relation.

Finally, we can state the contextual rule for the set of properties needed for determining the comparative similarity relation:

• Context When evaluating the counterfactual conditional $\phi \boxright \psi$ within a theory with models W, use the comparative similarity relation induced on W by any quasi-maximal set of properties minimally relevant for $\psi$ in $v_\phi ^{-1}[\top ] = \{ w \in W: v_\phi (w) = \top \}$.

Any quasi-maximal set of properties for $\psi$ in $v_\phi ^{-1}[\top ]$—the set of models in which $\phi$ is true—determines the same comparative similarity relation on W by definition. These are the properties of models that are relevant for the truth of $\psi$ among the $\phi$-models.

There is of course a sense in which each of the properties in the quasi-maximal set for the consequent make a difference for the truth of the counterfactual, but this does not mean that each minimally relevant property is “equally weighted” in any straightforward arithmetic way. (That is, the comparative similarity relation induced on W may not arise from a single semi-pseudometric on W that is an arithmetic sum of those induced from the aforementioned properties.) Nevertheless, there is also a definite sense in which a quasi-maximal set may contain “weighted” properties. For instance, consider two real-valued properties $P_1$ and $P_2$—viz., $v_{P_1}: W \rightarrow \mathbb {R}$ and $v_{P_2}: W \rightarrow \mathbb {R}$.¹⁴ Then one can define a new property Q with valuation $v_Q= av_{P_1} + bv_{P_2}$, for $a,b \in \mathbb {R}$. If $a \ne b$, then Q represents a property that is an “unequally weighted” combination of properties $P_1$ and $P_2$, and may well appear in a quasi-maximal set.

Regardless of whether the quasi-maximal set for the consequent contains such weighted properties, the contextual rule here is non-trivially so: it varies in general from counterfactual consequent to consequent. Contra van Fraassen (1980, p. 118), this context is determined by these semantics given the models of a particular theory. Just as physical theories don’t affirm much unconditionally—only what’s the case in all their models—but bestow their insight conditioned on “boundary conditions, initial conditions, parameter-values, auxiliary assumptions and what not” (Muller 2005, p. 95), they don’t affirm much about relevant similarity unless provided the context that a particular counterfactual conditional offers. This is the essential point: even if the technical details I have provided of how the relevant properties should be contextually determined require revision or adaptation to specific cases, the particular counterfactual conditional considered provides that determination with the resources a physical theory already provides.

6 Comparing variably strict conditionals with Maudlin’s modest proposal

Before illustrating the above account with a few examples, I pause for a comparative excursus. Maudlin (2007) has proposed an account of how to evaluate counterfactuals using physical theories that has some resemblances and some differences with mine and with that of Lewis (1973), which he discusses explicitly. After sketching his position I shall briefly compare it with my own, highlighting some of my account’s potential advantages: greater generality and formal precision.¹⁵

Maudlin takes as his starting point not models of theories, but laws, due to their commonly accepted role in scientific explanation: “scientific and commonsense explanations demand the postulation of [(fundamental) laws of temporal evolution] and their adjunct principles” (Maudlin 2007, p. 13) such as boundary conditions, the specification of particular forces, etc. Which temporally extended regularities are laws is not determined by anything else; they are ontologically primitive, but they themselves determine what’s possible or necessary, to the extent that they do, according to which states of affairs they permit or require, respectively. Indeed, “The content of the laws can be expressed without modal notions, and suffices to determine a class of models. The models can then be treated as ‘possible worlds’ in the usual way, and so provide truth conditions for claims about nomic possibility and necessity” (Maudlin 2007, p. 21).

They also provide truth conditions for counterfactual conditionals $\phi \boxright \psi$ at a spacetime world w through a three-step evaluation process (Maudlin 2007, pp. 22–23).

• 1. Choose a Cauchy surface C for w—a three-dimensional surface in the spacetime through which each maximal timelike worldine passes completely.

• 2. Construct a Cauchy surface $C'$ satisfying $\phi$ that is otherwise the same as C, inasmuch as this is possible according to the laws.

• 3. Apply the laws to $C'$ to develop a new model spacetime $w'$, and evaluate whether $\psi$ is true at $w'$.

The antecedent $\phi$ ideally should pick out both C and $C'$ uniquely, and if the laws are deterministic with respect to their initial-value problem, the resulting $w'$ will be unique as well. If not, then vagueness or non-determinism will yield through this recipe a collection of spacetime worlds $w'$. In any case, $\phi \boxright \psi$ is true at w if for all such $w'$, $\psi$ is true at $w'$.¹⁶

How, on Maudlin’s account, does one understand the ceteris paribus clause of step two? “In each case different cetera are paria, and which change is appropriate is decided, if at all, by context and background assumptions.” (Maudlin 2007, p. 24). But in contrast with Lewis (1973, 1986a), “our recipe makes no reference to an overall similarity between worlds, the nearest thing being a ceteris paribus condition that determines what counts as the appropriate carrying out of a command” (Maudlin 2007, p. 33). This contrast should not be overstated, however. After all, when there are many way of constructing some $C'$ that makes $\phi$ true that require some other modifications to w, which does one select? Maudlin does not make precise how this should be done. Regardless of whether this is a problem for Maudlin’s goals,¹⁷ it will not suffice for the present ones, which include articulating how the semantics for counterfactuals can be provided internally to a scientific theory. By contrast, the previous Section has outlined how the comparative similarity relation among models is determined from the properties of the models minimally relevant to the evaluation of a given counterfactual.

Another difference is the comparatively restricted scope of Maudlin’s account, which applies only to explicitly spatiotemporal theories (needed for the definition of a Cauchy surface) with a well-defined initial-value problem (needed in order to apply laws to the Cauchy surface to generate a model) and counterfactual conditionals whose antecedents specify a Cauchy surface (at least vaguely). Maudlin (2007, p. 13) does stress that “Some so-called laws of co-existence, such as the ideal gas law $PV = nRT$, are better construed as consequences of laws of temporal evolution” rather than laws. But this seems to be dependent on our evidence for an inter-theoretic reduction with kinetic theory, not a consequence of the theory itself; indeed, why should it have been impossible for Boyle to reason counterfactually with his law (that for a fixed amount of gas at a constant temperature $PV = \text {const.}$) 75 years before the development of kinetic theory? Of course, Maudlin is ultimately interested in the metaphysics of laws of nature, whereas I am presently interested in theory-based reasoning regardless of the theory’s metaphysical interpretation or viability. The metaphysical (im)possibility of the situations described by the models makes no difference in my account.

Setting these differences in goals aside, there are some special conditions for my own account under which Maudlin’s falls as a special case. Under the conditions outlined in the previous paragraph, suppose as well that the theory under consideration is deterministic, in the sense that the model $w'$ constructed in stage three of Maudlin’s procedure is unique. For a counterfactual conditional under all these conditions, his account and mine will always agree on the counterfactual’s truth value at a model, regardless of the comparative similarity relation (modulo the remarks of footnote 16). This is because if there is a unique model at which one needs to evaluate whether the conditional’s consequent holds, then the application of the whole apparatus of comparative similarity becomes trivial—it doesn’t matter which models are more comparatively similar to which, since there is only one model to check.

Under slightly more general conditions, suppose that there is not necessarily such a unique model, but that the consequent receives the same truth value in each of the models generated. In this case, too, Maudlin’s account and mine will always agree on the counterfactual’s truth value at a model, regardless of the comparative similarity relation (again modulo the remarks of footnote 16). In this case, which includes the previous one as a special case, the comparative similarity relation doesn’t matter because no matter how that relation selects among the antecedent-satisfying models, the semantic evaluation of the conditional will always be the same. (Here there is also agreement with the strict conditional described in Sect. 2.)

Thus the advantage of introducing this comparative similarity structure, and showing how it is determined from the theory and the counterfactual under evaluation, arises in more complicated cases. These include cases falling under the auspices of Maudlin’s account, but for which comparative similarity is needed for the “ceteris paribus” part of his recipe. It also includes cases involving theories that do not fit the strictures of Maudlin’s account: being spatiotemporal, having Cauchy surfaces and a well-defined initial-value problem, etc. These will both be illustrated with a few examples in the sequel, Sect. 7.

7 Application: elementary equilibrium thermodynamics

Elementary equilibrium thermodynamics is a statical theory: it does not concern in general the detailed changes of thermodynamical quantities over time, only their balance for various equilibrium states. Thus there is no such thing as an “initial-value problem” in the theory. (The conceit of the quasi-static process is that the thermodynamical system undergoing it proceeds, in some way or other, along a sequence of equilibrium states; the exact dynamics of this process are beyond the scope of the theory.) And because thermodynamical quantities are not generally spatiotemporal, the theory does not permit any adjudications of more or less spatially or temporally “widespread” variability among states of thermodynamic affairs. For these reasons neither Maudlin’s nor Lewis’s account of the truth conditions for counterfactual conditions readily applies.

But it is simple for the approach am I advancing. Consider systems of enclosed gases in a piston-cylinder device with pressure P, volume V, and absolute temperature T, each positive real numbers, models of which will be those described by the combined gas law: for any particular such gas, $PV/T = \text {const}$. This constant sets which models are accessible from which others. (In particular, they will divide into equivalence classes based on the value of this constant.) The device will fail (break) whenever the pressure, volume, or temperature of the gas rises to at least the thresholds $\bar{P}$, $\bar{V}$, or $\bar{T}$, respectively. Consider a particular sample of gas whose pressure is $\bar{P}/2$, volume is $\bar{V}/2$, and temperature is $\bar{T}/4$: for this sample, the device is not failing.

Consider further the following counterfactual conditionals:

• 1. If the gas were twice as hot, the device would not fail.

• 2. If the gas were twice as hot and the piston were fixed, the device would fail.

I interpret the antecedent as (colloquially) referring to the absolute temperature. In both cases, the property relevant to the consequent of the conditional is the maximum among the values of the pressure, volume, and temperature. The device fails in a model (which we can represent as property F) according to the following valuation on models parameterized by (P, V, T):

$$\begin{aligned} v_F(P,V,T) = {\left\{ \begin{array}{ll} \top &{}\text { if } \max \{P/\bar{P},V/\bar{V},T/\bar{T}\} \ge 1,\\ \bot &{}\text { if } \max \{P/\bar{P},V/\bar{V},T/\bar{T}\} < 1. \end{array}\right. } \end{aligned}$$

(6)

Since this is a qualitative property, its valuation space acquires the same semi-pseudometric as described in Eq. 1. This yields a relatively simple comparative similarity relation: models are at least as similar as each other at any model just in case they have the same verdict regarding whether the device fails.

To evaluate the first counterfactual at the model $(\bar{P}/2,\bar{V}/2,\bar{T}/4)$, one must consider the set of models with temperature $T = \bar{T}/2$ (that also satisfy the combined gas law). Note that for any model $(P,V,\bar{T}/2)$, $(\bar{P}/\sqrt{2},\bar{V}/\sqrt{2},\bar{T}/2) \le _{(\bar{P}/\sqrt{2},\bar{V}/\sqrt{2},\bar{T}/2)} (P,V,\bar{T}/2)$, since $(\bar{P}/\sqrt{2},\bar{V}/\sqrt{2},\bar{T}/2)$ is at least as similar to itself as any other model regarding the non-failure of the device. Thus $(\bar{P}/\sqrt{2},\bar{V}/\sqrt{2},\bar{T}/2)$ satisfies the first condition of the truth conditions described at the beginning of Sect. 3. It also satisfies the second, since by definition if $(P,V,\bar{T}/2) \le _{(\bar{P}/\sqrt{2},\bar{V}/\sqrt{2},\bar{T}/2)} (\bar{P}/\sqrt{2},\bar{V}/\sqrt{2},\bar{T}/2)$, then $v_F(P,V,\bar{T}/2) = \bot$. Thus the sentence is true. Intuitively, the models for which $T = \bar{T}/2$ that also satisfy the combined gas law are never more similar regarding the non-failure of the device as $(\bar{P}/\sqrt{2},\bar{V}/\sqrt{2},\bar{T}/2)$, and those equally similar are also ones in which the device does not fail.

To evaluate the second counterfactual at the model $(\bar{P}/2,\bar{V}/2,\bar{T}/4)$, one must consider the set of models with volume $V = \bar{V}/2$ and temperature $T = \bar{T}/2$ (that also satisfy the combined gas law). It turns out that there is only one such model: $(\bar{P},\bar{V}/2,\bar{T}/4)$, and $v_F(\bar{P},\bar{V}/2,\bar{T}/4) = \top$. So it then becomes trivial that the second counterfactual is true, since the only model accessible at which the antecedent is true is one in which the consequent is also true.

Although these two examples are very simple, they are essentially of the same form as the pair of counterfactual conditionals that (as described in Sect. 2) the strict conditional could never make true at once.¹⁸ This shows the semantics I have provided do not ultimately reduce to those of the strict conditional.

8 Implications: models, logics, and laws

Accounts of the formal semantics of counterfactual conditionals concerning physical phenomena have typically followed one of two paths. The first, most standard one, is to ground the conditionals’ truth conditions in an account of physical laws of nature. This is Lewis’s approach, with its sophisticated formal machinery of comparative similarity relations on possible worlds but also its essential reliance on miracles in the determination of comparative similarity among worlds. The second path is to deny that physical theories ground the conditionals’ truth conditions at all. This is van Fraassen’s approach, which, while avoiding the problems with Lewis’s, is a Pyrrhic victory for understanding how scientific theories can ground counterfactual reasoning. I have in this essay marked the trailhead, first imagined by Muller (2005), for a third path, that advances a semantics of comparative similarity among models of a theory whose contextuality is determined by the theory. In the remainder, I’d like to draw out the implications of following this path for the philosophy of other particular sciences, the logics of counterfactuals and relevance, and laws of nature.

First, although I have been using examples from physics to illustrate a path to formalized counterfactual reasoning, nothing on this path essentially demands that this reasoning concern physical phenomena described by a physical theory. In the first place, the only role of theory in the account is to provide a class of models of possible ways the phenomena they represent could be. There is no loss if the models do not arise from a theory, but instead from some endogenous modeling practices. Moreover, that the models are of physical phenomena is not essential. Any sufficiently formalized models, of whatever sort of phenomena they represent—physical, biological, social, etc.—can be the basis for counterfactual reasoning. Rather, the brambles to be cleared are those obscuring how to extend the approach from non-probabilistic to probabilistic models.

Second, certain aspects of the presented logic for counterfactual conditionals deserve further development. At a broad level, its advancement comes through the application of relevance concepts to these conditionals. The mixture of these two is not new: it is not always appreciated that C. I. Lewis devised the strict conditional not as a theory of counterfactuals but to advance a relevance logic for conditionals (Garson 2016, §5), and others have developed more sophisticated theories of counterfactual conditionals as relevant conditionals (Mares and Fuhrmann 1995; Mares 2004). What is the connection between these latter systems and the present one?

At a narrower level, there is a slightly subtle tension between Lewis’s semantics for VWU (or VCU) and my own. These V-logics assume a single comparative similarity relation on the nodes, while my own contextual semantics allows that structure to change depending on the propositions linked by the counterfactual connective. So, if these propositions do not themselves contain a counterfactual conditional, then only one similarity structure is used to evaluate the conditional at a node, hence my semantics matches with Lewis’s. The converse will hold when any nested counterfactuals are trivial, or induce the same comparative similarity relation, but otherwise this is not guaranteed. How this affects the proof theory of the logic, and its consequent differences with VWU (and VCU), are yet to be explored.

Third, one of the central objections to antirealism about laws of nature is that these laws seem to be central to scientific practices of reasoning counterfactually and causally. By contrast, the account of counterfactual reasoning presented notably contains no reference to laws of nature, obviating the first version of this objection. The development of a suitable counterfactual account of causality therefrom would then obviate the second. To accommodate laws’ common invocation in scientific reasoning, I would prefer a deflationary account of them rather than an error theory. On such an account, I would agree with van Fraassen (1989, p. 224) that “Apparent laws which frequently appear are often partial descriptions of special subclasses of models,” and that the particular axiomatizations of theories through these apparent laws summarize “important features by which models may be described and classified. The distinction between these features and others that characterize the model equally well is in the eye of the theoretician; it does not, to my mind, correspond to any division in nature” (van Fraassen 1989, p. 223). Or, rather, it need not so correspond—see further the discussion in Fletcher (2019, §6.2). Further development of this deflationary account of laws of nature, and its concomitant elaboration of causality, deserving as they are, must await another occasion.