Abstract
Many authors have noted that there are types of English modal sentences cannot be formalized in the language of basic first-order modal logic. Some widely discussed examples include “There could have been things other than there actually are” and “Everyone who is actually rich could have been poor.” In response to this lack of expressive power, many authors have discussed extensions of first-order modal logic with two-dimensional operators. But claims about the relative expressive power of these extensions are often justified only by example rather than by rigorous proof. In this paper, we provide proofs of many of these claims and present a more complete picture of the expressive landscape for such languages.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is well known that first-order modal logic faces fundamental limitations in expressive power. Some standard examples used to illustrate this include:
-
(E)
There could have been things other than there actually are.Footnote 1
-
(R)
Everyone who is actually rich could have been poor.Footnote 2
Informally, the first is true iff there is a possible world where something exists that does not exist in the actual world. The second has multiple readings, but on one reading, it is true iff there is a possible world where everyone who is rich in the actual world is poor in that world. It can been shown that no formula in basic first-order modal logic with actualist quantifiers (i.e., quantifiers ranging over existents) is equivalent to (E) or to (R).Footnote 3 We can regiment (E) using a possibilist existential quantifier \(\Sigma {}\) (i.e., a quantifier ranging over all possible objects) and an existence predicate \({\textsf {E}} \) as follows:
But one can prove that even with these additions, there is still no formula that is equivalent to (R).Footnote 4
In response to these expressive limitations, many authors have considered extending first-order modal logic with an “actually” operator \(@\).Footnote 5 They then point out that in the presence of \(@\) and the possibilist universal quantifier \(\Pi {}\), the following is equivalent to (R):
However, even with possibilist quantifiers and the actuality operator, sentences like the following seem to remain inexpressible:Footnote 6
-
(NR)
Necessarily, everyone who was rich could have been poor.
One could try to fix this problem by adding more and more operators to the language, some of which we will discuss below. But many such languages face further expressivity limitations themselves.Footnote 7 Corresponding expressive limitations also arise for first-order temporal logic, though we will mostly focus on the modal versions until the end of this paper.
Very often, these inexpressibility claims are justified in the literature only by example: all of the most straightforward attempts at formalizing these English sentences into first-order modal logic fail. While this style of argument may be convincing, it does not constitute a proof. One can sometimes find rigorous proofs for a variety of inexpressibility claims.Footnote 8 But only (Hodes 1984a, b, c) provides proofs of the inexpressibility of (R), (E), and sentences like them in extensions of first-order modal logic with two-dimensional operators such as \(@\).Footnote 9 And while these proofs are very interesting and involve a number of underappreciated techniques, they are quite complicated and difficult to generalize to other formal languages of interest.
In this paper, I will use a modular notion of bisimulation to characterize the expressive power of extensions of first-order modal logic with two-dimensional operators. After reviewing basic first-order modal logic (Sect. 2), I will provide a single proof method for characterizing the expressive power of a wide variety of first-order modal languages using bisimulations (Sect. 3). I will then present a variety of inexpressibility proofs using this technique (Sect. 4). I will conclude by generalizing these results to temporal logics and higher-dimensional logics (Sect. 5). The more intricate details are left to appendices (Appendices 1–4).
2 First-order modal logic
In this section, we review the standard possible worlds semantics for first-order modal logic. The technical details below are fairly standard except our points of evaluation need to be two-dimensional to account for operators like the actuality operator \(@\). While we have picked a particularly simple formulation of first-order modal logic, the inexpressibility results we explore in this paper apply to a wide range of formulations of first-order modal logic.Footnote 10
The signature for our plain vanilla first-order modal language  contains:
contains:
-
\({\textsf {VAR}} \) =
 (the set of (object) variables);
(the set of (object) variables); -
\({\textsf {PRED}} ^n\) =
 for each \(n \ge 1\) (the set of n-place predicates);
for each \(n \ge 1\) (the set of n-place predicates);
The set of formulas in  or
or  -formulas is defined recursively:
-formulas is defined recursively:

where \(P^n \in {\textsf {PRED}} ^n\) for any \(n \ge 1\), and  . The usual abbreviations for \(\bot \), \(\vee \), \(\rightarrow \), \(\leftrightarrow \),
. The usual abbreviations for \(\bot \), \(\vee \), \(\rightarrow \), \(\leftrightarrow \),  , and \(\Diamond \) apply. We may drop parentheses for readability. If the free variables of \(\varphi \) are among
, and \(\Diamond \) apply. We may drop parentheses for readability. If the free variables of \(\varphi \) are among  , we may write “
, we may write “ ” to indicate this.
” to indicate this.
To talk more easily about extensions of  , we will introduce a convention. Let
, we will introduce a convention. Let  be some new symbols with pre-defined syntax. The language obtained from
be some new symbols with pre-defined syntax. The language obtained from  by adding
by adding  is
is  . Some symbols that might be added include:
. Some symbols that might be added include:

where \(\approx \) is the identity relation, \({\textsf {E}} \) is an existence predicate, \(@\) is an “actually” operator, \({\mathop {\downarrow }}\) is a diagonalization operator (the inverse of \(@\)),Footnote 11\(\mathcal {F}\) is a “fixedly” operator,Footnote 12 is a quantifier over all actual objects,Footnote 13 and \(\Pi {}\) is the possibilist universal quantifier (its existential counterpart is \(\Sigma {}\)). The usual abbreviations apply. In what follows, we will let “\(\mathcal {L}\)” stand for any arbitrary
is a quantifier over all actual objects,Footnote 13 and \(\Pi {}\) is the possibilist universal quantifier (its existential counterpart is \(\Sigma {}\)). The usual abbreviations apply. In what follows, we will let “\(\mathcal {L}\)” stand for any arbitrary  where
where  are among the symbols above.
are among the symbols above.
Definition 1
(Models) A model is a tuple \(\mathcal {M} \) = \(\left\langle W,R,F,D,\delta ,I\right\rangle \) where:
-
W is a nonempty set (the state space);
-
\(R \subseteq W \times W\) (the \(\Box \)-accessibility relation);
-
\(F \subseteq W \times W\) (the \(\mathcal {F}\)-accessibility relation);
-
D is a nonempty set disjoint from W (the (global) domain);
-
\(\delta :W \rightarrow \wp \left( D\right) \) is a function (the local domain assignment), where for each \(w \in W\), \(\delta (w)\) is the local domain ofw;
-
\(I :{\textsf {PRED}} ^n \times W \rightarrow \wp (D^n)\) (for all \(n \ge 1\)) is a function (the interpretation function).
We will let \(\mathcal {M} \)’s state space be \(W^\mathcal {M} \), \(\mathcal {M} \)’s \(\Box \)-accessibility relation be \(R^\mathcal {M} \), etc. We will define  (and likewise for F). If \(R = W \times W\), we will say R is universal. If \(D =\bigcup _{w \in W} \delta (w)\) (i.e., D does not contain impossible objects), we will say D satisfies the domain constraint. We will let \(\mathbf U \) be the class of models where R and F are universal, \(\mathbf D \) be the class of models where D satisfies the domain constraint, and UD be their intersection.
(and likewise for F). If \(R = W \times W\), we will say R is universal. If \(D =\bigcup _{w \in W} \delta (w)\) (i.e., D does not contain impossible objects), we will say D satisfies the domain constraint. We will let \(\mathbf U \) be the class of models where R and F are universal, \(\mathbf D \) be the class of models where D satisfies the domain constraint, and UD be their intersection.
Let \(\mathcal {M} \) be a model. A variable assignment for\(\mathcal {M} \) is a function g mapping variables to elements in D. Let the set of variable assignments for \(\mathcal {M} \) be \({\textsf {VA}} (\mathcal {M} )\). If \(g \in {\textsf {VA}} (\mathcal {M} )\), then \(g^x_a\) is the result of modifying g by mapping x to a.
For readability, if  is a sequence (of terms, objects, etc.), we may write “\(\overline{\alpha } \)” in place of “
is a sequence (of terms, objects, etc.), we may write “\(\overline{\alpha } \)” in place of “ ”. \(\overline{\alpha } \) is assumed to be of the appropriate length, whatever that is in a given context. Let \(\left| \overline{\alpha } \right| \) be the length of \(\overline{\alpha } \). When f is some unary function, we may write “\(f(\overline{\alpha })\)” in place of “
”. \(\overline{\alpha } \) is assumed to be of the appropriate length, whatever that is in a given context. Let \(\left| \overline{\alpha } \right| \) be the length of \(\overline{\alpha } \). When f is some unary function, we may write “\(f(\overline{\alpha })\)” in place of “ ”. For instance, if g is a variable assignment, “\(g(\overline{x})\)” on this notation stands for “
”. For instance, if g is a variable assignment, “\(g(\overline{x})\)” on this notation stands for “ ”. Likewise, “\(g^{\overline{x}}_{\overline{a}}\)” stands for “
”. Likewise, “\(g^{\overline{x}}_{\overline{a}}\)” stands for “ ”.
”.
Since we want to consider operators like \(@\), our possible worlds semantics will be two-dimensional [as suggested in, e.g., Davies and Humberstone (1980, pp. 4–5)]. That is, indices will have to contain two worlds. The first world is to be interpreted as the world “considered as actual” and the second as the world of evaluation.
Definition 2
(Satisfaction for  ) The
) The  -satisfaction relation\(\Vdash \) is defined recursively, for all models \(\mathcal {M} = \left\langle W,R,F,D,\delta ,I\right\rangle \), all \(w,v \in W\) and all \(g \in {\textsf {VA}} (\mathcal {M} )\):
-satisfaction relation\(\Vdash \) is defined recursively, for all models \(\mathcal {M} = \left\langle W,R,F,D,\delta ,I\right\rangle \), all \(w,v \in W\) and all \(g \in {\textsf {VA}} (\mathcal {M} )\):

If \(\left| \overline{x} \right| \le \left| \overline{a} \right| \), then \(\mathcal {M} ,w,v \Vdash \varphi [\overline{a} ]\) if for all \(g \in {\textsf {VA}} (\mathcal {M} )\), \(\mathcal {M} ,w,v,g^{\overline{x}}_{\overline{a}} \Vdash \varphi (\overline{x})\).
Definition 3
(Validity) Let \(\mathbf C \) be a class of models. We will say \(\varphi \) is (generally)C-valid—written as \(\Vdash _\mathbf C \varphi \)—if \(\mathcal {M} ,w,v,g \Vdash \varphi \) for all \(\mathcal {M} \in \mathbf C \), all \(w,v \in W^\mathcal {M} \), and all \(g \in {\textsf {VA}} (\mathcal {M} )\). We will say \(\varphi \) is diagonallyC-valid—written as \(\Vdash _\mathbf C ^\text {d} \varphi \)—if \(\mathcal {M} ,w,w,g \Vdash \varphi \) for all \(\mathcal {M} \in \mathbf C \), all \(w \in W^\mathcal {M} \), and all \(g \in {\textsf {VA}} (\mathcal {M} )\). If \(\varphi \leftrightarrow \psi \) is (diagonally) \(\mathbf C \)-valid, we will say \(\varphi \) and \(\psi \) are (diagonally)C-equivalent. If \(\mathbf C \) is the class of all models, we may drop mention of \(\mathbf C \) and just say “valid” or “equivalent”.
We could have defined some of the additional symbols above in terms of others, assuming the others are present. For instance,  ,
,  , and
, and  are all valid (we will invoke these throughout without explicit mention of them). Thus, by the following lemma, we could have taken the lefthand side of these biconditionals to be abbreviations for their righthand side:
are all valid (we will invoke these throughout without explicit mention of them). Thus, by the following lemma, we could have taken the lefthand side of these biconditionals to be abbreviations for their righthand side:
Lemma 4
(Replacement of equivalents) Suppose \(\varphi \) and \(\psi \) have the same free variables. Let \(\theta '\) be a formula that results from replacing any number of instances of \(\varphi \) in \(\theta \) with \(\psi \). Then \(\Vdash _\mathbf C \varphi \leftrightarrow \psi \) implies \(\Vdash _\mathbf C \theta \leftrightarrow \theta '\).
This follows by a straightforward induction. If we replace \(\Vdash _\mathbf C \) in Lemma 4 with \(\Vdash _\mathbf C ^\text {d}\), then the result no longer holds (for instance, \(\Vdash ^\text {d} @P(x) \leftrightarrow P(x)\), but \(\nVdash ^\text {d} \Box @P(x) \leftrightarrow \Box P(x)\)). However, if \(\Vdash _\mathbf C ^\text {d} \varphi \leftrightarrow \psi \), then \(\Vdash _\mathbf C \star \varphi \leftrightarrow \star \psi \), where  , in which case we can replace \(\star \varphi \) with \(\star \psi \).
, in which case we can replace \(\star \varphi \) with \(\star \psi \).
We can think of Definition 2 as specifying a translation from the modal language into the language of possible worlds. We can make this more precise by formally defining the language of possible worlds, which is often called the correspondence language.Footnote 14 The correspondence language is a two-sorted first-order language: one sort for objects, and one sort for worlds. The signature for our two-sorted first-order language  contains \({\textsf {VAR}} \), \({\textsf {PRED}} \), and:
contains \({\textsf {VAR}} \), \({\textsf {PRED}} \), and:
-
\({\textsf {SVAR}} \) =
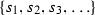 (the set of state variables).
(the set of state variables).
The set of formulas in or
or  -formulas is defined recursively:
-formulas is defined recursively:

where \(P^n \in {\textsf {PRED}} ^n\), \(x,y,\overline{y} \in {\textsf {VAR}} \), and \(s,t \in {\textsf {SVAR}} \). I will typically use \(\alpha ,\beta ,\gamma ,\dots \) for  -formulas to distinguish them from
-formulas to distinguish them from  -formulas.
-formulas.
To illustrate, here are the intended formalizations of (E), (R), and (NR), where \(s^*\) is meant to be interpreted as the actual world (which we will assume is the same as our starting world of evaluation, just for simplicity):Footnote 15
-
(E)
There could have been things other than there actually are.
 (3)
(3) -
(R)
Everyone who’s actually rich could have been poor.
 (4)
(4) -
(NR)
Necessarily, everyone who’s rich could have been poor.
 (5)
(5)
To define  ’s semantics, we need to modify the definition of a variable assignment for\(\mathcal {M} \) so that not only do variable assignments map variables to elements of D, but they also map state variables to elements of W. Then satisfaction in
’s semantics, we need to modify the definition of a variable assignment for\(\mathcal {M} \) so that not only do variable assignments map variables to elements of D, but they also map state variables to elements of W. Then satisfaction in  is just the standard notion of satisfaction for two-sorted first-order logic:
is just the standard notion of satisfaction for two-sorted first-order logic:
Definition 5
(Satisfaction for  ) The
) The  -satisfaction relation\(\vDash \) is defined recursively for all models \(\mathcal {M} \) and all \(g \in {\textsf {VA}} (\mathcal {M} )\):
-satisfaction relation\(\vDash \) is defined recursively for all models \(\mathcal {M} \) and all \(g \in {\textsf {VA}} (\mathcal {M} )\):

We say \(\alpha \) is C-valid—written as \(\vDash _\mathbf C \alpha \)—if \(\mathcal {M} ,g \vDash \alpha \) for all \(\mathcal {M} \in \mathbf C \) and all \(g \in {\textsf {VA}} (\mathcal {M} )\). Equivalence is defined likewise.
We can now make more precise the thought that Definition 2 is specifying a translation:
Definition 6
(Standard translation) Let \(\varphi \) be a \(\mathcal {L}\)-formula, and let \(s,t \in {\textsf {SVAR}} \). The standard translation of\(\varphi \)with respect to\(\left\langle s,t\right\rangle \),  , is defined recursively:
, is defined recursively:

where \(s'\) and \(t'\) are state variables not occurring anywhere in  . If \(\varPhi \) is a set of \(\mathcal {L}\)-formulas, then we will let
. If \(\varPhi \) is a set of \(\mathcal {L}\)-formulas, then we will let  .
.
The following lemma, which can be proved using a simple induction on formulas, states that \({\textsf {ST}} \) translates every \(\mathcal {L}\)-formula into an equivalent  -formula:
-formula:
Lemma 7
(Translation) Let \(\mathcal {M} \) be a model, \(w,v \in W^\mathcal {M} \), \(g \in {\textsf {VA}} (\mathcal {M} )\), \(s,t \in {\textsf {SVAR}} \), and \(\varphi \) an \(\mathcal {L}\)-formula. Then \(\mathcal {M} ,w,v,g \Vdash \varphi \) iff  .
.
In other words, Lemma 7 tells us that we can think of “\(\mathcal {M} ,w,v,g \Vdash \varphi \)” as a notational variant of “ ”. In what follows, we will implicitly identify an extension of
”. In what follows, we will implicitly identify an extension of  with its equivalent fragment of the two-sorted language. The question now is to what extent we can find a translation that goes the other way. To help answer this question, we can define a formal notion of expressivity relative to
with its equivalent fragment of the two-sorted language. The question now is to what extent we can find a translation that goes the other way. To help answer this question, we can define a formal notion of expressivity relative to  as follows:
as follows:
Definition 8
(Expressivity) Let \(\mathbf C \) be a class of models. We will say a set of  -formulas \(\varGamma \)C-expresses a set of
-formulas \(\varGamma \)C-expresses a set of  -formulas \(\varDelta \) if \(\varGamma \) is \(\mathbf C \)-equivalent to \(\varDelta \)—that is, for all \(\mathcal {M} \in \mathbf C \) and all \(g \in {\textsf {VA}} (\mathcal {M} )\), we have that \(\mathcal {M} ,g \Vdash \varGamma \) iff \(\mathcal {M} ,g \Vdash \varDelta \). If either \(\varGamma \) or \(\varDelta \) are singletons, we can drop the set brackets for readability. Where \(\mathcal {L}\) is a fragment of
-formulas \(\varDelta \) if \(\varGamma \) is \(\mathbf C \)-equivalent to \(\varDelta \)—that is, for all \(\mathcal {M} \in \mathbf C \) and all \(g \in {\textsf {VA}} (\mathcal {M} )\), we have that \(\mathcal {M} ,g \Vdash \varGamma \) iff \(\mathcal {M} ,g \Vdash \varDelta \). If either \(\varGamma \) or \(\varDelta \) are singletons, we can drop the set brackets for readability. Where \(\mathcal {L}\) is a fragment of  , we will say \(\varGamma \) is C-expressible in \(\mathcal {L}\) if there is a set of \(\mathcal {L}\)-formulas that \(\mathbf C \)-expresses \(\varGamma \). Where \(\mathcal {L}_1\) and \(\mathcal {L}_2\) are fragments of
, we will say \(\varGamma \) is C-expressible in \(\mathcal {L}\) if there is a set of \(\mathcal {L}\)-formulas that \(\mathbf C \)-expresses \(\varGamma \). Where \(\mathcal {L}_1\) and \(\mathcal {L}_2\) are fragments of  , we will say \(\mathcal {L}_2\)C-expresses\(\mathcal {L}_1\) or \(\mathcal {L}_1\) is C-included in \(\mathcal {L}_2\)—written as \(\mathcal {L}_1 \le _\mathbf C \mathcal {L}_2\)—if for any set of \(\mathcal {L}_1\)-formulas \(\varGamma \), there is a set of \(\mathcal {L}_2\)-formulas \(\varDelta \) that \(\mathbf C \)-expresses \(\varGamma \). We will write \(\mathcal {L}_1 <_\mathbf C \mathcal {L}_2\) if \(\mathcal {L}_1 \le _\mathbf C \mathcal {L}_2\) and \(\mathcal {L}_2 \nleq _\mathbf C \mathcal {L}_1\), and \(\mathcal {L}_1 \equiv _\mathbf C \mathcal {L}_2\) if \(\mathcal {L}_1 \le _\mathbf C \mathcal {L}_2\) and \(\mathcal {L}_2 \le _\mathbf C \mathcal {L}_1\).
, we will say \(\mathcal {L}_2\)C-expresses\(\mathcal {L}_1\) or \(\mathcal {L}_1\) is C-included in \(\mathcal {L}_2\)—written as \(\mathcal {L}_1 \le _\mathbf C \mathcal {L}_2\)—if for any set of \(\mathcal {L}_1\)-formulas \(\varGamma \), there is a set of \(\mathcal {L}_2\)-formulas \(\varDelta \) that \(\mathbf C \)-expresses \(\varGamma \). We will write \(\mathcal {L}_1 <_\mathbf C \mathcal {L}_2\) if \(\mathcal {L}_1 \le _\mathbf C \mathcal {L}_2\) and \(\mathcal {L}_2 \nleq _\mathbf C \mathcal {L}_1\), and \(\mathcal {L}_1 \equiv _\mathbf C \mathcal {L}_2\) if \(\mathcal {L}_1 \le _\mathbf C \mathcal {L}_2\) and \(\mathcal {L}_2 \le _\mathbf C \mathcal {L}_1\).
These definitions apply to extensions of  , viewed as fragments of
, viewed as fragments of  . Thus, where \(\varGamma \) is a set of
. Thus, where \(\varGamma \) is a set of  -formulas, and where \(\mathcal {L}\) is an extension of
-formulas, and where \(\mathcal {L}\) is an extension of  , we will say \(\varGamma \) is C-expressible in \(\mathcal {L}\) if there is a set of \(\mathcal {L}\)-formulas \(\varPhi \) such that \(\varGamma \) is \(\mathbf C \)-equivalent to
, we will say \(\varGamma \) is C-expressible in \(\mathcal {L}\) if there is a set of \(\mathcal {L}\)-formulas \(\varPhi \) such that \(\varGamma \) is \(\mathbf C \)-equivalent to  . Likewise, if \(\mathcal {L}_1\) and \(\mathcal {L}_2\) are extensions of first-order modal logic, we will write \(\mathcal {L}_1 \le _\mathbf C \mathcal {L}_2\) if for any set of \(\mathcal {L}_1\)-formulas \(\varPhi \), there is a set of \(\mathcal {L}_2\)-formulas \(\varPsi \) such that
. Likewise, if \(\mathcal {L}_1\) and \(\mathcal {L}_2\) are extensions of first-order modal logic, we will write \(\mathcal {L}_1 \le _\mathbf C \mathcal {L}_2\) if for any set of \(\mathcal {L}_1\)-formulas \(\varPhi \), there is a set of \(\mathcal {L}_2\)-formulas \(\varPsi \) such that  is \(\mathbf C \)-equivalent to
is \(\mathbf C \)-equivalent to  . Similarly for \(<_\mathbf C \) and \(\equiv _\mathbf C \).
. Similarly for \(<_\mathbf C \) and \(\equiv _\mathbf C \).
3 Bisimulation
To show that no formula (or set of formulas) of a modal language \(\mathcal {L}\) can express a certain formula \(\alpha \) of  , one must generally construct two models such that (a) they agree in \(\mathcal {L}\) on all \(\mathcal {L}\)-formulas (i.e., they are \(\mathcal {L}\)-equivalent), and (b) they disagree in
, one must generally construct two models such that (a) they agree in \(\mathcal {L}\) on all \(\mathcal {L}\)-formulas (i.e., they are \(\mathcal {L}\)-equivalent), and (b) they disagree in  on \(\alpha \). To make showing that such models are \(\mathcal {L}\)-equivalent easier, we can appeal to the notion of a bisimulation.Footnote 16 The notion of a bisimulation for first-order modal logic has not been discussed much until recently.Footnote 17 Below, we extend the notion of bisimulation in order to ensure modal equivalence for formulas involving two-dimensional operators.
on \(\alpha \). To make showing that such models are \(\mathcal {L}\)-equivalent easier, we can appeal to the notion of a bisimulation.Footnote 16 The notion of a bisimulation for first-order modal logic has not been discussed much until recently.Footnote 17 Below, we extend the notion of bisimulation in order to ensure modal equivalence for formulas involving two-dimensional operators.
A bisimulation is basically a back-and-forth game. In the standard back-and-forth game for (non-modal) first-order logic, there are two players, Abelard and Eloïse. Abelard aims to refute Eloïse’s attempt to show that the two models satisfy the same closed formulas. Abelard starts by picking an object from one of the models. Eloïse must then pick a matching object from the other model that satisfies the same atomic formulas. They continue in this manner, making sure at all times that the objects picked out so far from one model satisfy exactly the same atomic formulas that the objects picked out from the other model satisfy. If at any point the objects picked out from one model do not satisfy the same atomic formulas as the objects picked out from the other model, then Abelard wins. But if Eloïse manages to extend the game out for an infinite number of rounds, she wins. Two first-order models are elementarily equivalent (i.e., satisfy the same closed first-order formulas) if (but not only if) Eloïse has a winning strategy in this game for those models.
Likewise, two modal models satisfy the same  -formulas if Eloïse has a winning strategy for a back-and-forth game like the one above, with some modifications. In the modified game, the game is “located” at some world(s) in the two models. When Abelard picks an object from the model, he must pick an object that exists at the world where the game is located; likewise with Eloïse. Now the catch: Abelard can choose, at any time, to change the location of the game in either model to any accessible world from the current location. In order to keep playing, Eloïse must likewise pick a matching accessible world in the other model to relocate the game to. The game then relocates to those accessible worlds, and the game continues. As before, if the objects that have been picked out from one model do not satisfy the same atomic formulas at the game’s current location that are satisfied by the objects picked out from the other model, then Abelard wins. But if Eloïse manages to extend the game out for an infinite number of rounds, she wins. Two worlds in two models will satisfy the same
-formulas if Eloïse has a winning strategy for a back-and-forth game like the one above, with some modifications. In the modified game, the game is “located” at some world(s) in the two models. When Abelard picks an object from the model, he must pick an object that exists at the world where the game is located; likewise with Eloïse. Now the catch: Abelard can choose, at any time, to change the location of the game in either model to any accessible world from the current location. In order to keep playing, Eloïse must likewise pick a matching accessible world in the other model to relocate the game to. The game then relocates to those accessible worlds, and the game continues. As before, if the objects that have been picked out from one model do not satisfy the same atomic formulas at the game’s current location that are satisfied by the objects picked out from the other model, then Abelard wins. But if Eloïse manages to extend the game out for an infinite number of rounds, she wins. Two worlds in two models will satisfy the same  -formulas if Eloïse has a winning strategy in this game, where the game starts at those two worlds. More variations arise when different extensions of
-formulas if Eloïse has a winning strategy in this game, where the game starts at those two worlds. More variations arise when different extensions of  are considered. More precisely:
are considered. More precisely:
Definition 9
(Bisimulation) Let \(\mathcal {M} \) and \(\mathcal {N} \) be models. An  -bisimulation between\(\mathcal {M} \)and\(\mathcal {N} \) is a nonempty variably polyadic relation Z such that for all \(w,v \in W^\mathcal {M} \), all \(w',v' \in W^\mathcal {N} \), all finite \(\overline{a} \in D^\mathcal {M} \), and all finite \(\overline{b} \in D^\mathcal {N} \) where \(\left| \overline{a} \right| = \left| \overline{b} \right| \), we have that \(Z(w,v,\overline{a};w',v',\overline{b})\) only if:
-bisimulation between\(\mathcal {M} \)and\(\mathcal {N} \) is a nonempty variably polyadic relation Z such that for all \(w,v \in W^\mathcal {M} \), all \(w',v' \in W^\mathcal {N} \), all finite \(\overline{a} \in D^\mathcal {M} \), and all finite \(\overline{b} \in D^\mathcal {N} \) where \(\left| \overline{a} \right| = \left| \overline{b} \right| \), we have that \(Z(w,v,\overline{a};w',v',\overline{b})\) only if:
-
(Atomic)
 :
: 
-
(Zig)

-
(Zag)

-
(Forth)

-
(Back)
 .
.
We may write “\(\mathcal {M} ,w,v,\overline{a} \leftrightarrows \mathcal {N} ,w',v',\overline{b} \)” (where possibly \(\left| \overline{a} \right| = \left| \overline{b} \right| = 0\)) to indicate that \(\mathcal {M} ,w,v,\overline{a} \) and \(\mathcal {N} ,w',v',\overline{b} \) are  -bisimilar, i.e., that there is a bisimulation Z between \(\mathcal {M} \) and \(\mathcal {N} \) such that \(Z(w,v,\overline{a};w',v',\overline{b})\).
-bisimilar, i.e., that there is a bisimulation Z between \(\mathcal {M} \) and \(\mathcal {N} \) such that \(Z(w,v,\overline{a};w',v',\overline{b})\).
The notion of an  -bisimulation between\(\mathcal {M} \)and\(\mathcal {N} \) is defined similarly, except one must add the corresponding condition(s) below:
-bisimulation between\(\mathcal {M} \)and\(\mathcal {N} \) is defined similarly, except one must add the corresponding condition(s) below:

We may write “\(\mathcal {M} ,w,v,\overline{a} \leftrightarrows _{\mathcal {L}} \mathcal {N} ,w',v',\overline{b} \)” to indicate that \(\mathcal {M} ,w,v,\overline{a} \) and \(\mathcal {N} ,w',v',\overline{b} \) are \(\mathcal {L}\)-bisimilar. We may also sometimes write “ ”, where
”, where  , for readability.
, for readability.
Here are the various conditions phrased in terms of games. (Atomic) says that Eloïse loses unless \(\overline{a} \) satisfy the same atomic formulas in \(\mathcal {M} ,w,v\) that \(\overline{b} \) satisfy in \(\mathcal {N} ,w',v'\). (Zig) says that if Abelard decides to move the game to \(\left\langle w,u\right\rangle \) in \(\mathcal {M} \) where \(u \in R^\mathcal {M} [v]\), Eloïse must choose a \(u' \in R^\mathcal {N} [v']\) and relocate the game in \(\mathcal {N} \) to \(\left\langle w',u'\right\rangle \) to continue. Likewise for (Zag). (Forth) says that if Abelard picks an object \(a'\) from v, Eloïse must pick an object \(b'\) from \(v'\) to match it with. Likewise for (Back). (Eq) says that if Abelard picks an object that was already chosen, Eloïse must pick the matching object. (Ex) says that the objects picked have to agree in terms of existence, even when the game relocates. (Act) says that Abelard can force the game to relocate to \(\left\langle w,w\right\rangle \) and \(\left\langle w',w'\right\rangle \). Likewise for (Diag). The other clauses are as before, except with respect to different domains and relations.
Definition 10
(Modal equivalence) \(\mathcal {M} ,w,v,\overline{a} \) and \(\mathcal {N} ,w',v',\overline{b} \) are  -equivalent or modally equivalent if for all \(\mathcal {L}\)-formulas \(\varphi (\overline{x})\) (where \(\left| \overline{x} \right| \le \left| \overline{a} \right| \)), \(\mathcal {M} ,w,v \Vdash \varphi [\overline{a} ]\) iff \(\mathcal {N} ,w',v' \Vdash \varphi [\overline{b} ]\). We may write “\(\mathcal {M} ,w,v,\overline{a} \equiv _\mathcal {L}\mathcal {N} ,w',v',\overline{b} \)” to indicate that \(\mathcal {M} ,w,v,\overline{a} \) and \(\mathcal {N} ,w',v',\overline{b} \) are \(\mathcal {L}\)-equivalent.
-equivalent or modally equivalent if for all \(\mathcal {L}\)-formulas \(\varphi (\overline{x})\) (where \(\left| \overline{x} \right| \le \left| \overline{a} \right| \)), \(\mathcal {M} ,w,v \Vdash \varphi [\overline{a} ]\) iff \(\mathcal {N} ,w',v' \Vdash \varphi [\overline{b} ]\). We may write “\(\mathcal {M} ,w,v,\overline{a} \equiv _\mathcal {L}\mathcal {N} ,w',v',\overline{b} \)” to indicate that \(\mathcal {M} ,w,v,\overline{a} \) and \(\mathcal {N} ,w',v',\overline{b} \) are \(\mathcal {L}\)-equivalent.
Theorem 11
(Bisimulation implies modal equivalence) Where  , if \(\mathcal {M} ,w,v,\overline{a} \leftrightarrows _{\mathcal {L}} \mathcal {N} ,w',v',\overline{b} \), then \(\mathcal {M} ,w,v,\overline{a} \equiv _{\mathcal {L}} \mathcal {N} ,w',v',\overline{b} \).
, if \(\mathcal {M} ,w,v,\overline{a} \leftrightarrows _{\mathcal {L}} \mathcal {N} ,w',v',\overline{b} \), then \(\mathcal {M} ,w,v,\overline{a} \equiv _{\mathcal {L}} \mathcal {N} ,w',v',\overline{b} \).
In general, modal equivalence does not imply bisimulation.Footnote 18 However, it does when infinitary conjunction is present in the language. Consider the symbol  with the following formation rule: if \(\varPhi \) is a set of well-formed formulas (of any size), then
with the following formation rule: if \(\varPhi \) is a set of well-formed formulas (of any size), then  is a well-formed formula. Then it can be shown that
is a well-formed formula. Then it can be shown that  iff
iff  .Footnote 19 Thus, bisimulation is equivalent to infinitary modal equivalence. No bisimulation clauses need to be added for
.Footnote 19 Thus, bisimulation is equivalent to infinitary modal equivalence. No bisimulation clauses need to be added for  .
.
Adding infinitary conjunction to the language clearly increases the expressive power of the language. For example, one can regiment the sentence “There are infinitely many rich people” as  , where
, where  is short for the formula
is short for the formula  , and
, and  is short for the formula
is short for the formula  . However, infinitary conjunction does not increase the expressive power enough to overcome the particular expressive limitations discussed here, so we set it aside in what follows.
. However, infinitary conjunction does not increase the expressive power enough to overcome the particular expressive limitations discussed here, so we set it aside in what follows.
Now, recall the definition of expressibility (Definition 8).
Corollary 12
(Translation implies invariance) Let \(\alpha (\overline{x};s,t)\) be an  -formula. If
-formula. If  , and if \(\alpha \) is equivalent to the translation of some set of
, and if \(\alpha \) is equivalent to the translation of some set of  -formulas, then \(\mathcal {M} \vDash \alpha [\overline{a};w,v]\) iff \(\mathcal {N} \vDash \alpha [\overline{b};w',v']\). In other words, if \(\mathcal {M} ,w,v,\overline{a} \) and \(\mathcal {N} ,w',v',\overline{b} \) are
-formulas, then \(\mathcal {M} \vDash \alpha [\overline{a};w,v]\) iff \(\mathcal {N} \vDash \alpha [\overline{b};w',v']\). In other words, if \(\mathcal {M} ,w,v,\overline{a} \) and \(\mathcal {N} ,w',v',\overline{b} \) are  -bisimilar, but they disagree on \(\alpha \), then \(\alpha \) is not expressible as a set of
-bisimilar, but they disagree on \(\alpha \), then \(\alpha \) is not expressible as a set of  -formulas.
-formulas.
Corollary 12 says that if a  -formula is equivalent to the translation of an \(\mathcal {L}\)-formula (or a set of \(\mathcal {L}\)-formulas), then it is preserved under \(\mathcal {L}\)-bisimulations. As in propositional modal logic, the converse also holds (see Appendix 1 for the proof).Footnote 20
-formula is equivalent to the translation of an \(\mathcal {L}\)-formula (or a set of \(\mathcal {L}\)-formulas), then it is preserved under \(\mathcal {L}\)-bisimulations. As in propositional modal logic, the converse also holds (see Appendix 1 for the proof).Footnote 20
Theorem 13
(van Benthem Characterization Theorem) Let \(\alpha (\overline{x};s,t)\) be an  -formula such that \(\mathcal {M} \vDash \alpha [\overline{a};w,v]\) iff \(\mathcal {N} \vDash \alpha [\overline{b};w',v']\) given that \(\mathcal {M} ,w,v,\overline{a} \leftrightarrows _{\mathcal {L}} \mathcal {N} ,w',v',\overline{b} \). Then \(\alpha \) is equivalent to the translation of some \(\mathcal {L}\)-formula.
-formula such that \(\mathcal {M} \vDash \alpha [\overline{a};w,v]\) iff \(\mathcal {N} \vDash \alpha [\overline{b};w',v']\) given that \(\mathcal {M} ,w,v,\overline{a} \leftrightarrows _{\mathcal {L}} \mathcal {N} ,w',v',\overline{b} \). Then \(\alpha \) is equivalent to the translation of some \(\mathcal {L}\)-formula.
This together with Theorem 11 implies that \(\mathcal {L}\) is just the \(\mathcal {L}\)-bisimulation invariant fragment of  . For our purposes, however, Corollary 12 will be the key result in generating the inexpressibility results below.
. For our purposes, however, Corollary 12 will be the key result in generating the inexpressibility results below.
4 Inexpressibility
While Corollary 12 and Theorem 13 exactly characterize the expressive power of  and its various extensions, the characterization is a bit abstract, and it does not automatically tell us what the expressive power of these extensions are relative to one another. We now turn to illustrating the expressive limitations of
and its various extensions, the characterization is a bit abstract, and it does not automatically tell us what the expressive power of these extensions are relative to one another. We now turn to illustrating the expressive limitations of  and its extensions with concrete examples. Note that all of our models in this section fall in the class UD, so these inexpressibility results therefore apply to any class that includes UD.
and its extensions with concrete examples. Note that all of our models in this section fall in the class UD, so these inexpressibility results therefore apply to any class that includes UD.
To warm up, we start by showing that (E) is not expressible in  . Recall (E) says that there could have been things other than there are, which is formalized in
. Recall (E) says that there could have been things other than there are, which is formalized in  as (3):
as (3):

The proof strategy will always be the same: construct two modal models that are bisimilar, but that disagree on (3). Because we do not have \(\approx \) in  by default, this is actually very easy. Let \(\mathcal {E} = \left\langle W,R,F,D,\delta ,I\right\rangle \), where
by default, this is actually very easy. Let \(\mathcal {E} = \left\langle W,R,F,D,\delta ,I\right\rangle \), where  , R and F are universal,
, R and F are universal,  , and \(I(P,u) = \emptyset \). Let \(\mathcal {E} ' = \left\langle W,R,F,D',\delta ',I\right\rangle \), where everything is as in \(\mathcal {E} \), except
, and \(I(P,u) = \emptyset \). Let \(\mathcal {E} ' = \left\langle W,R,F,D',\delta ',I\right\rangle \), where everything is as in \(\mathcal {E} \), except  . See Fig. 1 for a picture.
. See Fig. 1 for a picture.
It is easy to see that w in \(\mathcal {E} \) does not satisfy (3): every possible object exists at w. However, w in \(\mathcal {E} '\) does satisfy (3): b is a possible object that does not exist at w. So \(\mathcal {E},w\) and \(\mathcal {E} ',w\) disagree on (3). So we just need to show that \(\mathcal {E},w,w \leftrightarrows \mathcal {E} ',w,w\). In fact, in this case, we can just take Z to map every world to every world, and every object to every object any number of times. To show this is a bisimulation, we just check each of the clauses from Definition 9 holds, which is easy to do. One might initially think that we will run into problems in trying to show (Back) holds; for if we consider Z(w, v, a; w, v, a), and we decide to pick b from \(\delta '(v)\), then we cannot pick b from \(\delta (v)\) to match it with. But since a and b do not disagree on any predicates, and since \(\approx \) is not present in the language,  cannot tell that a and b are distinct objects anyway. We do not have to match a to a and b to b every time. We can just as well match b in \(\delta '(v)\) with a in \(\delta (v)\).
cannot tell that a and b are distinct objects anyway. We do not have to match a to a and b to b every time. We can just as well match b in \(\delta '(v)\) with a in \(\delta (v)\).
What made this proof easy was the absence of \(\approx \). Now we will show that even  cannot express (E).Footnote 21 Consider first \(\mathcal {E} _1 = \left\langle W_1,W_1^2,W_1^2,\mathbb {N} ,\delta _1,I_1\right\rangle \), where the global domain is \(\mathbb {N} \) and the accessibility relations are both universal. For each nonempty finite or cofinite \(S \subseteq \mathbb {N} \), there is a world \(w_S \in W_1\) such that \(\delta _1(w_S) = S\). No other worlds are in \(W_1\). Again, the extension of all non-logical predicates will be empty at all worlds. The second model
cannot express (E).Footnote 21 Consider first \(\mathcal {E} _1 = \left\langle W_1,W_1^2,W_1^2,\mathbb {N} ,\delta _1,I_1\right\rangle \), where the global domain is \(\mathbb {N} \) and the accessibility relations are both universal. For each nonempty finite or cofinite \(S \subseteq \mathbb {N} \), there is a world \(w_S \in W_1\) such that \(\delta _1(w_S) = S\). No other worlds are in \(W_1\). Again, the extension of all non-logical predicates will be empty at all worlds. The second model  is similar to the first, but now the global domain contains an additional object \(\infty \). For each nonempty set S that is either finite or cofinite in
is similar to the first, but now the global domain contains an additional object \(\infty \). For each nonempty set S that is either finite or cofinite in  , there is a world \(w_S \in W_2\) such that \(\delta _2(w_S) = S\). See Fig. 2 for a picture.
, there is a world \(w_S \in W_2\) such that \(\delta _2(w_S) = S\). See Fig. 2 for a picture.
Since \(\delta _1(w_\mathbb {N} ) = \mathbb {N} = D\), \(w_\mathbb {N} \) in \(\mathcal {E} _1\) does not satisfy (3). But \(w_\mathbb {N} \) in \(\mathcal {E} _2\) does satisfy (3), since \(\infty \notin \delta _2(w_\mathbb {N} )\). So \(\mathcal {E} _1,w_\mathbb {N} \) and \(\mathcal {E} _2,w_\mathbb {N} \) disagree on (3). So we just need to show that \(\mathcal {E} _1,w_\mathbb {N} ,w_\mathbb {N} \leftrightarrows _{\approx } \mathcal {E} _2,w_\mathbb {N} ,w_\mathbb {N} \). Constructing the bisimulation is fairly straightforward (albeit tedious) once we work out what Eloïse’s winning strategy is. The construction of the bisimulation is given in Appendix 2, but the idea in terms of games is sketched below. To help describe the proof, let us introduce the following useful definition:
Definition 14
(Partial isomorphism) A partial isomorphism between\(\mathcal {M} ,w,v,\overline{a} \)and\(\mathcal {N} ,w',v',\overline{b} \) is a finite partial map \(\rho :D \rightarrow D'\) such that \(\rho (a_i) = b_i\) for \(i \le \left| \overline{a} \right| \) and:
-
(Predicate)
 :
: 

We write \(\mathcal {M} ,w,v,\overline{a} \simeq \mathcal {N} ,w',v',\overline{b} \) to indicate that there is a partial isomorphism between \(\mathcal {M} ,w,v,\overline{a} \) and \(\mathcal {N} ,w',v',\overline{b} \).
To say that \(\mathcal {M} ,w,v,\overline{a} \simeq \mathcal {N} ,w',v',\overline{b} \) is essentially to say that Eloïse can continue the game (i.e., Abelard has not won yet) at this stage of the game (even with \(\approx \) present).
Proposition 15
(Inexpressibility of (E)) \(\mathcal {E} _1,w_\mathbb {N} ,w_\mathbb {N} \leftrightarrows _{\approx } \mathcal {E} _2,w_\mathbb {N} ,w_\mathbb {N} \). But \(\mathcal {E} _2 \vDash \) (3)\([w_\mathbb {N} ]\) while \(\mathcal {E} _1 \nvDash \) (3)\([w_\mathbb {N} ]\). Hence, (3) is not expressible in  .
.
Proof
(Sketch) Our game starts at \(\mathcal {E} _1,w_\mathbb {N} ,w_\mathbb {N} \) and \(\mathcal {E} _2,w_\mathbb {N} ,w_\mathbb {N} \). We will describe a strategy for Eloïse such that, at every stage of the game, which we will represent as \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \), we have that \(\mathcal {E} _1,w_\mathbb {N} ,v_1,\overline{a} \simeq \mathcal {E} _2,w_\mathbb {N} ,v_2,\overline{b} \) (in other words: Eloïse can continue the game at every stage of the game). We construct the strategy by induction on Abelard’s move.
Vacuously, \(\mathcal {E} _1,w_\mathbb {N} ,w_\mathbb {N} \simeq \mathcal {E} _2,w_\mathbb {N} ,w_\mathbb {N} \). So suppose \(\left\langle w_\mathbb {N} ,v_1,\overline{a} '; w_\mathbb {N} ,v_2,\overline{b} \right\rangle \) is the current stage of the game, where \(\mathcal {E} _1,w_\mathbb {N} ,v_1,\overline{a} \simeq \mathcal {E} _2,w_\mathbb {N} ,v_2,\overline{b} \) and where \(\left| \delta _1(v_1) \right| = \left| \delta _2(v_2) \right| \), i.e., the size of \(\delta _1(v_1)\) and \(\delta _2(v_2)\) is the same. Abelard can decide either to pick an object from \(\delta _1(v_1)\) or \(\delta _2(v_2)\), or to relocate the game. By the fact that \(\mathcal {E} _1,w_\mathbb {N} ,v_1,\overline{a} \simeq \mathcal {E} _2,w_\mathbb {N} ,v_2,\overline{b} \) and that \(\left| \delta _1(v_1) \right| = \left| \delta _2(v_2) \right| \), it follows that  . So if Abelard decides to pick a new object from one of \(v_1\) and \(v_2\), Eloïse can always pick a matching object from the local domain of the other world to continue the game.
. So if Abelard decides to pick a new object from one of \(v_1\) and \(v_2\), Eloïse can always pick a matching object from the local domain of the other world to continue the game.
Suppose instead that Abelard decides to relocate the game. Eloïse should then choose a world in the other model so that the following holds of the new locations \(u_1\) and \(u_2\): (i) \(\left| \delta _1(u_1) \right| = \left| \delta _2(u_2) \right| \), and (ii) \(a_i \in \delta _1(u_1)\) iff \(b_i \in \delta _2(u_2)\). Since there are only finitely many \(\overline{a} \) at any given stage of the game, this will always be possible. And as long as (ii) holds, we will have that \(\mathcal {M} ,w_\mathbb {N} ,u_1,\overline{a} \simeq \mathcal {M} ,w_\mathbb {N} ,u_2,\overline{b} \). \(\square \)
Notice that this proof will fail under a variety of extensions of  . This is easy to see if the extension can express (3) directly, as does
. This is easy to see if the extension can express (3) directly, as does  and
and  :
:


But it is also instructive to see where the proof for Proposition 15 fails for these extensions. If we were to add \(\Pi {}\), then Abelard would be allowed to pick any object from the global domain of either model. In that case, partial isomorphism is no longer enough to guarantee that Eloïse can continue in this game. For Eloïse to continue the game at \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \), we also need to ensure that \(\left| \mathbb {N} - \delta _1(v_1) \right| = \left| \mathbb {N} ^\infty - \delta _2(v_2) \right| \). Otherwise, if say \(\left| \mathbb {N} - \delta _1(v_1) \right| < \left| \mathbb {N} ^\infty - \delta _2(v_2) \right| \), Abelard could keep picking objects from \(\mathbb {N} - \delta _1(v_1)\) until he ran out (since \(\left| \mathbb {N} - \delta _1(v_1) \right| < \left| \mathbb {N} ^\infty - \delta _2(v_2) \right| \) would imply that \(\mathbb {N} - \delta _1(v_1)\) is finite). Then he could pick whatever unmatched objects remain in \(\mathbb {N} ^\infty - \delta _2(v_2)\). In response, Eloïse would be forced to match Abelard’s object either with an object not in \(\mathbb {N} - \delta _1(v_1)\), thus violating (Ex) from Definition 9, or with an object in \(\mathbb {N} - \delta _1(v_1)\) that was already chosen, thus matching a previously unmatched object to a previously matched object and violating (Eq). So we need to be able to ensure that \(\left| \mathbb {N} - \delta _1(v_1) \right| = \left| \mathbb {N} ^\infty - \delta _2(v_2) \right| \) at every stage of the game, which we can do except at one very crucial point, viz., the beginning: \(\left| \mathbb {N} - \delta _1(w_\mathbb {N} ) \right| \ne \left| \mathbb {N} ^\infty - \delta _2(w_\mathbb {N} ) \right| \). In other words, Abelard can force a win just by picking \(\infty \) from \(D_2\), leaving Eloïse unable to pick a matching object while meeting (Ex). Without \(\Pi {}\), this winning strategy for Abelard is blocked.
If we add \(@\), then Abelard can force the location of the game in both models to move back to \(w_\mathbb {N} \). In the proof of Proposition 15 above, it is crucial that Eloïse can choose to relocate to a world similar enough to the actual world. For instance, suppose on round 1, Abelard chooses to move to  in \(\mathcal {E} _2\). Then Eloïse must choose to move to some
in \(\mathcal {E} _2\). Then Eloïse must choose to move to some  in \(\mathcal {E} _1\)—let us say
in \(\mathcal {E} _1\)—let us say  . Abelard can then choose \(\infty \) from
. Abelard can then choose \(\infty \) from  , forcing Eloïse to choose 5. At this point, if Abelard decided to relocate the game back to \(w_\mathbb {N} \) in both models, then he could choose 5 from \(\mathcal {E} _1\), and Eloïse would lose by violating (Eq). But without \(@\), while Abelard can choose to relocate the game to \(w_\mathbb {N} \) in \(\mathcal {E} _2\), say, Eloïse does not have to relocate the game to \(w_\mathbb {N} \) in \(\mathcal {E} _1\); she can, for instance, pick to relocate to
, forcing Eloïse to choose 5. At this point, if Abelard decided to relocate the game back to \(w_\mathbb {N} \) in both models, then he could choose 5 from \(\mathcal {E} _1\), and Eloïse would lose by violating (Eq). But without \(@\), while Abelard can choose to relocate the game to \(w_\mathbb {N} \) in \(\mathcal {E} _2\), say, Eloïse does not have to relocate the game to \(w_\mathbb {N} \) in \(\mathcal {E} _1\); she can, for instance, pick to relocate to  in \(\mathcal {E} _1\).
in \(\mathcal {E} _1\).
Let us now turn to showing a more difficult inexpressibility result, viz., that (R) is not expressible in  .Footnote 22 Recall (R) says that everyone who is actually rich could have been poor, which is formalized in
.Footnote 22 Recall (R) says that everyone who is actually rich could have been poor, which is formalized in  as (4):
as (4):

Let \(\mathbb {N} ^- \,{:}{=}\, \mathbb {Z} - \mathbb {N} \). We let \(\mathcal {R} _1 = \left\langle W_1,R_1,F_1,D_1,\delta _1,I_1\right\rangle \) and \(\mathcal {R} _2 = \left\langle W_2,R_2,F_2,D_2,\delta _2,I_2\right\rangle \), where \(D_1 = D_2 = \mathbb {Z} \) and the accessibility relations are universal for both models. There is a world \(w \in W_1\) that will act as our actual world, where every positive integer is rich (top half of circle), and every negative integer is poor (bottom half of circle). For each nonempty finite subset \(S \subseteq \mathbb {N} \), there is a world \(v_S \in W_1\) where the members of S do not exist, and otherwise the rich and the poor are flipped with respect to w; so at \(v_S\), the negative integers are rich, and the positive integers not in S are poor, and the positive integers in S do not exist. The extension of all other predicates is empty. The only difference between \(\mathcal {R} _1\) and \(\mathcal {R} _2\) is that \(\mathcal {R} _2\) includes an additional world \(v_\emptyset \in W_2\), where no integer fails to exist, and where the rich and poor are flipped with respect to w. See Fig. 3 for a picture.
\(\mathcal {R} _2 \vDash \) (4)[w], since \(v_\emptyset \) is the world where everyone rich in w is poor. But \(\mathcal {R} _1 \nvDash \) (4)[w], since in every world where something that is rich in w is poor, something that is rich in w does not exist (and hence is not poor). And once again, \(\mathcal {R} _1,w,w \leftrightarrows _{\approx ,@} \mathcal {R} _2,w,w\). The details are left to Appendix 2, but a proof is sketched in terms of games below.
Proposition 16
(Inexpressibility of (R)) \(\mathcal {R} _1,w,w \leftrightarrows _{\approx ,@} \mathcal {R} _2,w,w\). But \(\mathcal {R} _2 \vDash \) (4)[w] even though \(\mathcal {R} _1 \nvDash \) (4)[w]. Hence, (4) is not expressible in  .
.
Proof
(Sketch) Our game starts at \(\mathcal {R} _1,w,w\) and \(\mathcal {R} _2,w,w\). As before, we will describe a winning strategy for Eloïse such that, at every stage \(\left\langle w,v,\overline{a};w,v',\overline{b} \right\rangle \) of the  -bisimulation game, \(\mathcal {R} _1,w,v,\overline{a} \simeq \mathcal {R} _2,w,v',\overline{b} \).
-bisimulation game, \(\mathcal {R} _1,w,v,\overline{a} \simeq \mathcal {R} _2,w,v',\overline{b} \).
Again, vacuously, \(\mathcal {R} _1,w,w \simeq \mathcal {R} _2,w,w\). So suppose \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \) is the current stage of the game, where \(\mathcal {R} _1,w,u_1,\overline{a} \simeq \mathcal {R} _2,w,u_2,\overline{b} \) and where \(a_i\) is positive (i.e., in \(\mathbb {N} \)) iff \(b_i\) is positive. We will show that this continues to be true regardless of Abelard’s move. If Abelard decides to pick a new object from \(\delta _1(u_1)\) or \(\delta _2(u_2)\), it will either be positive or negative. Since there are infinitely many of both, Eloïse will have no trouble picking a new one; and since there was a partial isomorphism between \(u_1\) and \(u_2\), Eloïse only needs the new objects to agree on their sign.
Suppose instead that Abelard decides to relocate the game. If he decides to move the game in both models back to w, since \(a_i\) is positive iff \(b_i\) is positive, we will have \(\mathcal {R} _1,w,w,\overline{a} \simeq \mathcal {R} _2,w,w,\overline{b} \). (Likewise, if Abelard chooses to relocate to w in one model but lets Eloïse choose the other new location, she should still choose w for the reason above.) If he decides to relocate to some \(v_S\) where \(S \ne \emptyset \) in, say, \(\mathcal {R} _1\), let T be any set with the same cardinality as S such that \(a_i \in S\) iff \(b_i \in T\). Since there are only finitely many \(a_i\)s, there will always be such a T. Eloïse can choose to relocate to \(v_T\), and again, since \(a_i\) is positive iff \(b_i\) is positive, \(\mathcal {R} _1,w,v_S,\overline{a} \simeq \mathcal {R} _2,w,v_T,\overline{b} \). Likewise if Abelard chooses to relocate to some \(v_S\) in \(\mathcal {R} _2\).
The tricky part is determining what to do when Abelard decides to relocate to \(v_\emptyset \) in \(\mathcal {R} _2\). But since there are only finitely many \(a_i\)s, Eloïse can just choose a \(v_S\) where  . Then it will still be the case that \(\mathcal {R} _1,w,v_S,\overline{a} \simeq \mathcal {R} _2,w,v_\emptyset ,\overline{b} \). So no matter where Abelard decides to relocate, Eloïse can continue the game. \(\square \)
. Then it will still be the case that \(\mathcal {R} _1,w,v_S,\overline{a} \simeq \mathcal {R} _2,w,v_\emptyset ,\overline{b} \). So no matter where Abelard decides to relocate, Eloïse can continue the game. \(\square \)
Notice that the proof fails if we try to add either \(\Pi {}\), \({\mathop {\downarrow }}\), or \(\mathcal {F}\). It is easy to see this for \(\Pi {}\), since we can express (4) as (2):
To see where the proof above fails for  , consider what happens when Abelard decides to move from \(u_2\) to \(v_\emptyset \) in \(\mathcal {R} _2\). Eloïse will try to match that move in \(\mathcal {R} _1\) by moving from \(u_1\) to some \(v_S\) where
, consider what happens when Abelard decides to move from \(u_2\) to \(v_\emptyset \) in \(\mathcal {R} _2\). Eloïse will try to match that move in \(\mathcal {R} _1\) by moving from \(u_1\) to some \(v_S\) where  . But now, because of \(\Pi {}\), Abelard is free to pick any object in S (and hence not in \(\delta _1(v_S)\)), forcing Eloïse to match it with an object in \(\delta _2(v_\emptyset )\) (since \(\delta _2(v_\emptyset ) = D_2 = \mathbb {Z} \)), and hence violating (Atomic).
. But now, because of \(\Pi {}\), Abelard is free to pick any object in S (and hence not in \(\delta _1(v_S)\)), forcing Eloïse to match it with an object in \(\delta _2(v_\emptyset )\) (since \(\delta _2(v_\emptyset ) = D_2 = \mathbb {Z} \)), and hence violating (Atomic).
As for \({\mathop {\downarrow }}\) and \(\mathcal {F}\), the models above disagree on both of these formulas:


In particular, \(\mathcal {R} _2,w,w \vDash \) (8) and \(\mathcal {R} _2,w,w \vDash \) (9) (take \(v_\emptyset \) to be the world we shift to by \(\Diamond {\mathop {\downarrow }}\) or \(\left\langle \mathcal {F}\right\rangle @\)), but \(\mathcal {R} _1,w,w \nvDash \) (8) and \(\mathcal {R} _1,w,w \nvDash \) (9). While this does not show that (4) can be expressed as an  -formula, it does show \(\mathcal {R} _1\) and \(\mathcal {R} _2\) cannot be used to settle the matter. Using modified models, however, it is possible to settle the matter in the negative: (4) is not even UD-expressible in
-formula, it does show \(\mathcal {R} _1\) and \(\mathcal {R} _2\) cannot be used to settle the matter. Using modified models, however, it is possible to settle the matter in the negative: (4) is not even UD-expressible in  (see Appendix 3).Footnote 23
(see Appendix 3).Footnote 23
As a final example, we will show that even  cannot express (NR), which is formalized as (5):
cannot express (NR), which is formalized as (5):

Consider two models \(\mathcal {N} _1\! =\! \left\langle W_1,R_1,F_1,D_1,\delta _1,I_1\right\rangle \) and \(\mathcal {N} _2 \!=\! \left\langle W_2,R_2,F_2,D_2,\delta _2,I_2\right\rangle \). Again, \(D_1 = D_2 = \mathbb {Z} \) and the accessibility relations are universal. However, now all of \(\mathbb {Z} \) exists at every world in either model. Our actual world is z, an egalitarian world where no integer is either rich or poor. For every finite set \(S \subseteq \mathbb {N} \) and finite set \(T \subseteq \mathbb {N} ^-\), there is a world \(w_S^T\) where all the integers in \((\mathbb {N} - S) \cup T\) are rich, while all the integers in \((\mathbb {N} ^- - T) \cup S\) are poor (so our old w is now just \(w_\emptyset ^\emptyset \)). And for every nonempty finite set \(S \subseteq \mathbb {N} \), and every finite set \(T \subseteq \mathbb {N} ^-\), there is a world \(v_S^T\) like before, where the rich and poor are flipped with respect to \(w_S^T\). The only difference between \(\mathcal {N} _1\) and \(\mathcal {N} _2\) is the presence of worlds of the form \(v_\emptyset ^T\) in \(\mathcal {N} _2\). See Fig. 4 for a picture.Footnote 24
\(\mathcal {N} _1,z,z\) and \(\mathcal {N} _2,z,z\) both agree that (4) is true, since nothing in z is rich. But they disagree on whether (5) is true; without the presence of \(v_\emptyset ^T\), there is no world where everyone rich in \(w_\emptyset ^\emptyset \) (i.e., \(\mathbb {N} \)) is poor. Thus, \(\mathcal {N} _1 \nvDash \) (5)[z] but \(\mathcal {N} _2 \vDash \) (5)[z]. Furthermore:
Proposition 17
(Inexpressibility of (NR)) \(\mathcal {N} _1,z,z \leftrightarrows _{\approx ,@,\Pi {}} \mathcal {N} _2,z,z\). But \(\mathcal {N} _2 \vDash \) (5)[z] while \(\mathcal {N} _1 \nvDash \) (5)[z]. Hence, (5) is not expressible in  .
.
Proof
(Sketch) Our game starts at \(\mathcal {N} _1,z,z\) and \(\mathcal {N} _2,z,z\). We will describe a winning strategy for Eloïse such that at every stage of the game \(\left\langle z,u_1,\overline{a};z,u_2,\overline{b} \right\rangle \), not only do we have \(\mathcal {N} _1,z,u_1,\overline{a} \simeq \mathcal {N} _2,u_2,\overline{b} \), but also we have \(u_1 = z\) iff \(u_2 = z\), and we have \(u_1 = w^{T_1}_{S_1}\) for some \(S_1\) and \(T_1\) iff \(u_2 = w^{T_2}_{S_2}\) for some \(S_2\) and \(T_2\). Clearly this holds for the initial stage \(\left\langle z,z;z,z\right\rangle \). So suppose \(\left\langle z,u_1,\overline{a};z,u_2,\overline{b} \right\rangle \) is such a stage.
Because for each world u and each  , \(I_k({\textsf {Rich}},u)\) and \(I_k({\textsf {Poor}},u)\) are empty or infinite, the back-and-forth step is easy. So suppose Abelard decides to relocate the game in \(\mathcal {N} _1\). If he relocates to z, then Eloïse should also just relocate to z in \(\mathcal {N} _1\). Suppose now Abelard decides to relocate to some \(w^{T_1}_{S_1}\) in \(\mathcal {N} _1\). Define
, \(I_k({\textsf {Rich}},u)\) and \(I_k({\textsf {Poor}},u)\) are empty or infinite, the back-and-forth step is easy. So suppose Abelard decides to relocate the game in \(\mathcal {N} _1\). If he relocates to z, then Eloïse should also just relocate to z in \(\mathcal {N} _1\). Suppose now Abelard decides to relocate to some \(w^{T_1}_{S_1}\) in \(\mathcal {N} _1\). Define  and
and  . Then one can check that \(\mathcal {N} _1,z,w^{T_1}_{S_1}, \overline{a} \simeq \mathcal {N} _2,z,w^{T_2}_{S_2}, \overline{b} \). For instance, suppose \(a_i \in I_1({\textsf {Rich}},w^{T_1}_{S_1})\). Either \(b_i \in \mathbb {N} \) or \(b_i \in \mathbb {N} ^-\). If \(b_i \in \mathbb {N} \), then \(b_i \notin S_2\), so \(b_i \in I_2({\textsf {Rich}},w^{T_2}_{S_2})\). If \(b_i \in \mathbb {N} ^-\), then \(b_i \in T_2\), so \(b_i \in I_2({\textsf {Rich}},w^{T_2}_{S_2})\). Likewise, if \(a_i \in I_1({\textsf {Poor}},w^{T_1}_{S_1})\), then \(b_i \in I_2({\textsf {Poor}},w^{T_2}_{S_2})\). The same strategy works if Abelard chooses to relocate to some \(v^{T_1}_{S_1}\) in \(\mathcal {N} _1\). It also works if Abelard decides to relocate in \(\mathcal {N} _2\), except when he chooses \(v^{T_2}_{S_2}\) where the corresponding \(S_1\) as defined above would be empty. In that case, for no \(a_i \in \mathbb {N} \) is \(b_i \in I_2({\textsf {Rich}},v^{T_2}_{S_2})\). So Eloïse can choose \(S_1\) to be any nonempty subset of
. Then one can check that \(\mathcal {N} _1,z,w^{T_1}_{S_1}, \overline{a} \simeq \mathcal {N} _2,z,w^{T_2}_{S_2}, \overline{b} \). For instance, suppose \(a_i \in I_1({\textsf {Rich}},w^{T_1}_{S_1})\). Either \(b_i \in \mathbb {N} \) or \(b_i \in \mathbb {N} ^-\). If \(b_i \in \mathbb {N} \), then \(b_i \notin S_2\), so \(b_i \in I_2({\textsf {Rich}},w^{T_2}_{S_2})\). If \(b_i \in \mathbb {N} ^-\), then \(b_i \in T_2\), so \(b_i \in I_2({\textsf {Rich}},w^{T_2}_{S_2})\). Likewise, if \(a_i \in I_1({\textsf {Poor}},w^{T_1}_{S_1})\), then \(b_i \in I_2({\textsf {Poor}},w^{T_2}_{S_2})\). The same strategy works if Abelard chooses to relocate to some \(v^{T_1}_{S_1}\) in \(\mathcal {N} _1\). It also works if Abelard decides to relocate in \(\mathcal {N} _2\), except when he chooses \(v^{T_2}_{S_2}\) where the corresponding \(S_1\) as defined above would be empty. In that case, for no \(a_i \in \mathbb {N} \) is \(b_i \in I_2({\textsf {Rich}},v^{T_2}_{S_2})\). So Eloïse can choose \(S_1\) to be any nonempty subset of  . \(\square \)
. \(\square \)
Once again, however, this inexpressibility proof does not extend to languages with \({\mathop {\downarrow }}\), since we can express (5) as:
Likewise, if we restrict to the class of models where \(R = F\), we can express (5) with:
5 Generalizations
In the previous section, we saw a number of examples demonstrating how bisimulations can be used to prove inexpressibility results for a variety of two-dimensional logics. In this section, we turn to some more general results regarding the expressive power of two-dimensional modal languages and beyond.
The (\(\mathbf D \)-)expressive hierarchy for two-dimensional languages between  and
and  . Arrows represent strict increase in expressive power. If there is an upward path from \(\mathcal {L}_1\) to \(\mathcal {L}_2\) in the diagram on the left, then the inclusions between \(\mathcal {L}_1\), \(\mathcal {L}_2\), and their extensions with \({\textsf {E}} \), \(\approx \), or \(\Pi {}\) are represented in the right diagram
. Arrows represent strict increase in expressive power. If there is an upward path from \(\mathcal {L}_1\) to \(\mathcal {L}_2\) in the diagram on the left, then the inclusions between \(\mathcal {L}_1\), \(\mathcal {L}_2\), and their extensions with \({\textsf {E}} \), \(\approx \), or \(\Pi {}\) are represented in the right diagram
First, given that sentences like (E), (R), and (NR) are expressible in some languages but not others, it is natural to ask what exactly the relative expressive power of all these various languages are. For instance, combining the results in Sect. 4, we know that  . But how do languages like
. But how do languages like  and
and  compare? Is one stronger than the other? What if we add a possibilist quantifier to one or the other?
compare? Is one stronger than the other? What if we add a possibilist quantifier to one or the other?
Using bisimulation techniques like the ones in Sect. 4, we can mostly settle these questions for the two-dimensional languages discussed in this paper (though in what follows, I have excluded languages that include  ). The inclusions relative to the class of all models can be diagrammed as in Fig. 5 (for a proof of the accuracy of the diagram, see Appendix 4). The diagram is still accurate relative to \(\mathbf D \). Relative to \(\mathbf U \), adding \({\mathop {\downarrow }}\) or \(\mathcal {F}\) without \(@\) present is redundant. Moreover,
). The inclusions relative to the class of all models can be diagrammed as in Fig. 5 (for a proof of the accuracy of the diagram, see Appendix 4). The diagram is still accurate relative to \(\mathbf D \). Relative to \(\mathbf U \), adding \({\mathop {\downarrow }}\) or \(\mathcal {F}\) without \(@\) present is redundant. Moreover,  .Footnote 25 Relative to UD, we will have more inclusions. For instance, while
.Footnote 25 Relative to UD, we will have more inclusions. For instance, while  and
and  , we do have
, we do have  , using the translation
, using the translation  . Similarly,
. Similarly,  . However, there are still limitations:
. However, there are still limitations:  and
and  . For more details, see Appendix 4.
. For more details, see Appendix 4.
Second, all of these inexpressibility results carry over to temporal logic. In temporal logic, one also includes a backward-looking operator \({\Box }^{-1} \), in addition to \(\Box \), with the following semantic clause (where  ):
):

Usually, \(\Box \) and \({\Box }^{-1} \) are written respectively as \({\mathop {\mathsf {G}}}\) and \({\mathop {\mathsf {H}}}\) (for “it is always going to be” and “it has always been”), \(@\) is written as \({\mathop {\mathsf {N}}}\) (for “now”), and \({\mathop {\downarrow }}\) is written as \({\textsf {T}} \) (for “then”). The notion of a bisimulation can easily be generalized to temporal logic by including Zig-Zag clauses for both R and \({R}^{-1} \) (which are often written respectively as < and >).
All of the sentences considered in this paper have natural temporal analogues. Here are a few variations on some of the sentences we have been considering (where \({\textsf {R}} \) is replaced by <):
-
(FE)
There will be things other than there are now.
 (12)
(12) -
(PR)
It was the case that everyone now rich was poor.
 (13)
(13) -
(FPR)
Henceforth, everyone who is rich will have once been poor.
 (14)
(14)
All of our models in Sect. 4 have universal accessibility relations. However, allowing < to be universal would be too permissive in the context of temporal logic (there would be no difference between future and past!). Often, < is required to be at least a strict partial order (i.e., irreflexive, asymmetric, and transitive), thereby excluding models where it is universal. Thus, none of the results in Sect. 4 immediately carry over to temporal logic.
Fortunately, we can still piggyback on these inexpressibility results with the following trick. Suppose  where the accessibility relations of \(\mathcal {M} \) and \(\mathcal {N} \) are universal. Assume for simplicity that \(W^\mathcal {M} \) and \(W^\mathcal {N} \) are countable. Let \(f^\mathcal {M} :\mathbb {N} \rightarrow W^\mathcal {M} \) be a surjection such that \(f^\mathcal {M} (0) = w\) (and likewise for \(f^\mathcal {N} \)). Define a new model \(\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }\) where \(W^{\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }} {:}{=}\mathbb {Z} \times W^\mathcal {M} \),
where the accessibility relations of \(\mathcal {M} \) and \(\mathcal {N} \) are universal. Assume for simplicity that \(W^\mathcal {M} \) and \(W^\mathcal {N} \) are countable. Let \(f^\mathcal {M} :\mathbb {N} \rightarrow W^\mathcal {M} \) be a surjection such that \(f^\mathcal {M} (0) = w\) (and likewise for \(f^\mathcal {N} \)). Define a new model \(\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }\) where \(W^{\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }} {:}{=}\mathbb {Z} \times W^\mathcal {M} \),  , \(D^{\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }} {:}{=}D^\mathcal {M} \), \(\delta ^{\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }}(\left\langle i,f(n)\right\rangle ) {:}{=}\delta ^\mathcal {M} (f(n))\), and \(I^{\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }}(P,\left\langle i,f(n)\right\rangle ) {:}{=}I^\mathcal {M} (P,f(n))\). That is, each \(i \in \mathbb {Z} \) contains a copy of \(\mathcal {M} \), and the integer-world pairs are ordered lexicographically. Define \(\mathcal {N} _{\mathbb {Z} \times \mathbb {N} }\) similarly from \(\mathcal {N} \) using \(f^\mathcal {N} \).
, \(D^{\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }} {:}{=}D^\mathcal {M} \), \(\delta ^{\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }}(\left\langle i,f(n)\right\rangle ) {:}{=}\delta ^\mathcal {M} (f(n))\), and \(I^{\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }}(P,\left\langle i,f(n)\right\rangle ) {:}{=}I^\mathcal {M} (P,f(n))\). That is, each \(i \in \mathbb {Z} \) contains a copy of \(\mathcal {M} \), and the integer-world pairs are ordered lexicographically. Define \(\mathcal {N} _{\mathbb {Z} \times \mathbb {N} }\) similarly from \(\mathcal {N} \) using \(f^\mathcal {N} \).
From this, it follows that  . For instance, suppose we are playing the
. For instance, suppose we are playing the  back-and-forth game with \(\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }\) and \(\mathcal {N} _{\mathbb {Z} \times \mathbb {N} }\), and we are currently located at some stage \(\left\langle \left\langle i_1,u_1\right\rangle ,\left\langle i_2,u_2\right\rangle ,\overline{a};\left\langle i_1',u_1'\right\rangle ,\left\langle i_2',u_2'\right\rangle ,\overline{b} \right\rangle \). Then whenever Abelard makes a move, Eloïse need only consult the
back-and-forth game with \(\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }\) and \(\mathcal {N} _{\mathbb {Z} \times \mathbb {N} }\), and we are currently located at some stage \(\left\langle \left\langle i_1,u_1\right\rangle ,\left\langle i_2,u_2\right\rangle ,\overline{a};\left\langle i_1',u_1'\right\rangle ,\left\langle i_2',u_2'\right\rangle ,\overline{b} \right\rangle \). Then whenever Abelard makes a move, Eloïse need only consult the  back-and-forth with \(\mathcal {M} \) and \(\mathcal {N} \), and see how she would respond at stage \(\left\langle u_1,u_2,\overline{a};u_1',u_2',\overline{b} \right\rangle \). In particular, if Abelard chooses to relocate the game in \(\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }\) to \(\left\langle i_3,u_3\right\rangle \) where \(\left\langle i_3,u_3\right\rangle > \left\langle i_2,u_2\right\rangle \), then Eloïse can pick whatever \(u_3'\) she would have chosen had Abelard chose \(u_3\) in the back-and-forth game with \(\mathcal {M} \) and \(\mathcal {N} \), and then she can relocate the game in \(\mathcal {N} _{\mathbb {Z} \times \mathbb {N} }\) to \(\left\langle i_3',u_3'\right\rangle \) where \(\left\langle i_3',u_3'\right\rangle > \left\langle i_2',u_2'\right\rangle \) (she will always be able to find one, since there are infinitely many copies of \(\mathcal {N} \) after \(i_2'\)). The same strategy applies if Abelard picks \(\left\langle i_3,u_3\right\rangle \) with \(\left\langle i_3,u_3\right\rangle < \left\langle i_2,u_2\right\rangle \). Thus, our results in Sect. 4 can be extended to temporal logic.Footnote 26
back-and-forth with \(\mathcal {M} \) and \(\mathcal {N} \), and see how she would respond at stage \(\left\langle u_1,u_2,\overline{a};u_1',u_2',\overline{b} \right\rangle \). In particular, if Abelard chooses to relocate the game in \(\mathcal {M} _{\mathbb {Z} \times \mathbb {N} }\) to \(\left\langle i_3,u_3\right\rangle \) where \(\left\langle i_3,u_3\right\rangle > \left\langle i_2,u_2\right\rangle \), then Eloïse can pick whatever \(u_3'\) she would have chosen had Abelard chose \(u_3\) in the back-and-forth game with \(\mathcal {M} \) and \(\mathcal {N} \), and then she can relocate the game in \(\mathcal {N} _{\mathbb {Z} \times \mathbb {N} }\) to \(\left\langle i_3',u_3'\right\rangle \) where \(\left\langle i_3',u_3'\right\rangle > \left\langle i_2',u_2'\right\rangle \) (she will always be able to find one, since there are infinitely many copies of \(\mathcal {N} \) after \(i_2'\)). The same strategy applies if Abelard picks \(\left\langle i_3,u_3\right\rangle \) with \(\left\langle i_3,u_3\right\rangle < \left\langle i_2,u_2\right\rangle \). Thus, our results in Sect. 4 can be extended to temporal logic.Footnote 26
Finally, it seems as though two-dimensions is not enough to overcome the kind of expressive limitations discussed in this paper in full generality. Recall that while (NR) is not expressible as an  -formula, it is expressible as an
-formula, it is expressible as an  -formula. However, more complicated sentences can be constructed that reveal the expressive limitations of even
-formula. However, more complicated sentences can be constructed that reveal the expressive limitations of even  . The most natural examples use temporal modalities or mix modalities. For instance, here is a temporal example from Cresswell (1990, p. 29):
. The most natural examples use temporal modalities or mix modalities. For instance, here is a temporal example from Cresswell (1990, p. 29):
-
(H)
Once, everyone now alive who was not then miserable would eventually be happy.
To formalize this, it seems that we need to store two reference times, not just one. In  , we would formalize (H) as follows:
, we would formalize (H) as follows:

We can also get examples with metaphysical modality, although the more powerful the language is, the more contrived the examples have to be:
-
(RC)
There could have been a brave man such that everyone who was poor but kind in reality necessarily received money from that man.
The problem is that we need to be able to go back to both the actual world and the first world we shifted to while we are at the second world we shifted to; but we can only keep track of one reference world at a time. It has been noted in the literature that this point seems to generalize to higher-dimensional languages.Footnote 27 One gets the feeling that for any n, we can concoct a  -formula that requires keeping track of \((n + 1)\)-many worlds in our points of evaluation. But no proof of this claim has been offered in the literature.Footnote 28 Using the power of bisimulations, we can actually verify this claim. I will conclude by explaining how to generate further inexpressibility results for higher-dimensional languages. We will only explicitly prove that a certain three-dimensional language is not expressible in any two-dimensional language. Hopefully, it will be clear how the method can be schematized to show that some \((n+1)\)-dimensional languages are not expressible in any n-dimensional language.
-formula that requires keeping track of \((n + 1)\)-many worlds in our points of evaluation. But no proof of this claim has been offered in the literature.Footnote 28 Using the power of bisimulations, we can actually verify this claim. I will conclude by explaining how to generate further inexpressibility results for higher-dimensional languages. We will only explicitly prove that a certain three-dimensional language is not expressible in any two-dimensional language. Hopefully, it will be clear how the method can be schematized to show that some \((n+1)\)-dimensional languages are not expressible in any n-dimensional language.
First, we define an n-dimensional model to be any tuple of the form  where each \(R_i \subseteq W \times W\), and otherwise everything is as before. For instance, the models we have been working with in this paper have all been 2-dimensional models (where \(F = R_1\)). Second, for each \(k \ge 1\), we will introduce operators \(\Box _k\), \(@_k\), and \({\mathop {\downarrow }}_k\), which we might add to
where each \(R_i \subseteq W \times W\), and otherwise everything is as before. For instance, the models we have been working with in this paper have all been 2-dimensional models (where \(F = R_1\)). Second, for each \(k \ge 1\), we will introduce operators \(\Box _k\), \(@_k\), and \({\mathop {\downarrow }}_k\), which we might add to  . In what follows, we will define
. In what follows, we will define  and
and  . Third, where
. Third, where  is a sequence of worlds, and where \(1 \le k \le n\), let \(\sigma ^k_v\) be the result of replacing \(w_k\) in \(\sigma \) with v. Finally, satisfaction for
is a sequence of worlds, and where \(1 \le k \le n\), let \(\sigma ^k_v\) be the result of replacing \(w_k\) in \(\sigma \) with v. Finally, satisfaction for  will be relativized to \((n+1)\)-dimensional models, as well as a sequence of n-many worlds
will be relativized to \((n+1)\)-dimensional models, as well as a sequence of n-many worlds  , a world v, and a variable assignment \(g \in {\textsf {VA}} (\mathcal {M} )\), with the semantic clauses for the new operators stated below for \(1 \le k \le n\):
, a world v, and a variable assignment \(g \in {\textsf {VA}} (\mathcal {M} )\), with the semantic clauses for the new operators stated below for \(1 \le k \le n\):

Thus, \(\mathcal {F}\), \(@\), and \({\mathop {\downarrow }}\) are \(\Box _1\), \(@_1\), and \({\mathop {\downarrow }}_1\) respectively. Since  and
and  is essentially
is essentially  , it makes sense to call
, it makes sense to call  with this semantics an n-dimensional language. Generalizing the definition of a bisimulation to
with this semantics an n-dimensional language. Generalizing the definition of a bisimulation to  is straightforward.
is straightforward.
Using models similar to \(\mathcal {N} _1\) and \(\mathcal {N} _2\) from Fig. 4, we can show that  is not included in
is not included in  . We have already shown with Proposition 17 that
. We have already shown with Proposition 17 that  is not included in
is not included in  (or even in
(or even in  ), since
), since  distinguishes \(\mathcal {N} _1,z,z\) and \(\mathcal {N} _2,z,z\), even though \(\mathcal {N} _1,z,z \leftrightarrows _{\approx ,@_1,\Pi {}} \mathcal {N} _2,z,z\). We will show that the following
distinguishes \(\mathcal {N} _1,z,z\) and \(\mathcal {N} _2,z,z\), even though \(\mathcal {N} _1,z,z \leftrightarrows _{\approx ,@_1,\Pi {}} \mathcal {N} _2,z,z\). We will show that the following  -formula is not expressible in
-formula is not expressible in  :Footnote 29
:Footnote 29

The proof that  is not expressible in
is not expressible in  is a straightforward generalization of the proof below.
is a straightforward generalization of the proof below.
First, we describe our models \(\mathcal {N} _3\) and \(\mathcal {N} _4\). These models have been summarized in Fig. 6. All of the accessibility relations will be universal, and \(\mathcal {N} _3\) and \(\mathcal {N} _4\) will both be constant domain models (so the local domain of every world is the global domain). Let \(\mathbb {N} _1\), \(\mathbb {N} _2\), \(\mathbb {N} _3\), and \(\mathbb {N} _4\) be disjoint copies of \(\mathbb {N} \). In both models, there will be a unique world z where \(I_k(P_1,z) = I_k(P_2,z) = I_k(P_3,z) = \emptyset \) for  . There will be three types of worlds: \(\alpha \)-worlds, \(\beta \)-worlds, and \(\gamma \)-worlds. Each type of world will be uniquely specified by four sets \(S_1\), \(S_2\), \(S_3\), and \(S_4\), where \(S_k \subseteq \mathbb {N} _k\) and
. There will be three types of worlds: \(\alpha \)-worlds, \(\beta \)-worlds, and \(\gamma \)-worlds. Each type of world will be uniquely specified by four sets \(S_1\), \(S_2\), \(S_3\), and \(S_4\), where \(S_k \subseteq \mathbb {N} _k\) and  for
for  . Where
. Where  , we will denote the worlds as \(\eta _{S_1,S_2,S_3,S_4}\). Each of \(S_1\), \(S_2\), \(S_3\), and \(S_4\) is generally allowed to be empty, but in \(\mathcal {N} _3\), only \(\gamma \)-worlds where \(S_1 \ne \emptyset \) are allowed. For each
, we will denote the worlds as \(\eta _{S_1,S_2,S_3,S_4}\). Each of \(S_1\), \(S_2\), \(S_3\), and \(S_4\) is generally allowed to be empty, but in \(\mathcal {N} _3\), only \(\gamma \)-worlds where \(S_1 \ne \emptyset \) are allowed. For each  and each
and each  , \(I_k(P_i,\eta _{S_1,S_2,S_3,S_4}) = \emptyset \) with the following exceptions:
, \(I_k(P_i,\eta _{S_1,S_2,S_3,S_4}) = \emptyset \) with the following exceptions:
-
\(I_k(P_1,\alpha _{S_1,S_2,S_3,S_4}) = (\mathbb {N} _1 - S_1) \cup (\mathbb {N} _2 - S_2) \cup S_3 \cup S_4\)
-
\(I_k(P_2,\beta _{S_1,S_2,S_3,S_4}) = (\mathbb {N} _1 - S_1) \cup (\mathbb {N} _3 - S_3) \cup S_2 \cup S_4\)
-
\(I_k(P_3,\gamma _{S_1,S_2,S_3,S_4}) = (\mathbb {N} _1- S_1) \cup (\mathbb {N} _4 - S_4) \cup S_2 \cup S_3\).
We will start by explaining why \(\mathcal {N} _3,\left\langle z,z\right\rangle ,z \nVdash \) (16) while \(\mathcal {N} _4,\left\langle z,z\right\rangle ,z \Vdash \) (16). First, to explain why \(\mathcal {N} _3,\left\langle z,z\right\rangle ,z \nVdash \) (16), it suffices to note the following (where \(\alpha \) and \(\beta \) below have set \(S_1 = S_2 = S_3 = S_4 = \emptyset \), and w is any world):

This is simply because \(I(P_1,\alpha ) \cap I(P_2,\beta ) = \mathbb {N} \), but no \(\gamma \)-world has all of \(\mathbb {N} \) in its interpretation of \(P_3\). Second, to explain why \(\mathcal {N} _4,\left\langle z,z\right\rangle ,z \Vdash \) (16), consider the following formula:

Notice that \(\mathcal {N} _4,\left\langle w,v\right\rangle ,u \Vdash \) (17) holds vacuously unless w is an \(\alpha \)-world and v is a \(\beta \)-world. So suppose \(w = \alpha _{S_1,S_2,S_3,S_4}\) and \(v = \beta _{T_1,T_2,T_3,T_4}\). Then:
Now pick \(u = \gamma _{(S_1 \cup T_1),(T_2 - S_2),(S_3 - T_3),S_4'}\), where \(S_4'\) is disjoint from \(S_4 \cap T_4\). (We can always find such a \(\gamma \) since \(S_1 \cup T_1\) is allowed to be empty.) Then it is easy to see that  . Thus, \(\mathcal {N} _3,\left\langle z,z\right\rangle ,z\) and \(\mathcal {N} _4,\left\langle z,z\right\rangle ,z\) disagree on (16).
. Thus, \(\mathcal {N} _3,\left\langle z,z\right\rangle ,z\) and \(\mathcal {N} _4,\left\langle z,z\right\rangle ,z\) disagree on (16).
Now, in what follows, let us say that a 2D-partial isomorphism between \(\mathcal {M} ,\left\langle w,z\right\rangle ,v,\overline{a} \) and \(\mathcal {N} ,\left\langle w',z'\right\rangle ,v',\overline{b} \) is a map \(\rho \) such that \(\rho \) is a partial isomorphism between \(\mathcal {M} ,w,v,\overline{a} \) and \(\mathcal {N} ,w',v',\overline{b} \), and also a partial isomorphism between \(\mathcal {M} ,w,w,\overline{a} \) and \(\mathcal {N} ,w',w',\overline{b} \). In other words, 2D-partial isomorphisms must also satisfy (Predicate) and (Existence) at w and \(w'\). We will write \(\simeq _\text {2D}\) in place of \(\simeq \) for 2D-partial isomorphisms. It is easy to verify that 2D-partial isomorphism allows for Eloïse to continue the  -bisimulation game.
-bisimulation game.
Let us write \(\mathcal {M} ,w,z,v,\overline{a} \leftrightarrows ^2 \mathcal {N} ,w',z',v',\overline{b} \) to mean that \(\mathcal {M} ,w,z,u,\overline{a} \) and \(\mathcal {N} ,w',z',u',\overline{b} \) are  -bisimilar (I am dropping the angle brackets). Note \(\leftrightarrows ^2\) is just
-bisimilar (I am dropping the angle brackets). Note \(\leftrightarrows ^2\) is just  -bisimilarity, with an extra argument place for worlds in the middle; no clause in this notion of bisimilarity can do anything to or with the z and \(z'\) worlds. The conventions from before regarding adding additional operators, quantifiers, etc. all apply.
-bisimilarity, with an extra argument place for worlds in the middle; no clause in this notion of bisimilarity can do anything to or with the z and \(z'\) worlds. The conventions from before regarding adding additional operators, quantifiers, etc. all apply.
Theorem 18
(Higher-dimensional inexpressibility) \(\mathcal {N} _3,z,z,z \leftrightarrows _{\approx ,@_2,\Pi {}}^2 \mathcal {N} _4,z,z,z\).
Proof
Clearly, \(z,z,z \simeq _\text {2D} z,z,z\). Now, suppose \(w,z,v,\overline{a} \simeq _\text {2D} w',z,v',\overline{b} \), where:
-
\(w = z\) iff \(w' = z\) (likewise for v and \(v'\))
-
w is an \(\alpha \)/\(\beta \)/\(\gamma \)-world iff \(w'\) is an \(\alpha \)/\(\beta \)/\(\gamma \)-world (likewise for v and \(v'\))
-
\(w = v\) iff \(w' = v'\).
Using these assumptions, we will show that no matter what move Abelard makes, Eloïse can match his move so as to preserve these assumptions.
First, observe that no matter what worlds w and v are, for any  , all of the following sets are either empty or infinite (where
, all of the following sets are either empty or infinite (where  ):
):

Thus, if Abelard picks a new \(a \in \delta _3(u)\), then no matter what predicates it satisfies in w or v, Eloïse will have infinitely many new \(b \in \delta _4(u')\) to choose from which satisfy the same predicates in \(w'\) and \(v'\). Likewise if Abelard picks a new \(b \in \delta _4(u')\).
Next, suppose Abelard decides to relocate the game in \(\mathcal {N} _3\). Since this is the  -bisimulation game, he can either choose to replace w with another world, or v with another world (there are no clauses for reseting z). Clearly if he replaces one of these with z, Eloïse should match his move by replacing the corresponding world with z. If he replaces w with v, Eloïse should replace \(w'\) with \(v'\). Likewise if he replaces v with w. Suppose WLOG that he decides to replace v with a new \(\alpha \)-world \(u = \alpha _{S_1,S_2,S_3,S_4}\). Define:
-bisimulation game, he can either choose to replace w with another world, or v with another world (there are no clauses for reseting z). Clearly if he replaces one of these with z, Eloïse should match his move by replacing the corresponding world with z. If he replaces w with v, Eloïse should replace \(w'\) with \(v'\). Likewise if he replaces v with w. Suppose WLOG that he decides to replace v with a new \(\alpha \)-world \(u = \alpha _{S_1,S_2,S_3,S_4}\). Define:

Define \(u' = \alpha _{T_1,T_2,T_3,T_4}\). It is easy to check that \(a_i \in I_3(P_1,u)\) iff \(b_i \in I_4(P_1,u')\). (Suppose \(a_i \in I_3(P_1,u)\), and reason by cases depending on which \(\mathbb {N} _k\) contains \(b_i\). Likewise with \(a_i \notin I_3(P_1,u)\).) The other cases are symmetric (for both Zig and Zag), except if Abelard decides to replace \(v'\) with a \(\gamma \)-world where the corresponding \(S_1\) we define would be empty. In that case, define the other sets as before, and pick a new  and set
and set  . \(\square \)
. \(\square \)
6 Conclusion
As we have seen, there are a number of English modal claims that seem to resist regimentation in first-order modal logic, even if we add two-dimensional operators. Proofs of these claims in the literature are often quite complicated. But as we have shown, they can be simplified by first regimenting these English sentences as formulas in an extensional two-sorted language and then constructing bisimilar models that disagree on these extensional formulas. We illustrated this technique by showing that (E) is not expressible in  , that (R) is not expressible in
, that (R) is not expressible in  , and that (NR) is not expressible in
, and that (NR) is not expressible in  . We then classified the relative expressive power of the extensions of
. We then classified the relative expressive power of the extensions of  with operators like \(@\), \({\mathop {\downarrow }}\), and \(\mathcal {F}\), and finally showed how these inexpressibility results generalize to temporal languages and to higher-dimensional languages.
with operators like \(@\), \({\mathop {\downarrow }}\), and \(\mathcal {F}\), and finally showed how these inexpressibility results generalize to temporal languages and to higher-dimensional languages.
There are still a number of questions about the expressivity of extensions of first-order modal logic that have yet to be resolved. For one thing, we have yet to complete the classification of the expressive power of these languages relative to \(\mathbf U \) and UD, and one might also wonder whether these results hold in other kinds of models, such as the class of models with finite global domains.Footnote 30 More broadly, there is still a question about whether we can formally characterize sentences like (E), (R), and (NR).Footnote 31 Finally, there is still much to be learned about even more powerful extensions of first-order modal logic. For instance, the results in Sect. 5 suggest that the key to overcoming all of these expressive limitations is to move to a hybrid language, or some weaker Vlachian languages.Footnote 32 Bisimulation techniques can also be used to characterize the expressive power of first-order Vlachian logics and hybrid logics.Footnote 33 But there is still much to uncover about the full expressive landscape for these languages and their extensions.
Notes
Originally from Hazen (1976, p. 31).
Originally from Cresswell (1990, p. 34).
Hodes (1984c).
Wehmeier (2001).
See Garson (2001) for a tree of such formulations.
Davies and Humberstone (1980).
See Blackburn et al. (2001).
There is a general question as to whether the object quantifier in (R) and (NR) is possibilist or actualist. In general, I assume it should be actualist, in which case the object quantifiers in (4) and (5) should technically be \({\textsf {E}} \)-bounded. But to avoid clutter, we assume in the background that nothing can be rich or poor unless it exists (
 ), in which case it does not matter which type of quantifier we use in (4) and (5). None of our models will violate this constraint.
), in which case it does not matter which type of quantifier we use in (4) and (5). None of our models will violate this constraint.See Blackburn et al. (2001, Chap. 2) for an introduction to bisimulations.
See Blackburn et al. (2001, p. 68) for the proof in the propositional case.
See Goranko and Otto (2006) for a proof in the propositional case. Generalizing to first-order modal logic is straightforward.
A proof of this was suggested by Hazen (1976, p. 35). He describes his models as follows:
For suppose that [(3)] is false, that the actual world is the only one with infinitely many individuals, and that for every finite set of individuals in the actual world there is a world containing just those individuals, and consider the purely logical sentences true under those suppositions. Now suppose there is added to the system of possible worlds a new world for each old world, containing all the same individuals plus one new individual (the same for each new world) not in any old world. [(3)] will have become true, but no purely logical sentence of the modal language will have changed its truth value.
However, the proof is not correct as stated, since the second model, but not the first, satisfies the formula
 (there is no world where this new object exists by itself). The natural fix is to add another world to the second model which only contains the new object. The resulting models (which are like ours except the worlds with cofinite domains are removed) satisfy the same
(there is no world where this new object exists by itself). The natural fix is to add another world to the second model which only contains the new object. The resulting models (which are like ours except the worlds with cofinite domains are removed) satisfy the same  -formulas, but they are not bisimilar, since they are distinguished by the
-formulas, but they are not bisimilar, since they are distinguished by the  -formula
-formula  . However, if you restrict the
. However, if you restrict the  -bisimulation game to n-steps, for any finite n, then Eloïse has a winning strategy (that is, the models are n-bisimilar for every n); and this suffices to guarantee modal equivalence. Here, we ensure full bisimilarity by including worlds with cofinite domains. Thus, our proof shows that (3) is not even expressible in
-bisimulation game to n-steps, for any finite n, then Eloïse has a winning strategy (that is, the models are n-bisimilar for every n); and this suffices to guarantee modal equivalence. Here, we ensure full bisimilarity by including worlds with cofinite domains. Thus, our proof shows that (3) is not even expressible in  .
.Yanovich (2015, p. 87) claims to have shown that \(\Diamond \Pi {x}\left( @Q(x) \rightarrow Q(x)\right) \) is not expressible in
 . He proceeds, as we do, by constructing two models that disagree on this sentence, and then argues that they are bisimilar. The first model consists of two worlds w and u, where
. He proceeds, as we do, by constructing two models that disagree on this sentence, and then argues that they are bisimilar. The first model consists of two worlds w and u, where  and where in both w and u,
and where in both w and u,  satisfy Q(x) and
satisfy Q(x) and  do not satisfy Q(x). The second model consists of worlds \(w'\), \(u_1'\), and \(u_2'\), where
do not satisfy Q(x). The second model consists of worlds \(w'\), \(u_1'\), and \(u_2'\), where  . In \(w'\),
. In \(w'\),  satisfy Q(x) while
satisfy Q(x) while  do not. In \(u_1'\), only
do not. In \(u_1'\), only  satisfy Q, and in \(u_2'\), only
satisfy Q, and in \(u_2'\), only  satisfy Q. He then claims that w and \(w'\) are
satisfy Q. He then claims that w and \(w'\) are  -bisimilar. However, these models are not
-bisimilar. However, these models are not  -bisimilar. In fact, they do not even satisfy the same
-bisimilar. In fact, they do not even satisfy the same  -formulas: e.g., \(\Sigma {x}\left( Q(x) \wedge \Diamond \lnot Q(x)\right) \) distinguishes the two models. The claim that such sentences cannot be expressed in
-formulas: e.g., \(\Sigma {x}\left( Q(x) \wedge \Diamond \lnot Q(x)\right) \) distinguishes the two models. The claim that such sentences cannot be expressed in  is still correct, as can be verified with a bisimulation argument using the models \(\mathcal {N} _1,w,w\) and \(\mathcal {N} _2,w,w\) defined in Fig. 4 below (where \(w = w^\emptyset _\emptyset \)). Another proof that
is still correct, as can be verified with a bisimulation argument using the models \(\mathcal {N} _1,w,w\) and \(\mathcal {N} _2,w,w\) defined in Fig. 4 below (where \(w = w^\emptyset _\emptyset \)). Another proof that  cannot express (R) can be found in Wehmeier (2001).
cannot express (R) can be found in Wehmeier (2001).I claimed in Kocurek (2015, p. 215) that the proof of Proposition 16 extends to
 immediately. But this needs qualification. We can obtain a quick proof that (4) is not expressible in
immediately. But this needs qualification. We can obtain a quick proof that (4) is not expressible in  by restricting the accessibility relations in \(\mathcal {R} _1\) and \(\mathcal {R} _2\); but as Appendix 3 reveals, the proof of UD-inexpressibility is more challenging.
by restricting the accessibility relations in \(\mathcal {R} _1\) and \(\mathcal {R} _2\); but as Appendix 3 reveals, the proof of UD-inexpressibility is more challenging.I claimed to prove this in Kocurek (2015, pp. 215–216) using models like the ones presented here, except with \(T = \emptyset \) for all worlds. However, my proof was incorrect, since those models are distinguishable by the
 -formula
-formula  .
.The exact relation between
 ,
,  , and
, and  relative to \(\mathbf U \) is an open question. In particular, it is unknown whether
relative to \(\mathbf U \) is an open question. In particular, it is unknown whether  or even
or even  . Fig. 11 in Appendix 4 summarizes the remaining inclusions relative to \(\mathbf U \).
. Fig. 11 in Appendix 4 summarizes the remaining inclusions relative to \(\mathbf U \).Though our partial order was linear and discrete, this was not crucial to the construction. We could have, for instance, mapped each state in \(\mathcal {M} \) to a rational in the interval [0, 1), and have obtained a dense linear order. Alternatively, via tree unraveling, we could have obtained a branching structure.
Several conjectures have been made about how to construct such formulas. For instance, Needham (1975, pp. 73–74) gives a sentence he claims is not expressible in
 ; but van Benthem (1977, p. 417) shows it is. van Benthem then gives a genuine example of a temporal
; but van Benthem (1977, p. 417) shows it is. van Benthem then gives a genuine example of a temporal  -formula that is not expressible in
-formula that is not expressible in  . However, it should be noted that even though \(\mathcal {F}\) operators were not the focus of van Benthem (1977), the sentence he gives is expressible in
. However, it should be noted that even though \(\mathcal {F}\) operators were not the focus of van Benthem (1977), the sentence he gives is expressible in  , which is still two-dimensional. Forbes (1989, p. 89) also gives a schema that was supposed to show that \((n-1)\)-dimensional logic is not as expressive as n-dimensional logic. But as footnote 29 explains, the example is not correct either. Cresswell (1990, p. 30) suggests one can generate such sentences from (H) since, reading the conditional in (15) as a disjunction, “disjunctions can be extended with no upper limit.”
, which is still two-dimensional. Forbes (1989, p. 89) also gives a schema that was supposed to show that \((n-1)\)-dimensional logic is not as expressive as n-dimensional logic. But as footnote 29 explains, the example is not correct either. Cresswell (1990, p. 30) suggests one can generate such sentences from (H) since, reading the conditional in (15) as a disjunction, “disjunctions can be extended with no upper limit.”Forbes (1989, p. 87) gives a purported example of an n-dimensional formula not expressible as an \((n+1)\)-dimensional formulas. (Following Forbes, we restrict attention to models whose accessibility relations are universal.) Given a model \(\mathcal {M} \), let us say a sequence
 is an n-chain if \(\delta ^\mathcal {M} (w_i) \subset \delta ^\mathcal {M} (w_{i+1})\) for \(1 \le i < n\). Forbes (1989, p. 89) says “it is a very probable conjecture that ‘there is an n-chain of worlds’ cannot be expressed in [
is an n-chain if \(\delta ^\mathcal {M} (w_i) \subset \delta ^\mathcal {M} (w_{i+1})\) for \(1 \le i < n\). Forbes (1989, p. 89) says “it is a very probable conjecture that ‘there is an n-chain of worlds’ cannot be expressed in [ ], so that the hierarchy of modal languages is strictly increasing in expressive power...” Forbes also notes that
], so that the hierarchy of modal languages is strictly increasing in expressive power...” Forbes also notes that  can express “there is an n-chain of worlds”, but claims that it cannot express “there is an \(n+1\)-chain of worlds”. However, the conjecture is false. Define
can express “there is an n-chain of worlds”, but claims that it cannot express “there is an \(n+1\)-chain of worlds”. However, the conjecture is false. Define  . Then the claim that there is a 4-chain can be expressed as an
. Then the claim that there is a 4-chain can be expressed as an  -formula: \(\Diamond _1\Diamond _2\left( \theta _{1,2} \wedge \Diamond _1\left( \theta _{2,1} \wedge \Diamond _2\theta _{1,2}\right) \right) \). Likewise for \(n > 4\). Also, let
-formula: \(\Diamond _1\Diamond _2\left( \theta _{1,2} \wedge \Diamond _1\left( \theta _{2,1} \wedge \Diamond _2\theta _{1,2}\right) \right) \). Likewise for \(n > 4\). Also, let  and let
and let  . Then the claim that there is a 4-chain can be expressed as an
. Then the claim that there is a 4-chain can be expressed as an  -formula: \(\Diamond _1\Diamond \left( \chi \wedge \Diamond _1\left( \eta \wedge \Diamond \chi \right) \right) \). Again, this generalizes to n-chains where \(n > 4\).
-formula: \(\Diamond _1\Diamond \left( \chi \wedge \Diamond _1\left( \eta \wedge \Diamond \chi \right) \right) \). Again, this generalizes to n-chains where \(n > 4\).A theorem of Yanovich (2015, pp. 85–86) shows that one will not generally be able to use the bisimulation
technique proposed in this paper to establish inexpressibility over the class of models with finite domains. I suspect one could still establish such results, however, by constructing sequences of pairs of finite models that were n-bisimilar for each \(n \in \mathbb {N} \). But working out the details must be left for future work.
See Kocurek (2016) for one such syntactic characterization.
See Chang and Keisler (1990, Chap. 4).
See Bell and Slomson (2006, pp. 222–224).
Hodes (1984b, pp. 445–446) claimed to have a proof that
 . He also constructs two models which he claims satisfy the same
. He also constructs two models which he claims satisfy the same  -formulas, but disagree on the
-formulas, but disagree on the  -formula
-formula  . Here are the models \(\mathcal {A} \) and \(\mathcal {B} \) he describes (p. 445, his notation; A(w) and B(w) in Hodes’s notation means \(\delta ^\mathcal {A} (w)\) and \(\delta ^\mathcal {B} (w)\) in ours, and \(\left\langle w,a\right\rangle \in V(P)\) in his notation means \(a \in I(P,w)\) in ours; he also write \(\mathcal {A} ,0 \vDash \varphi \) in place of our \(\mathcal {A} ,0,0 \Vdash \varphi \)):
. Here are the models \(\mathcal {A} \) and \(\mathcal {B} \) he describes (p. 445, his notation; A(w) and B(w) in Hodes’s notation means \(\delta ^\mathcal {A} (w)\) and \(\delta ^\mathcal {B} (w)\) in ours, and \(\left\langle w,a\right\rangle \in V(P)\) in his notation means \(a \in I(P,w)\) in ours; he also write \(\mathcal {A} ,0 \vDash \varphi \) in place of our \(\mathcal {A} ,0,0 \Vdash \varphi \)):Let
 ,
,  . Let \(A(0) = B(0) = \omega \),
. Let \(A(0) = B(0) = \omega \),  , let V(P) be empty for all \(P \in {\textsf {Pred}} \), \(\mathcal {A} = \left( W,A,V\right) \), \(\mathcal {B} = \left( W',B,V\right) \). Clearly \(\mathcal {A} ,0 \vDash \theta _2\) but \(\mathcal {B} ,0 \nvDash \theta _2\).
, let V(P) be empty for all \(P \in {\textsf {Pred}} \), \(\mathcal {A} = \left( W,A,V\right) \), \(\mathcal {B} = \left( W',B,V\right) \). Clearly \(\mathcal {A} ,0 \vDash \theta _2\) but \(\mathcal {B} ,0 \nvDash \theta _2\).However, Hodes’s description of these models is incomplete, since crucially the local domain of 1 in \(\mathcal {B} \) is never specified, and the proof that follows gives no indication of what it might be. Moreover, given the proof requires that \(\mathcal {A},0,0 \Vdash \theta _2\) and \(\mathcal {B},0,0 \nVdash \theta _2\), we can infer that it would have to be that
 has exactly one member (since
has exactly one member (since  is the set of objects that do not exist at 0). But if that is right, then these models are distinguishable by the following
is the set of objects that do not exist at 0). But if that is right, then these models are distinguishable by the following  -formula:$$\begin{aligned} \Sigma {x}\Sigma {y}\left( x \not \approx y \wedge \lnot {\textsf {E}} (x) \wedge \lnot {\textsf {E}} (y) \wedge \Diamond ({\textsf {E}} (x) \wedge \lnot {\textsf {E}} (y))\right) . \end{aligned}$$
-formula:$$\begin{aligned} \Sigma {x}\Sigma {y}\left( x \not \approx y \wedge \lnot {\textsf {E}} (x) \wedge \lnot {\textsf {E}} (y) \wedge \Diamond ({\textsf {E}} (x) \wedge \lnot {\textsf {E}} (y))\right) . \end{aligned}$$The proof of Lemma 35 was inspired by an attempt to fix Hodes’s proof.
Here is the idea. First, every \(@\) in \(\varphi \) is in the immediate scope of a \(\mathcal {F}\), then \(\Vdash _\mathbf U \Box \varphi \leftrightarrow \mathcal {F}@\varphi \). So every \(\Box \) in a
 -formula can be replaced by \(\mathcal {F}@\). Second, note that
-formula can be replaced by \(\mathcal {F}@\). Second, note that  . So having replaced every \(\Box \) with \(\mathcal {F}@\), every \(\Pi {}\) is in the scope of a \(\mathcal {F}@\), so we can replace every \(\Pi {x}\) with
. So having replaced every \(\Box \) with \(\mathcal {F}@\), every \(\Pi {}\) is in the scope of a \(\mathcal {F}@\), so we can replace every \(\Pi {x}\) with  . The result is a \(\mathbf UD \)-equivalent
. The result is a \(\mathbf UD \)-equivalent  -formula.
-formula.
References
Areces, C., Blackburn, P., & Marx, M. (1999). Hybrid logic is the bounded fragment of first-order logic. In Proceedings of 6th workshop on logic, language, information and computation.
Areces, C., & ten Cate, B. (2007). Hybrid logics. In P. Blackburn, F. Wolter, & J. van Benthem (Eds.), Handbook of modal logic (pp. 821–868). New York: Elsevier.
Bell, J. L., & Slomson, A. B. (2006). Models and ultraproducts: An introduction. Princeton, NJ: Courier Corporation.
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal logic. Cambridge: Cambridge University Press.
Bricker, P. (1989). Quantified modal logic and the Plural De Re. Midwest Studies in Philosophy, 14, 372–394.
Chang, C. C., & Keisler, H. J. (1990). Model theory (3rd ed.). Princeton, NJ: Courier Corporation.
Correia, F. (2007). Modality, quantification, and many Vlach-operators. Journal of Philosophical Logic, 36, 473–488.
Cresswell, M. J. (1990). Entities and indices. Dordrecht: Kluwer.
Crossley, J. N., & Humberstone, L. (1977). The logic of “actually”. Reports on Mathematical Logic, 8, 11–29.
Davies, M., & Humberstone, L. (1980). Two notions of necessity. Philosophical Studies, 38, 1–30.
Fine, K. (1979). Failures of the Interpolation lemma in quantified modal logic. The Journal of Symbolic Logic, 44, 201–206.
Fine, K. (1981). Model theory for modal logic—Part III: Existence and predication. Journal of Philosophical Logic, 10, 293–307.
Fine, K. (2005). Prior on the construction of possible worlds and instants. In Modality and tense (pp. 133–175). Oxford: Oxford University Press.
Forbes, G. (1989). Languages of possibility. Cambridge, MA: Blackwell.
Fritz, P. (2012). Modal ontology and generalized quantifiers. Journal of Philosophical Logic, 14(1), 1–36.
Gabbay, D. M. (1981). Expressive functional completeness in tense logic. Aspects of Philosophical Logic 91–117.
Garson, J. W. (2001). Quantification in modal logic. In Handbook of philosophical logic (pp. 267–323). Dordrecht: Springer.
Gilbert, D. R. (2015). Actuality, quantifiers and actuality quantifiers. Logique et Analyse, 58(232), 457–486.
Goranko, V., & Otto, M. (2006). Model theory of modal logic. In P. Blackburn, J. van Benthem, & F. Wolter (Eds.), Handbook of modal logic. Elsevier.
Hazen, A. P. (1976). Expressive completeness in modal language. Journal of Philosophical Logic, 5, 25–46.
Hazen, A. P. (1990). Actuality and quantification. Notre Dame Journal of Formal Logic, 31, 498–508.
Hodes, H. T. (1984a). Axioms for actuality. Journal of Philosophical Logic, 13, 27–34.
Hodes, H. T. (1984b). On modal logics which enrich first-order S5. Journal of Philosophical Logic, 13, 423–454.
Hodes, H. T. (1984c). Some theorems on the expressive limitations of modal languages. Journal of Philosophical Logic, 13, 13–26.
Kocurek, A. W. (2015). On the expressivity of first-order modal logic with “actually”. In W. van der Hoek, W. H. Holliday & W. Wang (Eds.), Logic, rationality, and interaction: Proceedings 5th international workshop, LORI 2015, Taipei, Taiwan, October 28–30, 2015 (pp. 207–219). Berlin: Springer.
Kocurek, A. W. (2016). The problem of cross-world predication. Journal of Philosophical Logic 1–46.
Lewis, D. K. (1973). Counterfactuals and comparative possibility. Journal of Philosophical Logic, 2, 418–446.
Needham, P. (1975). Temporal perspective: A logical analysis of temporal reference in English. Ph.D. thesis, Upsala, Sweden.
Sider, T. (2010). Logic for philosophy. Oxford: oxford University Press.
Sturm, H., & Wolter, F. (2001). First-order expressivity for S5-models: Modal versus two-sorted languages. Journal of Philosophical Logic, 30, 571–591.
van Benthem, J. (1977). Tense logic and standard logic. Logique et Analyse, 80, 395–437.
van Benthem, J. (2010). Frame correspondences in modal predicate logic. 1–14.
Vlach, F. (1973). “Now” and “then”: A formal study in the logic of tense Anaphora. Ph.D. thesis, UCLA.
Wehmeier, K. F. (2001). World travelling and mood swings. In Trends in logic (pp. 257–260). Dordrecht: Springer.
Yanovich, I. (2015). Expressive power of “now” and “then” operators. Journal of Logic, Language and Information, 24, 65–93.
Acknowledgments
Many thanks to Melissa Fusco, Wes Holliday, and two anonymous reviewers for all their feedback on this paper. Thanks also to those who participated in UC Berkeley’s dissertation seminar in the Spring of 2016 for all their valuable comments and suggestions on an earlier draft of this paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: van Benthem’s characterization theorem
In this appendix, we prove Theorem 13. We essentially follow the proof of the corresponding theorem for propositional modal logic in Blackburn et al. (2001, Chap. 2.6). The crucial change is with the definition of a set of formulas being satisfiable.
Definition 19
(Satisfiability) Let  be some new variables not in \({\textsf {VAR}} \), and let
be some new variables not in \({\textsf {VAR}} \), and let  be the result of extending \(\mathcal {L}\) with
be the result of extending \(\mathcal {L}\) with  . Let
. Let  be a set of
be a set of  -formulas whose only variables not among
-formulas whose only variables not among  are \(\overline{x} \). Let \(\mathcal {M} \) be a model, and \(X \subseteq W^2\), and let \(\overline{b} \in D\).
are \(\overline{x} \). Let \(\mathcal {M} \) be a model, and \(X \subseteq W^2\), and let \(\overline{b} \in D\).
-
\(\varGamma \) is
 -satisfiable inXover\(\overline{b} \)(with respect to\(\mathcal {M} \)) if there is a \(\left\langle w,v\right\rangle \in X\) and some \(\overline{a} \in D/\delta (v)/\delta (w)\) such that \(\mathcal {M} ,w,v \Vdash \varGamma [\overline{a},\overline{b} ]\).
-satisfiable inXover\(\overline{b} \)(with respect to\(\mathcal {M} \)) if there is a \(\left\langle w,v\right\rangle \in X\) and some \(\overline{a} \in D/\delta (v)/\delta (w)\) such that \(\mathcal {M} ,w,v \Vdash \varGamma [\overline{a},\overline{b} ]\). -
\(\varGamma \) is finitely
 -satisfiable inXover\(\overline{b} \)(with respect to\(\mathcal {M} \)) if every finite subset of \(\varGamma \) is
-satisfiable inXover\(\overline{b} \)(with respect to\(\mathcal {M} \)) if every finite subset of \(\varGamma \) is  -satisfiable in X over \(\overline{b} \) (with respect to \(\mathcal {M} \)).
-satisfiable in X over \(\overline{b} \) (with respect to \(\mathcal {M} \)).
Note that if the only free variables in \(\varGamma \) are among  , then \(\varGamma \) is (finitely) \(\Sigma {}\)-satisfiable in X over \(\overline{b} \) iff it is (finitely)
, then \(\varGamma \) is (finitely) \(\Sigma {}\)-satisfiable in X over \(\overline{b} \) iff it is (finitely)  -satisfiable in X over \(\overline{b} \) iff it is (finitely)
-satisfiable in X over \(\overline{b} \) iff it is (finitely)  -satisfiable in X over \(\overline{b} \). We will just use the term “(finitely) satisfiable” when the distinction does not matter.
-satisfiable in X over \(\overline{b} \). We will just use the term “(finitely) satisfiable” when the distinction does not matter.
Definition 20
(Modal saturation) Assume \(\mathcal {F}\),  , and \(\Pi {}\) are not among
, and \(\Pi {}\) are not among  . A model \(\mathcal {M} \) is
. A model \(\mathcal {M} \) is  -saturated if for all \(w,v \in W\), all \(\overline{b} \in D\), and all sets
-saturated if for all \(w,v \in W\), all \(\overline{b} \in D\), and all sets  of
of  -formulas:
-formulas:
-
(a)
if \(\varGamma \) is finitely
 -satisfiable in
-satisfiable in  over \(\overline{b} \) (with respect to \(\mathcal {M} \)), then it is
over \(\overline{b} \) (with respect to \(\mathcal {M} \)), then it is  -satisfiable in
-satisfiable in  over \(\overline{b} \);
over \(\overline{b} \); -
(b)
if \(\varGamma \) is finitely
 -satisfiable in
-satisfiable in  over \(\overline{b} \) (with respect to \(\mathcal {M} \)), then it is
over \(\overline{b} \) (with respect to \(\mathcal {M} \)), then it is  -satisfiable in
-satisfiable in  over \(\overline{b} \).
over \(\overline{b} \).
If \(\mathcal {F}\) is among  , we just add the following clause:
, we just add the following clause:
-
(c)
if \(\varGamma \) is finitely
 -satisfiable in
-satisfiable in  over \(\overline{b} \) (with respect to \(\mathcal {M} \)), then it is
over \(\overline{b} \) (with respect to \(\mathcal {M} \)), then it is  -satisfiable in
-satisfiable in  over \(\overline{b} \).
over \(\overline{b} \).
If  is among
is among  , add the clauses above but with
, add the clauses above but with  replaced by
replaced by  .
.
Lemma 21
(Modal saturation implies the Hennessy–Milner property) Suppose \(\mathcal {M} \) and \(\mathcal {N} \) are  -saturated. Then
-saturated. Then  is an
is an  -bisimulation between \(\mathcal {M} \) and \(\mathcal {N} \). Hence, if
-bisimulation between \(\mathcal {M} \) and \(\mathcal {N} \). Hence, if  , then it follows that
, then it follows that  .
.
Proof
Suppose  . Clearly (Atomic) is satisfied (and likewise for (Ex) and (Eq) if \({\textsf {E}} \) or \(\approx \) are among
. Clearly (Atomic) is satisfied (and likewise for (Ex) and (Eq) if \({\textsf {E}} \) or \(\approx \) are among  ).
).
-
Zig-Zag.
Let \(u \in R^\mathcal {M} [v]\). Define
 . Let \(\varDelta \subseteq \varGamma \) be finite and nonempty. Then since \(u \in R^\mathcal {M} [v]\),
. Let \(\varDelta \subseteq \varGamma \) be finite and nonempty. Then since \(u \in R^\mathcal {M} [v]\),  . Since
. Since  (and since for each \(\psi \in \varDelta \), we could replace
(and since for each \(\psi \in \varDelta \), we could replace  with fresh new variables in \({\textsf {VAR}} \)), it follows that
with fresh new variables in \({\textsf {VAR}} \)), it follows that  . Hence, \(\varDelta \) is satisfiable in
. Hence, \(\varDelta \) is satisfiable in  over \(\overline{b} \). By
over \(\overline{b} \). By  -saturation, there is a \(u' \in R^\mathcal {N} [v']\) such that \(\mathcal {M} ,w,u' \Vdash \varGamma [\overline{b} ]\). Thus,
-saturation, there is a \(u' \in R^\mathcal {N} [v']\) such that \(\mathcal {M} ,w,u' \Vdash \varGamma [\overline{b} ]\). Thus,  . Likewise for the Zag clause. \(\checkmark \)
. Likewise for the Zag clause. \(\checkmark \) -
Back-Forth.
Let \(a' \in \delta ^\mathcal {M} (v)\). Define
 . Let \(\varDelta \subseteq \varGamma \) be finite and nonempty. Then
. Let \(\varDelta \subseteq \varGamma \) be finite and nonempty. Then  . Since
. Since  , it follows that
, it follows that 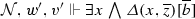 . Hence, \(\varDelta \) is
. Hence, \(\varDelta \) is  -satisfiable in
-satisfiable in  over \(\overline{b} \) with respect to \(\mathcal {N} \). By
over \(\overline{b} \) with respect to \(\mathcal {N} \). By  -saturation, \(\varGamma \) itself is
-saturation, \(\varGamma \) itself is  -satisfiable in
-satisfiable in  over \(\overline{b} \) with respect to \(\mathcal {N} \). So there is a \(b' \in \delta ^\mathcal {M} (v')\) such that \(\mathcal {N} ,w',v' \Vdash \varGamma [b',\overline{b} ]\). Thus,
over \(\overline{b} \) with respect to \(\mathcal {N} \). So there is a \(b' \in \delta ^\mathcal {M} (v')\) such that \(\mathcal {N} ,w',v' \Vdash \varGamma [b',\overline{b} ]\). Thus,  . Likewise for the Forth clause. \(\checkmark \)
. Likewise for the Forth clause. \(\checkmark \)
The \(\mathcal {F}\)-Zig-Zag-clauses are just like the Zig-Zag clause above, and the other quantifier Back-Forth clauses are just like the Back-Forth clauses above. The Act and Diag clauses are taken care of automatically by the fact that  (assuming \(@\)/\({\mathop {\downarrow }}\) is among
(assuming \(@\)/\({\mathop {\downarrow }}\) is among  ). \(\square \)
). \(\square \)
Definition 22
(Realization) Let  be
be  extended with
extended with  and \(\overline{t} \notin {\textsf {SVAR}} \). Let \(\overline{b} \in D\) and \(\overline{v} \in W\) where
and \(\overline{t} \notin {\textsf {SVAR}} \). Let \(\overline{b} \in D\) and \(\overline{v} \in W\) where  and \(\left| \overline{v} \right| = \left| \overline{t} \right| \). Let \(\mathcal {M} \) be a model, and let
and \(\left| \overline{v} \right| = \left| \overline{t} \right| \). Let \(\mathcal {M} \) be a model, and let  be a set of
be a set of  -formulas whose only free variables are among
-formulas whose only free variables are among  .
.
-
\(\varGamma \) is realized over\(\overline{b} \)and\(\overline{v} \)(with respect to\(\mathcal {M} \)) if there are some \(\overline{a} \in D\) and \(\overline{u} \in W\) such that \(\mathcal {M} \vDash \varGamma [\overline{a},\overline{b};\overline{u},\overline{v} ]\). We call \(\overline{b} \) and \(\overline{v} \)parameters.
-
\(\varGamma \) is finitely realized over\(\overline{b} \)and\(\overline{v} \)(with respect to\(\mathcal {M} \)) if every finite subset of \(\varGamma \) is realized over \(\overline{b} \) and \(\overline{v} \) (with respect to \(\mathcal {M} \)).
Definition 23
(Saturation) We will say \(\mathcal {M} \) is countably saturated if for every finite \(\overline{b} \in D\), every finite \(\overline{v} \in W\), and every set \(\varGamma \) of  -formulas (where
-formulas (where  and \(\left| \overline{v} \right| = \left| \overline{t} \right| \)) that is finitely realized over \(\overline{b} \) and \(\overline{v} \), \(\varGamma \) is also realized over \(\overline{b} \) and \(\overline{v} \).
and \(\left| \overline{v} \right| = \left| \overline{t} \right| \)) that is finitely realized over \(\overline{b} \) and \(\overline{v} \), \(\varGamma \) is also realized over \(\overline{b} \) and \(\overline{v} \).
Lemma 24
(Countable saturation implies modal saturation) If \(\mathcal {M} \) is countably saturated, then it is \(\mathcal {L}\)-saturated.
Proof
Let \(\mathcal {M} \) be a countably saturated model. Suppose a set  of
of  -formulas is finitely
-formulas is finitely  -satisfiable in
-satisfiable in  over \(\overline{b} \). Consider the set:
over \(\overline{b} \). Consider the set:

Let \(\varDelta \subseteq \varGamma \) be finite and nonempty. Since \(\varDelta \) is  -satisfiable in
-satisfiable in  , there is a \(u \in R[v]\) and some \(\overline{a} \in \delta (u)\) such that \(\mathcal {M} ,w,u \Vdash \varDelta [\overline{a},\overline{b} ]\). Let:
, there is a \(u \in R[v]\) and some \(\overline{a} \in \delta (u)\) such that \(\mathcal {M} ,w,u \Vdash \varDelta [\overline{a},\overline{b} ]\). Let:

Then \(\mathcal {M} \vDash \varDelta ^*[\overline{a},\overline{b};w,v,u]\). But \(\varDelta ^* \subseteq \varGamma ^*\) is finite. So every finite subset of \(\varGamma ^*\) is realized over \(\overline{b} \), w, v, and u. By countable saturation, there are some \(\overline{a} \in D\) and \(u \in W\) such that \(\mathcal {M} \vDash \varGamma ^*[\overline{a},\overline{b};w,v,u]\). But then \(u \in R[v]\), \(\overline{a} \in \delta (u)\), and \(\mathcal {M} ,w,u \Vdash \varGamma [\overline{a},\overline{b} ]\). So \(\varGamma \) is  -satisfiable in
-satisfiable in  . Likewise for
. Likewise for  -satisfiability in
-satisfiability in  , except you define:
, except you define:

Similarly for the other kinds of satisfiability. \(\square \)
It follows from Lemmas 21 and 24 that:
Corollary 25
(Countable saturation implies Hennessy–Miller property) If \(\mathcal {M} \) and \(\mathcal {N} \) are countably saturated, and it  , then it follows that
, then it follows that  .
.
Definition 26
(Ultraproducts) Let \(N \ne \emptyset \). An ultrafilter overN is a set \(U \subseteq \wp \left( N\right) \) where U is closed under supersets and finite intersections, \(\emptyset \notin U\), and for all \(S \in \wp \left( N\right) \), either \(S \in U\) or  . Let U be an ultrafilter over N. For each \(i \in N\), let \(W_i \ne \emptyset \). Then \(\prod _{i \in N} W_i\) is the set of functions \(f :N \rightarrow \bigcup _{i \in N} W_{i}\) where \(f(i) \in W_i\). We will say \(f \sim _U f'\) if
. Let U be an ultrafilter over N. For each \(i \in N\), let \(W_i \ne \emptyset \). Then \(\prod _{i \in N} W_i\) is the set of functions \(f :N \rightarrow \bigcup _{i \in N} W_{i}\) where \(f(i) \in W_i\). We will say \(f \sim _U f'\) if  . Define
. Define  . Finally, we will define the ultraproduct of\(W_i\)moduloU as the set
. Finally, we will define the ultraproduct of\(W_i\)moduloU as the set  . We will drop the subscript U when the ultrafilter in question is obvious from the context. An ultrapower is an ultraproduct where \(W_i = W\) for all \(i \in N\), which we may write as \(\prod _U W\).
. We will drop the subscript U when the ultrafilter in question is obvious from the context. An ultrapower is an ultraproduct where \(W_i = W\) for all \(i \in N\), which we may write as \(\prod _U W\).
Definition 27
(Ultrapowers of models) Let \(\mathcal {M} = \left\langle W,R,F,D,\delta ,I\right\rangle \) be a model. The ultrapower model of\(\mathcal {M} \)moduloU is the model \(\prod _U \mathcal {M} \) defined as follows:
-
\(W_U {:}{=}\prod _U W\)
-
\(R_U(\left[ f_1\right] ,\left[ f_2\right] )\) iff
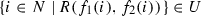
-
\(F_U(\left[ f_1\right] ,\left[ f_2\right] )\) iff
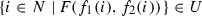
-
\(D_U {:}{=}\prod _U D\)
-
\(\left[ o\right] \in \delta _U\left( \left[ f\right] \right) \) iff
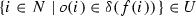
-
\(\left\langle \left[ o_1\right] ,\dots ,\left[ o_n\right] \right\rangle \in I_U(P,\left[ f\right] )\) iff
 .
.
It is a routine exercise to show that these definitions are well-defined, i.e., they do not depend on the representative of the equivalence class used in their statement.
Theorem 28
(Łoś ’s theorem) The following are equivalent:
-
(a)
\(\prod _U \mathcal {M} \vDash \alpha [\left[ o_1\right] ,\dots ,\left[ o_n\right] ]\).
-
(b)
 .
.
This can be proven by induction.Footnote 34 Now, define \({f_w}:{i}\mapsto {w}\) and \({o_a}:{i}\mapsto {a}\). If g is a variable assignment over \(\mathcal {M} \), define \({g_U}:{x}\mapsto {o_{g(x)}}\). Let the diagonal map be the map d from \(\mathcal {M} \) to \(\prod _U \mathcal {M} \) such that \(d(w) = f_w\) and \(d(a) = o_a\). Then it is a straightforward corollary of Theorem 28 that the diagonal map is an elementary embedding of \(\mathcal {M} \) into \(\prod _U \mathcal {M} \).
Say that U is countably incomplete if there is a countable subset of U whose intersection is not in U. A standard result from model theory shows that if U is countably incomplete, then \(\prod _U \mathcal {M} \) is countably saturated.Footnote 35 The important point, however, is that we can always find a countably saturated elementary extension of \(\mathcal {M} \) (viz., \(\prod _U \mathcal {M} \) where U is a countably incomplete ultrafilter). This is all we will need below.
Proof
(Theorem 13) Let  . It suffices to show (by the compactness of
. It suffices to show (by the compactness of  ) that \(\varGamma \vDash \alpha \). Suppose \(\mathcal {M} ,g \vDash \varGamma \). Define:
) that \(\varGamma \vDash \alpha \). Suppose \(\mathcal {M} ,g \vDash \varGamma \). Define:

It is easy to show that \(\varDelta \) is satisfiable (again by compactness). Let \(\mathcal {N} ,h \vDash \varDelta \). Then  by the way we defined \(\varDelta \). Now, by the results above, there exist elementary extensions \({e}:{\mathcal {M} }\preccurlyeq {\mathcal {M} '}\) and \({f}:{\mathcal {N} }\preccurlyeq {\mathcal {M} '}\) that are countably saturated. Since these are elementary embeddings:
by the way we defined \(\varDelta \). Now, by the results above, there exist elementary extensions \({e}:{\mathcal {M} }\preccurlyeq {\mathcal {M} '}\) and \({f}:{\mathcal {N} }\preccurlyeq {\mathcal {M} '}\) that are countably saturated. Since these are elementary embeddings:

By Corollary 25, since these are countably saturated:

Hence, by invariance under bisimulation, \(\mathcal {M} ',g' \vDash \alpha \) (where \(g'(x) = e(g(x))\). Since \({e}:{\mathcal {M} }\preccurlyeq {\mathcal {M} '}\), it follows that \(\mathcal {M} ,g \vDash \alpha \). \(\square \)
Appendix 2: Bisimulation proofs
In this appendix, we give more formal details regarding the bisimulation proofs from Sect. 4. We start with the proof of Proposition 15. Before reading, recall the definition of a partial isomorphism from Definition 14, and the definition of the models \(\mathcal {E} _1\) and \(\mathcal {E} _2\) (see Fig. 2 for a picture). Note that \(\mathcal {M} ,w,v,\overline{a} \simeq \mathcal {N} ,w',v',\overline{b} \) iff the map \(a_i \mapsto b_i\) is a partial isomorphism between them. In particular, for our models \(\mathcal {E} _1\) and \(\mathcal {E} _2\), if \(a_i \in \delta _1(v_1)\) iff \(b_i \in \delta _2(v_2)\) and \(a_i = a_j\) iff \(b_i = b_j\), then \(\mathcal {E} _1,w_\mathbb {N} ,v_1,\overline{a} \simeq \mathcal {E} _2,w_\mathbb {N} ,v_2,\overline{b} \), since this means \(a_i \mapsto b_i\) is a partial isomorphism. We will make use of this implicitly throughout.
We will define our bisimulation in stages. First, set  . Next, suppose we have constructed \(Z_i\) so that for all \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \in Z_i\), \(\left| \delta _1(v_1) \right| = \left| \delta _2(v_2) \right| \) and \(\mathcal {E} _1,w_\mathbb {N} ,v_1,\overline{a} \simeq \mathcal {E} _2,w_\mathbb {N} ,v_2,\overline{b} \). (Clearly this holds for \(Z_0\).) Define the following sets:
. Next, suppose we have constructed \(Z_i\) so that for all \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \in Z_i\), \(\left| \delta _1(v_1) \right| = \left| \delta _2(v_2) \right| \) and \(\mathcal {E} _1,w_\mathbb {N} ,v_1,\overline{a} \simeq \mathcal {E} _2,w_\mathbb {N} ,v_2,\overline{b} \). (Clearly this holds for \(Z_0\).) Define the following sets:

Set \(Z_{i+1} {:}{=}Z_i \cup Z_i^\text {ZZ-fin} \cup Z_i^\text {ZZ-cofin} \cup Z_i^\text {BF}\).
Lemma 29
(This construction can continue) If \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \in Z_{i+1}\), then \(\left| \delta _1(v_1) \right| = \left| \delta _2(v_2) \right| \) and \(\mathcal {E} _1,w_\mathbb {N} ,v_1,\overline{a} \simeq \mathcal {E} _2,w_\mathbb {N} ,v_2,\overline{b} \).
Proof
Suppose \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \in Z_{i+1}\). If \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \in Z_i\), then this is obvious. Otherwise, \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \) is either in \(Z_i^\text {ZZ-fin}\), \(Z_i^\text {ZZ-cofin}\), or \(Z_i^\text {BF}\).
-
Case 1: \(Z_i^\text {ZZ-fin}\). So \(v_1 = w_S\) and \(v_2 = w_T\) for some S and T. By the fact that \(\left| S \right| = \left| T \right| \), \(\left| \delta _1(v_1) \right| = \left| \delta _2(v_2) \right| \). And by construction, \(a_i \in S\) iff \(b_i \in T\), so \(a_i \in \delta _1(v_1)\) iff \(b_i \in \delta _2(v_2)\), and thus \(\mathcal {E} _1,w_\mathbb {N} ,v_1,\overline{a} \simeq \mathcal {E} _2,w_\mathbb {N} ,v_2,\overline{b} \). \(\checkmark \)
-
Case 2: \(Z_i^\text {ZZ-cofin}\). Same reasoning, only we know
 . \(\checkmark \)
. \(\checkmark \) -
Case 3: \(Z_i^\text {BF}\). We already know \(\left| \delta _1(v_1) \right| = \left| \delta _2(v_2) \right| \) since this was guaranteed by \(Z_i\). Moreover, both \(a \in \delta _1(v_1)\) and \(b \in \delta _2(v_2)\), so we still meet (Existence). And by the fact that \(a = a_i\) iff \(b = b_i\), we still meet (Equality). \(\checkmark \)
\(\square \)
Lemma 29 guarantees we can continue the construction. Finally, define \(Z \,{:}{=}\, \bigcup _{i \in \omega } Z_i\).
Proof
(Proposition 15) Suppose \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \in Z\). Then there is some i such that \(\left\langle w_\mathbb {N} ,v_1,\overline{a};w_\mathbb {N} ,v_2,\overline{b} \right\rangle \in Z_i\). By Lemma 29, \(\mathcal {E} _1,w_\mathbb {N} ,v_1,\overline{a} \simeq \mathcal {E} _2,w_\mathbb {N} ,v_2,\overline{b} \), so (Atomic) and (Eq) (as well as (Ex)) are satisfied.
-
Zig.
Let \(u_1 \in W_1\). Suppose that \(u_1 = w_S\) for some finite nonempty \(S \subseteq \mathbb {N} \). We want to show that there is a \(T \subseteq \mathbb {N} ^\infty \) such that \(\left\langle w_\mathbb {N} ,w_S,\overline{a};w_\mathbb {N} ,w_T,\overline{b} \right\rangle \in Z_i^\text {ZZ-fin}\). List the elements
 . Let
. Let  be n-many distinct elements from
be n-many distinct elements from  , and set
, and set  . Then \(T \subseteq \mathbb {N} ^\infty \) is also finite and nonempty, \(\left| S \right| = \left| T \right| \), and \(a_i \in S\) iff \(b_i \in T\). So \(\left\langle w_\mathbb {N} ,w_S,\overline{a};w_\mathbb {N} ,w_T,\overline{b} \right\rangle \in Z_i^\text {ZZ-fin}\). The case where \(u_1 = w_{\mathbb {N} - S}\) is essentially the same, except one does not need \(\left| S \right| = \left| T \right| \). \(\checkmark \)
. Then \(T \subseteq \mathbb {N} ^\infty \) is also finite and nonempty, \(\left| S \right| = \left| T \right| \), and \(a_i \in S\) iff \(b_i \in T\). So \(\left\langle w_\mathbb {N} ,w_S,\overline{a};w_\mathbb {N} ,w_T,\overline{b} \right\rangle \in Z_i^\text {ZZ-fin}\). The case where \(u_1 = w_{\mathbb {N} - S}\) is essentially the same, except one does not need \(\left| S \right| = \left| T \right| \). \(\checkmark \) -
Zag.
As above. \(\checkmark \)
-
Forth.
Let \(a \in \delta _1(v_1)\). If \(a = a_i\), then we can just pick \(b = b_i\), and note that \(\left\langle w_\mathbb {N} ,v_1,\overline{a},a_i;w_\mathbb {N} ,v_2,\overline{b},b_i\right\rangle \in Z_i^\text {BF}\). So suppose a is not among \(\overline{a} \). Since \(\left| \delta _1(v_1) \right| = \left| \delta _2(v_2) \right| \), we have that
 . And the former is not empty since
. And the former is not empty since  . So pick any
. So pick any  . Then we have that \(\left\langle w_\mathbb {N} ,v_1,\overline{a},a;w_\mathbb {N} ,v_2,\overline{b},b\right\rangle \in Z_i^\text {BF}\). \(\checkmark \)
. Then we have that \(\left\langle w_\mathbb {N} ,v_1,\overline{a},a;w_\mathbb {N} ,v_2,\overline{b},b\right\rangle \in Z_i^\text {BF}\). \(\checkmark \) -
Back.
As above. \(\checkmark \)
\(\square \)
Now for the proof of Proposition 16. As before, set  . Now suppose we have constructed \(Z_i\) and for all \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \in Z_i\), \(\mathcal {R} _1,w,u_1,\overline{a} \simeq \mathcal {R} _2,w,\overline{u} _2,\overline{b} \) and \(u_1 = w\) iff \(u_2 = w\). Define the following sets:
. Now suppose we have constructed \(Z_i\) and for all \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \in Z_i\), \(\mathcal {R} _1,w,u_1,\overline{a} \simeq \mathcal {R} _2,w,\overline{u} _2,\overline{b} \) and \(u_1 = w\) iff \(u_2 = w\). Define the following sets:

Then set: \(Z_{i+1} = Z_i \cup Z_i^\text {Act} \cup Z_i^\text {ZZ} \cup Z_i^{\mathrm{ZZ}\emptyset } \cup Z_i^\text {BF}\).
Lemma 30
(This construction can continue too) If \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \in Z_{i+1}\), then \(\mathcal {R} _1,w,u_1,\overline{a} \simeq \mathcal {R} _2,w,\overline{u} _2,\overline{b} \) and \(u_1 = w\) iff \(u_2 = w\).
Proof
Suppose \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \in Z_{i+1}\). It is easy to verify that \(u_1 = w\) iff \(u_2 = w\) by looking at the constructions above. If \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \in Z_i\), then we are done. So suppose \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \notin Z_i\).
First, (Predicate). If \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \in Z_i^\text {Act} \cup Z_i^\text {ZZ} \cup Z_i^{\mathrm{ZZ}\emptyset }\), then we know  . So \(\mathcal {R} _1,w,u_1',\overline{a} \simeq \mathcal {R} _2,w,u_2',\overline{b} \). But since \(u_1' = w\) iff \(u_2' = w\), that means \(a_i \in \mathbb {N} \) iff \(b_i \in \mathbb {N} \). So since \(u_1 = w\) iff \(u_2 = w\), \(\mathcal {R} _1,w,u_1,\overline{a} \) and \(\mathcal {R} _2,w,u_2,\overline{b} \) satisfy (Predicate). If instead \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle = \left\langle w,u_1,\overline{c},c;w,u_2,\overline{d},d\right\rangle \in Z_i^\text {BF}\), then \(\left\langle w,u_1,\overline{c};w,u_2,\overline{d} \right\rangle \in Z_i\), which (by the same reasoning as above) means \(c_i \in \mathbb {N} \) iff \(d_i \in \mathbb {N} \). And by construction of \(Z_i^\text {BF}\), \(c \in \mathbb {N} \) iff \(d \in \mathbb {N} \). So since \(u_1 = w\) iff \(u_2 = w\), again \(\mathcal {R} _1,w,u_1,\overline{a} \) and \(\mathcal {R} _2,w,u_2,\overline{b} \) satisfy (Predicate).
. So \(\mathcal {R} _1,w,u_1',\overline{a} \simeq \mathcal {R} _2,w,u_2',\overline{b} \). But since \(u_1' = w\) iff \(u_2' = w\), that means \(a_i \in \mathbb {N} \) iff \(b_i \in \mathbb {N} \). So since \(u_1 = w\) iff \(u_2 = w\), \(\mathcal {R} _1,w,u_1,\overline{a} \) and \(\mathcal {R} _2,w,u_2,\overline{b} \) satisfy (Predicate). If instead \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle = \left\langle w,u_1,\overline{c},c;w,u_2,\overline{d},d\right\rangle \in Z_i^\text {BF}\), then \(\left\langle w,u_1,\overline{c};w,u_2,\overline{d} \right\rangle \in Z_i\), which (by the same reasoning as above) means \(c_i \in \mathbb {N} \) iff \(d_i \in \mathbb {N} \). And by construction of \(Z_i^\text {BF}\), \(c \in \mathbb {N} \) iff \(d \in \mathbb {N} \). So since \(u_1 = w\) iff \(u_2 = w\), again \(\mathcal {R} _1,w,u_1,\overline{a} \) and \(\mathcal {R} _2,w,u_2,\overline{b} \) satisfy (Predicate).
Next, (Existence). This is trivial if \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \in Z_i^\text {Act}\), since \(\delta _1(w) = \delta _2(w) = \mathbb {Z} \). It is guaranteed by construction in all other cases.
Finally, (Equality). This is trivial in every case, except \(Z_i^\text {BF}\), in which case it is guaranteed by construction. \(\square \)
As before, define \(Z \,{:}{=}\, \bigcup _{i \in \omega } Z_i\).
Proof
(Proposition 16) Suppose \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \in Z\). Then there is an i such that \(\left\langle w,u_1,\overline{a};w,u_2,\overline{b} \right\rangle \in Z_i\). By Lemma 30, (Atomic) and (Eq) (as well as (Ex)) are satisfied.
-
Act.
By construction of \(Z_i^\text {Act}\), \(\left\langle w,w,\overline{a};w,w,\overline{b} \right\rangle \in Z_{i+1}\). \(\checkmark \)
-
Zig.
Let \(u_1' \in W_1\). If \(u_1' = w\), then this is covered by the above case. So let \(u_1' = v_S\) instead. Define
 where
where  is arbitrary. Then T is finite and nonempty, and \(a_i \in S\) iff \(b_i \in T\). So \(\left\langle w,v_S,\overline{a};w,v_T,\overline{b} \right\rangle \in Z_i^\text {ZZ}\). \(\checkmark \)
is arbitrary. Then T is finite and nonempty, and \(a_i \in S\) iff \(b_i \in T\). So \(\left\langle w,v_S,\overline{a};w,v_T,\overline{b} \right\rangle \in Z_i^\text {ZZ}\). \(\checkmark \) -
Zag.
As above, except in the case where we pick \(v_\emptyset \in W_2\). In that case, let \(S \subseteq \mathbb {N} \) be any finite nonempty set such that
 . Then \(\left\langle w,v_S,\overline{a};w,v_\emptyset ,\overline{b} \right\rangle \in Z_i^{\mathrm{ZZ}\emptyset }\). \(\checkmark \)
. Then \(\left\langle w,v_S,\overline{a};w,v_\emptyset ,\overline{b} \right\rangle \in Z_i^{\mathrm{ZZ}\emptyset }\). \(\checkmark \) -
Back.
Let \(a \in \delta _1(u_1)\) (we assume without loss of generality that
 ). If \(a \in \mathbb {N} ^-\), then pick any new \(b \in \mathbb {N} ^-\). If instead \(a \in \mathbb {N} \), then since \(\delta _2(u_2) \cap \mathbb {N} \) is infinite, pick any new \(b \in \delta _2(u_2) \cap \mathbb {N} \). Either way, \(\left\langle w,u_1,\overline{a},a;w,u_2,\overline{b},b\right\rangle \in Z_i^\text {BF}\). \(\checkmark \)
). If \(a \in \mathbb {N} ^-\), then pick any new \(b \in \mathbb {N} ^-\). If instead \(a \in \mathbb {N} \), then since \(\delta _2(u_2) \cap \mathbb {N} \) is infinite, pick any new \(b \in \delta _2(u_2) \cap \mathbb {N} \). Either way, \(\left\langle w,u_1,\overline{a},a;w,u_2,\overline{b},b\right\rangle \in Z_i^\text {BF}\). \(\checkmark \) -
Forth.
As above. \(\checkmark \)
\(\square \)
Other inexpressibility proofs are straightforward once the winning strategy for Eloïse is worked out.
Appendix 3: Inexpressibility in 
In this appendix, we will prove that (4) is not expressible as an  -formula. Recall (4):
-formula. Recall (4):

First, we define our models \(\mathcal {R} _3 = \left\langle W_3,R_3,F_3,D_3,\delta _3,I_3\right\rangle \) and \(\mathcal {R} _4 = \left\langle W_4,R_4,F_4,D_4,\delta _4,I_4\right\rangle \). Our global domains will contain \(\mathbb {Z} \) plus a disjoint copy of \(\mathbb {N} \), which we will call  . So \(D_3 = D_4 = \mathbb {Z} \cup \mathbb {N} _\infty \). All the accessibility relations are universal in their respective models. If \(T \subseteq \mathbb {N} \), let
. So \(D_3 = D_4 = \mathbb {Z} \cup \mathbb {N} _\infty \). All the accessibility relations are universal in their respective models. If \(T \subseteq \mathbb {N} \), let  . Please note: throughout this section, when we write
. Please note: throughout this section, when we write  , we mean \(\mathbb {N} _\infty - T\); when we write
, we mean \(\mathbb {N} _\infty - T\); when we write  where \(S \subseteq \mathbb {N} \), we mean \(\mathbb {N} - S\).
where \(S \subseteq \mathbb {N} \), we mean \(\mathbb {N} - S\).
For each finite nonempty\(S \subseteq \mathbb {N} \), and each finite \(T \subseteq \mathbb {N} \), \(W_1\) will contain a world \(w^T_S\) and a world \(v^T_S\). Intuitively, \(w^T_S\) is a world where (i) every negative integer is poor, (ii) every integer of \((\mathbb {N} - S)\) is rich, (iii) every object of \(T_\infty \) is rich, and (iv) nothing in  exists. \(v^T_S\) is like \(w^T_S\) except the rich and the poor are flipped. In addition, for any finite \(T \subseteq \mathbb {N} \), there will be a world of the form \(w^T_\emptyset \) in \(W_1\) (our actual world will be \(w {:}{=}w^\emptyset _\emptyset \)). \(W_2\) is like \(W_1\) except it also contains worlds of the form \(v^T_\emptyset \). See Fig. 7 for a picture.
exists. \(v^T_S\) is like \(w^T_S\) except the rich and the poor are flipped. In addition, for any finite \(T \subseteq \mathbb {N} \), there will be a world of the form \(w^T_\emptyset \) in \(W_1\) (our actual world will be \(w {:}{=}w^\emptyset _\emptyset \)). \(W_2\) is like \(W_1\) except it also contains worlds of the form \(v^T_\emptyset \). See Fig. 7 for a picture.
Observe \(\mathcal {R} _3 \nvDash \) (4)[w] while \(\mathcal {R} _4 \vDash \) (4)[w]. Furthermore, recall that the reason \(\mathcal {R} _1\) and \(\mathcal {R} _2\) could not be used to show that (4) is not expressible as an  -formula was because they disagreed on the following formulas at w:
-formula was because they disagreed on the following formulas at w:


Observe that this is no longer the case: w does not satisfy either (8) or (9) in \(\mathcal {R} _3\) or \(\mathcal {R} _4\).
Proposition 31
(Strengthened inexpressibility of (R)) \(\mathcal {R} _3,w,w \leftrightarrows _{\approx ,@,{\mathop {\downarrow }},\mathcal {F}} \mathcal {R} _4,w,w\).
Proof
Clearly \(\mathcal {R} _3,w,w \simeq \mathcal {R} _4,w,w\). So suppose that \(\mathcal {R} _3,s^{T_1}_{S_1},t^{T_2}_{S_2},\overline{a} \simeq \mathcal {R} _4,s^{T_1'}_{S_1'}, t^{T_2'}_{S_2'},\overline{b} \), where:

Notice in particular that \(\mathcal {R} _3,w,w \simeq \mathcal {R} _4,w,w\) meets all of these constraints vacuously. We will show using (I)–(V) that, regardless of Abelard’s move, Eloïse can continue the game in a way that preserves (I)–(V). Note throughout that if I use the same letter, say u, for \(u^T_S\) and \(u^{T'}_{S'}\), I mean for \(u^T_S\) to be a w-world iff \(u^{T'}_{S'}\) is a w-world.
First, suppose Abelard decides to pick an object \(a \in \delta _3(t^{T_2}_{S_2})\) (the case where he picks a \(b \in \delta _4(t^{T_2'}_{S_2'})\) is symmetric). If he does this, then obviously (I) and (V) are met regardless of what Eloïse picks. So she just needs to ensure (II)–(IV) are met. If \(a \in \mathbb {N} ^-\), then Eloïse can pick an arbitrary \(b \in \mathbb {N} ^-\) that has not already been picked. Otherwise, since \(a \in \delta _3(t^{T_2}_{S_2})\), that means  . There are two cases to consider:
. There are two cases to consider:
-
Case 1:
 . That means \(a \in (\mathbb {N} - (S_1 \cup S_2)) \cup (T_{1\infty } \cup T_{2\infty })\). But since \(S_1'\), \(S_2'\), \(T_1'\), and \(T_2'\) are all finite, there will be infinitely many \(b \in (\mathbb {N} - (S_1' \cup S_2')) \cup (T_{1\infty }' \cup T_{2\infty }')\) that have not been picked yet. So Eloïse can just pick an arbitrary one of those, in which case
. That means \(a \in (\mathbb {N} - (S_1 \cup S_2)) \cup (T_{1\infty } \cup T_{2\infty })\). But since \(S_1'\), \(S_2'\), \(T_1'\), and \(T_2'\) are all finite, there will be infinitely many \(b \in (\mathbb {N} - (S_1' \cup S_2')) \cup (T_{1\infty }' \cup T_{2\infty }')\) that have not been picked yet. So Eloïse can just pick an arbitrary one of those, in which case  and
and  . \(\checkmark \)
. \(\checkmark \) -
Case 2:
 . That means we need to ensure that
. That means we need to ensure that  while also ensuring that
while also ensuring that  . That means we need:
. That means we need: 
But since \(\left| (S_1 - S_2) \cup (T_{2\infty } - T_{1\infty }) \right| = \left| (S_1' - S_2') \cup (T_{2\infty }' - T_{1\infty }') \right| \), and since (II)–(IV) hold for \(\overline{a} \) and \(\overline{b} \), it is easy to show that:

Hence, there must be some \(b \in (S_1' - S_2') \cup (T_{2\infty }' - T_{1\infty }')\) that has not been picked yet. So Eloïse can just pick an arbitrary one of those. \(\checkmark \)
Next, suppose Abelard decides to relocate the game. If he uses the \(@\) or \({\mathop {\downarrow }}\) moves, then the constraints will all be vacuously satisfied. So suppose he decides to relocate the game in \(\mathcal {R} _3\) to \(\left\langle s^{T_1}_{S_1},u^{T_3}_{S_3}\right\rangle \). If \(T_3 = T_1\) and \(S_3 = S_1\), then Eloïse should pick \(u^{T_1'}_{S_1'}\). If \(T_3 = T_2\) and \(S_3 = S_2\), then she should pick \(u^{T_2'}_{S_2'}\). Otherwise, Eloïse can pick a \(T_3'\) and \(S_3'\) using a different method as follows. Define the following sets:

One can verify that if \(S_3' \subseteq \mathbb {N} \) and \(T_{3\infty }' \subseteq \mathbb {N} _\infty \) such that  and
and  , then
, then  iff
iff  . We will now show the following:
. We will now show the following:
Claim
There are \(S_3' \subseteq \mathbb {N} \) and \(T_{3\infty }' \subseteq \mathbb {N} _\infty \) such that:
-
1.

-
2.
 , and
, and -
3.
\(\left| (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty }) \right| = \left| (S_1' - S_3') \cup (T_{3\infty }' - T_{1\infty }') \right| \).
Suppose not. That is, suppose that every \(S_3' \subseteq \mathbb {N} \) and \(T_{3\infty }' \subseteq \mathbb {N} _\infty \) that satisfy (i) and (ii) fail to satisfy (iii). We will show that from this assumption, we can derive a contradiction.
First, suppose there is an \(S_3' \subseteq \mathbb {N} \) and \(T_{3\infty }' \subseteq \mathbb {N} _\infty \) satisfying (i) and (ii) such that \(\left| (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty }) \right| > \left| (S_1' - S_3') \cup (T_{3\infty }' - T_{1\infty }') \right| \). Let n be such that \(\left| (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty }) \right| = \left| (S_1' - S_3') \cup (T_{3\infty }' - T_{1\infty }') \right| + n\) (both sets are finite after all). Since \(T_{1\infty }'\) and \(T_{3\infty }'\) are finite, we can pick n arbitrary objects  and set
and set  . But then \(\left| (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty }) \right| = \left| (S_1' - S_3') \cup (T_{3\infty }'' - T_{1\infty }') \right| \), and (ii) is still met replacing \(T_{3\infty }'\) with \(T_{3\infty }''\).
. But then \(\left| (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty }) \right| = \left| (S_1' - S_3') \cup (T_{3\infty }'' - T_{1\infty }') \right| \), and (ii) is still met replacing \(T_{3\infty }'\) with \(T_{3\infty }''\). 
Hence, it must be that for every \(S_3' \subseteq \mathbb {N} \) and \(T_{3\infty }' \subseteq \mathbb {N} _\infty \) satisfying (i) and (ii), \(\left| (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty }) \right| < \left| (S_1' - S_3') \cup (T_{3\infty }' - T_{1\infty }') \right| \). Now, we can assume without loss of generality that  and
and  . Here is why. Suppose
. Here is why. Suppose  . Then pick a
. Then pick a  and set
and set  . Then \(\left| S_1' - S_3'' \right| < \left| S_1' - S_3' \right| \), so \(\left| (S_1' - S_3'') \cup (T_{3\infty }' - T_{1\infty }') \right| < \left| (S_1' - S_3') \cup (T_{3\infty }' - T_{1\infty }') \right| \). \(S_3''\) still satisfies (i), so by hypothesis, it still must be that \(\left| (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty }) \right| < \left| (S_1' - S_3'') \cup (T_{3\infty }' - T_{1\infty }') \right| \). So we can just keep adding objects from
. Then \(\left| S_1' - S_3'' \right| < \left| S_1' - S_3' \right| \), so \(\left| (S_1' - S_3'') \cup (T_{3\infty }' - T_{1\infty }') \right| < \left| (S_1' - S_3') \cup (T_{3\infty }' - T_{1\infty }') \right| \). \(S_3''\) still satisfies (i), so by hypothesis, it still must be that \(\left| (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty }) \right| < \left| (S_1' - S_3'') \cup (T_{3\infty }' - T_{1\infty }') \right| \). So we can just keep adding objects from  to \(S_3'\) in this way until
to \(S_3'\) in this way until  . Likewise, we can keep removing objects in \(T_{3\infty }'\) from
. Likewise, we can keep removing objects in \(T_{3\infty }'\) from  until
until  .
.
Thus, we may assume that  and
and  . It follows that
. It follows that  . But if \(b_i \in (S_1' - S_3') \cup (T_{3\infty }' - T_{1\infty }')\), then \(a_i \in (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty })\) by (III) and by the fact that (i) and (ii) imply that
. But if \(b_i \in (S_1' - S_3') \cup (T_{3\infty }' - T_{1\infty }')\), then \(a_i \in (S_1 - S_3) \cup (T_{3\infty } - T_{1\infty })\) by (III) and by the fact that (i) and (ii) imply that  iff
iff  . This gives rise to an injection from
. This gives rise to an injection from  to
to  , which means
, which means  .
.  This completes our proof of the claim above.
This completes our proof of the claim above.
Thus, Eloïse can just pick any such \(S_3'\) and \(T_{3\infty }'\), and it will have the desired properties. If instead Abelard decides to relocate the game in \(\mathcal {R} _4\), the strategy is the same: the reasoning above did not rely on Abelard’s \(S_3\) being nonempty. Finally, the case where Abelard decides to relocate the game in \(\mathcal {R} _3\) to \(\left\langle u^{T_3}_{S_3},t^{T_2}_{S_1}\right\rangle \) is symmetric. \(\square \)
Appendix 4: Mapping the expressive hierarchy
In this appendix, we map out in more detail the relative expressive power for various fragments of  . We will start by showing that, ignoring \({\textsf {E}} \), \(\approx \), and \(\Pi {}\), the relative expressive power for the remaining languages is accurately diagrammed by Fig. 8. This includes the strict inclusions and incomparabilities the diagram suggests. Note that for any class of models \(\mathbf C \), \(\le _\mathbf C \) is a preorder.
. We will start by showing that, ignoring \({\textsf {E}} \), \(\approx \), and \(\Pi {}\), the relative expressive power for the remaining languages is accurately diagrammed by Fig. 8. This includes the strict inclusions and incomparabilities the diagram suggests. Note that for any class of models \(\mathbf C \), \(\le _\mathbf C \) is a preorder.
Lemma 32
(Adding only \({\mathop {\downarrow }}\) does nothing)  .
.
Proof
First, note that, by induction, for any  -formula \(\varphi \), \(\mathcal {M} ,w,v,g \Vdash \varphi \) iff \(\mathcal {M} ,w',v,g \Vdash \varphi \). Thus, where \(\varphi \) is an
-formula \(\varphi \), \(\mathcal {M} ,w,v,g \Vdash \varphi \) iff \(\mathcal {M} ,w',v,g \Vdash \varphi \). Thus, where \(\varphi \) is an  -formula, let \(\varphi ^-\) be the result of removing every instance of \({\mathop {\downarrow }}\) from \(\varphi \). Then it is easy to show by induction (using this fact for the \({\mathop {\downarrow }}\)-case) that \(\Vdash \varphi \leftrightarrow \varphi ^-\). Hence,
-formula, let \(\varphi ^-\) be the result of removing every instance of \({\mathop {\downarrow }}\) from \(\varphi \). Then it is easy to show by induction (using this fact for the \({\mathop {\downarrow }}\)-case) that \(\Vdash \varphi \leftrightarrow \varphi ^-\). Hence,  , and therefore
, and therefore  . \(\square \)
. \(\square \)
Throughout, when I say “\(I^\mathcal {M} \) is empty” or “\(I^\mathcal {M} = \emptyset \)”, what I mean is that for all \(w \in W^\mathcal {M} \) and all predicates P, \(I^\mathcal {M} (P,w) = \emptyset \). Also, if \(\overline{a} \) is clear from context, I will use “\(a_i\)” to stand for an arbitrary element of \(\overline{a} \).
Lemma 33
(Adding \(\mathcal {F}\))  .
.
Proof
Let \(\mathcal {M} _1 = \left\langle W_1,R_1,F_1,D_1,\delta _1,I_1\right\rangle \), where  ,
,  ,
,  , and \(I_1 = \emptyset \). Let \(\mathcal {M} _2\) be just like \(\mathcal {M} _1\) except \(F_2 = \emptyset \). Then \(\mathcal {M} _1,w,w \leftrightarrows _{\approx ,@,{\mathop {\downarrow }},\Pi {}} \mathcal {M} _2,w,w\), but \(\mathcal {M} _1,w,w \nVdash \mathcal {F}\bot \) while \(\mathcal {M} _2,w,w \Vdash \mathcal {F}\bot \). \(\square \)
, and \(I_1 = \emptyset \). Let \(\mathcal {M} _2\) be just like \(\mathcal {M} _1\) except \(F_2 = \emptyset \). Then \(\mathcal {M} _1,w,w \leftrightarrows _{\approx ,@,{\mathop {\downarrow }},\Pi {}} \mathcal {M} _2,w,w\), but \(\mathcal {M} _1,w,w \nVdash \mathcal {F}\bot \) while \(\mathcal {M} _2,w,w \Vdash \mathcal {F}\bot \). \(\square \)
Where \(\mathcal {M} \) is a model, let \(\mathcal {M} ^{{\textsf {E}} \rightarrow P}\) be the model just like \(\mathcal {M} \) except \(I^{\mathcal {M} ^{{\textsf {E}} \rightarrow P}}(P,w) = \delta ^\mathcal {M} (w)\) for all \(w \in W^\mathcal {M} \). That is, \(\mathcal {M} ^{{\textsf {E}} \rightarrow P}\) effectively makes P an existence predicate. Define \(\mathcal {M} ^{\approx \rightarrow P}\) likewise. It will be useful to note the following:
Lemma 34
(Replacing \({\textsf {E}} \)) If \(\mathcal {M} ,w,v,\overline{a} \leftrightarrows _{\mathcal {L}({\textsf {E}})} \mathcal {N} ,w',v',\overline{b} \), then \(\mathcal {M} ^{{\textsf {E}} \rightarrow P},w,v,\overline{a} \leftrightarrows _{\mathcal {L}({\textsf {E}})} \mathcal {N} ^{{\textsf {E}} \rightarrow P},w',v',\overline{b} \). In addition, if \(I^\mathcal {M} (P,u) = \emptyset = I^\mathcal {N} (P,u')\) for all \(u \in W^\mathcal {M} \) and all \(u' \in W^\mathcal {N} \), then the converse holds as well. Likewise for \(\approx \) in place of \({\textsf {E}} \).
We can use this trick to bootstrap off of previous inexpressibility results which used \({\textsf {E}} \) or \(\approx \) for languages without \({\textsf {E}} \) or \(\approx \). For instance, it is relatively easy to show  . Take models \(\mathcal {E} _1\) and \(\mathcal {E} _2\) from Fig. 2. Since \(\mathcal {E} _1,w_\mathbb {N} ,w_\mathbb {N} \leftrightarrows _{\approx } \mathcal {E} _2,w_\mathbb {N} ,w_\mathbb {N} \), we can use Lemma 34 to conclude \(\mathcal {E} _1^{{\textsf {E}} \rightarrow P},w_\mathbb {N} ,w_\mathbb {N} \leftrightarrows _{\approx } \mathcal {E} _2^{{\textsf {E}} \rightarrow P},w_\mathbb {N} ,w_\mathbb {N} \), though they disagree on
. Take models \(\mathcal {E} _1\) and \(\mathcal {E} _2\) from Fig. 2. Since \(\mathcal {E} _1,w_\mathbb {N} ,w_\mathbb {N} \leftrightarrows _{\approx } \mathcal {E} _2,w_\mathbb {N} ,w_\mathbb {N} \), we can use Lemma 34 to conclude \(\mathcal {E} _1^{{\textsf {E}} \rightarrow P},w_\mathbb {N} ,w_\mathbb {N} \leftrightarrows _{\approx } \mathcal {E} _2^{{\textsf {E}} \rightarrow P},w_\mathbb {N} ,w_\mathbb {N} \), though they disagree on  .
.
However, this proof does not show that  , since the models are distinguishable by \(\Sigma {x}\lnot P(x)\). Lemma 35 strengthens this result to include \(\Pi {}\), again using Lemma 34:Footnote 36
, since the models are distinguishable by \(\Sigma {x}\lnot P(x)\). Lemma 35 strengthens this result to include \(\Pi {}\), again using Lemma 34:Footnote 36
Lemma 35
(Adding \(@\))  .
.
Proof
It is easy to show that if \(\varphi \) is an  -formula, then \(\Vdash _\mathbf U \mathcal {F}\varphi \leftrightarrow \varphi \) (just use the observation from the proof of Lemma 32). So every
-formula, then \(\Vdash _\mathbf U \mathcal {F}\varphi \leftrightarrow \varphi \) (just use the observation from the proof of Lemma 32). So every  -formula is \(\mathbf U \)-equivalent to an
-formula is \(\mathbf U \)-equivalent to an  -formula. But if \(\psi \) is an
-formula. But if \(\psi \) is an  -formula, then \(\Vdash _\mathbf U {\mathop {\downarrow }}\psi \leftrightarrow \psi \). Putting these together, every
-formula, then \(\Vdash _\mathbf U {\mathop {\downarrow }}\psi \leftrightarrow \psi \). Putting these together, every  -formula is \(\mathbf U \)-equivalent to an
-formula is \(\mathbf U \)-equivalent to an  -formula. So it suffices to find two
-formula. So it suffices to find two  -bisimilar models in UD that disagree on some
-bisimilar models in UD that disagree on some  -formula.
-formula.
Let \(\mathcal {M} _1 = \left\langle W_1,R_1,F_1,D_1,\delta _1,I_1\right\rangle \), where:

\(R_1\) and \(F_1\) are universal, \(D_1 = \mathbb {Z} \), \(\delta _1(w) = \mathbb {N} \), \(\delta _1(v_S) = (\mathbb {N} - S) \cup T\), and \(I_1 = \emptyset \). Let \(\mathcal {M} _2\) be like \(\mathcal {M} _1\) except that  , and
, and  . Observe:
. Observe:

However, we will show that \(\mathcal {M} _1,w,w \leftrightarrows _{\approx ,\Pi {}} \mathcal {M} _2,w,w\). Clearly \(w,w \simeq w,w\). Suppose \(w,u_1,\overline{a} \simeq w,u_2,\overline{b} \). Since \(\delta _1(u_1)\) and  are infinite, if Abelard picks an \(a' \in D_1\), then Eloïse can find a \(b' \in D_2\) so that \(w,u_1,\overline{a},a' \simeq w,u_2,\overline{b},b'\) by ensuring that \(a' \in \delta _1(u_1)\) iff \(b' \in \delta _2(u_2)\). Likewise if Abelard picks a \(b' \in D_2\). Now, suppose Abelard picks an \(u_1' \in W_1\). Define
are infinite, if Abelard picks an \(a' \in D_1\), then Eloïse can find a \(b' \in D_2\) so that \(w,u_1,\overline{a},a' \simeq w,u_2,\overline{b},b'\) by ensuring that \(a' \in \delta _1(u_1)\) iff \(b' \in \delta _2(u_2)\). Likewise if Abelard picks a \(b' \in D_2\). Now, suppose Abelard picks an \(u_1' \in W_1\). Define  and
and  . (If \(\left| S \right| \le 1\), add a couple of elements from
. (If \(\left| S \right| \le 1\), add a couple of elements from  to S. If \(\left| T \right| \le 1\), add a couple of elements from
to S. If \(\left| T \right| \le 1\), add a couple of elements from  to T.) Then \(a_i \in \delta _1(u_1)\) iff \(b_i \in \delta _2(v_S^T)\). So \(w,v_S^T,\overline{a} \simeq w,v_{S'}^{T'},\overline{b} \). Likewise if Abelard chooses a \(u_2' \in W_2\), even if \(u_2' = v\). Thus, using Lemma 34,
to T.) Then \(a_i \in \delta _1(u_1)\) iff \(b_i \in \delta _2(v_S^T)\). So \(w,v_S^T,\overline{a} \simeq w,v_{S'}^{T'},\overline{b} \). Likewise if Abelard chooses a \(u_2' \in W_2\), even if \(u_2' = v\). Thus, using Lemma 34,  . \(\square \)
. \(\square \)
Lemma 36
(Adding two operators)  .
.
Proof
First,  . Let \(\mathcal {M} _1 = \left\langle W_1,R_1,F_1,D_1,\delta _1,I_1\right\rangle \), where
. Let \(\mathcal {M} _1 = \left\langle W_1,R_1,F_1,D_1,\delta _1,I_1\right\rangle \), where  , \(R_1 = W_1 \times W_1\), \(F_1 = \emptyset \),
, \(R_1 = W_1 \times W_1\), \(F_1 = \emptyset \),  , and \(I_1 = \emptyset \). Let \(\mathcal {M} _2\) be like \(\mathcal {M} _1\) except
, and \(I_1 = \emptyset \). Let \(\mathcal {M} _2\) be like \(\mathcal {M} _1\) except  . Then \(\mathcal {M} _1,w,w \leftrightarrows _{\approx ,@,\mathcal {F},\Pi {}} \mathcal {M} _2,w,w\) (since \(F_1[w] = F_2[w] = \emptyset \)), but \(\mathcal {M} _1,w,w \Vdash \Box {\mathop {\downarrow }}\mathcal {F}\bot \), while \(\mathcal {M} _2,w,w \nVdash \Box {\mathop {\downarrow }}\mathcal {F}\bot \). So
. Then \(\mathcal {M} _1,w,w \leftrightarrows _{\approx ,@,\mathcal {F},\Pi {}} \mathcal {M} _2,w,w\) (since \(F_1[w] = F_2[w] = \emptyset \)), but \(\mathcal {M} _1,w,w \Vdash \Box {\mathop {\downarrow }}\mathcal {F}\bot \), while \(\mathcal {M} _2,w,w \nVdash \Box {\mathop {\downarrow }}\mathcal {F}\bot \). So  .
.
Next,  . Consider the models \(\mathcal {N} _1\) and \(\mathcal {N} _2\) from Fig. 4. Modify them so that \(F_1 = F_2 = \emptyset \), and call the resulting models \(\mathcal {N} _1'\) and \(\mathcal {N} _2'\). Then \(\mathcal {N} _1',z,z \leftrightarrows _{\approx ,@,\mathcal {F},\Pi {}} \mathcal {N} _2',z,z\), but they disagree on
. Consider the models \(\mathcal {N} _1\) and \(\mathcal {N} _2\) from Fig. 4. Modify them so that \(F_1 = F_2 = \emptyset \), and call the resulting models \(\mathcal {N} _1'\) and \(\mathcal {N} _2'\). Then \(\mathcal {N} _1',z,z \leftrightarrows _{\approx ,@,\mathcal {F},\Pi {}} \mathcal {N} _2',z,z\), but they disagree on  . Hence,
. Hence,  . \(\square \)
. \(\square \)
It is tedious, but straightforward, to show the following using the lemmas above:
Theorem 37
(Completeness of Fig. 8) Figure 8 is a complete diagram of the expressive power of the languages presented in that diagram.
Now we turn to extensions with \({\textsf {E}} \), \(\approx \), and \(\Pi {}\). It will help to define back-and-forth games for  and some of its fragments. First, an
and some of its fragments. First, an  -formula is almost\({\textsf {E}} \)-free if it can be built from atomics other than those of the form \({\textsf {E}} (x;s)\) using negation, conjunction, object quantification, state quantification, and \({\textsf {E}} \)-bounded object quantification. (Thus, \({\textsf {E}} \) only occurs as the bounds of object quantifiers.) Let
-formula is almost\({\textsf {E}} \)-free if it can be built from atomics other than those of the form \({\textsf {E}} (x;s)\) using negation, conjunction, object quantification, state quantification, and \({\textsf {E}} \)-bounded object quantification. (Thus, \({\textsf {E}} \) only occurs as the bounds of object quantifiers.) Let  be the \(\approx \)-free fragment,
be the \(\approx \)-free fragment,  be the \(\approx \)-free and almost \({\textsf {E}} \)-free fragment, and
be the \(\approx \)-free and almost \({\textsf {E}} \)-free fragment, and  be the \({\textsf {E}} \)-bounded fragment of
be the \({\textsf {E}} \)-bounded fragment of  .
.
Definition 38
(Back-and-forth system) Let \(\mathcal {M} \) and \(\mathcal {N} \) be models. A back-and-forth system between\(\mathcal {M} \)and\(\mathcal {N} \) is a nonempty variably polyadic relation Z such that whenever \(Z(\overline{w},\overline{a};\overline{v},\overline{b})\),  and
and  , and if \(Z(\overline{w},\overline{a};\overline{v},\overline{b})\), then:
, and if \(Z(\overline{w},\overline{a};\overline{v},\overline{b})\), then:
-
(\({\textsf {TS}} \) Atomic)
 :
: 
-
(\({\textsf {TS}} \) Eq) \(\forall {n,m \le \left| \overline{a} \right| :} a_n = a_m\) iff \(b_n = b_m\)
-
(\({\textsf {TS}} \) StEq)
 \(w_k = w_l\) iff \(v_k = v_l\)
\(w_k = w_l\) iff \(v_k = v_l\) -
(\({\textsf {TS}} \) Ex)
 iff \(b_n \in \delta ^\mathcal {N} (v_k)\)
iff \(b_n \in \delta ^\mathcal {N} (v_k)\) -
(\({\textsf {TS}} \) Acc)
 \(R(w_k,w_l)\) iff \(R(v_k,v_l)\) and \(F(w_k,w_l)\) iff \(F(v_k,v_l)\)
\(R(w_k,w_l)\) iff \(R(v_k,v_l)\) and \(F(w_k,w_l)\) iff \(F(v_k,v_l)\) -
(\({\textsf {TS}} \) Zig)
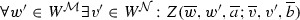
-
(\({\textsf {TS}} \) Zag)
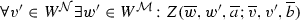
-
(\({\textsf {TS}} \) Forth)
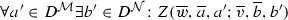
-
(\({\textsf {TS}} \) Back)
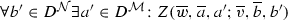 .
.
We may write \(\mathcal {M} ,\overline{w},\overline{a} \leftrightarrows _{{\textsf {TS}}} \mathcal {N} ,\overline{v},\overline{b} \) to indicate that \(\mathcal {M} ,\overline{w},\overline{a} \) and \(\mathcal {N} ,\overline{v},\overline{b} \) are back-and-forth equivalent. If we drop (\({\textsf {TS}} \) Eq) and (\({\textsf {TS}} \) StEq), we get a notion of a back-and-forth system for  . We get a notion of a back-and-forth system for
. We get a notion of a back-and-forth system for  if we drop (\({\textsf {TS}} \) Eq), (\({\textsf {TS}} \) StEq), and (\({\textsf {TS}} \) Ex) and we add:
if we drop (\({\textsf {TS}} \) Eq), (\({\textsf {TS}} \) StEq), and (\({\textsf {TS}} \) Ex) and we add:
-
(\({\textsf {TS}} \)\({\textsf {E}} \)-Forth)

-
(\({\textsf {TS}} \)\({\textsf {E}} \)-Back)
 .
.
If we replace (\({\textsf {TS}} \) Forth) and (\({\textsf {TS}} \) Back) with (\({\textsf {TS}} \)\({\textsf {E}} \)-Forth) and (\({\textsf {TS}} \)\({\textsf {E}} \)-Back), we get a notion of a back-and-forth system for  .
.
Definition 39
( -Equivalence) \(\mathcal {M} ,\overline{w},\overline{a} \) and \(\mathcal {N} ,\overline{v},\overline{b} \) are
-Equivalence) \(\mathcal {M} ,\overline{w},\overline{a} \) and \(\mathcal {N} ,\overline{v},\overline{b} \) are  -equivalent if for all
-equivalent if for all  -formulas \(\alpha (\overline{x};\overline{s})\) (where \(\left| \overline{x} \right| \le \left| \overline{a} \right| \) and \(\left| \overline{s} \right| \le \left| \overline{w} \right| \)), \(\mathcal {M} \vDash \alpha [\overline{a};\overline{w} ]\) iff \(\mathcal {N} \vDash \alpha [\overline{b};\overline{v} ]\). We may write “\(\mathcal {M} ,\overline{w},\overline{a} \equiv _{\textsf {TS}} \mathcal {N} ,\overline{v},\overline{b} \)” to indicate that \(\mathcal {M} ,\overline{w},\overline{a} \) and \(\mathcal {N} ,\overline{v},\overline{b} \) are
-formulas \(\alpha (\overline{x};\overline{s})\) (where \(\left| \overline{x} \right| \le \left| \overline{a} \right| \) and \(\left| \overline{s} \right| \le \left| \overline{w} \right| \)), \(\mathcal {M} \vDash \alpha [\overline{a};\overline{w} ]\) iff \(\mathcal {N} \vDash \alpha [\overline{b};\overline{v} ]\). We may write “\(\mathcal {M} ,\overline{w},\overline{a} \equiv _{\textsf {TS}} \mathcal {N} ,\overline{v},\overline{b} \)” to indicate that \(\mathcal {M} ,\overline{w},\overline{a} \) and \(\mathcal {N} ,\overline{v},\overline{b} \) are  -equivalent. Likewise for the various fragments of
-equivalent. Likewise for the various fragments of  .
.
It is easy to check that \(\mathcal {M} ,\overline{w},\overline{a} \leftrightarrows _{\textsf {TS}} \mathcal {N} ,\overline{v},\overline{b} \) implies \(\mathcal {M} ,\overline{w},\overline{a} \equiv _{\textsf {TS}} \mathcal {N} ,\overline{v},\overline{b} \), and likewise for the various fragments of  . Now, say \(\mathcal {L}_1 \le ^* \mathcal {L}_2\) if every \(\mathcal {L}_1\)-formula is equivalent to some \(\mathcal {L}_2\)-formula. This is more stringent than \(\le \), since some \(\mathcal {L}_1\)-formula might only be expressible as a set of \(\mathcal {L}_2\)-formulas. Observe by Definition 6 that
. Now, say \(\mathcal {L}_1 \le ^* \mathcal {L}_2\) if every \(\mathcal {L}_1\)-formula is equivalent to some \(\mathcal {L}_2\)-formula. This is more stringent than \(\le \), since some \(\mathcal {L}_1\)-formula might only be expressible as a set of \(\mathcal {L}_2\)-formulas. Observe by Definition 6 that  , that
, that  , and that
, and that  .
.
Lemma 40
(Adding \({\textsf {E}} \) and \(\approx \)) If  , then \(\mathcal {L}< \mathcal {L}({\textsf {E}}) < \mathcal {L}(\approx )\). Likewise if relativize to \(\mathbf D \), \(\mathbf U \), or UD.
, then \(\mathcal {L}< \mathcal {L}({\textsf {E}}) < \mathcal {L}(\approx )\). Likewise if relativize to \(\mathbf D \), \(\mathbf U \), or UD.
Proof
Recall the models \(\mathcal {E} \) and \(\mathcal {E} '\) from Fig. 1. It is easy to check that via our original bisimulation, \(\mathcal {E},w,w \leftrightarrows _{{\textsf {TS}}-\approx ,({\textsf {E}})} \mathcal {E} ',w,w\) (remember, you do not need to satisfy (\({\textsf {TS}} \) Eq) or (\({\textsf {TS}} \) Ex) in this back-and-forth game!). But these models are distinguishable by the  -formula
-formula  . So
. So  . Suppose now for reductio that \(\mathcal {L}({\textsf {E}}) \le \mathcal {L}\). Since
. Suppose now for reductio that \(\mathcal {L}({\textsf {E}}) \le \mathcal {L}\). Since  (easily verified by induction),
(easily verified by induction),  ,
,  . So \(\mathcal {L}({\textsf {E}}) \nleq \mathcal {L}\), and thus \(\mathcal {L}< \mathcal {L}({\textsf {E}})\).
. So \(\mathcal {L}({\textsf {E}}) \nleq \mathcal {L}\), and thus \(\mathcal {L}< \mathcal {L}({\textsf {E}})\).
As for \(\mathcal {L}({\textsf {E}}) < \mathcal {L}(\approx )\), revise \(\mathcal {E} \) and \(\mathcal {E} '\) by deleting the world w from the models. Call the resulting models \(\mathcal {E} _{-}\) and \(\mathcal {E} _{-}'\). Then \(\mathcal {E} _{-},v \leftrightarrows _{{\textsf {TS}}-\approx } \mathcal {E} _{-}',v\), but they disagree on  . So
. So  . But \(\mathcal {L}({\textsf {E}}) \le \mathcal {L}(\approx )\), so reasoning as before (noting that
. But \(\mathcal {L}({\textsf {E}}) \le \mathcal {L}(\approx )\), so reasoning as before (noting that  ), we have that \(\mathcal {L}({\textsf {E}}) < \mathcal {L}(\approx )\). \(\square \)
), we have that \(\mathcal {L}({\textsf {E}}) < \mathcal {L}(\approx )\). \(\square \)
Now, where \(\mathcal {L}_1\) and \(\mathcal {L}_2\) were languages in Fig. 8 such that \(\mathcal {L}_1 < \mathcal {L}_2\), we can show that the inclusions involving their extensions with \({\textsf {E}} \) or \(\approx \) can be diagrammed as in Fig. 9. First, the arrows that are present are immediate by Lemma 40 and by the fact that if \(\mathcal {L}_1 < \mathcal {L}_2\) in Fig. 8, then we already have \(\mathcal {L}_1 <^* \mathcal {L}_2\). Next, \(\mathcal {L}_1({\textsf {E}}) \nleq \mathcal {L}_2\), since if it were, we would have  , contrary to Lemma 40. Likewise, \(\mathcal {L}_1(\approx ) \nleq \mathcal {L}_2({\textsf {E}})\). Finally, observe that in the results used above to show that \(\mathcal {L}_2 \nleq \mathcal {L}_1\), we already showed that \(\mathcal {L}_2 \nleq \mathcal {L}_1(\approx ,\Pi {})\). Thus, \(\mathcal {L}_2 \nleq \mathcal {L}_1(\approx )\).
, contrary to Lemma 40. Likewise, \(\mathcal {L}_1(\approx ) \nleq \mathcal {L}_2({\textsf {E}})\). Finally, observe that in the results used above to show that \(\mathcal {L}_2 \nleq \mathcal {L}_1\), we already showed that \(\mathcal {L}_2 \nleq \mathcal {L}_1(\approx ,\Pi {})\). Thus, \(\mathcal {L}_2 \nleq \mathcal {L}_1(\approx )\).
Lemma 41
(Adding \(\Pi {}\)) If  , then \(\mathcal {L}< \mathcal {L}(\Pi {})\). Likewise if we relativize to \(\mathbf U \). Also, if
, then \(\mathcal {L}< \mathcal {L}(\Pi {})\). Likewise if we relativize to \(\mathbf U \). Also, if  , then \(\mathcal {L}<_\mathbf D \mathcal {L}(\Pi {})\).
, then \(\mathcal {L}<_\mathbf D \mathcal {L}(\Pi {})\).
Proof
Let \(\mathcal {M} _1 = \left\langle W_1,R_1,F_1,D_1,\delta _1,I_1\right\rangle \), where  ,
,  ,
,  ,
,  ,
,  . Let \(\mathcal {M} _2\) be just like \(\mathcal {M} _1\) except
. Let \(\mathcal {M} _2\) be just like \(\mathcal {M} _1\) except  . Then \(\mathcal {M} _1,w \leftrightarrows _{{\textsf {TS}} \upharpoonright {\textsf {E}}} \mathcal {M} _2,w\), but they disagree on the
. Then \(\mathcal {M} _1,w \leftrightarrows _{{\textsf {TS}} \upharpoonright {\textsf {E}}} \mathcal {M} _2,w\), but they disagree on the  -formula \(\Sigma {x}\lnot P(x)\). So
-formula \(\Sigma {x}\lnot P(x)\). So  . Reasoning as before, \(\mathcal {L}< \mathcal {L}(\Pi {})\).
. Reasoning as before, \(\mathcal {L}< \mathcal {L}(\Pi {})\).
Suppose now we restrict to \(\mathbf D \). Let \(\mathcal {M} _1 = \left\langle W_1,R_1,F_1,D_1,\delta _1,I_1\right\rangle \), where  ,
,  , \(\delta _1(w) = \mathbb {N} \),
, \(\delta _1(w) = \mathbb {N} \),  , \(I(P,w) = \emptyset \), and for each \(n \in \mathbb {N} \),
, \(I(P,w) = \emptyset \), and for each \(n \in \mathbb {N} \),  . Let \(\mathcal {M} _2\) be just like \(\mathcal {M} _1\) except
. Let \(\mathcal {M} _2\) be just like \(\mathcal {M} _1\) except  , where \(u \notin W_1\),
, where \(u \notin W_1\),  , \(F_2 = F_1\), \(\delta _2(u) = \mathbb {N} \), and \(I(P,u) = \emptyset \). One can show that \(\mathcal {M} _1,w,w \leftrightarrows _{\approx ,@,{\mathop {\downarrow }},\mathcal {F}} \mathcal {M} _2,w,w\). But, they disagree on the
, \(F_2 = F_1\), \(\delta _2(u) = \mathbb {N} \), and \(I(P,u) = \emptyset \). One can show that \(\mathcal {M} _1,w,w \leftrightarrows _{\approx ,@,{\mathop {\downarrow }},\mathcal {F}} \mathcal {M} _2,w,w\). But, they disagree on the  -formula \(\Box \Sigma {x} P(x)\). So
-formula \(\Box \Sigma {x} P(x)\). So  . So \(\mathcal {L}<_\mathbf D \mathcal {L}(\Pi {})\). \(\square \)
. So \(\mathcal {L}<_\mathbf D \mathcal {L}(\Pi {})\). \(\square \)
So once again, using Lemma 41 and the results above, we can verify that if \(\mathcal {L}_1\) and \(\mathcal {L}_2\) are in Fig. 8 and \(\mathcal {L}_1 < \mathcal {L}_2\), then their extensions involving \(\Pi {}\) can be represented in Fig. 10. This holds even if we add \({\textsf {E}} \) or \(\approx \). Thus, Fig. 5 from Sect. 4 is correct. Moreover, it is still correct even relative to \(\mathbf D \).
We now turn to asking to what extent these results hold relative to \(\mathbf U \) and UD. We only give a partial answer here. First, set aside \({\textsf {E}} \), \(\approx \), and \(\Pi {}\), and focus just on \(\mathbf U \). Then the diagram of expressive power looks something like Fig. 11 (whether we should include the dashed arrows has yet to be determined).
First, if \(\varphi \) is \(@\)-free, then \(\Vdash _\mathbf U (\mathcal {F}\varphi \leftrightarrow \varphi )\) and \(\Vdash _\mathbf U ({\mathop {\downarrow }}\varphi \leftrightarrow \varphi )\). So  . But still
. But still  by Lemma 35. And the remarks on page 4 (together with Lemma 34) show that
by Lemma 35. And the remarks on page 4 (together with Lemma 34) show that  and that
and that  . As for the lack of inclusion from
. As for the lack of inclusion from  to
to  :
:
Lemma 42
(\(\mathcal {F},@\) Not included in \(@,{\mathop {\downarrow }}\))  .
.
Proof
Let \(\mathcal {M} _1 = \left\langle W_1,R_1,F_1,D_1,\delta _1,I_1\right\rangle \) where:

\(R_1 = F_1 = W_1 \times W_1\), \(D_1 = \mathbb {Z} \), \(\delta _1(v^T_S) = (\mathbb {N} - S) \cup T\), and \(I_1 = \emptyset \). Let \(\mathcal {M} _2\) be just like \(\mathcal {M} _1\), except we allow \(\left| S \right| = 1\). Let \(w = v^\emptyset _\emptyset \). Observe that:

However, we will show \(\mathcal {M} _1,w,w \leftrightarrows _{\approx ,@,{\mathop {\downarrow }}} \mathcal {M} _2,w,w\). Clearly \(w,w \simeq w,w\). Suppose throughout that \(u_1,u_2,\overline{a} \simeq u_1',u_2',\overline{b} \) and that the following hold:
-
(I)
\(a_i \in \delta _1(u_1)\) iff \(b_i \in \delta _1(u_1)\)
-
(II)
\(u_1 = u_2\) iff \(u_1' = u_2'\)
-
(III)
 .
.
Observe that no matter what \(u_1\) and \(u_2\) are,  is infinite, and
is infinite, and  is finite. Likewise for \(u_1'\) and \(u_2'\).
is finite. Likewise for \(u_1'\) and \(u_2'\).
First, suppose Abelard picks a new \(a \in \delta _1(u_2)\). If \(a \in \delta _1(u_1)\), then since  is infinite, Eloïse will always be able to match a with a
is infinite, Eloïse will always be able to match a with a  . If instead \(a \notin \delta _1(u_1)\), then by (III), we can find a
. If instead \(a \notin \delta _1(u_1)\), then by (III), we can find a  to match a with. A symmetric argument applies if Abelard instead picks a \(b \in \delta _2(u_2')\).
to match a with. A symmetric argument applies if Abelard instead picks a \(b \in \delta _2(u_2')\).
Next, suppose Abelard decides to relocate the game. If he invokes (Act) or (Diag), then clearly (I)–(III) hold. So suppose he decides to pick a \(u_3 \in W_3\) to relocate to. Eloïse’s choice is obvious if \(u_3 = u_1\), so suppose \(u_3 \ne u_1\). We will construct a \(T_3'\) and a \(S_3'\) of the appropriate sort and show they meet (I)–(III). First, pick two elements  (note that
(note that  is infinite since each world has cofinitely many positive integers) and define:
is infinite since each world has cofinitely many positive integers) and define:

Note that where \(u_1' = v^{T_1'}_{S_1'}\),  is finite, so \(S_3'\) is finite and
is finite, so \(S_3'\) is finite and  . Second, define
. Second, define  . Observe that:
. Observe that:

Now, where  , pick k-many elements
, pick k-many elements  (notice that
(notice that  is infinite, since each world only has finitely many negative integers). Define
is infinite, since each world only has finitely many negative integers). Define  . We will show that if Eloïse chooses \(u_3' = v^{T_3'}_{S_3'}\), then all the necessary constraints are met.
. We will show that if Eloïse chooses \(u_3' = v^{T_3'}_{S_3'}\), then all the necessary constraints are met.
We first need to show \(u_1,u_3,\overline{a} \simeq u_1',v^{T_3'}_{S_3'},\overline{b} \)—in particular, \(a_i \in \delta _1(u_3)\) iff \(b_i \in \delta _2(u_3')\). Suppose \(a_i \in \delta _1(u_3)\). Either \(b_i \in \mathbb {N} \) or \(b_i \in \mathbb {N} ^-\). If \(b_i \in \mathbb {N} \), then \(b_i \notin S_3'\), so \(b_i \in \delta _2(u_3')\). If \(b_i \in \mathbb {N} ^-\), then \(b_i \in T_{3,0}' \subseteq T_3'\), so \(b_i \in \delta _2(u_3')\). Suppose instead \(a_i \notin \delta _1(u_3)\). Again, either \(b_i \in \mathbb {N} \) or \(b_i \in \mathbb {N} ^-\). If \(b_i \in \mathbb {N} \), then \(b_i \in S_3'\), so \(b_i \notin \delta _2(u_3')\). If \(b_i \in \mathbb {N} ^-\), then \(b_i \notin T_3'\), so \(b_i \notin \delta _2(u_3')\). No matter what, \(a_i \in \delta _1(u_3)\) iff \(b_i \in \delta _2(u_3')\).
Next, we need to show (I)–(III). (I) holds by default. Now, we assumed above \(u_3 \ne u_1\), so we need \(u_3' \ne u_1'\). But recall that we picked c, d so that \(c,d \in \delta _2(u_1')\). But \(c,d \in S_3'\), so \(c,d \notin \delta _2(u_3')\). Thus, \(u_3' \ne u_1'\). So (II) holds. Finally, using the calculations above, since  , we find that:
, we find that:

where  . So (III) holds. Thus, if Abelard relocates to \(u_3\), Eloïse can choose to relocate to \(u_3'\). And since \(\left| S_3' \right| > 1\), a symmetric argument applies if Abelard decides to relocate the game in \(\mathcal {M} _2\). The proof is completed with one application of Lemma 34. \(\square \)
. So (III) holds. Thus, if Abelard relocates to \(u_3\), Eloïse can choose to relocate to \(u_3'\). And since \(\left| S_3' \right| > 1\), a symmetric argument applies if Abelard decides to relocate the game in \(\mathcal {M} _2\). The proof is completed with one application of Lemma 34. \(\square \)
Now, because the proof of Lemma 40 only uses models in \(\mathbf U \) (in fact, in UD), we can still safely say that adding \({\textsf {E}} \) or \(\approx \) can be diagrammed as in Fig. 9. Adding \(\Pi {}\) makes things more complicated. Recall that relative to the class of all models, we could simply say that if  , then \(\mathcal {L}_i < \mathcal {L}_i(\Pi {})\), \(\mathcal {L}_1(\Pi {}) < \mathcal {L}_2(\Pi {})\), and \(\mathcal {L}_1(\Pi {})\) and \(\mathcal {L}_2\) were incomparable. However, showing that \(\mathcal {L}_2 \nleq \mathcal {L}_1(\Pi {})\) crucially relied on the fact that all of our inexpressibility proofs for showing \(\mathcal {L}_2 \nleq \mathcal {L}_1\) already showed that \(\mathcal {L}_2 \nleq \mathcal {L}_1(\Pi {})\). But because Lemma 42 left out \(\Pi {}\) (which is crucial, as we will see below), we cannot conclude that \(\mathcal {L}_2 \nleq _\mathbf U \mathcal {L}_1(\Pi {})\).
, then \(\mathcal {L}_i < \mathcal {L}_i(\Pi {})\), \(\mathcal {L}_1(\Pi {}) < \mathcal {L}_2(\Pi {})\), and \(\mathcal {L}_1(\Pi {})\) and \(\mathcal {L}_2\) were incomparable. However, showing that \(\mathcal {L}_2 \nleq \mathcal {L}_1(\Pi {})\) crucially relied on the fact that all of our inexpressibility proofs for showing \(\mathcal {L}_2 \nleq \mathcal {L}_1\) already showed that \(\mathcal {L}_2 \nleq \mathcal {L}_1(\Pi {})\). But because Lemma 42 left out \(\Pi {}\) (which is crucial, as we will see below), we cannot conclude that \(\mathcal {L}_2 \nleq _\mathbf U \mathcal {L}_1(\Pi {})\).
We can still verify by hand that in some cases, \(\mathcal {L}_2 \nleq \mathcal {L}_1(\Pi {})\). For one thing,  by Lemma 35. We also have that
by Lemma 35. We also have that  by Proposition 17. Likewise,
by Proposition 17. Likewise,  . But importantly, some of these languages without \({\textsf {E}} \) and \(\Pi {}\) that were distinct collapse when you add \({\textsf {E}} \) and \(\Pi {}\):
. But importantly, some of these languages without \({\textsf {E}} \) and \(\Pi {}\) that were distinct collapse when you add \({\textsf {E}} \) and \(\Pi {}\):
Lemma 43
(Collapse)  . Likewise if we add \(\approx \) to these languages.
. Likewise if we add \(\approx \) to these languages.
Proof
Throughout, let  . Note that the following are all \(\mathbf U \)-valid (where \(\alpha \) is an atomic formula):
. Note that the following are all \(\mathbf U \)-valid (where \(\alpha \) is an atomic formula):
Likewise, all of these are \(\mathbf U \)-valid:
Using these rules, we can push each \(@\) and each \({\mathop {\downarrow }}\) inwards as much as possible until \(@\) only occurs right before a \(\mathcal {F}\) or an atomic, and \({\mathop {\downarrow }}\) only occurs right before a \(\Box \). Moreover, we can delete any \(\mathcal {F}\) and \({\mathop {\downarrow }}\) if it does not scope over an \(@\), and repeat. After this entire process, the resulting formula will be \(\mathbf U \)-equivalent to our original. So assume without loss of generality that our formula has already gone through this pre-processing.
Now, say that an \(\mathcal {L}^*\)-formula is in normal form if it is either a non-modal formula, or if it is of the form:
where  (the quantifier block may be empty), \({\textsf {BC}} \) is some boolean combination of its components, \(\overline{\psi } \) are all non-modal, each
(the quantifier block may be empty), \({\textsf {BC}} \) is some boolean combination of its components, \(\overline{\psi } \) are all non-modal, each  , and \(\overline{\theta } \) are all in normal form. By induction, one can convert every \(\mathcal {L}^*\)-formula into one of normal form (essentially by pre-processing as above, and then replacing bound variables and pulling out quantifiers). Thus, we may assume without loss of generality that our formula is already in normal form.
, and \(\overline{\theta } \) are all in normal form. By induction, one can convert every \(\mathcal {L}^*\)-formula into one of normal form (essentially by pre-processing as above, and then replacing bound variables and pulling out quantifiers). Thus, we may assume without loss of generality that our formula is already in normal form.
Finally, suppose an \(\mathcal {L}^*\)-formula has been pre-processed and is in the form:
where \(\overline{\varphi } \) are all non-modal, and \(\overline{\psi } \), \(\overline{\theta } \), \(\overline{\chi } \), and \(\overline{\xi } \) are all in normal form (notice that since we pre-processed, each \(\psi \) is either an atomic or of the form \(\mathcal {F}\psi '\)). Then the following are \(\mathbf U \)-valid:
Thus, in our original formula, we can replace any \(\mathcal {F}\) with \({\mathop {\downarrow }}\Box \) or vice versa. \(\square \)
To sum up, the following questions have yet to be answered about the relative \(\mathbf U \)-expressive power of these languages:
-
Is
 ?
? -
Is
 ?
? -
Is
 or
or  ?
? -
Is
 or
or  ?
?
Answering these questions would settle the rest.
We now finally turn to UD. Excluding \({\textsf {E}} \), \(\approx \), and \(\Pi {}\), the diagram in Fig. 11 is still correct (again, the dashed arrows have not been determined). And again, Fig. 9 is still correct when adding either \({\textsf {E}} \) or \(\approx \). But adding \(\Pi {}\) is even trickier than before, since we can no longer appeal to Lemma 41. We still have the lack of inclusions mentioned above Lemma 43. We also have the following lack of inclusions:
Lemma 44
(Inexpressibility of \(@\) with \(\Pi {}\))  .
.
Proof
Recall that \(\mathcal {R} _1,w,w \leftrightarrows _{\approx ,@} \mathcal {R} _2,w,w\) (Fig. 3). But the models are distinguished by  . \(\square \)
. \(\square \)
Lemma 45
(Inexpressibility of \(@,\Pi {}\) with \(@,{\mathop {\downarrow }},\mathcal {F}\))  .
.
Proof
This immediately follows from Proposition 31. \(\square \)
However, we now have more inclusions. For example,  (just set
(just set  ).Footnote 37 Likewise,
).Footnote 37 Likewise,  , thoughthe proof is a bit more roundabout.Footnote 38 These inclusions are strict by Lemma 35. The questions mentioned above for \(\mathbf U \)-expressive power are still unanswered for UD-expressive power. And again, answering these questions suffices to settle the remaining inclusions.
, thoughthe proof is a bit more roundabout.Footnote 38 These inclusions are strict by Lemma 35. The questions mentioned above for \(\mathbf U \)-expressive power are still unanswered for UD-expressive power. And again, answering these questions suffices to settle the remaining inclusions.
Rights and permissions
About this article
Cite this article
Kocurek, A.W. On the expressive power of first-order modal logic with two-dimensional operators. Synthese 195, 4373–4417 (2018). https://doi.org/10.1007/s11229-016-1172-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-016-1172-3





 (the set of (object) variables);
(the set of (object) variables); for each
for each  (the set of state variables).
(the set of state variables).


 :
: 



 .
.
 -bisimilar models that disagree on (E)
-bisimilar models that disagree on (E)
 -bisimilar models disagreeing on (E)
-bisimilar models disagreeing on (E) :
: 

 -bisimilar models disagreeing on (R). The top half of each circle satisfies
-bisimilar models disagreeing on (R). The top half of each circle satisfies 
 -bisimilar models disagreeing on (NR)
-bisimilar models disagreeing on (NR)




 , we have that
, we have that  . For
. For  ), in which case it does not matter which type of quantifier we use in (
), in which case it does not matter which type of quantifier we use in ( (there is no world where this new object exists by itself). The natural fix is to add another world to the second model which only contains the new object. The resulting models (which are like ours except the worlds with cofinite domains are removed) satisfy the same
(there is no world where this new object exists by itself). The natural fix is to add another world to the second model which only contains the new object. The resulting models (which are like ours except the worlds with cofinite domains are removed) satisfy the same  -formulas, but they are not bisimilar, since they are distinguished by the
-formulas, but they are not bisimilar, since they are distinguished by the  -formula
-formula  . However, if you restrict the
. However, if you restrict the  -bisimulation game to n-steps, for any finite n, then Eloïse has a winning strategy (that is, the models are n-bisimilar for every n); and this suffices to guarantee modal equivalence. Here, we ensure full bisimilarity by including worlds with cofinite domains. Thus, our proof shows that (
-bisimulation game to n-steps, for any finite n, then Eloïse has a winning strategy (that is, the models are n-bisimilar for every n); and this suffices to guarantee modal equivalence. Here, we ensure full bisimilarity by including worlds with cofinite domains. Thus, our proof shows that ( .
. . He proceeds, as we do, by constructing two models that disagree on this sentence, and then argues that they are bisimilar. The first model consists of two worlds w and u, where
. He proceeds, as we do, by constructing two models that disagree on this sentence, and then argues that they are bisimilar. The first model consists of two worlds w and u, where  and where in both w and u,
and where in both w and u,  satisfy Q(x) and
satisfy Q(x) and  do not satisfy Q(x). The second model consists of worlds
do not satisfy Q(x). The second model consists of worlds  . In
. In  satisfy Q(x) while
satisfy Q(x) while  do not. In
do not. In  satisfy Q, and in
satisfy Q, and in  satisfy Q. He then claims that w and
satisfy Q. He then claims that w and  -bisimilar. However, these models are not
-bisimilar. However, these models are not  -bisimilar. In fact, they do not even satisfy the same
-bisimilar. In fact, they do not even satisfy the same  -formulas: e.g.,
-formulas: e.g.,  is still correct, as can be verified with a bisimulation argument using the models
is still correct, as can be verified with a bisimulation argument using the models  cannot express (R) can be found in Wehmeier (
cannot express (R) can be found in Wehmeier ( immediately. But this needs qualification. We can obtain a quick proof that (
immediately. But this needs qualification. We can obtain a quick proof that ( by restricting the accessibility relations in
by restricting the accessibility relations in  -formula
-formula  .
. ,
,  , and
, and  relative to
relative to  or even
or even  . Fig.
. Fig.  ; but van Benthem (
; but van Benthem ( -formula that is not expressible in
-formula that is not expressible in  . However, it should be noted that even though
. However, it should be noted that even though  , which is still two-dimensional. Forbes (
, which is still two-dimensional. Forbes ( is an n-chain if
is an n-chain if  ], so that the hierarchy of modal languages is strictly increasing in expressive power...” Forbes also notes that
], so that the hierarchy of modal languages is strictly increasing in expressive power...” Forbes also notes that  can express “there is an n-chain of worlds”, but claims that it cannot express “there is an
can express “there is an n-chain of worlds”, but claims that it cannot express “there is an  . Then the claim that there is a 4-chain can be expressed as an
. Then the claim that there is a 4-chain can be expressed as an  -formula:
-formula:  and let
and let  . Then the claim that there is a 4-chain can be expressed as an
. Then the claim that there is a 4-chain can be expressed as an  -formula:
-formula:  . He also constructs two models which he claims satisfy the same
. He also constructs two models which he claims satisfy the same  -formulas, but disagree on the
-formulas, but disagree on the  -formula
-formula  . Here are the models
. Here are the models  ,
,  . Let
. Let  , let V(P) be empty for all
, let V(P) be empty for all  has exactly one member (since
has exactly one member (since  is the set of objects that do not exist at 0). But if that is right, then these models are distinguishable by the following
is the set of objects that do not exist at 0). But if that is right, then these models are distinguishable by the following  -formula:
-formula: -formula can be replaced by
-formula can be replaced by  . So having replaced every
. So having replaced every  . The result is a
. The result is a  -formula.
-formula. -satisfiable inXover
-satisfiable inXover -satisfiable inXover
-satisfiable inXover -satisfiable in X over
-satisfiable in X over  -satisfiable in
-satisfiable in  over
over  -satisfiable in
-satisfiable in  over
over  -satisfiable in
-satisfiable in  over
over  -satisfiable in
-satisfiable in  over
over  -satisfiable in
-satisfiable in  over
over  -satisfiable in
-satisfiable in  over
over  . Let
. Let  . Since
. Since  (and since for each
(and since for each  with fresh new variables in
with fresh new variables in  . Hence,
. Hence,  over
over  -saturation, there is a
-saturation, there is a  . Likewise for the Zag clause.
. Likewise for the Zag clause.  . Let
. Let  . Since
. Since  , it follows that
, it follows that 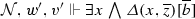 . Hence,
. Hence,  -satisfiable in
-satisfiable in  over
over  -saturation,
-saturation,  -satisfiable in
-satisfiable in  over
over  . Likewise for the Forth clause.
. Likewise for the Forth clause. 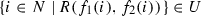
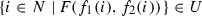
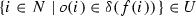
 .
. .
. .
.  . Let
. Let  be n-many distinct elements from
be n-many distinct elements from  , and set
, and set  . Then
. Then  . And the former is not empty since
. And the former is not empty since  . So pick any
. So pick any  . Then we have that
. Then we have that  where
where  is arbitrary. Then T is finite and nonempty, and
is arbitrary. Then T is finite and nonempty, and  . Then
. Then  ). If
). If 

 -bisimilar models that still disagree on (R)
-bisimilar models that still disagree on (R) . That means
. That means  and
and  .
.  . That means we need to ensure that
. That means we need to ensure that  while also ensuring that
while also ensuring that  . That means we need:
. That means we need: 


 , and
, and
 and
and 
 :
: 

 iff
iff 
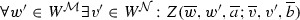
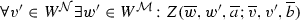
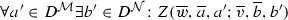
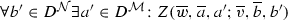 .
.
 .
.


 and
and 
 .
. ?
? ?
? or
or  ?
? or
or  ?
?