Abstract
In “Properties and the Interpretation of Second-Order Logic” (Hale, Philos Math 21:133–156, 2013) Bob Hale develops and defends a deflationary conception of properties where a property with particular satisfaction conditions actually (and in fact necessarily) exists if and only if it is possible that a predicate with those same satisfaction conditions exists. He argues further that, since our languages are finitary, there are at most countably infinitely many properties and, as a result, the account fails to underwrite the standard semantics for second-order logic. Here a more lenient version of the view is explored, which allows for the possibility of countably infinite predicates understood as the product of linguistic supertasks. This enriched deflationist account of properties—the Infinitary Deflationary Conception of Existence—supports the standard semantics for models with countable first-order domains, and allows one to prove the categoricity of the second-order Peano axioms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 The deflationary account of properties
In “Properties and the Interpretation of Second-order Logic” (Hale 2013), Bob Hale defends a ‘deflationary’ conceptionFootnote 1 of properties that can be used to legitimate the use of second-order logic in the face of traditional criticisms such as those of Quine (1970) (as we shall see, whether, and to what extent, standard, or ‘full’ semantics for second-order logic is legitimated by this move is another matter). The following sums up Hale’s basic approach:
...it is sufficient for the actual existence of a property or relation that there could be a predicate with appropriate satisfaction conditions. (Hale 2013, p. 133)
Hale briefly motivates the deflationary conception of properties along Fregean lines, and in analogy with a similar Fregean approach to objects.Footnote 2 The deflationary conception of objects has it that:
Roughly, objects are those things for which singular terms can stand, and a sufficient (and in my view necessary) condition for there to exist objects of a certain kind is that there could be true atomic statements featuring singular terms which, if they refer at all, stand for objects of that kind. (Hale 2013, p. 134, second emphasis added)Footnote 3
Along similar lines, the deflationary conception of properties has it that:
Roughly, properties and relations are those things for which predicates can stand, and a sufficient (and again, in my view necessary) condition for their existence is that there could be predicates with appropriately determinate satisfaction conditions. (Hale 2013, p. 134, final emphasis added.)
Before moving on to the positive project of the present essay, it is worth noting that the deflationary account of properties involves an apparently philosophically loaded theoretical term—“satisfaction conditions”. A full defense of the deflationary account of properties would require a full explication of exactly what this notion amounts to. Hale, in passing, equates satisfaction conditions with meanings:
Taking the meaning of a predicate to be its satisfaction-condition, two predicates stand for the same property if and only if they have the same meaning. (Hale 2013, p. 144)
but since he does not provide a full account of meaning, this is at best a partial characterization.
The following characterization of satisfaction conditions is sufficient for our purposes here: A satisfaction condition (for a predicate, property, or both) is whatever it is that makes it the case (or explains, etc.) that the predicate ‘stands for’ that property (and hence holds of the same objects as does the property). At a minimum, a satisfaction condition is (or is associated with) a total function that maps each possible world to a subcollection of the domain of that world—that is, it is (or is associated with) a function that assigns a (possibly empty) extension to the corresponding property or predicate at each world. Hale’s suggestion that satisfaction conditions are meanings is compatible with, but is not entailed by, this more superficial explication of the notion.
Given this intuitive (but ultimately primitive, and unanalyzed) notion of satisfaction condition, we can sum up the deflationary account of properties as follows:
Given a satisfaction condition \(\Sigma \), the following are necessarily equivalent:
-
There is a property with satisfaction condition \(\Sigma \).
-
Possibly, there is a predicate with satisfaction condition \(\Sigma \).
Of course, the deflationary account of properties is meant to complement the deflationary account of objects that motivated it. Since the deflationary account of objects will play a central role in the investigation of the deflationary conception of properties undertaken here, we require a similar formulation of how deflationism applies to objects and the terms that denote them. An initial (but ultimately unsatisfactory) stab in the direction of such an account is to simply state that an object exists if and only if it is possible that there is a singular term that denotes that object, but such an account ignores the fact that complex singular terms might denote different objects at different worlds, and it also ignores the fact that some singular terms fail to denote any object at some worlds.
Thus, just as we introduced satisfaction conditions to connect properties to predicates, we introduce a similar notion—denotation conditions—to connect singular terms with the objects they denote at different worlds. Roughly speaking, and along the lines of our treatment of satisfaction conditions above, a denotation condition is whatever it is that makes it the case (or explains, etc.) that the singular term ‘picks out’ a particular object at a particular world (if it picks out anything at all). At a minimum, a denotation condition is (or is associated with) a partialFootnote 4 function that maps each possible world on which it is defined to an object in the first-order domain of that world—that is, it is (or is associated with) a function that assigns a denotation to the corresponding singular term at each world in which it is defined (i.e. at each world at which the term in question has a denotation). Unsurprisingly, the claim that the denotation condition associated with a particular singular term is the meaning of that term is compatible with, but not entailed by, the explication of the notion just given. We can now flesh out the deflationary account of objects as follows:
Given a denotation condition \(\Delta \), the following are necessarily equivalent:
-
The object picked out by \(\Delta \) (if any) exists.
-
Possibly, there is a singular term with denotation condition \(\Delta \).Footnote 5
The deflationary account of properties is meant to play a central role in Hale’s defense of neo-logicism (a take on the foundations of mathematics to which I also ascribe): Neo-logicism requires a sufficiently robust version of second-order logic if it is to provide a reconstruction of arithmetic (and, in fact, all or most of mathematics) based on Fregean abstraction principles.Footnote 6 Interestingly, however, Hale denies that the deflationary approach delivers the standard semantics for second-order logic (i.e. the semantics, and resulting logic, obtained via the assumption that the domain of properties is, or is isomorphic to, the full powerset of the domain of objects). Instead, Hale argues that the deflationary conception provides a more limited domain of properties (corresponding to Henkin models of second-order logic, where the domain of properties is a possibly proper subset of the powerset of the domain of objects). His argument for this limitation on the deflationary conception can be summarized as follows:
Premise 1: Given a countably infinite domain of objects, standard semantics for second-order logic requires the existence of continuum-many non-coextensive properties.Footnote 7
Premise 2: Given the deflationary account of properties, the existence of continuum many non-coextensive properties requires the existence of continuum-many distinct predicates.Footnote 8
Premise 3: Our languages are finite—that is, they contain at most finitely many primitive bits of vocabulary and at most a recursively specifiable countable infinity of finitely long formulas, and hence at most a recursively specificable countable infinity of distinct predicates, built from this vocabulary.
Conclusion: Given a countably infinite domain of objects, the deflationary account of properties does not provide standard semantics for second-order logic.
In other words, if our languages only contain (and in principle can only contain) at best a countably infinite stock of predicates, then there exists at most a countable infinity of properties (see Hale 2013, pp. 145–146 for Hale’s version of this argument).
This argument consists, in essence, of two applications of modus tollens, and as a result is surely valid (even in many of the most non-classical of non-classical logics). In addition, the first premise is little more than an application of Cantor’s theorem (plus the definition of ‘standard semantics’), and the second premise is a straightforward consequence of the deflationary account of properties. Thus, whether the argument is sound (from the perspective of a defender of the deflationary account, at least), and thus whether its conclusion is true, hinges solely on the status of the third premise—that our languages, both possible and actual, are in principle limited to a countable infinity of finite expressions. After some further elucidation (and mild criticism) of Hale’s account, and some technical preliminaries, the remainder of this essay will be devoted to exploring the consequences that rejection of this premise has for the deflationary conception of properties.
Hale’s deflationism about properties provides an attractive account of the nature of properties, one that defuses Quinean objections to the use of properties as the range of second-order variables as ‘set theory in sheep’s clothing’ (see Quine 1970) by providing an independent (and intensional) account of the existence and nature of properties. But the advantages of second-order logic—that is, categoricity (and quasi-categoricity) theorems, the logical definability of Dedekind infinity and Frege’s ancestral, the derivability of second-order Peano Arithmetic from Hume’s Principle (i.e., Frege’s Theorem), etc.—do not stem merely from quantification over properties. In addition, many of these results depend on either the fact that the logic in question validates the full second-order comprehension schema, or stems from features of the standard semantics, or both (see Shapiro 1991 and the essays in Cook 2007b for details on the relevant results for pure second-order logic and the mathematics of logicism respectively). Thus, a semantics that countenances genuine quantification over properties but which allows for the existence of very few properties, relatively speaking, threatens to be useless for many of the purposes to which second-order systems were originally applied.
Hale is aware of this point, and in fact argues that the second-order logic that results from accepting only countably many properties, provided by a stock of countably many (possible and actual) predicates, is compact, complete, and satisfies both the upwards and downwards Löwenheim–Skolem theorem (see Hale 2013, pp. 144–151). Hale’s arguments for these metatheorems are flawed, however.Footnote 9 For example, let our theory \(\mathcal {T}\) consist of the following principle:
This theory clearly has a countable model on Hale’s account: given a countable first-order domain, its sole axiom requires only countably many singleton properties (plus closure under those operations required by Hale’s logic, which will introduce at most countably many additional propertiesFootnote 10). But if Hale is right and there can exist at most countably many properties, then the upward Löwenheim–Skolem theorem fails, since our theory \(\mathcal {T}\) requires that there be at least as many properties as there are objects, and thus can have no uncountable models. Similar problems plague the completeness and compactness results.Footnote 11
There is a philosophical confusion that seems to accompany Hale’s technical mistakes: Hale’s (incorrect) negative results regarding the expressive and representational strength of the second-order logic based on the deflationary account of properties depend on two explicit assumptions: first, as already noted, Hale assumes that our languages (both actual and possible) are finite in the relevant sense, and thus contain at most a countable infinity of predicates. Second, Hale notes that if we are to prove any theorems whatsoever regarding the logical power and limitations of second-order logic based on the deflationary approach, we need a more precise account of what properties are possible relative to a particular formal language. He suggests that one promising way to precisify this informal notion of possibility is in terms of definability, and that the relevant notion of definability is given via consideration of the resources of the (not necessarily formal) metalanguage for the particular formal language under consideration:
If one is to base a model-theoretic semantics on this conception, it is clearly necessary to be more precise about what is to be understood by ‘definable’—else it will not be determinate what the higher-order variables may take as values [...] To that end we may take the definable subsets of the individual domain—in the context of providing a semantics for a given second-order language—to be the subsets definable in our meta-language (Hale 2013, pp. 147–148.)
In short, given a particular formal language, the predicates that are possible relative to that language are exactly the predicates that are actually contained in the metalanguage for that formal language (or the properties definable in the metalanguage restricted to the domain of the object language, in those cases where the domain of the metalanguage is wider than that of the object language). Setting aside the underspecifity of this understanding of “definable”,Footnote 12 the problem is this: it is not clear that this understanding of definability (however one implements it precisely) is compatible with the idea that the collection of properties must be countable: if the properties in a model are exactly those definable in the metalanguage for that model, then presumably (in keeping with the idea that the deflationary account of properties is an extension of the deflationary account of objects) the objects in a model ought to be named in the metalanguage, or at least nameable in some possible extension of the metalanguage (for example, the one obtained by adding all possible names). If this is right, however, then, if the idea that there might be uncountable models is to even be coherent—that is, if the statement of the Löwenheim–Skolem theorems are to even make sense—then there must be possible metalanguages that contain uncountably many names. But (assuming standard logical resources) if we have uncountably many names, then we have uncountably many predicates, and hence we have uncountably many properties in (at least some) models after all. Thus, the following claims are incompatible:
-
A model \({\mathcal {M}}\) can contain an object if and only if that object is named or nameable (by a singular term) in the metatheory in which the model is constructed (or a metatheory in which the model could be constructed).
-
A model \({\mathcal {M}}\) can contain a property if and only if that property is named or nameable (by a predicate) in the metatheory in which the model is constructed (or a metatheory in which the model could be constructed).
-
There are models with uncountable domains of objects.
-
There are no models with uncountable domains of properties.
Of course, the deflationary conception of properties proper—that is, the simple idea that actual property existence covaries with possible predicate existence—is independent of both the assumption that the collection of properties must be countable and the assumption that the possible predicates are exactly those definable in the metatheory (or, more generally, that there must be some single language—metatheory or not—that contains all possible predicates in the first place). In addition, the deflationary conception is an extremely powerful idea, and most of Hale’s philosophical discussion and defense of the view is untouched by the mistaken metatheorems. As a result, it is worth investigating what happens when we abandon one or both of these problematic assumptions while retaining the more general ideas underlying the deflationary conception of properties.
In Sect. 2 I shall provide a more careful formulation of the idea that the existence of properties is tied to the possible existence of appropriate predicates, and (given two additional, and very weak, modal assumptions) I shall prove that even though this version of the deflationary view does not entail the existence of more than countably many properties (given a countably infinite first-order domain), it (plus the aforementioned modest modal assumptions) does entail the full comprehension schema for second-order logic. This result (which Hale 2013 does not address) is important, since it shows that, although the deflationary account might allow for (or even require) Henkin models, not any Henkin model will do—instead, the second-order domains of the Henkin models at issue must be, roughly put, closed under (finitary) Boolean operations and first- and second-order projections. Thus, this portion of the present essay is compatible with, and complementary to, the general perspective of Hale (2013): loosely put, that work focuses on those arbitrary collections of the first-order domain that might fail to correspond to a property, and the limitations that result, while Sect. 2 below focuses on the very rich structure of properties whose existence is nevertheless guaranteed by the deflationary account.
In Sect. 3, however, I shall depart significantly from the approach of Hale (2013), and consider infinitary languages. In particular, we shall look at languages that contain ‘expressions’ whose actual expression would seem to require the completion of a supertaskFootnote 13—that is, languages that contain countably infinite conjunctions, disjunctions, and the like. Interestingly, given this more lenient vantage point, we can prove (again, with two additional, and not quite so weak, modal assumptions) that the models appropriate to the deflationary conception of properties are standard models when the domain is countably infinite (which immediately entails the categoricity theorem for arithmetic and other theories with countably infinite intended interpretations), and I shall also sketch an argument that this semantics, although not equivalent to the standard semantics on uncountably infinite first-order domains, nevertheless provides a ‘weak’ type of categoricity result for second-order real analysis.
Of course, the interest of the material in Sect. 3 depends on whether these linguistic supertasks are genuinely possible in the relevant sense (we are doing metaphysics here, not merely mathematics!) Thus, in the final section I shall provide some reasons for thinking that the supertasks required for such infinitary languages are logically possible (even if not physically possible relative to our own modal location)—and surely logical possibility is the relevant notion of possibility in the present context. In doing so, I shall also address the reasons underlying Hale’s own rejection of this extension of the deflationary account.Footnote 14
Before moving on, a methodological observation is in order: The remainder of this paper is filled with ‘definitions’, ‘theorems’, ‘lemmas’, etc. The reader with adamantine mathematical scruples, however, might object to the use of such honorifics when describing the informal arguments given below—in particular, she might object to the fact that no rigorous syntax has been provided for the languages for which these results are being proved. Of course, in a perfect world (where this essay would be written by a perfect mathematician), such a rigorous presentation would be preferable, but there are practical difficulties with such an approach: the results to follow involve proving theorems about a space of possible worlds where different languages—including languages with different logical resources—are used in (and hence different predicates—and types of predicates—exist in) different possible worlds (e.g., possible worlds where infinitary conjunctions, disjunctions, etc. are actually expressed, presumably in contrast to the actual world where our natural languages are finitary). Setting this up in a formally precise manner (for example, with some worlds whose language is standard first-order, while others involve \(\mathcal {L}_{\omega ,\omega }\), etc.) would significantly complicate the presentation of the arguments of this paper, to (as far as I can ascertain) no philosophical benefit.Footnote 15 Thus, the ‘proofs’ given below, whose conclusions are identified with the terms ‘theorem’, ‘lemma’, etc., should be taken to be philosophically informal, yet rigorous proofs (in the sense of ‘informal rigor’ developed in Kreisel 1972) regarding informal philosophical notions. I see no reason, however, to doubt that precisified versions of these arguments will apply to any precisely specified version of the space of possible worlds, and the languages of those worlds, informally discussed in the sections to follow.Footnote 16
2 Deflationism and comprehension
In this section I shall prove that the deflationary conception of properties supports a semantics that validates the full second-order comprehension schema for second-order logic. Before doing so, however, some technical preliminaries need to be dealt with.
First, we need a somewhat more perspicuous notation for representing predicates, properties, singular terms, satisfaction conditions, denotation conditions, and the relation between them. Thus, the following definitions:
Definition 2.1
“\(SC_{pred}(\cdots , \cdots )\)” holds between a predicate \(\ulcorner \Phi (x)\urcorner \) and a satisfaction condition \(\Sigma \) if and only if \(\ulcorner \Phi (x)\urcorner \) has satisfaction condition \(\Sigma \)
“\(SC_{prop}(\cdots , \cdots )\)” holds between a property \(\Pi \) and a satisfaction condition \(\Sigma \) if and only if \(\Pi \) has satisfaction condition \(\Sigma \).
“\(DC_{term}(\cdots , \cdots )\)” holds between a singular term \(\ulcorner \tau \urcorner \) and a denotation condition \(\Delta \) if and only if \(\ulcorner \tau \urcorner \) has denotation condition \(\Delta \).
“\(DC_{obj}(\cdots , \cdots )\)” holds between an object \(x\) and a denotation condition \(\Delta \) if and only if \(\Delta \) is defined (at the current world) and ‘picks out’ \(x\).
As suggested in these definitions, I shall use \(\Pi \) when quantifying over properties, \(\Sigma \) and \(\Gamma \) when quantifying over satisfaction conditions, \(\Delta \) when quantifying over denotation conditions, \(\ulcorner \tau \urcorner \) and \(\ulcorner \sigma \urcorner \) when quantifying over singular terms, and \(\ulcorner \Phi (x) \urcorner \) and \(\ulcorner \Psi (x) \urcorner \) when quantifying over predicates (with subscripts when more than one occurrence is needed). In the latter instances, the corner quotes merely serve to emphasize that it is predicates and singular terms (i.e. expressions of some formal or natural language) that we are quantifying over—no particular naming or coding device is required or implied.Footnote 17
Given this notation, we can now provide a snappy, precise formulation of the deflationary conception of properties—one that is more amenable to formal manipulation and rigorous (albeit informal) proof than the rather loose explication provided in the previous section. First, we note explicitly an assumption that has been underlying the discussion so far—the Coextensionality PrincipleFootnote 18:
In other words, any property and predicate that have the same satisfaction condition necessarily hold of exactly the same objects. In addition, we need to guarantee that every property, and every predicate, has a satisfaction condition—hence the Satisfaction Condition Existence PrinciplesFootnote 19:
So far, the listed principles are uncontroversial (at least, they are given the coherence of the conception of satisfaction conditions outlined above). Formulating the more controversial portions of the deflationary concept is straightforward as well. The idea that a property exists if and only if there is a possible predicate with the appropriate satisfaction condition—a thesis we shall call Hale’s Property Principle—is formulated as:
Along similar lines, we will also have need for the following Weak Object PrincipleFootnote 20, which codifies part of the deflationary conception of objects (and is all that is needed in the results that follow)Footnote 21:
The Weak Object Principle captures the idea that the existence of any object requires that it is at least possible that there is a singular term that would refer to that object (note that the Weak Object Principle does not entail that the possible singular term actually refers to the object in question in the possible world(s) at which it exists).
Hale’s Property Principle (or its conjunction with the Weak Object Principle) does not, on its own, entail much about the existence of properties (for example, it entails very little in very weak modal logics such as K or T). Thus, we need to say a bit more about how we are understanding the relevant notion of possibility, and what modal logic governs this notion. A first stab at the relevant notion of possibility is to just lay down the obvious principle: A predicate is possible in the relevant sense just in case there is a possible worldFootnote 22 where a concrete (i.e. spoken, written, thought, etc.) instance of that predicate exists. It might well be the case that this understanding of which predicates are possible is sufficient for our purposes. Whether or not this is indeed the case is an open question, but one we need not answer here, since there is a more inclusive notion that subsumes this initial thought and better serves our purposes. On this understanding, a predicate is possible if and only if there is a possible world where the predicate is in the closure of the formation rules of some language where are least some expressions of that language exist as concrete instances in that world. In short, an expression is possible on this reading if it would be counted as grammatical within some language used within some possible world. Note that this understanding of possible predicate has it that all predicates of English (or Chinese, or whatever), regardless of whether an inscription of that predicate will fit within the physical universe, are possible because they are actual! This is as it should be, however, since we are concerned with determining which predicates are logically possible, and physical limitations such as the possible boundedness of physically possible worlds (like the actual world), the logically contingent fact that \(c\) is finite, etc. seem irrelevant to determining that.
With at least a rough understanding of the relevant notion of possibility now on the table, the next task is to determine which modal logic governs this notion. Here I will just defer to authority, and reproduce Hale’s succinct but compelling argument for S5:
I think we can show that the logic of absolute necessity is S5. The easiest way to see this is to consider the usual model-theoretic treatment of modality in terms of worlds. If the accessibility relation on worlds were less than universal, the notion of necessity captured in terms of truth at all worlds accessible from the given world would fairly obviously be a form of restricted or relative necessity. But if it is universal, we have S5. (Hale 2013, p. 135)Footnote 23
With issues regarding the underlying logical framework out of the way, we are now ready to show that the deflationary conception of properties supports the second-order comprehension schema. First, however, it is worth noting one of Hale’s central results—I include a proof that is roughly equivalent to his, but that is somewhat more formal and which includes explicit mention of satisfaction conditionsFootnote 24:
Theorem 2.2
(Hale 2013) Hale’s Property Principle entails that possible properties exist necessarily.
Proof
(Satisfaction condition \(\Sigma \) arbitrary, fixed.)

\(\square \)
Before giving our proof of the full second-order comprehension schema, it is worth noting that the following special case—the simple comprehension schema:
Simple Comprehension: For any unary predicate \(\ulcorner \Phi (x)\urcorner \) with only \(x\) free:
has a nearly trivial proof on the deflationary conception of properties:
Theorem 2.3
Hale’s Property Principle entails simple comprehension.
Proof
Let \(\ulcorner \Psi (y) \urcorner \) be any predicate. Then:

\(\square \)
The following corollary is worth noting:
Corollary 2.4
For any predicate \(\ulcorner \Psi (y) \urcorner \), Hale’s Property Principle entails:
Proof
Delete line 7 in the proof of Theorem 2.3 and replace line 8 (now 7) with the desired conclusion.\(\square \)
What we are interested in, however, is the full version of the second-order comprehension schema, which allows free first- and second-order variables in the predicate on the right-hand side in addition to the ‘comprehension’ variable, where these additional variables are (either implicitly or, as is the case here, explicitly) bound by initial universal quantifiers:
Full Comprehension: For any predicate \(\ulcorner \Phi (\cdots )\urcorner \) with:
free and containing no occurrences of the second-order variable \(\Pi \):
Now, as was already hinted at in Sect. 1 above, we cannot in fact prove the full second-order comprehension schema from Hale’s Property Principle alone. In addition, we need two additional modal principles governing the logical ‘behavior’ of expressions from world to world. The first we shall call the Finite Compossibility of Expressions Principle:
Although typographically complex, the intuitive import of this principle (which is really a schema, with distinct instances for each pair of finite cardinals \(n\) and \(m\)) is as follows: given a finite list of satisfaction conditions \(\Sigma _1, \Sigma _2, \ldots \Sigma _n\) and denotation conditions \(\Delta _1, \Delta _2 \ldots \Delta _m\), if there are possible worlds \(\omega _1, \omega _2, \ldots \omega _{n+m}\), predicates \(\ulcorner \Phi _1(x) \urcorner , \ulcorner \Phi _2(x) \urcorner \dots \ulcorner \Phi _n(x) \urcorner \), and singular terms \(\ulcorner \tau _1 \urcorner , \ulcorner \tau _2 \urcorner \dots \ulcorner \tau _m \urcorner \) such that, for each \(k\) where \(1 \le k \le n\), (i) \(\ulcorner \Phi _k(x) \urcorner \) exists in \(\omega _k\) and (ii) \(\ulcorner \Phi _k(x) \urcorner \) has satisfaction conditions \(\Sigma _k\), and, for each \(k\) where \(1 \le k \le m\) (i) \(\ulcorner \tau _k \urcorner \) exists in \(\omega _{n+k}\) and (ii) \(\ulcorner \tau _k \urcorner \) has denotation conditions \(\Delta _k\), then there is a single possible world \(\omega \), predicates \(\ulcorner \Psi _1(x) \urcorner , \ulcorner \Psi _2(x) \urcorner \dots \ulcorner \Psi _n(x) \urcorner \), and and singular terms \(\ulcorner \sigma _1 \urcorner , \ulcorner \sigma _2 \urcorner \dots \ulcorner \sigma _m \urcorner \) such that, for each \(k\) where \(1 \le k \le n\), (i) \(\ulcorner \Psi _k(x) \urcorner \) exists in \(\omega \) and (ii) \(\ulcorner \Psi _k(x) \urcorner \) has satisfaction conditions \(\Sigma _k\), and, for each \(k\) where \(1 \le k \le m\), (i) \(\ulcorner \sigma _k \urcorner \) exists in \(\omega \) and (ii) \(\ulcorner \sigma _k \urcorner \) has denotations conditions \(\Delta _k\). In short, if each expression in some finite sequence of expressions is individually possible (i.e. each exists at some possible world) then those expressions (or analogues of those expressions with the same satisfaction or denotation conditions) are compossible (i.e. there is a single world at which they, or their analogues, all existFootnote 25).
Of course, it is at least conceivableFootnote 26 that a collection of expressons could exist at a possible world while logical combinations of those expressions fail to exist in that world, even on the very lenient understanding of possible existence adopted earlier—say, if those predicates come from languages so different as to be completely incommensurable. We rule out this possibility with a second modal principle—the Finitary Predicate Construction Principle—which states that the possible simultaneous existence of the parts of a complex predicate is sufficient for the possible existence of that predicate itself. First, however, one last piece of terminology:
Definition 2.5
“\(Logic(\mathcal {F})\)” holds of a function \(\mathcal {F}\) if and only if \(\mathcal {F}\) is a logical operation mapping \(n\)-tuples of satisfaction and denotation conditions to satisfaction conditions.
I will not attempt to provide a necessary and sufficient specification of what, exactly, counts as a logical operation on satisfaction and denotation conditions,Footnote 27 but the following should make the rough idea clearer: a logical operation on satisfaction and denotation conditions is a function that maps each \(n\)-tuple of satisfaction and denotation conditions of the appropriate sort to a single satisfaction condition, and which is specifiable in terms of purely logical notions. For example, the logical operation on satisfaction conditions corresponding to conjunction is a binary function \(\mathcal {F}_\wedge \) where, for any predicates \(\ulcorner \Phi _1(x) \urcorner \) and \(\ulcorner \Phi _2(x) \urcorner \) and satisfaction conditions \(\Sigma _1\) and \(\Sigma _2\) such that \(\Sigma _1\) is the satisfaction condition for \(\ulcorner \Phi _1(x)\urcorner \) and \(\Sigma _2\) is the satisfaction condition for \(\ulcorner \Phi _2(x)\urcorner \), \(\mathcal {F}_\wedge (, \Sigma _1, \Sigma _2) = \Sigma _3\) where \(\Sigma _3\) is the satisfaction condition for the predicate \(\ulcorner \Phi _1(x) \wedge \Phi _2(x) \urcorner \). We can now formulate the the Finitary Predicate Construction Principle:
Informally, this principle states that if all of the subcomponent predicates and terms required for the construction of a complex predicate exist in a particular possible world, then there is a possible world where that complex predicate (or an analogue of it with the same satisfaction conditions) exists.
Let us call this formalization of the deflationary conception of objects and properties—that is:
the Deflationary Conception of Existence (or DCE). We can now show that the Deflationary Conception of Existence entails entails the full comprehension schema:
Theorem 2.6
The Deflationary Conception of Existence entails full comprehension.
Proof
Consider:
where \(\Sigma _{\Phi }\) is the (\(n + m + 1\)-ary) satisfaction condition for \(\Phi (\cdots )\) (whose existence is entailed by SCEP\(_{pred}\)). Let \(\Pi _1, \Pi _2, \ldots \Pi _n\) be any arbitrary properties, with satisfaction conditions \(\Sigma _{\Pi _1}, \Sigma _{\Pi _2}, \ldots \Sigma _{\Pi _n}\) respectively (existence of these is guaranteed by SCEP\(_{prop}\)), and \(a_1, a_2,\ldots a_m\) be any arbitrary objects. Then, by S5 we obtain:
and, by HPP, we obtain:

By WOP, there exist denotation conditions \(\Delta _1, \Delta _2, \ldots \Delta n\) such that:

By the FCEP, we then have:

Let \(\mathcal {F}\) be the logical operation (determined by the logical form of \(\Phi (\cdots )\))that takes:
as argument, and outputs the satisfaction condition corresponding to:
Then, by FPCP, we obtain:
Thus, there is a possible predicate with the relevant satisfaction condition, so by HPP the property in question actually (and hence, by Theorem 2.2, necessarilyFootnote 28) exists. Since \(\Pi _1, \Pi _2, \ldots \Pi _n\) and \(a_1, a_2,\ldots a_m\) were arbitrary, this completes the proof.\(\square \)
Before moving on to the infinitary case, it is worth noting that Theorem 2.6 supplies both good new and bad news. The good news is that this result shows that the Deflationary Conception of Existence not only provides us with a substantial and philosophically respectable account of the nature of properties, but it provides a conception that is able to underwrite a robust deductive theory. All of the deductions that are typically carried out within systems based on the standard semantics can also be carried out in the system based on the deflationary approach, since the deflationary approach supports the standard axioms and rules as laid out in, for example, Shapiro (1991). Simply put: although the Deflationary Conception of Existence may not support full semantics for second-order logic, it does imply the existence of enough properties to guarantee the validity of all of the standard axioms and rules that are typically used in deductive systems based on the standard semantics.
The bad news, however, is already implicit in our description of the good news: the Deflationary Conception of Existence seems compatible with (and, if only finitary predicates can exist, perhaps even requires) a domain of properties no more abundant than what is minimally required by nonstandard Henkin models that satify the full comprehension schema. Thus, given a countably infinite domain of objects, the collection of properties might (and, perhaps must) contain only a countable infinity of properties. Thus, it is worth seeing if, and how, we can do better, and in particular, it is worth determining whether there is a version of the deflationary conception of properties that will provide categority results for central mathematical theories such as second-order arithmetic and real analysis—a task to which I now turn.
3 Deflationism and linguistic super-tasks
The basic thought behind this section is that we can enrich the deflationary account of properties by allowing for the possibility (even if not the actuality) of expressions that consist of countably infinite strings of primitive voabulary, and hence the possibility (even if, again, not the actuality) of countably infinite predicates, by understanding such expressions as involving possible (if not actual) agents carrying out the supertasks required to write, utter, or think about such expressions.
Before moving on to the formal results, it is worth noting that Hale explicitly rejects this extension of the view for two reasons. The first involves familiar worries about whether or not supertasks are possible. The second reason is that Hale is concerned that what is required is not the possibility of carrying out various supertasks, but is instead the posisbility of carrying out non-countable hypertasks. As we shall see, the setup and results below defuse this hypertask worry. I shall return to briefly discuss and defend the logical possibility of supertasks in the concluding section.
The infinitary approach to deflationism regarding existence begins the same way as did the finitary approach, with Hale’s Property Principle and the Weak Object Principle as explicated in the previous sections (our background principles CP, SCEP\(_{prop}\) and SCEP\(_{pred}\) remain unchanged as well). We need not modify these principles, since they merely connect the actual existence of properties and objects with the possible existence of predicates and singular terms with the same satisfaction and denotation conditions respectively. The issue at issue is determining the conditions under which we may assume that various predicates at least possibly exist—Hale’s property principle, as originally formulated, will then apppriately connect these possible predicates to the corresponding properties.
Where modifications of the original finitary Deflationary Conception of Existence do come into play is in formulating infinitary analogues of our two modal principles governing the compossibility, and recombinability, of linguistic expressions. The first of these, which is an infinitary analogue of the Finite Compossibility of Expressions Principle, we shall call the Infinite Compossibility of Expressions Principle:
The Infinite Compossibility of Expressions Principle is typographically similar to the Finite Compossibility of Expressions Principle—the main difference is the inclusion of ellipsis indicating that we are now considering (countably) infinite sequences of satisfaction conditions and denotation conditions, and corresponding infinite sequences of predicates and terms.Footnote 29 In short, the Infinite Compossibility of Expressions Principle states that, if each expression in some countably infinite sequence of expressions is individually possible (i.e. each exists at some possible world) then those expressions (or analogues of those expressions with the same satisfaction or denotation conditions) are compossible (i.e. there is a single world at which they, or their analogues, all exist).
Note that Infinitary Compossibility of Expressions Principle does not require the possibility of hypertasks—even if each individual expression requires completion of a supertask for its existence, the simultaneous completion of all of these tasks in a single possible world requires merely the completion of a countably infinite sequence of countably infinite sequences of tasks, and hence is itself merely a supertask. Not also that the Infinite Compossibility of Expressions Principle does not, on its own, entail the existence of any infinitely long expressions. Instead, if all possible expressions are finite, then this principle merely entails that any countably infinite collection of such expressions co-exist in some possible world.
It is our second alternative principle that entails the existence of infinitely complex predicates. In order to formulate the principle we first need to generalize our notion of logical operations (i.e. “\(Logic(\mathcal {F})\)”) on satisfaction and denotation conditions so that the operations in question can operate on countably infinite sequences of satisfaction and denotation conditions (but still deliver in every case a single satisfaction condition as output). We still require that such an operation be specifiable in purely logical terms (although we now allow the logical resources in question to include infinitary conjunctions, infinitary strings of quantifiers, infinitely long predicates, etc.)Footnote 30 Given this, the Infinite Predicate Construction Principle is as follows:
Again, we seen little typographical difference between this principle and its finitary predecessor (FPCP) other than the inclusion of ellipsis indicating that we are now concerned with countably infinite sequences of satisfaction conditions, denotation conditions, predicates, and singular terms. Informally, this principle states that if all of the subcomponent predicates and terms required for the construction of a possibly (countably) infinitely complex predicate exist in a particular possible world, then there is a possible world where that complex predicate (or an analogue of it with the same satisfaction conditions) exists.
Let us call this stronger formalization of the deflationary conception of objects and properties—that is:
the Infinitary Deflationary Conception of Existence (or \(\infty \)DCE).
Our first result is suprisingly powerful given that it does not require anything like the full power of the Infinitary Deflationary Conception of Existence, but instead requires only Hale’s Property Principle, the Weak Object Principle, and the special case of the Infinitary Compossibility of Expressions Principle and the Infinitary Expression Construction Principle where the initial quantifiers are restricted to denotation conditions:
Theorem 3.1
The Infinitary Deflationary Conception of Existence entails that, for any countably infinite sequence of objects \(a_1, a_2, \ldots a_n, a_{n+1}\ldots \), there is a property holding of exactly \(a_1, a_2, \ldots a_n, a_{n+1}, \ldots \).
Proof
Let
be an arbitrary countably infinite sequence of possible objects. By the weak object principle, there is a sequence of denotation conditions \(\Delta _1, \Delta _1, \ldots \Delta _n, \Delta _{n+1}\) such that:

Thus, by the \(\infty \)CEP we obtain:

Let \(\mathcal {F}\) be the logical operation that takes:
as argument, and outputs the satisfaction condition corresponding to:
Then, by \(\infty \)PCP, we obtain:
Thus, there is a possible predicate with the relevant satisfaction condition, so by HPP the property in question actually (and hence, by Theorem 2.2, necessarilyFootnote 31) exists. Since \(a_1, a_2,\ldots a_n, a_{n+1} \ldots \) were arbitrary, this completes the proof.\(\square \)
Theorem 3.1 thus guarantees the existence of a property corresponding to any arbitrary countably infinite collection of objects. This is a vast improvement over the situation in the previous section, since this entails that any model whose first-order domain is finite or countably infinite will contain a property corresponding to each finite or countably infinite subcollection of the domain, hence a property corresponding to any subcollection of the domain. In short, if we allow for at least the logical possibility of supertasks (equivalently: formulas with countably infinitely many occurrences of primitive vocabulary), then we retain the standard semantics for the special (but important) case where the first-order domain is finite or countably infinite.
Presumably, it is this powerful result that underlies the worry that we have somehow smuggled hypertasks into the account. After all, if our account entails the existence of continuum many properties, and each property requires the possible existence of a corresponding predicate, then this entails the possible existence of continuum-many distinct predicates. First, it should be noted that, even if this worry were well-founded, it might not be the problem that it superficially appears to be, since we have defined possible predicate existence in terms of being in the extension of the formation rules for a language that is used within a possible world—hence, not every expression that exists in a world need actually be written or spoken within that world. This response, however, is somewhat unsatisfying, since it relies heavily on the particular—and particularly ‘thin’—analysis of possible existence adopted here. But it turns out that we need not worry, since there is no sense in which the principles adopted above entail that any possible world contains more than countably many predicates.
The confusion hinges on an ambiguity in the phrase “this entails the possible existence of continuum-many predicates” used in the previous paragraph. According to the Infinitary Deflationary Conception of Existence, if the actual world (or any world) contains a countably infinite collection of objects, then that world will also contain an uncountable (continuum-sized, at the least) collection of properties. Now, for each of these properties, there must be a possible predicate with the same satisfaction conditions. And Theorem 3.1 provides a recipe for finding each of these predicates (and the possible worlds that contain them). But there is no reason to conclude that all continuum-many of these predicates can be found together in a single possible world. Hence, if there need be no world that contains uncountably many distinct predicates (regardless of how we ultimately understand ‘exists’ when applied to predicates), there is no risk of the view requiring that actual or even merely possible agents perform linguistic hypertasks.
Of course, given any countably infinite collection of such predicates, there will, by \(\infty \)PCP, be a possible world containing all the predicates (or analogues of them with the same satisfaction conditions) in the collection. But again, constructing all the predicates in a countably infinite collection of predicates (even if each of the predicates is itself of countably infinite length or complexity) is merely a supertask.Footnote 32
The following two corollaries are important, since they show that the Infinitary Deflationary Conception of Existence allows us to precisely capture at least some mathematical structures of central interest (and they also show that the semantics provided by the Infinitary Deflationary Conception of Existence supports a second-order logic sufficient to carry out neo-logicist reconstructions of arithmetic and real analysis):
Corollary 3.2
On finite or countably infinite first-order domains, the semantics provided by the Infinitary Deflationary Conception of Existence is equivalent to standard semantics.
Proof
Straightforward consequence of Theorem 3.1.\(\square \)
Corollary 3.3
Second-order Peano arithmetic is categorical in the semantics provided by the Infinitary Deflationary Conception of Existence.
Proof
The property holding of exactly the standard natural numbers exists, by Theorem 3.1. Induction then implies that the standard natural numbers are the only objects in the domain. Hence the only model is the standard, countable model.\(\square \)
In addition, Theorem 3.1 provides us with the promised ‘near-categority’ result for real analysis:
Theorem 3.4
In the semantics provided by the Infinitary Deflationary Conception of Existence, any two models of second-order real analysis are order-isomorphic on their standard orderings.
Proof
(proof sketch): By Theorem 3.1, any such model of real analysis contains a property corresponding to each countably infinite set of reals, and hence contains a property corresponding to any Cauchy sequence. Thus, the second-order axiom:
entails that any countably infinite, bounded subset of the reals has a least upper bound as intended (since each such subset can be mimicked by an appropriate Cauchy sequence). This (plus the first-order axioms) suffices for order-isomorphism.\(\square \)
There is, of course, an obvious further question to ask: how do standard set theories such as (second-order) ZFC fare in the semantics provided by the Infinitary Deflationary Conception of Existence? This is an important question but a difficult one, so I will remain content, for the purposes of this essay, with labelling this issue ‘open’, and promising to return to it in later work.
There is one final issue that we can straightforwardly and definitely deal with, however: the status of the second-order comprehension schema within the semantics provided by the Infinitary Deflationary Conception of Existence. There are two main complications that we need to deal with.
First, we should note that the proof of Theorem 2.6 is not on its own sufficient to show that full comprehension holds in the present context. The reason for this is that our stronger infinitary principles entail the existence of more properties and corresponding predicates than were present in the finitary context within which we proved Theorem 2.6, and hence the initial universal quantifiers in the comprehension schema now have wider scope than they did in the finitary case. Nevertheless, even if that proof does not suffice in the present context, a straightforward typographical modification of it can be carried out for the Infinitary Deflationary Conception of Existence:
Theorem 3.5
The Infinitary Deflationary Conception of Existence entails the full comprehension schema.
Proof
Mimic the proof of Theorem 2.6, replacing FCEP and FPCP with \(\infty \)CEP and \(\infty \)PCP respectively.\(\square \)
It turns out, however, that in the present context we can do even better. Given that we are countenancing at least the possibility of infinitary predicates, it seems natural to explore whether the Infinitary Deflationary Conception of Existence supports the following countably infinitary generalization of the full comprehension schema:
Infinitary Comprehension: For any (possibly countably infinite) predicate \(\ulcorner \Phi (\cdots )\urcorner \) with:
free:
Perhaps surprisingly, the modifications required to transform the proof of Theorem 2.6 into a proof of the infinitary comprehension schema are only slightly more complicated than those required for Theorem 3.5 above:
Theorem 3.6
The Infinitary Deflationary Conception of Existence entails the infinitary comprehension schema.
Proof
Mimic the proof of Theorem 2.6, replacing FCEP and FPCP with \(\infty \)CEP and \(\infty \)PCP respectively, and inserting ellipsis when necessary.\(\square \)
Thus, even if we are not able to construct infinitary predicates in our own actual world, the Infinitary Deflationary Conception of Existence guarantees that properties corresponding to any such predicate exist (and exist necessarily), and further that the domain of properties is closed under finite and infinitary Boolean operations and first- and second-order projections. While this still falls short of providing standard semantics when the first-order domain is uncountable, it does guarantee that the second-order domain provides a powerful and abundant stock of properties over which we can quantify.Footnote 33
4 Logical possibility and supertasks
Thus, the Infinitary Deflationary Conception of Existence, although failing to provide the full, standard semantics for models with uncountable first-order domains, nevertheless:
-
1.
Provides a property corresponding to every finite or countably infinite collection from the first-order domain.
-
2.
Satisfies the full comprehension schema for properties, as well as the infinitary variant of comprehension.
-
3.
Provides categority results for theories with countably infinite intended interpretations.
-
4.
Provides ‘near’-categority results for real analysis.
The final task is to say a few things in favor of the Infinitary Deflationary Conception of Existence, and in particular, to provide some evidence that the sorts of supertasks whose possibility is required by the view (in particular, those required by the Infinitary Predicate Construction Principle) are in fact possible.
For the sake of argument, let us grant that we cannot actually speak, write, or think in languages that contain the sort of countably infinite expressions whose possible existence is entailed by the Infinitary Deflationary Conception of Existence (or, more carefully, we cannot speak, write, or think those expressions that are, in fact, countably infinitely long). The question, then, is whether this constraint is a contingent fact regarding our biology and psychology and the sort of world that we find ourselves in, or whether this reflects a more general, logical constraint on reasoning and language. In other words, does our local inability to entertain and reason with such expressions stem from the fact that such expressions are logically impossible, or merely from the fact that they are physically impossible (for us)?
The first thing to notice in answering this question is that there do exist actual languages (not merely possible ones) that include infinitary expressions of just the sort we are concerned with: logicians formulate, study, and prove theorems about infinitary languages, their semantics, and their logics all the time. Formal languages (including infinitary languages and their logics) are (or can be though of as) a certain type of set theoretic construction. Thus, it is a theorem of set theory that such languages exist. Existence theorems of this sort, however, clearly are not the appropriate way to settle the relevant possibility claims.Footnote 34 But they do suggest a strategy: We can determine what sorts of languages are possible in the relevant sense by determining which formal languages model linguistic constructions and behaviors that are, or seem to be, logically possible.
First, the easy cases. Languages with expressions of finite length only are in, since they closely model the languages that we actually do use to speak, write, and think. For the sake of argument let us assume that languages with expressions of uncountably infinite length are out (perhaps because we believe that the sort of possible world that could contain speakers, writers, and thinkers must have a temporal structure enough like our own—that is, its temporal order of instants must have a structure sufficiently similar to the real numbers—so as to rule out embedding uncountably infinite hypertasks into a finite durationFootnote 35). So the question is whether reasoners in some possible world could speak, write, and think in languages that contain countably infinitely long expressions (and, more specifically, whether they can speak, write, or think these infinite expressions).
There seems to me to be no reason to think that we should answer this question negatively. In fact, we can easily formulate instructionsFootnote 36 for writing the sort of countably infinite formulas at issue: Write the first symbol in half a minute, in a region no more than half an inch square; the second symbol in a quarter of a minute, in a region no more than a quarter inch square; the third symbol in an eighth of a minute, in a region no more than an eighth inch square; the fourth symbol\(\ldots \). Of course, thanks to the quantum structure of our universe, the finite upper bound on achievable speeds, etc., we are unable to carry out these instructions ourselves (in fact, we are unable to complete the supertask involved in writing them down, although we can provide a definite description precisely describing them). But, as noted above, this is not the issue. The issue is whether it is logically possible to carry out these instructions. And the answer to this question, I think, must be “yes”. There is no reason to think that there is anything logically absurd or impossible about these instructions, and no reason (other than a sort of provincial presupposition that possible reasoners ought be no more able than ourselves, and live in worlds no more congenial than our own) to think that there is anything logically absurd about either the sort of infinitary reasoner who could carry out such a set of instructions, or the sort of possible world in which such a reasoner would have to live in order to do so. To paraphrase Bertrand Russell, our inability to carry out supertasks amounts to nothing more than a mere medical impossibility.
If this is right, then the best formulation of the deflationary conception of properties and objects is one that takes the logical possibility of linguistic supertasks into account—that is, the best version of such a deflationism is something like the Infinitary Deflationary Conception of Existence. As we have seen, such a view does not get us quite everything that we might want, such as standard semantics for models with uncountably infinite first-order domains. But the Infinitary Deflationary Conception of Existence does provide substantially more representational and logical power than is provided by either first-order formalisms or the finitary version of the Deflationary Conception of Existence. In particular, the view seems to provide a robust enough domain of properties to support the sort of second-order reasoning required by neo-logicism—which is one of the motivations for Hale’s deflationary conception of properties in the first place.
Notes
Hale equates his deflationary approach to properties with so-called abundant conceptions, but prefers the former terminology since it emphasizes the existence conditions for properties rather than their profusion. Further, as we shall see, Hale’s reading the deflationist conception (as well as the alternative development of these ideas explored here) is less than fully ‘abundant’, since it does not imply the existence of a property for each arbitrary collection of objects. Hale’s deflationism should be carefully distinguished from minimalist views such as Thomas Hofweber’s internalism (Hofweber 2006). Although both views closely link existence claims regarding properties to the possible or actual existence of a corresponding predicate, internalism rejects the thought that such existence claims actually commit us to the existence of properties.
Hale refers to his earlier (Hale 2010) for a full defense of the deflationary approach to ontology.
It is important to note that on the deflationary conception object existence, like property existence, is a matter of what expressions might exist, not a matter of what expressions (contingently) do exist!
The astute reader will note that there is an asymmetry to our formulation of the deflationary account of properties and the deflationary account of objects—the former involves (or is associated with) a total function, while the latter involves a partial function. This is as it should be, however. If a predicate possibly exists, then the corresponding property exists at every possible world (although the extension of the property might vary from world to world, and be empty at some worlds). The possible existence of a singular term does not guarantee the existence of a corresponding object at every world, however.
The additional condition that the possible singular term, had it existed, would figure in true atomic statements has disappeared from this way of formulating the idea. Since in what follows we shall only be concerned with the inference from the first bullet-point to the second—i.e., that necessarily, for any object that exists, there is a possible singular term that would denote that object had it (the singular term) existed—this simplification is harmless.
Hale actually argues for an intensional account of property individuation, where two distinct properties might hold of the same objects, and might even necessarily hold of the same objects (see Hale 2013, pp. 139–144). Since the present concern is determining whether, and under what conditions, the deflationary account might provide ‘enough’ properties to validate the second-order comprehension schema, or support the standard semantics for second-order logic (or both), however, I ignore this complication.
Of course, two distinct predicates might stand for the same property, and, given the intentional individuation of properties outlined in Hale (2013), more than one property might be co-extensive with the same predicate (and perhaps even necessarily so). The point is that a single predicate cannot stand for two non-coextensive properties.
Since the point of the present essay is to (correctly) extend Hale’s philosophical ideas, rather than criticize those points where he gets the mathematics wrong, I leave it to the interested reader to identify the exact point at which Hale’s reasoning goes awry. See below, however, for some additional observations.
For example, a model containing countably many objects, and whose properties correspond to the finite and co-finite subsets of those objects, would suffice.
This paragraph owes much to helpful comments from Stewart Shapiro and an anonymous referee.
After all, a single object language can be studied from the perspective of many different metalanguages, with vastly different expressive resources.
A supertask is a task that requires performing a countable infinity of distinct sub-tasks within a finite period of time. A hypertask is a task that requires performing an uncountable infinity of tasks within a finite period of time.
Hale generously credits the present author with bringing the issue of infinitary expression and supertasks to his attention in the same footnote that contains his objections to such an extension of the view. He notes that “the whole issue deserves much fuller investigation and discussion” (Hale 2013, p. 146, footnote 29). The present essay is, needless to say, an attempt to provide some initial investigation, and to prompt fuller discussion, in the manner called for.
Of course, such a more rigorous approach might have mathematical benefits, but that is another matter!
Thanks are due to an anonymous referee for emphasizing the importance of this clarification, and apologies are due to the same referee for failing to address this concern in exactly the manner he or she would have preferred.
Care needs to be taken here: If we expand the language by adding a function \(\mathcal {F}(x)\) that takes the Gödel code of a predicate as argument, and outputs the satisfaction condition for that predicate (and there seems to be no good reason to object to such a function), then we can diagonalize on:
$$\begin{aligned} (\exists X)(SC_{prop}(X, \mathcal {F}(y)) \wedge \lnot X(x)) \end{aligned}$$to obtain a predicate \(\Phi (y)\) such that:
$$\begin{aligned} (\forall z)[\Phi (z) \leftrightarrow (\exists X)(SC_{prop}(X, \mathcal {F}(\ulcorner \Phi (y) \urcorner )) \wedge \lnot X(z)) \end{aligned}$$In short, we can construct a Russell/Liar-like predicate \(\Phi (y)\) such that, for any object \(a\), \(\Phi (y)\) holds of \(a\) if and only if there is a property with the same satisfaction conditions as \(\Phi (y)\) yet which fails to hold of \(a\). But by definition, any two things with the same satisfaction conditions hold of the same things (in every possible world!). So, in particular, we have
$$\begin{aligned} (\forall X)(SC_{prop}(X, \mathcal {F}(\ulcorner \Phi (y) \urcorner )) \rightarrow (\forall z)(X(z) \leftrightarrow \Phi (x))) \end{aligned}$$Contradiction.
Of course, this is not all that surprising: satisfaction conditions (and our \(SC_{(\dots )}\) predicates holding of them) are semantic notions, and it is well-known that naïve formulation of the principles governing semantic notions can lead to paradox. Thus, a more careful and precise formulation of the principles governing satisfaction conditions would involve applying whatever prophylactic one prefers in the more well-known instances of this sort of phenomenon (i.e., plug in one’s favored solution to the Liar paradox here: my own preference can be found in Cook 2007a, 2009). Given the straightforward nature of the arguments given below, however (and, in particular, the fact that they involve no diagonalization or other paradox-prone constructions), we can safely ignore this problem for the time being. Thanks go to an anonymous referee for pointing out this contradiction, and the need to address it.
We also assume the \(n\)-ary analogues of CP for all \(n \in \mathbb {N}\). For example, the binary version can be written as:
$$\begin{aligned} \text {CP}^2: \;&\Box (\forall \Sigma ^2)(\forall X^2)(\forall \ulcorner \Phi (y_1, y_2) \urcorner )((SC_{prop}(X^2, \Sigma )\wedge SC_{pred}(\ulcorner \Phi (y_1, y_2) \urcorner , \Sigma ^2)) \\&\rightarrow \Box (\forall z_1)(\forall z_2)(X(z_1, z_2) \leftrightarrow \Phi (x_1, x_2))) \end{aligned}$$with superscripts indicating the arity of properties and satisfaction conditions (a notational detail we shall suppress when arity is clear from context).
Additionally, it is worth noting that CP is ‘ungrammatical’ as written, since it includes both ‘mention’ of the predicate in question (i.e. \(\ulcorner \Phi (x)\urcorner \)) and its ‘use’ in the final biconditional clause. This could be rectified by introducing a satisfaction predicate \(Sat(x, y)\) such that:
For any predicate \(\ulcorner \Phi (y) \urcorner \):
$$\begin{aligned} (\forall x)(Sat(\ulcorner \Phi (y) \urcorner , x) \leftrightarrow \Phi (x)) \end{aligned}$$and then formulating the Coextensionality Principle as:
$$\begin{aligned} \text {CP}: \;&\Box (\forall \Sigma )(\forall X)(\forall \ulcorner \Phi (y) \urcorner )((SC_{prop}(X, \Sigma )\wedge SC_{pred}(\ulcorner \Phi (y) \urcorner , \Sigma )) \\&\rightarrow \Box (\forall z)(X(z) \leftrightarrow Sat(\ulcorner \Phi (y) \urcorner , x))) \end{aligned}$$The simplification introduced in the ‘incorrect’ formulation is harmless in the present (somewhat informal) context, however, and avoids the introduction of paradox-prone notions such as \(Sat(x, y)\). See footnote 17 above for more discussion of paradoxes, and how to deal with them, within the present approach.
Note that we do not assume that, for every satisfaction condition, there is a predicate or property that has that satisfaction condition—that is, we do not assume (and do not need):
$$\begin{aligned}&\Box (\forall \Sigma )(\exists \Pi )(SC_{prop}(X, \Sigma )\\&\Box (\forall \Sigma )(\exists \ulcorner \Phi (y) \urcorner )(SC_{prop}(\ulcorner \Phi (y) \urcorner , \Sigma ) \end{aligned}$$The adoption of the Weak Object Principle, rather than some stronger principle that arguably captures the entirety of the deflationary conception of objects in the same sense as Hale’s Property Principle captures the entirety of the deflationary conception of properties, allows us to sidestep, in a technical sense, the need to deal with cases where terms fail to refer.
Note that we do not need separate existence principles analogous to SCEP\(_{prop}\) and SCEP\(_{pred}\) for denotation conditions, since WOP entails that, for any object, there exists a denotation condition ‘picking out’ that object.
Hale prefers talk of possibilities rather than worlds, where the former (unlike traditional treatments of the latter) need not be assumed to be fully determinate or maximal. But he notes (and I agree) that this point is orthogonal to the concerns of both his and the current essay—see (Hale (2013), p. 135, footnote 5).
Hale talks here of absolute necessity, rather than logical necessity, and defines absolute necessity in terms of the counterfactual conditional as follows:
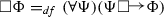
where the universal quantifier ranges over all propositions unrestrictedly. Thus, Hale’s absolute necessity is not necessarily the same as the notion of logical necessity being mobilized here. But, although absolute necessity and logical necessity might not be everywhere equivalent, I see no reason to think that they will fail to agree when the case at issue is the possible existence of linguistic items, and every reason to think they will be ‘locally’ equivalent in this case. Also, the reader unconvinved by Hale’s brief argument can find longer, more technically complex arguments that S5 is the logic of logical necessity in Burgess (1999) and Halldén (1963).
See (Hale (2013), pp. 135–136) for the original argument.
The parenthetical qualification is important: the Finite Compossibility of Expressions Principle does not require that it is the same predicates or singular terms that exist at a single possible world, but merely a sequence of predicates and terms with pairwise the same satisfaction or denotation conditions.
Of course, I make no assumption that conceivability its a reliable—or even useful—guide to possibility. In fact, conceivable or not, I believe that the ‘situation’ ruled out by the Finitary Predicate Construction Principle is, in fact, logically impossible. Thus, the point of the Finitary Predicate Construction Principle is not to restrict attention to only a certain kind of possible world (i.e those that satisfy the principle), but rather to highlight a particularly important observation regarding all possible worlds.
Providing such necessary and sufficient conditions would require, amongst other things, that we determine the exact location of the boundary that separates logical from non-logical vocabulary, which is both an extremely difficult task, and one that seems somewhat outside the remit of the present essay.
Note that this we could modify this step of the proof to prove a stronger, modal formulation of the full comprehension schema, along the lines of Corollary 2.4 above. Details are left to the interested reader.
As noted at the end of the introductory section, I shall use infinitary expressions of this sort in an intuitive manner, although the arguments here and below can be straightforwardly adapted in standard infinitary logics such as those studied in Keisler (1971).
Although I have left the specification of \(Logic(\mathcal {F})\) rather informal in order to maximize the general applicability of the results below, one can easily precisify this notion by identifying the infinitary logical operations with those logical operations definable in some preferred infinitary language (e.g, \(\mathcal {L}_{\omega ,\omega }\)).
As usual, this proof can be modified to provide a stronger, modal formulation of the theorem. Details are left to the interested reader.
Of course, the Infinitary Deflationary Conception of Existence does seem to require an uncountably infinite class of possible worlds if hypertasks are disallowed, since we need enough worlds to ‘spread out’ the various supertasks required for the vast number of distinct predicates whose possibility is entailed by the view. I see no reason to think that this sort of proliferation is at all problematic, however. At any rate, the defender of the deflationary account of objects who also believes that the (standard, classical) real numbers exist—and Hale is such a defender, see Hale (2000)—is already in a similar position: if continuum-many reals exist, then by the deflationary conception of objects continuum-many distinct singular terms must be possible. Either they are jointly possible, and there is a single world where a linguistic hypertask has been completed, or they are not jointly possible, and are spread out amongst continuum-many distinct possible worlds.
Note that the observation that the second-order semantics supported by the Infinitary Deflationary Conception of Existence satisfies the infinitary comprehension schema does not require that the language we use when quantifying over the first- or second-order domains of models in that semantics include the infinitary resources required to formulate this infinitary form of comprehension. On the contrary, this is the surprising power of Theorem 3.6—that it shows that the mere possibility of infinitary logical constructions entails that our own world contains an abundance of properties that cannot be defined merely in terms of the finitary resources available locally (assuming, of course, that we are in fact contingently restricted to finitary expressions in the actual world).
Further, if all that mattered were the possible or actual existence of formal languages with appropriate predicates, then we could easily retain full semantics tout court merely by pointing out that nothing prevents infinitary formal languages with formulas of arbitrary infinite length.
Note that this point, if correct (and I am not actually completely convinced that it is) does not rule out the logical possibility of hypertasks in general, but only rules out the possibility of linguistic hypertasks!
Of course, this particular sort of instruction schema will only work for formulas where the symbols are ordered in a simple \(\omega \)-sequence. But any countably infinite sequence can be embedded in a finite interval of the reals, and hence can be given a similar, although in some cases more complicated, set of instructions.
References
Cook, R. (2007a). Embracing revenge: On the indefinite extensibility of the liar. In J. Beall (Ed.), Revenge of the liar: New essays on the paradox (pp. 31–52). Oxford: Oxford University Press.
Cook, R. (2007b). The Arché paper on the mathematics of abstraction. Western Ontario Series in the Philosophy of Science (Vol. 71). Dordrecht: Springer.
Cook, R. (2009). What is a truth value, and how many are there? Studia Logica, 92, 183–201.
Burgess, J. (1999). Which modal logic is the right one? Notre Dame Journal of Formal Logic, 40(1), 81–93.
Hale, B. (2000). Reals by abstraction. Philosophia Mathematica, 8(2), 100–123.
Hale, B. (2010). The bearable lightness of being. Axiomathes, 20, 399–422.
Hale, B. (2013). Properties and the interpretation of second-order logic. Philosophia Mathematica, 21, 133–156.
Hale, B., & Wright, C. (2001). The reason’s proper study. Oxford: Oxford University Press.
Halldén, S. (1963). A pragmatic approach to model theory. Acta Philosophica Fennica, 16, 53–63.
Hofweber, T. (2006). Inexpressible properties and propositions. Oxford Studies in Metaphysics, 2, 155–206.
Keisler, H. (1971). Model theory for infinitary logic: Logic with countable conjunctions and finite quantifiers. Studies in logic and the foundations of mathematics (Vol. 62). Amsterdam: North Holland.
Kreisel, G. (1972). Informal rigour and completeness proofs. In I. Lakatos (Ed.), Problems in the philosophy of mathematics (pp. 138–157). Amsterdam: North Holland.
Quine, W. (1970). Philosophy of logic. Englewood Cliffs, NJ: Prentice Hall.
Shapiro, S. (1991). Foundations without foundationalism: The case for second-order logic. Oxford: Oxford University Press.
Acknowledgments
A huge thanks is due to Bob Hale, who tolerated many conversations and e-mails regarding this material (both before and after Hale 2013 was accepted for publication). He was, as always, extremely helpful and extremely patient, and provided many insightful suggestions that greatly improved the material above and its organization. Thanks are also due to Stewart Shapiro and Chris Menzel for helpful comments, and to a generous and insightful audience at the Between First- and Second-Order Logic workshop at UniLog 2013: The World Congress on Universal Logic in Rio de Janeiro, Brazil, where an early version of these ideas was presented.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cook, R.T. Possible predicates and actual properties. Synthese 196, 2555–2582 (2019). https://doi.org/10.1007/s11229-014-0592-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-014-0592-1