Dedicated hardware design for efficient quantum computations using classical logic gates

Abstract

This work presents a novel approach to quantum computing by proposing a customizable hardware design of a dedicated processor that emulates the execution of quantum algorithms. Unlike software-based quantum computation simulators, which run on standard general-purpose computers and suffer from reduced performance, this hardware design, which is based on classical concepts of bits, registers and memories, aims to leverage pure parallelism and pipelined execution for efficient quantum computations via emulation. The architecture includes several key components: memories, computation unit, measurement unit and control unit. The quantum state memory stores the individual and group states of qubits. This memory is crucial for maintaining the quantum information required for quantum operations. Basic operators are stored in dedicated operator memory. Additionally, a scratch memory allows for larger operators to be dynamically built at runtime. The computation unit is responsible for performing complex number multiplications, which form the basis of tensor and matrix products necessary for executing quantum operations. A measurement unit enables quantum state sampling, which is an essential aspect of quantum computation. Furthermore, a control unit is incorporated to ensure the correct operation of the quantum processor’s data path. It utilizes a microprogram to manage and coordinate the functional units. All the functional units communicate with each other through dedicated and shared data buses, depending on the frequency of information exchange. This enables efficient data transfer and coordination among the components. The proposed hardware design has been simulated and proved to be effective in executing quantum operations. By exploiting parallelism and employing a pipelined execution, this architecture overcomes the limitations of software-based simulators, delivering improved performance for emulating quantum algorithms. We use Grover’s search algorithm as a benchmark to evaluate the performance of the proposed hardware design and compare it to software-based simulation and to hardware-based algorithm-dedicated emulation.

1 Introduction

Quantum computing has garnered considerable research interest due to its potential to enhance processing speed through the use of algorithms with inherent parallelism. It offers the possibility of achieving polynomial time solutions for NP-complete problems [1,2,3]. However, the control of quantum states in real quantum computers remains challenging, with only a few qubits being controlled for a short duration. At the time of this work’s conclusion, the largest number of entangled qubits achieved under special conditions was twenty [4]. Companies have invested in the development of commercial real quantum devices. For instance, in 2015, D-Wave introduced a quantum computer with 1000 qubits, although not all were entirely entangled [5]. Four years later, D-Wave announced the next-generation Pegasus quantum processor chip, featuring 15 connections per qubit compared to the previous 6. They projected that the subsequent system would utilize the Pegasus chip, encompassing over 5000 qubits, and become available shortly [6].

While commercial real quantum processors are not yet available to the general public, quantum programming is being explored through simulators and libraries of quantum operation routines. Examples of these include QCL (Quantum Computation Language) [7], QCS (Quantum Computer Simulator), QuaSi, Fraunhofer Quantum Computing Simulator, QuCalc, QDensity, OpenQuacs, QML, JaQuzzi, Senko’s Quantum Computer, Shornuf, Simqubit and QHaskell [8,9,10]. For efficient software simulation, many sophisticated data structure has been proposed. Among others, tensor networks [11] and decision diagrams [12] provide successful implementations for the simulation of quantum computations on classical computers. However, these kinds of data structures are complex and dynamic, thus limiting their suitability for a hardware implementation, which require a concise internal representation and efficient management of dynamic memory.

Nowadays, various efficient quantum simulators, such as IBM’s quantum circuit composer [13] and Munich Quantum Toolkit [14], run effectively on standard general-purpose computers. However, simulators, being software products, often suffer from longer processing times due to sequential execution, although this can be partially mitigated by utilizing multiple processors and resource sharing [15, 16]. The usage of general-purpose processors and thus internal general data paths, which are not necessarily optimized for the low-level instructions used to simulate quantum operations, are the main reason for the execution bottleneck. Optimized data paths as well as custom-made parallelism are the main contributions in quantum hardware emulators with dedicated designs towards the acceleration of quantum operations. So, dedicated processors, custom-designed to emulate quantum operations efficiently, can offer significant advantages over simulators run on standard general-purpose processors, thus providing faster speed as well as a well-tailored parallelism to guarantee a good trade-off between cost and efficiency. By running on specialized processors, such as emulated quantum processors, the results of quantum operations can be obtained in a shorter time frame. Building dedicated hardware for quantum computing is a complex and ongoing research effort, involving various scientific disciplines, engineering challenges and optimization to achieve stable, reliable and scalable quantum computing emulators. As real quantum computing technology advances, dedicated hardware emulators should meanwhile help unlocking the full potential of quantum algorithms and applications.

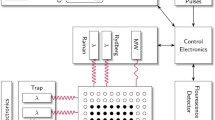
Dedicated hardware for quantum computing refers to specialized physical devices and components designed to implement and perform quantum computations. Unlike classical computers that rely on bits to represent information, quantum computers use quantum bits or qubits, which can represent multiple states simultaneously due to the principles of quantum superposition and entanglement. Real quantum processors, which are the key element in quantum computers, are built using various physical systems such as superconducting circuits [17], trapped ions [18], topological qubits [19] and photonic qubits [20]. Dedicated hardware emulators for quantum computing are nowadays necessary because quantum computations require dedicated and precise control over the idealized representations of qubits and quantum registers and the ability to manipulate the emulated quantum states with high fidelity and high processing speed.

This work introduces an architecture of an emulated quantum processor, designed to be implemented using classical hardware and embedded into classical general-purpose computers. The design should enable the acceleration of problem-solving, when compared with software-based quantum simulators and more versatility when compared to a hardware design, dedicated to implement a specific quantum algorithm. This work represents a pioneering effort, as it is the first attempt to implement a classical hardware-based emulation of a quantum processor, capable of emulating the execution of quantum operations. It does so via user directives inserted in a traditional program, as it is the case in physical real quantum computers, which by design receive their instructions from a classical program. As to this point in time, we were unable to find a similar work, wherein a hardware design of a quantum emulator based on classical concepts of memory, register and bits to emulate quantum computations, is proposed. Of course, as mentioned before, this has been done either using novel physical technologies, such as superconducting qubits [17], trapped Ions [18], photonic qubits [20] and topological qubits [19], or in software-based simulators, but not using emulation via a dedicated quantum processor as it is the case in this work. Dedicated hardware specifically designed for some quantum algorithms can be found in [21].

For the sake of simplicity and to lift any ambiguity, throughout the rest of this paper, physical quantum implementations, based on aforementioned advanced technologies for qubits, will be termed (real) quantum hardware or processors while software simulation and hardware emulation of quantum computations will be discriminated as simulated and emulated quantum processor or simply simulator and emulator, respectively. So, the processor hardware design, proposed in this work, which is based on classical logic concepts to emulate quantum computations, will be termed as emulated quantum processor (EQP) or simply emulator.

Some key issues that hardware design dedicated to quantum emulation include: (1) processing unit, allowing to manipulate the set of qubits and to emulate quantum operations; (2) state control units, which are specialized electronics and control systems to manipulate and maintain the internal representation of qubits states; (3) computation units, which are components responsible for emulating the execution of quantum operations on the qubit internal representations used in quantum algorithms; (4) memory units, which are representation, techniques and hardware to store and retrieve the internal representation of quantum information; and (5) measurement units, which allow interfacing with the quantum emulator, enabling the emulation of quantum states observation and transformation into a classical binary representation. Note that error correction unit that is fundamental in real quantum processors is not required in emulated quantum processor designs that are based on classical logic gates. Classical binary circuits do not experience a significant amount of bit flips errors due to the high external energy needed to change the electrical current [22].

Our work proposes a novel hardware architecture of a dedicated processor to accelerate the emulation of quantum operations. The design can be customized according to some parameters, such as the overall number of qubits of machine state, the maximum number of qubits that can be operated simultaneously and the number of qubits entanglements. The proposed quantum emulator works alongside a general-purpose processor. It is capable of emulating quantum operations efficiently using a custom-designed of parallelism and pipeline. The design leverages dedicated information bookkeeping memories to enable efficient access to information regarding to stored internal representation of qubits and emulate quantum operations with high efficiency. It does by optimizing the design’s data paths for efficient execution. It is worth noting that the current design does not require any error detection unit. We establish the superiority of the proposed solution over software-based simulation regarding time requirements and over hardware-based alternative when the design is dedicated to a given algorithm regarding versatility. The proposed design trades some performance for a larger versatility.

This paper is divided into seven sections. First of all, in Sect. 2, we provide an introduction to quantum computing, including a definition of the data model and the primary quantum operations. After that, in Sect. 3, we present and discuss recent related works of the literature. Subsequently, in Sect. 4, we describe the macro-architecture of the proposed quantum processor. There follows, in Sect. 5, the details of the micro-architecture regarding the data path and control path of the quantum processor. This includes the organization of the included memory. Later, in Sect. 6, we present and explain simulation results related to instruction execution within the quantum processor. Subsequently, in Sect. 7, we present and analyze the performance of the proposed processor design for a quantum algorithm with respect to memory and time requirements and compare it to that of software simulation and hardware emulation alternatives. Finally, in Sect. 8, we provide the concluding remarks and suggest promising directions for future research.

2 Quantum computations

Quantum computing is founded on the concept of the fundamental information unit known as the quantum bit, qubit or simply qubit. Unlike classical bits, which can only store a single value of 0 or 1, qubits can exist in a state of superposition. This means that a qubit can simultaneously hold both 0 and 1, with each state having its own amplitude. This unique property allows qubits to represent an infinite range of values, including the boundary states of 0 and 1, using probabilistic characteristics instead of deterministic ones.

Mathematically, a qubit can be represented as a vector in a two-dimensional orthonormal basis and can be used to express an infinite set of values through linear combinations in the complex number field. The common notation is $\vert 0\rangle =\begin{bmatrix} 1&0\end{bmatrix}^T$ and $\vert 1\rangle =\begin{bmatrix} 0&1\end{bmatrix}^T$. So, qubit $\vert v \rangle$ can be represented interchangeably by either forms: $\vert v \rangle =\begin{bmatrix} \alpha&\beta \end{bmatrix}^T$ or $\vert v \rangle =\alpha \vert 0\rangle +\beta \vert 1\rangle$, where $\alpha$ and $\beta$ are complex numbers representing the magnitude of each base vector. Thus, it features a qubit in simultaneously states 0 and 1, but with the respective coefficients for each state. The squared amplitude represents the probability that the qubit is in that corresponding state. The sum of the squared amplitudes is always 1, i.e., $\vert \alpha \vert ^2+\vert \beta \vert ^2 = 1$, preserving the vector norm.

The state of a quantum system can be represented by a vector that is a linear combination of the base vectors, with the dimension of the base being equal to $2^n$, where n is the number of qubits in the system. As a result, a vector representing the state of the quantum system contains not only as many states as the number of qubits, but $2^n$ states.

The quantum state of a machine is formed by a linear combination of collapsed states (base vectors) multiplied by their associated amplitudes. When an operation is performed on a vector, it is equivalent to performing the operation on each term of the linear combination. This results in an inherent parallelism, and for any given operator, say T, we can express it as in Eq. 1:

$$\begin{aligned} \begin{array}{lll} T\vert v \rangle &{}=&{}T(\alpha \vert 0\rangle +\beta \vert 1\rangle +\gamma \vert 2\rangle +\dots +\omega \vert 2^n-1\rangle )\\ &{}&{}\\ &{}=&{}\alpha T\vert 0\rangle +\beta T\vert 1\rangle +\dots +\omega T\vert 2^n-1\rangle .\\ \end{array} \end{aligned}$$

(1)

A qubit can be entangled with one or more other qubits, allowing for mutual interference, which is referred to as entanglement, and not just a group of isolated qubits [23]. Entanglement results in a grouping characteristic that is of particular interest in quantum computing, enabling applications such as super-dense coding and teleportation [24]. Measuring an entangled qubit results in the collapse of all qubits in the group, forcing them to collapse to either state $\vert 0\rangle$ or $\vert 1\rangle$ [23]. Entangled qubits cannot be factorized into individual states. This means that there are no states of isolated qubits that can be manipulated to result in an entangled state. Therefore, entangled qubits are operated on by specific quantum gates that act on the entire set of entangled qubits.

In contrast to classical computing, a qubit cannot be copied without consequence, as this would entail a measurement and thus alter the state of the qubit. The non-cloning theorem, as explained in [25], asserts that even if we had a machine with an input of two qubits, one of which is an unknown state $\vert \phi \rangle$ and the other an "inert" state $\vert v\rangle$, we cannot discover a unitary operator T that would output the state $\vert \phi \rangle \otimes \vert \phi \rangle$ without altering the initial state of the qubits. The tensor product operation is denoted by $\otimes$. The hypothetical operator T would need to reproduce the state of $\vert \phi \rangle$ in $\vert v\rangle$, regardless of the state of $\vert \phi \rangle$. However, the usual inner product between $\vert \phi \rangle$ and $\vert v\rangle$ would only be useful if it resulted in either the state 0 or 1, indicating orthogonality or equality between the states, respectively. For any other result, the operator T would fail. [25].

When a quantum operation is performed on a state of n qubits, with $n\ge 2$, a tensor product would be required, resulting in a column vector of $2^n$ rows. A quantum operator on such a set of qubits is a $2^n\times 2^n$ matrix. It is constructed from basic $2\times 2$ quantum operators. The tensor product of 2 matrices of any size is given by the product of each coefficient of the first matrix by its counterpart coefficient in the second matrix [23]. Quantum operators allow the execution of operations on one or more qubits. They have an equal number of inputs and outputs, maintaining the equivalence between the energy of the inputs and that of the outputs. Therefore, there should be no heat dissipation. These operators allow to know the conditions of the input data, as this information is preserved. With reversible operators, it possible to return the quantum system to its previous state, i.e., before applying the quantum operator in question [26].

For this works, we define basic quantum operators as those having dimension $2\times 2$, acting on a single qubit, the controlled NOT (CNOT) and Swap operators, whose size is $4\times 4$, acting on two qubits, and controlled Swap (CSwap) and Toffoli’s operators, whose size is $8\times 8$, acting on three qubits. Complex quantum operators can act on two or more qubits simultaneously. In this case, the operator is built using tensor products, as explained earlier. In this way, a quantum operator, with the exception of CNOT or Toffoli’s gate, can be constructed from tensor products between basic quantum operators, which allows the state reversibility characteristic. That is, from a certain quantum state, one can return to the previous state by applying the inverse operator of the last operator used [27].

Basic unary quantum operators include [23]: (1) The X operator, also known as the Pauli-X, allows a qubit rotation of $\pi$ around the x-axis and inverts the amplitudes associated with the base vectors. If applied to a qubit in a collapsed state, it results in the opposite collapsed state, similar to a classic NOT gate. (2) The Y, also known as the Pauli-Y, allows a qubit rotation of $\pi$ around the y-axis. It. (3) The Z operator, also known as the Pauli-Z, allows a qubit rotation of $\pi$ around the z-axis. (4) The I operator is the identity operator that preserves the state of the qubit it is applied to. (5) The H operator, also known as the Hadamard operator, transforms a qubit in the collapsed state ($\vert 0 \rangle$ or $\vert 1 \rangle$) into a superposition of both states with equal amplitude. The H operator coincides with its adjunct operator [28]. (6) The P$_\theta$ operator performs a phase shift dependent on the informed angle $\theta$. Operator P$_{\pi /4}$ is known as the T operator and P$_{\pi /2}$ as the S operator. The formal definition of these operators and their application to $\vert v\rangle = \alpha \vert 0\rangle + \beta \vert 1\rangle$ are shown in Table 1$^1$.

Table 1 Unary quantum operators: definition and application

Basic binary quantum operators include [29]: (1) The controlled NOT (CNOT) operator is one of the main operators in quantum computing because it has the ability to entangle qubits. This operator has two arguments: the control qubit and the target qubit. The CNOT operator inverts the state of the target qubit when the control qubit is in state 1. (2) The Swap operator swaps the contents of two qubits. (3) The controlled phase shift (CZ) operator is a fundamental gate used in quantum computing for various quantum algorithms and quantum error correction. It introduces a phase shift to the target qubit based on the state of the control qubit. It. The formal definition of these operators and their application are shown in Table 2$^1$.

Table 2 Binary quantum operators: definition and application

Basic ternary quantum operators include: (1) The controlled Swap (CSwap) operator, also known as the Fredkin operator, exchanges the second and third qubits if the first qubit, also called the control qubit, is in state $\vert 1\rangle$ [30]. (2) The Toffoli operator uses three qubits: two qubits for control and third as target. It reverses the state of the target qubit whenever the two control qubits are in state $\vert 1\rangle$. The formal definition of these operators and their application are shown in Table 3.¹

It is important to note that there are other unary operators not mentioned here as well as other multi-qubit quantum operations, supporting arbitrary numbers of qubits. Operators CNOT, Swap, CSwap and Toffoli are just common examples of multi-qubit operators. A complete summary of quantum operators and possible combinations together with their representative symbol, matrix and application can be found in [31].

Table 3 Ternary quantum operators: definition and application

3 Related works

Numerous research studies in the field have focused on simulating quantum operations, utilizing both software and hardware approaches. These works encompass the development of libraries, the implementation of quantitative circuits using programmable or reconfigurable devices and initiatives that extend beyond the use of hardware description languages. Additionally, there are efforts dedicated to designing modeling tools to facilitate the simulation of quantum operations.

3.1 Quantum hardware emulators

In the work by Khalid et al. [32], a quantum circuit model is presented, which describes various quantum algorithms and their corresponding analogies with digital circuit models. The authors focus on developing an FPGA-based emulator for quantum algorithms, with a particular emphasis on novel techniques for modeling quantum circuits. This includes addressing aspects such as qubit entanglement, probabilistic computation and precision-critical issues.

In the study conducted by Shende et al. [33], the authors analyze the logical efficiency of quantum circuits that perform generic quantum computations and the initialization of quantum registers.

Guowu et al. [34] propose an approach for synthesizing quantum circuits from non-commutative quantum gates, such as the controlled square root of not quantum gate (controlled-V). The authors utilize group theory to transform the synthesis problem into a multiple-valued optimization.

Hashemi et al. [35] explore the use of quantum-dot cellular automata (QCA), a nanotechnology, to propose a reconfigurable device (FPGA) with efficient, symmetric and reliable programmable switch matrix interconnection elements. The results demonstrate the high efficiency of the proposed designs in QCA-based FPGA routing.

Vandijk et al. [16] discuss the challenges involved in designing a scalable electronic interface for real quantum processors. They also highlight the specific requirements that vary based on the different existing qubit technologies.

3.2 Quantum software simulators

In Ömer’s work [36], the author explores the application of classical computing concepts, such as hardware abstraction, structured programming, data types, memory management and control flow, in the context of quantum computing. To facilitate this, the author introduces a quantum computing language called QCL. QCL includes an interpreter that enables the execution of quantum programs. It incorporates both quantum and non-quantum instructions, such as irreversible functions, local variables and conditional branching. By using the provided interpreter, users can experiment with non-classical features such as the reversibility of unitary transformations and the non-observability of quantum states within a procedural programming language.

Karafy et al. [37] propose a quantum simulator designed for users with limited knowledge of quantum mechanics. The simulator is based on the circuit model of quantum computation, where models of quantum gates act on the data structure modeling a quantum registers composed of multiple internal representation of quantum bits.

In the work by Raedt et al. [38], a massively parallel quantum computer simulator is presented. It utilizes a software component with portability features to simulate the behavior of universal quantum computers on parallel computing systems. The simulator supports various quantum algorithms across different computer architectures. The simulator outputs matrices that represent the quantum register state at each step of the quantum computation, as well as details regarding the measurement probabilities of the quantum registers. The well-known Deutsch’s algorithm and the quantum Fourier transform are demonstrated using the proposed simulator.

Maron et al. [39] focus on optimizing the execution library of a visual programming environment designed for the quantum geometric machine model. The model employs recursive mathematical functions to dynamically generate values that define quantum transformations, resulting in a significant reduction in memory consumption.

Nikahd et al. [15] introduce a general direct simulator called OWQS for the one-way quantum computation (1WQC) model. The simulator incorporates techniques such as qubit elimination, pattern reordering and implicit simulation of actions to greatly reduce the time and memory requirements for simulations. Furthermore, it employs measurement patterns with a generalized flow without calculating the measurement probabilities. Experimental results confirm the effectiveness and efficiency of the proposed model for quantum computing simulation.

In Willie’s work [40], useful extensions are presented for the programming language SyReC (Synthesis of Reversible Circuits), which enables the specification and automatic synthesis of reversible circuits. The authors also propose algorithms for optimizing the resulting circuits based on different objectives, such as time delay and circuit cost.

Fu et al. [41] propose a control architecture for fault-tolerant quantum computing based on the rotated planar surface code with logical operations. The architecture incorporates a two-level address mechanism that supports a scalable compilation model for a large number of qubits. It also includes architectural support for quantum error correction during runtime, significantly reducing the size of the quantum program and improving its scalability.

4 Macro-architecture of the proposed EQP

The emulated quantum processor proposed in this work is specifically designed to execute quantum operations on a set of qubits that constitute the quantum state of the machine. Acting as an isolated system, this emulator interacts with a host processor through a dedicated communication channel. The main processor sends formatted commands to the processor, instructing it to perform quantum operations on the qubits and manipulate the quantum state. Until the processor receives a command to read its state, the quantum state remains enclosed within the quantum machine representation, leading to the assumption of a collapsed state for each qubit.

First and foremost, and before we get to the details of proposed design, let us define the qubit internal representation used by this design. A qubit is represented internally by two complex numbers: one representing the amplitude of ket $\vert 0 \rangle$ and the other that of ket $\vert 1 \rangle$. Each of the complex numbers are held as two float numbers of 32 bits. So, a qubit is kept internally as four float numbers using 128 bits. The sequence of these four float numbers will be made clear, in the next section, when the structure of the quantum state memory is detailed.

The emulated quantum processor has the capability to execute quantum operations on one or more qubits of the machine state, utilizing either basic quantum operators or operators generated dynamically based on the requests from the main processor. Once a quantum instruction is executed, the processor waits for further instructions, remaining idle until then. It can provide the most recent machine quantum state upon request. The proposed emulator implements fundamental operators such as H, X, Y, Z, T, S, I and CNOT, while any other quantum operator can be executed if the corresponding basic operator matrix is loaded into the operator memory [42].

Figure 1 depicts the communication between the main processor (MP) and the proposed emulated quantum processor (EQP) using a half-duplex channel. The choice of a half-duplex configuration acknowledges the sequential nature of quantum algorithms, considering the potential dependence of the outcome on one or more qubits from previous operations. Although a full-duplex configuration is also feasible, it necessitates additional control mechanisms to manage data dependencies. Quantum operations are requested by the main processor using descriptive blocks that specify the desired basic quantum operation and the target qubit(s). For operations involving multiple qubits, multiple descriptors are needed to define the operation and the corresponding target qubits.

Fig. 1

Communication of the host processor and emulated quantum processor

Figure 2 provides an overview of the macro-architecture of the proposed quantum processor emulator. The interaction between EQP’s units is done via data, address and control buses. There are 5 data buses: (1) ODATA is a unidirectional data bus. It provides the calculation unit with the coefficients of the quantum operators’ matrices; (2) SDATA is a bidirectional data bus. It allows the exchange of intermediate results during the computation of the tensor products between operators of two or more bits; (3) QDATA is a bidirectional data bus. It allows the exchange of states of the qubits addressed by a quantum instruction, as sent by the main processor; (4) MDATA is a bidirectional data bus. It allows the exchange of the states of the observed qubits before and after measurements; (5) RANDOM is a unidirectional data bus of 32 bits. It forwards the generated random number, necessary for state measurement. The former four buses have 128 bits each.

Fig. 2

Emulated quantum processor macro-architecture

The control unit of the EQP, referred to as UCO, manages the operation of the data path within the architecture using a microprogram and dedicated components. It is responsible for recording, decoding and interpreting quantum descriptors that contain essential information about the quantum operation code and the target qubit(s). Processor EQP utilizes three memory components:

• 1. Memory MQS (Memory for Quantum State) stores the machine quantum state, which is the quantum state of the qubits.

• 2. Memory MOP (Memory for basic OPerator) stores the coefficients of basic operators used in quantum operations.

• 3. Memory MSC (Memory for SCratch computation) is a scratch memory that stores coefficients of quantum operators for two or more qubits. These coefficients are calculated based on the basic quantum operators. Further details about the memory organization can be found in [43].

The calculation unit of EQP is represented by the UCA unit. It performs tensor products and matrix products, which are essential for various quantum operations. Tensor product operations are required between qubits, between basic operators, and between the calculated operator and the basic operator. Matrix product operations, on the other hand, are necessary for combining an operator and a qubit.

The measurement unit, denoted as UMS, is responsible for performing the measurement of the quantum state. It utilizes a pseudorandom number generator component called RNG to assist in the measurement process. When requested by the main processor (MP), the UCO unit provides the measurement result or the probabilities associated with different possible states.

5 Micro-architecture of the proposed EQP

In this sequel, we describe the detailed micro-architecture of the composing memories and functional units of the proposed emulated quantum processor.

5.1 Quantum state memory

The quantum state memory (MQS) is a dual-port memory that allows both reading and writing operations but does not support simultaneous read and write operations at the same address. MQS is divided into two parts: MQB for qubit state memory and MQC for qubit control memory. Both parts have an equal number of addresses, and their contents are linked together for each address, creating a seamless extension of each other. The purpose of this separation is to enable updating of only one of the memories in certain situations during the execution of quantum instructions.

The number of addresses in MQS is sufficient to represent all possible states of the quantum machine. Here, nq represents the maximum number of qubits in the machine’s quantum state. The first nq addresses are reserved for storing the kets (quantum states) of non-entangled or the first states of entangled qubits. The remaining $2^{nq-1} - nq$ addresses are utilized to store the remaining quantum states regarding the set of entangled qubits. These entries complement the coefficients of the column vector stored in some of the nq initial addresses, which are required for the entangled qubits. It is important to note that this memory organization allows the machine to handle a maximum of nq qubit entanglements.

MQS is designed to hold two kets for each non-entangled qubit in the machine’s quantum state at each address. It is augmented with additional data to describe the amplitudes of each possible state relative to sets of two or more entangled qubits. At each address a in MQS, the data is divided into two parts:

• 1. The coefficients (real and imaginary parts) for both kets of the qubit are stored in MQB at address a. The word format in MQB consists of four fields of 32 bits each (64 bits for each ket), as illustrated in Fig. 3.

• 2. The addresses of the first and next qubits in the entangled qubit list, to which the qubit at address a belongs, are stored in MQC at address a. The format of MQC consists of two fields of $nq-1$ bits each and a third field of 1 bit, as depicted in Fig. 4.

Fig. 3

Word format of memory MQB

Fig. 4

Word format of memory MQC

It is important to note that a word at address $a-1$ of MQB holds the $a^{th}$ qubit of the quantum state when it is not yet entangled or one of the possible combinations regarding an entanglement the $a^{th}$ qubit is part of. So, for instance, let us assume a quantum machine of $nq = 10$ qubits. So, MQB and MQC have each $2^{9}$ locations, which is enough to store all possible $2^{10}$ states if the 10 qubits were all entangled. Recall that a single location in MQB holds the details of two possible states of an entanglement (see Fig. 3). Initially, the first 10 locations keep the 10 not yet entangled qubits. Let the three qubits, stored at address 2, 5 and 7, be entangled. Then, four locations in MQB are required to store all $2^3$ possible states regarding the entanglement and other four locations in MQC are required to keep control of this entanglement. So, the entangled states $\vert 0\rangle$ – $\vert 5\rangle$ will be kept in the proper qubits’ locations, i.e., states $\vert 0\rangle$ and $\vert 1\rangle$ at locations 2, $\vert 2\rangle$ and $\vert 3\rangle$ at location 5 and $\vert 4\rangle$ and $\vert 5\rangle$ at location 7. The remaining two states $\vert 6\rangle$ and $\vert 7\rangle$ will be stored in an available extra location in MQB. If these three qubits are the first to be entangled in the quantum machine, then this extra location will be of address 10. According to the MQC word format of Fig. 4, at locations 1, we would have the data 2/5/1, in location 5, the word would be set to 7/10/1, and at location 10, the stored word would be 10/10/1. This example shows that any possible entanglement, i.e., in terms of which qubits and/or how many qubits are involved, is fully functional.

Figure 5 illustrates the logic block of MQS, the memory component of the system. MQS handles input and output data through the QDATA bus, which is organized into four parts. These parts represent the real and imaginary components of the complex numbers that correspond to the amplitudes of the kets $\vert 0\rangle$ (even) and $\vert 1\rangle$ (odd) of the qubits. This specific organization of data is chosen to facilitate the design of unit UCA, as will be explained later. In the figure, the input pins for data, address and control signals are depicted in black, white and gray, respectively. On the other hand, the output pins for data and control signals are represented with hatched and dotted patterns, respectively. It is important to note that there are no output address signals in the design proposed.

Fig. 5

Logic block MQS for the quantum state memory

The logic block of memory MQB, which stores information about the complex numbers representing the amplitudes of the kets, is depicted in Fig. 6. In a quantum algorithm, the non-entangled state of a qubit can be temporary and may change due to entanglement. Therefore, the address initially assigned to a non-entangled qubit will be repurposed to store the first two coefficients of the column vector representing the set of entangled qubits to which it belongs. One coefficient corresponds to $\vert 0\rangle$ (even) and the other to $\vert 1\rangle$ (odd). The even and odd references are essential for understanding the design of unit UCA, which will be described later.

Fig. 6

Logic block MQB for the qubit memory

During the operation of EQP, each position in memory MQB is initialized with the tuple (1.0, 0.0, 0.0, 0.0) according to the format shown in Fig. 3. This means that the ket $\vert 0\rangle$ is represented by the values 1.0 in the real part and 0.0 in the imaginary part, while the ket $\vert 1\rangle$ is represented by 0.0 in both the real and imaginary parts. It is important to note that all data is stored in the IEEE754 standard floating-point number format, ensuring compatibility and accuracy.

In order to represent the qubit entanglement, each qubit in the quantum state is associated with the addresses of the first and next qubits in the sequence of entangled qubits it belongs to (see Fig. 4). Recall that the entanglement bit, included in the stored word, indicates whether a qubit is entangled or not. For entangled qubits, the entanglement bit is set to 1. In the case of a non-entangled qubit, both the first and next qubit addresses are set to the address of the qubit itself. This information is stored in memory MQC whose logic block is shown in Fig. 7.

Fig. 7

Logic block MQC for the qubit control memory

It is important to mention that the parameter anq represents the number of bits required to address a cell in both memories MQB and MQC. The binary decoding output of the address from memory MQS is used as a read/write selector for both MQB and MQC. To achieve this, two binary address decoders are utilized to decode $nq-1$ bits into the corresponding one-hot code of the address. As a result, anq is equal to $2^{nq-1}$ bits, providing sufficient addressing capability for both MQB and MQC.

To represent a sequence of e entangled qubits, $2^{e-1}$ locations are required in memory MQB, resulting in a total of $128 \times 2^{e-1}$ bits. Both the even and odd coefficients are stored in these locations to capture the entanglement. When performing a quantum operation on a set of qubits, knowing the address of the first qubit is crucial, as the operation involves a matrix product that starts with the first row of the column vector representing the entangled qubits. Since each MQB address contains information for two rows of the column vector of e qubits, the number of positions to be read during a quantum operation is $2^{e-1}$, considering that each MQB address contains four coefficients. Note that when resetting the quantum machine, each address a in MQC is initially set to the tuple (a, a, 0).

Therefore, the total number of bits in the quantum state memory MQS is the sum of the bits in memories MQB and MQC. Although both memories have the same addressable space, ranging from 0 to $2^{nq-1}$, their word sizes differ. Each position in MQB has a fixed size of 128 bits, while each position in MQC has a variable size depending on the number of qubits in the coprocessor. Each MQS word consists of $2nq - 1$ bits. Hence, for nq qubits, the size of memory MQS in terms of bits can be calculated as $Size_{MQS}= 2^{nq}\left( 2\times nq + 129\right)$.

5.2 Operator memory

The quantum operator memory, MOP, is a read-only memory that stores the coefficients of basic quantum operators. Each MOP address contains the coefficients of a given row of the operator matrix, organized in the same manner as memory MQB. For a basic $2\times 2$ quantum operator, its coefficients are stored in two consecutive MOP addresses. The logic block of memory MOP is illustrated in Fig. 8.

Fig. 8

Logic block MOP for the quantum operator memory

In MOP, the coefficients of the operator matrix are represented by the even and odd columns, which respectively store the real and imaginary parts. For a $2\times 2$ operator, the bits are arranged as follows: Bits $0 \dots 31$ represent the real part of the coefficient in the odd column, bits $32 \dots 63$ represent the imaginary part of the coefficient in the odd column, bits $64 \dots 95$ represent the real part of the coefficient in the even column, and bits $96 \dots 127$ represent the imaginary part of the coefficient in the even column.

The number of bits required to address memory MOP is denoted as aop and is calculated using the formula $Aop = \lceil \log _2\left( \frac{1}{2}\sum _{o=1}^{nop} 4^{noq_o}\right) \rceil$. Here, nop represents the number of basic operators, and $noq_o$ represents the number of qubits required by operator o. Thus, aop corresponds to half the total number of complex coefficients of the quantum operators implemented by EQP.

The storage arrangement of two complex numbers within an MOP address is compatible with the arrangement of ket coefficients in memory MQB. This compatibility enables the design of efficient tensor and matrix multipliers, as discussed in Sect. 5.5. The implemented quantum operators include I, X, Y, Z, H, S, T and CNOT. It is important to note that for all other existing quantum operators, their corresponding matrices can be derived from the implemented ones.

In the quantum program, quantum operators are referenced using a unique code associated with the initial address of the reserved range for that specific operator in MOP. Instead of using three bits to represent the eight operators and an additional lookup table to access the starting address of the operator matrix in MOP, we utilize only four bits to indicate the address of the word associated with the requested operator as stored in memory MOP.

The total number of bits in the operator memory, MOP, can be calculated by summing the space required to store all permitted basic operators by the coprocessor. Therefore, for the total of nop coefficients required for all considered basic operators, the size of memory MOP in terms of bits is given by: $Size_{MOP}= 128\times 2^{\left( \lceil \log _2\left( \frac{1}{2}\sum _{o=1}^{nop} 4^{noq_o}\right) \rceil \right) }$.

5.3 Scratch memory

The scratch memory (MSC) is a dual-port read–write memory designed to store the coefficients of quantum operators for multiple qubits. These coefficients are generated dynamically by performing tensor products of basic quantum operators. It is important to note that MSC has limitations when it comes to simultaneous reading and writing operations at the same address. The logic block of MSC is illustrated in Fig. 9.

Fig. 9

Logic block MSC for the scratch memory

Memory MSC utilizes a word structure similar to that of memory MQB, as depicted in Fig. 3. In a manner analogous to memory MOP, each MSC address contains two coefficients corresponding to a row of the operator matrix: one for the odd column and another for the even column. These coefficients serve as inputs to the two complex number multipliers embedded within the calculation unit UCA, which facilitate efficient computation of both tensor and matrix products. The total number of MSC addresses, denoted by a, is determined by the maximum number of qubits that can be operated simultaneously in the quantum machine, denoted by mq. Consequently, we have $a = 4^{mq}/2 = 2^{2mq-1}$, and thus, $amq = 2mq - 1$. It should be noted that mq is limited by the total number of qubits in the quantum machine, denoted as nq. Therefore, the upper bound on amq is $2nq - 1$.

Memory MSC is exclusively employed during the construction and temporary storage of quantum operators involving more than two qubits, based on the instructions extracted from the currently executing quantum program. The total number of bits required by MSC can be calculated as the sum of the space needed to accommodate the largest operator that the coprocessor can handle. This is determined by the parameter mq. Consequently, the size of memory MSC in terms of bits is $Size_{MSC} = 128 \times 2^{2mq-1}$ and its upper bound can be defined as ${\overline{Size}}_{MSC} = 128 \times 2^{2nq-1}$.

5.4 Measurement unit

The measurement unit UMS plays a crucial role in preparing the state of the quantum machine upon request from the main processor. When a quantum state is measured, each qubit of the coprocessor collapses into either the state $\vert 0\rangle$ or $\vert 1\rangle$. Many ways have been proposed to simulate state measurement in quantum computing in the computational basis of $\vert 0\rangle$ and $\vert 1\rangle$ state, depending on the model used and the level of interference on the machine quantum state. Among other, we have the following state measurement models:

• The projective measurement, after which the state collapses [44]. It is a fundamental method for performing state measurement in quantum computing. It allows the extraction of classical information from a quantum system by projecting the quantum state onto the specified basis.

• The quantum non-demolition measurement, which is a technique that allows the extraction of the information about a quantum state without disturbing it [45];

• The weak measurement, which involves performing a weak interaction with the quantum system, providing partial information about the state without fully collapsing it [46]. The outcome is based on averaging multiple weak measurements to yield the quantum state’s properties;

• The quantum state tomography, which is a technique used to fully characterize an unknown quantum state. It involves performing measurements in multiple bases to reconstruct the density matrix representing the quantum state [47]. Quantum state tomography is especially useful for verifying the fidelity of quantum operations and diagnosing errors in quantum circuits;

• The homodyne detection, which used for continuous-variable quantum systems, such as those in quantum optics. It involves measuring the quadrature amplitudes of a quantum state [48].

In the proposed design, we use the standard projective measurement model. We propose a simple yet effective implementation. It is noteworthy to point out that no specifics about a functional implementation of the measurement process have been found. In our approach, each of the $2^{nq}$ possible states for the nq qubits, either entangled or not, in the coprocessor (where $nq\ge 1$) is associated with a specific probability value, as explained in 2. We adopt the proportional selection model, commonly known as the “roulette” model, which is widely used in genetic algorithms during the selection phase of individuals to form the next-generation population [49]. In this model, the probability interval [0, 1[, which is the range covered by the pseudorandom number generator, is divided into n non-overlapping subintervals. The extension of each subinterval is proportional to the score assigned to the corresponding individual [49].

Applying the aforementioned concept to the possible quantum states of the coprocessor, where each state is treated as an individual, the associated probability determines the extension of the subinterval representing that quantum state. So, in the case of the measurement of a single non-entangled qubit defined by $\vert v\rangle = \alpha \vert 0\rangle + \beta \vert 1\rangle$, there two subintervals $\big [0.0, \vert \alpha \vert ^2\big [$ for a state outcome of a classical 0-bit and $\big [\vert \alpha \vert ^2, \vert \alpha \vert ^2+\vert \beta \vert ^2\big [$ for a state outcome of a classical 1 bit. Recall that $\vert \alpha \vert ^2+\vert \beta \vert ^2=1$.

Similarly, in the case of n entangled bits, with $1\le n\le nq$, defined as $\vert v\rangle =\sum \nolimits _{i=0}^{n-1} \alpha _i\vert i\rangle$, there are n subintervals with the first one defined by $\big [0.0, \vert \alpha _0\vert ^2\big [$ while the remaining subintervals related to states $\vert i\rangle$, for $1\le i\le n-1$, are defined as $\big [\sum \nolimits _{i=0}^{n-2} \vert \alpha _{i}\vert ^2, \sum \nolimits _{i=0}^{n-1} \vert \alpha _i\vert ^2 \big [$. Also, recall that $\sum \nolimits _{i=0}^{n} \vert \alpha _i\vert ^2 = 1$. Table 4 summarizes the subinterval configuration for n qubits. It is fundamental to emphasize that the subintervals re dependent on the qubits that are being observed. So, for every measurement, a new range configuration is yielded by the measurement process.

Table 4 Configuration for quantum state amplitudes for n entangled qubits

So, for instance, consider a measurement of quantum register of 2 entangled qubits and the squared amplitudes presented in the second column of Table 5. The corresponding subintervals are defined based on the values provided in the last column of the same table. The resulting roulette wheel for this case is illustrated in Fig. 10.

Table 5 Configuration example of state squared amplitudes for 2 entangled qubits

Fig. 10

Example roulette wheel configuration for proportional selection regarding the setting of Table 5

When a state measurement takes place, the range configuration is first set up based on the amplitudes associated with the specified qubits for which an observation is required. Then, a pseudorandom number r is drawn. The quantum state $\vert i\rangle$, for which r falls in its associated subinterval, is selected and the classical bitwise representation of state $\vert i\rangle$ is thus the outcome of the measurement process. All qubits involved in such measurement process are then collapsed to their corresponding state in $\vert i\rangle$. For instance, let us assume that the configuration of Table 5 is built based on the amplitudes of the 2-qubit register $\vert v\rangle =\vert q_0q_1\rangle$ for which a measurement operation is required. If random number $r=0.25$ is drawn, then the observed state $\vert 01\rangle$ is selected. Hence, qubits $q_0$ and $q_1$ will collapse to quantum states $\vert 0\rangle$ and $\vert 1\rangle$, respectively. So, the measurement process implement in such a way is completely stochastic and depends on the faithfully on the amplitudes of the observed qubits.

The micro-architecture of the measurement unit UMS is illustrated in Fig. 11. It consists of a local control unit CUnit, responsible for coordinating the different steps of a measurement operation. Upon receiving the signal StartMs, UMS obtains the coefficients from each address in the MQB memory, denoted as OddReRd, OddImRd, EvenReRd and EvenImRd. Using the functional unit RgCalc, it initiates the quantum state measurement process. First, it computes the upper limits for each sub-range based on the given coefficients. The lower limit of the first subinterval is always 0, while the subsequent subintervals have the higher limit of the previous range as their lower limit. The $2^{nq}$ values corresponding to the sub-ranges, where nq is the number of qubits in the coprocessor, are then stored in the local memory LMem, implemented as a lookup table and retrieved when necessary.

Fig. 11

Micro-architecture of the measurement unit UMS

Functional unit UMS determines the distribution and extension of the subintervals based on the tensor product of all qubits in MQB and the obtained amplitudes for each state. It compares these values with the generated pseudorandom number rand from the RNG unit in parallel, using the Cmp unit. The comparison is performed for all contents of the LMem positions simultaneously. A match is declared when the 1-bit result of the comparison is set for the state $\vert 2^i\rangle$, while the result for state $\vert 2^{i-1}\rangle$ is reset. The selected quantum state is then recorded in the MQB memory by setting the n qubits in MQB accordingly. For $\vert 0\rangle$ qubits, the coefficients (1.0, 0.0, 0.0, 0.0) are used, and for $\vert 1\rangle$ qubits, (0.0, 0.0, 1.0, 0.0) is used, based on the binary representation of the observed state $2^i$. It is important to note that all data are stored in the IEEE754 standard floating-point number format.

Furthermore, after a measurement operation, all qubits are assumed to be in a collapsed state, and any existing entanglements must cease to exist. Therefore, all entries in the MQC memory for the observed qubits are reinitialized. The content of each address a is set as (a, a, 0) according to the MQC word format shown in Fig. 4. Once this process is complete, the signal EndMs is triggered to indicate the completion of the measurement operation.

The proposed macro-architecture includes the RNG component, which utilizes the linear feedback shift register (LFSR) principle to generate pseudorandom numbers within the range [0, 1[. The LFSR is a type of shift register where the input bit is determined by a linear function based on the previous state, as illustrated in Fig. 12. The XOR operation is the only available linear function in this case. The register acts as an offset register, with its input bit being influenced by the XOR operation of certain bits within the register, causing a random change in its value. The specific bit positions that affect the next state are referred to as taps.

Fig. 12

Configuration of the LFSR for the generation of random numbers

In an LFSR register with n bits, the maximum period of cycles before the sequence repeats is equal to $2n - 1$. To ensure that the generated numbers fall within the interval [0, 1[, the function is applied to the eight most significant bits of the mantissa and the four least significant bits of the exponent. This configuration guarantees that the generated numbers remain within the specified interval [50, 51].

5.5 Quantum calculation unit

The calculation unit (UCA) plays a crucial role in computing complex numbers required for various quantum operations, including the tensor product of quantum operators, tensor product of qubits, matrix product between operators, quantum register of qubits and the summation of complex numbers. It receives data from three memories: MSC, MQS and MOP. The control unit (UCO) manages the operations of other components within EQP. The micro-architecture of UCO is depicted in Fig. 13, illustrating its connections and functions.

The UCA is connected to two input data buses and two output data buses, each with a width of 128 bits. The first input data bus is responsible for transmitting coefficient pairs from memory MQS, representing the column vector that represents a single qubit or a set of qubits. The second input data bus carries coefficient pairs from either memory MOP or MSC. MOP supplies coefficients of basic quantum operators, while MSC provides coefficients of operators constructed for two or more qubits.

Additionally, the UCA unit is connected to output data buses dedicated to writing data in MSC and MQS independently. The data intended for the MSC writing data bus pertains to intermediate results of the ongoing tensor product calculation. On the other hand, the data intended for the MQS writing data bus relates to the final result of the tensor product involving qubits or the matrix product between a quantum operator and a single qubit or a register of qubits.

Fig. 13

Micro-architecture of the calculation unit UCA

In the architecture depicted in Fig. 13, several registers play specific roles in the computation process. RMC1 and RMC2 are registers that store the coefficients of the qubit or operator currently undergoing multiplication. RMCTP1 and RMCTP2 hold the coefficients of the second row of basic quantum operators when performing a tensor product. RMCEX1${1\dots n}$ and RMCEX2${1\dots n}$ are a set of n registers designed to store data from the positions in MQS that are involved in the quantum operation before the operation is executed. The number of these registers is determined by $n=2^p - 2$, where p represents the maximum number of qubits on which an operator can act. RMCTP11 and RMCTP21 store the coefficients of the first row of the basic quantum operator, while RMCTP12 and RMCTP22 store the coefficients of the second row.

The components MULTC1 and MULTC2 function as multipliers of complex numbers, while SUMC1 and SUMC2 are adders of complex numbers. The first adder is responsible for summing up two partial products in a matrix multiplication between an operator and a set of qubits. The second adder accumulates the partial products of an operator matrix row with the column vector represented by one or more entangled qubits. This accumulation process is achieved by iteratively using the complex number register RSC. Register RSP holds the intermediate complex number resulting from the sum of computed partial products. It temporarily stores this value in MSC until the corresponding final result is available and can be written to the appropriate address in MQS.

The complex number multipliers, MULTC1 and MULTC2, are based on a simple precision floating-point arithmetic unit (FPU) [52]. Four multipliers, one adder and one subtractor are employed in this architecture. Considering two complex numbers as ordered pairs (A, B) and (C, D), where A and C represent the coefficients of the real part and B and D represent the coefficients of the imaginary part, their multiplication yields a complex number represented by the pair $(AC - BD, AD+BC)$. The four multiplications required to obtain the partial products AC, AD, BC and BD are performed in parallel. Once the products are ready, the sum $AD + BC$ and the difference $AC - BD$ are computed concurrently. The micro-architecture of the complex number multiplier is depicted in Fig. 14.

Fig. 14

Micro-architecture of the complex number multiplier

Since the FPU operates continuously, independent of a specific trigger, the complex number multiplier can be serially supplied with data, and the results are sequentially made available. Each FPU considers the data present at its input pins during the rising transition of the clock and the result is sampled during the rising transition of the clock as well. The number of clock cycles required to obtain the correct result is determined by the FPU’s latency parameter. For multipliers, this parameter is set to 3 clock cycles, while for adders and subtractors, it is set to 2.

To ensure efficient operation, different clock signals are used for the multiplier and adder/subtractor. This design allows the products to be available for use by the adder/subtractor before the next transition of the multiplier’s clock signal. Without this approach, a delay of 1 clock cycle would be introduced for every complex number multiplication, leading to significant delays when performing quantum operations involving multiple qubits.

The total number of complex number multiplications in a quantum operation involving $n \ge 2$ qubits can be calculated as $2^n + 4^n + 4^n = 2^n + 4^{n + 1} = 2^n + 2^{2(n+1)} = 2^{3n+2}$. This total includes the tensor product of the n qubits, augmented by the tensor product required to obtain the desired quantum operator from basic ones, and further augmented with the matrix multiplication between the obtained quantum operator and the result of the tensor product of the qubits involved in the operation. For example, a single quantum operation on 3 qubits would require the coprocessor to perform 6,144 clock cycles for floating-point multiplications.

5.6 Control unit

The control unit UCO plays a vital role in synchronizing the operation of EQP’s remaining components. It utilizes a microprogram and several auxiliary components to coordinate and manage the actions of the macro-architecture based on instructions from the main processor. By employing planned micro-orders and dedicated controllers, UCO effectively orchestrates the functionality of other components within EQP. The micro-architecture of UCO, illustrating its internal structure, can be seen in Fig. 15.

Fig. 15

Micro-architecture of the control unit UCO

Unit UCO includes one memory, two counters, five registers, five controllers and two address converters. Their functions are detailed as follows: (1) JumpCtrl handles conditional and unconditional jumps within the microprogram; (2) InstCtrl is the instruction controller; (3) MPR is the read-only control memory wherein the microprogram resides; (4) MPR-AddrReg is the address register of the control memory; (5) MIR is the micro-instruction register; (6) OpTPCtrl controls the computation of the tensor product of quantum operator, starting from basic ones; (7) OpTPRecCtrl manages the recording of tensor product in MSC; (8) QbNumReg stores the quantity of current qubits regarding the quantum operator in construction; (9) MOP-AddrReg is the address register of coefficients in memory MOP; (10) QbTPCtrl controls the computation of the tensor product of quantum bits as well as matrix product; (11) MSC-AddrRdCnt and MSC-AddrWrCnt are the address counters for reading and writing in memory MSC; (12) MQS-AddrRdReg and MQS-AddrWrReg are the address registers for reading and writing into memory MQS. (13) MSC-AddrRdConv and MSC-AddrWrConv are converters of reading and writing addresses of the tensor product coefficients in memory MSC, respectively. Moreover, unit UCO handles SADDR-Rd and SADDR-Wr, which are the address buses for accessing memory MSC in read and write modes, respectively; OADDR, which is the address bus for reading form memory MOP; QADDR-Rd and QADDR-Wr, which are the address buses for accessing memory MQS in read and write modes, respectively; and QDATA, which is the main data bus for memory MQS.

The main processor interacts with the emulated quantum processor by transmitting quantum operations in a sequential manner, with each operation consisting of a fixed-size instruction. The size of an instruction is predetermined and remains consistent throughout the communication. The execution of a quantum operation requires a specific number of instructions, which is determined by the number of qubits involved. The quantum instruction format comprises three essential components: the quantum operator code, the target qubit to which the operation is applied and a flag indicating whether it is the final instruction in the quantum operation. The structure of a quantum instruction is illustrated in Fig. 16, where m denotes the total number of available quantum operators and n represents the number of qubits in the quantum state. Once the last instruction flag is set to 1, the instruction controller (InstCtrl) ceases to await further instructions.

Fig. 16

Format of a quantum instruction

The InstCtrl component is responsible for receiving and storing the set of instructions for a quantum operation transmitted by the main processor. The logic block of the instruction controller is depicted in Fig. 17. When input control signals 1 and 2 are activated, the instruction controller can either request the next instruction of the quantum operation or reset the pointer to the instruction buffer. The output flags 3–5 indicate the status of any remaining instructions that are yet to be executed. Output data signals 6–8 provide information about the current instruction being executed, the number of qubits in the first instruction and the total number of instructions in the current quantum operation, respectively. Output address signal 9 indicates the last address that was read in memory MOP.

The input pins for data, address and control signals are represented by black, white and gray lines, respectively. On the other hand, the output pins for data, address and control signals are denoted by hatched west, hatched east and dotted lines, respectively.

Fig. 17

Logic block of component InstCtrl

The task coordination as performed by the UCO to execute quantum operations is accomplished through the execution of a microprogram stored in the control read-only memory MPR. This microprogram comprises a sequence of micro-instructions, given in the format shown in Fig. 18.

Fig. 18

Format of a micro-instruction

The micro-instruction format consists of three pieces of information. The first is the Micro-orders field, which contains a set of commands used to activate the data path components, including units UCA, UMS and the read/write operations of the different memories.

The second field of the micro-instruction is Flags, which consists of a collection of status flags used in micro-instructions that require conditional jumps. There are two conditional jump instructions: One checks whether a specific flag is set to high, while the other checks whether the flag state is different from high. The current design utilizes ten flags: MQBRdAddrZero and MQBWrAddrZero, indicating whether the address to read from/write to memory MQB is zero, respectively; NoInst, indicating an empty list of instructions; PlusOp, indicating the presence of more than one quantum operator in the current quantum operation; LastInst, signifying that the current instruction is the last in the quantum operation; EntangledBit, indicating the presence of at least one entangled qubit in the specified set of qubits; MSCRdAddrZero and MSCWrAddrZero, indicating whether the address to read from/write to memory MSC is zero, respectively; TPOpComplete and TPQbComplete, indicating the completion of the tensor product of the operators listed in the instructions and the qubits specified in the instructions, respectively.

The third field of the micro-instruction, termed as Address, serves multiple purposes. It can represent one of four items: the address of a qubit in memory MQB, an address in memory MOP when accessing the coefficients of a basic quantum operator, an MPR address to jump to or a specific value to be loaded when required. The number of bits p allocated for this field is determined by the largest size needed to accommodate any of the four cases.

The MPR address register is implemented as an up-counter with a preset option, enabling the sequencing of micro-instructions that do not deviate from the primary flow of the program. When a jump instruction occurs and the jump condition is met, the address provided in the micro-instruction is loaded into this counter. The JumpCtrl component, illustrated in Fig. 19, guarantees the update of the MPR register.

Fig. 19

Micro-architecture of controller JumpCtrl

Unit UCO is equipped with specialized components that facilitate the execution of tensor products between qubits and quantum operators, as well as the computation of matrix products. One of these components is QbTPCtrl, which is responsible for managing the read/write addresses for memory MQB, controlling the records of memory MQC and handling the multiplexers and registers of unit UCA. Component QbTPCtrl ensures the generation of the desired tensor product. This is detailed in Sect. 5.6.1. Another essential component is OpPTCtrl, which handles the sequencing and synchronization of the read/write addresses for memory MSC. It also manages the multiplexers and registers of unit UCA to produce the required composed operator from the available basic operators stored in memory MOP. Moreover, component OpPTCtrl ensures the proper execution and generation of the composed operator. This is detailed in Sect. 5.6.2. Comprehensive information on these controllers, their functionality and some illustrated examples of their operation can be found in [42].

5.6.1 Controller of the qubit tensor and matrix products

In order to produce the required tensor product, component QbTPCtrl takes control of the read/write addresses for memory MQB, the control records of memory MQC, as well as the multiplexers and registers of unit UCA to produce the requested tensor product. The tensor product of qubits requires not only the appropriate mathematical operation but also the handling of the control records associated with the qubits involved. Recall that these control records, depicted in Fig. 7, form a linked list that contains all the necessary information for the column vector representation of the entangled qubits.

When performing operations with entangled qubits, the linked records are processed sequentially, starting from the first record and following the link order until the last record. The intermediate results of the tensor product, obtained from the entangled qubits and the subsequent qubit as indicated in the associated records in MQC, are generated by multipliers MULTC1 and MULTC2. These results are then placed on the data bus of memory MQB, ready for a write operation. Component QbTPCtrl commands the tensor multiplication between the coefficients of the qubit set specified in the records and the qubit indicated in the next record. The address to be used in the read operation is stored in register MQS-AddrRdReg. The number of records needed in MQB to store the coefficients of the column vector representing the entangled qubits is $2^{q-1}$, where q is the number of qubits referenced in the associated records.

Controller QbTPCtrl is triggered to initiate the tensor product by a high-level input signal. When triggered, it takes control of the coprocessor components. The controller operates based on the following inputs:

• 1. Overall number of operators of the current quantum operation;

• 2. Number of the qubit of the first instruction in the current quantum operation;

• 3. Number of the qubit of the current instruction;

• 4. Control record of the qubit referred to in the current instruction;

• 5. Current micro-instruction;

• 6. Control register wherein the new control data will be stored in MCQ;

• 7. Address of the qubits wherein the data will be stored in MQB;

• 8. Address used to update the qubit number register.

Once the controller receives the flag indicating the completion of the requested tensor product computation, it enables the writing of the result into memory MQS. The address to be used for this write operation is stored in register MQS-AddrWrReg. It is important to note that registers MQS-AddrRdReg and MQS-AddrWrReg are implemented as up-counters with a preset option. This allows for sequential reads/writes during the initialization/measurement of qubits, facilitating the setup and observation of the quantum state of the machine. Additionally, the preset option enables the registers to use a target address for isolated read/write operations, as may occur in a tensor product between qubits or in a matrix product involving two or more qubits.

5.6.2 Controller of operator tensor product

Controller OpPTCtrl is responsible for controlling the sequencing and synchronization of the read/write addresses of memory MSC, as well as the multiplexers and registers of unit UCA, in order to generate the desired composed operator from the available basic operators stored in memory MOP. When triggered, this controller uses relative addresses to access the coefficients of the quantum operator stored in MSC memory, starting from the last pair of coefficients and moving towards the first pair. The converters MSC-AddrRdConv and MSC-AddrWrConv are utilized to determine the corresponding absolute addresses based on the relative addresses managed by OpPTCtrl. The relative address from which the reading starts depends on the number of qubits handled by the current quantum operator stored in MSC memory. The total number of addresses occupied in MSC by the operator is given by $2^{2oq-1}$, where oq represents the number of qubits involved in the operator.

During the construction of a two-qubit operator, the two basic operators to be multiplied are read from memory MOP, and the resulting tensor product is stored in memory MSC. For operators involving three or more qubits, the operator read from memory MSC is tensor multiplied with the operator provided by memory MOP. The resulting operator is then written back into memory MSC. Read and write operations in MSC may occur simultaneously but always at different addresses. During the construction of an operator for two or more qubits, OpPTCtrl follows a predetermined address sequence to reference the operator’s coefficients. This sequence starts from the first pair of coefficients in the first row and ends at the last pair of last row coefficients.

The address converters, MSC-AddrRdConv and MSC-AddrWrConv, are responsible for computing the destination address in MSC memory using $A_{abs}= 2^{mq-oq}\left( A_{rel} -A_{rel} \text{ mod } 2^{oq -1}\right) + A_{rel} \text{ mod } 2^{oq-1}$. Here $A_{abs}$ represents the absolute address while $A_{rel}$ relative one. Recall that oq denotes the number of qubits the operator that is being constructed will operate on while and mq the maximum number of qubits that the coprocessor can handle simultaneously.

Controller OpTPCtrl is responsible for activating the appropriate control signals for the multiplexers and registers of UCA in order to correctly input the coefficients into the multipliers MULTC1 and MULTC2. It also controls the enable signal for the write operation, which determines when the partial results of the operator tensor product are stored in memory MSC. This enable signal remains active for a duration of 4 clock cycles after the start of the tensor product, which corresponds to the latency of the complex number multiplier.

Additionally, OpTPCtrl provides the recording converters MSC-AddrRdConv and MSC-AddrWrConv with two signals that play a role in determining the read/write address in memory MSC. These signals are the column number of the selected coefficient from the first operator and the row number of the selected coefficient from the second operator. By utilizing these signals, the address converters can accurately compute the appropriate address for reading and writing operations in memory MSC.

Controller OpTPRecCtrl is responsible for recording the tensor product results in memory MSC. Its main function is to control the sequencing of MSC addresses where the results of the operator tensor products need to be written. The controller utilizes two key inputs: the largest relative address of the next quantum operator, which is obtained from a specific register, and the relative address counter MSC-AddrWrCnt. To initiate the recording process, OpTPRecCtrl requires a counting enable signal, which is provided by the current micro-instruction. This signal triggers the controller to start counting clock cycles, considering the latency of the complex number multiplier needed to compute the product. Once the countdown reaches its conclusion, the writing enable signal is activated. This signal indicates that the writing phase of the results has commenced. When the relative address reaches 0, the counter MSC-AddrWrCnt is reset, preparing it for the next recording operation.

Register QbNumReg functions as an up-counter and serves as a register. Its purpose is to store the number of qubits in the current operator. Various components, namely MSC-AddrRdCnt, MSC-AddrWrCnt, MSC-AddrRdConv and MSC-AddrWrConv, utilize this register to determine the largest relative address of the operator being constructed. During the iteration of the tensor product sequence between operators, QbNumReg is incremented at the end. This ensures that the register holds the updated value for the subsequent operator construction. When the construction of an operator commences, the initial value of QbNumReg is set to 2, indicating the presence of two qubits.

6 Simulation results

This section offers proof of the precise performance of the proposed design of EQP by showcasing simulations that highlight two specific aspects of its operation during the execution of a quantum instruction. For more details, refer to the relevant information provided in [42].

6.1 Operation on non-entangled qubits

In this simulation, we demonstrate that a non-entangled quantum operation on n qubits with $n \ge 2$ can be achieved by sequentially applying n quantum operations, each on a single qubit. Specifically, we apply the quantum operator NOT on two non-entangled qubits, resulting in the collapse of the qubits into the state $\vert 0\rangle$. A quantum NOT operator for 2 qubits that can be obtained from the one for 1 qubit is shown in Eq. 2:

$$\begin{aligned} NOT \otimes NOT = \begin{bmatrix} 0 &{} 1\\ 1 &{} 0 \end{bmatrix} \otimes \begin{bmatrix} 0 &{} 1\\ 1 &{} 0 \end{bmatrix} = \begin{bmatrix} 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 0 \end{bmatrix} \end{aligned}$$

(2)

The column vector formed by the tensor product of 2 qubits, each in state $\vert 0\rangle$, is defined as: $\vert 0 \rangle \otimes \vert 0 \rangle = [1 \;\;\;0] \otimes [1\;\;\; 0] = [1\;\;\; 0\;\;\; 0\;\;\; 0]^T$. The matrix-based representation of this operation is defined as: $(NOT \otimes NOT)(\vert 0\rangle \otimes \vert 0\rangle ) = [0\;\;\; 0\;\;\; 0\;\;\; 1]^T$.

The NOT operation is executed on two qubits in two distinct steps, with each qubit undergoing a separate NOT operation. The time diagram of this process is illustrated in Fig. 20, showcasing the execution of the two NOT operations on a single qubit.

Fig. 20

Matrix product of a NOT operation on two non-entangled qubits

For a closer look at the time period encompassing these two operations, a zoomed-in view is presented in Fig. 21. Figures 22 and 23 show, respectively, the time diagram of the first and second NOT operation.

Fig. 21

Amplified view of the two NOT operation on the qubit

Fig. 22

Detailed view of the first NOT operation

Fig. 23

Detailed view of the second NOT operation

The NOT operation on two qubits is accomplished using two descriptive instructions encoded in the signal CurrentInst. The first instruction, 02 01 1, represents the NOT operation on qubit #1 and is not the final instruction of this operation. The second instruction, 02 02 0, signifies the NOT operation on qubit #2 and serves as the last instruction of this operation. Initially, the signal NoInst is set to a high level until an instruction is provided by the host processor. Subsequently, the signal InstReq is activated multiple times until the final instruction in the current quantum operation is reached, while also verifying if at least one qubit is entangled in the current instruction. In the simulated example, this condition occurs twice. If there is no entangled qubit, the signal RstPtrInst is triggered, enabling the instruction controller InstCtrl to supply the data of the first instruction the next time the signal InstReq is issued. Once the final instruction of the quantum operation is selected, the signal LastInst is set to a high level. The signal InstReq is initially activated after initializing the instruction pointer. In the given example, the quantum NOT operators are applied to qubits in the collapsed state $\vert 0\rangle$. The calculations and results presented in the operation on one qubit are repeated separately for both qubits.

6.2 Operation on entangled qubits

When performing quantum operations on entangled qubits or when the operation results in entanglement between qubits, a quantum operator needs to be constructed using tensor product. This section presents three case studies:

• 1. Constructing a quantum operator for operating with 2 qubits when the memory MSC can only accommodate operators for 4 qubits.

• 2. Constructing a quantum operator for operating with 3 qubits when memory MSC can only store operators for 4 qubits.

• 3. Constructing a quantum operator for operating with 3 qubits when memory MSC can handle operators for 4 qubits.

In the case where the scratch memory MSC can only hold an operator for 4 qubits with 128 addresses, the example utilizes only 8 addresses to store the 16 coefficients of the NOT operator for 2 qubits, which is constructed from two NOT operators for 1 qubit.

The process begins by obtaining the coefficients of the first row from memory MOP, followed by retrieving the coefficients of the second row for the NOT operator on 1 qubit, which are stored in the registers of the calculation unit UCA. Subsequently, the coefficients of the second basic quantum operator are read from memory MOP and temporarily stored in the registers of unit UCA. The tensor product operation between these operators generates 8 coefficients, which are then stored in memory MSC. The timing diagram illustrating this process is presented in Fig. 24.

Fig. 24

Building a NOT operator for 2 qubits when the design can handle quantum operations that involve at most 4 qubits

When qubits are entangled or targeted by an operation that results in entanglement, a total of $2^n$ memory positions are required to store the coefficients of the column vector representing the entangled qubits, where n represents the number of qubits involved in the operation. Each memory address can hold two coefficients. As a result, the first $2^{nq-1}$ memory positions of memory MQB, which were initially designated for tracking the kets of each non-entangled qubit, are now utilized to store the initial pairs of coefficients that constitute the entangled column vector. If more than two qubits are involved, additional memory positions are allocated to store the remaining coefficients.

For instance, consider $nq=4$ and the tensor product on two qubits ($n=2$) that are in the collapsed state $\vert 0\rangle$: $[1\;\; 0]^T \otimes [1\;\; 0]^T = [1\;\; 0\;\; 0\;\; 0]^T$. Table 6 presents the values of the coefficient pairs stored at each memory address in MQB before and after the tensor product operation. In this particular example, the same two memory positions are sufficient to store the four coefficients of the resulting column vector.

Table 6 Contents of the first four addresses of memory MQB before and after performing the tensor product

Figure 25 shows the timing diagram regrading to the aforementioned tensor product. Markers READ and WRITE are separators of the signal groups, associated with the read and write operation of memory MQB, respectively.

Fig. 25

Memory MQB contents before and after a tensor product regarding the example of NOT operator and Table 6

7 Performance evaluation

In order to evaluate the performance of the proposed design, we synthesized the design of EQP for the Xilinx Virtex UltraScale FPGA XCVU095-2FFVA2104E. The system maximum frequency yielded is 52.0 MHz. With these characteristics, we run the quantum search algorithm, known as Grover’s algorithm. It is a well-known quantum search algorithm to speedup search in unsorted database [53]. The algorithm is designed to search an unsorted database of $N=2^n$ entries to find a specific target item. The items of the database are the possible states formed by n qubits, i.e., $\vert i\rangle$, for $1\le i \le n-1$, and the target is one of these states. Grover’s algorithm can also be used to search for more than one target.

The steps of the algorithm depend on the number of qubits n and the configuration of procured target state. It offers a quadratic speedup compared to classical search algorithms that require linear time in terms of N. The algorithm involves applying a series of quantum operations iteratively. There are many circuit designs for this algorithm. The used version of Grover’s algorithm for n qubits is depicted in Fig. 26 [44, 54].

Fig. 26

Steps of Grover’s quantum algorithm for n qubits searching for target $\vert n-1\rangle$

Grover’s algorithm consists of three main steps: (1) input state preparation, which allows to yield the quantum states representing the searched database items; (2) oracle, which allows the identify the target items within the input data changing distinctively the amplitude of the corresponding quantum state with respect to the remaining items of the database; (3) target’s amplitude amplification, also known as the diffuser, which allows to increase the amplitude of the amplitudes of the targets’ states while decreasing that of the remaining states (4) output state measurement, which allows to observe the final results of the search, wherein amplitudes associated with the target states should be significantly high with respect to that associated with the remaining states. Of course, the sum of the squared amplitudes for all states must be equal to 1. Steps 2 and 3 are iterated to achieve satisfactory identification of the targets via the corresponding high amplitudes. In each iteration, the state undergoes specific quantum gates that allow marking the target and others that amplify its amplitude and reduce that of the remaining items.

For the preparation of the input states, a set of Hadamard operators, implements the first step of the algorithm, allowing the generation of a uniform state superposition with an amplitude do $1/\sqrt{2^n}$. A controlled Z operator is included in the implementation of the second and third steps. The number of control qubits is $n-1$ so that the amplitude of state $\vert 2^{n-1}\rangle$ is inverted to $-1/\sqrt{2^n}$ while that of the remaining state remain unchanged. It is noteworthy to emphasize that this operator has not been constructed by the processor. Instead, we stored the adequate matrix of the controlled Z operator according to the required controls in MOP as a basic operator. The construction of this operator from basic ones, as described in Sect. 2, is not a straightforward process, as it needs a complex transpilation process to be converted to simpler basic operators [55, 56], which is clearly out of the scope of this work. The third step is implemented by a state reflection around the average amplitude by a set of Hadamard operators, a set of X operators and a controlled Z operator with $n-1$ control qubits.

The iterations create constructive interference, which leads to the desired state where the probability of measuring the target item is higher. The main steps of Grover’s algorithm need to be iterated both real and simulated quantum computers. In a simulated quantum processor, these iterations are still necessary because they are a fundamental part of how Grover’s algorithm works [53]. The ideal number of iteration is defined in [57] as $\pi /4\sqrt{N/m}$, wherein $N=2^n$ represents the number of entries in the searched unsorted database and m is the number of targets.

The simulations are executed on a personal computer equipped with 4GB RAM memory, using the ModelSim program on the Windows 7 operating system. In this case, the coprocessor is capable of handling operations on up to 6 qubits simultaneously. Of course, if we run the simulation on better equipped computer, we would be able to run operations that act on more qubits. So, for the processor performance evaluation, we run Grover’s algorithm, described in Fig. 26, for two to six qubits. Table 7 shows the memory and time requirements for the execution of Grover’s algorithm for quantum search in a unsorted database of n input qubits. The results are averages of 100 shots.

Table 7 Performance of the Grover search algorithm for different state number of qubits

For each case, we provide the number of qubits n, the bit configuration of the target state, the number of required iterations, the required memory, the overall execution time, the measured target amplitude (TA) and the average amplitudes of the nontarget states (NTAA). Note that the reported memory size is customized for the case, i.e., exactly what is required for the circuit. Memories MQS, MOP and MOP as well as the local memory used in UMS are set to the fit the qubits and operators, used in the circuit. The processor with a maximum quantum state of 6 qubits that can be handled simultaneously via all basic operators described in Sect. 2 requires 7,6204 Bytes, all memories included.

For comparison purposes, we focus on different ways to implement Grover’s algorithm. We compare the results regarding software simulation, hardware emulation and direct execution on real quantum hardware. For simulation, we consider a dedicated software implementation of the algorithm (GDSS) [21] and a general-purpose software implementation of Grover’s algorithm via a simulation (GPSS) [58]. For emulation, we consider a dedicated hardware, which is custom-designed for Grover’s algorithm (GDHE) [21] and a general-purpose hardware emulation of the algorithm using EQP, presented in this work. Finally, for real quantum hardware, we consider the execution of Grover’s algorithm on quantum computers IBM Q (GIBMQ) and IonQ (GIonQ) [59]. For each of the considered implementations, Table 8 shows the execution time of Grover’s algorithm for n input qubits. Note that for a more concise presentation of the timing figures, we opted to use different time unit: nanoseconds ($\times 10^{-9}s$), microseconds ($\times 10^{-6}s$) or seconds. Note that the timings are sourced from their respective cited works. Also, due to the variations in system configurations among the compared implementations, the comparability of the results is limited.

Table 8 Performance comparison of software-based simulation and hardware-based emulation of quantum computations

Before, we get to further details about the comparison, it is fundamental to note that the performance of implementations based on real quantum hardware are included here only for completeness. State-of-the-art real quantum hardware are slower than emulated quantum hardware for many reasons. Among these reasons, we can cite (1) error-proneness due to decoherence and gate imperfections, among other forms of noise, requiring error correction techniques to mitigate the effects of noise; (2) limited qubit connectivity, requiring additional operations and/or extra qubits to implement correct interactions; (3) high measurement time due to physical constraints; and (4) device calibration and initialization procedures to ensure proper operation. All these reasons lead to slower execution times in real quantum hardware when compared to an ideal simulation or emulation [60].

Considering the time unit by kind of implementations, it is clear that the hardware-based solutions of Grover’s algorithm (GDHE [21] and the one proposed in this work GPDP) are a way faster (of the order of $10^3\times$ than GDSS [21] and $10^6\times$ than GPSS [58]) than the software-based ones. Also, considering the same basis, it is clear that the dedicated software implementation of the algorithm GDSS [21] is $10^3\times$ faster than the one implemented on a general-purpose emulated quantum processor GPSS [58]. Moreover, the dedicated hardware GDHE [21] scales better than the one implemented on the emulated quantum processor, proposed in this work. The former allows to run the algorithm for 7 qubits while the proposed implementation does not. Also, except for the cases of 2 qubits, for which both designs the latter is 2.7$\times$ faster, the former performs better. The speedups for 3, 4, 5 and 6 qubits are about 1.3$\times$, 4$\times$, 13$\times$ and 45$\times$, respectively. Nonetheless, it is important to note that GDHE can only run Grover’s algorithm, and a new hardware needs to be designed for another quantum algorithm. In contrast, the same hardware processor that is used to get GDPE, can also be simply programmed to run any other quantum algorithm. The proposed solution trades speedup for higher versatility.

8 Conclusions

This paper introduces an adaptive hardware design of an emulated quantum processor that can be customized for various applications. The proposed design utilizes a completely parallel pipelined approach to perform the tensor product operation, which is a fundamental operation in quantum computing. The design operates on complex numbers and is expected to be highly efficient. The effectiveness of the design is demonstrated through simulations of representative quantum instructions.

The main units of the proposed macro-architecture consist of the calculation unit, the control unit and the measurement unit. The calculation unit plays a critical role in executing the extensive and computationally intensive complex number products and sums required by the coprocessor. The modular nature of the proposed micro-architecture of this unit allows for scalability, enabling the design to be expanded to achieve the desired level of parallelism. However, this expansion entails increased control complexity, widening of the data path, and potentially, the buses. The control unit is micro-architecture is optimized. It utilizes control memory and auxiliary components to handle various tasks. The control path automates elementary operations and contributes to simplifying the microprogram.

Simulations of typical computations are provided to validate the correct functioning of the coprocessor using typical quantum operations and instructions involving matrices and tensor products. The simulations utilize scalable and parameterizable code, executed on a personal computer equipped with 4GB RAM memory, using the ModelSim program on the Windows 7 operating system. In this particular case, the coprocessor is capable of handling operations on up to 6 qubits simultaneously.

The performance of the proposed processor is presented for Grover’s algorithm for unsorted database search. The time and memory requirements are shown for a given item search in databases of 4, 8, 16, 32 and 64 items, i.e., testing with Grover’s algorithm for 2, 4, 5 and 6 qubits. We also compare the performance of the proposed processor regarding execution time to a dedicated implementation of Grover’s algorithm: using a simulated quantum processor and via emulation using a dedicated hardware. For completeness, we also provide the algorithm execution times on two real quantum hardware. We establish clearly that proposed hardware design of the proposed emulated quantum processor is far faster than the software solution but somehow slower than the dedicated hardware implementation, which scales better than the proposed processor design. Nonetheless, the proposed processor is versatile and allows the implementation of any quantum algorithm by simply programming while the dedicated hardware is designed specifically for Grover’s algorithm. Another design, built from scratch, is required to implement another quantum algorithm.

There are several avenues for future work that can be explored to enhance the coprocessor design: (1) Increasing the number of multipliers in the calculation unit, always in powers of 2, would allow for the simultaneous execution of more matrix and tensor products. This would leverage the coprocessor’s capabilities and improve its overall performance. (2) Implementing a pipeline organization in the architecture could optimize quantum operations by utilizing auxiliary complex number multipliers. This approach would facilitate the matrix product calculation by performing it on already computed lines, reducing the waiting time for the required calculations. (3) Enhancing the scratch memory by incorporating additional read and write ports, along with a larger number of complex number multipliers, would accelerate the construction of quantum operators. This would enable faster processing and improve the efficiency of the coprocessor. (4) Introducing a new auxiliary scratch memory dedicated to storing operators constructed for multiple qubits could save time by avoiding the need for recalculating larger operators repeatedly. This would enhance performance and efficiency by eliminating redundant calculations.

The proposed future directions to improve the design efficiency will certainly increase the design size. However, it is expected that the increase would further accelerate the emulation of quantum operations, allowing the execution of bigger instances of quantum algorithms. Of course, based on state-of-the-art science and technology, it would be always true that such an emulator whose design cost does not exponentially scale with the number of handled qubits will be certainly not capable of universal quantum emulation. Nonetheless, the general idea for future work is to increase the level of parallelism during execution, finding a good trade-off between cost (hardware area) and throughout (execution time). This will always be sought during the design improvement. Exploring these directions in future research and development efforts would contribute to the ongoing improvement and optimization of the coprocessor design.