1 Introduction

Many optimization algorithms have been proposed for different types of problems; however, according to the “No free launch” theorem [1], no optimization algorithm can be appropriate for solving all types of problems. That is why new algorithms are still being proposed in the literature. Until 2021, optimization algorithms could be classified into three main categories: Evolutionary Algorithms (EA) such as Genetic algorithm [2], and Bird mating optimizer [3], Swarm Intelligence (SI) algorithms such as Particle Swarm Optimization (PSO) algorithm [4], Artificial Bee Colony algorithm [5], and Chimp optimization algorithm, and Physical Phenomena (PP) algorithms such as Passing Vehicle search [6], and Gravitational Search algorithm [7].

In 2021, a new optimization algorithm named Battle Royale Optimization (BRO) [8] added a new category named “Game-based” optimization algorithms [9] to the literature. The original version of the BRO algorithm was designed only for solving problems of a continuous nature, and it was incapable of solving problems of a discrete nature. Later, the Binary Battle Royale algorithm (BinBRO) was proposed for solving binary optimization problems. Still, all those algorithms can only solve single-objective problems. However, some problems have a multi-objective nature, in which there is more than one objective to be satisfied (minimized or maximized). As most real-world problems are multi-objective, tackling multi-objective problems is essential. For example, when making a trade, the trader is usually interested in low prices and high quality, while these two objectives are conflicting, i.e., achieving one goal may compromise another. Therefore, there is no universal solution that can minimize/maximize all objective functions for all problems; instead, there are Pareto optimal solutions, which offer the best trade-offs between conflicting objectives [10]. Multi-objective problems may have two or more objectives. Multi-objective problems with three or more objectives are known as “many-objective problems” [11].

In this paper, we propose the multi-objective version of the Battle Royale Optimization algorithm for the first time in the literature and compare its performance with the multi-objective version of five state-of-the art algorithms: the Gray Wolf optimization algorithm (MOGWO), the Multi-Objective Particle Swarm Optimization algorithm (MOPSO), the Multi-Objective Artificial Vultures Optimization algorithm (MOAVAO), the Arithmetic Optimization Algorithm for Multi-Objective Problems (MAOA), and the Multi-Objective Non-dominated Sorting Genetic Algorithm III (NSGA-III).

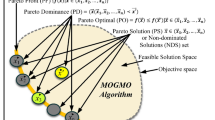
Multi-objective problems can be divided into constrained and unconstrained groups. In constrained problems, some constraints restrict the values that can be assigned to variables, while in unconstrained problems, no such restriction exists. The terminology for multi-objective problems is provided as follows:

  • Multi-objective problem A quadruple < V, D, F, S > represents a multi-objective problem, where V is a set of variables V = {v1, v2, …, vm} to be initialized by values taken from a set of domains D = { d1, d2, …, dm}, so that objectives F = {f1, f2, …, fp} are minimized (or maximized).

  • Constrained Multi-objective problem (CMOP) A CMOP is a multi-objective problem, in which, the goal is to find a vector of solutions, X, which optimizes f(X) subject to a set of inequality and equality constraints while satisfying some conflicting objectives:

$$\begin{aligned} g_{i} \left( {\text{X}} \right) & \le 0,\quad i = 1, \ldots ,m \\ h_{i} \left( {\text{X}} \right) & = 0,\quad i = 1, \ldots ,k \\ \end{aligned}$$

Where m and k are, respectively, the number of inequality and equality constraints. These constraints can be linear or nonlinear [12].

The feasible and infeasible solution A solution for CMOPs would be named as feasible if it satisfies all constraints, or infeasible otherwise.

On the other hand, S = {s1,s2,…,sp} as a set of candidate solutions can be divided into two subsets: population (dominated) and repository (non-dominated) candidate solutions. The non-dominated solutions are placed on a border so-called the Pareto front (PF).

  • Domination Solution x dominates solution y if x is as good as y for all objectives and better than it at least in one objective: x < y⇔∀i ∈ {1,…,p}fi(x) ≤ fi(y) and ∃i ∈ {1,…,p}fi(x) < fi(y).

  • Pareto optimal A candidate solution x is called Pareto optimal (PO) if there exists no other candidate solution y that can dominate x: x is PO⇔ ∃y ∈ S, such that y ≺ x.

  • Pareto Optimal set (PS) This set includes all Pareto optimal solutions: PS* = {si|si is PO}.

  • Pareto optimal front Given the Pareto Optimal set and objective function F, Pareto optimal front (POF) is the output values obtained by applying the objective functions to solutions in Pareto Optimal set: POF = {F(x) = (f1(x), f2(x), …, fp(x)) | x ∈ PS*}.

There are different categorizations of methods for solving multi-objective problems. Those categorizations generally differ in the way they choose the next move to achieve the global optima, i.e., they use different preference methods to find the preferred solutions. So, preference information is required to guide the search to the Pareto front area. The ultimate goal is to find a solution that is approved by a decision-maker. The decision-makers are either individual experts regarding the matter at hand or methods automatically applied to the selection procedure for choosing the next move. Hwang and Masud [13] classify the existing approaches for solving multi-objective problems into four different groups based on preference methods:

  • No-preference method In this approach, the MO problem is solved by employing a relatively straightforward method (classical single-objective optimization algorithms), and the obtained solution is delivered to the decision-maker; however, the suggestions of the decision-maker are not taken into consideration.

  • Posteriori methods In this approach, a decision-maker indicates its preferences a posteriori after receiving information about the trade-offs among the non-dominated solutions. Specifically, the decision-maker indicates which solution is the optimal one found so far. Our proposed algorithm, MOBRO, belongs to this category and determines the optimal solution in each iteration using the Roulette Wheel selection method. Like MOPSO [14], we use a grid mechanism for measuring the density of the PF area. The sparser areas in the PF have a higher probability of including the optimal solution(s). If more than one solution exists in the sparsest grid, one of them is randomly chosen as optimal.

  • Priori methods The objectives may be converted into a single objective by assigning a weight to each objective and then combining them. The associated weights should be defined in advance by the decision-makers.

  • Interactive methods In this approach, the objective functions, constraints, and their respective priorities are updated by getting user feedback on preferences several times throughout the optimization process.

Several research works have solved multi-objective problems using different methods. According to [15], multi-objective optimization algorithms generally rely either on non-dominated sorting methods or archive-based methods when searching for optimal solutions [14, 16]. The proposed approach, MOBRO, lies in the latter group (archive-based methods). One of the archive-based approaches has been proposed in [16], in which the authors propose a multi-objective version of the Gray Wolf optimization (GWO) algorithm, so-called MOGWO, by using a grid mechanism to detect and store the non-dominated solutions (in the archive) and choosing three solutions as leaders—global optima found so far—to guide other solutions in the population toward regions that may contain the global optimum. Social leadership was the main inspiration for GWO. As mentioned already, in archive-based multi-objective optimization algorithms, those solutions that are closer to the global optima are also stored in a separate set named a repository or archive. Despite its success in solving some single-objective problems, due to the nature of the original GWO algorithm, MOGWO suffers from a shortage of candidate leaders in the Pareto front as it requires three leaders (alpha, beta, and gamma), instead of one to solve the optimization problems. In other words, in some cases, the GWO algorithm is unable to provide more than one or two leaders. The most popular archive-based algorithm in the literature, a multi-objective version of the PSO algorithm (MOPSO), was proposed in [14]. In this work, the authors add a constraint-handling mechanism and a mutation operator to the original PSO algorithm to achieve a better exploration mechanism. ε-MOABC [11], as another archive-based algorithm, a multi-objective version of the Artificial Bee Colony algorithm uses a relaxed form of Pareto-dominance, named ε-dominance. A combined mutation operator is suggested in MOABC to prevent the basic ABC algorithm from being trapped in a local Pareto front. In [17], Mirjalili et al. adapt the Grasshopper optimization algorithm (GOA) for multi-objective optimization problems by using an archive and target selection technique to estimate the optimal solutions. The authors believe that GOA benefits from high exploration while showing a very fast convergence speed, and its balance between exploration and exploitation makes it an appropriate algorithm for multi-objective problems. The Ant colony algorithm has also been adapted to solve multi-objective problems [18]. This algorithm creates a pheromone matrix as an archive and stores the best N solutions in it. In [19], the authors propose a multi-objective version of the artificial vultures optimization algorithm (AVOA) for solving multi-objective optimization problems, so-called MOAVOA. The archive and grid mechanisms are also used in this algorithm. Another archive-based multi-objective arithmetic optimization algorithm (MAOA) is proposed in [20] for solving industrial engineering problems. The original AVOA is based on the distribution behaviour of four arithmetic operators. The most popular multi-objective algorithm among the sorting-based algorithms is probably NSGA III, proposed in [21], which is an evolutionary many-objective optimization algorithm using a reference-point-based non-dominated sorting approach based on the Genetic Algorithm for solving unconstrained multi-objective problems. This algorithm, as an extension of its previous version, NSGA II [22], attempts to preserve diversity among the solutions using a set of reference directions. There exist also other algorithms in the literature proposed for solving multi-objective problems [23,24,25,26]

It is very difficult to measure the performance of an optimization algorithm in theory; therefore, researchers apply their proposed optimization algorithms to benchmark datasets and compare them with other algorithms [27]. We evaluated the proposed algorithm, MOBRO, by applying it to four benchmark datasets: the CEC 2009 [28], CEC 2018 [29], ZDT [30], and DTLZ [31] datasets. The obtained results prove that MOBRO can solve unconstrained multi-objective problems; it also competes with other state-of-the-art MO optimization algorithms and, in most of the benchmark suites, surpasses them.

The remaining sections of the paper are designed as follows: Sect. 2 explains the proposed multi-objective version of the Battle Royale Optimization algorithm. Section 3 provides an experimental evaluation of the proposed method, and Sect. 4 provides conclusions and future works.

2 MOBRO: multi-objective battle royale algorithm

The original version of the Battle Royale optimization algorithm was recently proposed by Farshi (2020). This optimization algorithm, which drew inspiration from the Battle Royale video game, added a new category to optimization algorithms: “game-based” optimization algorithms. In this category, each solution competes with its nearest neighbor, and better solutions, according to fitness value (stronger soldiers in the game), attempt to overcome the worse ones (weaker soldiers). If a solution loses a specified number of times when competing with other solutions, it will be removed from the problem space and will be regenerated using Eq. 1. If the number of losses for a solution does not reach a threshold, it will be updated by Eq. 2, hoping that it will approach the best solution found so far in dimension d.

$${x}_{\mathrm{dam}.\mathrm{d}}=r\left({ub}_{d}-{lb}_{d}\right)+{lb}_{d}$$
(1)
$${x}_{\mathrm{dam}.\mathrm{d}}={x}_{\mathrm{dam}.\mathrm{d}}+r({x}_{\mathrm{best}.\mathrm{d}}-{x}_{\mathrm{dam}.\mathrm{d}})$$
(2)

In these equations, r is a random number generated using a uniform distribution in the range [0, 1]; Xdam,d, and Xbest,d are the position of the damaged (looser) and the best solution (found so far). The lower and the upper bounds of dimension d in the problem space are denoted by lbd and ubd.

To move a solution toward the best one, Akan and Akan [32] updated Eq. 2 as follows:

$$\begin{aligned} \lambda_{{{\text{dam}},\;d}} & = r_{1} x_{{{\text{best}},\;d}} + r_{2} \left( {\lambda_{{{\text{dam,}}\;d}} - x_{{{\text{dam}},\;d}} } \right), \\ x_{{{\text{dam}},\;d}} & = \lambda_{{{\text{dam}},\;d}} + x_{{{\text{dam}},\;d}} \\ \end{aligned}$$
(3)

where \({r}_{1}\) and \({r}_{2}\) are independent numerical values randomly chosen from the interval [0, 1], and \({\lambda }_{\mathrm{dam},d}\) is also a combination of randomly generated values taken from a uniform distribution [0, 1] that will be updated in each iteration. The updated movement strategy is more stochastic in exploration and exploitation.

The key point of this algorithm is that the safe zone (game field) shrinks down by Δ = Δ + round(Δ/2), where Δ is initialized by log10(MaxCircle); MaxCicle is the maximum number of generations. This space restriction will force all solutions to move toward the best one found so far. Diminishing the space is done based on Eq. 4, in which, SD(xd) is the standard deviation of the population in dimension d.

$$\begin{gathered} {\text{lb}}_{d} = x_{{{\text{best}},d}} - {\text{SD}}\left( {\overline{{x_{d} }} } \right) \hfill \\ {\text{ub}}_{d} = x_{{{\text{best}},d}} + {\text{SD}}\left( {\overline{{x_{d} }} } \right) \hfill \\ \end{gathered}$$
(4)

The overall methodology of MOBRO is provided as a pseudo-code in Algorithm 1 and also as a flowchart in Fig. 1. As seen in this algorithm, in the beginning, some solutions are randomly generated (initialized). As mentioned in the introduction, an attribute of the multi-objective version of BRO is using a set named archive (or repository). This set stores copies of non-dominated solutions. If a solution is not dominated by any other solution, it should be added to the archive. If any candidate solution inside the archive gets dominated by a new solution, the dominated solution will be replaced by a new (dominating) one. Solutions can remain in the archive as long as they are non-dominated [16]. In the MOBRO algorithm, the non-dominated solutions are determined, and a copy of them is added to the archive after evaluating the solutions.

Fig. 1
figure 1

The proposed algorithm, MOBRO, as a flowchart

Full size image
figure a

Then, the whole process is repeated for a predefined number of iterations. As the first task in each iteration, a flag solution (assumed to be the global optimum) is chosen out of solutions in the repository using a selection strategy based on the roulette wheel selection method [14]. Concretely, the Pareto Front region is divided into grids using a gridding mechanism, and one of the solutions in the least crowded region of the Pareto Front is selected as the flag (leader). The gridding mechanism keeps the candidate solutions in the archive as diverse as possible. Gridding recursively divides the Pareto front apace into grids and covers all solutions. If any solution lies outside the gridding region, gridding should be repeated. The solutions belonging to each grid are recorded, so the number of solutions in each grid can be easily calculated [16]. The advantages of this mechanism are twofold: (1) low computational cost; and (2) no need for a niche-size parameter setting [34].

Then the following process is repeated for all solutions in the population: Each solution is compared to its neighbors, starting from the nearest to the farthest. This comparison stops when one solution (the winner) dominates the other (the damaged one). If no solution could dominate the other, the winner and the loser tags are randomly assigned to a solution and its nearest neighbor. When a solution gets damaged, its fault counter will be incremented by one, while the same counter will be set to zero for the winner. If the fault counter does not reach a threshold value, a crossover task [32], given in Eq. 3, will be applied to the loser, hoping to make it closer to the best solution. The intuition behind this policy is that the loser is not in an appropriate state (the soldier is in danger) and should be updated to move to a better position. If this cross-over causes the loser to leave the safe zone, it will be brought back to the edge of the safe zone. However, if the fault counter of the loser reaches a threshold (one of the parameters of MOBRO), this solution will be deleted and regenerated as another one with new values (as a soldier is respawned in a random area inside the safe zone). In each iteration, a mutation task [14, 33] is also applied to the flag. The flag will be updated if this mutation improves it or will remain unchanged, otherwise. Note that, similar to the original BRO algorithm, the search space shrinks once in \(\Delta\) iterations based on Eq. 4. In all cases, the leader will be updated if the recently updated damaged solution dominates it. At the end of each iteration, a flag is chosen from the repository and is compared to the current flag. The current flag will be replaced by a new one if it dominates the current one.

As mentioned already, the search strategy explained above is repeated for all n solutions in the population, and again, the newly found non-dominated solutions, as well as the flag solution, are added to the repository (archive). If the repository becomes full, one of the existing solutions in its most crowded region will be removed. There are two reasons for removing the surplus solution from the repository: (1) newly added solutions might dominate the existing ones, and (2) the capacity of the repository becomes full. Finally, at the end of each iteration, a selection mechanism will be performed on the repository to update the flag.

3 Experimental results and performance evaluation

In this section, we first introduce the datasets and performance metrics used for evaluating the proposed algorithm and then provide the obtained results as well as a detailed discussion on them.

3.1 Dataset

As the theoretical evaluation of optimization algorithms in terms of their performance is difficult, benchmark datasets are used for this purpose. The benchmark multi-objective optimization problems of the competitions on evolutionary computation (CEC), CEC 2009 [28], and CEC 2018 [29] as well as two other datasets, ZDT [30] and DTLZ [31] have been used for the evaluation of the proposed algorithm and its comparison with five state-of-the-art algorithms. Tables 1 and 2, respectively, list the mathematical presentation of different test problems in the CEC 2009, ZDT, and DTLZ datasets, including 10, 6, and 7 test problems. Due to the long equations, the mathematical presentation of CEC 2018 is provided in Table S1 in the Appendix file. It is worth noting that the crossover task for the DTLZ dataset is performed by Eq. 2, but the same task is performed by Eq. 3 for other datasets.

Table 1 The mathematical representation of different test cases in CEC 2009 dataset
Full size table
Table 2 The mathematical representation of different test cases in the ZDT and DTLZ datasets
Full size table

3.2 Performance metrics

Different performance metrics have been proposed in the literature for evaluating different aspects of a multi-objective optimization algorithm [35]. These aspects include convergence, spread, and distribution. The proposed metrics in the literature do not directly measure one aspect in isolation; instead, they measure different aspects while assigning different weights to each one. We evaluated the proposed algorithm using three metrics: Inverted Generational Distance (IGD) [35], Spacing (SP) [36], and Maximum spread [21] or spread in short. These metrics are provided in Eqs. 5–7, respectively.

$$\mathrm{IGD}=\frac{\sqrt{{\sum }_{i=1}^{m}({r}_{i}- {e}_{i})}}{\mathrm{m}}$$
(5)

where m is the number of true solutions in the Pareto optimal set, \({r}_{i}\) and \({e}_{i}\) are, respectively, the real and closest found solutions to the true one. This metric is calculated for m times, which is the number of true solutions. IGD is sensitive to the number of points found by the algorithm [37]. This metric favors those algorithms providing a denser area for the solutions than those providing a more distributed version of the Pareto front. IGD is the most commonly used metric for evaluating the performance of many-objective optimization algorithms [35]. Furthermore, it is cheaper to compute, i.e., its time complexity is lower than some other metric’s such as hyper volume [38].

$$\mathrm{SP}(S)=\sqrt{\frac{1}{|S|-1}\sum_{i=1}^{|S|} {(\overline{d }{-d}_{i})}^{2}}$$
(6)

where |S| is the number of solutions in the Pareto optimal set (S), \(\overline{d }\) is the mean of all dis, and.

\(\left(d =\mathrm{ min}(\left|{f}_{1}^{i}\left(\overline{x }\right)-{f}_{1}^{j}(\overline{x })\right|+ \left|{f}_{2}^{i}\left(\overline{x }\right)-{f}_{2}^{j}(\overline{x })\right|\right))\), i,j = 1,2,…|S|, and \(\overline{x }\in\) |S|. The spacing metric considers the distance between a point and its closest neighbor in the Pareto front generated by the optimization algorithm to measure how evenly the estimated solutions are distributed. The value 0 for this metric indicates that the estimated solutions are spaced at equal distances [37].

$$\mathrm{MS}=\sqrt{{\sum }_{k=1}^{|F|}\mathrm{max}(\mathrm{ED}({a}_{i}- {b}_{i}))}$$
(7)

where ED is the Euclidean distance; \({a}_{i}\) and \({b}_{i}\) are, respectively, the maximum and minimum values in the \({i}_{th}\) objective; and |F| is the number of objectives. This metric measures the extent of the points along the Pareto front; it calculates the diversity of estimated points. In other words, it indicates the range of values covered by the solutions. Generally, a wider area including the estimated solutions in the Pareto front is desired, i.e., the larger the value of MS, the better it is. This metric is also known as the “extent metric” in literature.

Note that in all experiments on the CEC 2009, ZDT, and DTLZ benchmarks, we have utilized 100 solutions and a maximum of 1000 iterations. The main criterion in these benchmarks was the number of iterations. However, we used the Maximum Number of Function Evaluations (MNFE) as the termination criterion rather than relying on a 'Maximum Iteration Number for the CEC 2018 dataset. In CEC 2108 experiments, the number of objectives (M) in MaOP1-MaOP10 is set to 3. The number of variables (N) in all ten test problems is 20. The population size in each algorithm is pop = 100 × M and finally, the total number of function evaluations is set to pop × 500. Besides, the general parameters of the proposed algorithm as well as five other algorithms are listed in Table 3. We have run experiments with different values for the parameters used in MOBRO and concluded that MOBRO achieves its highest performance when using the values shown in Table 3. The parameter values of other algorithms have been taken from their publications. Note that four optimization algorithms (MOBRO, MOGWO, MOPOS, and NSGA-III) have been applied to the CEC 2009, ZDT, and DTLZ datasets, but all algorithms, including MOAVOA and MAOA, have been tested on the CEC 2018 dataset.

Table 3 The initial values of the parameters in optimization algorithms
Full size table

3.3 Results

All the experiments have been conducted on MATLAB R2019b, installed on Windows 10, on a computer with a Core i7-7700HQ processor running at 2.80 GHz and 32 GB of RAM. Since heuristic algorithms are inherently stochastic, they may generate relatively diverse results. Therefore, for each dataset, an average of 25 separate runs have been used. As the theoretical evaluation of optimization algorithms is difficult, benchmark datasets are used for this purpose. We calculated the value of three performance metrics explained in Sect. 3.1 and provided them in Tables 4, 6 and 8 separately for different datasets. For the sake of fair comparison, the obtained results are compared with five state-of-the-art algorithms: the non-dominated sorting genetic algorithm (NSGA-III), multi-objective particle swarm optimization (MOPSO), multi-objective gray wolf optimization (MOGWO), multi-objective arithmetic optimization algorithm (MAOA), and the multi-objective version of the artificial vulture optimization algorithm (MOAVOA). Note that the first three algorithms have been applied to three datasets (CEC 2009, ZDT, and DTLZ), but all five algorithms have been tested on the CEC 2018 dataset. As the number of runs for obtaining these results is 25, the best, worst, average, and standard deviations of these runs are also provided in these tables, i.e., according to, for example, IGD, the average case shows the average IGD value across a set of runs of each algorithm on the problem. The best case shows the lowest IGD value achieved by any run of the algorithm on the problem, and the worst case shows the highest IGD value achieved by any run of the algorithm on the problem. The SD shows the standard deviation of the IGD values across the set of runs for each algorithm. The rank of each optimization algorithm among others is also provided in Tables 5, 7 and 9.

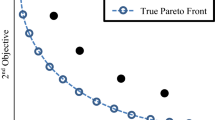
Based on the results in Table 4, UF1 function, the MOBRO algorithm achieves competitive results with state-of-the-art According to the obtained results on the CEC 2009 dataset, MOBRO has the lowest average IGD value among the four algorithms, followed by NSGA-III, MOGWO, and MOPSO. MOBRO also has the lowest best and worst IGD values and the lowest standard deviation. This suggests that MOBRO may be the most consistent and efficient algorithm among the four in terms of achieving good solutions. All four algorithms have small and consistent average values for the SP indicator, with an average value of around 0.02 and a standard deviation of around 0.03. A notable aspect of Table 4 is the best values for each algorithm, which are all very small. The best value for MOBRO is 0, indicating that the solutions in the Pareto front approximation are evenly spaced and perfectly distributed. This suggests that the algorithms can find a set of solutions that are very diverse and evenly distributed, covering a wide range of the objective space. Also, NSGA-III outperforms others in the worst case; however, other algorithms provide competitive results. The average values for the spread metric for all four algorithms are close to 1, with a standard deviation of around 0.01. This indicates that the algorithms have similar performance in terms of the average spread or dispersion of the solutions. The best values for the spread metric obtained by each algorithm are very close to 1, while MOGWO achieves the best value of 1.115994. Also, MOBRO provides the best value in terms of the worst case. Figure 2 (UF1) shows that MOBRO provides an accurate approximation of the true Pareto Optimal Front with the highest diversity as it is evenly spaced and distributed over the true Pareto Front. For the remaining functions (U2-U10), according to the results given in Table 4, all the algorithms provide satisfactory results. Nonetheless, as shown in Fig. 2 (UF2-UF10), MOBRO provides a more accurate approximation of the true Pareto optimal front with the highest diversity where its solutions are equally spaced and dispersed across the true Pareto front.

Table 4 Obtained results for the CEC 2009 dataset by MOBRO and three state-of-the-art optimization algorithms (UF)
Full size table
Fig. 2
figure 2figure 2figure 2

The Pareto fronts obtained by the applied algorithms on the all test problems

Full size image

By inspecting the obtained results on the CEC 2009 dataset, which are summarized in Table 5, the MOBRO algorithm ranks first according to the average, best, worst, and SD values of the IGD metric. Meanwhile, MOBRO ranks third, first, third, and third in average, best, worst, and SD, respectively, in terms of the spacing metric. Also, MOBRO ranks first, second, first, and fourth in average, best, worst, and SD, respectively, in terms of the spread metric. Finally, MOBRO ranks first alongside NSGA-III over the average on all metrics’ ranks.

Table 5 The ranks of each algorithm among others according to CEC 2009 dataset
Full size table

Table 6 provides the results obtained by the four different multi-objective optimization algorithms on the ZDT benchmark functions, while the ranks of the algorithms are summarized in Table 7. On the ZDT1 problem, in terms of average IGD, MOPSO has the lowest value, followed by MOBRO, NSGA-III, and MOGWO. Also, the best IGD values show a similar trend. The worst IGD values are somewhat lower for MOPSO and MOBRO compared to NSGA-III and MOGWO, but the difference is not as large as it is for the average and best values. This suggests that the worst solutions found by MOPSO and MOBRO were not as far from the true Pareto front as the worst solutions found by NSGA-III and MOGWO are. Finally, the standard deviation values show that the IGD values for MOPSO and BRO had smaller variations across the set of runs compared to NSGA-III and MOGWO. This indicates that the performance of MOPSO and MOBRO was more consistent across the runs, while the performance of NSGA-III and MOGWO was more variable. Based on the average spacing values provided in the table, MOBRO has the lowest average spacing value, followed by MOPSO, NSGA-III, and MOGWO. This ranking means that MOBRO outperforms the other algorithms in terms of producing a more focused set of solutions on the Pareto front, followed by MOPSO, NSGA-III, and MOGWO. Based on the best and worst spacing values, MOBRO has the narrowest range of spacing values, followed by MOPSO, NSGA-III, and MOGWO. This could indicate that MOBRO produces a more focused set of solutions on the Pareto front, while the other algorithms produce a more diverse set of solutions. The standard deviation of the spacing values also suggests that MOBRO has the most consistent set of spacing values, followed by MOPSO, NSGA-III, and MOGWO. This could further support the idea that MOBRO produces a more focused set of solutions.

Table 6 Obtained results for the ZDT dataset by MOBRO and three state-of-the-art optimization algorithms (ZDT)
Full size table
Table 7 The ranks of each algorithm among others according to the ZDT dataset
Full size table

Based on the values given in Table 6, MOBRO outperforms the other algorithms in terms of the spread metric for the ZDT1 optimization problem, with the greatest average, best, and worst values. However, MOPSO, although ranked 4th in the spread metric, has the lowest standard deviation, indicating that it has a more consistent set of values and potentially a smaller range of solutions. As mentioned already, due to the nature of the original GWO algorithm, in some cases MOGWO suffers from a shortage of candidate leaders in the Pareto front as it requires three leaders to find the optimal solution. For example, MOGWO is unable to provide any solution for the ZDT2 and ZDT3 test suits as it could not provide more than one or two candidate leaders in the Pareto Front. Moreover, it can be seen in Table 5 that the MOBRO algorithm outperforms its competitors in terms of spacing and spread indicators and ranks first according to average, best, and worst values. Considering all ZDT functions, MOBRO ranks second, third, second, and second in average, best, worst, and SD, respectively, in terms of the IGD metric. Finally, by taking the average over all metrics ranks on all ZDT datasets, MOBRO ranks first, followed by MOPSO, NSGA-III, and MOGWO. Figure 2 for ZDT1-ZDT6 shows that in most cases, the algorithms can find a very accurate approximation of the true Pareto optimal solutions with a good diversity that is evenly spaced and perfectly distributed. However, MOGWO is unable to provide solutions for ZDT2 and ZDT3.

Tables 8 and 9, respectively, represent the obtained results and the rankings of the four algorithms on the DTLZ dataset. Based on the average IGD value for the DTLZ1, NSGA-III ranks first by a large margin, and the following algorithms are MOGWO, MOBRO, and MOPSO, respectively, from second to last. Moreover, based on the spacing metric, the NSGA-III algorithm again ranks first in all cases (best, worst, average, and SD) on DTLZ1. However, according to Spread, the MOBRO algorithm ranks first in “average”, “best,” and “worst,” while MOPSO ranks first in “SD”. According to the obtained results, the DTLZ dataset appears to be more challenging than the other two datasets. As is shown in Table 8, MOGWO could not provide any solutions for the DTLZ7 test function in some runs of the algorithm. However, the best Pareto Front of all success runs for MOGWO have been plotted in Fig. 2 (DTLZ1).

Table 8 Obtained results for MOBRO as well as state-of-the-art optimization algorithms (DTLZ)
Full size table
Table 9 The ranks of all algorithms among others according to DTLZ dataset
Full size table

In a nutshell, according to all DTLZ functions, MOBRO ranks second, third, fourth, and third in average, best, worst, and SD, respectively, in terms of the IGD metric. Also, it ranks fourth, third, fourth, and fourth in average, best, worst, and SD, correspondingly, in terms of the spacing metric. According to the Spread metric, MOBRO ranks first in average, best, worst and ranks second in SD. Finally, by taking the average over all metrics’ ranks, the overall ranking of the four algorithms is NSGA-III, MOPSO, MOBRO, and MOGWO from best to worst. These results show that the distance between MOBRO's solutions for DTLZ and the true Pareto Front is not as close as others. Also, a higher spacing value for MOBRO indicates that the solutions are more evenly distributed within the set, while a lower spacing value for the competitors suggests that the solutions are more densely clustered. The spacing value depends on the optimization problem's context and goals. In some cases, a diverse or evenly distributed set of solutions is desired, while in others, a tightly clustered set is more appropriate.

Also, MOBRO ranks first based on the Spread metric in all the datasets. It proves that the obtained results by MOBRO can cover the true Pareto Front through hyper cubes better than its competitors.

Unlike other datasets (CEC 2009 ZDT and DTLZ), we used the number of function evaluation criterion instead of the number of iterations for measuring the performance of MOBRO on the CEC 2018 dataset. Tables 10 and 11, respectively, provide the obtained results for four different algorithms according to performance metrics and the rank of each algorithm, among others. The reason for not listing MOGWO in these tables is that MOGWO is unable to find an optimal solution for any of the datasets in CEC2018, as it requires three solutions in the Pareto Front, and when it cannot find these three, a runtime error occurs in this algorithm.

Table 10 Obtained results for the CEC 2018 dataset by MOBRO and four state-of-the-art optimization algorithms (UF)
Full size table
Table 11 The ranks of each algorithm among others according to CEC 2018 dataset
Full size table

According to Table10 and consequently Table 11, NSGA-III ranks first and MOBRO ranks second in terms of the IGD measure, followed by MOPSO, MOAVOA, and MAOA ranking from third to fifth. This superiority suggests that MOBRO and NSGA-III offer a better balance between convergence and diversity. This balance can be seen in their ability to approximate the true Pareto Front effectively. When looking at the Spacing measure, again, NSGA-III and MOBRO respectively rank the first and second, but this time, MOBRO obtains very competitive results to NSGA-III. The MOPSO, MAOA, and MOAVOA respectively rank from third to fifth. These ranks indicate that the estimated solutions by MOBO and NSGA-III are spaced at almost equal distances. In terms of the spread, MOBRO surpasses all other algorithms and ranks first. The second to fifth ranks are respectively achieved by NSGA-III, MOAVOA, MAOA, and MOPSO. Obtained results on this measure suggest that MOBRO and NSGA-III spread the obtained solutions with a higher distance over the Pareto Front. Note that for the first two factors, IGD and SP, lower values but for the third one, spread, higher values are desired. In summary, MOBRO and NSGA-III emerged as prominent candidates, providing a high solution quality and diversity, which can be chosen as trustable algorithms for solving multi-objective optimization problems in a specific domain.

We also measured the runtime for each algorithm when applied to the CEC 2018 dataset, provided in Table 12. According to this table, the fastest algorithm among the five is MAOA, while the slowest one is NSGA-III. This low speed can be assumed to be a disadvantage for the NSGA-III algorithm, despite its success in finding optimal solutions for many multi-objective problems. Finally, the Wilcoxon signed-rank test, which is widely used in the literature [39, 40], was used for a more accurate comparison of five optimization algorithms. Table 13 lists the statistical results obtained by this test. As can be seen in this table, MBRO overcomes MOPSO, MAOA, and MOAVOA in all benchmarks, but it could overcome NSGA-III in only 7 out of 10 datasets.

Table 12 Required CPU time for running each algorithm when applied to the CEC 2018 dataset
Full size table
Table 13 Pair-wise statistical comparison between MBRO and all competitors by Wilcoxon signed-rank test (α = 0.05)
Full size table

4 Conclusions

We proposed the multi-objective version of the Battle Royale optimization algorithm for solving unconstrained multi-objective optimization problems. The MOBRO algorithm is based on the Battle Royale optimization algorithm proposed in 2021, which is inspired by the Battle Royale games.

MOBRO uses an archive to store non-dominated solutions, and after finishing its search over the population, it provides several candidate solutions in the Pareto front. All solutions in the Pareto front are better than or at least as good as all other solutions in the population in satisfying the objectives. Although MOBRO is an archive-based optimization algorithm, we compared it with both evolutionary and swarm-based algorithms, where the former group uses the sorting scheme, but the latter group uses the archive-based scheme.

We compared the proposed algorithm with five state-of-the-art multi-objective optimization algorithms, MOPSO, NSGA-III, MOAVOA, MAOA, and MOGWO, based on three performance metrics: inverted generational distance (IGD) for measuring convergence, spacing (SP) for measuring how evenly the estimated solutions are distributed, and maximum spread for measuring the diversity of estimated points. These algorithms have been tested on four benchmark datasets: CEC 2009, CEC 2018, ZDT, and DTLZ. According to the obtained results, MOBRO ranked first in the ZDT and CEC 2009 datasets. In the CEC 2009 and DTLZ datasets, MOBRO ranked second and third, respectively. In terms of performance metrics, MOBRO is more efficient according to IGD and almost always ranks first based on this metric. This indicates that MOBRO has the best convergence among its competitors, but it ranks from first to last in different datasets based on the spacing metric. This suggests that according to the distribution of the estimated solutions and their diversity, MOBRO ranks first, second, third, or last in different test suits. Finally, according to the spread metric, MOBRO ranks first or second, indicating that its solutions are well distributed along the Pareto Front border. The limitation of the proposed approach is that it is designed for solving only the unconstrained multi-objective optimization problems, while some of the real-world problems are constrained. We aim to address this issue in our future work.