1 Introduction

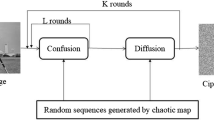
Due to the rapid progress in smart multimedia devices and communication technologies, securing multimedia data during the transmission process from sender to receiver is extremely critical in digital communication. For this reason, encryption and its applications are critical for improving security standards. Images always have a high value among all other multimedia types due to their visual impact [1]. Images are used to communicate information in various industries, including but not limited to medical, military, aerospace, banking, and education; therefore, they must be protected from unauthorized access [2]. The growing demand for robust image encryption systems has emerged as a consequence of the increased need for the Internet of Things and technological advancements [3]. Image encryption is mainly composed of two phases: confusion and diffusion. The pixels are shuffled throughout the confusion stage [4], while the pixel values are changed during the diffusion stage [5]. An efficient image encryption method includes treating an image as a stream of bits and then encrypting this stream utilizing traditional encryption methods like the Advanced Encryption Standard (AES), the International Data Encryption Algorithm (IDEA), and the Triple Data Encryption Algorithm (TDEA). These methods suffer from a strong correlation between neighbouring pixels and redundant data [6, 7]. As a result, different encryption approaches based on various technologies have been proposed to provide better security to images [8], such as frequency domain transformation [9], chaos theory [10], Deoxyribonucleic Acid (DNA) coding [11], and compressive sensing [12, 13]. One of the most well-known approaches is using chaotic maps with image encryption. Chaos-based image encryption algorithms provide robust results in terms of complexity, security, and speed due to their characteristics, such as pseudo-randomness, ergodicity, non-periodicity, and sensitivity to initial conditions. [14]. Due to the sensitivity of chaotic maps to initial conditions, the control parameters and initial conditions must be carefully selected. Otherwise, the results will be unsatisfactory, the secret keys can be predicted, and unauthorized individuals can access data [15]. Metaheuristics techniques have been used to optimize appropriate control parameters to overcome this problem. Figure 1 presents the block diagram of the proposed chaos-based image encryption algorithm. The main contributions of the proposed work are:

  1. (1)

    Presenting a novel approach utilizing metaheuristic optimization algorithms to enhance the security and robustness of image encryption based on chaotic maps, leveraging the chaotic maps as objective functions to improve the optimization process through the inherent complexity and randomness of chaotic sequences.

  2. (2)

    Extensive investigation and fine-tuning of control parameters for eight different chaotic maps using nine metaheuristic optimizers are conducted, resulting in the generation of highly secure encryption keys with improved randomness and complexity.

  3. (3)

    Proposing a novel confusion process using optimized chaotic sequences to permute image pixels, thereby strengthening the encryption scheme and introducing an additional layer of security.

  4. (4)

    Conducting a comparison between encryption methods with and without optimization, the potential of metaheuristic optimizers is evaluated, and the most effective technique in terms of security and robustness is identified.

  5. (5)

    Introducing a robust image security algorithm that effectively resists various attacks and distortions, focusing on mitigating the impact of periodic noise, thus enhancing image confidentiality and integrity.

  6. (6)

    Evaluating the performance of the eight proposed chaotic-based image encryption methods on different standardized images demonstrates the applicability and effectiveness of our approach across various image types and characteristics.

Fig. 1
figure 1

Structure diagram of the proposed system

Full size image

The rest of this paper is structured as follows. Section 2 presents an overview of related work. Section 3 illustrates chaotic maps. Section 4 demonstrates the different metaheuristic optimizers that are used in this paper. Section 5 presents the model proposed. Section 6 introduces our proposed model’s performance metrics and experimental results. Finally, the conclusions are shown in Sect. 7.

2 Related work

Mozaffari [16] has designed an image encryption system relying on bitplane decomposition and a local binary pattern technique, which converts the plain grayscale image to a group of binary images. After that, pixel substitution and permutation are performed using a genetic algorithm. Finally, the scrambled bitplanes are merged to create an encrypted image. This technology enhanced the encryption speed and allowed it to be used in real-time applications. Talhaoui et al. [17] have suggested an approach to encrypting images relying on the Bülban chaotic map, which produces only a few random columns and rows. Then the substitution-permutation process was used for pixels, and a circular shift was used for rows and columns. At last, the XOR operation and the modulo function are used together to mask the values of the pixels and avoid information leakage. This approach proved to be secure and fast for real-time image processing. Saravanan et al. [18] have proposed an optimized Hybrid Chaotic Map (HCM) approach for image encryption, integrating 2DLCM and PWLCM. Parameter optimization using the Chaos-Induced Whale Optimization Algorithm (CI-WOA) enhances performance and ensures efficient and secure image transmission. Rezaei et al. [19] have presented an evolutionary-based image encryption method using a two-dimensional Henon chaotic map. The parameters of the chaotic map, including α and β, are fine-tuned using the metaheuristic Imperialist Competitive Algorithm (ICA), which ensures that the generated pseudorandom numbers are unique, enhancing the security of the encryption process. Experimental results demonstrate the effectiveness of the proposed method in protecting image content against common attacks. Shahna et al. [20] have introduced a system for encrypting images relying on a symmetric key, cyclic shift operation, scan method, and chaotic map. Diffusion and confusion processes are implemented using the Henon chaotic map and Hilbert curve. Image scrambling involves both bit-level and pixel-level permutations. From the double-scrambled image, the final encrypted image is produced. The proposed technique provides high security. Ghazvini et al. [21] have suggested a hybrid image encryption technique based on chaotic maps and a genetic algorithm. During the confusion phase, Chen’s map of chaos was used, while the logistic-sine map was used during the diffusion phase. The encrypted image is then optimized using a genetic algorithm. The proposed technique is resistant to security attacks. Noshadian et al. [22] have performed an image encryption scheme that employs a chaotic logistic function to change the value of the pixels and a genetic algorithm to decrease the correlation among adjacent pixels. Wang et al. [23] have developed a scheme for encrypting images that relies on logistic maps, DNA sequences, and multi-objective particle swarm optimization. The chaotic logistic map and DNA encoding produce random DNA mask images. Then, particle swarm optimization is used to find the best balance between entropy and correlation. The suggested scheme has good security and is resistant to security attacks. Wang et al. [24] have proposed an image encryption method that uses particle swarm optimization (PSO) to select the parameters and initial values of chaotic systems for generating a high-chaotic sequence. The proposed approach uses the chaotic system parameters and initial values as particles, making it more computationally efficient for real-time applications. The encryption algorithm includes key selection, chaotic sequence pre-processing, block scrambling, expansion, confusion, and diffusion, with the PSO-optimized chaotic sequence used for scrambling and diffusion. Experimental results demonstrate that the proposed method is secure. Ferdush et al. [25] have proposed a method for encrypting images that uses a logistic map, a genetic algorithm, and particle swarm optimization. The logistic map is first used to create the initial population. Then, the genetic algorithm is used to encrypt the image, and the particle swarm optimizer is used to make the best-encrypted image. The entropy of the proposed method is high. Alghafis et al. [26] have utilized an image encryption technique based on chaotic sequencing and DNA. Random sequences are generated using logistic, Henon, and Lorenz chaotic systems. Then, pixel confusion and diffusion are created using DNA computations in combination with the chaotic systems. The security tests revealed that this algorithm is well-suited to encrypt digital images and can also protect the privacy of other digital contents, such as audio and video files. Latha et al. [27] proposed an optimized two-dimensional (2D) chaotic mapping for image encryption. A metaheuristic fitness-based Sea Lion optimization algorithm is used to fine-tune the initial parameters of the chaotic system. This algorithm tries to maximize the information entropy model for chaotic key generation, which leads to the best initial parameters. The experimental results demonstrate that the proposed model has high entropy. Kumar et al. [28] have proposed an algorithm to encrypt images by combining the Henon map with a one-dimensional elementary cellular automaton. The diffusion process uses an elementary cellular automaton, and pseudo-random numbers are generated using the Henon map. The proposed algorithm is resistant to statistical attacks. Babaei et al. [29] have developed a method for encrypting images using DNA, a chaotic map, and recursive cellular automata (RCA). The logistic map is utilized for a cellular shift of the image rows and columns during the permutation phase. The RCA and DNA are then utilized to alter the pixel intensity during the diffusion phase. The proposed algorithm is secure and has good entropy. Ghazanfaripour et al. [30] have presented an approach for encrypting images based on hill diffusion, column-row diffusion, and a 3D scale-invariant modular chaotic map. Column-row diffusion and hill diffusion are used for adjacency pixel mixing in the plain image and pixel substitution. Pixel permutation is done by utilizing 3D scale-invariant chaotic maps. The proposed algorithm has a large key space but takes a long time to execute.

3 Chaotic maps

Chaotic maps are subsets of nonlinear dynamical methods like noise signals but are much more specific [32]. One of the essential things about chaotic maps is that they are very sensitive to initial conditions, which indicates that a slight change in the starting value will significantly affect the output, making them suitable for encrypting images [33, 34]. In this paper, eight chaotic maps have been studied, and their properties have been analysed in order to produce chaotic sequences:

3.1 Logistic map

The following equation has been utilized to define the logistic map:

$$x_{n + 1} = ax_{n} \left( {1 - x_{n} } \right)$$
(1)

where \(x\) is the chaotic sequence in the range [0 1], \(n\) is the iteration number, and \(a\) is the control parameter having values in the range [0 4] [35], while the system is chaotic when \(a\), ϵ [3.5699456, 4] [36].

3.2 Sine map

The sine map has been calculated using the following mathematical definition:

$$x_{n + 1} = asin\left( {\pi x_{n} } \right)$$
(2)

where \(x\) is the chaotic sequence in the range [0 1], \(n\) is the iteration number, and \(a\) is the control parameter with values in the range [0 1] [37], while the system is chaotic when \(a\) ϵ [0.87,1] [38].

3.3 Gauss map

Gauss map is also known as mouse map; the gauss map is mathematically formulated as [39]:

$$x_{{n + 1}} = \left\{ \begin{gathered} 10 \hfill \\ \frac{1}{{\,\bmod \,\left( {x_{n} ,1} \right)}}\,\,\,{\text{Otherwise}} \hfill \\ \end{gathered} \right..$$
(3)

where, \(x\) is the chaotic sequence in the range [0 1], and \(n\) is the iteration number [40].

3.4 Circle map

Circle map is one-dimensional chaotic map, and is mathematically formulated as [41]:

$$X_{i + 1} = \bmod \left( {x_{i} + {\text{b}} - \left( {\frac{{\text{a}}}{2\pi }} \right)\sin \left( {2\pi x_{i} } \right),1} \right)$$
(4)

where \(x\) is the chaotic sequence in the range [0 1], It has two parameters a and b, the power of non—linearity is represented by parameter a, while the externally applied frequency is represented by parameter b [42].

3.5 Tent map

The following mathematical definition gives the equation of the tent map:

$$X_{{n + 1}} = \left\{ {\begin{array}{*{20}c} {rx_{n} ~~~~~~~~~~~~~~~~~~~~~{\text{i}}f~~0 < x_{n} < 0.5} \\ {r\left( {1 - x_{n} } \right)~~~~~~~~~~~~{\text{i}}f~~0.5 \le x_{n} < 1} \\ \end{array} } \right.$$
(5)

where \(x\) is the chaotic sequence in the range [0 1], \(n\) is the number of iterations, and \(r\) is the control parameter with values in the range [0 2], while the system is chaotic when \(r\) ϵ [1.4, 2] [43].

3.6 Chebyshev map

The following formula describes the Chebyshev map:

$$x_{n + 1} = \cos \left( {{\text{acos}}^{ - 1} \left( {x_{n} } \right)} \right.)$$
(6)

where \(x\) is the chaotic sequence in the range [−1 1], \(n\) is the iteration number, and \(a\) is the control parameter with values in the range [0 2], while the system is chaotic when \(a\) ϵ [1 2] [44].

3.7 Singer map

The singer map is mathematically formulated as:

$$x_{n + 1} = \mu \left( {7.86x_{n} - 23.31x_{n}^{2} + 28.75x_{n}^{3} - 13,3x_{n}^{4} } \right)$$
(7)

where \(x\) is the chaotic sequence in the range [0 1], \(n\) is the iteration number, and \(\mu\) is the control parameter with values in the range [0 2], while the system is chaotic when \(\mu\) ϵ [0.9 1.08] [45].

3.8 Piecewise map

The piecewise map is calculated using the following equation:

$$x_{{i + 1}} = \left\{ {\begin{array}{*{20}l} {\frac{{x_{n} }}{a}} \hfill & {if} \hfill & {0 \le x_{n} \le a} \hfill \\ {\frac{{x_{n} - a}}{{0 \cdot 5 - a}}} \hfill & {if} \hfill & {a \le x_{n} < 0.5} \hfill \\ {\frac{{1 - a - x_{n} }}{{0 \cdot 5 - a}}} \hfill & {if} \hfill & {0.5 < x_{n} < 1 - a} \hfill \\ {\frac{{1 - x_{n} }}{a}} \hfill & {if} \hfill & {1 - a \le x_{n} < 1} \hfill \\ \end{array} } \right.$$
(8)

where \(x\) is the chaotic sequence in the range [0 1], \(n\) is the number of iterations, and \(a\) is the control parameter with values in the range [0 2], while the system is chaotic when \(a\) ϵ [1.4, 2] [46]. Figure 2 shows the bifurcation diagram of the chaotic maps, where horizontal axis denotes the parameter r and vertical axis denotes x and each trajectory of the map about x with a fixed x is plotted as dots on the figure.

Fig. 2
figure 2

The bifurcation diagram of a Logistic map, b Sine map, c Gauss map, d Circle map, e Tent map, f Chebyshev map, g Singer map, and h Piecewis map

Full size image

4 Metaheuristics optimizers

Meta-heuristic optimizers are generally used to obtain optimal solutions. In this paper, the chaotic maps’ initial conditions and control parameters are fine-tuned using the following meta-heuristic optimizers:

4.1 Genetic algorithm (GA)

GA belongs to the wider family of evolutionary algorithms (EA). It involves four steps: selection, mutation, crossover, and inheritance [47, 48]. To simulate the evolution process, GA generates several solutions called population [49]. The initial population is represented using the following equation:

$$x = \left\{ {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right\}$$
(9)

GA uses a fitness evaluation function to determine the fitness value of each solution:

$$f\left( {x_{1} } \right),f\left( {x_{2} } \right),f\left( {x_{3} } \right), \ldots \ldots \ldots , f\left( {x_{n} } \right)$$
(10)
$$P_{i} = \frac{{f\left( {x_{i} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{N} f\left( {x_{i} } \right)_{ } }}$$
(11)

where, \(x\) represents the chromosome, n indicates the size of chromosomes population, \(i\) is the number of chromosomes, and \({P}_{i}\) is the selection probability of the ith chromosome. Accordingly, the crossover and mutation operators have been applied to the best solutions to generate a new population. It chooses the best chromosomes to crossover exactly as it does in nature [50]. Random individuals’ random genes are changing using mutation. The mutation is used to avoid local optimum solutions [51].

4.2 Particle swarm optimization

Eberhart and Kennedy proposed PSO at the end of the 20th century based on their research about bird foraging and migration behaviour [52]. Each group member’s unique perception ability allows them to recognize the best local and global individual positions and adjust their next behavior accordingly [53]. Individuals are viewed as particles in a multi-dimensional search space in the algorithm, with each particle representing a potential solution to the optimization problem. The particle characteristics are described using four parameters: velocity, fitness value, and position [54]. The fitness function determines the fitness value. The particle changes its moving direction and distance independently based on the optimal global fitness value and reaches the best solution by iteration [55]. The population of n particles exists in a D-dimensional space represented by the following equations:

$$x = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$$
(12)
$$x_{i} = \left[ {x_{i1} ,x_{i2} , \ldots_{ } ,x_{iM} } \right]$$
(13)

The following equations express the location, velocity and position of the ith particle [56]:

$$X_{i} = \left( {x_{i1}^{ } ,x_{i2}^{ } , \ldots ,x_{{{\text{i}}D}}^{ } } \right)^{ }$$
(14)
$$V_{i} = \left( {v_{i1}^{ } ,v_{i2}^{ } , \ldots ,v_{{{\text{i}}D}}^{ } } \right)^{ }$$
(15)
$$P_{best} = \left( {p_{i1}^{ } ,p_{i2}^{ } , \ldots ,p_{{{\text{i}}D}}^{ } } \right)^{ }$$
(16)
$$g_{best} = \left( {g_{i1}^{ } ,g_{i2}^{ } , \ldots ,g_{iD}^{ } } \right)^{ }$$
(17)

where, \(X_{i}\) is the current location, \(V_{i}\) is the current velocity, \(P_{best}\) is the best local position, and \(g_{best}\) is the best global position. The velocity and position are updated as follows:

$$\nu_{id} \left( {t + 1} \right) = \nu_{id} \left( t \right) + c_{1} \times {\text{Rand}} \times \left[ {Pbest_{id} \left( t \right) - x_{id} \left( t \right)} \right] + c_{2} \times {\text{Rand}} \times \left[ {Gbest_{d} \left( t \right) - x_{id} \left( t \right)} \right]$$
(18)
$$x_{id} \left( {t + 1} \right) = x_{id} \left( t \right) + \nu_{id} \left( {t + 1} \right)$$
(19)

where, \(c_{1}\) represents the cognitive acceleration coefficient, and \(c_{2}\) is the social acceleration coefficients.rticles tend to move towardgood areas in the search space in response to information spreadingthrough the swarm. A particle moves to a new position calculatedby the velocity updated at each time step tby Eq. (3). Equation (4) is then used to calculate the new velocity as the sum of the previou

4.3 Whale optimization algorithm

Mirjalili presented WOA for solving and optimizing problems [57]. This algorithm was inspired by the bubble-net attacking technique used by humpback whales [58]. As a result, the WOA is often used in many fields, such as image encryption, energy, structural optimization, management, and so on [59]. Whales have a unique way of chasing a group of krill or small fish in which they build a nine-shaped net with bubbles that capture the fish, allowing them to easily eat the fish. This technique is known as “spiral bubble-net feeding” [60]. The WOA consists of the following three stages:

  1. (I)

    Encircling prey

Whales use the following formulas to encircle A group of krill or small fish:

$${\vec{\text{D}}} = \left| {\vec{C} \cdot \overrightarrow {{X^{*}_{ } }} \left( t \right) - \vec{X}\left( t \right)} \right|$$
(20)
$$\vec{X}\left( {t + 1} \right) = \overrightarrow {{X^{*}_{ } }} - \vec{A} \cdot \vec{D}$$
(21)
$$A = 2ar - a$$
(22)
$$C = 2r$$
(23)

where \({\vec{\text{X}}}\) represents the position vector, \(\overrightarrow{{{\mathrm{X}}^{*}}}\) represents the position vector of the best solution, t represents the current iteration, A and C represent coefficient vectors, a is reduced linearly from 2 to 0, and r is a random vector in the range of [0, 1].

  1. (II)

    Bubble-net attacking method:

The mathematical model for exploitation phase is as follows:

$$\vec{X}\left( {t + 1} \right) = \vec{D}^{^{\prime}} \cdot {\text{e}}^{bl} \cdot \cos \left( {2\pi L} \right) + \overrightarrow {{X^{*} }} \left( t \right)$$
(24)
$$\vec{D}^{^{\prime}} = \left| {\vec{x}^{*} - \vec{x}\left( t \right)} \right|$$
(25)

where L denotes a random number between − 1 and 1, b denotes a constant that specifies the logarithmic shape and is the distance between the prey and the whale. Assume that the whale will follow a shrinking mechanism or a spiral path, with a 50% chance of each [61]. The following formula is used to represent this:

$$\vec{X}\left( {t + 1} \right) = \left[ {\begin{array}{*{20}c} {\overrightarrow {{X^{{\text{*}}} }} - \vec{A} \cdot \vec{D}} & {\left( {if} \right){\text{~}}P < 0.5} \\ {\vec{D}^{{\text{'}}} \cdot {\text{e}}^{{bl}} \cdot \cos \left( {2\pi L} \right) + \overrightarrow {{X^{{\text{*}}} }} \left( t \right)} & {\left( {if} \right){\text{~}}P \ge 0.5} \\ \end{array} } \right]$$
(26)

where P is a random number in the range [0, 1].

  1. (III)

    Search for prey

The mathematical model for Exploration phase is as follows:

$$\vec{D} = \left| {\vec{C} \cdot \vec{X}_{{{\text{rand}} }} - \vec{X}} \right|$$
(27)
$$\vec{X}\left( {t + 1} \right) = \vec{X}_{{{\text{rand}} }} - \vec{A} \cdot \vec{D}$$
(28)

where \(\vec{X}_{{{\text{rand}} }}\) is position vector selected randomly from the current population.

4.4 Dragonfly algorithm

DA is a randomized search optimizer mimicking a dragonfly swarm’s flying movement [62, 63]. Dragonfly swarms follow the following rules: separation, alignment, cohesion, attraction, and deflection [64, 65]:

  1. (I)

    Separation (S) The swarms are separated from other individuals in this step, avoiding clashes with neighbours [65]. Separation is calculated using the following equation:

    $$s_{i} = - \mathop \sum \limits_{j = 1}^{N} X - X_{j}$$
    (29)

Where X represents the current individual’s position, \({X}_{j}\) represents the position of j-th neighbouring, and N represents the number of neighbouring individuals.

  1. (II)

    Alignment (A) This phase describes the process of a dragonfly’s speed adjusting to the speed vectors of other nearby dragonflies in the swarm [66]. This phase is expressed using the following equation:

    $$A_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} v_{j} }}{N}$$
    (30)

    Where \(v_{j}\) is the velocity of the close individual (j).

  1. (III)

    Cohesion (C) This phase refers to the swarm’s attraction to the centre of the swarm’s team [67]. The cohesion is calculated using the following equation:

    $$c_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} X_{j} }}{N} - X$$
    (31)

    Where \(X_{j}\) denotes the location of the jth close individual, and \(X\) denotes the location of the current individual.

  1. (IV)

    Attraction This phase shows the attraction of swarms toward the food origin [68]. The attraction is calculated using the following equation:

    $$F_{i} = X^{ + } - X$$
    (32)

Where, \(x^{ + }\) denotes the position of the food source, and X denotes the current individual’s location.

  1. (V)

    Distraction In this phase, the dragonfly is diverted from the enemy [69]. The distraction is computed using the following equation:

$$E_{i} = X^{ - } + X$$
(33)

Where, \(X^{ - }\) denotes the location of the enemy, and X denotes the current individual’s location. To locate the best solution to a specified optimization problem, DA assigns a step vector and a position vector to every search agent in the swarm [71]. The step vector is calculated using the following equation:

$$\Delta X_{t + 1} = \left( {sS_{i} + aA_{i} + cC_{i} + fF_{{i^{ + e} }} E_{i} } \right) + \omega \Delta X_{t}$$
(34)

The position vector is updated using the following equation:

$$X_{t + 1} = X_{t} + \Delta X_{t + 1}$$
(35)

where \(s,a, c, f, and e\) denote the weighting factors for separation, alignment, cohesion, attraction, and distraction, and t denotes the current iteration.

4.5 Grey wolf optimization

GWO is an algorithm inspired by swarm intelligence [72], and it is based on the leadership hierarchy and hunting behaviour of grey wolves in their natural habitat [73]. The leadership hierarchy in the model simulation is divided into four wolf types [74]: alpha (the highest level), beta, delta, and omega (the lowest level). The first level begins with the best solution in alpha and progresses downward in order [75, 76]. The steps of GWO are as follows:

  1. (I)

    Encircling prey The following equations are used to represent the encircling process [76]:

$${\vec{\text{D}}} = \left| {{\vec{\text{C}}} \cdot \overrightarrow {{{\text{X}}_{{\text{P}}} }} \left( {\text{t}} \right) - {\vec{\text{X}}}\left( {\text{t}} \right)} \right|.$$
(36)
$$\vec{X}\left( {t + 1} \right) = \overrightarrow {{X_{P} }} - \vec{A} \cdot \vec{D}$$
(37)

where \(\vec{A}\) denotes random vectors, \(X_{P}\) denotes the prey’s position vector, t denotes the current iteration, victor \(\vec{C}\) has random range of [0 2], and \(\vec{X}\) denotes grey wolf’s position vector. The vectors of coefficients \(\vec{A}\) and \(\vec{C}\) are obtained with the following equations:

$$\vec{A} = 2\vec{a} \cdot \overrightarrow {{r_{1} }}$$
(38)
$$\vec{C} = 2 \cdot \overrightarrow {{r_{2} }}$$
(39)
  1. (II)

    Hunting is a behavior driven by alpha, while beta and delta might occasionally play a role [77]. The following formulas demonstrate hunting behavior:

    $$\overrightarrow {{D_{\alpha } }} = \left| {\overrightarrow {{C_{1} }} \cdot \vec{X}_{\alpha } - \vec{X}} \right|$$
    (40)
    $$\vec{D}_{\beta } = \left| {\overrightarrow {{C_{2} }} \cdot \vec{X}_{B} - \vec{X}} \right|$$
    (41)
    $$\vec{D}_{\delta } = \left| {\vec{C}_{3} \cdot \vec{X}_{\delta } - \vec{X}} \right|$$
    (42)
    $$\vec{X}_{1} = \vec{X}_{\alpha } - \vec{A}_{1} \cdot \left( {\vec{D}_{\alpha } } \right)$$
    (43)
    $$\vec{X}_{2} = \vec{X}_{\beta } - \vec{A}_{2} \cdot \left( {\vec{D}_{\beta } } \right)$$
    (44)
    $$\vec{X}_{3} = \vec{X}_{\delta } - \vec{A}_{3} \cdot \left( {\vec{D}_{\delta } } \right)$$
    (45)
    $$\vec{X}\left( {t + 1} \right) = \frac{{\vec{X}_{1} + \vec{X}_{2} + \vec{X}_{3} }}{3}$$
    (46)

    Where \(\vec{X}_{\alpha } ,{ }\vec{X}_{\beta } ,{ }\&\, \vec{X}_{\delta }\) denote the first three best solutions at iteration \(t\).

  1. (III)

    Attacking Prey When the prey stops moving, the hunting process ends, the wolves attack, and the values of \(\overrightarrow{a}\) and \(\overrightarrow{A}\) are decreased mathematically [78].

  2. (IV)

    Search for prey The search phase mainly uses the α, β, and δ positions. Grey wolves look for prey individually before banding together to attack it. To model divergence mathematically [79], the \(\overrightarrow{A}\) is a random value in which if \(\overrightarrow{A}\) > 1, the wolves will diverge, and if \(\overrightarrow{A}\) < 1, the wolves will converge [80].

4.6 Moth-flame optimization

MFO is an algorithm inspired by swarm intelligence [82]. Moreover, it is based on the moths’ transverse orientation navigation method [83]. In MFO, individuals are called moths (M), a population is a group of moths, and the best solution for each moth is called flame (F) [84]. Only one flame for each moth is considered the best solution. This flame will be updated if a better solution arises during the iterations [85]. Moths and flames are generally represented as n * d matrices, where m denotes the number of moths and d denotes the number of dimensions [86]. Following is the moth population matrix:

$${\text{M }} = \left[ {\begin{array}{*{20}c} {m_{1,1} } & {m_{1,2} } & \cdots & {m_{1,d} } \\ {m_{2,1} } & {m_{2,2} } & \cdots & {m_{2,d} } \\ \vdots & \vdots & \ddots & \vdots \\ {m_{n,1} } & {m_{n,2} } & \cdots & {m_{n,d} } \\ \end{array} } \right]$$
(47)

where N denotes the moth population, \({m}_{1}, {m}_{2}, \cdots ,{m}_{n}\) denotes n moths. The moth’s fitness is calculated once per iteration and saved in a vector called (OM) [87]. Following is the moth’s fitness vector:

$${\text{OM }} = \left[ {\begin{array}{*{20}c} {OM_{1} } \\ {OM_{2} } \\ {OM_{3} } \\ {OM_{N} } \\ \end{array} } \right]$$
(48)

The following is the flame matrix (F) and its fitness vector (OF):

$${\text{F }} = \left[ {\begin{array}{*{20}c} {f_{1,1} } & {f_{1,2} } & \cdots & {f_{1,d} } \\ {f_{2,1} } & {f_{2,2} } & \cdots & {f_{2,d} } \\ \vdots & \vdots & \ddots & \vdots \\ {f_{n,1} } & {f_{n,2} } & \cdots & {f_{n,d} } \\ \end{array} } \right].$$
(49)
$${\text{OF }} = \left[ {\begin{array}{*{20}c} {Of_{1} } \\ {Of_{2} } \\ {Of_{3} } \\ {Of_{n} } \\ \end{array} } \right]$$
(50)

where F denotes flame set, \(f_{1} , f_{2} , \cdots ,f_{n}\) denotes n flames. MFO algorithm is composed of the 4 phases listed below [88]:

In the first phase, the moth’s location is updated. The equation to find the best optimal value is given as:

$$M_{i} = S\left( {M_{i} ,F_{j} } \right)$$
(51)

where \(M_{i}\) denotes the ith moth, Fj denotes the jth Flame, and \(S\) denotes the moth’s spiral function.

In the second phase, the moth’s spiral function is calculated using the following equations:

$$S\left( {M_{i} ,F_{j} } \right) = D_{i} *{\text{e}}^{bt} *\cos \left( {2\pi t} \right) + F_{j}$$
(52)
$$D_{i} = \left| {F_{j} - M_{i} } \right|$$
(53)

where \({D}_{i}\) denotes the distance from the ith moth to the jth Flame, t denotes a random value between − 1 and 1, and b denotes the spiral shape factor.

In the third phase, the number of flames is updated using the attenuation function [89, 90]. The attenuation function is defined using the following equation:

$$Nf = round\left( {N - R*\frac{N - 1}{T}} \right)$$
(54)

where R denotes the current number of iterations, T denotes the maximum iterations number, and N denotes the maximum flame number.

In the fourth phase, the best moth is obtained if the termination criterion is met. [91].

4.7 Sine cosine algorithm

SCA is a population-based optimizer that starts with a randomly generated population [92, 93]. The location of solutions is updated using sine and cosine equations [94]. The optimization process uses the exploration phase to find the most desirable location in the search area and the exploitation phase to find the best solution in the proposed region [95]. SCA is expressed as follows:

$$x_{i}^{t + 1} = x_{i}^{t} + r_{1} *\left( {\sin \left( {r_{2} } \right)} \right)*\left| {r_{3} P_{i}^{t} - x_{i}^{t} } \right|$$
(55)
$$x_{i}^{t + 1} = x_{i}^{t} + r_{1} *\left( {\cos \left( {r_{2} } \right)} \right)*\left| {r_{3} P_{i}^{t} - x_{i}^{t} } \right|$$
(56)

where \(x_{i}^{t}\) denotes the current solution’s position, \(r_{1}\) denotes a control parameter responsible for achieving the balance between exploitation and exploration, \(r_{2}\), and \(r_{3}\) denote random values, and \(P_{i}^{t}\) denotes the target solution. The two SCA equatns are combined into a single Equation:

$$x_{i}^{t} = \left[ {\begin{array}{*{20}c} {x_{i}^{t + 1} = x_{i}^{t} + r_{1} *\left( {\sin \left( {r_{2} } \right)} \right)*\left| {r_{3} P_{i}^{t} - x_{i}^{t} } \right|} & {\left( {{\text{i}}f} \right) r_{4} < 0.5} \\ {x_{{\text{i}}}^{{t^{ + 1} }} = x_{i}^{t} + r_{1} *\left( {\cos \left( {r_{2} } \right)} \right)*\left| {r_{3} P_{i}^{t} - x_{i}^{t} } \right|} & {\left( {{\text{i}}f} \right) r_{4} \ge 0.5} \\ \end{array} } \right].$$
(57)

r1, r2, r3, and r4 are updated using the following equations:

$$r_{1} = a - t\frac{a}{T}$$
(58)
$$r_{2} = 2*\pi *{\text{rand}}\left( \right)$$
(59)
$$r_{3} = 2*{\text{rand}}\left( \right)$$
(60)
$$r_{4} = {\text{rand}}\left( \right)$$
(61)

where \(a\) denotes a constant, \(T\) denotes the maximum number of iterations, \({r}_{2}\) denotes the next solution’s movement direction, \({r}_{3}\) is utilized to identify a random weight for the destination, and \({r}_{4}\) is utilized to toggle between sine and cosine functions [96].

4.8 Multi verse optimization

MVO is a population-based optimizer inspired by the big bang theory and the multi-verse theory [97], which starts with a randomly generated population [98]. MVO algorithm comprises three main principles: White hole, Black hole, and Wormhole [99, 100]. The search space is explored by white holes and black holes, while the search space is exploited by warm holes [101]. Individual development for each population can be conducted using one of the theories concerning the existence of multiple universes [102]. For each iteration, every solution is referred to as a “universe” [103]. The universes are sorted depending on the inflation rates, and one of them is picked to have a white hole using the roulette wheel [104]. MVO is expressed mathematically as follows:

$${\text{U }} = \left[ {\begin{array}{*{20}c} {x_{1}^{1} } & {x_{1}^{2} } & \cdots & {x_{1}^{d} } \\ {x_{2}^{1} } & {x_{2}^{2} } & \cdots & {x_{2}^{d} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{n}^{1} } & {x_{n}^{2} } & \cdots & {x_{n}^{d} } \\ \end{array} } \right]$$
(62)
$$X_{i}^{J} = \left\{ {\begin{array}{*{20}c} {X_{k}^{J} , r_{1} < NI\left( {U_{i} } \right)} \\ {X_{i}^{J} , r_{1} \ge NI\left( {U_{i} } \right)} \\ \end{array} } \right\}$$
(63)

where d denotes the number of the parameters, n denotes the universe’s number, \({X}_{i}^{J}\) denotes the jth parameter of the ith universe, \({X}_{k}^{J}\) denotes the jth parameter of the kth universe, r1 denotes a random value with range [0 1], and \(NI\left({U}_{i}\right)\) denotes the ith universe’s normalized swell rate. An additional operation used to create local modifications for each universe is outlined below [105]:

$$X_{i}^{J} = \left\{ {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\left( {x_{j} + TDR^{ } *\left( {ub - lb} \right)*^{ } r_{4} + lb} \right),r_{3} < 0.5} \\ {\left( {x_{j} - TDR^{ } *\left( {ub - lb} \right)*^{ } r_{4} + lb} \right),r_{3} \ge 0.5} \\ \end{array} } \right\}, r_{2} < WEP } \\ {X_{i}^{J} , r_{2} \ge WEP^{ } } \\ \end{array} } \right\}.$$
(64)

where \(x_{j}\) denotes the jth parameter of the best universe, \(ub\) denotes the upper limit, \(lb\) denotes the lower limit, TDR denotes travelling distance rate, WEP denotes wormhole existence probability, and r2, r3, and r4 denote random number with range [0 1]. The wormhole existence probability and the Travelling distance rate are calculated using the following equations [106]:

$$WEP_{ } = WEP_{\min } + t*\left( {\frac{{WEP_{max} - WEP_{min} }}{{t_{max} }}} \right)$$
(65)
$$\left( {TDR} \right) = 1 - \left( {\frac{t}{{t_{max} }}} \right)^{1/n}$$
(66)

where \(WEP_{max} \& WEP_{min}\) denotes two constantans in which (\(WEP_{max} = 1\, \& \, WEP_{min} = 0.1)\), t denotes iteration, \(t_{max}\) denotes the maximum iterations number, and \(1/n\) denotes exploitation accuracy constant.

4.9 Ant-lion optimization

ALO is inspired by nature and relies on ant lion hunting mechanisms [107]. It simulates the intelligent behaviour of ant lions through the life cycle of larvae [108]. In the ALO, the roulette wheel and random walks of ants are used to eliminate local optima [109]. The ALO algorithm is divided into six stages, which are as follows [110]:

  1. (I)

    Random walk of prey

Ants (prey) are supposed to walk randomly [111], The following cumulative sum equation represents the random walk:

$$x\left( t \right) = \left[ {0,Cumsum\left( {2r\left( {t_{i} } \right)} \right) - 1, \ldots ,Cum\sin \left( {2r\left( T \right)} \right) - 1} \right]$$
(67)

where \(Cumsum\) denotes the sum, \(t_{i}\) denotes random walk step at the i-th iteration, \(T\) denotes the total number of iterations, and \(r\left( t \right)\) denotes a random function, which is represented in the following equation:

$$r\left( t \right) = \left\{ {\begin{array}{*{20}c} {1,{ }rand\left( {0,1} \right) > 0.5} \\ {0,{ }rand\left( {0,1} \right) \le 0.5} \\ \end{array} } \right.$$
(68)

A normalization of position in search space is described using Eq. (69):

$$X_{j}^{t} = \frac{{\left( {X_{j}^{t} - a_{j} } \right) \times \left( {d_{j}^{t} - c_{J}^{t} } \right)}}{{b_{j} - a_{j} }} + c_{j}$$
(69)

where, \(X_{j}^{t}\) denotes the position of j-th variable at iteration t, \(a_{j}\) and \(b_{j}\) denote the minimum and maximum of random walk in the j-th variable, and \(c_{J}^{t}\) and \(d_{j}^{t}\) denote the minimum and maximum of the j-th variable at iteration t.

  1. (II)

    Building traps

Antlion traps affect the random walk ants [112], as shown by the following equations:

$$c_{j}^{t} = Antlion_{j}^{t} + c^{t} ,$$
(70)
$$d_{j}^{t} = Antlion_{j}^{t} + d^{t}$$
(71)

where \(Antlion_{j}^{t}\) represents the j-th position of the antlion at the iteration t.

  1. (III)

    Setting trap

ALO selects antlions based on their fitness value using a roulette wheel to mimic the antlions’ hunting process [113].

  1. (IV)

    Sliding of prey in a trap

Once the ants drop into the trap, the antlion tosses sand into the pit’s centre [114]. As a result, the following equations denote the ant’s movement:

$$c^{t} = \frac{{c^{t} }}{I},$$
(72)
$${\text{d}}^{t} = \frac{{{\text{d}}^{t} }}{I}$$
(73)

where \(I\) denotes a factor based on the ratio of a current iteration to the number of total iterations.

  1. (V)

    Catching a prey/rebuilding a trap

The following equation defines the final prey capture and repositioning of ant lions.

$$Antlion_{j}^{t} = Ant{ }_{j}^{t} \,\,\,if{ }\left( {Ant_{i}^{t} } \right) > f\left( {Antlion_{j}^{t} } \right)$$
(74)

where \(Ant_{i}^{t}\) denotes the ant’s position at the t-th iteration.

  1. (VI)

    Elitism rule

The ant’s position is updated based on the roulette wheel’s average and the elite antlion’s movement [115, 116], which is expressed using the following equation:

$$Ant_{i}^{t} = \frac{{\left( {R_{A}^{t} } \right) + \left( {R_{E}^{t} } \right)}}{2}$$
(75)

where \(R_{A}^{t}\) represents the random walk taken by an ant across antlion picked during the process of the roulette wheel selection, and \(R_{E}^{t}\) represents the random walk of the same ant across the elite antlion at the t-th iteration.

5 Proposed algorithm

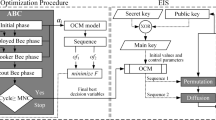
Encryption-based chaotic maps are extremely sensitive to initial conditions and control parameters; therefore, the generated sequence will not be chaotic if these parameters are not chosen precisely. The attacker could break the secret key and read the data. Manually picking these seed values takes a long time and is very tedious. As a result, metaheuristic optimizers are used to optimize these parameters. In this algorithm, we compare the performance of different metaheuristic optimizers to tune the control parameters of eight different chaotic maps.

  • First: Meta heuristic optimizing

Meta-heuristic optimizers are used to fine-tune the chaotic maps’ initial conditions and control parameters. In this paper, we compare the performance of nine different meta-heuristic optimizers. The basic steps of optimization are summarized as follows:

  • Step 1 Produce the initial population of individuals.

  • Step 2 Set the objective function, the chaotic map function, whose initial condition and control parameters will be tuned.

  • Step 3 Assessing every individual in the population using the objective function.

  • Step 4 A new population is formed by altering existing population solutions using evolutionary processes.

  • Step 5 The search parameter is updated continuously until it reaches the terminating criteria regarding the number of iterations.

  • Step 6 The algorithm will look for the best solution that meets the objective function at each iteration.

  • Step 7 The obtained solution is used as the chaotic map’s initial condition and control parameter.

  • Second: Chaotic level Confusion:

The original image’s pixels are permuted to decrease the correlation among neighbouring pixels. The basic steps of confusion are summarized as follows:

  • Step 1 Input the original image (I) with dimensions M*N, where M is the row size, and N is the column size.

  • Step 2 Convert the original image (I) to a 1*MN-dimensional vector (V).

  • Step 3 The tuned initial condition and control parameters are used to generate the chaotic sequence vector \(\left( x \right)\).

  • Step 4 The elements of the chaotic sequence vector are sorted using the following equation:

$$\left[ {so,{\text{i}}n} \right] = {\text{sort}}\left( x \right)$$
(76)

where \(so\) is the newly sorted chaotic sequence vector, and \({\text{i}}n\) is the index of the sorted vector.

  • Step 5

    se the following equation to scramble the position of the original image vector (V):

$$V_{2} \left( {\text{i}} \right) = V\left( {in\left( i \right)^{ } } \right)$$
(77)

Figure 3 shows a simple illustration of the chaotic level permutation process. Fig. 4.

  • Third diffusion level

Fig. 3
figure 3

Chaotic level Permutation process

Full size image
Fig. 4
figure 4

Block Diagram of the Encryption Process

Full size image

The key image is used at this level to diffuse the permuted image. Following is a summary of the fundamental steps of the diffusion level:

  • Step 1 In order to obtain the diffusion vector (D), the following equation is iterated M*N times:

$$D\left( {t + 1} \right) = \cos \left( {p\cos^{ - 1} \left( {D\left( t \right)} \right)} \right.$$
(78)

  • Step 2: The 1*MN diffusion vector (D) is multiplied by 255, rounded off, and the absolute value (k) is calculated as follows:

    $$k = abs(round\left( {D{*}255} \right)$$
    (79)

  • Step 3 The obtained vector is converted from decimal to binary using the de2bin function, and then the bits are shifted using a one-bit circular shifting process.

  • Step 4 The shifted vector is converted from binary to decimal (R), and the obtained vector is combined with victor (k) using the exclusive OR operation to generate a key stream.

  • Step 5 The generated key stream is XORed with the permuted image to generate the encrypted image. Fig. 4 shows the block diagram of the proposed encrypting scheme. Algorithm 1 presents the pseudo-code for the Grey Wolf Optimization Algorithm with the Logistic Map. It illustrates one of the approaches used in our study to fine-tune the control parameters of chaotic maps for image encryption. It is important to note that similar procedures were applied to the eight chaotic maps using the nine metaheuristic optimizers. Integrating these optimizers with the respective chaotic maps allowed us to optimize their initial conditions and control parameters, enhancing the overall encryption process. Algorithm 2 represents the pseudo-code for the whole encryption process.

figure a
figure b

6 Results

6.1 Lyapunov exponent

The Lyapunov exponent (LE) provides a numerical measure for assessing the sensitivity of control parameters in chaotic maps. Its mathematical representation is as follows:

$$LE = \mathop {lim}\limits_{n \to \infty } \frac{1}{n}\mathop \sum \limits_{n = 0}^{n - 1} {\text{ln}}\left| {f^{\prime}\left( {x_{i} } \right)} \right|$$
(80)

where \(f^{\prime}\left( {x_{i} } \right)\) represents the derivative function of the function f(x), f(x) represents a 1D chaotic map. The parameter n denotes the number of iterations of the chaotic map. Table 1 shows Lyapunov exponents for optimized chaotic maps using metaheuristic optimizers compared to non-optimized maps. A higher Lyapunov exponent indicates stronger chaotic behaviour. The optimized chaotic maps have significantly higher (LE) values, indicating increased chaos. Notably, the optimized maps have higher (LE) values than the non-optimized ones, demonstrating the effectiveness of optimization in enhancing chaotic behaviour.

Table 1 Lyapunov exponents
Full size table

6.2 Performance metrics

The following performance metrics are used to measure and compare the performance of encryption algorithms based on eight optimized chaotic maps:

6.2.1 Statistical attack analysis

6.2.1.1 Histogram analysis

It represents the frequency of an image’s pixel distribution. The histograms of the primary image are non-uniform. In contrast, the histograms of encrypted images should be uniform to resist statistical attacks. The histograms of plain and encrypted images are shown in Fig. 5. It is noticeable that the histogram distributions of the plain images are unequal. In contrast, the histogram distributions of the encrypted images using encryption algorithms based on the eight chaotic maps are uniform, indicating that each chaotic map resists statistical attacks.

Fig. 5
figure 5figure 5

a Original images, b Original image’s histogram, The histogram of the encrypted images using c Logistic map, d Sine map, e Gauss map, f Circle map, g Tent map, h Chebyshev map, i Singer map, and j Piecewis map

Full size image
6.2.1.2 Entropy analysis

Entropy measures the randomisation of the encrypted image’s pixel intensities. An encryption algorithm with an entropy value of approximately 8 is a robust algorithm. The entropy is calculated using the following formulas:

$$E\left( X \right) = \mathop \sum \limits_{i = 0}^{L - 1} p\left( {x_{i} } \right)\log_{2} \frac{1}{{p\left( {x_{i} } \right)}}$$
(81)

where, \({\text{E}}\left( {\text{X}} \right){ }\) denotes the entropy of the plain image X, \({\text{p}}\left( {{\text{x}}_{{\text{i}}} } \right){ }\) denotes the occurrence probability, and \({\text{L}}\) denotes total number of the tested pixels. The results in Fig. 6 demonstrate that the encrypted images’ entropy is near the optimal value. However, encrypted images using Tent Chaotic map optimized with SCA has the best entropy. Table 2 demonstrates entropy comparison with other recent algorithms. From the previous results, it is concluded that the proposed algorithm provides the highest entropy value and is robust against entropy attacks.

Fig. 6
figure 6

Entropy of different images

Full size image
Table 2 Entropy Comparison with other recent algorithms
Full size table
6.2.1.3 Correlation analysis

The correlation coefficient measures how closely two adjacent pixels in a picture are related. It is a term that describes the degree of similarity between two neighbouring pixels in the vertical, horizontal, and diagonal directions. A robust algorithm for image encryption decreases the correlation among neighbouring pixels in the encrypted image. The following formulas are used to calculate the correlation coefficient:

$$r_{{xy_{ } }} = \frac{{{\text{cov}} \left( {x,y} \right)}}{{\sqrt {D\left( x \right)} \sqrt {D\left( y \right)} }},$$
(82)
$${\text{cov}} \left( {x,y} \right) = \frac{1}{L}\mathop \sum \limits_{i = 1}^{L} \left( {x_{i} - E\left( x \right)} \right)\left( {y_{i} - E\left( y \right)} \right)$$
(83)
$$E\left( x \right) = \frac{1}{L}\mathop \sum \limits_{i = 1}^{L} x_{i} ,$$
(84)
$$E\left( y \right) = \frac{1}{L}\mathop \sum \limits_{i = 1}^{L} y_{i} ,$$
(85)
$$D\left( x \right) = \frac{1}{L}\mathop \sum \limits_{i = 1}^{L} \left( {x_{i} - E\left( x \right)} \right)^{2} ,$$
(86)
$$D\left( x \right) = \frac{1}{L}\mathop \sum \limits_{i = 1}^{L} \left( {y_{i} - E\left( y \right)} \right)^{2} ,$$
(87)

where x denotes the original image, y denotes the cipher image, and L denotes the number of pixels. Figures 7, 8, 9 and 10 illustrate the correlation of neighboring pixels in the three directions for the four images before and after encryption. As per Figs. 7, 8, 9 and 10, the correlation distribution of neighboring pixels in plain images is generally centered along the diagonal, indicating a significant relationship among neighboring pixels. While the correlation of the encrypted images is distributed randomly over the entire area, demonstrating a weak correlation between adjacent pixels. Table 3 displays the numerical results of the correlation among neighbouring pixels of the encrypted images, whereas the results achieved for the encrypted images are close to zero. Table 4 shows the comparison results with other methods. The correlation coefficients of our encryption algorithm are better than the results of the other method. Tables 3 and 4 prove that the proposed algorithm resists correlation attacks.

Fig. 7
figure 7

Shows the correlation for cameraman plain image and the encrypted image

Full size image
Fig. 8
figure 8

Shows the Correlation for Elaine plain image and encrypted image

Full size image
Fig. 9
figure 9

Shows the Correlation for Lena plain image and the encrypted image

Full size image
Fig. 10
figure 10

Shows the Correlation for Peppers plain image and encrypted image

Full size image
Table 3 Shows the correlation of the encryption algorithms using eight optimized chaotic Maps
Full size table
Table 4 Correlation comparison with others
Full size table

6.2.2 Peak signal to noise ratio analysis (PSNR)

PSNR gives the error between the plain image and the decrypted image. The PSNR is computed based on the mean squared error (MSE).

$$MSE = \frac{1}{M*N}\mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{n = 1}^{N} \left| {X\left( {m,n} \right) - X_{d} \left( {m,n} \right)} \right|^{2} ,$$
(88)
$$PSNR = 10*\log_{10} \left[ {\frac{{255^{2} }}{MSE}} \right],$$
(89)

where, \({\text{X}}\left( {{\text{m}},{\text{n}}} \right)\) presents the original image, \({\text{X}}_{{\text{d}}} \left( {{\text{m}},{\text{n}}} \right)\) presents the decrypted image, and M*N presents the size of both images. All of the PSNR values for the images are 99%, meaning that the original and decrypted images are the same, demonstrating that the proposed model is robust.

6.2.3 Robust analysis

The encryption scheme’s robustness indicates recovering valuable data even when noise disturbs the encrypted image or some data is lost during transmission. In the tests, some noise and different data loss amounts are added.

6.2.3.1 Noise attack analysis

Salt and Pepper, Gaussian, Poisson, and Speckle noise have been added to the encrypted images of Cameraman, Elaine, Lenna, and peppers. Figures 11(a–d) show the encrypted images with the Salt and Pepper intensity of 0.05, the Gaussian noise variance of 0.01, the Poisson, and the Speckle noise, respectively. Figures 11(e–h) show the corresponding decrypted images. From Fig. 11, it can be seen that the decrypted images are clearly visible, which indicates that the algorithm is robust against noise attacks. Moreover, Fig. 12 shows a PSNR comparative analysis of the eight chaotic maps with and without optimization. It can be recognized from Figs. 11 and 12 that Gauss chaotic map with Dragonfly optimizer has the best visual recovery and most reasonable PSNR.

Fig. 11
figure 11

Results of Cipher image with a Salt andPepper noise of intensity 0.05. b Gaussian noise of mean 0 and variance 0.01. c Poisson noise. d Speckle noise; Decryption image with e Salt and Pepper of intensity 0.05; Decryption image with f Gaussian noise of mean 0 and variance 0.01. g Poisson noise. h Speckle noise

Full size image
Fig. 12
figure 12figure 12

PSNR of the recovered images comparative analysis- Different Chaotic maps with different optimizers and with no optimizer

Full size image
6.2.3.2 Periodic noise

In order to test the algorithm’s robustness, periodic noise has been added to images. The following steps have been taken to recover the image:

  1. (1)

    Convert the image from the spatial domain to the frequency domain by computing the fast Fourier transform.

  2. (2)

    Find the periodic noise spikes in the frequency image and block them.

  3. (3)

    Convert the image back to the spatial domain using the inverse Fourier transform.

Figure 13 demonstrates that despite adding periodic noise, the essential details of the original image can still be retrieved. Figure 14 shows that the decrypted images’ PSNRs are high, demonstrating that the proposed algorithm strongly resists periodic noise attacks.

Fig. 13
figure 13

Results of Periodic noise attack on images “cameraman,” “Elaine,” “Lenna,” and “Peppers”: (a–d) Ciphertext images. (e–h) Decrypted images

Full size image
Fig. 14
figure 14

PSNRs of the Periodic noise decrypted images and the corresponding plain image

Full size image
6.2.3.3 Cropping attack

Different degrees of cropping attack tests have been applied to the encrypted images. The cipher images are cropped by 2.25, 12.5, 25, and 50%, respectively, and then decrypted. Figure 16 shows that the decrypted image obtained from the non-optimized Singer chaotic map reveals a partial loss of information, highlighting the importance of chaotic map optimization in achieving a robust image encryption algorithm, where optimization plays a crucial role in preserving the integrity of the encrypted data during decryption. Moreover, Fig. 17 shows the PSNR between the original and recovered images Even though the Singer Chaotic map has the highest PSNR, cropped cipher images can only be reconstructed with optimization, and part of the data is lost, as shown in Figs. 15, 16, and 17. The Gauss chaotic map gives a good PSNR, and the primary information of the plain images can be recovered. It can be concluded that the Gauss Chaotic map has the best numerical and visual results compared to the other chaotic maps, and the Dragonfly algorithm is the best optimizer in terms of robust analysis.

Fig. 15
figure 15

Results of cropping attacks on cipher image using Gauss chaotic map optimized by dragonfly with: a 6.25% cropped. b 12.5% cropped. c 25% cropped. d 50% cropped; Decryption image with e 6.25% cropped. f 12.5% cropped. g 25% cropped. h 50% cropped

Full size image
Fig. 16
figure 16

Results of cropping attacks on cipher image using Singer chaotic map without optimization with: a 6.25% cropped. b 12.5% cropped. c 25% cropped. d 50% cropped; Decryption image with e 6.25% cropped. f 12.5% cropped. g 25% cropped. h 50% cropped

Full size image
Fig. 17
figure 17figure 17

Comparative analysis of PSNRs of the decrypted images after applying different percentages of cropping attack to the encrypted -Different Chaotic maps with different optimizers and with no optimizer

Full size image
6.2.3.4 Cropping attack with noise

In this test, a 25% cropping attack with noise has been added to cipher images. It can be shown from Fig. 18 that the decrypted images using the optimized chaotic map successfully reconstructed the original content (Fig. 19), whereas Fig. 20, representing the non-optimized chaotic map, failed to reconstruct the decrypted images. This emphasizes the significance of optimization in achieving robust image encryption. Figure 20 shows the PSNR between the original image and the reconstructed images that match it. Based on these results, it can be declared that the Gauss Chaotic Map encryption algorithm is robust against noise attacks.

Fig. 18
figure 18

Results of 25% cropping attacks on cipher image using Gauss chaotic map optimized by dragonfly with a Salt andPepper noise of intensity 0.05. b Gaussian noise of mean 0 and variance 0.01. c Poisson noise. d Speckle noise; Decryption image with e Salt and Pepper of intensity 0.05; Decryption image with f Gaussian noise of mean 0 and variance 0.01. g Poisson noise. h Speckle noise

Full size image
Fig. 19
figure 19

Results of 25% cropping attacks on cipher image using Singer chaotic map without optimization with a Salt andPepper noise of intensity 0.05. b Gaussian noise of mean 0 and variance 0.01. c Poisson noise. d Speckle noise; Decryption image with e Salt and Pepper of intensity 0.05; Decryption image with f Gaussian noise of mean 0 and variance 0.01. g Poisson noise. h Speckle noise

Full size image
Fig. 20
figure 20figure 20

Comparative analysis of PSNRs of the decrypted images after applying noise and cropping attack to the encrypted -Different Chaotic maps with different optimizers and with no optimizer

Full size image

6.2.4 Key analysis

6.2.4.1 Key space analysis

The analysis of the key space refers to the collection of all possible encryption keys. A robust encryption algorithm must be sensitive to secret keys and have enough space to withstand any brute-force attack. The proposed algorithm uses the chaotic map parameters, initial conditions, and the parameters of the diffusion equation as keys. The key space of the proposed algorithm for the different types of chaotic maps with a computation precision of \(({10}^{-16})\) is shown in Table 5, which demonstrates that the key space of the proposed encryption algorithm is sufficiently large to resist brute-force attacks, with the Circle Chaotic map having the most robust key space. Table 6 compares the key spaces of different encryption techniques. The proposed algorithm has a large key space and is resistant to brute-force attacks, as seen in Table 6.

Table 5 Key Space of each Chaotic Map
Full size table
Table 6 Comparisons of the image encryption algorithms key space
Full size table
6.2.4.2 Key sensitivity analysis

Key sensitivity examines the sensitivity of a cipher image to a very slight change in the secret key. Figure 21a indicates decryption with the correct key x = 0.777; the encrypted image is identical to the original image; then the ciphered image is decrypted using one bit changed key x = 0.7770000000000000001. as shown in Fig. 21b, shows that the cipher image could not be decrypted then the ciphered image is decrypted using a one-bit changed key x = 0.7770000000000000001. As shown in Fig. 21b, the cipher image could not be decrypted. Consequently, the proposed algorithm is highly sensitive to secret keys.

Fig. 21
figure 21

Decrypting Lena image using the a correct key and b wrong key

Full size image

6.2.5 Differential analysis

6.2.5.1 Number of pixel change rate

It is the proportion of changed pixel numbers between two encrypted images with a one-pixel change in the original image. The following are the formulas used to compute the NPCR:

$$NPCR = \mathop \sum \limits_{i = 1}^{M} \mathop \sum \limits_{j = 1}^{N} \frac{{D\left( {i,j} \right)}}{M*N}*100\%$$
(90)
$$D\left( {{\text{i}},j} \right) = \left\{ {\begin{array}{*{20}c} {0, otherwise} \\ {1, if\,\, Y_{1} \left( {i,j} \right) = Y_{2} \left( {i,j} \right) } \\ \end{array} } \right.$$
(91)

where \(Y_{1} \left( {i,j} \right) \& Y_{2} \left( {i,j} \right)\) denote two encrypted images corresponding to the same original image differing only in one bit, and M*N is the size of the images.

6.2.5.2 Unified average changing intensity

It calculates the average difference in intensity between two ciphered images, which corresponds to a change of one pixel in the original image. The following equation is utilized to calculate the UACI:

$$UACI = \frac{1}{M \times N}\left[ {\mathop \sum \limits_{i = 1}^{M} \mathop \sum \limits_{j = 1}^{N} \frac{{Y_{1} \left( {i,j} \right) - Y_{2} \left( {i,j} \right)}}{255}} \right] \times 100\%$$
(92)

where \({Y}_{1}\left(i,j\right) and {Y}_{2}\left(i,j\right)\) denote two ciphered images corresponding to the same plain image, differing only by one bit, and M*N is the size of the images. Table 7 shows the results of UACI and NPCR for encryption algorithms using the eight optimized chaotic maps. As seen from Table 4, all results of UACI and NPCR are closer to theoretical values except when using all the chaotic maps without optimization, giving the lowest UACI and NPCR. From the previous results, the optimized eight chaotic maps demonstrate effective resistance to differential attacks. Tables 7 and 8 compare UACI and NPCR with other encryption algorithms, which indicates that the proposed algorithm has the highest sensitivity and is competitive with other proposed encryption methods (Table 9).

Table 7 UACI and NPCR comparison
Full size table
Table 8 Comparisons of the image NPCR of encrypted image
Full size table
Table 9 Comparisons of the image UACI of encrypted image
Full size table

6.2.6 Computational speed analysis

It is the time required to execute the algorithm, measured in seconds or milliseconds. Figure 22 compares the time of execution for the eight optimized chaotic maps. It can be observed that the chaotic tent map has a relatively higher computational time than the other chaotic maps. The results regarding computational time for all images demonstrate that the gauss chaotic map has the lowest computational time compared to the other chaotic maps and that using the chaotic maps without optimization has the highest computational time. The proposed algorithm provides the fastest encryption speed, as shown in Table 10.

Fig. 22
figure 22

Encryption time/ decryption time (sec) of the proposed algorithm

Full size image
Table 10 Comparisons of time complexity of encrypted and decryption process
Full size table

7 Conclusion

This paper aims to propose an image encryption scheme using optimized chaotic maps. Eight chaotic maps (logistics, sine, gauss, circle, tent, Chebyshev, singer, and piecewise map) are optimized using various metaheuristic optimizers. The encryption process involves chaotic confusion and pixel diffusion. Performance metrics such as entropy, histogram, cross-correlation, computation time, NPCR, UACI, noise attack, data loss, and key analysis are employed to evaluate the proposed scheme. The evaluation of the proposed encryption scheme yielded significant findings. The correlation coefficient values of encrypted images are nearly zero, indicating high security. The histogram analysis reveals uniform distributions, preventing information leakage. The execution time for encryption is recorded as 0.1556 ms, demonstrating real-time applicability. The key space reaches 10^80, ensuring a large key space for robustness. The NPCR value is measured at 99.63%, and the UACI value is 32.92%, further indicating the effectiveness of the encryption scheme. Moreover, the analysis of noise and cropping attacks confirms the robustness of the proposed scheme. Comparative evaluations against other algorithms support the superior performance of the optimized encryption algorithms.