1 Introduction

As a product of the combination of random algorithm and local search algorithm, the meta-heuristic algorithm proposes new feasible solutions for solving some complex engineering optimization problems. Compared with traditional algorithms, meta-heuristic algorithms search for spaces that may contain high-quality solutions by simulating natural or physical phenomena to give a better “global optimal solution.” When encountering difficult non-convex problems formed by complex engineering problems, the meta-heuristic algorithm is more effective than the gradient algorithm that is common in the past. This is mainly because of several major advantages of meta-heuristic algorithms: 1. The principle is simple and easy to implement; 2. Does not rely on gradient information; 3. It can be combined with different disciplines to solve diversified problems. 4. Able to give a better “global optimal solution.”

In recent years, with the continuous development of meta-heuristic algorithms, it can be divided into the following three categories. The first category is evolution-based algorithms. Evolutionary algorithms can simulate biological evolutionary behavior in nature. The most famous one is the genetic algorithm GA [1] proposed by learning Darwin’s biological evolution theory. In addition, there are genetic programming GP [2] and evolutionary strategy ES [3]. The second category is physics-based algorithms. Commonly used in this type of algorithms are the simulated annealing algorithm for learning natural annealing phenomena in nature [4], and the gravitational search algorithm GSA [5], which is inspired by Newton’s law of universal gravitation. Similar to these algorithms are the Moth–flame optimization algorithm MFO [6], the small world search algorithm WCA [7], the central force algorithm CFO [8] and the hydrological cycle algorithm WCA [9]. The third category is swarm-based algorithms. This type of algorithms is proposed after learning the clusters of biological populations and predation behavior in the natural world. For example, the particle swarm algorithm PSO [10] proposed by J. Kennedy and R. C. Eberhart et al. was inspired by the swarm behavior of birds. After decades of development, it has been widely used in different disciplines and achieved good results. Similar algorithms include gray wolf optimization algorithm GWO [11] inspired by wolf hunting behavior, sparrow search algorithm SSA [12], salvia colony algorithm SSA [13] and ant colony algorithm ACO [14].

Whale Optimization Algorithm (WOA) [15] is a swarm-based intelligent optimization algorithm proposed by Mirjalili et al in 2016. This algorithm simulates the unique bubble net predation behavior of humpback whales. Because of its simple structure and strong search capability, WOA is widely used in power economic dispatching, robot path planning, image segmentation, time series forecasting and other complex optimization problems. For example, Saha et al. [16] applied the improved WOA to the control of switched reluctance motors, and the test results showed that the algorithm has stable performance and reliability. Kong et al. [17] used the improved WOA to solve the complex parameter reduction problem, and the experimental results showed that the improved WOA has excellent performance. Sulaiman et al. [18] used the improved WOA to solve the PEHE multi-objective optimization problem. The experimental results show that this scheme is better than other meta-heuristic algorithms.

At the same time, more in-depth researches and applications have also revealed the shortcomings of WOA itself. Aiming at the problems that WOA’s convergence accuracy and convergence speed are insufficient, Gaganpreet Kaur et al. [19] proposed a way to combine WOA with chaos strategy. The test results show that the convergence speed of WOA has been improved to a certain extent. Coincidentally, Li et al. [20] also used the tent map in the chaotic map to initialize the population of WOA and achieved good results. These research contents not only put forward some improvement directions, but also show the importance of population initialization. In 2019, Hemasian-Etefagh et al. [21] proposed the idea of whale grouping to improve the convergence of WOA. Facts show that when WOA search methods and search capabilities are changed, WOA performance can be significantly improved. For example, Kaveh et al. [22] changed the original formula in WOA and applied it to specific engineering problems. The experimental results show that the performance of the improved WOA has been significantly improved. Along this research direction, more scholars have discovered the connection between the position update formula and population diversity. Ma et al. [23] introduced the inertia weight into the MFO, which effectively enriched the moth population and allowed the algorithm to maintain a higher search efficiency. At the same time, the introduction of inertia weight also effectively strengthens the adaptability of the algorithm itself. Qiu Xingguo et al. [24] used the sobel sequence, inertial weights and nonlinear strategies in the improvement of WOA. This scheme makes the initial population of WOA more abundant, so that the improved algorithm can continue to maintain a good search ability in the later stages of the iteration. At the same time, some scholars have also optimized WOA by introducing new content or combining WOA with other algorithms. Xiao Shuang et al. [25] combined Lévy flight with adaptive weights to increase the convergence speed of WOA, and achieved the best performance in comparison with other optimization schemes. Luo et al. [26] successfully introduced the differential mutation operator into WOA, and the addition of the mutation operator effectively improved the quality and reliability of solutions. Zhang et al. [27] combined WOA with the golden sine algorithm (GoldenSA) [28]. After extensive testing, they found that the golden sine operator can effectively accelerate the convergence speed of the algorithm. In general, these schemes have effectively improved the deficiencies of the algorithm to a certain extent. But in some typical non-convex problems, their performance is still very limited. Especially in some complex engineering problems, they still face the problem of premature convergence. In order to solve this problem effectively, this paper proposes a whale optimization algorithm based on dynamic pinhole imaging and adaptive strategies(DAWOA). The main contributions of this article are as follows:

  • The theory of dynamic pinhole imaging is proposed and used to update the position of search agents. This strategy can adjust the position of the leader adaptively, allowing it to quickly approach the global optimal solution, thereby accelerating the convergence speed of the algorithm.

  • Adaptive inertia weights based on dynamic boundaries and dimensions can adjust the algorithm in a feedback manner. It will adjust itself according to the location information of the individual population, so as to better balance the exploitation and the exploration capabilities of the algorithm.

  • The local mutation strategy can dynamically adjust the shape of the logarithmic spiral according to the number of iterations, thereby changing the search range of the whale population. And, this can make the individual whale search state closer to the real whale.

At present, there are few studies on dynamic pinhole imaging and adaptive strategies in WOA algorithms. This analysis forms the basis of this work. The rest of the paper is structured as follows: Sect. 2 introduces the basic whale optimization algorithm. Section 3 discusses the three strategies proposed. Test problems and numerical results analysis are presented and discussed in Sects. 4 and 5, respectively. Section 6 is a summary of this paper and prospects for future work.

2 Principle and mathematical model of WOA

2.1 Shrink envelope

At this phase, the whale population will approach prey constantly. The number of whale populations is N and the dimension is d. The algorithm assumes that the position of the current optimal individual (search agent) is the global optimal position, and other whale individuals will use this as the target area to update their positions. The mathematical formula for this stage is:

$$\begin{aligned} D = \left| {C\overrightarrow{X} *\left( t \right) - X\left( t \right) } \right| \end{aligned}$$
(1)
$$\begin{aligned} \overrightarrow{X} \left( {t + 1} \right) = \overrightarrow{X} *\left( t \right) - A \cdot \overrightarrow{D}, \end{aligned}$$
(2)

where t is the current iteration number, A and C are coefficients. \(\overrightarrow{X} \mathrm{{*}}(t)\) is the current position vector of the best individual whale, and \(\overrightarrow{X} (t)\) is the position vector of the current whale.The mathematical model of coefficients A and C is as follows:

$$\begin{aligned} \overrightarrow{A} = 2\overrightarrow{a} \cdot \overrightarrow{{r_1}} - \overrightarrow{a} \end{aligned}$$
(3)
$$\begin{aligned} C = 2{r_2} \end{aligned}$$
(4)
$$\begin{aligned} a = 2 - 2t/{T_{\max }}, \end{aligned}$$
(5)

where \({r_1}\) and \({r_2}\) are random numbers in (0, 1), the value of a will linearly decrease from 2 to 0 with the number of iterations. t is the current number of iterations, and \({T_{\max }}\) is the maximum number of iterations.

2.2 Development phase

At this phase, the whale population will attack the prey. During the attack, the whale will continue to spirally update its position. Its mathematical model is as follows:

$$\begin{aligned} \overrightarrow{X} (t + 1) = \overrightarrow{X\mathrm{{*}}} (t) + {D_p}{e^{bl}}\cos (2\pi l) \end{aligned}$$
(6)
$$\begin{aligned} {D_p} = \left| {\overrightarrow{X} *(t) - \overrightarrow{X} (t)} \right| ,\end{aligned}$$
(7)

where \({D_p}\) is the distance between the whale and the prey, \(\overrightarrow{X} \mathrm{{*}}(t)\) is the current position vector of the best individual whale. It is worth noting that b is a constant, used to define the shape of the logarithmic spiral. l is a random number in \((-1,1)\). In this link, the whale must continue to shrink and envelope while spiraling close to the prey. In this process, the whale population will repeat the behavior of the first stage. For this synchronous behavior model, in order to simulate the actual offensive process, assuming that the probability of the whale choosing the spiral update position is the same as the probability of choosing the shrink envelope, that is, \(p = 0.5\). Then, the mathematical formula at this stage can be expressed as:

$$\begin{aligned} \overrightarrow{X} (t + 1) = \left\{ {\begin{array}{*{20}{c}} {\overrightarrow{X} *(t) - A \cdot D}&{}{P < 0.5}\\ {\overrightarrow{X} *(t) + {D_p}{e^{bl}}\cos (2\pi l)}&{}{P \ge 0.5} \end{array}} \right. \end{aligned}$$
(8)

In the development stage, the value of A will change continuously with the change of the value of a. And, the value of a can be any value in [-1,1]. Simply put, the individual whale can be in any position between the current position and the optimal position.

2.3 Search phase

At this stage, the whale population will conduct a large-scale search. The algorithm will randomly select a whale individual as the search agent to change the original predation area of the whale population. In this way, the whale population will conduct a more extensive search. Therefore, we only need to make small changes to Eq(1)(2) to get the mathematical model of this stage:

$$\begin{aligned} D = \left| {C*{{\overrightarrow{X} }_\mathrm{rand}} - \overrightarrow{X} (t)} \right| \end{aligned}$$
(9)
$$\begin{aligned} \overrightarrow{X} (t + 1) = {\overrightarrow{X} _\mathrm{rand}} - A \cdot D, \end{aligned}$$
(10)

where \({\overrightarrow{X} _\mathrm{rand}}\) is the position vector of the randomly selected whale, which will be regarded as a new search agent. At this stage, due to \(\left| A \right| \ge 1\), the whale population will be forced to leave its current location for a more extensive search. It is worth noting that the existence of this stage allows the algorithm to effectively avoid local optima.

3 whale optimization algorithm based on dynamic pinhole imaging and adaptive strategy

This section will give a detailed introduction to the three improvement strategies in the proposed improved algorithm (DAWOA).

3.1 Dynamic pinhole imaging strategy

Generally speaking, the actual operation of an algorithm should be divided into two stages: particle divergence and particle shrinkage. Good population initialization can often bring faster convergence speed and higher convergence accuracy for the algorithm. If most of the population individuals can be initialized near the optimal solution, then in the particle shrinking phase of the algorithm, the population individuals only need a small amount of movement and search to reach the optimal value, which is undoubtedly a very ideal situation. In 2005, Tizhoosh proposed the Opposite-based learning theory [29], which revealed an efficient scheme for initializing the population. If the population individuals produce an opposite individual at the opposite position of the current position, the probability that the two individuals are closer to the optimal solution is 50%. Therefore, only a few operations are required to generate a higher quality population. This can be reminiscent of the theory of pinhole imaging in optics. Compared with ordinary Opposite-based learning, the pinhole imaging theory is more accurate and can produce more diversified points of opposition.

Fig. 1
figure 1

Dynamic pinhole imaging strategy

Full size image

Figure 1 shows a typical theoretical model of pinhole imaging. Applying it to the search space of the population, the following mathematical model can be obtained:

$$\begin{aligned} \frac{{{\mathrm{Xbest}_{i,j}} - (U{b_{i,j}} + L{b_{i,j}})/2}}{{(U{b_{i,j}} + L{b_{i,j}})/2 - {X_{i,j}}}} = \frac{{{L_p}}}{{{L_{ - p}}}}, \end{aligned}$$
(11)

where \({\mathrm{Xbest}_{i,j}}\) is the location of the current best individual (search agent), \({X_{i,j}}\) is the opposite position in the theory of pinhole imaging. \(U{b_{i,j}}\) and \(L{b_{i,j}}\) are the dynamic boundaries of the i-th whale in the j-th dimension, \({L_p}\) and \({L_{ - p}}\) are the length of the virtual candle in the current best position and the opposite position, respectively. It is worth noting that the position of the candle in the figure is also the position of the search agent, but the point representing the individual whale does not have an effective length. Therefore, the ratio of the two candles can be set as a variable K. From this, you can get:

$$\begin{aligned} {X_{i,j}} = \frac{{(K + 1)(U{b_{i,j}} + L{b_{i,j}}) - 2{\mathrm{Xbest}_{i,j}}}}{{2K}} \end{aligned}$$
(12)

It is not difficult to see from Eq.(12) that when two candles have the same length, this strategy evolves into a basic reverse learning strategy. Adjusting the value of K properly can change the position of the opposite point, allowing individual whales to have more search opportunities. In this paper, K is set to \(1.5 \times {10^4}\). In this way, every iteration, a new opposite point will be generated near the center line of the search space. When the opposite point is in a better position, its position will become a new boundary.

3.2 Adaptive strategy

When the algorithm is iterated to the later stage, the diversity of population individuals will decrease sharply. For the search space, the reduction of diversity will cause most of the population individuals to stagnate near the local optimal position. At this time, only a small number of whale populations are continuing to search, and the result is that the algorithm converges prematurely and falls into a local optimum. WOA is a swarm-based algorithm. Compared with an evolution-based algorithm, a swarm-based algorithm does not use a greedy strategy to discard poor values. WOA will retain the information of the previous generation for use in the next iteration. Therefore, an effective balance of algorithm’s development and exploration capabilities is the key to enhancing the algorithm’s search capabilities. To put it simply, introducing the inertia weight into the original WOA formula can effectively balance the local development capabilities and global search capabilities of WOA, thereby enriching the diversity of whale populations. This allows the algorithm to maintain a certain intensity of the search state in the later stages of the iteration, so as to avoid the population from falling into the local optimum. The updated Eqs. (8, 10) is as follows:

$$\begin{aligned} \overrightarrow{X} (t + 1) = \left\{ {\begin{array}{*{20}{c}} {\omega \cdot \overrightarrow{X} *(t) - A \cdot D}&{}{P < 0.5}\\ {\omega \cdot \overrightarrow{X} *(t) + {D_p}{e^{bl}}\cos (2\pi l)}&{}{P \ge 0.5} \end{array}} \right. \end{aligned}$$
(13)
$$\begin{aligned} \overrightarrow{X} (t + 1) = \omega \cdot {\overrightarrow{X} _\mathrm{rand}} - A \cdot D, \end{aligned}$$
(14)

where \(\omega\) is the adaptive inertia weight that can be adjusted with the number of iterations adaptively. The mathematical model is as follows:

$$\begin{aligned} \omega = \frac{{\mathrm{{C}} \times \sqrt{t} }}{M} \times (1 - \frac{t}{{{T_{\max }}}}) \end{aligned}$$
(15)
$$\begin{aligned} M = \sqrt{H + {N^2}} \end{aligned}$$
(16)
$$\begin{aligned} H = \frac{{\sum \nolimits _{j = 1}^N {{{(U{b_{i,j}} - L{b_{i,j}})}^2}} }}{t}, \end{aligned}$$
(17)

where \(C = 0.1\), t is the current iteration number, \({T_{\max }}\) is the maximum number of iterations, and N is the dimension. At the beginning of the iteration, almost only H and \(\sqrt{t}\) play a role. As the number of iterations progresses, when the position of the optimal solution is from farther to nearer, the value of M will decrease, and the value of \(\omega\) will increase at this time. This will allow the population individuals to escape from their current positions and conduct exploration with a larger search radius, thereby effectively enhancing the algorithm’s extensive search capabilities to avoid falling into local optima. When the optimal solution is located farther away, the value of \(\omega\) will decrease relative to the previous iteration. As a result, individual whales will search in the high-quality solution space with a more precise spiral path to strengthen the local development capabilities of the algorithm. At the later stage of the iteration, H will hardly change again, and \(\omega\) at this time will become a steadily decreasing variable. This allows each individual whale to have a stronger search ability and a more diverse location. In fact, the purpose of this strategy is to tap the potential of individual populations and allow each individual whale to improve its own performance to varying degrees. In other words, as long as a small number of enhanced whales jump out of the local optimum successfully, they can lead the optimized population to the global optimum.

3.3 Local mutation strategy

When a population individual finds a space that may contain high-quality solutions, using an effective strategy to approach the target area can not only help the algorithm quickly lock the optimal value, but also fully search this space. The advantage of this is that it can prevent the population individuals from gathering at a point in the space, which will cause the algorithm to stagnate. In Eq. (13), the parameter b can determine the shape of the logarithmic spiral. In other words, b determines the search path of the individual whale near the target area. Under normal circumstances, b is a fixed value, which will lead individual whales to perform local development in a fixed pattern in each iteration. When the better solution keeps a certain distance from the logarithmic spiral search path, these optimal values will lose their attractiveness to the whale population. Therefore, adding an appropriate mutation to b can help the individual whale better discover the global optimal solution that may exist in the surrounding space. This approach is similar to the actual hunting behavior of individual animals in nature.In the process of exploration, they will have a certain probability to deviate from the original path to develop possible prey because of the smell of the prey. The specific mathematical model is as follows:

$$\begin{aligned} b = \left(9 + \mathrm{rand})(1 - \frac{t}{{{T_{\max }}}}\right) \end{aligned}$$
(18)

It is not difficult to see from Eq. (18) and Fig. 2 that as the iteration progresses, the search area will gradually shrink, so the logarithmic spiral will also continue to become smaller. Individuals of the population can perform more careful repeated searches in a limited space. When the iteration progresses to the later stage, the movement of the whale population will becomes very gradual, which can effectively increase the utilization of the current space. The mutation mechanism will give the population individuals more opportunities to explore possible solutions.

Fig. 2
figure 2

Local mutation strategy

Full size image

As a summary, the effective combination of the three strategies can bring the initial population closer to the optimal solution, and the richness and quality of the population will be higher. In the search process, adaptive inertial weights can help the algorithm find a dynamic balance point in exploration and development. The local mutation mechanism can adjust the whale’s search range dynamically. As shown in Fig. 3, the original WOA will increase the possibility of falling into a local optimum due to insufficient population richness and too random initial position (Fig. 3a, b). The improved algorithm has richer population diversity and stronger search ability. The search agent in the current iteration process can also be initialized at a position closer to the optimal value (Fig. 3c, d). In this way, the algorithm can effectively jump out of the local optimal to find a better global optimal solution.

Fig. 3
figure 3

DAWOA’s search process

Full size image

3.4 Analysis of DAWOA’s computational complexity

The time complexity of the algorithm is the time resources consumed by the computer during the actual operation of the algorithm, which is an important reference for the actual performance of the algorithm. As far as DAWOA is concerned, the main factors that determine the time complexity are the total number of iterations (T), population initialization, fitness sorting, three position update formulas, dynamic pinhole imaging strategy, adaptive inertial weighting and local mutation mechanism. Given that the number of populations is n and the dimension is D, then the time complexity for population initialization is \(O(n \times D)\). Since the sorting process must be performed once in each iteration, its time complexity is \(O(T \times {n^2})\). Considering that the adaptive inertia weight and the WOA position update formula change together, the time complexity of the three formulas is \(O(T \times n \times D)\). The dynamic pinhole imaging strategy needs to be compared and updated during each iteration. Therefore, its time complexity is \(O(T \times n \times D)\). The local mutation strategy is equivalent to the successive change of parameter b, so its time complexity is \(O(T \times n \times D)\). If the worst case is considered, the upper limit of the total time complexity of DAWOA is \(O(T \times ({n^2} + n \times d))\).

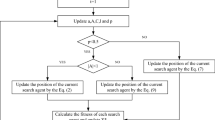
The pseudo-code of DAWOA algorithm is shown in Table 1.

Table 1 Pseudo code of DAWOA
Full size table

4 Simulation experiment and numerical result analysis

20 well-known benchmark functions [30,31,32,33] composed of unimodal functions (F1–F7), multimodal functions (F8–F13) and fixed-dimensional functions (F14–F20) will be used to test the specifics of the improved algorithm Performance, some specific information of these test functions are shown in Table 2. In the test process, DAWOA will be used to compare the numerical results and convergence status with WOA, SSA, the recently proposed optimization algorithms EWOA [34] and MWOA [35].

Table 2 Benchmark function
Full size table

4.1 Simulation test environment and evaluation standards

Simulation test environmentThe test environment for this experiment is as follows: Intel(R) core(TM) i5-6300HQ CPU @2.30 GHz 2.30 GHZ processor, 8G memory. The MATLAB version is MATLAB (2019b). During the test, the population size N is set to 30, and the maximum number of iterations \({T_{\max }}\) is set to 500. In addition to the fixed dimension function, other test functions will be tested in the three dimensions of 10/30/50. Different algorithms will independently perform 30 tests of the same dimension in each test function and record the test results.

Evaluation standardsIn addition to introducing the mean (Mean) and standard deviation (Std) as the test criteria, this test will also introduce the Wilcoxon signed rank test [36] to compare the performance of each algorithm more reliably. Among the above detection standards, the average value test is used to detect the general performance and convergence accuracy of the algorithm; the standard deviation test is used to detect the overall stability of the algorithm. As a common nonparametric paired test, the Wilcoxon signed rank test is a fast and effective detection method. It only needs to provide a small number of samples for reliable numerical analysis. The rules of the inspection method are very simple. In the numerical test results, if the target algorithm is better than the comparison algorithm, it is recorded as \({R_ + }\); otherwise, it is recorded as \({R_ - }\). Generally, speaking, the greater the number of \({R_ + }\), the greater the advantage of the target algorithm. In order to facilitate recording and comparison, in the table, “+” will be used to indicate that the target algorithm is better than the comparison algorithm, “−” is used to indicate that the target algorithm is inferior to the comparison algorithm, and “=” indicates that the two algorithms are in the same degree of superiority and inferiority, and Gm represents the difference between the number of “+” and the number of “−”.

Experimental parameter settingIn the comparative experiment in this chapter, the parameter settings of each algorithm are shown in Table 3.

Table 3 Experimental parameter setting
Full size table

4.2 Unimodal function test and result analysis

Unimodal test functions are mainly complex spherical or valley-shaped numerical problems. They only have a global minimum but are difficult to find. Therefore, it can be used to test the exploitation capabilities of the algorithm. As shown in Tables 4, 5, and 6, among the three dimensions, DAWOA almost occupies a dominant position in all unimodal functions, showing strong competitiveness. For the test functions F1–F4, although the convergence speed of MWOA is faster than DAWOA in every dimension, DAWOA has more obvious advantages in the remaining unimodal functions. For example, the test function F5 (Rosenbrock), which is a typical non-convex function, requires complex numerical calculations to solve it. The global minimum of the Rosenbrock function is located in a narrow parabolic valley. Although this valley is easy to find, it is difficult to converge to the lowest point. As shown in Figs. 4, 5, and 6, the performance of WOA, MWOA, EWOA and SSA in the test function F5 are all unsatisfactory. However, the improved DAWOA can reduce the numerical result to 4 decimal places, which is undoubtedly a big improvement. When the dimensions are 10 and 30, DAWOA’s performance in F6 is second only to SSA. But when the dimension rose to 50, DAWOA recovered its own advantages. As shown in Fig. 4, during the convergence process, there were several cliff-like declines in the curve. This shows that the dynamic pinhole imaging strategy has been trying to adjust the position of the leader to help it quickly approach the optimal area. At the same time, adaptive inertia weights are also helping the population to maintain an efficient search state, thereby accelerating the convergence of the algorithm. The above conclusion fully shows that the local development capability of the algorithm has been significantly improved.

Table 4 Comparison of test results of different algorithms
Full size table
Fig. 4
figure 4

Convergence curve comparison of some unimodal test functions (30 dimensions)

Full size image
Fig. 5
figure 5

Convergence curve comparison of some unimodal test functions (10 dimensions)

Full size image
Fig. 6
figure 6

Convergence curve comparison of some unimodal test functions (50 dimensions)

Full size image

4.3 Multimodal function test and result analysis

Different from the unimodal functions, the multimodal functions have many local optimal values. Moreover, the scale of this type of problem will increase exponentially as the dimensionality increases. Therefore, the multimodal function can effectively test the exploration capabilities of the algorithm. In combination with Tables 4, 5, and 6, it can be seen that DAWOA performs significantly better than WOA, EWOA, MWOA and SSA in multimodal functions. For the test function F8, this is a typical multimodal function with a large number of local optimal values, and its shape is similar to a hill. Compared with WOA, EWOA and SSA, DAWOA’s numerical results in F8 have made a big leap. Although the test result of MWOA is very close to the theoretical value, the convergence accuracy of DAWOA is significantly higher. This is because the addition of adaptive inertial weights increases the diversity of the whale population, allowing population individuals to be evenly distributed in the solution space, thereby effectively avoiding local optima. Figs. 7, 8, and 9 show the convergence curves of several algorithms in functions F8, F11 and F12. In the early iteration of the algorithm, the dynamic aperture imaging strategy is playing an active role. The algorithm quickly approaches the target area, and the convergence curve drops sharply. As the number of iterations progressed, the local mutation strategy began to operate. After a short search, the whale population avoided the many local best points in the solution space and successfully reached the target area. When the dimensionality gradually increases, the complexity of the search space will increase significantly. It is not difficult to see from Table 5 and Table 6 that the increase in dimensions has not affected DAWOA’s dominant position, and the collaborative work of the three strategies has helped it open up a broader search space. The above results fully demonstrate that the improved algorithm has good extensive search capabilities.

Table 5 Comparison of the numerical results of unimodal and multimodal functions (10 dimensions)
Full size table
Table 6 Comparison of the numerical results of unimodal and multimodal functions (50 dimensions)
Full size table
Fig. 7
figure 7

Convergence curve comparison of some multimodal functions (30 dimensions)

Full size image
Fig. 8
figure 8

Convergence curve comparison of some multimodal functions (10 dimensions)

Full size image
Fig. 9
figure 9

Convergence curve comparison of some multimodal functions (50 dimensions)

Full size image

4.4 Fixed dimension function test and result analysis

Fixed-dimensional functions are a type of complex multimodal functions with specific dimensional requirements. This type of problem can effectively test the overall performance of the algorithm, especially the ability to jump out of the local optimum. As far as the test function itself is concerned, most of the global optimal values of fixed-dimensional functions are not 0. This has the advantage of making the type of unknown solution space more comprehensive, and it also provides a more reliable test result and numerical basis for the specific performance test of the algorithm. It can be seen from Table 4 that so far, DAWOA has achieved the best performance in most of the test functions. In the test function F16 (Branin function), the improved algorithm is slightly worse than EWOA, but the numerical results obtained by DAWOA are already very close to the theoretical values. It can be seen from Fig. 10 that in the test functions F15, F17, F18, F19 and F20, after the improved algorithm quickly approximates the region where the optimal value is located, the population individuals do not gather near a local optimal value. The local mutation mechanism allows them to continue to maintain an efficient search state after reaching the local optimal area, which allows some whale individuals to perceive the location of a better solution successfully. In the test functions F15, F18, F19, F20, there are several obvious gradient drops in the convergence curve, which shows that the adaptive inertia weight effectively balances the algorithm’s extensive search capabilities and local development capabilities, allowing the information retained by the previous generation to be fully used. Therefore, the algorithm quickly found a better value after a short search and escaped the trap of local optimization. The total number of iterations in this test is only 500, which not only effectively reflects the search ability of the algorithm, but also makes the changes in the convergence curve more clear. In short, the cause of this phenomenon is easy to understand. The adaptive inertia weight is constantly receiving feedback information while adjusting the performance of the algorithm. In this way, the algorithm can successfully find a dynamic balance point between the exploration capability and the development capability to help the population quickly jump out of the local optimal value. The above data fully shows that the improved algorithm has a high success rate in solving such complex problems, and has a stronger ability to avoid local minimums.

Fig. 10
figure 10

Comparison of convergence curves of some fixed-dimensional test functions

Full size image

4.5 Analysis of the effectiveness of DAWOA

In order to verify the effectiveness of each strategy in DAWOA, this section introduces effectiveness analysis. Adding the three strategies to WOA in the order of dynamic pinhole imaging strategy, local mutation strategy, and adaptive strategy can form three new algorithms: WOA-1, WOA-2 and WOA-3. In addition, this section selects three benchmark test functions to compare and test the four algorithms. The three benchmark functions are the unimodal function F1, F5 and the multimodal function F8 in turn. In order to ensure the fairness of the experiment, the dimension is uniformly set to 30. As shown in Table 7 and Fig. 11, no matter which test function it is, the three strategies of DAWOA are all effective. And, with the continuous addition of strategies, DAWOA’s performance is also continuously enhanced. This fully shows that the three strategies can not only work individually, but also work together to make the algorithm perform more comprehensively. At the same time, the specific effects of these strategies can also be briefly summarized as follows:

  1. (1)

    Dynamic pinhole imaging strategy (WOA-1). It is not difficult to see that the effect of the dynamic pinhole imaging strategy is significant. This shows that as the number of iterations increases, the dynamic pinhole imaging strategy has been actively adjusting the position of the whale. This approach allows some whales to quickly jump to the vicinity of the optimal solution, thereby greatly improving the quality of leaders.

  2. (2)

    Adaptive strategy (WOA-2). Although the dynamic pinhole imaging strategy helped the whale obtain a higher-quality search area, the search ability of the individual whale has not been strengthened, which may cause WOA to fall into a local optimum to a large extent. It can be seen from Table 7 that the adaptive strategy can continuously adjust the search ability of the whale population under the action of the dynamic boundary to help the population quickly reach the target area. This approach can effectively improve the search capabilities of the algorithm.

  3. (3)

    Local mutation strategy (WOA-3). The significance of the local mutation strategy is to strengthen the local development capabilities of the algorithm. When the current two strategies help the algorithm approach the region where the optimal solution is located, the local mutation strategy can dynamically adjust the spiral search range of the algorithm following the number of iterations. With the continuous shrinking of the dynamic boundary, the dynamically reduced spiral path can effectively enhance the local search capability of the algorithm, allowing the algorithm to perform a more detailed search. This approach can significantly improve the convergence accuracy of the algorithm.

Table 7 Test results of the four algorithms in some benchmark functions
Full size table
Fig. 11
figure 11

Comparison of the convergence curves of the four algorithms in some benchmark functions

Full size image

4.6 Principle analysis

In order to more fully explain the role of the three strategies in DAWOA, this section will analyze DAWOA from a theoretical perspective. Undoubtedly, the search process of most algorithms can be divided into particle shrinkage and particle divergence phases. Therefore, we will discuss the advantages of DAWOA from the perspective of these two phases:

  1. (1)

    Particle divergence phase. At this phase, the population individuals of the algorithm will spread as far as possible across the entire search space to obtain richer diversity. However, for WOA, its exploration process is not sufficient, and the quality of leaders is not high enough. Although the exploration phase of WOA has a high priority, it must share the search process with the spiral update location phase. Therefore, the probability at this stage can be expressed as follows:

    $$\begin{aligned} {P_{\left| A \right| \ge 1}} = \frac{1}{2}\int _1^2 {\int _{{1a}}^1 {\mathrm{d}(2r - 1)da \approx 0.1535} } \end{aligned}$$
    (19)

    It is not difficult to see that this probability is much lower than expected. This is also the reason why WOA tends to fall into local optimum. When the dynamic pinhole imaging strategy comes into play, individuals in the population have more diverse positions. In many cases, some low-quality population individuals can quickly jump to the vicinity of the optimal solution under the action of these strategies, which undoubtedly brings more possibilities to the algorithm.

  2. (2)

    Particle shrinkage phase. For many typical non-convex problems, the algorithm is easy to find the target area. However, the ability of local search limits the accuracy of most algorithms, and WOA is no exception. The fixed search range makes it difficult for WOA to be attracted by the optimal solution near the search path, which leads to insufficient convergence accuracy. The local mutation strategy proposed in this paper can make the shape of the logarithmic spiral change with the number of iterations, which can to a large extent strengthen the development ability of the algorithm. At the same time, this strategy also contains an uncontrolled mutation, which can create a lot of opportunities for the algorithm when whales perform local searches. In this way, DAWOA can perform a more careful search during the particle shrinkage phase.

In addition, even if the algorithm has a better location and more flexible search range, if the whale’s search ability is not improved, the performance of the algorithm will hardly be changed significantly. Therefore, this paper also proposes an adaptive strategy: the adaptive strategy allows the whale population to adjust its search ability according to changes in the environment to obtain a better global optimal solution. In this way, DAWOA can obtain more comprehensive performance under the synergy of the three strategies.

As a summary, the numerical experiment results in this section effectively prove the effectiveness of the improved algorithm. a). The unimodal function test results fully demonstrate the feasibility of the dynamic pinhole imaging strategy. Compared with EWOA, WOA and SSA, DAWOA can quickly find the global optimal value and converge. b). Multimodal function test results show that adaptive inertial weights based on dynamic boundary feedback can effectively increase the diversity of the population, make the distribution of population individuals more even, and it is easier to avoid local optima. c). The results of the fixed-dimensional function test show that when the search space becomes more complex, adaptive strategies and local mutation strategies can effectively balance the exploitation and exploration capabilities of the algorithm. This can prevent the population from gathering near the local optimal points that are easy to find in the space, leading to premature convergence of the algorithm. The effectiveness analysis further confirmed the above conclusions. In the following sections, DAWOA will be applied to more challenging engineering problems to further test its performance.

5 The application of DAWOA in engineering problems

The purpose of algorithm optimization is to better solve real-world problems. In order to test the actual effectiveness of DAWOA, four complex constrained engineering optimization problems will be used to test the specific performance of DAWOA. Among them, the specific parameters of the four engineering problems come from optimization literature [23, 37]. The detailed description of the problem and the analysis of the test results will be divided into four subsections to form the entire content of this section.

5.1 The problem of pressure vessel

The pressure vessel problem is a common optimization problem with complex mixed constraints in engineering. As shown in Fig. 12, this problem requires that the overall value be minimized while considering the cost of the structure, material, manufacturing, and welding of the vessel. Moreover, there are only four important design variables for the pressure vessel problem:

\({X_1}\)—Thickness of the two lids of the container.

\({X_2}\)—The thickness of the container shell.

\({X_3}\)—Inner radius of the container.

\({X_4}\)—The length of the cylinder in the middle of the container.

Table 8 shows the best data comparison between DAWOA and WOA, LSA-SM, DE, ACO, GA, RCGA-rdn [38], MBA, DMMFO [23], GSA and ES. Most of the data used for comparison comes from the literature [15, 23, 39]. It is not difficult to see that the performance of DAWOA is better than other comparison algorithms, and the numerical results obtained by DAWOA are even better.

Fig. 12
figure 12

Problem of pressure vessel

Full size image
Table 8 Comparison of results of pressure vessel problems
Full size table

5.2 The problem of cantilever beam

The purpose of the cantilever beam problem is to minimize the weight of the square-section cantilever beam. As shown in Fig. 13, five hollow blocks of different sizes constitute a typical cantilever beam. Among them, the number of hollow blocks determines the number of parameters, and Xi is the side length of the square block. Table 9 is the comparison of the numerical results of DAWOA and some algorithms. Among them, the test data of all the comparison algorithms are from the literature [15, 37,38,39]. It is not difficult to see that DAWOA is still the best optimizer among them.

Fig. 13
figure 13

Problem of cantilever beam

Full size image
Table 9 Comparison of numerical results of cantilever beam problem
Full size table

5.3 The problem of three-bar truss

The three-bar truss problem is a complex structural optimization problem. An obvious feature of this problem is that the algorithm is required to find the minimum value in a narrow search space. Therefore, the three-bar truss problem has a fairly broad research prospect. As shown in Fig. 14, there are two adjustable variables in the three-bar truss problem. The focus of the problem is to keep the weight of the entire structure as small as possible. DAWOA was used to compare with MBA, CS, GOA, WDO [40], Ray [41], MFO, and the comparison results are shown in Table 10. Among all the algorithms, DAWOA’s numerical results are better than other algorithms and have the most reliable performance.

Fig. 14
figure 14

Problem of three-bar truss

Full size image
Table 10 Comparison of results of three-bar truss problems
Full size table

5.4 The problem of tension/compression spring

The tension/compression spring problem was first proposed by Belegundu in 1982. It is a very common and well-known constrained engineering optimization problem. As shown in Fig. 15, the problem contains three important parameters, the purpose is to minimize the weight of the entire spring while ensuring the performance of the spring. Table 11 is the comparison result of DAWOA and some algorithms. The data of these algorithms comes from literature [15, 40]. It can be seen from the comparison results that the numerical results obtained by DAWOA are the best among all the algorithms (Table 11).

Fig. 15
figure 15

Problem of tension/compression spring

Full size image
Table 11 Comparison of results of tension/compression spring problems
Full size table

As a summary, this section tests the performance of DAWOA in four well-known engineering optimization problems with complex constraints. From the comparison of numerical results, DAWOA performs better than other comparison algorithms. These experimental results fully show that DAWOA can effectively solve some practical problems and has a certain practicability.

6 Conclusion and future work

This paper proposes three strategies to help WOA improve its performance. The dynamic pinhole imaging strategy inspired by optics allows the leader to quickly approach areas that may contain high-quality solutions, thereby effectively accelerating the convergence speed of the algorithm. Adaptive inertial weights based on dynamic boundaries and dimensions can properly balance the exploitation and exploration capabilities of the algorithm, making the algorithm’s population diversity richer. So as to effectively strengthen the search ability of the algorithm and prevent the algorithm from premature convergence. The local mutation strategy can dynamically adjust the search range of the algorithm according to the number of iterations, so that the whale population can have more diverse spiral paths. The improved algorithm has been extensively tested in 20 well-known benchmark functions and four complex constrained engineering optimization problems, and compared with other optimization algorithms presented in the literature. The test results show that the improved algorithm has faster convergence speed and higher convergence accuracy, and can effectively jump out of the local optimum.

Although the performance of the improved algorithm DAWOA has been significantly improved to a certain extent, its performance in some test functions will gradually decrease when the dimension increase. This situation reflects the deficiencies of DAWOA to a certain extent. If the leader is always unable to reach the vicinity of the global optimal solution, no matter how many iterations, the entire whale population will most likely fall into a local optimum. How to ensure that the leader’s position update is efficient and reliable, this is the problem we are about to solve. In the future, we will conduct more in-depth research on WOA for ultra-high-dimensional large-scale problems and multi-objective problems to solve more real-world problems.