NestMSA: a new multiple sequence alignment algorithm

Abstract

Multiple sequence alignment (MSA) is a core problem in many applications. Various optimization algorithms such as genetic algorithm and particle swarm optimization (PSO) have been used to solve this problem, where all of them are adapted to work in the bioinformatics domain. This paper defines the MSA problem, suggests a novel MSA algorithm called ‘NestMSA’ and evaluates it in two domains: Web data extraction and removing different URLs with similar text (DUST). The suggested algorithm is inspired by the PSO optimization algorithm. It is not a generalization of a two-sequence alignment algorithm as it processes all the sequences at the same time. Therefore, it looks globally at the same time on all sequences. Different from other PSO-based alignment algorithms, swarm particles in the proposed NestMSA algorithm are nested inside the sequences and communicated together to align them. Therefore, global maximum is guaranteed in our algorithm. Furthermore, this work suggests a new objective function which both maximizes the number of matched characters and minimizes the number of gaps inserted in the sequences. The running time complexity and the efficiency of NestMSA are addressed in this paper. The experiments show an encouraging result as it outperforms the two approaches DCA and TEX in the Web data extraction domain (95% and 96% of recall and precision, respectively). Furthermore, it gives a high-performance result in the DUST domain (95%, 93% and 92% of recall, precision and SPS score, respectively).

1 Introduction

Sequence (string) alignment is a common and a core problem in many fields such as information extraction, removing DUST, bioinformatics, NLP, financial data analysis and others. Aligning of characters in multiple data sequences is a challenge because these characters have many variations. The first variation is called missed characters/patterns, in which a character (a pattern of different consecutive characters) may be missed (has no occurrences) in a sequence. Gaps (referred by—in this paper) are inserted among the sequence characters in place of these missed characters. In the second variation, called repetitive characters/patterns, a character (a pattern) may have more than one occurrence in a sequence. The third variation is called multi-order characters/patterns. Characters (patterns) in this variation may have multiple ordering in different sequences. The fourth and last variation is the existence of what are called disjunctive (mutative) characters, in which a character (a pattern) in a sequence may appear as an alternative to another character (pattern) in some other different sequences. Multiple sequence alignment aims to arrange sequences of characters in order to recognize missed (gaps), repetitive, multi-order and disjunctive (mutative) characters.

Many research algorithms have been proposed to solve the MSA problem, although it is still of great necessity for different reasons. First, some proposed algorithms solve the multiple sequence alignment problem as a generalization of the pair-wise alignment problem (i.e., align the sequences two by two until finally cover the whole sequences). The results of these pair-wise alignment methods usually are affected by the order of the sequences to be aligned and will not be applicable to unseen sequences. Second, many recent MSA algorithms use optimization models such as particle swarm optimization (PSO), although global maximum alignment is not guaranteed as they consider the whole sequences as a solution (a particle) and then try to modify each particle (inserting gaps in the sequences) step by step until reaching a best local solution of this particle. The global best solution is then gained by tracking the local best solutions for all working particles. Third, to the best of our knowledge, all of these algorithms are adapted to work in the bioinformatics domain (e.g., DNA, RNA or Protein alignment) [1], although MSA is a core for other domains such as Web data extraction and removing DUST. Thus, MSA is still demanded to be addressed in such domains. In the field of Web data extraction, data to be extracted are embedded in the Document Object Model (DOM) tree of a Web page. Tree alignment is used to solve the data extraction problem (Depta [2] and FiVaTech [3]). For simplicity, tree alignment is usually solved by converting the multiple tree alignment problem into the multiple sequence alignment. In the field of detecting and removing duplicate Web pages without fetching their contents (DUST), Web pages URLs get tokenized into tokens and then are aligned to generate a set of normalization rules (regular expressions). Later, these expressions are used by search engines to avoid crawling duplicate URLs [4, 5].

In this paper, the multiple sequence alignment problem is defined and a new alignment algorithm called ‘NestMSA’ is proposed to solve this problem. Our proposed algorithm tries to handle the above-mentioned variations: missed patterns, repetitive patterns, multi-order patterns and disjunctive patterns. Similar to the peer matrix alignment algorithm (a heuristic-based one) in [6], our proposed algorithm processes multiple sequences and aligns all of them at the same time. It is not a generalization of a two-sequence alignment algorithm. Therefore, NestMSA has a global view for the whole sequences to be aligned. NestMSA is inspired by the particle swarm optimization algorithm. Different from other PSO-based MSA algorithms, swarm particles in the proposed algorithm are nested/reside inside the sequences and they are communicated together to align these sequences step by step. In other words, a particle in NestMSA corresponds to a character inside the sequences, while a particle in other PSO-based alignment algorithms corresponds to the whole sequences to be aligned. Another contribution in this paper is that a new objective function which tries to both maximize the number of matched characters and minimize the number of gaps inserted is provided. Therefore, global maximum is guaranteed in the proposed algorithm. Furthermore, different from most optimization-based MSA algorithms, the proposed algorithm will be evaluated and addressed in the two different domains: Web data extraction and removing DUST.

The rest of the paper is organized as follows. Section 2 presents related works. Section 3 introduces the particle swarm optimization algorithm, while the MSA problem is formulated in Sect. 4. The proposed PSO-based algorithm with a simple example is presented in Sect. 5. The experimental study is described in Sect. 6. Finally, our work is concluded in Sect. 7.

2 Related works

Multiple sequence alignment has been solved by using many approaches in different fields [7,8,9]. In the bioinformatics domain, there are four main different approaches. The first approach is an exact approach in which dynamic programming is used to align two sequences. It converts the MSA problem into the problem of finding the shortest path in a weighted direct acyclic graph. Dynamic programming gives good alignment results for two sequences. When extended to multiple sequence alignment, the algorithm showed poor results as the lengths and the number of sequences increased. In the second approach, called a progressive approach, the algorithm first finds the most similar sequences and then incrementally aligns the other sequences to the initial alignment. An example of this approach is CLUSTAL X (an updated version of CLUSTAL W, which is also an extension of a previous version CLUSTAL) [10]. The third approach is a consistency-based approach. It considers that an optimum alignment occurred when optimal pair-wise alignments have been reached. A common example is T-COFFEE [11]. It uses a library of pair-wise alignments from the sequences to be aligned, then it finds both the best global and the local alignments. After that, it gets a final alignment which has the highest level of consistency within the library. The last approach is called an iterative approach. The alignment algorithm in the iterative approach begins with a generated initial alignment, and then it refines the alignment until no more improvement could be obtained. GA and PSO are the most common algorithms used for this iterative approach. Our proposed algorithm is an iterative PSO-based method.

Many approaches in the bioinformatics domain adapt PSO algorithm to solve the MSA problem in which the objective is to maximize a scoring function among the sequences to be aligned. Examples of such approaches are [12,13,14]. They consider a particle in the swarm as a set of multiple sequences to be aligned. A particle is represented as a set of vectors, where each vector holds positions of the gaps in a sequence to be aligned. The scoring function used to keep track of the global best particle position is based on the alignment score of each pair of sequences. The alignment score between two sequences is the summation of the scores assigned to match each pair of symbols in these two sequences. The only difference among these approaches is the way that the particles are initialized. The former approach initializes the particles randomly, while the latter one generates the initial particles using the solution obtained from ClustalX algorithm [10]. There are two main differences between such PSO-based algorithms and our proposed algorithm. First, to the best of our knowledge, all PSO-based algorithms are adapted and addressed in the bioinformatics domain. Second, a particle in all of the PSO-based algorithms corresponds to a whole peer matrix with gaps added among the sequences, while a particle in our proposed algorithm corresponds to just a symbol in a matrix row as we shall discuss later.

MSA is not addressed and tested in the Web data extraction domain, although most of the proposed approaches in this domain are solved by using MSA. Some of these approaches are OLERA [15], RoadRunner [16], DEPTA [2], VIPER [17], FiVaTech [3], AFIS [18], TEX [19] and DCA [20]. Wrappers (extraction rules) that are used to extract data from Web pages in OLERA are constructed by acquiring a rough example from the user. It applied the two main techniques: pattern mining and string alignment. OLERA considered the problem of multiple string alignment as a generalization of two-string alignment. RoadRunner assumed that the input pages are similar and each one is a sequence of tokens. Extraction rules are recognized by aligning two pages (sequences), and then the alignment result is compared with a third page (sequence). DEPTA identified data record boundaries by using string edit distance. After that, attributes in these records are identified using partial tree alignment. ViPER recognized and ranked data records with respect to the users visual perception of the input Web page. It handled missed and multi-valued data by using the edit distance after applying the tandem repeats algorithm. String alignment in VIPER is based on the global matching and the text content. To simplify the multiple alignment problem, it used a divide-and-conquer approach. AFIS formulated the problem of data extraction as alignment of Document Object Model (DOM) Trees leaf nodes. AFIS is an unsupervised approach which deduces schema of detail pages that include all product information to be extracted. It applied divide-and-conquer and longest increasing sequence (LIS) algorithms to mine landmarks from input. Finally, FiVaTech is an unsupervised page-level data extraction approach. It applied the three techniques: tree matching, tree alignment and pattern mining, to solve the data extraction problem. First, FiVaTech merged all input DOM trees into a single tree (pattern tree), which is then used to detect the template and the schema of the site. To merge multiple trees, the tree alignment problem is converted into the multiple string alignment problem. FiVaTech is used in this work to collect a dataset which consists of peer matrixes to be aligned.

To the best of our knowledge, the only two MSA algorithms that are suggested and addressed in the field of Web data extraction are TEX and DCA (that is why both have been chosen in our experiment to be compared with our proposed one). Although the two methods use MSA, the methodologies of the two algorithms are different. TEX is an unsupervised information extraction approach that tried to identify a Web site template (shared patterns) and then removed this template from the input site pages. Different from DCA and FiVaTech, TEX did not use the pages DOM trees, rather it considered each input page as a sequence of tokens. Given a set of multiple sequences/pages $S=\{T_{1}, T_{2}, \ldots , T_{n}\}$, where $n \ge 2$ as input, TEX tried to separate the template used to generate these pages from the data to be extracted. In order to achieve that, TEX used a simple multiple string alignment which is based on a searching algorithm that looks for shared patterns. It iteratively searched for a shared pattern of sizes $\max , \max -1, \ldots , \min$, in order (min and max values are calculated experimentally). If a shared pattern is found, TEX expanded the set S by replacing each sequence $T_{i}$ with three other sequences: prefix, separator and suffix of the detected pattern in the sequence $T_{i}$, and so on until no shared patterns are found.

In DCA [20], Oviliani and Chang emphasized the necessity to have a high-performance multiple string alignment algorithm to solve the Web data extraction problem (from singleton Web pages). Given more than one DOM tree as input, each sequence of leaf nodes in a DOM tree is added as a row in a matrix which is finally aligned in two phases: a template mining phase and an alignment phase. Leaf nodes are classified into one of the three categories: mandatory template, optional template and mandatory data. The first two, parts of the Web site template, are used as landmarks to achieve the alignment process, while the last one corresponds to the data to be extracted. In the template mining phase, a divide-and-conquer approach is applied to recursively detect landmarks (mandatory templates) via longest increasing sequence (LIS). Further, optional templates are detected and merged across segments to remove false-positive mandatory templates. In the alignment phase, non-template leaf nodes are aligned to generate a consistent output for multi-order attribute-value pairs and merge similar/disjunctive columns to generate the output matrix.

Detecting and removing DUST is another domain which is recently solved by MSA algorithms [4]. Rodrigues et al. have suggested an approach called DUSTER, which aligns multiple URLs with duplicated content. It then uses the alignment results to construct high-quality, general and precise normalization rules. The derived rules could be used by a web crawler to avoid fetching DUST. To align a set of multiple URLs, they used the progressive alignment strategy which is a generalization of pair-wise sequence alignment.

3 Particles swarm optimization

Given a fitness function that describes a problem to be optimized, classical optimization algorithms use the first derivative of this fitness function to get the optima on a given constrained surface. Recently, many optimization algorithms have been suggested to solve the problem without calculating the derivative which is very difficult, especially for discontinuous optimization spaces. Examples of such algorithms are: GA [21, 22] and PSO [23,24,25]. Particle swarm optimization is a stochastic search algorithm and an alternative solution to the nonlinear optimization problem. The algorithm has been inspired by the social behavior of animals such as bird flocking, fish schooling and so on. It was introduced in 1995 by Kennedy and Eberhart. In PSO, the population (swarm) consists of a set of particles (solutions). The PSO algorithm works as follows. Initially, particles in the swarm are distributed randomly in the search space in such a way that each particle $p_{i};\,(1 \le i \le m)$ has an initial position $x_{i}(t_{\circ })$ and moves toward a randomly chosen direction. Each particle keeps track of its best previous position $\mathfrak {I}_{i}$ and a global best position $g$ which is shared by all other particles. After each particle has moved to a new position, iteratively it improves its new position by flying toward both its best position and the global best position. PSO will be terminated when the maximum number of iterations (calculated based on some stop criteria) has been reached. Considering maximization problems, the particle best position and the global best position are calculated based on an objective (fitness) function $f(x);\,x \in R^{N}$; where $N$ is the dimension of the search space. The local best position $\mathfrak {I}_{i}$ of the particle $p_{i}$ and the global best $g$ of all particles at the iteration number $t+1$ are defined, respectively, as:

$$\begin{aligned} \mathfrak {I}_{i}(t+1) &= {} {\left\{ \begin{array}{ll} \mathfrak {I}_{i}(t), &{}\text {if}\ f(x_{i} (t+1)) \le f(\mathfrak {I}_{i} (t)) \\ x_{i} (t+1), &{}\text {if}\ f(x_{i} (t+1)) > f(\mathfrak {I}_{i} (t)) \end{array}\right. } \end{aligned}$$

(1)

$$\begin{aligned} g(t+1) &= {} \mathfrak {I}^{*}_{i}(t+1);\text { such that } f(\mathfrak {I}^{*}_{i}(t+1))=\max _{\{i=1, \ldots , m\}} \{ \mathfrak {I}_{i}(t+1) \} \text { and } m \ge 1 \end{aligned}$$

(2)

The position $x_{i}$ of the particle $p_{i}$ is updated using the following formula:

$$\begin{aligned} x_{i}(t+1)= x_{i}(t) + \upsilon _{i}(t+1) \end{aligned}$$

(3)

The velocity $v_{i}$ of the particle $p_{i}$ at iteration $t+1$ is calculated by:

$$\begin{aligned} \upsilon _{i}(t+1)= \omega \upsilon _{i}(t) + c_{1} r_{1}(t) [\mathfrak {I}^{*}_{i}(t) - x_{i}(t)]+ c_{2} r_{2}(t) [g(t) - x_{i}(t)] \end{aligned}$$

(4)

where

• (i) The term $\omega \upsilon _{i}(t)$ is called an inertia component which prevents drastic change in the direction of the particle.

• (ii) The term $c_{1} r_{1}(t) [\mathfrak {I}^{*}_{i}(t)$ is called a cognitive component which directs the particle to fly toward its previous best position.

• (iii) The term $c_{2} r_{2}(t) [g(t) - x_{i}(t)]$ is called a social component which directs the particle to fly toward the best position found by the particles neighborhood (the global best).

• (iv) The constant $\omega$ is called an inertia weight.

• (v) The two constants $c_{1}$ and $c_{2}$ are positive constants that accelerate the cognitive component and the social component, respectively.

Fig. 1

Particles $p_{s}$ (for all symbols in a row $r$) nested at the row to align it

4 MSA problem formulation

Given a finite set $A$ of arbitrary symbols (called an Alphabet set), a sequence $S_{i}$ of length $n_{i}$ is defined as a series of ordered symbols taken from the alphabet $A$ (i.e., $S_{i}=\{s_{1i}, s_{2i}, \ldots , s_{n_{i}i}\}$, where $n_{i}=|S_{i}|$. The jth symbol in the sequence $S_{i}$ is denoted by $s_{ji}$$(j=1,\, ,n_{i})$. We define the term multi-sequence matrix or simply called peer matrix as follows.

Definition 1

(Peer matrix) Given a set of $c$ sequences $T={S_{1},S_{2},\ldots ,S_{c} }$ taken from the alphabet $A$, where the sequence $S_{i}$ has a length $n_{i} (i=1,\ldots ,c)$, a peer matrix $M$ is defined as the matrix whose columns are the sequences $S_{1},S_{2},\ldots ,S_{c}$.

That is:

$$\begin{aligned} M= \begin{bmatrix} s_{11} &{}s_{12} &{}\ldots &{}s_{1c} \\ s_{21} &{}s_{22} &{}\ldots &{}s_{2c} \\ \ldots &{}\ldots &{}\ldots &{}\ldots \\ s_{n_{1}1} &{}s_{n_{2}2} &{}\ldots &{}s_{n_{c}c} \end{bmatrix} \end{aligned}$$

Multiple sequence alignment is now defined as follows.

Definition 2

(Multiple sequence alignment) Given a peer matrix M formed from multiple sequences taken from the alphabet set $A$, multiple sequence alignment is the problem of finding a matrix $M^{\prime }$ (called an aligned matrix) from the original matrix $M$ such that:

$$\begin{aligned} M^{\prime }= \begin{bmatrix} s^{\prime }_{11} &{}s^{\prime }_{12} &{}\ldots &{}s^{\prime }_{1c} \\ s^{\prime }_{21} &{}s^{\prime }_{22} &{}\ldots &{}s^{\prime }_{2c} \\ \ldots &{}\ldots &{}\ldots &{}\ldots \\ s^{\prime }_{n_{1}1} &{}s^{\prime }_{n_{2}2} &{}\ldots &{} s^{\prime }_{n_{c}c} \end{bmatrix} \end{aligned}$$

where $M^{\prime }$ is taken from a new alphabet $A^{\prime } = A \bigcup \{$—$\}$ and it has all of the following constraints:

• 1. The sequences (columns) $S^{\prime }_{1},S^{\prime }_{2},\ldots ,S^{\prime }_{c}$ of $M^{\prime }$ are defined over the new alphabet $A^{\prime }$.

• 2. The sequences $S^{\prime }_{1},S^{\prime }_{2},\ldots ,S^{\prime }_{c}$ of $M^{\prime }$ have the same length $n=\max \{|S^{\prime }_{i}|; i=1,\ldots ,c\}.$

• 3. $S^{\prime }_{i} (i=1,\ldots ,c)$ reverts to the original $S_{i}$ by removing all the inserted gap characters.

• 4. For each row $r$ in the matrix $M^{\prime }$, there exists at least one symbol $s^{\prime }_{ri}$ which is not a gap; i.e., $s^{\prime }_{ri} \ne$ ‘—.’ This means that it is not possible to have a row in the matrix $M^{\prime }$ that only has gaps.

• 5. Number of matched characters (symbols) in each row of $M^{\prime }$ is maximized.

• 6. Number of gaps inserted in the matrix $M^{\prime }$ is minimized.

In the multiple sequence alignment of DNA sequences, the alphabet $A$ is ${A, C, T, G}$. Similarly, the RNA alphabet is ${A, C, U, G}$, while the alphabet for protein MSA is ${A, C, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, W, Y}$. In the NLP domain, the alphabet is a set of all tokens/words defined by the language. In the domain of detecting and removing DUST, the alphabet is a set of URL tokens that have been described by the EBNF-based grammar [4] (e.g., the URL http://domain/story?id=num is tokenized to have the following 11 tokens:$\{{<}{http}{>}, {<}:{>}, {<}/{>}, {<}/{>}, {<}domain{>}, {<}/{>}, {<}story{>},{<}?{>},{<}id{>},{<}={>},{<}num{>}\}$. Finally, for the Web data extraction problem, the alphabet is a set of identifiers (symbols) where each one corresponds to a subtree (a leaf node) from a Web page DOM tree that includes some data to be extracted. Matched/similar subtrees (leaf nodes) take the same identifier (symbol) where similarities could be measured by using tree-edit distance, visual features comparison, or any other measurement way. This means, for the last two domains, removing DUST and Web data extraction, the peer matrix contains sequences of symbols/characters that correspond to URL tokens or subtrees from the DOM tree, respectively.

Fig. 2

A multiple sequence alignment example

Figure 2a shows a simple example of four sequences alignment problem. The matrix to be aligned $M$ consists of the four sequences: $S_{1}=\{a,b,c,b,c,d,e,m\}$, $S_{2}=\{a,c,b,c,f,g\}$, $S_{3}=\{a,b,c,h,i,m,n\}$ and $S_{4}=\{a,b,c,b,c,j,k,m\}$ of lengths 8, 6, 7 and 8, respectively. The matrix $M$ has 8 rows (indexed at the left hand side 1–8). Multiple sequence alignment of the matrix $M$ is the problem of finding a matrix such as $M^{\prime }$ shown in Fig. 2b in which:

• 1. Gaps (‘—’) are inserted among the symbols of the sequences in $M$.

• 2. All sequences in $M^{\prime }$ have the same length (9).

• 3. Each sequence in $M^{\prime }$ reverts to its original one in $M$ by removing all the gaps inserted in this sequence.

• 4. There is no row in $M^{\prime };$ which only has the gap character.

• 5. Number of matched characters (symbols) in $M^{\prime }$ is maximized.

• 6. Number of gaps inserted to the matrix is minimized.

After the alignment has been completed, missed values, repetitive patterns and disjunctive patterns could be identified in the aligned matrix. For example, the aligned matrix $M^{\prime }$ in Fig. 2b shows that the symbol ‘a’ is mandatory/required in all the four sequences, the pattern of two symbols $\{`b{\text {'}},`c{\text {'}}\}$ is repetitive and has a missing symbol ‘b,’ the four patterns $\{`d{\text {'}},`e{\text {'}}\}$, $\{`f{\text {'}},`g{\text {'}}\}$, $\{`h{\text {'}},`i{\text {'}}\}$ and $\{`j{\text {'}},`k{\text {'}}\}$ are disjunctive, and finally the two symbols ‘m’ and ‘n’ are missed.

5 The proposed algorithm: NestMSA

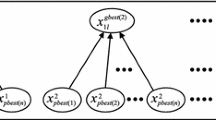
Given a peer matrix $M$ that is constructed from a set of sequences $T=\{S_{1},S_{2},\ldots , S_{c}\}$ as defined above, NestMSA adapts the behavior of PSO to align $M$ and get an aligned matrix such as $M^{\prime }$ shown in Fig. 2b. Different from all other PSO-based multiple sequence alignment works, NestMSA is iteratively applied to align each row in the matrix. After all rows are aligned, the alignment problem is then solved and the aligned matrix such as $M^{\prime }$ is obtained. As shown in Fig. 1, for each row $r$ in the matrix $M$, particles in our algorithm will be initially distributed (nested) over the row $r$. Then, these particles start flying down to decide which one shall be moved (replaced by gaps). The particle with the global best (if there) shall be moved down (as the particles are distributed over the whole row symbols, so the global best solution is guaranteed). Number of swarm particles $m$ in the row $r$ is less than or equal to number of columns (sequences) $c$ (i.e., $m \le c$) as each particle $p_{s_{i}}$ will work with one symbol $s_{i} (i=1,\ldots ,m)$ in the row, and at the same time, the row may have more than one occurrence of this symbol. That is, all occurrences of the symbol $s_{i}$ in the row $r$ are carried by a particle $p_{s_{i}}$. So, position $x_{s_{i}}(r)$ of the particle $p_{s_{i} }$ is defined by using the row $r$ that contains the symbol $s_{i}$ as well as locations of the symbol $s_{i}$ in the different columns (indexes of the columns that contain $s_{i}$) in the row r. That is:

$$\begin{aligned} x_{s_{i}}(r)= [r, i_{1}, i_{2}, \ldots ] \end{aligned}$$

(5)

where $i_{1}$ is the index of the first occurrence of $s_{i}$ in the row $r$, $i_{2}$ is the index of the second occurrence of $s_{i}$ in $r$, and so on. After the $m$ swarm particles $\varPhi$ have been nested at row $r$, they iteratively fly down (row by row at each iteration), keep track and share the global best position which could be used to decide which particle (symbol) should be moved to align the row. Again, this process is repeated until either one particle (symbol) only remains at the row or none of the particles can fly. If one particle only remains at the row, it is considered as an aligned row. If all of the particles cannot fly, we consider the symbols associated with these particles as disjunctive. A symbol will move down to align the row $r$ based on the global best position $g$ of the $m$ particles in the swarm at the row $r$. Figure 3 shows our proposed algorithm (NestMSA_RowAlignment($r$, $M$)) which is iteratively called to align the row $r$ in the matrix $M$. It is important to note that, in this section, we use the term move to make an actual modification in the matrix to be aligned, while the term fly shall be used to decide which particle to move (without any actual modification in the matrix). The algorithm is working as follows.

Fig. 3

The proposed algorithm (NestMSA_RowAlignment) to align a row $r$

The algorithm starts by initializing the swarm population and creates a set of $m$ particles (line 1) as discussed above. If the swarm has only one particle (i.e., there are different occurrences of only one symbol), the row is considered as aligned and the algorithm is terminated (lines 2–3; no particle will be moved). Otherwise, the algorithm does the following to decide which particle to move. For each particle $p_{s_{i}}$ ($i=1,\ldots ,m$) in the swarm (lines 5–17), the particle position $x_{s_{i}}(r)$ is identified as in Eq. 5 and the particle's best position is initialized by the value $x_{s_{i}}(r)$ (lines 5–7). This means that the initial position of the particle will be at row $r$ (i.e., $t_{\circ }=r$). Each particle will iteratively fly one step down until stop criteria become true. The position of the particle at each iteration $t$ ($t=r+1,\ldots , r+l$) is defined as:

$$\begin{aligned} x_{s_{i}}(t)= [t, i_{1}, i_{2}, \ldots ]; \text { where } t=r+1, \ldots , r+l \end{aligned}$$

(6)

The number of iterations $l$ is called the flying span. This means that the particle $p_{s_{i}}$ will fly carrying the symbol $s_{i}$ down in the same column (i.e., only the row will be changed when the particle fly down, while indexes of the columns that contain the symbol are not changed). The flying span $l$ is calculated using a combination of one or more of the following stop criteria:

• (i) The flying span (the number of iterations) $l$ is a fixed number. In our experiment, we calculate this fixed value by subtracting the longest sequence (that does not contain the particle symbol $s_{i}$) length and the row value $r$, as the particle does not fly alone. This means the particle $p_{s_{i}}$ will fly down until no other symbols are shown in the row.

• (ii) For each fly of the particle $p_{s_{i}}$, the objective function at the new position ($t=r+1,\ldots ,r+l$) does not increase for a fixed value of $l$. Experimentally, we set the value of $l$ as 5.

• (iii) Particle $p_{s_{i}}$ flies to a new position $x_{s_{i}}(t)=[t, i_{1}, i_{2}, \ldots ];\,t=r+1, \ldots , r+l$, and stops when the symbol $s_{i}$ appears in the row $t$ at some different indexes $j$ (in other words, there is a column of index $j \not \in \{i_{1},i_{2},\ldots \}$ in the matrix at row $t$ which has the symbol $s_{i}$). This means the particle $p_{s_{i}}$ at indexes $i_{1},i_{2},\ldots$ is flying until it finds the symbol $s_{i}$ down in a row at an index $j \ne i_{k}$; $k=1,2,\ldots$, otherwise the stop criteria ii and i are applied, in order.

At each iteration $t$ ($\text {ranged from } r \text { to } r+l$), the particle position is modified by increasing the row number by 1 (lines 9–10). The objective function at the next row (will be discussed later) is updated (line 11) after the particle symbol is flying down to row $t$ (i.e., after the matrix has been virtually modified). Then, the value of the new objective function will be used to calculate both the particle best position $\mathfrak {I}_{i}$ (lines 12–13) as in Eq. 1 and the global best position for all particles as in Eq. 2 (lines 14–15). The global best position was initialized before the particles start flying. This initial global best value is called $g_{\circ }$ in the algorithm (line 4). After the global best position $g=[t^{\prime }, i_{1}, i_{2}, \ldots ]$ is tracked/shared by all particles, it is returned by the algorithm (line 22). Hence, all occurrences (indexed by $i_{1}, i_{2},\ldots$) of the symbol with this global best position will be moved down a distance equal to ($t^{\prime } - r$) in the matrix $M$. At the same time, each gap added to the matrix is replaced by—. If the global best position does not change (i.e., $g=g_{\circ }$), the algorithm is terminated after recognizing all the different symbols $s_{i}$; $i=1, \ldots ,m$ in the row $r$ as disjunctive/mutative (lines 18–21; no particle will be moved).

As discussed above, the proposed algorithm adapts the particle swarm optimization as follows. First, it simply considers the particles initial positions as the row to be aligned. Second, the velocity of the particle at iteration $t+1$ will improve the particle position at iteration $t+1$ by just changing the row value $t$ in the particle position $x_{s}(t)= [t, i_{1}, i_{2}, \ldots ]$ at iteration $t$. This means that the flying directions of the particles depend only on the inertia component and ignored both the cognitive components and the social component.

To analyze the algorithm that aligns a row $r$ of $m$ different symbols, we consider the number of comparisons between two symbols as the cost measure to determine the running time. Updating the objective function at line 11 in Fig. 3 requires $(c-1) \times (k-r)$ comparisons (see Eq. 8 in the next subsection), where $c$ and $k$ are the number of columns (sequences) and the longest sequence length, respectively. The inner loop (lines 8–16 in the figure) stops after $l$ iterations (flying span) which is calculated based on the three criteria mentioned above. So, the inner loop requires $l \times (c-1) \times (k-r)$ comparisons. This will be repeated (the outer loop—lines 5–17) for each different symbol (particle) in $r$ (i.e., the outer loop has $m$ iterations). Experimentally, as mentioned above, the flying span $l$ based on the three criteria applied in the algorithm is less than 5. Therefore, the running time complexity of the algorithm is $O(m \times c \times k)$.

5.1 Particle objective function

Before we go further in this subsection to discuss how to calculate the objective function of a particle $p_{s}$ at position $x_{s} (t)=[t,i_{1},i_{2},\ldots ]$ in a matrix $M$, we introduce some important definitions.

Definition 3

(Aligned row) Given a matrix $M$ as discussed in Sect. 4, a row $r$ is called an aligned row if it only contains different occurrences of the same symbol $s$.

Definition 4

(Full row) An aligned row $r$ is called full if no gaps (—) are added in the row $r$. That is, the number of occurrences of the symbol in the row is equal to the number of columns in the matrix.

Definition 5

(Row weight) Weight of the row $r$ is calculated as:

$$\begin{aligned} \omega (r)=\left\{ \begin{array}{ll} \omega _{1}\times \frac{x}{c}; &{}\text { if }\ r \text { is not aligned }\\ \omega _{2}\times \frac{n_{s}}{c};&{} \text { if }\ r \text { is aligned }\\ \omega _{3}; &{} \text { if }\ r \text { is Full } \end{array}\right. \end{aligned}$$

(7)

where $\omega _{1}$, $\omega _{2}$ and $\omega _{3}$ are the penalties of the row if it is not aligned, aligned and full, respectively. Experimentally, as we shall mention later, we chose the values for these penalties as: $\omega _{1}=0.25$ (for the non-aligned row), $\omega _{2}=0.5$ (for the aligned row) and $\omega _{3}=1$ (for a full aligned row), although other values could be more suitable for other experiments. For example, when evaluating the proposed MSA algorithm in the field of Web data extraction, we used a higher value of $\omega _{3}$ ($\omega _{3}=2$) if the symbol in a full aligned row corresponds to a leaf node in the DOM tree which is a part of the Web page template (not classified as data to be extracted). The value $n_{s}$ is the number of occurrences of the symbol $s$ in the aligned row $r$, and $c$ is the total number of columns in the matrix $M$ ($c > 1$). The value $x$ is calculated for the non-aligned row $r$ as follows. The value of $x$ is equal to zero if every symbol in the row $r$ occurred at most once, otherwise $x$ is equal to the max number of occurrences (matches) of some symbol in $r$. The proposed algorithm is a single objective optimization problem. The objective function $f$ of the particle $p_{s}$ at position $x_{s}(r)$ in the matrix $M$ is calculated based on the accumulated weights of all rows from $r$ to the last row ($\sum _{j=r}^{k} \omega (j)$). Also, as discussed in Sect. 4, the objective function has a converse relationship with the number of gaps $Gaps(r)$ added to the matrix from row $r$ to the last row, and a positive relationship with the number of aligned rows $A(r)$ in $M$ from the row $r$ to the last row ($k$). Finally, we define a row context value $C(r)$ as the maximum number of matched characters (symbols) in the current row $r$ ($C(r) \ge 1$). The objective function $f$ should be increased when $C(r)$ is increased. Therefore, the objective function is formulated as follows.

$$\begin{aligned} f(x_{s}(r)) = \frac{A(r)\times C(r)}{1+Gaps(r)} \times \sum _{j=r}^{k} \omega (j) \end{aligned}$$

(8)

5.2 An illustrative example

Fig. 4

Snapshots of the matrix $M$ shown in Fig. 1a during the alignment process

To clarify our proposed algorithm in Fig. 3, it will be applied to solve the alignment problem on the fictional matrix $M$ shown in Fig. 2a. To align the first row ($r=1$), the algorithm NestMSA_RowAlignment will create a swarm $\varPhi$ that includes only one particle $p_{a}$ as the row has only one symbol $a$. So, it returns null because the row is already aligned (lines 2–3 in Fig. 3). To align the second row ($r=2$), a swarm $\varPhi$ that contains the two particles $p_{b}$ and $p_{c}$ is created as the row has two symbols ($b$ and $c$). To decide which symbol to move to align this row, each of the two particles will fly down in the matrix iteratively and the global best position will be tracked and calculated. Based on this calculated global best position, the algorithm will decide which particle (symbol) to move in order to align the row. Sometimes, the algorithm is called more than one time to align the row. The initial global best position at the second row is $g_{\circ }=x_{b}(2)=[2,1,3,4]$ where the symbol ‘b’ has occurred at indexes 1, 3 and 4 at the row. Objective function (Eq. 8) at the initial position $g_{\circ }$ is calculated as:

$f(g_{\circ }) = \frac{1\times 3}{1+0} \times 0.875 = 2.625$,

where $\sum _{j=2}^{8} \omega (j) = 0.25 \times \frac{3}{4} + 0.25 \times \frac{3}{4} + 0.25 \times \frac{2}{4} + 0.25 \times \frac{2}{4} + 0 + 0 + 0.5 \times \frac{2}{4}= 0.875$, $A(2) = 1$ (as there is only one aligned row, the eighth row, in the range from row 2 to row 8) and $Gaps(2)=0$ (as no gaps added to the rows from 2 to 8 till now). Also, the row context value is $C(r)=3$, because the symbol ‘b’ has a maximal occurrence value (3 occurrences in the second row). Now, either of the two particles $p_{b}$ or $p_{c}$ is flying down if a global best position $g$ is found such that $f(g) > f(g_{\circ })=2.625$, otherwise no flying is done.

To decide which symbol to move in the second row, the first particle will start flying and it stops after 1 iteration at $t=3$ (applying the third stop criterion iii discussed above). Figure 4a shows the matrix $M$ after flying the particle $p_{b}$ to the third row. At that time, the particle new position is $x_{b}(3)=[3,1,2,3,4]$, the objective function $f(x_{b}(2))$ after the particle flying is $f(x_{b}(2))=\frac{4 \times 1}{1+3} \times 2.625 = 2.625$, and so the particle's best and the global best positions will not be changed as the objective function when the particle $p_{b}$ is flying down is the same as the objective function at its initial position (i.e., $f(g)=f(g_{\circ })=2.625$. Note that the algorithm will use a copy of the matrix $M$ to be modified when particles are flying and calculate the global best position without changing the original matrix.

For the second particle $p_{c}$ in the swarm, it also flies and stops after 1 iteration. Figure 4b shows the matrix $M$ after the particle $p_{c}$ flies to the third row. At that time $x_{c}(3)=[3,1,2,3,4]$, $f(x_{c}(2))=\frac{3 \times 3}{1+1} \times 2.0 = 6.0$, and so the particle best and the global best positions will be: $\mathfrak {I}_{c}=x_{c}(3)$ and $g=x_{c}(3)$, respectively. Since the objective function at the global best position is greater than the one at the initial position (i.e., $f(g)=6.0>f(g_{\circ })=2.625$), the algorithm will return the last modified global best $g=x_{c}(3)=[3,1,2,3,4]$. Therefore, after all particles have been communicated, the second row will be aligned by moving the symbol (‘c’) at index 2 a distance $3-2=1$. This means that the second row will be aligned by moving ‘c’ to the third row and adding a gap at that place to get a matrix $M$ shown in Fig. 4b.

Aligning the second row shown in Fig. 4 is a good example which demonstrates the strength of the proposed objective function in the algorithm. Comparing the two matrixes in Fig. 4a, b, each of the two matrixes could be a solution to our alignment problem. The objective function at the second row will take the responsibility to choose one of these two matrixes (the one that maximizes the objective function value). That is why, this function may need to be adapted when applying to other fields. It is clear from the calculated objective function values at the second row that the more aligned rows and the minimum added gaps give the larger objective value.

Similar to the first row, the swarm for the third row has only one particle $p_{c}$, so it returns null as the row is aligned (see Fig. 4b). For the fourth row, the swarm includes the two particles $p_{b}$ and $p_{h}$. The initial global best position is $g_{\circ }=x_{b}(4)=[4,1,2,4],$ where the symbol ‘b’ at the fourth row has indexes 1, 2 and 4, and then $f(g_{\circ })=(1 \times 3)/(1+0) \times 0.625 = 1.875$. Similar to aligning the second row, using the first stop criterion (i), the particle $p_{b}$ will fly 3 times ($r=$5,6 and 7). After the particle $p_{b}$ stops flying, the global best position will be $g=x_{b}(7)=[7,1,2,4]$. After the particle $p_{h}$ stops flying, the global best is updated to be $g=x_{h}(6)=[6,3]$ at which $f(x_{h}(4))=(4 \times 3)/(1+2) \times 1.25 = 5.0$. So, the algorithm at the fourth row of the matrix $M$ shown in Fig. 4b will return $g=x_{h}(6)=[6,3]$. This means that the row will be aligned by moving the symbol ‘h’ at the fourth row a distance $6-4=2$ and adding gaps in that places. The matrix obtained after this step is shown in Fig. 4c.

In the sixth row of the matrix in Fig. 4c, the swarm creates the four particles: $p_{d}$, $p_{f}$, $p_{h}$ and $p_{j}$. The initial global best position is $g_{}\circ =x_{d}(6)=[6,1]$ where the symbol ‘d’ at the sixth row has an occurrence at index 1, and then $f(g_{\circ })=1.0$. Each of the four particles will fly down, but the global best and the local best will not be modified as none of them fly to a position at which the objective function is greater than $f(g_{\circ })=1.0$. This means that the global best for the four particles remains $g_{\circ }$. Therefore, the algorithm terminates after identifying the four symbols ‘d,’ ‘f,’ ‘h’ and ‘j’ as disjunctive/mutative. Similarly, the algorithm identifies the four symbols ‘e,’ ‘g,’ ‘i’ and ‘k’ as disjunctive in the seventh row. Finally, the last two rows are aligned. Gaps are added in the row when it is identified by the algorithm as an aligned row and it was not full. The result will be the matrix shown in Fig. 4d which is the same as the one in Fig. 2b ($M^{\prime }$).

6 Experiments

In this paper, we focused on measuring the performance of the proposed algorithm and comparing it with other algorithms in the two domains: Web data extraction and removing DUST, although it could be adapted to be used in other domains. Sequences in these domains are usually of small sizes. Each character in the sequence corresponds to either a datum to be extracted (DOM subtree) from Web pages or an URL token as mentioned before. Three experiments are conducted in this paper, two of them are used to evaluate the algorithm in the field of Web data extraction, while the third one is used to evaluate the algorithm in the domain of removing DUST. The first experiment is conducted to measure the performance of the proposed algorithm on a dataset of peer matrixes that are generated by a Web data extraction system. The second experiment tries to compare the proposed algorithm with the two alignment algorithms in TEX [19] and DCA [20]. Finally, the third experiment is conducted to measure the performance of the algorithm on a set of dup-clusters (each dup-cluster is a set of different URLs with similar contents) gathered from the common crawl dataset. All the experiments are conducted on a standard Intel Core i7-4600U 2.7 GHz CPU with 8G RAM running window 10.

Recall and precision are used to measure the performance of the algorithm in the first two experiments. We use the same formulas applied in both DCA and TEX in order to achieve the comparison. Given an aligned matrix $M^{\prime }_{\mathrm{alg}}$ extracted by an algorithm called ‘$alg$’ and the aligned matrix $M^{\prime }_{\mathrm{manually}}$ extracted manually by experts, recall ($R_{r}$) and precision ($P_{r}$) for each row $r$ in the aligned matrix $M^{\prime }_{\mathrm{alg}}$ are calculated as follows:

$$\begin{aligned} R_{r}= & {} \frac{\# \text {correct aligned symbols in } M^{\prime }_{\mathrm{alg}} \text { at row } r}{\# \text { symbols in } M^{\prime }_{\mathrm{manually}} \text { at row } r}\\ P_{r}= & {} \frac{\# \text {correct aligned symbols in } M^{\prime }_{\mathrm{alg}} \text { at row } r}{\# \text { symbols in } M^{\prime }_{\mathrm{alg}} \text { at row } r} \end{aligned}$$

Now, recall ($R$) and precision ($P$) could be calculated for each matrix by dividing the number of correctly extracted rows ($CR$) by the total number of rows in $M^{\prime }_{\mathrm{manually}}$ ($GA$) and the total number of rows in $M^{\prime }_{\mathrm{alg}}$ ($ER$), respectively. Similar to DCA, we consider a row as correctly extracted if $R_{r} \ge 0.85$. Therefore, recall ($R$), precision ($P$) and F-measure ($F$) are calculated as follows:

$$\begin{aligned} R=\frac{CR}{GA}, \;\; P=\frac{CR}{ER},\;\; F=\frac{2 \times R \times P}{R + P} \end{aligned}$$

(9)

For the first experiment, a dataset is generated for the purpose of this work by the help of a Web data extraction system [3, 26] and a simple GUI. The tools developed for the Web data extraction system FiVaTech are used to automatically collect all the matrixes to be aligned. The research purpose-designed GUI is used to simplify the manual labeling and alignment process of the collected matrixes. (C++ is the core language for this GUI as FiVaTech is written using it.) A total of 1200 peer matrixes taken from 51 Web sites (Testbed for Information Extraction from Deep Web (TBDW) Version 1.02 dataset¹) are collected, and their corresponding alignments are created to measure the performance of the proposed algorithm. We ignore to collect peer matrixes formed from subtrees near the roots of the DOM trees as many of them already have aligned rows (full aligned in many cases). We add a constraint on the characters (data) in the peer matrixes to be taken from DOM trees at least 4 levels from the root (${<}body{>}$ tag). Particularly, we take 200 peer matrixes from each level (4, 6, 8, 10 and greater than 10) in the DOM trees (a total of 1200 matrixes). Figure 5 shows the average time cost for each block of 200 matrixes (in milliseconds). Also, both the average number of sequences and the average sequence lengths for each block are shown in the figure. As shown in the figure, the time cost to align peer matrixes near the root of the DOM trees is very small and it is increased gradually when the dimensions of the matrixes increased. The average time cost for the whole 1200 matrixes is approximately equal to 0.42 ms.

Fig. 5

Time cost for the algorithm NestMSA

Table 1 Results of applying the algorithm on the dataset using 3 different stop criteria

Table 2 The performance of the proposed algorithm

To guarantee that the results are not biased to the used dataset, we used the following heuristic to find the most appropriate penalties for the non-aligned, aligned and full aligned rows. We fix the value of $\omega _{2}$ to be 0.5, start $\omega _{1}$ and $\omega _{3}$ with the values 0.1 and 0.6, respectively, and finally measure the precision and recall. After that, iteratively we add 0.05 to each of the two values of $\omega _{1}$ and $\omega _{3}$, and again measure the precision and recall at each iteration. Finally, we chose the penalties values with the maximum F-measure. If more than one iteration has a maximum F-measure, we chose the highest $\omega _{1}$ and $\omega _{3}$ values.

Table 1 shows the results of applying our proposed algorithm on the dataset in three different cases when each of the three stopping criteria discussed in Sect. 5 is used to calculate the particles' flying span (columns 2, 3 and 4), respectively. For each case, the total number of gaps, the total number of matched symbols, the total number of disjunctive symbols, the total number of full aligned rows and the average alignment score are calculated and compared with the manually generated aligned matrixes. The alignment score is calculated using Eq. 8 for each matrix (resulted by the proposed algorithm), and then the average of these matrixes scores is calculated. We set 1 to the value $C(r)$ in Eq. 8. The total number of gaps is calculated after ignoring gaps added at the end of the sequences to have the same length. Also, when calculating the number of matched symbols, we only consider the rows that have more than one occurrence of a symbol. As shown in Table 1, applying the last criterion gives better results. The performance of the algorithm in the three different stopping cases is measured by using recall, precision and F-measure (defined in Eq. 9). Table 2 shows that there is no significant difference when applying either of the first two criteria (i and ii), while the last criterion (iii) gives better performance.

For the second experiment, we use the 22 Web sites in the DCA dataset² that are used for the comparison between TEX and DCA. The average number of pages in each site is 30 pages, while the average number of sequence lengths is 292. To compare our proposed algorithm with the two algorithms DCA and TEX, we used recall, precision and F-measure that are defined in Eq. 9. Table 3 shows that our proposed algorithm outperforms both DCA and TEX. The performance of the proposed algorithm is: $R = 0.95$, $P = 0.96$, $F = 0.96$. The average number of the manually aligned rows (called golden answer in DCA) is 47 rows per website, while the average number of aligned rows extracted by the proposed algorithm is 47.27 which is much closer. TEX suffered from false-positive data attributes. It produced the highest number of aligned rows, resulting in low precision.

Finally, the last experiment is conducted on a collection Web pages URLs crawled from the common crawl dataset,³ which is an open repository of Web crawl data. We developed a simple tool to choose only Web sites supporting Google's suggestion [27], in which the canonical URLs are explicitly specified. The data are collected from 10 Web sites. (The 10 sites are extracted using the three categories: Sports, Travel and Business.) The average number of dup-clusters in a Web site is 275, while the total number of dup-clusters (peer matrixes) in the ten sites is 3170. The minimum number of URLs in a dup-cluster is 2, and the maximum number is 49. Our aim in this experiment is evaluating the performance of the proposed MSA algorithm in the DUST domain; we are not focusing on finding or evaluating the normalization rules that transform a group of URLs having the same formation into a canonical formation. We used the same measures used in the two experiments ($R$, $P$ and $F$) discussed before as well as the common score metric Sum of Pairs (SPS). Table 4 shows the results of the 10 Web sites. As shown in the table, the performance of the algorithm is high (recall, precision and F averages are 0.95, 0.93 and 0.94, respectively). The SPS score values (the average is 0.92) are calculated based on the distance scoring among the sequences.

Table 3 Performance comparison between our algorithm and both DCA and TEX

Table 4 Performance of the proposed algorithm in removing dust domain

7 Conclusion

This paper suggested a new multiple sequence alignment algorithm (NestMSA) that is inspired by the particle swarm optimization behavior. Different from all other researches that adapt PSO to solve the multiple sequence alignment problem, particles in our proposed algorithm are nested and communicated among the sequences (at one row in the matrix) to guarantee obtaining the global maximum. A new objective function is also suggested which considers all the characteristics of the multiple sequence alignment problem. To improve the efficiency of the algorithm, a combination of three different stopping criteria are applied to reduce the particles' flying span. The proposed algorithm considered the variations occurred in the multiple sequence alignment problem such as missing patterns, repetitive patterns and disjunctive patterns. We addressed the problem of MSA in the two domains Web data extraction and removing DUST as very few works are done although those are very important domains. But, we will consider the problem of DNA sequences alignment in which the sequences are very long with multiple nested repetitive regions in our future work.