Implementation of scalable bidomain-based 3D cardiac simulations on a graphics processing unit cluster

Abstract

Computational models of the human cardiac cells provide detailed properties of human ventricular cells. The execution time for a realistic 3D heart simulation based on these models is a major barrier for physicians to study and understand the heart diseases, and evaluate hypotheses rapidly toward developing treatments. Graphics processing unit (GPU)-based parallelization efforts to this date have been shown to be more effective than parallelization efforts on the CPU-based clusters in terms of addressing the 3D cardiac simulation time challenge. In this paper, we review all GPU-based studies and investigate both the cardiac cell models and cardiac tissue models in 3D space. We propose algorithmic optimizations based on red black successive over-relaxation method for reducing the number of simulation iterations and convergence method for dependence elimination between neighboring cells of the heart tissue. We investigate data transfer reduction and 2D mesh partitioning strategies, evaluate their impact on thread utilization, and propose a strongly scalable cardiac simulation. Our implementation results with reducing the execution time by a factor of five compared to the state-of-the-art baseline implementation. More importantly, our implementation is an important step toward achieving real-time cardiac simulations as it achieves the strongest scalability among all other cluster-based implementations.

1 Introduction

Chronic heart failure (CHF) occurs when the heart is damaged and unable to sufficiently pump blood throughout the body. CHF affects millions of Americans each year, and it is the leading cause of hospitalization of the patients over the age of 65 [1]. In addition, cardiac arrhythmias and sudden cardiac death, specifically due to ventricular tachycardia (VT) and ventricular fibrillation (VF) in patients with CHF, are among the most common causes of death in the industrialized world [2]. Despite decades of research, the relationship between CHF and VT/VF is poorly understood.

Computational models of the human cardiac cells exist and provide detailed properties of human ventricular cells, such as the major ionic currents, calcium transients, and action potential duration (APD) restitution, and important properties of wave propagation in human ventricular tissue, such as conduction velocity (CV) restitution (CVR). The complexity of detailed 3D models has led cardiac researchers to less accurate models, such as the monodomain model, that are computationally tractable. However, for studying cases such as the defibrillation in which the stimuli are applied extracellularly, the bidomain model is the desirable method.

Several studies [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] have focused on making 3D heart simulations a feasible option for cardiac researchers through exploitation of high-performance computing systems and parallelization of various cardiac models.

The program architecture of heart simulation involves iterative and inherently data parallel computations over cardiac cells, which makes it an ideal match for the fine-grained parallel computing capability offered by the GPUs. In our earlier work [3], we presented the parallel implementation of 3D heart simulation for a tissue size of $256\times 256\times 256$ cells and reported an execution time reduction factor of 637 based on a single GPU (Tesla C1060) over the serial version executing on a single CPU. In this study, we revisit our earlier implementation and map it onto a cluster of Nvidia K20X GPUs. We propose algorithmic optimizations, which significantly reduce the amount and the complexity of computations needed and accordingly reduce the execution time by a factor of two for the tissue size of $256\times 256\times 256$. Moreover, we evaluate the scalability of our earlier implementation on a multi-GPU system. We show that the intensive amount of data transfer overhead between the GPUs poses as a bottleneck from scalability point of view. Therefore, we investigate ways to achieve a strong scalability through reduction in the amount of data transferred among the GPUs and 2D mesh partitioning strategies. We show that there is a tight coupling between the data partitioning strategy and utilization of the threading power of the GPUs. We evaluate the impact of various partitioning strategies to minimize the data communication overhead while maximizing the thread utilization on a single GPU basis and identify the optimal partitioning strategy. We implement a strongly scalable cardiac simulation, which provides the strongest scalability among all other cluster-based implementations [15, 16] to the best over our knowledge. We show that the scalable and algorithmically optimized implementation reduces the execution time by up to a factor of five compared to our earlier work. We finally extend our analysis to monodomain model and show that our data partitioning approach when applied to this model also results in a scalable implementation.

This paper is organized as follows. In Sect. 2, mathematical foundations of the cardiac simulation and numerical strategies for describing the electrical behavior of heart are presented. In Sect. 3, we give an overview of the related work. In Sect. 4, we discuss the details of our parallelization approach on a single GPU, introduce two algorithmic optimizations, and evaluate the impact of our optimizations on the execution time performance. In Sect. 5, we present our optimization strategies for achieving strong scalability on a GPU cluster, which involves data reduction and 2D mesh partitioning among the GPUs. This is followed by Sect. 6, in which we discuss the implementation of a less accurate model and expose the trade-off between execution time and simulation accuracy. Finally, we present our conclusions in Sect. 7.

2 Mathematical model

Modeling the electrophysiological behavior of the heart involves coupling a cell model with a tissue model. A cell model provides the description of electrical activities that produce cardiac action potentials (APs). A tissue model provides the description of interactions among the cardiac cells. There is a large body of work on capturing the behavior of a heart cell through models that primarily vary in a number of variables with a trade-off in computation complexity and model accuracy. Similarly, tissue models have been introduced offering a choice between the accuracy and computation complexity. In the following subsections, we justify our choices for the cell and tissue models with a brief overview on each.

2.1 Cardiac cell models

Cardiac cell models [24,25,26,27,28,29,30,31] describe the electrical activities at the cellular level by taking into account both physical and chemical properties of that cell.

The excitement of a cell against a stimulus generates a charging followed by a discharging activity within the cell, and forms the AP. The voltage difference is the source of current flow in the form of change in ionic (sodium, and calcium) concentrations across a single cell. The voltage level is determined by the equations governing that specific cell model.

The TNNP [26] is a model with 19 variables, which includes detailed properties of human ventricular cells. This model has been shown to provide highly accurate analysis for clinical applications [27]. As shown by [32], TNNP offers the best trade-off between accuracy and computation time. For example, Karma [24] is a model successfully used for preserving important properties of cardiac cells including AP rate of rise, APD and CVR curves. This model is based on only two variables (membrane voltages and a gate variable) offering high computation efficiency. However, it offers limited accuracy in generating the AP curve, since it does not take into account critical phenomena such as spatial inhomogeneities, and electromechanical coupling, which play an important role for studying the abnormal heart rhythm [24]. The IMW [25] is a superior model than the TNNP since it is formed of 67 variables offering higher accuracy in describing the cardiac cell. However, the tight dependencies between operations over these variables as shown by Bartocci et al. [9] turn the execution into a sequential flow with limited parallelism. This makes this model less clinically applicable in comparison with the TNNP model.

The TNNP model is widely used by Majumder et al. [33, 34] and Nayak et al. [35] to study alternans and electrical instability, ionic current abnormalities, effects of inhomogeneities, and relationships between CV and fibroblast coupling parameters.

In TNNP model, the AP, which describes electrophysiological behavior of a single cell, is modeled by a set of ordinary differential equations (ODEs) as shown in (1) and (2) where $V_m$ is membrane voltage, t is time, $I_{\mathrm{{stim}}}$ is the externally applied stimulus current, $C_m$ is the cell capacitance per unit surface area, $I_{\mathrm{{ion}}}$ is the total membrane ionic current, $S_i$ are variables (ion concentrations and gates) that contribute to the modeling of $I_{\mathrm{{ion}}}$, and f is a function.

$$\begin{aligned} \frac{\mathrm{{d}}V_m}{\mathrm{{d}}t} &= - \frac{I_{\mathrm{{ion}}}(V_m,S_i)+I_{\mathrm{{stim}}}}{C_m} \end{aligned}$$

(1)

$$\begin{aligned} \frac{\mathrm{{d}}S_i}{\mathrm{{d}}t}&= f(t,S_i) \end{aligned}$$

(2)

$I_{\mathrm{{ion}}}$ consists of several types of ionic currents (${\mathrm{{Na}}}^+$, ${\mathrm{{Ca}}}^{2+}$, ${\mathrm{{K}}}^+$, etc.) as shown in (3).

$$\begin{aligned} I_{\mathrm{{ion}}}=I_{\mathrm{{Na}}}+I_{\mathrm{{K}}1}+I_{\mathrm{{to}}}+I_{\mathrm{{Kr}}}+I_{\mathrm{{Ks}}}+I_{\mathrm{{CaL}}}+I_{\mathrm{{NaCa}}}+I_{\mathrm{{NaK}}}+I_{\mathrm{{pCa}}}+I_{\mathrm{{pK}}}+I_{\mathrm{{bCa}}}+I_{\mathrm{{bNa}}} \end{aligned}$$

(3)

Each ionic current is calculated based on the membrane voltage, ion concentrations, and gates ($S_i$). The full specifications of these equations are presented in [26].

2.2 Cardiac tissue models

A cardiac tissue can be modeled as bidomain or monodomain. Bidomain refers to regions both inside a cardiac cell (intracellular) and its surrounding cells (extracellular) as shown in Fig. 1. The monodomain model is an approximation of the bidomain model, which assumes extracellular region has infinite conductivity. Although monodomain model is not as physiologically accurate as the bidomain model, it is utilized in large-scale simulations, since it allows reducing the computation complexity. However, for studying certain cases such as the defibrillation in which the stimuli are applied extracellularly, the bidomain model is the desirable method [36]. Defibrillation is a treatment for life-threatening cardiac dysrhythmias such as VT and VF. Therefore, we focus on implementing the bidomain model as a general-purpose solution for studying a wide range of heart diseases such as VT/VF.

Fig. 1

The equivalent electric circuit of cardiac cell based on bidomain model

The bidomain model is formulated by a series of data-dependent partial differential equations (PDEs) for describing the electrical interactions of cardiac cells.

The bidomain PDEs are shown in (4) and (5), where $\sigma$ is conductivity, $\Phi$ is potential, $V_m$ is membrane voltage, which is the potential difference between intercellular and extracellular potential ($V_m = \Phi _i - \Phi _e$), $I_{\mathrm{{ion}}}$ is the ionic current represented by the TNNP model and $I_{\mathrm{{stim}}}$ is the stimulus applied on a cell or a region of cells.

$$\begin{aligned} -\nabla .(\sigma _o \nabla \Phi _o)&= C_m\frac{\delta V_m}{\delta t} + I_{\mathrm{{ion}}}+I_{\mathrm{{stim}}} \end{aligned}$$

(4)

$$\begin{aligned} \nabla .((\sigma _i + \sigma _o)\nabla \Phi _o)&= -\nabla .\sigma _i \nabla V_m \end{aligned}$$

(5)

The space surrounding each cell is termed as the interstitial region. Intracellular and interstitial regions are bounded by the extracellular region. The parameters that belong to specific region of a cell are denoted by subscripts of o, i, and e, which stand for intracellular, extracellular, and interstitial region, respectively.

The PDEs simply state that the current flow entering the intracellular region leaves the extracellular region by crossing the interstitial region (cell membrane).

Boundary conditions are necessary to solve the PDEs. We assume cardiac tissue is surrounded in a saline bath. As an electrically isolated medium, no charge can be accumulated on the surface of the tissue. This can be formulated using (6).

$$\begin{aligned} \nabla ^2\Phi _e = 0 \end{aligned}$$

(6)

The first step to solve ODEs and PDEs is temporally and spatially discretization of the equations for which there are different methods, namely finite element method (FEM) and finite difference methods (FDM). Although FEM is better suited for solving PDEs in the environments with irregular geometry, FDM methods are more efficient in terms of execution time considering environment with regular geometry [37]. Therefore, we use FDM to approximate the aforementioned equations with difference equations. The difference equation obtained from discretizing the continuous domains (1) and (2) using forward difference method are shown in (7) and (8), respectively. We use central difference method to approximate (4)–(6) which are presented in (9)–(11).

$$\begin{aligned} (V_m)^{n+1}&= (V_m)^n - \frac{\Delta t}{C_m}(I_{\mathrm{{ion}}}+I_{\mathrm{{stim}}}) \end{aligned}$$

(7)

$$\begin{aligned} (S_i)^{n+1}&= (S_i)^n +\Delta t(f(t,((S_i)^n)) \end{aligned}$$

(8)

$$\begin{aligned} (\Phi _o)^{n}_{i,j,k}&= \frac{\mathrm{{Term}}1 + {\mathrm{{Term}}}2 + (I_{\mathrm{{ion}}}+I_{\mathrm{{stim}}})^n_{i,j,k}}{2\sum _{i,j,k}(\sigma _{ix}+\sigma _{ox})\slash \Delta x^2} \\ {\mathrm{{Term}}}1&= (\sigma _{ix}+\sigma _{ox})\frac{(\Phi _o)^n_{i+1,j,k}+(\Phi _o)^n_{i-1,j,k}}{\Delta x^2} \\&\quad +\, (\sigma _{iy} +\sigma _{oy})\frac{(\Phi _o)^n_{i,j+1,k}+(\Phi _o)^n_{i,j-1,k}}{\Delta y^2} \\& \quad +\, (\sigma _{iz} +\sigma _{oz})\frac{(\Phi _o)^n_{i,j,k+1}+(\Phi _o)^n_{i,j,k-1}}{\Delta z^2} \\ {\mathrm{{Term}}}2&= \sigma _{ix}\frac{(V_m)^n_{i+1,j,k}+(V_m)^n_{i-1,j,k}-2(V_m)^n_{i,j,k}}{\Delta x^2} \\&\quad +\, \sigma _{iy}\frac{(V_m)^n_{i,j+1,k}+(V_m)^n_{i,j-1,k}-2(V_m)^n_{i,j,k}}{\Delta y^2} \\&\quad +\, \sigma _{iz}\frac{(V_m)^n_{i,j,k+1}+(V_m)^n_{i,j,k-1}-2(V_m)^n_{i,j,k}}{\Delta z^2}) \end{aligned}$$

(9)

$$\begin{aligned} (V_m)^{n+1}_{i,j,k}&= (V_m)^n_{i,j,k} - \frac{\Delta t}{C_m} \left\{ \sigma _{ox}\frac{(\Phi _o)^n_{i+1,j,k}+(\Phi _o)^n_{i-1,j,k}-2(\Phi _o)^n_{i,j,k}}{\Delta x^2} \right. \\& \quad +\, \sigma _{oy}\frac{(\Phi _o)^n_{i,j+1,k}+(\Phi _o)^n_{i,j-1,k}-2(\Phi _o)^n_{i,j,k}}{\Delta y^2} \\& \quad \left. +\, \sigma _{oz}\frac{(\Phi _o)^n_{i,j,k+1}+(\Phi _o)^n_{i,j,k-1}-2(\Phi _o)^n_{i,j,k}}{\Delta z^2} \right\} \end{aligned}$$

(10)

$$\begin{aligned} (\Phi _e)^n_{i,j,k}&= \frac{1}{2\left( \frac{\sigma _{ex}}{\Delta x^2}+\frac{\sigma _{ey}}{\Delta y^2}+\frac{\sigma _{ez}}{\Delta z^2}\right) }\left\{ \sigma _{ex}\frac{(\Phi _e)^n_{i+1,j,k}+(\Phi _e)^n_{i-1,j,k}}{\Delta x^2} \right. \\&\quad \left. +\,\sigma _{ey}\frac{(\Phi _e)^n_{i,j+1,k}+(\Phi _e)^n_{i,j-1,k}}{\Delta y^2} +\sigma _{ez}\frac{(\Phi _e)^n_{i,j,k+1}+(\Phi _e)^n_{i,j,k-1}}{\Delta z^2}\right\} \end{aligned}$$

(11)

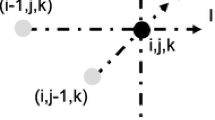
In the discretized form of (7)–(11), $\Delta t$ is time step; $\Delta x$, $\Delta y$, and $\Delta z$ are spatial steps; n represents the index of time step; and (i, j, k) represents mesh node indices in 3D space. Based on Taylor’s series expansion [37], the truncation error for the first order forward method is proportional to $\Delta t$ and for the second-order central difference method truncation error is proportional to $\Delta x^2$, assuming same spatial steps in each of the three directions. This is how we model a cardiac tissue with a mesh of cells.

3 Related work

Cardiac models have been parallelized in numerous forms on various platforms that resulted in significant speed-ups [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Among these studies, the graphics processing unit (GPU)-based parallelization efforts to this date have been shown to be much more effective than parallelization over the CPU clusters [8, 12, 16]. Therefore, our focus is on the GPU-based implementations in this paper. We review all GPU-based studies here to set the stage for our contributions as we investigate both the cardiac cell and tissue models equations in 3D space.

The study by Biffard and Leon [4] is one of the first investigations, which demonstrates the benefits of GPU for heart cell simulations. They use a 2D automaton model to implement cardiac tissue simulation on a GPU, where next state of each cell depends on its current state and the state of its neighboring cells. In the automaton model, cell updates are governed by fixed set of rules rather than differential equations. As a result, this approach simplifies the computation complexity with a trade-off in simulation accuracy.

Rocha et al. [5] investigate the 2D implementation of monodomain equations solvers for TNNP and LR-I [28] cardiac ionic models. They compare their implementation on a quad-core CPU with the one on an Nvidia GPU. Similar to the conclusions of the study by Vigmond et al. [6], they show that ODEs are better suited for parallelization on the GPU over the PDEs, and for the cardiac simulations, PDEs are the bottleneck.

Amorim et al. [7] compare OpenGL and CUDA implementations of the 2D bidomain equations in terms of performance and programmability. For each programming approach, they evaluate the impact of various implementation strategies on performance, and show the best strategy implemented in CUDA results in reducing the execution time by 22% more than the one implemented in OpenGL on a GeForce 8800GT GPU.

Amorim et al. [8] use the CellML [38] standard based on Extensible Markup Language (XML) for describing the cardiac cell models. They approach the problem of parallelizing differential equation solvers on GPUs through tool-assisted loop conversions. Specifically, they convert the differential equations embedded in a CellML file to a CUDA library that can be used in cardiac simulation. This allows them to rapidly evaluate multiple 2D cardiac models (TNNP, LR-I, MSH [29], BNK [30]) in terms of their computational complexity and execution time with mesh sizes ranging from $128\times 128$ to $1024\times 1024$. Their results indicate that the implementations of all the models on GPU run faster than the implementations on CPU. The speed-up gained from TNNP and LR-I models is higher than the MSH and BNK models as they offer better parallelization on the GPU. However, as opposed to the TNNP model, LR-I model is not applicable to human heart because it has been developed for describing AP in a single cell of guinea pigs heart.

Bartocci et al. [9] exhaustively investigate the complexity of 2D cardiac models with number of state variables ranging from two-variable Karma [24] model to 67-variable IMW [25] model. They present a detailed analysis on the effect of shared and texture memories on execution time, and show that texture memory-based implementation has better performance in terms of execution time for all the models and all the mesh sizes. Even though texture memory-based implementation is applicable for 3D simulation, it is not suitable for achieving high performance as updating texture memory directly from the device memory is not supported for the 3D objects [39].

There is a natural trade-off between accuracy of the 3D heart simulations and efficiency of the underlying parallel computations. Utilizing shorter time step ($\Delta t$) provides higher simulation accuracy while increasing the number of iterations and in turn increasing the execution time linearly. Therefore, identifying the time step is a balance between simulation accuracy and the execution time. One approach to deal with this trade-off problem is to adjust the time step duration at run time based on the phase of the simulation. Garcia et al. [10, 11] evaluate the impact of adaptively adjusting the time step on execution time and accuracy in a series of studies. In their earlier work [10], based on the 1D heart model, they show that the dynamic time step method implemented on a single GPU allows reducing the execution time of the simulations by 25%. However, for the case of CHF type of studies, heart cells go through unexpected and irregular transactions, which force a reduction in the time step. In their subsequent study [11], they show that the overhead of calculations used for determining the new step in each iteration becomes prohibitive particularly for cases where sudden changes in APs occur frequently. Therefore, the authors conclude that even though dynamically adjusting the time step amount helps improve the simulation accuracy, this method results in increasing the execution time.

Jararweh et al. [12] evaluate speed-up gain when porting cardiac simulation from CPU platform to GPU platform. For the cardiac simulation, they utilize the TNNP cell model and bidomain tissue model. Moreover, they exploit a machine learning approach to further speed up their simulation on a single GPU. This approach is based on the fact that rate of changes in potential of the cell over time varies in various phases of the AP. Therefore, not all the phases of AP require the same time resolution. Their implementation adjusts the time step for each phase with a machine learning method based on the values of five time-dependent gates. By utilizing this approach, they achieve a six times speed-up over the traditional approach (fixed time step). However, their approach suffers from a misclassification rate of 16.38%. Recently, we proposed a new method for detecting the phase of 3D heart simulation and evaluated based on the monodomain model [13]. We achieved a misclassification rate of 1% and reduced the execution time by a factor of 28.4 on a single GPU and 191 on a 16-GPU-based implementation. After presenting our implementation approach for the bidomain model, later we will revisit our monodomain implementation, show that some of the parallelization strategies used for the bidomain model are applicable to the monodomain model and quantify the speed-up achieved over the monodomain implementation as well.

Yu et al. [14] propose a 3D anatomic model of the human heart along with a cardiac electrophysiological model. They map the compute-intensive ODE and PDE solvers onto the GPU. In addition, the authors use OpenGL for visualizing anatomic cardiac model. Even though they are able to simulate the entire APD in real time, the implementation is not practical for accurately analyzing the cardiac cells since they simplify the model significantly by excluding the micro-scale details of ionic and molecular cell properties.

Chai et al. [15] perform a high-resolution 3D cardiac simulation by solving monodomain ODE equations for two different heart models using two different differential equation solvers. They analyze the execution time and scalability of the implementation on a GPU cluster using up to 128 GPUs. Although they implement a strongly scalable partitioning strategy, they are not able to achieve linear scalability.

We are aware of other heart simulations using GPU such as [16,17,18,19]. However, these studies target animal heart such as rabbit and sheep. These models significantly differ from human heart in various aspects, namely shape, structure, and properties of the cells, which make them unsuitable for clinical studies involving human heart. In this study, our simulation targets practical medical application for treatment and study of human heart disease; therefore, we exclude them from our analysis. However, we will refer to the implementation of Neic et al. [16] when evaluating the parallel efficiency (scalability) of our implementation as it is the state of the art in terms of scalable bidomain implementation on a GPU cluster to the best of our knowledge.

In summary, human heart simulations have mainly concentrated on single GPU-based implementations. More recent studies have benefited from the GPU clusters [15, 16]. Based on them, we observe that scalability of the implementation is an important barrier.

In Table 1, we show the categorization of GPU-based cardiac simulation studies in terms of the cell and tissue models they are built on along with the tissue size, tissue dimension and programming approach as each of these features plays a critical role on the simulation quality and execution time performance

Table 1 Features of other implementations including cell and tissue models, platform, programming language, tissue size and dimension

4 Implementation details

We use Extremely LarGe Advanced TechnOlogy (El Gato) computing system at the University of Arizona. This system includes 2176 Intel cores, Mellanox FDR InfiniBand network with a fully non-blocking fat tree topology, 26TB of RAM, 140 Nvidia Tesla K20X GPUs, 40 5110P Intel PHIs, and 190TB of DDN SFA12K shared storage. The Mellanox FDR InfiniBand network has Raw Signaling Rate of 14.1 Gb/s, Effective Data Rate of 13.64 Gb/s, and Aggregated ($4\times$) Throughput of 54.5 Gb/s. It can achieve latency as low as 0.7 ms. Each GPU node includes two Tesla K20X GPUs and two 8-core Intel Xeon Processors (E5-2650 v2 2.60 GHz with 256 GB 1800 MHz RAM). This node has PCIe Gen3 x16 bus with the speed of 15.75 GB/s. We use a single Xeon processor in this system for measuring the execution time of the sequential code. The K20X has 6 GB of global memory. During our simulations on a single GPU, we target mesh sizes from $32\times 32\times 32$ to $256\times 256\times 256$ due to the global memory limitation. During our simulations on GPU clusters for conducting scalability analysis, for each mesh size we vary the number of GPUs from 1 to 16. We also increase the mesh size to $512\times 512\times 512$ and conduct execution time and scalability evaluations on 4, 8, and 16 GPU configurations. For obtaining accurate timing measurements on the system, we request the required nodes for exclusive use with no other job running on that node. By doing so, scheduler solely runs our job on the requested nodes. We use CUDA version 8.0 and OpenMPI version 1.8 for internode communications.

We also use the parallel efficiency metric for measuring the scalability of our implementation and comparing with respect to other implementations. Parallel efficiency is the ratio of speed-up to the number of processing elements. The efficiency value of one indicates linear scalability, whereas the value below one indicates sublinear efficiency [40].

In the following subsections, we first present the sequential and single GPU implementations. We then present our optimization strategies on a single GPU with performance analysis.

4.1 Sequential implementation

We first solve (7) and (8) to obtain voltage values at each time step. Then, we use these values to solve bidomain equations (9)–(11) for potential values. As shown in these equations, potential of each cell is expressed as a function of its six neighboring cells in 3D space. This generates a system of equations for a given mesh size of $256\times 256\times 256$. There are two classes of iterative methods to solve difference equations, namely stationary and non-stationary methods. In general, non-stationary iterative methods provide a better convergence and accuracy. However, in this study we utilize the stationary Jacobi iterative method similar to [7, 12], which provides SIMD-level parallelism making it an ideal match for parallelizing on the GPU architecture. In this method, we start with initial values for $256\times 256\times 256$ unknown potentials, and execute several (spatial) iterations to approximate the unknown values. The approximations at a given iteration are based on the values from previous iteration. As we go through spatial iterations, the approximations become more accurate; that is, the error of evaluation becomes smaller. To calculate the error of this numerical method, in our earlier work [3] we used the Euclidean norm as shown in (12).

$$\begin{aligned} \Vert e^s\Vert _2= \sqrt{\sum _{i,j,k}\left( (\Phi _o)^s_{i,j,k}-(\Phi _o)^{s-1}_{i,j,k}\right) ^2} \end{aligned}$$

(12)

This equation calculates the sum of the squares of the difference between the new potential and the old potential in consecutive spatial iterations for all of the cells in the 3D mesh. In this equation, s represents the index of spatial step. The error tolerance ($\varepsilon =\Vert e^s\Vert /\Vert e^0\Vert$) of $10^{-1}$ as the convergence criteria is used in Jacobi iterative method. We set the time step ($\Delta t$) to 0.02 ms. Therefore, simulation of one APD (360 ms) needs 18,000 time steps. Space step indicates the level of spatial resolution. We set the space step to 0.03 mm in all 3D directions ($\Delta x$, $\Delta y$, and $\Delta z$). These values are the same as the ones suggested by Ten Tusscher et al. [26].

As explained in Algorithm 1, the cardiac simulation starts with an initialization of the TNNP model variables including voltage, time-dependent gates, and ionic currents. This phase is followed by a time-stepping loop executed for 18,000 temporal iterations of a single AP. This loop involves the ODE solvers of TNNP model, a space-stepping loop for solving the system of PDEs of bidomain model, potential update, and voltage update stages. The stimuli are applied to certain cells at specific time steps during the simulation based on the dynamic restitution protocol [26].

Figure 2 shows the execution time of simulating 3D cardiac tissues with various mesh sizes ranging from $32\times 32\times 32$ to $512\times 512\times 512$ cells on a general-purpose processor. As we can see, the execution time increases linearly with the mesh size. We also observe that 10 temporal iterations of cardiac simulation for a mesh compromised of $512\times 512\times 512$ cells (134 million) on a CPU take 221 min which corresponds to about 9 months for the simulation of an APD (18,000 temporal iterations). We report this execution time only for highlighting the significance of the computation time for 3D simulations, which is prohibitive for conducing medical studies on CHF.

In the following subsections, we will present our implementation and optimization approaches incrementally. We first present the single GPU-based implementation followed by two algorithmic optimizations.

Fig. 2

Cardiac simulation (10 temporal iterations) time (s) on a CPU with respect to change in mesh size (based on logarithmic scale base 8) shows linear increase in execution time

4.2 Single GPU implementation

In our earlier GPU-based implementation, the CPU still remains in charge of the control flow of simulation that was explained in Algorithm 1, while the compute-intensive tasks are offloaded to the GPU. We create a kernel for each stage of the simulation flow as shown in Fig. 3a. The CPU executes the loops involved in the simulation and launches the kernels on the GPU. We employ the data parallelization at cell level for the ODE solvers of TNNP model; that is, we distribute the workload by assigning the required computations of each cell to one thread. Based on (9)–(11), the membrane voltage and intracellular potential of each cell are computed using the data from the cell itself together with the six neighboring cells also known as seven-point stencil computation. The parallelization for this task is also implemented at cell level.

Fig. 3

Execution flow with two parallelization strategies a 4-kernel; b 6-kernel

[3] conducted a series of experiments on parallelization and task partitioning strategies for the GPU architecture using Tesla C1060 GPU. Figure 3b shows the best-case task partitioning strategy with six kernels. However, the performance difference in terms of execution time between 6-kernel-based and 4-kernel-based implementations shows a negligible difference of 1%. In addition, in [3], the time step was chosen to be 0.035 ms, which required only 10,000 time steps to complete the simulation. In this study, we increase the number of time steps by increasing the resolution of the simulation. Since each temporal iteration requires six kernel launches for this implementation, based on the second strategy, the kernel launch overhead is expected to increase. Therefore, in this study, we choose to keep our task partitions compact to reduce kernel launch overhead and partition the tasks into four kernels only. In this implementation, we employ standard GPU memory optimization strategies such as coalesced memory accesses.

As the access to global memory is costly, minimizing these memory transactions is crucial in program performance. One of the effective strategies to reduce the bandwidth is memory coalescing. The memory coalesced access happens when the threads in the block access the continuous address from the memory. To this end, we use a proper data structure similar to the one in [3]. This data structure contains 22 arrays of variables including 19 variables of TNNP [26] model (ion and gate values), membrane voltage, new membrane voltage, and total ionic current as shown in Fig. 4. When scanning the 3D space, the access pattern is also designed in such a way that subsequent threads access the subsequent cells to ensure coalescing.

Fig. 4

Instances (a) of the data structure (b) for $256\times 256\times 256$ mesh. Thread blocks are organized in z direction

For the case of $256\times 256\times 256$, we report the hardware utilization values and performance metrics in Table 2. As reported in this table, the archived occupancies of Kernels 1 and 2 are lower than Kernels 3 and 4, because of the higher number of registers per thread. The K20X is capable of running 2048 threads per multiprocessor. Hence, for achieving the maximum occupancy, Kernel 2 needs $53\times 2048=106\hbox {K}$ registers per multiprocessor, which exceeds the number of available registers (64K) per multiprocessor. In the memory bandwidth column, we see that the Kernel 3 has a lower bandwidth in comparison with the other kernels. The reason is that in Kernel 3, there are two memory transactions (one write and one read) per thread, while in the other kernels there are seven transactions (six reads and one write) per thread as shown in (7)–(11). As seen in the table, Kernel 3 is more compute-intensive in terms of execution time than the other kernels while achieving low bandwidth utilization. Therefore, as a part of our optimization strategy we target particularly this kernel and investigate algorithmic optimizations as we will discuss in the following subsection.

Table 2 Statistics of hardware utilization and performance metrics by a single GPU for Kernel (K) 1, 2, 3, and 4 ($256\times 256\times 256$ mesh, 100 temporal iterations)

Table 3 shows how the execution time for Nimmagadda’s implementation [3] scales on the K20x GPU with respect to its published implementation on the Tesla C1060 GPU. It is a reasonable assumption that the execution time scales linearly with number of processor cores, and processor core clock of the underlying GPU. Based on these two hardware features, we would expect to observe about six times reduction in execution time, which is almost consistent with what we achieve based on Table 3.

Table 3 Execution time (s) for the Nimmagadda’s [3] implementation based on a single K20X GPU (baseline) ($256\times 256\times 256$ mesh, 18,000 temporal iterations)

The drawback of the implementation by Nimmagadda et al. [3] is its error tolerance ($\varepsilon$) of $10^{-1}$. As shown by recent studies [41], the error tolerance should be less than $10^{-3}$. Therefore, in this study we reduce the error of the numerical method used for solving the PDEs by employing an error tolerance of $10^{-3}$ instead of $10^{-1}$. This two orders of magnitude increase in the resolution results in a linear increase in the execution time to 19,106 s as reported in Table 4. For the remainder of this paper, all the implementations are based on the new error tolerance value. This implementation forms the baseline for our evaluations.

Table 4 The execution time (s) for the implementations with the error tolerance ($\varepsilon$) of $10^{-1}$, and $10^{-3}$ (baseline); Kernel 3 elimination; and RBSOR method ($256\times 256\times 256$ mesh, 18,000 temporal iterations)

4.3 Algorithmic optimizations

Figure 5 shows how various kernels contribute to the total execution time. As we can see, 44% of the execution time is spent on Kernel 3, which calculates the error of solving the PDEs. To remove this calculation overhead, we utilize the maximum norm in (13) as the criteria for error calculation instead of Euclidean norm.

$$\begin{aligned} \Vert e^s\Vert _\infty = \max _{i,j,k}{|(\Phi _o)^s_{i,j,k}-(\Phi _o)^{s-1}_{i,j,k}|} \end{aligned}$$

(13)

Fig. 5

The percentage of the time spent on various kernels of the program ($256\times 256\times 256$ mesh)

To make sure that the accuracy of simulation is consistent by using different error criteria, we choose error tolerance in such a way that the number of spatial iterations remains unchanged. Based on the max norm criteria, we need to calculate the maximum over all the cells similar to Euclidean norm. However, we slightly modify the iterative process of deciding whether to perform next spatial iteration or not. To do so, instead of calculating the maximum norm, and then comparing it with an error tolerance (global error), each thread can compare the error of calculation at each cell (local error) with the error tolerance and update a global variable only if the local error exceeds the error tolerance. In this approach, each thread can update the global variable in parallel because of the lack of data dependency between threads for performing this operation. Therefore, at each spatial iteration, by the time the last unknown variable is solved we have the error calculated as well and we are able to eliminate Kernel 3 without an overhead for Kernel 2. As a result of the elimination, the execution time is improved by 39% as reported in Table 4.

As shown in Fig. 5, most of the simulation time is spent on solving the PDEs, because as opposed to the ODEs, they are calculated using the Jacobi iterative method that takes several spatial iterations. One way to reduce this time is to decrease the number of spatial iterations needed for solving the PDEs. To do so, we use successive over-relaxation (SOR) [42] iterative method instead of Jacobi method. Considering (9), the difference between these two methods is that in Jacobi method, the values of $(\Phi _o)^{s+1}$ in the cells are not calculated until entire iteration (s) is calculated, while in SOR method, the values of $(\Phi _o)^s$ are used for the computation of $(\Phi _o)^{s+1}$ as soon as they are calculated. In other words, in a particular iteration, with Jacobi method, all the known values are from previous iteration, while in the SOR method, the values used for computations include both the new values calculated in the current iteration and values from the previous iteration. Therefore, the SOR method has a faster rate of convergence because it uses the values as soon as they become available.

However, when it comes to parallel computations, SOR method suffers from data dependency between calculations of each cell during each spatial iteration. To overcome this issue, we utilize the red/black SOR (RBSOR) method [42], which resolves this data dependency. In this method, the cells are divided into two subsets with different colors (red and black) such that there is no data dependency between calculations of the cells with the same color as shown in Fig. 6. Therefore, the calculations of the cells with the same color can be parallelized. The PDEs are solved in two phases. First, the calculations of the red cells are performed and they are updated as shown in (14) where $i+j+k$ is even. This is followed by calculating and updating black cells as shown in (15) where $i+j+k$ is odd. In (14) and (15), Term2 is the same as the one in (9) and $\omega$ is relaxation parameter. This parameter affects convergence rate of the BRSOR iterative method. There are analytical approaches for determining the relaxation parameter [43]. However, we take an experimental approach by programmatically sweeping and evaluating various relaxation parameters. To do so, we run Algorithm 1 and count the total number of iterations to solve (9) for $\omega$ values in the range 1–2 with step size of 0.01 as suggested by [44]. Then, we pick the $\omega$ value that results with the lowest number of iterations. Our analysis shows that relaxation parameter of 1.83 provides the best convergence rate.

$$\begin{aligned} (\Phi _o)^{s+1}_{i,j,k}&= (1-\omega )(\Phi _o)^{s}_{i,j,k} + \omega \left( \frac{\mathrm{{Term}}1 + {\mathrm{{Term}}}2 + (I_{\mathrm{{ion}}}+I_{\mathrm{{stim}}})^s_{i,j,k}}{2\sum _{i,j,k}(\sigma _{ix}+\sigma _{ox})\slash \Delta x^2}\right) \\ {\mathrm{{Term}}}1&= (\sigma _{ix}+\sigma _{ox})\frac{(\Phi _o)^s_{i+1,j,k}+(\Phi _o)^{s}_{i-1,j,k}}{\Delta x^2} \\&\quad +\, (\sigma _{iy} +\sigma _{oy})\frac{(\Phi _o)^{s}_{i,j+1,k}+(\Phi _o)^s_{i,j-1,k}}{\Delta y^2} \\&\quad +\, (\sigma _{iz} +\sigma _{oz})\frac{(\Phi _o)^{s}_{i,j,k+1}+(\Phi _o)^s_{i,j,k-1}}{\Delta z^2} \end{aligned}$$

(14)

$$\begin{aligned} (\Phi _o)^{s+1}_{i,j,k}&= (1-\omega )(\Phi _o)^{s}_{i,j,k} + \omega \left( \frac{\mathrm{{Term}}1 + {\mathrm{{Term}}}2 + (I_{\mathrm{{ion}}}+I_{\mathrm{{stim}}})^s_{i,j,k}}{2\sum _{i,j,k}(\sigma _{ix}+\sigma _{ox})\slash \Delta x^2}\right) \\ {\mathrm{{Term}}}1&= (\sigma _{ix}+\sigma _{ox})\frac{(\Phi _o)^{s+1}_{i+1,j,k}+(\Phi _o)^{s+1}_{i-1,j,k}}{\Delta x^2} \\&\quad +\, (\sigma _{iy} +\sigma _{oy})\frac{(\Phi _o)^{s+1}_{i,j+1,k}+(\Phi _o)^{s+1}_{i,j-1,k}}{\Delta y^2} \\&\quad +\, (\sigma _{iz} +\sigma _{oz})\frac{(\Phi _o)^{s+1}_{i,j,k+1}+(\Phi _o)^{s+1}_{i,j,k-1}}{\Delta z^2} \end{aligned}$$

(15)

In the first phase, the calculations of red cells depend only on the data from black cells, which are available from previous iterations and vice versa in the second phase. Table 5 shows the statistics for the two implementations of Kernel 2 using Jacobi and RBSOR. Based on RBSOR method, Kernel 2 operates on the half of the cells (either black or red) at a time, while in Jacobi-based method it operates on all the cells at a time. Therefore, we launch Kernel 2 in RBSOR implementation with half of the thread blocks that we launched in Jacobi implementation. Accordingly, we expect that the average execution time to be reduced by 50%; however, the results in Table 5 show that the execution time is reduced by 35%. This is because, in RBSOR-based implementation, the accesses of threads to global memory are strided. This non-coalesced accesses cause reduction in memory throughput and accordingly increase in the execution time of the kernel as shown in Table 5. The coalesced memory access pattern can be achieved by reordering of cells such that the cells with the same color are grouped. However, since different kernels operate on the 3D mesh of the cells, reordering affects their functionality. Despite the non-coalesced access pattern, the total execution time of Kernel 2 is reduced by 36%. As reported in Table 4, the total execution time of this kernel is accordingly improved by 26% in comparison with the implementation with Kernel 3 elimination. This is because of the reduction in the total number of spatial iterations for solving the PDEs. We will refer to this implementation as algorithmically optimized (AO) version. In overall, we conclude that the RBSOR and the Kernel 3 elimination-based implementation reduce the execution time by a factor of two.

Fig. 6

Red/black reordering technique

Table 5 Comparison of Kernel 2 implementations based on Jacobi and RBSOR methods on a single GPU ($256\times 256\times 256$ mesh, 100 temporal iterations)

5 GPU cluster implementation

Nimmagadda et al. [3] evaluated the scalability of the baseline implementation on a four-GPU system with a single CPU as the controller and its DRAM acting as the shared memory for the GPU devices using OpenMP. In this study, our aim is to investigate the scalability of our baseline implementation on a distributed memory system using message passing interface (MPI). In this parallel implementation, multiple processes are created and run on the host CPUs of a cluster. These CPU processes are responsible for synchronization, launching the kernels, and data partitioning among the GPUs.

In the case of four GPUs, we divide the entire 3D mesh equally across the GPUs with planes perpendicular to x direction as shown on Fig. 7. We refer to this as 1D partitioning strategy. For the seven-point stencil calculation, each cell needs to communicate the membrane voltage to the neighboring cells in the 3D directions. With this partitioning strategy, data associated with the cells in the interface regions are exchanged between the GPUs. Data transfer from memory of one GPU device to the memory of the other GPU device is handled through the host CPU as shown in Fig. 8.

Fig. 7

Partitioning of the 3D mesh across four GPUs. The interface regions (shaded areas) have inter-GPU data dependency, which are exchanged among GPUs. The numbers on partitions show the processes number that controls the calculation of these partitions. The numbers on arrows show the order in which the inter-GPU transfers are completed

Fig. 8

Inter-GPU communication

The order of data transfer transactions between GPUs is also shown in Fig. 7. Nodes 0 and 2 simultaneously send data using MPI_Send() routine to nodes 1 and 3, respectively. MPI_Send() routine is a synchronous (blocking) operation, such that a process does not return (blocked) until its data transfer has been completed. As soon as processes 1 and 3 indicate the completion of data transfer, then processes 0 and 2 simultaneously send data to 1 and 3, respectively. After this transaction, processes 1 and 2 exchange their data in a similar fashion. Therefore, for this case, there are four sequential data transfers in total. In half of the transactions, there are two parallel data transfer and in the other half there is only one. We represent this as 1 and 2. It is not suitable to utilize other communication methods such as collective communication (message broadcasting) and asynchronous communication for our application. The collective communication method involves the communication among all processes. However, in our application the data have to be exchanged between pairs of nodes only. In asynchronous communication, as opposed to synchronous (blocking) messaging, the send and receive operations are completed without waiting for completion of the data transfer. In our simulation, the next operation depends on the data received from the MPI communication; therefore, all nodes need to complete data transfer before starting the next iteration.

Figure 9 shows the breakdown of total execution time to computation and communication time with respect to number of GPUs for the mesh size of $256\times 256\times 256$. We observe that this partitioning strategy is not scalable as the rate of reduction in execution time reduces and starts saturating as we increase the number of GPUs. Nimmagadda’s implementation [3] showed almost linear reduction as the number of GPUs is scaled from one to four on a shared memory system. We also observe a similar trend in the distributed system-based implementation. In both of the implementations, we observe the execution time reduces by a factor more than $3.6\times$ using four GPUs. However, the current implementation does not show scalability over eight and 16 GPUs. Figure 9 also shows the percentage ratio of communication time to total execution time for each GPU configuration. Despite the reduction in computation time, the data transfer time overhead due to the MPI communication becomes a performance bottleneck with the 1D partitioning strategy. To address this scalability issue, we design and analyze two optimization strategies.

Fig. 9

Scalability analysis based on the communication time over total time with respect to number of GPUs ($256\times 256\times 256$ mesh, 18,000 temporal iterations)

5.1 Data reduction optimization

In the AO implementation, the whole data structure in the interface regions is transferred from one GPU to another GPU, while only membrane voltage (or intracellular potential) is used for cell interaction calculations. To transfer this variable individually, we create a strided MPI datatype. As shown in Fig. 10, the array of membrane voltage is copied with the specified stride. Apart from strided MPI data type, as the transfer is staged through CPU memory, we also utilize strided memory copy between global and host memories. This reduction in the size of transferred data results in less communication time and accordingly improved scalability. For the mesh size of $512\times 512\times 512$, an instance of data structure contains the variables for 512 cells. In other words, it has 22 arrays, each of which consists of 512 elements. The elements of the array are floating point variables with the size of 4 bytes (B). Therefore, the size of an instance of the data structure is $512\times 22\times$4B = 44KB. After using the strided MPI datatype, the size of transferred data for 512 cells becomes $512\times 1\times 4\hbox {B} = 2\hbox {KB}$ since only the array of membrane voltage (or intracellular potential) is transferred. This results in 95% reduction in the data transfer amount for each time step of the simulation. As shown in Fig. 10, this optimization approach reduces the communication time significantly (by a factor of 11); however, by increasing the number of GPUs, the amount of the data needed to be exchanged increases. To overcome this limitation factor, we introduce another partitioning strategy in the next subsection.

Fig. 10

MPI strided datatype for $512\times 512\times 512$ mesh

5.2 Partitioning optimization

In this subsection, we evaluate the impact of various mesh partitioning strategies across multiple GPUs on communication time overhead and computation time. For a configuration that offers multiple partitioning options, we present a case study on partitioning strategies among eight GPUs. For this case, there are three possible partitioning strategies as shown in Fig. 11. As we can see from this figure, there are 7, 4, and 3 cuts for 1D Fig. 11a, 2D Fig. 11b and 3D Fig. 11c partitioning strategies, respectively. Accordingly, the total data transfer for these partitioning strategies are 28KB, 32KB, and 6KB. Therefore, we expect 3D partitioning results in best communication overhead. However, applying cuts in three directions limits the number of threads per block on the GPU. Assume that for the mesh of $512\times 512\times 512$, we apply cuts perpendicular to x and y directions. In this case as shown in Fig. 11b, the threads are organized in z direction where each thread block operates on 512 cells with 512 threads concurrently. This would result in launching 262,144 thread blocks ($512\times 512$). When we apply the cut in 3 directions Fig. 11c, then we divide the mesh size perpendicular to z direction by half reducing the number of threads per block to 256. This would result in doubling the number of thread blocks. The K20X GPUs have 14 multiprocessors, and the maximum number of resident blocks per multiprocessor is 16. Plus, there can be a maximum of 224 active thread blocks on the device. Therefore, the thread blocks are scheduled iteratively in rounds. Reducing the thread block size doubles the number of iterations. Given that each thread is assigned to a single cell and the operations over the single cell are the same across the threads, the execution time for a thread block of size 256 and size 512 is expected to be close to each other. Intuitively, we expect 3D scenario to increase the execution time by a factor of 2.

Therefore, we conclude that the 2D partitioning is the desirable strategy for our cluster-based simulation. Now that we have concluded the advantage of 2D partitioning, we analyze the communication time overhead with respect to number of GPUs based on the 1D and 2D partitioning strategies identified for each configuration. For the 1D partitioning, as shown in Table 6, we see an increase in the communication time with the number of GPUs. This is because of the increase in the number of parallel data transfers. For the 2D partitioning strategy, we see a decrease in communication with respect to the number GPUs. That is because despite an increase in number of parallel data transfers, the total data transfer decreases. Therefore, we conclude that the size of data transfer has a stronger effect than number of parallel data transfers. Although the contribution of data transfer overhead is small relative to the time spent on computation, as the number of GPUs increases the relative importance of the data transfer overhead will become an important factor in terms of the scalability of the implementation. Therefore, the partitioning strategy and quantifying its benefits are an important task.

Fig. 11

Possible partitioning strategies for the 3D mesh across 8 GPUs; a 1D partitioning, b 2D partitioning, c 3D partitioning

Table 6 Statistics of 1D and 2D partitioning strategies (PS) for $512\times 512\times 512$ mesh and 18,000 temporal iterations (the letter in the parenthesis shows the direction with which the cut is associated)

As reported in Table 6, we present the total amount of data transfers between neighboring GPU pairs during each iteration for the case of $512\times 512\times 512$. For the worst-case scenario, a single GPU sends 2KB of data and receives the same amount of data during each iteration. Throughout the 18,000 steps, the total amount of data transfers is around 70MB. This data are transferred between GPUs on the same node through PCIe bus and between GPUs on different nodes through the network. As mentioned in Sect. 4, the bandwidth of the network and PCIe bus is 54.5 Gb/s and 15.75 GB/s, respectively. Therefore, the communication overhead of our implementation is far from stressing the PCIe bus or network bandwidth.

5.3 Results

We present the total execution time for the final version of our implementation, which benefits from both algorithmic and communication optimizations for various mesh sizes with respect to the number of GPUs in Fig. 12. Since we set the thread block size equal to the mesh size, Kernel 2 is launched with $(32\times 32)/2 = 512$ thread blocks for the $32\times 32\times 32$ mesh. However, not all the thread blocks can be executed simultaneously because of two limitations, namely maximum of 16 thread blocks and 2028 threads per multiprocessor. Based on these limitations, simulating this mesh would take three rounds to complete on a single GPU and two rounds to complete on two GPUs. Subsequent GPU configurations (4, 8 and 16) would complete the execution in one round. Therefore, we do not observe any improvement in execution time if we utilize more than four GPUs. Apart from this, we observe that the execution time increases with 8 and 16 GPUs compared to the 4-GPU configuration, because communication time in these two configurations is higher than the 4 GPU configuration. The number of rounds for the mesh size of $64\times 64\times 64$ is 10, 5, 3, 2, and 1 for the configurations with 1, 2, 4, 8, and 16 GPUs, respectively. For this and the larger meshes (128, 256, and 512), we observe that execution time improves as we increase the number of GPUs because of the decreasing trend in the number of rounds. We use the same approach for analyzing the execution time over various mesh sizes. On a single GPU, for the mesh sizes ranging from $32\times 32\times 32$ to $256\times 256\times 256$, there are 3, 10, 37, 293 rounds of executions, respectively. Therefore, the execution time increases with the mesh size. It is worth mentioning that the execution time is not exactly proportional to the number of the rounds, because the reported numbers of rounds are based on the Kernel 2 only. Even though the number of rounds varies across different kernels, our analysis is still fairly accurate because more than 90% of the computation time is spent on Kernel 2.

Fig. 12

Execution time (s) for final implementations with various mesh sizes over 1 to 16 GPUs (18,000 temporal iterations)

To show the scalability of the final version, we report the parallel efficiency of the final implementations for meshes with $128\times 128\times 128 \approx 2\hbox {M}$, $256\times 256\times 256 \approx 17\hbox {M}$, and $512\times 512\times 512 \approx 134\hbox {M}$ cells as well as one of the state-of-the-art bidomain implementations by Neic et al. [16] in Table 7. Besides using a different cell model (rabbit ventricles), the implementation by Neic et al. [16] is based on a cluster with Nvidia Tesla C2070 GPUs each with 6 GB RAM. The data presented in Table 7 are generated based on the execution time results reported in [16]. Since this is one of the only two studies on a GPU cluster and achieves a very good scalability, we treat it as a benchmark for evaluating the quality of our implementation.

Starting with two GPUs, as we double the resources up to 16 GPUs, the parallel efficiency decreases with a fast rate for the final implementation with 2M cells. The parallel efficiency over all the number of GPUs improves for the larger meshes. That is because the ratio of the communication to computation time increases by utilizing more number of GPUs, and accordingly the overhead of partitioning the data becomes a performance bottleneck. Improvement obtained from partitioning the workload among multiple GPUs needs a reasonable ratio of the computation to communication similar to the cases of $256\times 256\times 256$ and $512\times 512\times 512$. Therefore, for small mesh sizes, one GPU is the best hardware configuration for simulation.

Table 7 The parallel efficiency of the final implementations and Neic et al. [16] with respect to the number of GPUs

The parallel efficiency of Neic et al. [16] implementation with 41M cells outperforms the final implementation for $256\times 256\times 256$ mesh up to 8 GPUs. However, for 16 GPUs, final implementation has better parallel efficiency. This shows that for the higher number of GPUs, our implementation has stronger scalability than Neic et al. [16]. The significance of our work is shown by the final implementation for $512\times 512\times 512$ mesh which has completely linear scalability. Finally, we conclude that the final implementation is scalable to higher number of GPUs, if sufficient amount of workload for computation is provided for each GPU.

The serial code written in a naive way takes 844 hours to complete on a single CPU core at 2.6 GHz with 256 GB memory for a $256\times 256\times 256$ mesh. Serial version, of course, can be restructured for multithreaded and vectorized forms by a performance programmer with SIMDization techniques for further performance improvement. Our aim is to simply set a reference point for the CPU execution time and not a performance comparison. With the final implementation on 16 GPUs, we achieve a reduction in $4787\times$ over the serial implementation.

5.4 Correctness of implementation

We visualize the propagation of electrical waves through the simulation that is written to the text files, and then they are processed for offline visualization. Figure 13 shows the excitation propagation in 3D cardiac tissue in different time steps. Figure 13 at $t = 60\hbox {ms}$ shows position of the applied stimulus and its propagation through the whole tissue in the subsequent time steps. We conduct some experiments to validate the 3D simulation with spiral wave propagation shown in Fig. 14. We compare the AP curves for each cell between our implementation and the TNNP with the tissue size of $16\times 16\times 16$. The relative root mean square (RRMS) error between the two implementations is $1.32\times 10^{-3}$, which is comparable with the results reported in [5]. Figure 15 shows the two AP curves for a single cell. The literature in cardiac simulation finds such RRMS acceptable [45].

Fig. 13

Excitation propagation in a cardiac tissue with $32\times 32\times 32$ cells

Fig. 14

Spiral wave in a $256\times 256$ tissue

Fig. 15

AP curves of a single cardiac in a our implementation; b Ten Tusscher’s implementation [26]

6 Monodomain implementation

The monodomain model is a simplification of the bidomain model in which it is assumed that the anisotropic ratio for the intra- and extracellular domains is equal, that is $\sigma _i = k \sigma _e$. As a result, we can derive the relationship between ionic and transmembrane voltage shown in (16) using (4) and (5).

$$\begin{aligned} -\nabla .(\sigma _i \nabla V_m) = C_m\frac{\delta V_m}{\delta t} + I_{\mathrm{{ion}}}+I_{\mathrm{{stim}}} \end{aligned}$$

(16)

Using the center difference formula [37], we discretize (16) as shown in (17).

$$\begin{aligned} \begin{aligned} (V_m)^{n+1}_{i,j,k}&= (V_m)^n_{i,j,k} + \Delta t \left\{ \sigma _{ix}\frac{(V_m)^n_{i+1,j,k}+(V_m)^n_{i-1,j,k}-2(V_m)^n_{i,j,k}}{\Delta x^2} \right. \\&\quad +\, \sigma _{iy}\frac{(V_m)^n_{i,j+1,k}+(V_m)^n_{i,j-1,k}-2(V_m)^n_{i,j,k}}{\Delta y^2} \\&\quad \left. +\, \sigma _{iz}\frac{(V_m)^n_{i,j,k+1}+(V_m)^n_{i,j,k-1}-2(V_m)^n_{i,j,k}}{\Delta z^2}\right\} - \frac{\Delta t}{C_m}(I_{\mathrm{{ion}}}+I_{\mathrm{{stim}}}) \end{aligned} \end{aligned}$$

(17)

For solving bidomain equations, an iterative method is inevitable because of the system of dependent PDEs (9)–(11); however, the monodomain equation (17) can be solved using Euler forward method. Since this method is not iterative, the algorithmic optimizations, namely Kernel 3 elimination and RBSOR method, are not applicable to this implementation. Nevertheless, other optimizations applied to the bidomain model such as the 2D partitioning, data reduction, memory coalescing are applicable to this model. Figure 16 shows the execution time of monodomain implementation with the GPU and MPI communication optimizations versus the bidomain implementation over various numbers of GPUs. As we can see, the execution time of bidomain is greater than the one for monodomain by a factor of seven independent of the number of GPUs because of the time spent on solving the system of bidomain PDEs. Recently, we introduced an autonomic framework [13] that allows the end user to set the desired execution time and simulation accuracy as two constraints. The framework relies on machine learning to adjust the granularity of the simulation time step for meeting the accuracy requirement and the number of GPUs for meeting the execution time requirement. In this framework, we implemented the baseline version of the monodomain model. Figure 16 compares the execution time of this baseline monodomain implementation and the one with the applicable optimizations discussed in this paper. Since the algorithmic optimizations are not applicable to the monodomain model, there is no difference in execution time for the case of single GPU. However, as we increase the number of GPUs, the speed-up with respect to the baseline monodomain implementation improves, which is similar to what we observed for the bidomain implementations shown in Fig. 16.

Fig. 16

Execution time (s) comparison of bidomain, the baseline and optimized monodomain implementations with respect to number of GPUs ($256\times 256\times 256$ mesh, 18,000 temporal iterations)

7 Conclusion

Simulating one APD (360 ms real time) for a $256\times 256\times 256$ mesh takes 844 hours on a high-end general-purpose processor. We were able to reduce the total execution time from 844 hours to 145 min on a single GPU benefiting from eliminating the overhead of the error calculation and RBSOR method. Apart from the algorithmic optimization and fined-grained parallelization (cell level) on GPU architecture, we exploited coarse-grained parallelization (mesh partitioning) on high-performance computing systems, which provides not only higher scale of execution time improvement, but also the capability of simulating tissues with the size of the whole organ of the human heart. Implementing this hybrid parallelization approach, we were able to scale down execution time from 145 to 10 min. Moreover, we address the challenges of design and implementation of a linearly scalable solution to exploit potential of HPC systems. We identified the bottlenecks associated with MPI communication overhead. We achieve parallel efficiency of one for the mesh size of $512\times 512\times 512$ cells that minimizes the communication overhead.

Finally, our implementation is a step toward achieving real-time cardiac simulations, which would help physicians to better understand the behavior of a complex system, and evaluate multiple hypotheses rapidly toward developing patient-specific treatments for CHF.