OFDM waveform design based on mutual information for cognitive radar applications

Abstract

We propose a novel optimization method based on wideband orthogonal frequency division multiplexing (OFDM) signals to detect random extended targets with known covariance matrix in the presence of additive white Gaussian noise. Mutual information is used as our criterion for waveform design under transmitted power constraint. We utilize the advantage of OFDM signal to intelligently design the complex weights of the transmitted waveform. For making complete use of the transmission power, a novel iterative algorithm is introduced based on maximizing mutual information criterion between the target impulse response and the received echoes. We have derived the optimal Neyman–Pearson detector for the corresponding hypothesis testing problem and provided different numerical experiments to demonstrate the achieved performance improvement when the proposed method is applied.

1 Introduction

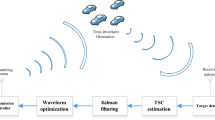
Cognitive radar is an emerging approach which enables radar to intelligently investigate propagation channel using all available information, including previous measurements, work priorities and external databases [1,2,3,4,5]. Based on the prior knowledge about targets and environments, the transmitted signals can be adaptively optimized to improve system performance and efficiency. Adjusting radar transmitted waveform to adapt to the radar environment is one of the important roles in cognitive radar. Therefore, adaptive waveform design in the presence of interference, particularly multipath and clutter, is attracting the attention in modern radar systems like cognitive radar [6]. Figure 1 shows the block diagram of cognitive radar seen as a dynamic closed-loop feedback system [1].

Fig. 1

Block diagram of a cognitive radar system [1]

The basic idea is to optimize criteria such as the probability of target detection, output signal-to-noise ratio (SNR), and mutual information, with respect to the transmitted waveform, in order to achieve better estimation or detection performance [7,8,9,10,11,12].

It has been shown in the literature that use of multicarrier signals can resolve the multipath components and provide additional frequency diversity due to different scattering centers of extended targets [13]. The advantage of using OFDM signals has been studied extensively for communications [14,15,16,17,18,19,20] and also in various radar applications, such as block channel equalization in the frequency domain, [21], constant envelope OFDM signal design with favorable ambiguity functions [22], OFDM chirp waveform diversity design scheme with sparse modeling [23]. It is shown in [24] that by using OFDM signals the micro-Doppler frequency of a multi-scatterer target can be estimated with performance close to Cramer–Rao lower bound (CRLB)

Tang et al. [25] have demonstrated that the optimal transmitted waveform in a multiple-input and multiple-output (MIMO) radar system should be matched with the target to maximize mutual information and enhance the performance of radar system. Zhu et al. [26] address the problem of designing the optimal radar waveform based on maximizing locally most powerful detection metric. It is shown that the signal should place all its energy at the minimum value of noise to target power spectral density (PSD). An iterative algorithm to optimize the coding matrix of the extended binary phase shift keying-based multicarrier phase-coded signal is proposed in [27]. It is shown that by optimization of the coding matrix, the target detection performance has been remarkably improved.

Sen et al. [28] have been addressed a new method for detecting moving targets in the presence of multipath reflections and used the generalized likelihood ratio (GLR) test to design the complex weights of the transmitted waveform for the next coherent processing interval.

In this paper, a new approach to design the transmitted OFDM signal is developed based on the underlying radar scene characteristics. We utilize the mutual information criterion to optimally design the parameters of the transmitted OFDM waveform. Based on the proposed criterion, a new power allocation scheme has been introduced. Simulation results show that such a design method for complex weights of the transmitted waveform will lead to an optimum use of transmitted power. It is shown that by using the optimized waveforms one can achieve better detection performance and greater mutual information.

An extended target model with multiple relatively fixed scattering centers and known velocity is considered in this study. The additive noise component is assumed to have zero-mean complex Gaussian distribution with a covariance matrix independent of the target. We also present the optimal NP detector assuming that the noise covariance matrix is unknown.

The structure of the remainder of this paper is as follows. In Sect. 2, we present the OFDM measurements model for an extended target case.

Based on this model, in Sect 3, we investigate the waveform design problem for OFDM radar by maximizing mutual information criterion. We derive the optimal solution to this problem and show the power allocation scheme by different numerical experiments. It is shown that to achieve the maximum mutual information, the proposed waveform should be matched with the target, which means that the complex weights of an OFDM signal should match to the eigenvalues of the target covariance matrix.

In Sect 4, the performance of the proposed waveform design method is evaluated and compared with the other three different waveforms. Conclusions are given in Sect 5.

Notation: Bold small letters denote vectors, bold capital letters denote matrices. $(.)^\mathrm{T}$, $(.)^H$, diag(.), E., $I_M$ , Re(.), Tr(.), logdet(.) and $\mathrm{vec}(.)$ denote transpose, conjugate transpose, the diagonal matrix, expectation operator, $M \times M$ identity matrix, real part, trace, logarithm-determinant of matrix and vectorization operator, respectively.

2 Background: problem formulation

A multicarrier OFDM signal consists of subcarriers at baseband and can be described by the following equation:

$$\begin{aligned} s(t)=\sum _{l=0}^{L-1}a_{l}\exp (j2{\pi }l{\Delta }ft) \end{aligned}$$

(1)

We consider an OFDM signaling system with L active subcarriers, a bandwidth of B Hz, and pulse duration of T seconds. ${\Delta }f=B/(L+1)={1/T}$ denotes the subcarrier spacing, and the sequence $a_l$ represents the complex weights transmitted over the subcarriers. Let $f_c$ be the carrier frequency of modulation, then the transmitted signal can be represented as:

$$\begin{aligned} \tilde{s}(t)=2 Re\left\{ \sum _{l=0}^{L-1}a_{l}\exp (j2{\pi }f_lt)\right\} \end{aligned}$$

(2)

where

$$\begin{aligned} f_l=f_c+l{{\Delta }f} \quad \quad l=0,1,\ldots ,L-1 \end{aligned}$$

(3)

We assume extended target model in this paper and corresponding to the specific range cell containing the target, the received signal due to only the lth subcarrier is given by:

$$\begin{aligned} \tilde{y_l}(t)=x_l\tilde{s}({\gamma }(t-\tau _l))+\tilde{e_l}(t) \end{aligned}$$

(4)

where $x_l$ is a complex weight that represents the scattering coefficient of the target along the lth subchannel; $\gamma =1+\beta$ with $\beta =2<\vec {v},\vec {u}>/c$ is the relative Doppler shift, $\vec {v}$ is target velocity vector, $\vec {u}$ represents the direction-of-arrival (DOA) unit-vector between the radar and target, and c is the speed of propagation; $\tau _l$ is the round-trip delay due to each scatterer point and c is the speed of propagation [29]. ${e_l}(t)$ is the measurement noise along the lth subchannel. Therefore, the received signal over all subchannels can be formulated as:

$$\begin{aligned} \tilde{y}(t)&=\sum _{l=0}^{L-1}\tilde{y_l}(t)\nonumber \\&=2 Re\left\{ \sum _{l=0}^{L-1}a_{l}x_le^{(j2{\pi }f_l{\gamma }(t-\tau _l))}\right\} +\sum _{l=0}^{L-1}\tilde{e_l}(t)\nonumber \\&=2 Re\left\{ \sum _{l=0}^{L-1}a_{l}x_le^{(j2{\pi }(f_c+l\Delta {f}){(1+\beta )} (t-\tau _l))}\right\} +\sum _{l=0}^{L-1}\tilde{e_l}(t)\nonumber \\&=2 Re\left\{ \sum _{l=0}^{L-1}a_{l}x_le^{(j2{\pi }l\Delta {f}{(1+\beta )}(t-\tau _l))} \nonumber \right. \\&\quad \left. \times \, e^{-j2{\pi }f_c(1+\beta )\tau _l} e^{j2{\pi }f_c\beta {t}}e^{j2{\pi }f_ct}\right\} +\sum _{l=0}^{L-1}\tilde{e_l}(t) \end{aligned}$$

(5)

Assuming that all the scatterer delays are approximately equal, $\tau _l=\tau _0 \quad for \quad l=0,1,\ldots ,L-1$ where $\tau _0$ denotes the round-trip delay corresponding to the range cell under consideration. Therefore, the corresponding complex envelope is represented as Eq. (6).

$$\begin{aligned} y_{\mathrm{OFDM}}(t)=&\sum _{l=0}^{L-1}a_{l}x_le^{j2{\pi }l\Delta {f}{(1+\beta )} (t-\tau _0)} \nonumber \\&\times \, e^{-j2{\pi }f_c(1+\beta )\tau _0} e^{j2{\pi }f_c\beta {t}} +\sum _{l=0}^{L-1}e_l(t) \end{aligned}$$

(6)

The information of the round-trip delays can be automatically incorporated into the model by choosing $t=\tau _0+nT_{\mathrm{PRI}} ,n=0,1,\ldots ,N-1$, where $T_{\mathrm{PRI}}$ is the pulse repetition interval (PRI) and N is the number of pulse in a pulse train. By this assumption, the discrete complex envelope of the received signal at the output of the lth subchannel is given by:

$$\begin{aligned} y_{l_{\mathrm{OFDM}}}(n)=a_lx_l\phi _l(n)+e_l(n) \quad n=0,1,\ldots ,N-1 \end{aligned}$$

(7)

where

$$\begin{aligned} \phi _l(n)= e^{-j2{\pi }f_l\tau _0} e^{j2{\pi }f_l\beta {n}T_{\mathrm{PRI}}} \end{aligned}$$

(8)

Stacking the measurements of all subchannels into one column vector of dimension $L\times {1}$ , we have:

$$\begin{aligned} y_{\mathrm{OFDM}}(n)=A(a)X\phi (n)+e(n) \end{aligned}$$

(9)

where

• $y_{\mathrm{OFDM}}(n)=[y_{0_{\mathrm{OFDM}}}(n),y_{1_{\mathrm{OFDM}}}(n),\ldots ,y_{L-1_{\mathrm{OFDM}}}(n)]$.

• $A=\mathrm{diag}(a)$ is $L\times {L}$ complex diagonal matrix that contains the transmitted weights a.

• $X=\mathrm{diag}(x_l)$ is a diagonal matrix where its diagonal elements are the scattering coefficients of the target at the lth subchannel.

• $\phi (n) =[\phi _0(n),\phi _1(n),\ldots ,\phi _{L-1}(n)]$ is an $L\times {1}$ vector containing the doppler information of the target at the lth subchannel.

• $e(n)=[e_0(n),e_1(n),\ldots ,e_{L-1}(n)]^T$ is an $L\times {1}$ vector of measurement noise.

Then, concatenating all data columnwise into an $L \times {N}$ matrix we obtain the OFDM measurement model given in Eq. (10).

$$\begin{aligned} Y_{\mathrm{OFDM}}=AX\Phi +E=A\tilde{\Phi }+E \end{aligned}$$

(10)

where

• $Y_{\mathrm{OFDM}}=[y_{{\mathrm{OFDM}}}(0),y_{{\mathrm{OFDM}}}(1),\ldots ,y_{{\mathrm{OFDM}}}(N-1)]$.

• $\tilde{\Phi }=[\tilde{\Phi }(0),\tilde{\Phi }(1),\ldots ,\tilde{\Phi }(N-1)]$, where $\tilde{\Phi }=X\Phi$ is an $L \times {N}$ matrix related to the channel response.

• $E=[e(0),e(1),\ldots ,e(N-1)]$ is an $L \times {N}$ matrix of measurement noise.

3 Proposed method

The application of information theory in radar system design was first considered by Woodward and Davies [30,31,32,33]. Mutual information criterion suggests the maximization of mutual information between the unknown channel and received signal as a function of transmitted training symbols. In recent years, it has been shown in some researches that waveforms designed based on information theory lead to the water-filling solution, i.e., the energy is distributed in accordance with the quality of each target scattering mode [25] and [34]. In this paper, a new method to design the complex weights of transmitted waveform is addressed to maximize the mutual information criterion.

If the transmitted waveform matrix A in Eq. (10) is known, the conditional mutual information between Y and $\tilde{\Phi }$ is given by [7]:

$$\begin{aligned} MI(Y_{\mathrm{OFDM}};\tilde{\Phi }|A)&=h(Y_{\mathrm{OFDM}}|A)-h((Y_{\mathrm{OFDM}}|\tilde{\Phi },A))\nonumber \\&=N[\mathrm{logdet}(AR_{\tilde{\Phi }}A^H+R_n)-\mathrm{logdet}(R_n)] \end{aligned}$$

(11)

where MI(x; y) denotes the mutual information between x and y, h(x) denotes the entropy of x and $R_x=E[xx^H]$ is the covariance matrix.

To make the optimization problem nontrivial, the power constraint to this optimization problem is added. Considering AWG noise, the optimization problem is stated as follows:

$$\begin{aligned} A_{\mathrm{opt}}&={{\mathrm{arg\,max}}}_A[MI(Y_{\mathrm{OFDM}};\tilde{\Phi }|A)] \quad s.t \ AA^H\le P_t\nonumber \\&={{\mathrm{arg\,max}}}_A(N[\mathrm{logdet}(AR_{\tilde{\Phi }}A^H+R_n)-\mathrm{logdet}(R_n)])\nonumber \\&\qquad \qquad s.t \ AA^H\le P_t \end{aligned}$$

(12)

where $P_t$ is the total transmitted power in dB. Suppose $B=AR_{\tilde{\Phi }}A^H+R_n$ and denote the eigenvalues and main diagonal elements of B as $\lambda _l(B)$ and $d_l(B)$. Then, according to the function stated in [35]:

$$\begin{aligned} f(\lambda (B))=\mathrm{logdet}(B)=\sum _{l=0}^{L-1}log(\lambda _l(B)) \end{aligned}$$

(13)

It is proved that this function is a Schur-concave problem in which $f(\lambda (B))\le f(d(B))$ and the upper bound is achieved when $\lambda (B)=d(B)$. This is true if and only if B was a diagonal matrix. Singular value decomposition (SVD) of the transmitted matrix is utilized as $A=U_s\Lambda _s V_s$ where $U_s$ and $V_s$ are unitary matrices and $\Lambda _s$ is a diagonal matrix. By substituting d(B) derived in Appendix B into Eq. (13), the optimization problem can be written as:

$$\begin{aligned} A_{\mathrm{opt}}&={{\mathrm{arg\,max}}}_{\beta _l}\left( \sum _{l=0}^{L-1} (\sigma ^2 +\Lambda _s^2(l,l) R_{\tilde{\Phi }} (l,l))\right) \nonumber \\&\qquad \qquad s.t \ tr \ \Lambda _s\Lambda _s^H\le P_t \end{aligned}$$

(14)

Since $\Lambda _s$ is a diagonal matrix, if the interference covariance matrix $R_{\tilde{\Phi }}$ be diagonal, the whole assumptions will be held true and we can reach the upper bound which is the solution of our maximization problem. The interference covariance matrix $R_{\tilde{\Phi }}$ is computed as:

$$\begin{aligned} R_{\tilde{\Phi }}&=E\{X_{L\times L}\Phi _{L\times N}\Phi _{L\times N}^HX_{L\times L}^H\}\nonumber \\&=E\{X_{L\times L}[\Phi _0 \Phi _1 \ldots \Phi _{L-1}]_{L\times N}[\Phi _0 \Phi _1 \ldots \Phi _{L-1}]_{N\times L}^H X_{L\times L}^H] \end{aligned}$$

(15)

By substituting $\Phi _l(n)$ from Eq. (8) into Eq. (15), it can be easily shown that $R_{\tilde{\Phi }}$ will be reduced to (16).

$$\begin{aligned} R_{\tilde{\Phi }}&=E\{X[NI_{L\times L}+11^H]X^H\}\nonumber \\&=NE\{XX^H\}+E\{X(11^H)X^H\}=(N+1)C_X \end{aligned}$$

(16)

In the preceding equation, $C_X=E\{XX^H\}$ is the covariance matrix of the extended target which is computed by:

$$\begin{aligned} C_X=E \left\{ \begin{pmatrix} x_1 &{}\quad 0 &{}\quad \dots &{}\quad 0 \\ 0 &{}\quad x_2 &{} \quad \dots &{}\quad 0\\ &{}\quad &{}\quad \ddots \\ 0&{}\quad \dots &{}\quad 0 &{}\quad x_{L} \end{pmatrix} \begin{pmatrix} x_1^H &{} 0 &{}\dots &{}0 \\ 0 &{} x_2^H &{} \dots &{}0\\ &{} &{} \ddots \\ 0&{}\dots &{}0 &{} x_{L}^H \end{pmatrix} \right\} \end{aligned}$$

(17)

Since it is assumed that $E\{x_l\}=0$ , the diagonal elements of the covariance matrix are $E\{x_lx_l^H\}$ and nondiagonal elements are zero, so it will be reduced to the diagonal form of Eq.  (18).

$$\begin{aligned}&\quad C_X= E \left\{ \begin{pmatrix}\\ x_1x_1^H &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ 0 &{}\quad x_2 x_2^H &{}\quad \ldots &{}\quad 0\\ &{} \quad &{}\quad \ddots \\ 0&{}\quad \dots &{}\quad 0 &{}\quad x_{L} x_{L}^H \end{pmatrix} \right\} \end{aligned}$$

And finally the covariance matrix of the extended target will be expressed as:

$$\begin{aligned}&\quad C_X= \begin{pmatrix}\\ \sigma ^2_{x,1}&{}\quad 0 &{}\quad \dots &{}\quad 0 \\ 0 &{}\quad \sigma ^2_{x,2} &{}\quad \dots &{}\quad 0\\ &{}\quad &{}\quad \ddots \\ 0&{}\quad \dots &{}\quad 0 &{}\quad \sigma ^2_{x,L} \end{pmatrix} \end{aligned}$$

(18)

Now, by substituting Eq. (18) into Eq. (14) we can rewrite the optimization problem given in Eq. (19).

$$\begin{aligned} A_{\mathrm{opt}}&={{\mathrm{arg\,max}}}_{\beta _l}\left( \sum _{l=0}^{L-1} \log (\sigma ^2+(N+1)\beta _l\sigma ^2_{x,l})\right) \nonumber \\&\qquad \qquad s.t \ \sum _{l=0}^{L-1} \beta _l \le P_t \end{aligned}$$

(19)

where the power transmitted along the lth subcarrier is $\beta _l=|\Lambda _s(l,l)^2|$ and $\sigma ^2_{x,l}$ is the lth diagonal element of $C_{X}$. Now the optimization problem can be solved by the method of Lagrange multipliers. Therefore, the functional in (20) can be constructed.

$$\begin{aligned} L(\lambda )=\sum _{l=0}^{L-1} \log \left( \sigma ^2+(N+1)\beta _l\sigma ^2_{x,l}\right) -\lambda \left( \sum _{l=0}^{L-1}\beta _l-P_t\right) \end{aligned}$$

(20)

Differentiating $L(\lambda )$ with respect to $\beta _l$ and setting the result equal to 0, we reach to Eq. (21).

$$\begin{aligned} \frac{(N+1)\sigma ^2_{x,l}}{\sigma ^2+\beta _l(N+1)\sigma ^2_{x,l}}-\lambda =0 \end{aligned}$$

(21)

Since $\beta _l\ge 0$, the optimal waveform can be found from:

$$\begin{aligned} \beta _l=\max \left( -\frac{1}{\lambda }-\frac{\sigma ^2}{(N+1)\sigma ^2_{x,l}},0\right) \end{aligned}$$

(22)

where the parameter $\lambda$ can be calculated from equation (23).

$$\begin{aligned} \sum _{l=0}^{L-1}\max \left( -\frac{1}{\lambda }-\frac{\sigma ^2}{(N+1)\sigma ^2_{x,l}},0\right) =P_t \end{aligned}$$

(23)

According to the above equation, the more target scattering values, the more allocated power. The proposed power allocation scheme is so that the transmitted signal matches its weights ($A_{\mathrm{opt}}$) to the target scattering values in the frequency domain. Such an algorithm will lead to improving the mutual information criterion in comparison with other power allocation algorithms.

4 Simulation results

In this section, the performance of the proposed waveform design method is evaluated via several experiments. First, we provide a description of the simulation setup and then discuss different numerical examples. We have considered stochastic extended targets with a large number of scatterer points where located in the range cell centered at 3 km with respect to radar (positioned at the origin). The scattering coefficients of the target (i.e., the entries of X) are unknown and generated from a $CN(0, C_X)$ complex normal distribution where the covariance matrix $C_X$ is known. Such an assumption corresponds to, for example, the situation where the radar is searching for specific targets with known signatures in the underlying radar scene. We have also considered additive white Gaussian noise model with power $\sigma ^2$ through all simulation results.

The radar system parameters are chosen to realize the overall system that are as follows:

• Carrier frequency $f\mathrm{c}=9$ GHz.

• Pulse repetition interval $T_{\mathrm{PRI}}=200$$\upmu$s

• Pulse width $T=250$ ns

• Subcarrier spacing $\Delta f=4$ MHz

• Available bandwidth $B=60$ MHz

• Number of coherent pulses $N=16$

• Number of subcarriers $L=16$

• Total transmitted power $P_t=10$ dBW

We may change the number of subcarriers L and total transmitted power in different experiments.

4.1 Power allocation scheme

In this section, the proposed power allocation method, conventional equal power waveform, locally most powerful (LMP)-based waveform [26] and the GLR-based waveform [28] are investigated and compared. We consider a random extended target in which the scattering coefficients are assumed to be unknown but its covariance matrix $C_X$ is known. The total transmitted power is $P_t=10 dBW$ and the number of subcarriers is set to be 16.

A conventional OFDM radar system in which their complex weights of the transmitted signal are given by $a_l=\frac{P_t}{L}$ in the first N pulse is regarded to be compared with the proposed method.

Sen et al. [28] have presented an adaptive waveform design problem where the complex weights of the transmitted signal have been chosen based on maximizing the following expression:

$$\begin{aligned} A_{\mathrm{opt}}=&{{\mathrm{arg\,max}}}_A tr(\Sigma ^{-1}AX\Phi \Phi ^HX^HA^H) \nonumber \\&\qquad \qquad s.t \ \sum _{i=0}^{L-1} aa^H \le P_t \end{aligned}$$

(24)

It has been shown that the optimal solution, $A_{\mathrm{opt}}$, is the eigenvector corresponding to the largest eigenvalue of $tr(AX\Phi \Phi ^HX^HA^H)$.

Note that in our problem X and $\Sigma$ are known and we assume that the measurement noise is temporally white.

Fig. 2

Diagonal elements of target covariance matrix

Fig. 3

Illustration of power allocation. a Weights of equal power waveform. b Weights of LMP-based waveform. c Weights of GLR-based waveform. d Weights of the proposed waveform ($L=16$, $P_t=10\,dBW$)

Zhu et al. [26] have also provided a waveform that allocates all its energy at the frequency where the ratio of the target PSD to the noise PSD ($\frac{C_X}{R_n}$) is maximum. Hence, from the perspective of our problem only one weight of transmitted signal which corresponds to the highest value of $\frac{C_X}{R_n}$ is chosen to be transmitted in the channel.

To compare the advantages and disadvantages of each method, some numerical analysis is done which are presented in the following.

Figure 2 shows the diagonal elements of the covariance matrix of an arbitrary stochastic extended target. Figure 3 illustrates the power allocation of each waveform based on the target covariance matrix shown in Fig. 2.

There is a significant difference between the proposed and other methods indicated in Fig. 3. It is remarkable that in the proposed power allocation scheme, the energy is distributed proportionally to the quality of each target scattering value. In other words, the more target scattering values, the more allocated power. In contrast, in the GLR-based waveform, most of the power is assigned to subcarriers corresponding to the prevailing target covariance matrix values. The LMP-based waveform power allocation is so that the total transmitted power is assigned to one subcarrier, which has the highest target covariance matrix value, and the power of other subcarriers is considered to be zero.

4.2 Evaluating the overall performance of the proposed method

In this section, we evaluate the performance of the proposed waveform design method via several measures and demonstrate its advantages compared to equal power waveform, GLR-based waveform, and LMP-based waveform.

4.2.1 Mutual information performance

Here, the performance of the proposed method is presented under different transmitted power constraints. Figures 4 and  5 show the mutual information and relative entropy of the equal power waveform, GLR-based waveform, LMP-based waveform and the proposed waveform for different total transmitted powers. It can be seen that the proposed waveform results in significantly better performance compared to the other waveforms.

Fig. 4

Mutual information of the proposed waveform compared with other waveforms

We can also find that when the total transmitted power becomes higher, the difference between the mutual information of the proposed waveform and equal power waveform becomes smaller while there is a remarkable gap with two other methods.

4.2.2 Detection performance

We construct the decision problem regarding a binary hypothesis testing problem which can be formulated as Eq. (25).

$$\begin{aligned} {\left\{ \begin{array}{ll} H_0:\ Y_{\mathrm{OFDM}}=E, \ \mathrm{No} \ \ \mathrm{Target}\\ H_1:\ Y_{\mathrm{OFDM}}=AX\Phi +E, \ \mathrm{Target} \ \ \mathrm{Exists} \end{array}\right. } \end{aligned}$$

(25)

In Appendix A, we have derived optimal Neyman–Pearson detector for the above hypothesis testing problem. The numerical value of the amplitude threshold is determined by fixing the probability of false alarm $P_{\mathrm{fa}}=0.01$. Figure 6 indicates the probability of target detection achieved by the proposed method and other power allocation waveforms for different total transmitted powers.

Fig. 5

Relative entropy of the proposed waveform compared with other waveforms

We have performed Monte Carlo simulations based on $10^5$ independent trials to obtain the results. For the OFDM measurement model, the entries of 100 different target covariance matrix have been realized from the $CN(0, C_X)$ distribution and then scaled to satisfy the required signal-to-noise ratio (SNR), defined as Eq. (26).

$$\begin{aligned} \mathrm{SNR}_{\mathrm{OFDM}}=\frac{\frac{1}{N}\sum _{i=1}^{N}(A(a)X\Phi )(A(a)X\Phi )^H}{\sigma ^2} \end{aligned}$$

(26)

In order to illustrate the advantage of using the proposed OFDM signal, the performance for all algorithms is shown in Figs. 6 and 7. As indicated in Fig. 6, the detection probability of the proposed waveform is superior compared to other three algorithms when the transmitted signal has enough power to split between different subcarriers ($P_t>5$ dBW). When the total transmitted power is low ($P_t<5$ dBW), the LMP-based and GLR-based waveforms perform better than the proposed method; however, LMP-based power allocation scheme has two significant disadvantages compared with other waveforms. The first problem is that this waveform is unable to estimate the channel in the next coherent pulse intervals (CPI) because of single-frequency transmission and thus could not be a good choice for cognitive radar application. The second problem is lack of access to other benefits of OFDM such as high resolution, ability to overcome with fading effect and so on.

Fig. 6

Detection probability of different waveforms versus total transmitted power

Figure 7 represents the received SNR versus total transmitted power. From Fig. 7, one can find that, regarding the received SNR, the improvement in the proposed waveform over the other waveforms is obvious and there is an average gain of about 3dB yielded by the proposed power allocation method.

Fig. 7

Recieved SNR versus total transmitted power

The difference in MI and $P_d$ arises from the choice of different power allocation schemes and proves the superiority of the proposed power allocation algorithm over other power assignment methods. The performance of the proposed power allocation algorithm in higher transmitted powers is superior to other power allocation methods. Such a performance represents a reliable and rigorous approach for designing radar transmitted waveforms in scenarios in which the transmitter has enough power to allocate.

5 Conclusion

In this paper, we have addressed the problem of OFDM waveform design in cognitive radar applications. We have developed a measurement model for a random extended target having multiple dominant scattering centers. We investigated radar waveform design based on optimizing the mutual information (MI) criterion. It was shown that transmitted radar waveforms which have good results in higher MI will also result in higher target detection accuracy as one of the main motivations of this work. Indeed, the optimum solution leads to the best power allocation for the transmitted signal coefficients such that the proposed waveform is matched to the radar channel. We have also derived an optimal Neyman–Pearson detector for the hypothesis testing problem and the detection performance of the proposed waveform has been compared to the other conventional and recently developed waveforms. Simulation results provide compelling evidence that the proposed OFDM method represents a reliable and rigorous approach for designing radar transmitted waveforms in scenarios in which its transmitter has enough power to allocate. For future works, the approach can be used in many different applications such as transmission of data on wireless networks and sensory systems [36,37,38] to improve the performance and reliability of data communication links, content security and management in remote sensing and pattern recognition systems [39,40,41,42,43,44,45,46,47,48]. Toward radar systems and applications, it might also be usable for different radar systems such as tracking radars and imaging platforms [49,50,51] as the next area of application.

Appendices

Appendix A: Optimal Neyman–Pearson detector

The PDF of OFDM received signal can be computed as [52]:

$$\begin{aligned} P_0(Y_{\mathrm{OFDM}})&=\frac{1}{\pi ^{LN}\sigma ^{2N}}\exp \left\{ -\frac{tr[Y_{\mathrm{OFDM}}Y_{\mathrm{OFDM}}^H]}{\sigma ^2}\right\} \nonumber \\ P_1(Y_{\mathrm{OFDM}})&=\frac{1}{\pi ^{LN}\mathrm{det}^N((N+1)AC_xA^H+\sigma ^2)}\nonumber \\&\quad \times \, \exp \{-tr[((N+1)AC_xA^H+\sigma ^2))^{-1}Y_{\mathrm{OFDM}}Y_{\mathrm{OFDM}}^H]\} \end{aligned}$$

(27)

The log-likelihood function can be simplified by Eq. (28).

$$\begin{aligned} l(Y_{\mathrm{OFDM}})=&\log \frac{P_1(Y_{\mathrm{OFDM}})}{P_0(Y_{\mathrm{OFDM}})} \nonumber \\ =&\frac{1}{\sigma ^2}tr[Y_{\mathrm{OFDM}}Y_{\mathrm{OFDM}}^H] \nonumber \\&-tr[((N+1)AC_xA^H+\sigma ^2))^{-1}Y_{\mathrm{OFDM}}Y_{\mathrm{OFDM}}^H]+K \end{aligned}$$

(28)

where $K=\pi ^{LN}\sigma ^{2N}-\pi ^{LN}\mathrm{det}((N+1)AC_xA^H)$ is a constant term which is not dependent on $Y_{\mathrm{OFDM}}$. Therefore, the optimal Neyman–Pearson detection statistics is stated by Eq. (29).

$$\begin{aligned} T(Y_{\mathrm{OFDM}})&=\frac{1}{\sigma ^2}tr[Y_{\mathrm{OFDM}}Y_{\mathrm{OFDM}}^H] \nonumber \\&\quad -tr[((N+1)AC_xA^H+\sigma ^2))^{-1}Y_{\mathrm{OFDM}}Y_{\mathrm{OFDM}}^H] \end{aligned}$$

(29)

If T(Y) exceeds a given threshold, we say a target exists.

Appendix B: Computing the diagonal elements of matrix B

We suppose $B=AR_{\tilde{\Phi }}A^H+R_n$ and now we want to compute diagonal elements of B as $d_l(B)$. Assuming AWGN noise with known power $P_n=\sigma ^2$, we can write matrix B by equation (30).

$$\begin{aligned} B&=AR_{\tilde{\Phi }}A^H+\sigma ^2 I \nonumber \\&=U_s\Lambda _s V_s R_{\tilde{\Phi }} (U_s\Lambda _s V_s)^H+\sigma ^2 I \nonumber \\&=\Lambda _s V_s^H R_{\tilde{\Phi }} V_s \Lambda _s^H+\sigma ^2 I \end{aligned}$$

(30)

Since $V_s$ is a unitary matrix, it must be equal to the eigen-matrix (matrix of eigenvectors) of $R_{\tilde{\Phi }}$. Now, since $R_{\tilde{\Phi }}$ is a diagonal matrix, its eigen-matrix is $I_L$. Thus, we can write $V_s=P$, where P is a permutation matrix, and we have:

$$\begin{aligned} B=\Lambda _s R_{\tilde{\Phi }} \Lambda _s^H+\sigma ^2 I \end{aligned}$$

(31)

Finally, the diagonal elements of matrix B can be written as Eq. (32).

$$\begin{aligned} d(B)=\sigma ^2 +\Lambda _s^2(l,l) R_{\tilde{\Phi }} (l,l) \end{aligned}$$

(32)