1 Introduction

During the past half-century, there have been various efforts to improve computer performance [1,2,3]. As one of the results from the efforts, multicomputer has become emergent. Multicomputer consists of multiple processors connected together, and we call the structure of the connected processors interconnection network. Interconnection network has been studied and applied in many fields, such as parallel processing topology, physical interconnection of the VLSI internal processors for Network on Chip (NoC) [4,5,6,7], logical interconnection among various sensors in the wireless sensor network (WSN) [8,9,10], analytical model for DNA in biology [11,12,13] and sorting problem [14,15,16]. Due to special and subject-specific limitations for each field presented above, the criteria can be different to evaluate various types of interconnection networks. Especially for parallel processing computer and NoC that have a physically connected structure, it is considered advantageous to have network cost that requires O(1) to reduce the cost to expand network for better scalability.

An interconnection network defines the linking structure among processors, which can be expressed in a graph with nodes corresponding to the processor and edges corresponding to the communication link. The number of edges combined with a node is called a degree. The minimum number of edges between two nodes is called a distance, and the maximum distance within a network is called a diameter. Interconnection networks are classified into networks based on hypercube [17] or star graph [18], where the degree increases in proportion to the number of nodes whenever the network is expanded; on the other hand, in the networks based on mesh [19], the degree is constant even when the network is expanded. Extending network, herein, means increasing number of nodes in the network.

The fixed-degree network is not necessarily adding edge(s) whenever the network is expanded. But it is necessary to add more edges to extend hypercube-like and star graph-like networks. For this reason, fixed-degree networks are better than the others in terms of network extensibility. For the store-and-forward routing where the message latency time is proportional to the distance between two nodes, it is beneficial to use unfixed-degree network that has more degrees of vertices, but shorter diameter. On the other hand, for the wormhole routing where the message latency time is not affected much by the distance between two nodes, it is appropriate to use fixed-degree network which has larger diameter, but better scalability.

Two-dimensional (2D) fixed-degree network can be designed to layout triangle, rectangle, pentagon and hexagon side by side on two-dimensional space. The examples of 2D fixed-degree network are torus [19], honeycomb mesh [20], honeycomb torus [20], diagonal mesh [21] and hexagonal torus [22], and these have been commercialized to MasPar Intel Paragon, XP/S, Touchstone DELTA System and Mosaic C [23]. The examples of 3D fixed-degree network are 3D mesh [24], 3D torus [24], 3D hexagonal mesh [23], 3D honeycomb mesh [25], diamond network [26] are 3D prismatic twisted torus [27], and these are commercialized to Cray T3D, MITs J-Machine and Tera Computer [28].

Network cost is defined by a product of degree and diameter. There is a trade-off between degree and diameter. When two interconnection networks with the same number of nodes are compared, less network cost means that one performs better with less expensive hardware installation cost and fast message transfer time. The reason to find interconnection network with less network cost is that people would like to guarantee fast message transfer time while maintaining less number of links. Thus, network cost is an important measure for the evaluation of interconnection networks [29]. Peterson graph is known to be the most cost-effective in terms of the network cost among all graphs having 10 nodes.

Interconnection network was first proposed as a graph, such as mesh, hypercube and star graph and more. Interconnection networks have been proposed with less network cost. There are several ways to improve network cost. First of all, edges can be added/removed to/from a simple graph. The networks constructed by adding edges are torus [19] and folded hypercube [31], and ones constructed by removing edges are matrix star [32] and half hypercube [33]. Secondly, two graphs can be combined. The examples of product network using CARTESIAN product operation [34] are hyper Petersen [35], cross-cube [36] and folded Petersen [37]. Last way to improve network cost is to use hierarchical interconnection network (HIN). For this, we make multiple clusters to construct networks and group (connect) these clusters to construct HIN. The examples of HIN are hierarchical cubic network HCN(m, m) [38], hierarchical folded-hypercube network HFN(m, m) [39], hierarchical star HS(k, k) [40], hierarchical hypercube network HHN(m, h) [41], hierarchical hypercube d-HHC [42].

In interconnection networks, the average distance between two arbitrary nodes is short as there are more edges. When there is the same number of nodes, average distance between two nodes is shorter in hypercube than in mesh although the hypercube has more edges. HIN was proposed to reduce the number of edges while maintaining short average distance between nodes [43]. HCN(m, m) is constructed based on hypercube \(Q_m\) as a cluster and 2m number of clusters are connected in the shape of \(Q_m\). HS(k, k) is constructed based on star graph \(S_k\) as a cluster, and k! number of clusters are connected in the shape of \(S_k\). HCN and HS are defined with only two levels. However, HHN(m, h) expends HCN(m, m) to h levels. In HHN(m, m), the degree is 2m and it is increased as the network is expanded. As listed in Table 2, the degree is increased proportionally as the number of levels is increased in most of the traditional hieratical networks. Due to this property, it has disadvantages to have increased network cost and communication links when the network is expanded.

In this paper, we propose hierarchical interconnection network where the number of nodes is recursively expanded at the rate of \(10^n\) although the degree is unchanged with a constant, 5. The next section presents the properties (routing, Hamilton path and spanning tree) of Petersen graph and folded Petersen graph. In Sect. 3, we define HPN(n) newly proposed in this paper and analyze various properties, such as spanning tree, broadcasting algorithm and embedding. We also propose routing algorithm and compare corresponding diameter with ones in other networks.

2 Related works

2.1 Routing, Hamilton path and spanning tree in Petersen graph

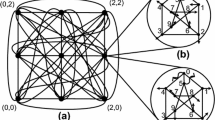
Petersen graph is a basic building to construct HPN(n). The Petersen graph incorporates a regular graph and a node (edge)-symmetric graph. It has a degree of 3, diameter 2, connectivity 3 and girth 5 [44]. There are several ways to assign node addresses. In the routing algorithm of the Petersen graph in this section, an address consisting of permutations of double digits is used; in other sections, for convenience in indicating the node address, an address consisting of single digits in parentheses is used. The Petersen graph and the spanning tree of the Petersen graph are shown in Fig. 1.

Fig. 1
figure 1

Petersen graph and spanning tree of Petersen graph. a Petersen graph. b Spanning tree of Petersen graph

Full size image

In the Petersen graph, \(P=(V_p, E_p)\). \(\{x,y\}\in \{1,2,3,4,5\}, x<y\), \(\{x',y'\}\in \{\{1,2,3,4,5\} - \{x,y\}\}, x'<y'\). The meaning of \(x,y\in \{1,2,3,4,5\}\) is “x and y are elements of set {1,2,3,4,5}”. Node \(V_p = xy\). Edge \(E_p = (xy, x'y')\). It is assumed that in the Petersen graph, node \(U=u_1u_2\) is a start node and node \(V=v_1v_2\) is a destination node. The routing algorithm from U to V is as given below [45].

Summary 1

(Case 1) If \(\{u_1, u_2\} \cap \{v_1, v_2\} = \phi \), U is adjacent to V.

(Case 2) If \(\{u_1, u_2\} \cap \{v_1, v_2\} \ne \phi \), it reaches V via the node composed of \(\{1, 2, 3, 4, 5\} - (\{u_1, u_2\} \cup \{v_1, v_2\})\) from U.

Summary 2

Petersen graph contains a spanning tree with degree of 3 as depicted in Fig. 1b. Since Petersen graph is node (edge)-symmetric graph, arbitrary node can be a root node of spanning tree.

Summary 3

For all-port model, the one-to-all broadcasting in the Petersen graph is edge disjoint and broadcasting time is 2. Initially, node 0 has a message. As presented in Fig. 1b, node 0 sends a message to its 3 child nodes in the first step. In the second step, those 3 child nodes send the messages to all leaf nodes. As shown in the figure, all the paths where the messages are traversing to get to the leaf nodes are edge disjoint. Since Petersen graph is node (edge)-symmetric graph, Summary  3 is valid even though any arbitrary node has a message initially.

2.2 Folded Petersen graph FP\(_k\)

The k-dimensional folded Petersen graph, FP\(_k = P \times \cdots \times P = \mathrm{FP}_{k-1} \times P\), is the iterative Cartesian product on the Petersen graph, P. FP\(_k = (V_k, E_k)\) where

$$\begin{aligned} V_k = {v_kv_{k-1}v_{k-2}\ldots v_{i+1}v_iv_{i-1}\ldots v_2v_1} (0 \le v_i\le 9,\quad 1 \le i \le k). \end{aligned}$$

Each node consists of k numbers where each number can be from 0 through 9, inclusive; in this paper, each number is also called “symbol”. There are two types of edges. Internal edges connect nodes inside of the basic module, and external edges connect nodes in different modules. Internal edge connects two nodes where all symbols of the two nodes match except for \(v_1\). External edge connects two nodes where only one symbol does not match among all symbols except for \(v_1\). In this case, those two symbols must be adjacent in Petersen graph.

$$\begin{aligned} E_k= & {} (v_kv_{k-1}v_{k-2}\ldots y_i\ldots v_2v_1, v_kv_{k-1}v_{k-2}\ldots z_i\ldots v_2v_1)\, \hbox {where} \\&\,y_i\,\hbox { and }\,z_i\,\hbox { are adjacent in Petersen graph.} \end{aligned}$$

FP\(_k\) has \(10^k\) nodes and the degree of 3k. Due to the space limitation, we do not include the details of FP\(_k\), which can be found in [37]. The routing in FP\(_k\) is the same as the conversion of starting node symbol to make it the same as destination node symbol. The conversion of one symbol follows Summary 1, and it starts from the most significant bit (MSB) to the least significant bit (LSB) one bit by one bit.

3 Hierarchical Petersen network HPN(n)

3.1 Definition of HPN(n)

HPN is an undirected graph, and HPN(1) is Petersen graph. HPN(2) is constructed by substituting all nodes in HPN(1) by Petersen graph, and HPN(3) is constructed by substituting all nodes in HPN(2) by Petersen graph. In this way, HPN(n) is constructed by substituting all nodes in HPN\((n-1)\) by Petersen graph. Conversely, HPN\((n-1)\) is constructed by substituting Petersen graph in HPN(n) by one node. Node expansion is recursive, and the number of nodes is increased in multiple of 10. All nodes are connected by “rotate” operations on symbols in a nodes address. Since there may be a loop by applying “rotate” operation on nodes with the exact same symbols, P(x) and M(x) are defined in Definition 1 to resolve the issue. HPN is based on Petersen graph as a basic module. The address of each basic module is represented as nonnegative integer. HPN(n) with \(10^n\) nodes is called n-level HPN. The address of a n-level HPN consists of n numbers and node \(U = u_nu_{n-1}u_{n-2} \ldots n_{i+1}u_iu_{i-1} \ldots u_2u_1\). Definition 1 shows “left rotate (LR)” and “right rotate (RR)” operations to define an edge. % is used for modulo operation in the rest of this paper. \(P(x) = (x + 2) \% 10\) and \(M(x) = (x + 8) \% 10\).

Definition 1

(A) LR operation is denoted as LR(U) and LR\((U) = u_{n-1}u_{n-2} \ldots n_{i+1}u_iu_{i-1} \ldots u_2P(u_1)u_n \).

(B) RR operation is denoted as RR(U) and RR\((U) = u_1u_nu_{n-1}u_{n-2} \ldots n_{i+1}u_iu_{i-1} \ldots u_4u_3M(u_2) \).

For example, if node \(U=123\) in HPN(3), LR\((U)=251\) and RR\((U)=310\). If node \(U=719\), LR\((U)=117\) and RR\((U)=979\).

Figure 2 shows the structure of HPN(3). Figure 2a, b is not included in HPN. n-level hierarchical Petersen network is HPN\((n) = (V_{hp}, E_{hp})\) where \(n \ge 3\). A node in HPN(n) is defined as \(V_{hp} = u_nu_{n-1}u_{n-2} \ldots n_{i+1}u_iu_{i-1} \ldots u_2u_1\) where \(0 \le u_i \le 9, 1 \le i \le n\).

Fig. 2
figure 2

HPN(3)

Full size image

Each node consists of n digits, and each digit can be from 0 through 9, inclusive. There are two types of edges; internal edges connect nodes inside of the basic module, and external edges connect nodes in different modules. Internal edges are ones used in Petersen graph. Let’s examine an arbitrary internal edge and its two incident nodes. All the symbols in the two nodes are the same except for LSB, and their LSBs are xy and \(x'y'\) in the edge \(E_p = (xy, x'y')\) in Petersen graph. External edge is defined as follows:

$$\begin{aligned} \hbox {LR edge} = (U, \hbox {LR}(U))\, \hbox {and RR edge} = (U, \hbox {RR}(U)). \end{aligned}$$

Basic module is \(u_nu_{n-1}u_{n-2} \ldots n_{i+1}u_iu_{i-1} \ldots u_2x\) where \(0 \le x \le 9\). For example, basic module 54x in HPN(3) consists of 10 nodes, \(540, 541, 542,\ldots , 548\) and 549. A node 542 is connected to node 445 via LR edge and to node 252 via RR edge. A node 542 is connected to nodes 541, 543 and 546 via internal edges. Basic module 54x is connect to 10 nodes, x52, via RR edges and to other 10 nodes, 4x5, via LR edges.

Suppose that |HPN(n)| represents the number of nodes in HPN(n). HPN(n) consists of 10 clusters that contains \(|HPN(n-1)|\) number of nodes and \(|HPN(n)| = |HPN(n-1)| \times 10\). HPN\((n-1)\) consists of 10 clusters that contains \(|HPN(n-2)|\) number of nodes and \(|HPN(n-1)| = |HPN(n-2)| \times 10\). For instance, there are 10 clusters \((0xx, 1xx, 2xx, 3xx,\ldots , 8xx\) and 9xx) in HPN(3), and there are 100 nodes in each cluster. In particular, 10 nodes (000, 100, 200, 300,..., 800 and 900; one in each cluster) are connected to the basic module 02x. Therefore, all 10 clusters are connected. Cluster 0xx consists of 10 basic modules as a cluster \((00x, 01x, 02x, 03x,\ldots , 08x\) and 09x) where each module contains 10 nodes. The 10 nodes (000, 010, 020,..., 080 and 090) in each module are connected to basic module, 00x. Therefore, all 10 clusters are connected. Therefore, HPN is a connected graph. In other words, a node 00000 in HPN(5) is connected to all nodes in a basic module 0000x, and 0000x is connected to 000xx by a LR edge. This is the procedure to expand network connections using LR edge, and if this process is repeated 3 times, all nodes in HPN(5) are connected. In this way, if the same process is repeated \(n-1\) times for any arbitrary basic module in HPN(n) using LR edges, all nodes in HPN(n) are connected. Unlike expanded hypercubes [46] and Hyperwave [47], HPN(n) proposed in this paper does not require additional network controller node to connect clusters; network controller is a device without memory and processor and used only for communication. HPN is a regular graph where the degrees of all nodes are the same. Since it is also an undirected graph, the number of edges is \((5 \times 10^n) \div 2 = 2.5 \times 10^n\).

HPN(n) has degree of 5, \(10^n\) nodes and \(2.5 \times 10^n\) edges.

3.2 Simple routing, improved routing and diameter of HPN(n)

This section presents simple routing algorithm, improved routing algorithm and diameter of HPN(n). Let U be a starting node and denoted as \(u_nu_{n-1} \ldots u_2u_1\). Similarly, let V be a destination node and denoted as \(v_nv_{n-1}\ldots v_2v_1\). Deciding routing path is equivalent to the process of conversion from the starting address to destination address using the definition of the graph HPN(n). For routing, we simply change a symbol \(u_i\) to \(v_t\) and move it to the location t. After that, rule is applied to all symbols in starting node. We call this procedure “\(u_i\) is mapped to \(v_t\)”. The way to change \(u_i\) to \(v_t\) follows Summary 1 and happens at LSB. It is denoted as \(ch(u_i, v_t)\). The path derived from \(ch(u_i, v_t)\) is called “internal path,” and the path distance is denoted as dist\((u_i, v_t)\). Changing the location of \(u_i\) follows definition 1, and the corresponding path is called “external path.” Internal and external paths are presented as \(\rightarrow \) and \(\Rightarrow \), respectively.

3.2.1 Simple routing

There are two types of simple routings; RR routing that uses only RR operation and LR routing that uses only LR operation. Figure 3 shows a starting node mapped to a destination node in simple routing.

Fig. 3
figure 3

Example of RR routing and LR routing. a RR routing. b LR routing

Full size image

RR routing operates as follows; when RR operation is used to move symbols, \(u_2\) is changed to \(M(u_2)\) and moved to LSB. Therefore, \(ch(u_i, v_t)\) is equivalent to \(ch(M(u_i), v_t)\) where \(t = (i + 1) \% n\) (when \(i=n-1, t = n\)). Algorithm 1 shows RR routing algorithm.

figure a

Example 1

Assume that \(U=732\) and \(V=594\) in HPN(3). The path by RR routing is as follows: \(732 \rightarrow 733 \rightarrow 739 \Rightarrow 971 \rightarrow 970 \rightarrow 975 \Rightarrow 593 \rightarrow 594\).

Example 2

Assume that U=15732 and V=38594 in HPN(5). The path by RR routing is as follows: \(15732 \rightarrow 15733 \rightarrow 15739 \Rightarrow 91571 \rightarrow 91570 \rightarrow 91575 \Rightarrow 59155 \rightarrow 59159\rightarrow 59158 \Rightarrow 85913 \Rightarrow 38599 \rightarrow 38593 \rightarrow 38594.\)

LR routing is as follows: When symbol is relocated using LR operations, \(u_1\) is changed to \(P(u_1)\) and moved to \(u_2\) location. Therefore, \(ch(u_i, v_t)\) is equivalent to \(ch(u_i, M(v_t))\) where \(t = (i - 1) \% n\) (when \(i=1, t=n\)). Algorithm 2 shows LR routing algorithm.

figure b

Example 3

Assume that \(U=732\) and \(V=594\) in HPN(3). The path by LR routing is as follows: \(732 \rightarrow 736 \rightarrow 735 \Rightarrow 971 \rightarrow 970 \rightarrow 975 \Rightarrow 593 \rightarrow 594\).

Example 4

Assume that \(U=15732\) and \(V=38594\) in HPN(5). The path decided by LR routing is as follows: \(15732 \rightarrow 15731 \Rightarrow 57331 \rightarrow 57335 \rightarrow 57336 \Rightarrow 73385 \rightarrow 73384 \rightarrow 73383 \Rightarrow 33857 \Rightarrow 38593 \rightarrow 38594\).

3.2.2 Improved routing

When changing the starting node address to the destination node address, we have to decide each symbol in the starting node (\(u_i\) where \(1 \le i \le n\)) is mapped to which symbol in the destination node (\(v_j\) where \(1 \le j \le n\)). For example, \(u_1\) must be mapped to one of \(v_i\)s (\(1 \le i\le n\)). In RR routing, \(u_1\) is mapped to \(v_2\). In LR routing, \(u_1\) is mapped to \(v_n\). LL and RR routings are the ways to minimize an external path length to \(n-1\). These routings do not consider internal path length, which could become 2n in the worst cast. Improved routing selects a mapping with the shortest internal path length among n possible mappings. This decision problem is NP hard [14, 41]. In this situation, we calculate every possible case (n) and choose the minimum value instead of finding optimal value. According to the definition of an edge in HPN(n), if \(u_k\) is mapped to \(v_t\), \(u_{k+1}\) is mapped to \(v_{t+1}\) since the order of the symbols cannot be changed. Therefore, the number of possible symbol mappings between starting node and destination node is n. If \(u_1\) is mapped to \(v_t\), for example, the improve routing algorithm in terms of t is shown in Algorithm 3. Improved algorithm chooses the case with the shortest path value from the n cases. Due to notational complexity, \(M(u_j)\) and \(M(v_j)\) are not shown in Algorithm 3 as they are calculated in RR() and LR() operations.

figure c

When \(t=1\), the length of external path is n. When \(t=2\), RR routing is used and when \(t=n\), LR routing is used. The distance of external paths of LR and RR routings is \(n-1\).

3.2.3 Diameter

Theorem 1

The diameter of HPN(n) is \(3n-1\).

Proof

In the improved routing, the number of internal paths is n for all n cases and the diameter of Petersen graph is 2. Therefore, the sum of internal path distance for routing can be at most 2n. When \(t=1\), the length of external path is n. When \(t=n\) and \(t=2\), the length of external path is \(n-1\). When \(3 \le t \le \lceil \frac{n}{2}\rceil \), the length of external path is \(n+t-1\). When \(\lceil \frac{n}{2}\rceil < t \le n-1\), the length of external path is \(n+n-t\). In the worst case, when \(t=\frac{n}{2}\), the external path length is 1.5n. The length of internal path is 0 in the best case and 2n in the worst case. Assume that the internal path is 2n long for all n possible cases. Then the improved routing algorithm will select the route with the shortest external path. In this case, the length of external path is \(n-1\). Therefore, the diameter is \(3n-1\) according to the improved routing algorithm.

Table 1 Comparison of degree, diameter and network cost between HPN(n) and fixed-degree interconnection networks
Full size table

Now, HPN is compared to various interconnection networks. First of all, Table 1 shows the comparison of degree, diameter and network cost between HPN(n) and fixed-degree interconnection networks [20]. For this comparison, network cost per one network node (which is calculated as total network cost divided by total number of nodes) is used. In Table 1, N represents the number of nodes. Since \(\sqrt{N}> \root 3 \of {N} > \log _{10} N\), HPN outperforms over other networks in terms of network cost.

Table 2 Comparison of degree, diameter and network cost between HPN(n) and other hierarchical interconnection networks
Full size table
Fig. 4
figure 4

Comparison of network cost between HPN(n) and other hierarchical interconnection networks

Full size image

Secondly, HPN is compared to hierarchical interconnection networks. Table 2 shows the comparison for degree, diameter and network cost between HPN(n) and other hierarchical interconnection networks. For better and simpler representation of the network cost comparison, network costs regarding the number of nodes are shown in Fig. 4. As the interconnection networks do not have the same number of nodes, network costs are calculated with an approximation in the figure. As the number of nodes increases, the network cost for HPN(n) does not increase much compared to other networks as shown in the figure.

3.3 Spanning tree of HPN

Spanning tree is the tree structure that connects all nodes in a graph. If spanning tree can be constructed in HPN, it means HPN is a connected graph. In addition, spanning tree provides an algorithm to connect all nodes with less cost. This algorithm can be used in various ways, such as broadcasting algorithms (one-to-many and many-to-many broadcasting) and performance improvement for fault tolerance.

The process to construct a spanning tree is simple. First, we add all nodes located in the same basic module to the spanning tree as described in Summary 2. Secondly, we add all nodes connected by RR edges to all nodes in the basic module to the spanning tree. Repeat these two steps. The following shows formal procedure to construct spanning tree ST. In HPN(n), the root node of spanning tree is denoted as \(R = u_nu_{n-1}u_{n-2} \ldots u_2u_1\). Initially, ST is an empty set.

Procedure

  1. 1.

    Based on basic module \(u_nu_{n-1}u_{n-2} \ldots u_4u_3u_{2x}\), spanning tree is constructed with R node as a root node according to Summary 2 and it is added to ST.

  2. 2.

    Let TN be the set of nodes, connected to all nodes in a basic module that is the most recently added to ST using RR edges. Then, TN is added to ST.

  3. 3.

    According to Summary 2, spanning tree is constructed with TN as a root node based on the basic module consisting of majority of TNs. The rest except for TN is added to ST.

  4. 4.

    Repeat (2) and (3) \(n-1\) times.

There are two limitations in Procedure (2). Firstly, a node N with \(u_n=u_{n-1}=\cdots =u_2=u_1\) does not add child node connected to N by RR edge. Secondly, when Procedure (2) is executed, existing nodes are not added again to ST.

Figure 5 shows a step-by-step procedures how spanning tree is constructed in HPN(5). Step 1 in Fig. 5 depicts first round of Procedures (1), (2) and (3). The rest (steps 2, 3 and 4) are acquired by repeating Procedures (2) and (3).

Fig. 5
figure 5

Spanning tree of HPN(5)

Full size image

Theorem 2

HPN(5) contains a spanning tree with degree of 4, and it is a connected graph.

Proof

For an arbitrary node in a spanning tree, the degree is the same as the number child nodes. The degree of spanning tree is the largest degree among all nodes in it. The spanning tree constructed in Procedure (3) has degree of 3 according to Summary 2. In the next step, the nodes connected via RR edges are to be added to spanning tree and no child nodes will be added to these nodes. Therefore, spanning tree has degree of 4.

If an arbitrary graph contains a spanning tree, the graph is a connected graph. In Fig. 5, we would like to examine the node addresses surrounded with square. First of all, spanning tree is constructed using 10 nodes in Petersen graph 1234x, which is a basic module. In step 1, 10 x123x basic modules are added to spanning tree where the 10 basic modules are connected to the nodes in 1234x via RR edges. These 10 basic modules (\(10^2\) number of nodes) cover all domain without overlapping and/or left-over area at n level of HPN. For this spanning tree, the total number of nodes is \(10^1 + 10^2\). In \(n-2\) step (step 3), \(10^{n-2}\) basic modules (\(10^{n-1}\) nodes) are added to spanning tree. \(10^{n-2}\) basic modules cover all domain without overlapping and/or any left-over area at 2-level of HPN. For this spanning tree, the total number of nodes is \(10^1 + 10^2 + \cdots + 10^{n-1}\). In \(n-1\) step (step 4), \(10^{n-1} - (10^0 + 10^1 + \cdots + 10^{n-2})\) basic modules are added to spanning tree. These added basic modules cover all domain without overlapping and/or any left-over area at 1-level of HPN. For this spanning tree, the total number of nodes is as follows:

\(= 10^1 + 10^2 + \cdots + 10^{n-1} + (10^{n-1} - (10^0 + 10^1 + \cdots + 10^{n-2})) \times 10\)

\(= 10^1 + 10^2 + \cdots + 10^{n-1} + 10^n - (10^0 + 10^1 + \cdots + 10^{n-1})\)

\(= 10^n\).

As the spanning tree contains all nodes in HPN, HPN is a connected graph.

3.4 One-to-all broadcasting algorithm

In a network, nodes often need to communicate with each other for various reasons, such as data migration, message collection, job allocation and message dissemination. We assume a communication model where each communication channel is half-duplex and each node has all-port capability. This section presents broadcasting algorithm based on the spanning tree introduced in Sect. 3.3. and its procedure.

Suppose that the node with initial message is \(S = s_ns_{n-1}s_{n-2}\ldots s_2s_1\). Algorithm 4 shows one-to-all broadcasting algorithm.

figure d

In step 1, message is transmitted to 10 nodes, \(s_ns_{n-1}s_{n-2} \ldots s_2x\) from node S according to Summary 3. In step 2, a message is transmitted from the node \(s_ns_{n-1}s_{n-2} \ldots s_2x\) to the node \(xs_ns_{n-1}s_{n-2} \ldots M(s_2)\) where they are connected via RR edge. If the same symbols in the address are the same \((s_n=s_{n-1}=s_{n-2}= \cdots =s_2=s_1)\) for any node, the node stops transmitting the message. In step 3, the message is transmitted to \(xs_ns_{n-1}s_{n-2} \ldots x\) from the node \(xs_ns_{n-1}s_{n-2} \ldots M(s_2)\) according to Summary 3. When steps 2 and 3 are repeated \(n-2\) times, the broadcasting terminates.

Theorem 3

For HPN(n), one-to-all broadcasting time (BT) is \(3n-1\) and the broadcasting algorithm is edge disjoint.

Proof

According to Summary 3, the BT in steps 1 and 3 is 2. In step 2, BT is 1. For HPN(n), therefore, BT\( = 2 + (1 + 2){(n - 1)} = 3n - 1\). The path for the message traverse is the same as the one in spanning tree shown in Sect. 3.3. Therefore, the path is edge disjoint.

3.5 Embedding HPN(n) into FP\(_k\)

Once a new interconnection network is designed, parallel algorithms suited to the network structure are designed at the same time but it costs much in terms of research efforts. Research on network embedding focuses on the efficiency for which an algorithm developed for one certain interconnection network G can be used in a new interconnection network H. If the algorithm developed for G can be efficiently embedded into H with lower cost, then the overall cost can be reduced. Embedding f of guest graph G in host graph H means that V(G) is mapped in V(H) and edge E(G) in the path in H. In graph G, the dilation of edge e is the length of the path \(\rho (e)\) in H and the dilation of embedding f is the maximum value among dilations for all edges of G. In graph H, the congestion of edge \(e'\) is the number of \(\rho (e)\) included in \(e'\), and the congestion of embedding f is the maximum value among congestions for all edges of H. The expansion of an embedding is the ratio of the number of nodes in H to the number of nodes in G [48]. So, guest graph is HPN(n) and host graph is FP\(_k\).

Let the node in HPN(n) be \(U=u_nu_{n-1}u_{n-2}\ldots u_2u_1\) and the node in FP\(_k\) be \(V=v_kv_{k-1}v_{k-2}\ldots v_2v_1\). When \(n = k\), the nodes with the same address are exactly mapped because the total number of nodes \(10^n\) and the address allocation are the same in HPN(n) and FP\(_k\). According to this node mapping, the basic module \(u_nu_{n-1}u_{n-2}\ldots u_2x\) in HPN(n) is mapped to the basic module \(v_kv_{k-1}v_{k-2}\ldots v_2x\) in FP\(_k\). These two basic modules are automorphism, which means that the internal edge \((u_nu_{n-1}u_{n-2}\ldots u_2y, u_nu_{n-1}u_{n-2}\ldots u_2z)\) in HPN(n) is mapped to the internal edge \((v_kv_{k-1}v_{k-2}\ldots v_2y, v_kv_{k-1}v_{k-2}\ldots v_2z)\) in FP\(_k\). In this case, y and z are the adjacent nodes in Petersen graph. The external edge \((U, \mathrm{RR}(U))\) in HPN(n) is mapped to the path in FP\(_k\) with the starting node U and the destination node RR(U). Another external edge \((U, \mathrm{LR}(U))\) in HPN(n) is mapped to the path in FP\(_k\) with the starting node U and the destination node LR(U). Figure 6 shows that a basic module 174x in HPN(4) is mapped to the basic module 174x in FP\(_4\).

RR edge \((u_ku_{k-1}u_{k-2}\ldots u_2u_1, u_1u_ku_{k-1}u_{k-2}\ldots M(u_2))\) is mapped to the path with the starting node \(S=u_ku_{k-1}u_{k-2}\ldots u_2u_1\) and the destination node \(T = u_1u_ku_{k-1}u_{k-2}\ldots M(u_2)\). LR edge \((u_ku_{k-1}u_{k-2}\ldots u_2u_1, u_{k-1}u_{k-2}\ldots u_2P(u_1)u_k)\) is mapped to the path with the starting node \(S = u_ku_{k-1}u_{k-2}\ldots u_2u_1\) and the destination node \(T = u_{k-1}u_{k-2}\ldots u_2P(u_1)u_k\). The path is ruled by folded Petersen routing presented in Sect. 2.2.

Fig. 6
figure 6

Embedding 174x in HPN(4) into 174x in FP\(_4\)

Full size image

Theorem 4

When \(n = k\), HPN(n) is one-to-one mapped to FP\(_k\) and is embedded into expansion 1, dilation 2k and congestion 4.

Proof

As all nodes in HPN(n) are mapped to all nodes with the same addresses in FP\(_k\), expansion is 1 and it is one-to-one embedding. In addition, since a basic module in HPN(n) is mapped to the one with the same address in FP\(_k\), the dilation of an internal edge is 1. RR edge in HPN(n) is mapped to the path in FP\(_k\) with the starting node \(S=u_ku_{k-1}u_{k-2}\ldots u_2u_1\) and the destination node \(T = u_1u_ku_{k-1}u_{k-2}\ldots M(u_2)\). As dist\((u_i, u_{i+1} \% k)\) = 2 or 1 (for all is), the path distant is 2k in the worst case. The case with LR edge is similar to RR edge and the dilation is also 2k.

Congestion is more complicated. Since basic module in HPN(n) is one-to-one mapped to basic module in FP\(_k\), an internal edge in HPN(n) is mapped to an internal edge in FP\(_k\) where the two edges have the exact same symbols. Since internal edges are not overlapped, there is no need to check further. To calculate congestion, we have to examine two cases for which an external edge in HPN(n) is mapped to which external edge in FP\(_k\); (1) check which path in FP\(_k\) is mapped to external edges of 10 nodes in the basic module in HPN(n). (2) check all other cases which does not belong to case (1). For the rest of this section, symbol x means don’t care where \(1 \le x \le 9\).

For the first case, suppose that there are 10 nodes in basic module \(u_nu_{n-1}\ldots u_3u_2x\) in HPN(n). Ten RR edges connected to these 10 nodes are \((u_nu_{n-1}u_{n-2}\ldots u_2x,\) \( xu_nu_{n-1}u_{n-2}\ldots u_3M(u_2))\), and 10 paths in FP\(_k\), which are mapped to the 10 RR edges, are as follows:

$$\begin{aligned} u_nu_{n-1}u_{n-2}\ldots u_2x\Rightarrow & {} xu_{n-1} \ldots u_3u_2x \Rightarrow xu_n \ldots u_3u_2x \Rightarrow \cdots \Rightarrow xu_n \ldots u_4u_2x \\\Rightarrow & {} xu_n \ldots u_4u_3x \Rightarrow xu_nu_{n-1} \ldots u_3M(u_2) \end{aligned}$$

These 10 paths include x at the same location. Therefore, they are edge disjoint.

Suppose that there are 10 nodes in basic module \(u_nu_{n-1}\ldots u_3u_2x\) in HPN(n). Ten LR edges connected to these 10 nodes are \((u_nu_{n-1}\ldots u_3u_2x,\) \( u_{n-1}u_{n-2}\ldots u_3u_2P_x(u_n))\), and 10 paths in FP\(_k\), which are mapped to the 10 LR edges, are as follows:

$$\begin{aligned} u_nu_{n-1}\ldots u_3u_2x\Rightarrow & {} u_{n-1}u_{n-1}\ldots u_3u_2x \Rightarrow u_{n-1}u_{n-2}\ldots u_3u_2x \Rightarrow \cdots \\\Rightarrow & {} u_{n-1}u_{n-2} \ldots u_2u_2x \Rightarrow u_{n-1}u_{n-2} \ldots u_2P(x)x \\\Rightarrow & {} u_{n-1}u_{n-2}\ldots u_3u_2P_x(u_n) \end{aligned}$$

These 10 paths include x at the same location. Therefore, they are edge disjoint.

For the second case, assume that x is at the MSB; the result will be the same no matter where x is. Suppose that there are 10 nodes in HPN(n), \(xu_{n-1}u_{n-2}\ldots u_2u_1\). Ten RR edges connected to these 10 nodes are \((xu_{n-1}u_{n-2}\ldots u_2u_1,\) \( u_1xu_{n-1}u_{n-2}\ldots u_3M(u_2))\), and 10 paths in FP\(_k\), which are mapped to the 10 RR edges, are as follows:

$$\begin{aligned} xu_{n-1}u_{n-2}\ldots u_2u_1\Rightarrow & {} u_1u_{n-1}u_{n-2}\ldots u_2u_1 \Rightarrow u_1xu_{n-2}\ldots u_2u_1\\\Rightarrow & {} u_1xu_{n-2}\ldots u_4u_2u_1 \Rightarrow u_1xu_{n-2}\ldots u_4u_3u_1 \\\Rightarrow & {} u_1xu_{n-1}u_{n-2}\ldots u_3M(u_2) \end{aligned}$$

These 10 paths pass through a node \(u_1u_{n-1}u_{n-2}\ldots u_2u_1\). If the node is 154321, the path \(xu_{n-1}u_{n-2}\ldots u_2u_1 \Rightarrow u_1u_{n-1}u_{n-2}\ldots u_2u_1 \Rightarrow u_1xu_{n-2}\ldots u_2u_1\) is \(x54321 \Rightarrow 154321 \Rightarrow 1x4321\). The following shows all 10 paths listed in detail.

$$\begin{aligned} \begin{array}{lccccccccc} \hbox {Path (1)} &{} 054321 &{} &{} &{} \Rightarrow &{} 154321 &{} \Rightarrow &{} &{} &{} 104321 \\ \hbox {Path (2)} &{} &{} &{} &{} &{} 154321 &{} \Rightarrow &{} 104321 &{} \Rightarrow &{} 114321\\ \hbox {Path (3)} &{} 254321 &{} &{} &{} \Rightarrow &{} 154321 &{} \Rightarrow &{} 164321 &{} \Rightarrow &{} 124321\\ \hbox {Path (4)} &{} 354321 &{} \Rightarrow &{} 254321 &{} \Rightarrow &{} 154321 &{} \Rightarrow &{} 194321 &{} \Rightarrow &{} 134321\\ \hbox {Path (5)} &{} 454321 &{} \Rightarrow &{} 054321 &{} \Rightarrow &{} 154321 &{} \Rightarrow &{} 104321 &{} \Rightarrow &{} 144321\\ \hbox {Path (6)} &{} 554321 &{} \Rightarrow &{} 054321 &{} \Rightarrow &{} 154321\\ \hbox {Path (7)} &{} 654321 &{} \Rightarrow &{} 254321 &{} \Rightarrow &{} 154321 &{} \Rightarrow &{} &{} &{} 164321\\ \hbox {Path (8)} &{} 754321 &{} \Rightarrow &{} 854321 &{} \Rightarrow &{} 154321 &{} \Rightarrow &{} 164321 &{} \Rightarrow &{} 174321\\ \hbox {Path (9)} &{} 854321 &{} &{} &{} \Rightarrow &{} 154321 &{} \Rightarrow &{} 194321 &{} \Rightarrow &{} 184321\\ \hbox {Path (10)} &{} 954321 &{} \Rightarrow &{} 854321 &{} \Rightarrow &{} 154321 &{} \Rightarrow &{} &{} &{} 194321\\ \end{array} \end{aligned}$$

An edge (054321, 154321) passes through paths (1), (5) and (6). An edge (254321, 154321) passes through paths (3), (4) and (7). An edge (854321, 154321) passes through paths (8), (9) and (10). As these three edges are mapped to internal edges in HPN(n), congestion is 4. An edge (154321, 104321) passes through paths (1) and (5). An edge (154321, 164321) passes through paths (3) and (8). An edge (154321, 194321) passes through paths (9) and (10). Since these three edges are mapped to internal edges in HPN(n), congestion is 3. Therefore, when HPN(n) is embedded to FP\(_k\), congestion is 4.

4 Conclusion

Interconnection network can be categorized in three topologies; mesh family having constant degrees, hypercube family and star graph family consisting of various degrees. In mesh family, the node increase rate is very minimal when the network is expanded. On the other hand, there would be more nodes in hierarchical interconnection network than hypercube family or star graph family when the network is expanded. In addition, the number of degree is also increased. The proposed HPN(n) keeps the number of degree to 5 unchanged when the network is expanded while its size is relatively large, \(10^n\). It is very advantageous over other interconnection networks.

HPN(n) is a hierarchical network with degree of 5 and \(10^n\) number of nodes. When the number of nodes is N, for HPN, the diameter is 3log\(_{10}N-1\) and the network cost is 15log\(_{10}N-1\). As listed in Table 1, the network cost and diameter are \(O(\sqrt{N})\) in most fixed-degree networks. In addition, the degree is O(N) in most hierarchical networks as presented in Table 2. In this paper, we analyzed fundamental topological properties and showed that it contains a spanning tree with degree of 4. Additionally, we proposed edge-disjoint one-to-all broadcasting algorithm with time complexity \(3n-1\) and embedded (one-to-one) HPN(n) into FP\(_k\) with dilation 2k. As a result, HPN(n) with fixed degree and diameter of \(O(\mathrm{log}_{10}N)\) has improved network cost over existing hierarchical and fixed-degree networks.