1 Introduction

Given a natural number e, an addition chain, AC, for e is a finite sequence of numbers having three properties: (1) the first number is one, (2) every element is the sum of two earlier elements, and (3) the given number occurs at the end of the sequence. The sequence can be written as : \(a_0=1,a_1, a_2,\ldots , a_r=e\) such that \(a_i=a_j+a_l,\) \(i\ge 1,\) and \( l\le j<i\).

The AC problem is used to reduce the number of multiplications needed in modular exponentiation, \(x^e\,\) mod \(\,m,\) where x, e,  and m are positive integers. In [19], the authors suggested a sequential algorithm to find a short AC for e and then they used this short AC to reduce the number of modular multiplications required for parallel modular exponentiations. Moreover, the addition chain can be used to improve the computations of inversions in finite fields [16].

The sequential algorithms for AC can be classified into two groups. The first group contains algorithms that find the AC with minimal length. These algorithms are based on different techniques such as depth-first, breadth-first and branch and bound [2, 3, 7, 22]. The running times of these algorithms are non-polynomial time.

The second group contains algorithms that generate a short (necessary minimal length) chain. These algorithms are based on different techniques and run in polynomial in n. Examples for these techniques are continued fraction, binary, m-ary, window, factor, power tree, genetic, and ant colony [3,4,5,6, 8, 11,12,13,14,15, 17, 18, 20]. For example, the short chain generated by the binary method for \(e=65\) is \(a_0=1, a_1=a_0+a_0=2, a_2=a_1+a_1=4, a_3=a_2+a_2=8, a_4=a_3+a_3=16, a_5=a_4+a_4=32, a_6=a_5+a_5=64, a_7=a_6+a_1=65\) and the length of the chain is 7. We can also generate another short chain for \(e=65\) by using the factoring method as follows. The integer 65 can be factored to 5 and 13. The addition chains for 5 and 13 are (1, 2, 4, 5) and (1, 2, 4, 8, 12, 13), respectively. Therefore, the final addition chain for 65 is 1, 2, 4, 5, 10, 20, 40, 60, 65 and has length 8.

In case of parallelism, two algorithms are proposed based on the left–right binary method under parallel random access machine (PRAM). The two algorithms are designed based on EREW PRAM (exclusive read exclusive write). The first one [8] depends on parallelizing the addition operation only as in Proposition 3, Sect. 2.2. So, the algorithm consists of n sequential iterations. In each iteration, the \(\frac{n}{\log {n}}\) processors are used to parallelize the addition of two numbers of n-bits each. The algorithm uses \(\frac{n}{\log {n}}\) processors to run the algorithm in \(O(n/\log n)\) parallel time. The algorithm is optimal but not fast.

The other parallel algorithm [10] is based on a new formula to generate the elements of the chain in a parallel way. The formula uses two other operations, division and subtraction. The algorithm uses \(O( n^{2} \log n \log \log n)\) processors and runs in \(O((\log {n})^2)\) parallel time. The algorithm is fast, but it has two main drawbacks: (1) the algorithm is not optimal, and (2) the algorithm uses the division and subtraction operations.

As a conclusion of previous works, the optimal parallel algorithm for short AC has not polylogarithmic time, \(O((\log n)^k)\) and k is a constant. On the other side, the fastest parallel algorithm for short AC is not optimal. Therefore, the main target of this paper is to design an optimal parallel algorithm in polylogarithmic time.

The paper presents two parallel addition chain algorithms for the natural number e of n-bits. The strategy used in the proposed algorithms is the right–left binary algorithm. The first algorithm runs in \(O((\log {n})^2)\) parallel time using \(n^2\log \log {n}\) processors. The algorithm is modified to be optimal based on using the barrel shifter circuit. Using \(\frac{n^2}{(\log {n})^2}\) processors on EREW PRAM, the modified algorithm runs in \(O((\log {n})^2)\).

The structure of the paper is organized as an introduction and four sections. In Sect. 2, we mention basic definitions and facts about our problem. We also give an overview about the right–left binary sequential algorithm. In Sect. 3, we give the parallel right–left binary algorithm to compute an addition chain of short length on EREW PRAM. We also compute its complexity. In Sect. 4, we modified the proposed algorithm to be optimal in the sense of cost. The conclusion of this paper appears in Sect. 5.

2 Preliminaries

In this section we give the preliminaries related to design optimal short chain on EREW PRAM. This section consists of three subsections. The first subsection presents a brief description of the model of parallelism used in the proposed parallel algorithm. In the second subsection, we review some definitions and results needed in the paper. Then, in the third subsection, we review the sequential right–left binary algorithm to generate a short addition chain.

2.1 Model of computation

The model of parallelism that is used in the proposed algorithm is the parallel random access machine (PRAM). The model is an extension of the sequential model of computation (the Random Access Machine, or RAM). PRAM consists of p identical processors that communicate through a common memory. Based on the mechanism on how to handle the simultaneous memory accesses, we have four submodels of PRAM. In this paper, we will use one of them which is exclusive read, exclusive write (EREW) PRAM. In this model, the concurrent read/write from/to the same memory cell is not allowed.

2.2 Definitions and previous results

We mention some definitions and previous results needed to design our parallel algorithm.

Definition 1

[1] A parallel algorithm for problem Q is optimal if the product of the number of processors and the time complexity of the parallel algorithm is equal to the time of the fastest sequential algorithm for Q.

Definition 2

[1] The prefix operation for the array \(X=(x_{1},x_{2},\ldots ,x_{n})\) is the array \(S=(s_{1},s_{2},\ldots ,s_{n}),\) where \(s_{i}=x_{1}\oplus x_{2}\oplus \ldots \oplus x_{i}\), \(\forall 1\le i \le n\).

In Definition 2, if the binary operator \(\oplus \) is equal to \({+}\) then the problem is called prefix-sums, while if \(\oplus = *, \) then the problem is called prefix-products.

Definition 3

[1, 9] The Nick’s class, NC, consists of the problems that are solved using a polynomial number of processors \(n^{O(1)}\) in polylogarithmic \(O(\log ^{O(1)}{n})\) time.

Proposition 1

[1] The sequential time required to compute the prefix operation of the array \(X=(x_{1},x_{2},\ldots ,x_{n})\) is O(n),  while the same problem can be solved using \(p\le \frac{n}{\log {n}}\) EREW PRAM processors in time \(O(\log {n}+\frac{n}{p}).\)

Proposition 2

[1, 8] Given two integers, x and y,  of n-bits each. Computing \(x\pm y\) takes O(n) sequential time.

Proposition 3

[1, 8, 21] Given two integers, x and y,  of n-bits each. Based on EREW PRAM, the addition of x and y using \(\frac{n}{\log {n}}\) processors has parallel time \(O(\log {n}),\) while the multiplication of x and y using \(O(n\log {n}\log \log {n})\) processors has parallel time \(O(\log {n}).\)

We use the notations \(x\, +_{_p}\,y\) and \(x\,*_{_p}\,y\) to represent the addition and multiplication of two integer numbers in parallelism.

2.3 Sequential right–left binary algorithm

We review the sequential right–left binary algorithm that generates a short chain. Let e be a natural number of n bits. The number e can be written as binary \(e=(e_{n-1}, e_{n-2},\ldots ,e_1,e_0)_2,\) where \(e_{i} \in \{0,1\},\) \(0\le i\le n-1.\) We also assume that \(v(e)=|\{e_i,\) s.t. \(e_i=1, 0\le i\le n-1\}|.\) The steps of the algorithm are as follows [8, 11].

Step 1:

Set \(a_0=1.\)

Step 2:

Generate \(n-1\) elements of the chain by doubling the previous element as \(a_i=a_{i-1}+a_{i-1}, \forall 1\le i\le n-1.\)

Step 3:

Generate \(v(e)-1\) elements of the chain by adding the element \(a_i\) to the last generated element if the ith bit of e equals 1, \(0\le i\le n-2.\) i.e. \(a_j= a_{j-1}+a_i, \forall n\le j\le n+v(e)-2.\)

Example 1

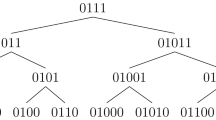
Given \(e=52039=(1100101101000111)_2\). Figure 1 shows the execution of the right–left binary method on e. Figure 1(i) represents Step 1; while Fig. 1(ii) represents the generation of 15 elements of the AC as described in Step 2. Figure 1(iii) represents the generation of the remainder elements of AC, where \(a_{16}=a_{15}+a_{0}, a_{17}=a_{16}+a_1, a_{18}=a_{17}+a_2, a_{19}=a_{18}+a_6, a_{20}=a_{19}+a_8, a_{21}=a_{20}+a_{9}, a_{22}=a_{21}+a_{11}, a_{23}=a_{22}+a_{14}.\)

Fig. 1
figure 1

Tracing of right–left binary algorithm on \(e=52039\)

Full size image

3 Parallel algorithm for AC

We introduce a fast algorithm to compute a short AC for the number e of n-bits on PRAM. The n bits \((e_{n-1}, e_{n-2},\ldots ,e_1,e_0)_2\) of the number e are stored in the shared memory of the PRAM. The number of processors used in the proposed algorithm is \(O(n^2 \log {\log {n}}).\)

Our introduced algorithm is based on the right–left binary strategy. We have two main steps in this method. The first one is Step 2 and it is used to compute the addition chain for the number \(2^{n-1}.\) The addition chain for the number \(2^{n-1}\) is the sequence \(1, 2, 4, 8,\dots ,2^{n-1}.\) This chain can be generated in parallel by applying the prefix-product algorithm on the sequence \(\{1, 2, 2, 2, 2,\dots , 2\}\) of n numbers. The other main step is Step 3. The step is used to generate the reminder elements of AC which correspond to the 1 bits in the binary representation of e. The elements can be computed in parallel by selecting the element \(a_j\) from the chain, \(\{a_0=1, a_1=2, a_2=4,\dots , a_{n-1}=2^{n-1}\},\) if \(e_{j}=1, \forall 0\le j<n-1.\) We can compute the rest of the chain by applying the parallel prefix-sum algorithm on the selected elements and the element \(a_{n-1}=2^{n-1}.\)

We use the notation A(i : j) to represent the elements \(a_i,a_{i+1},\dots ,a_{j}.\) We also assume that \(w=\log {n}\) and \(N=\frac{n}{\log {n}}.\) Our parallel algorithm on EREW PRAM consists of four main steps:

The first step of the proposed algorithm is initialization. We use n processors to initialize the first element of A with 1 and the next \(n-1\) elements of A with 2.

The second main step is computing the addition chain for \(2^{n-1}.\) The minimal length addition chain for \(2^{n-1}\) is \(1, 2, 4, \ldots , 2^{n-1}.\) It can be computed by using the prefix-product algorithm on \(A(0:n-1)\) and \(n^2\log \log {n}\) processors as follows.

  • For each subarray \(A_i=A(i\,w:(i+1)\,w-1), 0\le i< N,\) compute \(a_{i\,w+j}=a_{i\,w+j}\,*_{_p}\,a_{i\,w+j-1}\), \(\forall \, 1\le j<w .\)

  • Repeat the following \(\log {N}\) iterations, \(1\le h\le \log {N}:\) compute \(a_{(i+1)w-1}=a_{(i+1)w-1}\, *_{_p}\, a_{(i-2^{h-1}+1)w-1}\), \(\forall \, 2^{h-1}\le i< N.\)

  • For each subarray \(A_i, 1\le i< N,\) compute \(a_{i\,w+j}=a_{i\,w+j}\, *_{_p} \, a_{i\,w-1}\), \(\forall \, 0 \le j< w-1.\)

Note that we assign \(n \log n \log \log n\) processors to each partition, \(A_i, 0\le i<n/\log n.\) For each partition, we do \(\log n\) iterations sequentially. The \(n \log n \log \log n\) processors used to compute \(*_p\) in parallel. So, we used \(n^2 \log \log n\) processors to execute the second step.

The third main step is determining the elements of \(A(0:n-2)\) that will be used in the rest of chain. We select \(v(e)-1\) elements from \(A(0:n-2)\) and store them in the array \(A(n:n+v(e)-2).\) The ith selected element \((1\le i\le v(e)-1)\) is the element \(a_j \in A(0:n-2)\) such that \(e_{j}\) is the ith one of \(e=(e_{n-1}\ldots e_1 e_0)_2.\) This step can be done as follows.

  • Each processor \(p_i, 0\le i< N,\) computes the number of ones in \((e_{((i+1)w)-1}, \ldots ,e_{i\,w})_2.\) Let \(x_i=v((e_{((i+1)w)-1},\ldots ,e_{i\,w})_2)\)

  • Each processor \(p_i, 0\le i< N-1,\) assigns \(x_i\) to \(x_{i+1}.\) The processor \(p_{N-1}\) assigns n to \(x_0.\)

  • Apply the prefix-sum algorithm on \(X(0:N-1).\)

  • Each processor \(p_i, 0\le i< N,\) does the following test on the \((i+1)\)th w bits of e: if \(e_{i\,w+j}\) equals 1 then (1) save \(a_{i\,w+j}\) at the location \(x_{i}\) in the array A,  where \(0 \le j< w;\) and (2) update \(x_{i}=x_{i}+1.\)

    Note that when \(i=N-1,\) we test \(w-1\) bits \((e_{n-2},\dots ,e_{n-w})\) only.

The fourth step is computing the rest of the chain. Compute the remaining elements of the addition chain by applying the prefix-sum algorithm on \(A(n-1:n+v(e)-2).\) This step can be done as follows.

  • Let \(m=v(e)-1, \,m'=\log m, \, M'=\frac{m}{m'}.\)

  • For each subarray \(A_i=A(n-1+i\,w:n-2+(i+1)w), 0\le i< M',\) compute \(a_{n+i\,m'+j-1}=a_{n+i\,m'+j-1}\, +_{_p} \, a_{n+i\,m'+j-2}, \forall \, 1 \le j< m'.\)

  • Repeat the following \(\log {N'}\) iterations, \(1\le h\le \log {M'}:\) compute \(a_{n+(i+1)m'-2}=a_{n+(i+1)m'-2}\, +_{_p} \,a_{n+(i-2^{h-1}+1)\,m'-2}, \,\,\,\forall 2^{h-1}\le i< M'.\)

  • For each subarray \(A_i, 1\le i< M',\) compute \(a_{n+i\,m'+j-1}=a_{n+i\,m'+j-1}\, +_{_p} \,a_{n+i\,m'-2},\,\,\,\forall 0 \le j < \log {w}-1.\)

Note that we assign \(\frac{n}{\log {n}}\) processors to each partition, \(A_i.\) For each partition, we do \(\log n\) iterations sequentially. The \(\frac{n}{\log {n}}\) processors used to compute \(+_p\) in parallel. So, we used n processors, at most, to execute the fourth step.

Example 2

Using the same value of e in Example 1, the tracing of the proposed algorithm to generate the AC for e is shown in Fig. 2. Figure 2(i) represents the initialization step; while the prefix-product of \(a_0,a_1,\dots ,a_{n-1=15}\) is shown in Fig. 2(ii). Figure 2 \(\,(iii)\) represents the elements of \(A(0:n-2)\) that will be used in the rest of chain. The prefix-sums for \(a_{15},a_{16},a_{17},a_{18},\dots ,a_{23}\) is shown in Fig. 2(iv).

Fig. 2
figure 2

Tracing of parallel right–left binary algorithm on \(e=52039\)

Full size image

Now, the complete proposed algorithm is as follows.

figure a

It is easy to compute the number of sequential and parallel operations performed by the proposed algorithm. Step 1 requires n processors to execute it in O(1) time. By using at most \(O(n^2 \log \log {n})\) processors, the time required for Steps 2.1, 2.2, and 2.3 are \(O((\log {n})^2),\) \(O(\log {n}\log {\frac{n}{\log {n}}})\) and \(O((\log {n})^2)\), respectively. Therefore, Step 2 takes \(O((\log {n})^2)\) time. The time complexity for Step 3 is \(O(\log {n}).\) Because the running time of Steps 3.1, 3.2, 3.3, 3.4 and 3.5 are O(1),  \(O(\log {n}),\) O(1),  \(O(\log {\frac{n}{\log {n}}}),\) and \(O(\log {n})\), respectively, using at most \(O(\frac{n}{\log {n}})\) processors. By using at most \(O(\frac{n^2}{(\log {n})^2})\) processors, the time complexity for Steps 4.1, 4.2 and 4.3 are \(O(\log {n}\,\log {m}),\) \(O(\log {n}\,\log {(\frac{m}{\log {m}})})\) and \(O(\log {n}\,\log {m})\), respectively. So, Step 4 takes \(O((\log {n})^2)\) time. Therefore, by using \(O(n^2 \log \log {n})\) processors on EREW PRAM, the time complexity of the proposed algorithm is \(O((\log {n})^2).\) The storage of the algorithm is \(O(\frac{n}{\log {n}}),\) since we have only one auxiliary array, X,  of length \(\frac{n}{\log {n}}.\)

4 Optimal parallel algorithm for AC

The PAC algorithm has polylogarithmic time, but not optimal. The goal of this section is to modify the proposed algorithm to be the optimal algorithm while keeping the time as it is. The algorithm is based on using the barrel shifter circuit. A barrel shifter is a combinational logic circuit consisting of three parts. \((1)\,\) k data inputs. \((2)\,\) k data outputs. (3) A group of control inputs that determine the mechanism of shifting the data between input and output [23]. The circuit is able to perform shift (left and right) logical, rotate (left and right) operations in a single cycle. These operations, shifting and rotating are important in many applications such as arithmetic operations, bit-indexing, and variable-length coding. Currently, a barrel shifter exists as a part of a microprocessor.

For example, if \(n=8\) and the original data equals 11010001 then we can shift the data (in a single clock cycle ) by 4 positions using the barrel shifter and produce 00011101.

The first two steps of PAC algorithm can be modified as follows.

figure b

By using n processors, the two steps (1 and 2) run in O(1) time. Hence, we required \(O(\frac{n^2}{(\log {n})^2})\) processors to run the modified algorithm in \(O((\log {n})^2)\) time. The running time of the sequential addition chain algorithm, \(O(n^2),\) is reduced to \(O((\log {n})^2).\) The algorithm is simple, fast and optimal.

Table 1 shows the comparison between the different algorithms for short chain using the binary method, where S(n) represents the storage of the algorithm. The comparison between different parallel algorithms is based on optimality, running time and storage criteria. In parallel computation, especially on PRAM, a parallel algorithm for AC is optimal if the cost, product of parallel time and number of processors, is equal to the best sequential time \(O(n^2)\) [11]. For the optimality measure, we have two optimal parallel algorithms. The first one in the ref. [8], while the second is the proposed algorithm. For the running time measure, the fastest algorithms are the algorithm in the ref. [10] and the proposed algorithm. For the storage measure, the memory-consumed for the algorithm in the ref. [8] is minimal. Therefore, the fast and optimal parallel algorithm for AC is the proposed algorithm.

5 Conclusion

In this work, we have studied the generation of a short AC for the n bits number e. We have developed a new algorithm based on the right–left binary algorithm and barrel shifter circuit. The algorithm is designed on EREW PRAM and uses \(O(\frac{n^2}{(\log {n})^2})\) processors. The time complexity of the algorithm is \(O((\log {n})^2)\) which is belongs to Nick’s class. The algorithm is simple, fast and optimal.

Table 1 Comparison between different algorithms
Full size table

The future study of this work is to parallelize the different strategies such as window and m-ary methods to find a short chain and then compare it with the proposed algorithm. We also try to implement the proposed algorithm on different platforms of high-performance systems such as multi-core and GPU to measure the speedup of the proposed algorithm.