An Asymptotic Analysis of Methods for Predicting the Fracture Toughness of Multiaxial Carbon Fiber Composite Laminates Using the Elastic Constants of the 0° Plies

Carbon fiber composite laminates are an important alternative to metal in many mechanical structural applications. Carbon fiber composite laminates usually have multidirectional plies with different angles. In this study, a simple analytical model is derived to predict the notch strength of these multidirectional plies from the unidirectional strength of the 0° ply. The first method considers the orthogonal analysis of the forces introduced in each ply at the Cartesian coordinates in each of the 2 axes with their direction, and then calculates the resulting forces. The second method considers the percentage of layers inside the laminates and then orthogonally analyzes the induced forces on the entire laminate sheets. The resulting stress induced by these forces is calculated according to the theory of maximum failure shear or principal stress. In addition, the fracture toughness ${{\text{G}}}_{{\text{IC}}}$ was predicted based on the strength of the unnotched laminates calculated by previous methods. In addition, the size effect of the open-hole specimen was measured based on the predicted fracture toughness and strength of the unnotched laminates. The model was compared with available experimental and other published models. The optimum values for the two methods of fracture toughness were determined. The average percent accuracy of size effect prediction based on the first method is 3.24%, while it is 6.82% for the second method.

Nomenclature

${\sigma }_{un}$, ${\sigma }_{la}$ – un-notch strength

$\overline{{A }_{90}}$, $\overline{{A }_{\theta }}$, and $\overline{{A }_{0}}$ area of laminate in 90°, angle ply, and 0°

$\overline{{A }_{lay}}$, $\overline{{A }_{ply}}$, and $\overline{{A }_{lax}}$ – area of laminate in $y$, angle ply, and in $x$

$\left[A\right]$ – stiffness matrix

${A}_{90}$ – area of 90° ply

${A}_{la}$ – area of laminate

${A}_{ply}$ and ${A}_{plx}$ – area of ply in $x$ and $y$ directions

${A}_{\theta }$ – area of angle ply

${E}_{1}$, ${E}_{2}$, ${G}_{12}$, and ${\nu }_{12}$ – elastic constant in 1 and 2 principal directions

${E}_{eff}$ – modified effective Young modulus

${E}_{x}$, ${E}_{y}$, ${G}_{xy}$, and ${\nu }_{xy}$ – elastic constant in $x$ and $y$ Cartesian coordinates

${F}_{0}$ – force induced in zero direction

${F}_{lay}$ – ply force induced in $y$ direction

${F}_{x}$ and ${F}_{y}$ – total component of force in $x$ and $y$ directions

${F}_{\theta }$ – force induced in angle direction

${I}_{1}$ – ones matrix

${Q}_{xy}$ – the reduced stiffness

${X}_{t}$ and ${X}_{c}$ – uniaxial tensile and compression strength

${f}_{ij}$ – transformation function calculating in Appendix [1]

${\delta }_{c}$ – critical crack opening

${\delta }_{ij}$ – Kronecker delta

${\varepsilon }_{f}$ – fracture strain

${\lambda }_{90}$, ${\lambda }_{\theta }$, and ${\lambda }_{0}$ – percent of ply in 90°, angle, and 0°, respectively

$\tilde{\sigma }$ – average stress

${\sigma }_{90}$ – uniaxial stress in 90° ply

${\sigma }_{lay}$ – stress through laminates in $y$ direction

${\sigma }_{n}$ – nominal strength

${\sigma }_{\theta }$ – uniaxial stress through angle ply

${G}_{IC}$ – mode I fracture toughness, kJ/m²

$x$ and $y$ – Cartesian coordinates

$\psi$ – calculated equivalent Young modulus

$N$ – total number of plies

$nx$ – number of ply in $x$ direction

$ny$ – number of plies in $y$ direction

$t$ – total thickness of laminate

$\theta$ – angle of ply inclination

Introduction. Carbon fiber composite laminate structures are a competitive alternative to many metals due to their excellent specific strength and specific weight, especially in the aerospace, marine and offshore industries [2,3,4]. In the design of such materials, stress concentration factors [5] are usually used, which are caused by discontinuity or interfaces between plies or layers such as delaminations [6]. Therefore, the applicability of such types of materials depends mainly on a fast and robust model to determine their strength under accurate applications.

Finite element methods can predict the strength of laminates with good accuracy, but they are time consuming and not preferable in optimization [5, 7] or material selection proposals [8]. Moreover, most mesh element methods need to be refined, which increases the computation time. Therefore, analytical methods based on the cohesive zone model can be proposed and overcome the limitation of FEM difficulties with satisfactory accuracy and speed [9,10,11]. A direct relationship between the fracture toughness and the notched impact strength of a structural plate was established by Tan [12]. The cohesive zone model uses a fictitious crack [13] and relates the cohesive stress across the crack surface and the critical crack opening [14]. The cohesive zone model used to predict the nominal strength of composite laminates with open holes can have different forms: linear [9], exponential [1] and even bilinear [15]. Fracture toughness for aerospace and aircraft wings should be precisely defined to improve safety [16]. Therefore, to define it completely, two main parameters are required: fracture toughness and notched impact strength of composite laminates. Many analytical models [1, 17,18,19] have been derived to predict the nominal strength of cracked composite laminates. The failure modes would be concentrated in a process zone ahead of the crack tip if the thickness of the plies is sufficiently thin, while for thicker plies, failure occurs by delamination. For composite structures, the nominal strength decreases as the size or geometry of the structure increases [20]. Therefore, in order to predict the size effect well, methods are needed to calculate the energy lost due to crack propagation [21].

Furtado et al. [5] proposed an analytical model to predict the strength of open hole carbon fiber reinforced polymer laminates. This model used three characteristic material properties such as fracture toughness, Young’s modulus and notched impact strength, these parameters were calculated using invariant-based models, the results were acceptable, but the model lacks generality of layers and stacking sequences with large percentage error, neglecting the availability of many angular layers with 90° or without. In this context, it was reported in [22] that the longitudinal fracture toughness of Hexcel IM7-8552 carbon epoxy multidirectional laminates can be predicted using unidirectional laminates based on linear elastic fracture mechanics (LEFM) concepts and lamination theories, but the accuracy of these models required increasing caution and more experience to be implemented. Therefore, a simplification based on geometry and orientation was performed by Mohammed et al [23]. In addition, a comparative study was presented by Abdellah [24] to predict the fracture toughness of T800/924C CFRP. Here, the cohesive zone model was applied in reverse to predict the fracture toughness with the definition of the size-effect curve profile of the open-hole specimen, and the results were compared with the results of the study by Soutis and Curtis [25], in which the nominal strength of open-hole specimens was predicted using the cohesive zone model based on the experimentally measured fracture toughness and a predicted notch-free strength. Since the two parameters of the cohesive zone model are a characteristic property, it was not necessary to measure each time the specimen geometry changed due to holes, cracks, or other shape discontinuities. Moreover, the cohesive zone models are based on physical properties with exact sense [26].

The linear elastic failure theories for isotropic material have been used [27,28,29,30] to predict the failure of composite materials, but their applicability and reliability are still problematic and require much work. Micromechanical models have been used to accurately predict the stiffness and strength models of composite laminates using length, stochastic fiber orientation, fiber volume fraction, and void volume fraction [31]. The strain energy failure criterion has been used to predict the tensile strength of composite laminates, but was limited to some assumptions. Recently, natural vibration was used as a nondestructive test [32] o measure the fracture toughness and size effect of composite laminates. In the study, the equivalent Young modulus of the glass fiber composite structure was first predicted from the natural frequencies, and then the modified hook law was used according to the LEFM approach with high accuracy and lower % error.

It is clear that the elasticity theories need to be further investigated in order to apply them in the calculation of strength and elastic stiffness of composite laminates. Therefore, the present study attempts to establish a robust model to predict the notch-free strength of laminates with angular plies and quasi-isotropic plies, and to propose a model to predict the fracture toughness of composite laminates and the strength of CFRP composite panels with open holes. Another objective of the present study is to compare the results of the proposed models with other available models to determine the optimization and accuracy of the model. In addition, the size-response curve of the open-hole sample is determined.

In the first section, the analytical model is explained, and in the second section, the results of the model are compared with those of other publications to obtain optimization tables. Finally, the results are summarized.

1. Un-Notch Strength. The following macromechanical analysis method is an attempt to calculate the strength ${\sigma }_{un}$ of unidirectional composite laminates from the strength of unidirectional laminates in tension ${X}_{t}$ or in compression ${X}_{c}$. Then the equivalent Young modulus is calculated using the stiffness of unidirectional laminates ${E}_{1}, {E}_{2}, {\nu }_{12},$ and ${G}_{12}$. Based on the prediction of multidirectional strength without notch, fracture strain and equivalent Young modulus, it is possible to calculate fracture toughness ${G}_{IC}$ by theories of elastic fracture mechanics. Finally, the size effect of open holes can be predicted using the linear cohesive law.

1.1. Method 1-a. Simple method based on equilibrium forces in each ply for balanced laminates with $\theta$-angle, 0° and 90° ply. The problem is divided into four segments (top and bottom) in the $y$-axis direction and (right and left) in the $x$-axis direction, as shown in Fig. 1. The positive direction is clockwise.

Fig. 1.

Cartesian coordinates of multidirectional laminates with $\theta$-angle position: (a) upper and lower segment; (b) right and left segment.

Analysis the forces in only $y$ directions without consider forces in $x$ direction (Fig. 1a) as follows:

$${F}_{lay}=\sum {F}_{y}={F}_{0}+{F}_{\theta }{\text{cos}}\left(\theta \right)+{F}_{\theta }{\text{cos}}\left(\theta \right),$$

(1)

where ${F}_{lay}$ is the total laminates force in $y$ direction. As the force through fiber is equal the stress through laminates multiplied by area ${\sigma }_{lay}{A}_{la}$ therefore the previous equation can be rewritten as

$${\sigma }_{lay}{A}_{la}=\sum {F}_{y}{A}_{ply}={\sigma }_{90}{A}_{90}+{\sigma }_{\theta }{A}_{\theta }{\text{cos}}\left(\theta \right)+{\sigma }_{\theta }{A}_{\theta }{\text{cos}}\left(\theta \right),$$

(2)

where ${A}_{la}$ is laminate area per unit width equal (${A}_{la}=Nt$), where $t$ is laminates thickness, $N$ is total laminates plies, and ${A}_{ply}$ ply area which equal to (${A}_{ply}=(N/ny)t$). Therefore, substitution into Eq. (2) give the following expression:

$${\sigma }_{lay}=\sum {F}_{y}{A}_{ply}=\frac{{\sigma }_{90}}{ny}+\frac{{\sigma }_{\theta }}{\mathit{ny}}{\text{cos}}\left(\theta \right)+\frac{{\sigma }_{\theta }}{ny}{\text{cos}}\left(\theta \right),$$

(3)

where $ny$ is total ply in $y$ direction which is equal to ($ny=\sum ({n}_{90}+{n}_{\theta })$), where ${n}_{90}$ and ${n}_{\theta }$ are 90° and $\theta$ plies, respectively. Repeat the pervious analysis at the bottom side of the laminates.

The same analysis is carried out for the right and lift section in $x$ direction of the laminates (Fig. 1b), it is obtained the strength in $x$ direction as follows:

$${\sigma }_{lax}=\sum {F}_{x}{A}_{plx}=\frac{{\sigma }_{0}}{nx}+\frac{{\sigma }_{\theta }}{\mathit{nx}}{\text{sin}}\left(\theta \right)+\frac{{\sigma }_{\theta }}{nx}{\text{sin}}\left(\theta \right),$$

(4)

where $nx$ is total ply in $x$ direction which is equal to ($nx=\sum ({n}_{0}+{n}_{\theta })$), where ${n}_{0}$ and ${n}_{\theta }$ are 0° and $\theta$ plies, respectively. Then the multidirectional laminate strength (${\sigma }_{la}$) is the product of the strengths in the $y$ and $x$ direction as follows:

$${\sigma }_{la}=2\sqrt{{\sigma }_{lax}^{2}+{\sigma }_{lay}^{2}}.$$

(5)

1.2. Method 1-b. For laminates without 90° or without $\theta$, the Cartesian coordinate from Fig. 2 is used. And the thickness of the laminates can be calculated as follows:

Fig. 2.

Cartesian coordinates of multidirectional laminates with $\theta$ angle ply.

For strength in $y$ direction, it is as follows:

$${\sigma }_{lay}=\sum {F}_{y}{A}_{ply}={\sigma }_{90}{\lambda }_{90}+{\sigma }_{\theta }{\lambda }_{\theta }{\text{cos}}\left(\theta \right)+{\sigma }_{-\theta }{\lambda }_{-\theta }{\text{cos}}\left(2\pi -\theta \right).$$

(6)

For strength in $x$ direction, it is as follows:

$${\sigma }_{lax}=\sum {F}_{x}{A}_{plx}={\sigma }_{0}{\lambda }_{0}+{\sigma }_{\theta }{\lambda }_{\theta }{\text{sin}}\left(\theta \right)+{\sigma }_{-\theta }{\lambda }_{-\theta }{\text{sin}}\left(2\pi -\theta \right).$$

(7)

The laminates consider one plate with $x$, $y$ component and the resultant force is as follows:

$${\sigma }_{la}=2\sqrt{{\sigma }_{lax}^{2}+{\sigma }_{lay}^{2}}.$$

(8)

Here ${\lambda }_{90}$, ${\lambda }_{0}$, ${\lambda }_{\theta }$, and ${\lambda }_{-\theta }$ are percent of 90°, 0°, and $\pm \theta$ ply in the whole laminates thickness.

1.3. Method 2. This method is similar to method 1-b, but is considered a general method for quasi-isotropic laminates with all stacking sequences, based on orthogonal force analysis of two sides of the laminates and ply percentages through the laminates. Both maximum principal stress theory and maximum shear stress theory are used. Referring to Fig. 2, the force analysis is as follows:

$${F}_{lay}=\sum {F}_{y}={F}_{90}+{F}_{\theta }{\text{cos}}\left(\theta \right)+{F}_{\theta }{\text{cos}}\left(2\pi -\theta \right).$$

(9)

And the $x$ component of force is as follows:

$${F}_{lax}=\sum {F}_{x}={F}_{0}+{F}_{\theta }{\text{sin}}\left(\theta \right)+{F}_{\theta }{\text{sin}}\left(2\pi -\theta \right).$$

(10)

By substituent stress $\sigma$ instead of forces, these equations can be rewritten as follows:

$${\sigma }_{lay}\times \overline{{A }_{lay}}=\sum {F}_{y}\overline{{A }_{ply}}={\sigma }_{90}\overline{{A }_{90}}+{\sigma }_{\theta }\overline{{A }_{\theta }}{\text{cos}}\left(\theta \right)+{\sigma }_{\theta }\overline{{A }_{\theta }}{\text{cos}}\left(2\pi -\theta \right),$$

(11)

where $\overline{{A }_{la}}$ is the total laminate area per unit width and equal to $\overline{{A }_{lay}}=\left({\lambda }_{90}+{\lambda }_{\theta }+{\lambda }_{-\theta }+{\lambda }_{0}\right)t$ also $\overline{{A }_{lax}}=\left({\lambda }_{90}+{\lambda }_{\theta }+{\lambda }_{-\theta }+{\lambda }_{0}\right)t$ and $\overline{{A }_{ply}}$ ply area per width which equal to ($\overline{{A }_{ply}}={(N}_{ply}/N)t={\lambda }_{ply}t$). Therefore, substitution into Eq. (11) give the following expression:

$${\sigma }_{lay}=\sum {F}_{y}\overline{{A }_{ply}}={\sigma }_{90}{\lambda }_{90}+{2\sigma }_{\theta }{\lambda }_{\theta }{\text{cos}}\left(\theta \right)+2{\sigma }_{\theta }{\lambda }_{-\theta }{\text{cos}}\left(2\pi -\theta \right).$$

(12)

Repeat the steps for the $x$ direction, it is obtained the following expression:

$${\sigma }_{lax}=\sum {F}_{y}\overline{{A }_{plx}}={\sigma }_{0}{\lambda }_{0}+{2\sigma }_{\theta }{\lambda }_{\theta }{\text{cos}}\left(\theta \right)+2{\sigma }_{\theta }{\lambda }_{-\theta }{\text{cos}}\left(2\pi -\theta \right).$$

(13)

Note the number 2 is used to obtain to sides of the laminates right and left segments.

Then the maximum failure shear stress theory can be applied [25, 30, 33] for some quasi-isotropic laminates to obtain the resultant strength as follows:

$${\sigma }_{la}=\frac{{\sigma }_{lay}-{\sigma }_{lax}}{2},$$

(14)

or the maximum principal failure stress theory can be expressed as follows:

$${\sigma }_{la}=\frac{{\sigma }_{lay}+{\sigma }_{lax}}{2}.$$

(15)

2. Fracture Toughness. The fracture toughness ${G}_{IC}$ is an important property to obtain the size-response curve or to predict the nominal strength of composite plates with open holes using the cohesion law [1, 22, 23]. The cohesive law relates the strength σ at the onset of failure to the progressive crack opening $\delta$ [10, 34, 35], as shown in Fig. 3. The notch-free failure strength of laminates for which ${\sigma }_{la}$ was previously measured is related to the GIC by linear cohesion laws as follows [24, 25]:

Fig. 3.

Linear cohesive law.

$${G}_{Ic}={\int }_{0}^{{\delta }_{c}}{\sigma }_{la}d\delta ={\sigma }_{la}{\delta }_{c}.$$

(16)

Now the critical crack opening displacement ${\delta }_{c}$ can be calculated using the proposed equation by Hahn and Rosenfield [36] and Perez [37], under the following stress condition at fracture:

For plan stress condition:

$${\delta }_{c}=t{\varepsilon }_{f}.$$

(17)

For plane strain condition:

$${\delta }_{c}=t{\varepsilon }_{f}\left(1-{\nu }_{xy}^{2}\right).$$

(18)

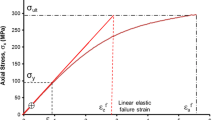
To calculate the strain at break ${\varepsilon }_{f}$, the equivalent Young modulus $\psi$ is first calculated from the unidirectional elastic stiffness of unidirectional laminates using lamination theories. The indices 1 and 2 represent the lamina properties in the fiber direction and in the transverse direction, respectively [38] (see Fig. 4). The reduced stiffness [39] ${Q}_{ij}$ can be expressed by the elastic constant of the laminae as follows:

Fig. 4.

Angle ply transformation system.

$$\begin{array}{c}{Q}_{11}=\frac{{E}_{1}}{1-{\nu }_{12}{\nu }_{21}}, {Q}_{22}=\frac{{E}_{12}}{1-{\nu }_{12}{\nu }_{21}},\\ {Q}_{12}=\frac{{{\nu }_{12}E}_{2}}{1-{\nu }_{12}{\nu }_{21}}, {Q}_{66}={G}_{12}, {\nu }_{21}= {\nu }_{12}\frac{{E}_{2}}{{E}_{1}}.\end{array}$$

(19)

For symmetric layup, the average stress $\tilde{\sigma }$ through laminates thickness $t$ can be calculated using Eqs. (20):

$$\tilde{\sigma }=\left[A\right]\frac{\left\{\epsilon \right\}}{t}, \left(\begin{array}{c}{\tilde{\sigma }}_{x}\\ {\tilde{\sigma }}_{y}\\ {\tilde{\sigma }}_{z}\end{array}\right)=\left(\begin{array}{ccc}{A}_{11}& {A}_{12}& {A}_{16}\\ {A}_{12}& {A}_{22}& {A}_{26}\\ {A}_{16}& {A}_{26}& {A}_{66}\end{array}\right)\left(\begin{array}{c}{\varepsilon }_{x}\\ {\varepsilon }_{y}\\ {\varepsilon }_{z}\end{array}\right),$$

(20)

where $A$ is the stiffness matrix where can calculate from the following relationship [Eqs. (21)] for multidirectional laminates with $\theta$ angle plies:

$$\begin{array}{c}{A}_{11}={A}_{11}^{90}+{A}_{11}^{0}+{A}_{11}^{\theta }, {A}_{22}={A}_{22}^{90}+{A}_{22}^{0}+{A}_{22}^{\theta },\\ {A}_{12}={A}_{12}^{90}+{A}_{12}^{0}+{A}_{12}^{\theta }, {A}_{66}={A}_{66}^{90}+{A}_{66}^{0}+{A}_{66}^{\theta },\\ {A}_{ij}^{90}={\lambda }_{90}{Q}_{ij}{t}_{90}, {A}_{ij}^{0}={\lambda }_{0}{Q}_{ij}{t}_{0}, {A}_{11}^{\theta }={\lambda }_{\theta }\left(\frac{{Q}_{11}}{4}+\frac{{Q}_{22}}{4}+\frac{{Q}_{12}}{4}+{Q}_{66}\right){t}_{\theta }={A}_{22}^{\theta },\\ {A}_{12}^{\theta }={\lambda }_{\theta }\left(\frac{{Q}_{11}}{4}+\frac{{Q}_{22}}{4}+\frac{{Q}_{12}}{4}-{Q}_{66}\right){t}_{\theta }, {A}_{66}^{\theta }={\lambda }_{\theta }\left(\frac{{Q}_{11}}{4}+\frac{{Q}_{22}}{4}-\frac{{Q}_{12}}{2}\right){t}_{\theta },\end{array}$$

(21)

where ${t}_{90}$, ${t}_{0}$, and ${t}_{\theta }$ are ply thickness of 90°, 0°, and $\theta$ direction, respectively.

Substitution into Eqs. (22) give an expression for elastic constant in $x$ and $y$ directions:

$${E}_{x}={A}_{11}-\frac{{A}_{12}^{2}}{{A}_{22}}, { E}_{y}={A}_{22}-\frac{{A}_{12}^{2}}{{A}_{11}}, { G}_{xy}={A}_{66}, { \nu }_{xy}=\frac{{A}_{12}}{{A}_{22}}.$$

(22)

Then after the elastic constant in $x$, $y$ directions calculated the equivalent Young modulus is then can be determine form Eqs. (23) as follows:

$$\psi =\frac{\sqrt{2{E}_{x}{E}_{y}}}{\sqrt{\sqrt{\frac{{E}_{y}}{{E}_{x}}}+\frac{{E}_{y}}{2{G}_{xy}}-{\nu }_{xy}}}.$$

(23)

Substitution into Hooke’s law for linear material behaviors into Eq. (24) as follows:

$${\varepsilon }_{f}=\frac{{\sigma }_{la}}{\psi }.$$

(24)

To evaluated the effective Young modulus ${E}_{eff}$, rearrange Eq. (16) and modification respect to (17), it is given Eq. (25) as follows:

$${E}_{eff}=\frac{{\sigma }_{la}^{2}}{{G}_{IC}}t.$$

(25)

3. Nominal Strength and Size Effect. The linear cohesion law, shown in Fig. 3, is used to determine the nominal strength of open hole specimens of carbon fiber laminates. The two main parameters fracture toughness GIC and laminate strength ${\sigma }_{la}$ determined in the previous sections must be fully described and defined, then Eq. (26) [9, 10] is applied as follows:

$${\sigma }_{n}={\delta }_{c}{\left[\frac{{\delta }_{c}}{{\sigma }_{la}}{\delta }_{ij}+{f}_{ij}\right]}^{-1}{I}_{1},$$

(26)

where ${\delta }_{ij}$ is knocker delta and ${I}_{1}$ is one matrix, and ${f}_{ij}$ is the transformation function completely derived in [9, 10].

4. Results and Discussion. Figures 5 and 6 and Table 1 show the predicted failure strength of multidirectional laminates. It can be observed that the percent error in tension is 4.37 and –2.72 for La0 and 9.297 and 1.897 for La1 for method a1 and method 2, respectively; moreover, the percent error is 0.70 and –6.13 for La2. For compression, these values increase to –14.63 and –20.45, respectively. The same results for compression for the other material La1, as the percent errors are 17.439 and 9.461 for method a1 and method 2, respectively. The average percent errors for all materials (La0, La1, and La2) in tension and compression were 9.29 and 8.13 for method 1-a and method 2, respectively, which is based on the maximum shear stress theory. These values are lower than the average percent error of 9.8 produced by other unit circle models [5].

Fig. 5.

Comparison model methods with experimental data [5, 19, 33, 40, 44] and other available models [5] in tension case for CFRP.

Fig. 6.

Comparison among model methods with experimental data [5, 19, 33, 40, 44] and other available models [5] in compression based on Eq. (15).

Table 1. Comparison of Predicted Failure Strength of Quasi-Isotropic Laminates Using the Present Models with Experimental and Other Available Published Models for Different CFRP Material Systems with Layered Structure {Maximum Shear Stress [Eq. (15)]}

Figure 7 and Table 2 show the failure strength predicted by method 1-a and method 2, which is based on maximum principal stress theory, for CFRP laminates under compression. The percent errors for La3 are –0.97 and 5.24 for method 1-a and method 2, respectively, which is based on maximum principal stress theory. This theory was selected for these material systems with relatively lower fracture toughness than those listed in Table 1. It is found that La5 has a lower % error –0.82 when method 1-a is used, while the % error increases by 57% for method 2. However, moderate % errors –17.53 and 10.61 were observed for sample La4. This result is due to unbalanced stacking sequences. In general, method 1-a gives the lowest average % error –6.44 corresponding to 11.092 for the model of Soutis and Curtis [25].

Fig. 7.

Comparison among model methods with experimental data [25, 41], and other available models in compression case for CFRP.

Table 2. Comparison of Predicted Failure Strength of Quasi-Isotropic Laminates Using the Present Models with Experimental and Other Available Published Models for Different CFRP Material Systems with Layered Structure {Maximum Principal Stress [Eq. (16)]}

Figure 8 and Table 3 show the prediction of the failure strength of CFRP laminates with an angular layer [$\theta$/0]2s or a laminate with only one transverse layer [0/90]. These types of superstructures were calculated using method 1-b because it has the same aspects as method 1-a. The comparison of the percentage error shows that it is generally lower for both methods, but differs for specimen La10 because there is no angular layer to reduce the size effect and balance the loads by a specific direction, since the superstructure has a loss when loaded by the exact direction. The percentage errors were –6.25 and –3.36 for La6, while they were 6.57 and 5.12 for La7, with positive sense, moreover, the percentage errors for La8 and La9 were 4.09, –6.8182 and –2.6, –28.3614 for method 1-b and method 2, respectively. Although the percent error –3.13 in the case of La10 has a lower value for method 2, it is very large at 30% for method 1-b, which can be attributed to the loss of shear load due to arbitrary angular positions [5, 40,41,42,43]. Finally, the model within the two methods has a lower average % error of 9.9 and 9.3, while the average % error of the model proposed by Soutis and Curtis[25] is larger at 18.

Fig. 8.

Comparison among model methods with experimental data [25, 41] and other available models in compression based on Eq. (16).

Table 3. Comparison of Predicted Failure Strength of T800/ 924C CFRP with [$\theta$/0]_2s and without Angular Laminate Using the Present Models with Experimental and Another Available Published Model

Table 4 shows the comparison between the predicted fracture toughness measured by the proposed Eq. (16) and the notched impact strength calculated by method 1. It is observed that the percentage errors vary between lower and higher values, with the lowest value of percentage errors being –1.76 and –5.86 for La4 and La5, respectively (see Fig. 9). It is noted that the calculated equivalent $\psi$ for La0 is the same as the values of fracture toughness were used for plane stress condition [Eq. (17)], as it is suitable for high values of fracture toughness for less thin laminates by thickness [24]. The percent errors listed in Table 5 obtained by method 2 generally have lower values for most specimen types, although the La4 material has the highest value of –19.66 due to its high predicted strength of 896 MPa and therefore does not match its experimental fracture toughness [25] (see Fig. 9). The optimum values for the two methods are listed in Table 6 and Fig. 10. The optimum values are mainly obtained from the second proposed method.

Table 4. Comparison of Prediction of Fracture Toughness Based on Un-Notch Strength of Method 1-a

Fig. 9.

Comparison among model methods with experimental data [25, 26, 41] to predict the fracture toughness of different CFRP laminates.

Table 5. Comparison of Prediction of Fracture Toughness Based on Un-Notch Strength of Method 2

Table 6. Optimum Values for Fracture Toughness

Fig. 10.

Optimum values of the fracture toughness of different CFRP laminates with different methods and experimental data [25, 26, 41].

The linear cohesion law provides considerable data for predicting the nominal strength of open-hole CFRP laminate structures. The cohesion law methods must define two main material properties, the notched impact strength and the fracture toughness ${G}_{IC}$, and the value of the nominal strength differs from the method in which the equivalent Young modulus is calculated, even in the present study [25, 41]. Figures 11 and 12 show the nominal strength of the open hole predicted using the calculated Young modulus $\psi$ and the effective Young modulus ${E}_{eff}$ based on method 1-a and method 2, respectively. The percent error values for the open hole strength were 6.17 and –1.03 for La0. However, different percent error values were obtained for the other specimens, which can be attributed to the changed values of $\psi$ and ${E}_{eff}$. The optimal values are listed in Table 7. It can be seen that the optimal values obtained by method 1-a with the equivalent Young modulus $\psi$ for samples La3 and La10 have a percent error of 7.67 and –2.5, respectively. The percent error determined by method 2 with the equivalent Young modulus ${E}_{eff}$ for La4 was 2.5, while it was 5.67 for La5 with the equivalent Young modulus $\psi$.

Fig. 11.

Nominal strength of open hole CFRP laminates predicted based on un-notch strength calculated by method 1-a respect to experimental data [25, 26, 41].

Fig. 12.

Nominal strength of open hole CFRP laminates predicted based on un-notch strength calculated by method 2 respect to experimental data [25, 26, 41].

Table 7. Optimum Values for Open Hole Strength

Figure 13 shows the size effect curve predicted using the linear cohesion law based on the predicted notched impact strength by method 1-a and method 2. Although the two methods provide a remarkably good prediction, method 1-a fits better due to its good fracture toughness and low notched impact strength predicted with a lower % error of 822. The average % accuracy of size effect prediction based on method 1-a is 3.24%, while it is 6.82% for method 2.

Fig. 13.

Size effect curve prediction using un-notch and fracture toughness calculated with the proposed model compared to experimental data [26].

Conclusions. The notched impact strength of CFRP is a very important characteristic property, so it is of great importance to determine it. In the present study, it was predicted using two simple analytical methods based on the elastic strength and stiffness of unidirectional plies with an angle of 0° and lamination theory. A comparison study was proposed to determine the degree of accuracy of each method. Based on the predicted strength of different CFRP material systems and different layers, both the fracture toughness curve (${G}_{IC}$) and the size effect curve were defined and the following optimal results were reported:

1. The second method, based on the ply ratio and force analysis through the whole laminate plate, is more suitable and gives a lower % error.

2. The maximum failure shear stress theory is well suited for CFRP laminates with higher fracture toughness, while the maximum principal failure stress theory is better suited for materials with fracture toughness of 25–40 kJ/m².

3. The equivalent modulus of elasticity, calculated based on the percentage of plies in the elastic stiffness of the laminates using the laminate theory, is well suited to measure open hole strength.

4. The average percentage accuracy of predicting the size effect based on method 1-a is 3.24%, while it is 6.82% for method 2.