Introduction. The specific mechanical features of rubber parts, which allow them to perform their functions in some operating conditions more effectively than when using other structural materials, complicate the calculation and design of such parts. Rubber, as a structural material, has a number of such specific features. The most significant among them are the following: low compressibility, viscoelasticity, dissipative heating, nonlinearity of deformation, ability to withstand significant deformations without destruction and others. Depending on the operating conditions of parts, one or another property is of predominant importance for their performance. Therefore, if rubber structural elements are dampers of vibrations of rather high frequency, then the manifestation of dissipative heating during operation must be taken into account when creating such elements. Weak compressibility is decisive in the vast majority of rubber application because it affects the deformation processes and, accordingly, should be taken into account when designing structures. Analysis of the operating conditions of the shock absorbers under investigation shows that after installation, they are under static load conditions due to the weight of buildings and machines. When vibration sources appear, a periodic dynamic component is often added to the static load.

On this basis, when designing the design and dimensions of shock absorbers, it is advisable to perform static and dynamic calculations.

The static calculation involves determining the components of the stress-strain state of the shock absorber and comparing them with some limit values (for example, the ultimate strength of rubber, the maximum value of shock absorber contraction, etc.). Such estimates and subsequently taking them into account when choosing the size of shock absorbers, their number for a particular machine or structure allow us to increase the service life of shock absorbers and their reliability.

Taking into account all the special properties of rubber in design is quite a difficult task and leads to cumbersome mathematical models. To simplify the model and make it more convenient for practical application, it is necessary to identify at the initial stage those features of the material that are decisive for the required mode of operation.

In static calculation, i.e., when the shock absorber is deformed under the weight of the building, it is advisable to take into account such properties of rubber as weak compressibility and viscoelasticity.

The main problem that arises when weak compressibility is taken into account is that in the equations of state that relate stresses and strains, elastic coefficients appear that tend to infinity (when Poisson’s ratio tends to 0.5). As a result, uncertainty arises, and the mathematical model gives inadequate results.

Various rheological models are used to describe viscoelastic properties. The viscoelastic properties of rubbers are most adequately described in the integral form on the basis of the hereditary Boltzmann–Volterra theory using different difference kernels.

The use of some types of kernels, such as exponential kernels, allows us to make some mathematical transformations in an analytical way. In addition, as a rule, in the exponential relaxation kernel, the kernel parameters include instantaneous and long-term elastic moduli. These parameters have been determined experimentally for a wide range of materials, in contrast to other types of kernels, whose parameters are not always determined.

The description of weak compressibility and viscoelasticity in the mathematical model significantly complicates it and leads to the impossibility to studyit by analytical methods even for structures of relatively simple geometric shape. Therefore, it is advisable to use numerical methods in calculations. One of the most widespread numerical methods is the finite element method (FEM), which provides the ability to solve the above problems.

Analysis of Research. Given simplifying hypotheses, the damping properties of rubber structural elements were studied by analytical methods [1,2,3]. An experimental study of the deformation and strength properties of rubber shock absorbers in various designs is given in [4, 5]. Additionally, based on the Ritz method, a calculation of a rubber shock absorber under viscoelastic deformation was carried out [4]. The deformation properties of a rubber-metal shock absorber, taking into account friction in the presence of free contact between the rubber and metal elements, are described in [6].

The use of numerical methods allows taking into account a greater number of mechanical properties of rubber. For instance, a study of large deformations of a number of axisymmetric rubber structures based on a semilinear model of the material was carried out using the finite element method [7]. A variational approach for a weakly compressible neo-Hookean material was used in the finite element calculation of the deformation of an arch-type rubber shock absorber [8]. A finite element moment scheme taking into account the weak compressibility of the rubber material was used to calculate linear and nonlinear problems in [9, 10]. The modeling of the weak compressibility of the material using a special finite element is given in [11].

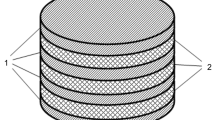
Statement of the Problem. We determine the parameters of the stress-strain state of a rubber shock absorber used in the vibration isolation of the machines of the general, mining and metallurgical, agro-industrial complexes and others. The above shock absorber was designed at the Institute of Geotechnical Mechanics of the National Academy of Sciences of Ukraine (Dnipro). The structure of the shock absorber, besides the rubber element, consists of two metal plates (Fig. 1).

Fig. 1
figure 1

Rubber shock absorber.

Full size image

The shock absorber is widely used in vibratory machines for the discharge and delivery of uranium ore and in the protection of heavy mining machines from dynamic loads.

In the process of operation, the shock absorber experiences a significant axial load P; in addition, with the passage of time, there appears a certain asymmetry in operation, which is manifested in the occurrence of additional tangential loads Q. Let us calculate the amount of contraction for two cases of load action - only axial load and a combination of axial and shear loads.

Numerical Approach. Let us build a scheme for calculating rubber structures by the finite element method under viscoelastic deformation based on the Lagrange variational principle, according to which

$$ \delta \Pi =\delta W-\delta A, $$
(1)

where Π is the potential energy of the medium, W is the deformation energy of the medium, and A is the work of external forces.

To construct the resolving equations of the finite element method, we consider in detail the deformation energy, which is represented in the general form as follows:

$$ \delta W-\int \underset{V}{\int}\int {\sigma}^{ij}{\delta \varepsilon}_{ij} dV, $$
(2)

where εij and σij are the components of the strain and stress tensors, respectively, and V is the volume of the medium under consideration. To model the viscoelastic behavior of the material, we use the hereditary Boltzmann–Volterra theory. Let us take the relaxation kernel in the exponential form, which contains instantaneous and long-term mechanical characteristics, given that in practice, as a result of experiments for most grades of rubbers and other materials, instantaneous and long-term elastic moduli are obtained, which characterize the viscoelastic properties of the material in the form of the relation [12]:

$$ {\sigma}^{ij}={C}_0^{ij kl}{\varepsilon}_{kl}(t)-\left({C}_0^{ij kl}-{C}_{\infty}^{ij kl}\right)\int_0^t{e}^{-\left(t-\tau \right)}{\varepsilon}_{kl}\left(\tau \right) d\tau, $$
(3)

where \( {C}_0^{ijkl} \) and \( {C}_{\infty}^{ijkl} \) are the instantaneous and long-term elastic constant tensors of the material, respectively. Taking into account the weak compressibility of rubber, it is advisable to separate the shear and volume components in deformation. Then, expression (3) takes the form

$$ {\displaystyle \begin{array}{c}{\sigma}^{ij}=2{\upmu}_0{g}^{ik}{g}^{jl}{\varepsilon}_{kl}(t)+{\lambda}_0{g}^{ij}\uptheta (t)-2\left({\upmu}_0-{\upmu}_{\infty}\right){g}^{ik}{g}^{jl}\int_0^t{e}^{-\left(t-\tau \right)}{\varepsilon}_{kl}\left(\tau \right) d\tau \\ {}-\left({\lambda}_0-{\lambda}_{\infty}\right){g}^{ij}\int_0^t{e}^{-\left(t-\tau \right)}\uptheta \left(\tau \right) d\tau, \end{array}} $$
(4)

where gik are the components of the metric tensor, μ and λ are Lamé constants, and θ is the function volume change function.

After substitution of (4) in (2) and further transformations, the variation of strain energy will take the form

$$ {\displaystyle \begin{array}{c}\delta W=\int \underset{V}{\int}\int \Big(2{g}^{ik}{g}^{jl}\left({\upmu}_0{\varepsilon}_{kl}(t)-\left({\upmu}_0-{\upmu}_{\infty}\right)\int_0^t{e}^{-\left(t-\tau \right)}{\varepsilon}_{kl}\left(\tau \right) d\tau \right)\delta {\varepsilon}_{ij}(t)\\ {}+{g}^{ij}\left({\lambda}_0\uptheta (t)-\left({\lambda}_0-{\lambda}_{\infty}\right)\int_0^t{e}^{-\left(t-\tau \right)}\uptheta \left(\tau \right) d\tau \right)\delta \uptheta (t)\Big) d V.\end{array}} $$
(5)

Rubber is a weakly compressible material, and calculations at Poisson’s ratio close to 0.5 give increasing errors. To eliminate this drawback in the finite element method, a moment scheme of finite elements for weakly compressible materials was proposed, which is described in detail in [9] and consists in a special representation in the form of decomposition into a number of components of the displacement vector, strain tensor and volume change function. According to this scheme, for a hexagonal eight-node finite element, the components of the strain tensor are represented as

$$ {\displaystyle \begin{array}{c}{\varepsilon}_{11}={e}_{11}^{(000)}+{e}_{11}^{(010)}{\uppsi}^{(010)}+{e}_{11}^{(001)}{\uppsi}^{(001)}+{e}_{11}^{(011)}{\uppsi}^{(011)},\\ {}{\varepsilon}_{22}={e}_{22}^{(000)}+{e}_{22}^{(100)}{\uppsi}^{(100)}+{e}_{22}^{(001)}{\uppsi}^{(001)}+{e}_{22}^{(101)}{\uppsi}^{(101)},\\ {}{\varepsilon}_{33}={e}_{33}^{(000)}+{e}_{33}^{(100)}{\uppsi}^{(100)}+{e}_{33}^{(010)}{\uppsi}^{(010)}+{e}_{33}^{(110)}{\uppsi}^{(110)},\\ {}{\varepsilon}_{12}={e}_{12}^{(000)}+{e}_{12}^{(001)}{\uppsi}^{(001)},\\ {}{\varepsilon}_{13}={e}_{13}^{(000)}+{e}_{13}^{(010)}{\uppsi}^{(010)},\\ {}{\varepsilon}_{23}={e}_{23}^{(000)}+{e}_{23}^{(100)}{\uppsi}^{(100)},\end{array}} $$
(6)

Here, a set of power coordinate functions has the form:

$$ {\uppsi}^{(pqr)}=\frac{{\left({x}_1\right)}^p{\left({x}_2\right)}^q{\left({x}_3\right)}^r}{p!q!r!}, $$
(7)

where xi(i = 1,⋯,3) is a system of local coordinates associated with afinite element and e(pqr)ij are expansion coefficients.

$$ {\varepsilon}_{ij}={\left\{{e}_{ij}\right\}}^T\left\{\uppsi \right\}. $$
(8)

The strain tensor expansion coefficients e(pqr)ij are determined by the relations:

$$ {\displaystyle \begin{array}{c}{e}_{11}^{(pqr)}=\sum_{\upmu =0}^p\sum_{v=0}^q\sum_{\upeta =0}^r{\upomega}_{k\prime}^{\left(\upmu +1\;v\;\upeta \right)}{f}_{\left(p+1-\upmu\;q-v\;r-\upeta \right),}^{k\prime}\\ {}{e}_{22}^{(pqr)}=\sum_{\upmu =0}^p\sum_{v=0}^q\sum_{\upeta =0}^r{\upomega}_{k\prime}^{\left(\upmu\;v+1\;\upeta \right)}{f}_{\left(p-\upmu\;q+-v\;r-\upeta \right),}^{k\prime}\\ {}{e}_{33}^{(pqr)}=\sum_{\upmu =0}^p\sum_{v=0}^q\sum_{\upeta =0}^r{\upomega}_{k\prime}^{\left(\upmu\;v\;\upeta +1\right)}{f}_{\left(p-\upmu\;q-v\;r+1-\upeta \right),}^{k\prime}\\ {}{e}_{12}^{(pqr)}=\frac{1}{2}\sum_{\upmu =0}^p\sum_{v=0}^q\sum_{\upeta =0}^r\left({\upomega}_{k\prime}^{\left(\upmu\;v+1\;\upeta \right)}{f}_{\left(p+1-\upmu\;q-v\;r-\upeta \right)}^{k\prime }+{\upomega}_{k\prime}^{\left(\upmu +1\;v\upeta \right)}{f}_{\left(p-\upmu\;q+1-v\;r-\upeta \right)}^{k\prime}\right),\\ {}{e}_{13}^{(pqr)}=\frac{1}{2}\sum_{\upmu =0}^p\sum_{v=0}^q\sum_{\upeta =0}^r\left({\upomega}_{k\prime}^{\left(\upmu\;v\;\upeta +1\;\right)}{f}_{\left(p+1-\upmu\;q-v\;r-\upeta \right)}^{k\prime }+{\upomega}_{k\prime}^{\left(\upmu +1\;v\upeta \right)}{f}_{\left(p-\upmu\;q-v\;r+1-\upeta \right)}^{k\prime}\right),\\ {}{e}_{23}^{(pqr)}=\frac{1}{2}\sum_{\upmu =0}^p\sum_{v=0}^q\sum_{\upeta =0}^r\left({\upomega}_{k\prime}^{\left(\upmu\;v\;\upeta +1\;\right)}{f}_{\left(p-\upmu\;q+1-v\;r-\upeta \right)}^{k\prime }+{\upomega}_{k\prime}^{\left(\upmu\;v+1\;\upeta \right)}{f}_{\left(p-\upmu\;q-v\;r+1-\upeta \right)}^{k\prime}\right),\end{array}} $$
(9)

where the designation:

$$ {f}_{\left(\upmu \kern0.5em v\kern0.5em \upeta \right)}^{k\prime }={\left.\frac{\partial^{\upmu +v+\upeta}{z}_{k\prime }}{{\left(\partial {x}_1\right)}^{\upmu}{\left(\partial {x}_2\right)}^v{\left(\partial {x}_3\right)}^{\upeta}}\right|}_{x_1={x}_2={x}_3=0}, $$
(10)

is adopted, where zk′(k′ = 1, …, 3) is the global Cartesian coordinate system.

Then, in the matrix form, the strain tensor expansion coefficients (9) can be represented in terms of displacement approximation coefficients in the global coordinate system \( {\upomega}_{k\prime}^{(pqr)} \) as follows:

$$ \left\{{e}_{ij}\right\}=\left\{{F}_{ij}^{k\prime}\right\}\left\{{\omega}_{k\prime}\right\}. $$
(11)

Considering that the displacement approximation coefficients \( {\upomega}_{k\prime}^{(pqr)} \) do not have any mechanical meaning, they in turn are represented through nodal displacement values \( {u}_{k\prime}^L \) (L – node number) of the finite element:

$$ \left\{{\upomega}_{k\prime}\right\}=\left[A\right]\left\{{u}_{k\prime}^L\right\}. $$
(12)

The matrix [A] is a matrix of transformation of traditional finite element shape functions to power functions (7). Then, we have finally for strains:

$$ {\varepsilon}_{ij}={\left(\left\{{F}_{ij}^{k\prime}\right\}\left[A\right]\left\{{u}_{k\prime}^L\right\}\right)}^T\left\{\uppsi \right\}. $$
(13)

We do the same with the volume change function. According to the moment scheme, it takes the form [9]:

$$ \uptheta ={e}_{11}^{\left(\alpha \kern0.5em \upbeta \kern0.5em \upgamma \right)}{g}^{11}+{e}_{22}^{\left(\alpha \kern0.5em \upbeta \kern0.5em \upgamma \right)}{g}^{22}+{e}_{33}^{\left(\alpha \kern0.5em \upbeta \kern0.5em \upgamma \right)}{g}^{33}. $$
(14)

Taking into account the representation of strains (9) and (10) and relation (12) in matrix form, we have:

$$ \uptheta ={\left(\left\{{F}_{\uptheta}^{k\prime}\right\}\left[A\right]\left\{{u}_{k\prime}^L\right\}\right)}^T\left\{\uppsi \right\}. $$
(15)

Let us substitute relations (13) and (15) into the expression for strain energy (5), in which we take into account that the nodal displacement values are functions of time. After matrix transformations, we have:

$$ {\displaystyle \begin{array}{c}\delta W=\delta {\left\{{u}_{k\prime}^L(t)\right\}}^T\int \underset{V}{\int}\int \left(2{g}^{ik}{g}^{jl}\right({\upmu}_0{\left[A\right]}^T{\left\{{F}_{ij}^{k\prime}\right\}}^T\left\{\uppsi \right\}{\left\{\uppsi \right\}}^T\left\{{F}_{kl}^{m\prime}\right\}\left[A\right]\left\{{u}_{m\prime}^L(t)\right\}\\ {}-\left({\upmu}_0-{\upmu}_{\infty}\right)\int_0^t{e}^{-\left(t-\tau \right)}{\left[A\right]}^T{\left\{{F}_{ij}^{k\prime}\right\}}^T\left\{\uppsi \right\}{\left\{\uppsi \right\}}^T\left\{{F}_{kl}^{m\prime}\right\}\left[A\right]\left\{{u}_{m\prime}^L\left(\tau \right)\right\} d\tau \Big)\\ {}+{g}^{ij}\Big({\lambda}_0{\left[A\right]}^T{\left\{{F}_{\uptheta}^{k\prime}\right\}}^T\left\{\uppsi \right\}{\left\{\uppsi \right\}}^T\left\{{F}_{\uptheta}^{m\prime}\right\}\left[A\right]\left\{{u}_{m\prime}^L(t)\right\}\\ {}-\left({\lambda}_0-{\lambda}_{\infty}\right)\int_0^t{e}^{-\left(t-\tau \right)}{\left[A\right]}^T{\left\{{F}_{\uptheta}^{k\prime}\right\}}^T\left\{\uppsi \right\}{\left\{\uppsi \right\}}^T\left\{{F}_{\uptheta}^{m\prime}\right\}\left[A\right]\left\{{u}_{m\prime}^L\left(\tau \right)\right\} d\tau \left)\right) dV.\end{array}} $$
(16)

Analyzing relation (16), we can distinguish the elastic components of the finite element stiffness matrix

$$ {\displaystyle \begin{array}{c}\left[{K}^{k\prime m\prime}\right]=\left[{K}_{ij}^{k\prime m\prime}\right]+\left[{K}_{\uptheta}^{k\prime m\prime}\right],\\ {}\left[{K}_{ij}^{k\prime m\prime}\right]=\int \underset{V}{\int}\int 2{\upmu}_0{g}^{ik}{g}^{jl}{\left[A\right]}^T{\left\{{F}_{ij}^{k\prime}\right\}}^T\left\{\uppsi \right\}{\left\{\uppsi \right\}}^T\left\{{F}_{kl}^{m\prime}\right\}\left[A\right] dV,\\ {}\left[{K}_{\uptheta}^{k\prime m\prime}\right]=\int \underset{V}{\int}\int {\lambda}_0{g}^{ij}{\left[A\right]}^T{\left\{{F}_{\uptheta}^{k\prime}\right\}}^T\left\{\uppsi \right\}{\left\{\uppsi \right\}}^T\left\{{F}_{\uptheta}^{m\prime}\right\}\left[A\right] dV,\end{array}} $$
(17)

and additions to the stiffness matrix due to the viscoelastic properties of the material:

$$ {\displaystyle \begin{array}{c}\left[\varDelta {K}^{k\prime m\prime}\right]=\left[\varDelta {K}_{ij}^{k\prime m\prime}\right]+\left[\varDelta {K}_{\uptheta}^{k\prime m\prime}\right],\\ {}\left[\varDelta {K}_{ij}^{k\prime m\prime}\right]=\int \underset{V}{\int}\int 2\left({\upmu}_0-{\upmu}_{\infty}\right){g}^{ik}{g}^{jl}{\left[A\right]}^T{\left\{{F}_{ij}^{k\prime}\right\}}^T\left\{\uppsi \right\}{\left\{\uppsi \right\}}^T\left\{{F}_{kl}^{m\prime}\right\}\left[A\right] dV,\\ {}\left[\varDelta {K}_{\uptheta}^{k\prime m\prime}\right]=\int \underset{V}{\int}\int \left({\lambda}_0-{\lambda}_{\infty}\right){g}^{ij}{\left[A\right]}^T{\left\{{F}_{\uptheta}^{k\prime}\right\}}^T\left\{\uppsi \right\}{\left\{\uppsi \right\}}^T\left\{{F}_{\uptheta}^{m\prime}\right\}\left[A\right] dV.\end{array}} $$
(18)

Then, expression (16) takes the form:

$$ \delta W=\delta {\left\{{u}_{k\prime}^L(t)\right\}}^T\left(\left[{K}^{k\prime m\prime}\right]\left\{{u}_{m\prime}^L(t)\right\}\right.-\int_0^t{e}^{-\left(t-\tau \right)}\left.\left[\varDelta {K}^{k\prime m\prime}\right]\left\{{u}_{m\prime}^L\left(\tau \right)\right\}\right). $$
(19)

Taking into account relation (19) and considering that only surface loads act on the structure, the variation of the total potential energy of the system will be represented in the form:

$$ {\displaystyle \begin{array}{c}\delta \varPi =\delta {\left\{{u}_{k\prime}^L(t)\right\}}^T\Big(\left[{K}^{k\prime m\prime}\right]\left\{{u}_{m\prime}^L(t)\right\}\\ {}-\int_0^t{e}^{-\left(t-\tau \right)}\left[\varDelta {K}^{k\prime m\prime}\right]\left\{{u}_{m\prime}^L\left(\tau \right)\right\} d\tau \Big)-\delta \left\{{u}_{k\prime}^L{(t)}^T\right\}\left\{{P}_{k\prime}^L\right\}.\end{array}} $$
(20)

The vector of nodal loads is found through the vector of surface loads [P], acting on the surfaces S, and the finite element shape function matrix [NL]:

$$ \left\{{P}_{k\prime}^L\right\}=\underset{S}{\iint }{\left[{N}_L\right]}^T\left[P\right]\kern0.5em dS. $$

According to the Lagrange variational principle, we have:

$$ \left[{K}^{k\prime m\prime}\right]\left\{{u}_{m\prime}^L(t)\right\}-\int_0^t{e}^{-\left(t-\tau \right)}\left[\varDelta {K}^{k\prime m\prime}\right]\left\{{u}_{m\prime}^L\left(\tau \right)\right\} d\tau =\left\{{P}_{k\prime}^L\right\}. $$
(21)

Let us divide the time interval [0; t] into n parts with step Δtm = tm − tm − 1, (m = 1, n). Then, relation (21) will take the form:

$$ \left[{K}^{k\prime m\prime}\right]\left\{{u}_{m\prime}^L\left({t}_n\right)\right\}-\left[\varDelta {K}^{k\prime m\prime}\right]\sum \limits_{m=1}^n\int_{t_{m-1}}^{t_m}{e}^{-\left({t}_n-\tau \right)}\left\{{u}_{m\prime}^L\left(\tau \right)\right\} d\tau =\left\{{P}_{k\prime}^L\right\}. $$
(22)

If we assume that in each time interval, the displacements have a linear dependence on time, i.e.,

$$ \left\{{u}_{m\prime}^L\left(\tau \right)\right\}=\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}+\left(\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}\right)\frac{\tau -{t}_{m-1}}{t_m-{t}_{m-1}}. $$
(23)

After substituting (23) into (22) and integrating, we obtain the expression:

$$ {\displaystyle \begin{array}{c}\left[{K}^{k\prime m\prime}\right]\left\{{u}_{m\prime}^L\left({t}_n\right)\right\}-\left[\varDelta {K}^{k\prime m\prime}\right]\\ {}\times \sum_{m=1}^n\Big({e}^{-\left({t}_n-{t}_m\right)}\left(\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\frac{\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}}{t_m-{t}_{m-1}}\right)\\ {}+{e}^{-\left({t}_n-{t}_{m-1}\right)}\left(\frac{\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}}{t_m-{t}_{m-1}}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}\right)\Big)=\left\{{P}_{k\prime}^L\right\},\end{array}} $$
(24)
$$ {\displaystyle \begin{array}{c}\left(\left[{K}^{k\prime m\prime}\right]-\left[\varDelta {K}^{k\prime m\prime}\right]\left(1+\frac{e^{-\left({t}_n-{t}_{n-1}\right)}-1}{t_n-{t}_{n-1}}\right)\right)\left\{{u}_{m\prime}^L\left({t}_n\right)\right\}\\ {}=\left\{{P}_{k\prime}^L\right\}-\left[\varDelta {K}^{k\prime m\prime}\right]\left({e}^{-\left({t}_n-{t}_{n-1}\right)}+\frac{e^{-\left({t}_n-{t}_{n-1}\right)}-1}{t_n-{t}_{n-1}}\right)\left\{{u}_{m\prime}^L\left({t}_{n-1}\right)\right\}\\ {}+\left[\varDelta {K}^{k\prime m\prime}\right]\sum_{m=1}^{n-1}\Big({e}^{-\left({t}_n-{t}_m\right)}\left(\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\frac{\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}}{t_m-{t}_{m-1}}\right)\\ {}+{e}^{-\left({t}_n-{t}_{m-1}\right)}\left(\frac{\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}}{t_m-{t}_{m-1}}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}\right)\Big).\end{array}} $$
(25)

As a result, we come to a resolving system of linear algebraic equations, which is solved in an iterative process:

$$ \left[{\tilde{K}}^{k\prime m\prime}\right]\left\{{u}_{m\prime}^L\left({t}_n\right)\right\}=\left\{{P}_{k\prime}^L\right\}=\left[\varDelta {\tilde{Q}}_{n-1}^{k\prime m\prime}\right]+\sum \limits_{m=1}^{n-1}\left[{\tilde{Q}}_m^{k\prime m\prime}\right]. $$
(26)

Here, the stiffness matrix of viscoelastic weakly compressible material at the moment of time tn is

$$ \left[{\tilde{K}}^{k\prime m\prime}\right]=\left[{K}^{k\prime m\prime}\right]-\left[\varDelta {K}^{k\prime m\prime}\right]\left(1+\frac{e^{-\left({t}_n-{t}_{n-1}\right)}-1}{t_n-{t}_{n-1}}\right), $$

the vector of additional load due to the viscoelastic properties of the material on the time interval [tn-1; tn] is

$$ \left[\varDelta {\tilde{Q}}_{n-1}^{k\prime m\prime}\right]=\left[\varDelta {K}^{k\prime m\prime}\right]\left({e}^{-\left({t}_n-{t}_{n-1}\right)}+\frac{e^{-\left({t}_n-{t}_{n-1}\right)}-1}{t_n-{t}_{n-1}}\right), $$

the vector of additional load due to viscoelastic properties of the material on the mth time interval [tm-1; tm] is

$$ {\displaystyle \begin{array}{c}\left[{\overset{\sim }{Q}}_m^{k\prime m\prime}\right]=\left[\varDelta {K}^{k\prime m\prime}\right]\Big({e}^{-\left({t}_n-{t}_{n-1}\right)}\left(\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\frac{\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}}{t_m-{t}_{m-1}}\right)\\ {}+{e}^{-\left({t}_n-{t}_{m-1}\right)}\left(\frac{\left\{{u}_{m\prime}^L\left({t}_m\right)\right\}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}}{t_m-{t}_{m-1}}-\left\{{u}_{m\prime}^L\left({t}_{m-1}\right)\right\}\right)\Big).\end{array}} $$

The described approach was implemented using the software package MIRELA+ with the help of which the stress-strain state of the shock absorber was determined.

Numerical Results. Using the proposed numerical approach, the stress-strain state of a cylindrical rubber shock absorber under viscoelastic behavior was determined.

Dimensions of the shock absorber (Fig. 1): H = 0.1 m, D = 0.18 m. Rubber material – rubber grade 2956 with the following mechanical characteristics [13]: instantaneous shear modulus μo=1.76 MPa; long-term shear modulus μ∞ = 0.74 MPa; Poisson’s ratio ν = 0.499, considered unchanged over time, and rubber grade 1562 with the following mechanical characteristics [13]: instantaneous shear modulus μo=0.78 MPa; long-term shear modulus μ∞ = 0.51 MPa; Poisson’s ratio ν = 0.499. The maximum contraction of the structure as a function of time for the combination of axial (P = 0.6 MPa) and shear (Q = 0.3 MPa) loads is shown in Fig. 2.

Fig. 2
figure 2

Dependence of the relative contraction of the rubber shock absorber on time: for rubber 2959: (1) under axial load, (2) under axial and shear loads; for rubber 1562: (3) under axial load; (4) under axial and shear loads.

Full size image

The design calculation was performed using different finite element meshes with gradual mesh thickening. Figure 2 shows the calculation results for a 7×17×15 finite element mesh, when its further thickening leads to a slight change in the results.

The analysis of the obtained results shows that the qualitative picture of the dependence of the contraction on time for both rubber grades is the same, and that the absolute value of the contraction of shock absorbers made of less rigid rubber 1562 is approximately 2 times greater than that for rubber 2959. For both cases of loading, the influence of the viscoelastic properties of the rubber grade under study is especially significant in the first 3–5 s after the application of the load. During this time, the contraction increases by 20–25% and then settles down and further increases by no more than 5–10%. In the case of axial load, the contraction is 15–17% less than in the case of a combination of axial and shear load, both in elastic and in viscoelastic deformation.

Conclusion. In summary, it can be stated that the viscoelastic properties of rubber significantly affect the parameters of the stress-strain state of shock absorbers, and that taking them into account allows us to refine the modeling of the deformation process and adjust the design of the shock absorber.