Introduction. Thin-layer rubber-metal elements have gained widespread acceptance in different modern engineering industries as elastic hinges of helicopter rotor blades, steering gear supports, simple bridge supports, etc. Such elements are used in heavy-laden designs to provide the rigid fixing of the construction in one direction with its free displacement in the other one. The major trend today is to use rubber elements in designing high-rise buildings to protect them from the vibration effects of artificial (vehicles, metro, etc.) and natural (seismicity) origin.

The thin-layer rubber-metal element is an elastic entity that consists of thin rubber and metal layers laminated into a pack of two or more layers with an enhanced load-carrying capacity (> 30 MPa) in the direction normal to the layer and high compliance (50–200% strain) in the transverse one.

Research Analysis. Damping properties of rubber vibration absorbers were first investigated with analytical methods [1,2,3,4,5,6]. Different alternatives of vibration absorber designs were proposed to improve their functionality and reduce the risk of vibration and seismic effects [7,8,9]. The collision protection problem for closely-spaced constructions in earthquake-prone regions was solved with rubber spacers installed in expected collision locations, and the impact interaction was numerically simulated using the nonlinear inelastic force model [10]. The effect of friction in the case of free contact between rubber and metal elements on the deformation behavior of the rubber-metal absorber was examined in [11].

The account of a greater number of deformation properties typical of rubber materials makes it necessary to apply the numerical methods for calculations. The semilinear material model became the basis for the finite element approach to the calculation of axisymmetric problems of mechanics for incompressible elastomers in the region of large strains [12]. The stress-strain state of several elastomer structures was determined. The finite element approach to the calculation of rubber arch absorber deformation was evolved in the variational statement based on the weakly compressible non-Hookian material model [13]. The calculation of rubber absorbers with the moment finite element scheme for weakly compressible materials in the nonlinear statement is given in [14, 15]. A special finite element for weakly compressible materials is proposed in [16].

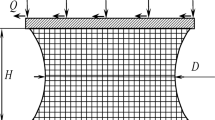
Statement of the Problem. The basic element of the rubber-metal pack is the rubber layer h high intervening between the two metal plates (Fig. 1). The lower plate is fixed in position on the horizontal base, and the upper one is subjected to the vertical force. The rubber element exhibits the thickness reduction δ under the action of the force P.

Fig. 1.
figure 1

Thin-layer ruber (1) and metal (2) elements.

Full size image

The thickness reduction was calculated for the two cases of fixing the rubber layer and metal plates. In the first case, the rubber layer is vulcanized onto the metal plates (rigid fixing), in the second one, it can slide freely over the cross-section without friction.

The stress-strain state calculation for thin-layer rubber-metal elements should consider rheological rubber properties, its weak compressibility, etc.

Rubber belongs to the materials, which can absorb large strains without failure. The range of the liner stress–strain relation in the general case is the function of the base mix, filling ratio, vulcanization conditions, etc. For unfilled and slightly filled rubber, the linearity can be retained to 80% strain or more, for highly filled one, it is only to 1–10% [17].

For rubber materials, a great number of the nonlinear laws of state, e.g., Peng–Landel, Seth, Lindley, and others, was proposed. The choice of a law of state for each rubber brand is a specific problem. Moreover, their application to some rubber brands is retarded by lack of data on steels involved in the equations of state. The vibration absorber thickness reduction is defined below in view of nonlinearity of the two types: geometrical and viscoelastic based on the hereditary Boltzmann–Volterra theory with known relaxation kernels for a wide range of rubbers [18].

Experimental investigations demonstrated that the majority of rubbers was weakly compressible. Design calculations quite often assume that rubber is an incompressible material under deformation in the closed volume and its Poisson’s ratio equals 0.5. However, for the so-called thin-layer rubber-metal elements, the weak compressibility with the true Poisson’s ratio in the range of 0.48–0.4995 should be considered [19].

This study makes use of the moment finite element scheme for weakly compressible materials, which possesses all the advantages of the finite element method and permits of calculating the stress-strain state of the constructions from such materials (Poisson’s ratio is from 0.49 to 0.4999999999), as opposed to the traditional FEM which produces errors already at Poisson’s ratio of 0.49.

Analytical and Numerical Approaches. Analytical solutions for the thickness reduction evaluation of thin-layer rubber-metal elements can be obtained only with simplifications that simulate the behavior of rubber elements with the thickness of tens and hundreds smaller than their sizes in plan. The simplifications consist in bounded displacements along the x- and y-axes (along the axes that coincide with the median surface area of the rubber layer).

The analytical problem solution for the rigid fixing of rubber layer ends was gained with the approach described in [6]. Combine the x-, y-plane of the system of Cartesian coordinates with the median surface area of the rubber layer. The displacement components along the x-, y-, z-directions are denoted by ux, uy, uz, respectively.

The displacements ux and uy are the rapidly varying functions of the z-coordinate and slowly varying ones in relation to x and y [5]. The displacements uz are independent of x and y or vary slowly with those coordinates.

A number of terms in the Cauchy equations for shear strains is proposed to be neglected, and it is suggested that the strain γxy is small in comparison with γxz and γyz [6]. With these assumptions, the calculations are based only on the strains γxz and γyz. The stresses τxy were also not considered.

The above hypotheses used in the stress-strain state evaluation for the rubber layer resulted in deriving the thickness reduction–load relation [6]

$$ \updelta =\frac{2}{3}\frac{h^3}{\uppi \upmu {R}^4}P, $$
(1)

where δ is the thickness reduction of the rubber layer, h and R are its thickness and radius, μ is the instantaneous shear modulus, and P is the load.

This formula is valid only for elastic rubber deformation and the above boundary conditions at the ends. Solutions under viscoelastic deformation are obtained with the finite element method. To eliminate complicated mathematical operations associated with the specific behavior of rubber materials, the modified finite element method, viz the moment finite element scheme for weakly compressible materials, is applied [15].

This scheme is based on the triple approximation of displacement fields, strains, and a volume variation function [15]. The order of expansion of strains and a volume variation function is chosen so as to eliminate all strain components that respond to rigid displacements and a “false shear” effect and all volume variation function components that responsed to a weak rubber compressibility.

The approximation of displacements has the form

$$ {u}_{k\prime }=\sum \limits_{pqr}{\upomega}_{k\prime}^{(pqr)}{\uppsi}^{(pqr)}, $$
(2)

where \( {\upomega}_{k\prime}^{(pqr)} \) are the expansion coefficients, ψ(pqr) is the set of power coordinate functions,

$$ {\uppsi}^{(pqr)}=\frac{{\left({x}^1\right)}^p{\left({x}^2\right)}^q{\left({x}^3\right)}^r}{p!q!r!}, $$
(3)

where p, q, and r are the exponents of the approximating polynomial for the corresponding directions.

Strain tensor components are approximated by the Maclaurin expansion of the components εij in the origin of coordinates

$$ {\upvarepsilon}_{ij}=\sum \limits_{stg}^{(ij)}{e}_{ij}^{(stg)}{\uppsi}^{(stg)}, $$
(4)

where \( {e}_{ij}^{(stg)} \) are the expansion coefficients of the strain components.

Approximation of the volume variation function is written as

$$ \uptheta =\sum \limits_{\upalpha \upbeta \upgamma}{\upxi}^{\left(\upalpha \upbeta \upgamma \right)}{\uppsi}^{\left(\upalpha \upbeta \upgamma \right)}, $$
(5)

where ξ(αβγ) are the expansion coefficients of the volume variation function.

In expansions (4) and (5), a number of terms is eliminated in accordance with certain rules of the moment finite element scheme for weakly compressible materials, and the stiffness matrix of a finite element is composed on the basis of those expansions.

The account of rheological rubber properties is effected with the hereditary Boltzmann–Volterra theory. Then Hooke’s law can be written in the operator form

$$ {\tilde{\upsigma}}^{ij}={\tilde{C}}^{ij kl}{\upvarepsilon}_{kl}. $$
(6)

Here \( {\tilde{C}}^{ijkl} \) is the integral operator

$$ {\tilde{C}}^{ijkl}\upphi ={C}_0^{ijkl}\left[\upphi (t)-\underset{0}{\overset{t}{\int }}R\left(t-\uptau \right)\upphi \left(\uptau \right)d\uptau \right], $$
(7)

where R(t − τ) is the difference kernel of relaxation, \( {C}_0^{ijkl} \) are the elastic constant tensor components defined via the metric tensor components gij and the Lame coefficients μ0 and λ0 (instantaneous value)

$$ {C}_0^{ij kl}={\upmu}_0\left({g}^{ik}{g}^{jl}+{g}^{il}{g}^{jk}\right)+{\uplambda}_0{g}^{ij}{g}^{kl}. $$
(8)

The application of operator (7) would require the nonlinear problem solution. Therefore, for the finite element method, the integral operator is written in the finite difference representation

$$ {\tilde{C}}_0^{ijkl}\upphi ={C}_0^{ijkl}\left[\upphi \left({t}_n\right)-\sum \limits_{m=0}^{n-1}\underset{t_m}{\overset{t_{m+1}}{\int }}R\left(t-\uptau \right)\upphi \left(\uptau \right)d\uptau \right]. $$
(9)

The expression for the stress tensor components in view of Eq. (9) takes on the form

$$ {\tilde{\upsigma}}^{ij}={C}_0^{ij kl}\left[{\upvarepsilon}_{kl}\left({t}_n\right)-\sum \limits_{m=0}^{n-1}{\upvarepsilon}_{kl}\left({t}_m\right)\underset{t_m}{\overset{t_{m+1}}{\int }}R\left(t-\uptau \right)d\uptau \right]. $$
(10)

The variation of the total potential energy with regard to the stress tensor relation is written as

$$ \updelta \prod =\underset{V}{\iiint}\left[{C}_0^{ij kl}{\upvarepsilon}_{kl}\left({t}_n\right){\updelta \upvarepsilon}_{ij}-\sum \limits_{m=0}^{n-1}{\overset{\ast }{R}}_m{C}_0^{ij kl}{\upvarepsilon}_{kl}\left({t}_m\right){\updelta \upvarepsilon}_{ij}\right] dV-\updelta A, $$
(11)

where \( {\overset{\cdot }{R}}_m=\underset{t_m}{\overset{t_{m+1}}{\int }}R\left(t-\uptau \right)d\uptau \).

The first term in the square brackets in (11) describes the elastic strain energy variation and is the basis of composing the stiffness matrix of a finite element [Ks ′ t′] for the fixed time tn

$$ \underset{V}{\iiint }{C}_0^{ij kl}{\upvarepsilon}_{kl}\left({t}_n\right){\updelta \upvarepsilon}_{ij} dV={K}^{s\prime t\prime}\left({t}_n\right){u}_{s\prime}\left({t}_n\right)\updelta {u}_{t\prime }, $$
(12)

where Ks ′ t′(tn) is the stiffness matrix at the time t = tn and us′(tn) is the vector of displacements.

The second term in (11) describes the hereditary component of the stiffness matrix, which can be written as

$$ \sum \limits_{m=0}^{n-1}{\overset{\ast }{R}}_m\underset{V}{\iiint }{C}_0^{ij kl}{\upvarepsilon}_{kl}\left({t}_m\right){\updelta \upvarepsilon}_{ij} dV=\sum \limits_{m=0}^{n-1}{\overset{\ast }{R}}_m{K}^{s\prime t\prime}\left({t}_m\right){u}_{s\prime}\updelta {u}_{t\prime }. $$
(13)

If the body is subjected only to distributed surface loads, which are reduced to concentrated node forces in the finite element method, the variational principle based on the potential energy in view of (12) and (13) can be presented as

$$ \left[{K}^{s\prime t\prime}\left({t}_n\right){u}_{s\prime}\left({t}_n\right)-\sum \limits_{m=0}^{n-1}{\overset{\ast }{R}}_m{K}^{s\prime t\prime}\left({t}_n\right){u}_{s\prime}\left({t}_n\right)-{F}^{t\prime}\left({t}_n\right)\right]\updelta {u}_{t\prime }=0, $$
(14)

where Ft′(tn) is the surface load.

Since the variation of displacements is nonzero, the expression in the square brackets should equal zero that is the system of linearized equations of hereditary viscoelasticity

$$ {K}_{(n)}{\overline{u}}^{(n)}=\sum \limits_{m=0}^{n-1}{\overline{Q}}_{(m)}+{\overline{P}}_{(n)}, $$
(15)

where K(n) is the global stiffness matrix of the construction, \( {\overline{u}}^{(n)} \) is the vector of node displacements, \( {\overline{P}}_{(n)} \) is the vector of node loads, \( {\overline{Q}}_{(m)} \) is the vector of additional node loads, which simulates the viscoelastic behavior of the material and is defined in the iterative process on each mth iteration \( {\overline{Q}}_{(m)}={\overset{\cdot }{R}}_m{K}^{s\prime t\prime}\left({t}_m\right){u}_{s\prime}\left({t}_m\right) \).

For solving the nonlinear problem, the combined Newton–Kantorovich method of parametric continuation (load, time) is applied [15]. This method permits of getting the linearized solutions at each parametric step. In the case of viscoelastic deformation, the linearized system of equations is solved with the right-hand side that admits the introduction of the additional load vector at each time step, which simulates the viscoelasticity of the material.

For solving the geometrically nonlinear problem, the total loads are divided into several steps. The nonlinear problem is also solved at each step with the combined Newton–Kantorovich method.

For getting the system of resolving equations, the finite strain tensor is written as

$$ {\upvarepsilon}_{ij}={\upvarepsilon}_{ij}^{(l)}+{\upvarepsilon}_{ij}^{(n)}, $$
(16)

where \( {\upvarepsilon}_{ij}^{(l)} \) is the linear part of the strain tensor, \( {\upvarepsilon}_{ij}^{(l)}=\frac{1}{2}\left({C}_j^{m\prime }{u}_{m\prime, i}+{C}_i^{m\prime }{u}_{m\prime, j}\right) \), um′ are the components of the displacement vector, \( {C}_j^{m\prime } \) are the components of the transformation tensor, and \( {\upvarepsilon}_{ij}^{(n)} \) is the nonlinear part of the strain tensor, \( {\upvarepsilon}_{ij}^{(n)}=\frac{1}{2}{u}_{m\prime, i}{u}_{,j}^{m\prime } \).

Then the stress tensor takes on the form

$$ {\upsigma}^{ij}={C}^{ij kl}\left({\upvarepsilon}_{ij}^{(l)}+{\upvarepsilon}_{ij}^{(n)}\right)={\upsigma}_{(l)}^{ij}+{\upsigma}_{(n)}^{ij}, $$
(17)

where \( {\upsigma}_{(l)}^{ij} \) is the linear part of the stress tensor, \( {\upsigma}_{(l)}^{ij}={C}^{ij kl}{\upvarepsilon}_{ij}^{(l)} \), and \( {\upsigma}_{(n)}^{ij} \) is the nonlinear part of the stress tensor, \( {\upsigma}_{(n)}^{ij}={C}^{ij kl}{\upvarepsilon}_{ij}^{(n)} \).

The variation of the internal strain energy in view of (16) and (17) may be written as

$$ \updelta W=\underset{V}{\iiint }{\upsigma}_{(l)}^{ij}{\updelta \upvarepsilon}_{ij}^{(l)} dV+\underset{V}{\iiint}\left({\upsigma}_{(l)}^{ij}+{\upsigma}_{(n)}^{ij}\right){\updelta \upvarepsilon}_{ij}^{(n)} dV+\underset{V}{\iiint }{\upsigma}_{(n)}^{ij}{\updelta \upvarepsilon}_{ij}^{(l)} dV. $$
(18)

Then its linear part is the basis for composing the stiffness matrix of the construction

$$ \underset{V}{\iiint }{\upsigma}_{(l)}^{ij}{\updelta \upvarepsilon}_{ij}^{(l)} dV={K}^{s\prime t\prime }{u}_{s\prime}\updelta {u}_{t\prime }. $$
(19)

The nonlinear part of the variation in (18) is written as follows:

$$ \underset{V}{\iiint}\left({\upsigma}_{(l)}^{ij}+{\upsigma}_{(n)}^{ij}\right){\updelta \upvarepsilon}_{ij}^{(n)} dV+\underset{V}{\iiint }{\upsigma}_{(n)}^{ij}{\updelta \upvarepsilon}_{ij}^{(l)} dV={N}^{s\prime t\prime }{u}_{s\prime}\updelta {u}_{t\prime }. $$
(20)

The variational principle based on potential energy in terms of the derived relations takes on the form

$$ \left[{K}^{s\prime t\prime }{u}_{s\prime }+{N}^{s\prime t\prime }{u}_{s\prime }-{F}^{t\prime}\right]\updelta {u}_{t\prime }=0. $$
(21)

Since the variation of displacements is nonzero, expression in the square brackets (21) should be equal to zero that is the system of linearized resolving equations of the geometrically nonlinear problem

$$ {K}_{(n)}{\overline{u}}^{(n)}={\overline{P}}_{(n)}-{\overline{N}}_{(n)}, $$
(22)

where \( {\overline{N}}_{(n)} \) is the vector of nonlinear terms, \( {\overline{N}}_{(n)}={N}^{s\prime t\prime }{u}_{s\prime } \).

After solving system (22), the geometry of construction and stiffness matrix are recalculated. Then the next step of loads should be done, and the iterative process of calculation based on (22) is repeated.

Numerical Results. The three-dimensional calculation of a thin-layer rubber-metal element with different R/h values is carried out using the above approaches.

Determine the stress-strain state of a thin rubber layer subjected to vertically applied force. Compare the calculation results obtained with analytical formula (1), including simplifications, and the data of the numerical method using the moment finite element scheme.

The application of formula (1) is restricted with the condition R/h = 2–6 (smaller value corresponds to rigid rubbers) with a permissible error of 10% [6]. Therefore, the sizes of a rubber element were chosen within a given range, and the thickness reduction at different loads was calculated by formula (1).

The layer material is rubber of 2956 brand with the following mechanical characteristics: instantaneous shear modulus μ = 1.76 MPa, Poisson’s ratio ν = 0.49. The Rabotnov kernel was chosen as the rubber relaxation kernel with the parameters: α = −0.6, β = 1.06, and γ = 0.58.

The calculation of the construction is performed with different finite element networks subjected to gradual condensation. The results for a 9 × 17 × 17 finite element network, with its further condensation leading to inconsiderable result variations, are demonstrated in Fig. 2.

Fig. 2.
figure 2

Finite element model of a vibration absorber.

Full size image

The calculation results at R = 0.2 m and different h and P = 100 kN are illustrated with Figs. 3 and 4.

Fig. 3.
figure 3

Relative thickness reduction of a vibration absorber δ/h with rigid end fixing vs R/h: (1) analytical solution by formula (1); (2), (3) numerical nonlinear elastic and viscoelastic solutions.

Full size image
Fig. 4.
figure 4

Relative thickness reduction of a vibration absorber δ/h with free end fixing vs R/h: (1) and (2) numerical nonlinear elastic and viscoelastic solutions.

Full size image

The comparison of numerical results under triaxial elastic deformation with rigid end fixing (Fig. 3) and the analytical solution [6] demonstrates a qualitatively identical relative thickness reduction against R/h, though the numerical values are somewhat different based on the deformation nonlinearity. Moreover, at the ends of the range R/h = 2–6, the linear solution approaches the nonlinear one, which is explained by the limitations of analytical formula (1) due to the application of symplifying hypotheses. The numerical solution of the viscoelastic problem (t = 10 s) over the whole range of R/h = 2–6 results in slightly larger thickness reduction values as compared to those obtained in the solution of the elastic problem, which is caused by the material creep. However, this difference is insignificant, and at R/h ~ 6 i.e., a thin rubber layer, both solutions are practically coincide. The reason is that the rigid end fixing in compression provides the rubber layer deformation in the radial direction, thus, it is in the state of compression and due to weak compressibility offers the resistance to deformation in the axial direction, including creep strains.

In the case of unfixed rubber layer ends, the material can freely be deformed in the radial direction, therefore, the thickness reduction in the vertical direction grows more than twice in comparison with the fixed ends. Moreover, the relative thickness reduction is little dependent on R/h. For fixed ends, the viscoelastic solution gives the thickness reduction that is 8–12% larger than under elastic deformation, which is also caused by the higher deformability of the rubber layer in the axial direction.

Conclusion. Deformation of rubber vibration absorbers in view of nonlinearity permits of refining their stress-strain state at static loads and correcting the problem in the dynamic statement.