Introduction. Thick-walled cylinders are widely used in mechanical engineering, civil engineering, aerospace, chemical engineering, etc. [1,2,3,4,5,6,7,8]. In mechanical engineering, the shrink fit between a transmission shaft and sleeve, shaft and hub belong to a combined thick-walled cylinder [9,10,11,12,13,14]. To improve the ultimate bearing capacity, the method of increasing wall thickness is limited when the inner radius of a thick-walled cylinder is fixed. However, two or more thick-walled cylinders are used to form multilayered combined cylinders by means of interference fit, and the stress distribution is more reasonable than that of a single integral thick-walled cylinder [15]. Multilayered combined thick-walled cylinders are mostly designed with equal strength; that is, when the container fails, the inner and outer cylinders are simultaneously damaged [16,17,18]. Many researchers have studied the optimization design and stress intensity factor for combined thick-walled cylinders by the Tresca yield criterion, but it is not applicable to tensile-compressive anisotropic materials and does not consider the intermediate principal stress. Until now, the limit analysis of multiple thick-walled cylinders rarely reported in the literature. The elastoplastic bearing capacity solutions herein for double-layered and multilayered combined thick-walled cylinders are presented with unified strength theory (UST), which fully considers the influence of the intermediate principal stress and strength difference. In addition, the separate radius, assemblage pressure and shrink range fundamental solutions are derived from the UST.

1. Theoretical Method.

1.1. Unified Strength Theory. The UST was developed based on orthogonal octahedron of a twin shear element model, which mathematical expression was introduced in [19]

$$ F={\upsigma}_1-\frac{\upalpha}{1+b}\left(b{\sigma}_2+{\sigma}_3\right)={\sigma}_s,\kern1em {\sigma}_2\le \frac{\sigma_1+\upalpha {\sigma}_3}{1+\upalpha}, $$
(1a)
$$ F\hbox{'}=\frac{1}{1+b}\left({\sigma}_1+b{\sigma}_2\right)-\upalpha {\sigma}_3={\sigma}_s\kern1em {\sigma}_2\ge \frac{\sigma_1+\upalpha {\sigma}_3}{1+\upalpha}, $$
(1b)

where α and b are defined as α = σt/σc and \( b=\frac{\left(1+\upalpha \right){\uptau}_s-{\sigma}_t}{\sigma_t-{\uptau}_s}, \) F and F′ are functions of principal stress strength theory, σ1, σ2 , and σ3 are the major, intermediate, and minor principal stresses, respectively, σt , σc , and τs are the tensile, compressive and shear yield strengths, respectively, α denotes the tension-compression strength ratio, and b is a preset parameter of different failure criteria, which range is 0 ≤ b ≤ 1.

1.2. Yield Condition. Under axisymmetric plane strain conditions, the tangential stress σθ and radial stress σr are the principal stresses σ1 and σ3 , respectively; the axial stress σz is the mean principal stress σ2. If σ1 ≥ σ2 ≥ σ3, the following expression is valid:

$$ {\sigma}_1={\sigma}_{\uptheta}>0,\kern1em {\sigma}_2={\sigma}_z,\kern1em {\sigma}_3={\sigma}_r<0. $$
(2)

A simple empirical correlation was introduced by Yu et al. [20]: \( {\sigma}_z=\frac{m}{2}\left({\sigma}_r+{\sigma}_{\uptheta}\right), \) where m is an empirical constant with 0 ≤ m ≤ 1. It was assumed that, m = 2v (v is Poisson’s ratio) in the elastic zone and m → 1 in the plastic zone. Using Eq. (2), the intermediate principal stress σ2 can be given as \( {\sigma}_2=\frac{m}{2}\left({\sigma}_1+{\sigma}_3\right). \) Because α ≤1, the condition \( {\upsigma}_2\le \frac{\upsigma_1+{\upalpha \upsigma}_3}{1+\upalpha} \) should be adopted. Then, Eq. (1) can be reduced to

$$ {\upsigma}_{\uptheta}=\frac{\upalpha}{1+b}\left( bm\frac{\upsigma_r+{\upsigma}_{\uptheta}}{2}+{\upsigma}_r\right)={\upsigma}_{\mathrm{s}}. $$
(3)

Equation (3) can be rewritten as follows:

$$ \frac{2+2b-\upalpha bm}{2+2b}{\sigma}_{\uptheta}-\frac{\upalpha bm+2\upalpha}{2+2b}{\upsigma}_r={\upsigma}_s, $$
(4)

where Eq. (4) is the yield condition of a thick-walled cylinder based on the UST.

2. Fundamental Solutions of Double-Layered Cylinder. A thick-walled cylinder with inner radius ri and outer radius ro bears inner pressure p1 and outer pressure p2 . The elastic stresses can be derived as in [19]:

$$ {\displaystyle \begin{array}{c}{\upsigma}_r=\frac{r_i^2{r}_o^2\left({p}_2-{p}_1\right)}{r_o^2-{r}_i^2}\frac{1}{r^2}+\frac{r_i^2{p}_1-{r}_o^2{p}_2}{r_o^2-{r}_i^2},\\ {}{\upsigma}_{\uptheta}=\frac{r_i^2{r}_o^2\left({p}_2-{p}_1\right)}{r_o^2-{r}_i^2}\frac{1}{r^2}+\frac{r_i^2{p}_1-{r}_o^2{p}_2}{r_o^2-{r}_i^2},\end{array}} $$
(5)

where σr and σθ are radial and tangential stresses, respectively.

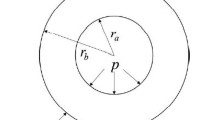
2.1. Assemblage Pressure. Figure 1a shows a double-layered cylinder made of the same material with an inner radius ri , outer radius ro , and separate radius rc . Figure 1b and 1c shows a combined cylinder composed of the inner cylinder (with inner radius ri and outer radius rc + δ1) and outer cylinder (with inner radius rc + δ2 and outer radius ro), respectively. It is assumed that the material of both cylinders is identical. When assembling, the outer cylinder needs to be heated to increase it inner radius and place it over the inner one. Upon cooling, a certain contact (assemblage) pressure between both cylinders is generated.

Fig. 1.
figure 1

Double-layered thick-walled cylinder: (a) double-layered cylinder; (b) inner cylinder; (c) outer cylinder.

Full size image

As shown in Fig. 1b and 1c, the shrink range δ in the assemblage zone is determined as

$$ \updelta ={\updelta}_2-{\updelta}_1. $$
(6)

According to theory of elasticity, the assemblage pressure equation takes the following form [15]:

$$ p=\frac{E\updelta}{r_c}\frac{\left({r}_c^2-{r}_i^2\right)\left({r}_o^2\right)}{2{r}_c^2\left({r}_o^2-{r}_i^2\right)}, $$
(7)

where E is the cylinder material’s elastic modulus under plane strain conditions.

Equation (7) implies that the assemblage pressure p can be determined if the shrink range δ and separate radius rc are given; thereby, the assemblage stress generated in the inner and outer cylinders can be obtained.

2.2. Separate Radius and Assemblage Shrink Range. The optimal solution of the separate radius rc and shrink range δ for assemblage containers made of the same material can be established by utilizing the inner wall of the inner cylinder and inner wall of the outer cylinder simultaneously to satisfy the yielding condition. It is assumed that the inner cylinder bears inner pressure p1 and assemblage pressure p at r=rc. To ensure that the inner and outer cylinders yield at the same time, the inner cylinder at r=ri should have the same pressure as that of the outer cylinder at r=rc, where the stress at the interface can be expressed from Eq. (4) as

$$ \left(\frac{2+2b-\upalpha bm}{2+2b}{\upsigma}_{\uptheta}-\frac{\upalpha bm+2\upalpha}{2+2b}{\upsigma}_r\right). $$

(1) An inner cylinder comes under internal pressure p1 at the inner wall and external pressure q at the outer wall. Then, the external pressure q is defined as

$$ q=p+{\upsigma}_r\left|{}_{r={r}_c},\right. $$
(8)

where \( {\upsigma}_r\left|{}_{r={r}_c}\right. \) denotes the radial stress at r=rc under the internal pressure p1, which is formulated as follows:

$$ {\upsigma}_r\left|{}_{r={r}_c}=\frac{r_i^2\left({r}_c^2-{r}_o^2\right)}{r_c^2\left({r}_c^2-{r}_i^2\right)}\right.{p}_1. $$
(9)

(2) An outer cylinder bears inner pressure q at the inner wall and zero pressure at the outer wall, i.e., \( {\upsigma}_r\left|{}_{r={r}_o}\right.=0. \) For the inner cylinder, the following equation obtained from Eq. (5) at r=ri is given as

$$ {\left(\frac{2+2b-\upalpha bm}{2+2b}{\upsigma}_{\uptheta}-\frac{\upalpha bm+2\upalpha}{2+2b}{\upsigma}_r\right)}_{r={r}_i}=\frac{2+2b-\upalpha bm}{2+2b}\frac{\left[\left({r}_i^2+{r}_c^2\right){p}_1-2{r}_c^2q\right]}{r_c^2-{r}_i^2}+\frac{\upalpha bm+2\upalpha}{2+2b}{p}_1. $$
(10)

For the outer cylinder, the stress component is deduced by setting r=rc in Eq. (5) as

$$ {\left(\frac{2+2b-\upalpha bm}{2+2b}{\upsigma}_{\uptheta}-\frac{\upalpha bm+2\upalpha}{2+2b}{\upsigma}_r\right)}_{r={r}_i}=\frac{2+2b-\upalpha bm}{2+2b}\frac{r_o^2+{r}_c^2}{r_o^2-{r}_c^2}q+\frac{\upalpha bm+2\upalpha}{2+2b}q. $$
(11)

By integrating Eqs. (10) and (11), the following equation can be manipulated as

$$ q=\frac{\left[\left(2+2b+2{\upalpha \mathrm{r}}_c^2\right){r}_c^2+\left(2+2b-\upalpha bm-2\upalpha \right){r}_i^2\right]\left({r}_o^2-{r}_c^2\right)}{\left(6+6b-2\upalpha bm+2\upalpha \right){r}_o^2{r}_o^2-\left(2+2b-2\upalpha bm-2\upalpha \right){r}_i^2{r}_c^2-\left(2+2b+2\upalpha \right)\left({r}_o^2{r}_i^2+{r}_c^4\right)}{p}_1, $$
(12)

where k1, k2, and k3 are defined as k1 = 2 + 2b + 2α, k2 = 2 + 2b − 2αbm − 2α, and k3 = 6 + 6b − 2αbm + 2α, respectively. Then, Eq. (12) can be simplified as

$$ q=\frac{\left[{k}_1{r}_c^2+{k}_2{r}_i^2\right]\left({r}_o^2-{r}_c^2\right)}{k_3{r}_o^2{r}_c^2-{k}_2\Big({r}_i^2{r}_c^2-{k}_1\left({r}_o^2{r}_i^2+{r}_c^4\right)}{p}_1. $$
(13)

By substituting Eq. (13) into \( \left(\frac{2+2b-\upalpha bm}{2+2b}{\upsigma}_{\uptheta}-\frac{\upalpha bm+2\upalpha}{2+2b}{\upsigma}_r\right), \) the function of rc is determined as

$$ f\left({r}_c\right)=\frac{\left({k}_1{r}_o^2+{k}_3{r}_c^2\right)\left({k}_1{r}_c^2+{k}_2{r}_i^2\right)}{\left(2+2b\right)\left[{k}_3{r}_o^2{r}_c^2-{k}_2{r}_c^2{r}_i^2-{k}_1\left({r}_o^2{r}_i^2+{r}_c^4\right)\right]}{p}_1. $$
(14)

The function equation f has a minimum value, where the function must satisfy df/drc=0. Then, the separate radius is given as

$$ {r}_c=\sqrt{r_o{r}_i}. $$
(15)

By introducing Eq. (15) into Eq. (13), the following expression is obtained:

$$ q=\frac{\left({k}_1{r}_o+{k}_2{r}_i\right)\left({r}_o-{r}_i\right)}{k_3{r}_o^2-{k}_2{r}_i^2-2{k}_1{r}_o{r}_i}{p}_1. $$
(16)

Then, the assemblage pressure p is generated as

$$ {\left.p=q-{\upsigma}_r\right|}_{r={r}_c}=\frac{k_1{r}_o^3+\left({k}_2-{k}_3\right){r}_o^2{r}_i+{k}_1{r}_o{r}_i^2}{\left({r}_o+{r}_i\right)\left({k}_3{r}_o^3-{k}_2{r}_i^2-2{k}_1{r}_o{r}_i\right)}. $$
(17)

If the combined cylinder yields, by integrating Eq. (16) and using the yield condition with Eq. (10), that is, \( \frac{2+2b-\upalpha bm}{2+2b}\frac{\left[\left({r}_i^2+{r}_c^2\right){p}_1-2{r}_c^2q\right]}{r_c^2-{r}_i^2}+\frac{\upalpha bm+2\upalpha}{2+2b}{p}_1={\upsigma}_s, \) the internal pressure p1 can be transmuted as

$$ {p}_1=\frac{k_3{r}_o^2-{k}_2{r}_i^2-2{k}_1{r}_o{r}_i^2}{{\left({k}_1{r}_o+{k}_2{r}_i\right)}^2}\left(2+2b\right){\upsigma}_s. $$
(18)

By integrating Eqs. (5), (15), and (17), the assemblage shrink range can be expressed as

$$ \updelta =\frac{2\sqrt{r_o{r}_i}}{E}\frac{k_1{r}_o^3+\left({k}_2-{k}_3\right){r}_o^2{r}_i+{k}_1{r}_o{r}_i^2}{k_3{r}_o^3-\left(2{k}_1+{k}_3\right){r}_o^2{r}_i+\left(2{k}_1-{k}_2\right){r}_o{r}_i^2-{k}_2{r}_i^3}{p}_1. $$
(19)

3. Elastoplastic Analysis of the Double-Layered Cylinder. An infinitely long cylinder with yield strength σs1 of the inner cylinder and yield strength σs2 of the outer cylinder satisfies σs1>σs2. Figure 2 shows a double-layered cylinder with inner radius ra, outer radius rb, and separate radius rc which is subjected to uniform pressure p1. When both the inner and outer cylinders reach the plastic limit state, the plastic ultimate load of the combined cylinder can be determined.

Fig. 2.
figure 2

Double-layered cylinder with different yield limits.

Full size image

The stress equilibrium equation for a thick-walled cylinder can be obtained as [15]

$$ \frac{d{\upsigma}_r}{dr}+\frac{\upsigma_r-{\upsigma}_{\uptheta}}{r}. $$
(20)

By combining Eqs. (4) and (20), the following equation is obtained:

$$ \frac{d{\upsigma}_r}{dr}+\frac{2+2b-2\upalpha -2\upalpha bm}{r\left(2+2b-\upalpha bm\right)}{\upsigma}_r=\frac{2+2b}{r\left(2+2b-\upalpha bm\right)}{\upsigma}_s. $$
(21)

By integration, the radial stress σr is derived as

$$ {\upsigma}_r={Cr}^{\frac{2\upalpha \_2\upalpha bm-2-2b}{2+2b-\upalpha bm}}+\frac{\upsigma_s}{1-\upalpha}, $$
(22)

where C is an unascertained coefficient.

With the stress boundary situation, σr = -p1 and σs =σs1 at r=ri, the constant C can be expressed as

$$ c=\left(-{p}_1-\frac{\upsigma_{s1}}{1-\upalpha}\right){\left(\frac{1}{r_i}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}, $$
(23)

where pl is the plastic limit internal pressure. Then, Eq. (22) takes the following form:

$$ {\upsigma}_r=\left(-{p}_l-\frac{\upsigma_{s1}}{1-\upalpha}\right){\left(\frac{1}{r_i}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}+\frac{\upsigma_{s1}}{1-\upalpha}. $$
(24)

With the outer boundary condition, σr = -q at r=rc, the following formula is given by

$$ {p}_l-q=\left(-{p}_l-\frac{\upsigma_{s1}}{1-\upalpha}\right)\left[{\left(\frac{r_c}{r_i}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}-1\right]. $$
(25)

The plastic limit pressure q of the outer cylinder takes the following form [21]:

$$ q=\left(\frac{\upsigma_{s2}}{1-\upalpha}\right)\left[{\left(\frac{r_c}{r_o}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}-1\right]. $$
(26)

After substituting Eq. (26) into Eq. (25), pl is taken as

$$ {\displaystyle \begin{array}{c}{p}_l=\frac{\upsigma_{s1}}{1-\upalpha}\left[{\left(\frac{r_c}{r_i}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}-1\right]+{\left(\frac{r_i}{r_c}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}\frac{\upsigma_{\mathrm{s}2}}{1-\upalpha}\left[{\left(\frac{r_c}{r_o}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}-1\right]\\ {}={p}_{l1}{\left(\frac{r_i}{r_c}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}{p}_{l2}.\end{array}} $$
(27)

It can be seen from Eq. (27) that the plastic allowable pressure of a combined cylinder with different materials is not a simple superposition of the plastic ultimate bearing capacity of a two-layer cylinder. This result is different from the analysis result based on the Tresca yield. The plastic allowable bearing capacity of the combined cylinder with the same material can be obtained by setting σs1=σs2=σs in the above equation as follows:

$$ {p}_l=\frac{\upsigma_s}{1-\upalpha}\left[{\left(\frac{r_i}{r_o}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}-1\right], $$
(28)

where m is an empirical coefficient, which value is presented by theory and experiment [20]. For simplicity, the general approximation is m = 1, then Eq. (28) is reduce to:

$$ {p}_l=\frac{\upsigma_s}{1-\upalpha}\left[{\left(\frac{r_i}{r_o}\right)}^{\frac{2\upalpha +2\upalpha bm-2-2b}{2+2b-\upalpha bm}}-1\right], $$
(29)

where the degradation formula in Eq. (29) herein is the same as the corresponding result in [21].

It can be seen from the above equation that the structural plastic ultimate capacity with the same material is related to the radius ratio ri/ro, strength parameter b, and tension-compression ratio α and is independent of the separate radius rc and assemblage pressure p. That is, a composite cylinder of the same material can be considered a single-layered cylinder of the same thickness when solving for the plastic limit bearing capacity.

4. Elastic Analysis of the Multilayered Thick-Walled Cylinder. The stress distribution of multilayered cylinder related to n cylinders is more rational than that of single-layered cylinder. Figure 3 demonstrates a multilayered cylinder set with inner radii and outer radii (ri, r1), (r1, r2), (r2, r3), … (rn, ro) in sequence with the same material that bears an evenly supported pressure pi.

Fig. 3.
figure 3

Multilayered thick-walled cylinder.

Full size image

By assuming a multilayered thick-walled cylinder subjected to internal pressures q1, q2, ..., qn, between the layers, the following expression can be obtained when the inner surface of each layer yields:

$$ \Big\{{\displaystyle \begin{array}{c}{p}_e-{q}_1={\upsigma}_s\frac{r_1^2-{r}_i^2}{r_1^2+{r}_i^2\frac{\upalpha}{1+b}{r}_1^2-\upalpha {r}_1^2},\\ {}{q}_1-{q}_2={\upsigma}_s\frac{r_1^2-{r}_i^2}{r_2^2+{r}_i^2\frac{\upalpha}{1+b}{r}_2^2-\upalpha {r}_1^2},\\ {}\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ {}{q}_n={\upsigma}_s\frac{r_o^2-{r}_n^2}{r_o^2+{r}_n^2+\frac{\upalpha}{1+b}{r}_o^2-\upalpha {r}_n^2}.\end{array}} $$
(30)

By adding the above n equations, we can obtain

$$ {p}_e={\upsigma}_s\left[\frac{r_1^2-{r}_i^2}{r_1^2+{r}_i^2+\frac{\upalpha}{1+b}{r}_1^2-\upalpha {r}_i^2}+\frac{r_2^2-{r}_1^2}{r_2^2+{r}_1^2+\frac{\upalpha}{1+b}{r}_2^2-\upalpha {r}_1^2}+\dots +\frac{r_o^2-{r}_n^2}{r_o^2+{r}_n^2+\frac{\upalpha}{1+b}{r}_o^2-\upalpha {r}_n^2}\right]. $$
(31)

If the elastic ultimate pressure can have a maximum value, where the pressure must satisfy \( \frac{\partial {p}_e}{\partial {r}_1}=\frac{\partial {p}_e}{\partial {r}_2}=\dots =\frac{\partial {p}_e}{\partial {r}_n}=0. \) Then, the following equation is derived as

$$ \frac{r_1}{r_i}=\frac{r_2}{r_1}=\frac{r_3}{r_2}=\dots =\frac{r_o}{r_n}={\left(\frac{r_o}{r_n}\right)}^{\frac{1}{n+1}}. $$
(32)

As shown in Eq. (32), when the radius of each layer satisfies \( {\left(\frac{r_o}{r_i}\right)}^{\frac{1}{n+1}}, \) the maximum value of pe can be established as

$$ {p}_e={\upsigma}_sn\frac{1-{\left(\frac{r_i}{r_o}\right)}^{\frac{2}{n+1}}}{\left(1+\frac{\upalpha}{1+b}\right)+\left(1-\upalpha \right){\left(\frac{r_i}{r_o}\right)}^{\frac{2}{n+1}}}. $$
(33)

Equation (33) can be reduced to the Tresca criterion solution with α = 1 and b = 0 [15].

5. Results and Discussion.

5.1. Degradation Validation of Solutions. The parameter b exhibits the impact extent that the intermediate principal stress can induce the failure of multiple cylinder. With a specific value of b, the UST can come down to various existing failure criteria. For instance, the UST simplifies to the Tresca criterion with α = 1 and b = 0. The von Mises criterion can be estimated with α = 1 and b = 1/3. When the parameter α varies between 0 and 1, the Mohr–Coulomb failure criterion is established with b = 0.

5.2. Parametric Studies. Supposing that the multiple cylinder is constituted of the same material. The effects of the tension-compression ratio _ (the value is set to 0.2, 0.4, 0.6, 0.8, and 1.0) and the strength theory parameter b (the value is set to 0, 0.25, 0.5, 0.75, and 1.0) on the plastic limit pressure pl are investigated, as shown in Fig. 4. As shown in Fig. 4a, the ratio of pl/σs decreases with increasing α values. The tensile strength and compressive strength impact the failure of thick-walled cylinders. pl s _ has a minimum value where the coefficient satisfies α = 1. Figure 4 shows that the ratio of increases with parameter b. The pl/σs value is increased by 33.3% when b =1 compared with that of b = 0 for ro/ri = 4.0 and α = 1. The parameter b value represents different strength theories, which have a large impact on the limit solution of the combined cylinder. Figure 4b illuminates that the increasing rate of pl/𝜎s is relatively obvious for different ro/ri values.

Fig. 4.
figure 4

pl/σs versus the coefficients α and b with different ro/ri.

Full size image

Figure 5 shows the elastic limit pressure pe/σs versus the different parameters. As shown in Fig. 5a and b, the ratio of pe/σs improves with increasing b values. The significant differences in the results with various b values are a clear indication that the intermediate principal stress effect should be rationally considered. In observing Fig. 5c, the value of pe/σs increases with the increase in the number of cylinder layers n. From Fig. 5a–c, pe/σs is taken as the minimum value when α = 1. A significant difference with various α is a clear indication that the error might arise if tension-compression ratio is not properly considered. The influence of the tension-compression ratio α can be better applied to the ultimate load analysis of various materials. According to the solution in this paper, the effect of the tensile-compression ratio can be discussed, and test guidance can be given. Moreover, Fig. 5d illustrates that the influence of the radius ratio ro/ri on the pe/σs value is obvious with an increasing tension-compression strength ratio.

Fig. 5.
figure 5

pe/σs versus the coefficient α, b, n, and ro/ri.

Full size image

Conclusions. Considering intermediate principal stress and different tension-compression strengths, the elastoplastic unified solutions of double-layered and multilayered cylinders are derived on the basis of the UST. Moreover, the fundamental solutions of the separate radius, assemblage pressure and shrink range are derived for double-layered thick-walled cylinders. The effects of failure criteria parameter b, tensile-compressive strength ratio α, radius ratio ro/ri, and combined cylinder layers n on the ultimate results are significant. Furthermore, structural strength potentialities are fully achieved with the UST. The final solutions have general application and are universal for use. In conclusion, the proposed formulation of allowable limit pressure for multiple cylinder is more consistent with the true results by considering the intermediate principal stress and cylinder layers. According to the solutions in this paper, we can discuss the influence degree of the tension-compression ratio and different strength criteria and solve the related problems of thick-walled cylinder pressure vessels with different criteria.