1 Introduction

In many areas, high-frequency data are monitored in time and space. For example, (i) in medicine, a patient’s state can be diagnosed by time-related recordings (e.g. electroencephalogram, electrocardiogram) or/and images (e.g. fMRI) and (ii) in finance, the stocks markets are naturally recorded in time and space. Analyzing such data requires adapted techniques, mainly because of the high dimension and their complex time and space correlation structure. Since the pioneer works of Ramsey and Silverman (2005), this data is well-known in statistics as functional data and, nowadays, it is a well-established statistical research domain. Viewed as a sample of a random variable with values in some infinite dimensional space, functional data is mostly associated with a random variable indexed by a continuous parameter such as the time, wavelengths, or percentage of some cycle.

Dimension reduction techniques are used in order to tackle the issue of high dimension and correlation. Among these, the most basic and elementary one is the selection of privileged features of data by expert’s knowledge (see e.g Saikhu et al. (2019); Javed et al. (2020)). Some other works focused on deep learning models, in particular, long short-term memory models have been proposed for time series (Hochreiter and Schmidhuber 1997; Karim et al. 2017, 2019). They have the advantage of being less dependent on prior knowledge but are usually not interpretable. Maybe the most used methodologies for dealing with functional data are based on building latent models such as principal component analysis/regression (PCA, PCR) (Ramsey and Silverman 2005; Jacques and Preda 2014; Escabias et al. 2004 and partial least squares (PLS) Aguilera et al. (2010); Preda et al. (2007).

In this paper we are focused on supervised classification with binary response Y and multivariate functional data predictor \(X = (X^{(1)}, \ldots , X^{(d)})^{\mathop {\mathrm {\top }}\limits }\), where for \(j=1,\ldots ,d\), \(X^{(j)}\) are univariate functional random variables, \(X^{(j)}=\{X^{(j)}(t), t\in \mathcal {I}_j\}\), and \(\mathcal {I}_j\) is some compact continuous index set.

The supervised classification of univariate functional data (\(d=1\)) has been the source of various contributions. James and Hastie (2001) extended multivariate linear discriminant analysis (LDA) to irregularly sampled curves. As maximizing the between-class variance with respect to the total variance leads to an ill-posed problem, Preda et al. (2007) proposed a partial least square-based classification approach for univariate functional data. Using the concept of depth, López-Pintado and Romo (2006) introduced robust procedures to classify functional data. Non-parametric approaches have also been investigated, using distances and similarities measures, see e.g Ferraty and Vieu (2003), and Galeano et al. (2015) for an overview of the use of Mahalanobis distance. Tree-based techniques applied to functional data classification are quite recent: Maturo and Verde (2022) introduced tree models using functional principal component scores as features, and Möller and Gertheiss (2018) presented a tree based on curve distances.

In the multivariate functional data setting, the supervised classification is mainly investigated when all domains \(\mathcal {I}_j\) are identical, \(\mathcal {I}_j=[0, T]\) for \(j=1, \ldots , d\) and \( T> 0\), that is, all the d-components of X are defined on the same domain. Under this assumption, Blanquero et al. (2019) proposed a methodology that allows for optimal selection of the most informative time instants in the data. In Górecki et al. (2015), regression models are used to classify multivariate functional data by reduction dimension techniques based on basis projection. Recently, Gardner-Lubbe (2021) proposed a linear discriminant analysis. To avoid the ill-posed problem of the maximization of the between variance in the functional case, the authors use discretization techniques, by pooling data at specific time points.

The classification of multivariate functional data with different domains (the domains \(\mathcal {I}_j\) are different) is rarely explored. This framework is more flexible and makes possible the use of different types of data simultaneously (e.g. time series, images) (Happ and Greven 2018). To the best of our knowledge, only Golovkine et al. (2022) proposed a supervised classification method in this setting. They introduced a tree-based method for unsupervised clustering and demonstrated the applicability of their method to supervised classification. Their method is based on principal component analysis for multivariate functional defined on different domains (MFPCA), presented in (Happ and Greven 2018).

The use of MFPCA as ordinary principal component analysis (PCA) for supervised learning leads to some non-trivial issues, such as the number and the selection of the principal components to be retained in the model. Therefore, the partial least square (PLS) approach has been an interesting alternative, as the obtained PLS components are based on the relationship between predictors and the response. Since the introduction of PLS regression on univariate functional data predictors in Preda and Saporta (2002), many contributions have been proposed, particularly in the univariate functional framework. As already mentioned above, Preda et al. (2007) demonstrated the ability to use PLS for linear discriminant analysis. In Aguilera et al. (2010) the authors show the relationship between the PLS of univariate functional and ordinary PLS on the coefficients obtained from basis expansion approximation. An alternative non-iterative functional partial least square for regression is developed in Delaigle and Hall (2012), and they demonstrate consistency and establish convergence rates. For interpretability purposes, Guan et al. (2022) has recently introduced a modified partial least squares approach to obtaining the sparsity of the coefficient function.

To the best of our knowledge, PLS regression for multivariate functional data has been explored only in one domain setting. In Dembowska et al. (2021), the authors proposed a two-step approach for dealing with multivariate functional covariates. The first step consists of computing independently the PLS components for each (univariate) dimension \(X^{(j)}, j=1, \ldots , d\). Then, they extract new uncorrelated features based on linear combinations of the obtained PLS components. In Beyaztas and Shang (2022) the aim is to provide a robust version of PLS for multivariate functional data. They have extended Aguilera et al. (2010) basis expansion results on multivariate functional data and proposed a partial robust M-regression in this framework.

We extend the recent contribution in Beyaztas and Shang (2022) by investigating more exhaustively PLS procedures, in particular, we derive the relationship between the PLS regression with univariate functional data (FPLS) and the PLS regression with multivariate functional data (MFPLS). This relationship provides a way to estimate the PLS components for multivariate functional data from the corresponding univariate ones. In the one-domain setting, it provides, from a computational point of view, a new estimating procedure. In the case of different domains, this relationship makes it possible to treat each univariate functional data with a different domain separately and then combine the FPLS components to obtain the MFPLS ones.

The different dimension framework makes it possible to mix functional data of heterogeneous types (e.g. images and time series). Inspired by the Tree Penalized Linear Discriminant Analysis (TPLDA) introduced in Poterie et al. (2019), we propose a tree classifier based on PLS regression scores. Similarly to the TPLDA, our tree model uses a predefined structure group of dimensions.

The paper is organized as follows. Section 2 presents the PLS methodology for binary classification. It introduces the PLS regression with multivariate functional data defined on different domains and establishes the relationship with the univariate functional PLS approach. The presentation of the TMFPLS methodology ends this section. Section 3 presents simulation studies for regression and classification purposes and compares the performances of our approaches with existing methods. We also apply the MFPLS and TMFPLS methods to benchmark data for multivariate time series classification in Sect. 4. A discussion is given in Sect. 5. The appendix contains detailed proofs of some theoretical results. The supplementary material includes additional figures related to the numerical experiments.

2 Methods

2.1 Basic principles and notations

We are dealing with multivariate functional data defined on different domains in a similar framework as Happ and Greven (2018). As a general model for multivariate functional data analysis, let X be a stochastic process represented by a d-dimensional vector of functional random variables \(X =(X^{(1)}, \ldots , X^{(d) } )^{\mathop {\mathrm {\top }}\limits }, \) defined on the probability space \((\Omega , \mathcal {A}, \mathbb {P})\).

In the classical setting ( Ramsey and Silverman (2005); Jacques and Preda (2014); Górecki et al. (2015)), the components \(X^{(j)}\), \(j=1, \ldots , d\), are assumed real-valued stochastic processes defined on some finite continuous interval [0, T]. In our setting, we consider the general framework where each component \(X^{(j)}\) is defined on some specific continuous compact domain \(\mathcal {I}_j\) of \(\mathbb {R}^{d_j}\), with \(d_j \in \mathbb {N}-\{0\}\). Thus, for \(d_j = 1\) we deal in general with time or wavelength domains whereas for \(d_j=2\), the domain \(\mathcal {I}_j\) indexes images or more complex shapes. It is also assumed that \(X^{(j)}\) is a \(L_2\)-continuous process, and it has squared integrable paths, i.e. each trajectory of \(X^{(j)}\) belongs to the Hilbert space of the square-integrable functions defined on \(\mathcal {I}_j\), \(L_2(\mathcal {I}_j)\). These general hypotheses ensure that integrals involving the variables \(X^{(j)}\) are well-defined. Let define \(\mathcal {H}= L_2(\mathcal {I}_1) \times ... \times L_2(\mathcal {I}_d)\) be the Hilbert space of vector functions

$$\begin{aligned} \mathcal {H}=&{} \left\{ f = (f^{(1)}, \ldots , f^{(d)})^{\mathop {\mathrm {\top }}\limits }, f^{(j)} \in L_{2}(\mathcal {I}_j), \ j=1, \ldots , d\right\} \end{aligned}$$

endowed with the inner product

$$\begin{aligned} \langle \langle f, g\rangle \rangle _\mathcal {H} \!\!=\!\! \sum _{j=1}^d \langle f^{(j)}, g^{(j)}\rangle _{L_2(\mathcal {I}_j) } \!\!=\!\! \sum _{j=1}^d \int _{\mathcal {I}_j} f^{(j)}(t)g^{(j)}(t) dt. \end{aligned}$$

where dt is the Lebesgue measure on \(\mathcal {I}_j\). In the following, if there’s no confusion, the index \(\mathcal {H}\) will be omitted and \(\vert \vert \vert , \vert \vert \vert \) will denote the norm induced by \(\langle \langle , \rangle \rangle \).

2.2 The linear functional regression model

When the aim is the prediction (the supervised context), the stochastic process X is associated to a response variable of interest Y through the conditional expectation \(\mathbb {E}(Y\vert X).\)

Let consider the real-valued response variable Y be defined on the same probability space as X,

$$\begin{aligned} Y:\Omega \rightarrow \mathbb {R}. \end{aligned}$$

Without loss of generality, we assume that Y and X are zero-mean,

$$\begin{aligned} \mathbb {E}(Y) = 0,\; \mathbb {E}(X^{(j)}(t)) = 0 , j =1, \ldots , d \; t \in \mathcal {I}_j \end{aligned}$$
(1)

and Y has a finite variance.

The functional linear regression model assumes that \(\mathbb {E}(Y\vert X)\) exists and is a linear operator as a function of X. Thus, we have:

$$\begin{aligned} Y=\langle \langle X, \beta \rangle \rangle + \epsilon , \end{aligned}$$
(2)

where

  • \(\beta \in \mathcal {H}\) denotes the regression parameter (coefficient) function,

    $$\begin{aligned} \beta = \left( \beta ^{(1)}, \ldots , \beta ^{(d)}\right) ^{\mathop {\mathrm {\top }}\limits }, \end{aligned}$$

  • \(\epsilon \) denotes the residual term which is assumed to be of finite variance \(\mathbb {E}(\epsilon ^2)= \sigma ^2\) and uncorrelated to X.

In the integral form, the model in (2) is written as:

$$\begin{aligned} Y= \sum _{j=1}^{d}\int _{\mathcal {I}_j}X^{(j)}(t)\beta ^{(j)}(t)dt + \epsilon . \end{aligned}$$
(3)

Under the least squares criterion, the estimation of the coefficient function \(\beta \) is, in general, an ill-posed inverse problem (Aguilera et al. 2010; Preda and Saporta 2002; Preda et al. 2007). From a theoretical point of view, this is due to the infinite dimension of the predictor X, which makes that its covariance operator is not invertible (Cardot et al. 1999). Hence, dimension reduction methods such as principal component analysis (Happ and Greven 2018) and expansion of X into a basis of functions (Aguilera et al. 2010) can be used in order to obtain an approximation of linear form in (3).

2.2.1 Expansion (of the predictor) into a basis of functions

For each dimension j \(\mathcal {H}\), \(j=1, \ldots , d\), let consider in \(L_2(\mathcal {I}_j)\) the set \(\Psi ^{(j)} = \{\psi ^{(j)}_1, \ldots , \psi ^{(j)}_{M_j}\}\) of \(M_j\) linearly independent functions. Denote with \(M = \sum _{j=1}^{d}M_j\).

Assuming that the functional predictor X and the regression coefficient function \(\beta \) admit the expansions

$$\begin{aligned} X^{(j)}(t) = \sum _{k=1}^{M_j} a_{k}^{(j)} \psi ^{(j)}_k(t), \ \ \ \; \beta ^{(j)}(t) = \sum _{k=1}^{M_j} b^{(j)}_k \psi ^{(j)}_k(t), \end{aligned}$$
(4)

\(\forall t \in \mathcal {I}_j, \; j = 1,\ldots , d\), the functional regression model in (3) is equivalent to the multiple linear regression model:

$$\begin{aligned} Y= (\textrm{F}a)^{\mathop {\mathrm {\top }}\limits } b + \epsilon \end{aligned}$$
(5)

where

  • a is the vector of size M obtained by concatenation of vectors \(a^{(j)}= (a^{(j)}_1, a^{(j)}_2, \ldots , a^{(j)}_{M_j} )^{\mathop {\mathrm {\top }}\limits }\), \(j = 1, \ldots , d, \)

  • b is the coefficient vector of size M obtained by concatenation of vectors \(b^{(j)}= (b^{(j)}_1, b^{(j)}_2, \ldots , b^{(j)}_{M_j} )^{\mathop {\mathrm {\top }}\limits }\), \(j = 1, \ldots , d, \) and

  • \(\textrm{F}\) is the block matrix of size \(M\times M\) with diagonal blocks \(\textrm{F}^{(j)}\), \(j = 1, \ldots , d\),

$$\begin{aligned} \textrm{F}= \begin{pmatrix} \textrm{F}^{(1)} &{} 0 &{} \ldots &{} 0 \\ 0&{} \textrm{F}^{(2)}&{} \ldots &{} 0 \\ \vdots &{} &{} &{} \vdots \\ 0 &{} 0 &{} \ldots &{} \textrm{F}^{(d)} \end{pmatrix}. \end{aligned}$$
(6)

For each \(j = 1,\ldots , d\), \(\textrm{F}^{(j)}\) is the matrix of inner products between the basis functions, with elements \(\textrm{F}^{(j)}_{k,l} = \langle \psi _{k}^{(j)}, \psi _{l}^{(j)}\rangle _{L_2(\mathcal {I}_j)}\), \(1\le k,l\le M_j\).

Hence, under the assumption of basis expansion hypothesis (4), the estimation of the coefficient function, \(\beta \), is equivalent to the estimation of the coefficient vector b in a classical multiple linear regression model with a design matrix involving the basis expansion coefficients of the predictor (the vector a) and the metric provided by the choice of the base’s functions (the matrix F).

The least-square criterion for the estimation of b yields in some settings (e.g. large number of basis functions) to multicollinearity and high dimension issues, similar to the univariate setting (see (Aguilera et al. 2010) for more details). Two well-established methods of estimation, principal component regression (PCR) and partial least squares regression (PLS) are reputed for the efficiency of their estimation algorithm and the interpretability of the results. As mentioned in Jong (1993) in the finite-dimensional setting and in Aguilera et al. (2010) for the functional one, for a fixed number of components, the PLS regression fits closer than the PCR. Thus, the PLS regression provides a more efficient solution (sum of square errors criterion). Numerical experiments confirm these results for the regression with univariate functional data (see for more details Delaigle and Hall (2012); Guan et al. (2022)).

In the next section, we present the proposed PLS regression of multivariate functional data.

2.3 PLS regression with multivariate functional data: MFPLS

PLS regression penalizes the least squares criterion by maximizing the covariance between linear combinations of the predictor variables X (the PLS components) and the response Y. It is based on an iterative algorithm building at each step PLS components as predictors for the final regression model. In the multivariate setting, analogously to the univariate case (Preda and Saporta 2002), the weights for the linear combinations are obtained as the solution to the Tucker criterion:

$$\begin{aligned} \max _{w \in \mathcal {H} }\text {Cov}^2(\langle \langle w, X \rangle \rangle , Y), \end{aligned}$$
(7)

with \(w = (w^{(1)}, \ldots , w^{(d)})^{\mathop {\mathrm {\top }}\limits }\) such that \(\vert \vert \vert w\vert \vert \vert _{\mathcal {H}}=1. \)

The following proposition establishes the solution to the above maximization problem.

Proposition 1

The solution of (7) is given by

$$\begin{aligned}{} & {} w^{(j)}(t)=\frac{\mathbb {E}(X^{(j)}(t)Y)}{\sqrt{\sum _{k=1}^d\int _{\mathcal {I}_k}\mathbb {E}^2(X^{(k)}(s)Y)ds}},\nonumber \\{} & {} \quad \forall t\in \mathcal {I}_j,\, j=1, \ldots , d. \end{aligned}$$
(8)

\(\square \)

Let denote by \(\xi \) the PLS component defined as the linear combination of variables X given by the weights w, i.e.,

$$\begin{aligned} \xi = \langle \langle X, w \rangle \rangle = \sum _{k=1}^{d}\int _{\mathcal {I}_k}X^{(k)}(t)w^{(k)}(t)dt. \end{aligned}$$

The iterative PLS algorithm works as follows:

  • Step 0: Let \(X_{0}=X\) and \(Y_{0}=Y\).

  • Step h, \(h\ge 1\): Define \(w_h\) as in Proposition 1 with \(X = X_{h-1}\) and \(Y= Y_{h-1}\). Then, define the h-th PLS component as

    $$\begin{aligned} \xi _h = \langle \langle X_{h-1}, w_h \rangle \rangle \text {, } \end{aligned}$$

    Compute the residuals \(X_h\) and \(Y_h\) of the linear regression of \(X_{h-1}\) and \(Y_{h-1}\) on \(\xi _h\),

    $$\begin{aligned} \begin{array}{l} X_h = X_{h-1} - \rho _{h}\xi _{h}, \\ Y_h = Y_{h-1} - c_{h}\xi _{h}, \\ \end{array} \end{aligned}$$

    where \(\rho _h = \displaystyle \frac{\mathbb {E}(X_{h-1}\xi _{h})}{\mathbb {E}(\xi _h^{2})} \in \mathcal {H}\) and \(c_h = \displaystyle \frac{\mathbb {E}(Y_{h-1}\xi _{h})}{\mathbb {E}(\xi _h^{2})} \in \mathbb {R}\).

  • Go to the next step (\(h = h+1)\).

Moreover, the following proprieties, stated in the univariate setting (Proposition 3 in Preda and Saporta (2002)), are still valid in the multivariate case. Let L(X) denotes the linear space spanned by X.

Proposition 2

For any \(h \ge 1\), \(\{\xi _k \}_{k=1}^h\) forms an orthogonal system of L(X) and the following expansion formula hold:

  • \(Y= c_1 \xi _{ 1}+ c_{ 2} \xi _{ 2} +...+ c_{ h} \xi _{ h} + Y_{h},\)

  • \(X^{(j)}(t)= \rho _{1}^{(j)}(t) \xi _{ 1} + \rho _{2}^{(j)}(t) \xi _{ 2} +...+ \rho _{h}^{(j)}(t) \xi _{h} + X_{h}^{(j)}(t),\) \(\forall t\in \mathcal {I}_j,\, j=1, \ldots , d. \)

\(\square \)

The right-hand side term of the expansion of Y provides the PLS approximation of order h of (2),

$$\begin{aligned} \langle \langle X, \beta \rangle \rangle \approx c_1 \xi _{ 1}+ c_{ 2} \xi _{ 2} +...+ c_{ h} \xi _{ h} \end{aligned}$$
(9)

and the residual part,

$$\begin{aligned} \varepsilon \approx Y_{h}. \end{aligned}$$

Nevertheless, the above properties don’t furnish the direct relationship between Y and X as in (2). In order to do that, let’s write the components \(\xi _h\) as a linear function of X, i.e., as a dot product in \(\mathcal {H}\).

Lemma 1

Let \(\{v_{ k}\}_{k=1}^h\), \(v_k\) \(\in \text {span}\{w_1,\ldots ,w_h\}\), be defined by:

$$\begin{aligned} v_{ h}^{(j)}(t)= & {} w_{ h}^{(j)}(t) - \sum _{k=1}^{h-1} \langle \langle \rho _{ k}, w_ { h} \rangle \rangle v_{k}^{(j)} (t),\;\nonumber \\{} & {} t\in \mathcal {I}_j \ j= 1, \ldots , d. \end{aligned}$$
(10)

Then, \(\{v_{ k}\}_{k=1}^h\) forms a linearly independent system in \(\mathcal {H}\) and

$$\begin{aligned} \xi _{h} = \langle \langle v_{ h}, X \rangle \rangle =\sum _{j=1}^{d}\int _{\mathcal {I}_j}X^{(j)}(t)v_h^{(j)}(t)dt. \end{aligned}$$

\(\square \)

Thus, as for the principal component analysis X (Happ and Greven 2018), the PLS regression computes the components as the dot product of X and the functions \(\{v_k\}_{k=1}^h\). These components are suitable for regression, as they capture the maximum amount of information between X and Y according to Tucker’s criterion. Obviously, by Lemma 1 and (9) we can write:

$$\begin{aligned} c_1 \xi _{ 1}+ c_{ 2} \xi _{ 2} +...+ c_{ h} \xi _{ h} = \langle \langle X, \beta _{h} \rangle \rangle \end{aligned}$$

with

$$\begin{aligned} \beta _{h}= \sum _{i=1}^{h} c_i v_i. \end{aligned}$$
(11)

Thus, the PLS regression model obtained with h components is given by

$$\begin{aligned} Y= \langle \langle X, \beta _{h} \rangle \rangle + \varepsilon _h, \end{aligned}$$

with \(\varepsilon _h = Y_h\).

Remark 1

For \(h\ge 1\), let \(\mathcal {V}_h=\begin{pmatrix} v_1&\ldots&v_h \end{pmatrix}\) and \(\mathcal {W}_h=\begin{pmatrix} w_1&\ldots&w_h \end{pmatrix}\) be two row-vectors of \(\mathcal {H}^h\). From Lemma 1, the relationship between \(\mathcal {V}_h\) and \(\mathcal {W}_h\) given in (10) can be written in matrix form as

$$\begin{aligned} \mathcal {V}_h = \mathcal {W}_h- \textrm{P}_{h} \mathcal {V}_h, \end{aligned}$$
(12)

where \(\textrm{P}_{h}\) is the \({h\times h}\) matrix,

$$\begin{aligned} \textrm{P}_{h} = \left( \begin{array}{ccccc c } 0 &{} \langle \langle \rho _1, w_2 \rangle \rangle &{} \langle \langle \rho _1,w_3 \rangle \rangle &{}\ldots &{} \langle \langle \rho _1, w_{h-1} \rangle \rangle &{}\langle \langle \rho _1, w_h \rangle \rangle \\ 0 &{} 0 &{} \langle \langle \rho _2,w_3 \rangle \rangle &{} \ldots &{}\langle \langle \rho _2, w_{h-1} \rangle \rangle &{}\langle \langle \rho _2, w_h \rangle \rangle \\ \vdots &{} &{} &{} \ldots &{} &{} \vdots \\ 0&{} 0 &{} 0&{} \ldots &{} 0 &{}\langle \langle \rho _{h-1}, w_h \rangle \rangle \\ 0&{} 0 &{} 0 &{} \ldots &{} 0 &{} 0 \\ \end{array}\right) \end{aligned}$$

Let \(\mathbb {I}_{h \times h}\) be the identity matrix of size \(h \times h\). Since \(\mathbb {I}_{h \times h} + \textrm{P}_{h}\) is non-singular, then equation (12) yields to

$$\begin{aligned} \mathcal {V}_h=(\mathbb {I}_{h \times h } + \textrm{P}_{h} )^{-1} \mathcal {W}_h. \end{aligned}$$
(13)

As the functions \(\{w_{k}\}_{k=1}^h\) are computed directly from Proposition 1, the equation (13) provides a straightforward way to obtain the weights \(\{v_k\}_{k=1}^h\) and, therefore by (11), we obtain the coefficient function approximation \(\beta _h\).

Remark 2

It is worth noting that, contrary to eigenfunctions of the PCA of X Happ and Greven (2018), \(\{ v_k \}_{k=1}^h\) is not an orthogonal system by the inner product \(\langle \langle ,\rangle \rangle \). Nonetheless, it provides orthogonal PLS components, i.e. \(\mathbb {E}(\xi _{k} \xi _{l} ) = \mathbb {E}(\xi _{k}^2) \delta _{k,l}\), where \(\delta _{k,l} \) is the Kronecker symbol.

The next part focuses on the relationship between the partial least squares regression of univariate functional data (FPLS) and the proposed multivariate version (MFPLS) given by Proposition 1. More precisely, we show that the MFPLS regression can be solved by iterating FPLS within a two-stage approach.

2.3.1 Relationship between MFPLS and FPLS

For each j in \(1, \ldots d\), let \(\tilde{w}_1^{(j)}\) be the weight function corresponding to the first PLS component obtained by FPLS regression of Y on dimension \(X^{(j)}\) (Proposition 2 in Preda and Saporta (2002)),

$$\begin{aligned} \tilde{w}_1^{(j)}(t)= \frac{\mathbb {E}(X^{(j)}(t)Y) }{ \sqrt{\int _{\mathcal {I}_j} \mathbb {E}^2(X^{(j)}(s)Y)ds} }, \; t \in \mathcal {I}_j. \end{aligned}$$

Obviously, the functions \(\tilde{w}^{(j)}_1\) and \(w^{(j)}_1\) (as defined in Proposition 1) are related by the following relationship

$$\begin{aligned} w^{(j)}_1=u_{1, j} \tilde{w}^{(j)}_1, \ \end{aligned}$$
(14)

with \(u_{1, j} = \displaystyle \frac{ || \mathbb {E}(X^{(j)}Y) ||_{L_2(\mathcal {I}_j)} }{|||\mathbb {E}(XY)|||} \in \mathbb {R}\)

and \(|| \cdot ||_{L_2(\mathcal {I}_j) }\) stands for the norm induced by the usual inner product in \(L_2(\mathcal {I}_j) \).

Let note that the vector \( u_1=\begin{pmatrix} u_{1,1},..., u_{1,d}\end{pmatrix}^{\mathop {\mathrm {\top }}\limits } \) is such that \( \vert \vert u\vert \vert _{\mathbb {R}^{d} }=1\). Hence, we can establish a relationship between the PLS components of MFPLS and FPLS in the following way. For each j in \(1, \ldots , d\), let denote by \(\xi ^{(j)}_1\) the first PLS component obtained by the FPLS regression of Yon the j-th dimension of X. Then, the first PLS component of the MFPLS of Yon X, \(\xi _1\), is obtained as the first PLS component of the PLS regression of Yon \(\{\xi _{1}^{(1)}, \ldots , \xi _{1}^{(d)}\}\).

Based on the iterative PLS process, that relationship can be applied to the computation of higher-order MFPLS components.

That relationship allows us to define a new methodology for the computation of MFPLS regression when the functional predictor X is approximated into a basis of functions.

2.3.2 Using the basis expansion for the MFPLS algorithm

Under the hypothesis (4), for any \(j = 1, \ldots d\), let denote with \(\Lambda ^{(j)}\) the vector

$$\begin{aligned} \Lambda ^{(j)}= \left( \textrm{F}^{(j)}\right) ^{1/2}a^{(j)} \end{aligned}$$

where \(\left( \textrm{F}^{(j)}\right) ^{1/2}\) is the squared root of the matrix \(\textrm{F}^{(j)}\) and \(a^{(j)}\) is the vector of (random) coefficients of the expansion of \(X^{(j)}\) in the basis of functions \(\{\psi ^{(j)}_1, \ldots , \psi ^{(j)}_{M_j}\}\).

Then, Proposition 2 in Aguilera et al. (2010) makes the MFPLS procedure equivalent to the following algorithm.

MFPLS algorithm

  • Step 0: Let \(\Lambda _{0}^{(j)}=\Lambda ^{(j)}\) for all \(j =1, \ldots , d\) and \(Y_{0}=Y\).

  • Step h, \(h\ge 1\):

    1. 1.

      For each \(j =1, \ldots , d\),

      • define \(\xi ^{(j)}_h\) as the first PLS component obtained by the ordinary PLS regression of \(Y_{h-1}\) on \(\Lambda _{h-1}^{(j)}\),

        $$\begin{aligned} \xi ^{(j)}_{h} = \sum _{k=1}^{M_j}\Lambda ^{(j)}_{h-1, k} \theta _{h,k}^{(j)}, \end{aligned}$$
        (15)

        where \(\theta _h^{(j)} \in \mathbb {R}^{M_j}\) is the associated weight vector.

    2. 2.

      Define the h-th MFPLS component \(\xi _h\) as the first PLS component of the regression of \(Y_h\) on \(\{\xi ^{(1)}_h, \ldots , \xi ^{(d)}_h\}\),

      $$\begin{aligned} \xi _h=\sum _{k=1}^{d}\xi ^{(k)}_{h}u_{h,k}, \end{aligned}$$
      (16)

      where \(u_{h}\in \mathbb {R}^{d}\) is the associated weight vector.

    3. 3.

      • For each \(j=1, \ldots , d\), compute the residuals \(\Lambda ^{(j)}_h\) of the linear regression of \(\Lambda ^{(j)}_{h-1}\) and \(Y_{h-1}\) on \(\xi _h\),

        $$\begin{aligned} \Lambda ^{(j)}_h = \Lambda ^{(j)}_{h-1} - r^{(j)}_h{\xi _{h}}, \end{aligned}$$

        where \( r^{(j)}_h=\displaystyle \frac{\mathbb {E}(\xi _h\Lambda ^{(j)}_{h-1})}{\mathbb {E}(\xi _h^2) } \in \mathbb {R}^{M_j} \).

      • compute the residual \(Y_h\) of the linear regression of \(Y_{h-1}\) on \(\xi _h\),

        $$\begin{aligned} Y_h = Y_{h-1} - c_{h}\xi _{h}, \end{aligned}$$

        where \(c_h = \displaystyle \frac{\mathbb {E}(Y_{h-1}\xi _{h})}{\mathbb {E}(\xi _h^{2})} \in \mathbb {R}\).

  • Go to the next step (\(h = h+1)\).

Remark 3

  1. 1.

    The number of PLS components (h) retained in the approximation of the regression model (9) is usually chosen by cross-validation, optimizing some criteria as the Mean Squared Error (MSE) or, for binary classification, the Area under the ROC Curve (AUC).

  2. 2.

    The approach of Beyaztas and Shang (2022) is an extension of the basis expansion result from Aguilera et al. (2010). It was proposed for one domain definition. Note that our approach is more flexible since it allows different intervals. The case of one domain is then a special case of the proposed methodology (see Sect. 3.1.1 for numerical comparison).

  3. 3.

    Let introduce in the step h - point 3 of the algorithm the computation of functions \(w_h^{(j)}\) and \(\rho _h^{(j}\), \(j = 1,\ldots , d\), as

    $$\begin{aligned} w_h^{(j)}&= u_{h, j} \textrm{H}^{(j)}\theta _{h}^{(j)} \psi ^{(j)}, \\ \rho _h^{(j)}&=\textrm{H}^{(j)}r_h^{(j)}\psi ^{(j)} \end{aligned}$$

    where \( \textrm{H}^{(j)}= \left( \textrm{F}^{(j)}\right) ^{-1/2}\). Then, by Lemma 1, the functions \(\{v_k\}_{k=1}^{h}\) can also be computed through the MFPLS algorithm, allowing to compute the regression coefficient function in (11).

  4. 4.

    Computational details: Let consider \((\mathcal {X}_1, \mathcal {Y}_1), \ldots , \mathcal {(X}_n,\mathcal {Y}_n)\) be an i.i.d. sample of size \(n \ge 1\) of (X, Y). Then, for each \(j = 1, \ldots , d\), the vector \(a^{(j)}\) is represented by the sample \(n\times M_j\) matrix of coefficients \(\textbf{A}^{(j)}\),

    $$\begin{aligned} \textbf{A}^{(j)} = \begin{pmatrix} a^{(j)}_{1,1} &{} \ldots &{} a^{(j)}_{1,l} &{} \ldots &{}a^{(j)}_{1,M_j}\\ \vdots &{} &{} \vdots &{} &{} \vdots \\ a^{(j)}_{k,1} &{} \ldots &{} a^{(j)}_{k,l} &{} \ldots &{}a^{(j)}_{k,M_j}\\ \vdots &{} &{} \vdots &{} &{} \vdots \\ a^{(j)}_{n,1} &{} \ldots &{} a^{(j)}_{n,l} &{} \ldots &{}a^{(j)}_{n,M_j}. \end{pmatrix} \end{aligned}$$

    and

    $$\begin{aligned} \mathbf {\Lambda }^{(j)}= \textbf{A}^{(j)}(\textrm{F}^{(j)})^{1/2}. \end{aligned}$$

    Let define \(\textbf{Y} =(\mathcal {Y}_1, \ldots , \mathcal {Y}_n)^{\mathop {\mathrm {\top }}\limits }\). Then, the matrix version of the MFPLS algorithm (step h) can be rewritten as:

  5. 1

    For each \(j=1, \ldots , d\), define \(\varvec{\xi }_h^{(j)}\in \mathbb {R}^n\) as the first PLS component obtained by the ordinary PLS of \(\textbf{Y}_h\) on \(\mathbf {\Lambda }_{h-1}^{(j)}\)

  6. 2

    The h-th MFPLS \(\varvec{\xi }_h\) is the first component obtained by the ordinary PLS of \(\textbf{Y}_h\) on \(\left( \varvec{\xi }^{(1)}_h, \ldots , \varvec{\xi }^{(d)}_h\right) \).

  7. 3

    For \(j=1, \ldots , d\), the residuals \(\varvec{\Lambda }_h^{(j)}\) are computed by

    $$\begin{aligned} \mathbf {\Lambda }_h^{(j)}= \mathbf {\Lambda }_{h-1}^{(j)}- \varvec{\xi }_h \textbf{r}^{(j)}_h \end{aligned}$$

    with \(\textbf{r}_h^{(j)}=\displaystyle \frac{1}{\varvec{\xi }_h^{\mathop {\mathrm {\top }}\limits } \varvec{\xi }_h}\varvec{\xi }_h^{\mathop {\mathrm {\top }}\limits }\mathbf {\Lambda }^{(j)}_{h-1} \) is the projection coefficient. And the residual \(\textbf{Y}_{h}\) is

    $$\begin{aligned} \textbf{Y}_h= \textbf{Y}_{h-1}- \varvec{\xi }_h\textbf{c}_h \end{aligned}$$

    with \(\textbf{c}_h=\displaystyle \frac{1}{\varvec{\xi }_h^{\mathop {\mathrm {\top }}\limits } \varvec{\xi }_h}\varvec{\xi }_h^{\mathop {\mathrm {\top }}\limits } \textbf{Y}_{h-1} \).

Although the proposed methodology is for regression problems with scalar response, it can be used for binary classification by using the relationship between linear discriminant analysis and linear regression (Aguilera et al. 2010; Preda et al. 2007). The next section addresses a classification application based on PLS regression.

2.3.3 From PLS regression to PLS binary-classification

Using the previous notations, let X be the predictor variable (not necessarily zero-mean) and Y be the response. The binary classification setting assumes that Y is a Bernoulli variable, \(Y \in \{0, 1\}\), \(Y\sim \mathcal {B}(\pi _1)\) with \(\pi _1= \mathbb {P}(Y=1)\). The PLS regression can be extended to binary classification after a convenient encoding of the response.

Let define the variable \(Y^*\) as

$$\begin{aligned} Y^* = \left\{ \begin{array}{ll} \sqrt{\frac{\pi _1}{\pi _0}} &{}\text {, if } Y=0\\ - \sqrt{\frac{\pi _0}{\pi _1}} &{}\text {, if } Y=1, \end{array} \right. \end{aligned}$$
(17)

with \(\pi _0 =1-\pi _1\).

Then, the coefficient function \(\beta \) of the regression of \(Y^{*}\) on X corresponds (up to a constant) to that defining the the Fisher discriminant score denoted by \(\Gamma (X)\):

$$\begin{aligned} \Gamma (X)= \alpha + \langle \langle X,\beta \rangle \rangle , \end{aligned}$$

with \(\alpha \)= -\(\langle \langle \mu , \beta \rangle \rangle \), and \(\mu = \mathbb {E}(X) \in \mathcal {H}\).

Finally, the predicted class \(\hat{Y}_0\) of a new curve \(X_{0}\) is given by

$$\begin{aligned} \hat{Y}_0 = \left\{ \begin{array}{ll} 0&{} \text {if } \Gamma (X_{0}) > 0\\ 1 &{} \text {otherwise. } \end{array} \right. \end{aligned}$$

See for more details Preda et al. (2007).

In this paper we estimate the coefficient function \(\beta \) by the MFPLS approach.

2.4 MFPLS tree-based methods

Alternatives to linear models such Support Vector Machine or SVM (see e.g Rossi and Villa (2006); Blanquero et al. (2019a)), clusterwise regression (see e.g Preda and Saporta (2005); Yao et al. (2011); Li et al. (2021)) could be extended to multivariate functional data. In this section, we present a tree-based methodology (TMFPLS) combined with MFPLS models. The variable selection feature of tree methods is particularly adapted in the framework of multivariate functional data and allows predicting the response throughout more complex but still interpretable relationships. It represents in some way a generalization of the finite-dimensional setting presented in Poterie et al. (2019) to the case of multivariate functional data. The procedure consists in split a node of the tree by successively selecting an optimal discriminant score (according to some impurity measure) among discriminant scores obtained from MFPLS regression models with different subsets of predictors. In the presented methodology, we limit our attention to the case of binary classification (\(Y \in \{ 0, 1\}\) ).

2.4.1 The algorithm

Let consider \((\mathcal {X}_1, \mathcal {Y}_1), \ldots , \mathcal {(X}_n,\mathcal {Y}_n)\) be an i.i.d. sample of size \(n \ge 1\) of (X, Y), where Y is a binary response variable and \(X = (X^{(1)}, \ldots , X^{(d)})\) a multivariate functional one. Moreover, we assume that there exists a well-defined group structure (potentially overlapping) of the dimensions of X, i.e. there exists K subgroups, \(K\ge 1\), \(\mathcal {G}_1, \ldots , \mathcal {G}_K\) of variables \(\{X^{(1)}, \ldots , X^{(d)}\}\). Notice that groups are not necessarily disjoint. These groups of variables define the candidates to be used to split the node of the tree (the score will be calculated with the only variables in the candidate group).

Inspired by Poterie et al. (2019)’s methodology, our algorithm is composed of two main steps. In a nutshell, with the help of MFPLS methodology, the first step provides the results of the splitting according to candidates groups \(\mathcal {G}_1, \ldots , \mathcal {G}_K\) whereas the second one selects the best splitting candidate using an impurity criterion. These two steps are applied to all current nodes (start with the root node containing all the sample – n observations) until the minimum purity threshold is reached.

Consider the current node of the tree to be split:

  • Step 1: The MFPLS candidate scores. For each candidate group of variable \(\mathcal {G}_{i}\), \(i = 1, \ldots , K\), perform MFPLS of Y on \(\mathcal {G}_{i}\) and denote with \(\Gamma ^{i}\) the estimated MFPLS score (prediction) obtained with the group \(\mathcal {G}_{i}\). Then, the result of the split with \(\Gamma ^{i}\) is represented by two new sub-nodes obtained according to the predictions of the observations \((\mathcal {X}_j, \mathcal {Y}_j)\) in the current node: \(\{\Gamma ^{i} (\mathcal {X}) > 0 \}\) and \(\{\Gamma ^{i} (\mathcal {X}) \le 0 \}\).

  • Step 2: Optimal splitting. Select the optimal splitting according to group \(\mathcal {G}^{*}\) which maximizes the decrease of impurity function \(\Delta \mathcal {Q}\) (see (Poterie et al. 2019) for more details),

    $$\begin{aligned} \mathcal {G}^*=\mathop {\mathrm {arg\,max}}\limits _{\mathcal {G}\in \{\mathcal {G}_1, \ldots , \mathcal {G}_K \} }\Delta \mathcal {Q}^{\mathcal {G}}. \end{aligned}$$

    Therefore, the optimal splitting for the current node is the one obtained with the MFPLS score \(\Gamma \) corresponding to \(\mathcal {G}^*\).

A node is terminal if its impurity index is lower than a defined purity threshold. In order to avoid overfitting, a pruning method can be employed. Here, we use the same technique as in Poterie et al. (2019), i.e. the optimal depth of the decision tree (\(m^*\)) is estimated using a validation set.

3 Simulation study

This section deals with finite sample properties on simulated data to evaluate the performances of MFPLS and TMFPLS approaches with competitor methods based on MFPCA. Two different cases are presented. In the first one, all the components \(X^{(j)}\) of X are defined on the same one domain \(\mathcal {I}=[0,T]\), \(T > 0\). In the second case, X is a bivariate functional vector \(X = (X^{(1)}, X^{(2)} )^{\mathop {\mathrm {\top }}\limits }\) with \(X^{(1)}=(X^{(1)}(t))_{t\in \mathcal {I}_1}\) and a two-domain variable \(X^{(2)}=(X^{(2)}(t))_{t\in \mathcal {I}_2\times \mathcal {I}_2}\), where \(\mathcal {I}_1, \mathcal {I}_2 \subset \mathbb {R}\). Thus, in this second one, a sample from the functional variable X corresponds to a set of curves and 2-D images of domains \(\mathcal {I}_1\) and \(\mathcal {I}_2\times \mathcal {I}_2\) respectively.

All computation results reported in this section were obtained using a computer that has a Windows 10 operating system, 11th Gen Intel(R) Core(TM) i7-1165G7 2.80GHz and 16.00Go Go of RAM memory.

3.1 One domain case

3.1.1 Setting 1: scalar response

Since the main concurrent MFPLS was proposed for regression (Beyaztas and Shang 2022), we conduct in this section the regression simulation framework described in Beyaztas and Shang (2022) and compare their method with MFPLS.

Consider the domain \(\mathcal {I}= [0,1]\) and the 3-dimensional functional predictor \(X= (X^{(1)}, X^{(2)}, X^{(3)} )^{\mathop {\mathrm {\top }}\limits } \):

$$\begin{aligned} X^{(j)}(t)=\sum _{k=1}^5 \gamma _k \upsilon _k(t),\; \text { } t\in \mathcal {I},\, j= 1, 2, 3, \end{aligned}$$

with \(\gamma _k \sim \mathcal {N}(0, 4k^{-3/2} ) \) and \(\upsilon _k(t) = \sin {k\pi t}- \cos {k \pi t}\), \(k=1, \ldots , 5\).

The functional coefficient \(\beta \) is defined by

$$\begin{aligned} \beta (t) =\begin{pmatrix} \sin (2\pi t), \sin (3\pi t), \cos (2\pi t) \end{pmatrix}^{\mathop {\mathrm {\top }}\limits }. \end{aligned}$$

Then, the regression model generating the data is given by

$$\begin{aligned} Y= \langle \langle X, \beta \rangle \rangle + \epsilon , \end{aligned}$$

where \(\epsilon \sim \mathcal {N}(0, \sigma ^2)\).

We define the noise variance as

$$\begin{aligned} \sigma ^2= \frac{\mathbb {E}(\langle \langle X, \beta \rangle \rangle ^2) }{\text {SNR} }, \end{aligned}$$

where SNR is the signal-to-noise ratio. We consider 5 values of SNR: SNR \(\in \{0.5, 1.62, 2.75, 3.88, 5\} \).

The approach proposed in Beyaztas and Shang (2022) is a generalization of the result in Aguilera et al. (2010) to the multivariate case (MFPLS_D). It exploits an equivalence between the PLS of multivariate functional covariates and ordinary PLS of the projection scores of covariates in basis functions. Our method has a different procedure, as we compute multivariate PLS components using the univariate PLS components (see Sect. 2.3.2).

As in Beyaztas and Shang (2022) we use 200 equidistant discrete times points on \(\mathcal {I}\) where raw data of X are observed, and 400 independent copies of X are simulated. Among these copies, \(50\%\) are used for learning and the remaining for validation.

We also compare our method to principal component regressionFootnote 1(MFPCR). A number of 200 replications of the three different inference procedures are done.

The number of components in all approaches is chosen by 10-fold cross-validation procedures. To transform the raw data into functions, smoothing is used with 20 quadratic splines basis functions.

Performances of the three approaches are measured by the mean squared prediction error (MSPE):

$$\begin{aligned} \text {MSPE}= \frac{1}{200}\sum _{i\in V_{\text {set} }}(Y_i - \hat{Y}_i)^2 \end{aligned}$$

with \(\hat{Y}_i\) is the predicted response for the \(i-th\) observation in the validation sample (\(V_\text {set}\)), \(Y_i\) the true value.

The results of the experiences are summarized in Table 1.

All methods provide comparable results. Although the proposed method (MFPLS) is more time-consuming (around 60 milliseconds), Table 1 shows that MFPLS and MFPLS_D give similar performances.

3.1.2 Setting 2: binary response

In the following experiment, we focus on a classification problem with one-dimensional domain \(\mathcal {I}= [0,1]\).

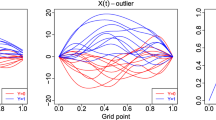
Here, we build two different classes (Class 1 and Class 2) of functional data, visualized in Fig. 2. They are related to some pattern (a shape with peaks) appearing at some locations of the curves. This simulation setting is a kind of visual pattern-recognition problem (Fukushima 1988). The pattern of interest is identifiable by eyes but challenging to detect with algorithms. An example may be epileptic spikes detection in electroencephalogram recordings (see for instance Abd El-Samie et al. (2018) for more details).

The performances of MFPLS, TMFPLS, and linear discriminant analysis on principal component scores (MFPCA-LDA) are compared in this simulation study.

Consider the domain \(\mathcal {I}=[0, 1]\), and the 2-dimensional functional predictor \(X=(X^{(1)}, X^{(2)})^{\mathop {\mathrm {\top }}\limits } \):

$$\begin{aligned}&X^{(1)}(t) = \sum _{s=1}^4 a_{s} h_s(t) + \epsilon ^{(1)}(t)\;,\\&X^{(2)}(t)=\sum _{s=1}^4 (1- a_{s}) h_s(t) + \epsilon ^{(2)}(t) , \end{aligned}$$

where

  • \(a=\begin{pmatrix} a_1&a_2&a_3&a_4 \end{pmatrix}^\top \) is a random vector taking values in \(\{ -1, 0, 1 \}^4\). Note that in this case, a can possibly take \(3^4=81\) different values, which are denoted by \(V_1, \ldots , V_{81}\).

  • \(h_1, \ldots , h_4\) are triangle functions:

    $$\begin{aligned} h_s(t)= \left( 1- 10|t- u_s|\right) _+, s=1, \ldots , 4, \end{aligned}$$

    with \(u_1=0.2\), \(u_2=0.4\), \(u_3=0.6\), and \(u_4=0.8\).

  • \(\epsilon ^{(1)}\) and \(\epsilon ^{(2)}\) are two independent white noises functions with variance \({Var}(\epsilon ^{(j)}(t))=0.20\), for \(j=1, 2\) and \(t\in \mathcal {I}\).

We consider that \(V_1=\begin{pmatrix} 1&1&0&0 \end{pmatrix}^\top \), \(V_2=\begin{pmatrix} 0&1&1&0 \end{pmatrix}^\top \), \(V_3=-V_1\) and \(V_4=-V_2\). The vectors \(V_5, \ldots , V_{81}\) are the 76 other possible values of a. Let the response variable Y be

$$\begin{aligned} Y = \left\{ \begin{array}{ll} 1 &{} \text{ if } a \in \{V_1, V_2, V_3, V_4 \} {\textbf { }} \\ 0 &{} \text{ if } a \in \{V_5, \ldots , V_{81}\} \end{array} \right. \end{aligned}$$

If \(a_s\ne 0\), \(s=1, \ldots , 4\), this means we observe a peak on \(X^{(1)}\) at the position \(t=u_s\), which could be positive (\(a_s=1\)) or negative (\(a_s=-1\)). Then, \(Y=1\), if two consecutive peaks (both negatives or positives) occur at the beginning of \(X^{(1)}\). Namely the peaks of interest are observed at \(t=0.2, 0.4\) or \(t=0.4, 0.6\). The four cases where \(Y=1\) are illustrated in Fig. 1.

Fig. 1
figure 1

Examples of \(N=25\) realizations of X for \(Y=1\) (Setting 2)

Full size image
Fig. 2
figure 2

Example of curves X in Setting 2, under both scenarios. Class 1 (red curves, \(Y=1\)) and class 0 (blue curves, \(Y=0\)). Scenario 2 (right) shows more heterogeneity in class 1 compared to Scenario 1 (left)

Full size image

According to the distribution of a, we study two scenarios (see Fig. 2):

  • Scenario 1: Positive peaks. \(\mathbb {P}(a=V_1)=\mathbb {P}(a=V_2)=\frac{1}{4}\) and \(\mathbb {P}(a=V_3)=\mathbb {P}(a=V_4)=0\). \(\mathbb {P}(a=V_5)= \mathbb {P}(a=V_6)= \ldots = \mathbb {P}(a=V_{81})=\frac{1}{162}\).

  • Scenario 2: Positive and negative peaks. \(\mathbb {P}(a=V_1)=\mathbb {P}(a=V_2)=\mathbb {P}(a=V_3)= \mathbb {P}(a=V_4)=\frac{1}{8}\). \(\mathbb {P}(a=V_5)= \mathbb {P}(a=V_6)= \ldots = \mathbb {P}(a=V_{81})=\frac{1}{162}\).

Remark 4

  • In the two scenarios \(\mathbb {P}(Y=1)=\mathbb {P}(Y=0)=0.5\).

  • In Scenario 1, the curves X where \(Y=1\) are composed exclusively of the realizations of events \(V_1\) and \(V_2\); in \(X^{(1)}\), they have consecutive positive peaks at \(t=0.2, 0.4\), or at \(t=0.4, 0.6\).

  • Scenario 2 is more complex. The four cases: \(V_1\), \(V_2\), \(V_3\) and \(V_4\) have the same probability to occur. In this case, the curves X for \(Y=1\) are more heterogeneous compared to Scenario 1. The four cases, represented in Fig. 1, theoretically have the same proportion in the sample.

The functional form of X is reconstructed using 20 quadratic spline functions with equidistant knots. For a given scenario, we did 200 experiments. At each, 75 % of the data are used for learning and 25 % for validation.

Table 1 Means and standard deviations (in parentheses) of MSPEs obtained and estimation times in the experiments
Full size table

The number of components for the MFPLS (in both models) is chosen by 10-fold cross-validation. Moreover, MFPCA-LDA is performed for comparison. It consists, firstly in the estimation of principal components (using Happ (2017) package) and then applying linear discriminant analysis to them. As in the previous model, the number of components is chosen by 10-fold cross-validation. We also compute the approach proposed in Beyaztas and Shang (2022) (MFPLS\(\_\)D). To use it for classification, the transformation proposed in Sect. 2.3.3 is employed. The number of components in MFPLS\(\_\)D is also chosen by 10-fold cross-validation.

By defining the set of groups as \(\mathcal {G}_1=1, \mathcal {G}_2=2, \mathcal {G}_{3}=\{1,2\}\), the decision tree looks for the best splits among those obtained using separately univariate functions and the ones obtained using both dimensions. In order, to have an estimation of the optimal depth \(m^*\), we randomly take 75% of learning data to train an intermediate TMFPLS, and 25% for pruning (by AUC metric). This procedure is repeated 10 times and \(\hat{m}^*\) is the frequent value among the 10 repetitions. The final tree is then trained on the whole learning data, with the maximum tree depth fixed to \(\hat{m}^*\), and the minimum criterion of impurity at 1%.

3.1.3 Results

Table 2 Results of Setting 2. For the two scenarios, the presented metrics (AUC, Sensibility, etc.) are the means and the standard deviations (in parentheses) of those obtained in the experiences
Full size table

In Scenario 1, Table 2 shows that AUC differences are about 8% between MFPLS and TMFPLS. Furthermore, MFPCA-LDA and MFPLS\(\_\)D are competitive with MFPLS. Table 2 also exhibits that the training procedure of TMFPLS is time-consuming compared to the other methods, about 66 times more than the time for training MFPLS. This can be explained by the fact that at each split in the tree, we used a cross-validation procedure to choose the number of components. Also, the results clearly show that MFPLS\(\_\)D is the fastest method.

Scenario 2 shows more differences between the methods: MFPLS, MFPLS\(\_\)D and MFPCA-LDA are non-effective compared to TMFPLS. Hence, TMFPLS outperforms these methods in a complex task classification such as Scenario 2. It is worth noting that in this case, the (mean) time for the estimation of TMFPLS has significantly increased compared to Scenario 1.

This is because the estimated trees in Scenario 1 have fewer ramifications than the estimated ones in Scenario 2. As an illustration, we can refer to Figs. 3 and 5, which represent examples of trees estimated respectively from Scenario 1 and Scenario 2. These trees are randomly selected among the 200 estimated for each scenario. Moreover, Figs. 4 and 6 present the associated discriminant functional coefficients used for splitting rules in the trees. We provide insight on how to interpret them.

In Scenario 1, the tree uses in the first splitting rule (depth=0) a coefficient function that only depends on the first dimension. The fact that this function has a negative peak at \(t=0.4\) can be interpreted as if a curve X has a low value of \(X^{(1)}\) at this region, it will belong to the left node of depth\(=1\). Note that this node has exclusively curves of class \(Y=0\). This makes sense since in Scenario 1, X curves where \(Y=1\) are defined as having peaks in \(X^{(1)}\) at points (0.2, 0.4) or (0.4, 0.6). In other words, a high value at \(t=0.4\) characterizes the class \(Y=1\).

At the depth\(=1\), the coefficient function depends only on the second dimension. The resulting separation doesn’t lead to total purity in the node, however, the coefficient states that curves X in the right node with high values of \(X^{(2)}\) at (0.2, 0.4) are more frequent in class \(Y=0\). This last rule is not senseless, since Fig. 1 shows that curves X for \(a=V_1\) don’t have peaks in \(X^{(2)}\) at \(t=0.2\) and \(t=0.4\).

Using only these two coefficients, we can say that for curve X if at \(t=0.4\) \(X^{(1)}\) doesn’t have a peak, X is of class \(Y=0\). However, if \(X^{(1)}\) has a peak at \(t=0.4\), and \( X^{(2)}\) has small values at regions (0.2, 0.4), X is probably of class \(Y=1\). The other coefficient functions help to refine the predictions by giving more and more precise rules at each step.

Fig. 3
figure 3

Example of post-pruned tree in Scenario 1(Setting 2). Dimension(s) used for the splitting is in red

Full size image
Fig. 4
figure 4

Scenario 1: TMFPLS estimated coefficient functions (from left to right) at each split

Full size image

In the scenario 2, the goal is to estimate a more complex rule of classification, since the amplitudes (\(a_1, a_2, a_3, a_4\)) can be either positive or negative for curves X of class \(Y=1\). As already mentioned, compared to Scenario 1, the example estimated tree (Fig. 5) has more ramifications. As in the classical tree, it is challenging to give a clear interpretation of TMFPLS in a such case, especially, when using only Fig. 5 and Fig. 6. There are numerous coefficient functions that we have to take into account. One need, which we should address in the future, is to provide more insightful visualizations in this case. However, this tree shows how TMFPLS can be flexible and can therefore be used in a complex classification framework.

Fig. 5
figure 5

Example of post pruned tree in Scenario 2( Setting 2)

Full size image
Fig. 6
figure 6

Scenario 2: Coefficient functions in the estimated tree

Full size image

3.2 Different domains case

3.2.1 Setting 3: Image and time series classification

Our approach allows the use of images and time series simultaneously. In this part, we highlight the use of various domains instead of focusing only on one dimension domain.

Framework Consider the domains \(\mathcal {I}_1=[0, 50]\), \(\mathcal {I}_2=[0,1] \times [0,1]\), and \(X=(X^{(1)}, X^{(2)})^{\mathop {\mathrm {\top }}\limits } \):

$$\begin{aligned} X^{(1)}(t)&=Z_1h(t) + \epsilon ^{(1)}(t)\text {, } t \in \mathcal {I}_1 \\ X^{(2)}(t)&= Z_2q(t) + \epsilon ^{(2)}(t) \text {, }t \in \mathcal {I}_2. \end{aligned}$$

The noise term \(\epsilon =(\epsilon ^{(1)}, \epsilon ^{(2)})^{\top }\) is composed of two independent dimensions: the first one \(\epsilon ^{(1)}\) is a white noise of variances \(\sigma ^2\), while the second one \(\epsilon ^{(2)}\) is a gaussian random field. \(\epsilon ^{(2)}\) is associated with a Matern covariance model, with sill, range, and nugget parameters equal to 0.25, 0.75, and \(\sigma \), respectively (see (Ribeiro et al. 2001) for more details). The variables \(Z_1\) and \(Z_2\) are Bernoulli variables with values in \(\{0,1\}\). The (deterministic) functions h and q are given by:

$$\begin{aligned}&\; h(t) = 3.14 \left( 1-\frac{\vert t-10\vert }{4}\right) _+ \\&q(s) = -2\log \left( \sqrt{(s^{(1)}-0.5)^2 + (s^{(2)}-0.5)^2} \right) \end{aligned}$$

where \((.)_+\) denotes the positive part, \(t\in \mathcal {I}_1\), \(s=(s^{(1)}, s^{(2)}) \in \mathcal {I}_2 \).

The response variable Y is constructed as follows:

$$\begin{aligned} Y = \left\{ \begin{array}{ll} 1 &{} \text{ if } Z_1Z_2 =1 \\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

In other words, \(Y=1\) if and only if both variables \(Z_1\), \(Z_2\) are simultaneously 1 (see Fig. 7).

Fig. 7
figure 7

Construction of class 1 (\(Y=1\)), curve X(t) in Setting 3, under SNR=0.5 If Y=0, X is random noise \(\epsilon \) (left figures)

Full size image

50 equidistant discrete points and \(50\times 50\) pixels are observed respectively for the first and the second dimension. To get the functional form of X, the first and second components are projected respectively into the space spanned by 20 quadratic spline functions, and the 4 two-dimensional splines (Happ 2017).

The variances of the functions q and h along their domain are approximately 1. The signal-to-noise ratio (SNR) is then (approximately) the same on both dimensions and depends only on \(\sigma \)

$$\begin{aligned} \text {SNR}=\frac{1}{\sigma ^2}. \end{aligned}$$

By controlling the parameter \(\sigma \), we consider several values of SNR: 0.5, 0.7, 1.2, 2.1 and 4.9.

We set \(\mathbb {P}(Z_1=1)=\mathbb {P}(Z_2=1)=3/4\), then \(\mathbb {P}(Y=1) = 9/16\simeq 0.56\). A set of 500 curves are simulated: 75% are used for learning, while the remaining 25% is for the validation set.

For each value of SNR, three MFPLS models are computed. The two first use exclusively one dimension of the predictor: MFPLS(1) uses \(X^{(1)}\) and MFPLS(2) \(X^{(2)}\). The third one uses both functional components (MFPLS). The purpose is to assess the amount of performance using one-dimensional domain and multiple-dimensional domain. We also compute MFPCA-LDA for comparison purposes, the principal component analysis is performed by Happ (2017) package.

The number of components in the two approaches: MFPLS and MFPCA-LDA are chosen by 10-fold cross-validation using AUC. We did 200 simulations: models are assessed by AUC on the validation set.

Table 3 Means and the standard deviations (in parentheses) of the obtained AUC on the 200 experiences
Full size table

Table 3 shows that MFPLS gives better results than MFPCA-LDA for the lowest value of SNR, and the difference between the methods disappears with the increase of SNR. Using partially the data (models MFPLS(1) and MFPLS(2)) to predict the class variable is less efficient than using both dimensions. Namely, Table 3 clearly shows the advantage of using both of the components of the functional variables.

This simulation demonstrates the ability of our method to classify different domain data. In addition, as it’s specially designed for supervised learning, it can be more effective than principal component analysis-based techniques such as MFPCA-LDA in a noisy context.

4 Real data application: Multivariate time series classification

In this section, we compare the proposed methods with black box models (LSTM, Random Forest, etc...) on benchmark data (Table 4, from Table 1 of (Karim et al. 2019)), ranging from online character recognition to activity recognition. These data, suitable for multivariate functional time series data and binary classification, have been used by various works to assess new methodologies (see e.g. Pei et al. (2017); Schäfer and Leser (2017)).

Table 4 Datasets summary. T denotes the number of sampling time points, d: the data dimensions, and Ratio of the train-test split. All datasets are available in https://github.com/titu1994/MLSTM-FCN/releases/tag/v1.0
Full size table
Table 5 Comparison of MFPLS, TMFPLS, and other non-FDA classification methods by their accuracies (%) in the test set. Bold metrics correspond to the best accuracy for each dataset, and underline indicate the second best. [1]: Tuncel and Baydogan (2018), [2]: Schäfer and Leser (2017), [3]:RF, [4]: SVM-Poly, [5]: DTW
Full size table

The proposed models (MFPLS, TMFPLS) are compared with discriminant analysis (MFPCA-LDA) on scores obtained by Multivariate functional principal component analysis (Happ 2017), and non-functional models; the Long Short-Term Memory Fully Convolutional Network (LSTM-FCN) and Attention LSTM-FCN (ALSTM-FCN), proposed by Karim et al. (2019). We also present the benchmark of these last models named SOTA, which gives the best performances among Dynamic time warping (DTW), Random Forest (RF), SVM with a linear kernel, SVM with a 3rd-degree polynomial kernel (SVM-Poly), and other state-of-the-art methods (see Karim et al. (2019) for more details).

The challenge is to show that our models based on regression can be competitive. The splitting of the data into training and test samples (see Table 4) is that of Karim et al. (2019). The different models mentioned above are compared by the accuracy metric, the rate of well-predicted classes obtained on the test datasets.

4.1 Choice of hyperparameters

As for some datasets (CMUsubject, KickVsPunch, etc...), the sample size is small (less than 50 observations, see Table 5) the number of components in MFPLS and MFPCA is chosen by 20-fold cross-validation (contrary to 10-fold in previous parts). The maximum tree depth \(m^*\) is an important hyperparameter. It may significantly affect the performance of our tree-based model, as it helps to prevent the overfitting of TMFPLS. We estimate \(m^*\) by cross-validation alike procedure. More precisely, we randomly take 75% of learning data to train an intermediate TMFPLS and 25% for pruning. This procedure is repeated 10 times and let \(\hat{m}^*\) be the most occurred number from these 10. The final tree is then trained on the whole learning data, with the maximum tree depth fixed to \(\hat{m}^*\). As in the previous section, group are defined as \(\mathcal {G}_1=1, \ldots , \mathcal {G}_d=d, \mathcal {G}_{d+1}=\{1,..., d \} \), to see whether FPLS gives better splitting than MFPLS. Testing several combinations of dimensions takes time, the ideal choice of groups would be guided by some prior knowledge of the data structure.

Two strategies are used for the number of components in the decision tree: TMFPLS H-1 denotes the decision tree where only one component in MFPLS is used, and TMFPLS H-CV is the decision tree where the number of components is estimated by 20-fold cross-validation as in MFPLS. The first tree is faster to train than the second one, and it’s less likely to overfit the data. However, the second one is expected to be a more efficient model, since it is able to estimate more complex coefficient functions \(\beta \).

For all functional data methods, we use 30 B-Splines basis functions by dimension to have a functional representation (Ramsey and Silverman 2005) of each dataset (see Fig. 8 in Appendix Appendix B for the smoothed functions). This number of basis functions is chosen arbitrarily small compared to the minimum number of discrete time points (117) of the original raw datasets.

4.2 Results

Table 5 shows that, in most cases, our models (MFPLS, TMFPLS) and MFPCA-LDA are competitive with that of Karim et al. (2019) and SOTA. In about half of the cases, TMFPLS or MFPLS reach the highest or the second-highest accuracy. TMFPLS is generally more performing than MFPLS. Note also that MFPCA-LDA is competitive with the proposed methodologies. The main difference between MFPCA-LDA and MFPLS is that for the first one, components are searched with no regard to the response variable Y.

For the KickVsPunch dataset, the performance of TMFPLS H-1 is better than the one by TMFPLS H-CV. This is because TMFPLS H-CV could easily overfit when the training sample is small (\(\text {N}_{\text {Train}}<20\)). This is one of the well-known drawbacks of the decision tree. Tuning hyperparameters is then crucial and may have a huge impact on performances.

5 Conclusion and discussion

Statistical learning of multivariate functional data evolving in complex spaces leads to challenging questions that need the development of new methods and techniques. In this paper, we are interested in some of these methods in the case of different functional domain settings. Namely, we propose least squares regression and classification models for multivariate functional predictors. The first classification model relies on the partial least square (PLS) regression (MFPLS) while the second one (TMFPLS) combines PLS with a decision tree. Technical arguments on the PLS methods are given. The finite sample performance of the regression and classification models are assessed by simulations and real data (EEG, Ozone, wafer,...) applications where we compare the proposed methods with some benchmarks, in particular a PLS regression model of the literature (Beyaztas and Shang 2022) and well known principal components regression and some machine learning models.

A main specificity of our proposed models is that the multivariate functional data considered are defined on different domains compared to the literature. This allows dealing with heterogeneous types of data (e.g. images, time series, etc.) with a potentially large number of applications as shown by the given classification case study on images and functional time series. We also give a relationship between the partial least square of multivariate functional data with its univariate counterparts. To the best of our knowledge, the proposed tree classification model is new.

The finite sample properties show our models’ competitiveness with regard to some existing methods. The multivariate time series classification case study highlights the competitive performance of MFPLS and TMFPLS with black-box models (LSTM, RF,...) on benchmark data. These performances may be improved by using prior knowledge of the benchmark data (groups of variables, suitable preprocessing,...).

In this paper we focus on continuous functional predictors, a possible extension of the proposed models would be including additional type (e.g, qualitative) of covariates.

The EEG and ozone data considered in the finite sample study may have spatial dependence. The classification approaches seem not affected by these data dependencies, but this deserves future investigation.

As in a number of functional data analysis, a tuning parameter related to the number of basis functions used to smooth the raw data or reduce the dimension of the functional space, has to be selected. In this paper, we fix or use a cross-validation approach for the choice of this parameter. Other alternatives may be based on bootstrap methods or criteria like AIC, BIC.

This work highlights the good behavior of TMFPLS and a way to deal with non-linearity in classification problems of multivariate functional data. However, with heterogeneous high-dimensional data, tree-based methods may be challenging. An alternative method could be cluster-wise regression techniques by extending the univariate case studied by Preda and Saporta (2005) to our context. Some other methods as lasso classification techniques can also be explored (see e.g Godwin (2013)).