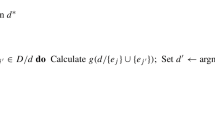1 Introduction

The usual aim of the so-called “optimal” design of experiments is to perform experimental trials in a way that enables efficient estimation of the unknown parameters of an underlying statistical model (see, e.g., Fedorov 1972; Pázman 1986; Pukelsheim 2006; Atkinson et al. 2007; Goos and Jones 2011; Pronzato and Pázman 2013). The literature provides optimal designs in analytical forms for many specific situations; for a given practical problem at hand, however, analytical results are often unavailable. In such a case, it is usually possible to compute an optimal or nearly optimal design numerically (e.g., Chapter 4 in Fedorov 1972, Chapter 5 in Pázman 1986, Chapter 12 in Atkinson et al. 2007, and Chapter 9 in Pronzato and Pázman 2013).

In this paper, we propose a simple algorithm for solving one of the most common optimal design problems: computing efficient approximate designs for experiments with uncorrelated observations and several independent factors. The proposed algorithm employs a specific strategy to adaptively explore the grid of factor-level combinations without the need to enumerate all elements of the grid. The key idea of this algorithm is to form exploration sets composed of star-like subsets and other strategically selected points; therefore, we refer to this algorithm as the “galaxy” exploration method (GEX).

If the set of all combinations of factor levels is finite and not too large, it is possible to use many available efficient and provably convergent algorithms to compute an optimal design (e.g., those of Fedorov 1972; Atwood 1973; Silvey et al. 1978; Böhning 1986; Vandenberghe et al. 1998; Uciński and Patan 2007; Yu 2011; Sagnol 2011; Yang et al. 2013; Harman et al. 2020). However, in the case of multiple factors, each with many levels, the number of factor-level combinations is often much larger than the applicability limit of these methods.

The main advantage of GEX is that it can be used to solve problems with an extensive number of combinations of factor levels, e.g., \(10^{15}\) (5 factors, each with 1000 levels), and obtain an optimal design in several seconds. Note that factors with large, yet finite, numbers of levels often correspond to practical requirements on the factor resolution. Even in the theoretical case of fully continuous factors, GEX can be applied; the factors can simply be densely discretized (to, say, 3 decimal places). We will show that this straightforward approach usually outperforms intricate state-of-the-art methods that can choose the factor levels anywhere in given continuous intervals (e.g., those of Pronzato and Zhigljavsky 2014; Duarte et al. 2018; Lukemire et al. 2019; Xu et al. 2019; García-Ródenas et al. 2020). As a byproduct, we demonstrate that it is rarely necessary to discretize each factor to an enormous number of levels to admit an approximate design that is almost perfect compared to the optimum achievable with fully continuous factors.

Let k be the number of experimental factors. Suppose that for any trial, the factors can be independently chosen from predefined finite sets \({\mathfrak {X}}_1,\ldots ,{\mathfrak {X}}_k \subset {\mathbb {R}}\) of permissible levels, without mutual constraints. The design space \({\mathfrak {X}}\) is then the set of all combinations of the factor levels, formally, \({\mathfrak {X}}= {\mathfrak {X}}_1 \times \cdots \times {\mathfrak {X}}_k\). Geometrically, \({\mathfrak {X}}\) is a finite grid of “design points” \(\mathbf{x}=(x_1,\ldots ,x_k)^T\).

An approximate experimental design is any probability measure \(\xi \) on \({\mathfrak {X}}\). For \(\mathbf{x}\in {\mathfrak {X}}\), the interpretation of \(\xi (\mathbf{x})\) is the proportion of trials to be performed at \(\mathbf{x}\). The value \(\xi (\mathbf{x})\) is often referred to as the “weight” of \(\mathbf{x}\). The set of all design points \(\mathbf{x}\) with nonzero weights is called the support of \(\xi \) and is denoted by \(\mathrm {supp}(\xi )\).

In practical experiments, an approximate design \(\xi \) must be converted into an “exact” design of size N determined by the available experimental resources.Footnote 1 The exact design assigns nonnegative integer numbers \(n_1,\ldots ,n_s\) of trials to properly selected points \(\mathbf{x}_1,\ldots ,\mathbf{x}_s\) such that \(\sum _{i=1}^s n_i=N\). A standard strategy is to select the points \(\mathbf{x}_1,\ldots ,\mathbf{x}_s\) that form the support of an optimal or nearly optimal approximate design \(\xi \) and then compute the integer numbers of trials through appropriate “rounding” of the numbers

$$\begin{aligned} N\xi (\mathbf{x}_1),\ldots ,N\xi (\mathbf{x}_s); \end{aligned}$$

see, e.g., Pukelsheim and Rieder (1992). Alternatively, since the support size s is usually small, it may be feasible to compute the integers \(n_1,\ldots ,n_s\) by specialized procedures for optimal exact designs (e.g., Chapter 12 of Atkinson et al. 2007) restricted to \(\mathrm {supp}(\xi )\).

Computational strategies employing optimal approximate designs lead to exact designs that are typically very efficient (albeit not perfectly optimal) within the class of all exact designs of size N on the full \({\mathfrak {X}}\), especially when N is large. Importantly, the approximate design approach leads to an optimization problem that is generally much simpler than the problem of computing a perfectly optimal exact design of a given size N. Moreover, the approximate optimal design, once computed, can be rounded to an exact design of any size. In addition, the optimal approximate design can be utilized to provide informative lower bounds on the quality of candidate exact designs.

In the rest of this paper, we will use the term “design” specifically to refer to an approximate experimental design.

The quality of a design \(\xi \) is usually expressed as a function of the normalized information matrix

$$\begin{aligned} \mathbf{M}(\xi )=\sum _{\mathbf{x}\in {\mathfrak {X}}} \xi (\mathbf{x}) \mathbf{f}(\mathbf{x})\mathbf{f}^T(\mathbf{x}), \end{aligned}$$
(1)

where \(\mathbf{f}: {\mathfrak {X}}\rightarrow {\mathbb {R}}^m\), \(m \ge 2\), is known. To avoid uninteresting pathological situations, we will assume that \(\mathbf{f}(\mathbf{x}_1),\ldots ,\mathbf{f}(\mathbf{x}_m)\) are linearly independent for some \(\mathbf{x}_1,\ldots ,\mathbf{x}_m \in {\mathfrak {X}}\). An information matrix of the form given in (1) is typical of models with independent, real-valued observations with nonzero variance, where the stochastic distribution of each observation y depends on the design point \(\mathbf{x}\) chosen for the corresponding trial as well as on the unknown m-dimensional vector \(\theta \) of model parameters.

For linear regression, that is, if \(\mathrm {E}(y(\mathbf{x}))=\mathbf{h}^T(\mathbf{x})\theta \) and \(\mathrm {Var}(y(\mathbf{x}))=\sigma ^2/w(\mathbf{x})\), where \(\mathbf{h}:{\mathfrak {X}}\rightarrow {\mathbb {R}}^m\) and \(w: {\mathfrak {X}}\rightarrow (0,\infty )\) are known and \(\sigma ^2 \in (0, \infty )\) may be unknown, we have

$$\begin{aligned} \mathbf{f}(\mathbf{x})=\sqrt{w(\mathbf{x})}\mathbf{h}(\mathbf{x}). \end{aligned}$$

However, if \(\mathrm {E}(y(\mathbf{x}))=\eta (\mathbf{x},\theta )\), where \(\eta : {\mathfrak {X}}\times {\mathbb {R}}^m \rightarrow {\mathbb {R}}\) is nonlinear in \(\theta \), the situation is generally much more difficult. In this paper, we adopt the usual simplification, called the approach of “local” optimality, which makes use of a “nominal” parameter \(\theta _0\) that is assumed to be close to the true value (see, e.g., Chernoff 1953 or Chapter 17 in Atkinson et al. 2007 and Chapter 5 in Pronzato and Pázman 2013). If, for each \(\mathbf{x}\in {\mathfrak {X}}\), the observation \(y(\mathbf{x})\) is normally distributed with a possibly unknown constant variance \(\sigma ^2\) and \(\eta (\mathbf{x},\cdot )\) is differentiable in \(\theta _0\), then the approach of local optimality leads to

$$\begin{aligned} \mathbf{f}(\mathbf{x}) = \mathbf{f}(\mathbf{x}, \theta _0) = \left. \frac{\partial \eta (\mathbf{x},\theta )}{\partial \theta } \right| _{\theta = \theta _0} \end{aligned}$$

and

$$\begin{aligned} \mathbf{M}(\xi ) = \mathbf{M}(\xi , \theta _0) = \sum _{\mathbf{x}\in {\mathfrak {X}}} \xi (\mathbf{x}) \mathbf{f}(\mathbf{x},\theta _0) \mathbf{f}^T(\mathbf{x},\theta _0). \end{aligned}$$

For a generalized linear model (GLM) for which the mean value of the observations is \(\eta (\mathbf{x},\theta )=g^{-1}(\mathbf{h}^T(\mathbf{x})\theta )\), where \(g: {\mathbb {R}}\rightarrow {\mathbb {R}}\) is a strictly monotonic and differentiable link function and \(\mathbf{h}: {\mathfrak {X}}\rightarrow {\mathbb {R}}^m\) is known, we have

$$\begin{aligned} \mathbf{f}(\mathbf{x}) = \mathbf{f}(\mathbf{x}, \theta _0) = \sqrt{w(\mathbf{x},\theta _0)} \mathbf{h}(\mathbf{x}) \end{aligned}$$

for some \(w:{\mathfrak {X}}\times {\mathbb {R}}^m \rightarrow (0,\infty )\). In Table 1, we provide the form of w for several common classes of GLMs (for more details on computing optimal designs in GLMs, see, e.g., Khuri et al. 2006; Atkinson and Woods 2015). Since in the approach of local optimality, the nominal parameter \(\theta _0\) is treated as a constant, we henceforth write \(\mathbf{f}(\mathbf{x})\) and \(\mathbf{M}(\xi )\) instead of \(\mathbf{f}(\mathbf{x}, \theta _0)\) and \(\mathbf{M}(\xi , \theta _0)\), respectively, for both linear and nonlinear models.

Table 1 Selected GLM classes and the corresponding functions \(w(\mathbf{x},\theta _0)\). The symbol f denotes the standard normal density, and F denotes the standard normal cumulative distribution function
Full size table

The size of an information matrix (and, implicitly, the quality of the corresponding design) is measured in terms of an optimality criterion \(\varPhi \). For clarity, we will focus on the most common criterion of D-optimality, but the method proposed in this paper can be trivially adapted to a large class of criteria (cf. Sect. 4). The D-optimal design problem is to find a design \(\xi ^*\) that maximizes

$$\begin{aligned} \varPhi (\mathbf{M}(\xi )) = \left\{ \det (\mathbf{M}(\xi ))\right\} ^{1/m} \end{aligned}$$

over the set \(\Xi \) of all designs. The D-optimal design minimizes the volume of the confidence ellipsoid for the vector of unknown parameters.Footnote 2 The criterion \(\varPhi \) is concave, positive homogeneous and Loewner isotonic on the set of all \(m \times m\) nonnegative definite matrices. Note also that the set \(\Xi \) is convex and compact, that is, the problem of D-optimal design is convexFootnote 3 and always has at least one optimal solution. The information matrix of all D-optimal designs is nonsingular and unique, although for some models, even some that appear in practice, the D-optimal design itself is not unique.

The D-efficiency of a design \(\xi \) relative to a design \(\zeta \) with \(\varPhi (\mathbf{M}(\zeta ))>0\) is defined as \(\mathrm {eff}(\xi |\zeta )=\varPhi (\mathbf{M}(\xi ))/\varPhi (\mathbf{M}(\zeta ))\). The D-efficiency of a design \(\xi \) (per se) means the D-efficiency of \(\xi \) relative to the D-optimal design \(\xi ^*\). The D-efficiency of \(\xi \) with nonsingular \(\mathbf {M}(\xi )\) satisfies (see, e.g., Pukelsheim 2006, Section 5.15)

$$\begin{aligned} \mathrm {eff}(\xi |\xi ^*) \ge \frac{m}{\max _{\mathbf{x}\in {\mathfrak {X}}} d_\xi (\mathbf{x})}, \end{aligned}$$
(2)

where \(d_\xi (\mathbf{x}) = \mathbf{f}^T(\mathbf{x})\mathbf{M}^{-1}(\xi )\mathbf{f}(\mathbf{x})\). The function \(d_\xi (\cdot )\) is called the “variance function” because it is proportional to the variance of the least squares estimator of \(\mathbf{f}^T(\cdot )\theta \) in the linear regression model. Equation (2) implies the so-called equivalence theorem for D-optimality: A design \(\xi \) is D-optimal if and only if \(\max _{\mathbf{x}\in {\mathfrak {X}}} d_\xi (\mathbf{x}) =m\); otherwise, \(\max _{\mathbf{x}\in {\mathfrak {X}}} d_\xi (\mathbf{x}) > m\) (see Kiefer 1959). Therefore, provided that the maximum of \(d_\xi (\cdot )\) over \({\mathfrak {X}}\) can be reliably determined, it is possible to construct a lower bound on the D-efficiency of \(\xi \) or prove its optimality. However, if \({\mathfrak {X}}\) is large and multidimensional, maximization can be challenging because \(d_\xi (\cdot )\) is typically nonlinear and multimodal, even for linear regression models.

In the rest of this paper, we will drop the prefix “D-”, e.g., a D-optimal design will simply be called an “optimal design”.

We are not aware of any method that specifically targets optimal design problems on very large discrete grids. For the case of factors that are discrete with an enormous number of practically possible levels, the usual approach is to consider the factors to be fully continuous. Therefore, methods that operate on continuous spaces are natural competitors for the method proposed in this paper, and we briefly discuss them in the rest of this section.

If one or more factors are assumed to be continuous, the simplest approach is to discretize those factors and turn the problem into one that can be solved using discrete-space methods. Naturally, discrete-space solvers then generally cannot find a design that is perfectly optimal on the original, continuous \({\mathfrak {X}}\). Nonetheless, our experience shows that the loss in efficiency is usually negligible if a continuous factor is discretized to, say, 1000 levels. Such discretization can be handled with modern hardware and state-of-the-art discrete-space methods for problems with only one or two continuous factors or problems with one continuous factor and a few binary factors.

There are also other situations with continuous factors in which it is possible to directly apply the existing discrete-space methods. For instance, for some models, there exist theoretical results that limit the support of an optimal design to a relatively small finite subset. As an example, for a fully quadratic linear model on a cube, the search can be restricted to the set of centers of the faces of the cube of all dimensions (see Heiligers 1992).

However, direct discretization may not be sufficient if there are more than two continuous factors or if we require a fine resolution of the levels. In such cases, choosing a method such as the one proposed in this paper can be of significant benefit.

For computing optimal designs when all or some of the factors are continuous, there are many methods that do not employ a fixed discretization of \({\mathfrak {X}}\). To present a brief survey thereof, we choose to split them into two categories.

1.1 Methods that use standard continuous-space algorithms

The problem of optimal design with continuous factors can be directly solved by means of common nonlinear programming methods; for example, the Nelder–Mead algorithm is used in Chaloner and Larntz (1989), a quasi-Newton method is applied in Atkinson et al. (2007) (see Section 13.4), semi-infinite programming is used in Duarte and Wong (2014), and multiple nonlinear programming methods are applied in García-Ródenas et al. (2020). Some papers utilize nonlinear programming methods in a specific way or for a particular class of models; see, for instance, Gribik and Kortanek (1977) and Papp (2012).

In addition to classical nonlinear programming methods, various metaheuristics have been recently proposed to compute optimal designs with continuous factors; see, e.g., Wong et al. (2015) for particle swarm optimization, Xu et al. (2019) or Stokes et al. (2020) for differential evolution, Lukemire et al. (2019) for quantum-behaved particle swarm optimization, and Zhang et al. (2020) for competitive swarm optimization. A thorough empirical evaluation of the performance of nonlinear programming methods and metaheuristics, including genetic algorithms, is given by García-Ródenas et al. (2020).

A typical feature of nonlinear programming methods and metaheuristics is that a fixed-size support of the design is merged with a vector of weights to form a single feasible solution to the optimization problem at hand. This transforms an infinite-dimensional convex problem into a finite one, which is, however, not convex in the coordinates of the support points. Then, these algorithms simultaneously adjust the support and the corresponding weights. A major advantage is that this approach can be used with almost any criterion; it is necessary only to implement the evaluation of the criterion as a subroutine. A disadvantage is that these methods either require a search for an appropriate support size or are rendered less efficient by using a relatively large support size as provided by the Carathéodory theorem (see, e.g., Theorem 2.2.3 in Fedorov 1972). In addition, because the problem is nonconvex, convergence to a good design is usually not guaranteed, and even when convergence is reached, it can be slow. One reason for the slow speed is that with the direct application of nonlinear programming and metaheuristics, the convexity of the problem in the design weights is not exploited.

1.2 Methods that use a discrete-space solver on “adaptive grids”

An alternative idea is to use a discrete-space method applied to a finite set, which is sequentially updated in the continuous space to (hopefully) approach the support of the optimal design. We call this strategy “adaptive support”. The general idea of an adaptive search for the optimal support has been present in the literature from the beginning; for instance, the classical Fedorov-Wynn algorithm is based on iterative improvements to the support of the design, although for each new support, the design weights are adjusted only by means of a simple transformation (Fedorov 1972, Chapter 4). The general possibility of using adaptive supports has also been mentioned in Wu (1978a) and Wu (1978b). More recently, a randomized adaptive support approach has been suggested by Dror and Steinberg (2006).Footnote 4 Furthermore, Stufken and Yang (2012) (Section 6) have proposed “...a multi-stage grid search that starts with a coarse grid that is made increasingly finer in later stages”. Adaptation of the support is also central to the computational methods of Yang et al. (2013) and Pronzato and Zhigljavsky (2014). These methods apply classical convex optimization to find optimal weights on a fixed discrete set, and in each step, they enrich the support set with the global maximum of the variance function. Most recently, Duarte et al. (2018) have employed semidefinite programming and an adaptive replacement of the support with a specific set of local maximizers of the variance function.

Our proposed algorithm, GEX, is more closely related to the class of continuous-space methods reviewed in Sect. 1.2 than to those discussed in Sect. 1.1.

2 The algorithm

In GEX, we apply a discrete-space optimal design algorithm to suitably chosen exploration sets \({\mathfrak {X}}_{exp}\). In the course of the computation, the exploration sets are sequentially updated with the aim of approaching the support of the true optimal design for the model at hand. An outline of GEX is presented as Algorithm 1 below. The input to the algorithm includes the problem itself in the form of a subroutine that, for each permissible \(\mathbf{x}\in {\mathfrak {X}}\), computes the vector \(\mathbf{f}(\mathbf{x})\). The values \(\mathrm {eff}_{opt}<1\), \(\mathrm {eff}_{grp} \le 1\), \(N_{loc} \in \{0,1,\ldots \}\) and \(\mathrm {eff}_{stop}<1\) are parameters chosen by the user; their meaning is explained later in this section.

figure a

In Steps 1 and 2, we select an initial finite exploration set \({\mathfrak {X}}_{exp} \subseteq {\mathfrak {X}}\) and use a discrete-space method to calculate an efficient design \(\xi _{new}\) on \({\mathfrak {X}}_{exp}\). In Step 3, we alternately construct a finite exploration set \({\mathfrak {X}}_{exp}\) based on the current design and compute a new efficient design on \({\mathfrak {X}}_{exp}\). The algorithm stops once the last optimization on \({\mathfrak {X}}_{exp}\) does not lead to a significant improvement. Note that this form of the stopping rule implies that the number of loops in Step 3 is bounded.

Although the general scheme of GEX is simple, judicious specification of the basic steps can make a crucial difference in the overall performance. In the following subsections, we detail our choices regarding the procedures INI, OPT and EXP.

2.1 INI

In Step 1 of Algorithm 1, we construct an initial exploration set \({\mathfrak {X}}_{exp} \subseteq {\mathfrak {X}}\). In our specification, \({\mathfrak {X}}_{exp}\) is constructed as the union of two sets, \({\mathfrak {X}}_{grid}\) and \({\mathfrak {X}}_{rnd}\). The set \({\mathfrak {X}}_{grid}\) is a grid formed by the combinations of the extreme levels of all factors and the median levels of all nonbinary factors. The set \({\mathfrak {X}}_{rnd}\) is a random selection of points in \({\mathfrak {X}}\). The size of \({\mathfrak {X}}_{grid}\) is at most \(3^k\), which is reasonably small for as many as \(k \lesssim 13\) factors, and for many models used in practice, \({\mathfrak {X}}_{grid}\) constructed in the proposed way contains highly informative points. For our numerical study, we chose the size of \({\mathfrak {X}}_{rnd}\) to be 1000; a sensitivity analysis suggests that the performance of the algorithm is similar for a wide range of sizes of \({\mathfrak {X}}_{rnd}\).

2.2 OPT

In Steps 2 and 3c of Algorithm 1, we apply a discrete-space algorithm that computes a design \(\xi _{new}\) on \({\mathfrak {X}}_{exp}\) with an efficiency of at least \(\mathrm {eff}_{opt}\) (among all designs on \({\mathfrak {X}}_{exp}\)) and then prunes the support of \(\xi _{new}\) by means of a grouping procedure parametrized by the value of \(\mathrm {eff}_{grp}\). In more detail, the assignment process \(\xi _{new} \leftarrow \) OPT (\({\mathfrak {X}}_{exp}\), \(\mathbf{f}\), \(\mathrm {eff}_{opt}\), \(\mathrm {eff}_{grp}\)) consists of the steps shown below.

figure b

As the underlying discrete-space optimization procedure, we choose the REX algorithm of Harman et al. (2020). It has several advantages compared to other methods: REX is not only fast and applicable to relatively large problems, but crucially, the resulting designs do not have a tendency to contain many design points with small “residual” weights. The parameter \(\mathrm {eff}_{opt}\) is the lower bound on the efficiency that is used to stop the computation. In our numerical studies, we chose \(\mathrm {eff}_{opt} = 1 - 10^{-6}\).

In Step 2 of Algorithm 1, the initial design for REX is based on the modified Kumar-Yildirim method as described in Harman and Rosa (2020), which is rapid and always provides a design with a nonsingular information matrix. If this relatively advanced initialization method were to be replaced by the uniform random selection of m distinct points, the efficiency of the resulting design (and the speed of computation) would not be much affected. However, the Kumar-Yildirim method guarantees nonsingularity of the information matrix of the initial design, which is an important aspect of the algorithm.Footnote 5 In contrast to Step 2, in Step 3c, the REX algorithm is initialized with \(\xi _{old}\).

Each REX computation is followed by a specific form of grouping of nearby support points. For continuous spaces, a grouping method has previously been recommended by Fedorov (1972), page 109. In our case, the factors are discrete, but the levels can be very close to each other; consequently, grouping nearby support points generally improves the performance. We have identified that for all studied models, it is sufficient to use a nearest-distance approach to decrease the support size of the constructed design on a discrete space.

More precisely, let \(\xi _0\) be the design obtained via the original discrete-space procedure, such as REX. Let \(\mathbf{x}_1,\ldots ,\mathbf{x}_s\) be the support points of \(\xi _0\).Footnote 6 The procedure GRP determines the pair \((\mathbf{x}_k,\mathbf{x}_l)\), \(k<l\), consisting of the two nearest support points and assigns the pooled weight \(\xi _0(\mathbf{x}_k)+\xi _0(\mathbf{x}_l)\) to the point \(\mathbf{x}_k\) if \(\xi _0(\mathbf{x}_k) \ge \xi _0(\mathbf{x}_l)\) or to the point \(\mathbf{x}_l\) if \(\xi _0(\mathbf{x}_k) < \xi _0(\mathbf{x}_l)\), which results in a design \(\xi _1\). If the efficiency of \(\xi _1\) is at least \(\mathrm {eff}_{grp}\) relative to the design originally returned by REX, then the pooling operation is accepted, and the process is repeated. In our study, we chose \(\mathrm {eff}_{grp}=1-10^{-6}\). We remark that removing GRP (e.g., by setting \(\mathrm {eff}_{grp}=1\)) results in marginally more efficient designs, but it makes the computation slower. More importantly, not using GRP results in designs that are populated by a large number of points with small weights.

2.3 EXP

In the key Step 3b, we construct a new exploration set \({\mathfrak {X}}_{exp}\) based on a set of local maxima of the variance function as well as a long-range variation of the support of the current design. In detail, \({\mathfrak {X}}_{exp} \leftarrow \) EXP (\({\mathfrak {X}}\), \(\mathbf{f}\), \(\xi _{old}\), \(N_{loc}\)) consists of the steps summarized below.

figure c

The procedure LOC returns the results of randomly initialized hill climbing maximizations of the current variance function \(d \xi _{old}(\cdot )\) over \({\mathfrak {X}}\). The number of maximizations starting from random points in \({\mathfrak {X}}\) is given by the parameter \(\mathrm {N}_{loc}\); for our numerical study, we chose \(\mathrm {N}_{loc} = 50\). Decreasing \(N_{loc}\) slightly worsens the final design but also makes the computation faster. Removing the \({\mathfrak {X}}_{loc}\) part of \({\mathfrak {X}}_{exp}\) altogether often makes the computation much faster, but for some models, it systematically leads to suboptimal designs.

As in all local search methods, the efficiency depends on the system of neighborhoods considered for each feasible solution \(\mathbf{x}\in {\mathfrak {X}}\).

We use a “star-set” neighborhood \({\mathfrak {S}}(\mathbf{x})\), which consists of all points lying in a “star” centered at \(\mathbf{x}\): \({\mathfrak {S}}(\mathbf{x})\) is the set of points in \({\mathfrak {X}}\) that differ from \(\mathbf{x}\) in at most one coordinate. Formally,

$$\begin{aligned} {\mathfrak {S}}(\mathbf{x})= \big \{ \, {\tilde{\mathbf{x}}} \in {\mathfrak {X}}\, \vert&\text {There exists an } i \in \{1,\ldots ,k\} \text { such that }\\&{\tilde{x}}_i \in {\mathfrak {X}}_i \text { and } {\tilde{x}}_j = x_j \text { for all } j \ne i \, \big \}. \end{aligned}$$

We search the neighborhood of the current point \(\mathbf{x}\), move to the point in \({\mathfrak {S}}(\mathbf{x})\) with the highest value of the variance function, and repeat this process as long as there is an increase in the variance function. Neighborhoods of the form of \({\mathfrak {S}}(\mathbf{x})\) seem to be suitable for optimal design problems on multidimensional grids, as they allow us to explore such grids quite thoroughly yet do not grow exponentially in size with respect to the dimensionality k of the design space. Moreover, the neighborhoods \({\mathfrak {S}}(\mathbf{x})\) have the added advantage that they are fast to computationally enumerate.

The crucial procedure for the construction of the exploration sets is STAR, which is specifically chosen to suit the grid-like structure of the design space studied in this paper. The best solution requires a balanced compromise between exploration and exploitation. Our experience leads us to choose star sets again (hence the name “galaxy exploration”). For a given \(\xi _{old}\), the set \({\mathfrak {X}}_{star}\) is the union of all star-set neighborhoods centered at the support points of \(\xi _{old}\). Formally,

$$\begin{aligned} {\mathfrak {X}}_{star} = \bigcup _{\mathbf{x}\in \mathrm {supp}(\xi _{old})} {\mathfrak {S}}(\mathbf{x}); \end{aligned}$$

such a star set is illustrated in Fig. 1. Note that the REX algorithm produces efficient designs with “sparse” supports, which means that the size of \({\mathfrak {X}}_{star}\) does not grow greatly during the GEX computation.

Fig. 1
figure 1

\({\mathfrak {X}}_{star}\) for a design with 3 support points, where \({\mathfrak {X}}\) is a discretized square \([-1,1]^2\). The support points are denoted by black circles, and the gray dots form the star sets

Full size image

2.4 Summary

Algorithm 2 shows the final formulation of GEX, with all steps described in detail.

figure d

Similar to the methods of Sect. 1.2, in particular Pronzato and Zhigljavsky (2014) or Duarte et al. (2018), our method applies a discrete-space solver to a subset of \({\mathfrak {X}}\) and adaptively modifies this subset. However, unlike the method of Pronzato and Zhigljavsky (2014) and many others, GEX does not attempt to calculate the global maximum of the variance function but instead utilizes a set of local maximizers. The general idea of using a set of local maximizers is similar to that of Duarte et al. (2018), but in GEX, we accomplish it in a significantly different way. Importantly, we include the star sets around the support points of the current \(\xi \), meaning that the exploration set is much larger than merely a set of local maximizers of the variance function, which enables GEX to better explore the design space. Note also that the \({\mathfrak {X}}_{star}\) part of the exploration set is similar to the set implicitly utilized in the coordinate-exchange method for exact designs (see Meyer and Nachtsheim 1995), where in each iteration, one coordinate of one design point is updated via a line search. Nonetheless, we compute approximate, not exact, designs and, crucially, do not consider the coordinates of the points one at a time; rather, all single-coordinate changes to all points are considered simultaneously as a batch (with a set of local maximizers of the variance function), to which an efficient internal discrete-space solver is applied.

In summary, GEX is practically and numerically simple to apply in the sense that it requires no theoretical analysis of the model at hand and no special numerical solvers or libraries, except for the standard procedures of linear algebra. The algorithm has only a few tunable parameters, which are directly interpretable and can be set to fixed default values that perform very well for a wide class of models (as we will demonstrate in Sect. 3).

In each iteration, GEX finds a design that is at least as good as the previous one, and is guaranteed to stop in a finite number of iterations. Nevertheless, GEX does not necessarily converge to the theoretical optimum, even if we let the terminating parameter \(\text {eff}_{stop}\) approach 1; it is possible to construct artificial problems for which it produces considerably suboptimal designs with high probability. Moreover, for extremely large design spaces \({\mathfrak {X}}\), it is difficult to verify that the design provided by GEX is optimal or, more generally, that it has an efficiency above a certain threshold. However, this difficulty is not specific to the proposed method; it is rather a feature of the optimization problem that we are attempting to solve. Obtaining a perfectly reliable lower bound on the efficiency of a design would require either computationally processing all vectors \(\mathbf{f}(\mathbf{x})\), \(\mathbf{x}\in {\mathfrak {X}}\) (cf. inequality (2)), or utilizing mathematical properties specific to the model, which might demand an exceedingly large amount of effort and/or expert knowledge.

Finally, we note that GEX automatically determines the support size of the resulting design. This property is beneficial in the sense that the application of GEX does not require a search for a proper support size. However, this also means that we do not have control over the support size.Footnote 7 If we require efficient designs with a strict upper bound on the support size, nonlinear programming techniques or heuristics (cf. Sect. 1.1) may be a better choice than GEX.

2.5 Notes

In some cases, the information matrix of the D-optimal design is ill-conditioned. If this occurs, we can use the well-known fact that regular reparametrization, i.e., replacing the vectors \(\mathbf{f}(\mathbf{x})\) with \({\tilde{\mathbf{f}}}(\mathbf{x})={\mathbf {R}}\mathbf{f}(\mathbf{x})\), where \({\mathbf {R}}\) is nonsingular, does not alter the D-optimal design. If \({\mathbf {R}}\) is chosen to be close to the inverse of the square root of the optimal information matrix, such reparametrization may greatly improve the condition number of the matrices used in GEX. In particular, we applied this approach to enhance the numerical stability of the computation of optimal designs for Model 10 described in Sect. 3. We chose \({\mathbf {R}}={\mathbf {M}}^{-1/2}\), where \({\mathbf {M}}\) is the information matrix of the design computed for the initial \({\mathfrak {X}}_{exp}\) via the modified Kumar-Yildirim method.

During the execution of the algorithm, points that cannot support optimal designs can be removed by using the results of Harman and Pronzato (2007) in order to decrease the size of the problem and potentially speed up the computations. However, in our experience, the removal of redundant points does not provide a significant increase in the speed of GEX. This is likely due to the nature of the discrete-space engine REX, which tends to work with designs with small supports and, as such, does not benefit much from the elimination of unpromising parts of the design space.

Fig. 2
figure 2

The time profiles of the efficiencies of the designs \(\xi _{new}\) computed by REX in Steps 2 and 3c of GEX. For each problem (see the numbers above the panels), we executed 3 independent runs of GEX; each run is represented by a separate piecewise-linear curve. The efficiencies are expressed on a logarithmic scale, with efficiencies of 0, 0.9, 0.99, 0.999, ..., \(1-10^{-9}\), and \(>1-10^{-9}\) corresponding to the values 0, 1, 2, 3, ..., 9, and 10, respectively, on the vertical axis

Full size image

3 A numerical study

For a numerical study, we selected 5 prominently published recent papers that focus on presenting algorithms for computing D-optimal designs on continuous or mixed design spaces, namely,

  • Pronzato and Zhigljavsky (2014) (adaptive grids combined with projected gradients and vertex exchange optimization),

  • Duarte et al. (2018) (a different approach to adaptive grids combined with semidefinite programming),

  • Lukemire et al. (2019) (quantum-behaved particle swarm optimization),

  • Xu et al. (2019) (differential evolution), and

  • García-Ródenas et al. (2020) (multiple nonlinear programming and metaheuristic methods).

From each paper, we chose two test problems, as summarized in Table 3. The chosen problems include a linear regression model, two nonlinear models with homoscedastic normal errors, a Poisson model, a probit model, and several logistic regression models. The number of factors, k, varies from 2 to 10, and the number of parametric dimensions, m, varies from 4 to 16. We used these test problems to illustrate the behavior of GEX and numerically compare its performance with that of the competing methods.

Figure 2 shows the typical behavior of GEX on the problems in Table 3. We see that the designs \(\xi _{new}\) generated in the main loop of GEX monotonically improve and ultimately converge to the optimum.Footnote 8 The variability of the computation time is moderate.Footnote 9 The usual number of discrete-space optimizations before the stopping rule is satisfied is 3 to 6. We observe that the efficiency growth generally does not decline with increasing computation time. Moreover, with increasing problem difficulty, the number of discrete-space optimization runs required to achieve the optimal design does not tend to grow.

Some additional general observations from the computational study of GEX can be summarized as follows:

  • Depending on the test problem from Table 3, the runs of the subroutine REX consume between 10 and 60 percent, and the runs of the subroutine LOC consume between 15 and 85 percent of the overall computation time. Other subroutines take negligible amounts of time. Consequently, the speed of GEX is mostly determined by the speed of the underlying discrete-space optimization and the procedure that computes the sets of local optima of the variance functions.

  • The results of GEX are highly robust with respect to the choice of the initial exploration set. Even if \({\mathfrak {X}}_{exp}\) constructed by the subroutine INI only consists of 1000 random points of \({\mathfrak {X}}\) (that is, if \({\mathfrak {X}}_{grid}\) is not used), there is only a small variation in the resulting designs. In particular, for each model from Table 3, the fully random initial exploration set leads, with a large probability, to the same size of the support and the same value of the criterion (within 6 significant digits); cf. Table 4.

We provide R (R Development Core Team 2020) codes that are completely free to use and require minimal technical expertise to be applied to any D-optimal design problem on a cuboid grid; see www.iam.fmph.uniba.sk/ospm/Harman/design/.

Table 2 The design produced by GEX for Model 6. The first column gives the index i of the identified support point, the columns labeled \(x_{i1}\) to \(x_{i5}\) list the values of the factors, and \(\xi (\mathbf{x}_i)\) is the weight of the corresponding support point \(\mathbf{x}_i\)
Full size table

For illustration, in Table 2, we present the detailed design for Model 6 as computed by GEX. All other designs can be obtained within a few seconds by running the provided R script. Note that due to the nature of GEX, the resulting designs are “tidy”, i.e., there is no need to remove design points with very small weights or round the positions of the support points to a reasonable number of decimal places.

In optimal experimental design, the numerical comparison of competing computational methods is a challenging task. The reason is that there are no generally adopted benchmark suites and no guidelines for reporting the results of such comparisons. Often, the source code is not available or is fine-tuned to the few problems studied in the source paper. Moreover, the quality of the resulting designs depends on the computation time in a method-specific way and can be strongly influenced by the choice of hardware, programming language and implementation details; a seemingly minor change can lead to a several-fold speed-up or slow-down. Despite these methodological difficulties, however, at least a brief comparison is necessary because there are a plethora of heuristic or theoretical ideas applicable to the computation of optimal designs, and failing to realize that a proposed method is much worse than existing alternatives can be detrimental to readers.

Table 3 Descriptions of the benchmark models, the nominal parameter \(\theta _0\) used and the design space \({\mathfrak {X}}\)
Full size table
Table 4 Comparison of GEX with the competing methods on the benchmark models in Table 3
Full size table

In Table 4, we provide the computation times, support sizes and criterion values for the optimal or nearly optimal designs as reported in the corresponding papersFootnote 10 and as provided by an R implementation of GEX. We used Microsoft R Open 3.5.3 and a 64-bit Windows 10 system with an Intel Core i7-9750H processor operating at 2.60 GHz.

The authors of the competing methods used either MATLAB or C++, both of which almost always permit a faster implementation of a given algorithm than R does. Except for Pronzato and Zhigljavsky (2014), the cited authors used standard modern hardware.

The benchmark results for Models 2 and 3 were obtained by running the algorithm of Pronzato and Zhigljavsky (2014) 11 times using our hardware and the MATLAB code kindly provided by the authors. For these two models, the authors also provide analytically calculated optimal designs based on the results of Schwabe (2012); thus, it can be shown that the designs obtained by GEX for these models have efficiencies of at least 99.999% relative to the provably optimal designs. For Models 1 and 4, the CPU times and benchmark design were taken from Table 9 in Duarte et al. (2018). The results for Models 5 and 9 from Lukemire et al. (2019) were obtained by running the compiled instance of the program written in C++ provided by the authors, with the number of iterations set to 2000 and the required number of support points predetermined by GEX. We ran each instance 11 times and recorded the computation times and criterion values for the resulting designs. The benchmark designs for Models 8 and 10 can be found in Tables 5 and 11 of Xu et al. (2019) and the computation times are based on personal communication with the lead author of Xu et al. (2019). Finally, the results for Models 6 and 7 are available in Table 11 of García-Ródenas et al. (2020); note that the listed results encompass the time and efficiency performance of 5 different algorithms.

From Table 4, it is clear that GEX produces designs with higher efficiency than the competing methods in a shorter computation time, sometimes by several orders of magnitude. The only close competitor is the algorithm from Pronzato and Zhigljavsky (2014). In fact, the designs for Models 2 and 3 obtained by this algorithm are slightly better than the designs for the same models obtained by GEX, although the difference is not within 6 significant digits of the criterion values displayed in Table 4. However, the practical applicability of the algorithm from Pronzato and Zhigljavsky (2014) is limited to models with small numbers of factors; if the number of factors is greater than 2, the computation becomes exceedingly slow. Moreover, in contrast to GEX, the application of this algorithm may require theoretical analysis specific to the problem.

Nevertheless, we stress that all compared algorithms have their own advantages; for instance, they may be more appropriate for computing efficient designs for very general models or special optimality criteria.

4 Final comments

We have proposed a conceptually simple approach and its concrete and efficient specification, which we call the galaxy exploration method (GEX). The proposed algorithm can be used for computing D-optimal or nearly D-optimal approximate experimental designs on large grids and, by means of dense discretization, on continuous multidimensional cuboid spaces.

With a suitable transformation or embedding, GEX can also be applied to compute efficient designs on noncuboid design spaces. For instance, suppose that the experimental design space is the unit disk \({\mathfrak {D}}\) in a plane. Then, we have the following two options for facilitating the application of GEX:

  1. 1.

    Use the radial and angular coordinates of the design points as independent factors. More formally, transform \({\mathfrak {D}}\) into a cuboid design space \({\mathfrak {X}}= [0, 1] \times [0, 2\pi ]\) by means of the polar transformation.

  2. 2.

    Embed \({\mathfrak {D}}\) into the larger design space \({\mathfrak {X}}= [-1,1] \times [-1,1]\) and extend the set \(\mathbf{f}(\mathbf{x})\), \(\mathbf{x}\in {\mathfrak {D}}\), with artificial \(\mathbf{f}(\mathbf{x})={\mathbf {0}}\) for all \(\mathbf{x}\in {\mathfrak {X}}\setminus {\mathfrak {D}}\).

While feasible, assessing the actual performance of GEX under such transformations and embeddings, or adapting the principle of GEX itself to noncuboid design spaces, will require further research.

Although we have focused on D-optimality in this paper, GEX can be directly adapted to any other criterion for which there exist a simple analogue of the variance function and an appropriate discrete-space solver. This is the case for the popular c-, A-, and I-optimality criteria (see, e.g., Harman and Jurík 2008; Harman et al. 2020) as well as for other criteria.

In this paper, we have used the approach of local optimality to compute efficient designs for nonlinear models. Note that locally optimal designs not only are useful by themselves but also are crucial for several methods of constructing robust experimental designs; as examples, let us mention so-called maximin efficient designs (see, e.g., Müller and Pázman 1995; Dette et al. 2006) and the clustering methodology developed by Dror and Steinberg (2006). For other approaches to experimental design of nonlinear models, such as the pseudo-Bayesian and minimax approaches, the potential for utilizing GEX will require further research. In the meantime, we refer the reader to alternative algorithms, such as those proposed by Chen et al. (2015), Masoudi et al. (2017), Lukemire et al. (2019), and Masoudi et al. (2019).

The performance of GEX can be undoubtedly improved even further, for instance, through modification of the exploration sets, clever adaptive changes to the levels of each factor, or parallelization of the computation. These are also interesting topics for further research.