Computer experiment designs for accurate prediction

Abstract

Computer experiments using deterministic simulators are sometimes used to replace or supplement physical system experiments. This paper compares designs for an initial computer simulator experiment based on empirical prediction accuracy; it recommends designs for producing accurate predictions. The basis for the majority of the designs compared is the integrated mean squared prediction error (IMSPE) that is computed assuming a Gaussian process model with a Gaussian correlation function. Designs that minimize the IMSPE with respect to a fixed set of correlation parameters as well as designs that minimize a weighted IMSPE over the correlation parameters are studied. These IMSPE-based designs are compared with three widely-used space-filling designs. The designs are used to predict test surfaces representing a range of stationary and non-stationary functions. For the test conditions examined in this paper, the designs constructed under IMSPE-based criteria are shown to outperform space-filling Latin hypercube designs and maximum projection designs when predicting smooth functions of stationary appearance, while space-filling and maximum projection designs are superior for test functions that exhibit strong non-stationarity.

1 Introduction

A deterministic computer simulator is the implementation, in computer code, of a mathematical model that relates the input and output variables of a physical system. As mathematical descriptions of such systems have become more sophisticated, the use of deterministic simulators as experimental vehicles has become more widespread in many applications: engineering design (Forrester et al. 2008; Nekkanty 2009; Villarreal-Marroquín et al. 2013); biomechanics (Ong et al. 2008; Leatherman et al. 2014b); the physical sciences (Montgomery and Truss 2001; Higdon et al. 2004); the life sciences (Fogelson et al. 2003; Hajagos 2005; Upton et al. 2006).

A computer experiment is performed by varying the inputs to a computer simulator and observing the effects on the simulator output. When physical experiments cannot be conducted because of ethical considerations or because they require a prohibitive budget or excessive time, computer experiments are sometimes conducted in their place. This paper evaluates criteria for the initial design of computer experiments with small to moderate numbers of inputs.

When the simulator is treated as a “black-box” function, i.e., the relationship between the inputs and outputs is of unknown form and may be complex, space-filling designs are often used for the computer experiment. Space-filling designs spread points over the input space of interest, see Bates et al. (1995). Two widely-used classes of space-filling designs are maximin Latin hypercube designs (LHDs) and minimum average reciprocal distance LHDs (see, for example, McKay et al. 1979; Morris and Mitchell 1995; Welch 1985; Johnson et al. 1990; Audze and Eglais 1977; Bates et al. 2003; Liefvendahl and Stocki 2006).

More recently, there has been an increasing emphasis on space-filling designs under criteria that also force projections of the design to be space-filling (e.g., Welch 1985; Draguljić et al. 2012). Joseph et al. (2015) introduced maximum projection (MaxPro) designs which minimize a criterion that integrates the reciprocal interpoint distance over projections onto all possible dimensions and which are very economically computed.

The focus of this paper is on the choice of the initial design of a computer experiment to enhance the prediction accuracy of empirical best linear unbiased predictors when applied to stationary and non-stationary test functions. Some authors have evaluated designs with respect to criteria not related to prediction, see, for example, Bursztyn and Steinberg (2006). However, other studies have compared designs’ prediction accuracies, either theoretically or empirically. Sacks et al. (1989a) compared integrated mean squared prediction error (IMSPE) optimal designs with $n=9$ runs in $d=2$ dimensions. These designs were constructed to minimize the IMSPE for a stationary Gaussian process surface with Gaussian correlation, defined in Eq. (2), using specified values of the correlation parameters $(\rho _1, \rho _2)$, thus local IMSPE optimal designs. The authors concluded that local IMSPE optimal designs constructed assuming $\rho _1 = \rho _2=0.78$ were robust for predicting a range of stationary Gaussian process surfaces having alternative correlation values. In an empirical comparison of four classes of designs (including local IMSPE optimal and maximin LHDs), Johnson et al. (2011) concluded that, for predicting four test functions, the four design classes had similar empirical prediction errors. In a comparison of five classes of designs (including local IMSPE optimal and maximin LHDs), Silvestrini et al. (2013) concluded that all the designs performed similarly with respect to IMSPE when $n \ge 10d$ and that the designs’ prediction accuracy did not improve dramatically when n increased to 15d. These authors also showed that empirical prediction errors for maximin LHDs and local IMSPE optimal designs were very similar in a case study example.

This paper presents a more comprehensive comparison of the empirical prediction accuracy of local IMSPE optimal designs, three classes of space-filling designs, and a class of weighted IMSPE optimal designs. These comparisons show differences in the prediction accuracy of these design classes and provide examples where IMSPE-based designs are likely to be preferred to traditional space-filling designs. (Alternatives to space-filling designs may be preferred under other design criteria, too. See, for example, Pronzato and Müller 2012). Designs having dimensions $d=3$, 5, 8, 10, and 20 are assessed in Sects. 6 and 7. Prediction accuracy comparisons are made over four test-beds of Kriging-based surfaces that are constructed with fixed or stochastically selected correlation parameters, and two hard-to-predict non-stationary test-bed surfaces. Each test-bed contains 100 representative surfaces.

In contrast to the literature cited above, Sects. 6 and 7 show that in maximizing prediction accuracy, the local IMSPE optimal and the weighted IMSPE optimal designs outperform the two types of space-filling LHDs and the MaxPro designs over the wide range of smooth functions of stationary appearance examined in this paper. However, for the strongly non-stationary test surfaces studied, the space-filling LHDs and MaxPro designs outperform the IMSPE-based designs.

The specific local IMSPE optimal designs investigated in this paper minimize the IMSPE for a stationary Gaussian process surface having a given Gaussian correlation parameter $\varvec{\rho }=(\rho _1$ $, \ldots ,$ $\rho _d)^T$, where $\rho _i$ is the parameter for the i th input, d is the number of simulator inputs, and T denotes transpose.

Even if the surface to be predicted arises from a stationary Gaussian process, the process’s exact value of $\varvec{\rho }$ is unlikely to be known in advance. Consequently, a second group of designs to be compared are those that minimize a weighted average of IMSPE values for a given distribution of $\varvec{\rho }$ values; such designs are called Weighted IMSPE (W-IMSPE) optimal designs. While these designs may be regarded as Bayesian, our emphasis is to regard the weighting as simply an alternative methodology for design construction (in the spirit of Efron (2014)). We show that the computational time to construct W-IMSPE designs is substantial and that, perhaps surprisingly, little benefit in prediction accuracy is obtained over local IMSPE optimal designs.

This paper is organized as follows. Section 2 presents the Gaussian process model for simulator output and the corresponding best linear unbiased predictor of the output at untested inputs. Section 3 states the local IMSPE and W-IMSPE objective functions and gives an example of each design. Section 4 describes the computational algorithms used to construct local IMSPE optimal and W-IMSPE optimal designs and provides details for the numerical computation of the W-IMSPE design objective function. Section 5 describes the designs and stationary surfaces used for the simulation study of Sect. 6. This simulation study compares the prediction accuracy of several local IMSPE optimal and W-IMSPE optimal designs with that of three types of space-filling designs for stationary surfaces. An additional comparison of the prediction accuracy of these designs, but for non-stationary surfaces, is shown in Sect. 7. Design recommendations are made from both simulation studies. Section 8 gives a summary of the paper and discusses limitations and extensions of the results.

2 The Gaussian process model

Let $y(\varvec{x})$ denote the real-valued output of a computer simulator when run at a $d \times 1$ input vector $\varvec{x}$. The input space is assumed to be a d-dimensional rectangle that is scaled to $\left[ 0,1\right] ^d$. Assume that $y(\varvec{x})$ can be modeled as a realization of the Gaussian process

$$\begin{aligned} Y(\varvec{x})= \sum _{i=1}^p f_i (\varvec{x}) \beta _i + Z(\varvec{x}) =\varvec{f}^T(\varvec{x})\varvec{\beta } + Z(\varvec{x}), \end{aligned}$$

(1)

where $\varvec{f}^T(\cdot )= \left[ f_1(\cdot ), f_2(\cdot ), \ldots , f_p(\cdot )\right]$ are known regression functions, $\varvec{\beta }=\left[ \beta _1, \beta _2, \ldots ,\beta _p \right] ^T$ is a vector of unknown regression coefficients, and the regression deviations are described by a stationary Gaussian process, $Z(\varvec{x})$, $\varvec{x} \in \left[ 0,1\right] ^d$. The $Z(\varvec{x})$ process is assumed to have zero mean, variance $\sigma _Z^2$, and separable Gaussian correlation function

$$\begin{aligned} R(\varvec{x}_{u}-\varvec{x}_{v} \mid \varvec{\rho }) = \prod _{j=1}^d \rho _j ^{ 4\left( x_{uj} - x_{vj}\right) ^2}, \end{aligned}$$

(2)

for $\varvec{x}_{u}, \varvec{x}_{v} \in [0,1]^{d}$ which have $j{\mathrm{th}}$ elements, $1 \le j \le d$, $x_{u j}$ and $x_{v j}$, respectively, $\varvec{\rho }=(\rho _1, \rho _2,\ldots ,\rho _d)^T$, and $\rho _j\in \left( 0,1\right)$ (see, for example, Sacks et al. 1989a, b; Currin et al. 1991; Higdon et al. 2004). The parameter $\rho _j$ is the correlation between the outputs at inputs $\varvec{x}_{u}$ and $\varvec{x}_{v}$ for which $\vert x_{uj} - x_{vj}\vert = 0.5$, and $x_{u\ell }=x_{v\ell }$ for $\ell \ne j$. The equivalent parameterization $\theta _j=-4 \ln (\rho _j)$ of $\rho _{j}$ is often used so that $\theta _j > 0$ and $\rho _j^{4}=e^{-\theta _j}$, $1 \le j \le d$. The parameterization used here is one of several that have been proposed in the literature for providing an increase in numerical stability for extreme values of the correlation parameters (see, for example, Higdon et al. 2004; MacDonald et al. 2015). The methodology in this paper can be implemented similarly for other separable but non-Gaussian correlation functions.

Suppose $\varvec{y}^n = \left[ y(\varvec{x}_1), y(\varvec{x}_2),\ldots , y(\varvec{x}_n)\right] ^T$ is the $n \times 1$ vector of simulator (training) outputs computed at the n inputs which are the rows of the $n \times d$ design matrix $\varvec{X}=[\varvec{x}_1, \varvec{x}_2, \ldots , \varvec{x}_n]^T$. When $\varvec{\rho }$ is known, Sacks et al. (1989a) show that the best linear unbiased predictor of $y(\varvec{x}_0)$, $\varvec{x}_0 \in [0,1]^{d}$, is

$$\begin{aligned} \widehat{y}(\varvec{x}_0) = \varvec{f}_{0}^T \widehat{\varvec{\beta }} + \varvec{r}_{0}^T\varvec{R}^{-1}(\varvec{y}^n-\varvec{F}\widehat{\varvec{\beta }}), \end{aligned}$$

(3)

where $\varvec{f}_{0}=\varvec{f}(\varvec{x}_0)=[f_1(\varvec{x}_0), \ldots , f_p(\varvec{x}_0)]^T$ is the $p \times 1$ vector of known regressors at $\varvec{x}_0$; $\varvec{F}$ is the $n \times p$ matrix of known regressors having $(i,j){\mathrm{th}}$ element $f_j(\varvec{x}_i)$ for $1 \le i \le n, 1\le j \le p$. Also, $\widehat{\varvec{\beta }}=$ $({\varvec{F}^T} {\varvec{R}^{-1}} \varvec{F})^{-1} \varvec{F}^T \varvec{R}^{-1} \varvec{y}^n$ is the generalized least squares estimator of $\varvec{\beta }$; $\varvec{r}_{0}$ is the $n \times 1$ vector $\left( R(\varvec{x}_0-\varvec{x}_1\mid \varvec{\rho }), \ldots ,\right.$ $\left. R(\varvec{x}_0-\varvec{x}_n\mid \varvec{\rho })\right) ^T$ and $\varvec{R}$ is the $n \times n$ matrix $\left( R\left( \varvec{x}_i-\varvec{x}_j \mid \varvec{\rho } \right) \right)$ whose elements are defined by the correlation function (2).

Because $\varvec{\rho }$ is assumed known, $\widehat{y}(\varvec{x}_0)$ is an idealized predictor which has many positive features. First, the overall mean structure is specified by a regression while local deviations from the trend are described by a flexible stationary Gaussian process. Second, because $\widehat{y}(\varvec{x}_0)$ is the mean of the conditional distribution of $(Y(\varvec{x}_0) \mid \varvec{Y}^n = \varvec{y}^{n})$ where $\varvec{Y}^n=\left[ Y(\varvec{x}_1), Y(\varvec{x}_2),\ldots , \right.$ $\left. Y(\varvec{x}_n)\right] ^T$, it is straightforward to calculate the uncertainty, and hence the mean squared prediction error (MSPE), of $\widehat{y}(\varvec{x}_0)$ using the variance of $(Y(\varvec{x}_0) \mid \varvec{Y}^n = \varvec{y}^{n})$. Finally, $\widehat{y}(\varvec{x}_0)$ interpolates the training data. Assuming $\varvec{\rho }$ is known, the MSPE of $\widehat{y}(\varvec{x}_0)$ will be used to construct local IMSPE optimal and W-IMSPE optimal designs (see Sect. 3 for the design criteria and Sect. 4 for the construction methods). An empirical version of (3) that uses an estimate of $\varvec{\rho }$ will be utilized in Sects. 6 and 7 to study the prediction accuracy of various designs.

3 IMSPE-based and space-filling designs

Local IMSPE and W-IMSPE optimal designs are constructed in this paper to predict well for a given $\varvec{\rho }$ or in repeated use for a distribution of $\varvec{\rho }$ values. The predictor $\widehat{y}( \varvec{x}_0)$ in (3) depends on the design $\varvec{X}$ and on the model parameters through $\varvec{r}_0$ and $\varvec{R}$ (defined in Sect. 2). For fixed $\varvec{X}$, $\varvec{\rho }$, and $\sigma _Z^2$, one measure of prediction accuracy of $\widehat{y}( \varvec{x}_0)$ at $\varvec{x}_0$ is the MSPE

$$\begin{aligned}&{\mathrm{MSPE}} \left( \varvec{x}_0, \varvec{X}\mid \sigma _Z^2, \varvec{\rho } \right) = E_{Y} \left\{ \left( Y(\varvec{x}_0) - \widehat{y}(\varvec{x}_0) \right) ^{2} \right\} \end{aligned}$$

(4)

$$\begin{aligned}&\quad =\sigma _Z^2\left( 1 - \begin{bmatrix} \varvec{f}_{0}^T ~~ \varvec{r}_{0}^T \end{bmatrix} \begin{bmatrix} \varvec{0}&\varvec{F}^T \\ \varvec{F}&\varvec{R} \end{bmatrix}^{-1} \begin{bmatrix} \varvec{f}_{0}\\ \varvec{r}_{0}\end{bmatrix}\right) , \end{aligned}$$

(5)

where $\varvec{0}$ is a $p \times p$ matrix of zeros and the expectation in (4) is taken over the joint distribution of $(Y(\varvec{x}_0),$ $\varvec{Y}^n)$.

For known $\varvec{\rho }$ and $\sigma _Z^2$, a local IMSPE optimal design is an $n \times d$ design matrix $\varvec{X}$ that minimizes

$$\begin{aligned}&{\mathrm{IMSPE}} \left( \varvec{X}\mid \sigma _Z^2, \varvec{\rho } \right) = \int _{[0,1]^d} {\mathrm{MSPE}} \left( \varvec{x}_0, \varvec{X}\mid \sigma _Z^2, \varvec{\rho } \right) \mathrm {d} \varvec{x}_0 \nonumber \\&\quad =\sigma _Z^2 \left( 1 - {\mathrm {tr}} \left( \begin{bmatrix} \varvec{0}&\varvec{F}^T \\ \varvec{F}&\varvec{R} \end{bmatrix}^{-1} \int \begin{pmatrix} \varvec{f}_{0} \varvec{f}_{0}^T &{} \varvec{f}_{0} \varvec{r}_{0}^T \\ \varvec{r}_{0} \varvec{f}_{0}^T &{} \varvec{r}_{0} \varvec{r}_{0}^T \\ \end{pmatrix} \mathrm {d} \varvec{x}_0 \right) \right) , \end{aligned}$$

(6)

which is the MSPE in (5) averaged over the input space $[0,1]^{d}$. Here ${\mathrm {tr}}(\varvec{A})$ is the trace of matrix $\varvec{A}$ and the integration in (6) is performed element-wise over $[0,1]^d$ (see Sacks et al. 1989a, b).

An important special case of (6) (cf. Sacks et al. 1989b) that is used here to construct both local and weighted IMSPE optimal designs is when the Gaussian process has constant mean, say $\beta _0$. In this case $\varvec{f}_{0} =1$, $\varvec{F}=\varvec{1}_n$, and Eq. (6) reduces to

$$\begin{aligned}&{\mathrm{IMSPE}} \left( \varvec{X}\mid \sigma _Z^2, \varvec{\rho } \right) \nonumber \\&\quad =\sigma _Z^2 \left( 1 - {\mathrm {tr}} \left( \begin{bmatrix} \varvec{0}&\varvec{1}_n^T \\ \varvec{1}_n&\varvec{R} \end{bmatrix}^{-1} \int \begin{pmatrix} 1 &{} \varvec{r}_{0}^T \\ \varvec{r}_{0} &{} \varvec{r}_{0} \varvec{r}_{0}^T \\ \end{pmatrix} \mathrm {d} \varvec{x}_0 \right) \right) . \end{aligned}$$

For the Gaussian correlation function (2), the integral of the $i^{th}$ element, $R(x_0-x_i\vert \varvec{\rho })$, of $\varvec{r}_{0}$ is

$$\begin{aligned} \left[ \int _{[0,1]^d} \varvec{r}_{0} \mathrm {d} \varvec{x}_0 \right] _i&= \int _{[0,1]^d} \prod _{k=1}^d \rho _k ^{ 4\left( x_{0k} - x_{ik} \right) ^2} \mathrm {d} x_{0k} \\&= \prod _{k=1}^d \left( \sqrt{\frac{\pi }{\gamma _k}} \left( \varPhi \left( \sqrt{2 \gamma _k} \left( 1-x_{ik}\right) \right) \right. \right. \\&\qquad \qquad \qquad \qquad \left. \left. - ~ \varPhi \left( - \sqrt{2 \gamma _k} x_{ik}\right) \right) \right) , \end{aligned}$$

for $1 \le i \le n$ where $\gamma _k=-4 \ln (\rho _k)$ and $\varPhi (\cdot )$ denotes the cumulative distribution function of the standard normal distribution. The integral of the $(i,j)^{th}$ element of $\varvec{r}_{0} \varvec{r}_{0}^T$ is

$$\begin{aligned}&\left[ \int _{[0,1]^d} \varvec{r}_{0} \varvec{r}_{0}^T \mathrm {d} \varvec{x}_0 \right] _{ij} \\&= \int _{[0,1]^d} \prod _{k=1}^d \rho _k ^{4\left( x_{0k} - x_{ik}\right) ^2} \rho _k ^{4\left( x_{0k} - x_{jk} \right) ^2} \mathrm {d} x_{0k} \\&= \prod _{k=1}^d \left( exp\left\{ - \frac{1}{2}\gamma _k \left( x_{ik} - x_{jk} \right) ^2 \right\} \sqrt{\frac{\pi }{2 \gamma _k}} \right. \\&\qquad \quad \left. \times ~ \left( \varPhi \left( \sqrt{4 \gamma _k} \left( 1-\frac{x_{ik}+x_{jk}}{2}\right) \right) \right. \right. \\&\qquad \quad \qquad \qquad \left. \left. - ~ \varPhi \left( - \sqrt{4 \gamma _k} \frac{x_{ik}+x_{jk}}{2}\right) \right) \right) , \end{aligned}$$

for $1\le i,j\le n$. Because ${\mathrm{IMSPE}} \left( \varvec{X}\mid \sigma _Z^2, \varvec{\rho } \right) = \sigma _Z^2 \times {\mathrm{IMSPE}} \left( \varvec{X}\mid \sigma _Z^2 =1, \varvec{\rho } \right)$, a design that minimizes

$$\begin{aligned} {\mathrm{IMSPE}}^\star \left( \varvec{X}\mid \varvec{\rho } \right) \equiv {\mathrm{IMSPE}} \left( \varvec{X}\mid 1, \varvec{\rho } \right) \end{aligned}$$

(7)

equivalently minimizes ${\mathrm{IMSPE}} \left( \cdot \mid \sigma _Z^2, \varvec{\rho } \right)$ for all $\sigma _Z^2 > 0$. Thus a local IMSPE optimal design depends only on the model correlation parameters $\varvec{\rho }$ and not the process variance $\sigma _Z^2$.

If $\varvec{\rho }$ is not known, but either information about the ranges of its components or detailed subject matter knowledge of the possible values of the components is available, then the minimization of an average of ${\mathrm{IMSPE}}^{\star }$ with weights $\pi \left( \varvec{\rho }\right)$ is an appropriate design criterion. From a Bayesian perspective, the weight $\pi \left( \varvec{\rho }\right)$ is a prior distribution on $\varvec{\rho }$. An $n \times d$ design matrix $\varvec{X}$ that minimizes

$$\begin{aligned} {W}\left( \varvec{X}\mid \pi \right) = \int _{[0,1]^d} {\mathrm{IMSPE}}^{\star } \left( \varvec{X}\mid \varvec{\rho } \right) \pi \left( \varvec{\rho }\right) \mathrm {d} \varvec{\rho } \end{aligned}$$

(8)

is called a weighted IMSPE (or W-IMSPE) optimal design.

As an example when $d=3$ and $n=30$, Fig. 1a shows the 3-d scatterplot of a local IMSPE optimal design over $[0,1]^3$, denoted $\varvec{X}_a$, for $\varvec{\rho }= (0.75, 0.75$,$0.75)^T$. Figure 1b shows the scatterplot of the W-IMSPE optimal design, denoted $\varvec{X}_b$, corresponding to the weight function

$$\begin{aligned} \pi (\rho _{1},\rho _{2},\rho _{3}) \propto \prod _{k=1}^{3} \rho _{k}^{4} (1- \rho _{k})^{12}. \end{aligned}$$

(9)

From a Bayesian perspective, (9) states that $\rho _{1}$, $\rho _{2}$, $\rho _{3}$ are independent and identically distributed (i.i.d.) as beta (5,13) random variables. The beta (5,13) distribution has mode 0.25 and standard deviation 0.10. Thus $\pi (\varvec{\rho })$ accounts for (small) differences from equality of $\rho _{1}$, $\rho _{2}$, and $\rho _{3}$ and may predict better for slightly less uniform training/test surfaces.

The minimum interpoint (average reciprocal) distance is 0.2803 (1.4613) for $\varvec{X}_a$ and 0.2975 (1.6631) for $\varvec{X}_b$. Thus, while the local IMSPE optimal design has two points in the design that are slightly closer than any two points in the W-IMSPE optimal design, it is more space-filling “on average” than the W-IMSPE optimal design under the average reciprocal distance measure. It also includes points nearer the edge of the design space than the W-IMSPE optimal design. This illustrates the difficulty of selecting designs by space-fillingness, since it will be shown that the design in Fig. 1a has prediction accuracy inferior to that of the design in Fig. 1b.

For comparison, Fig. 1c shows the 3-d scatterplot of the maximin LHD, denoted $\varvec{X}_c$, for $(n,d) =$ (30, 3) obtained from van Dam et al. (2013). Its minimum interpoint distance is 0.3600 (by construction, larger than those of either IMSPE-based design), and its average reciprocal distance (1.5969) falls between the corresponding distance for the other two designs.

Fig. 1

For $(n,d) =(30,3)$, 3-d scatterplots of a $\varvec{X}_a$: a local IMSPE optimal design in $\left[ 0,1\right] ^3$ for $\varvec{\rho }= (0.75, 0.75,0.75)^T$; b $\varvec{X}_b$: a W-IMSPE optimal design in $\left[ 0,1\right] ^3$ for the weight function in (9); and c $\varvec{X}_c$: a maximin LHD in $\left[ 0,1\right] ^3$

The next section will discuss computational methods for constructing IMSPE-based designs. Sections 6 and 7 will present the results of an empirical comparison of prediction accuracy using the IMSPE-based, maximum projection, and space-filling designs that are listed in Sect. 5. It will be shown that the (less space-filling) local IMSPE optimal and W-IMSPE optimal designs result in smaller empirical prediction errors than the space-filling LHDs for the stationary test-beds studied, while the opposite is true for the non-stationary test-beds studied.

4 Computational methods for constructing IMSPE-based designs

This section describes the optimization methods used to find the local IMSPE optimal and W-IMSPE optimal designs discussed in Sect. 3, as well as the methods used to numerically evaluate ${W}\left( \varvec{X}\mid \pi \right)$ in (8).

Define ${\mathcal {D}}_{n,d}$ to be the class of all designs $\varvec{X}$ with n runs and d inputs in the transformed space $[0,1]^d$ with each pair of design points having Euclidean distance at least 0.001 apart. To find the design $\varvec{X}$ in ${\mathcal {D}}_{n,d}$ that minimizes $\hbox {IMSPE}^{\star }(\varvec{X}\mid \varvec{\rho })$ in (7) for a given $\varvec{\rho }$ or the design in ${\mathcal {D}}_{n,d}$ that minimizes $W(\varvec{X}\mid \pi )$ in (8) for a specific $\pi (\varvec{\rho })$, this paper used a modified particle swarm optimization (PSO) algorithm to identify a design to serve as the starting point for a gradient-based quasi-Newton search for the best design.

Briefly, PSO begins with a set of $N_{\mathrm{des}}$ starting designs spread over the design space ${\mathcal {D}}_{n,d}$. At the start of a given iteration, each design $\varvec{X}$ is moved separately to a new design that is “between” the global best design among all designs generated thus far and the best design restricted to those along its own path. For a detailed description of this heuristic approach and an illustrative example, see Leatherman et al. (2014a). For this paper, the PSO parameter settings followed the recommendations of Kennedy and Eberhart (1995) and Yang (2010), and the PSO algorithm was run with $N_{\mathrm{des}} =4nd$ starting designs and $N_{\mathrm{its}} = 2N_{\mathrm{des}}$ iterations. Since, in this paper, PSO is followed by a quasi-Newton optimizer, these values of $N_{\mathrm{des}}$ and $N_{\mathrm{its}}$ are much smaller than the number of designs and iterations that would have been required for a search using solely PSO.

The local IMSPE optimal designs described in Sect. 5 and compared in Sects. 6 and 7 were constructed using PSO followed by a quasi-Newton search. In this construction, the formulas in Sect. 3 allowed for closed-form evaluation of IMSPE$^{\star }(\varvec{X}\mid \varvec{\rho })$. However, there is no closed form available for $W(\varvec{X}\mid \pi )$. Thus, this paper used quasi Monte Carlo numerical integration based on a low discrepancy sequence to approximate $W(\varvec{X}\mid \pi )$. Many low discrepancy sequences have been used in statistics and other disciplines; two recent surveys of these methods are given by Kincaid and Cheney (2002) and Givens and Hoeting (2012). This paper used the widely-available Sobol’ sequence to integrate (8) (cf. Morokoff and Caflisch 1995; Niederreiter 1992).

The W-IMSPE objective function ${W}\left( \varvec{X}\mid \pi \right)$ was approximated by

$$\begin{aligned} {{{W}_a\left( \varvec{X}\mid \pi \right) ~=~}} \frac{1}{2^k} \sum _{j=1}^{2^k} {\mathrm{IMSPE}}^{\star } \left( \varvec{X}\mid \varvec{\rho }_j \right) \pi \left( \varvec{\rho }_j\right) , \end{aligned}$$

(10)

where $\varvec{\rho }_j$ is the $j{\mathrm{th}}$ point of the $2^k$-point Sobol’ sequence in d dimensions. The d correlation parameters were taken to be mutually independent, thus $\pi (\varvec{\rho })$ is of the form $\prod _{i=1}^d\pi _{i}(\rho _i)$ where $\pi _{i}(\varvec{\cdot } )$ is the probability density of $\rho _i$.

Two modifications were used to increase the accuracy of the ${W}_a\left( \varvec{X}\mid \pi \right)$ approximation of ${W}\left( \varvec{X}\mid \pi \right)$: a rescaling and shifting of the $\{\varvec{\rho }_{j} \}_{j=1}^{2^k}$ points, and a selection of the minimal k that allows accurate approximation. The first modification is based on the observation that, for fixed k and the selected $\pi (\varvec{\cdot })$, many terms in (10) can have extremely small $\pi (\varvec{\rho }_{j})$ yielding terms with a wide range of magnitudes. One can improve the approximation by using only those $\varvec{\rho }_{j}$ having significant $\pi \left( \varvec{\rho }_j\right)$ contributions to the sum in (10). For this paper, this is accomplished by transforming the range of integration of each $\varvec{\rho }_{j}$ from $[0,1]^d$ to $\prod _{i=1}^d [a_i, b_i]$, where $0< a_i< b_i < 1$ are selected so that all component pdfs $\pi _{i}(\rho _i)$, $1 \le i \le d$, of $\pi (\varvec{\rho })$ satisfy $\pi _{i}(\rho _i) \ge 10^{-10}$ for $\rho _i \in [a_i, b_i].$

The second modification is to select the minimal k so that ${W}_a\left( \varvec{X}\mid \pi \right)$ computed with $2^k$ terms provides an accurate estimate of ${W}\left( \varvec{X}\mid \pi \right)$. The length $2^k$ of the Sobol’ sequence needed for this purpose depends upon d, the dimension of the ${W}\left( \varvec{X}\mid \pi \right)$ integral. As d increases, longer Sobol’ sequences are required. For example, the ideal value of k was determined to be 16 for $d=3$ by calculating (10) for several designs using an increasing sequence of k values, and selecting the smallest k for which the sum (10) becomes stable.

Two additional modifications were made in the implementation of the algorithm. First, since the use of the ideal k became computationally prohibitive on the compute machines available for this paper as d increased, an adaptive number of draws was used in the optimization. The idea is that initially a smaller k can be used because ${W}_a\left( \varvec{X}\mid \pi \right)$ differences are likely to be larger, while bigger k values must be used when making the final ${W}_a\left( \varvec{X}\mid \pi \right)$ comparisons because these values are likely to be more nearly equal. Specifically, for each initial design with $d=3$ inputs studied in Sect. 5, approximately the first $90\%$ of the $N_{\mathrm{its}}$ iterations were performed with a ‘cheaply’ estimated $W(\varvec{X}\mid \pi )$ by calculating (10) with $2^{11}$ Sobol’ draws. The value of $k=11$ was chosen because the study of k described in the previous paragraph showed that $k=11$ allowed the ${W}_a\left( \varvec{X}\mid \pi \right)$ values to be reasonably close to their converged value for $d=3$. The remaining 10% of the iterations used the more accurate $k=16$.

A second modification to the algorithm enhanced the ability of the PSO algorithm to escape from local minima. After computing 90% of the $N_{\mathrm{its}}$ PSO iterations, a randomly selected set of 5% of the $N_{des}$ designs was replaced by a space-filling set of alternative designs. Then the remaining 10% of the PSO iterations were conducted starting with this modified set of designs and using the more accurate k. The best design constructed by PSO in this way was taken as the starting design for a single run of a quasi-Newton algorithm (as implemented in the MATLAB code fmincon.m) to produce the final W-IMSPE optimal design. The quasi-Newton algorithm used the larger, d-dependent, value of k to calculate (10).

MATLAB code for constructing the local and the weighted IMSPE optimal designs, as well as data files of the specific designs used in this paper are posted on the first author’s website http://stat.wvu.edu/~erl/CompExpDesgs_Pred/.

5 Designs compared and test-bed surfaces

This section describes the set of designs to be compared in Sects. 6, 7, and the Supplementary Material, and the collection of test functions used to compare them. The sample sizes n and numbers of inputs d considered in providing design recommendations were

$$\begin{aligned} (n,d)\in \left\{ (15, 3), (30,3),(25,5), (50,5), (40,8), (80,8), \right.&\\ \left. (100,10), (100,20) \right\} .&\end{aligned}$$

5.1 The designs compared

All local IMSPE optimal and W-IMSPE optimal designs in this paper were constructed using the optimization methodology described in Sect. 4 using a constant mean $\varvec{f}^T(\varvec{x})\varvec{\beta }=\beta _0$ for the Gaussian process in (1). The local IMSPE optimal designs minimized $\hbox {IMSPE}^{\star }(\varvec{X} \mid \varvec{\rho })$ over $\varvec{X}\in {\mathcal {D}}_{n,d}$ for the three common-correlation $\varvec{\rho }$ listed in Table 1. The W-IMSPE optimal designs were constructed to minimize $W_a(\varvec{X}\mid \pi )$ over $\varvec{X}\in {\mathcal {D}}_{n,d}$ for weight functions $\pi (\varvec{\rho })$ of the form $\prod _{i=1}^{d} \pi (\rho _{i})$ where $\pi (\rho )$ was a common, marginal beta density for (the independent) $\rho _{i}$, $1 \le i \le d$. W-IMSPE optimal designs were constructed only for $\pi (\rho )$ having mode at most 0.5 because a pilot study showed that using $\pi (\rho )$ with larger modes resulted in greater prediction errors than the $\pi (\rho )$ selected for this study. The three selected weight functions are denoted $W_{.25W}$, $W_{.25N}$, and $W_{.5N}$ (Table 1), where the numerical subscripts represent the mode of the distribution and the letter W or N in the subscript denotes whether the distribution had a “wide” or “narrow” spread, i.e., had standard deviation 0.10 or 0.057, respectively.

Table 1 Notation for the local IMSPE optimal and W-IMSPE optimal designs studied in this paper; the local IMSPE designs use $\varvec{\rho } = \rho \times \varvec{1}_d$, and the W-IMSPE designs use common $\pi (\varvec{\cdot })$

For $(n,d) =$ (15, 3) and (30, 3), local IMSPE optimal and W-IMSPE optimal designs were constructed for all six correlation and weight functions listed in Table 1. For $d \ge 5$, only the three local IMSPE optimal designs were constructed because of their computational feasibility for the larger (n, d) cases and their good prediction performance for $d=3$ (see Sect. 6).

Sections 6 and 7 compare the local IMSPE optimal and W-IMSPE optimal designs from Table 1 with maximin LHDs, minimum average reciprocal distance LHDs, and MaxPro designs. The LHDs used in this paper were obtained from the website of van Dam et al. (2013). The MaxPro designs were constructed using the R package (2016) MaxPro (Ba and Joseph 2015) based on the software’s default initialization and update values.

5.2 Test-beds of stationary functions

In all, six test-beds of functions $y(\cdot )$ were constructed to compare the prediction accuracy of the designs listed in Sect. 5.1. The construction of four stationary test-bed families is described in this subsection and the construction of two non-stationary test-bed families is presented in Sect. 7.

The method of Trosset (1999) was used to provide families of stationary Kriging interpolator test surfaces; each such surface has the form

$$\begin{aligned} y_{\mathrm{test}}(\varvec{w}) = \hat{\beta }_{0}+\varvec{r}(\varvec{w})^T \varvec{R}^{-1} \left( \varvec{Y}^{500}-\varvec{1}_{500}\ \hat{\beta }_0 \right) , \end{aligned}$$

(11)

for $\varvec{w}\in \left[ 0,1\right] ^d$, where $\varvec{Y}^{500}$ is a $500 \times 1$ vector drawn from a Gaussian process $Y(\varvec{x})$ at $\varvec{x} \in \varvec{L}$, where $\varvec{L}$ is an (approximate) maximin LHD in $\left[ 0,1\right] ^d$ of size $500 \times d$. The process $Y(\varvec{x})$ was taken to have mean $\beta _0=100$, variance $\sigma _Z^2=10$, and the Gaussian correlation function in (2), with $\varvec{\rho }=(\rho _1,\rho _2,\ldots ,\rho _d)^T$ specified in the next paragraph. From the description below (3), $\varvec{R}$ is the $500 \times 500$ matrix of correlations with the given $\varvec{\rho }$, and $\varvec{r}(\varvec{w})$ is the $500 \times 1$ vector of correlations with same $\varvec{\rho }$. For numerical stability, a nugget of size $10^{-6}$ was added to the diagonal of $\varvec{R}$ when computing (11).

The following four correlation families were used to generate the test-bed of response surfaces using (11):

• 1. Deterministically Common Correlation: Two test-bed families have $\rho _1=\rho _2=\ldots =\rho _d=\rho$ and are denoted ${\mathrm{DC}}_{.25}$ and ${\mathrm{DC}}_{.5},$ corresponding to $\rho = .25$ and .50, respectively.

• 2. Stochastically Common Correlation: Two test-bed families have $\rho _1,$ $\rho _2,$ $\ldots ,$ $\rho _d$ independently drawn from a common beta distribution and are denoted ${\mathrm{SC}}_{.25}$ and ${\mathrm{SC}}_{.5},$ corresponding to ${\mathrm{beta}}(5,13)$ and ${\mathrm{beta}}(11.34,$ 11.34), respectively, where the subscript denotes the mode of the distribution.

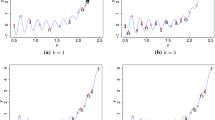
The common $\rho _{i}$ correlation for each input that is used by ${\mathrm{DC}}_{.25}$ and ${\mathrm{DC}}_{.5}$ when forming $\varvec{Y}^{500}$, allows each input to have the same opportunity to influence $y_{\mathrm{test}}(\varvec{w})$. However, because $\rho _1, \ldots , \rho _d$ need not be equal for ${\mathrm{SC}}_{.25}$ and ${\mathrm{SC}}_{.5}$, the inputs have (stochastically) different influences on $y_{\mathrm{test}}(\varvec{w})$ for these two test-beds. Representative draws $y_{\mathrm{test}}(\varvec{w})$ from the ${\mathrm{DC}}_{.25}$ and ${\mathrm{DC}}_{.5}$ families are shown in Fig. 2.

Fig. 2

Examples of draws $y_{\mathrm{test}}(\varvec{w})$ from the stationary test-bed (11) with $d=2$ using a $\varvec{\rho }= (.25, .25)^T$, b $\varvec{\rho }= (.50, .50)^T$

The four test-bed families described in the previous paragraph were selected to show clear distinction between the designs being assessed. Other families such as $DC_{.75}$, originally considered but not included here, produced surfaces for which outputs were nearly constant across the input space, so that all designs had similar performance. The four test-beds used in the current study produced substantial variation among the draws from $y_{\mathrm{test}}(\varvec{w})$ in (11).

One hundred surfaces were drawn from each test-bed family. This number was determined using an approximate sample size calculation for $d = 3$ and $d = 5$ to allow a difference in the empirical root mean squared prediction error (to be defined in (13) below) of 0.15 to be detected with probability .96 if a paired t-test were to be conducted at level .05 (Bechhofer et al. 1995). (This was based on the fact that a pilot study showed a typical range of the empirical root mean squared prediction error was 0.8–1.5.) Thus, in total, there were $4 \times 100 = 400$ surfaces drawn for each input size $d=3,5,8,10,$ and 20. The same set of 400 surfaces was used to evaluate the $15 \times 3$ and $30 \times 3$ designs, and likewise for the $25 \times 5$ and $50 \times 5$ designs, and also the $40 \times 8$ and $80 \times 8$ designs.

6 Comparison of designs for predicting stationary surfaces

Because the designs in this paper are constructed specifically for prediction, the local IMSPE optimal and the W-IMSPE optimal designs in Table 1 are compared with each other and then with the space-filling LHDs and MaxPro designs in terms of their relative prediction accuracy. Prediction is performed using

$$\begin{aligned} \widehat{y}^{E}(\varvec{x}_0) = \widehat{{\beta }}_{0} + \widehat{\varvec{r}}(\varvec{w})^T \widehat{\varvec{R}}^{-1} \left( \varvec{y}^n-\varvec{1}_{n} \widehat{{\beta }}_{0} \right) , \end{aligned}$$

(12)

which is an empirical best linear unbiased predictor that is based on a constant-mean Gaussian process with an unknown process variance $\sigma ^{2}_{Z}$ and the Gaussian correlation function (2) having unknown correlation parameter values $\varvec{\rho } = (\rho _{1}, \ldots , \rho _{d})^T$. Here $\varvec{y}^n$, $\widehat{\varvec{r}}(\varvec{w}) = \left( R \left( \varvec{w}-\varvec{x}_j \mid \widehat{\varvec{\rho }} \right) \right)$ and $\widehat{\varvec{R}} = \left( R \left( \varvec{x}_i-\varvec{x}_j \mid \widehat{\varvec{\rho }} \right) \right)$ are defined as in (3) but with $\widehat{\varvec{\rho }}$ estimated using restricted maximum likelihood (REML), while $\widehat{\beta }_{0} =$ $\left( \varvec{1}_{n}^{T} \widehat{\varvec{R}}^{-1} \varvec{y}^n\right) /$ $\left( \varvec{1}_{n}^{T} \widehat{\varvec{R}}^{-1} \varvec{1}_{n} \right)$. In this paper, all REML estimates of $\varvec{\rho }$ and $\widehat{y}^{E}(\varvec{x}_0)$ were calculated using the software MATLAB Parametric Empirical Kriging (MPErK) (2013).

Given a design $\varvec{X}$ and a test-bed output function $y_{\mathrm{test}}(\varvec{w})$, $\varvec{w}\in [0,1]^d$, training data $\varvec{y}^n$ were computed at the design points $\varvec{x}_1, \ldots , \varvec{x}_n$ in design $\varvec{X}$, REML estimates of $\varvec{\rho }$ were calculated, and $\widehat{y}^{E}(\varvec{x})$ in (12) was evaluated at a space-filling set of g test points in $[0,1]^d$. The prediction accuracy of design $\varvec{X}$ for the test function $y_{\mathrm{test}}(\varvec{w})$ was quantified by the empirical root mean squared prediction error defined as

$$\begin{aligned} {{{\mathrm{PE}}}}&(\varvec{X},y_{\mathrm{test}}(\varvec{x})) = \sqrt{\frac{1}{g} \sum _{i=1}^{g} \left( \widehat{y}^E(\varvec{x}_i) - y_{\mathrm{test}}(\varvec{x}_i) \right) ^2}\, . \end{aligned}$$

(13)

The g test points were formed as follows. For $d=3$, the test points formed an equally-spaced grid having 50 values/input ($0, 1/49, 2/49,\ldots ,1$) yielding a total of $g=50^3=$ 125,000 points. For $d=5$, the test points were again an equally-spaced grid but now containing 10 points/input $\left( 0,1/9, 2/9,\ldots ,1 \right)$; thus $g=10^5=$ 100,000 total points. The use of grids became infeasible for $d \in \{8,10, 20\}$. Instead, to ensure adequate coverage of $[0,1]^{d}$ for these cases, a d-dimensional Sobol’ sequence of size $g=2^{17} =$ 131,072 points was used as the test set of inputs. The number of Sobol’ points was selected based on a pilot study which showed that, for these three d cases, $g=2^{17}$ gave accurate values of $\hbox {PE}(\varvec{X},y_{\mathrm{test}}(\varvec{x}))$ (13) for several closed-form functions $y_{\mathrm{test}}$ with known root mean squared prediction errors.

In what follows, we use the notation in Sect. 5.2 for the test functions, the names in Table 1 for the IMSPE-based designs (that is, $I_{.25}, I_{.5}, I_{.75}$ and $W_{.25W},$ $W_{.25N}$, $W_{.5N}$), and the notation MmL, mAL, MaxPro for the maximin LHDs, the minimum average reciprocal distance LHDs, and the maximum projection designs, respectively.

For each test-bed $T\in \{DC_{.25}, DC_{.5},$ $SC_{.25},$ $SC_{.5}\}$, 100 random test functions $S_{T,i}$, $i = 1,2,\ldots ,100,$ were drawn. Then for each design $\varvec{X}$ in

$$\begin{aligned} \{&I_{.25}, I_{.5}, I_{.75}, MmL, mAL, MaxPro, \nonumber \\&W_{.25W}, W_{.25N}, W_{.5N} \}, \end{aligned}$$

(14)

training data were formed by evaluating each $S_{T,i}$ at $\varvec{X}$. To simplify notation, $\hbox {PE}(\varvec{X},y_{\mathrm{test}}(\varvec{x}))$ in (13) calculated for $S_{T,i}$ and using design $\varvec{X}$ is denoted $\hbox {PE}(\varvec{X}, {T,i})$.

For $d=3$ the designs were compared as follows. For each fixed $n \in \{ 15, 30\}$, test-bed T, and design $\varvec{X}$ in (14), $\hbox {PE}(\varvec{X}, {T,i})$ was determined separately for each of the 100 test functions $S_{T,i}$, $i = 1,2,\ldots ,100,$ drawn from T. For each test function $S_{T,i}$, $i = 1,2,\ldots ,100,$ let $\varvec{X}^*_{{T,i}}$ denote the design having the smallest value of $\hbox {PE}(\varvec{X}, {T,i})$ among the nine designs. Because the test functions $y_{\mathrm{test}}(\varvec{x})$ can vary substantially in their complexity, even when drawn from the same test-bed, the empirical root mean squared prediction error was normalized by calculating $\hbox {PE}(\varvec{X}, {T,i})$ relative to the best prediction over all the designs evaluated; i.e., by

$$\begin{aligned} {\mathrm{rPE}}(\varvec{X}, {T,i}) = {\mathrm{PE}}(\varvec{X}, {T,i}) / {\mathrm{PE}}(\varvec{X}^*_{{T,i}}, {T,i})\,. \end{aligned}$$

(15)

Note that while designs can be compared for each fixed d, n, and T via $\hbox {rPE}(\varvec{X}, {T,1})$, ..., $\hbox {rPE}(\varvec{X}, {T,100})$, one cannot compare designs for different d, n, or T. For example the empirical root mean squared prediction error is (almost always) smaller for larger n so that a design which appears “better” for a larger n compared with a design that uses a smaller n may only reflect sample size differences. However, an interesting comparison of the effect of sample size will be described in the Discussion of Sect. 8.

Returning to the $d =3$ comparisons, for each $n \in \{15, 30\}$, and for each test-bed family T, the values of $\hbox {rPE}(\varvec{X}, T,1)$, ..., $\hbox {rPE}(\varvec{X}, T,100)$ were ordered from largest to smallest, and plotted (see Fig. 3 for the $\hbox {rPE}(\varvec{X}, {T,i})$ comparisons when $n=30$ and the Supplementary Material for the $n= 15$ comparisons). All rPE plots group values greater than 1.4; i.e., rPE values greater than or equal to 1.4 are shaded with the same intensity. Designs that have the best or close-to-the-best prediction accuracy of 1.0 have bars with the large light area. So, for example, for the $DC_{.25}$ test functions in Fig. 3 (the top left panel), approximately 40% of the leftmost bar is almost white, indicating that the design $I_{.25}$ led to the best, or close to the best, predictions across 40 of the 100 $DC_{.25}$ test surfaces. Only about 20% of the time did this design exceed 30% larger prediction errors than the best design, i.e., only about 20% of the draws from $DC_{.25}$ resulted in $\hbox {rPE}(\varvec{X}, {T,i})$ values $\ge 1.3$.

Fig. 3

For $(n,d)=(30,3)$, the ordered $\hbox {rPE}(\varvec{X}, {T,i})$ values (15) for 100 $S_{T,i}$ test functions from $T{\in }\{DC_{.25}, DC_{.5},$ $SC_{.25}, SC_{.5}\}$ when using training data based on $\varvec{X}{\in } \{I_{.25},$ $I_{.5},$ $I_{.75}$, MmL, mAL, MaxPro, $W_{.25W}, W_{.25N}, W_{.5N} \}$

From the darkness of the bars in Fig. 3 below and Fig.1 of the Supplement, it is clear that, for $d=3$ and both $n = 15$ and 30, the MmL, mAL, and MaxPro space-filling designs have an inferior prediction performance for these stationary test functions than most of the IMSPE-based designs. Second, in searching for designs that perform well for all four stationary test-beds and for both sample sizes n, no design criterion uniformly dominates all others over all scenarios, but $I_{.25}, I_{.5}, W_{.25W}, W_{.5N}$ all have good prediction performance, at least for some scenarios. Because designs $W_{.25W}$ and $W_{.5N}$ do not perform consistently better than $I_{.25}$ and $I_{.5}$ but require considerably more time to construct (see Table 1 of the Supplementary Material), the weighted designs will be omitted from consideration for the larger d cases.

As for $d=3$, the d = 5, 8, and 10 input cases use $n = 5 \times d$ and $10 \times d$ training runs, but the $d=20$ case uses only $n = 5\times d$ training runs due to the large number of inputs. Figures 4, 5, and 6 plot rPE$(\varvec{X}, {T,i})$ values (15) for $(n,d)=(80,8),$ (100, 10),  and (100, 20), respectively. The additional (n, d) cases are plotted in the Supplementary Material.

Fig. 4

For $(n,d)=(80,8)$, the ordered $\hbox {rPE}(\varvec{X}, {T,i})$ values (15) for 100 $S_{T,i}$ test functions from $T{\in }\{DC_{.25},$ $DC_{.5},$ $SC_{.25},$ $SC_{.5}\}$ when using training data based on $\varvec{X}{\in } \{I_{.25},$ $I_{.5},$ $I_{.75}, MmL, mAL, MaxPro\}$

Comparing the sizes of the dark areas of the plots shows that the $DC_{.5}$ and $SC_{.5}$ test-beds are predicted less consistently across designs than test-beds $DC_{.25}$ and $SC_{.25}$. Examining the $n = 10\times d$ cases, the $I_{.25}$ local IMSPE-optimal designs have smaller $\hbox {rPE}(\varvec{X}, {T,i})$ values than the other five designs.

Fig. 5

For $(n,d)=(100,10)$, the ordered $\hbox {rPE}(\varvec{X}, {T,i})$ values (15) for 100 $S_{T,i}$ test functions from $T{\in }\{DC_{.25}, DC_{.5},$ $SC_{.25}, SC_{.5}\}$ when using training data based on $\varvec{X}{\in } \{I_{.25},$ $I_{.5}, I_{.75}$, MmL, mAL, MaxPro}

Fig. 6

For $(n,d){=}(100,20)$, the ordered $\hbox {rPE}(\varvec{X}, {T,i})$ values (15) for 100 $S_{T,i}$ test functions from $T\in \{DC_{.25}, DC_{.5},$ $SC_{.25}, SC_{.5}\}$ when using training data based on $\varvec{X}{\in } \{I_{.25},$ $I_{.5}, I_{.75}$, $MmL, mAL, MaxPro\}$

In the difficult-to-predict $(n,d)= (100,20)$ case, Fig. 6 shows that $I_{.25}$ is again the dominant local IMSPE optimal design, and $I_{.75}$ is clearly inferior. The space-filling MmL and MaxPro designs are at least as effective as $I_{.25}$ for all test-beds and dominate $I_{.25}$ for $DC_{.5}$ and $SC_{.5}$.

Fig. 7

Non-stationary $y_\mathrm{test}(\varvec{w})$ draws from a $\hbox {NS}_{\mathrm{edge}}$ and from b $\hbox {NS}_{\mathrm{mid}}$

In summary, we recommend using the $I_{.25}$ design when predicting smooth functions that are consistent with being a draw from a stationary process. The situation of effect sparsity has not been considered in this paper, and is left for future work.

7 Comparison of designs for predicting non-stationary surfaces

This section extends the comparison of the designs’ prediction accuracy to non-stationary functions. Two test-beds of strongly non-stationary functions are considered. For $d=3$ the nine design classes in (14) that are compared in Sect. 6 are also evaluated for these two test-beds; again because of computational expense, only the first six designs are compared for $d \ge 5$. As will be seen, the prediction results are in striking contrast to those of Sect. 6.

Both test-beds studied in this section start with the base function

$$\begin{aligned} y_{\mathrm{test}}(\varvec{w})&= 10^{d/2} \prod _{i=1}^d \left[ \sin \left( a_i \left( w_i-b_i \right) ^4 \right) \right. \cos \left( 2\left( w_i - b_i\right) \right) \nonumber \\&\left. + \,\frac{w_i - b_i}{2} \right] , \end{aligned}$$

for $\varvec{w}\in \left[ 0,1\right] ^d$, which was proposed initially by Xiong et al. (2007) and was also used by Ba and Joseph (2012). The test function $y_{\mathrm{test}}(\varvec{w})$ has non-stationary activity occurring near the edges of $\left[ 0,1\right] ^d$. The first non-stationary test-bed, denoted $\hbox {NS}_{\mathrm{edge}}$, takes $a_1, a_2, \ldots , a_d$ to be i.i.d. $\hbox {Uniform}(20,35)$ draws and $b_1, b_2, \ldots , b_d$ to be i.i.d. $\hbox {Uniform}(0.5,0.9)$ draws. The second test-bed, denoted $\hbox {NS}_{\mathrm{mid}}$, uses the function $y_{\mathrm{test}}(\left| \varvec{v} - .5 \right| )$, $\varvec{v} \in \left[ 0,1\right] ^d$, and the same distributions for the $\{ a_i\}$ and $\{ b_i\}$ as does $\hbox {NS}_{\mathrm{edge}}$. The non-stationary activity in this second formulation occurs near the middle of $\left[ 0,1\right] ^d$. Panels (a) and (b) of Fig. 7 show, for $d=2$, one function drawn from each of $\hbox {NS}_{\mathrm{edge}}$ and $\hbox {NS}_{\mathrm{mid}}$, respectively. One hundred test surfaces were drawn from each of the $\hbox {NS}_{\mathrm{edge}}$ and $\hbox {NS}_{\mathrm{mid}}$ families for each d studied.

Fig. 8

For $(n,d)=(30,3)$, the ordered $\hbox {rPE}(\varvec{X}, {T,i})$ values for 100 $S_{T,i}$ test functions from $T {\in } \{\mathrm{NS}_{\mathrm{edge}}$, ${\mathrm{NS}}_{\mathrm{mid}}\}$ when using training data based on $\varvec{X}{\in } \{I_{.25}, I_{.5}, I_{.75}$, $MmL, mAL, MaxPro, W_{.25N}, W_{.25W}, W_{.5N}\}$

Fig. 9

For $(n,d)=(25,5)$, the ordered $\hbox {rPE}(\varvec{X}, {T,i})$ values for 100 $S_{T,i}$ test functions from $T\in \{\mathrm{NS}_{\mathrm{edge}}, {\mathrm{NS}}_{\mathrm{mid}}\}$ when using training data based on $\varvec{X}\in \{I_{.25}, I_{.5}, I_{.75}$, $MmL, mAL, MaxPro\}$

Fig. 10

For $(n,d)=(50,5)$, the ordered $\hbox {rPE}(\varvec{X}, {T,i})$ values for 100 $S_{T,i}$ test functions from $T\in \{\mathrm{NS}_{\mathrm{edge}}, {\mathrm{NS}}_{\mathrm{mid}}\}$ when using training data based on $\varvec{X}\in \{I_{.25}, I_{.5}, I_{.75}$, $MmL, mAL, MaxPro\}$

Sorted $\hbox {rPE}(\varvec{X}, {T,i})$ values are shown in Figures 8, 9, 10, and 11 for the $(n,d) = (30,3), (25,5), (50,5),$ and (80, 8), respectively; corresponding figures for the remaining design sizes studied are in the Supplementary Material. When $d = 3$ and $n = 10/\hbox {input}$, the space-filling designs mAL and MmL are among the best of the nine designs considered, together with the locally optimal $I_{.25}$ design and the weighted $W_{.25W}$ design. The larger gray areas in the $\hbox {NS}_{\mathrm{mid}}$ plots indicate that the draws from $\hbox {NS}_{\mathrm{mid}}$ are less consistently predicted by the nine designs in (14) than are draws from $\hbox {NS}_{\mathrm{edge}}$.

For $d \ge 5$, and the $\hbox {NS}_{\mathrm{mid}}$ draws, the space-filling design mAL outperforms the MmL and MaxPro designs which, in turn, outperform all three local IMSPE optimal designs. This conclusion is refined by fixing $d=5$ and comparing the results for the smaller data case of $n = 5/\hbox {input}$ in Fig. 9 with the larger data case of $n = 10/\hbox {input}$ in Fig. 10. The designs mAL, MmL, and MaxPro have nearly equivalent performance for the smaller data case but mAL is substantially better than the other two types of design once there are “adequate” runs, here $10/\hbox {input}$, to detect mid domain non-stationarities.

For the large d cases and draws from $\hbox {NS}_{\mathrm{edge}}$, $I_{.25}$ is a tiny bit better than $I_{.5}$ or $I_{.75}$ while mAL is a better design than MmL and MaxPro, and becomes comparable to $I_{.25}$ especially for large d, i.e., say $d \ge 10$. The figures in the Supplementary Material confirm this trend. Finally, the $d \ge 5$ plots make clear that space-filling designs produce prediction errors which are, on average, 40% smaller than locally optimal designs for draws from $\hbox {NS}_{\mathrm{mid}}$, i.e., the locally optimal designs have $\hbox {rPE}(\varvec{X}, {T,i})$ values $\ge 1.4$ for over half the draws from $\hbox {NS}_{\mathrm{mid}}$. However, the more easily predicted draws from $\hbox {NS}_{\mathrm{edge}}$ have predictions using local designs that are virtually comparable to those from the space-filling designs.

Fig. 11

For $(n,d)=(80,8)$, the ordered $\hbox {rPE}(\varvec{X}, {T,i})$ values for 100 $S_{T,i}$ test functions from $T\in \{\mathrm{NS}_{\mathrm{edge}}, {\mathrm{NS}}_{\mathrm{mid}}\}$ when using training data based on $\varvec{X}\in \{I_{.25}, I_{.5}, MmL, mAL, MaxPro\}$

8 Summary and discussion

This paper compares the prediction accuracy of two groups of designs in terms of their empirical root mean squared prediction errors when predicting stationary or non-stationary simulator output. One group of designs uses IMSPE-based design criteria and the other group uses space-filling criteria. Three of the IMSPE-based design criteria use (7) with a fixed and common correlation, and three use (8). Each of the designs was used to collect training data from test-bed functions, both stationary and non-stationary, and predictions were made using the empirical best linear unbiased predictor at a comprehensive set of additional inputs for these functions. The empirical prediction errors for each function were compared to determine designs that produced the best predictions.

Based on the test functions examined in this paper, the $I_{.25}$ design is recommended when predicting smooth “stationary” surfaces. Although, for the small $d = 3$ case, $I_{.5}$, $W_{.25W}$, and $W_{.5N}$ also perform well. However, not showing any predictive improvement over local IMSPE optimal designs and requiring substantially greater computational effort, the W-IMSPE optimal designs are eliminated from further consideration. Similarly, $I_{.5}$ can slightly underperform $I_{.25}$ for larger d cases. The stationary test-bed functions were selected to show clear distinction between the designs being assessed. Other families, such as $DC_{.75}$, produced surfaces for which outputs were nearly constant across the input space, so that all designs had similar performance.

For functions having pronounced non-stationary activity near the “middle” of the input domain, the space-filling LHDs and maximum projection designs were the best three designs. The minimum average reciprocal distance LHD, mAL, was particularly dominant for the “large” d cases. For functions having non-stationary activity nearer the “edge” of the input domain, both the mAL and $I_{.25}$ designs are recommended.

The authors recognize that many additional criteria could have been applied to form space-filling designs. It has not been the objective of this paper to provide a comprehensive review of the predictive performance of every class of space-filling designs that has been proposed in the literature. Rather, we have selected designs constructed using three widely-used space-filling criteria and compared these designs with two classes of IMSPE-based designs using one important statistical basis, empirical prediction accuracy. The results suggest that other space-filling designs will show a similar dichotomy in their performance, when compared with IMSPE-based designs.

The situation of effect sparsity has not been considered in this paper, and is left for future work.

Fig. 12

For $d=3$, boxplots of the ratios of the $\hbox {PE}(\varvec{X}, {T,i})$ values when $n=15$ to $n=30$ for 100 $S_{T,i}$ test functions drawn from $T\in \{DC_{.25}, DC_{.5}, SC_{.25}, SC_{.5}\}$ when using training data based on $\varvec{X}\in \{I_{.25}, I_{.5}, I_{.75}$, MmL, mAL, MaxPro, $W_{.25W}, W_{.25N}, W_{.5N} \}$

Fig. 13

For $d=3$, boxplots of the ratios of the $\hbox {PE}(\varvec{X}, {T,i})$ values when $n=15$ to $n=30$ for 100 $S_{T,i}$ test functions drawn from $T\in \{\mathrm{NS}_{\mathrm{edge}}, \mathrm{NS}_{\mathrm{mid}}\}$ when using training data based on $\varvec{X}\in \{I_{.25}, I_{.5}, I_{.75}$, MmL, mAL, MaxPro, $W_{.25W}, W_{.25N}, W_{.5N} \}$

Tables 1 and 2 of the Supplementary Material show the computation times for constructing the IMSPE-based designs in this paper. It would be of interest to make a more complete study of the effect on construction time of increasing the number of input variables d and the number of runs n.

Figures 12 and 13 provide a quantitative assessment of the effect on the prediction error of doubling the number of runs from 15 to 30 when $d=3$. For each of the 100 test functions drawn from the four stationary test-beds $\hbox {DC}_{.25}$, $\hbox {DC}_{.5}$, $\hbox {SC}_{.25}$, and $\hbox {SC}_{.5}$ and for each of the nine design types, Fig. 12 shows side-by-side boxplots of the 100 ratios of the value of the empirical root mean squared prediction error, $\hbox {PE}(\varvec{X}, {T,i})$ in (13), when $n=15$ divided by the corresponding values when $n=30$. Intuition suggests that, if $n=30$, $\hbox {PE}(\varvec{X}, {T,i})$ should be smaller than if $n=15$; this is true for most test-bed functions. Figure 12 shows that this is essentially true for all test-bed function draws from every stationary test-bed $\times$ design combination. The $\hbox {DC}_{.25}$ and $\hbox {SC}_{.25}$ panels show the boxplots of the ratios of $\hbox {PE}(\varvec{X}, {T,i})$ for test-beds have a median of about 2, i.e., there is a 50% reduction in empirical prediction error when doubling the number of runs. The $\hbox {DC}_{.5}$ and $\hbox {SC}_{.5}$ panels show that doubling the number of runs produces test-bed median $\hbox {PE}(\varvec{X}, {T,i})$ ratios between 2 and 3, i.e., the prediction error decreases by 50–67% when doubling the number of runs. Finally, the ratios for these two test-beds have greater range that those of the $\hbox {DC}_{.25}$ and $\hbox {SC}_{.25}$ test-beds.

Figure 13 shows comparative boxplots of the same ratio for the $\hbox {NS}_{mid}$ and $\hbox {NS}_{edge}$ non-stationary test-beds. The most important conclusion that is drawn from Fig. 13 is that the median ratios of empirical root mean squared prediction errors for both test-beds and all designs are approximately 1, i.e., for half the test-bed functions, doubling the number of runs from 15 to 30 increases the prediction error. For most test-bed $\times$ design cases, all 100 ratios are less than 2 so that even when doubling the number of runs produces smaller prediction errors, there is never more than a 50% decrease in the prediction error. This dramatic result emphasizes the critical importance of the experimental design; designs constructed for one model can perform poorly when used to predict functions from test-beds that violate the assumptions underlying the design construction.