1 Introduction

The idea of using tempered transitions has gained increased attention in Bayesian statistics as a method to improve the efficiency of Markov chain Monte Carlo (MCMC) algorithms in terms of exploring the target posterior distribution. Sophisticated methods such as the Metropolis-coupled MCMC (Geyer 1991), the simulated tempering (Marinari and Parisi 1992; Geyer and Thompson 1995), the sequential Monte Carlo (Del Moral et al. 2006), and the annealed sampling (Neal 1996, 2001) incorporate transitions to overcome the slow mixing of the MCMC algorithms in multi-modal densities; see Behrens et al. (2012) for an insightful review.

Here, we work on the ideas of path sampling (Gelman and Meng 1994, 1998) where simulated output of tempered transitions schemes can be are employed in order to estimate the ratio of two intractable normalizing constants. In particular, let \(q_0(\varvec{\theta })\) and \(q_1(\varvec{\theta })\) be two unnormalized densities and \(z_0\), \(z_1\) be their normalizing constants leading to

$$\begin{aligned} p_t(\varvec{\theta })=\frac{q_t(\varvec{\theta })}{z_t }, \quad \text{ where } \; z_t=\int _{\varvec{{\varTheta }}} q_t(\varvec{\theta })\,d\varvec{\theta }, \quad \text{ for } \; t=0,1. \end{aligned}$$
(1)

Gelman and Meng’s (1998) method is based on the construction of a continuous and differentiable path \(q_t(\varvec{\theta })=h(q_1,q_0,t)\) which is used to estimate the ratio of normalizing constants \(\lambda =z_1/z_0\) via the thermodynamic integration (TI) identity

$$\begin{aligned} \log \lambda= & {} \int _0^1 \int _{\varvec{{\varTheta }}} \frac{d \,\log \,q_t(\varvec{\theta })}{dt}\,p_t(\varvec{\theta })\, d \varvec{\theta }\,dt \nonumber \\= & {} \int _0^1 E_{p_t} \big \{U(\varvec{\theta })\big \} dt, \end{aligned}$$
(2)

where \(U(\varvec{\theta }) = \frac{d \,\log \,q_t(\varvec{\theta })}{dt}\) and \(E_{p_t} \big \{U(\varvec{\theta })\big \}\) stands for the expectation over the sampling distribution \(p_t(\varvec{\theta })\). The scalar \(t \in [0,1]\) is often referred to as the temperature parameter, since the TI has its origins in thermodynamics and specifically in the calculation of the difference in the free energy of a system. Here we focus on geometric paths (Neal 1993) of the form

$$\begin{aligned} q_t(\varvec{\theta })=q_1(\varvec{\theta })^t q_0(\varvec{\theta })^{1-t}, \end{aligned}$$
(3)

for specific choices of \(q_0(\varvec{\theta })\) and \(q_1(\varvec{\theta })\). For example, Friel and Pettitt (2008) have used the path \(q_t(\varvec{\theta })= f( \varvec{y} | \varvec{\theta } )^{t} f( \varvec{\theta } )\) and therefore set the unnormalized posterior as \(q_1\) and the prior as \(q_0\). In the general case, (2) under geometric paths becomes

$$\begin{aligned} \log \lambda = \int _0^1 \int _{\varvec{{\varTheta }}} \log \frac{q_1(\varvec{\theta })}{q_0(\varvec{\theta })}\, p_t(\varvec{\theta })\, d\varvec{\theta }\, dt. \end{aligned}$$
(4)

since \(U(\varvec{\theta }) = \log q_1(\varvec{\theta }) - \log q_0(\varvec{\theta })\) .

The ideas of the thermodynamics have important applications on a variety of scientific fields, such as physics, chemistry, biology and computer science (machine learning, pattern recognition) among others. As Gelman and Meng (1998) note, methods related to the TI have been developed by researchers from different disciplines working independently and in parallel (Frenkel 1986; Binder 1986; Ogata 1989). Within Bayesian statistics, a straightforward application of the TI refers to model comparison. In fact, current research in Bayesian statistics focuses on three interesting topics, namely

  1. (a)

    on using the TI method to estimate the marginal likelihood and/or the Bayes factor (BF, Kass and Raftery 1995),

  2. (b)

    on the connection between the TI and measures of divergence between probability distributions,

  3. (c)

    and finally, on assessing the sources of error when estimating \(\lambda \) based on (b).

In Sect. 2 we present existing and new thermodynamic identities for Bayesian model comparison (a). We also consider an alternative approach for path sampling, based on the stepping-stone identity considered in Neal (1993) and applied in this context by Xie et al. (2011) and Fan et al. (2011). Any blanks in the list of previously reported estimators based on the two different approaches are filled in by introducing new estimators using a identity-path selection rationality. We further discuss the implementation of the two alternative approaches in the direct Bayes factor estimation and we introduce the compound paths which can be used to efficiently switch between competing models of different dimension located at the endpoints of the path.

With regard to (b), Friel and Pettitt (2008), Calderhead and Girolami (2009), Lefebvre et al. (2010) and Behrens et al. (2012) under different motivations and scopes, outline the close relationship between the TI and the relative entropy, best known in statistics as the Kullback-Leibler divergence (KL; Kullback and Leibler 1951), which can be derived at the endpoints of the TI. In Sect. 3, we examine what happens at the intermediate points, \(t\in (0,1)\), and we describe the mechanism which eventually produces the relative entropy at the initial (\(t=1\)) and final (\(t=0\)) states.We introduce the functional KL, defined at each temperature, which is implemented to show that (4) is directly linked to other measures of divergence between probability distributions, such as the Chernoff information (Chernoff 1952), the Bhattacharyya distance (Bhattacharyya 1943) and Rényi’s relative entropy (Rényi 1961). In this context, we show that there is an optimal point \(t^*\), where the sampling distribution is equidistant (in the KL sense) from the endpoint densities and where the ratio of interest \(\lambda \) could be derived directly, avoiding the thermodynamic integration.

In Sect. 3, based on our findings on the uncertainty at the intermediate points, we further examine and geometrically represent the structure of the thermodynamic integral. This approach provides insight and assists us to understand the path sampling estimators of \(\lambda \) in terms of error, assessing (b). In particular, the path-related variance is geometrically approached and it is highlighted that any variance reduction in the thermodynamic estimators should primarily focus on the path implemented. We identify why large discretisation error occurs and we discuss on its reduction by adopting more efficient (in terms of error) paths and subsequently well designed tempering schedules.

The paper closes with an illustration of the methods and estimators discussed here in a common regression example (previously used by Friel and Pettitt 2008 and Lefebvre et al. 2010 for marginal likelihood estimation) and in a demanding latent trait model implementation using a simulated dataset.

2 Bayesian model comparison using tempered transitions

Let us consider two competing models, \(m_1\) and \(m_0\), with equal prior probabilities. Then, the Bayes factor (BF; Jeffrey 1961; Jeffreys 1935; Kass and Raftery 1995) is derived as the ratio of the marginal likelihoods

$$\begin{aligned} f(\varvec{y}|\,m_i) = \int _{\varvec{{\varTheta }}} f (\varvec{y} |\,\varvec{\theta },m_i) \pi (\varvec{\theta }|\,m_i)\, d\varvec{\theta } \end{aligned}$$
(5)

for each model \(m_1\) and \(m_0\); where \(\varvec{y}\) denotes the data matrix and \(\pi (\varvec{\theta }|m_i)\) is the prior density of the parameter vector under the model \(m_i\). The integral involved in the marginal likelihood (Eq. 5) is often high dimensional making its analytic computation infeasible. Therefore a wide variety of MCMC based methods have been developed for its estimation; see, for example, in Chib (1995); Gelman and Meng (1998); Lewis and Raftery (1997) among others.

Since the marginal likelihood is the normalizing constant of the posterior distribution \(f(\varvec{\theta }|\varvec{y},m_i)\) it can be estimated by path sampling. Recently, such methods have been considered by Lartillot and Philippe (2006), Friel and Pettitt (2008) and Lefebvre et al. (2010). Oates et al. (2015) in addition combine the thermodynamic integration with control variables.

2.1 The stepping-stone identity

In this section we consider an alternative approach that is based on the stepping-stone sampling, an importance sampling example considered for the estimation of the marginal likelihood in Xie et al. (2011) and Fan et al. (2011). Closely related ideas are also discussed in the context of the free energy estimation in Neal (1993, see section 6.2 and references within); see also in Meng and Wong (1996) and Liang and Wong (2001) for earlier uses of the stepping stone identity in path link Monte Carlo algorithms. The stepping-stone sampling considers finite values \(t_i \in \mathcal{T}\), that are placed according to a temperature schedule. The ratio of the normalizing constants can be expressed as

$$\begin{aligned} \lambda = \frac{z_{1}}{z_{0}}=\frac{z_{t_n}}{z_{t_{n-1}}}\frac{z_{t_{n-1}}}{z_{t_{n-2}}} \dots \frac{z_{t_{1}}}{z_{t_0}}=\prod _{i=0}^{n-1} \frac{z_{t_{i+1}}}{z_{t_{i}}}. \end{aligned}$$

Hence, the ratio of the normalizing constants are derived using \(z_{t_{i+1}}/z_{t_{i}}\) as an intermediate step which can be estimated from t specific MCMC samples based on the identity

$$\begin{aligned} \frac{z_{t_{i+1}}}{z_{t_{i}}}= \int _{\varvec{{\varTheta }}} \frac{q_{t_{i+1}}(\varvec{\theta })}{q_{t_{i}}(\varvec{\theta })} ~p_{\,t_{i}}(\varvec{\theta }) \,d\varvec{\theta }; \end{aligned}$$

see Xie et al. (2011) for details. For geometric paths, the stepping-stone identity for \(\lambda \) is then given by

$$\begin{aligned} \lambda = \prod _{i=0}^{n-1}\int _{\varvec{{\varTheta }}} \left\{ \frac{q_1(\varvec{\theta })}{q_0(\varvec{\theta })} \right\} ^{{\varDelta }(t_i)}p_{\,t_{i}}(\varvec{\theta })\,d\varvec{\theta }. \end{aligned}$$
(6)

Xie et al. (2011) presented the stepping-stone sampling specifically for estimating the marginal likelihood (under a certain geometric path) while Fan et al. (2011) modified the initial marginal likelihood estimator in order to improve its properties (both estimators are addressed later on in this section). However, as outlined here, the stepping-stone sampling can be considered as a general method, alternative to path sampling, that can be applied for the estimation of ratios of unknown normalisation constants.

In this section we outlined that the identities (4) and (6), are two closely related alternative tempered transition methods for the estimation of normalizing constants using geometric paths. Therefore, any estimator currently developed via thermodynamic integration has its corresponding stepping-stone estimator and vice versa. This method-path approach allows us to further introduce new estimators based on the counterpart existing ones.

2.2 Marginal likelihood estimators

In order to avoid confusion, hereafter we will name each estimator based on the method (thermodynamic or stepping-stone) and on the path implemented for its derivation.

The power posteriors (Lartillot and Philippe 2006; Friel and Pettitt 2008) and the stepping stone (Xie et al. 2011) marginal likelihood estimators are using the same geometric path but they are based on different identities, approaching the same problem using a different perspective. In fact, both methods implement the geometric path

$$\begin{aligned} q_t^{PP }(\varvec{\theta })=\left\{ f(\varvec{y}|\,\varvec{\theta })\pi (\varvec{\theta })\right\} ^t\pi (\varvec{\theta })^{1-t}=f(\varvec{y}|\,\varvec{\theta })^t\pi (\varvec{\theta }), \end{aligned}$$
(7)

which will be referred to hereafter as the prior-posterior path. The prior posterior path links a proper prior for the model parameters, \(q_0(\varvec{\theta })=\pi (\varvec{\theta })\), with the corresponding unnormalized posterior density, \(q_1(\varvec{\theta })=f(\varvec{\theta |}\,\varvec{y})\,\pi (\varvec{\theta })\). Setting the prior-posterior in (4) and (6), yields the thermodynamic and the stepping-stone prior-posterior identities (PP\(_T\) and PP\(_S\) respectively) for the marginal likelihood

$$\begin{aligned}&\log f(\varvec{y}) =\int _0^1 E_{p_t^{PP }}\left\{ \log f(\varvec{y}|\,\varvec{\theta })\right\} \,dt ~~\text{ and } \\&f(\varvec{y}) = \prod _{i=0}^{n-1}\int _{\varvec{{\varTheta }}}\left\{ \log f(\varvec{y}|\,\varvec{\theta }) \right\} ^{{\varDelta }(t_i)} p_{\,t_{i}}^PP (\varvec{\theta })\,d\varvec{\theta } \end{aligned}$$

where \(p_t^PP (\varvec{\theta }|\varvec{y})\) is the density normalized version of (7).

Fan et al. (2011) modified the estimator of Xie et al. (2011) based on the ideas of Lefebvre et al. (2010), who considered other options rather than the prior at the zero end of the TI. Provided that \(g(\varvec{\theta })\) is an importance function which approximates the posterior, the geometric path implemented by Fan et al. (2011) can be named as the importance-posterior path

$$\begin{aligned} q_t^IP (\varvec{\theta })=\left\{ f(\varvec{y}|\,\varvec{\theta })\, \pi (\varvec{\theta })\right\} ^tg(\varvec{\theta })^{1-t}. \end{aligned}$$

It should be noted that the density \(g(\varvec{\theta })\) is required to be proper so that \(z_0=1\). It is possible to be constructed by implementing the posterior moments available from the MCMC output at \(t=1\), provided that the shape of the posterior allows so.

The thermodynamic and stepping-stone importance-posteriors (IP\(_T\) and IP\(_S\) respectively) are derived by the identities

$$\begin{aligned}&\log f(\varvec{y}) = \int _0^1 E_{p_t}^IP \left[ \log \frac{f(\varvec{y}|\,\varvec{\theta })\,\pi (\varvec{\theta })}{g(\varvec{\theta })}\right] dt ~~\text{ and }~~ \nonumber \\&f(\varvec{y}) = \prod _{i=0}^{n-1}\int _{\varvec{{\varTheta }}}\left\{ \frac{f(\varvec{y}|\,\varvec{\theta })\,\pi (\varvec{\theta })}{g(\varvec{\theta })} \right\} ^{{\varDelta }(t_i)} p_{\,t_{i}}^IP (\varvec{\theta })\,d\varvec{\theta }, \end{aligned}$$
(8)

where \(p_t^IP (\varvec{\theta })\) is the density normalized version of \(q_t^IP (\varvec{\theta })\).

The TI identity appearing in (8) has the attractive feature of sampling from \(g(\varvec{\theta })\), rather than the prior, for \(t=0\). It also retains the stability ensured by averaging in log scale according to the thermodynamic approach.

Therefore, in specific model settings, the estimators based on the thermodynamic importance posteriors can perform more efficiently than estimators based on the other expressions, provided that an importance function can be formulated.

Although techniques for finding efficient importance functions exist (see for example in Perrakis et al. 2014), the later this task is far from trivial. Depending upon the shape of the posterior (multi-modal, high dimensional) the construction of an envelope function can be a challenging problem (see for instance Owen and Zhou 2000). The prior-posterior path is therefore superior in terms of general applicability, since an approximation of the posterior is not required.

It is our belief that beyond the four expressions reviewed here, others may be developed within this broad framework, by choosing the appropriate path for particular models, coming with thermodynamic and stepping-stone variants.

2.3 Bayes factor direct estimators

The BF is by definition a ratio of normalized constants. Therefore, (4) and (6) can be implemented to construct direct BF estimators, rather than applying the methods to each model separately. Lartillot and Philippe (2006) implemented the thermodynamic integration, in order to link two competing (not necessary nested) models, instead of densities. That was achieved by choosing the appropriate path, in a way that eventually produces directly a BF estimator. Lartillot and Philippe (2006) were motivated by the fact that lack of precision on each marginal likelihood estimation, may alter the BF interpretation. They argue, that a simultaneous estimation of the two constants can ameliorate that to some extend. The idea is to employ a bidirectional melting-annealing sampling scheme, based on the model-switch path:

$$\begin{aligned}&q_t^{MS }(\varvec{\theta }) \\&\quad =\bigg \{f(\varvec{y}|\,\varvec{\theta }, m_1)\,\pi (\varvec{\theta }| \, m_1)\bigg \}^{t}\bigg \{f(\varvec{y}|\,\varvec{\theta }, m_0)\,\pi (\varvec{\theta }| \, m_0)\bigg \}^{1-t}. \end{aligned}$$

Lartillot and Philippe’s (2006) thermodynamic model-switch (MS\(_T\)) identity for the BF is given by

$$\begin{aligned} \log BF_{10}=\int _0^1 E_{p_t^{MS }}\left[ \log \left\{ \frac{f(\varvec{y}|\,\varvec{\theta }, m_1)\,\pi (\varvec{\theta }| \, m_1)}{f(\varvec{y}|\,\varvec{\theta }, m_0)\,\pi (\varvec{\theta }| \, m_0)}\right\} \right] dt\nonumber \\ \end{aligned}$$
(9)

where the expectation is taken over \(p_t^{MS }(\varvec{\theta }|\varvec{y})\) which is the density obtained after normalizing the model-switch path \(q_t^{MS }(\varvec{\theta })\). Based on (6), the stepping-stone counterpart for the model switch identity (MS\(_S\)) becomes are as follows

$$\begin{aligned} BF_{10}= \prod _{i=0}^{n-1}\int _{\varvec{{\varTheta }}}\left\{ \frac{f(\varvec{y}|\, \varvec{\theta }, m_1)\,\pi (\varvec{\theta }| \, m_1)}{f(\varvec{y}|\, \varvec{\theta }, m_0)\,\pi (\varvec{\theta }| \, m_0)}\right\} ^{{\varDelta }(t_i)} p_{\,t_{i}}^{MS }(\varvec{\theta }|\,\varvec{y})\,d\varvec{\theta }, \end{aligned}$$

In case where \(\varvec{\theta }\) is common between the two models (for instance if the method is used to compare paths under different endpoints, see Lartillot and Philippe 2006 for an example) the method is directly applicable. Otherwise, if \(\varvec{\theta }=( \varvec{\theta }_{m_1},\varvec{\theta }_{m_0} )\), pseudo-priors need to be assigned at the endpoints of the path to retain the dimension balance between the two models in a similar manner as in transdimensional MCMC methods such as the reversible jump MCMC algorithm (Green 1995), the Carlin and Chib (1995) Gibbs sampler and the Gibbs variable selection of Dellaportas et al. (2002). Such pseudo-priors should reflect the corresponding posteriors and their specification can be a challenging task. Rough choices of pseudo-priors can be based on small pilot MCMC runs of the bigger model (in nested model comparison) or for both models (in non-nested model comparison) in a similar manner as in reversible jump MCMC implementation; see for example in Forster and Dellaportas (1999). Nevertheless, this task needs further investigation which the authors intend to address in the future.

Having in mind the direct estimation of Bayes factors, more complicated estimators may be derived using compound geometric paths. With the term compound paths we refer to paths that consist of a hyper geometric path, \(Q_t (\varvec{\theta })\), used to link two competing models and a nested path \(q_t(\varvec{\theta },i)\) for each endpoint function \(Q_i\), for \(i=0,1\). The two intersecting paths form a quadrivial, \((Q\circ q)_t(\varvec{\theta })= Q_1(\varvec{\theta })^t Q_0(\varvec{\theta })^{1-t}\) with \(t\in [0,1]\) that can be defined as

$$\begin{aligned}&(Q\circ q)_t(\varvec{\theta }) \\&\quad = \bigg [ q_1(\varvec{\theta },1)^t q_0(\varvec{\theta },1)^{1-t}\bigg ]^t\, \bigg [ q_1(\varvec{\theta },0)^t q_0(\varvec{\theta },0)^{1-t}\bigg ]^{1-t}. \end{aligned}$$

The multivariate extension is discussed in detail in Gelman and Meng (1998). The endpoint target densities are given by \(q_i(\varvec{\theta },i)\) for \(t=0\) and \(t=1\) respectively estimating the ratio \(z_{1}/z_{0} = \int q_1(\varvec{\theta },1) d\varvec{\theta } \times \left[ \int q_0(\varvec{\theta },0) d\varvec{\theta } \right] ^{-1}. \) The densities \(q_i(\varvec{\theta },j)\) for \(i,j = 0, 1\) and \(i \ne j\) serve as linking densities within each nested path. Therefore, following the importance-sampling logic, they should play the role of approximating (importance) functions for each \(q_i(\varvec{\theta },i)\).

For the specific case of the Bayes factor estimation, the objective is to retrieve the marginal likelihoods at the endpoints and therefore it is reasonable to consider as nested paths the prior-posterior and the importance-posterior paths, discussed in the previous section. The importance-posterior BF quadrivial, for instance, is as follows

$$\begin{aligned} (Q\circ q)^{{IP}}_t(\varvec{\theta })= & {} \Bigg [\bigg \{f(\varvec{y}|\,\varvec{\theta }, m_1) \pi (\varvec{\theta }|\, m_1)\bigg \}^{t} g(\varvec{\theta }|\, m_1)^{1-t}\Bigg ]^{t} \nonumber \\&\times \Bigg [\bigg \{f(\varvec{y}|\,\varvec{\theta }, m_0) \pi (\varvec{\theta }|\, m_0)\bigg \}^{1-t}g(\varvec{\theta }|\, m_0)^{t} \Bigg ]^{1-t} \end{aligned}$$

leading to the thermodynamic (\(Q_{IP_T}\)) and stepping-stone (\(Q_{IP_S}\)) expressions

$$\begin{aligned}&\displaystyle \log BF_{10} \\&\quad =\displaystyle \int _0^1 E_{P_t}\left[ \log \frac{\bigg \{f(\varvec{y}|\, \varvec{\theta }, m_1)\,\pi (\varvec{\theta }|\, m_1)/g(\varvec{\theta }|\, m_1)\bigg \}^{2t} g(\varvec{\theta }|\, m_1)}{\bigg \{f(\varvec{y}|\,\varvec{\theta }, m_0)\, \pi (\varvec{\theta }|\, m_0)/g(\varvec{\theta }|\, m_0)\bigg \}^{2(1-t)} g(\varvec{\theta }|\, m_0)}\right] dt \end{aligned}$$

and

$$\begin{aligned}&\displaystyle BF_{10}=\prod _{i=0}^{n-1}\int _{\varvec{{\varTheta }}} \\&\quad \times \log \frac{\bigg \{f(\varvec{y}|\,\varvec{\theta }, m_1)\,\pi (\varvec{\theta }|\, m_1)/g(\varvec{\theta }|\, m_1)\bigg \}^{2 T_i }g(\varvec{\theta }|\, m_1)}{\bigg \{f(\varvec{y}|\,\varvec{\theta }, m_0)\,\pi (\varvec{\theta }|\, m_0)/g (\varvec{\theta }|\, m_0)\bigg \}^{2(1-T_i)}g(\varvec{\theta }|\, m_0)} \,P_{t_i}(\varvec{\theta }) \, d \varvec{\theta }, \end{aligned}$$

where \(P_t(\varvec{\theta })=(Q\circ q)^{{IP}}_t (\varvec{\theta })/Z_t\), \(Z_t= \int _{\varvec{{\varTheta }}}(Q\circ q)^{{IP}}_t \,d\varvec{\theta }\), \(t\in [0,1]\). In the thermodynamic expression, t is the melting temperature and \(1-t\) the annealing one, assuming that the procedure starts at \(t=0\) and gradually increases to \(t=1\). The hyper-path ensures that while the model \(m_1\) is melting, the model \(m_0\) is annealing. At the same time, the importance-posterior path serving as the nested one, links the posterior with the importance at each model separately. In the stepping-stone counterpart expression the melting and annealing temperatures are given by \(T_i=(t_{i+1}+t_{i})/2\) for any \(i = 0,1,\dots , n-1\).

From the expressions \(Q_{IP_S}\) and \(Q_{IP_T}\) we may derive the analogue ones for the prior-posterior quadrivial (\(Q_{PP_T}\) and \(Q_{PP_S}\)) by substituting the importance densities \(g(\varvec{\theta }|\,m_i)\) with the corresponding priors \(\pi (\varvec{\theta }|\,m_i), ~(i=0,1)\). The quadrivial expressions, univariate and multivariate, are under ongoing research and it is not yet clear to the authors which applications could benefit from their complete structure. The optimal tempering scheme is also an open issue. However, as shown in the applications at Sect. 4, they are associated with reduced Monte Carlo error.

3 Entropy measures and path sampling

In Statistics, entropy is used as a measure of uncertainty which, unlike the variance, does not depend on the actual values of a random variable \(\varvec{\theta }\), but only on their associated probabilities. Here, we use the term entropy measures in a broad definition to refer to measures of divergence between probability distributions that belong to the family of \(f-\) divergences (Ali and Silvey 1966; Csiszár 1963). Such measures are widely used in statistics (Liese and Vajda 2006), information theory (Cover and Thomas 1991) and thermodynamics (Crooks and Sivak 2011).

The most commonly used \(f-\)divergence is the Kullback - Leibler (Kullback and Leibler 1951)

$$\begin{aligned} KL(p_1 \parallel p_0)= & {} \int _{\varvec{{\varTheta }}} p_1(\varvec{\theta })\log \frac{p_1(\varvec{\theta })}{ p_0(\varvec{\theta })}\, d\varvec{\theta }\nonumber \\= & {} \int _{\varvec{{\varTheta }}} p_1(\varvec{\theta })\log p_1(\varvec{\theta }) \,d\varvec{\theta } \nonumber \\&-\int _{\varvec{{\varTheta }}} p_1(\varvec{\theta })\log p_0(\varvec{\theta })\, d\varvec{\theta }\nonumber \\= & {} -H(p_1)+cH(p_1 \parallel p_0), \end{aligned}$$
(10)

with \(cH(p_1 \parallel p_0)\) being the cross entropy and \(H(p_1)\) the differential entropy; see for details in Cover and Thomas (1991). The KL-divergence is always non-negative but it is not a distance or a metric with the strict mathematical definition, since neither the symmetry nor the triangle inequality conditions are satisfied. In information theory, it is mostly referred to as the relative entropy and is a measure of the information lost when \(p_0(\varvec{\theta })\) is used as an approximation of \(p_1(\varvec{\theta })\). Subsequently, a symmetric version of KL can naturally be defined as

$$\begin{aligned} J(p_1, p_0)=KL(p_1 \parallel p_0)+ KL (p_0 \parallel p_1), \end{aligned}$$

which dates back to Jeffreys’ investigations of invariant priors (Jeffreys 1946) and is often called as the symmetrized KL-divergence or J-divergence.

The relationship between the KL-divergence and the thermodynamic integral was described by Friel and Pettitt (2008) and further studied by Lefebvre et al. (2010). In particular, the KL-divergences between \(p_1(\varvec{\theta })\) and \(p_0(\varvec{\theta })\) can be derived by the endpoints of the expectation of \(E_{p_t} \big \{ U( \varvec{\theta })\}\) appearing thermodynamic equation (4) since

$$\begin{aligned}&KL(p_1 \parallel p_0)= E_{p_1} \big \{ U( \varvec{\theta }) \big \} -\log \lambda ~~\text{ and } \\&KL(p_0 \parallel p_1)= - E_{p_0} \big \{ U( \varvec{\theta }) \big \} +\log \lambda ~. \end{aligned}$$

The findings presented by Friel and Pettitt (2008) and Lefebvre et al. (2010) refer therefore to the endpoints of a geometric path. The question which naturally arises here is which is the role of entropy at the intermediate points, \(t\in (0,1)\). In the following, we address this issue and we illustrate how other \(f-\)divergences are related to the thermodynamic integral (4) and thus can be estimated as path sampling byproducts.

3.1 The normalised thermodynamic integral

In this section, we draw attention to the normalized thermodynamic integral (NTI) given by

$$\begin{aligned} NTI = \int _0^1\int _{\varvec{{\varTheta }}}p_t(\varvec{\theta })\, \log \frac{p_1(\varvec{\theta })}{p_0(\varvec{\theta })}\,d\varvec{\theta } \, dt. \end{aligned}$$
(11)

The NTI links the normalised densities \(p_0\), \(p_1\) and equals zero for any geometric path. It can be expressed via the thermodynamic integral using the identity

$$\begin{aligned} NTI = \int _0^1 \int _{\varvec{{\varTheta }}} p_t(\varvec{\theta })\, \log \frac{q_1(\varvec{\theta })}{q_0(\varvec{\theta })}\,d\varvec{\theta }\, dt - \log \lambda ~. \end{aligned}$$

This identity will be used to connect the thermodynamic integral with \(f-\)divergences other than the KL, at the intermediate points of [0,1].

3.1.1 The functional KL and \(f-\) divergences

The NTI (11) essentially represents the area between the temperature axis and the following curve

$$\begin{aligned} {\mathcal {KL}}_t=\int _{\varvec{{\varTheta }}} p_t(\varvec{\theta })\log \frac{p_1(\varvec{\theta })}{ p_0(\varvec{\theta })}\, d\varvec{\theta } =E_{p_t} \big \{ U(\varvec{\theta }) \big \} - \log \lambda ~, \end{aligned}$$
(12)

as depicted in Fig. 1. Hereafter, the \({\mathcal {KL}}_t\) is refered to as the functional KL-divergence of order t and reduces to \({\mathcal {KL}}_0=-KL(p_0 \parallel p_1)\) and to \({\mathcal {KL}}_1=KL(p_1 \parallel p_0)\) at the endpoints of the geometric path, in accordance with the findings of Friel and Pettitt (2008) and Lefebvre et al. (2010). The \({\mathcal {KL}}_t\) denotes the difference between the KL divergences of \(p_t\) with the two endpoint densities \(p_1\) and \(p_0\) since

$$\begin{aligned} {\mathcal {KL}}_t= & {} -cH(p_t \parallel p_1)+cH(p_t \parallel p_0) \\= & {} KL(p_t \parallel p_1)-KL(p_t \parallel p_0). \end{aligned}$$

Hence, it can be interpreted as a measure of relative location of the sampling distribution \(p_t\), relative to \(p_1\) and \(p_0\). That is, for any \(t \in [0,1]\), the \({\mathcal {KL}}_{t}\) indicates whether \(p_{t}\) is closer to \(p_0\) (negative values) or to \(p_1\) (positive values), while \({\mathcal {KL}}_{t}=0\) at the point where the two endpoint densities are equidistant from the sampling distribution. The sampling distribution \(p_t(\varvec{\theta })\) is the Boltzmann–Gibbs distribution pertaining to the Hamiltonian (energy function) \({\mathcal {H}}_t(\varvec{\theta })=-t\log p_1(\varvec{\theta })-(1-t)\log p_0(\varvec{\theta })\). A key observation here is that when adopting geometric paths, the sampling distribution embodies the Chernoff coefficient \(\mu (t)=\int _{\varvec{{\varTheta }}} p_1(\varvec{\theta })^t p_0(\varvec{\theta })^{1-t} d\varvec{\theta }\) (Chernoff 1952) since

$$\begin{aligned} p_t(\varvec{\theta }) = \frac{ \big \{ z_1 p_1(\varvec{\theta }) \big \} ^t \big \{ z_0 p_0(\varvec{\theta }) \big \}^{1-t}}{\int _{\varvec{{\varTheta }}} q_1(\varvec{\theta })^t q_0(\varvec{\theta })^{1-t} d\varvec{\theta }}=\frac{\ p_1(\varvec{\theta }) ^t p_0(\varvec{\theta }) ^{1-t}}{\mu (t)},\nonumber \\ \end{aligned}$$
(13)

for any \(~t\in [0,1]\). In view of (13) the NTI becomes

$$\begin{aligned}&\int _0^1\int _{\varvec{{\varTheta }}} \frac{\ p_1(\varvec{\theta }) ^t p_0(\varvec{\theta }) ^{1-t}}{\mu (t)}\, \log \frac{p_1(\varvec{\theta })}{p_0(\varvec{\theta })}\,d\varvec{\theta } \, dt \nonumber \\&\quad = \int _0^1 \frac{d\log \mu (t)}{dt}\, dt=\bigg [ \log \mu (t)\bigg ]_0^1=0, \end{aligned}$$
(14)

since

$$\begin{aligned} \frac{d\log \mu (t)}{dt} = \frac{1}{\mu (t)} \int \frac{d\{\,p_1(\varvec{\theta }) ^t p_0(\varvec{\theta }) ^{1-t}\}}{dt}~ dt. \end{aligned}$$

From (14) it is straightforward to see that the NTI up to any point \(t\in (0,1)\) is directly related to the Chernoff t-divergence (Chernoff 1952; Parzen 1992; Kakizawa et al. 1998; Rauber et al. 2008), given by

$$\begin{aligned} C_t(p_1\parallel p_0) = - \log \int _{\varvec{{\varTheta }}} p_1(\varvec{\theta })^t p_0(\varvec{\theta })^{1-t} d\varvec{\theta }=-\log \mu (t),\nonumber \\ \end{aligned}$$
(15)

as described in detail in the following lemma.

Lemma 1

The normalised thermodynamic integral (11) up to any point \(t\in (0,1)\) given by

$$\begin{aligned} NTI(t) = \int _0^t\int _{\varvec{{\varTheta }}} p_u(\varvec{\theta }) \log \frac{p_1(\varvec{\theta })}{p_0(\varvec{\theta })}\,d\varvec{\theta } \, du \end{aligned}$$
(16)

is equal to minus the Chernoff t-divergence of the endpoint densities, that is

$$\begin{aligned} NTI(t)= \log \mu (t)= -C_{t}(p_1\parallel p_0). \end{aligned}$$
(17)

The proof of Lemma 1 is obtained in straightforward manner as (14). \(\square \)

Based on Lemma 1, it occurs that the Chernoff \(t-\)divergences can be directly computed from the NTI. Subsequently, a number of other divergences related to Chernoff can be obtained from NTI. The Bhattacharyya distance (Bhattacharyya 1943) occurs at \(t=0.5\), that is

$$\begin{aligned} Bh(p_1,p_0)= & {} C_{0.5}(p_1\parallel p_0) \\= & {} -\log \int _{\varvec{{\varTheta }}} \sqrt{p_1(\varvec{\theta }) p_0(\varvec{\theta })} d\varvec{\theta }=-\log \rho _B. \end{aligned}$$

The Bhattacharyya coefficient \(\rho _B\) can be implemented in turn to derive the Bhattacharyya-Hellinger distance (Bhattacharyya 1943; Hellinger 1909) since \(He(p_1,p_0)= \sqrt{1-\rho _B}\). Based on the Chernoff t-divergence we may also derive the Rényi t-divergence \(R_t(p_1\parallel p_0) = C_{t}(p_1\parallel p_0)/(1-t)\) (Rényi 1961) and the Tsallis t-relative entropy \(T_t(p_1\parallel p_0) = \big [\exp \big \{-C_{t}(p_1\parallel p_0)\big \}-1\big ]/(1-t)\).

Fig. 1
figure 1

Graphical representation of the NTI: the plot of \({\mathcal {KL}}_t(\varvec{\theta })\) over t

Full size image

The graphical representation of the NTI (Fig. 1) reveals the relationship of the thermodynamic integral with a number of entropy measures. The cross entropy differences between \(p_t\) and the endpoint distributions (\(p_0\) and \(p_1\)) are depicted on the vertical axis. The KL-divergences between \(p_0\) and \(p_1\) are located at the endpoints of [0, 1]. The projection of the \({\mathcal {KL}}_t\) curve on the vertical axis represents the \(J-\)divergence. The Chernoff \(t-\)divergence for any \(t_i \in [0,1]\) is given by the area between the curve and the t-axis from \(t=0\) to \(t=t_i\), while the Bhattacharyya distance is given by the corresponding area from zero up to \(t=0.5\). All these measures can be estimated as path sampling byproducts. An algorithm to estimate the \(f-\)divergences mentioned here using path sampling, is presented at the Appendix.

To summarize, it occurs that the NTI given in (11) can offer another link between Bayesian inference, information theory and thermodynamics (or statistical mechanics). For instance, under the Hamiltonian \({\mathcal {H}}_t(\varvec{\theta })\), Merhav (2010, section 3.3) discuss the excess or dissipated work in thermodynamics and its relation to the data processing theorem in information theory, with the NTI emerging in the case of reversible processes. In a more general framework, Crooks and Sivak (2011) consider conjugate trajectories, that is forward (from \(t=0\) to \(t=1\)) and backward processes (from \(t=1\) to \(t=0\)), to derive the physical significance of the \(f-\)divergences considered here, in terms of non-equilibrium dynamics. Further parallelism between the NTI and statistical mechanics is not attempted here, leaving this part to the experts on the field.

In the next section we focus on the point \(t^*\) (hereafter optimal temperature) where the functional \({\mathcal {KL}}_t\) equals zero and discuss on further results related to it.

3.1.2 Optimal temperature \(t^*\)

The solution of the equation \({\mathcal {KL}}_{t^*}=0\) defines the point \(t^*\) where the sampling distribution is equidistant (in the KL sense) from the endpoint densities, that is, \( KL(p_{t^*} \parallel p_1)=KL(p_{t^*} \parallel p_0)\). The main observation here is that at the optimal temperature it holds \(E_{p_{t^*}} \big \{ U(\varvec{\theta }) \big \}=\log \lambda \), according to the definition (12). Therefore, there is a temperature point where the ratio of interest \(\lambda \) may be derived directly, avoiding the thermodynamic integration.

In other words, in the case that \(t^*\) is known, the ratio of the normalizing constants \(\lambda \) can be estimated in a single MCMC run (with \(t=t^*\)), rather than employing the entire path using multiple simulations. However this is rarely the case and, using the inverse logic, \(t^*\) can be estimated by path sampling.

Before proceeding any further, we may first outline the reversibility property of the NTI, which is based on the anti-symmetry property \(C_t(p_1 \parallel p_0)=C_{1-t}(p_0 \parallel p_1)\), considered in Crooks and Sivak (2011).

  1. Reversibility property:

    For any intermediate point \(t\in (0,1)\) it holds that

    $$\begin{aligned} NTI(t)= & {} - \overline{NTI}(t) ~\text{ with }~ \overline{NTI}(t) \nonumber \\= & {} \int _t^1\int _{\varvec{{\varTheta }}} p_u(\varvec{\theta }) \log \frac{p_1(\varvec{\theta })}{p_0(\varvec{\theta })}\,d\varvec{\theta } \, du. \end{aligned}$$
    (18)

The reversibility property implies that the maximum area occurs at \(t^*\) and it is equal to NTI\((t^*)\). This result leads us to the Chernoff information (Parzen 1992), as described in Lemma 2 which follows.

Lemma 2

The Chernoff information, defined as

$$\begin{aligned} C(p_1 \parallel p_0) = \max _{t \in [0,1]} C_t(p_1\parallel p_0) \end{aligned}$$

is equal to \(NTI(t^*)\) with \(t^*\) being the solution of equation \({\mathcal {KL}}_t=0\), i.e.

$$\begin{aligned} C(p_1 \parallel p_0) = NTI (t^*) ~\text{ with }~ t^* \in [0,1]: \mathcal{KL}_{t^*} = 0. \end{aligned}$$

Proof

Consider the continuous and differentiable function \(g(t)=NTI(t)=\log \mu (t)\). Then \(g'(t)=d\log \mu (t)/dt={\mathcal {KL}}_t \) and \(g''(t)=V_{p_t} \Big \{ \log \frac{p_1(\varvec{\theta })}{p_0(\varvec{\theta })} \Big \} > 0\); where \(V_{p_t} \Big \{ \log \frac{p_1(\varvec{\theta })}{p_0(\varvec{\theta })} \Big \}\) is the variance of \(\log \frac{p_1(\varvec{\theta })}{p_0(\varvec{\theta })}\) with respect to \(p_t (\varvec{\theta })\). Since \(g'(t^*) = {\mathcal {KL}}_{t^*} =0\) and \(g''(t^*)>0\), then \(g(t^*)= \min _{t \in [0,1]} \log \mu (t)\). Hence, from (17) we have that

$$\begin{aligned} C(p_1 \parallel p_0)= & {} \max _{t \in [0,1]} C_t(p_1\parallel p_0) \\= & {} \min _{t \in [0,1]} NTI(t) = NTI( t^* ). \end{aligned}$$

\(\square \)

The optimal \(t^*\) is a unique point in [0,1] and can be estimated using the algorithm presented in the Appendix. Subsequent to the approximation of the optimal temperature, the Chernoff information can be estimated, which is generally a non-trivial and cumbersome procedure. For instance, Nielsen (2011) describe a geodesic bisection optimization algorithm that approximates \(C(p_1 \parallel p_0)\) for multidimensional distributions which belong to the exponential family, based on Bregman divergences (named after Bregman, who introduced the concept in Bregman 1967). Julier (2006) provides also an approximation for Gaussian mixture models. The MCMC method based on the TI presented here is an alternative method that can be used for any choice of \(p_0\) and \(p_1\) distributions.

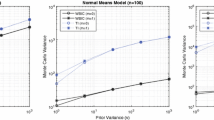
To sum up, in this section we have proved that a unique temperature \(t^*\) exists, where: (a) the mean energy \(E_{p_{t^{*}}} \big \{ U(\varvec{\theta }) \big \}\) equals the free energy \(\lambda \), (b) the sampling distribution at this temperature is equidistant from the endpoint densities, and (c) the area between the graph and the thermodynamic path equals the Chernoff information. The optimal temperature is required for the computation of the widely applicable Bayesian information criterion (Watanabe 2013, WBIC) implying a clear connection between the thermodynamic integral and the information criteria. For the computation of WBIC, Watanabe (2013) approximates \(t^*\) using asymptotic arguments while Mononen (2015) studies the same problem in the field of Gaussian process regression models. Both approaches directly aim at the calculation of the optimal temperature in order to estimate WBIC. Here we investigate the quest of the optimal temperature under a different perspective since the aim is to study its properties and its connection with the thermodynamic integration rather than to be used for the estimation of the target quantity. Thus, the computation of the optimal temperature requires the evaluation of the thermodynamic integral. As Friel et al. (2016) point out, our findings may provide a basis for the development of new solid methods for the estimation of the optimal temperature. For instance, according to point (b), \(t^*\) heavily depends on the endpoint densities. Thus, different prior distributions lead to different optimal temperatures; see Table 3 for an illustration. This result lines up with the study of Friel et al. (2016). The algorithm we provide in the Appendix for the computation of the optimal temperature is rigorous but it provides a wide understanding of the placement of the optimal temperature in the [0, 1] interval based on the particular selected path. Furthermore, it can be used in future studies to assess the quality of the approximation of the \(t^*\) in real life examples.

In the next section we focus on the study of the MCMC estimators of \(\log \lambda \) constructed using TI and geometric paths.

3.2 MCMC path sampling estimators and associated error

Numerical approaches are typically used to compute the external integral of (2), such as the trapezoidal or Simpson’s rule (Ogata 1989; Neal 1993; Gelman and Meng 1998, among others). The numerical approaches require the formulation of an n-point discretisation \(\mathcal{T} = \{t_0, t_1, \dots , t_n\}\) of [0, 1], such that \(0=t_0<{\cdots }< t_{n-1}<t_n=1\), which is called temperature schedule. A separate MCMC run is performed at each \(t_i\) with target distribution the corresponding \(p(\varvec{\theta }|\,t_i)\), \(i=0,...,n\). The MCMC output is then used to estimate \(\mathcal{E}_{t} = E_{p_{t}}\left\{ U(\varvec{\theta })\right\} \) by the sample mean \(\widehat{\mathcal{E}}_t\) of the simulated values \(\{\varvec{\theta }^{(r)}\}^{R}_{r=1}\) generated from \(p_{t}\) for each \(t\in \mathcal{T}\). The final estimator is derived by

$$\begin{aligned} \log \widehat{\lambda }= & {} \sum _{i=0}^{n-1}(t_{i+1}-t_i) \frac{\widehat{{\mathcal {E}}}_{t_{i+1}} + \widehat{{\mathcal {E}}}_{t_{i}}}{2}; \end{aligned}$$
(19)

see also in Friel and Pettitt (2008).

At a second step, the posterior output at each \(t_i\) and \(\log \widehat{\lambda }\) can be employed to estimate \(t^*\) and the Chernoff information. Here we provide an algorithm for that purpose, which yields also the estimated Chernoff \(t-\)divergences for any \(t\in (0,1)\) and subsequently the \(f-\)divergences described in Sect. 3.1.

In this section we study two important sources of error for path sampling estimators: the path-related variance and the discretisation error. The path-related variance is the error related to the choice of the path which, for geometric ones, is restricted to the selection of the endpoint densities. On the other hand, for any given path, the discretisation error is related to the choice of the temperature schedule \(\mathcal{T}\) and is derived from the numerical approximation of the integral over [0, 1]. In order to examine these two error sources, we provide a geometric representation of TI (Eq. 4) and NTI (Eq. 11) identities. This leads us to a better understanding of the behaviour of the path sampling estimators.

3.2.1 Path-related variance

The total variance of \(\log \widehat{\lambda }\) has been reported by Gelman and Meng (1998) in the case of stochastic t with an appropriate prior distribution attached to it. Further results were also presented by Lefebvre et al. (2010) for geometric paths. They have showed that the total variance is associated with the \(J-\)divergence of the endpoint densities and therefore with the choice of the path. Here we focus on the t-specific variances \(V_t=V_{p_t}\{U(\varvec{\theta })\}> 0\) of \(U(\varvec{\theta })\) (hereafter local variance) which are the components of the total variance.

Figure 2 is a graphical representation of TI. To be more specific, the curve represents the \(\mathcal{E}_t \) values for each \(t\in [0,1]\) while the area between the t-axis and the curve gives the thermodynamic integral (2). In this figure, the error of the TI estimators is depicted by the steepness of the curve of \(\mathcal{E}_t\). This result is based on the fact that the partition function \(z_t\) is the cumulant generating function of \(U(\varvec{\theta })\) (Merhav 2010, section 2.4) and therefore the first derivative of \(\mathcal{E}_t\) is given by the local variance \(V_t\), that is \(\mathcal{E}_t' = V_t\). It follows that the slope of the tangent of the curve at each t equals to \(V_t\). Therefore, the graphical representation of two competing paths can provide valuable information about the associated variances of their corresponding estimators.

Fig. 2
figure 2

Graphical representation of the TI: the plot of the curve \(\mathcal{E}_t = E_{p_t}\{U( \varvec{\theta })\}\) over t, based on two paths \(q_t\) (black line) and \(q'_t\) (grey line). For each path, the \(J-\)distance between the endpoints coincides with the slope of the corresponding secant, sec(0, 1). The slope of the tangent \(tan(t_i)\) equals the local variance \(V_{t_i}\)

Full size image

In the case of geometric paths particularly, \(J(p_1,\,p_0)\) coincides with the slope of the secant defined at the endpoints of the curve and lays below the curve of the strictly increasing (in terms of t) function \(\mathcal{E}_t\). Therefore, it can be used as an indicator of the slope of the curve and the result of Lefebvre et al. (2010) has a direct visual realisation. The result can be generalised for any other pair of successive points, say \((t_i, \mathcal{E}_{t_i})\) and \((t_{i+1}, \mathcal{E}_{t_{i+1}})\), with the corresponding slope (or gradient) of the secant \(sec(t_i,t_{i+1})\) given by

$$\begin{aligned} \nabla sec(t_i,t_{i+1})= & {} \frac{ \mathcal{E}_{t_{i+1}} - \mathcal{E}_{t_{i+1}} }{t_{i+1}-t_i} = \frac{ \mathcal{KL}_{t_{i+1}} -\mathcal{KL}_{t_{i}}}{t_{i+1}-t_i}. \end{aligned}$$
(20)

The latter is derived from (12) and it reflects the fact that the slopes of the curves depicted in Figs. 1 and 2 are identical. Additionally, \(\mathcal{KL}_t\) can be written in terms of the KL-divergence between the successive sampling densities \(p_{t_i}\) and \(p_{t_{i+1}}\) since, from (13) we obtain

$$\begin{aligned} KL(p_{t_i} \parallel p_{t_{i+1}})= & {} \int _{\varvec{\theta }} p_{t_i}(\varvec{\theta })\log \bigg \{p_1(\varvec{\theta })^{t_i-t_{i+1}}p_0(\varvec{\theta })^{t_{i+1}-t_{i}}\bigg \} \,d\varvec{\theta } \nonumber \\&+\,\log \frac{\mu (t_{i+1})}{\mu (t_{i})}\nonumber \\= & {} -(t_{i+1}-t_i) \mathcal{KL}_{t_i}+\log \frac{\mu (t_{i+1})}{\mu (t_{i})}. \end{aligned}$$
(21)

Using (20) and (21), we can associate the \(J-\)divergence between two successive points with the slope of the secant \(sec(t_i,t_{i+1})\) since

$$\begin{aligned} \nabla sec(t_i,t_{i+1})=\frac{J(p_{t_{i}},p_{t_{i+1}})}{(t_{i+1}-t_i)^2} \end{aligned}$$
(22)

generalizing the result of Lefebvre et al. (2010) for the endpoints of the graph where the slope of the sec(0, 1) is given by \(J(p_1,p_0)\). For successive points closely placed to each other (that is, for \({\varDelta }(t_{i})=t_{i+1}-t_{i} \rightarrow 0\)) the slope of the secant approximates the corresponding slope of the tangent of the curve and therefore the local variance. Hence, the \(J-\)divergence between any two successive points is indicative of the slope of the curve and consequently of the associated variance. For example, in Fig. 2 for values of t close to zero the slope of curve is very steep indicating high local variability.

The local variances of the path sampling estimators discussed here depend on the selection of the path. In the next section, we proceed with the study of the discretisation error and its effect on the path sampling estimators based on both the TI and NTI identities for any fixed geometric path.

3.2.2 Discretisation error

Calderhead and Girolami (2009) expressed the discretisation error in terms of differences of relative entropies of successive (in terms of t) sampling distributions. The result of Calderhead and Girolami (2009) can be written for any geometric path as follows

$$\begin{aligned} \log \widehat{\lambda }= & {} \sum _{i=0}^{n-1} \frac{\widehat{z}_{t_{i+1}}}{\widehat{z}_{t_{i}}} = \frac{1}{2}\sum _{i=0}^{n-1} \, (t_{i+1}-t_i) \, \left\{ \widehat{{\mathcal {E}}}_{t_{i+1}}+\widehat{{\mathcal {E}}}_{t_{i}} \right\} \nonumber \\&+\,\frac{1}{2} \sum _{i=0}^{n-1} \left\{ \widehat{KL}(p_{t_i}\parallel \,p_{t_{i+1}})-\widehat{KL}(p_{t_{i+1}}\parallel p_{t_{i}}) \right\} ,\nonumber \\ \end{aligned}$$
(23)

Calderhead and Girolami (2009) consider the case for \({\varDelta }(t_i) \rightarrow 0\) in (23) and outline that the first summation is equivalent to the trapezium rule used for numerical integration with the associated error expressed in terms of the asymmetries between the KL divergences defined between \(p_{t_i}\) and \(p_{t_{i+1}}\). In view of (21), expression 23 becomes

$$\begin{aligned} \log \widehat{\lambda }= & {} \frac{1}{2}\sum _{i=0}^{n-1} \, {\varDelta }(t_i) \, \left\{ \widehat{{\mathcal {E}}}_{t_{i+1}}+\widehat{{\mathcal {E}}}_{t_{i}} \right\} \nonumber \\&-\,\frac{1}{2} \sum _{i=0}^{n-1} \, {\varDelta }(t_i) \left( \widehat{{\mathcal {KL}}}_{t_i}+\widehat{{\mathcal {KL}}}_{t_{i+1}}\right) , \end{aligned}$$
(24)

since \( \sum _{i=0}^{n-1}\log \frac{\mu (t_i)}{\mu (t_{i+1})}=0\). The second term in the right side of (24) is the approximation of the NTI (using the trapezoidal rule), which indeed it should be zero. According to the discussion in Sect. 3.2.1, the relative entropies in (23), as well as the areas above and below the t-axis which represent the Chernoff divergences, are not expected to be zero. They both represent the path-related variance which is independent (and pre-existing) of the discretisation error. The discretisation error consists of the asymmetries that occur under any particular tempering schedule either in the TI or in NTI. The symmetry is a feature of the thermodynamic integration and it represents the trade-off between uncertainty in the forward and backward trajectories. Therefore, the error manifests as lack of symmetry in the assessment of the uncertainty due to the discretisation, as explained below.

While the path-related variance is independent from the discretisation error, the reverse argument does not hold. In fact, the discretisation error is highly influenced and dependent upon the path-related variance. Consider two pairs of successive points, located close to the zero and unit endpoints in Fig. 1, say \(t^{(0)}_i, t^{(0)}_{i+1}\) and \(t^{(1)}_j, t^{(1)}_{j+1}\) respectively, for \(i,j=1,...,n\). Further assume that the distances between the points within each pair are equal, say \(\delta > 0\). For the first pair, the corresponding \({\mathcal {KL}}_t\)s on the vertical axis are distant due to the steepness of the curve. On the contrary, for the second pair the corresponding \({\mathcal {KL}}_t\)s are very close, due to the fact that the slope of the curve is almost horizontal. Therefore, using the trapezoidal rule, for equally spaced pairs of points we approximate a large part of the curve towards the zero end and a small part of the curve towards the unit end. In order to achieve the same degree of accuracy at both ends, the second pair of points need to be closer. In conclusion, the temperature schedule should place more points towards the end of the path where the uncertainty (slope) is higher. For instance, the powered fraction (PF) schedule (Friel and Pettitt 2008)

$$\begin{aligned} {\mathcal {T}}_{PF}=\{t_i\}_{i=1}^n ~~\text{ such } \text{ as }~~ t_i=(i/n)^{\mathcal {C}}, \quad {\mathcal {C}}=1/a>1, \end{aligned}$$
(25)

places more points towards the zero endpoint of the path. Xie et al. (2011) proposed a closely related geometric schedule where the \(t_i\)s are chosen according to evenly spaced quartiles of a Beta(a, 1) distribution. Friel et al. (2014) proposed an adaptive algorithm for the temperature schedule that takes under consideration the local variances in order to locate the high uncertainty points. The algorithm traces the points on the curve and assigns an increased number of \(t_i\)s close to their regions. Then, the error is considerably decreased with a small computational price. Hug et al. (2016) also study a closely related approach, which relies on Simpsons rule, and demonstrated improved performance in high dimensional problems.

A temperature schedule which places more points towards the end of the path where the uncertainty is higher, is not efficient for the bidirectional paths presented in Sect. 2.3. Using for instance (25) in one of the directions, it would have reduced the path related variance for the one direction but it would have the exact opposite effect in the other direction. Therefore, the uniform schedule is more efficient in this case and improvement in the estimation can be achieved by uniformly placing more temperature points in [0,1].

Table 1 Marginal likelihood estimates—Pine data
Full size table

4 Illustrative examples

4.1 Regression modelling in the pine dataset

For the illustration of the estimators discussed in Sect. 2 we implement the pine data set, which has been studied by Friel and Pettitt (2008) and Lefebvre et al. (2010) in the context of path sampling. The dataset consists of measurements taken on 42 specimens of Pinus radiata. A linear regression model was fitted for the specimen’s maximum compressive strength (y), using their density (x) as independent variable, that is

$$\begin{aligned} y_i\,{=}\,\,\alpha {+}\beta (x_i{-}\bar{x})+\epsilon _i, \quad \epsilon _i \sim N(0,\sigma ^2), \quad i=1,\ldots ,42.\nonumber \\ \end{aligned}$$
(26)

The objective in this example is to illustrate how each method and path combination responds to prior uncertainty. To do so, we use three different prior schemes, namely:

  • \({\varPi }_1{:} (\alpha , \beta )' \sim N\left\{ (3000,185)', (10^6,10^4)'\right\} \), \(\sigma ^2\sim IG(3,1.8 \times 10^5)~\),

  • \({\varPi }_2{:}~~ (\alpha , \beta )' \sim N\left\{ (3000,0)', (10^5,10^3)'\right\} \), \(\sigma ^2\sim IG(3,1.8 \times 10^4)~\),

  • \({\varPi }_3{:}~~(\alpha , \beta )' \sim N\left\{ (3000,0)', (10^5,10^3)'\right\} \), \(\sigma ^2\sim IG(0.3,1.8 \times 10^4)\),

where IG(a, b) denotes the inverse gamma distribution with shape a and rate b. The marginal likelihoods were estimated over \(n_1=50\) and \(n_2=100\) evenly spaced temperatures. At each temperature, a Gibbs algorithm was implemented and 30,000 posterior observations were generated; after discarding 5000 as a burn-in period. The posterior output was divided into 30 batches (of equal size of \(R_b =\) 1000 points) and all estimators were computed within each batch. The mean over all batches was used as the final estimate, denoted by \(\log \widehat{\lambda }_{i}\) for each prior \({\varPi }_i\), \(i=1,2,3\). In order the estimators to be directly comparable in terms of error, the batch means method (Schmeiser 1982, Bratley et al. 1987) was preferred. In particular, the standard deviation of the \(\log \widehat{\lambda }\) over the 30 batches was considered as the estimated error, denoted hereafter by \(\widehat{MCE}\). Lefebvre et al. (2010) used \(n=1001\) equally spaced points to compute the gold standard for \(\log \hat{\lambda }_{1}=-309.9\). Following the same approach we derived \(\log \hat{\lambda }_{2}=-323.3\) and \(\log \hat{\lambda }_{3}=-328.2\). These values are considered as benchmarks in the current study. Finally, the importance functions for each model were constructed from the posterior means and variances at \(t=1\).

The estimations for the marginal likelihoods are presented in Table 1. The values that were obtained based on the importance-posterior path, reached the gold standards even when \(n=50\). The thermodynamic (IP\(_{T}\)) and the stepping–stone (IP\(_{S}\)) counterparts performed equally well and were associated with similar errors. On the contrary, the estimators that are based on the prior-posterior path yielded different values depending on the method. In particular, the stepping–stone estimator (PP\(_{S}\)) was fairly close to the gold standards with low error, for all prior schemes. The thermodynamic estimator (PP\(_{T}\)) on the other hand, underestimated the marginal likelihood and exhibited higher errors than all other methods. Logarithms of the ratios of the estimated marginal likelihoods along with the estimated BF values directly derived by the model-switch methods are further presented in Table 2. The thermodynamic and stepping-stone analogues of MS, Q\(_{PP}\) and Q\(_{IP}\), yielded estimates with similar values and errors.

Table 2 Estimated \(\varvec{\log }\) ratio of the marginal likelihoods—Pine data
Full size table
Table 3 Estimated \(f-\)divergences for Pine data
Full size table

In this example, we have used a uniform temperature schedule, moderate number of points n and non informative priors. It was therefore reasonable to expect that the prior-based methods would be associated with higher error (that could be addressed with more suitable temperature schedules) but thi approach was followed in order to highlight the path-related variance and also allow for direct comparisons with the bidirectional methods. The interesting result here was that the stepping–stone estimator addressed the prior uncertainty more successfully. In fact, the thermodynamic and stepping–stone approaches coincided only when the gold standard was reached, which means that the discretisation error (23) was minimized. The next step in our analysis was to employ a temperature schedule that places more points towards the prior in order to reduce the uncertainty. The powered fraction (25) schedule (Friel and Pettitt 2008) was used with \({\mathcal {C}}=5\). For \(n=100\), the PP\(_T\) yielded the benchmark values for the marginal likelihoods, namely \(\log \hat{\lambda }_{1}=310.0 ~(0.01)\), \(\log \hat{\lambda }_{2}=323.5 ~(0.01)\) and \(\log \hat{\lambda }_{2}=328.3 ~(0.02)\). The results were almost identical for the PP\(_S\).

Once the thermodynamic procedure yielded the benchmark values, we proceeded with the estimation of the entropy measures (see Sect. 3.1) presented in Table 3. The precision for the point \(t^*\) was set to the third decimal point and the extra MCMC runs costed less than a minute of computational time. The Bhattacharyya and Bhattacharyya-Hellinger values indicate that the priors \({\varPi }_1\), \({\varPi }_2\) and \({\varPi }_3\) where very distant from the corresponding posteriors. On the contrary, the importance functions were close approximations of their matching posterior densities. This fact completely explains the differences in the estimation, reflecting the increased local variances encountered by the PP\(_T\) as opposed to IP\(_T\). That is, the estimated distances between the end-point densities are in line with the path-related variance and therefore knowledge of the distances facilitates the prior selection, the evaluation of the importance function and the selection of the most efficient path.

4.2 Marginal likelihood for latent trait models in a simulated dataset

According to our results, the uncertainty in the pine data example was manageable under a suitable tempering schedule. This will not always be the case, especially in high dimensional problems. Here we consider also a factor analysis model with binary items which belongs to the family of the generalised linear latent trait models (GLLTM; Moustaki and Knott 2000). The GLLTM consist of three components: (i) the multivariate random component \(\mathbf Y \) of the observed variables, (ii) the linear predictor denoted by \(\eta _j \) and (iii) the link function \(\upsilon (\cdot )\), which connects the previous two components. Hence, a GLLTM can be summarized as:

$$\begin{aligned} Y_j \vert \mathrm{\mathbf{Z}}\sim ExpF,\eta _j = \alpha _j + \sum \limits _{\ell = 1}^k {\beta _{j\ell } Z_\ell }, \,\,\text{ and } \; \upsilon _j \Big ( {\mu _j (\mathrm{\mathbf{Z}})} \Big ) = \eta _j \nonumber \\ \end{aligned}$$
(27)

for \(j=1,\ldots p\) ; where ExpF is a member of the exponential family and \(\mu _{j}\)(Z) = E(Y\(_{j}\vert \) Z). With regard to the prior, a multivariate standard normal distribution is typically assumed for the latent variables \(\mathbf Z \). For the model parameters \(\varvec{\theta }=\{\alpha _j,~\beta _{j\ell }\}\) (\(j=1,\ldots p\), \(\ell =2,\ldots ,k\)) we use the low information prior presented in Vitoratou et al. (2014) based on the ideas of Ntzoufras et al. (2000) and Fouskakis et al. (2009, equation 6). For binary variables, this prior corresponds to a N(0, 4) distribution for all non-constrained loadings and for all \(\alpha _j\). For all the \(\beta _{jj}\) parameters a standardized normal prior is used for each \(\log \beta _{jj}\) inducing prior a standard deviation for \(\beta _{jj}\) approximately equal to 2, in analogy with the rest non-zero parameters \(\beta _{jl}\). To summarize, the prior is given by:

$$\begin{aligned} \pi (\beta _{j\ell }) = \left\{ \begin{array}{lll} 0 ~\text{ with } \text{ probability }~ 1&{}\quad \text{ if } &{} j<\ell \\ LN(0,1) &{}\quad \text{ if } &{} j=\ell \\ N(0,4) &{}\quad \text{ if } &{} j>\ell \end{array} \right. \end{aligned}$$

where \(Y\sim LN(\mu , \sigma ^2)\) is the log-normal distribution with the mean and the variance of \(\log Y\) being equal to \(\mu \) and \(\sigma ^2\), respectively. The dataset consists of \(N=400\) responses, \(p=4\) observed items and \(k=1\) latent variable and was previously considered in Vitoratou et al. (2014), within the context of marginal likelihood estimation. Using the same importance functions as in Vitoratou et al. (2014), we applied the PP and the IP paths, to derive the estimated marginal likelihood. Due to the dimensionality of the model, \(n=200\) runs were used and 30,000 posterior observations from a Metropolis within Gibbs algorithm were derived at each temperature point (burn in period: 10,000 iterations, thinned by 10).

The batch means for the thermodynamic and stepping-stone importance posteriors were \(-978.1\) and \(-977.9\) respectively, with associated MCE errors 0.018 and 0.013. ed These values are in agreement with the estimates obtained by Vitoratou (2013, section 6.3) using several marginal likelihood estimators including, among others, the bridge harmonic (\(-977.4\)) and the bridge geometric (\(-977.5\)) estimators (Gelman and Meng 1998).

The corresponding values under the prior posterior path were \(-995.4\) and \(-995.1\) with associated MCE errors 0.032 and 0.027, respectively. The low MCEs indicated that the error was not stochastic but rather due to the temperature placement. Even though the powered fraction (25) schedule was used to place more values close to the prior (\({\mathcal {C}}=5\)), the uncertainty was not successfully addressed. The estimators did not improve when the process was replicated for \(n=500\). This example indicates that in high dimensional models with non informative priors, the PP\(_T\) and PP\(_S\) estimators can be deteriorated by discretisation error even for large n.

5 Discussion

In this paper we have started our quest from general thermodynamic approaches using geometric paths, concluding to marginal likelihood and Bayes factors estimators. We further passed from the normalized thermodynamic integration to \(f-\) divergences and the path-related error.

We have focused our attention on the most popular implementation of thermodynamic integration in Bayesian statistics: the estimation of the marginal likelihood and the Bayes factors. We have first presented an alternative thermodynamic approach based on the stepping-stone identity (Neal 1993), introduced in biology by Xie et al. (2011) and Fan et al. (2011). We presented in parallel the available in the literature estimators under the two different approaches (thermodynamic and stepping-stone) and further made a distinction between methods according to the specific path implemented (prior-posterior or importance-posterior). By this way, we were able to introduce new appropriate estimators (based on equivalent paths) filling in the blanks in the list of the marginal likelihood and Bayes factors estimators. We have also introduced compound Bayes factor estimators which are based on nested, more complex, paths which seem to perform efficiently when estimating directly Bayes factors instead of marginal likelihoods.

Our study through these topics offers a direct connection between thermodynamic integration and divergence measures such as Kullback–Leibler and Chernoff divergences, as well as f-divergences and entropy measures emerging as special cases or functions of them. By this way, we were able to offer an efficient MCMC based thermodynamic algorithm for the estimation of the Chernoff information for a general framework which was not available in the past. While entropy measures are mostly implemented in information theory, Pardo (2006) provides a detailed guide concerning the implementation of divergences in standard statistical problems such as hypothesis testing, model comparison and parameter estimation. The Chernoff information, for instance, is used to identify an upped bound of the probability of error of the Bayes rule in classification problems with two possible decisions including hypothesis testing; see Nussbaum and Szkoła (2009) and Cover and Thomas (1991) for details. Several further readings can be found related to applications of other f-divergences in statistical inference; see for example in Sanei Tabass and Borzadaran Mohtashami (2015) for the use of Tsallis entropy in parameter estimation, in Morales et al. (2000) for the implementation of the Rényi distance in goodness-of-fit assessment, and in Chaudhuri et al. (1991) for the implementation of Bhattacharyya distance in time series context.

The study of the thermodynamic identities and integrals in terms of the f-divergences has lead us to an understanding of the error sources of the TI estimators. All these are accompanied with detailed graphical and geometric representation and interpretation offering insight to the thermodynamic approach of estimating ratios of normalizing constants. The unified framework in thermodynamic integration presented in this article offers new highways for research and further investigation. Below we discuss only some of the possible future research directions.

First, we have shown interesting properties of the optimal temperature \(t^*\), namely (a) the mean energy \(E_{p_{t^{*}}} \big \{ U(\varvec{\theta }) \big \}\) equals the free energy \(\lambda \); (b) the sampling distribution at \(t^*\) is equidistant from the endpoint densities; and (c) the area between the graph and the thermodynamic path equals to the Chernoff information. Moreover, the latter point subsequently leads also to the computation of other f- divergences. Point (b) leads to the conclusion that \(t^*\) will be sensitive to the choice of the endpoints, leading to different optimal temperatures for different prior specifications; see Table 3 for an illustration. This optimal temperature is directly connected with the information criteria and is required for the computation of the widely applicable Bayesian information criterion; see for details in Watanabe (2013). Nevertheless, in contrast to Watanabe (2013), the aim of this work is not the computation \(t^*\) in order to simplify the thermodynamic computations. For this reason, \(t^*\) is obtained as a by-product which leads to the computation of divergences. Moreover, these findings provide fruitful insights that may lead to innovative research pathways concerning the study of information criteria. Although the algorithm we provide for the computation of the optimal temperature is rigorous, it may serve as the gold standard for the evaluation of computational methods for \(t^*\).

The second research direction is associated with the study of a possible link between the deviance information criterion, DIC, (Spiegelhalter et al. 2002) and thermodynamic integration. It is well-known that the estimation of the number of efficient parameters is highly problematic in mixture models. A possible connection between TI and DIC may offer alternative efficient estimation methods in cases where multi-modal posterior densities are involved.

The development of a stochastic TI approach where the temperature will be treated as a unknown parameter is another intriguing research field. In this case, a suitable prior should be elicitated in order to a-priori support points where higher uncertainty of \(\widehat{{\mathcal {E}}}_t\) is located. Such a stochastic approach will eliminate the discretisation error which is an important source of variability for TI estimators.

Finally, MCMC samplers used for Bayesian variable selection is another interesting area of implementation of the TI approach. In such cases, interest may lie on the estimation of the normalizing constants over the whole model space and the direct estimation of posterior inclusion probabilities of each covariate. This might be extremely useful in large spaces with high number of covariates where the full exploration of the model space is infeasible due to its size and due to the existence of multiple neighborhoods of local maxima placed around well-fitted models.

6 Appendix

6.1 Estimation of the Chernoff \(t-\) divergences and information

Following Lemma 2, the Chernoff information is given by \(NTI(t^*)\). Therefore, in order to compute the Chernoff information we need first to estimate \(t^*\) for which \({\mathcal {KL}}_{t^*}\) is zero. The computation of \(t^*\) can be achieved by adding a number of steps in the path sampling procedure according to the following algorithm.

  1. Step 1

    Perform n MCMC runs to obtain \(\widehat{\mathcal{E}}_t\) for all \(t \in \mathcal{T}\) and \(\log \widehat{\lambda }\) from (19).

  2. Step 2

    Calculate \(\widehat{{\mathcal {KL}}}_t = \widehat{{\mathcal {E}}}_t - \log \widehat{\lambda }\) for all \(t \in \mathcal{T}\).

  3. Step 3

    Identify interval \(\left( t_{i^*}^-, t_{i^*+1}^+\right) \) where the sign of \({\mathcal {KL}}_t\) changes; where

    $$\begin{aligned} t_i^-= & {} \max \big ( t \in \mathcal{T} : \widehat{{\mathcal {KL}}}_t < 0 \big ) ~~\text{ and }~~ \\ t_i^+= & {} \min \big ( t \in \mathcal{T} : \widehat{{\mathcal {KL}}}_t > 0 \big )~. \end{aligned}$$

    Note, that \({\mathcal {KL}}_t\) will be negative for any \(t<t^*\) and positive otherwise since since \(\frac{d \mathcal{KL}_t }{dt} = V_{p_t} \Big \{ \log \frac{p_1(\varvec{\theta })}{p_0(\varvec{\theta })} \Big \}>0\) and therefore \(\mathcal{KL}_t\) it is an increasing function of t.

  4. Step 4

    Perform extra MCMC cycles by further discretising \(\left( t_{i^*}^-, t_{i^*+1}^+\right) \) until the required precision is achieved.

  5. Step 5

    Update \(\mathcal{T}\) and n to account for the new points \(t_i\in \left( t_{i^*}^-, t_{i^*+1}^+\right) \) used in Step 5.

  6. Step 6

    Once the \(t^*\) is estimated, the MCMC output already available from the runs in Steps 1 and 4 can be used to estimate the Chernoff information. In particular, it is estimated as described in (19) having substituted \(\widehat{{\mathcal {E}}}_t\) by \(\widehat{{\mathcal {KL}}}_t\) for all \(t\in \mathcal{T}\) and only accounting for \(t_i \le t^*\) in the summation. Therefore, the Chernoff information is estimated by \(\widehat{NTI}(t^*)\) given by

    $$\begin{aligned} \log \widehat{NTI}(t^*)= & {} \sum _{ i \in \mathcal{I}:\, t_{i+1} \le \,t^* } (t_{i+1}-t_i) \frac{\widehat{{\mathcal {KL}}}_{t_{i+1}} + \widehat{{\mathcal {KL}}}_{t_{i}}}{2} \nonumber \\= & {} \sum _{ i \in \mathcal{I}:\, t_{i+1} \le \, t^* } (t_{i+1}-t_i) \frac{\widehat{{\mathcal {E}}}_{t_{i+1}} + \widehat{{\mathcal {E}}}_{t_{i}} }{2}\nonumber \\&\quad - t^* \log \widehat{\lambda }, \end{aligned}$$
    (28)

    where the \(\mathcal{I} = \{ 0, 1, \dots , n\}\) and \(n=|\mathcal{T}|\).

In the special case where the path sampling is combined with output from MCMC algorithms which involve tempered transitions (see Calderhead and Girolami 2009 for details), the estimation of the Chernoff information comes with low computational cost. This approach can be attractive and useful in the case of multi-modal densities. The same algorithm can be also implemented to compute the rest of the f-divergences measures discussed in Sect. 3.1. In fact, their estimation is less demanding since it requires one additional MCMC run, in order to derive the estimated \({\mathcal {KL}}_{t_i}\) at the point of interest; for instance at \(t_i\)=0.5 we derive the \(Bh(p_1,\,p_0)\) and \(He(p_1,\, p_0)\) divergences.