On the use of Markov chain Monte Carlo methods for the sampling of mixture models: a statistical perspective

Abstract

In this paper we study asymptotic properties of different data-augmentation-type Markov chain Monte Carlo algorithms sampling from mixture models comprising discrete as well as continuous random variables. Of particular interest to us is the situation where sampling from the conditional distribution of the continuous component given the discrete component is infeasible. In this context, we advance Carlin & Chib’s pseudo-prior method as an alternative way of infering mixture models and discuss and compare different algorithms based on this scheme. We propose a novel algorithm, the Frozen Carlin & Chib sampler, which is computationally less demanding than any Metropolised Carlin & Chib-type algorithm. The significant gain of computational efficiency is however obtained at the cost of some asymptotic variance. The performance of the algorithm vis-à-vis alternative schemes is, using some recent results obtained in Maire et al. (Ann Stat 42: 1483–1510, 2014) for inhomogeneous Markov chains evolving alternatingly according to two different $\pi ^{*}$-reversible Markov transition kernels, investigated theoretically as well as numerically.

1 Introduction

To sample from mixture probability distributions $\pi ^{*}$ of a discrete and a continuous random variable, denoted by $M$ and $Z$, respectively, is a fundamental problem in statistics. In this paper we study the use of different data-augmentation-type Markov chain Monte Carlo (MCMC) algorithms for this purpose. Of particular interest to us is the situation where sampling from the conditional distribution of $Z$ given $M$ is infeasible.

In many applications the most natural approach to sampling from $\pi ^{*}$ goes via the Gibbs sampler, which samples alternatingly from the conditional distributions $M \mid Z$ and $Z \mid M$. Since the component $M$ is discrete, the former sampling step is most often feasible (at least when $\pi ^{*}$ is known up to a normalising constant). On the contrary, drawing $Z \mid M$ is in general infeasible; in that case this sampling step is typically metropolised by replacing, with a Metropolis-Hastings probability, the value of $Z$ obtained at the previous iteration by a candidate drawn from some proposal kernel. This yields a so-called Metropolis-within-Gibbs—or hybrid—sampler.

However, when the modes of the mixture distribution are well-separated, implying a strong correlation between $M$ and $Z$, the Gibbs sampler has in general very limited capacity to move flexibly between the different modes, and exhibits for this reason most often very poor mixing (see Hurn et al. (2003) for some discussion). Since this problem is due to model dependence, it effects the standard Gibbs as well as the hybrid sampler. In order to cope with this well-known problem, we consider Carlin & Chib’s pseudo-prior method (Carlin and Chib 1995) as an alternative way to infer mixture models. The method extends the target model with a set of auxiliary variables that are used to help moving the discrete component. When the distribution of the auxiliary variables (determined by a set of pseudo-priors) is chosen optimally (an idealised situation however), the method produces indeed i.i.d. samples from the marginal distribution of $M$ under $\pi ^{*}$. Given $M$, the $Z$ component is sampled from $Z \mid M$ in accordance with the Gibbs sampler, with possible metropolisation in the case where exact sampling is infeasible. The latter scheme will be referred as the Metropolised Carlin & Chib-type (MCC) sampler.

Surprisingly, it turns out that passing directly and deterministically the value of the $M$th auxiliary variable, obtained through sampling from the pseudo-priors at the beginning of the loop, to the $Z$ component yields a Markov chain that is still $\pi ^{*}$-reversible (see Lemma 8). Moreover, using some recent results obtained in Maire et al. (2014) on the comparison of asymptotic variance for inhomogeneous Markov chains, we are able to prove (see Theorem 7) that this novel MCMC algorithm, referred to as the Frozen Carlin & Chib-type (FCC) sampler, generates a Markov chain whose sample path averages have always higher asymptotic variance than those of the MCC sampler for a large class of objective functions. This is well in line with our expectations, as the MCC sampler “refreshes” more often the $Z$ component. On the other hand, since this component is already modified through sampling from the pseudo-priors, which, when well-designed, should be close to the true conditional distribution $Z \mid M$, we may expect that the additional mixing provided by the MCC sampler is only marginal. This is also confirmed by our simulations, which indicate only a small advantage of the MCC sampler to the FCC sampler in terms of autocorrelation. As the FCC algorithm omits completely the Metropolis-Hastings operation of the MCC sampler, it is considerably more computationally efficient. Thus, we consider the FCC sampler as a strong alternative to the MCC sampler in terms of efficiency (inverse standard error per unit CPU).

The paper is structured as follows: in Sect. 2 we introduce some notation and describe precisely the mixture model framework under consideration. Section 3 describes the Carlin & Chib-type MCMC samplers studied in the paper. In Sect. 4 we prove that the involved algorithms are indeed $\pi ^{*}$-reversible and provide a theoretical comparison of the MCC and FCC samplers. Finally, in the implementation part, Sect. 5, we illustrate and compare numerically the algorithms on two examples: a toy mixture of Gaussian distributions and a model where the mixture variables are only partially observed. The latter is applied to two different settings including the estimation of a warping parameter for handwritten digits analysis.

2 Preliminaries

2.1 Notation

We assume throughout the paper that all variables are defined on a common probability space $(\varOmega , \mathcal {F}, \mathbb {P})$. We will use upper case for random variables and lower case for realisations of the same, and write “$X \leadsto x$” when $x$ is realisation of $X$. We write “$X \sim \mu$” to indicate that the random variable $X$ is distributed according to the probability measure $\mu$. For any $\mu$-integrable function $h$ we let $\mu (h) :=\int h(x) \mu (dx)$ be the expectation of $h(X)$ under $\mu$. Similarly, for Markov transition kernels $M$, we write $Mf(x) :=\int f(x') M(x, dx')$ whenever this integral is well-defined. For any two probability measures $\mu$ and $\mu '$ defined on some measurable spaces $(\mathsf {X}, \mathcal {X})$ and $(\mathsf {X}', {\mathcal {X}}')$, respectively, we denote by $\mu (dx)\mu '(dx')$ the product measure on . For $(m, n) \in \mathbb {Z}^2$ such that $m \le n$, we denote by $[\![m, n ]\!] :=\{m, m + 1, \ldots , n\} \subset \mathbb {Z}$. Moreover, we denote by $\mathbb {N}^{*}:=\mathbb {N}\setminus \{ 0 \}$ the set of positive integers.

Finally, given some probability measure $\pi$ on $(\mathsf {X}, \mathcal {X})$ we recall, first, that a Markov transition kernel $M$ is called $\pi$ -reversible if $\pi (dx) M(x, dx') = \pi (x') M(x', dx)$ and, second, that $\pi$-reversibility of $M$ implies straightforwardly that this kernel allows $\pi$ as a stationary distribution.

2.2 Mixture models

Throughout this paper, our main objective is to sample a probability distribution $\pi ^{*}$ on some product space , where $n$ is at least $2$ and is some (typically uncountable) measurable space, associated with the $\sigma$-field . Thus, a $\pi ^{*}$-distributed random variable comprises a $[\![1, n ]\!]$-valued (discrete) random variable $M$ and a -valued (typically continuous) random variable $Z$.

In the following we assume that $\pi ^{*}(dm\times dz)$ is dominated by a product measure $|dm| \nu (dz)$, where $|dm|$ denotes the counting measure on $[\![1, n ]\!]$ and $\nu$ is some nonnegative measure on , and denote by $\pi ^{*}(m, z)$ the corresponding density function on . We may then define the marginal probability functions

$$\begin{aligned} \pi ^{*}(m)&:=\int \pi ^{*}(m, z) \nu (dz) \\ \pi ^{*}(z)&:=\sum _{m= 1}^n \pi ^{*}(m, z) \end{aligned}$$

(w.r.t. $|dm|$ and $\nu$, respectively) on $[\![1, n ]\!]$ and , respectively, as well as the conditional probability functions

$$\begin{aligned} \pi ^{*}(m\mid z)&:= \frac{\pi ^{*}(m, z)}{\pi ^{*}(z)} , \nonumber \\ \pi ^{*}(z\mid m)&:= \frac{\pi ^{*}(m, z)}{\pi ^{*}(m)} \end{aligned}$$

(1)

(w.r.t. $|dm|$ and $\nu$, respectively) on $[\![1, n ]\!]$ and , respectively.

Remark 1

We stress at this stage that our focus is set on the problem of how to sample efficiently from a given mixture model; in particular, Bayesian model selection problems, where the dimensionality of the parameter vector is typically not fixed (see, e.g., Green (1995), Petralias and Dellaportas (2013)), fall outside the scope of this paper.

3 Markov chain Monte Carlo methods for mixture models

Using the conditional distributions (1), a natural way of sampling $\pi ^{*}$ consists in implementing a standard Gibbs sampler simulating a Markov chain with transitions described by the following algorithm—the Markov chain superscript refers to the algorithm index.

Remark 2

Since $M$ is a discrete random variable it is most often possible to sample $M\; \sim \pi ^{*}(dm\mid z)$. In contrast, sampling $Z\; \sim \pi ^{*}(dz\mid m)$ is not always possible. In that case, one may replace Step (ii) by a Metropolis-Hastings step, yielding a Metropolis-within-Gibbs algorithm (see [Robert and Casella (2004), section 10.3.3] for details).

Using the output of Algorithm 1, any expectation $\pi ^{*}(f)$, where $f$ is some $\pi ^{*}$-integrable objective function on , can be estimated by the sample path average

A well-known problem with this approach is that even though Algorithm 1 generates a Markov chain with stationary distribution $\pi ^{*}$, the discrete component tends in practice to get stuck in a few states. Indeed, when the variable $Z$ is sampled from its conditional distribution given $M = m$, the probability of jumping to another index $m' \ne m$ is proportional to $\pi ^{*}(m', z)$, which may be very low when the index component $M$ is informative concerning the localisation of $Z$. This will lead to poor mixing and, consequently, high variance of any estimator $\hat{\pi }^{(1)}_n(f)$. To be specific, let $h$ be some function on $[\![1, n ]\!]$ and assume that we run the Gibbs sampler in Algorithm 1 to estimate $\int h(m) \pi ^{*}(dm)$. Then is itself a Markov chain with transition kernel $G(m, dm') :=\int \pi ^{*}(dz\mid m) \pi ^{*}(dm' \mid z)$ and starting with , we have, as $\pi ^{*}$ is invariant under $G$,

where, by Jensen’s inequality,

Consequently,

Combining this with the fact that $G$ is $\pi ^{*}(dm)$-reversible, we obtain

Moreover, using again that $G$ is $\pi ^{*}(dm)$-reversible,

Finally, letting $f(m,z) \equiv h(m)$, we obtain

showing that the Gibbs sampler approximates the index less accurately than i.i.d. sampling from $\pi ^{*}(dm)$.

The pseudo-prior method of B. P. Carlin and S. Chib (Carlin and Chib 1995) was introduced in the context of model selection and can successfully be adapted to mixture models. By introducing some auxiliary variables, this method increases the number of moves of the index component. The algorithm may be regarded as a Gibbs sampler-based data-augmentation algorithm targeting the distribution $\pi$ defined on the extended state space by

$$\begin{aligned} \pi (dm\times du) :=\pi ^{*}(dm\times du_m) \bigotimes _{j \ne m} \rho _j(du_j) , \end{aligned}$$

(2)

where and the probability measures $\{\rho _j ; j \in [\![1, n ]\!] \}$ are referred to as pseudo-priors (the terminology comes from Carlin and Chib (1995)). We assume that also the pseudo-priors are dominated jointly by the nonnegative measure $\nu$ and use the same symbols $\rho _j$ for denoting the corresponding densities. As a consequence, the measure $\pi$ defined in (2) admits the density

with respect to . In the following, the density $\pi$ is assumed to be positive, i.e., $\pi (m, u) > 0$ for all .

Remark 3

The pseudo-priors constitute a design parameter of the method that has to be tuned by the user provided that (i) the pseudo-priors are analytically tractable and (ii) can be sampled from. Even though the Markov chain is in general ergodic for any choice of the pseudo-priors, the design of the same impacts significantly the performance of the algorithm in practice. Methods for designing the pseudo-priors are often problem specific; still, some possible guidelines are provided in Sect. 5.

Denote by the Markov chain generated by this algorithm, which we will in the following refer to as the Carlin & Chib-type (CC-type) sampler and whose transitions comprise the $n + 1$ sub-steps described in Algorithm 2 below.

Intuitively, Algorithm 2 allows jumps between different indices to occur more frequently than in the Gibbs sampler; indeed, in Step (ii) the probability of moving to the index $m'$ is

$$\begin{aligned} \pi (m' \mid u) \propto \pi ^{*}(m',u_{m'})/ \rho _{m'}(u_{m'}), \end{aligned}$$

(3)

where the right hand side is close to $\pi ^{*}(m')$ if the pseudo-priors are chosen such that $\rho _{\ell }(z)$ is close to $\pi ^{*}(z\mid \ell )$ for all . The optimal case where $\rho _\ell (z) \equiv \pi ^{*}(z\mid \ell )$ implies, via (3), that

$$\begin{aligned} \pi (m' \mid u)\propto \pi ^{*}(m'). \end{aligned}$$

Thus, in this case, Step (ii) draws actually $M'$ according to the exact marginal $\pi ^{*}(dm)$ of the class index random variable regardless the value of $u$, which implies that the algorithm simulates i.i.d. samples according to $\pi ^{*}$. This actually gives a more efficient approximation than that produced by the Gibbs sampler, whose variance w.r.t. the index component is, as we remarked previously, always larger than that obtained through i.i.d. sampling from $\pi ^{*}(dm)$. However, this ideal situation requires the quantity $\pi ^{*}(z\mid \ell )$ to be tractable, which is typically not the case.

As in Remark 2, one may replace Step (iii) in Algorithm 2 by a Metropolis-Hastings step if sampling from $\pi ^{*}(dz\mid m')$ is infeasible. This is most often the case when $\pi ^{*}(dm\times dz)$ is the a posteriori distribution of $(M, Z)$ conditionally on one or several observations (see Sect. 5.2 for an example). In that case $\pi ^{*}$ is known only up to a normalizing constant, which prevents sampling from the conditional density $\pi ^{*}(dz\mid m')$. The resulting algorithm will in the following be referred to as the Metropolised CC-type (MCC) sampler and is presented in Algorithm 3, where $\{R_\ell ; \ell \in [\![1, n ]\!] \}$ is a set of proposal kernels on . Assume for simplicity that all these kernels are jointly dominated by the reference measure $\nu$ and denote by $\{r_\ell ; \ell \in [\![1, n ]\!] \}$ the corresponding transition densities with respect to this measure. Throughout the paper, we will assume that $r_\ell (u,z)>0$ for all $\ell \in [\![1, n ]\!]$ and all . Introducing also the Metropolis-Hastings acceptance probability

(4)

the MCC algorithm is described as follows.

Note that Step (iii) generates, given $u_{m'}$, $U_{m'}' \sim K_{m'}(u_{m'}, du')$, where

$$\begin{aligned}&K_\ell (u, du') :=R_\ell (u, du') \alpha _\ell (u, u') \nonumber \\&\quad +\delta _u(du') \left( 1 - \int R_\ell (u, du'') \alpha _\ell (u, u'') \right) \nonumber \\&\quad ((u, \ell ) \in \mathsf {Z}\times [\![1, n ]\!]) . \end{aligned}$$

(5)

It can be easily checked (using (4)) that $K_{m'}$ is indeed a Metropolis-Hastings kernel with respect to $\pi (dz \mid m')$; it is thus $\pi (dz \mid m')$-reversible. Moreover, in the particular case where $R_\ell (u, du') = \pi ^{*}(du' \mid \ell )$ for all $\ell \in [\![1, n ]\!]$, the MCC algorithm and Algorithm 2 coincide.

Remarkably, it turns out that Step (iii) in Algorithm 3 may be omitted, which may, in some cases, imply a significant gain of computational complexity. The MCC algorithm sampler then simplifies to what we will refer to as the Frozen CC-type (FCC) sampler, which is described formally in Algorithm 4.

Figure 1 compares the transitions of Algorithms 2, 3, and 4, and shows clearly that the algorithms differ only in the way the continuous component is updated. More specifically, from the diagram it is clear that the three algorithms under consideration can be regarded as inhomogeneous Markov chains evolving alternatingly according to two different kernels comprising Steps (i)–(ii) and Steps (iii)–(iv), respectively. The first kernel updates $(m, z)$ according to a $\pi ^{*}$-reversible transition. The second kernel may, as for the CC and MCC algorithms, correspond to some specific $\pi ^{*}$-reversible kernel or can, as in the FCC algorithm, be simply the identity kernel (which is, being reversible with respect to any distribution, straightforwardly $\pi ^{*}$-reversible). Depending on the context, this shortcut makes FCC considerably less computationally demanding. Nevertheless, as stated in Theorem 7 below, FCC is always less efficient in terms of asymptotic variance than the corresponding MCC sampler. Intuitively, this stems from the fact that once the index $M'$ is drawn, the associated continuous component is selected deterministically without being “refreshed” (on the contrary to Step (iii) in Algorithm 3). In addition, as our numerical simulations indicate that the gain of the asymptotic variance obtained by refreshing, as in the MCC sampler, this component instead of freezing the same as in the FCC sampler seems to be limited (see Sect. 5 for details), we definitely regard the FCC algorithm as a strong challenger of the MCC sampler.

Fig. 1

Comparison of the CC-type samplers

4 Theoretical results

4.1 Comparison of asymptotic variance of inhomogeneous Markov chains

In this section we recall briefly the main result of [Maire et al. (2014), Theorem 4], which is propelling the coming analysis. The following—now classical—orderings of Markov kernels turn out to be highly useful.

Definition 1

Let $P_{0}$ and $P_{1}$ be Markov transition kernels on some state space $(\mathsf {X}, \mathcal {X})$ with common invariant distribution $\pi$. We say that $P_{1}$ dominates $P_{0}$

• on the off-diagonal, denoted $P_{1} \succeq P_{0}$, if for all $\mathsf {A} \in \mathcal {X}$ and $\pi$-a.s. all $x \in \mathsf {X}$,

  $$\begin{aligned} P_{1}(x, \mathsf {A} \setminus \{ x \}) \ge P_{0}(x, \mathsf {A} \setminus \{ x \}) . \end{aligned}$$

• in the covariance ordering, denoted $P_{1} \succcurlyeq P_{0}$, if for all ,

  $$\begin{aligned}&\int f(x) P_{1}f(x) \pi (dx) \le \int f(x) P_{0}f(x) \pi (dx) . \end{aligned}$$

The covariance ordering, which was introduced implicitly in [Tierney (1998), p. 5] and formalised in Mira (2001), is an extension of the off-diagonal ordering, since, according to [Tierney (1998), Lemma 3], $P_{1} \succeq P_{0}$ implies $P_{1} \succcurlyeq P_{0}$. Moreover, it turns out that for reversible kernels, $P_{1} \succcurlyeq P_{0}$ implies that the asymptotic variance of sample path averages of chains generated by $P_{1}$ is smaller than or equal to that of chains generated by $P_{0}$ (see the proof of [Tierney (1998), Theorem 4]).

In algorithms of Gibbs-type, the ordering in Definition 1 is usually not applicable, since the fact that all candidates are accepted with probability one prevents the chain from remaining in the same state. The ordering is however still meaningful when a component is discrete.

In the following, let $P_{i}$ and $Q_{i}$, $i \in [\![0, 1 ]\!]$, be Markov transition kernels on $(\mathsf {X}, \mathcal {X})$ and let and be inhomogeneous Markov chains evolving as follows:

(6)

This means that for all $k \in \mathbb {N}$ and $i \in \{0, 1\}$,

• ,

• ,

where , $n \in \mathbb {N}$. Now, impose the following assumption.

(A1) (i) $P_{i}$ and $Q_{i}$, $i \in [\![0, 1 ]\!]$, are $\pi$ -reversible,

(ii) $P_{1} \succcurlyeq P_{0}$ and $Q_{1} \succcurlyeq Q_{0}$.

As mentioned above, $P_{1}\succeq P_{0}$ implies $P_{1}\succcurlyeq P_{0}$; thus, in practice, a sufficient condition for (A1) (ii) is that $P_{1} \succeq P_{0}$ and $Q_{1} \succeq Q_{0}$. Under these assumptions, Maire et al. (2014) established the following result.

Theorem 4

[Maire et al. (2014)] Assume that $P_{i}$ and $Q_{i}$, $i \in [\![0, 1 ]\!]$, satisfy (A1) and let , $i \in [\![0, 1 ]\!]$, be Markov chains evolving as in (6) with initial distribution $\pi$. Then for all such that for $i \in [\![0, 1 ]\!]$,

(7)

it holds that

$$\begin{aligned} v_{1}(f) \le v_{0}(f) , \end{aligned}$$

(8)

where

(9)

Remark 5

As shown in [Maire et al. (2014), Proposition 9], under the assumption that the product kernels $P_{i} Q_{i}$, $i \in [\![0, 1 ]\!]$, are both $V$ -geometrically ergodic (according to Definition 7 in the same paper), the absolute summability assumption (7) holds true for all objective functions $f$ such that $f$ and , $i \in [\![0, 1 ]\!]$, have all bounded $\sqrt{V}$-norm; see again Maire et al. (2014) for details.

4.2 The MCC sampler versus the FCC sampler

In the light of the remarks following Algorithm 4 it is reasonable to assume that the CC-type sampler (Algorithm 2) and the MCC sampler provides more accurate estimates than the FCC sampler. However, since is not $\pi ^{*}$-reversible, [Tierney (1998), Theorem 4] does not allow these two algorithms to be compared. Nevertheless, using Theorem 4 we may provide a theoretical justification advocating the MCC and CC-type samplers ahead of the FCC sampler in terms of asymptotic variance. To do this we decompose the transition kernels of and into products of two $\pi ^{*}$-reversible kernels. More specific, let and be the inhomogeneous Markov chains defined on through, for $i\in [\![3, 4 ]\!]$,

(10)

Here we have introduced the kernels

• $\displaystyle :=\!\idotsint \! \left( \prod _{j \ne m} \rho _j({d} u_j) \right) \! \delta _z({d} u_m) \pi ({d} \check{m} \!\mid \! u) \delta _{u_{\check{m}}}({d} \check{z}),$

• ,

• (where $K_{\check{m}}$ is defined in (5)),

• .

Setting , $k \in \mathbb {N}$, $i\in [\![1, 2 ]\!]$, it can be checked easily that and have indeed exactly the same distribution as the output of Algorithm 3 and Algorithm 4, respectively. Using the decomposition (10), we may obtain the following results.

(A2) It holds that

where $\omega (m,u):=\pi ^{*}(m,u)/\rho _m(u)$.

Theorem 6

The Markov chains and generated by Algorithms 3 and 4, respectively, have $\pi ^{*}$ as invariant distribution. Moreover, under (A2) , the chains are uniformly ergodic.

Proof

The first part of the theorem is established by noting that defined above is reversible with respect to any distribution, and in particular it is $\pi ^{*}$-reversible. Moreover, according to Lemma 8 (below), and are also $\pi ^{*}$-reversible. This completes the proof of the first part.

To prove the second part, note that for each $i \in [\![3, 4 ]\!]$, the transition kernel of is $P_{i}Q_{i}$. Moreover, since $P_{4}Q_{4}=P_{4}=P_{3}$, it is enough to establish that $P_{3}$ and $P_{3}Q_{3}$ are uniformly ergodic. By definition, for all $(m,u_m) \in \mathsf {Y}$,

$$\begin{aligned}&P_{3}((m,u_m),d\ell \times dv) \nonumber \\&\quad =\sum _{k \in [\![1, n ]\!]}\idotsint \left( \prod _{i \ne m} \rho _i(du_i) \right) \pi (k \mid u)\delta _k(d\ell )\delta _{u_k}(dv),\nonumber \\ \end{aligned}$$

(11)

and plugging the expression

$$\begin{aligned} \pi (k \mid u)=\frac{\omega (k,u_k)}{\sum _{j = 1}^n \omega (j,u_j)} , \end{aligned}$$

where $\omega$ is defined in (A2) , into (11) yields

$$\begin{aligned}&P_{3}((m,u_m),d\ell \times dv) \nonumber \\&\quad = \sum _{k \ne m} \kappa (m,u_m,k,v) \nu _k(d\ell \times dv) \nonumber \\&\qquad +\check{\kappa }(m,u_m) \delta _{(m,u)}(d\ell \times dv) , \end{aligned}$$

(12)

where we have defined

$$\begin{aligned}&\nu _k(d\ell \times dv) :=\delta _k(d\ell )\nu (dv), \\&\kappa (m,u_m,k,u_k) :=\rho _k( u_k) \int \prod _{i \ne m, i \ne k} \rho _i(du_i) \frac{\omega (k,u_k)}{\sum _{j}\omega (j,u_j)} , \\&\check{\kappa }(m,u_m) :=\int \prod _{i \ne m} \rho _i(du_i) \frac{\omega (m,u_m)}{\sum _{j}\omega (j,u_j)} . \end{aligned}$$

Note that (A2) implies

$$\begin{aligned} \underline{\kappa }(k,v) :=\inf _{(m,u)\in \mathsf {Y}} \kappa (m,u,k,v)>0; \end{aligned}$$

(13)

thus, for all , we obtain

$$\begin{aligned}&P_{3}^2((1,u),\mathsf {A}) \nonumber \\&\quad \ge \iint P_{3}((1,u),dk \times dw) \mathbb {1}_{\{2\}}(k)\nonumber \\&\qquad \times P_{3}((2,w),d\ell \times dv) \mathbb {1}_{\{1\}}(\ell )\mathbb {1}_\mathsf {A}(\ell ,v) \nonumber \\&\quad \ge \int \underline{\kappa }(2,w) \nu (dw) \int _\mathsf {A} \underline{\kappa }(1,v) \nu _1(d\ell \times dv) . \end{aligned}$$

(14)

Now, fix $m\ne 1$; then, reusing (13) yields

$$\begin{aligned}&P_{3}^2((m,u),\mathsf {A})\\&\quad \ge \iint P_{3}((m,u),dk \times dw) \mathbb {1}_{\{1\}}(k)\\&\qquad \times P_{3}((2,w),d\ell \times dv) \mathbb {1}_{\{1\}}(\ell )\mathbb {1}_\mathsf {A}(\ell ,v) \\&\quad \ge \int _\mathsf {A} \underline{\kappa }(1,v)\check{\kappa }(1,v) \nu _1(d\ell \times dv) . \end{aligned}$$

Consequently, for all $(m,u) \in \mathsf {Y}$ and all $\mathsf {A} \in \mathcal {Y}$,

$$\begin{aligned} P_{3}^2((m,u),\mathsf {A}) \ge \varepsilon \bar{\eta }_1(\mathsf {A}), \end{aligned}$$

where $\bar{\eta }_1:=\eta _1/\eta _1(\mathsf {Y})$, $\varepsilon :=\eta _1(\mathsf {Y})$, and

$$\begin{aligned}&\eta _1(d\ell \times dv):=\\&\quad \left( \int \underline{\kappa }(2,w) \rho _{2}(dw) \wedge \check{\kappa }(1,v)\right) \underline{\kappa }(1,v) \nu _1(d\ell \times dv). \end{aligned}$$

This establishes that $P_{3}=P_{4}Q_{4}$ is uniformly ergodic.

We now turn to the product $P_{3}Q_{3}$. By definition of $Q_{3}$, we have $Q_{3}((m,u),d\ell \times dv)=\delta _m(d\ell ) K_m(u, dv)$. Thus, we obtain, using (5),

(15)

where by assumption,

Using (15) twice, we obtain for all $(m,u) \in \mathsf {Y}$ and all $\mathsf {A}\in \mathcal {Y}$,

(16)

which implies, along the lines of (14),

$$\begin{aligned} (P_{3}Q_{3})^2((1,u),\mathsf {A})\ge \epsilon _1 \int _{\mathsf {A}}g_1(v) \nu _1(d\ell \times dv), \end{aligned}$$

where

Similarly, for all $m \ne 1$,

$$\begin{aligned} (P_{3}Q_{3})^2((m,u),\mathsf {A})\ge \int _{\mathsf {A}}g_2(v) \nu _1(d\ell \times dv), \end{aligned}$$

where

Thus, along previous lines, for all $(m, u) \in \mathsf {Y}$ and all $\mathsf {A} \in \mathcal {Y}$,

$$\begin{aligned} (P_{3}Q_{3})^2((1,u),\mathsf {A}) \ge \epsilon \bar{\eta }_2(\mathsf {A}), \end{aligned}$$

where $\bar{\eta }_2:=\eta _2/\eta _2(\mathsf {Y})$, $\epsilon :=\eta _2(\mathsf {Y})$, and

$$\begin{aligned} \eta _2(d\ell \times dv) :=(\epsilon _1 g_1(v)) \wedge g_2(v) \nu _1(d\ell \times dv), \end{aligned}$$

implying that $P_{3}Q_{3}$ is uniformly ergodic. The proof is completed. $\square$

Theorem 7

Let , $i\in [\![3, 4 ]\!]$, be the Markov chains (10) starting with for $i\in [\![3, 4 ]\!]$. Then, under (A2) , for all real-valued functions $h$ on $[\![1, n ]\!]$, it holds that

Proof

By Theorem 6, the processes and are both inhomogeneous Markov chains that evolve alternatingly according to the $\pi ^{*}$-reversible kernels and , $i\in [\![1, 2 ]\!]$, respectively. Moreover, , and since has no off-diagonal component, . Now, define Markov chains , $i \in [\![3, 4 ]\!]$, as in (10) with , and set $f(m,z) \equiv h(m)$. By construction, for all $(i, k) \in [\![3, 4 ]\!] \times \mathbb {N}^{*}$, implying that

(17)

where finiteness follows since are the index components of the Markov chain , which is uniformly ergodic by Theorem 6, and since the function $h$ is bounded (being defined on a finite set). Moreover, for all $n \in \mathbb {N}^{*}$,

implying, by (17), that

Finally, by (17) we may apply Theorem 4 to the chains , $i \in [\![0, 1 ]\!]$, which establishes immediately the statement of the theorem. $\square$

Lemma 8

The Markov kernels and are both $\pi ^{*}$-reversible.

Proof

Write, using the identity

$$\begin{aligned}&\nu (dz) \delta _{z}(du_m) \delta _{u_{\check{m}}}(d\check{z}) \prod _{j \ne m} \nu (du_j) \\&= \delta _{u_m}(dz) \delta _{u_{\check{m}}}(d\check{z}) \prod _{j = 1}^n \nu (du_j) , \end{aligned}$$

for any nonnegative measurable function $f$ on $(\mathsf {Y}, \mathcal {Y})$,

Thus, integrating first over $z$ and $\check{z}$ and defining

$$\begin{aligned}&A(m, \check{m}, u) \\&\quad :=\pi ^{*}(m, u_{m}) \pi ^{*}(\check{m},u_{\check{m}}) \frac{\prod _{j \ne m} \rho _j(u_j) \times \prod _{j\ne \check{m}} \rho _j(u_j)}{\sum _{k = 1}^n\pi ^{*}(k, u_k) \prod _{\ell \ne k} \rho _{\ell }(u_\ell )} \end{aligned}$$

yields

Now, the symmetry $A(m, \check{m}, u) = A(\check{m}, m, u)$ implies the identity

(18)

and as $f$ was chosen arbitrarily, (18) implies that

which establishes the $\pi ^{*}$-reversibility of .

We show that is $\pi ^{*}$-reversible. Again, let $f$ be some nonnegative measurable function on $(\mathsf {Y},\mathcal {Y})$. Then, using that $K_m$ is reversible with respect to $\pi ^{*}(dz \mid m)$ for all $m \in [\![1, n ]\!]$, we obtain, denoting $\check{y}:=(\check{m}, \check{z})$ and $y :=(m, z)$,

$$\begin{aligned}&\idotsint f(\check{y}, y) \pi ^{*}(d\check{y}) K_{\check{m}}(\check{z},dz) \delta _{\check{m}}(dm) \\&\quad =\idotsint f(\check{y}, y) \pi ^{*}(d\check{m}) \pi ^{*}(d\check{z}\mid \check{m}) K_{\check{m}}(\check{z},dz) \delta _{\check{m}}(dm) \\&\quad =\idotsint f(\check{y}, y) \pi ^{*}(d\check{m}) \pi ^{*}(dz \mid \check{m}) K_{\check{m}}(z,d\check{z}) \delta _{\check{m}}(dm) \\&\quad =\!\idotsint \! f(\check{y}, y) \pi ^{*}(dm)\pi ^{*}(dz \mid m) K_m(z,d\check{z}) \delta _m (d\check{m}) . \end{aligned}$$

This implies

which completes the proof. $\square$

5 Numerical illustrations

In this section we compare numerically the performances of the different algorithms described in the previous section. The comparisons will be based on three different models: first, a simple toy model consisting of a mixture of two Gaussian strata; second, a model where only partial observations of the mixture variables are available; third, a real-world high-dimensional missing data inference problem where the posterior distribution of a class index and a deformation field is estimated given a set of template patterns and a specific observation. All implementations are in Matlab, running on a MacBook Air with a $1.8$ GHz Inter Core i7 processor (for the first two examples) and a Dell Precision T1500 with a $3.3$ GHz Inter Core i5 processor (for the third example).

5.1 Mixture of Gaussian strata

Let $\mathsf {Y}= [\![1, 2 ]\!] \times \mathbb {R}$ (i.e., in this case) and consider a pair of random variables $(M, Z)$ distributed according to the Gaussian mixture model

$$\begin{aligned} \pi ^{*}(m, z) = \frac{1}{2} \phi (z; \mu _m, \sigma ^2) \quad ((m, z) \in \mathsf {Y}) , \end{aligned}$$

(19)

where $\sigma > 0$, $(\mu _1, \mu _2) = (-1, 1)$, and $\phi (z; \mu , \sigma ^2)$ denotes the Gaussian probability density function with mean $\mu$ and variance $\sigma ^2$. Even though it is straightforward to generate i.i.d. samples from this simple toy model, we use it for illustrating and comparing the performances of the algorithms proposed in the previous; in particular, since $\pi ^{*}(z\mid m)$ is simply a Gaussian distribution in this case, it is possible to execute Step (iii) in Algorithm 2 (which is, as mentioned, far from always the case; see the next example). For small values of $\sigma$, such as the value $\sigma = \sqrt{.2}$ used in this simulation, the two modes are well-separated, implying a strong correlation between the discrete and continuous components. As a consequence we may expect the naive Gibbs sampler to exhibit a very sub-optimal performance in this case. In order to improve mixing we introduced Gaussian pseudo-priors

$$\begin{aligned} \rho _\ell (u) :=\phi (u; \tilde{\mu }_\ell , \tilde{\sigma }^2_\ell )\quad ((\ell , u) \in [\![1, 2 ]\!] \times \mathbb {R}) \end{aligned}$$

on $\mathbb {R}$, where $(\tilde{\mu }_1, \tilde{\mu }_2, \tilde{\sigma }_1^2, \tilde{\sigma }_2^2) = (-.5, .5, .205, .205)$, and executed, using these pseudo-priors, Algorithms 2, 3, and 4. Note that the slight over-dispersion of the pseudo-priors provides a model that satisfies (A2 ), which allows Theorem 7 to be used for comparing theoretically the algorithms. Moreover, the naive Gibbs sampler was implemented for comparison. Algorithm 3 used the proposal

$$\begin{aligned} R_\ell (u, dz) = \rho _\ell (dz) \quad ((\ell , u) \in [\![1, 2 ]\!] \times \mathbb {R}) , \end{aligned}$$

yielding an algorithm that can be viewed as a hybrid between Algorithms 2 and 4 in the sense that it “refreshes” randomly the continuous component $U_{m'}$ obtained after Step (ii) by replacing, with the Metropolis-Hastings probability $\alpha _{m'}$, the same by a draw from $\rho _m'$. Cf. Algorithms 2 and 4, where $U_{m'}$ is refreshed systematically according to $\rho _m'$ and kept frozen, respectively. For each of these algorithms we generated an MCMC trajectory comprising 301,000 iterations (where the first 1,000 iterations were regarded as burn-in and discarded) and estimated the corresponding autocorrelation functions. The outcome, which is displayed in Fig. 2 below, indicates increasing autocorrelation for the CC, MCC, FCC, and Gibbs algorithms, respectively, confirming completely the theoretical results obtained in the previous section. Interestingly, the FCC algorithm has, despite being close to twice as efficient in terms of CPU with our implementation, only slightly higher autocorrelation than the MCC algorithm for both the components; indeed, for the mixture index component the plots of the corresponding estimated autocorrelation functions are more or less indistinguishable. As expected, the Gibbs sampler suffers from very large autocorrelation as it tends to get stuck in the different modes, while the CC algorithm has the highest performance at a computational complexity that is comparable to that of the FCC algorithm in this case (due to Matlab’s very efficient Gaussian random number generator). Qualitatively, similar outcomes are obtained if the parametrisations of the target distribution or the pseudo-priors are changed.

Fig. 2

Plot of estimated autocorrelation for the standard Gibbs sampler (solid line), Algorithm 2 (dashed line), Algorithm 3 (dotted line), and Algorithm 4 (dash-dotted line) when applied to the model (19). The estimates are based on 300,000 MCMC iterations, a $M$-component, b $Z$-component

5.2 Partially observed mixture variables

In this example we consider a model with two layers, where a pair $Y = (M, Z)$ of random variables, forming a mixture model $\tilde{\pi }$ on of the form described in Sect. 2.2, is only partially observed through some random variable $X$ taking values in some other state space $(\mathsf {X}, \mathcal {X})$. More specifically, we assume that the distribution of $X$ conditionally on $Y$ is given by some Markov transition density $g$ on $\mathsf {Y}\times \mathsf {X}$, i.e.,

$$\begin{aligned} X \mid (M, Z) \sim g((M, Z), x) \lambda (dx) , \end{aligned}$$

where $\lambda$ is some reference measure on $(\mathsf {X}, \mathcal {X})$. When operating on a model of this form one is typically interested in computing the conditional distribution of the latent variable $Y$ given some distinguished value $X = x \in \mathsf {X}$ of the observed variable. This posterior distribution has the density

$$\begin{aligned}&\pi ^{*}(m, z\mid x) = \frac{g((m, z), x) \tilde{\pi }(m, z)}{\iint g((m, z), x) \tilde{\pi }(m, z) |dm|\nu (dz)}\\&\quad ((m, z, x) \in \mathsf {Y}\times \mathsf {X}) \end{aligned}$$

w.r.t. the product measure $|dm|\nu (dz)$. Since the observation $x$ is fixed, we simply omit this quantity from the notation and write $\pi ^{*}(m, z\mid x) = \pi ^{*}(m, z)$. Note that $\pi ^{*}$ is again a mixture model on $\mathsf {Y}$, and our objective is to sample from this distribution.

In order to evaluate, in this framework, the performances of the MCMC samplers discussed in the previous section we consider two different setups, namely

• 1. a Gaussian mixture model related to the toy example in Sect. 5.1.

• 2. a real-world image analysis problem consisting in sampling jointly a high-dimensional warping parameter and a cluster index, parameterising typically a mixture of deformable template models (Allassonnière et al. 2007).

The two setups are summarised in Table 1.

Table 1 Specifications of the two setups studied in Sect. 5.2

5.2.1 Gaussian mixture model

Let, as in the previous example, $\mathsf {Y}= [\![1, 2 ]\!] \times \mathbb {R}$, and consider the Gaussian mixture model

$$\begin{aligned} \tilde{\pi }(m, z) = \alpha _m\phi \left( z; {\mu _m}{\sigma ^2}\right) \quad ((m, z) \in [\![1, 2 ]\!] \times \mathbb {R}) , \end{aligned}$$

(20)

where $\alpha _1 = 1/4$, $\alpha _2 = 3/4$, $\mu _1 = -1$, $\mu _2 = 1$, and $\sigma = \sqrt{.2}$. (Note that letting $\alpha _1 = \alpha _2 = 1/2$ yields the mixture model (19) of the previous example.) In addition, we let $(M, Z)$ be partially observed through

$$\begin{aligned} X = Z^2 + \varsigma \varepsilon , \end{aligned}$$

(21)

where $\varsigma = \sqrt{.1}$ and $\varepsilon$ is a standard Gaussian noise variable which is independent of $Z$. Consequently, the measurement density (with respect to Lebesgue measure) is given by $g((m, z), x) = \phi (x; z^2, \varsigma ^2)$, $x \in \mathbb {R}$, in this case. For the fixed observation value $x = .4$ we sampled from the posterior distribution

$$\begin{aligned} \pi ^{*}(m, z)&\propto \alpha _m\phi (z; \mu _m, \sigma ^2) \phi (x; z^2, \varsigma ^2)\\&((m, z) \in [\![1, 2 ]\!] \times \mathbb {R}) \end{aligned}$$

and estimated the posterior index probability $\alpha ^*_2 = \pi ^{*}(m) |_{m= 2}$ and the posterior mean $\mu ^* :=\int z \pi ^{*}(dz)$ using Algorithms 3 and 4. Note that we are unable to sample directly the conditional distribution $\pi ^{*}(z\mid m)$ in this case due to the nonlinearity of the observation equation (21); thus, Algorithm 2 is excluded from our comparison. In addition, we implemented the Gibbs sampler in Algorithm 1 with Step (ii) replaced by a Metropolis-Hastings operation, yielding a Metropolis-within-Gibbs (MwG) sampler. This Metropolis-Hastings operation as well as in the corresponding operation in Step (iii) of the MCC sampler (Algorithm 3) used the conditional prior distribution as proposal, e.g.,

$$\begin{aligned} R_\ell (u, dz) = \tilde{\pi }(dz\mid \ell ) \quad ((\ell , u) \in [\![1, 2 ]\!] \times \mathbb {R}) . \end{aligned}$$

This distribution was also used for designing the pseudo-priors in the MCC and FCC algorithms, e.g.,

$$\begin{aligned} \rho _\ell (dz) = \tilde{\pi }(dz\mid \ell ) \quad ((\ell , u) \in [\![1, 2 ]\!] \times \mathbb {R}) , \end{aligned}$$

and consequently the MCC sampler can, as in the previous example, be viewed as a “random refreshment”-version (using the terminology of Maire et al. (2014)) of the FCC sampler. We note that $\omega (m, u) \propto \alpha _m \phi (x; u^2, \varsigma ^2)$ is uniformly bounded in $(m, u) \in [\![1, 2 ]\!] \times \mathbb {R}$, providing a model satisfying (A2 ); we may hence compare theoretically the algorithms using Theorem 7.

After prefatory burn-ins comprising $1,\!000$ iterations, trajectories of length $300,\!000$ were generated using each algorithm. The resulting autocorrelation function estimates are displayed in Fig. 3, which shows that the FCC and MCC algorithms are clearly superior, in terms of autocorrelation, to the MwG sampler. Even though the MCC sampler has, as expected from Theorem 7, a small advantage to the FCC sampler in terms of autocorrelation, both samplers exhibit very similar mixing properties. This is particularly appealing in the light of the CPU times reported in Table 2, which shows that the FCC sampler is almost twice as fast as the MCC sampler for our implementation. Tables 2 and 3 report also the posterior mean and probability estimates obtained using the output of the different algorithms, and apparently the slow mixing of the MwG sampler rubs off on the precision of the corresponding estimate. The true values $\alpha _2^* = .750$ (which is very close to the corresponding prior probability $\alpha _2$ for the given observation $x = .4$) and $\mu ^* = .315$ were obtained using numerical integration. The asymptotic variance estimates of the different samplers were obtained using the method of overlapping batch means (see Meketon and Schmeiser (1984)), where each batch contained $4{,}481$ ($= \lfloor 300,\!000^{2/3} \rfloor$) values (this batch size is consistent with the recommendations of [Flegal and Jones (2010), Section 4]), and as a measure of precision per computational effort we defined efficiency as inverse asymptotic standard error over computational time. As clear from Tables 2 and 3, MCC and FCC have, as expected, a clear advantage over MwG in terms of efficiency for both estimators. Moreover, FCC is about $1.8$ and $1.5$ times more efficient than MCC for the discrete and continuous components, respectively.

Fig. 3

Plot of estimated autocorrelation for the Metropolis-within-Gibbs sampler (solid line), Algorithm 3 (dotted line), and Algorithm 4 (dash-dotted line) when applied to the model (21), a $M$-component, b $Z$-component

Table 2 Estimates of the posterior index probability $\alpha _2^*$ delivered by the MwG, MCC, and FCC algorithms for the partially observed mixture model (21) together with the corresponding asymptotic standard errors, CPU times, and efficiencies (inverse standard error per unit CPU time)

Table 3 Estimates of the posterior mean $\mu ^*$ delivered by the MwG, MCC, and FCC algorithms for the partially observed mixture model (21) together with the corresponding asymptotic standard errors, CPU times, and efficiencies (inverse standard error per unit CPU time)

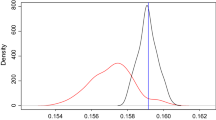
Figure 4 displays the estimate of the marginal posterior density $\pi ^{*}(z)$ obtained by applying a Gaussian kernel smoothing function to the output of the FCC algorithm. The exact posterior, obtained using numerical integration, is plotted for comparison.

Fig. 4

Probability density estimate based on the sequence generated by Algorithm 4 (dashed line) for the partially observed mixture model (21) together with the exact posterior density (solid line)

5.2.2 Sampling a high-dimensional warping parameter for handwritten digits

We now consider the problem of warping a random observation of a $16\times 16$ pixels handwritten digit “$5$” from the MNIST dataset (LeCun and Cortes 2010) with a (known) collection of prototype patterns, referred to as templates, of the digit in question; see Fig. 5a. In this setting, $M$, taking values in $[\![1, 4 ]\!]$, is the template number and $Z$, taking values in $\mathsf {Z}=\mathbb {R}^{72}$, is the warping parameter. As in the previous example, the variables $(M, Z)$ are only partially observed through a single data point, namely the digit displayed in Fig. 5b, and we impose the same prior distribution as in (20), with $\alpha _m = 1/4$ and $\mu _m = \mathbf {0}_{|\mathsf {Z}|}$ for all $m\in [\![1, 4 ]\!]$. We refer to Table 1 for a detailed comparison between this model and the model of the previous example.

Fig. 5

Templates $\{f(m,\mathbf {0}_{|\mathsf {Z}|})\}_{m=1}^4$ (the vector $\mathbf {0}_{|\mathsf {Z}|}$ corresponds to no deformation) and observed digit, a Templates, b Observed handwritten digit

The latent data $(M, Z)$ are only partially observed through the deformable template model

$$\begin{aligned} X = f(M, Z) + \varsigma \varepsilon , \end{aligned}$$

(22)

where $f : [\![1, 4 ]\!] \times \mathbb {R}^{72} \rightarrow \mathbb {R}^{16} \times \mathbb {R}^{16}$ is a deterministic mapping distorting the $M$th template by the deformation parameterised by $Z$; see, e.g., Allassonnière et al. (2007) and the references therein for more details.

We aim at comparing the performances of the MwG, MCC, and FCC algorithms for the task of sampling the posterior distribution

$$\begin{aligned}&\pi ^{*}(m, z) \propto \alpha _m\phi (z; \mu _m, \sigma ^2) \phi (x; f(m,z), \varsigma ^2) \\&((m, z) \in [\![1, 4 ]\!] \times \mathbb {R}^{72}) . \end{aligned}$$

Setting, as in Sect. 5.2.1, $\rho _m(dz) = \tilde{\pi }(dz\mid m)$ for all $m \in [\![1, 4 ]\!]$ turns out to be too naive in this case; indeed, the high dimension of $\mathsf {Z}$ makes the prior highly non-informative, and the latter therefore differs significantly from the posterior $\pi ^{*}(dz\mid m)$ (to which the pseudo-priors should be close in the optimal scenario). Thus, the framework under consideration calls for more sophisticated design of the pseudo-priors. Laplace’s approximation suggests that a Gaussian distribution with mean and covariance matrix given by

$$\begin{aligned} \left\{ \begin{array}{l} z^{*}(m) :=\arg \max _{z \in \mathsf {Z}} \log \pi ^{*}(z\mid m) , \\ \varsigma ^2(m) :=(- \nabla ^2 \log \pi ^{*}(z\mid m)|_{z= z^{*}(m)})^{-1} , \end{array}\right. \end{aligned}$$

respectively, would provide a better proxy for $\pi ^{*}(dz\mid m)$. However, in the deformable template model context, the function $f$ in (22) is highly nonlinear and does not allow the log-likelihood to be maximised on closed-form. Optimisation in this space is very demanding from a computational viewpoint, and replacing $z^{*}(m)$ by a proxy is risky as the Hessian matrix needed for determining $\varsigma ^2(m)$ is not necessarily invertible at that point.

Another alternative consists in sampling $4$ independent Markov chains targeting $\pi ^{*}(dz\mid m)$, $m \in [\![1, 4 ]\!]$, respectively, and to let $\rho _m(z) = \phi (z; \hat{\mu }(m), \hat{\gamma }^2(m))$, $z\in \mathsf {Z}$, for each $m$, where $\hat{\mu }(m)$ and $\hat{\gamma }^2(m)$ are the sampling mean and covariance estimate, respectively. Although appearing maybe not overly elegant at a first glance, this method turns out to be very useful in most situations lacking an obvious, natural choice of pseudo-priors. Moreover, since we only need a rough approximation of the posterior distribution, we can stop the simulation of these auxiliary chains after a limited number of iterations. In this setting, we stopped the Markov chains after collecting $500$ samples from each chain, and discarded, as burn-ins, the first $100$ samples of each chain in the estimation. Obviously, this step adds a computational burden to the main sampling scheme; nevertheless, we have in the following taken this additional time into consideration when evaluating the outcome of the simulations. Moreover, we concede that this way of designing the pseudo-priors may not be reasonable in situations when the number $n$ of mixture components is very large; on the other hand, in such a case any CC-type approach is inappropriate due to the prohibitive number of auxiliary variables. Finally, a transition of the MwG algorithm is performed by a Metropolis-Hastings step with a Gaussian random walk proposal (with variance $\zeta ^2 = .1$) for each component of the parameter. This is also the common choice of the Markov kernels $R_m$, $m \in [\![1, 4 ]\!]$, used in the MCC algorithm.

We compare the three algorithms through the estimation of the posterior weights (Table 4; Fig. 6) and the asymptotic variance of the class index (Table 5). Moreover, we compare the qualities of the image reconstructions provided by the different algorithms in two ways, namely

• 1. Graphically by displaying, in Fig. 8, some realisations of templates warped by the deformation parameter sampled by the three algorithms.

• 2. Quantitatively by plotting, first, in Fig. 7, the mapping $\mathbb {R}\ni t \mapsto S_t$, where each statistic $S_t$ is defined by

  $$\begin{aligned}&S_t :=\sum _{m=1}^n \Vert x-f(m, \bar{z}_m^{(t)}) \Vert ^2 , \\&\bar{z}_\ell ^{(t)} :=\sum _{j \in \mathbb {N}: \tau (j)\le t} z_j \mathbb {1}_{m_j=\ell } \Bigg /\sum _{j \in \mathbb {N}: \tau (j)\le t} \mathbb {1}_{m_j=\ell } , \end{aligned}$$

  with $\tau :\mathbb {N}\rightarrow \mathbb {R}$ providing the CPU time needed for completing a given number of Markov transitions and, second, in Fig. 9, the estimated autocorrelation of one deformation parameter.

Fig. 6

Evolution of the class $m = 1$ posterior weight estimate delivered by the MwG (solid line), the MCC (dotted line), and the FCC (dash-dotted line) algorithms for the partially observed mixture model (22). The dashed line represents the class $1$ asymptotic posterior weight, estimated after $100,\!000$ iterations of MCC

Fig. 7

Evolution of the statistic $S_t$ as a function of the CPU time $t$ for the MwG (solid line), the MCC (dotted line), the MCC$^\dag$ (dashed line), and FCC (dash-dotted line) algorithms within the framework of the partially observed mixture model (22). MCC$^\dag$ refers to a version of the MCC algorithm using the naive pseudo-priors

Fig. 8

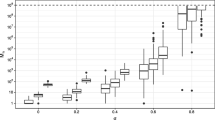
Illustration of the template number and deformation parameter sampling for the MwG, MCC and FCC algorithms. On the left hand side (a), the first, second, and third rows correspond to the MwG, MCC, and FCC algorithms, respectively, while each column corresponds to a Wraped templates $f(M_{k} , Z_{k})$ observed at different Markov chain iterations $k\, \epsilon \, \{5, 150, 500, 1000, 5000\}$. The table on the right hand side (b) provides the template numbers sampled by each chain at the corresponding iterations

Fig. 9

Plot of estimated autocorrelation for the MwG (solid line), MCC (dotted line), and FCC(dash-dotted line) algorithms when applied to the model (22)

Table 4 Estimates of the posterior weights delivered by the MwG, MCC, MCC${^{\dag }}$ (defined as MCC using the naive pseudo-priors), and FCC algorithms for the partially observed mixture model (22)

Table 5 Estimates of the class $m = 1$ posterior probability (given the observation in Fig. 5b) delivered by the MwG, MCC, and FCC algorithms together with the corresponding asymptotic standard error estimates (estimated using the method of overlapping batch means), CPU times, and efficiencies (for MwG, the efficiency had no meaning since the estimate is biased)

These results confirm those obtained through the previous simulations: quantitatively, the difference in mixing between MCC and FCC is indeed minor and both these algorithms outperform significantly the MwG algorithm, which gets stuck most of the time in the class $3$ (see Table 4). In this context, the huge gap in efficiency between FCC and MCC is particularly striking and stems from the high dimension of the deformation parameter, which, consequently, is very costly to sample using the Markov kernel—a burden avoided by FCC, which uses only the Gaussian pseudo-prior samples (Table 2). The FCC computational performance can also be observed graphically in Figs. 7 and 6. We conclude that FCC is a strong competitor in situations where the design of the pseudo-priors is demanding.

Qualitatively, both FCC and MCC allow deformations that are consistent with the observed data-point to be sampled, whereas MwG do so for only one template. Figure 8 shows that the digit displayed in Fig. 5b can be reconstructed from any of the four templates Fig. 5a using the sampled deformations, a fact that is quantitatively confirmed using the statistic $S_t$ Fig. 7.

Finally, note that these results depend strongly on the quality of the pseudo-priors: when using the naive pseudo-priors (defined as $\rho _m(dz) = \tilde{\pi }(dz\mid m)$ for all $m \in [\![1, 4 ]\!]$), the MCC behaves very similarly to the MwG; see Table 4 and Fig. 7. This shows that, in this example, the tradeoff between doing more MCMC iterations vs delaying the MCMC sampling scheme to specify decent pseudo-priors turns in favor of the latter.

Remark 9

The theoretical results developed in Theorem 7 are restricted to test functions $h$ depending on the $M$-component only; however, the case of test functions depending on the $Z$-component (or even the pair $(M, Z)$), for which a comparison of the asymptotic variance between MCC and FCC is not available, is of course of interest as well. Nevertheless, the results displayed in Table 3, Fig. 3b, and Fig. 9 indicate, not surprisingly, that the mixing properties, with respect to the $Z$ component, of the different algorithms seem to depend heavily on the ability (which is well-described by our theoretical results) of the same to move flexibly between different strata indices.

Remark 10

Following Carlin and Chib’s pseudo-priors spirit, it would be possible to design, in a similar off-line scheme, a finely tuned proposal kernel to improve the Metropolis-within-Gibbs mixing performances. Such an approach is actually related to the recent development in Particle MCMC methods and in particular to the Particle independent Metropolis-Hastings sampler (PIMH) (Andrieu et al. 2010), in which a target-matching proposal is constructed from a set of weighted particles. However, adapting a PIMH algorithm to infer mixture distributions may also be difficult to setup in practice (choice of instrumental kernel, number of particles, risk of degeneracy, etc.). Moreover, a frozen equivalent to such an algorithm, which typically exists in Carlin and Chib’s context thanks to the intermediate extended state space, would not exist, hence preventing to balance out the pre-processing step’s computational burden as with the FCC.

6 Conclusion

We have compared some data-augmentation-type MCMC algorithms sampling from mixture models comprising a discrete as well as a continuous component. By casting Carlin & Chib’s pseudo-prior into our framework we obtained a sampling scheme that is considerably more efficient than the standard Gibbs sampler, which in general exhibits poor state-space exploration due to strong correlation between the discrete and continuous components (as a result of the highly multimodal nature of the mixture model). In the case where simulation of the continuous component $Z$ conditionally on $M$ is infeasible, we used a metropolised version of the algorithm, referred to as the MCC sampler, that handled this issue by means of an additional Metropolis-Hastings step in the spirit of the hybrid sampler. In this case our simulations indicate, interestingly, that the loss of mixing caused by simply passing, as in the FCC algorithm, the value of the $M$th auxiliary variable, generated by sampling from the pseudo-priors at the beginning of the loop, directly to $Z$ without any additional refreshment is limited. Thus, we consider the FCC algorithm, which we proved to be $\pi ^{*}$-reversible, as strong contender to the MCC sampler in terms of efficiency (variance per unit CPU).

Our theoretical results comparing the MCC and FCC samplers deal exclusively with mixing properties of the restriction of the MCMC output to the discrete component, and the extension of these results to the continuous component is left as an open problem. However, we believe that the discrete component is indeed the quantity of interest, as our simulations indicate that the degree mixing of the discrete component gives a limitation of the degree of mixing of the bivariate chain due to the multimodal nature of the mixture.

There are several possible improvements of the FCC algorithm. For instance, following Petralias and Dellaportas (2013), only a subset of the pseudo-priors (namely those with indices belonging to some neighborhood of the current $M$) could be sampled at each iteration, yielding a very efficient algorithm from a computational point of view. Such an approach could be also used for handling the case of an infinitely large index space (i.e. $n = \infty$).