1 Introduction

Solar ultraviolet radiation shining on the Earth’s upper atmosphere ionizes part of the neutral atmosphere. A number of forces then act on this ionized plasma to drive electric currents throughout the ionization region. These forces include:

  1. 1.

    Electromagnetic fields: Electric and magnetic fields in the ionosphere influence plasma motion through the Lorentz force. Magnetic fields in the ionosphere region are generated from a variety of sources, including the Earth’s core, lithosphere, magnetosphere, and currents flowing in the ionosphere itself. Ionospheric electric fields can arise in two ways. First, a global ionospheric electric field will be generated and act on the ionized plasma to ensure a total divergence-free current. Second, electric fields present in other regions, such as the magnetosphere, can propagate along magnetic field lines into the ionosphere to further affect the electrodynamics of the region.

  2. 2.

    Collisions with neutral molecules: Neutral winds apply a force on the plasma through momentum exchange by collisions. The spatial and temporal structure of this force is highly complex, as neutral winds in the atmosphere are driven by solar heating, Joule heating, momentum transfer from drifting ions, and vertically propagating tides and gravity waves from below the thermosphere. All of these processes will influence the neutral atmosphere, providing it a rich and complex structure of neutral velocity and density, which will in turn modulate the ionized plasma through collisions.

  3. 3.

    Pressure gradients: Pressure-gradient forces arise from variations in the plasma pressure throughout the ionosphere. Gradients in plasma pressure, coupled with the geomagnetic field, cause non-zero net particle velocities in a direction perpendicular to both the pressure gradient and magnetic field directions. This results in a net plasma drift, with ions and electrons drifting in opposite directions, and hence an electric current.

  4. 4.

    Gravity: Similar to the pressure-gradient force, the gravitational force acts on the plasma in the ionosphere, which when coupled with the geomagnetic field, causes the plasma to drift in a direction perpendicular to both the gravitational and magnetic fields.

Much of the electrodynamics of the low and mid-latitude ionosphere is dominated by the neutral wind frictional force, as well as the electric field which maintains a global divergence-free current. The pressure-gradient and gravitational current systems are typically much weaker than wind-driven currents during the daytime, although they can be stronger at night. In fact, while the magnetic fields produced by ionospheric wind-driven currents (such as the equatorial electrojet and Solar-quiet (Sq) systems) are readily observed in surface observations, the magnetic signatures of the pressure-gradient and gravitational currents can only be seen in measurements made by low-Earth orbiting (LEO) satellites, flying close to these current sources in the \(F\)-region. The magnetic signatures of these currents in LEO satellite data can be on the order of several nT, and so it is important to understand the spatial and temporal structure of both of these ionospheric current systems.

In Sect. 2 we review the basics of ionospheric electrodynamics, focusing on the role played by the gravitational and pressure-gradient driven current systems. In Sect. 3, we review the studies which have presented magnetic observations of these two current systems, which so far have been collected mainly by space-based instruments. In Sect. 4, we review papers which have studied the gravity and pressure-gradient currents using in-situ measurements of plasma density. In Sect. 5, we review physics-based modeling progress in understanding these \(F\)-region currents, including their full 3D flow patterns, polarization electric field structure, and closure mechanisms.

2 Theoretical Background

A full treatment of the electrodynamic equations which govern the ionosphere is beyond the scope of this work, but the interested reader can find further details in the texts by Kelley (1989), Baumjohann and Treumann (1997), Chen (2006), Schunk and Nagy (2009). Here, we will simply state the main ideas needed to understand the origin of the gravitational and pressure-gradient current systems in the ionosphere.

If we ignore ionospheric processes which occur on short time scales of less than about one minute, we can treat ionospheric electrodynamics as being approximately steady-state, with a time-invariant global electric field and divergence-free current density. The current density can be expressed as (Richmond 1995a; Richmond and Maute 2014)

$$ \mathbf{J} = \mathbf{J}_{w} + \mathbf{J}_{g} + \mathbf{J}_{p} + \sigma\mathbf{E} $$
(1a)

with

$$\begin{aligned} \mathbf{J}_{w} &= \sigma\mathbf{U} \times\mathbf{B} \end{aligned}$$
(1b)
$$\begin{aligned} \mathbf{J}_{g} &= \frac{n m_{i}}{B^{2}} \mathbf{g} \times\mathbf{B} \end{aligned}$$
(1c)
$$\begin{aligned} \mathbf{J}_{p} &= \frac{-1}{B^{2}} \nabla P \times\mathbf{B} \end{aligned}$$
(1d)

where \(\mathbf{J}_{w}\), \(\mathbf{J}_{g}\), \(\mathbf{J}_{p}\) are the current densities due to neutral wind, gravitational and pressure-gradient forces respectively, \(\mathbf{E}\) is the global electrostatic electric field which maintains a total divergence-free current (with components \(\mathbf{E}_{w}\), \(\mathbf{E}_{g}\), \(\mathbf{E}_{p}\) associated separately with \(\mathbf{J}_{w}\), \(\mathbf{J}_{g}\), \(\mathbf{J}_{p}\) respectively), \(\mathbf{U}\) is the neutral wind velocity field, \(\mathbf{B}\) is the geomagnetic field, \(n\) is the electron density, \(m_{i}\) is the ion mass (assuming a single ion species), \(\mathbf{g}\) is the gravitational acceleration, \(P = n k_{B} (T_{i} + T_{e})\) is the plasma pressure, \(k_{B}\) is the Boltzmann constant, \(T_{i}\) and \(T_{e}\) are the ion and electron temperatures respectively, and finally \(\sigma\) is the conductivity tensor given in matrix form as

$$ \sigma= \sigma_{P} I + ( \sigma_{\parallel} - \sigma_{P} ) \mathbf{b} \mathbf{b}^{T} + \sigma_{H} [\mathbf{b}]_{\times} $$
(2)

Here, \(\sigma_{\parallel}\), \(\sigma_{P}\), \(\sigma_{H}\) are the parallel, Pedersen, and Hall conductivities respectively, \(\mathbf{b}\) is a unit vector in the magnetic field direction, and \([\mathbf{b}]_{\times}\) represents the skew-symmetric matrix defined by the cross product with \(\mathbf{b}\). For a given basis representation \(\mathbf{b} = (b_{1},b_{2},b_{3})^{T}\),

$$ [\mathbf{b}]_{\times} = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & -b_{3} & b_{2} \\ b_{3} & 0 & -b_{1} \\ -b_{2} & b_{1} & 0 \end{array}\displaystyle \right ) $$
(3)

Equation (2) follows from Richmond and Maute (2014), Eq. (2), and is equivalent to the expression given in Forbes (1981), Eq. (10), but is defined independently of a particular coordinate system. Expressions for the conductivities \(\sigma_{\parallel}, \sigma_{P}, \sigma_{H}\) can be found in Forbes (1981) and Kelley (1989), Appendix B. The expressions for \(\mathbf{J}_{g}\) and \(\mathbf{J}_{p}\) given in Eqs. (1c) and (1d) are approximations which ignore the effects of neutral collisions. Since these two currents are most prominent in the \(F\)-region this is generally an acceptable approximation. Full equations for \(\mathbf{J}_{g}\) and \(\mathbf{J}_{p}\) can be found in Richmond (2016).

During the daytime, the Pedersen and Hall conductivities are most significant in the lower ionosphere, below about 200 km (Richmond 1979). The neutral winds at these altitudes, which include large contributions from atmospheric tidal modes, move the conducting plasma across the geomagnetic field, generating electromotive forces which produce significant current flow. This is known as the ionospheric dynamo, and further details may be found in the reviews presented by Richmond (1979, 1989, 1995b). At mid and low latitudes in the ionospheric \(E\)-region, this results in the Solar-quiet (Sq) and equatorial electrojet (EEJ) current systems, which are the dominant ionospheric sources as seen in both ground and satellite magnetic observations. These wind-driven currents are represented by the terms \(\mathbf{J}_{w} + \sigma\mathbf{E}_{w}\) in Eqs. (1a)–(1d) which depend on the ionospheric conductivity \(\sigma\), the neutral wind field \(\mathbf{U}\), and the wind-generated electric field \(\mathbf{E}_{w}\). While most of the ionospheric wind-driven current at mid and low latitudes flows in the lower ionospheric \(E\)-region during daytime, \(F\)-region winds also generate electric currents at higher altitudes (Rishbeth 1971, 1997) which can contribute up to 15 % of the total ionospheric current flow (Rishbeth 1981). During nighttime, the ionospheric conductivity in the \(E\)-region drops substantially, which stops much of the wind-driven current flow in the lower ionosphere. However, the \(F\)-region Pedersen conductivity is significant enough to support a dynamo current during nighttime which can produce ground magnetic perturbations of up to 1 nT (Rishbeth 1971).

Above 200 km altitude, the gravitational and pressure-gradient forces on the plasma can be of the same order as the neutral wind collisional force and, consequently, \(\mathbf{J}_{g}\) and \(\mathbf{J}_{p}\) can be of the same order as \(\mathbf{J}_{w}\). Both \(\mathbf{J}_{w}\) and \(\mathbf{J}_{g}\) depend on the ion density, while \(\mathbf{J}_{p}\) depends on the gradient of ion density. \(\mathbf{J}_{w}\) also depends on the ion-neutral collision frequency, which decreases exponentially with increasing height, and so \(\mathbf{J}_{w}\) can become smaller than \(\mathbf{J}_{g}\) and \(\mathbf{J}_{p}\) in the topside ionosphere. At low latitudes \(\mathbf{J}_{w}\) tends to be mainly in the vertical/meridional direction, while \(\mathbf{J}_{g}\) and \(\mathbf{J}_{p}\) tend to be more in the zonal direction. All three produce non-negligible effects in the magnetic measurements of LEO satellites flying through the \(F\)-region. While all of these current systems are stronger during the daytime, when there is higher plasma density, it is difficult to separate their signals from the much stronger \(E\)-region currents in magnetic observations, and so most studies of these current systems have focused on nighttime measurements. The gravity-driven electric current arises from the combined effect of the gravitational and geomagnetic Lorentz forces acting on the ionized plasma. When placed in a magnetic field, a charged particle will gyrate around the magnetic field lines. When an additional force \(\mathbf{F}\) is applied to the particle of charge \(q\), it will drift in the \(\mathbf{F} \times \mathbf{B}\) direction with a velocity given by

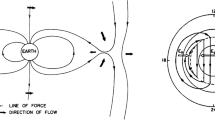
$$ \mathbf{v}_{F} = \frac{1}{q} \frac{\mathbf{F} \times\mathbf{B}}{B^{2}} $$
(4)

For an ion of mass \(m_{i}\) in a gravitational field, the force is \(\mathbf{F} = m_{i} \mathbf{g}\), and the resulting drift velocity will produce the current density \(\mathbf{J}_{g}\) given in Eq. (1c). Figure 1 illustrates single particle trajectories under the influence of perpendicular gravitational and magnetic fields, as one would find near the magnetic equator, ignoring collisions. The gravity current \(\mathbf{J}_{g}\) is proportional to the electron density \(n\), which is assumed to equal the ion density for a two-component plasma. The largest concentration of plasma is found in the low-latitude equatorial ionization anomaly (EIA), which spans an altitude range of roughly 250–500 km. At these altitudes, the dominant ion species is \(O^{+}\), and so we can assume this ion is the primary carrier of the gravity current in the \(F\)-region. Figure 2 shows profiles of typical ionospheric plasma densities in the EIA region as predicted by the International Reference Ionosphere (IRI) 2012 model (Bilitza et al. 2011). In the EIA region, the combined densities of the non-\(O^{+}\) ions are about two orders of magnitude less than \(N_{O^{+}}\). The EIA can be understood by considering a charged particle in an electric field, which will experience a force \(\mathbf{F} = q \mathbf{E}\), resulting in a drift velocity which is independent of the charge of the particle, according to Eq. (4). Therefore, electrons and ions drift in the same direction leading to zero net current. In the equatorial \(F\)-region, there is a prominent zonal component of the ionospheric electric field, which drives vertical drift, lifting plasma to the upper \(F\)-region, where it then diffuses downward along magnetic field lines (Anderson 1981; Stening 1992; Stolle et al. 2008). The result is an enhancement of \(F\)-region plasma density about \(15\mbox{--}20^{\circ}\) north and south of the magnetic equator. This enhanced density region is strongest during the daytime, but persists late into the evening, providing a medium for gravity current flow long after sunset.

Fig. 1
figure 1

Trajectories of charged particles in a gravitational and magnetic field

Full size image
Fig. 2
figure 2

Ionospheric density profiles output from the IRI-2012 model for northern hemisphere EIA peak (\(15^{\circ}\) magnetic latitude) at 1500 LT, using F10.7 input of 150 sfu. Electron density is shown in red, \(O^{+}\) density in green, and other combined ion densities (\(H^{+},He^{+},O_{2}^{+},NO^{+},N^{+}\)) in blue

Full size image

At low-latitudes where the ionospheric gravity current is most significant, the magnetic field points approximately northward, and so the \(\mathbf{g} \times\mathbf{B}\) gravity current flows magnetically eastward. This gives rise to the question of how this current system closes upon itself. While direct observational evidence of a “return current” has not yet been presented, the modeling study of Richmond and Maute (2014) found a westward return current through the \(E\) region driven by the electric field term \(\sigma\mathbf {E}_{g}\) of Eqs. (1a)–(1d). This will be further discussed in Sect. 5.

Turning now to the pressure-gradient current \(\mathbf{J}_{p}\), we see that a gradient in plasma pressure \(P = n k_{B} (T_{e} + T_{i})\) is responsible for causing ion and electron drift. In the ionosphere, the largest pressure gradients are also found in the EIA region. To understand the origin of this current, we first consider ions placed in a magnetic field with a density gradient \(\nabla n\). The ions will gyrate around the magnetic field lines as usual, but since there are less ions in the direction of decreasing density, the velocity component perpendicular to \(\mathbf{B}\) and \(\nabla n\) will no longer average to zero. This is illustrated in Fig. 3, which sketches a circular region of plasma with density increasing toward the center, depicted by the color shading. This can be thought of as a latitudinal cross section of the EIA region, with the horizontal axis representing longitude and the vertical axis representing altitude, though on very different spatial scales. The magnetic field is then pointing northward and into the plane of the figure. The circular current loops represent ion gyrations around the magnetic field lines, whose magnetic moments will act to reduce the ambient field. In this figure, the middle region represents the largest gradient in density, and the zoomed view illustrates that for a small volume, there is an asymmetry in the number of particles gyrating. Therefore, due to the density gradient, there is an excess particle gyration velocity where the density is larger, and so the component of gyration velocity perpendicular to \(\mathbf{B}\) and \(\nabla n\) no longer averages to zero. This results in a net drift of the ions in the \(-\nabla n \times\mathbf{B}\) direction, as indicated by the arrows. Though the electron motion is omitted from the figure, they will gyrate in the opposite sense as the ions and will therefore drift in the opposite direction. The current due to this ion/electron drift will act to reduce the ambient magnetic field, which is why the pressure-gradient current is also called diamagnetic. A temperature gradient will also lead to a drift, since the gyroradius of a particle in a lower temperature region will be smaller than that of a particle in a higher temperature region. The difference in gyro-radii will again cause a non-zero average velocity and thus a net current.

Fig. 3
figure 3

Illustration of a diamagnetic current due to a gradient in plasma density. The dark blue center region corresponds to high density, while the lighter outer region corresponds to low density, similar to the structure of the equatorial ionization anomaly. The circular loops represent positive ions gyrating around the magnetic field lines with magnetic moments which oppose the ambient field \(\mathbf{B}\). The arrows represent the flow pattern of the diamagnetic current caused by non-zero average velocities of ions and electrons due to the density gradient, as depicted in the zoom window (see text for further details)

Full size image

An alternative picture to single particles gyrating around field lines is to consider the balance between the plasma pressure and the Lorentz force in a steady-state plasma in equilibrium:

$$ (\nabla P)_{\perp} = \mathbf{J} \times\mathbf{B} $$
(5)

This expression arises from considering the fluid equation of motion describing mass flow of a plasma, and neglecting temporal variations as well as forces such as gravity and neutral wind friction (see for example Eq. 5-85 of Chen 2006). In the ionosphere, the component of \(\nabla P\) parallel to \(\mathbf{B}\) is normally balanced by collisions with neutrals and by gravity, but at low-latitudes, this component is usually smaller than the perpendicular component, and so for the rest of this discussion we will assume \((\nabla P)_{\parallel} \approx0\) and drop the ⊥ symbol. Inserting Maxwell’s equation \(\nabla\times\mathbf{B} = \mu_{0} \mathbf{J}\) into Eq. (5), we find

$$ \nabla P = \frac{1}{\mu_{0}} ( \nabla\times\mathbf{B} ) \times\mathbf{B} = \frac{1}{\mu_{0}} \biggl[ ( \mathbf{B} \cdot \nabla ) \mathbf{B} - \frac{1}{2} \nabla B^{2} \biggr] $$
(6)

or

$$ \nabla \biggl( P + \frac{B^{2}}{2 \mu_{0}} \biggr) = \frac{1}{\mu_{0}} ( \mathbf{B} \cdot\nabla ) \mathbf{B} $$
(7)

Since \(B^{2}/(2\mu_{0})\) is the magnetic pressure, the left hand side represents the gradient of the total pressure (plasma plus magnetic), while the right hand side represents the magnetic tension due to the curvature of the field lines. To determine the reduction in a magnetic field inside a plasma with pressure \(P\), one could solve Eq. (7), which is generally a difficult problem for an arbitrary field \(\mathbf{B}\). However, Lühr et al. (2003) observed that at low-latitudes, such as in the EIA region, to a good approximation the geomagnetic field line curvature can be neglected, and so the right hand side of Eq. (7) can be set to zero. This assumption leads to the condition

$$ P + \frac{B^{2}}{2\mu_{0}} = \text{constant} $$
(8)

meaning that any increase in plasma pressure will immediately be balanced by a decrease in magnetic pressure, and vice versa. Using this relation, if we let \(\mathbf{B}_{0} = B_{0} \hat{\mathbf{b}}_{0}\) be the ambient magnetic field with no plasma present (i.e., \(P = 0\)), then the magnetic field in a plasma with pressure \(P\) will be reduced by some amount \(\delta\mathbf{B}\). Since the diamagnetic current produces a field which opposes the ambient field, we can say \(\delta\mathbf{B} = -\delta B \hat{\mathbf{b}}_{0}\), where \(\delta B\) represents the magnitude of the reduction. Therefore the total magnetic field will be

$$ \mathbf{B} = \mathbf{B}_{0} + \delta\mathbf{B} = ( B_{0} - \delta B ) \hat{\mathbf{b}}_{0} $$
(9)

From Eq. (8), we then find

$$ \frac{B_{0}^{2}}{2\mu_{0}} = P + \frac{B^{2}}{2\mu_{0}} = P + \frac{ ( B_{0} - \delta B )^{2}}{2\mu_{0}} $$
(10)

Solving this equation for the magnitude of the diamagnetic reduction \(\delta B\) yields

$$ \delta B = B_{0} ( 1 - \sqrt{1 - \beta} ) $$
(11)

where

$$ \beta= \frac{P}{B_{0}^{2} / (2\mu_{0})} $$
(12)

is the ratio of plasma pressure to magnetic pressure. In the ionosphere, \(\beta\ll1\), as can be verified by using typical measured values, i.e., \(n = 4 \cdot10^{12}~\text{m}^{-3}\), \(T_{i} + T_{e} = 2000~\mbox{K}\), \(B_{0} = 30000~\mbox{nT}\), and so expanding Eq. (11) to first order in \(\beta\) yields

$$ \delta B_{L} = \frac{\mu_{0} P}{B_{0}} $$
(13)

where we have added a subscript \(L\) to credit this formula to the work of Lühr et al. (2003). Magnetic field reductions of up to 5 nT have been reported in the EIA region at LEO satellite altitudes due to pressure-gradient currents (Lühr et al. 2003; Alken 2016), and so researchers interested in studying other geomagnetic signals have made use of this formula to remove pressure-gradient effects from satellite data. Equation (13) has been used for both correcting satellite measurements and comparing with modeling results in studies of the equatorial electrojet (Lühr et al. 2004; Lühr and Maus 2006; Manoj et al. 2006), \(F\)-region dynamo current systems (Lühr and Maus 2006), ionospheric plasma irregularities (Stolle et al. 2006; Park et al. 2012; Lühr et al. 2014a,b), geomagnetic secular acceleration (Chulliat and Maus 2014), geomagnetic main field modeling (Maus et al. 2006, 2010), lithospheric field modeling (Maus et al. 2007), and magnetospheric field modeling (Maus and Lühr 2005; Lühr and Maus 2010). In practice, the unperturbed field \(B_{0}\) in the expression for \(\delta B_{L}\) is replaced with an in-situ field measurement from a satellite-based magnetometer to determine the diamagnetic reduction at the satellite’s location. Lowes (2007) investigated possible differences that could arise between the field measured by the magnetometer located in an instrument cavity, free from ionospheric plasma, and the true field outside the cavity, and found that the magnetometer will measure the true field, allowing a straight-forward use of the \(\delta B_{L}\) formula provided the plasma densities and temperatures are also known.

It should be noted that the gravity and pressure-gradient currents often have a tendency to cancel in the topside ionosphere. Both are driven by forces on the plasma, and in the topside ionosphere the vertical pressure-gradient force often tends to balance the gravitational force. This balance would be exact in a horizontally stratified ionosphere in diffusive equilibrium. While the topside ionosphere tends to adjust towards diffusive equilibrium along the direction of the magnetic field, the ionosphere is not necessarily horizontally stratified, owing to horizontal density and temperature gradients. Below the \(F\)-region peak diffusive equilibrium does not exist, and both the gravity and pressure-gradient currents generally flow in the magnetic-eastward direction.

3 Magnetic Observations of Currents

The first observations of an ionospheric pressure-gradient current were presented by Lühr et al. (2003) using combined magnetic field and electron density measurements from instruments on board the CHAMP (Reigber et al. 2003) satellite. CHAMP (CHAllenging Minisatellite Payload) was equipped with both vector fluxgate and absolute scalar magnetometers as well as a Langmuir probe for plasma density and temperature measurements. The CHAMP mission lasted from July 2000 until September 2010, and flew in a near-polar orbit with an \(87^{\circ}\) inclination and an initial altitude of 454 km which decayed to about 250 km by the end of its mission. This altitude range allowed CHAMP to sample most of the EIA region during its mission, making it an ideal platform for studying the \(F\)-region gravity and pressure-gradient current systems. Figure 4 is reproduced from Lühr et al. (2003) and shows simultaneous total field residuals and electron density measurements for three different CHAMP orbits taken during different local times. During the 12 LT and 20 LT tracks, clear local minima are observed in the total field data near the peaks in the electron density in both hemispheres, corresponding to southward magnetic fields in the EIA region. The dashed lines in the figure show the corrected total field residuals using Eq. (13), and it can be seen that the local minima features are largely removed by the correction. Interestingly, the corrected data for 12 LT shows a non-negligible adjustment to the equatorial electrojet current signature near the magnetic equator, indicating significant pressure-gradient current flow outside the EIA region at low-latitudes.

Fig. 4
figure 4

Concurrent magnetic field and electron density measurements for three different local times, top: 04 LT, middle: 12 LT, bottom: 20 LT. Full lines in the magnetic field frames show observations, broken lines reflect readings corrected for the diamagnetic effect. Times in the plot titles indicate UT. Reprinted from Lühr et al. (2003) with permission from John Wiley and Sons

Full size image

The first observational evidence of an ionospheric gravity-driven current was presented by Maus and Lühr (2006) also using CHAMP satellite magnetic measurements. Maus and Lühr (2006) studied night-time magnetic field residuals after removing core, crustal and magnetospheric contributions. They assumed the resulting residuals were primarily driven by the gravity and pressure-gradient terms of Eqs. (1a)–(1d) and attempted to model these effects separately to match the observed data. They used Eq. (13) as a model for the pressure-gradient contribution using in-situ measurements of the electron density and plasma temperatures from the CHAMP Langmuir probe instrument. For the gravity contribution, they assumed that the divergent part of \(\mathbf{J}_{g}\) is exactly balanced by the \(\sigma\mathbf{E}_{g}\) term, which effectively ignores the neutral wind current. They found this approximate model agreed well with their observations (see Figs. 2 and 3 of their paper) and provided some statistics on the latitudinal extent of the gravity current, its approximate strength and its seasonal dependence.

While Maus and Lühr (2006) studied the \(F\)-region current signatures when CHAMP was still flying at a relatively high altitude, above most of the current flow in the EIA region, Alken (2016) combined the entire CHAMP database with Swarm satellite measurements to study the \(F\)-region currents from both above and below the flow region. Swarm (Friis-Christensen et al. 2006) is a constellation of three satellites launched in November 2013. A lower pair of satellites (A and C) fly side-by-side in orbits with inclination \(87.4^{\circ}\) with current altitudes of about 460 km. The third satellite (B) has an \(88^{\circ}\) inclination an a higher altitude of about 530 km. Each satellite is equipped with vector fluxgate and absolute scalar magnetometers. Figure 5 is reproduced from Alken (2016) and shows a high altitude single track measurement from Swarm B (left) and a low altitude single track measurement from CHAMP (right). This figure shows the first observational evidence of a sign change in the \(B_{x}\) (northward) component for the low-altitude CHAMP measurements made below most of the current flow in the EIA region, which is a clear indication of the presence of a gravity current. For measurements made above the EIA region, an eastward gravity current would produce a southward field in the vicinity of the EIA peaks. However, the pressure-gradient current is diamagnetic and therefore always points in the southward direction, so high-altitude measurements alone cannot easily distinguish these two separate current systems. In fact for high-altitude measurements, the \(B_{x}\) (northward) and \(B_{z}\) (vertical) vector magnetic field components look very similar for both of the \(\mathbf{J}_{g}\) and \(\mathbf{J}_{p}\) currents. At low altitudes, the eastward gravity current flow produces a northward magnetic signature in the EIA region (and hence a sign change in \(B_{x}\)), while the pressure-gradient effect would continue to point southward. The right column of Fig. 5 shows a northward perturbation in the low-altitude \(B_{x}\) and total field observations from CHAMP (flying near 288 km altitude), which contrasts with the southward perturbation observed in the higher altitude Swarm B track (near 500 km altitude) in the left column (data recorded at different times). This data was not corrected for the diamagnetic effect, and so this indicates that for the CHAMP measurement, the gravity current was strong enough to completely reverse the southward field produced by the pressure-gradient current. Alken (2016) also presented a comprehensive analysis of the seasonal structure of the gravity and pressure-gradient currents, and found they are strongest during spring/fall, in close agreement with the seasonal behavior of the EIA. He also analyzed the local time structure and found these currents can persist until midnight, even under solar minimum conditions, which could have implications for geomagnetic main field modeling.

Fig. 5
figure 5

Left column: \(B_{x}\), \(B_{z}\) and total field magnetic residuals, including in-situ electron density measurements for a single track from Swarm B on 5 February 2014. Vertical lines are drawn at \(-15.5^{\circ}\) and \(10.5^{\circ}\) quasi-dipole (QD) latitude. Right column: \(B_{x}\), \(B_{z}\) and total field magnetic residuals for a single track from CHAMP on 22 May 2010. Electron density measurements were not available for CHAMP on this day. Vertical lines are drawn at \(-13^{\circ}\) and \(9.5^{\circ}\) QD latitude. Both satellites were in local times between 1930 and 2000. Reprinted from Alken (2016) with permission from John Wiley and Sons

Full size image

In addition to single-track magnetic measurements, the Swarm satellite constellation offers the possibility of directly measuring \(F\)-region currents by using two satellites flying in close proximity to each other. Over short time intervals, the two satellite orbits will map out two opposite sides of a series of quadrilaterals, and the magnetic measurements along the two paths can be used along with Ampere’s law to estimate the current flow normal to the plane enclosed by the quadrilaterals. Nominally, the Swarm A and C satellites fly side-by-side at similar altitudes, which allows the recovery of the vertical component of the current. This method is currently being used to provide an official Level-2 field-aligned current (FAC) product for the Swarm mission (Ritter et al. 2013). A recent study of Swarm-derived field-aligned and radial current measurements has been performed by Lühr et al. (2015). Field-aligned currents determined from conjunctions between Swarm and the Cluster mission have been reported by Dunlop et al. (2015). At the beginning of the Swarm mission, the constellation was organized such that two satellites were flying together along the same meridian but separated in altitude. This configuration allows the estimation of the horizontal zonal currents. First results of applying the Ampere’s law technique to this configuration were recently reported by Tozzi et al. (2015) and Lühr et al. (2016). Both studies found westward nighttime current densities at Swarm altitude of order \(10~\mbox{nA/m}^{2}\). Lühr et al. (2016) additionally analyzed daytime \(F\)-region current densities and found primarily eastward flow of order \(20~\mbox{nA/m}^{2}\). While the measured current contains contributions from all of the source terms in Eqs. (1a)–(1d), they were able to identify a prominent gravity-driven eastward current at low-latitudes.

4 In-Situ Plasma Density Comparisons with Magnetic Measurements

The CHAMP and Swarm satellites are all equipped with Langmuir probes for measuring in-situ plasma density and temperatures. Since the magnetic fields generated by both the gravity and pressure-gradient currents depend not only on local plasma parameters but on the plasma structure throughout the EIA region, an interesting question arises as to how correlated are the magnetic signatures of these currents with the in-situ density and temperature measurements made by the satellites along their orbits. In the case of the pressure-gradient current, as derived by Lühr et al. (2003), Equation (13) shows that only the plasma pressure at the measurement point of interest is relevant, but this is less clear for the gravity current. Alken (2016) investigated this question and performed orbit-by-orbit correlations between Langmuir probe density measurements and corresponding magnetic field perturbations and found large correlations, greater than 80 %, for satellite altitudes above about 450 km (see Fig. 2 of that paper). For lower altitudes, when currents are flowing above and below the satellite, the magnetic signal tends to cancel out and the correlations become less meaningful.

5 Physics-Based Modeling Progress

While the last decade and a half of high-quality magnetic satellite missions have provided new observations of the \(F\)-region gravity and pressure-gradient current systems, they often provide only a small localized glimpse of these large current flows as they fly by. To gain insight into the full 3D structure of these current systems, including the mechanisms by which the currents close, it is necessary to turn to physics-based modeling. Eccles (2004) presented the first study of the gravity and pressure-gradient current systems using a coupled ionospheric electrodynamics model with empirical models specifying the state of the neutral atmosphere. He solved for the individual electric fields generated by the \(\mathbf{J}_{w}\), \(\mathbf{J}_{g}\), and \(\mathbf{J}_{p}\) terms of Eqs. (1a)–(1d), first by solving the equations with all terms included, and then solving the equations with the desired term omitted. He found that the pressure-gradient electric field has negligible effects on the low-latitude electrodynamics. However, his study also found the gravity electric field can alter vertical plasma drift velocities by 10–15 m/s near sunrise and sunset. Alken et al. (2011) investigated the current flow patterns of the gravity and pressure-gradient currents using the Thermosphere-Ionosphere-Electrodynamics General Circulation Model (TIE-GCM). TIE-GCM is a self-consistent model of the upper atmosphere which includes the dynamics, energetics and the chemistry as described in Qian et al. (2014) and references therein. The ionospheric electrodynamics in TIE-GCM is self-consistent and ensures that the total current is divergence free

$$ \nabla\cdot\mathbf{J} = 0 $$
(14)

with the current defined by Eqs. (1a)–(1d). The TIE-GCM electrodynamics solver uses the realistic IGRF geomagnetic main field and is more fully described by Richmond (1995a), Richmond and Maute (2014). Alken et al. (2011) performed model runs of the TIE-GCM electrodynamics solver using empirical input models for the thermosphere and ionospheric densities and temperatures, and isolated the effects of different sources by omitting terms in Eqs. (1a)–(1d) similar to Eccles (2004). They found a wide band of gravity current flow following the EIA density enhancement, which continued into the nighttime due primarily to a Pedersen current. They also presented the flow pattern of the poloidal pressure-gradient current, calculated its magnetic perturbation and compared with the prediction of Lühr et al. (2003) given in Eq. (13). They found overall agreement with the theoretical prediction, although there were some small discrepancies which could be attributed to neglecting the influence of field-aligned currents in the modeling, or a possible influence of field line curvature perturbing the diamagnetic effect.

An assumption in the TIE-GCM current and magnetic perturbation calculation is that most of the current flows in an assumed thin ionospheric current sheet in the \(E\)-region (Richmond 1995a). This is a valid approximation for calculating the wind driven current and for determining ground magnetic perturbations using an equivalent current as described in Richmond (1974) and Richmond and Maute (2014). Doumbia et al. (2007), Zaka et al. (2010), Marsal et al. (2012) used this approach to calculate ground magnetic perturbations, and found reasonable agreement with observations on large spatial and temporal scales. However, for calculating the magnetic perturbation at LEO height in a region of current sources due to gravity and plasma pressure-gradient current the true height variation of the current has to be taken into account.

A new three-dimensional current model was therefore developed which includes an ionospheric electrodynamo, and which calculates the ionospheric current system and its magnetic signal at the ground and at LEO heights. The model spans altitudes from 80 km to approximately 1000 km and is discretized along magnetic field lines. The vertical grid spacing is defined by fixed-height surfaces which, in the present study, are separated by height increments of about 2 km at the lowest altitudes and increasing with altitude, to about 20 km at 400 km and increasingly greater above 400 km. These height surfaces also define the apex heights of the magnetic field lines used in the discretization. The field lines intersect the 80 km lower boundary at irregular latitudes, with steps ranging from \(0.13^{\circ}\) near the magnetic equator to \(3.05^{\circ}\) at mid-latitudes. The discretization is chosen such that the strong height and latitudinal variations in the low-latitude \(E\)-region can be resolved. Along the field line volume elements are introduced with the current determined at the surfaces of each element. Magnetic field lines are assumed to be equipotential, and a two-dimensional partial differential equation for the electric potential \(\varPhi\) with respect to apex latitude and longitude is formulated along the lines of Richmond (1995a) and Richmond and Maute (2014). Further details of the 3D ionosphere model can be found in Maute and Richmond (2016).

With the solution for \(\varPhi\), the three-dimensional ionospheric current \(\mathbf{J}\) is calculated from Eqs. (1a)–(1d) numerically in a way that strictly preserves its divergence-free nature, consistent with Equation (14). The ionospheric electrodynamics are forced as in TIE-GCM by the neutral wind, gravity and plasma pressure-gradient current as well as magnetosphere-ionosphere coupling current at high latitude and current from the lower atmosphere (Lucas et al. 2015). The latter two are neglected in this study. Knowing the electric field \(\mathbf{E}\), the current perpendicular to \(\mathbf{B}\) can be calculated using Eqs. (1a)–(1d). The current density parallel to \(\mathbf{B}\) is determined by the divergence of the perpendicular current integrated along a field line. The current at each height is mapped to a regular grid in Quasi-Dipole latitude and represented by the horizontal current density components \(J_{f_{1}}\) and \(J_{f_{2}}\) (magnetic-eastward and -northward, respectively) and the radial component \(J_{r}\) (Richmond 1995a; Laundal and Richmond 2016).

The simulated magnetic-eastward current densities, shown in Figs. 6(a) and 6(b), are due to \(\mathbf{J}_{g} + \sigma\mathbf{E}_{g}\) and \(\mathbf{J}_{p} + \sigma\mathbf{E}_{p}\) respectively. The results are for September equinox and solar maximum during the daytime at 14 local time (LT) when the EIA is developed and the plasma density is large. The gravity-driven current is eastward in the central and upper F-region, where its spatial variation mainly reflects the plasma mass density. The gravity current is larger at day than at night, and current continuity requires that the difference be mainly balanced by field-aligned current to lower altitudes, where it is closed by conductive current, largely through westward current in the day-time \(E\)-region. Associated with this closure current is a day-time westward electric field. In the equatorial electrojet region the westward electric field sets up a more intense downward/equatorward polarization field through the Cowling effect. This downward/equatorward field is approximately equal to the westward field multiplied by the ratio of field-line-integrated Hall to Pedersen conductivities. This downward/equatorward polarization effect extends even to regions outside the equatorial electrojet, and the associated westward Hall current adds to the westward Pedersen current driven by the westward electric field. These currents are represented as the layer of westward current below 200 km in Fig. 6(a). The magnitude of the equatorial westward current density in the \(E\)-region is larger than the eastward current density in the \(F\)-region though its cross-sectional area is smaller.

Fig. 6
figure 6

Magnetic eastward current density \(J_{f_{1}}\) in \(\mbox{nA/m}^{2}\) (a and b) and scalar magnetic field perturbations in nT (c and d) due to \(\mathbf{J}_{g} + \sigma\mathbf{E}_{g}\) (a and c) and \(\mathbf{J}_{p} + \sigma\mathbf{E}_{p}\) (b and d) for September equinox and solar maximum conditions (\(F_{10.7}=200~\mbox{sfu}\)) at approximately 14 LT over magnetic latitude

Full size image

Figure 7 (left) depicts the zonal and vertical current densities slightly off the magnetic equator due to \(\mathbf{J}_{g} + \sigma\mathbf{E}_{g}\). The color map shows the plasma mass density. As expected, there is eastward current associated with the density. In this plane there is also a strong vertical current density in the lower \(F\)-region and \(E\)-region; only the portion of this vertical current density above 230 km is shown, as it gets much stronger at \(E\)-region heights. This vertical current density varies strongly with latitude, such that its latitude-averaged value over low latitudes at a given longitude and height is much smaller than the local value shown in Fig. 7 suggesting that most of this current is closing in the meridional plane at low latitudes. The vertical current tends to close in the meridional plane by flowing poleward in the lower-\(F\) and \(E\)-regions and upward along low-latitude field lines as suggested by Rishbeth (1971) for the \(F\)-region dynamo current. We intend to investigate the three-dimensional structure of these currents further in a future study.

Fig. 7
figure 7

Equatorial current systems (vectors) at \(0.5^{\circ}\) quasi dipole latitude due to \(\mathbf{J}_{g} + \sigma\mathbf{E}_{g}\) (left) and \(\mathbf{J}_{p} + \sigma\mathbf{E}_{p}\) (right) for the same conditions as in Fig. 6. The \(O^{+}\) mass density (\(10^{-14}~\mbox{kg}/\mbox{m}^{3}\)) and electron density (\(\mbox{m}^{-3}\)) are represented by the contours in the left and right panels, respectively. The vertical component \(J_{r}\) of the vectors is scaled to account for the different dimensions in height and longitude of the plot. The current density is not plotted below 200 km. The red vertical line indicates 14 LT

Full size image

The scalar magnetic perturbation associated with \(\mathbf{J}_{g} + \sigma \mathbf{E}_{g}\) is shown in Fig. 6(c). This is the magnetic perturbation measured in the direction of the geomagnetic field. It is positive over most of the region shown, owing to the strong influence of the westward electrojet current and, at altitudes below 400-500 km, to the northward magnetic perturbations produced by the high-altitude eastward current and low-altitude westward current. This combined effect could be responsible for the observed northward \(B_{x}\) perturbation seen in the low-altitude (288 km) CHAMP data of Fig. 5, even in the presence of a southward pressure-gradient magnetic field.

The plasma pressure-gradient current is also mainly in the zonal direction (see Fig. 6(b)) due to strong vertical gradients in the plasma density. The current reverses sign approximately at the peak of the plasma density, with the plasma temperature variation modifying the height. Below the plasma density peak gravity and pressure-gradient currents enhance each other while above the peak the vertical pressure-gradient force tends to balance the gravitational force, and the two currents roughly cancel. The plasma pressure-gradient current is weakly divergent owing to variations of the magnetic-field strength, as shown in the following equation:

$$ \nabla\cdot\mathbf{J}_{p} = -\nabla\cdot \biggl[\frac{1}{B^{2}} \nabla P \times\mathbf{B} \biggr] = \biggl( \nabla\frac{1}{B^{2}} \times \mathbf{B} \biggr) \cdot\nabla P $$
(15)

with the curl of a gradient field and the curl of the (essentially main) magnetic field \(\mathbf{B}\) field being zero. If \(\nabla\frac{1}{B^{2}}\) were constant, \(\mathbf{J}_{p}\) would be divergence-free. However, because \(\frac{1}{B^{2}}\) does have a relatively weak gradient, the divergence of \(\mathbf{J}_{p}\) is non-zero, although it is generally small in comparison with the divergence of \(\mathbf{J}_{g}\). Figure 8 depicts the dominant flow of \(\mathbf {J}_{p}\) along contours of constant \(P\) as well as the regions of weak convergence and divergence. Note that \(\nabla\frac{1}{B^{2}} \times\mathbf{B}\) points toward magnetic west. Where the plasma pressure increases toward the east (in the morning), net current flows from the \(F\)-region down into the \(E\)-region along field lines to offset the unbalanced net zonal current, and where the plasma pressure decreases toward the east (typically in the late afternoon and evening) current flows up from the \(E\)-region to the \(F\)-region. An electric field is established in association with the currents into and out of the \(E\)-region, typically eastward during the day. This electric field is considerably smaller than that associated with the gravitational current, but it produces the eastward \(E\)-region current seen in Fig. 6(b). The perturbation of the scalar magnetic field (Fig. 6(d)) is predominantly within the \(F\)-region and negative, as expected from the diamagnetic effect of the plasma pressure. Nonetheless, an extension of the negative scalar perturbation to lower altitudes above the weak eastward equatorial electrojet is also seen in Fig. 6(d).

Fig. 8
figure 8

Schematic of daytime plasma pressure gradient driven current system (not to scale). The thick black line indicates a line of constant plasma pressure P separating the areas of high pressure indicated by H and low pressure shown by L. Pressure-gradient-driven current \(\mathbf {J}_{p}\) flows along constant-pressure contours. Its strength depends inversely on the magnetic-field strength, so there is somewhat more westward \(\mathbf{J}_{p}\) in the topside ionosphere than eastward \(\mathbf{J}_{p}\) in the bottomside ionosphere. The imbalance in \(\mathbf{J}_{p}\) feeds field-aligned current \(\mathbf {J}_{\parallel}\) that flows from the \(F\)-region to the \(E\)-region in the morning, where \(\nabla P\) is eastward, and from the \(E\)-region to the \(F\)-region in the late afternoon, where \(\nabla P\) is westward. The field-aligned current sets up an eastward electric field \(\mathbf{E}\) on the day side that drives eastward Pedersen current \(\sigma_{P} \mathbf{E}\), and the eastward field sets up an upward/poleward polarization electric field \(\mathbf{E}_{p}\) that drives additional eastward Hall current \(\sigma_{H} \mathbf{E}_{p}\), especially in the equatorial electrojet

Full size image

Figure 7 (right) shows the electron density distribution (contours) overlain by the magnetic-zonal and vertical current density slightly off the magnetic equator. It illustrates the tendency of the plasma pressure-gradient current to close in the \(F\)-region along lines of constant plasma pressure. The day-time eastward electric field sets up an upward/poleward polarization electric field through the Cowling effect. As is the case for the gravity-driven currents, vertical Pedersen and Hall currents associated with the plasma pressure gradient flow below 200 km that can be stronger than the \(F\)-region currents, but these are not shown in the figure.

Nighttime current density is much smaller than daytime values, as seen in Fig. 7. Alken et al. (2011) found nighttime gravity-driven current density descending and becoming stronger later at night with decreasing height of the plasma. Although \(\mathbf{J}_{g}\) weakens as the plasma density decays during the night, the associated polarization electric field can get stronger to maintain current flow in the form of Pedersen current in the lower \(F\) layer that supplements the relatively weak night-time conductive current in the \(E\)-region. Very small gravity-driven and pressure-gradient-driven currents persist till midnight in the simulation, with \(F\)-region currents flowing mainly between 300–350 km at midnight following the descent of the \(F\)-region. For the pressure-gradient current a weak increase in the eastward current is present in Fig. 7 at the bottom side of the plasma peak around \(-140^{\circ}\) magnetic longitude (approximately 22 LT). For the case in Fig. 7, the low-latitude nighttime eastward current density in the \(F\)-region due to gravity and pressure-gradient current is comparable in size with the \(F\)-region wind dynamo current, with values at 300–350 km of approximately \(25~\mbox{nA/m}^{2}\) for \(\mathbf{J}_{p} + \sigma\mathbf{E}_{p}\), \(10~\mbox{nA/m}^{2}\) for \(\mathbf{J}_{g} + \sigma\mathbf{E}_{g}\), and \(-15~\mbox{nA/m}^{2}\) for \(\mathbf{J}_{w} + \sigma\mathbf{E}_{w}\). In the \(E\)-region \(\mathbf{J}_{w} + \sigma\mathbf{E}_{w}\) dominates over \(\mathbf{J}_{p} + \sigma\mathbf{E}_{p}\) and \(\mathbf{J}_{g} + \sigma\mathbf{E}_{g}\) at all times. Further studies are planned to examine the complex three-dimensional current structure due to gravity and pressure-gradient driven current during the day- and night time.

6 Conclusions

We have reviewed studies of the ionospheric gravity and plasma pressure gradient current systems from both an observational and physics-based modeling viewpoint. Observations of these current systems have come mainly from low Earth orbiting satellite missions over the last decade and a half, and the magnetic perturbations associated with these currents have been found to reach up to 5–7 nT in satellite measurements. While the strongest currents flow during the day, these current systems can persist long after sunset, producing measurable magnetic perturbations up to about midnight. Since the main flow of both current systems is heavily aligned with the EIA structure, it can be difficult to separate the two effects in satellite measurements, although the diamagnetic perturbation formula of Lühr et al. (2003) can help to remove the pressure-gradient effect from observations.

Physics-based modeling results have allowed us to visualize the full 3D flow patterns of these two current systems throughout the \(E\)- and \(F\)-regions. In this paper we present new results of the gravity and pressure gradient current systems as calculated by a fully 3D ionospheric electrodynamics model based on the TIE-GCM. For the gravity current, the model shows an eastward flow in the EIA region during the daytime and evening, with a westward return current through the \(E\)-region due to polarization electric fields. The model further indicates additional current closure in the meridional plane which will be investigated in a future study. The pressure-gradient current flow is primarily zonal due to strong vertical gradients in plasma density in the EIA region, but exhibits some vertical flow as well to maintain a divergence-free current. The current flows poloidally around the EIA region and also exhibits a small eastward current in the \(E\)-region due to polarization electric fields.