1 Introduction

Analyzing the relationship between the parameters of the 11-yr solar sunspot-cycle is important for understanding the mechanism that drives the solar cycle (Bracewell, 1986; Dicke, 1988; Hathaway, Wilson, and Reichmann, 1994; Cameron and Schüssler, 2007; Pesnell, 2008; Petrovay, 2020). Two key parameters of the solar cycle are the maximum amplitude [\(R_{\mathrm{max}}\)] and the cycle length [\(P\), period between two successive minima]. But they are related rather than independent and may change over time. It has been found that \(R_{\mathrm{max}}\) is inversely correlated with the period of the same cycle (\(P\), Waldmeier, 1939; Solanki et al., 2002; Hathaway, Wilson, and Reichmann, 2002), of the previous cycle (\(P_{\mathrm{-1}}\), Waldmeier, 1939; Hathaway, Wilson, and Reichmann, 1999), and with that of three cycles earlier (\(P_{\mathrm{-3}}\), Solanki et al., 2002; Du, Wang, and He, 2006). This suggests that the solar dynamo may carry some memory from one cycle over into the next (Solanki et al., 2002; Dikpati, de Toma, and Gilman, 2006). Sunspot cycles are asymmetric, with a short rise time [\(T_{\mathrm{a}}\)] and a long decay time [\(T_{\mathrm{d}}\)]; large amplitudes tend to take less time to reach their maxima than small ones do (Waldmeier, 1939), the so-called “Waldmeier effect” (Usoskin and Mursula, 2003; Du and Wang, 2012; Hathaway, 2015; Takalo and Mursula, 2018; Chowdhury et al., 2019). The amplitude of an odd-numbered cycle tends to be larger than that of the previous even-numbered one, the G-O rule (Gnevyshev and Ohl, 1948). It is usually believed that \(T_{\mathrm{d}}\) is correlated with neither \(R_{\mathrm{max}}\) nor \(T_{\mathrm{a}}\) (Waldmeier, 1939; Wilson, 1993; Usoskin and Mursula, 2003). But, \(R_{\mathrm{max}}\) was found to be anti-correlated with \(T_{\mathrm{d}}\) of three cycles earlier (Du and Du, 2006).

The above conclusions are based on the total sunspot number values of the whole disk. When analyzing the solar activity in the northern and southern hemispheres separately, it was found that there is a North-South (N-S) asymmetry between the two hemispheres in sunspot areas (Newton and Milsom, 1955; Berdyugina and Usoskin, 2003; Deng et al., 2016), sunspot numbers (Temmer, Veronig, and Hanslmeier, 2002; Chowdhury et al., 2019), solar magnetic fields (Knaack, Stenflo, and Berdyugina, 2005), and other solar activity indicators (Temmer et al., 2001; Roy et al., 2020). These results imply that there may be two independent driving mechanisms in the two hemispheres (Veronig et al., 2021). Analyzing the solar activity in the northern and southern hemispheres separately is helpful for understanding the possible different mechanisms (Spoerer, 1889; Maunder, 1904; Waldmeier, 1971; Hathaway, 2015; Veronig et al., 2021).

The amount of data that can be used to analyze the solar activity in the two hemispheres is far less than that for sunspot numbers. Recently, Veronig et al. (2021) have reconstructed the hemispheric sunspot numbers (HSNs) back to the year 1874. We use the newly reconstructed HSNs to compare the correlations between the parameters of the solar cycle for the total sunspot numbers and HSNs.

First, we introduce the data in Section 2. Then, in Section 3, we compare the correlations between the cycle parameters using linear and quadratic fits, especially the correlation between the amplitude and rise time the Waldmeier effect (Section 3.1), the correlation between the amplitude and the preceding minimum (Section 3.2), and the correlation between the decay and rise times (Section 3.3). The correlation between the amplitude and cycle length is analyzed in Section 4. The different behaviors of the correlations in even- and odd-numbered cycles are compared in Section 5. Finally, the results are discussed and summarized in Section 6.

2 Data

Recently, Veronig et al. (2021) reconstructed the hemispheric sunspot numbers (HSNs) back to the year 1874 based on three different data sets of HSNs and hemispheric sunspot areas. They applied the relative fractions of the northern and southern activity, derived from the daily measurements of hemispheric sunspot areas from 1874 to 2016 from the Greenwich Royal Observatory and the National Oceanic and Atmospheric Administration, to divide the total sunspot number [\(R_{\mathrm{T}}\), TSN] for the whole disk into two parts for the northern [\(R_{\mathrm{N}}\), NSN] and southern hemisphere [\(R_{\mathrm{S}}\), SSN]. The daily, monthly mean, and 13-month smoothed monthly mean HSNs cover fully Solar Cycles 12 – 24 (from May 1874 to October 2020). They can be downloaded from the Sunspot Index and Long-term Solar Observations (SILSO) website (wwwbis.sidc.be/silso/extheminum).

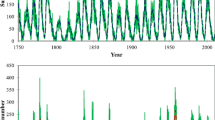
The “13-month smoothed monthly mean” HSNs are based on an “optimized smoothing technique” (OST: Podladchikova, Van der Linden, and Veronig, 2017) to find an optimization (tradeoff) between the closeness of the fit curve to the data and the smoothness of the curve, as shown in Figure 1a for the northern hemisphere [\(R_{\mathrm{N}}\)] and Figure 1b for the southern hemisphere [\(R_{\mathrm{S}}\)]. For comparison, the conventional “13-month running mean” (MRM, with half weights at the two ends) sunspot numbers of the northern [\(R'_{\mathrm{N}}\)] and southern hemisphere [\(R'_{\mathrm{S}}\)] are shown in Figures 1c and 1d, respectively. Figure 1e shows the “13-month running mean total sunspot number” [\(R_{\mathrm{T}}\)] of the second [V2] version (Clette et al., 2016; Clette and Lefèvre, 2016) for the same period, also from the SILSO website (wwwbis.sidc.be/silso/DATA/SN_ms_tot_V2.0.txt).

Figure 1
figure 1

The smoothed monthly mean sunspot numbers (solid) of (a) the northern [\(R_{\mathrm{N}}\)] and (b) southern [\(R_{\mathrm{S}}\)] hemisphere based on an “optimized smoothing technique [OST]”, and (c) the northern [\(R'_{\mathrm{N}}\)], (d) southern [\(R'_{\mathrm{S}}\)] hemisphere, and (e) total [\(R_{\mathrm{T}}\)] based on the “13-month running mean (MRM)” smoothing method. The vertical dashed lines indicate the peak times of \(R_{\mathrm{T}}\) for comparison. The blue dotted line connects the cycle maxima and minima. The red vertical solid line indicates the peak time of Cycle 13 in (a) and (c).

Full size image

Table 1 lists the parameters of the solar cycle for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\), directly from the smoothed monthly mean HSNs based on the OST (Podladchikova, Van der Linden, and Veronig, 2017; Veronig et al., 2021). These parameters are very close to those in Table 1 in Veronig et al. (2021).

Table 1 Parameters of the solar cycle for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\). Column 1 represents the cycle number [\(n\)]. Columns 2 – 7 are derived from \(R_{\mathrm{T}}\): column 2 is the start time [\(t_{\mathrm{min}}\)] of the cycle (in YYYY-MM format); column 3 is the minimum sunspot number [\(R_{\mathrm{min}}\)] at the beginning of the cycle; column 4 is the peak time [\(t_{\mathrm{max}}\)] of the cycle (in YYYY-MM format); column 5 is the maximum amplitude [\(R_{\mathrm{max}}\)] of the cycle; column 6 is the rise time [\(T_{\mathrm{a}}\), in months] from minimum to maximum, and column 7 is the decay time [\(T_{\mathrm{d}}\), in months] from the maximum to the end of the cycle. Columns 8 – 11 and 12 – 15 are derived from \(R_{\mathrm{N}}\) and \(R_{\mathrm{S}}\), respectively. The last two rows indicate the average and the standard deviation.
Full size table

When there are several dates with the same cycle minimum [\(R_{\mathrm{min}}\)], the time of this minimum [\(t_{\mathrm{min}}\)] is defined as the median time of these dates. When there are two dates with the same minimum, the time of this minimum is defined as the second date out of the two. With this definition, if there are two zeros near a solar minimum, the first zero belongs to the previous cycle and the second one belongs to the next cycle.

2.1 Differences in Cycle Parameters Computed with Two Smoothing Methods

The cycle parameters computed using the MRM (not shown) are slightly different from those computed using the OST (see Table 1), taken from the SILSO website. These differences are listed in Table 2. The entries in the table have the following meaning. For the northern hemisphere, \(\Delta t_{\mathrm{min}}=t'_{\mathrm{min,N,MRM}}-t_{\mathrm{min,N,OST}}\) is the difference in the time of solar minimum between the MRM and OST sunspot numbers in the northern hemisphere. For the southern hemisphere, \(\Delta t_{\mathrm{min}}=t'_{\mathrm{min,S,MRM}}-t_{\mathrm{min,S,OST}}\) is the difference in the time of solar minimum between the MRM and OST sunspot numbers in the southern hemisphere, and so on. The last row (av.) indicates the absolute average over cycles \(n=12\) – 24.

Table 2 Differences in the cycle parameters between the MRM- and OST-HSNs. The parameters \(\Delta t_{\mathrm{min}}\), \(\Delta t_{\mathrm{max}}\), \(\Delta T_{\mathrm{a}}\), and \(\Delta T_{\mathrm{d}}\) are in units of months (mo.). The last row indicates the absolute average value.
Full size table

Table 2 shows that in the northern hemisphere, for Cycle 13, \(\Delta T_{\mathrm{a,N}}\,(13)=31\) months and \(\Delta T_{\mathrm{d,N}}\,(13)=-28\) months. The reason for these very large values is that the highest peak of Cycle 13 is the first one (indicated by a red vertical solid line in Figure 1a) based on the OST, while it is the last one (indicated by a red vertical solid line in Figure 1c) based on the MRM. Apart from this cycle, the differences are, in general, not large. In the northern hemisphere, the average values of \(|\Delta t_{\mathrm{min}}|\), \(|\Delta R_{\mathrm{min}}|\), \(|\Delta t_{\mathrm{max}}|\), \(|\Delta R_{\mathrm{max}}|\), \(|\Delta T_{\mathrm{a}}|\), and \(|\Delta T_{\mathrm{d}}|\) are 1.2, 0.3, 3.9, 3.8, 4.7, and 4.5 (or 1.2, 0.3, 1.8, 3.9, 2.5, and 2.6 if not including Cycle 13), respectively. In the southern hemisphere, the average values of \(|\Delta t_{\mathrm{min}}|\), \(|\Delta R_{\mathrm{min}}|\), \(|\Delta t_{\mathrm{max}}|\), \(|\Delta R_{\mathrm{max}}|\), \(|\Delta T_{\mathrm{a}}|\), and \(|\Delta T_{\mathrm{d}}|\) are 0.6, 0.3, 0.8, 2.4, 1.2, and 1.4, respectively. These are smaller than the corresponding values in the northern hemisphere.

2.2 Cycle Parameters

Figure 2 shows the cycle parameters \(R_{\mathrm{min}}\) (a), \(R_{\mathrm{max}}\) (b), \(T_{\mathrm{a}}\) (c), and \(T_{\mathrm{d}}\) (d) for \(R_{\mathrm{T}}\) (solid), \(R_{\mathrm{N}}\) (dotted), and \(R_{\mathrm{S}}\) (dashed), respectively. From them, the following can be noted:

  1. i)

    \(R_{\mathrm{min}}\) (Figure 2a) tends to follow the same trend as \(R_{\mathrm{T}}\) [\(R_{\mathrm{min,T}}\), solid], \(R_{\mathrm{N}}\) [\(R_{\mathrm{min,N}}\), dotted], and \(R_{\mathrm{S}}\) [\(R_{\mathrm{min,S}}\), dashed]. There are some exceptions, though. For example, \(R_{\mathrm{min,N}}(13)\) is a local dip, in contrast to the local peaks of \(R_{\mathrm{min,T}}(13)\) and \(R_{\mathrm{min,S}}(13)\); \(R_{\mathrm{min,S}}(20)\) is lower than \(R_{\mathrm{min,S}}(19)\), in contrast to the cases of \(R_{\mathrm{min,T}}(20)\) and \(R_{\mathrm{min,N}}(20)\); \(R_{\mathrm{min,S}}(23)\) is higher than \(R_{\mathrm{min,S}}(22)\), in contrast to the cases of \(R_{\mathrm{min,T}}(23)\) and \(R_{\mathrm{min,N}}(23)\);

    Figure 2
    figure 2

    Cycle parameters \(R_{\mathrm{min}}\) (a), \(R_{\mathrm{max}}\) (b), \(T_{\mathrm{a}}\) (c), and \(T_{\mathrm{d}}\) (d) for \(R_{\mathrm{T}}\) (solid), \(R_{\mathrm{N}}\) (dotted), and \(R_{\mathrm{S}}\) (dashed).

    Full size image
  2. ii)

    \(R_{\mathrm{max}}\) (Figure 2b) tends to follow the same trend as \(R_{\mathrm{T}}\) [\(R_{\mathrm{max,T}}\), solid], \(R_{\mathrm{N}}\) [\(R_{\mathrm{max,N}}\), dotted], and \(R_{\mathrm{S}}\) [\(R_{\mathrm{max,S}}\), dashed]. There are also some exceptions, though. For example, \(R_{\mathrm{max,N}}(13)\) is not a local peak, in contrast to the local peaks of \(R_{\mathrm{max,T}}(13)\) and \(R_{\mathrm{max,S}}(13)\); \(R_{\mathrm{max,N}}(18)\) is lower than \(R_{\mathrm{max,N}}(17)\), in contrast to the cases of \(R_{\mathrm{max,T}}(18)\) and \(R_{\mathrm{max,S}}(18)\);

  3. iii)

    For \(T_{\mathrm{a}}\) (Figure 2c), the trends in the data corresponding to the total disk and those corresponding to the hemispheres differ significantly;

  4. iv)

    \(T_{\mathrm{d}}\) (Figure 2d) tends to follow the same trend as \(R_{\mathrm{T}}\) [\(T_{\mathrm{d,T}}\), solid], \(R_{\mathrm{N}}\) [\(T_{\mathrm{d,N}}\), dotted], and \(R_{\mathrm{S}}\) [\(T_{\mathrm{d,S}}\), dashed]. There are also some exceptions, though. For example, \(T_{\mathrm{d,N}}(18)\) is smaller than \(T_{\mathrm{d,N}}(17)\), in contrast to the case of \(T_{\mathrm{d,S}}(18)\); \(T_{\mathrm{d,S}}(20)\) is a local dip, in contrast to the local peaks of \(T_{\mathrm{d,T}}(20)\) and \(T_{\mathrm{d,N}}(20)\).

These results reflect the different behavior of the solar cycle in the northern and southern hemispheres. In addition, Table 1 shows that the rise time [\(T_{\mathrm{a}}\)] is shorter than the decay time [\(T_{\mathrm{d}}\)] for the total sunspot number (Waldmeier, 1939). In the northern hemisphere, this statement is also true. However, in the southern hemisphere, there are two cycles (\(n=17\) and 20) for which \(T_{\mathrm{a}}>T_{\mathrm{d}}\).

For comparison, the solar minima and maxima are indicated (connected) by the dotted lines in Figure 1. The vertical dashed lines indicate the peak times of the total sunspot number [\(R_{\mathrm{T}}\)]. From Figure 1, one may note that the highest peak of \(R_{\mathrm{T}}\) is mainly contributed by that of \(R_{\mathrm{N}}\) (Figure 1a) in Cycles 14, 17, 20, and 22, that of \(R_{\mathrm{S}}\) (Figure 1b) in Cycles 12, 13, 18, 19, 23, and 24, and by both \(R_{\mathrm{N}}\) and \(R_{\mathrm{S}}\) in the remaining cycles. If the highest peak of \(R_{\mathrm{N}}\) or \(R_{\mathrm{S}}\) does not correspond to that of \(R_{\mathrm{T}}\), it tends to form the secondary peak, such as those of \(R_{\mathrm{N}}\) for Cycles 12, 18, 23, and 24, and those of \(R_{\mathrm{S}}\) for Cycles 14 and 22.

3 Correlations Between the Cycle Parameters

In this section, we compare the correlation coefficients [\(r\)] between the cycle parameters \(R_{\mathrm{min}}\), \(R_{\mathrm{max}}\), \(T_{\mathrm{a}}\), and \(T_{\mathrm{d}}\) using the data for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), \(R_{\mathrm{S}}\), \(R'_{\mathrm{N}}\), and \(R'_{\mathrm{S}}\), as listed in Table 3. The correlation coefficients differ slightly in most cases depending on the two different smoothing methods. For example, the correlation coefficient between \(R_{\mathrm{max}}\) and \(R_{\mathrm{min}}\) (\(T_{\mathrm{a}}\)) is \(r=0.51\) (−0.54) when using \(R_{\mathrm{S}}\), and it is \(r=0.47\) (−0.46) when using \(R'_{\mathrm{S}}\). However, the correlation coefficient between \(T_{\mathrm{a}}\) and \(R_{\mathrm{max}}\) (\(T_{\mathrm{d}}\)) using \(R_{\mathrm{N}}\), \(r=0.36\,(-0.83)\), is much stronger than that using \(R'_{\mathrm{N}}\), \(r=0.10\,(-0.68)\). This is caused by the different peak times of Cycle 13 (Figures 1a and 1c) based on the two different smoothing methods. This is further discussed in Section 6. We analyze some of these correlations using \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\) in this section.

Table 3 Linear correlation coefficients [\(r\)] between cycle parameters.
Full size table

We use a threshold \(r_{\mathrm{c}}\) of the correlation coefficient [\(r\)] at the 50% confidence level to indicate whether two parameters are correlated. If \(|r|\) is larger (smaller) than \(r_{\mathrm{c}}\), the two parameters are said to be correlated (uncorrelated). For example, \(r_{\mathrm{c}}=0.20\) (0.21) when using a linear (quadratic) fit for \(N=13\) data points.

3.1 The Waldmeier Effect

First, we analyze the well known Waldmeier (1939) effect by which stronger cycles tend to rise faster (Usoskin and Mursula, 2003; Hathaway, 2010; Du and Wang, 2012; Takalo and Mursula, 2018; Chowdhury et al., 2019), as shown in the first row of Figure 3. The solid lines in the figure indicate the linear fits given by the following equations,

$$ R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrllr} 349.6 &-\ 3.49 T_{\mathrm{a}}, &r = -\,0.57, & \mathrm{CL} = 96\%, & \sigma =43.3, &\mathrm{for\ } R_{\mathrm{T}}, \\ 43.4 &+\ 1.12 T_{\mathrm{a}}, &r = +\,0.36, & \mathrm{CL} = 79\%, & \sigma =29.7, &\mathrm{for\ } R_{\mathrm{N}}, \\ 171.2 &-\ 1.28 T_{\mathrm{a}}, &r = -\,0.54, & \mathrm{CL} = 95\%, & \sigma =20.6, &\mathrm{for\ } R_{\mathrm{S}}, \\ \end{array}\displaystyle \right . $$
(1)

where \(r\) is the linear correlation coefficient, CL is the confidence level, and \(\sigma \) is the standard deviation of the regression.

Figure 3
figure 3

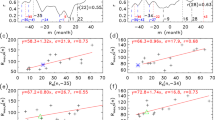
Scatter plots of \(R_{\mathrm{max}}\) against \(T_{\mathrm{a}}\) (first row), \(R_{\mathrm{max}}\) against \(R_{\mathrm{min}}\) (second row), and \(T_{\mathrm{d}}\) against \(T_{\mathrm{a}}\) (third row) for \(R_{\mathrm{T}}\) (left column), \(R_{\mathrm{N}}\) (middle column), and \(R_{\mathrm{S}}\) (right column). The solid (dotted) line represents a linear (quadratic) fit, with a correlation coefficient of \(r\) (\(r_{2}\)), whose confidence level is higher than 50% if it is stronger than \(r_{\mathrm{c}}=0.20\) (0.21). The two dashed lines indicate the 1-\(\sigma \) error from the linear fit. The asterisk indicates the point of Cycle 19. The triangles indicate some cycles for discussion.

Full size image

Figure 3a shows that \(R_{\mathrm{max}}\) is inversely correlated with \(T_{\mathrm{a}}\) for the total sunspot number [\(R_{\mathrm{T}}\)], \(r=-0.57\) (CL = 96%). The data point of Cycle 19 (indicated by an asterisk) is far from the others (far beyond the 1-\(\sigma \) error of the linear fit, indicated by the two dashed lines), and this cycle was an anomalous one (Kane, 2007; Ramesh and Lakshmi, 2012; Petrovay, 2020) in terms of the correlation between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\). In the southern hemisphere (\(R_{\mathrm{S}}\), Figure 3c), this correlation also holds [\(r=-0.54\), CL = 95%], but Cycle 19 is not an anomalous cycle. However, in the northern hemisphere (\(R_{\mathrm{N}}\), Figure 3b), \(R_{\mathrm{max}}\) has an increasing trend with \(T_{\mathrm{a}}\), and the correlation is weak [\(r=0.36\), CL = 79%].

The correlation coefficient in the southern hemisphere is close to that for the whole disk, while the correlation coefficient in the northern hemisphere differs from that in the southern hemisphere. The solar activity in the southern hemisphere obeys the Waldmeier effect (the anti-correlation between the amplitude and rise time), while the solar activity in the northern hemisphere does not obey the Waldmeier effect. This would imply that the solar activity in the northern hemisphere evolves differently from that in the southern hemisphere (Spoerer, 1889; Maunder, 1904; Waldmeier, 1971; Hathaway, 2015; Veronig et al., 2021). As pointed out by Veronig et al. (2021), the peak time for \(R_{\mathrm{N}}\) is about 7.6 months earlier than that for \(R_{\mathrm{S}}\) on average. The average value of \(T_{\mathrm{a}}\) in the northern hemisphere [49 months] is eight months shorter than that in the southern hemisphere [57 months, see Table 1]. Figure 1a shows that, for Cycles 12, 13, and 24, the highest peak of \(R_{\mathrm{N}}\) is the first of the two (or more) peaks and occurs much earlier than that of \(R_{\mathrm{T}}\). The average time shift is −23 months [see Table 1 in Veronig et al. (2021)], causing \(T_{\mathrm{a}}\) to be too short (Table 1). The above positive correlation is largely related to these cycles (triangles in Figure 3b) and the anomalous Cycle 19 (asterisk). If the values of \(T_{\mathrm{a}}\) in these cycles for \(R_{\mathrm{N}}\) are replaced by those for \(R_{\mathrm{T}}\), the correlation coefficient between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\) returns a negative value, \(r=-0.46\) (CL = 90%). If these cycles are not included, the correlation coefficient between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\) for \(R_{\mathrm{N}}\) [\(r=-0.44\), CL = 80%] is close to that for \(R_{\mathrm{S}}\) [\(r=-0.43\), CL = 78%]. Therefore, the positive correlation discussed above might lead to confusing results that the prediction for the solar activity in the northern hemisphere might not be reliable.

The dotted lines in Figure 3 show the quadratic fits to a function of the form

$$ y = c_{0} + c_{1}x + c_{2}x^{2}. $$
(2)

For \(y=R_{\mathrm{max}}\) and \(x=T_{\mathrm{a}}\) (first row) we find,

$$ \small R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrrlr} 626.2 & -\ 14.5 T_{\mathrm{a}} +\ 0.107T^{2}_{\mathrm{a}}, &r_{2} = 0.58, & \mathrm{CL}=96\%, &\sigma = 42.7, &\mathrm{for\ } R_{\mathrm{T}}, \\ -96.1 & +\ \ \ 7.1 T_{\mathrm{a}} -\ 0.061T^{2}_{\mathrm{a}}, &r_{2} = 0.40, & \mathrm{CL}=82\%, &\sigma = 29.1, &\mathrm{for\ } R_{\mathrm{N}}, \\ 114.6 & +\ 0.87 T_{\mathrm{a}} -\ 0.020T^{2}_{\mathrm{a}}, &r_{2} = 0.54, & \mathrm{CL}=94\%, &\sigma = 20.5, &\mathrm{for\ } R_{\mathrm{S}}, \\ \end{array}\displaystyle \right . $$
(3)

where \(r_{2}\) (always positive) is the correlation coefficient between \(y=R_{\mathrm{max}}\) and the quadratic fit \(y\), shown in Table 4 for comparison.

Table 4 Correlation coefficients [\(r_{2}\)] of quadratic fits between the cycle parameters.
Full size table

The top panels of Figure 3 show that the correlation coefficients using quadratic fits, \(r_{2}=0.58\) (CL = 96%), 0.40 (CL = 82%), and 0.54 (CL = 94%), are only slightly stronger than (or equal to) those using linear fits for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\), respectively, namely, \(|r|=0.57\) (CL = 96%), 0.36 (CL = 79%), and 0.54 (CL = 95%).

3.2 Correlation Between the Amplitude and Preceding Cycle Minimum

It is well known that the amplitude [\(R_{\mathrm{max}}\)] is weakly correlated with the preceding cycle minimum (\(R_{\mathrm{min}}\), Hathaway, 2010; Du and Wang, 2010; Ramesh and Lakshmi, 2012; Petrovay, 2020), as shown in the second row of Figure 3. The linear equations are

$$ R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrllr} 141.3 & +\ 4.0 R_{\mathrm{min}}, &r = 0.39, & \mathrm{CL} = 82\%, & \sigma =48.4, &\mathrm{for\ } R_{\mathrm{T}}, \\ 89.8 & +\ 2.1 R_{\mathrm{min}}, &r = 0.21, & \mathrm{CL} = 52\%, & \sigma =31.1, &\mathrm{for\ } R_{\mathrm{N}}, \\ 82.8 & +\ 5.3 R_{\mathrm{min}}, &r = 0.51, & \mathrm{CL} = 94\%, & \sigma =21.0, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(4)

The correlation between \(R_{\mathrm{max}}\) and \(R_{\mathrm{min}}\) is not strong for \(R_{\mathrm{T}}\) [\(r=0.39\), CL =82%, Figure 3d], \(R_{\mathrm{N}}\) [\(r=0.21\), CL = 52%, Figure 3e], and \(R_{\mathrm{S}}\) [\(r=0.51\), CL = 94%, Figure 3f]. The correlation in the northern hemisphere [\(r=0.21\)] is much weaker than that in the southern hemisphere [\(r=0.51\)], which is related to the anomalous Cycle 19. If Cycle 19 is excluded, the discrepancy is not that large: \(r=0.67\) (CL = 99%), 0.45 (CL = 87%), and 0.62 (CL = 97%) for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\), respectively.

The dotted lines in the second row of Figure 3 show the quadratic fits given by

$$ \small R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrrlr} 150.2 + 1.4 R_{\mathrm{min}} + 0.14R^{2}_{\mathrm{min}}, &r_{2} = 0.39, & \mathrm{CL} = 81\%, &\sigma = 48.3, &\mathrm{for\ } R_{\mathrm{T}}, \\ 80.7 + 8.0 R_{\mathrm{min}} - 0.58R^{2}_{\mathrm{min}}, &r_{2} = 0.27, & \mathrm{CL} = 62\%, &\sigma = 30.6, &\mathrm{for\ } R_{\mathrm{N}}, \\ 82.4 + 5.7 R_{\mathrm{min}} - 0.047R^{2}_{\mathrm{min}}, &r_{2} = 0.51, & \mathrm{CL} = 92\%, &\sigma = 21.0, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(5)

The correlation coefficients using quadratic fits, \(r_{2}=0.39\) (CL = 81%), 0.27 (CL = 62%), and 0.51 (CL = 92%), are close to those using linear fits for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\), respectively, namely, \(r=0.39\), 0.21, and 0.51.

3.3 Correlation Between the Decay and Rise Times

It has been known that the correlation between the decay time [\(T_{\mathrm{d}}\)] and rise time [\(T_{\mathrm{a}}\)] is very weak (Waldmeier, 1939; Wilson, 1993; Usoskin and Mursula, 2003; Du, 2006). The third row of Figure 3 shows scatter plots of \(T_{\mathrm{d}}\) against \(T_{\mathrm{a}}\), corresponding to the linear equations:

$$ T_{\mathrm{d}}=\left \{ \textstyle\begin{array}{rrrrllr} 101.5 & -\ 0.42 T_{\mathrm{a}}, &r = -\,0.41, & \mathrm{CL} = 85\%, & \sigma = 8.0, &\mathrm{for\ } R_{\mathrm{T}}, \\ 144.0 & -\ 1.28 T_{\mathrm{a}}, &r = -\,0.83, & \mathrm{CL} > 99\%, & \sigma = 8.8, &\mathrm{for\ } R_{\mathrm{N}}, \\ 104.4 & -\ 0.55 T_{\mathrm{a}}, &r = -\,0.50, & \mathrm{CL} = 93\%, & \sigma = 9.7, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(6)

The correlation is indeed not strong for \(R_{\mathrm{T}}\) [\(r=-0.41\), CL = 85%, Figure 3g] and \(R_{\mathrm{S}}\) [\(r=-0.50\), CL = 93%, Figure 3i]. However, for \(R_{\mathrm{N}}\), the anti-correlation between \(T_{\mathrm{d}}\), and \(T_{\mathrm{a}}\) is very strong [\(r=-0.83\), CL > 99%, Figure 3h]. Cycle 19 is not an anomalous cycle for the correlation between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\).

The weaker correlation in the southern hemisphere may be related to the later peaks (of about eight months) in the southern hemisphere with respect to those in the northern hemisphere: \(T_{\mathrm{a}}\) [\(\overline{T}_{\mathrm{a,S}}=57\) months] is longer and \(T_{\mathrm{d}}\) [\(\overline{T}_{\mathrm{d,S}}=72\) months] is shorter in the southern hemisphere than in the northern hemisphere [\(\overline{T}_{\mathrm{a,N}}=49\) and \(\overline{T}_{\mathrm{d,N}}=81\) months, respectively] (see Table 1). This is caused by Cycles 12, 14, and 23 (triangles in Figure 3i), which have the maximum differences of \(T_{\mathrm{a}}\), \(\Delta T_{\mathrm{a}}=T_{\mathrm{a,N}}-T_{\mathrm{a,S}}\) between \(R_{\mathrm{N}}\) and \(R_{\mathrm{S}}\) [−31, −22, and −24 months, see Table 1]. When they are not included, the correlation coefficient between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\) for \(R_{\mathrm{S}}\) [\(r=-0.84\), CL > 99%] is equal to that for \(R_{\mathrm{N}}\) [\(r=-0.84\), CL > 99%].

The above result means that the correlation between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\) is not very low for the solar activity in the southern hemisphere [\(r=-0.50\)], and this correlation is very strong for the solar activity in the northern hemisphere [\(r=-0.83\)]. One can use this correlation to predict the decay time and the end time of a cycle (or the beginning of the next cycle) if the rise time is known, which was not easy to be accurately predicted in the past.

The dotted lines in the third row of Figure 3 are quadratic fits given by

$$ T_{\mathrm{d}}=\left \{ \textstyle\begin{array}{rrrrlr} 56.9 & +\ 1.4 T_{\mathrm{a}} -\ 0.017T^{2}_{\mathrm{a}}, &r = 0.43, & \mathrm{CL} = 85\%, &\sigma = 7.9, &\mathrm{for\ } R_{\mathrm{T}}, \\ 129.6 & -\ 0.67 T_{\mathrm{a}} -\ 0.0063T^{2}_{\mathrm{a}}, &r = 0.83, & \mathrm{CL} > 99\%, &\sigma = 8.8, &\mathrm{for\ } R_{\mathrm{N}}, \\ 351.5 & -\ 9.96 T_{\mathrm{a}} +\ 0.086T^{2}_{\mathrm{a}}, &r = 0.83, & \mathrm{CL} > 99\%, &\sigma = 6.2, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(7)

The correlation coefficients using quadratic fits, \(r_{2}=0.43\) (CL = 85%) and 0.83 (CL > 99%), are stronger than those using linear fits, \(|r|=0.41\) and 0.50 for \(R_{\mathrm{T}}\) and \(R_{\mathrm{S}}\), respectively. Using the quadratic fit, the correlation coefficient in the southern hemisphere [\(r_{2}=0.83\), CL > 99%] is equivalent in strength to that in the northern hemisphere [\(r_{2}=0.83\)].

The above analysis notes that the correlation coefficients of the quadratic fits are only slightly stronger than those of the linear fits in most cases. Therefore, in general, a linear fit is sufficient. In addition, Table 3 shows that for \(R_{\mathrm{T}}\), \(R_{\mathrm{min}}\) is negatively correlated with \(T_{\mathrm{a}}\) [\(r=-0.41\) at CL = 85%] and positively correlated with \(T_{\mathrm{d}}\) [\(r=0.33\) at CL = 74%], and \(R_{\mathrm{max}}\) is uncorrelated with \(T_{\mathrm{d}}\) [\(r=0.10< r_{\mathrm{c}}=0.20\), CL < 50%]. For \(R_{\mathrm{N}}\) (\(R'_{\mathrm{N}}\)), \(R_{\mathrm{min}}\) is uncorrelated with \(T_{\mathrm{a}}\), \(r=0.09\) (−0.16) at CL < 50% (< 50%), and uncorrelated with \(T_{\mathrm{d}}\), \(r=-0.17\) (0.09) at CL < 50% (< 50%). The correlation coefficient between \(R_{\mathrm{max}}\) and \(T_{\mathrm{d}}\) is negative for \(R_{\mathrm{N}}\) (\(R'_{\mathrm{N}}\)) in the northern hemisphere, \(r=-0.53\) (−0.51) at CL = 95% (93%), but positive for \(R_{\mathrm{S}}\) (\(R'_{\mathrm{S}}\)) in the southern hemisphere, \(r=0.32\) (0.25) at CL = 71% (60%). The correlation between \(R_{\mathrm{max}}\) and \(T_{\mathrm{d}}\) of three cycles earlier is slightly stronger for \(R_{\mathrm{T}}\) [\(r=-0.63\), CL = 95%] and \(R_{\mathrm{N}}\) [\(r=-0.61\), CL = 96%], but very weak for \(R_{\mathrm{S}}\) [\(r=-0.15< r_{\mathrm{c}}=0.23\), CL < 50%]. These results imply that the solar activity evolves partially differently in the two hemispheres.

4 Correlation Between the Amplitude and Cycle Length

It is well known that \(R_{\mathrm{max}}\) is anti-correlated with the cycle length, \(P=T_{\mathrm{a}}+T_{\mathrm{d}}\) (the period between two successive minima), of the same cycle (Waldmeier, 1939; Solanki et al., 2002; Hathaway, Wilson, and Reichmann, 2002), as shown in the first row of Figure 4. Their linear fitting equations are

$$ R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrllr} 487.4 & -\ 2.39 P, &r = -\, 0.43, & \mathrm{CL} = 87\%, &\sigma = 47.5, &\mathrm{for\ } R_{\mathrm{T}}, \\ 328.5 & -\ 1.77 P, &r = -\,0.51, & \mathrm{CL} = 94\%, &\sigma = 27.3, &\mathrm{for\ } R_{\mathrm{N}}, \\ 151.9 & -\ 0.41 P, &r = -\,0.18, & \mathrm{CL} < 50\%, &\sigma = 24.0, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(8)

\(R_{\mathrm{max}}\) is inversely correlated with the cycle length [\(P\)] for \(R_{\mathrm{T}}\) [\(r=-0.43\), CL = 87%] and \(R_{\mathrm{N}}\) [\(r=-0.51\), CL = 94%]. But, they are uncorrelated in the southern hemisphere [\(r=-0.18<\) \(r_{\mathrm{c}}=0.20\), CL < 50%]. This is due to the positive correlation between \(R_{\mathrm{max}}\) and \(T_{\mathrm{d}}\), \(r=0.32\) (see Table 3).

Figure 4
figure 4

Scatter plots of cycle amplitude \(R_{\mathrm{max}}\) against cycle period \(P\) (first row), \(P_{\mathrm{-1}}\) (second row), and \(P_{\mathrm{-3}}\) (third row) using data for \(R_{\mathrm{T}}\) (left column), \(R_{\mathrm{N}}\) (middle column), and \(R_{\mathrm{S}}\) (right column). The correlation coefficient is at a confidence level higher than 50% if it is stronger than \(r_{\mathrm{c}}=0.20\), 0.21, and 0.23 for \(P\), \(P_{\mathrm{-1}}\), and \(P_{\mathrm{-3}}\), respectively. The asterisk indicates Cycle 19. The triangles indicate some cycles for discussion.

Full size image

\(R_{\mathrm{max}}\) was found to be anti-correlated with the cycle length of the previous cycle (\(P_{\mathrm{-1}}\), Waldmeier, 1939; Hathaway, Wilson, and Reichmann, 1999), as shown in the second row of Figure 4. Their linear fitting equations are

$$ R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrllr} 502.9 & -\ 2.48 P_{\mathrm{-1}}, &r = -\,0.46, & \mathrm{CL} = 88\%, & \sigma = 46.5, &\mathrm{for\ } R_{\mathrm{T}}, \\ 316.3 & -\ 1.67 P_{\mathrm{-1}}, &r = -\,0.47, & \mathrm{CL} = 89\%, & \sigma = 27.9, &\mathrm{for\ } R_{\mathrm{N}}, \\ 159.9 & -\ 0.47 P_{\mathrm{-1}}, &r = -\,0.21, & \mathrm{CL} = 50\%, & \sigma = 24.6, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(9)

\(R_{\mathrm{max}}\) is weakly anti-correlated with \(P_{\mathrm{-1}}\) for \(R_{\mathrm{T}}\) [\(r=-0.46\), CL = 88%], \(R_{\mathrm{N}}\) [\(r=-0.47\), CL = 89%], and \(R_{\mathrm{S}}\) [\(r=-0.21\), CL = 50%]. The correlation in the southern hemisphere \([r=-0.21]\) is much weaker than that in the northern hemisphere \([r=-0.47]\).

The amplitude was also found to be anti-correlated with the cycle length of three cycles earlier (\(P_{\mathrm{-3}}\), Solanki et al., 2002; Du, Wang, and He, 2006), as shown in the bottom panels of Figure 4. The linear fitting equations are

$$ R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrllr} 600.3 & -\ 3.17 P_{\mathrm{-3}}, &r = -\,0.51, & \mathrm{CL} = 89\%, & \sigma = 43.1, &\mathrm{for\ } R_{\mathrm{T}}, \\ 250.2 & -\ 1.11 P_{\mathrm{-3}}, &r = -\,0.34, & \mathrm{CL} = 68\%, & \sigma = 29.0, &\mathrm{for\ } R_{\mathrm{N}}, \\ 266.0 & -\ 1.25 P_{\mathrm{-3}}, &r = -\,0.48, & \mathrm{CL} = 86\%, & \sigma = 20.9, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(10)

The correlation in the northern hemisphere [\(r=-0.34\), CL = 68%] is weaker than that in the southern hemisphere [\(r=-0.48\), CL = 86%]. For the correlation between \(R_{\mathrm{max}}\) and \(P_{\mathrm{}}\), \(P_{\mathrm{-1}}\), and \(P_{\mathrm{-3}}\), the point of Cycle 19 is outside the 1-\(\sigma \) error of the linear fit. For comparison, Table 5 lists the correlation coefficients between \(R_{\mathrm{max}}\) and \(P\) of the same cycle, \(P_{\mathrm{-1}}\) of the previous cycle, and \(P_{\mathrm{-3}}\) of three cycles earlier for the data of \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), \(R_{\mathrm{S}}\), \(R'_{\mathrm{N}}\), and \(R'_{\mathrm{S}}\).

Table 5 Correlation coefficients [\(r\)] between \(R_{\mathrm{max}}\) and \(P\) of the same cycle, \(P_{\mathrm{-1}}\) of the previous cycle, and \(P_{\mathrm{-3}}\) of three cycles earlier for the data of \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), \(R_{\mathrm{S}}\), \(R'_{\mathrm{N}}\), and \(R'_{\mathrm{S}}\).
Full size table

For \(P\) and \(P_{-1}\) in the southern hemisphere, the correlations are very weak, \(r=-0.18\) at CL < 50% (Figure 4c) and \(r=-0.21\) at CL = 50% (Figure 4f), respectively. The latter is caused by the shortest cycle length [116 months] in Cycles 15 and 22 (triangles in Figure 4f). For example, the start time of Cycle 15 seems to be determined late, and the end time seems to be determined early (Figure 1b). When they are not included, the correlation [−0.47, CL = 85%] is near that for \(R_{\mathrm{N}}\) [−0.45, CL = 83%]. The former is caused by the short cycle length in Cycles 15 [116 months] and 16 [121 months] and the longest cycle length in Cycle 23 [151 months] shown by the triangles in Figure 4c. When these are not included, the correlation is much higher [−0.50, CL = 88%].

5 The Different Behavior of Even- and Odd-Numbered Cycles

It is well known that the solar activity may show different behavior in even- and odd-numbered cycles (Gnevyshev and Ohl, 1948; Yoshida, 2014; Javaraiah, 2016; Du, 2020; Takalo, 2020; Kakad and Kakad, 2021). This aspect is analyzed in this section for the relationships discussed in Section 3.

5.1 The Waldmeier Effect

The scatter plots of \(R_{\mathrm{max}}\) against \(T_{\mathrm{a}}\) using data for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\) are shown in the top panels of Figures 5 and 6 for the even- and odd-numbered cycles, respectively.

Figure 5
figure 5

Scatter plots of \(R_{\mathrm{max}}\) against \(T_{\mathrm{a}}\) (first row), \(R_{\mathrm{max}}\) against \(R_{\mathrm{min}}\) (second row), and \(T_{\mathrm{d}}\) against \(T_{\mathrm{a}}\) (third row) for \(R_{\mathrm{T}}\) (left column), \(R_{\mathrm{N}}\) (middle column), and \(R_{\mathrm{S}}\) (right column) in even-numbered cycles. The correlation coefficient is at a confidence level higher than 50% if it is stronger than \(r_{\mathrm{c}}=0.28\).

Full size image
Figure 6
figure 6

Similar to Figure 5 but in odd-numbered cycles. The correlation coefficient is at a confidence level higher than 50% if it is stronger than \(r_{\mathrm{c}}=0.31\). The asterisk indicates Cycle 19.

Full size image

For the even-numbered cycles (Figures 5a, 5b, and 5c), the linear fitting equations are

$$ R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrllr} 350.4 & -\ 3.91 T_{\mathrm{a}}, &r = -\,0.85, & \mathrm{CL} > 99\%, & \sigma = 24.4, &\mathrm{for\ } R_{\mathrm{T}}, \\ 44.4 & +\ 0.79 T_{\mathrm{a}}, &r = +\,0.43, & \mathrm{CL} = 69\%, & \sigma = 17.9, &\mathrm{for\ } R_{\mathrm{N}}, \\ 242.4 & -\ 2.55 T_{\mathrm{a}}, &r = -\,0.82, & \mathrm{CL} = 99\%, & \sigma = 14.4, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(11)

The correlation coefficient between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\) is negative and strong for \(R_{\mathrm{T}}\) [\(r=-0.85\), CL > 99%] and \(R_{\mathrm{S}}\) [\(r=-0.82\), CL = 99%], but positive and weak for \(R_{\mathrm{N}}\) [\(r=0.43\), CL = 69%]. This means that the rise rate [\(\overline{R}_{\mathrm{max}}/\overline{T}_{\mathrm{a}}\)] in the northern hemisphere behaves differently from that in the southern hemisphere. The negative correlations are stronger than those using the data of all cycles for \(R_{\mathrm{T}}\) and \(R_{\mathrm{S}}\), \(r=-0.57\) (Figure 3a) and −0.54 (Figure 3c), respectively.

For the odd-numbered cycles (Figures 6a, 6b, and 6c), the linear fitting equations are

$$ R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrllr} 273.5 & -\ 1.45 T_{\mathrm{a}}, &r = -\,0.21, & \mathrm{CL} < 50\%, & \sigma = 48.0, &\mathrm{for\ } R_{\mathrm{T}}, \\ 25.1 & +\ 1.88 T_{\mathrm{a}}, &r = +\,0.55, & \mathrm{CL} = 80\%, & \sigma = 30.1, &\mathrm{for\ } R_{\mathrm{N}}, \\ 123.7 & -\ 0.29 T_{\mathrm{a}}, &r = -\,0.17, & \mathrm{CL} < 50\%, & \sigma = 20.6, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(12)

The correlation coefficient between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\) is also positive for \(R_{\mathrm{N}}\) [\(r=0.55\), CL = 80%]. But they are uncorrelated for \(R_{\mathrm{T}}\) [\(r=-0.21< r_{\mathrm{c}}=0.31\), CL < 50%] and \(R_{\mathrm{S}}\) [\(r=-0.17\), CL < 50%] in the odd-numbered cycles. For convenience, the linear correlation coefficients between the cycle parameters in the even- and odd-numbered cycles are listed in Table 6.

Table 6 Linear correlation coefficients [\(r\)] between cycle parameters in even- and odd-numbered cycles.
Full size table

5.2 Correlation Between the Amplitude and Preceding Cycle Minimum

For the even-numbered cycles (Figures 5d, 5e, and 5f), the equations for the linear fitting between \(R_{\mathrm{max}}\) and \(R_{\mathrm{min}}\) are

$$ R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrllr} 89.7 & +\ 7.2 R_{\mathrm{min}}, &r = 0.81, &\mathrm{CL} = 98\%, & \sigma = 27.1, &\mathrm{for\ } R_{\mathrm{T}}, \\ 69.0 & +\ 3.2 R_{\mathrm{min}}, &r = 0.57, &\mathrm{CL} = 85\%, & \sigma = 16.3, &\mathrm{for\ } R_{\mathrm{N}}, \\ 65.6 & +\ 10.0 R_{\mathrm{min}}, &r = 0.71, &\mathrm{CL} = 95\%, & \sigma = 17.9, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(13)

The correlation is strong for \(R_{\mathrm{T}}\) [\(r=0.81, \mathrm{CL}=98\%\)] and \(R_{\mathrm{S}}\) [\(r=0.71, \mathrm{CL}=95\%\)], and slightly weaker for \(R_{\mathrm{N}}\) [\(r=0.57, \mathrm{CL}=85\%\)]. These correlations are much stronger than those using the data of all cycles, \(r=0.39\) (Figure 3d), 0.21 (Figure 3e), and 0.51 (Figure 3f), for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\), respectively.

For the odd-numbered cycles (Figures 6d, 6e, and 6f), the equations for the linear fitting between \(R_{\mathrm{max}}\) and \(R_{\mathrm{min}}\) are

$$ R_{\mathrm{max}}=\left \{ \textstyle\begin{array}{rrrrllr} 196.1 & +\ 0.84 R_{\mathrm{min}}, &r = 0.09, &\mathrm{CL} < 50\%, & \sigma = 49.0, &\mathrm{for\ } R_{\mathrm{T}}, \\ 105.9 & +\ 2.72 R_{\mathrm{min}}, &r = 0.23, &\mathrm{CL} < 50\%, & \sigma = 35.2, &\mathrm{for\ } R_{\mathrm{N}}, \\ 100.4 & +\ 2.18 R_{\mathrm{min}}, &r = 0.31, &\mathrm{CL} < 50\%, & \sigma = 19.9, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(14)

The correlation coefficients for \(R_{\mathrm{T}}\,[r=0.09< r_{\mathrm{c}}=0.31]\), \(R_{\mathrm{N}}\,[r=0.23< r_{\mathrm{c}}]\), and \(R_{\mathrm{S}}\,[r=0.306< r_{\mathrm{c}}=0.309]\) are all at a confidence level CL < 50% and are much weaker than those in the even-numbered cycles, \(r=0.81\), 0.57, and 0.71, respectively.

5.3 Correlation Between the Decay and Rise Times

For the even-numbered cycles (Figures 5g, 5h, and 5i), the equations for the linear fitting between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\) are

$$ T_{\mathrm{d}}=\left \{ \textstyle\begin{array}{rrrrllr} 109.6 & -\ 0.61 T_{\mathrm{a}}, &r = -\,0.63, &\mathrm{CL} = 91\%, & \sigma = 7.4, &\mathrm{for\ } R_{\mathrm{T}}, \\ 141.1 & -\ 1.23 T_{\mathrm{a}}, &r = -\,0.85, &\mathrm{CL} > 99\%, & \sigma = 8.1, &\mathrm{for\ } R_{\mathrm{N}}, \\ 93.7 & -\ 0.42 T_{\mathrm{a}}, &r = -\,0.35, &\mathrm{CL} = 60\%, & \sigma = 9.0, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(15)

It means that \(T_{\mathrm{d}}\) is inversely correlated with \(T_{\mathrm{a}}\). But the negative correlation for \(R_{\mathrm{N}}\) [\(r=-0.85\), CL > 99%] is much stronger than that for \(R_{\mathrm{S}}\) [\(r=-0.35\), CL = 60%], and similar to those obtained using the data of all cycles in Figures 3h and 3i (\(r=-0.83\) vs. −0.50).

For the odd-numbered cycles (Figures 6g, 6h, and 6i), the equations for the linear fitting between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\) are

$$ T_{\mathrm{d}}=\left \{ \textstyle\begin{array}{rrrrllr} 78.6 & +\ 0.08 T_{\mathrm{a}}, &r = +\,0.07, &\mathrm{CL} < 50\%, & \sigma = \ \, 7.9, &\mathrm{for\ } R_{\mathrm{T}}, \\ 147.3 & -\ 1.35 T_{\mathrm{a}}, &r = -\,0.81, &\mathrm{CL} = 97\%, & \sigma = 10.3, &\mathrm{for\ } R_{\mathrm{N}}, \\ 103.5 & -\ 0.48 T_{\mathrm{a}}, &r = -\,0.49, &\mathrm{CL} = 72\%, & \sigma = 10.5, &\mathrm{for\ } R_{\mathrm{S}}. \\ \end{array}\displaystyle \right . $$
(16)

\(T_{\mathrm{d}}\) is uncorrelated with \(T_{\mathrm{a}}\) for \(R_{\mathrm{T}}\) [\(r=0.07< r_{\mathrm{c}}=0.31\), CL < 50%], in contrast to the result for even-numbered cycles [\(r=-0.63\)]. \(T_{\mathrm{d}}\) is highly anti-correlated with \(T_{\mathrm{a}}\) for \(R_{\mathrm{N}}\) [\(r=-0.81\), CL = 97%], in a similar way to the result for even-numbered cycles [\(r=-0.85\)]. The anti-correlation between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\) for \(R_{\mathrm{S}}\) [\(r=-0.49\), CL = 72%] is stronger than that in the even-numbered cycles [\(r=-0.35\)].

In summary, the correlations between the cycle parameters tend to be stronger in the case of even-numbered cycles than for odd-numbered ones.

6 Discussion and Conclusions

We analyzed some typical relationships between the cycle parameters using \(R_{\mathrm{N}}\) and \(R_{\mathrm{S}}\) (Figure 3) smoothed by the “optimized smoothing technique” (OST: Podladchikova, Van der Linden, and Veronig, 2017). The first is the well known Waldmeier (1939) effect for the anti-correlation between the amplitude [\(R_{\mathrm{max}}\)] and rise time [\(T_{\mathrm{a}}\)] (Usoskin and Mursula, 2003; Hathaway, 2010; Du and Wang, 2012; Takalo and Mursula, 2018; Chowdhury et al., 2019). In the southern hemisphere [\(R_{\mathrm{S}}\)], \(R_{\mathrm{max}}\) is inversely correlated with \(T_{\mathrm{a}}\), \(r=-0.54\) (Figure 3c), which is the major contributor to the total sunspot number [\(R_{\mathrm{T}}\)], \(r=-0.57\) (Figure 3a). In the northern hemisphere [\(R_{\mathrm{N}}\)], the correlation between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\) does not follow the Waldmeier effect: \(R_{\mathrm{max}}\) is positively correlated with \(T_{\mathrm{a}}\), \(r=0.36\). This is largely related to some special cycles (Figure 3b) that have their peak times much earlier than those in the southern hemisphere (Figure 1a).

The strength of the correlation between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\) depends on the timings of solar minimum [\(t_{\mathrm{min}}\)] and maximum [\(t_{\mathrm{max}}\)]. Lantos (2000) found that the correlation [\(r=0.88\)] between \(R_{\mathrm{max}}\) and the slope at the inflection point is stronger than that [\(|r|=0.61\)] between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\) for \(R_{\mathrm{T}}\) of the old version [V1.0]. To eliminate the effect of the timings of solar minimum and maximum, Cameron and Schüssler (2008) analyzed the growth rate (slope) of \(R_{\mathrm{T}}\) within a certain range of \(30\leqslant R_{\mathrm{T}}\leqslant 50\) (old version) and found that it has a high correlation [0.82] with \(R_{\mathrm{max}}\). Veronig et al. (2021) pointed out that the peak growth rate gives an even higher correlation with the amplitude [0.9] in both hemispheres. The timing of the solar minimum is affected by the temporal overlapping of cycles (Cameron and Schüssler, 2007). The timing of solar maximum is influenced by which peak is the highest if there are double or multiple peaks. Therefore, analyzing the slope using the sunspot numbers above the minimum and below the maximum can eliminate the effect of their timings, especially if there are not significant differences in the values around a minimum or maximum during several months (e.g., Cycle 13 in Figure 1a).

The second typical relationship is that between the amplitude [\(R_{\mathrm{max}}\)] and the preceding cycle minimum [\(R_{\mathrm{min}}\)], although their correlation is not strong (Du and Wang, 2010; Hathaway, 2010; Ramesh and Lakshmi, 2012; Petrovay, 2020). The correlation coefficient between \(R_{\mathrm{max}}\) and \(R_{\mathrm{min}}\) is \(r=0.51\) in the southern hemisphere (Figure 3f) and \(r=0.21\) (or 0.45 excluding the anomalous Cycle 19) in the northern hemisphere (Figure 3e). This positive correlation can be explained by: (1) the temporal overlapping of adjacent cycles as the sunspot cycle actually begins a few years before the solar minimum, and (2) the anti-correlation between the rise time and the amplitude: a larger amplitude shifts the start time earlier with a larger minimum (Cameron and Schüssler, 2007). The weaker correlation in the northern hemisphere may be related to the larger \(R_{\mathrm{min}}\) in the northern hemisphere [\(\overline{R}_{\mathrm{min,N}}=4.0\)] than that in the southern hemisphere [\(\overline{R}_{\mathrm{min,S}}=2.9\), see Table 1] due to the overlapping of cycles (Cameron and Schüssler, 2007, 2008) by the shorter \(T_{\mathrm{a}}\) [\(\overline{T}_{\mathrm{a,N}}=49\)]: a shorter rise time shifts the start time earlier with a larger minimum [\(R_{\mathrm{min}}\)].

The third relationship is about the correlation between the decay time [\(T_{\mathrm{d}}\)] and the rise time [\(T_{\mathrm{a}}\)]. This correlation is well known to be very weak (Waldmeier, 1939; Wilson, 1993; Usoskin and Mursula, 2003). For \(R_{\mathrm{T}}\), the correlation between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\) is indeed very weak, \(r=-0.41\) (Figure 3g). However, in the southern hemisphere, the correlation is slightly stronger, \(r=-0.50\) (Figure 3i), and in the northern hemisphere, the correlation is very strong, \(r=-0.83\) (Figure 3h).

When using the “13-month running mean” (MRM) sunspot numbers of the northern [\(R'_{\mathrm{N}}\)] and southern hemisphere [\(R'_{\mathrm{S}}\)], there is only a little change in the above correlations in most cases (Table 3). However, the correlation coefficient between \(T_{\mathrm{a}}\) and \(R_{\mathrm{max}}\) (\(T_{\mathrm{d}}\)) using \(R_{\mathrm{N}}\), \(r=0.36\,(-0.83)\), becomes lower when using \(R'_{\mathrm{N}}\), \(r=0.10\,(-0.68)\), as shown in Figure 7a (7b). In this case, Cycle 13 is outside the 1-\(\sigma \) error of the linear fit.

Figure 7
figure 7

Scatter plots of \(R'_{\mathrm{max}}\) (a) and \(T'_{\mathrm{d}}\) (b) against \(T'_{\mathrm{a}}\) using \(R'_{\mathrm{N}}\) (smoothed by the 13-month running mean, in the northern hemisphere). Scatter plots of \(R'_{\mathrm{max}}\) (c) and \(T'_{\mathrm{d}}\) (d) against \(T'_{\mathrm{a}}\) using \(R'_{\mathrm{N}}\) , but the peak of Cycle 13 is taken as the first one: \(T'_{\mathrm{a}}(13)=37\) and \(T'_{\mathrm{d}}(13)=114\). The solid line is a linear fit, and the two dashed lines indicate the 1-\(\sigma \) error from the linear fit, and the asterisk indicates Cycle 13. The threshold is \(r_{\mathrm{c}}=0.20\) at CL = 50%.

Full size image

As can be seen in Figure 1, the highest peak of Cycle 13 is the first one (Figure 1a) for \(R_{\mathrm{N}}\) smoothed by the OST, while it is the last one (Figure 1c) for the MRM \(R'_{\mathrm{N}}\), leading to the large differences in \(\Delta T_{\mathrm{a}}\,[=31]\) and \(\Delta T_{\mathrm{d}}\,[=-28]\) in this cycle (Table 2). Now, we use the first peak of Cycle 13 (July 1892), \(T'_{\mathrm{a}}\,(13)=37\) and \(T'_{\mathrm{d}}\,(13)=114\) (months), and reanalyze the correlations in Figures 7a and 7b. These are shown in Figures 7c and 7d, respectively.

For the correlation between \(R'_{\mathrm{max}}\) and \(T'_{\mathrm{a}}\) (Figure 7c), Cycle 13 is within the 1-\(\sigma \) error of the linear fit. Their correlation coefficient [\(r=0.32\), CL = 72%] is much higher than that in Figure 7a [\(r=0.10\), CL < 50%] and close to that using \(R_{\mathrm{N}}\) in Figure 3b [\(r=0.36\)]. For the correlation between \(T'_{\mathrm{d}}\) and \(T'_{\mathrm{a}}\) (Figure 7d), Cycle 13 is still outside the 1-\(\sigma \) error of the linear fit. Their correlation coefficient [\(r=-0.80\), CL > 99%] is much stronger than that in Figure 7b [\(r=-0.68\), CL = 99%] and closer to that using \(R_{\mathrm{N}}\) in Figure 3h [\(r=-0.83\)]. Therefore, the differences in the correlation coefficients related to \(T_{\mathrm{a}}\) (and \(T_{\mathrm{d}}\)) in Table 3 are mainly due to the different peak times of Cycle 13 based on the OST and MRM smoothing methods. Determining the rise time in terms of the later maximum may destroy the correlation with the cycle amplitude (Cameron and Schüssler, 2008). These findings show that the optimized smoothing method (Podladchikova, Van der Linden, and Veronig, 2017) is superior to the traditional 13-month running mean in analyzing long-term variations in solar activity, as it provides a more robust determination of the cycle peaks and subsequently more robust relations between various solar cycle parameters.

The amplitude [\(R_{\mathrm{max}}\)] was also found to be anti-correlated with the cycle length [\(P=T_{\mathrm{a}}+T_{\mathrm{d}}\)] of the same cycle (Waldmeier, 1939; Solanki et al., 2002; Hathaway, Wilson, and Reichmann, 2002), of the previous cycle (\(P_{-1}\) Waldmeier, 1939; Hathaway, Wilson, and Reichmann, 1999), and with that of three cycles earlier (\(P_{\mathrm{-3}}\), Solanki et al., 2002; Du, Wang, and He, 2006). In the northern hemisphere, \(r=-0.51\) (Figure 4b), −0.47 (Figure 4e), and −0.39 (Figure 4h) for \(P\), \(P_{-1}\), and \(P_{\mathrm{-3}}\), respectively. These are the major contributor to those for the total sunspot number [\(R_{\mathrm{T}}\)], \(r=-0.43\) (Figure 4a), −0.46 (Figure 4d), and −0.51 (Figure 4g) for \(P\), \(P_{-1}\), and \(P_{\mathrm{-3}}\), respectively. This negative correlation has been explained by Cameron and Schüssler (2007) due to the overlapping effect of cycles. The negative correlation between \(R_{\mathrm{max}}\) and \(P_{-3}\) may be related to the modulation of long-term periods or the memory of 2 – 3 solar cycles (Solanki et al., 2002; Dikpati, de Toma, and Gilman, 2006). In the southern hemisphere, \(R_{\mathrm{max}}\) is nearly uncorrelated to \(P\) [\(r=-0.18\) at CL < 50%, Figure 4c] and \(P_{-1}\) [\(r=-0.21\) at CL = 50%, Figure 4f]. But these correlations are related to the timings of solar minima.

According to the above analysis, we realized that the correlations between the cycle parameters depend (more or less) on the timings of solar minima and maxima, which are not obviously identifiable and are related to the smoothing method to some extent. Different smoothing methods lead to different timings of solar minima and maxima (e.g., Figures 1a and 1c). For example, as there are fluctuations around the peak of Cycle 13 (Figure 1a), it is hard to clearly point out which point is more reasonable as a peak. For a solar minimum without sunspots over a period of time, e.g., from January to November 1912 (Figure 1a), unexpected small sunspots appearing at any time during this period could change the timing of the minimum. The main characteristic parameters of the solar cycle might require smoother sunspot numbers (Cameron and Schüssler, 2007).

Finally, in Section 5, we analyzed the different behavior of the above correlations in even- and odd-numbered cycles (Gnevyshev and Ohl, 1948; Yoshida, 2014; Javaraiah, 2016; Du, 2020; Takalo, 2020; Kakad and Kakad, 2021). The correlations between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\), between \(R_{\mathrm{max}}\) and \(R_{\mathrm{min}}\), and between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\) in even-numbered cycles tend to be stronger than those in odd-numbered ones for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\) (with two exceptions of the positive correlation between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\) for \(R_{\mathrm{N}}\) and the negative correlation between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\) for \(R_{\mathrm{S}}\)). They are similar to the correlation between \(R_{\mathrm{max}}\) and the value of \(R_{\mathrm{T}}\) at a certain time (three years) before the solar minimum (Yoshida, 2014; Du, 2020). The “even-odd” cycle pair constitutes a 22-yr magnetic cycle (Hale, 1924), having a much better behavior in the first half (“rising phase”) than in the second one (“declining phase”), similar to the 11-yr cycle. The weaker correlation in the odd-numbered cycles may be caused by the larger number of active regions (and solar flares, CMEs, etc.) and a more nonlinear behavior in odd-numbered cycles than in even-numbered ones (Du, 2020), similar to the case of the declining phase relative to the rising phase of the 11-yr cycle. The differences in the above correlations between the northern and southern hemispheres for even- or odd-numbered cycles are similar to those for all the cycles.

Based on the above analysis, our main results are summarized as follows:

  1. i)

    The anti-correlation between the amplitude [\(R_{\mathrm{max}}\)] and rise time [\(T_{\mathrm{a}}\)] for \(R_{\mathrm{T}}\) [\(r=-0.57\)] comes mainly from the contribution in the southern hemisphere [\(R_{\mathrm{S}}\)], \(r=-0.54\). In the northern hemisphere [\(R_{\mathrm{N}}\)], this correlation does not follow the Waldmeier effect: \(R_{\mathrm{max}}\) is positively correlated with \(T_{\mathrm{a}}\), \(r=0.36\);

  2. ii)

    The correlation between \(R_{\mathrm{max}}\) and the preceding minimum [\(R_{\mathrm{min}}\)] for \(R_{\mathrm{T}}\) [\(r=0.39\)] comes mainly from the contribution in the southern hemisphere [\(r=0.51\)]. This correlation is very weak in the northern hemisphere [\(r=0.21\)];

  3. iii)

    The anti-correlation between the decay time [\(T_{\mathrm{d}}\)] and rise time [\(T_{\mathrm{a}}\)] is weak for \(R_{\mathrm{T}}\) [\(r=-0.41\)], not strong in the southern hemisphere [\(r=-0.50\)], but very strong in the northern hemisphere [\(r=-0.83\)];

  4. iv)

    The anti-correlation between \(R_{\mathrm{max}}\) and the cycle length [\(P=T_{\mathrm{a}}+T_{\mathrm{d}}\)] is not strong for \(R_{\mathrm{T}}\,[r=-0.43]\) and for \(R_{\mathrm{N}}\,[r=-0.51]\), and very weak for \(R_{\mathrm{S}}\,[r=-0.18]\);

  5. v)

    The Waldmeier effect (the anti-correlation between \(R_{\mathrm{max}}\) and \(T_{\mathrm{a}}\)) is much more apparent in even-numbered cycles than in odd-numbered ones for both \(R_{\mathrm{T}}\) [\(r=-0.85\) vs. −0.21] and \(R_{\mathrm{S}}\) [\(r=-0.82\) vs. −0.17]. In the northern hemisphere, the Waldmeier effect no longer holds in both even- [\(r=0.43\)] and odd-numbered cycles [\(r=0.55\)];

  6. vi)

    The correlations between \(R_{\mathrm{max}}\) and \(R_{\mathrm{min}}\) in even-numbered cycles, \(r=0.81\), 0.57, and 0.71, are much stronger than those in odd-numbered ones, \(r=0.09\), 0.23, and 0.31 for \(R_{\mathrm{T}}\), \(R_{\mathrm{N}}\), and \(R_{\mathrm{S}}\), respectively;

  7. vii)

    For \(R_{\mathrm{T}}\), the anti-correlation between \(T_{\mathrm{d}}\) and \(T_{\mathrm{a}}\) is good in even-numbered cycles [\(r=-0.63\)] and near zero in odd-numbered cycles [\(r=0.07\)]. In the northern hemisphere, the correlation is very strong in both even- [\(r=-0.85\)] and odd-numbered cycles [\(r=-0.81\)]. In the southern hemisphere, the correlation is much weaker in both even- [\(r=-0.35\)] and odd-numbered cycles [\(r=-0.49\)].

In short, the correlations of \(R_{\mathrm{max}}\) with \(T_{\mathrm{a}}\) and \(R_{\mathrm{min}}\) in the southern hemisphere are much stronger than those in the northern hemisphere. While the correlation of \(T_{\mathrm{d}}\) with \(T_{\mathrm{a}}\) and that of \(R_{\mathrm{max}}\) with \(P\) in the northern hemisphere are much stronger than those in the southern hemisphere. This seems to imply that the solar activity in the northern hemisphere evolves partially differently from that in the southern hemisphere. But these correlations depend on the timings of solar minima and maxima, which are related to the smoothing method. Smoother sunspot numbers may be more suitable for analyzing the main characteristic parameters of the solar cycle (Cameron and Schüssler, 2007).

If two parameters of the solar cycle are found to be well correlated in the northern or southern hemisphere, the correlation can be used to predict one parameter from another in that hemisphere. For example, the end time of a cycle or the start time of the next cycle is also important in solar cycle prediction. However, the methods used to predict the time of minimum [\(t_{\mathrm{min}}\)] are far less in number than those used to predict the amplitude [\(R_{\mathrm{max}}\)]. The correlation between the decay time [\(T_{\mathrm{d}}\)] and rise time [\(T_{\mathrm{a}}\)] is very weak (Waldmeier, 1939; Wilson, 1993; Usoskin and Mursula, 2003) for the total sunspot number [\(r=-0.41\)]. But this correlation is slightly stronger in the southern hemisphere [\(r=-0.50\)] and very strong in the northern hemisphere [\(r=-0.83\)]. This correlation can be used to predict the decay time and then the time of solar minimum in the northern (or southern) hemisphere. Once the time of solar minimum in the northern or southern hemisphere is known, one can analyze the relationship between the amplitude and the value at the preceding declining phase in that hemisphere, similar to that for the total sunspot number using the value three years before the solar minimum (Cameron and Schüssler, 2007; Yoshida and Yamagishi, 2010; Han and Yin, 2019; Du, 2020). If the amplitude is found to be correlated with the value at a certain time before the solar minimum, the correlation can be used to predict the former in that or both hemispheres. Through analyzing the relationship of \(T_{\mathrm{d,T}}\) with both \(T_{\mathrm{d,N}}\) and \(T_{\mathrm{d,S}}\), the former and then the time of solar minimum for the total sunspot number may be predicted. One can also analyze the shapes of the solar cycle in both hemispheres using mathematical functions and extrapolate the remaining parts based on the observation in the initial few years. Combining the results of the two hemispheres, the shape of the total sunspot numbers can be analyzed (e.g., double peaks).