Coronal Quasi-periodic Fast-mode Propagating Wave Trains

Abstract

Quasi-periodic, fast-mode propagating (QFP) wave trains in the corona have been studied intensively over the last decade, thanks to the full-disk, high spatio-temporal resolution, and wide-temperature coverage observations taken by the Atmospheric Imaging Assembly (AIA) onboard the Solar Dynamics Observatory (SDO). In the AIA observations, the QFP wave trains are seen to consist of multiple coherent and concentric wavefronts emanating successively near the epicenter of the accompanying flares. They propagate outwardly either along or across coronal loops at fast-mode magnetosonic speeds from several hundred to more than 2000 km s⁻¹, and their periods are in the range of tens of seconds to several minutes. Based on the distinctly different properties of QFP wave trains, they might be divided into two distinct categories: narrow and broad ones. For most QFP wave trains, some of their periods are similar to those of the quasi-periodic pulsations (QPPs) in the accompanying flares, indicating that they are probably different manifestations of the same physical process. Currently, candidate generation mechanisms for QFP wave trains include two main categories: the pulsed energy excitation mechanism associated with magnetic reconnection and the dispersion-evolution mechanism related to the dispersive evolution of impulsively generated broadband perturbations. In addition, the generation of some QFP wave trains might be driven by the leakage of three- and five-minute oscillations from the lower atmosphere. As one of the discoveries of SDO, QFP wave trains provide a new tool for coronal seismology to probe the corona parameters, and they are also useful for diagnosing the generation of QPPs, flare processes including energy release, and particle acceleration. This review aims to summarize the main observational and theoretical results of spatially resolved QFP wave trains in extreme-ultraviolet observations and presents briefly a number of questions that deserve further investigation.

1 Introduction

The solar atmosphere is divided into the photosphere, the chromosphere, the transition region, and the corona based on their distinctly different physical properties. The outermost atmosphere layer of the Sun, the corona, is made of high-temperature magnetized plasma, which extends at a height of about 5 Mm above the photosphere into the heliosphere. In the low corona ($\leq 1.3~\mathrm{{R_{\odot }}}$), the magnetic-field strength ranges from 0.1 – 0.5 Gauss in the quiet Sun and in coronal holes to 10 – 50 Gauss in active-region resolved elements, with typical temperatures (electron densities) of 1 – 2 MK ($10^{9}~\mathrm{cm^{-3}}$) in the quiet Sun and 2 – 6 MK ($10^{11}~\mathrm{cm^{-3}}$) in active regions. These physical parameters determine that the coronal plasma, consisting of electrons and ions, is magnetically confined where charged particles are guided by magnetic-field lines in a helical gyromotion along the magnetic-field lines (e.g. Aschwanden, 2005).

The tenuous and hot corona stores a large amount of energy, mainly in the highly non-potential magnetic field of active regions. Generally, the stored energy can be released impulsively by magnetic reconnection and cause large-scale solar eruptions, such as flares (Shibata and Magara, 2011), filament/jet eruptions (Mackay et al., 2010; Shen, 2021), and coronal mass ejections (CMEs, Chen, 2011). These energetic solar eruptions will inevitably excite various types of magnetohydrodynamic (MHD) waves in the corona (e.g. Nakariakov and Verwichte, 2005; Li et al., 2020a; Van Doorsselaere et al., 2020; Nakariakov and Kolotkov, 2020; Nakariakov et al., 2021; Tian et al., 2021; Wang et al., 2021). In addition, the leakage of photospheric and chromospheric oscillations into the corona can also lead to the generation of coronal waves (e.g. Beckers and Tallant, 1969; De Moortel et al., 2002; Sych et al., 2009; Shen and Liu, 2012b), and mode conversion should occur in the chromosphere where the plasma pressure is approximately equal to the magnetic pressure (e.g. Bogdan et al., 2003). Generally, there are three MHD wave modes, including the Alfvén, slow-, and fast-magnetosonic waves. Alfvén waves are incompressible in the linear regime and can only cause Doppler shifts in observed line measurements, while slow- and fast-magnetosonic waves are compressive and can cause compression and rarefaction of the plasma density. Hence, compressional magnetosonic waves can be directly imaged by detecting intensity variations, since the optically thin emission measure in extreme ultraviolet (EUV) and soft X-rays is directly proportional to the square of electron density, and thus to the observed flux (Aschwanden, 2005). However, one should be cautious with this as the column-depth perturbations should also be taken into account (e.g. Cooper, Nakariakov, and Williams, 2003; Gruszecki, Nakariakov, and Van Doorsselaere, 2012). MHD waves not only carry energy away from their excitation sources and dissipate it into the medium where they propagate, but also reflect the physical properties of the waveguides and the background corona. Therefore, the investigation of MHD waves is very important for understanding the heating of the upper solar atmosphere, the acceleration of the solar wind, and the physical parameters of the solar atmosphere with the method of coronal seismology (e.g. Nakariakov and Verwichte, 2005; De Moortel and Nakariakov, 2012; Nakariakov et al., 2016; Wang et al., 2021). In addition, since MHD waves accompany solar eruptions, they are also important for diagnosing the driving mechanism and energy-release process of solar eruptions.

Rapidly propagating, large-scale disturbances in the solar atmosphere were first observed in the chromosphere with ground-based H$\alpha$ telescopes; they appear as arc-shaped bright fronts and have been named Moreton waves (e.g. Moreton, 1960; Moreton and Ramsey, 1960). Moreton waves propagate rapidly at a speed of 500 – 2000 km s⁻¹, so they can reach a long distance of the order of $10^{5}\mbox{ km}$ and cause the oscillation of remote filaments (e.g. Eto et al., 2002; Shen et al., 2014a,b). Since it is hard to understand the long-distance propagation of Moreton waves in the dense chromosphere (see Chen, 2016), Uchida (1968) interpreted them as the chromospheric response of coronal fast-mode magnetosonic waves or shocks. Uchida’s model not only naturally explained the observed features of Moreton waves, but also predicted the existence of large-scale fast, propagating magnetosonic waves or shocks in the lower corona. The high temperature of the corona causes the coronal plasma to radiate mainly in the EUV and X-ray wavebands. However, due to the strong absorption of this radiation by the Earth’s atmosphere, routine observation of the lower corona can only be made in space. Therefore, the large-scale, fast, propagating disturbances in the corona were not discovered until 1998 by the Extreme-ultraviolet Imaging Telescope (EIT: Delaboudinière et al., 1995) onboard the Solar and Heliospheric Observatory (SOHO), which followed the discovery of chromospheric Moreton waves by about 40 years (Moses et al., 1997; Thompson et al., 1998). The observational characteristics of large-scale corona disturbances are similar to those of chromospheric Moreton waves, such as the arc-shaped or circular diffuse wavefronts centered around the epicenter of the associated flares. Therefore, they were quickly thought to be the long-awaited coronal counterparts of chromospheric Moreton waves, i.e. fast-mode MHD waves or shocks excited by flare-ignited pressure pulses (e.g. Thompson et al., 1999; Wang, 2000; Wu et al., 2001). However, this interpretation has been challenged by many follow-up studies, due to characteristics such as much lower speeds compared to Moreton waves (Klassen et al., 2000) and stationary wavefronts (Delannée and Aulanier, 1999). During the past two decades, observational and theoretical studies have been intensively performed to study the driving mechanism and physical nature of these large-scale coronal disturbances. Thanks to the high spatio-temporal resolution observations taken by the Atmospheric Imaging Assembly (AIA: Lemen et al., 2012) onboard the Solar Dynamic Observatory (SDO), now we have recognized that a large-scale propagating coronal disturbance is typically composed of a fast-mode magnetosonic wave or shock followed by a slower wavelike feature, in which the former is often driven by a CME, corresponding to the coronal counterpart of a chromospheric Moreton wave (e.g. Ma et al., 2011; Shen and Liu, 2012c; Cheng et al., 2012), while the origin and physical nature of the latter is still unclear (Liu and Ofman, 2014; Warmuth, 2015; Chen, 2016; Shen et al., 2020). It should be pointed out that a bewildering multitude of names have been used in the past for large-scale, fast propagating coronal disturbances, such as “EIT waves”, “(large-scale) coronal waves”, “(large-scale) coronal propagating fronts” and “EUV waves”. In this article, we tend to use the term “EUV waves” based on their main observational waveband.

The launch of SDO started a resurgence of interest in the research of coronal MHD waves, due to its unprecedented observational capabilities. AIA onboard SDO observes the Sun uninterruptedly with a full-Sun (1.3 solar diameters) field-of-view, has seven EUV channels covering a wide temperature range from $6\times 10^{4}$ to $2\times 10^{7}$ K, and high signal-to-noise (sensitivity) for two- to three-second exposures. The temporal cadence and spatial resolution of the images taken by AIA are respectively 12 seconds and 1.2^′′ (Lemen et al., 2012). The combination of these excellent observational capabilities makes AIA the best ever instrument for the detection of coronal MHD waves with small intensity amplitudes. Since the launch of SDO in 2010, besides the great achievements in the study of single pulsed global EUV waves, quasi-periodic fast-mode propagating (QFP) wave trains have also been directly imaged (Liu et al., 2010, 2011). Direct imaging observations of QFP wave trains were very scarce, although they had long been theoretically predicted (Roberts, Edwin, and Benz, 1984) and confirmed by numerical studies with similar characteristics (e.g. Murawski and Roberts, 1993b, 1994; Murawski, Aschwanden, and Smith, 1998). This was mainly attributed to the limited observational capabilities of previous solar telescopes, such as their limited spatio-temporal resolution, low sensitivity, narrow temperature coverage, and small fields of view. As one of the discoveries of SDO, QFP wave trains have attracted a lot of attention; they have been identified as fast-mode magnetosonic waves using a three-dimensional MHD simulation (Ofman et al., 2011). So far, there are dozens of QFP wave trains that have been analyzed in detail with multi-wavelength observations, and remarkable theoretical attention has been given to their excitation, propagation, and damping mechanisms. The investigation of QFP wave trains is very important at least in the following aspects: First, as a new phenomenon accompanying solar eruptions, it is worthwhile to study their basic physical properties and the physical connections with solar eruptions. Second, since the QFP wave trains often show some common periods with those of the quasi-periodic pulsations (QPPs) in the accompanying flares, the study of the QFP wave trains can shed light on our understanding of the unresolved generation mechanisms of flare QPPs that appear as quasi-periodic intensity variation patterns with characteristic periods typically ranging from a few seconds to several minutes and can be seen in a wide range of wavelength bands from radio to $\gamma$-ray light curves (e.g. Young et al., 1961; Parks and Winckler, 1969; Kane et al., 1983; Nakariakov et al., 2010; Kupriyanova et al., 2010; Van Doorsselaere et al., 2011; Ning, 2014; Zhang, Li, and Ning, 2016; Milligan et al., 2017; Chen et al., 2019; Yuan et al., 2019; Hayes et al., 2020; Kashapova et al., 2020; Li et al., 2020b,c,d,e, 2021b; Clarke et al., 2021; Lu et al., 2021; Li et al., 2021a; Li, 2022). Third, QFP wave trains provide a new seismological tool to diagnose the physical parameters of the solar corona that are currently difficult or even impossible to measure. In addition, since the damping of fast-mode magnetosonic waves is rapid, they are thought to be important for balancing the typical radiative-loss rates of active regions (e.g. Porter, Klimchuk, and Sturrock, 1994; Liu et al., 2011).

The aim of this review is to summarize the main theoretical and observational results of spatially resolved QFP wave trains in the EUV wavelength band, focusing on recent advances and seismological applications. Liu and Ofman (2014) published a preliminary review on QFP wave trains seven years ago, based on only six published events at that time. The present review mainly focuses on new observational and theoretical advances, but also includes previous theoretical and observational studies. Other types of coronal MHD waves are not covered in this review; interested readers can refer to many excellent review articles published in recent years (e.g. Nakariakov and Verwichte, 2005; Warmuth, 2015; McLaughlin et al., 2018; Li et al., 2020a; Van Doorsselaere et al., 2020; Shen et al., 2020; Wang et al., 2021; Nakariakov and Kolotkov, 2020; Nakariakov et al., 2021; Zimovets et al., 2021).

2 Observational Signature

2.1 Pre-SDO Observation

Space-borne solar telescopes before SDO were not good for the detection of QFP wave trains, mainly because of their lower observational capabilities such as spatio-temporal resolution and sensitivity. Although the TRACE has a superior spatial resolution, but its lower temporal resolution, lower sensitivity, and smaller field-of-view are all not conducive for the detection of QFP wave trains. Therefore, sporadic imaging detections of possible coronal QFP wave trains have been mainly reported during solar total eclipse and coronagraph observations by detecting intensity, velocity, and line-width fluctuations (e.g. Pasachoff and Landman, 1984; Cowsik et al., 1999; Pasachoff et al., 2002; Katsiyannis et al., 2003). In addition, indirect signals from QFP wave trains have also been studied using radio observations. During the total solar eclipse on 1995 October 24, Singh et al. (1997) detected intensity variations with periods of 5 – 56 seconds. Possible evidence of periodic MHD waves has also been reported in other studies using coronagraph observations (e.g. Koutchmy, Zhugzhda, and Locans, 1983; Ofman et al., 1997; Sakurai et al., 2002). Some estimations have shown that these observed oscillations and periodic MHD waves carry enough energy to heat the active-region corona and could contribute significantly to solar wind acceleration in open magnetic-field structures if they are Alfvén or fast-mode magnetosonic waves.

A more reliable imaging detection of QFP wave trains occurred during the total solar eclipse on 11 August 1999 using the Solar Eclipse Corona Imaging System (SECIS: Williams et al., 2001). Detailed analysis results showed that the detected oscillations could be a QFP wave train that travels along active-region loops (Williams et al., 2002), whose period, speed, wavelength, and intensity amplitude were about 6 seconds, 2100 km s⁻¹, 12 Mm, and 5.5%, respectively. In a subsequent article, the authors detected more periods of the wave train in the range of 4 – 7 seconds, indicating the periodicity of the wave train’s nature (Katsiyannis et al., 2003). After the launch of the Transition Region And Coronal Explorer (TRACE: Handy et al., 1999), Verwichte, Nakariakov, and Cooper (2005) probably observed a QFP wave train that propagated along an open magnetic-field structure above a post-flare arcade using the 195 Å wavelength images. The measurements showed that the wave train had a period of 90 – 220 seconds and propagated at a speed of 200 – 700 km s⁻¹ at a height of 90 Mm above the solar surface. In addition, a quasi-periodic, large-scale, global EUV wave train was reported by Patsourakos, Vourlidas, and Kliem (2010), by using 171 Å imaging observations taken by the Extreme Ultraviolet Imager (EUVI: Wuelser et al., 2004) onboard the Solar Terrestrial Relations Observatory (STEREO: Kaiser et al., 2008). In their observation, multiple large-scale coherent EUV wavefronts propagating over the disk limb were seen ahead of the CME bubble, and the authors proposed that the quasi-periodic EUV wave train was driven by fine, expanding, pulse-like, lateral structures in the CME bubble, because the wavefronts appeared as the lateral expansion of the CME bubble slowed and terminated.

2.2 General Properties

Unambiguous signatures of QFP wave trains were directly imaged in EUV images taken by the AIA instrument onboard SDO (Liu et al., 2010, 2011; Shen and Liu, 2012b), and they were identified as fast-mode magnetosonic waves by Ofman et al. (2011) using a three-dimensional MHD model of a bipolar active-region structure. Since the initial discovery, the wave train has attracted a lot of attention, and a mass of observational and numerical studies have been performed to investigate their excitation mechanisms and physical properties. The occurrence of QFP wave trains is rather common and is frequently associated with single pulsed global EUV waves, flares, and CMEs. According to the first 4.5 years observation of SDO, Liu et al. (2016) performed a simple statistical study of QFP wave trains based on the database of global EUV waves cataloged at LMSAL (Nitta et al., 2013, www.lmsal.com/nitta/movies/AIA_Waves), and the authors found that about one third of global EUV waves associated with flares and CMEs are accompanied by QFP wave trains. This occurrence rate is clearly underestimated for all flare activities, because many QFP wave trains are not accompanied by global EUV waves and CMEs. Until now, more than thirty QFP wave trains have been analyzed in detail in the literature. The physical parameters and main associated solar activities of the published QFP wave trains are listed in Table 1. In these events, the QFP wave trains exhibit recurrence characteristics in some active regions along specific trajectories (e.g. Yuan et al., 2013; Zhang et al., 2015; Miao et al., 2020; Zhou et al., 2021a) and refraction and reflection effects during their interaction with coronal structures or at the remote footpoints of closed-loop systems (e.g. Liu et al., 2011; Shen et al., 2018b,a, 2019). In particular, turbulent cascade caused by the counter-propagation of two QFP wave trains along the same closed-loop system was also observed (Ofman and Liu, 2018).

Table 1 Physical parameters of the published QFP wave trains.

Based on Table 1, we can make a simple statistical study of QFP wave trains. It can be seen that QFP wave trains propagate at high speeds of about 305 – 2394 km s⁻¹ and with strong decelerations of 0.1 – 4.1 km s⁻²; they can propagate for a long distance over 500 Mm ($> 0.7~{\mathrm{R_{\odot }}}$) before their disappearance. It should be noted that the values of these parameters could be higher, since they are typically measured in the plane of the sky. Their occurrence is typically accompanied by flares, and they first appear at a distance greater than 100 Mm from the flare epicenter. Such a distance is consistent with the theoretical prediction of the initial periodic phase of an impulsively generated fast magnetosonic wave, during which the intensity amplitude takes time to be amplified for detection (Roberts, Edwin, and Benz, 1983, 1984). In addition, the observability of fast-mode magnetosonic waves is also significantly affected by the observation angle (Cooper, Nakariakov, and Williams, 2003). The amplitude of the QFP wave trains shows first an increasing and then a decreasing trend as they propagate outwards along funnel-like loops, and this might be due to the combined result of the amplification caused by the density stratification and the attenuation resulting from the geometric expansion of the waveguide (Yuan et al., 2013). According to Table 1, QFP wave trains are typically associated with large-scale solar activity including flares, CMEs, and global EUV waves. One can see that the associated flares can either be energetic GOES soft X-ray M-class (e.g. Nisticò, Pascoe, and Nakariakov, 2014; Kumar, Nakariakov, and Cho, 2017), low-energy events such as small brightening patches (Shen et al., 2018b; Miao et al., 2020), and possible reconnection events that can not even cause small GOES flares (Qu, Jiang, and Chen, 2017; Li et al., 2018b). This result might indicate that the occurrence of QFP wave trains does not need too much energy. Alternatively, the presence of special physical conditions might be an important factor instead, because in some active regions recurrent flares at the same location are often associated with recurrent QFP wave trains along the same trajectory.

We checked the correlation between QFP wave trains and CMEs based on the CACTUS (www.bis.sidc.be/cactus/) and CDAW (www.cdaw.gsfc.nasa.gov/CME_list/) databases. Of the 32 published QFP wave trains, 26 are associated with CMEs, which means that the association rate of QFP wave trains with CMEs is about $26/32\approx 80\%$. The average speeds of CMEs accompanied by QFP wave trains are in the range of 174 – 1466 km s⁻¹, which suggests that QFP wave trains are associated with both slow and fast CMEs and no clear preference between the two types of CMEs can be found. For the QFP wave trains propagating along coronal loops, we also checked their correlation with global EUV waves. It was found that 18 of the 27 QFP wave trains were associated with global EUV waves, which corresponds to an association rate of about $18/27\approx 70\%$. Moreover, of the global EUV waves that were accompanied by QFP wave trains, five were not associated with CMEs (Kumar and Manoharan, 2013; Shen et al., 2018b,c; Miao et al., 2020). In other words, these QFP wave trains have been associated with failed solar eruptions without association with CMEs, and the fraction of this kind of QFP wave train is about $5/18 \approx 30\%$. The QFP wave trains not associated with global EUV waves were almost all associated with CMEs. This is probably the reason why the association rate between QFP wave trains and CMEs (80%) is higher than that between global EUV waves (70%). We note that Liu et al. (2016) found that all the QFP wave trains associated with global EUV waves are also associated with flares and CMEs. In addition, based on a simple study of two flare-productive active regions AR 12129 and AR 12205, the authors found an interesting trend of preferential association of QFP wave trains with successful solar eruptions accompanied by CMEs. Here, based on a survey of published events, we would like to point out that not all QFP wave trains are simultaneously accompanied by both global EUV waves and CMEs, and that the association rate with successful solar eruptions is higher than that with failed ones (80% vs. 20%).

Because the occurrence of QFP wave trains is tightly associated with flares, we further checked the temporal relationship between the start time of QFP wave trains and the start and peak times of the associated flares (see Table 1). One can see that the start of QFP wave trains can either be before or after the peak times of the accompanying flares. For those QFP wave trains that appeared before the flare peak times, their start times are usually about 1 – 57 minutes later than the beginning of the accompanying flares, but about 3 – 51 minutes earlier than the flare peak times. For the QFP wave trains that occurred after the peak times of the accompanying flares, their beginning times are about 0 – 17 minutes later than the flares’ peak times. Among the 32 published QFP wave trains, there are 24 (8) cases that occurred before (after) the peak times of the accompanying flares. Therefore, we can draw a preliminary conclusion that most QFP wave trains occur during the impulsive phase of flares (24/32 = 75%). It seems that the energy level of flares is not the key physical condition for determining the start time of a QFP wave train, because for energetic GOES soft X-ray M-class flares, the associated QFP wave trains can occur either in the impulsive (e.g. Kumar and Manoharan, 2013; Nisticò, Pascoe, and Nakariakov, 2014; Kumar, Nakariakov, and Cho, 2017; Zhou et al., 2022) or the decay (e.g. Kumar, Nakariakov, and Cho, 2016; Ofman and Liu, 2018) phases. The start times of the QFP wave trains are probably associated with the durations of the flares. Taking the cases accompanied by M-class flares as an example, one can find that the impulsive phase of the flares with short duration tends to launch QFP wave trains during their impulsive phase (e.g. Kumar and Manoharan, 2013; Nisticò, Pascoe, and Nakariakov, 2014; Kumar, Nakariakov, and Cho, 2017; Zhou et al., 2022), while those with long duration are likely to excite QFP wave trains during their decay phase (e.g. Kumar, Nakariakov, and Cho, 2016; Ofman and Liu, 2018). The lifetimes of the published QFP wave trains are typically in the range of 6 – 65 minutes, which is comparable to that of the impulsive phases of the accompanying flares (3 – 68 minutes). The longest duration among all published QFP wave trains was reported by Ofman and Liu (2018), which reached up to about two hours. In this case, the flare had a long impulsive phase of about 57 minutes, and the QFP wave train started at the beginning of the decay phase of the accompanying flare.

2.3 Classification

A typical QFP wave train is composed of multiple coherent and concentric arc-shaped wavefronts emanating successively from near the epicenter of the accompanying flare and propagating outwards either along or across coronal loops (e.g. Liu et al., 2011; Shen and Liu, 2012b; Liu et al., 2012; Shen et al., 2019). Imaging observational results based on high spatio-temporal resolution AIA data indicate that QFP wave trains might be broken down into two main, distinct categories based on their significantly different physical characteristics: narrow and broad QFP wave trains. The main difference between the two types of QFP wave trains include the physical parameters of the observed waveband, propagation direction, angular width, intensity, amplitude, and energy flux (see Table 1). Narrow QFP wave trains are typically observed in the AIA 171 Å channel (occasionally appearing in the AIA 193 Å and 211 Å channels, see Liu et al., 2010 and Shen et al., 2013a); they propagate along the apparent direction of the magnetic-field within a relatively small angular extent of about 10 – 80 degrees and typically result in intensity fluctuations with a small amplitude of about 1% – 8% relative to the background corona (see the top row of Figure 1). The energy flux carried by narrow QFP wave trains is basically in the range of $0.1-4.0 \times 10^{5}~{\mbox{erg}\,\mbox{cm}}^{-2}\,{\mbox{s}}^{-1}$ (e.g. Liu et al., 2011; Shen and Liu, 2012b; Shen, Song, and Liu, 2018). Broad QFP wave trains are frequently observed in all AIA EUV channels and can cause intensity fluctuations with a large amplitude of about 10 – 35% relative to the background corona (see the bottom row of Figure 1). They propagate across magnetic-field lines in the quiet-Sun with a large angular extent of about 90 – 360 degrees and carry an energy flux of about 10 – 19 $\times 10^{5}~{\mbox{erg}\,\mbox{cm}}^{-2}\,{\mbox{s}}^{-1}$ (Liu et al., 2012; Shen et al., 2019; Zhou et al., 2021b, 2022). In comparison, the two types of QFP wave trains have different, distinct propagation preferences with respect to the magnetic-field orientation, and the temperature-coverage range of broad QFP wave trains is significantly wider than narrow QFP wave trains. In addition, all physical parameters, including angular width, intensity amplitude, and energy flux of broad QFP wave trains are evidently greater than those of narrow QFP wave trains.

Figure 1

Examples of the two types of QFP wave trains. The top row shows the narrow QFP wave train on 20 May 2011 using the AIA 171 Å running-difference images, which occurred close to the east limb of the solar disk and was analyzed in detail by Shen and Liu (2012b) and Yuan et al. (2013). The bottom row shows the broad QFP wave train on 24 April 2012 using the AIA 193 Å running-ratio images, which occurred on the east limb of the solar disk and propagated along the solar surface (see Shen et al., 2019, for details). The wave trains manifest themselves as a chain of arc-shaped bright fronts propagating outward from the accompanying flare epicenter.

Besides the above differences, the two types of QFP wave trains also show some similarities such as their propagation speed, deceleration, period, and wavelength (see Table 1). Specifically, for narrow (broad) QFP wave trains, the physical parameters of propagation speed, deceleration, period, and wavelength are in the ranges of 305 – 2394 (370 – 1416) km s⁻¹, 0.1 – 5.8 (0.1 – 4.1) km s⁻², 25 – 500 (36 – 240) seconds and 24 – 429 (58 – 170) Mm, respectively. In some events, broad QFP wave trains can be captured by coronal loops and become narrow QFP wave trains, which might mean the transformation of the former into the latter. For example, Shen et al. (2019) reported a broad QFP wave train propagating across the solar surface, whose eastern portion was trapped in a closed-loop system and propagating at a speed relatively faster than the on-disk component. In two other events reported by Shen et al. (2018c) and Miao et al. (2019), the authors observed the transformation of single pulsed global EUV waves into narrow QFP wave trains along coronal loops. Successful capture of global EUV waves by coronal loops was also reported by Zhou et al. (2021b), where a trapped EUV wave showed an interesting process where it first slowed down but then accelerated owing to variations in the physical parameters along the loop structure. In such a case, the global EUV waves are captured by coronal loops during their interaction, and the formation of the narrow QFP wave trains is probably due to the dispersive evolution of the initial disturbances caused by the global EUV waves. In a one-dimensional numerical simulation performed by Yuan et al. (2015), the authors showed that weak, fast wave trains can be formed by dispersion due to a series of partial reflections and transmissions of single pulsed EUV wavefronts during their interaction with loop-like coronal structures (Yuan, Li, and Walsh, 2016). As pointed out by Yuan et al. (2015), successful capture of an EUV wave may require the width of the coronal-loop system to be approximately half the initial width of the EUV wavefront. We note that the fast-mode global EUV waves were observed to convert into slow-mode magnetosonic waves during their interaction with coronal loops (Chandra et al., 2016; Zong and Dai, 2017; Chandra et al., 2018). Chen et al. (2016) numerically studied this phenomenon and found that the conversion occurs near the plasma $\beta \approx 1$ layer in front of the magnetic quasi-separatrix layer; the authors argued that such a mode-conversion process can account for the so-called stationary wavefronts formed when global EUV waves pass through quasi-separatrix layers (Delannée and Aulanier, 1999).

2.4 Kinematics

Kinematics is the most fundamental property of any propagating disturbance, generally characterized by speed and acceleration. If the propagating disturbance is a MHD wave, it should exhibit wave phenomena such as reflection, refraction, and diffraction effects during its interaction with coronal structures with a steep speed gradient (e.g. Shen and Liu, 2012a; Shen et al., 2013b; Zhou et al., 2021c). Therefore, one can simply start from the speed and propagation behavior to determine the physical nature of a propagating disturbance in the solar atmosphere. For example, if a propagating intensity disturbance in the solar atmosphere exhibits wave phenomena and propagates at slow (fast) magnetosonic wave speed, one can simply say that the disturbance is probably a slow (fast) magnetosonic wave (e.g. Shen and Liu, 2012c).

For QFP wave trains, there are two frequently used methods to measure their speed. The most popular method is to construct time–distance diagrams along straight paths or sectors across the wavefronts by composing the one-dimensional intensity profiles at different times along a specific path using running- or base-difference time-sequence images (see Figure 2a). In a time–distance diagram, the wavefronts appear as enhanced bright ridges, and the average speed can be obtained by fitting these ridges with a linear function, while the acceleration can be estimated by fitting the ridges with a quadratic function. The other method is to construct a $k\mbox{--}\omega$ diagram using the method of Fourier analysis of a three-dimensional data cube in $(x, y, t)$ coordinates, where the field-of-view should cover the propagation region of the QFP wave train (see Figure 2b). The details of this method can be found in many articles (e.g. DeForest, 2004; Liu et al., 2011; Shen and Liu, 2012b). In the $k\mbox{--}\omega$ diagram, the wave signature is represented by a steep, narrow ridge that describes the dispersion relation of the QFP wave train, and the slope of the ridge gives the average phase [$v_{ \mathrm{ph}}=\nu /k$] and group [$v_{\mathrm{gr}}={\mathrm{d}}\nu /{\mathrm{d}}k$] velocities (e.g. Liu et al., 2011; Shen and Liu, 2012b). The ridge in the $k\mbox{--}\omega$ diagram also reveals the frequency distribution in the QFP wave train, which appears as discrete power peaks representing the dominant frequencies of the wave train (e.g. Shen, Song, and Liu, 2018; Shen et al., 2018a). For a specific dominant frequency, one can obtain the Fourier-filtered images with a narrow Gaussian function centered at the dominant frequency (see Figure 2 c).

Figure 2

Kinematic analysis of the narrow QFP wave train on 30 May 2011. Panel a is the time–distance diagram along the propagation direction of the wave train, in which each bright intensity ridge represents a wavefront (adapted from Shen and Liu, 2012b). Panel b is the $k\mbox{--}\omega$ map, in which the red curve shows the power peaks along the straight ridge. Panel c is a Fourier-filtered image around the dominant frequency of 15.6 Hz (adapted from Shen and Liu, 2012b).

As shown in Table 1 for the published events, the projected speeds of the narrow and broad QFP wave trains are in the range of 305 – 2394 km s⁻¹ and 370 – 1416 km s⁻¹, while their decelerations are in the range of 0.1 – 5.8 km s⁻² and 0.1 – 4.1 km s⁻², respectively. These results indicate that the deceleration of the QFP wave trains is quite strong, and it seems that the faster waves are accompanied by stronger decelerations, consistent with the statistical result of the global EUV waves (Long et al., 2017a). The speed of the QFP wave trains do not show any preferential correlation with neither successful nor failed solar eruptions. Specifically, the speeds of the six QFP wave trains that were not associated with CMEs (i.e. failed eruptions) are in the range of 322 – 1670 km s⁻¹, while those of the other events that were accompanied by CMEs (successful eruptions) are in a similar range of 305 – 2394 km s⁻¹. Even for events that are associated with fast CMEs whose average speeds are greater than 1000 km s⁻¹, the speeds of the accompanying QFP wave trains can either be slow (668 km s⁻¹; Zhou et al., 2022) or fast (1860 km s⁻¹; Ofman and Liu, 2018). The speed of QFP wave trains does not show any preferential correlation with the energy class of the accompanying flares. For both low- and high-energy flares, the speeds of the accompanying QFP wave trains are all in the same range from several hundred to over 2000 km s⁻¹. These results might imply that the speed of the QFP wave trains is mainly determined by the physical property of the medium in which they propagate, such as the plasma density and the magnetic strength defined by the dispersion relation of fast magnetosonic waves. In addition, these results also suggest that the QFP wave trains should be freely propagating linear or slightly nonlinear fast magnetosonic waves, as suggested by the small Mach number (1.01) of a narrow QFP wave train (Zhou et al., 2021b).

2.5 Periodicity and Origin

The periodicity of the QFP wave trains contains important physical information about the eruption source regions and the medium in which they propagate. Investigating the generation and characteristics of periodicity in QFP wave trains can help us probe the eruption mechanism of solar eruptions and the physical properties of the supporting medium. Generally, the periods of a QFP wave train can be isolated by using the methods of Fourier analysis and wavelet analysis (Torrence and Compo, 1998, www.atoc.colorado.edu/research/wavelets). Sometimes one can also directly measure periods from time–distance diagrams. Based on the published events (see Table 1), the periods of the narrow QFP wave trains are in a wide range of 25 – 550 seconds, while those of the broad QFP wave trains are in the range of 36 – 240 seconds. Because the temporal cadence of the EUV channels of AIA is 12 seconds, we are not able to detect periods of less than 24 seconds (Liu and Ofman, 2014). However, this insufficiency can be compensated for by high temporal resolution radio observations. For example, some spatially unresolved events observed in radio wavelengths are similar to QFP wave trains with short periods of seconds (e.g. Karlický, Mészárosová, and Jelínek, 2013; Kolotkov, Nakariakov, and Kontar, 2018) and even subseconds (e.g. Mészárosová, Karlický, and Rybák, 2011; Yu and Chen, 2019). In addition, high temporal resolution data taken during solar eclipses are also important for detecting the short periods of QFP wave trains (e.g. Williams et al., 2002; Katsiyannis et al., 2003; Samanta et al., 2016).

Observational studies have shown that a QFP wave train often contains multiple periods. It has been confirmed in many events that some prominent periods of QFP wave trains are temporally correlated with QPPs in the accompanying flares, but others are not (e.g. Liu et al., 2011; Shen and Liu, 2012b). In particular cases, the periods of a QFP wave train are all associated with the QPPs in the accompanying flare (e.g. Shen et al., 2013a, 2018a; Zhou et al., 2022). However, there are still many cases whose periods are completely unassociated with the accompanying flares (e.g. Shen, Song, and Liu, 2018; Shen et al., 2019). These results suggest that the periodicity of QFP wave trains may be diverse and that some of them are probably associated with flare QPPs.

Generally, a flare QPP is loosely defined as the periodic intensity variations in flare light curves seen in a wide wavelength range from radio to $\gamma$-rays, with characteristic periods ranging from a fraction of a second to several tens of minutes (Nakariakov et al., 2019). In addition, since for a light curve obtained by observing the Sun as a star, i.e. without spatial resolution, it is hard to say what kind of physical process is responsible for the appearance of QPPs in the light curve. Because of these reasons, so far a handful of possible mechanisms have been proposed to account for the generation of flare QPPs (see Nakariakov and Melnikov, 2009; Van Doorsselaere, Kupriyanova, and Yuan, 2016; McLaughlin et al., 2018; Nakariakov et al., 2019; Kupriyanova et al., 2020; Zimovets et al., 2021, and references therein). As pointed out by Nakariakov and Melnikov (2009), the possible mechanisms for QPPs can be divided into two categories: pulsed energy release and MHD oscillations, and both can be relevant for the generation of QFP wave trains (Liu et al., 2011; Shen and Liu, 2012b; Shen et al., 2013a, 2018a). Pulsed energy release can take place in different situations and forms, but is commonly associated with various nonlinear processes in magnetic reconnection, such as the dynamic evolution of plasmoids (e.g. Kliem, Karlický, and Benz, 2000; Ni et al., 2015; Liu, Chen, and Petrosian, 2013; Li et al., 2018b; Cheng et al., 2018; Miao et al., 2021), oscillatory reconnection (e.g. Craig and McClymont, 1991; McLaughlin et al., 2009; McLaughlin, Thurgood, and MacTaggart, 2012; McLaughlin et al., 2012; Thurgood, Pontin, and McLaughlin, 2017; Hong et al., 2019; Xue et al., 2019; Thurgood, Pontin, and McLaughlin, 2019) and modulation resulting from external quasi-periodic disturbances (e.g. Nakariakov et al., 2006; Chen and Priest, 2006; Sych et al., 2009; Shen and Liu, 2012b; Jess et al., 2012; Jelínek and Karlický, 2019). MHD oscillations are relevant to the inherent physical properties of the wave hosts and the surrounding medium, which can modulate flare energy release (or plasma emission) and therefore result in QPPs and QFP wave trains whose periodicities are prescribed either by certain resonances or by a dispersive narrowing of the initially broad spectra (Roberts, Edwin, and Benz, 1983; Foullon et al., 2005; Nakariakov and Melnikov, 2009).

Observationally, the periods of QFP wave trains are comparable to the typical period of flare QPPs; both are in the range from a few seconds to several minutes. In addition, while QFP wave trains are mainly observed in flare impulsive and decay phases, QPPs can appear in all flare stages from the pre-flare to the decay phase. In some cases, the two phenomena can occur simultaneously and with similar periods, suggesting their intimate physical connection. However, the detailed physical relationship between the two phenomena is yet to be resolved. In our view, the QFP wave trains and the simultaneous flare QPPs might represent different aspects of a common physical process, such as pulsed energy release or MHD oscillations in flares. In terms of their origin, QFP wave trains could be viewed as a subclass of QPPs in general, since some proposed physical processes for the generation of QPPs might not cause simultaneous QFP wave trains (for example, the oscillation of coronal loops). In addition, in some studies (e.g. Mészárosová et al., 2009b; Kolotkov, Nakariakov, and Kontar, 2018), QPPs observed in radio wavelengths were thought to be produced by the modulation of the local plasma density by QFP wave trains. In this case, QPPs are actually the result or indirect signal of QFP wave trains. Because of these correlations, currently the proposed generation mechanisms for QFP wave trains are mainly analogous to those for flare QPPs (see Section 3 for details), since the latter have been investigated for more than half a century after their discovery (see Nakariakov and Melnikov, 2009; Van Doorsselaere, Kupriyanova, and Yuan, 2016; McLaughlin et al., 2018; Nakariakov et al., 2019; Kupriyanova et al., 2020; Zimovets et al., 2021, and references therein).

2.6 Amplitude and Intensity Profile

The physical nature of the QFP wave trains is also characterized by the peculiar variation pattern of the wavefront intensity profiles. For example, the intensity profiles of global EUV and Moreton waves often show simultaneously increasing width and decreasing amplitude during the initial propagation stage, consistent with the nature of nonlinear fast-mode or shock waves. For freely propagating linear or weakly nonlinear fast-mode magnetosonic waves, the integral over the entire wave pulse should be constant, as reported in several studies of global EUV waves (see Warmuth, 2015, and references therein). Commonly, an intensity profile is defined as the intensity distribution along a specific path perpendicular to the wavefronts, which is a function of distance at a particular time. The intensity profile is often expressed as a relative intensity change (i.e. $I/I_{0}$) or 100% change (i.e. $(I-I_{0})/I_{0}$) from the pre-event background. Here $I$ and $I_{0}$ are the emission intensities at a certain time and the pre-event background emission intensity, respectively.

In practice, one often first generates a time–distance diagram and then obtains an intensity profile at a specific distance from the excitation source of a QFP wave train. Observational results indicate that the peak intensity amplitudes of narrow and broad QFP wave trains are very different. Taking the published events as an example (Table 1), the values of peak intensity amplitudes for narrow and broad QFP wave trains are in the range of 1% – 8% and 10% – 35%, respectively. It is noted that both the narrow and broad QFP wave trains retain their variation ranges in peak intensity amplitudes at stable levels for different events, and they do not show any notable physical connection with other parameters and the accompanying activities such as flares and CMEs. This may suggest that the intensity amplitudes of QFP wave trains are basically determined by the physical parameters of the supporting medium. Since narrow QFP wave trains propagate along coronal loops in which the magnetic-field strength and plasma density are typically higher than the quiet-Sun region where broad QFP wave trains propagate, we propose that the peak intensity amplitudes of QFP wave trains are probably affected by physical parameters, such as magnetic-field strength and plasma density of the medium, and the propagation direction of QFP wave trains with respect to the magnetic-field direction. The very different intensity amplitudes of the two types of QFP wave trains are probably mainly caused by their different propagation media. As found by Pascoe, Goddard, and Nakariakov (2017), geometrical waveguide dispersion suppresses the nonlinear steepening of trapped narrow QFP wave trains, while broad QFP wave trains propagating in the quiet-Sun region do not experience dispersion and can steepen significantly into shocks.

For narrow QFP wave trains, Liu et al. (2011) and Shen and Liu (2012b) checked the intensity profiles in the propagation direction at several consecutive times and found that the spatial profiles can be fitted with a sinusoidal function from which physical information about phase speed, period, wavelength, and amplitude can be obtained. Moreover, a variation trend of weak broadening and decreasing amplitude of the wavefronts can be identified during the propagation. In addition, the authors also checked the temporal variation of the intensity profiles, which are then used for analysis with the aid of the wavelet-analysis technique. Shen et al. (2018b) reported the successive interactions of a narrow QFP wave train with two strong magnetic regions; they found that although the propagation direction changes significantly after the interactions, the peak intensity amplitudes of the wave train remain at the same level. Yuan et al. (2013) traced the detailed temporal evolution of the intensity amplitude of the narrow QFP wave train on 30 May 2011; they found that the intensity amplitude first underwent an increasing and then a decreasing process (see also Shen et al. (2018a) and the right panel of Figure 3). The authors further checked the evolution of a specific wavefront and found that the wavefront extended gradually along the waveguide, and the transverse distribution of the intensity profile perpendicular to the wave vector exhibited a Gaussian profile (see the left panels of Figure 3). For broad QFP wave trains, investigation of the variations in intensity profiles are scarce. Shen et al. (2019) found the obvious broadening of the width and decreasing amplitude of the intensity profiles during the propagation of the broad QFP wave train on 24 April 2012 (see Figure 4), and the initial steep intensity profiles weakened quickly with time (Kumar, Nakariakov, and Cho, 2017; Zhou et al., 2022). In addition, the Alfvén Mach number of the broad QFP wave train was estimated to be 1.39 by Shen et al. (2019), indicating that the wave train was shocked significantly. These characteristics suggest that broad QFP wave trains are more similar to global EUV waves that are strong shocks during the initial stage, but then quickly decay into linear or weakly non-linear, fast-mode magnetosonic waves (e.g. Shen and Liu, 2012c).

Figure 3

Intensity profile and amplitude of the narrow QFP wave train on 30 May 2011 (adapted from Yuan et al., 2013). The upper-left panel shows the temporal evolution of a specific wavefront at different times from the bottom up, while the left-lower panel is the intensity profile of the wavefront at the time of 72 seconds. The red curves in the left panels are the corresponding Gaussian fitting curves of the intensity profiles. Right panel shows the wave amplitudes of the three sub-QFP wave trains plotted as a function of distance from the flare epicenter. The red diamonds, green triangles, and blue squares denote the parameters of Train-1, -2, and -3, respectively.

Figure 4

Intensity profile of the broad QFP wave train along the solar surface on 24 April 2012 (adapted from Shen et al., 2019). The left panel is a time–distance diagram made from AIA 193 Å running-ratio images, in which the black dashed box shows the region where the intensity profiles are checked. The right panel shows the percentage intensity profiles of the wave train at different times based on the AIA 193 Å images, in which the red arrows indicate the first three wavefronts of the wave train.

2.7 Thermal Characteristic

AIA takes EUV images in seven channels covering a wide temperature range from 0.05 MK in the transition region to 20 MK in the flaring corona (Lemen et al., 2012). The EUV observing channels of AIA and their peak response temperatures are 304 Å (He ii; $T\approx 0.05$ MK), 171 Å (Fe ix; $T\approx 0.6$ MK), 193 Å (Fe xii; $T\approx 1.6$ MK; Fe xxiv; $T\approx 20$ MK), 211 Å (Fe xiv; $T\approx 2.0$ MK), 335 Å (Fe xvi; $T\approx 2.5$ MK), 94 Å (Fe xviii; $T\approx 6.3$ MK), 131 Å (Fe viii; $T\approx 0.4$ MK; Fe xxi; $T\approx 10$ MK). Such a wide temperature coverage provides an unprecedented opportunity to diagnose the thermal properties of QFP wave trains. Observations showed that narrow QFP wave trains are best seen in the AIA 171 Å channel (occasionally in the AIA 193 Å and 211 Å channels), indicating narrow temperature range. In contrast, broad QFP wave trains cover a wider temperature range, which can be observed in all of the AIA EUV channels (best seen in 193 Å and 211 Å channels) as global EUV waves.

According to the explanation given by Liu et al. (2016), the narrow temperature of narrow QFP wave trains is possibly due to two reasons: The first is owing to the physical property in the waveguide structures and the low intensity amplitude of narrow QFP wave trains. It is probably that the temperature of the wave-hosting plasma is close to the AIA 171 Å channel’s peak-response temperature. In addition, due to the low intensity amplitude of narrow QFP wave trains, it is hard for them to cause large temperature departures, unlike the large intensity amplitude caused by broad QFP wave trains. These possible conditions might account for the absence of narrow QFP wave trains in other AIA EUV channels. The second is possibly due to the sensitivity of the detectors used for the different AIA channels. Since the AIA 171 Å channel has a much higher photon-response efficiency than any other channels by at least one order of magnitude, it is particularly sensitive to small intensity variations. The two reasons might work either separately or together. However, so far the exact reasons for the narrow temperature dependence of the narrow QFP wave trains remain unclear.

In the broad QFP wave train on 8 September 2010, Liu et al. (2012) observed the darkening at 171 Å and brightening at 193 Å and 211 Å of the wavefronts, which was followed by a recovery in the opposite direction (see Figure 5). This process indicates the initial heating and subsequent cooling of the coronal plasma and can be interpreted as adiabatic heating due to compression followed by cooling with subsequent expansion/rarefaction driven by a restoring pressure-gradient force. A similar signature was previously reported in global EUV waves (see Liu and Ofman, 2014, and references therein). Such adiabatic compression caused by EUV waves can cause a considerable heating of the coronal plasma. For example, Schrijver et al. (2011) estimated that a mild adiabatic compression can result in a maximum density increase of about $10\%$ and a temperature increase of about $7\%$.

Figure 5

Base-ratio temporal profiles of emission intensity from azimuthal cuts at selected positions shown by the plus signs in Figure 4 in Liu et al. (2012). The general trend of darkening at 171 Å and brightening at 193 and 211 Å indicates heating in the EUV wave pulse ahead of the CME.

2.8 Energy Flux and Coronal Heating

QFP wave trains carry energy away from their excitation sources, and the energy is dissipated into the corona in which the waves propagate. Therefore, QFP wave trains can inevitably result in the heating of the corona. Earlier observations have suggested that short-period oscillations might make a significant contribution to the energy input into the coronal loops (e.g. Williams et al., 2001). The SDO/AIA observational results show that the energy flux carried by narrow and broad QFP wave trains is in the range of about (0.1 – 4.0)$\times 10^{5}~{\mbox{erg}\,\mbox{cm}}^{-2}\,{\mbox{s}}^{-1}$ and (1 – 2)$\times 10^{6}~{\mbox{erg}\,\mbox{cm}}^{-2}\,{\mbox{s}}^{-1}$, respectively. Obviously, such an energy flux level is sufficient to sustain the temperature of active-region coronal loops, because the typical energy-flux density requirement for heating coronal loops is estimated to be about $10^{5}~{\mbox{erg}\,\mbox{cm}}^{-2}\,{\mbox{s}}^{-1}$ (Withbroe and Noyes, 1977; Aschwanden, 2005). It is noted that the energy-flux carried by broad QFP wave trains is at least one order of magnitude higher than that of narrow QFP wave trains. While narrow QFP wave trains are mainly attributed to plasma heating of active-region coronal loops, broad QFP wave trains are more efficient for the plasma heating in the quiet-Sun regions.

The energy-flux carried by a QFP wave train can be estimated from the kinetic energy of the perturbed plasma that propagates at the group speed. The energy of the perturbed plasma is

$$ E = (\frac{1}{2} \rho v_{\mathrm{1}}^{2}) v_{\mathrm{gr}}, $$

(1)

where $v_{\mathrm{1}}$ is the disturbance amplitude of the locally perturbed plasma (Aschwanden, 2004), and $v_{\mathrm{gr}}$ is the group speed of the wave. Generally, for a rough estimation, one can use the measurable phase speed [$v_{\mathrm{ph}}$] of a dispersive wave train to replace the group speed [$v_{\mathrm{gr}}$] in Equation 1. For non-dispersive wave trains, their phase speeds are equal to the values of the group speeds. In addition, in the optically thin corona, the emission intensity $I$ is directly proportional to the square of the plasma density $\rho$, i.e. $I \propto \rho ^{2}$. Therefore, the density modulation of the background density ${\mathrm{d \rho }}/{\rho }$ can be written as ${\mathrm{d}I}/{2I}$. So, the energy flux of the perturbed plasma can be written as

$$ E \geq \frac{1}{8} \rho v_{\mathrm{ph}}^{3} (\frac{\mathrm{d}I}{I})^{2}, $$

(2)

if we assume that ${v_{\mathrm{1}}}/{v_{\mathrm{ph}}}$ is equal to or greater than ${\mathrm{d \rho }}/{\rho }$. Obviously, the energy flux estimated by this equation is determined by the coronal electron density $\rho$, perturbation amplitude of the emission intensity $\mathrm{d}I$, and the phase speed $v_{\mathrm{ph}}$ of the QFP wave trains. Since the intensity amplitude of narrow QFP wave trains are all in the range of 1% – 8%, the corresponding energy fluxes estimated based on this equation are all in the order of $\approx 10^{5}~{\mbox{erg}\,\mbox{cm}}^{-2}\,{\mbox{s}}^{-1}$. In contrast, the energy fluxes of broad QFP wave trains are about one order of magnitude higher than narrow QFP wave trains, which mainly result from their higher perturbation amplitude of the emission intensity (10% – 35%). Here, we would like to point out that the estimated energy fluxes of QFP wave trains are underestimated since the energy flux decreases quickly by orders of magnitude with height due to the spreading of the waves over a large area as a result of magnetic-field divergence (Ofman et al., 2011). However, in practice, many estimations are based on the measurement of the intensity variation far from their origin.

Observations showed that the occurrence of QFP wave trains are quite common in the corona, although many of them cannot yet be detected with our current telescopes (Liu et al., 2016). Besides the association with relatively strong flares (GOES soft X-ray C- and M-classes), they can also be excited by many low-energy small flares (GOES soft X-ray B-class, Liu et al., 2010; Shen, Song, and Liu, 2018), small coronal brightenings (Shen et al., 2018b; Miao et al., 2020), and some signatures of possible magnetic-reconnection events that cannot even be recognized as flares in the GOES soft X-ray light curves (e.g. Qu, Jiang, and Chen, 2017; Li et al., 2018b). In addition, due to the large-scale propagation nature of QFP wave trains, they are expected to further trigger many subsequent nano-flares (Parker, 1988) or magnetic-reconnection events in the corona with the complicated magnetic field, and these small flaring activities can probably further cause mini-QFP wave trains. The energy dissipation of these undetected small-scale energetic events can further contribute more heating to the coronal plasma. Therefore, the contribution of QFP wave trains to the heating of the coronal plasma might be more significant than we currently think (Van Doorsselaere et al., 2020).

2.9 Interaction with Coronal Structure

The highly structured corona is an inhomogeneous and anisotropic medium full of hot magnetized plasma, which is filled with strong magnetic structures such as active regions, coronal holes, and filaments. The Alfvén and fast-mode magnetosonic speeds at the boundary of these structures exhibit a strong speed gradient owing to the sudden changes of the magnetic-field strength and plasma density. In addition, the plasma density falls off faster than the decrease of the magnetic-field strength in the low corona. Therefore, the Alfvén and fast-mode magnetosonic speeds in the low corona increase with height in the quiet-Sun regions (Mann et al., 1999). The large-scale propagation of QFP wave trains will inevitably interact with regions with strong gradients of Alfvén and fast-mode magnetosonic speeds, and they will exhibit wave phenomena such as reflection, refraction, and transmission. In addition, QFP wave trains can also excite oscillations of filaments and coronal loops during their propagation. Evidence of reflection, refraction and transmission effects of single pulsed global EUV waves has been reported in many studies; interested readers can refer to several recent reviews (Liu and Ofman, 2014; Warmuth, 2015; Long et al., 2017b; Shen et al., 2020).

Narrow QFP wave trains propagating along open, funnel-like coronal loops do not interact with coronal structures. However, their propagation speed is affected by the increase of the characteristic fast-mode speed with height. In some cases, QFP wave trains propagate along closed coronal loops, which are reflected at the remote end of the loop system. Liu et al. (2011) observed bidirectional propagation of QFP wave trains in a closed-loop system that connects the conjugate flare ribbons, but the authors were unclear whether the bidirectional wave trains were generated independently or the same wave train was reflected repeatedly between the conjugate loop footpoints. Ofman and Liu (2018) first reported the detection of counter-propagating QFP wave trains along the same closed trans-equatorial coronal loop system, which were associated with two flares successively occurred in two neighboring active regions on 22 May 2013. The counter-propagating QFP wave trains propagated at large speeds of the order of > 1000 km s⁻¹ and interacted in the middle section of the loop system, which further excited trapped kink-mode and slow-mode MHD waves in the coronal loops (see the top and the middle rows of Figure 6). The authors have further performed a three-dimensional MHD simulation for this event, and the results agree well with the observations (see the bottom row of Figure 6). The unambiguous reflection of a QFP wave train at the far end of the closed guiding coronal loop was observed by Shen et al. (2019); in their case the incoming and reflected waves propagate at a similar speed of about 900 km s⁻¹, and the guiding closed-loop system exhibited obvious kink oscillations. In addition, single-pulse global EUV waves trapped in closed-loops are also observed in some events, which can also trigger the transverse kink oscillation of the guiding loops (Kumar and Innes, 2015; Zhou et al., 2021b).

Figure 6

Interaction between counter-propagating narrow QFP wave trains in the trans-equatorial coronal loop system on 22 May 2013 (adapted from Ofman and Liu, 2018). Panel a shows the outward-propagating QFP wave train of the primary flare, while Panel b shows the interaction between the two counter-propagating QFP wave trains of the primary flare on the left and the second flare on the right. The green arrows in Panel a indicate the outward-propagating wavefronts, the two white arrows in Panel b indicate the locations of the two flares, and the two green ones indicate the interaction sites. The bottom row shows the corresponding numerical simulation results of the event, in which the left and the right panels represent the density and velocity perturbations in the $x$–$z$ plane at $y=0$, respectively. The magnetic-field lines and the velocity direction (right panel only) are overlaid as white curves and arrows, respectively.

When multiple active regions exist simultaneously on the Sun, they are often connected by interconnected coronal loops. Shen et al. (2018b) reported a special narrow QFP wave train propagating along such closed, interconnected coronal loops, which passed through two different magnetic polarities and its propagation direction also changed significantly after each interaction with the magnetic polarities (see Figure 7). It was noted that the propagation speeds before and after each of the interactions showed little difference. This interesting phenomenon was interpreted as refraction of the QFP wave train due to the strong speed gradients within the strong magnetic regions on the path. The refraction of the narrow QFP wave trains was also seen by Shen et al. (2018a), the northern part of the wavefronts became broader and more bent during their passing through a strong magnetic-field region. It also caused the different propagation speeds of the northern (1485 km s⁻¹) and southern (884 km s⁻¹) parts of the wave train.

Figure 7

AIA 171 Å running-ratio images show the interaction of the narrow QFP wave train on 14 February 2011 with remote strong magnetic polarities (adapted from Shen et al., 2018b). The red curves marks the forefront of the wavefronts, and the white arrows indicate the propagation direction. The green symbols P1, N1, P2, N2, and P3 mark the regions with strong magnetic fields, where the letters P and N represent positive and negative magnetic polarities, respectively.

For large-scale, broad QFP wave trains propagating across the solar surface, they are more liable to interact with remote coronal structures. In the event studied by Shen et al. (2019), the on-disk propagating wavefronts interacted with a remote active region and showed a significant deformation around the middle section of the wavefronts, similar to what had been observed for global EUV waves (Li et al., 2012; Shen et al., 2013b; Yang et al., 2013). This phenomenon was interpreted as the transmission of a fast-mode magnetosonic wave through an active region in which the central characteristic fast-mode magnetosonic wave speed is faster than that at the rim. It was noted that the QFP wave train also resulted in the transverse oscillation of a remote filament and a closed coronal loop. Liu et al. (2012) studied a limb event in which broad QFP wave trains were observed in both south and north directions over the limb. The propagating wavefronts caused an uninterrupted chain sequence of deflections and/or transverse oscillations of remote coronal structures, including a flux-rope coronal cavity and its embedded filament with delayed onsets consistent with wave travel time at an elevated speed (by ≈ 50%) within it, which indicates that the wavefronts penetrated through a topological separatrix surface into the cavity. The sequential response of remote coronal structures to the arrival of large-scale broad QFP wave trains reminds us that global EUV waves can also cause a chain of oscillations of separate filaments (Shen et al., 2014a) and even simultaneous transverse and longitudinal oscillations of different filaments (Shen et al., 2014b; Pant et al., 2016). Recently, Zhou et al. (2022) observed the interaction of an on-disk broad QFP wave train with a remote low-latitude coronal hole. During the successive transmission of the wavefronts through the coronal hole, intriguing refraction and reflection effects of the wave were identified around the coronal hole’s west boundary. Since the coronal hole had a C-shape, the northern and southern arms of the refracted wavefronts propagated towards each other and finally merged into one on the eastern side of the coronal hole. This phenomenon was interpreted as interference of broad QFP wave trains, where the coronal hole acts as a concave lens. As mentioned above, the observations and wave effects provide compelling evidence for the interpretation of the QFP wave trains as fast-mode magnetosonic waves.

2.10 Possible Manifestations of QFP Wave Trains in Radio

In addition to direct-imaging observations in the EUV wavelength band, quasi-periodic patterns or fine structures in the radio dynamic spectrum are generally thought to be the possible indirect signals from spatially resolved QFP wave trains in the EUV. In principle, quasi-periodic fine structures in the radio dynamic spectrum can be produced by means of coherent modulation of the local coronal plasma density (Chernov, 2010), and this periodic modulation can result from the propagation of QFP wave trains in the low corona (Karlický, Mészárosová, and Jelínek, 2013; Karlický, 2013; Sharykin, Kontar, and Kuznetsov, 2018; Kolotkov, Nakariakov, and Kontar, 2018). Roberts, Edwin, and Benz (1983) developed a theory for interpreting the observed short period (a second or sub-second) pulsations in Type-IV radio bursts by means of studying the development and propagation of an impulsively generated QFP wave train within a dense coronal loop, and the authors proved that an impulsive disturbance (such as a flare) can naturally give rise to quasi-periodic pulsations owing to the dispersive evolution of the disturbance (Roberts, Edwin, and Benz, 1984). From then on, this theory has been applied to explain various quasi-periodic features in radio observations (see Li et al., 2020a, and references therein), such as Type-IIIb bursts (see the upper-left panel in Figure 8, Kolotkov, Nakariakov, and Kontar, 2018), fiber bursts (see the upper-right panel in Figure 8, Mészárosová, Karlický, and Rybák, 2011; Karlický, Mészárosová, and Jelínek, 2013) and wiggly zebra patterns (see the bottom panel in Figure 8, Kaneda et al., 2018). Both fiber bursts and zebra patterns are particular quasi-periodic fine structures in solar Type-IV radio bursts, while Type-IIIb bursts are a fine spectral structuring in Type-III bursts characterized by multiple narrowband bursts with slow frequency drift (de La Noe and Boischot, 1972; Sharykin, Kontar, and Kuznetsov, 2018). These fine structures in the radio spectrum are believed to be important sources of information for probing coronal plasma parameters and diagnosing flare processes (see Chernov, 2006, and references therein).

Figure 8

Candidate signatures in the radio dynamic spectra for coronal QFP wave trains. The upper-left panel shows the dynamic spectrum of a Type-III radio burst that occurred on 16 April 2015 and was observed by LOFAR in the frequency band of 35 – 39 MHz, in which the fine horizontal striae that can be fitted by a linear function (green lines) are the Type-IIIb radio bursts. The regions of apparent clustering of the striae into three distinct groups are indicated by “I”, “II”, and “III” and separated by the horizontal-dashed lines (adapted from Kolotkov, Nakariakov, and Kontar, 2018). The upper-right panel shows an example of radio-fiber bursts on 23 November 1998 (Karlický, Mészárosová, and Jelínek, 2013), which was observed by the Ondřejov radio spectrograph (Jiricka et al., 1993). The bottom panel shows an example of radio-zebra pattern structures in a Type-IV radio burst on 21 June 2011 (adapted from Kaneda et al., 2018), which was observed by the Assembly of Metric-band Aperture TElescope and Real-time Analysis System (AMATERAS: Iwai et al., 2012).

Solar radio observations typically have high temporal resolution but no spatial resolution. Even with interferometer observations, the spatial resolution is still very low. Therefore, the physical connections between various quasi-periodic fine structures in the radio and spatially resolved QFP wave trains in the EUV are still unclear. One often connects quasi-periodic radio structures with QFP wave trains in the EUV by comparing their physical parameters such as periods, speeds, and temporal correlation. In the works published by Mészárosová et al. (2009, 2011, 2013), the periods of the radio pulsations are in the range of 60 – 80 and 0.5 – 1.9 seconds. The longer periods are similar to those measured in spatially resolved EUV observations of QFP wave trains, while the short ones are unclear, because current AIA EUV observations cannot detect periods lower than 24 seconds (Liu and Ofman, 2014). Similar physical parameters are also derived from the observations of Type-IIIb radio bursts (Sharykin, Kontar, and Kuznetsov, 2018). For example, Kolotkov, Nakariakov, and Kontar (2018) studied the Type-IIIb radio bursts observed in a dynamic spectrum of a Type-III radio burst (see also Karlický, Mészárosová, and Jelínek, 2013; Sharykin, Kontar, and Kuznetsov, 2018). The authors proposed that the formation of the observed Type-IIIb radio bursts was probably caused by the modulation of the field-aligned propagating electron beam by a QFP wave train along the same bundle of funnel-like coronal loops. Therefore, the observed radio emissions in the Type-III radio burst also carry the same periodic information as the QFP wave train (see Figure 9). Based on this scenario, the authors further derived the physical parameters including speed, period, and amplitude of the possible QFP wave train and their corresponding values are respectively about 657 km s⁻¹, three seconds, and a few percent, in agreement with those detected in spatially resolved QFP wave trains in EUV observations.

Figure 9

A scenario for the generation of quasi-periodic striations (Type-IIIb bursts) in the dynamic spectrum of Type-III bursts by a QFP wave train (adapted from Kolotkov, Nakariakov, and Kontar, 2018).

Theoretically, the temporal signature of an impulsively generated QFP wave train propagating along coronal loops with different density-contrast ratios is expected to produce a characteristic tadpole wavelet spectrum, i.e. a narrow spectrum tail precedes a broad-band head, which indicates that the instantaneous period of the oscillations in the wave train decreases gradually with time (Nakariakov et al., 2004). In observations, the possible QFP wave train detected in the solar eclipse on 11 August 1999 shows such a special signature (Katsiyannis et al., 2003). In some studies, if a tadpole wavelet spectra can be observed in radio observations, one often speculates the existence of a possible QFP wave train in the low corona, even though the wave signature is not observed in EUV imaging observations. For example, Mészárosová et al. (2009a,b) and Mészárosová, Karlický, and Rybák (2011) detected similar tadpole wavelet spectra in solar decimetric Type-IV radio bursts and interpreted the detected radio pulsations as the result of possible QFP wave trains traveling along loops through the radio source and modulating the gyrosynchrotron emission. In combination with imaging observations and radio interferometric maps, Mészárosová et al. (2013) showed that a radio source that exhibits the wavelet tadpole feature was located at the null point of a fan–spine structure in the low corona, and the authors suggested that this might imply the passage of a QFP wave train.

In the studies mentioned above, the authors detected similar physical parameters (e.g. period and speed) in radio observations as in the EUV and similar characteristic tadpole wavelet spectra predicted by the theory. However, it is still unclear whether various quasi-periodic radio features genuinely result from the modulation of the local coronal plasma by QFP wave trains. First, in all the above studies, the authors did not observe the simultaneous appearance of spatially resolved QFP wave trains. Conversely, most QFP wave trains in the EUV are not accompanied by quasi-periodic radio fine structures. Second, in practical observations, the wavelet spectra of spatially resolved QFP wave trains in the EUV do not exhibit the tadpole feature.

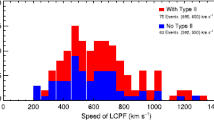
Recently, Goddard et al. (2016) observed a chain of discrete, quasi-periodic radio bursts preceding a Type-II radio burst, which were found to be associated with a CME and an ambiguous QFP wave train in the low corona. The authors found that the speeds and heights of the radio bursts are comparable to the CME leading edge in time, and that the period of the radio bursts is similar to that of the QFP wave train. Therefore, they interpreted the observed radio bursts as the result of the interaction between the QFP wave train and the CME leading edge (see Figure 10). For some spatially resolved QFP wave trains in the EUV, the generation of QFP wave trains was found to be highly correlated in start time with radio bursts (Yuan et al., 2013; Shen et al., 2018a), or that their periods are similar to the associated quasi-periodic Type-III radio bursts (Kumar, Nakariakov, and Cho, 2017). Type-III radio bursts are typically associated with electron beams accelerated to small fractions of the speed of light by magnetic reconnection, and their appearance often suggests bursty energy releases in the low corona. Therefore, in some studies the generation of QFP wave trains is suggested to be caused by the dispersive evolution of impulsively generated broadband disturbances (e.g. Yuan et al., 2013; Kumar, Nakariakov, and Cho, 2017).

Figure 10

Left panel shows the Learmonth radio spectra of 03 November 2014, which shows the discrete regions of enhanced emissions (radio bursts) in association with a Type-II radio burst. These radio bursts are proposed to be caused by the interaction of a QFP wave train with the leading edge of the accompanying CME (adapted from Goddard et al., 2016). The three lanes of the fundamental Type-II radio bursts are indicated by F1, F2, and F3, while the corresponding harmonic emission are indicated by H1, H2 and H3, respectively. The small radio bursts are indicated by the red arrows and symbols R1, R2, R3, and R4. The time axis refers to the time elapsed since 22:00 UT. The right panel is a schematic synopsis for illustrating the generation of the radio sparks in the radio spectra.

3 Theory and Modeling

As a booming research field in solar physics, the corresponding theory and numerical simulation have made significant advances since the discovery of QFP wave trains. Although there are various aspects that have not yet been fully addressed, the current numerical and analytical results have been in reasonably good agreement with observations, including morphology, periodicity, and velocity, as well as other properties (e.g. Ofman et al., 2011; Pascoe, Nakariakov, and Kupriyanova, 2013; Pascoe, Goddard, and Nakariakov, 2017; Ofman and Liu, 2018). In terms of the generation mechanism, studies are mainly focused on two interconnected scenarios similar to the generation of flare QPPs (see also Section 2.5). The first scenario is that a QFP wave train can be formed due to the dispersive evolution of an impulsively generated broadband perturbation, and the wave periodicity is determined by the physical properties of the waveguide and its surroundings (e.g. Roberts, Edwin, and Benz, 1983, 1984; Murawski and Roberts, 1994; Nakariakov et al., 2004). The second scenario is that a QFP wave train can be attributed to a pulsed energy release involving the magnetic-reconnection process, and that the wave periodicity is basically determined by the wave source (e.g. Yang et al., 2015; Takasao and Shibata, 2016).

3.1 Dispersion Evolution Mechanism

The corona hosts many filamentary structures of enhanced plasma density (low Alfvén speed) with respect to the background, such as coronal loops, fibrils, and plumes. These coronal structures act as waveguides for fast propagating magnetosonic waves that are highly dispersive when their wavelengths are comparable or longer than the width of the waveguides, and the wave-dispersion properties are seriously affected by the parameters of the waveguide and the surroundings (e.g. Lopin and Nagorny, 2015, 2017, 2019). Since a fast-mode, propagating, magnetosonic wave with different frequencies travels at different group speeds in an inhomogeneous structure, an impulsively generated broadband perturbation, i.e. a Fourier integral over all frequencies and wave numbers (wave packets; such as a flare), can naturally give rise to the generation of QFP wave trains in a waveguide at a distance from the initial site (Roberts, Edwin, and Benz, 1983). In the coronal context, the speeds of fast propagating magnetosonic waves along coronal loops are of the order of the Alfvén speed, which can vary from the minimum Alfvén speed inside of a loop to the maximum Alfvén speed outside the loop (Aschwanden, 2005). Roberts, Edwin, and Benz (1983, 1984) analytically analyzed the development of QFP wave trains in coronal loops that were modeled as straight slabs with sharp boundaries. The authors found that the group speeds of QFP wave trains with longer-wavelength spectral components propagate faster than those with shorter ones, and they qualitatively predicted that a QFP wave train experiences three distinct phases including periodic, quasi-periodic, and decay phases (see Figure 11).

Figure 11

A sketch of the evolution of a fast sausage wave evolved from an impulsively generated perturbation in the low-$\beta$ extreme, which exhibits three distinct phases, including periodic, quasi-periodic, and decay phases (adapted from Roberts, Edwin, and Benz, 1984). $h$ is the distance from the initial perturbation, $v_{\mathrm{A}}$ and $v_{\mathrm{Ae}}$ are respectively the internal and external Alfvén speeds of the slab, and $c^{\mathrm{min}}_{\mathrm{g}}$ is the minimum group velocity.

The periodic phase starts at a certain distance $[h]$ from the perturbation source with low amplitude and constant frequency, whose start and end times are $h/v_{\mathrm{Ae}}$ and $h/v_{\mathrm{A}}$, respectively, where $v_{\mathrm{Ae}}$ and $v_{\mathrm{A}}$ are the external and internal Alfvén speeds of the waveguide, respectively. During the periodic phase, the oscillation amplitude steadily grows, and the start (end) time represents the arrival time of the fastest (slowest) signal component of the perturbation. The quasi-periodic phase after the periodic phase but before the decay phase, which starts at a time $h/v_{\mathrm{A}}$ and ends at a time $h/c^{\mathrm{min}}_{\mathrm{g}}$, where $c^{\mathrm{min}}_{\mathrm{g}}$ is the minimum group speed. It can be seen that the end time of the quasi-periodic phase is determined by the minimum group speed of the perturbation. The quasi-periodic phase has a larger amplitude and a higher frequency than the earlier periodic phase, which is most detectable in observations. The quasi-periodic phase is followed by the decay phase, during which the amplitude of the perturbation declines quickly (see Figure 11). Initial numerical studies have been performed successfully to study these distinct phases of the QFP wave trains (Murawski and Roberts, 1993c,a,b, 1994; Murawski, Aschwanden, and Smith, 1998), and the average periods are found to be of the order of the wave travel time across the waveguides and are in agreement with previous analytical results (Roberts, Edwin, and Benz, 1983, 1984).

Nakariakov et al. (2004) numerically modeled the developed stage of a QFP wave train in a smooth slab of a low-$\beta$ plasma. They found that the quasi-periodicity arises from the geometrical dispersion of the wave train and is determined by the transverse profile of the loop, and that the period and the spectral amplitude are determined by the steepness of the transverse density profile and the density-contrast ratio in the loop. In addition, the authors have further analyzed the time-dependent power spectrum using the wavelet transform technique, which yields that the QFP wave train has a special tadpole shape in the Morlet wavelet spectra, i.e. a narrow-spectrum tail precedes a broad-band head (see the left column of Figure 12). Comparing with Roberts, Edwin, and Benz (1984), the periodic and quasi-periodic phases correspond respectively to the tadpole tail and head, while the decay phase corresponds to the tadpole-head maximum. The typical feature of the tadpole wavelet spectra was used as a characteristic signature to identify the presence of possible QFP wave trains in both observational and numerical studies, when direct imaging of QFP wave trains in EUV was not available (e.g. Mészárosová et al., 2009b; Karlický, Jelínek, and Mészárosová, 2011; Jelínek, Karlický, and Murawski, 2012; Karlický, Mészárosová, and Jelínek, 2013; Mészárosová et al., 2013, 2014). Recently, Kolotkov et al. (2021) modeled the linear dispersive evolution of QFP wave trains in plasma slabs with varying steepness of the transverse density profile, in which they showed that the development of a QFP wave train evolved from an initial impulsive perturbation undergoes three distinct phases, which are fully consistent with that qualitatively predicted by Roberts, Edwin, and Benz (1983, 1984). In contrast to wave trains in smooth waveguides that produce the tadpole structures (Nakariakov et al., 2004), it is interesting that the wavelet power spectrum develops into a boomerang structure that has two pronounced arms in the longer- and shorter-period parts of the spectrum (see the right column of Figure 12). The authors further pointed out that the duration of the different phases and how prominent they are in the whole temporal profile of the wave train depend on the parameters of the waveguide and the wave perturbation symmetry, and that this characteristic signature can be used as a seismological indicator of the transverse structuring of a hosting plasma waveguide. It should be pointed out here that in practice most direct imaging of QFP wave trains in the EUV do not show such a tadpole or boomerang structure in the wavelet spectra. It seems that such a special tadpole wavelet spectrum is more likely to appear in QFP wave trains with shorter periods of a few seconds (Katsiyannis et al., 2003).

Figure 12

Wavelet power spectra of dispersively formed QFP wave trains in waveguides. The left column is a numerical simulation of an impulsively generated QFP wave train along a coronal loop with a smooth boundary, in which the top panel shows the density-variation profile of the wave train, while the bottom panel is the wavelet transform analysis of the signal demonstrating the characteristic tadpole wavelet signature. The vertical lines in the top panel show the pulse arrival time if the density were uniform; the dotted line uses the external density; and the dashed line the density at the center of the structure (adapted from Nakariakov et al., 2004). The right column shows the temporal profile (top) and wavelet power spectrum (bottom) of a fully developed fast sausage wave train in a steep plasma waveguide. The three distinct developing phases of the wave train are indicated, and the wavelet spectra show a boomerang shape (adapted from Kolotkov et al., 2021).

In a series of recent theoretical works, attention is mainly paid to the geometric effects (e.g. Jelínek, Karlický, and Murawski, 2012; Pascoe, Nakariakov, and Kupriyanova, 2013; Mészárosová et al., 2014; Shestov, Nakariakov, and Kuzin, 2015) and transverse plasma-density structuring (e.g. Yu et al., 2015, 2016, 2017; Li et al., 2018a) of the waveguide on the formation and evolution of QFP wave trains. In particular, Oliver, Ruderman, and Terradas (2014, 2015) analytically demonstrated that QFP wave trains experience stronger attenuation for longer axisymmetric (or shorter transverse) perturbations, while the internal-to-external density ratio has a smaller effect on the attenuation. For typical coronal loops, axisymmetric (transverse) wave trains travel at a speed of 0.75 – 1 (1.2) times the Alfvén speed of the waveguide and with periods of the order of seconds. To efficiently excite a QFP wave train, a larger spatial extent (compared to the waveguide width) and a longer temporal duration of the initial impulsive driver are probably necessary conditions (e.g. Nakariakov, Pascoe, and Arber, 2005; Yu et al., 2017; Goddard, Nakariakov, and Pascoe, 2019). Shestov, Nakariakov, and Kuzin (2015) concluded that the characteristics of QFP wave trains depend on the fast-mode magnetosonic speed in both internal and external media, the smoothness of the transverse profile of the equilibrium quantities and also the spatial size of the initial impulsive perturbation.

Propagation of QFP wave trains can be both trapped and leaky in nature, especially for axisymmetric sausage waves of long wavelengths in smooth slabs (Murawski and Roberts, 1993a). An initial impulsive perturbation can result in the propagation of both trapped and leaky waves inside and outside a coronal loop, respectively. The trapped and leaky waves occur as a result of total reflection and refraction around the boundary of a waveguide (Murawski and Roberts, 1994; Pascoe, Nakariakov, and Kupriyanova, 2014). In contrast to previous studies in which coronal loops were considered as straight slabs or cylinders, Pascoe, Nakariakov, and Kupriyanova (2013, 2014) performed two-dimensional numerical simulations to study the evolution of impulsively generated QFP wave trains in a funnel geometry resembling active-region coronal loops and coronal holes (e.g. Liu et al., 2011; Shen and Liu, 2012b; Shen, Song, and Liu, 2018), where the funnel expands with height and with a field-aligned enhanced or reduced plasma density in comparison to the surroundings. In both an overdense waveguide and an underdense “anti-waveguide”, trapped and leaky QFP wave trains appear respectively inside and outside the waveguides, and the leaky QFP wave trains experience refraction that turns the local wave vector in the vertical direction due to refraction caused by the variation of the magnetic-field strength with height (see Figure 13). In comparison, both the trapped and leaky wave trains propagate in perpendicular directions in the case of straight waveguides. In contrast to the case of an overdense waveguide, the leaky wave train in the case of an underdense anti-waveguide is much more pronounced than the corresponding trapped component. In addition, the trapped wave train in the case of an underdense anti-waveguide exhibits less dispersive evolution than in the case of an overdense waveguide.

Figure 13

Numerical simulation results of developing QFP wave trains in funnel geometry overdense waveguide left column (adapted from Pascoe, Nakariakov, and Kupriyanova, 2013) and underdense anti-waveguide right column (adapted from Pascoe, Nakariakov, and Kupriyanova, 2014). For each column, the top (bottom) panel shows the velocity (density) perturbations, while the line contours outline the equilibrium density profile.

It has been demonstrated by numerical simulations that the propagation properties of the trapped and leaky QFP wave trains are completely different. Pascoe, Goddard, and Nakariakov (2017) showed that the nonlinear steepening of the trapped wave train is suppressed by the geometrical dispersion associated with the waveguide, while the leaky wave train does not undergo dispersion once it leaves the waveguide and therefore it can steepen into shock waves (see Figure 14). The formation of shock waves from the leaky wave train could possibly account for the direct observation of broad QFP wave trains in the low corona (e.g. Liu et al., 2012; Shen et al., 2019; Zhou et al., 2021b, 2022) or quasi-periodic Type-II radio bursts in association with one flare. Nisticò, Pascoe, and Nakariakov (2014) reported an interesting event in which both narrow and broad QFP wave trains are possibly simultaneously detected in one event, and their observations are thought to be consistent with the trapped and leaky wave trains identified in their numerical simulations (Pascoe, Nakariakov, and Kupriyanova, 2013; Pascoe, Goddard, and Nakariakov, 2017).

Figure 14

Numerical study of the nonlinear steepening of trapped and leaky wave trains inside and outside a straight slab (adapted from Pascoe, Goddard, and Nakariakov, 2017). The left panel shows the density perturbations, in which the trapped and leaky wave trains are indicated by the two arrows. The upper-right panel shows the density of the slab, in which a guided slow-mode shock and a fast-mode wave trains can be identified propagating in opposite directions along the slab. The lower-right panel shows the intensity profile at the center of the slab ($y=0$) as shown in the upper-right panel.

3.2 Pulsed Energy Excitation Mechanism

Pulsed-energy excitation mechanisms of QFP wave trains are related to the magnetic-reconnection process that converts magnetic-field energy to kinetic and thermal energy of the plasma and non-thermal high-energy particle energies (e.g. Fletcher et al., 2011; Shibata and Magara, 2011; Lin et al., 2015). Magnetic reconnection is a complex and highly nonlinear process referring to the breaking and reconnecting of oppositely directed magnetic-field lines in a highly conducting plasma due to finite resistivity (Priest and Forbes, 2002), which is essential to launch intermittent energy-release pulses and therefore cause QPPs in light curves from radio to $\gamma$-ray and QFP wave trains. In observations, some periods of QFP waves are found to be consistent with those of QPPs, which might suggest their common origin. In addition, this also implies the existence of an intimate relationship between QFP wave trains and nonlinear processes in magnetic reconnection (see Section 2.5).

Generally, theoretical and numerical studies have revealed that the launch of a fast magnetic reconnection requires the development of turbulence and the fragmentation of a thin current sheet into many small-scale plasmoids (magnetic islands or flux ropes in three-dimensions, Furth, Killeen, and Rosenbluth, 1963; Lazarian and Vishniac, 1999; Shibata and Tanuma, 2001). The formation of plasmoids is owing to the tearing-mode or plasmoid instability of the current sheet when its Lundquist number and aspect ratio are large enough (e.g. Ni et al., 2012, 2015). Plasmoids in a current sheet are typically generated repetitively and exhibit characteristics such as coalescence and bi-directional outward ejections at about the Alfvén speed. These motions reduce the magnetic flux in the current sheet, which in turn enables new magnetic flux to continuously enter the current sheet to achieve a fast reconnection speed (Shibata and Magara, 2011). So far, many numerical simulations have successfully produced such a physical process and the presence and dynamic characteristics of plasmoids are also observed indirectly in various solar eruptions from radio to $\gamma$-rays (see Shibata and Takasao, 2016; Ni et al., 2020, and reference therein). In some studies, flare QPPs have been related to the repetitive generation, coalescence, and ejections of plasmoids in current sheets, in which plasmoids are considered as a trap for accelerated particles that can result in drifting pulsating structures in the radio spectrum (e.g, Kliem, Karlický, and Benz, 2000; Karlický, 2004; Karlický and Bárta, 2007; Bárta, Karlický, and Žemlička, 2008). Jelínek et al. (2017) numerically showed the merging of two plasmoids, and the resulting larger plasmoid oscillated with a period of about 25 seconds; in the meantime, the downward plasmoids interact with the underlying flare arcade and cause the oscillation of the latter with a period of about 35 seconds. These periods are consistent with those observed in flare QPPs and QFP wave trains. In addition, plasmoid contraction or squashing are suggested as a promising mechanism for particle acceleration (e.g. Drake et al., 2006; Guidoni et al., 2016), and particles are shown to gain more energy at multiple X-points between plasmoids (Li and Lin, 2012; Li, Wu, and Lin, 2017; Xia and Zharkova, 2018).

Recent numerical simulations have studied the physical relationship between the nonlinear processes in magnetic reconnection and the generation of QFP wave trains. Ofman et al. (2011) first performed a three-dimensional MHD model in which they identified that the observed QFP wave trains are fast magnetosonic waves driven by quasi-periodic drivers at the base of the flaring region. The simulated QFP wave trains, driven by periodic velocity pulsations at the lower coronal boundary, propagate outward in a magnetic funnel and are evident through density fluctuations due to compressibility. The authors confirmed that the simulated QFP wave trains have similar physical properties to those obtained in real observations, including their amplitude, wavelength, and speeds (see the left column of Figure 15). Using real observations as a guideline, Ofman and Liu (2018) investigated the excitation, propagation, nonlinearity, and interaction of counter-propagating QFP wave trains in a large-scale, trans-equatorial coronal-loop system using time-dependent periodic boundary conditions at the two ends of the loop system. Besides QFP wave trains, trapped fast-(kink) and slow-mode waves are also identified in the closed-loop system. These results suggest that the counter-propagating QFP wave trains in closed coronal loops can potentially lead to a turbulent cascade that carries significant energy for coronal heating in low-corona magnetic structures. Yang et al. (2015) performed a 2.5-dimensional numerical MHD simulation to study the generation of QFP wave trains using the interchange reconnection scenario; they found that QFP wave trains can be launched by the impingement of plasmoids ejected outward from the current sheet upon the ambient magnetic-field in the outflow region, and a one-to-one correlation between the energy release and wave generation can be identified. The wave properties are also found to be similar to the observed QFP wave trains (see the right column of Figure 15). However, as pointed out by the authors, the simulated QFP wave train propagates isotropically from the wave source rather than along funnel-like loop structures as narrow QFP wave trains. Therefore, QFP wave trains excited by the impingement of plasmoids on the ambient magnetic field in the outflow region could possibly be used to explain the generation of broad QFP wave trains.

Figure 15

The left column shows the simulation results (adapted from Ofman et al., 2011), in which the top and the bottom panels display the velocity component $V_{x}$ and the density difference in the $xz$-plane at the center of the model, respectively. The right column shows the simulation results presented by Yang et al. (2015), in which the top and the bottom panels show the horizontal velocity $V_{x}$ and the running-difference of the synthesized emission at 171 Å wavelength, respectively. The white-dashed box in the top panel indicates the field-of-view of the bottom panel.

Takasao and Shibata (2016) described an alternative physical picture for the generation of QFP wave trains through a two-dimensional MHD simulation of the flare process, which includes essential physics such as magnetic reconnection, heat conduction and chromospheric evaporation. It was found that QFP wave trains are spontaneously excited by the oscillating region above the flaring loop filled with evaporated plasma, and the oscillation of this region is controlled by the backflow of the reconnection outflow. Therefore, the authors claimed that the backflow of the reconnection outflow can act as an exciter of QFP wave trains (see Figure 16). The oscillation region has a U-shaped structure due to the continuous impingement of the reconnection outflow, and therefore the generation process of QFP wave trains is similar to the sound wave generated by an externally driven tuning fork. Miao et al. (2021) observed simultaneous bi-directional narrow QFP wave trains originating from the same flaring region, and the authors suggested that their observation might be a good example to support such a magnetic tuning-fork model. Here, it should be noted that the propagation of the simulated QFP wave train in Takasao and Shibata (2016) is also isotropic, like that in Yang et al. (2015). It is hard to understand why the observed bi-directional narrow QFP wave trains in Miao et al. (2021) can be interpreted by the magnetic tuning-fork model. We think that this model should be more suitable for broad QFP wave trains, but it could also be used to interpret narrow QFP wave trains when the isotropic propagating wave train is captured by, and therefore trapped in, some inhomogeneous coronal structures such as coronal loops (e.g. Shen et al., 2019).

Figure 16

Numerical simulation results presented by Takasao and Shibata (2016). The upper-left panel shows the density map overlaid with magnetic-field lines, and the above-the-loop-top region is plotted as an inset. The bottom-left panel shows the running-difference image of the density perturbation, in which multiple wavefronts can be clearly identified. The right panel is a schematic illustrating the generation of QFP wave trains due to above-the-loop-top oscillation, in which the pink arrows indicate the dynamic pressure gradient, the black-vertical arrow indicates the downward reconnection outflow, the short black arrows indicate the generated QFP wave trains, and the longer black arrows indicate the magnetic-field lines.

Wang, Chen, and Ding (2021) performed a three-dimensional radiative MHD simulation to model the formation of active regions through magnetic-flux emergence from the convection zone into the corona, in which the eruption of a magnetic-flux rope produced a C-class flare and a QFP wave train with a period of about 30 seconds between the erupting flux rope and a preceding global EUV wave that was driven by the erupting flux rope (see Figure 17). Obviously, the propagation of the generated QFP wave train is a broad QFP wave train perpendicular to the magnetic-field lines (Liu et al., 2012; Shen et al., 2019; Zhou et al., 2021b, 2022) rather than along the magnetic-field lines as narrow QFP wave trains (Liu et al., 2011; Shen and Liu, 2012b; Shen et al., 2013a, 2018a). Therefore, this simulation provided an additional numerical model for the generation of broad QFP wave trains as well as for the simultaneously preceding global EUV wave. The generation of the QFP wave train by Wang, Chen, and Ding (2021) occurs spontaneously without any artificial exciters as used in previous simulations (e.g. Ofman et al., 2011; Pascoe, Nakariakov, and Kupriyanova, 2013). The authors proposed that the excitation of the QFP wave train was possibly due to pulsed energy release in the accompanying flare, as proposed in Liu et al. (2012). However, the authors also pointed out that the essential physical cause of the excitation mechanism still needs further investigation using higher spatio-temporal resolution three-dimensional simulations. This is true because there may be other excitation mechanisms for broad QFP wave trains. For example, Shen et al. (2019) proposed that the generation of broad QFP wave trains behind the CME-driven global EUV wave can possibly be driven by the pulsed energy release caused by the periodic unwinding and expanding twisted thin threads in the erupting filament, because the period of the observed QFP wave train is similar to the unwinding filament threads instead of the QPPs in the accompanying flare. In addition, the generation of broad QFP wave trains is possibly in association with the fine structure of CMEs. We note the appearance of large-scale, quasi-periodic EUV wavefronts ahead of the CME in numerical simulations with a period of about 84 – 168 seconds (see Figure 1 of Chen et al. (2002) and Figure 2 of Chen, Fang, and Shibata (2005) for details). Although the authors did not analyze these interesting wavefronts, their period is quite consistent with those of the broad QFP wave trains (Shen et al., 2019). Besides, Patsourakos, Vourlidas, and Kliem (2010) also observed the appearance of broad QFP wave trains ahead of a CME, where the authors proposed that the wave train was excited by the fine expanding pulse-like lateral structures in the CME. Recently, Shen et al. (2022) found that the generation of a broad QFP wave train can be driven by the sequential stretching of expansion of the newly formed reconnected magnetic-field lines, it is also a good observation supporting the scenario of pulsed energy release in magnetic reconnection.

Figure 17

Simulation results presented by Wang, Chen, and Ding (2021). The top and middle rows display the synthetic 171 Å and 94 Å running-difference images, respectively. The leading EUV wavefront and the following QFP wave train are indicated respectively by the yellow and green arrows in Panel c. The three red arrows in the Panels b and e are used to generate the time–distance diagrams plotted in the bottom row (based on the synthetic 171 Å running-difference images).

Other nonlinear physical processes in association with pulsed energy release in magnetic reconnection include i) the mechanism of oscillatory reconnection, which couples the resistive diffusion at X-type null points with the global advection of the outer fields (e.g. Craig and McClymont, 1991; McLaughlin et al., 2009; McLaughlin, Thurgood, and MacTaggart, 2012; McLaughlin et al., 2012; Thurgood, Pontin, and McLaughlin, 2017; Hong et al., 2019; Xue et al., 2019; Thurgood, Pontin, and McLaughlin, 2019), ii) patchy magnetic reconnection shows as supra-arcade downflows (e.g. Linton and Longcope, 2006; McKenzie and Savage, 2009; Savage, McKenzie, and Reeves, 2012; Cai et al., 2019; Xue et al., 2020; Reeves et al., 2020), and iii) the fluctuation of current sheets result from super-Alfvénic beams and Kelvin–Helmholtz instability nonlinear oscillations (e.g. Ofman and Sui, 2006; Li et al., 2016). In addition, periodicities in the magnetic reconnection can also be launched by external quasi-periodic disturbances from lateral or lower layers of the solar atmosphere through interaction and therefore modulating the reconnection process (e.g. Nakariakov et al., 2006; Chen and Priest, 2006; Sych et al., 2009; Shen and Liu, 2012b; Jess et al., 2012; Jelínek and Karlický, 2019). Basically, all of these possible physical processes are potentially able to produce both flare QPPs and QFP wave trains. However, although a number of numerical and theoretical studies have been performed to investigate the excitation mechanism of flare QPPs based on these scenarios (Nakariakov and Melnikov, 2009; Van Doorsselaere, Kupriyanova, and Yuan, 2016; McLaughlin et al., 2018; Kupriyanova et al., 2020; Zimovets et al., 2021), the physical relationship between these processes and the generation of QFP wave trains has not yet been established. Therefore, in the future more attention should be paid to these candidate mechanisms for the generation of QFP waves.

3.3 Discussion of the Current Models

The current models have shown that the two kinds of possible generation mechanisms of QFP wave trains are both supported by some observational evidence (e.g. Liu et al., 2011; Shen and Liu, 2012b; Nisticò, Pascoe, and Nakariakov, 2014; Shen, Song, and Liu, 2018; Shen et al., 2019; Yuan et al., 2013). However, for a particular event, whether the generation of the QFP wave train is associated with a specific mechanism or a combination of both is still unclear. Here, we would like to offer a preliminary discussion about this problem based on previous observational and theoretical studies.

The dispersion-evolution mechanism was first developed to interpret the short period-pulsations of a few seconds observed in radio emission, and these pulsations were thought to be the manifestation of plasma emission modulated by QFP wave trains propagating in inhomogeneous coronal structures such as coronal loops that act as overdense plasma tubes (Roberts, Edwin, and Benz, 1983, 1984). Obviously, QFP wave trains formed by the dispersion-evolution mechanism require the presence of overdense waveguides. In actual observations, many spatially resolved narrow QFP wave trains in the EUV can satisfy such a requirement as they propagate along coronal loops. In addition, it has been widely accepted that such a dispersively formed QFP wave train should lead to a characteristic tadpole structure in the time-dependent wavelet spectra (Nakariakov et al., 2004) if the driver is a broadband perturbation (Nakariakov, Pascoe, and Arber, 2005). Up to now, the characteristic tadpole structure has not been detected in all published narrow QFP wave trains observed by AIA. This might be attributed to the relatively longer period (25 – 550 seconds, see Table 1) of the narrow QFP wave trains observed by the AIA, since we note that a tadpole wavelet spectrum was detected in the QFP wave train observed by SECIS during the total solar eclipse on 11 August 1999, where the period was about six seconds Katsiyannis et al. (2003). Besides, as what had been pointed out in Nakariakov, Pascoe, and Arber (2005), the absence of tadpole wavelet spectra from narrow QFP wave trains could also be due to the more monochromatic and narrowband driver.

For broad QFP wave trains propagating in a homogeneous quiet-Sun region where the magnetic field has a strong vertical component, they are non-dispersive in nature and their propagation can be viewed as perpendicular to the magnetic field. As seen in the simulations (e.g. Murawski and Roberts, 1993a; Pascoe, Nakariakov, and Kupriyanova, 2013), an impulsive perturbation can dispersively evolve into both trapped and leaky wave trains inside and outside the waveguide. Pascoe, Goddard, and Nakariakov (2017) showed that broad QFP wave trains can be formed by the steepening of the leaky component of a dispersively formed wave train in an overdense waveguide, while the trapped component does not experience nonlinear steepening; the trapped and leaky wave trains have the same periods of about six seconds, and their velocity amplitudes are estimated to be respectively about 30% and 10% with respect to the local Alfvén speeds. This simulation might imply that broad QFP wave trains formed by the leaky component of dispersively formed QFP wave trains should also have relatively short periods, as we discussed in the above paragraph. The pulsed-energy excitation mechanism includes various forms, as stated in Section 3.2, in which the dynamic evolution of plasmoids and their interaction with magnetic structures in the reconnection-outflow region often excite broad QFP wave trains with periods of dozens of seconds (e.g. Yang et al., 2015; Takasao and Shibata, 2016; Jelínek et al., 2017; Wang, Chen, and Ding, 2021), in quantitative agreement with the lower limit of the period of published broad QFP wave trains observed by AIA (36 – 240 seconds, see Table 1). In addition, broad QFP wave trains with longer periods of several minutes are probably associated with other kinds of pulsed-energy release processes in association with magnetic reconnection. For example, the periodic untwisting motion of twisted erupting filament threads (Shen et al., 2019), the intermittent generation and stretching (or expansion) of reconnected magnetic-field lines (Shen et al., 2022), and the sequentially eruption of coronal loops (Patsourakos, Vourlidas, and Kliem, 2010).

Based on the above discussions, it is noted that both narrow and broad QFP wave trains can be produced by the two different generation mechanisms. In general, it appears that the dispersion-evolution mechanism seems more preferable for the generation of QFP wave trains with short periods of about a few seconds, while the dispersion-evolution mechanism seems more preferable for the generation of QFP wave trains with relatively long periods of typically about a dozen seconds to a few minutes. In principle, the two different generation mechanisms do not contradict each other. For the dispersion-evolution mechanism, it requires that the initial perturbation should be broadband. For the dispersion-evolution mechanism, the initial perturbation is more monochromatic. Here, we would like to point out that these preliminary thoughts are premature and need to be verified with high spatio-temporal resolution observations and theoretical work in the future.

4 Seismological Application

Seismology is the study of earthquakes and seismic waves that move through and around the Earth. This technique has been extended to other areas of science, such as helioseismology, stellar seismology, as well as MHD spectroscopy of laboratory plasma. Coronal seismology uses MHD waves and oscillations to probe unknown physical parameters of the solar corona (Nakariakov and Verwichte, 2005), which was originally proposed by Uchida (1970) for global and Roberts, Edwin, and Benz (1984) for local seismology. In principle, coronal seismology requires the combined application of theoretical modeling knowledge and observational parameters of MHD waves and oscillations, which yields the mean parameters of the corona that are currently inaccessible in the absence of in-situ instruments, such as the magnetic-field strength and Alfvén velocity and coronal dissipative coefficients (De Moortel, 2005; De Moortel and Nakariakov, 2012). So far, different types of MHD waves have been detected in the corona, and the technique of coronal seismology has also been successfully applied to estimate various coronal parameters (Nakariakov and Kolotkov, 2020). In previous studies, particular attention has been paid to deriving the elusive coronal magnetic field, and the results are often comparable to those obtained by using other direct or indirect methods including polarimetric measurements using Zeeman and Hanle effects (Lin, Penn, and Tomczyk, 2000; Lin, Kuhn, and Coulter, 2004), extrapolations using photospheric magnetograms (Zhao and Hoeksema, 1994; Liu and Lin, 2008), and radio observations of gyrosynchrotron emission with a coronal-density model (Gary and Hurford, 1994; White and Kundu, 1997; Ramesh, Kathiravan, and Sastry, 2010; Subramanian, Ebenezer, and Raveesha, 2010). Here, we only briefly review the applications of coronal seismology using QFP wave trains; for other types of waves, the reader can refer to several recent reviews (e.g. De Moortel, 2005; Nakariakov and Verwichte, 2005; De Moortel and Nakariakov, 2012; Jess et al., 2015; Liu and Ofman, 2014; Li et al., 2020a; Nakariakov and Kolotkov, 2020).

For a linear fast-mode magnetosonic wave in a homogeneous medium, its propagation is weakly dependent on the direction of the wave vector with respect to the magnetic field, which means that it propagates in any direction. The restoring force is the resultant force of the magnetic and gas-pressure gradient forces, and the speed is determined by the Alfvén speed and the sound of speed the local plasma medium. Theoretically, the speed of a fast-mode magnetosonic wave $[v_{\mathrm{f}}]$ in a uniform medium is

$$ v_{\mathrm{f}}=[\frac{1}{2}(v^{2}_{\mathrm{A}}+c^{2}_{\mathrm{s}}+\sqrt{(v^{2}_{\mathrm{A}}+c^{2}_{ \mathrm{s}})^{2}-4v^{2}_{\mathrm{A}}c^{2}_{\mathrm{s}}{\mathrm{cos}}^{2}\theta _{\mathrm{B}}})]^{1/2}, $$

(3)

where $c_{\mathrm{s}}$, $v_{\mathrm{A}}$, and $\theta _{\mathrm{B}}$ are the sound speed, Alfvén speed, and the angle between the wave vector and the magnetic field, respectively. Specifically, the mathematical expressions for $c_{\mathrm{s}}$ and $v_{\mathrm{A}}$ are

$$\begin{aligned} c_{\mathrm{s}}& = \sqrt{ \frac{\gamma {\mathrm{k_{B}}} T}{\bar{\mu }{\mathrm{m}}_{\mathrm{p}}}} \end{aligned}$$

(4)

$$\begin{aligned} {\mathrm{and}}~v_{\mathrm{A}}&=\frac{B}{\sqrt{4\pi \rho }}= \frac{B}{\sqrt{4\pi \bar{\mu }{\mathrm{m}}_{\mathrm{p}}n}}, \end{aligned}$$

(5)

respectively, where $\gamma =5/3$ is the adiabatic exponent for fully ionized plasmas, $\mathrm{k_{B}}$ is the Boltzmann constant, $T$ is the temperature, $\bar{\mu }$ the mean molecular weight, ${\mathrm{m_{p}}}$ is the proton mass, $B$ is the magnetic-field strength, $\rho$ is the mass density, and $n$ is the total particle number density. According to Priest (1982), $\bar{\mu }$ and $n$ are often respectively taken as 0.6 and $1.92n_{\mathrm{e}}$, with $n_{\mathrm{e}}$ as the electron density.

Obviously, for a fast-mode magnetosonic wave traveling in a particular direction, its speed depends on coronal parameters including the temperature, plasma density, and magnetic-field strength. Particularly, if a wave propagates perpendicular to the magnetic field (i.e. $\theta _{\mathrm{B}}=90^{\circ }$), Equation 3 reduces to a simple form of

$$ v_{\mathrm{f}} = \sqrt{v^{2}_{\mathrm{A}}+c^{2}_{\mathrm{s}}}, $$

(6)

and the magnetic-field strength of the medium in which the wave propagates can be estimated by measuring the wave speed and coronal parameters, including plasma density and temperature. In the case of $\theta _{\mathrm{B}}=0^{\circ }$, i.e. the wave propagates along the magnetic field, Equation 3 becomes

$$ v_{\mathrm{f}} = v_{\mathrm{A}}=\frac{B}{\sqrt{4\pi \rho }}, $$

(7)

namely, the fast-mode magnetosonic wave speed is equal to the Alfvén speed. Therefore, one can simply measure the wave speed and the plasma density to estimate the magnetic-field strength of the waveguide.

In the corona, magnetic-field lines are believed to be highlighted by coronal loops due to the coupling of hot plasma and magnetic field. Therefore, coronal loops commonly manifest the orientation and distribution of the coronal magnetic field. In practice, since narrow QFP wave trains travel along coronal loops, their propagation is along magnetic fields. Therefore, one often uses Equation 7 to estimate the magnetic-field strength of the guiding magnetic field. Williams et al. (2002) estimated that the magnetic-field strength of an active-region loop is about 25 Gauss. Liu et al. (2011) obtained that the magnetic-field strength of an active-region funnel-like loop is greater than 8 Gauss. Shen et al. (2019) derived that the magnetic-field strength of a closed transequatorial loop is about 6 Gauss. Zhou et al. (2021b) estimated that the magnetic-field strength of an interconnecting loop is about 5.6 Gauss, in agreement with the result (about 5.2 Gauss) derived from the simultaneous global EUV wave. Miao et al. (2021) reported a bi-directional QFP wave event, in which simultaneous QFP wave trains are observed in two opposite funnel-like loops rooted in the same active region. The magnetic-field strengths of the two funnel-like loops are estimated to be respectively about 12.8 and 11.3 Gauss, consistent with the results obtained by using magnetic-field extrapolation. Radio observations of possible QFP wave trains have also been used to estimate the magnetic-field strengths of coronal loops, which are found to be in the range of 1.1 – 47.8 Gauss (Mészárosová, Karlický, and Rybák, 2011; Kolotkov, Nakariakov, and Kontar, 2018). It should be pointed out that these results were all obtained using average parameters (plasma density and wave speed) along the entire loop structure. In practice, since narrow QFP wave trains decelerate rapidly as they propagate outwards, it should be better to estimate the magnetic-field strengths of the different sections of the waveguiding loop. According to this line of thought, Shen et al. (2013a) obtained that the magnetic-field strengths of the footpoint, middle, and outer sections of an active-region loop are about 5.4, 4.5, and 2.2 Gauss, respectively. This indicates that the strength of the magnetic-field decreases rapidly with increasing height of active-region coronal loops. Here, it should be pointed out that the above magnetic-field strength estimations based on Equation 7 are only approximations, but with a certain accuracy. As introduced in Section 3.1 (for more details one can refer to many books or reviews, e.g. Aschwanden, 2005; Roberts and Nakariakov, 2003; Nakariakov and Verwichte, 2005), the speeds of QFP wave trains propagating along coronal loops are of the order of the Alfvén speed, which is greater than the Alfvén speed of a loop but less than the Alfvén speed outside the loop. Therefore, derived values based on Equation 7 should be approximately consistent with the lower limit of the values estimated based on the theory of QFP wave trains along inhomogeneous waveguides.

In the simulation performed by Nakariakov et al. (2004), the authors found that the mean wavelength of the QFP wave train is comparable to the width of the guiding loop. Since the fast-mode wave speed is equal to the Alfvén speed of the waveguide, the relationship among wavelength [$\lambda$], period $[P]$, and wave speed [$v_{\mathrm{f}}$] can be written as

$$ P=\frac{\lambda }{v_{\mathrm{f}}} \approx \frac{w}{v_{\mathrm{A}}}, $$

(8)

where $w$ and $v_{\mathrm{A}}$ are the width and Alfvén speed of the guiding loop. Therefore, with the measurable physical parameters of period and wave speed, one can estimate the width of the guiding loop. For example, in the absence of imaging observations, Mészárosová, Karlický, and Rybák (2011) and Mészárosová et al. (2013) estimated loop widths using results derived from radio observations, which are in the range of about 1 – 30 Mm.

If simultaneous slow- and fast-mode waves are observed in the same waveguide, one can further estimate the plasma-$\beta$ of the medium, which is defined as the ratio of gas pressure to magnetic pressure (Van Doorsselaere et al., 2011). Zhang et al. (2015) reported the first imaging observation of simultaneous slow- and fast-mode wave trains propagating along the same coronal loop at speeds about 80 and 900 km s⁻¹, respectively. Assuming that the speeds of the observed slow- and fast-mode wave trains are respectively equal to the sound speed and Alfvén speed of the waveguide, the plasma-$\beta$ can be expressed by the slow- [$v_{ \mathrm{s}}$] and fast-mode [$v_{\mathrm{f}}$] characteristic speeds, i.e.

$$ \beta =\frac{2\mu p}{B^{2}} \approx \frac{2}{\gamma }( \frac{v_{\mathrm{s}}}{v_{\mathrm{f}}})^{2}, $$

(9)

where $p$, $\mu$, $\gamma$, and $B$ are the gas pressure, the permeability, the adiabatic index, and the magnetic-field magnitude, respectively. In the corona, the value of $\gamma$ ranges from 1 to 5/3 for isothermal and adiabatic sases, respectively. For the case analyzed by Zhang et al. (2015), the authors derived that the value of the plasma-$\beta$ ranges from 0.009 to 0.015, confirming the low-$\beta$ nature of the low corona.

Broad QFP wave trains commonly travel parallel to the solar surface, which has a strong vertical magnetic-field component. Therefore, the propagation of broad QFP wave trains is assumed to be perpendicular to the magnetic field, and one often uses Equation 6 to derive the magnetic-field strength of the supporting medium. This method is the same as magneto-seismology with global EUV waves (see Liu and Ofman, 2014; Warmuth, 2015, and references therein), and one must first determine the sound speed and the plasma density of the supporting medium. For example, Zhou et al. (2022) used the observation of a broad QFP wave train to estimate the magnetic-field strength in the quiet Sun, which yields a result of about 4.7 Gauss.

The large extent of propagation of broad QFP wave trains provides the potential to trigger oscillations of remote coronal structures such as coronal loops and filaments. The transverse oscillation of these coronal structures can be interpreted as the global, kink, standing mode of the loops, and one can use the measured oscillation parameters for coronal seismology (Aschwanden et al., 1999; Nakariakov et al., 1999; Nakariakov and Verwichte, 2005). According to Nakariakov and Ofman (2001), the observed wavelength of a global, kink, standing mode is twice the length of the loop; one can estimate the phase speed [$C_{\mathrm{k}}$] based on the observable period [$P$] and the loop length [$L$] with the formula

$$ P=\frac{2L}{C_{\mathrm{k}}}. $$

(10)

Assuming that in the low-$\beta$ coronal plasma the magnetic field is almost equal inside and outside the waveguide, the equation of the kink speed can be rewritten as

$$ C_{\mathrm{k}}=\sqrt{ \frac{\rho _{i}v^{2}_{\mathrm{Ai}}+\rho _{\mathrm{e}}v^{2}_{\mathrm{Ae}}}{\rho _{\mathrm{i}}+\rho _{\mathrm{e}}}} \approx v_{\mathrm{Ai}}\sqrt{\frac{2}{1+\rho _{\mathrm{e}}/\rho _{\mathrm{i}}}}, $$

(11)

where $\rho _{\mathrm{i}}$ ($\rho _{\mathrm{e}}$) is the internal (external) density and $v_{\mathrm{Ai}}$ ($v_{\mathrm{Ae}}$) is the internal (external) Alfvén speed. As the density contrast [$\rho _{\mathrm{e}}/\rho _{\mathrm{i}}$], the density inside the waveguide [$\rho _{\mathrm{i}}$] and the kink speed [$C_{\mathrm{k}}$] can be measured from observations, one can estimate the magnetic-field strength [$B$] of the waveguide using Equation 10, which can be rewritten as

$$ B = v_{\mathrm{Ai}}\sqrt{4\pi \rho _{\mathrm{i}}}=\frac{L}{P}\sqrt{8\pi \rho _{ \mathrm{i}}(1+\rho _{\mathrm{e}}/\rho _{\mathrm{i}})}. $$

(12)

This formula can be written as a more practical formula with measurable parameters for the distance between the footpoints of the loop [$d$], the number density inside the loop [$n_{\mathrm{i}}$], the number-density contrast [$n_{\mathrm{e}}/n_{\mathrm{i}}$] and the period of the loop oscillation [$P$], i.e.

$$ B \approx 7.9 \times 10^{-13} \frac{d}{P}\sqrt{n_{\mathrm{i}} + n_{\mathrm{e}}}, $$

(13)

where the magnetic-field [$B$] is in Gauss, the distance [$d$] in meters, the number densities $n_{\mathrm{i}}$ and $n_{\mathrm{e}}$ in m⁻³, and the period [$P$] in seconds (Roberts and Nakariakov, 2003).

Ofman and Liu (2018) studied the transverse oscillation of a coronal loop caused by the counter-propagation of two quasi-simultaneous narrow QFP wave trains within it. The authors first measured the width and length of the loop and then derived the background and loop density using the technique of differential emission measure (DEM: see Cheung et al., 2015, for instance). With the knowledge of the loop length, the oscillation period and the background and loop density, the magnetic-field strength of the loop is estimated to be about 5.3 Gauss with Equation 12. Such a value is consistent with their numerical model, which can produce similar observational characteristics to those obtained from the real observations. Shen et al. (2019) reported an interesting broad QFP wave train that propagated simultaneously along a transequatorial loop and on the solar surface, and the trapped part of the wave train resulted in the transverse oscillation of the loop system. Using the same methods as Ofman and Liu (2018), the authors estimated that the magnetic-field strength of the transequatorial loop is about 6 Gauss. In addition, the authors also estimated the magnetic-field strength of the loop with Equation 7, using the physical property of the wave train, which yields a value of about 8.3 Gauss. This result is obviously inconsistent with that obtained by using the oscillation property of the loop. The different magnetic-field strengths for the same loop derived from different methods are mainly because the broad QFP wave train was actually a shock rather than a linear fast-mode magnetosonic wave. Therefore, the authors further derived the Alfvén Mach number and then estimated the magnetic-field strength of the loop using the characteristic fast-mode speed obtained by dividing the measured wave speed by the Alfvén Mach number. Finally, the authors obtained the same result as that derived from the loop oscillation, which also confirmed the reliability of the two seismic methods.

Filament (or prominence) oscillations include transverse and longitudinal oscillations, and their oscillation parameters have also been applied into prominence seismology with various inversion techniques (see Arregui, Oliver, and Ballester, 2018, and reference therein). In previous studies, filament oscillations were commonly observed to be caused by the interaction of global EUV waves (e.g. Shen and Liu, 2012a; Shen et al., 2014a,b, 2017; Zhang and Ji, 2018). Liu et al. (2012) observed the transverse oscillation of the limb cavity, as well as the hosting prominence, which caused the passing of a broad QFP wave train. Taking the oscillation as a global standing transverse oscillation, as observed in coronal loops, the authors derived that the cavity’s magnetic-field strength is about 6 Gauss with a pitch angle of about $70^{\circ }$, suggesting that the observed cavity is a highly twisted flux rope. Shen et al. (2019) studied the transverse oscillation of a remote filament caused by the interaction of an on-disk propagating broad QFP wave train. The authors estimated the radial component of the magnetic field of the filament using the method proposed by Hyder (1966) with the measured parameters of the oscillation period and the damping time, and the derived value is about 12.4 Gauss. These results are in agreement with those obtained by inversion of full-Stokes observations (e.g. Casini et al., 2003).

5 Conclusions and Prospects

As one of the discoveries of SDO/AIA, spatially resolved QFP wave trains in the EUV wavelength band have attracted a lot of attention in the last decade. In this article, we have reviewed the observational properties, possible formation mechanisms, and the associated coronal seismology applications of coronal QFP wave trains. Generally, a QFP wave train consists of multiple coherent and concentric wavefronts emanating successively from near the epicenter of the accompanying flare and propagating outward either along or across coronal loops at fast-mode magnetosonic speed from several hundred to more than 2000 km s⁻¹. Based on the statistical study of published QFP wave trains observed by the AIA, we propose that QFP wave trains can be divided into two distinct categories: narrow and broad QFP wave trains. Although both narrow and broad QFP wave trains are fast-mode magnetosonic waves in physical nature with similar speeds, periods, and wavelengths, they also show distinct differences, including physical properties of observation wavelength, propagation direction, angular width, intensity amplitude, and energy flux. The energy flux carried by the QFP wave trains is found to be enough for heating the local low-corona plasma, and the measured parameters such as period, amplitude, and speed can be used for seismic diagnosis of currently undetectable coronal parameters such as magnetic-field strength.

Observations suggest that the generation of QFP wave trains is intimately associated with flare QPPs owing to their similar period and close temporal association, and that the two different phenomena might manifest different aspects of the same physical process. Detailed theoretical and numerical studies revealed that the periodicity origins of QFP wave trains are diverse, but they can be summarized as two interconnected groups dubbed the dispersion-evolution mechanism and the dispersion-evolution release excitation mechanism. The dispersion-evolution mechanism refers to a QFP wave train that develops from the dispersive evolution of an impulsive generated broadband perturbation in an inhomogeneous, overdense waveguide, because for a wave packet that represents a Fourier integral over all frequencies and wave number, different frequencies propagate with different phase and group speeds. In this regime, the periodicity of the wave train is not necessarily connected with the wave source, but can be created by the dispersive evolution of the initial perturbation based on the physical conditions inside and outside the waveguide. For the dispersion-evolution excitation mechanism, it means that the generation of a QFP wave train is periodically driven by pulsed energy releases owing to some nonlinear physical processes in association to magnetic reconnection, such as the repetitive generation, coalescence, and ejection of plasmoids, oscillatory reconnection and modulation of magnetic reconnection by external disturbances. Quasi-periodic motions in solar eruptions, such as the unwinding motion of erupting twisted filament threads and the expansion of coronal loops, can also launch broad QFP wave trains in the corona. In addition, it is also noted that some periods in the QFP wave trains are possibly connected to leakage of photospheric and chromospheric three- and five- minute oscillations into the corona. The generation mechanism of QFP wave trains may be diverse and more complicated than we thought; therefore, it should be pointed out that a specific QFP wave train might be generated by a single physical process or by the combination of different ones.

Despite the significant progress achieved in both theoretical and observational aspects of the study of coronal QFP wave trains over the last decade, thanks to the high spatio-temporal resolution and full-disk, wide temperature coverage observations taken by SDO and the tremendous improvement in computational and calculation techniques, there are still many important open questions that deserve further in-depth investigation. The following is a list of some outstanding issues.

• i) Statistical surveys considering large samples should be performed to explore the common properties of QFP wave trains. So far, only Liu et al. (2016) has performed a preliminary survey based on the database of global EUV waves, where the authors found a high occurrence rate of QFP wave trains. In addition, the present review, as well as Liu and Ofman (2014), also provides a simple statistical study of QFP wave trains observed by the AIA using published events. Since the intensity variations caused by narrow QFP wave trains are too small to be observed in the direct EUV images, one should alternatively use the running-difference or running-ratio images to search for narrow QFP wave trains. Coupled with the difficulties caused by AIA’s massive data base, one needs to develop sophisticated automatic-detection software to perform a complete survey and obtain more reliable physical parameters and other properties of QFP wave trains.

• ii) The excitation mechanisms of QFP wave trains are still unclear, although various possible mechanisms have been proposed in previous studies. High spatio-temporal resolution, multi-angle observations, three-dimensional radiation MHD simulations using more realistic initial conditions, and data-driven simulations that use multi-wavelength observations in tandem with MHD simulations are all required to clarify the real excitation mechanism of QFP wave trains as well as the waveguide properties. In addition, more attention should be paid to the possible excitation of QFP wave trains by the leakage of photospheric and chromospheric three- and five- minute oscillations into the corona. As discussed in Section 3.3, one needs to consider which mechanism is more suitable for what kind of QFP wave trains, or are there any new generation mechanisms?

• iii) QFP wave trains are typically associated with flares, but not all flares cause QFP wave trains. In addition, QFP wave trains show no obvious dependence on flare-energy class. It is worth investigating which type of flare tends to favor the occurrence of QFP wave trains. Our survey based on the published events suggests that broad QFP wave trains are associated with more energetic flares than the narrow ones. Liu et al. (2016) found an interesting trend of preferential association of QFP wave trains with successful solar eruptions accompanied by CMEs based on the study of two flare-productive active regions. Wang and Zhang (2007) found that failed and successful solar eruptions tend to occur closer to the magnetic center and the edge of active regions, respectively. Do QFP wave trains also have such a location preference that they occur more frequently in association with flares close to the edge of active regions? These special trends of preferential association with flares need further statistical investigations using large statistical samples of QFP wave trains.

• iv) The relationship between QFP wave trains and QPPs in solar and stellar flares deserves further in-depth investigation. These investigations can help us diagnose the flaring process and the physical properties of the waveguides, the solar and stellar coronal conditions, as well as the generation mechanism of QFP wave trains.

• v) Studies based on high temporal resolution radio observations combined with EUV imaging observations are important to investigate the fine physical processes involved in the generation of QFP wave trains. The relationship between narrow and broad QFP wave trains is worth studying to answer why they appear together in some events but separately in other individual ones. Does this mean different generation mechanisms or different propagation conditions? For broad QFP wave trains propagating in large-scale areas, they will inevitably interact with remote coronal structures such as coronal holes, active regions, filaments, and coronal loops. The phenomena occurring during these interactions can be applied to coronal seismology to diagnose the physical properties of the structures and the local coronal conditions.

• vi) Since QFP wave trains carry energy away from eruption source regions and propagate along or across magnetic-field lines, it is important to investigate their possible roles in energy transport, coronal heating, and the acceleration of solar wind.

Future studies of QFP wave trains will benefit from joint observations by ground-based and space-borne solar telescopes. Especially, the massive database of SDO remains to be fully exploited with sophisticated automatic-detection techniques. Solar Orbiter, launched in 2020, operates both in and out of the ecliptic plane images the polar regions of the Sun (Müller et al., 2020); the EUV imager and spectrometer onboard can make further contributions to the investigation of QFP wave trains. In addition, the combination of SDO and Solar Orbiter can make a stereoscopic diagnosis of QFP wave trains. Other solar telescopes including the 4-meter Daniel K. Inouye Solar Telescope (DKIST: Rast et al., 2021), the Advanced Space-based Solar Observatory (ASO-S: Gan et al., 2019), the Goode Solar Telescope (GST: Cao et al., 2010; Goode et al., 2010), the New Vacuum Solar Telescope (NVST: Liu et al., 2014), the Interface Region Imaging Spectrograph (IRIS: De Pontieu et al., 2014), and the Parker Solar Probe (PSP: Fox et al., 2016) are all important for diagnosing the eruption source region and the associated magnetic-reconnection process. A combination of the measurements of magnetic field, spectroscopy, imaging, and in-situ observations provided by these solar telescopes and high temporal-resolution radio telescopes will undoubtedly lead to a significant breakthrough in the comprehensive understanding of coronal QFP wave trains in the future.