Simultaneous Longitudinal and Transverse Oscillations in an Active-Region Filament

Abstract

We report on the co-existence of longitudinal and transverse oscillations in an active-region filament. On March 15, 2013, an M1.1 class flare was observed in Active Region AR 11692. A coronal mass ejection (CME) was found to be associated with the flare. The CME generated a shock wave that triggered the oscillations in a nearby filament, situated south-west of the active region as observed from National Solar Observatory (NSO) Global Oscillation Network Group (GONG) H$\alpha$ images. In this work we report the longitudinal oscillations in the two ends of the filament, which co-existed with the transverse oscillations. We propose a scenario in which an incoming shock wave hits the filament obliquely and triggers both longitudinal and transverse oscillations. Using the observed parameters, we estimate the lower limit of the magnetic field strength. We use a simple pendulum model with gravity as the restoring force to estimate the radius of curvature. We also calculate the mass accretion rate that causes the filament motions to damp quite fast.

1 Introduction

Filaments support both longitudinal and transverse oscillations (see, Arregui, Oliver, and Ballester, 2012). The oscillations in the filaments can be used to diagnose the local plasma conditions and magnetic field by applying the principle of magnetohydrodynamic (MHD) seismology (see, Nakariakov and Verwichte, 2005; Andries, Arregui, and Goossens, 2005). These oscillations are broadly classified as large amplitude (Tripathi, Isobe, and Jain, 2009) and small amplitude (Oliver and Ballester, 2002) oscillations. Large amplitude transverse oscillations, where a filament oscillates as whole, are often associated with the disturbances coming from nearby flares (Ramsey and Smith, 1966; Isobe and Tripathi, 2006; Okamoto et al., 2004; Hershaw et al., 2011; Schmieder et al., 2013; Pant et al., 2015). In contrast, large amplitude longitudinal oscillations are always found to be associated with small energetic events such as a subflare at one leg of the filament (Jing et al., 2003), a small flare in a nearby active region (Jing et al., 2006; Vršnak et al., 2007; Li and Zhang, 2012) or jets (Luna et al., 2014). There have been several reports on large amplitude longitudinal oscillations (Jing et al., 2003, 2006; Vršnak et al., 2007; Luna and Karpen, 2012; Luna, Díaz, and Karpen, 2012; Zhang et al., 2012; Luna et al., 2014). Luna and Karpen (2012) developed a one-dimensional (1D) self-consistent model that explained both restoring force and damping of large amplitude longitudinal oscillations. The model is analogous to an oscillating pendulum assuming the radius of curvature of the magnetic dip as the length of the pendulum. Luna et al. (2014) used this model to explain the strong damping of large amplitude longitudinal oscillations observed in filament threads. Recently, Luna et al. (2016) performed 2D non-linear time-dependent MHD simulations where a magnetic field can become distorted in response to the mass loading. The authors have reported that a simple pendulum model can be used to characterise the large amplitude longitudinal oscillations even in a scenario where the magnetic field responds to the plasma motions.

Damping of oscillations have been observed in large amplitude transverse oscillations (Hershaw et al., 2011; Pant et al., 2015). Goossens, Andries, and Arregui (2006), Arregui et al. (2007) used seismology to combine the damping time and period of oscillations in a consistent manner to estimate the magnetic field strength and inhomogeneity length scale in the coronal loops. Arregui et al. (2008) applied the same technique to the oscillating threads of a prominence. Pant et al. (2015) applied this technique to estimate the magnetic field and the inhomogeneity length scale of a filament as whole.

In addition to transverse oscillations, large amplitude longitudinal oscillations are also found to be damped (Luna and Karpen, 2012; Luna et al., 2014). Unlike transverse oscillations, which are now believed to be damped by resonant absorption, the damping mechanisms in longitudinal oscillations are not well understood. Several damping mechanisms have been proposed, e.g. energy leakage (Kleczek and Kuperus, 1969), dissipation (Tripathi, Isobe, and Jain, 2009), but these mechanisms are under debate. However, mass accretion due to the condensation of filament material (Luna and Karpen, 2012; Luna et al., 2014, 2016; Ruderman and Luna, 2016) is shown to be a promising way to explain the damping of longitudinal oscillations in a filament. Recently, Ruderman and Luna (2016) have reported the evidence of strong damping of longitudinal oscillations in the filament threads that are modelled as a curved magnetic tube.

Shen et al. (2014) reported that an incoming shock wave can trigger longitudinal and transverse oscillations in filaments depending on the interaction angle between the filament and the shock wave. Gilbert et al. (2008) has reported the co-existence of two transverse oscillation modes in a filament, one in the plane of sky and another along the line of sight. These modes occurred in response to a Moreton wave. Both modes were perpendicular to the filament axis. In this work, we report a unique observation of the co-existence of large amplitude damped longitudinal oscillations and large amplitude damped transverse oscillations in an active-region filament. The article is organised as follows. In Section 2 we describe the observations. In Section 3 we discuss the methods of the data analysis. We present the results in Section 4, which is followed by the discussion and conclusions in Section 5.

2 Observation

An M1.1 class flare was observed by the GOES satellite in Active Region AR 11692 on March 15, 2013. The flare was associated with a halo coronal mass ejection (CME). The flare created a global disturbance in the active region. The CME associated with the flare produced a shock wave. To observe shock fronts, we created running-difference images of AIA 193 Å. The shock fronts are marked with red and orange arrows in Figure 1. It is evident from Figure 1 that the shock fronts are moving outward.

Figure 1

Difference images of AIA 193 Å at four different time instances. Arrows in red and orange represent the shock front.

A filament was lying to the south-west of the active region as seen in H$\alpha$ images from NSO/GONG (Figure 2). NSO/GONG provides full-disk observation of the Sun in 6563 Å (H$\alpha$). It has a pixel resolution of ${\sim}\,1.07''$ and a cadence of 1 sec. The observational data used in this study are obtained from 06:00:54 UT to 10:22:54 UT. The flare started at 05:46:00 UT, peaked at 06:58:00 UT, and ended at 08:35:00 UT as recorded in the GOES catalogue. We note that immediately after the onset of the flare, oscillations were triggered in the filament.

Figure 2

NSO/GONG H$\alpha$ image of the filament lying south-west of Active Region AR 11692. The image was taken on March 15, 2013 at 06:55:22 UT. The bright ribbons correspond to the M1.1 class flare. Two broad artificial slices along the axis of the filament, used to generate x – t maps, are overplotted. Three artificial slits perpendicular to the axis of the filament are overplotted in green, red, and yellow, which were used in Pant et al. (2015) to investigate the transverse oscillations.

Filaments consist of fine threads that are not often seen in GONG H$\alpha$ images because of its poor spatial resolution. Therefore, we used the images from the extreme ultraviolet (EUV) passbands of the Atmospheric Imaging Assembly (AIA) onboard the Solar Dynamics Observatory (SDO). The AIA instrument provides almost simultaneous full-disk images of the Sun in seven EUV bands. It has a spatial resolution of $1.3''$, a pixel size of $0.6''$, and a cadence of 12 s (Lemen et al., 2012). We find that the filament consists of several threads that are seen more clearly in AIA 171 Å than in any other EUV passband of AIA. Therefore, we use AIA 171 Å for the further analysis. Moreover, we find that shortly after the oscillations started, the full-disk images of the Sun were not available from 06:22:23 UT to 07:36:00 UT. Thus, the first cycle of oscillations is not seen in AIA 171 Å.

We overplot the contours of the filament as seen in GONG H$\alpha$ over the magnetogram obtained from the Helioseismic and Magnetic Imager (HMI) onboard SDO (Figure 3). We find that the filament lies above the region that separates positive and negative polarities. We note from the movie (available online) that at 06:11:59 UT, i.e. before eruption, the filament material as enclosed in two different contours is part of the same filament (Pant et al., 2015, right panel of Figure 1).

Figure 3

Left: GONG H$\alpha$ image taken on March 15, 2013 at 09:28:45 UT. Right: HMI magnetogram taken at 09:28:59 UT. Overplotted red contours outline the position of the filament.

By careful inspection of the H$\alpha$ images in the movie (available online), it appears that both longitudinal and transverse oscillations are present simultaneously in the filament. In the movie we mark the filament in AIA images with a green arrow. The transverse oscillations in the filament under study have been reported in Pant et al. (2015). In this article we focus on longitudinal oscillations at two parts of the filament adjacent to its two ends.

3 Data Analysis

3.1 GONG H$\alpha$

To investigate the longitudinal oscillations in GONG H$\alpha$ images, we place two artificial broad slices, slit 1 and slit 2 along the axis of the filament as shown in Figure 2. The length (width) of the first and second slice is 130 pixel (15 pixel) and 60 pixel (20 pixel), respectively. The filament is oscillating in both transverse and longitudinal directions simultaneously. We choose broad slices so that the filament material remains inside the slices in spite of the transverse oscillations.

To further characterise the longitudinal oscillations in the filament, first we create a time-distance (x – t) map with time in x-axis and distance along the slice in y-axis for slits 1 and 2. The intensity along each column of the x – t map is fitted with a Gaussian curve. The mean value and one-sigma error of the intensity is estimated. Finally, the x – t map is fitted with a damped sinusoidal function to investigate the oscillation characteristics. Since the filament is oscillating and the amplitude of the oscillations is decreasing with time, it can be fitted with a damped sinusoidal function (assuming the mass of the filament to be constant) and represented as (Aschwanden et al., 1999),

$$ y(t)=c+A_{\sin}\sin(\omega t+\phi_{\sin})e^{-t/\tau_{\sin}}, $$

(1)

where $c$ is a constant, $A_{\sin}$ is the amplitude, $\tau_{\sin}$ is the damping time, $\omega$ is the angular frequency, and $\phi_{\sin}$ is the initial phase of sinusoidal function. The least-squares fitting is done using the function MPFIT.pro in Interactive Data Language (IDL) (Markwardt, 2009). It has been shown that if a filament accretes mass, then the Bessel function describes the oscillations better than the damped sinusoid (Luna and Karpen, 2012). Therefore, we fit the x – t map using a damped zeroth-order Bessel function of the first kind, represented by

$$ y(t)=c_{1}+A_{\mathrm{bes}} J_{0} (\omega t+ \phi_{\mathrm{bes}})e^{-t/\tau_{\mathrm{bes}}}, $$

(2)

where $c_{1}$ is a constant, $A_{\mathrm{bes}}$ is amplitude, $\omega$ is the angular frequency, $\tau_{\mathrm{bes}}$ is the damping time, and $\phi_{\mathrm{bes}}$ is the phase of the Bessel function.

3.2 AIA 171 Å

We repeat the analysis on AIA 171 Å images, but with only one artificial slice. The filament material at the position of slit 2 is not clearly seen in AIA 304, 171, and 193 Å because of overlying post-flare loops (see movie).

4 Results

4.1 GONG H$\alpha$

The period, damping time, and amplitude estimated from the fitting of a damped sinusoidal function represented by Equation (1) are summarised in Table 1. The period, damping time, and amplitude estimated from the fitting of a damped zeroth-order Bessel function of the first kind represented by Equation (2) is summarised in Table 2. In the right panel of Figure 4, we overplot dashed green lines at three time instances. It is evident that both ends of the filament started oscillating in different phase. It is also worth noting that the oscillations started at different times in the two ends of the filament.

Figure 4

The upper left panel shows the x – t map of slit 1. The starting time is March 15, 2013 at 06:00:54 UT. The thick black vertical strip represents a data gap between 07:07:54 UT to 07:18:54 UT. The time period, amplitude, and damping time obtained from fitting is mentioned at the top of the plot. The lower left panel is the same as the upper left panel, but for slit 2. In the upper right panel we plot the fitted damped sinusoidal curve with a one-sigma error bar. The lower right panel is the same for slit 2. Three vertical dashed lines over plotted at three time instances show that the oscillations started with different phases. The dotted black curve represents the best-fit damped sinusoidal function, while the orange curve represents the damped Bessel function.

Table 1 Table of parameters of the damped sine fitting

Table 2 Table of parameters of the modified Bessel function fitting

4.2 AIA 171 Å

The oscillation period is found to be 57±3 min, which is similar to the period estimated at the position of slit 1 in GONG H$\alpha$. The damping time is estimated to be 100 min, which is longer than the damping time estimated using slit 1 in GONG H$\alpha$ images. The oscillation amplitude is found to be 10 Mm, which is less than the amplitude measured in GONG H$\alpha$ images. The main reason for the long damping time and smaller amplitude is that the first oscillation cycle is missed in AIA 171 Å images, therefore the oscillations start after 100 min, as shown in Figure 5 (right panel). We note from Figure 4 (top right panel) that the estimated damping time of oscillations and amplitude are strongly dependent on the first oscillation cycle. If the first oscillation cycle is missed, then the damping time is longer and the amplitude is smaller. Another reason can be that the filament threads apparently merge and separate during the oscillations. This may be attributed to the fact that multiple threads are stacked along the line of sight. If they are not moving in phase, then it may appear that they are merging and separating. This is probably also related to the presence of transverse oscillations because this effect is not reported in earlier studies (Luna and Karpen, 2012) where only longitudinal oscillations were present. Therefore, choosing the thread that is associated with the oscillations is very challenging (see right panel of Figure 5). It is worth noting at this point that we did not fit a damped Bessel function to the AIA dataset because, as said above, the first oscillation cycle is missed, thus the Bessel function will not give the correct estimate of the damping time.

Figure 5

The left panel shows the AIA 171 Å image taken at March 15, 2013 at 08:51:23 UT with artificial slice overplotted on the filament. The right panel represents the x – t map corresponding to the curve artificial slice shown in the left panel. The starting time is March 15, 2013 at 06:00:54 UT. The thick black vertical strip represents the data gap between 07:07:54 UT to 07:18:54 UT. The black curve represents the best-fit sinusoidal function. The time period, amplitude, and damping time obtained from fitting is listed at the top.

4.3 Radius of Curvature of the Magnetic Dip

Filament material is supported by the magnetic fields against gravity. We use a simple pendulum model to estimate the oscillation parameters (Luna and Karpen, 2012). Assuming the restoring force to be gravity, we obtain the following equation

$$ \omega=\frac{2\pi}{P}=\sqrt{\frac{g_{0}}{R}}, $$

(3)

where $g_{0}$ is the Sun’s surface gravity, $\omega$ is the oscillation frequency, $P$ is the period of oscillation, and $R$ is the radius of curvature. Using Equation (3), the radius of curvature in GONG H$\alpha$ images is estimated to be ∼ 80 Mm and 85 Mm at the position of dip 1 (where the first slice is placed) and dip 2 (where the second slice is placed; see Figure 2), respectively. Similarly, the radius of curvature at the location of dip 1 (see left-hand panel of Figure 5, where the artificial slice is placed) in AIA 171 Å is estimated to be 80 Mm.

4.4 Estimation of Magnetic Field Strength

We calculate a lower limit of the magnetic field strength, assuming that magnetic stress is balanced by the weight of the filament material present in a dip (Luna and Karpen, 2012), using the following expression,

$$ B(G) \geq26 \biggl( \frac{n_{e}}{10^{11}} \biggr)^{\frac{1}{2}} P , $$

(4)

where $B$ is the magnetic field, $n_{e}$ is the electron number density in cm⁻³, and $P$ is the oscillation period in hours. Here we use the typical value of the electron number density $10^{11}~\mbox{cm}^{-3}$ as reported in Labrosse et al. (2010). Therefore, the minimum magnetic field strength is estimated to be ∼ (25 ± 1) G in dips 1 and 2, which is consistent with the typical values of the measured magnetic fields in the filaments (Labrosse et al., 2010; Mackay et al., 2010). Since the period of oscillation is estimated to be the same using AIA 171 Å, the estimated magnetic field strength remains unchanged.

4.5 Estimation of the Mass Accretion Parameter

In the model given by Luna and Karpen (2012), the damping of longitudinal oscillations in threads of the filaments is explained by the accretion of filament material. We calculate the mass accretion rate from the best-fit parameters of the damped Bessel function (represented by Equation (2)), using the following relation (Luna et al., 2014),

$$\alpha=\frac{\omega m_{0}}{\phi_{\mathrm{bes}}}, $$

where $m_{0}$ is the initial mass of the filament, and $\omega$ and $\phi_{\mathrm{bes}}$ are obtained from fitting the damped Bessel function. The mass of a filament, $m_{0}$, can be calculated as $m_{0}=1.27 m_{p} n_{e} \pi r^{2} L$, where $r$ and $L$ are the radius and the length of the thread of the filament. We take the typical radius of a filament thread to be 100 km as assumed in Luna et al. (2014). The length of the thread is estimated using an x – t map, as shown in Figure 4 (top panel). As explained above, the artificial slit is placed along the length of the filament. Thus the extent of the brightness along each column of the x – t map gives an estimate of the length of the filament thread at a particular time instance. The length of the filament thread is measured at various time instances (i.e. along different columns) from the start to the end of the oscillations. Finally, we estimate the mean value of the length of the filament thread ∼ 23± 7 Mm at the position of slit 1. Following the above procedure, the length of the filament thread at the position of slit 2 is estimated to be ∼ 10±4 Mm. It should be borne in mind that estimating the length of the filament thread at the position of slit 2 is uncertain because the oscillations are not clearly seen in the x – t maps, as shown in the bottom panel of Figure 4. Under these assumptions, we estimated the mass accretion rate at the position of slits 1 and 2 to be ∼ ($51 \pm 17\times10^{6}~\mbox{kg}\,\mbox{hr}^{-1}$) and ($192 \pm 72 \times 10^{6}~\mbox{kg}\,\mbox{hr}^{-1}$), respectively. The derived mass accretion rate at the position of slit 1 is comparable to those reported in earlier studies (Luna et al., 2014). It should be noted that at the position of slit 2 the mass accretion rate is higher, while the damping time is longer. One of the reasons for this discrepancy is the uncertainty in the fitting parameters. The mass accretion rate depends on the phase of the Bessel function, which is estimated from the best-fit parameters. Therefore, if the fitting of a function is poor, then the value of phase will have large errors and thus cannot be trusted.

4.6 Possible Existence of Both Longitudinal and Transverse Waves Driven by Kink Oscillations

In this subsection we investigate the possibility that both longitudinal and transverse oscillations may be driven by kink oscillations. We assume the filament has the shape of a cylinder embedded in a uniform plasma with low plasma $\beta$. The magnetic field is assumed to be constant inside the cylinder, and the effects of gravity are ignored. The model set-up is similar to the one described in Yuan and Van Doorsselaere (2016). To derive the variation of thermodynamic quantities, linearised ideal MHD equations are used (see Ruderman and Erdélyi, 2009),

$$\begin{gathered} \rho=- \nabla \cdot (\rho_{0} \xi), \end{gathered}$$

(5)

$$\begin{gathered} \rho_{0} \frac{\partial^{2} \mathbf{ \xi} }{\partial t^{2}}=-\nabla(p + \mathbf{b}\cdot\mathbf{B}_{0}/ \mu_{0}) + \frac{1}{\mu} \bigl[( \mathbf{B}_{0}\cdot\nabla)\mathbf{b} + (\mathbf{b}\cdot\nabla) \mathbf{B}_{0}\bigr], \end{gathered}$$

(6)

$$\begin{gathered} \mathbf{b}=\nabla\times(\boldsymbol{ \xi} \times\mathbf{B}_{0}), \end{gathered}$$

(7)

$$\begin{gathered} p - C_{s} ^{2} \rho= \mathbf{\xi} \cdot \bigl(C_{s} ^{2} \nabla\rho_{0} - \nabla p_{0}\bigr), \end{gathered}$$

(8)

where $\xi$ is the Lagrange displacement vector, $\rho$, $p$, and b are perturbed quantities, while $\rho_{0}$, $p_{0}$, and B ₀ are unperturbed quantities. Neumann boundary conditions are assumed at $r=a$

$$\begin{gathered}{} [P_{T}]_{r=a}=0, \\ [\xi_{r}]_{r=a}=0, \end{gathered}$$

and Dirichlet boundary conditions are assumed at $r=0,\infty$

$$\begin{gathered} P_{T}|_{r=0}< \infty, \\ \xi^{2}|_{r=0}=\infty, \\ P_{T}|_{r\rightarrow\infty}=0, \\ \xi|_{r\rightarrow\infty}=0, \end{gathered}$$

where $P_{T}$ is the total pressure.

For a filament, we define $\omega$, $\omega_{A}$, $\omega_{T}$ as kink, Alfvén, and tube oscillation frequency, respectively, and the tube speed, $C_{T}$, is given by $C_{T}=\frac{C_{A}C_{s}}{\sqrt{C_{A}^{2}+C_{s}^{2}}}$, where $C_{A}=\frac{B_{0}}{\sqrt{\mu_{0}\rho_{0}}}$ is the Alfvén speed and $C_{s}=\sqrt{ \frac{\gamma p_{0}}{\rho_{0}}}$ is the sound speed. $B_{0}$, $p_{0}$, and $\rho_{0}$ are the equilibrium magnetic field, plasma pressure, and plasma density, respectively, and $\mu_{0}$ is the magnetic permeability in free space. For a kink mode ($m=1$), the total pressure perturbation, $P_{T1}=p + \mathbf{b}\cdot\mathbf{B}_{0}/ \mu_{0}$, in the filament is assumed to be

$$ P_{T1} = A R(r) \cos(\omega t) \sin(kz) \cos(\phi) , $$

(9)

where $A$ is the amplitude of the total perturbed pressure. Since a kink mode is not axisymmetric, $\cos(\phi)$ dependence is assumed. Substituting Equation (9) into Equations (5) – (8) yields

$$ \frac{\mathrm{d}^{2}P_{T1}}{\mathrm{d}r^{2}}+\frac{\mathrm{d}P_{T1}}{r\,\mathrm{d}r}-\biggl(\kappa^{2}_{r}+ \frac {1}{r^{2}}\biggr)P_{T1}=0, $$

(10)

where

$$ \kappa^{2}_{r} = \frac{(\omega_{s}^{2}-\omega^{2})(\omega _{A}^{2}-\omega^{2})}{(\omega_{s}^{2}+\omega_{A}^{2})(\omega _{T}^{2}-\omega^{2})}k^{2}, $$

(11)

where $\omega_{s}^{2}=k^{2} C_{s}^{2}$. Equation (10) should also hold true for $R(r)$. In this work we confine ourselves to the inside of the flux tube. From solving Equation (10) for $R(r)$, we therefore obtain

$$R=J_{1}\bigl(|\kappa_{r}|r\bigr) . $$

In cylindrical coordinates, $v_{r}$ is the perturbed velocity amplitude of the transverse oscillation and $v_{z}$ is the perturbed velocity amplitude of the longitudinal oscillation. Inside the cylinder, the perturbed radial and axial components of the velocity amplitude are defined as (see Yuan and Van Doorsselaere, 2016, for details)

$$v_{r}=-\frac{r\,\mathrm{d}R}{R\,\mathrm{d}r} \sin(\omega t) \sin(kz) \cos(\phi) $$

and

$$v_{z} = - \frac{C_{T}^{2}}{C_{A}^{2}}kr\frac{\omega^{2}-\omega _{A}^{2}}{\omega^{2}-\omega_{T}^{2}} \sin(\omega t) \cos(kz) \cos (\phi). $$

Thus, the axial-to-radial velocity amplitude ratio is given by the following expression:

$$ \frac{v_{z}}{v_{r}}=k\frac{C_{T}^{2}}{C_{A}^{2}}\frac{R}{\frac {\mathrm{d}R}{\mathrm{d}r}} \frac{\omega^{2}-\omega_{A}^{2}}{\omega^{2}-\omega _{T}^{2}}\operatorname{cot}(kz) . $$

(12)

We take the length of slit 2 as the length of the filament, which is estimated to be 90 Mm. The radius of the filament is estimated to be ∼ 1 Mm. It is important to note that here we assume the length of the flux tube (modelled as a filament) as the length of the slit covering the filament material because here we compare longitudinal oscillations with the transverse oscillations as reported by Pant et al. (2015), where the authors assumed that the filament was oscillating as a whole in the transverse direction. To estimate the ratio of the axial-to-radial velocity amplitude, we choose three slit positions that we show in green, red, and yellow lines in Figure 2; these were used by Pant et al. (2015). From observations, we find that the ratio of the longitudinal velocity amplitude to the transverse velocity amplitude at these locations is 3.92, 3.26, and 2.22, respectively. Using Equation (12), we estimate the ratio to be $4 \times 10^{-4}$, $2 \times 10^{-4}$, and $1 \times 10^{-5}$, respectively, assuming the typical value of the sound speed in the chromosphere to be 15 km s⁻¹, the Alfvén speed at the three slit positions as 82, 88, and 91 km s⁻¹, respectively, and the perturbation frequency (assumed to be equal to the kink oscillation frequency) to be 117, 124, and 128 km s⁻¹, respectively (see, Pant et al., 2015). It should be borne in mind that a linear analysis is presented here. Considering the observed displacement to be large, non-linear effects would become important. Therefore to model such events, more studies are needed. Nevertheless, from the above analysis, we note that it is almost impossible to detect longitudinal oscillation in low-$\beta$ plasma as a result of a fast kink mode in our observation. Therefore, large amplitude longitudinal oscillations cannot be the kink mode.

5 Interaction of the Shock with the Filament

In this section, we explore the most likely mechanism for driving the longitudinal and transverse oscillations in a filament channel. Shen et al. (2014) reported that shock waves can interact with filaments in two possible geometries. If shock waves occur such that the normal vector to the shock wave is perpendicular to the filament axis, then a filament oscillates in the transverse direction, while if the shock wave interacts with a filament such that the normal vector of the shock wave is parallel to the filament axis, then a filament oscillates in the longitudinal direction. Here we propose a more general scenario, where a shock wave interacts obliquely with the filament such that the filament material oscillates in both transverse and longitudinal directions, as revealed from our observations. The position of the shock fronts in our observations are clearly seen in Figure 1. However, it should be borne in mind that from observations it is not straightforward to determine the direction of the shock with respect to the filament because the filament is in close proximity to the active region and is associated with overlying loops that expand in response to the shock wave. This makes it extremely difficult to determine the orientation of the shock wave.

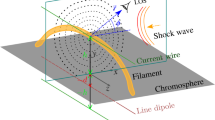
We depict this by a cartoon in Figure 6. We show that when a shock wave hits a filament obliquely, the normal vector to the wave front, $\hat{n}$ (shown in dark red), can be decomposed into perpendicular ($n_{\bot}$) and parallel ($n_{||}$) components as shown in Figure 6 in blue. The component parallel to the filament axis triggers the longitudinal oscillations in the filament, while the component perpendicular to the filament axis triggers the transverse oscillations in the filament. Thus the shock front interacts with the filament at dip 1 and displaces the filament material in both transverse and longitudinal directions. Similarly, in dip 2 the shock front displaces the plasma in both transverse and longitudinal directions, but at a different time. With this schematic picture we can explain the different start times of the longitudinal oscillation at the two ends of the filament. However, with this scenario, we would expect the transverse oscillations to be present at the locations of both dips, but transverse oscillations are only observed at the location of dip 1. It is worth noting that this is the simple geometry. In principle, many parts of the shock wave can interact with the filament at different orientations and can excite different modes. More detailed studies are needed to confirm this.

Figure 6

A cartoon depicting the interaction of a shock wave with a filament. The filament has two magnetic dips, dip 1 and dip 2. The filament material is shown in green. The shock wave front is represented by red curves. The normal vector to the shock wave front is shown in dark red. Arrows in blue represent the parallel and perpendicular components of the normal vector.

6 Summary and Conclusions

In this work, we find the co-existence of longitudinal and transverse oscillations in an active-region filament as observed by NSO/GONG H$\alpha$. The oscillations are triggered by the interaction of a shock wave with the filament. We find that the oscillations in the two ends of the filament started with different phases, but with an almost identical oscillation period. We note that the longitudinal oscillations at the two slit positions started at different times (see Figure 4), possibly because the shock wave front interacted with the two parts of the filament at different time instances. We depict this with a schematic diagram (see Figure 6).

The damping time at the position of slit 1 is estimated to be 46 minutes. This is slightly too long compared to the earlier reports (Tripathi, Isobe, and Jain, 2009) and comparable to what is reported in Luna et al. (2014). Luna and Karpen (2012) suggested that the mass accretion of the filament material is responsible for damping. We find the mass accretion rate to be $51 \pm 17 \times10^{6}~\mbox{kg}\, \mbox{hr}^{-1}$ at the position of slit 1 and $192 \pm 72 \times10^{6}~\mbox{kg} \,\mbox{hr}^{-1}$ at the position of slit 2, which is comparable with the earlier reports (Luna et al., 2014). We performed the filament seismology and estimated the magnetic field strength at two dip locations. We estimated the lower limit of the magnetic field strength ∼ (25 ± 1) G at the location of both the slices, which is consistent with typical values of the measured magnetic field from observation (Mackay et al., 2010). We also calculate the radius of curvature of the two magnetic dips of the filament as 80 Mm and 85 Mm for dips 1 and 2, respectively.

Based on our observations, we exclude the possibility that transverse and longitudinal oscillations could be simultaneously driven by a fast kink mode. Longitudinal oscillations due to a kink wave may be present, but their amplitude is much smaller than the amplitude of the longitudinal oscillations observed in this case. This shows that transverse and longitudinal oscillations exist independently in the filament under study.