Flux Accretion and Coronal Mass Ejection Dynamics

Abstract

Coronal mass ejections (CMEs) are the primary drivers of severe space weather disturbances in the heliosphere. Models of CME dynamics have been proposed that do not fully include the effects of magnetic reconnection on the forces driving the ejection. Both observations and numerical modeling, however, suggest that reconnection likely plays a major role in most, if not all, fast CMEs. Here, we theoretically investigate the accretion of magnetic flux onto a rising ejection by reconnection involving the ejection’s background field. This reconnection alters the magnetic structure of the ejection and its environment, thereby modifying the forces acting upon the ejection, generically increasing its upward acceleration. The modified forces, in turn, can more strongly drive the reconnection. This feedback process acts, effectively, as an instability, which we refer to as a reconnective instability. Our analysis implies that CME models that neglect the effects of reconnection cannot accurately describe observed CME dynamics. Our ultimate aim is to understand changes in CME acceleration in terms of observable properties of magnetic reconnection, such as the amount of reconnected flux. This flux can be estimated from observations of flare ribbons and photospheric magnetic fields.

1 Introduction

In a coronal mass ejection (CME), magnetic forces in the low corona accelerate a hot (${\sim}\,1$ MK) mass (${\sim}\,10^{15}\mbox{ g}$) of magnetized plasma at high speed (from a few hundred km s⁻¹ at the slow end of the observed range to 2000 km s⁻¹ or more at the fast end) into interplanetary space. These events are the primary drivers of severe space weather disturbances at Earth (Kahler, 1992). While CMEs are believed to be driven by the release of magnetic energy stored in electric currents in the solar corona (e.g., Forbes 2000), key aspects of their initiation and subsequent evolution are not well understood. Characterizing the processes at work during the eruption process is therefore essential to understand their dynamics.

Here, we present a model of the development of fast CMEs, the “flux accretion” CME model, which describes how reconnection affects the dynamics and structure of fast CMEs as they form. Simply put, the central thesis of the model is that magnetic reconnection underneath a rising ejection can accelerate the ejection both: i) directly, by momentum transfer from the reconnection outflow jet; and ii) indirectly, from the reconnection-modified magnetic structure of the ejection and its surrounding magnetic field. As explained in detail in subsequent sections, we believe the second, indirect acceleration mechanism is the dominant influence. The model is not directly focused on CME initiation, but rather on the evolution of CMEs after their rise has been triggered.

The effect of reconnection on CME dynamics is ignored in models of CME acceleration that only include forces that would be present if reconnection did not modify the ejection and its background field. For instance, Kliem and Török (2006) model CMEs as the expansion of a torus. Their model requires reconnection to occur for the torus to “slide” through overlying field, but they neglect dynamic effects due to changes in the ejection’s magnetic field arising from this reconnection. Most importantly, reconnection would cause poloidal flux that was initially external to the expanding torus to become entrained with it. This additional flux would produce a hoop force leading to greater acceleration of the torus than would occur without the added poloidal flux.

We argue that reconnection should fuel further reconnection, as magnetic flux external to the ejection is pulled into the low-density void created by the ejection’s increasingly rapid rise. Note that this “pull” reconnection (e.g., Yamada et al. 1997, Kusano et al. 2012) is driven by the evolution of the global system; no local driver of reconnection inflow is needed. We remark that hints of the CME’s rapid acceleration driving further reconnection to occur were seen in simulations that exhibited numerically problematic cavitation in the wakes of CMEs after reconnection began (MacNeice et al., 2004): the numerical difficulties arose when very low densities occurred near strong Lorentz forces in the outflow region. Note also that the sites of reconnection will tend to rise with time, as the low-density region trails the rising ejection.

The reinforcing interplay between the upward motion of the ejection and the reconnection – feedback – is effectively a macroscopic instability, which we refer to as a reconnective instability. We adopt this term because it is distinct from resistive instabilities, such as the tearing mode (Furth, Killeen, and Rosenbluth, 1963), since this feedback need not arise from the presence of resistivity per se: in some magnetic field configurations, the presence of resistivity (which enables reconnection) might not produce any feedback between reconnection and large-scale dynamics. For example, a current sheet (or “current ribbon” in 3D) should develop when the footpoints of an initially potential pair of bipoles are displaced a small distance, causing the coronal field, subject to fixed field-line connectivity, to evolve slightly away from the potential state (e.g., Longcope 1996). Onset of reconnection in such a system should decrease the current in the sheet.¹ In contrast, Longcope and Forbes (2014) found that “kinematic and quasi-static” flux transfers via reconnection across a current sheet in some configurations that they investigated “resulted in an increase in the size and strength of the current sheet.” They noted that if “large-scale dynamics” intensify some initial, local reconnection process, then a “resistive eruption mechanism” could operate. Sturrock (1989) qualitatively discussed a similar possibility. This suggests that, depending on how a large-scale system responds to a differential change in magnetic connectivity within the system, the configuration might be “reconnectively stable” or “reconnectively unstable.” Because this feedback effect would be inherently dynamic and nonlinear, it is not easily tractable with analytic methods. A large-scale reconnective instability would be distinct from both ideal MHD instabilities, which assume the field’s connectivity is fixed, and resistive instabilities, which do not necessarily produce feedback to the reconnection process. In a sense, the breakout configuration proposed by Antiochos, DeVore, and Klimchuk (1999) was intentionally engineered to become reconnectively unstable as the large-scale field is evolved by shearing on its boundary. While reconnective stability could be investigated in equilibrium configurations, a reconnective instability in CMEs might arise as a secondary instability when the system is already evolving away from equilibrium due to some other (perhaps ideal), primary instability (e.g., a kink instability).

It is possible that global-scale dynamics might depend sensitively upon the details of the reconnection process. In the pull-reconnection framework, the ejection will rise regardless of how quickly flux reconnects. The speed of this rise, however, likely will be affected by the rate at which the operating reconnection mechanism processes flux, because both the reconnection outflow and the ejection structure will differ from cases in which reconnection proceeded at different rates. This motivates theoretical or numerical investigations of eruption dynamics with varied reconnection parameters.

Our model fits within the overall framework of the “standard model” of eruptive flares, often called the CSHKP model (after Carmichael–Sturrock–Hirayama–Kopp–Pneumann, by Svestka and Cliver 1992; for a more recent review, see Webb and Howard 2012), which was essentially created to explain the formation and evolution of the two-ribbon emission pattern frequently associated with CMEs in terms of reconnection beneath a rising ejection. In the model, this reconnection leads, either directly or indirectly, to the acceleration of particles, which propagate downward along the newly reconnected magnetic fields toward the transition region and upper chromosphere. Here, they interact with the denser plasma to create hard X-rays via bremsstrahlung and heat the surrounding plasma. (Hudson 2011 and Benz 2008 provide excellent reviews.) The resulting intensity enhancements typically form two parallel, elongated emission structures, known as flare ribbons. Ribbons are often observed in H$\alpha$ and UV images (e.g., in the 1600 Å channel of the TRACE satellite; Handy et al. 1999), although some CMEs occur without ribbons or other obvious emission signatures (e.g., Robbrecht, Patsourakos, and Vourlidas 2009). Flare ribbons always straddle the polarity inversion line (PIL; where the photospheric radial magnetic field changes sign) beneath the ejection. It is presumed that the ribbon emission occurs on conjugate footpoints of newly reconnected magnetic flux. Observations typically show ribbons moving apart from each other (perpendicular to the PIL); in the CSHKP model, this arises naturally as reconnection successively acts on flux tubes with footpoints that are farther and farther apart.

Flare ribbons overlie strongly magnetized areas of the photosphere within and near active regions (ARs), and it was long ago hypothesized that the rate of (unsigned) magnetic flux being swept out by the ribbons as they move apart should be related to the rate of coronal magnetic reconnection (Forbes and Priest 1984, Poletto and Kopp 1986; for a recent observational study, see Hinterreiter et al. 2018). In a study of 13 halo CMEs with flares, Qiu and Yurchyshyn (2005) reported a very strong correlation between the total unsigned magnetic flux swept out by ribbons over the course of each event – which we hereafter refer to as the ribbon flux – and the CME speed: they found a linear correlation coefficient of 0.89. In a related study, Qiu et al. (2004) reported an association between the rate of flux being swept out by ribbons and CME acceleration. These findings are consistent: the time integral of acceleration yields velocity, and the time integral of the rate of magnetic flux being swept by ribbons (∝ acceleration) yields the total magnetic flux swept by ribbons (∝ velocity). Bein et al. (2012) suggested a “feedback relationship” between CME acceleration and the rate of magnetic reconnection that, in principle, is directly related to the rate of flux being swept out by ribbons. In numerical simulations of a CME’s formation and acceleration, Karpen, Antiochos, and DeVore (2012) also found that their model ejection’s acceleration was closely tied to the onset of fast reconnection beneath the rising ejection. More recently, Lynch et al. (2016) found a similar association between the onset of reconnection underneath a “stealth” ejection and acceleration of that ejection.

The idea that reconnection can affect the acceleration of CMEs dates at least to work by Anzer and Pneuman (1982), who noted that reconnection under the eruption “produces an increasing outward magnetic pressure gradient” across the CME. In addition, as Moore et al. (2001) later noted, reconnection under an eruption can also cut “magnetic tethers” (inward magnetic tension) restraining an eruption. Vršnak et al. (2004) observed that a “two-ribbon flare appears as a consequence of …fast magnetic field reconnection,” and then explicitly referred to a “feed-back relationship between the CME motion and the flare energy release.” More recently, Inoue et al. (2018) invoked “a nonlinear positive feedback process between the flux tube evolution and reconnection,” in which their numerically simulated ejection’s rise drove tether-cutting reconnection that, in turn, enabled the ejection to rise farther. Zhang and Dere (2006) also explored the idea of positive feedback between reconnection and CME acceleration. A concise passage in that paper’s concluding section discusses several ideas that we explore further below. We therefore quote this succinct paragraph in full:

“The temporal coincidence [between CME acceleration and flare radiative flux] also suggests that the CME run-away process and the magnetic reconnection process may mutually feed each other. The two processes not only start at the same time, but also end at almost the same time based on observations. The magnetic tether-cutting process is known to be very effective in accelerating the CME flux rope (Vršnak et al., 2004). First, it reduces the tension of the overlying restraining field by cutting the tie with the photosphere. Second, it increases the magnetic pressure below the flux rope by adding the poloidal flux through reconnection. Third, it enhances the outward hoop force due to the curvature of the flux rope thanks to the poloidal flux added. The escape of the flux rope reduces the magnetic pressure below, and thus induces an inflow toward the central current sheet; the current sheet is caused by the magnetic stretch as a result of the rising flux rope. Therefore, a faster rise of the flux rope causes a faster inflow, which results in a faster tether-cutting reconnection. At the same time, a faster reconnection causes a stronger outward force and thus a faster CME acceleration. The whole process, through flux rope rising, magnetic field stretching underneath, inflow tether-cutting reconnection, and further accelerating, forms a closed loop of positive feeding, which leads to the simultaneous CME acceleration and flare energy release.”

Vršnak (2006) described the ejection process in very similar terms. Both pictures are mostly consistent with our view. In the pull-reconnection scenario that we envision, there is actually cavitation behind the rising ejection, between it and the reconnection site. Nearer to the trailing edge of the rising ejection, concave-up post-reconnection flux can exert additional magnetic pressure on the ejection, thereby modifying the hoop force. While Zhang and Dere separate the pressure and hoop effects in their second and third items above, in our view these two points essentially refer to the same effect. (In the context of CMEs, the hoop force was probably first introduced by either Anzer (1978) or Mouschovias and Poland (1978).) In addition to these ideas, we also believe that upward-moving post-reconnection flux below the core of the ejection exerts a force on the ejection arising directly, from the momentum flux in the reconnection outflow. We discuss these issues in greater detail below.

Our chief aims here are i) to highlight additional observations of CME properties consistent with the key role of reconnection in producing fast CMEs, and ii) to extend foregoing qualitative picture by quantitatively characterizing how reconnection affects CME dynamics. What is new in this work? To our knowledge, estimates of reconnection-related changes to CME dynamics have not been analyzed in the terms we consider: as functions of the properties of reconnecting fields.

The remainder of this paper is organized as follows. In Section 2, we outline four observations that motivate our view of magnetic reconnection as a key driver of many eruptions, rather than a by-product of some other mechanism (e.g., an ideal instability) that powers ejections. In Section 3, we discuss our model in the framework of the CSHKP model, and distinguish aspects of the flux accretion model from other models of CME initiation and dynamics. In Sections 4 and 5, we use simplistic models of reconnection and changes in CME structure, respectively, to characterize the effects that reconnection can have on CME dynamics. In Section 6, we conclude with a brief discussion of the significance of flux accretion for CMEs.

2 Review of Relevant Observations

The key observations implicating reconnection in the development of CMEs are:

• i) Reconnection is typical when CMEs occur: Patterns of emission in the solar atmosphere interpreted as signatures of reconnection (flare ribbons and post-flare arcades) are generic features of many, if not most, CMEs. Observers have reported the existence of “stealth CMEs” (e.g., Robbrecht, Patsourakos, and Vourlidas 2009, Lynch et al. 2010), which lack low coronal signatures (LCSs) such as dimmings, coronal waves, and flares. Stealth events are believed to be a minority of CMEs. In a study of 34 events with STEREO, Ma et al. (2010) found that about $1/3$ had no LCSs, and that the speeds of their stealth events were typically slow, below 300 km s⁻¹.

• ii) Reconnection fluxes and CME speeds are correlated: As noted above, CME velocity is correlated with ribbon flux. In addition to the study by Qiu and Yurchyshyn (2005), Gopalswamy et al. (2017a) estimated reconnection fluxes using post-eruption arcades and report correlation coefficients between reconnection fluxes and CME speeds near 0.6 in a sample of about four dozen CMEs. In a sample of 16 events, most of which were also in the sample analyzed by Qiu and Yurchyshyn (2005), Deng and Welsch (2017) computed a linear fit of CME speed as a function of ribbon flux, and found the no-ribbon-flux intercept to be about 550 km s⁻¹, roughly the speed of the slow solar wind. This suggests that reconnection might be a key factor in accelerating CMEs to speeds much faster than the slow solar wind. Further, the close temporal association between CME accelerations and flare energy release reported by Zhang and Dere (2006) – major acceleration starts and ends as the flare energy release starts and ends – implicates reconnection in the acceleration process.

• iii) CME masses and speeds are correlated: The velocities of CMEs are correlated with their masses. This mass–speed relationship was noted long ago, as in Figure 4 of Vourlidas et al. (2002), which shows that the average mass of CMEs tends to be higher when their accelerations are larger. (Since the fitted accelerations were assumed constant [Vourlidas et al. 2000], higher acceleration directly implies higher velocities.) Vršnak, Vrbanec, and Čalogović (2008) also noted that “the driving force is greater in more massive CMEs.” The mass–speed relationship can also be verified directly from the CDAW CME catalog.² Figure 1 shows a scatter plot of speeds versus masses, and a relationship between the two can be discerned. A least-absolute-deviation fit to the logarithms of each was performed, and is overplotted. For the $N = 17792$ CMEs with masses and linear speeds listed in the catalog’s text version from 1996 January – 2016 May, the linear and rank-order correlation coefficients between CME linear speeds and logarithms of mass were $0.42 \pm0.01$ and $0.40 \pm0.1$, respectively, where the 1-$\sigma$ confidence intervals were computed using Fisher’s $z$-transform. While this correlation is statistically significant, it is not strong, indicating that factors other than mass strongly influence CME speed. Uncertainties in estimating CME masses and true speeds, made by assuming plane-of-sky position and velocity, respectively, introduce some scatter into this correlation. We note that for halo events, the linear and rank-order correlations are stronger: $0.48 \pm0.03$ and $0.55 \pm0.03$, respectively. (We also note that these correlations do not arise from CMEs’ velocities scaling with their sizes: the linear and rank-order correlations between non-halo CMEs’ linear speeds and angular widths are weaker, at 0.29 and 0.18, respectively.) Because magnetic flux is frozen to the plasma outside the small diffusion region where the reconnection occurs, magnetic flux that is accreted onto an ejection should increase its mass. This process was modeled by Lin, Raymond, and van Ballegooijen (2004a), who found that reconnection approximately doubles the ejection mass compared to the mass of the pre-eruptive structure in their model. They also found more mass added when a stronger background magnetic field was present, due to the higher inflow speed. An example of mass loading from flare reconnection can be seen in the lower panels of Figure 4 of the breakout simulations described by MacNeice et al. (2004). It should be noted, though, that causality might run the other way: the mass–speed correlation might arise because faster CMEs become more massive by collecting ambient material at their leading edges, via a “snow-plow” effect. Entrainment of solar wind plasma onto the CME is, however, uncertain (e.g., Feng et al. 2015.) One difference between the processes would be the density distribution: snow plowing should increase density at the CME’s front, while mass loading from the reconnection outflow would increase the density in the trailing half of the CME. It is probable that both processes are at work. (Reconnection also adds mass in what was previously external flux at the eruption’s leading edge to the ejection, but would not, by itself, strongly affect the mass density at that leading edge.) But this does suggest an observational question: how does mass distribution within CMEs compare between fast and slow CMEs?

  Figure 1

  

  A scatterplot of CMEs’ linear speeds versus their masses, from the CDAW CME catalog. A least-absolute-deviation fit to the logarithms of each is overplotted. Although a large amount of scatter is present, a trend is clear. (Quantization visible in this plot arises from two-digit precision used for masses in the catalog. The effect is most visible where changes in the tenth digit are fractionally largest – i.e., just to the right of each power of 10.)

• iv) Reconnection fluxes and ICME poloidal fluxes are correlated: As reported by Qiu et al. (2007), the ribbon fluxes in CMEs are correlated with the poloidal magnetic flux inferred from in situ flux-rope fitting. Gopalswamy et al. (2017a,b) found similar results. These associations are consistent with the picture that the key properties of the structures of interplanetary CMEs (ICMEs) that are measured in-situ are produced during the eruption process. The physical picture is that flux overlying an eruption becomes entrained with the eruption via magnetic reconnection beneath the rising ejection, and this entrained flux forms the poloidal flux in interplanetary flux ropes. If true, then the flux in flare ribbons, which reflects the amount of flux reconnected in the corona, should closely match the poloidal flux in interplanetary flux ropes. We also remark that in situ observations suggest that interplanetary flux ropes possess several turns (e.g., eight in a case studied by Larson et al. 1997), far beyond the number expected to be stable in a pre-eruptive structure.

3 Flux Accretion and Existing CME Models

Many models of CME initiation have been proposed, and we discuss some below. While some of these focus on the initiation of CMEs, and not necessarily their further development and acceleration, it is still worthwhile to consider their consistency with the observations above. All share a property: the pre-eruption state is marked by a balance between outward magnetic pressure from the confined fields that will erupt and inward magnetic tension from overlying fields. In each case, evolution of some component of the system disrupts this balance. Because magnetic reconnection will generally modify the structure of an erupting flux system, we refer to the core of the fields that will erupt as a proto-ejection – a not-yet-fully formed eruptive structure. After an eruption has begun, the reconnection process causes the magnetic structure of the material that is erupting to evolve.

• i) The tether-cutting model (Moore and Roumeliotis, 1992; Moore et al., 2001) is focused on the initiation of CMEs. In it, initial reconnection within sheared fields of a highly stressed magnetic configuration removes downward tension that was inhibiting the upward expansion of the stressed fields. Having thus cut some of its tethers, the proto-ejection that was poised for rapid rise is free to do so. Reconnection then plays an ongoing role in the eruption. Moore and Roumeliotis (1992) state that continuing reconnection:

  “further untethers the core field, providing a positive feedback that sustains the magnetic explosion …The whole process of coordinated eruption and reconnection is driven by the magnetic pressure of the unleashed core field.”

  The role of reconnection is described similarly in the later paper by Moore et al. (2001):

  “During the explosion, the reconnection within the core of the sigmoid progressively cuts more and more of the tethers, allowing the unleashed part of the core field to expand upward, the new short loops to implode downward, and the crossed arms of the sigmoid and surrounding inner envelope field to flow into the reconnection site.”

  These descriptions do suggest a basis for the observed correlation between ribbon fluxes and CME speed: more reconnection cuts more tethers, enabling faster escape of the proto-ejection. But they ignore any effect from the increased hoop force on the ejection due to flux added by the reconnection. As with the model of Kliem and Török (2006) mentioned above (and discussed further below), this view holds that reconnection removes downward forces restraining the ejection but does not result in any additional upward forces driving the ejection. The acceleration of the ejection predicted by the tether-cutting view would differ from that if the hoop force were increasing during the eruption. The tether-cutting model also does not account for the observed correlation between CMEs’ masses and speeds. If the sole effect of reconnection is to cut tethers, why should more massive CMEs be faster?

• ii) In the framework of the breakout model (Antiochos, DeVore, and Klimchuk, 1999), reconnection occurs in two regions: initially, it occurs only above a proto-ejection, which removes strapping fields that were inhibiting its rise. Strapping fields essentially act as tethers, but instead of being cut by reconnecting below the proto-ejection, as in the tether cutting model, they are cut from above by reconnection with fields external to the erupting system. Subsequently, after the proto-ejection has begun to rise, flare reconnection begins beneath the rising ejection. This flare reconnection is a generic feature of many CME simulations, including those outside the breakout framework, such as the flux cancellation model (e.g., Amari et al. 2010). Accordingly, flare reconnection is not a unique characteristic of the breakout model. Unlike the tether cutting model, the breakout model provides no natural explanation of why CME speeds should be correlated with ribbon fluxes. Like the tether-cutting model, the breakout model does not predict the correlation between CME speed and ejection mass.

• iii) As noted above, Kliem and Török (2006) describe an eruption evolving via the torus instability that involves reconnection. But their description does not incorporate any changes to the force driving the escaping torus due to the effects of reconnection on the magnetic structure of the escaping field. Thus, it provides no explanation for the correlations between either CME speed and ribbon flux, or CME speed and mass.

• iv) A kink instability might lead to onset of an eruption (e.g., Williams et al. 2005). Since this initiation mechanism does not, by itself, address the subsequent evolution of an eruption, this mechanism also cannot directly account for the correlations between CME speed and either ribbon flux or ejection mass.

Again, these models are focused on CME initiation, not subsequent evolution of the eruption. Our model also operates within this conceptual framework, although our primary focus is on the development rather than the initiation of the eruption. Our primary criticism of the models of CME processes above is that they are incomplete – i.e., that they should be modified, not rejected. It should also be remarked that all the models above operate within the “storage-and-release” paradigm, in which the coronal field possesses enough magnetic energy prior to the onset of the eruption to power it – i.e., any external forcing might trigger an eruption, but would not supply any significant energy to it.

The consequences of reconnection for CME dynamics have been modeled before. Lin, Raymond, and van Ballegooijen (2004b) analytically considered 2.5D reconnection in Cartesian geometry in a current sheet that formed in the wake of a flux rope that had suddenly jumped to a higher position due to loss of equilibrium at a lower, initial position. They note that some amount of reconnection is necessary for the flux rope to escape, and modeled the reconnection kinematically. With a reconnection rate near 0.1 $M_{\mathrm{A}}$, where $M_{\mathrm{A}}$ is the upstream Alfvén Mach number of the inflow, their modeled evolution was similar to that observed in long-duration eruptive events. Lin et al. (2005) analyzed sequences of EUV imager, spectrograph, and coronagraph observations to constrain the properties of reconnection in a current sheet in the wake of a CME and reported reconnection rates in the range 0.01 – 0.23 $M_{\mathrm{A}}$, broadly consistent with those modeled by Lin, Raymond, and van Ballegooijen (2004b).

An alternative CME paradigm was proposed by Chen (1996), in which a pre-existing, stable coronal flux rope would be driven to erupt ideally by a sudden increase of the poloidal flux wrapping around the rope. In this geometry, the field along the axis of the flux rope is toroidal, a nomenclature we will use below. In Chen’s model, this flux increase is driven ideally, by photospheric flows at the time of the eruption, in effect supplying power to drive the CME as it happens. A careful analysis of observed photospheric flows near the time of a CME by Schuck (2010) found the predictions of the model to be strongly inconsistent with the data, with model parameters and observed quantities differing by orders of magnitude. As Vršnak et al. (2004) and Forbes et al. (2006) noted, however, coronal reconnection during a CME can add poloidal flux to an erupting flux system in much the same way as Chen’s hypothesized flows would. If so, then aside from its unrealistic driving mechanism, the model’s predictions of CME dynamics could be accurate in some cases (e.g., Chen et al. 2006).

4 Momentum Transfer from the Reconnection Outflow

Although many numerical models of CMEs exhibit flare-type reconnection, relatively little is known about the significance of this reconnection in accelerating ejections, versus acceleration that would have occurred by ideal mechanisms alone – e.g., after strapping fields were reconnected away in the breakout model, or after sufficient photospheric flux were canceled in the flux cancellation model. While some amount of reconnection is essentially inevitable in numerical MHD models, we suggest that its nearly ubiquitous presence in simulations of CMEs is related to its key role in the eruption process on the actual Sun. We note that the role of reconnection versus ideal evolution could be investigated in studies with a “reconnection-controlled” model, like the FLUX finite-element code employed by Rachmeler et al. (2010).

In this section and the next, we investigate how magnetic reconnection in the wake of a rising ejection – flare reconnection – can accelerate that ejection.

We focus in this section on how flare reconnection can directly transfer momentum from the outflow jet to the ejection, thereby accelerating it. In the standard CSHKP model of an eruptive flare, magnetic reconnection occurs below a rising ejection, with outflow jets directed upward and downward. The downward-moving flux eventually forms post-flare loops, and the upward-moving flux eventually merges with the rising ejection. Reconnection likely occurs in a kinetic-scale diffusion region, within which magnetic flux is not frozen into the plasma.

As post-reconnection flux first enters the outflow region, field lines are $\Lambda$- or V-shaped (for downward and upward outflows, respectively), with sharp kinks near the diffusion region. While the plasma flow directly exiting the diffusion region should be essentially Alfvénic, magnetically connected plasma over a larger volume will be moving much more slowly. But the strong magnetic tension from the large-scale kink in the field will rapidly accelerate magnetically linked plasma to the perpendicular Alfvén speed, $v_{\mathrm{A} \perp} = \sqrt{B _{\perp}^{2}/(4 \pi\rho)}$. Figure 2 illustrates the geometry. (As usual, we define $B_{\perp}$ to be the component of the magnetic field in the 2D plane containing the X-point associated with the reconnection.) This process of dipolarization (e.g., Priest and Forbes 2000) implies a nonzero momentum flux $\mathcal{F}_{\boldsymbol {p}}$ is present in each outflow region, with magnitude

$$ \mathcal{F}_{\boldsymbol {p}} = (\rho v_{\mathrm{A} \perp}) v_{\mathrm{A} \perp} = \frac{B_{\perp}^{2}}{4 \pi} . $$

(1)

A key point is that the dipolarization occurs over a much larger scale than the diffusion region, with the acceleration coming from the large-scale structure of the magnetic field. Eventually the upward-moving flux catches up to the slower-moving ejection, and slows to the proto-ejection’s speed – in the process, transferring its excess momentum to the proto-ejection as it merges with it.

Figure 2

A schematic illustration of post-reconnection flux moving through the outflow region at equally spaced time intervals. The diffusion region shown is unrealistically large compared to the scale of magnetic variations shown here; in the actual solar corona, kinetic scales (on the order of meters) are far below the scale of observable structure (on the order of a few hundred kilometers). The opening angle of the outflow region was chosen arbitrarily. The key point is that the dipolarization of post-reconnected fields occurs over a much larger area than the diffusion region.

Integrated over a solar eruption, how much momentum might be transferred by this mechanism? Leroy, Bommier, and Sahal-Brechot (1983) and Casini et al. (2003) report typical axial magnetic fields of ${\sim}\,10$ G or more along the axes of non-active-region coronal prominences above the limb, with fields tilted by about $20^{\circ}$ with respect to prominence axes. If a prominence with a 10 G field erupts as a CME, a perpendicular field strength of ${\sim}\,3$ G is plausible. Assuming $B_{\perp}= 3~\mbox{G}$ implies a momentum transfer from the outflow jet of roughly 1 (g cm s⁻¹) per cm² per s. While the diffusion region is likely on ion kinetic scales (perhaps on the order of a few meters for typical fields in the corona), the outflow only becomes Alfvénic after it expands and accelerates. Hence, momentum transport from the outflow occurs over macroscopic area, and might be a few Mm across and a few tens of Mm long, meaning this could occur over an area of ${\sim}\, (3 \times10^{8}\mbox{ cm}) (3 \times10^{9}\mbox{ cm}) \simeq10^{18}~\mbox{cm}^{2}$. Zhang and Dere (2006) studied acceleration in a few dozen CMEs, and report the median duration of the “main” acceleration phase of 50 minutes, implying the strongest burst of momentum flux might perhaps last 3000 s. These roughly estimated parameters imply a net momentum transfer near $3\times10^{21}~\mbox{g}\,\mbox{cm}\,\mbox{s}^{-1}$.

A CME with a mass of $10^{15}$ g and a speed of 300 km s⁻¹ (e.g., Vourlidas et al. 2000) has a momentum of $3 \times10^{22}$ g cm s⁻¹. This suggests momentum transfer from the reconnection outflow might supply ${\sim}\,10\%$ of the momentum of a CME with typical mass and modest speed. Different choices for the reconnection field strength, the area of the outflow region or duration of the reconnection could substantially alter this very uncertain estimate.

Many CMEs are much faster than this, but such CMEs typically originate from within active regions, where coronal field strengths might be a factor of 10 or more larger. Given the $B_{\perp}^{2}$ scaling of $\mathcal{F}_{\boldsymbol {p}}$ in Equation 1, it is possible that momentum transfer from the reconnection outflow supplies a substantial part of an active region CME’s final momentum. The size of the reconnection outflow region can be larger in active regions, too. To cite a large case, Aschwanden and Alexander (2001) report the length of the post-flare arcade in the Bastille Day event of July 2000 to be about 200 Mm. The width of the upward outflow region in the simulations of Karpen, Antiochos, and DeVore (2012) is nearly the width of the sheared PIL at the model’s base. If similar photosphere-to-coronal scaling is present on the Sun, the width of the accelerated outflow in the Bastille Day event might still be about 3 Mm. The axial field might be of order 100 G. Because the reconnection typically proceeds from more sheared to less sheared field lines (e.g., Aschwanden and Alexander 2001, Su, Golub, and Van Ballegooijen 2007), the average reconnecting component might be 30 G. The associated GOES curves show a rise time of a bit less than 20 minutes, implying momentum transfer over ∼ 1000 s. With these parameter choices, the momentum transfer would be about $5 \times10^{23}$ g cm s⁻¹. This is about 20% of the CME’s momentum of $2.3 \times10^{24}$ g cm s⁻¹, from the CDAW CME catalog’s linear speed and mass of 1674 km s⁻¹ and $1.4~\times10^{16}$ g, respectively.

The observations discussed in Section 2 imply that both a CME’s mass and speed are correlated with reconnected flux, so its momentum should be, too. So momentum transfer from flare-reconnection outflow is partly consistent with the observations. Our parameter estimates, however, are very uncertain, so we cannot tightly constrain the significance of the reconnection outflow for CME dynamics. We expect that more detailed assessments of the role of the reconnection outflow in CME acceleration can be investigated by analyzing the results of existing numerical models of CMEs. For instance, in the simulations performed by Karpen, Antiochos, and DeVore (2012), the morphology of outflows where the reconnection jet meets the body of the ejection in their Figure 14 suggests that the jet’s flows distort – and therefore exert forces on – the ejection.

5 Reconnection-Induced Changes in External Forces

In the CSHKP model, reconnection in the wake of a rising ejection alters field line connectivity between the background magnetic field and the ejection. In general, this modifies the forces on the ejection, a scenario that we investigate in this section. We emphasize that models that do not account for changes in forces on CMEs arising from reconnection-driven field evolution must be incomplete: their predictions for CME height versus time, for instance, will not be based upon valid physics. A key point is that we explicitly assume that the eruption is already underway: the proto-ejection is already moving upward, due to an unbalanced force, so our focus is not on initiation.

When flux surrounding an ejection reconnects underneath it, some of the reconnected flux then becomes entrained with the ejection. We refer to this entrainment as flux accretion. This accretion can simultaneously increase the outwardly directed forces driving the ejection and decrease the inwardly directed forces restraining it, for some of the reasons outlined in the text passage from Zhang and Dere (2006) cited above. As noted previously, because magnetic flux is frozen to the plasma outside the small diffusion region where the reconnection occurs, flux accretion will increase the mass and size of an ejection. Recently, Compagnino, Romano, and Zuccarello (2017) used statistical matching criteria to associate flares and CMEs based upon their timing, and report a correlation between flare radiative flux in the GOES 1 – 8 Å band and CME mass. This is consistent with the idea that reconnection both leads to flare emission and adds mass to associated CMEs.

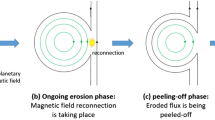
Figure 3 qualitatively illustrates an idealization of this process. In the figure, we assume that a finite amount of reconnection has occurred, but we now ignore the dynamical relaxation that would occur with realistic reconnection, since that effect was discussed above. Hence, in this sketch, the post-reconnection field lines have already dipolarized. This assumption of very simplistic field geometries for the pre- and post-reconnection fields greatly simplifies our comparisons between the two. It should be noted that each vector shown in Figure 3 represents a force density (i.e., the force per unit volume at a given point).

Figure 3

Left: A schematic illustration of some magnetic force densities present in a 2D, non-force-balanced magnetic configuration, at a given time $t_{i}$. By hypothesis, the configuration is not in equilibrium, and a net upward Lorentz force acts upon the CME (in the $z$ direction here). The solid black lines show a sample of magnetic field lines, meant to approximately convey field strengths. The dashed black lines show two separatrix surfaces, one of which encloses the ejection (closed, dashed circle). The red vector shows the upward component of then magnetic pressure gradient within the ejection due to upwardly decreasing field strength, and blue vectors show the inward magnetic tension forces at two points that act to restrain the ejection. The vertical dotted line denotes a current sheet in the wake of the rising ejection. Here, field lines’ shapes are unphysical; our focus is on their connectivity. Right: An illustration of some magnetic force densities present in a 2D, non-force-balanced magnetic configuration, but at a slightly later time, $t_{i} + \Delta t$. In this case, coronal magnetic flux that was anchored at the photosphere between points C and D in the left panel has reconnected in the wake of the rising ejection. Hence, the flux between C and D that previously overlay the ejection has been accreted onto the ejection, and now lies within the dashed circle enclosing the ejection. The newly reconnected, concave-up flux near the base of the ejection, between the points C’ and D’, exerts an upward magnetic tension, shown acting at the point labeled T’, that cancels the previously unbalanced downward magnetic tension from flux above the ejection, shown acting at the point labeled T. This reconnection implies that the downward magnetic tension T that formerly restrained the ejection as an external force acting upon it is now an internal force that cancels with the newly created upward magnetic tension force T’. Since some restraining force was removed, the net upward force on the ejection is therefore larger.

To quantitatively investigate the process, we now analyze the momentum equation for the ongoing ejection. We assume that the combined configuration of the CME and its background field is not in equilibrium, and a net upward Lorentz force acts upon the CME. Some process having triggered the eruption, we then wish to consider the effects of reconnection upon its further development.

A key challenge arising from this assumption is that simplifying assumptions typically adopted to study pre-eruptive configurations – for example, that the magnetic field is “force-free,” i.e., that $(\boldsymbol {J} \times \boldsymbol {B}) = 0$ (see, e.g., Schrijver et al. 2008) do not apply. Unfortunately, it is difficult, without resorting to numerical simulations, to model the spatial variation of $\boldsymbol {B}$, as would be required to analyze how reconnection modifies the $(\boldsymbol {J} \times \boldsymbol {B})$ force.

Consequently, we idealize the ejection as an object distinct from its coronal surroundings, and we estimate the net forces on it. Newton’s second law for the CME at a given instant in time $t_{i}$ is given approximately by

$$ \frac{\mathrm{d}\boldsymbol {p}}{\mathrm{d}t} = -(P_{\mathrm{out}} S_{\mathrm{out}} - P_{\mathrm{in}} S_{\mathrm{in}}) + \boldsymbol {F}_{\mathrm{Lorentz},\,\mathrm{ext}} - m \boldsymbol {g} - \boldsymbol {F}_{\mathrm{drag}}, $$

(2)

where $\boldsymbol {p}$ is the CME’s momentum, equal to $m_{\mathrm{eff}} \boldsymbol {v}$; $\boldsymbol {v}$ is the CME’s center-of-mass velocity, $m_{\mathrm{eff}}$ is the CME’s effective mass, equal to the CME’s mass $m$ plus its virtual mass (e.g., Forbes et al. 2006, equal to the mass of the background plasma that it displaces); $P_{\mathrm{in}}$ and $P_{\mathrm{out}}$ are the plasma (gas) pressures on the CME’s inner (or back, or bottom) and outer (or front, or top) surfaces, respectively, and $S_{\mathrm{in}}$ and $S_{\mathrm{out}}$ are the corresponding surface areas; $\boldsymbol {g}$ is the gravitational acceleration due to the Sun at the location of the CME’s center of mass; $\boldsymbol {F}_{\mathrm {Lorentz},\,\mathrm{ext}}$ is the Lorentz force on the ejection by external fields; and $F_{\mathrm{drag}}$ is the drag on the CME. We further assume that: the coronal plasma is magnetically dominated (e.g., Forbes 2000), so that the gravity and pressure gradient terms can be neglected; and that drag on the rising proto-ejection is negligible in the high-$\beta$ plasma near the Sun while reconnection is ongoing (Cargill et al., 1996). We then have

$$ \frac{\mathrm{d}\boldsymbol {p}}{\mathrm{d}t} = \boldsymbol {F}_{\mathrm{Lorentz},\,\mathrm{ext}}. $$

(3)

Although we have assumed a net upward Lorentz force is exerted on the proto-ejection, external fields exert both downward and upward forces on it. The dominance of Lorentz forces is only expected to hold low in the corona.

We next consider the change $\Delta \boldsymbol {F}_{\mathrm{Lorentz}}$ in net external Lorentz force on the CME due to the reconnection of a small amount of flux $\Delta\Phi$, assumed to occur over a small time interval (relative to the duration of the eruption) $\Delta t$. Observations of supra-arcade downflows (SADs) thought to represent cross sections of magnetic structures in reconnection outflow suggest the reconnection is patchy (McKenzie and Savage, 2009), and creates structures on length scales on the order of a few Mm (Savage and McKenzie, 2011). Considering a single reconnection event in isolation is consistent with assuming that the reconnection is patchy (Linton and Longcope, 2006; Linton, DeVore, and Longcope, 2009).

5.1 Reduction in Downward Magnetic Tension

First, as emphasized in Figure 3, some component of the downward magnetic tension acting on the CME is canceled after reconnection occurs. The force density from downward magnetic tension prior to the reconnection was

$$ \boldsymbol {f}_{\mathrm{tension}} = \frac{1}{4\pi} (\boldsymbol {B} \cdot \boldsymbol {\nabla } ) \boldsymbol {B}, $$

(4)

integrated over the volume containing the to-be-reconnected flux overlying the ejection. (Here and elsewhere we will use $\boldsymbol {f}$ for force densities, and $\boldsymbol {F}$ for forces, which are volume-integrated force densities.) To simplify this analysis, we first assume no guide field (a component of the field into the plane of the figure) is present where the reconnection occurs, an assumption we will relax later. We refer to this field as purely poloidal, and denote the reconnecting field’s strength as $B_{\mathrm{P}}$. This means the component of the field into the page is not contributing to the change in tension due to the reconnection that we compute here. Idealizing the overlying flux tube as forming a half-toroid with major radius $R$ and constant cross sectional area $\Delta A$ along its length, the pre-reconnection force $\Delta F$ in the downward direction integrated over the sub-volume that overlies the ejection and whose flux reconnects is then

$$\begin{aligned} \Delta F_{\mathrm{tension}} =& \frac{1}{4\pi} \int \mathrm{d}V \, \bigl| \hat{z} \cdot(\boldsymbol {B} \cdot \boldsymbol {\nabla } ) \boldsymbol {B} \bigr| \end{aligned}$$

(5)

$$\begin{aligned} =& \frac{1}{4\pi} \int \mathrm{d}V \, \frac{B_{\mathrm{P}}^{2}}{R} \, \biggl| \hat{z} \cdot\frac{\partial\hat{b}}{\partial\theta} \biggr| \end{aligned}$$

(6)

$$\begin{aligned} =& \frac{1}{4\pi} \int\frac{B_{\mathrm{P}}^{2}}{R}\, \mathrm{d}A \int_{-\pi/2}^{ \pi/2} R\, \mathrm{d}\theta\cos\theta \end{aligned}$$

(7)

$$\begin{aligned} \simeq& \frac{B_{\mathrm{P}} \, \Delta\Phi}{4\pi} \biggl( \frac{1}{R} (2R) \biggr) = \frac{\Delta\Phi B_{\mathrm{P}}}{2\pi}, \end{aligned}$$

(8)

where $\hat{b} = \hat{\theta}= \cos(\theta) \hat{x} - \sin (\theta) \hat{z}$, $\theta$ is the angular position around the ejection’s axis (with $\theta= 0$ along $\hat{z}$, and increasing clockwise), $\mathrm{d}V = \mathrm{d}A \, R \,\mathrm{d}\theta$, $\Delta\Phi= B_{\mathrm{P}} \, \Delta A$ is the flux that will be reconnected, and we approximate the tension term’s magnitude as $B_{\mathrm{P}}^{2}$ over the radius of curvature, $R$ (Spruit, 1981).

Physically, this force is not eliminated by reconnection in our idealized model. Rather, this small component of the overall downward force is canceled by the formation of concave up flux, resulting in a net change in Lorentz force directed upward equal to $\Delta\Phi B/2 \pi$. Strictly, the pre-reconnection downward tension force density was present in a volume external to the ejection, so it did not act directly on the ejection itself (as, for instance, gravity and external pressure can). For the ejection to rise, however, the forces driving it would have had to also accelerate plasma in this external volume upward, too. By both incorporating this external flux into the erupting system and canceling its downward force, reconnection thereby reduces this impediment to the ejection’s rise.

We note that our result is a simplistic approximation, for a few reasons. First, it is clear that any realistic reconnection model would not yield the geometries depicted in Figure 3, from which the result in Equation 8 was derived. As discussed in the previous subsection, post-reconnection field lines start with sharp vertices, then dipolarize while traversing the outflow region and become more rounded. The field geometry shown in Figure 3 is meant represent the already-dipolarized state, to enable characterizing the effect of reconnection on forces that act on the ejection independent of the outflow-driven momentum flux that we already analyzed. Nonetheless, the already-dipolarized, post-reconnection fields underneath the ejection will not precisely mirror fields above the ejection, so the upward and downward forces will not exactly cancel as we have described. In fact, from the typical decrease in total pressure (gas plus magnetic) with height in the corona, the field strength below the ejection’s core will be greater than that above the core – meaning the upward-directed tension force would be stronger. This point will be revisited in Section 5.3.

A second complication is that the ejection will rise during the time interval $\Delta t$ that the reconnection and subsequent dipolarization occur. The combination of this rising motion with the decreasing total pressure in the solar atmosphere with height, which we have ignored, will cause the ejection’s structure to evolve over $\Delta t$. Here, we simply ignore changes in the CME’s structure due to its upward displacement during this brief interval.

A third complication is that we have ignored the 3D structure of the eruption. Perhaps most importantly, our simplistic picture neglects the proto-eruption’s axial field – the component of the magnetic field in the direction normal to the plane containing Figure 3. Observations of prominences and soft-X-ray over PILs generally indicate the existence of an important component of the magnetic field along the PIL. A component of the field along the PIL corresponds to a nonzero guide field in the ensuing reconnection above the PIL. Accordingly, we now incorporate the effect of this guide field into our estimate of the change in tension force due to the reconnection. We assume the total field strength remains fixed, and focus on how reconnection modifies the tension force as the reconnecting field’s direction varies with respect to the proto-ejection’s axis. Figure 4 illustrates an idealized configuration before, during and after a reconnection event, with a guide field present. The field’s configuration is consistent with observations showing that lower-lying loops are more closely parallel to the PIL than higher loops (Martin and McAllister, 1996; Schmieder et al., 1996). In the figure, the presence of a guide field alters the post-reconnection field’s morphology from the purely 2D case: it leads to accretion of helical instead of circular flux. We define the $B_{\parallel}$ to point in the invariant direction (the $y$ direction in Figure 3, into/out of the figure plane), with $B_{\mathrm{P}}$ being perpendicular to the invariant direction (within the plane of Figure 3). For a field line pitch angle $\omega$ with respect to the guide field $B_{\parallel}$, and $\tan\omega= B_{\mathrm{P}}/B _{\parallel}$, the infinitesimal of length, $\mathrm{d}s$, along the helical field line segment is

$$ \mathrm{d}s = \sqrt{\mathrm{d}s_{\mathrm{P}}^{2} + \mathrm{d}s_{\parallel}^{2}} = \sqrt{(R \, \mathrm{d} \theta)^{2} + (R \, \mathrm{d}\theta)^{2}(B_{\parallel}/B_{\mathrm{P}})^{2}} = (R \, \mathrm{d}\theta) \sqrt{1 + \cot^{2} \omega}. $$

(9)

So the segment arching over the proto-ejection is longer, by an amount $\sqrt{1 + \cot^{2} \omega}$, meaning that the volume over which the tension force acts (the volume of the reconnected flux tube) is larger compared to that integrated in deriving Equation 8. But, with fixed total field strength, $B_{\mathrm{tot}} = \sqrt{B_{\mathrm{P}} ^{2} + B_{\parallel}^{2}}$, nonzero $B_{\parallel}$ means $B_{\mathrm{P}}$ is smaller, with $B_{\mathrm{P}} = B_{\mathrm{tot}}/\sqrt{1 + \cot^{2} \omega}$. This, in turn, means that the force density is also smaller, $B_{\mathrm{P}}^{2}/R = B_{\mathrm{tot}}^{2}/[R (1 + \cot^{2} \omega)]$. This lower force density can be understood in terms of the larger radius of curvature of the reconnected flux tube, which traverses a longer distance when crossing underneath the proto-ejection. The net effect of including the guide field is that the reduced force density, integrated over the larger volume, is smaller than the result in Equation 8, yielding

$$ \Delta F_{\mathrm{tension}} = \frac{\Delta\Phi B_{\mathrm{tot}}}{2\pi} \frac{1}{\sqrt{1 + \cot^{2} \omega}}. $$

(10)

But this result can also be understood in terms of the field’s components: $B_{\parallel}$ does not contribute to the tension, so the $B_{\mathrm{P}}$ in Equation 8 is replaced with $B_{\mathrm{tot}}/\sqrt{1 + \cot^{2} \omega}$ here. With $\omega= 20^{ \circ}$, the factor $1/\sqrt{1 + \cot^{2} \omega}$ is equal to 0.34. So the reduction in tension due to tether-cutting reconnection with a relatively small pitch angle is significantly smaller than our estimate without a guide field (a pitch angle of $90^{\circ}$). As noted previously, the angle between the reconnecting field and the PIL will vary from more to less parallel over the course of an eruption. So the decrease in restraining force on a proto-ejection produced by tether-cutting reconnection should vary in a typical event, as i) the shear angle of reconnecting fields decreases as the reconnection proceeds and ii) the strength of reconnecting fields decreases as flux farther from the active region core reconnects.

Figure 4

An illustration of evolving connectivity due to magnetic reconnection in the presence of a guide field during an eruption. Top left: A schematic, overhead view of field lines above a PIL prior to an eruption. Flux represented by the blue line forms the proto-ejection, and is drawn thickest to aid visualization of the connectivity configuration, as viewed from the bottom side of the top-left image. Note that magnetic shear – how closely the field runs parallel to the PIL – decreases with increasing height: the blue (lowest-lying) field line is the most sheared, the red (highest) field line is relatively unsheared. Top middle: An overhead view of the configuration after the proto-ejection has begun to rise. Cavitation in its wake draws in flux, represented by the magenta field lines. The upper magenta field line is shown as a dashed line to more clearly display connectivity. Bottom middle: an end-on view of the configuration in the top-middle image, as viewed from the bottom of that image. Top right: overhead view of the configuration after flux represented by the magenta lines has reconnected, forming two post-reconnection flux domains: one containing flux that winds around the ejection (dashed magenta line) and one containing shorter flux (solid magenta line) that runs beneath it. Bottom right: an end-on view of the configuration in the top-right image, as viewed from the bottom of that image. Flux represented by the dashed magenta field line has accreted onto the ejection. Note that this entrained flux is longer than the pre-reconnection magenta lines, and contains two segments with downward magnetic tension (above the blue line) and one with upward magnetic tension (below the blue line). Flux represented by the solid magenta field line might be observed as a post-flare loop.

We digress briefly to consider another significant result of this analysis: even though a magnetic flux $\Delta\Phi$ reconnected in the corona, there is a flux of $(4 \Delta\Phi)$ in the associated photospheric footpoints. If ribbon emission were produced at the footpoints of reconnecting coronal fields, then four footpoints would produce ribbon emission. This counts flux at both ends of each reconnected flux tube, because emission is believed to appear at both. Thus, four distinct ribbons could appear, a situation that Goff et al. (2007) refer to as a quadrupolar flare. But it is also possible that emission from each same-polarity pair of footpoints will occur within the same, contiguous ribbon.

Ribbon emission often precedes emission from post-flare loops, rooted in the ribbons, which have a morphology similar to the solid magenta line in the right column of Figure 4. But is there something different about ribbon emission at the footpoints of helical loops – corresponding to the dashed magenta line in the figure’s right column – that do not subsequently produce bright, post-flare loops? The enhanced density from chromospheric evaporation that brightens short post-flare loops might be too dilute to brighten longer loops, since emission measure scales as density squared. Or is there a quantitative difference in ribbon emission at footpoints of these longer loops? If the reconnection process accelerates ribbon-causing non-thermal particles near the reconnection site, then all four footpoints should produce similar ribbon emission. Chandra et al. (2009) and Zhao et al. (2016) relate observed ribbon emission to helical field lines, based upon their J- or reversed-J-shaped morphology (e.g., Williams et al. 2005, Green et al. 2007), and report that emission from such footpoints is more faint. This suggests that the acceleration of ribbon-causing non-thermal particles does not solely involve processes near the reconnection site. A major difference between the long and short post-reconnection loops is that the latter dipolarize downward into layers of the solar atmosphere that are much more dense and contain much higher field strengths. This contraction itself could lead to particle acceleration directly, by betatron acceleration (e.g., Somov and Bogachev 2003), or indirectly, via wave excitation (e.g., Fletcher and Hudson 2008).

We have also ignored dynamic effects arising from curvature along the axis of the erupting flux system, which we address in our discussion of the hoop force (Section 5.3) shortly.

5.2 Global-Scale Magnetic Pressure Variations

In addition to the reduction in downward-directed magnetic tension force restraining the CME, magnetic reconnection would, considered by itself, increase the magnetic pressure underneath the CME. This is because the reconnection introduces additional magnetic flux into the volume underlying the CME, without changing the amount of magnetic flux above the CME. If the CME were not rising, this would enhance the difference in magnetic pressure across the CME, which would increase the upward force upon it. In Figure 3, for instance, reconnection of the flux between points C and D at the photosphere adds the fluxes between points C’ and D’, and between points C” and D” into the space below the CME’s bottom boundary. This change increases the average flux density – equivalently, magnetic field strength – beneath the ejection. The higher average field strength underneath the ejection implies an increased upward magnetic pressure acting the ejection from below.

This increased magnetic flux density underneath the CME might be thought to supply pressure that acts like the gas behind a bullet in a gun barrel: the pressure difference across the bullet accelerates it. As noted in the introduction, however, in our pull-reconnection scenario, an ejection can rise sufficiently fast that there is a decrease in the average magnetic pressure in its wake, rather than an excess. So, compared to a stationary flux rope, the upward magnetic pressure behind a rapidly rising rope could be smaller. Note, however, our emphasis on “average” here; to the extent that the upward-dipolarizing, post-reconnection flux catches up with the CME, $B^{2}$ near the CME’s trailing edge would be higher than farther into its wake. So the force from the magnetic pressure gradient is not necessarily monotonically upward. We need to consider the increase in magnetic pressure at the trailing edge of the CME due to the reconnection, our focus in the next subsection.

5.3 CME-Scale Magnetic Pressure Variations: Changed Hoop Force

We now consider how magnetic reconnection affects the hoop force on an erupting flux system. We first briefly review the hoop force (Section 5.3.1). Then, treating a proto-ejection as a torus with a purely poloidal external field, we derive expressions for the hoop force (Section 5.3.2) and the change in this force due to the reconnection (Section 5.3.3). Finally, we consider the effect of a toroidal component in field external to the torus (Section 5.3.4).

5.3.1 The Hoop Force in CMEs

Erupting flux systems must be, in a rough sense, $\Omega$-shaped: the photospheric footpoints of fields participating in an eruption do not move significantly during the event, but the flux in the corona balloons outward into the heliosphere. Curvature of the magnetic field along the axis of the $\Omega$-shaped erupting flux system – the axial field being due to the flux system’s toroidal component – implies that a large-scale, downward magnetic tension force is present. (This large-scale, downward tension force from axial curvature is not expected to change directly due to reconnection, so we do not consider it further.)

Set against this inward force from curvature of the eruption’s toroidal field, the component of the field winding around the eruption’s axis – the poloidal field, $\boldsymbol {B}_{\mathrm{P}}$ – tends to exert an outward hoop force (e.g., Anzer 1978) on the ejection. We analyze the hoop force arising from poloidal flux that winds around a toroidal volume. We assume the cross section of the torus is circular, with the geometry illustrated in Figure 5. The hoop force can be understood qualitatively in the following way (Freidberg, 1987): i) poloidal flux passing through each differential area in the torus’s hole $(\Delta A_{\mathrm{in}} = \Delta r _{\mathrm{in}} r_{\mathrm{in}} \, \Delta\phi)$ must pass through a conjugate differential area outside the torus $(\Delta A_{\mathrm{out}} = \Delta r _{\mathrm{out}} r_{\mathrm{out}} \, \Delta\phi)$; ii) the area of the outside half of the torus’s surface, $S_{\mathrm{out}}$, is larger than the inside half of its surface, $S_{\mathrm{in}}$, since the differential surface area, $\mathrm{d}S$, increases linearly with distance from the center of the hole ($\mathrm{d}S \propto r \, \mathrm{d}\phi$); iii) if $\Delta r_{\mathrm{out}} = \Delta r_{ \mathrm {in}}$, then $B_{\mathrm{P}}$ decreases as $1/r$ (and $B_{\mathrm{P}}$ falls off more rapidly if $\Delta r_{\mathrm{out}} > \Delta r_{\mathrm{in}}$), meaning that $B_{\mathrm{P}}$ must be weaker on the outside half of the torus’s surface than on its inside half; iv) but the inward and outward magnetic pressure forces on the torus scale as $B_{\mathrm{P}}^{2}$ times $S_{\mathrm{out}}$ and $S_{\mathrm{in}}$, respectively, so the inverse-square decay of magnetic pressure with distance implies that the surface-integrated inward pressure force on $S_{\mathrm{out}}$ is less than the outward force on $S_{\mathrm{in}}$. Hence, the poloidal field exerts a net outward force. If this outward force were sufficient to overcome inward tension from curvature of the toroidal field, and no other forces were present, then the major radius of the torus would increase. This expansion might be inhibited by magnetic fields external to the torus. But if fields external to the torus decay sufficiently rapidly with distance, then the torus will accelerate outward (Kliem and Török, 2006).

Figure 5

An illustration of quantities used in describing the torus geometry used in hoop force calculations. Left: This end-on view of a cross section of the torus’s volume shows major and minor axes, $r$ and $R$, respectively. The poloidal angle, $\theta$, about the torus’s axis increases clockwise, and the azimuthal angle, $\phi$, increases into the page. Newly dipolarized flux is depicted as a shaded semicircle at the torus’s inner edge, and its conjugate flux fills the hashed area at the outer edge. Magnetic flux densities at the inside, middle, and outside surfaces are labeled as $B_{\mathrm{in}}$, $B_{\mathrm{mid}}$, and $B_{\mathrm{out}}$, respectively. Right: This side (edge-on) view shows a segment of the torus. Newly dipolarized flux is depicted as a shaded patch at the torus’s inner edge, and its conjugate flux fills the hashed area at the outer edge.

As a starting point for our analysis, we assumed that our flux system was not in force balance: it was already erupting. So a hoop force, or something akin to it, must already be present. But how does reconnection affect this force?

The key assumption that we make about the evolution of the post-reconnection field is that the concave-up flux from the flare reconnection under the proto-ejection does, indeed, catch up to it. Stated another way: the reconnection adds flux to the ejection faster than the ejection’s flux moves outward. That flux catches up to the ejection is evident in the lower panels of Figure 4 of the breakout simulations described by MacNeice et al. (2004), which show that the erupting flux system maintains a circular cross section as flux is added to it. (In Figure 3d of the paper by Karpen, Antiochos, and DeVore (2012), the simulated eruption’s cross section is deformed by the reconnection jet to become somewhat concave, suggesting that post-reconnection flux easily overtakes the outward-moving eruption.) The catch-up of post-reconnection flux is consistent with our earlier treatment of momentum transfer to the ejection from the reconnection outflow. Essentially, this flux dipolarizes as it catches up to the CME’s trailing edge, and its dipolarization is arrested (in the co-moving frame) by backwards-directed magnetic pressure at that edge. Given this assumption, magnetic pressure from the post reconnection flux will exert an additional upward force on the CME. Due to the cavitation farther back in the CME wake, however, the hoop force might be less than the estimate that we derive below, which might therefore represent an upper bound.

It should be noted here that an ejection’s evolution will differ if reconnection is assumed not to occur. If the major radius $r$ of an axisymmetric torus with nonzero poloidal field increases ideally, the poloidal flux density, $B_{\mathrm{p}}$, must decrease, because the same amount of poloidal flux is spread out over a larger area. Accordingly, the hoop force will also decrease. When reconnection occurs in the wake of an expanding torus, however, the accretion of additional flux onto the erupting system means that $B_{\mathrm{P}}$ at its trailing edge will generally not decrease with increasing $r$ in the same manner as the ideal case. In particular, the added flux can affect $B_{\mathrm{P}}$ there in two ways: i) by increasing magnetic pressure at the rear of the ejection, which keeps flux compressed; and ii) increasing the pitch angle at the rear of the ejection, as less-sheared fields reconnect and accrete onto the CME. The hoop force must still weaken as the ejection moves outward, but reconnection should decrease the rate at which the hoop force weakens with distance. We also remark that, due to this reconnection, the magnetic helicity of the erupting flux system is not conserved. We discuss some aspects of helicity evolution in Appendix A.

5.3.2 Hoop Force on a Torus Segment

Before we estimate the change in the hoop force from the reconnection, we first analyze the hoop force itself. We assume that the field at the surface of the torus is purely poloidal, and derive the inward and outward components of the hoop force due to external poloidal flux $\Delta\Phi$ in contact with the segment’s annular surface. The poloidal flux $\Delta\Phi$ at the inner edge of the torus segment matches a corresponding flux $\Delta\Phi$ at its outer edge, so the poloidal flux densities are related via

$$ \frac{B_{\mathrm{in}}}{B_{\mathrm{out}}} = \frac{\Delta\Phi/\Delta A_{\mathrm{in}}}{ \Delta\Phi/\Delta A_{\mathrm{out}}} = \frac{\Delta A_{\mathrm{out}}}{\Delta A _{\mathrm{in}}} = \frac{\Delta R_{\mathrm{out}} \, \Delta\phi(r + R)}{\Delta R_{\mathrm{in}} \, \Delta\phi(r - R)} = \frac{(r + R)}{(r - R)}. $$

(11)

Here, $\Delta\Phi$ refers to reconnected flux, but $\Delta\phi$ refers to an angular interval in the toroidal coordinate, $\phi$. We remark that we have assumed $\Delta R_{\mathrm{in}} = \Delta R_{\mathrm{out}}$ here; if $\Delta R_{\mathrm{out}} > \Delta R_{\mathrm{in}}$, then the outside magnetic field strength (and pressure force) will be weaker. Consistent with this expression for $B_{\mathrm{in}}/B_{\mathrm{out}}$, we model the variation of the poloidal field with $\theta$ to be

$$ B_{\mathrm{P}}(\theta) = B_{\mathrm {mid}} \biggl( \frac{r}{r + R \cos\theta} \biggr), $$

(12)

where $B_{\mathrm {mid}}$ is the poloidal field strength at the lateral, mid-position of the torus (i.e., $\theta= \pm\pi/2$). The outward and inward forces on the inner and outer halves of the segment, respectively, are given by the magnetic pressure, $B_{\mathrm{P}}(\theta)^{2}/8 \pi$ on each, projected onto the (outward) radial direction, integrated over the area of each half. Infinitesimal areas on the inner and outer halves of the segment are

$$\begin{aligned} \mathrm{d}S_{\mathrm{in}} =& (r - R \cos\theta) \, \mathrm{d}\phi R \, \mathrm{d}\theta, \end{aligned}$$

(13)

$$\begin{aligned} \mathrm{d}S_{\mathrm{out}} =& (r + R \cos\theta) \, \mathrm{d}\phi R \, \mathrm{d}\theta. \end{aligned}$$

(14)

To find the inward force on the outer segment of the torus, we integrate $\theta$ from $(-\pi/2, \pi/2)$ over the outside surface, and $\phi$ over the range $\Delta\phi$. Projection onto the outward direction introduces a factor of $-\cos(\theta)$. This yields (Dwight 1961, p. 105, integral 446.00)

$$\begin{aligned} F_{\mathrm{outer}} =& \int \mathrm{d}S_{\mathrm{out}} \frac{B_{\mathrm{mid}}^{2}}{8\pi} \biggl( - \frac{r^{2} \cos\theta}{(r + R \cos\theta)^{2}} \biggr) \end{aligned}$$

(15)

$$\begin{aligned} =& - r^{2} \, \Delta\phi R \frac{B_{\mathrm{mid}}^{2}}{8\pi} \int_{- \pi/2}^{\pi/2} \, \mathrm{d}\theta\frac{\cos\theta}{r + R \cos\theta} \end{aligned}$$

(16)

$$\begin{aligned} =& r^{2} \, \Delta\phi R \frac{B_{\mathrm{mid}}^{2}}{8\pi} \biggl[ - \frac{\theta}{R} + \frac{2r}{R\sqrt{r^{2} - R^{2}}} \tan ^{-1} \biggl( \frac{\sqrt{r - R}}{\sqrt{r + R}} \tan(\theta/2) \biggr) \biggr] \bigg| _{-\pi/2}^{\pi/2} \end{aligned}$$

(17)

$$\begin{aligned} =& r^{2} \, \Delta\phi\frac{B_{\mathrm{mid}}^{2}}{2\pi} \biggl[ \frac{ r }{\sqrt{r^{2} - R^{2}}} \tan^{-1} \biggl( \frac{\sqrt{r - R}}{\sqrt{r + R}} \biggr) - \frac{\pi}{4} \biggr] \end{aligned}$$

(18)

$$\begin{aligned} =& r^{2} \, \Delta\phi\frac{B_{\mathrm{mid}}^{2}}{4} \biggl[ \frac{ r }{\sqrt{r ^{2} - R^{2}}} \biggl( \frac{2}{\pi} \biggr) \tan^{-1} \biggl( \frac{\sqrt{r - R}}{\sqrt{r + R}} \biggr) - \frac{1}{2} \biggr] . \end{aligned}$$

(19)

The outward force on the inner segment of the torus involves an analogous integration, with a projection factor of $+\cos(\theta)$ and complementary domain, yielding

$$ F_{\mathrm{inner}} = r^{2} \, \Delta\phi\frac{B_{\mathrm{mid}}^{2}}{4} \biggl[ \frac{ r }{\sqrt{r^{2} - R^{2}}} \biggl( \frac{2}{\pi} \biggr) \tan^{-1} \biggl( \frac{\sqrt{r + R}}{\sqrt{r - R}} \biggr) - \frac{1}{2} \biggr] ~. $$

(20)

In the limit that torus’s minor radius $R$ were to expand to approximately its major radius, then the force on the inner surface would diverge, and the force on the outer surface would remain finite. The inverse tangents in Equations 19 and 20 are related via the identity $(\tan^{-1}[x] + \tan^{-1}[1/x]) = \pi/2$, so their values are coupled. The hoop force on the torus segment is given by the sum of $F_{\mathrm{outer}}$ and $F_{\mathrm{inner}}$, which yields

$$\begin{aligned} F_{\mathrm{hoop}} =& F_{\mathrm{inner}} + F_{\mathrm{outer}} = r^{2} \, \Delta \phi\frac{B_{\mathrm{mid}}^{2}}{2\pi} \biggl( \frac{\pi}{2} \biggr) \biggl[ \frac{ r }{\sqrt{r^{2} - R^{2}}} - 1 \biggr] \end{aligned}$$

(21)

$$\begin{aligned} =& r^{2} \, \Delta\phi\frac{B_{\mathrm{mid}}^{2}}{4} \biggl[ \frac{ r }{\sqrt{r ^{2} - R^{2}}} - 1 \biggr] . \end{aligned}$$

(22)

This is manifestly positive (outward).

Figure 6 plots the radial dependence of the terms in square brackets in the expressions for $F_{\mathrm{outer}}$, $F_{\mathrm{inner}}$, and $F_{\mathrm{hoop}}$ (from Equations 19, 20, and 22, respectively) as functions of major radius $r$. In the limit that the torus’s major radius $r$ expands to become much larger than its minor radius (so $r \gg R$),

$$\begin{aligned} F_{\mathrm{hoop}} \simeq& r^{2} \, \Delta\phi\frac{B_{\mathrm{mid}}^{2}}{4} \bigl[ \bigl(1 + (1/2) (R/r)^{2}\bigr) - 1 \bigr] \\ \simeq& R^{2} \, \Delta\phi\frac{B_{\mathrm{mid}}^{2}}{8}. \end{aligned}$$

(23)

As shown in Appendix B, the hoop force per unit length here scales as $I^{2}/r$, where $I$ is the total electric current within the torus, consistent with the result derived by Shafranov (1966). Therefore, if the evolution were ideal, the net outward force per unit length would decrease like $1/r$ if the major radius $r$ grew much greater than its minor radius $R$.

Figure 6

Plots of the radial dependence of the terms in square brackets in Equations 19, 20, and 22, corresponding to the outward $F_{\mathrm{inner}}$ (dashed), inward $F_{\mathrm{outer}}$ (dash/dots), and $F_{\mathrm{hoop}}$ (solid). For comparison, the curve $1/r$ is plotted (dotted line).

5.3.3 Change in Hoop Force Due to Reconnection

How does reconnection affect the hoop force on the ejection? The addition of flux should widen the proto-ejection, i.e., the minor radius $R$ of the ejection should increase. To analyze this effect, we must account for the change in minor radius by $\Delta R$ as $\Delta\Phi$ is added. This depends on the flux density at the proto-ejection’s trailing edge. In the frame co-moving with the ejection, the upward motion of the dipolarizing post-reconnection flux $\Delta\Phi$ is arrested by the back reaction of magnetic pressure at that trailing edge. This implies that magnetic pressures, and therefore field strengths, are approximately equal at the proto-ejection’s trailing edge and in the arrested flux. So the addition of flux $\Delta\Phi$ at the same field strength implies

$$\begin{aligned} \Delta\Phi =& B_{\mathrm{in}} \Delta R \, (r - R) \, \Delta\phi= \biggl[ B_{\mathrm{mid}} \frac{r}{r - R} \biggr] \Delta R \, (r - R) \, \Delta \phi \end{aligned}$$

(24)

$$\begin{aligned} =& B_{\mathrm{mid}} \, r \Delta R \, \Delta\phi \end{aligned}$$

(25)

$$\begin{aligned} \frac{\Delta\Phi}{\Delta R} =& B_{\mathrm{mid}} \, r \, \Delta\phi, \end{aligned}$$

(26)

where $B_{\mathrm{in}}$ is the field strength at the proto-ejection’s trailing edge, which is related to $B_{\mathrm{mid}}$ by Equation 12.

The change in hoop force, $\Delta F_{\mathrm{hoop}}$, due to the differential increase in $R$ is then the difference of two versions of Equation 22, evaluated for minor radii $R+\Delta R$ and $R$. Assuming $\Delta R$ is small compared to $(r-R)$, we have

$$\begin{aligned} \Delta F_{\mathrm{hoop}} =& \frac{B_{\mathrm{mid}}}{4} \frac{\Delta\Phi}{ \Delta R} r \biggl[ \frac{ r}{\sqrt{r^{2} - (R+\Delta R)^{2}}} - \frac{ r }{\sqrt{r^{2} - R^{2}}} \biggr] \end{aligned}$$

(27)

$$\begin{aligned} =& \frac{B_{\mathrm{mid}} \, \Delta\Phi}{4 \, \Delta R}r^{2} \biggl[ \frac{ 1}{\sqrt{r^{2} - R^{2} -2 R \, \Delta R - \Delta R^{2}}} - \frac{ 1 }{\sqrt{r^{2} - R^{2}} } \biggr] \\ =& \frac{B_{\mathrm{mid}} \, \Delta\Phi}{4 \, \Delta R}\frac {r^{2}}{\sqrt{r ^{2} - R^{2}}} \biggl[ \biggl( 1 - \frac{2 R \, \Delta R + \Delta R ^{2}}{(r^{2} - R^{2})} \biggr) ^{-1/2} - 1 \biggr] \end{aligned}$$

(28)

$$\begin{aligned} \simeq& \frac{B_{\mathrm{mid}} \, \Delta\Phi}{4 \, \Delta R} \frac{r ^{2}}{\sqrt{r^{2} - R^{2}}} \biggl[ 1 + \frac{R \, \Delta R }{(r ^{2} - R^{2})} - 1 \biggr] \end{aligned}$$

(29)

$$\begin{aligned} \simeq& \frac{B_{\mathrm{mid}} \, \Delta\Phi}{4} \frac{r^{2}}{\sqrt{r ^{2} - R^{2}}}\frac{R}{(r^{2} - R^{2})} \end{aligned}$$

(30)

$$\begin{aligned} \simeq& \frac{B_{\mathrm{mid}} \, \Delta\Phi}{4} \frac{r^{2} R}{(r^{2} - R^{2})^{3/2}} \end{aligned}$$

(31)

$$\begin{aligned} =& \frac{B_{\mathrm{mid}} \, \Delta\Phi}{4} \biggl[ \frac{(R/r)}{ ( 1 - (R/r)^{2} ) ^{3/2}} \biggr]. \end{aligned}$$

(32)

The coefficients in this result are similar in form to those in Equation 8, but the change in force depends on the ejection’s height $r$ and half-width $R$. For $r \gg R$, Equation 32 implies

$$ \Delta F_{\mathrm{hoop}, r \gg R} = \frac{B_{\mathrm{mid}} \, \Delta\Phi}{4} \biggl( \frac{R}{r} \biggr). $$

(33)

The results in Equations 32 and 33 can also be derived by differentiating the expressions in Equations 22 and 23, respectively, with respect to $R$, and expressing the result in terms of $\Delta\Phi$.

Figure 7 plots the variation with $(R/r)$ of the term in the square brackets in Equation 32, and includes the scaling predicted by Equation 33 for comparison. To the extent that CMEs evolve with constant angular width (e.g., Zhao, Plunkett, and Liu 2002), the ratio $(R/r)$ would remain fixed as major radius $r$ increases. The mean and median CME widths in the CDAW catalog dataset referenced above are $50^{\circ}$ and $63^{ \circ}$, respectively. These probably overestimate the actual angular widths of typical erupting flux ropes due to tilts of flux ropes’ axes along the line of sight. So a typical value for $(R/r)$ might be $1/3$, corresponding to a torus cross section that subtends an angle of $37^{\circ}$, for which

$$ \Delta F_{{\mathrm {hoop}}, r = 3R} = \frac{B_{\mathrm{mid}} \, \Delta\Phi}{4} \frac{(1/3)}{(8/9)^{3/2}} = \frac{B_{\mathrm{mid}} \, \Delta\Phi}{4} \frac{9}{64 \sqrt{2}} \simeq0.1 B_{\mathrm{mid}} \, \Delta\Phi. $$

(34)

This is a bit smaller than the change in tension force for a purely poloidal field, $\Delta F_{\mathrm {tension}} \simeq0.16 B_{\mathrm{tot}} \Delta\Phi$ from Equation 8, and a bit larger than the change in tension force for guide-field reconnection with field line pitch $\omega= 20^{\circ}$, $\Delta F_{\mathrm {tension}} \simeq0.05 B_{\mathrm{tot}} \Delta\Phi$ from Equation 10.

Figure 7

The solid line plots the term in square brackets in Equation 32 as $(R/r)$ varies. The dashed line plots $(R/r)$ versus $(R/r)$. To the extent that CMEs propagate with fixed angular width (e.g., Zhao, Plunkett, and Liu 2002), the ratio $(R/r)$ should be constant as $r$ increases.

Equation 32 and subsequent results assume that the reconnected flux $\Delta\Phi$ is completely dipolarized. The total change in hoop force should also account for how the hoop force increases as $\Delta\Phi$ evolves from the pre-dipolarized state to the post-dipolarized state. In Appendix C, we consider this change in force due to dipolarization, and we find that the change in force predicted by Equation 32 could be a lower estimate.

5.3.4 Toroidal and Poloidal External Field

The derivation above has neglected any toroidal component in the reconnecting field external to the torus. The presence of a toroidal component, $B_{\mathrm{T}}$, in the reconnecting field alters the relationships we derived above (Equations 19, 20, 22, and 32). The modified inward force on the outer surface, $F_{\mathrm{outer}}'$, is given by

$$ F_{\mathrm{outer}}' = \int \mathrm{d}S_{\mathrm{out}} \frac{(B_{\mathrm{P}}^{2} + B_{\mathrm{T}}^{2})}{8 \pi}, $$

(35)

and the modified outward force on the inner surface, $F_{\mathrm{inner}}'$, is given by

$$ F_{\mathrm{inner}}' = \int \mathrm{d}S_{\mathrm{in}} \frac{(B_{\mathrm{P}}^{2} + B_{\mathrm{T}}^{2})}{8 \pi}. $$

(36)

For fixed total field strength $B$, nonzero $B_{\mathrm{T}}$ implies the poloidal field, $B_{\mathrm{P}}$, is weaker. We assume, however, that the dependence of $B_{\mathrm{P}}$ on $\theta$ is unchanged, because Equation 11 must still apply: every unit of poloidal flux threading the interior of the torus must map to a larger area exterior to it.

Without developing a particular model of a field with a toroidal component, we can, with some basic assumptions, make some inferences about the effect that a nonzero toroidal field component, $B_{\mathrm{T}}$, would have on the hoop force. We start with the simplifying assumptions that i) fields in the torus and external to it are axisymmetric (invariant in the toroidal direction), and ii) there is no net current across (perpendicular to) the plane of the torus. Physically, assumption ii) is equivalent to requiring that net charge does not accumulate on either side of the torus; such an accumulation could not persist.

We now show that these assumptions imply that $B_{\mathrm{T}}$ must also decrease as the inverse of radial distance from torus center. Consider the closed path shown in the left panel of Figure 8, which lies in the plane of the figure. By Ampère’s law, the net electric current, $I_{n}$, normal to the plane of the figure that is enclosed by the loop, is proportional to $\oint \boldsymbol {B} \cdot \mathrm{d}\boldsymbol {\ell}$ around the loop. Axisymmetry implies that the line integrals across the torus, $\int B_{r} \,\mathrm{d}r$ for segment two and $-\int B_{r}\, \mathrm{d}r$ for segment four, must cancel. The integrations along segments one and three then imply

$$ I_{n} \propto \oint \boldsymbol {B} \cdot \mathrm{d}\boldsymbol {\ell}= \Delta\phi\bigl[ r_{3} B_{\mathrm{T}}(r_{3}) - r_{1} B_{\mathrm{T}}(r_{1}) \bigr]. $$

(37)

The radial coefficient of each term implies that, for $I_{n}$ to vanish, $B_{\mathrm{T}}$ must decrease as the inverse of distance from the torus center. The assumed axisymmetry implies that this result is valid even if $I_{n} \ne0$ for $r < r_{1}$. In accordance with this result, when comparing Equations 35 and 36, we know that $\mathrm{d}S$ increases linearly with distance from torus center, but $(B_{\mathrm{T}}^{2} + B_{\mathrm{P}}^{2})$ decreases quadratically with distance from torus center, so $|F_{\mathrm{inner}}'| > |F_{\mathrm{outer}}'|$, and again the hoop force is outward as in the case of purely poloidal field.

Figure 8

Left: The solid lines depict a cross section of a torus segment, viewed from the side, and the dashed lines show an Ampèrian loop in the plane of the cross section. Right: The two long, thin flux tubes crossing below the torus (solid being nearer the viewer, dashed farther) depict reconnecting fields with nonzero $B_{\mathrm{T}}$ below a rising ejection. Upward-dipolarized, post-reconnection flux (the upper, thick, half-dashed, half-solid flux tube) is in contact with the inner surface of the torus over a longer distance than with purely poloidal reconnecting field. The volume integral in Equations 39 and 40 runs over the length of the upward-dipolarized flux tube.

Our argument that $B_{\mathrm{T}}$ should scale as $1/r$ does rest upon somewhat restrictive assumptions, which might not apply on the Sun. In particular, our assumption of patchy reconnection implies that the assumed axisymmetry is, at best, only approximately correct.

As shown in the right panel of Figure 8, reconnection of fields below the torus with nonzero $B_{\mathrm{T}}$ will lead to post reconnection flux (upper, half-dashed, half-solid tube) in contact with the inner surface of the torus. This post-reconnection field would exert an outward force $F_{\mathrm{inner}}'$ on the torus.

5.4 Comparing Changes in Hoop and Tension Forces

To better understand reconnection-driven changes in forces acting on CMEs, it is useful to compare the changes in tension and hoop forces.

As a preliminary remark, we note that the presence of axial curvature of the erupting flux system, which is ultimately responsible for the hoop force, could, in principle, modify the tension force from the poloidal field. In Appendix D, we show that axial curvature does not affect the tension of a poloidal flux tube with $B_{\mathrm{P}}$ given by Equation 12.

Taking the ratio of the change in hoop force for $r \gg R$, from Equation 33, to the change in tension force, from Equation 8, yields

$$ \frac{\Delta F_{\mathrm{hoop}, r \gg R}}{\Delta F_{\mathrm {tension}}} \simeq \frac{(R/r) \, \Delta\phi B_{\mathrm{mid}}/4}{\Delta\phi B_{\mathrm{mid}}/2 \pi} \simeq\frac{\pi}{2} \biggl( \frac{R}{r} \biggr). $$

(38)

Hence, the force changes from these effects are similar in magnitude for $R$ comparable to $r$.

Using instead the change in tension force due to reconnection with a guide field, from Equation 10 with a value of $\omega= 20^{\circ}$, reduces the tension force by a factor of $1/3$. In this case, with $(R/r)$ = 1/3 as discussed previously, $\Delta F _{\mathrm{hoop}}$ due to the widening of the proto-ejection would be commensurate with or slightly larger than $\Delta F_{\mathrm {tension}}$.

5.5 Changes in CME Acceleration

We now seek to characterize the change in the CME’s acceleration due to these changes in external forces acting on the eruption. To do so, we derive the first-order difference in the time rate of change of momentum between two instants, $t_{1}$ and $t_{2}$, separated in time by $\Delta t$. Recall that a flux $\Delta\Phi_{B}$ accreted onto the CME increases its mass by $\Delta m$ because the flux is frozen to the plasma outside the diffusion region. (Here, $\Delta\Phi_{B}$ refers to the total flux in the flux tube, not just the flux from the reconnecting component of $\boldsymbol {B}$.) The mass in the segment of the flux tube that is added to the ejection is

$$\begin{aligned} \Delta m =& \int\rho\, \mathrm{d}V = \int\rho\, \mathrm{d}A \, \mathrm{d}L \end{aligned}$$

(39)

$$\begin{aligned} =& \int\frac{\rho}{B} \, \Delta\Phi_{B} \, \mathrm{d}L = \Delta \Phi_{B} \int\frac{\rho}{B} \, \mathrm{d}L. \end{aligned}$$

(40)

The integral here runs over the upward-dipolarized, thick flux tube in the right panel of Figure 8. (Notice that the presence of a toroidal field component – a guide field – in reconnection beneath the ejection yields accretion of post-reconnection flux tubes that are longer than if purely poloidal fields reconnected.) For field strengths of a few gauss, lengths of a few tens of Mm, and mass densities near $10 ^{-15}$ g cm⁻³ (a few times $10^{8}$ electrons per cm³), the added mass per unit reconnected flux is around ${\sim}\,10^{-6}$ g/Mx. For events with a few times $10^{21}$ Mx of reconnected flux (Qiu and Yurchyshyn, 2005; Kazachenko et al., 2017), the increase in mass of a proto-ejection by flux accretion would be of order ${\sim}\,10^{15}$ g. The mean of nonzero CME masses in the CDAW catalog is $1.6 \times10^{15}$ g.

The time rate of change in momentum is given by

$$ \frac{\mathrm{d}\boldsymbol {p}}{\mathrm{d}t} = \frac{\mathrm{d}m_{\mathrm{eff}}}{\mathrm{d}t} \boldsymbol {v} + m_{\mathrm{eff}} \frac{\mathrm{d}\boldsymbol {v}}{\mathrm{d}t}. $$

(41)

Assuming the increase in the CME’s effective mass is very small compared to the total effective mass, we neglect $\mathrm{d}m_{\mathrm{eff}}/\mathrm{d}t$ here and in the following steps. We then have

$$\begin{aligned} \frac{\mathrm{d}\boldsymbol {p}(t_{2})}{\mathrm{d}t} - \frac{\mathrm{d}\boldsymbol {p}(t_{1})}{\mathrm{d}t} =& \boldsymbol {F}(t _{2}) - \boldsymbol {F}(t_{1}), \end{aligned}$$

(42)

$$\begin{aligned} m_{\mathrm{eff}} \biggl( \frac{\mathrm{d}\boldsymbol {v}(t_{2})}{\mathrm{d}t} - \frac{\mathrm{d}\boldsymbol {v}(t _{1})}{\mathrm{d}t} \biggr) \simeq& \Delta \boldsymbol {F}, \end{aligned}$$

(43)

$$\begin{aligned} \Delta \boldsymbol {a} \simeq& \frac{\Delta \boldsymbol {F}}{m_{\mathrm{eff}}} , \end{aligned}$$

(44)

where the changes in tension and hoop forces due to the reconnection are given by Equations 10 and 32, respectively. For reconnection of a small amount of flux $\Delta \Phi$, both Equations 10 and 32 scale as the product of the reconnecting field strength multiplied by the reconnected flux,

$$ \Delta a \propto\frac{B \Delta\Phi}{m_{\mathrm{eff}}}. $$

(45)

Hence, these assumptions predict that the rate of acceleration of a CME increases linearly with reconnected flux.

How significant is the acceleration from reconnection-driven changes in the forces (Equations 10 and 32) acting on a CME? Our formalism analyzes the change in Lorentz forces from reconnection of a discrete amount of flux, $\Delta\Phi$. In Section 4, we considered reconnection for a total field strength of 10 G with a 3 G poloidal component. The SADs identified by Savage and McKenzie (2011) and McKenzie and Savage (2011) suggest that patchy reconnection occurs over areas on the order of 10 Mm². Accordingly, we consider reconnection of a 10 Mm² patch of 3 G field, corresponding to $\Delta\Phi= 3 \times10^{17}$ Mx, and an effective CME mass $m_{\mathrm{eff}} = 2 \times10^{15}$ g. For the tension force, the contribution to Equation 44 from 10 alone, with $\omega= 20^{\circ}$, would imply an increase in acceleration of ${\sim}\,24$ cm s⁻². For the hoop force, with $(R/r) = 3$, the increase in acceleration would be ∼ 38 cm s⁻². Roughly, the two effects both act to accelerate the ejection with similar magnitude, and the combined $\Delta a$ from both is on the order of 0.6 m s⁻².

Qiu and Yurchyshyn (2005), Kazachenko et al. (2017), and Gopalswamy et al. (2017a) report typical reconnection fluxes $10^{21}$ Mx for the CMEs in their samples. Qiu and Yurchyshyn (2005) also suggest that this could be an underestimate, because not all reconnected flux exhibits ribbon emission that is detectable by their methods. It should be noted, however, that their approach might produce an overestimate: if the reconnection is patchy, and both footpoints in each polarity produce ribbon emission captured by their method, then some reconnected flux is double counted. These two effects – missing some flux from weakly emitting footpoints, and double counting some flux – might offset each other, so we assume the flux estimates from Qiu and Yurchyshyn (2005) approximate the true reconnected flux. Simply summing $3 \times10^{3}$ similar reconnection events, each of $3 \times10^{17}$ Mx, to reconnect ${\sim}\,10^{21}$ Mx of flux would yield a total acceleration near 2000 m s⁻². Also, this analysis assumes that each reconnection event accelerates the final mass of the CME – but the CME mass should initially be smaller, and grow as reconnection accretes mass onto it. Moreover, several events studied by Qiu and Yurchyshyn (2005), Kazachenko et al. (2017), and Gopalswamy et al. (2017a) have substantially higher ribbon fluxes.

For comparison, using data from the LASCO C1 coronagraph (Brueckner et al., 1995) before it failed, Zhang and Dere (2006) report accelerations for 50 CMEs, with a mean value of 300 m s⁻², and a standard deviation of 600 m s⁻². Vršnak (2006) reports a few CMEs with accelerations near 1000 m s⁻². The accelerations implied by our crude estimates of Lorentz force changes due to reconnection are much larger than those observed in most CMEs, an issue we revisit shortly. It should be clear from Equations 10 and 32 that this too-high acceleration does not depend upon our choice that $\Delta\Phi= 3 \times10^{17}$ Mx – the key factors are the typical field strength of the post-reconnection field as it accretes onto the ejection, and the total amount of reconnected flux over the course of the eruption.

We now consider our model of reconnection-driven changes in forces on CMEs in the context of observations that show CMEs’ speeds scale with the reconnected flux. Equation 45 suggests that CME accelerations, not speeds, should scale with the amount of reconnected flux. This inconsistency with observations might be reconciled by the field-strength dependence in Equation 45, which implies that the added force on the ejection from reconnected flux will diminish with increasing height, because field strengths decrease with height.

While we have focused on changes in forces on an ejection due to reconnection, Lorentz forces from external fields not directly involved in reconnection also act on the ejection, both to drive and to resist the ejection’s rise. In addition to weakening forces from reconnected fields, the decrease of magnetic field strengths as the ejection moves outward will also reduce all other Lorentz forces acting on it. Equations 19 and 20 were derived for a small section of a torus, but they are also valid for external hoop forces acting on a longer torus section in the absence of reconnection. The ratio of inward to outward hoop forces, plotted as $|F_{\mathrm{outer}}/F _{\mathrm{inner}}|$ in Figure 9, aids consideration of how the total hoop force on the ejection changes as the ejection rises. At initiation of the eruption, $r$ is nearest $R$, so $|F_{\mathrm{outer}}/F_{\mathrm{inner}}|$ is smallest, and the acceleration is largest. As $r$ increases relative to $R$, however, $|F_{\mathrm{inner}}|$ decreases relative to $|F_{\mathrm{outer}}|$, so the external forces slowing the ejection increase substantially relative to the external forces driving it. Consistent with this, Vršnak (2006) estimated the accelerations of flare sprays, eruptive prominences, and the leading edges of white-light CMEs, and found a trend of decreasing acceleration with distance; see especially his Figure 2. The effect of decreasing field strength with height could be investigated using MHD models of erupting CMEs.

Figure 9

This plot shows the ratio of the inward magnetic pressure force, $|F_{\mathrm{outer}}|$, which acts on the ejection’s outer face, to the outward magnetic pressure force, $|F_{\mathrm{inner}}|$, which acts on its inner face. This ratio increases from near zero at $(r/R) \simeq 1$ to about 0.85 for large $(r/R)$.

Another factor that we have ignored is drag force on the CME. Vršnak, Vrbanec, and Čalogović (2008) analyzed CME accelerations, and found drag to be dynamically significant over the height range that they analyzed, (2 – 30) $R_{\odot}$. They expressed the drag force as

$$ F_{\mathrm {drag}} \sim\rho_{\mathrm {amb}} (v - v_{\mathrm {amb}})^{2} C_{D} A, $$

(46)

where $C_{D}$ is the dimensionless drag coefficient, $\rho_{\mathrm {amb}}$ is the density of the ambient plasma through which the CME propagates, $v_{\mathrm {amb}}$ is the speed of the ambient plasma, and $A$ is the effective area the ejection perpendicular to its relative motion with respect to the background plasma. In the outer corona and heliosphere, $v_{\mathrm {amb}}$ is the solar wind speed. In assessing drag forces on H$\alpha$ flare surges within 0.25 $R_{\odot}$, Vršnak (2006) noted that drag forces can be relatively strong there, because the ambient plasma speed is zero and ambient densities are highest. Increases in CME speed and area due to flux accretion would, all else equal, increase drag forces on the CME. (We have also ignored changes in gravity as the ejection rises, because that the gravitational energies of many CMEs are dwarfed by their kinetic energies – e.g., Emslie et al. 2012.)

6 Summary and Conclusions

Several observations indicate that magnetic reconnection in flare-associated CMEs plays a central role in the development such ejections. i) Emission patterns consistent with reconnection are common. ii) Estimates of reconnected flux inferred from these emission patterns are correlated with CME speeds, so a causal link between reconnection and CME accelerations is plausible. iii) The masses of CMEs are correlated with their speeds. iv) Estimates of reconnected flux are correlated with fitted poloidal fluxes in CME flux ropes. Taken together, these observations implicate reconnection in the formation and acceleration of some CMEs.

We noted that reconnection tends to add mass to CMEs. This occurs because reconnection joins external flux with the ejection as it rises, and plasma is frozen to this flux outside of the small diffusion region where the reconnection occurs. If reconnection had no other effect besides adding mass to the erupting flux system, the ejection would slow. We expect, however, that reconnection should also affect the Lorentz forces acting on the ejection.

Accordingly, we then sought to quantify, using order-of-magnitude estimates, how reconnection might affect the dynamics of a rising ejection. First, we estimated the momentum flux into a rising ejection due to outflow from the flare reconnection underneath it. We found that the reconnection outflow might be responsible for ${\sim}\,10$% of the final momentum of a moderate-speed CME, although the uncertainties in this estimate are large – it is plausible that momentum transfer from the reconnection outflow supplies significantly more or less than this.

Second, we considered simple models of the magnetic structure of an ejection before and after reconnection of a small amount of flux $\Delta\Phi$. We started by estimating the resulting changes in the net magnetic tension on the ejection, and found that downward magnetic tension was reduced by an amount proportional to $B \Delta\Phi$, where $B$ is the strength of the reconnecting field component and $\Delta\Phi$ is the amount of reconnected flux. We then estimated the change in upward magnetic pressure, due to the increased hoop force from accretion of post-reconnection flux onto the ejection, which was also proportional to $B \Delta\Phi$, where $B$ is the total field strength.

A key result of our analysis is that changes in tension and hoop forces due to reconnection are commensurate. This implies that a tether-cutting model of dynamics misses half of the story: “hoop adding” is just as important. This also highlights a significant difference between breakout reconnection above a proto-ejection, which reduces downward tension from overlying fields, and flare reconnection below a proto-ejection, which both reduces downward tension forces and adds hoop forces. Because the added hoop force is on the order of the reduced tension force, if the reconnecting fields were the same at each location, then flare reconnection would produce about twice the change in Lorentz force as breakout reconnection. But the decrease in field strength with height together with the field-strength dependence of the change in force implies that flare reconnection should much more strongly affect a proto-ejection’s acceleration than breakout reconnection. This accords with the results reported by Karpen, Antiochos, and DeVore (2012).

For reasonable choices of reconnecting field strengths and CME mass, we estimated the change in CME acceleration due to changes in Lorentz forces alone. This yielded rough estimates of CME accelerations near 2000 m s⁻². Such accelerations are, however, larger than the observed accelerations of most CMEs. We hypothesize that the decrease in Lorentz forces on the CME with increasing height above the solar surface (e.g., in Figure 9), combined with drag on the ejection, both neglected in our model, can reconcile the discrepancy between observed CME accelerations and those predicted by our model. Another possibility, discussed in Section 5.5 above, is that the reconnected flux estimated from flare ribbons and magnetograms, by double counting flux in each polarity, overestimates the actual reconnected flux.

We hope the rough estimates made here will be tested with data from MHD simulations of ejections. In particular, it would be illuminating to compare the contributions of momentum flux from the reconnection outflow, reduction in magnetic tension, and increase in hoop force to the overall momentum budgets of model CMEs.

Appendices

Appendix A: Evolution of Magnetic Helicity

Magnetic reconnection not only alters the Lorentz forces acting on an erupting flux rope, it also changes the rope’s magnetic helicity (e.g., Berger et al. 1998). To consider the effect of reconnection on the ejection’s helicity, we idealize the erupting flux system as a toroidal rope of purely azimuthal flux, $\Phi_{\mathrm{T}}$, formed by the ejection’s core, surrounded by purely poloidal flux, $\Phi_{\mathrm{P}}$. The mutual helicity of the two flux systems, $|H_{\mathrm {mut}}| = |2\Phi_{\mathrm{P}} \Phi_{\mathrm{T}}|$, quantifies linkages between the two flux systems. If the poloidal or azimuthal flux systems contained internal, “self” linkages, then the total helicity would be the sum of these self helicities and the mutual helicity. Because magnetic helicity is an ideal MHD invariant, no ideal process can lead to the increase of poloidal flux wrapping around the azimuthal core field. (Ideal processes could, however, cause poloidal flux to bunch up, leading to regions with stronger $B_{\mathrm{P}}$.)

When reconnection occurs in the wake of the outward-moving toroidal rope, however, it adds flux that wraps around the rope. Helicity is approximately globally conserved in fast reconnection (e.g., Berger 1999), and this increase in the helicity of the erupting flux system is offset by an opposing change in mutual helicity between the erupting system and surrounding fields. Figure 10 illustrates key aspects of this evolution. For simplicity, both flux tubes shown are assumed to have no internal twist; relaxing this assumption would not substantively alter results of the analysis. Essentially, some of the mutual helicity between the rising, toroidal system (A in the figure) and the initially overlying, external flux system (B in the figure) is transformed into self helicity of the erupting system (toroid plus reconnected flux that encircles it) (Berger et al., 1998).

Figure 10

Left: Flux systems A and B, each assumed untwisted, have a mutual helicity that is greater than zero, due to their positive crossing number. Middle: System A is erupting upward through B. Right: Flux from B has reconnected with itself, and thereby formed two flux systems, one that is closed and linked to system A and one that is anchored at the photosphere. The mutual helicity between A and the flux from system B that is anchored at the photosphere has changed sign, since the sign of their crossing has changed. Globally, helicity is conserved here, though it has been transferred between mutual and self helicities.

This transfer of helicity between the erupting and background flux systems may be seen by considering the sign of the crossing between the external flux and toroidal flux, which changes when the rising flux passes through the external field by driving the latter to reconnect with itself. Initially (left panel), their mutual helicity is $H_{i} = +\Phi_{A} \Phi_{B} (b_{+} + b_{-})/\pi$, and in the final state (right panel), their mutual helicity is $H_{f} = -\Phi_{A} \Phi _{B}(a_{+} + a_{-})/\pi$. (Demoulin, Pariat, and Berger (2006) review the sign convention for angles: the mutual helicity is defined from footpoint angles of the overlying loop; angles swing from the footpoint with the same sign as the apex loop’s footpoint toward the opposite-sign footpoint; and counterclockwise is positive.) The difference in mutual helicities is

$$ \Delta H_{\mathrm {mut}} = H_{f} - H_{i} = - \Phi_{A} \Phi_{B} (a_{+} + a _{-} + b_{+} + b_{-})/\pi= -2 \Phi_{A} \Phi_{B}. $$

(47)

The difference in mutual helicities from the changed crossing sign has been added to the self helicity of the erupting system: the flux that reconnected to encircle the rising flux contributes to the erupting system’s self helicity. The linking number of fluxes in the erupting system is $+1$, so the helicity within that system is $+2 \Phi_{A} \Phi _{B}$.

More detailed studies of helicity evolution due to reconnection in an eruption with reconnection have been undertaken (e.g., Priest and Longcope 2017).

Appendix B: Large-$r$ Scaling of Hoop Force

From Equation 23, the hoop force $F_{\mathrm{hoop}}$ on a length of torus $r \, \Delta\phi$ scales as $R^{2} \, \Delta \phi(B_{\mathrm{mid}}^{2}/8)$ for $r \gg R$. The force per unit length therefore scales as

$$ \frac{F_{\mathrm{hoop}}}{r \, \Delta\phi} \sim\frac{R^{2} B_{\mathrm{mid}} ^{2}}{r}. $$

(48)

Shafranov (1966) derived an expression for the hoop force per unit length in terms of the total azimuthal electric current, $I$, finding that the force per unit length scaled as $I^{2}/r$. In our model, with the poloidal field in Equation 12, the electric current along the torus’s axis is

$$\begin{aligned} I =& \frac{c}{4\pi} \oint \boldsymbol {B} \cdot \mathrm{d}\boldsymbol {L} = \frac{c}{4 \pi} \int_{-\pi}^{\pi} \frac{B_{\mathrm{mid}} \, r}{r + R \cos\theta} R \, \mathrm{d}\theta \end{aligned}$$

(49)

$$\begin{aligned} =& \frac{c r R B_{\mathrm{mid}}}{4\pi} \biggl[ \frac{2}{\sqrt{r ^{2} - R^{2}}} \tan^{-1} \biggl( \frac{\sqrt{r - R}}{\sqrt{r + R}} \tan(\theta/2) \biggr) \bigg\vert _{-\pi}^{\pi} \biggr] \end{aligned}$$

(50)

$$\begin{aligned} =& \frac{c r R B_{\mathrm{mid}}}{4\pi} \frac{2 \pi}{\sqrt{r^{2} - R ^{2}}} = \frac{c r R B_{\mathrm{mid}}}{2 \sqrt{r^{2} - R^{2}}}. \end{aligned}$$

(51)

Therefore, in our model, $I^{2}/r$ varies with $r$ as

$$ I^{2}/r \sim\frac{r R^{2} B_{\mathrm{mid}}^{2}}{(r^{2} - R^{2})} = \frac{R ^{2} B_{\mathrm{mid}}^{2}}{r (1 - (R/r)^{2})} . $$

(52)

In the $r \gg R$ limit, then,

$$ I^{2}/r \sim\frac{R^{2} B_{\mathrm{mid}}^{2}}{r} . $$

(53)

This matches the scaling of our force per unit length, from Equation 48. Figure 6 shows a comparison of $1/r$ (dotted line) with the radial dependence of the term in square brackets in the expression for $F_{\mathrm{hoop}}$ in Equation 22 (solid line).

Appendix C: Pre- to Post-Dipolarization Change in Hoop Force

Another aspect of the change in hoop force is more subtle: the total change in force on the proto-ejection by the addition of reconnected flux $\Delta\Phi$ is likely larger than the value given in Equation 32. To see why, we must consider how the net force exerted by the reconnected field on the ejection changes as a result of the dipolarization.

We define $t_{i}$ to be an instant after this flux has reconnected but before it has fully dipolarized, and $t_{f}$ to be after full dipolarization. At $t_{i}$, the field strength on the inner side of the proto-ejection is weaker than assumed in deriving Equation 20, as shown in the left magnetic field configuration in Figure 11. Consequently, the pre-dipolarization, inner-surface component of the hoop force, $F_{\mathrm {inner,pre}}$, is weaker than $F_{\mathrm{inner}}$ derived above. We assume that flux arching over the proto-ejection’s leading edge is unchanged by the reconnection, so always acts on the proto-ejection with the same inward pressure force $F_{\mathrm{outer}}$. This implies that the instantaneous hoop force acting on the proto-ejection due to just the annulus of reconnected flux is strongest after complete dipolarization, as depicted in the right panel of Figure 11. This force is equal to the value given in Equation 32, which can also be understood as the net pressure force due to only the annulus of reconnected flux $\Delta\Phi$ that wraps around the proto-ejection,

$$ \Delta F_{\mathrm{hoop}} = F_{{\mathrm {inner}}, \Delta\Phi} + F_{{\mathrm {outer}}, \Delta\Phi}, $$

(54)

where the $\Delta\Phi$ subscripts indicate that these forces are due only to the reconnected flux, and $F_{\mathrm{outer}, \Delta\Phi}$ is negative.

Figure 11

Left: Prior to complete dipolarization of post-reconnection flux, the flux density behind the ejection, $B_{\mathrm {pre}}$, is less than the inner-edge flux density $B_{\mathrm{in}}$ assumed in deriving Equation 20. The distance from the reconnection site to the trailing edge of the proto-ejection is assumed to be ${\sim}\, r/2$. The inward pressure force on the proto-ejection’s outer surface due to the reconnected flux, $F_{{\mathrm {outer}},\Delta \Phi}$, assumed to be unchanging, is depicted as a blue vector. The pre-dipolarization outward pressure force on its inner surface due to the reconnected flux, $F_{{\mathrm {inner,pre}},\Delta\Phi}$, is depicted as a red vector. For the configuration shown, at time $t_{i}$, the net pressure force from the annulus of reconnected flux is inward (negative). Right: After complete dipolarization at $t_{f}$, the outward pressure force from the reconnected flux (denoted $F_{{\mathrm {inner}},\Delta\Phi}$) is larger, and the net (outward) pressure force from the annulus of reconnected flux is strongest, and equal to $\Delta F_{\mathrm{hoop}}$ from Equation 32. The total change in the magnetic pressure force on the proto-ejection is the net pressure force at $t_{f}$ minus the net pressure force at $t_{i}$, $\Delta F_{fi}$ and this difference can exceed the value for $\Delta F_{\mathrm{hoop}}$.

This instantaneous force, however, is not the same as the change in pressure force acting on the proto-ejection due to the accretion of reconnected flux. The change in pressure force on the ejection from $t_{i}$ to $t_{f}$ is the difference between the net forces at $t_{f}$ and $t_{i}$,

$$\begin{aligned} \Delta F_{fi} =& (F_{\mathrm{inner}, \Delta\Phi} + F_{\mathrm{outer}, \Delta\Phi}) - (F_{\mathrm{inner, pre}, \Delta\Phi} + F_{\mathrm{outer},\Delta\Phi}) \end{aligned}$$

(55)

$$\begin{aligned} =& (F_{{\mathrm{inner}}, \Delta\Phi} - F_{{\mathrm{inner,pre}}, \Delta\Phi}), \end{aligned}$$

(56)

where the subscripts denote the outward and inward forces (subscripted inner and outer, respectively) on the proto-ejection from the reconnected flux $\Delta\Phi$. It can be seen that if $|F_{\mathrm{inner,pre}, \Delta\Phi}| < |F_{\mathrm{outer}, \Delta\Phi}|$, then $\Delta F_{fi} > \Delta F_{\mathrm{hoop}}$ from Equation 32. We remark that, much like the magnetic tension force from a flux tube $\Delta\Phi$ that is inward prior to tether-cutting reconnection, the net force due to inward and outward magnetic pressures from a flux tube $\Delta\Phi$ might also be inward in the pre-dipolarization state (i.e., $(F_{\mathrm{inner,pre}, \Delta\Phi} + F_{\mathrm{outer}, \Delta\Phi}) < 0$ in Equation 55).

How much weaker would the pre-dipolarization magnetic field, $B_{\mathrm{pre}}$, have to be for the pre-dipolarization force to be inward? As a first step to addressing this question, we use Equation 20 to crudely approximate the outward pressure force prior to complete dipolarization, $F_{\mathrm{inner,pre},\Delta\Phi}$, to be

$$ F_{\mathrm{inner,pre}, \Delta\Phi} \simeq(B_{\mathrm{pre}}/B_{\mathrm{in}})^{2} F_{\mathrm{inner}, \Delta\Phi}. $$

(57)

We expect that the behavior of $F_{\mathrm{inner}, \Delta\Phi}$ follows $F_{\mathrm{inner}}$, and similarly that $F_{\mathrm{outer}, \Delta\Phi}$ follows $F_{\mathrm{outer}}$. It is helpful to refer again to Figure 9, which plots the ratio of $|F_{\mathrm{outer}}/F _{\mathrm{inner}}|$ as a function of major radius $r$, in units of minor radius $R$. For $(r/R)$ near unity, $|F_{\mathrm{outer}}| \ll |F_{\mathrm{inner}}|$, but $|F_{\mathrm{outer}}|$ is more comparable to $|F_{\mathrm{inner}}|$ at larger $(r/R)$. For the ratio $(r/R) = 3$ assumed above, $|F_{\mathrm{outer}}/F_{\mathrm{inner}}|$ is near 0.6, implying that a ratio of $(B_{\mathrm {pre}}/B_{\mathrm{inner}})$ of 0.7, for instance, would yield an initially inward force:

$$ F_{\mathrm{inner,pre}, \Delta\Phi} + F_{\mathrm{outer}, \Delta\Phi} \simeq0.49 F_{\mathrm{inner}, \Delta\Phi} - 0.6 F_{\mathrm{inner}, \Delta\Phi} < 0. $$

(58)

A flux density of 0.7 times the dipolarized value would occur if the average thickness of the shaded region in Figure 11 were more than about $(0.7)^{-1} \simeq1.4$ times the final thickness, $\Delta R$.

It might be suggested that having an $F_{\mathrm{inner,pre}, \Delta \Phi}$ weaker than $F_{\mathrm{outer}, \Delta\Phi}$ is somehow unphysical, and that $(F_{\mathrm{inner}, \Delta\Phi} + F_{\mathrm{outer}, \Delta\Phi})$ must for some reason always be outward for an accelerating CME. But our analysis does not consider all forces on an ejection, just forces from a single flux tube $\Delta\Phi$, and forces from individual tubes may oppose the ejection. As noted above, a similar analysis is implicit in the tether-cutting model, which supposes that many individual tethers oppose an eruption’s upward motion, but nonetheless that eruption can have a net outward force.

How much larger is the change in hoop force $\Delta F_{fi}$ than the estimate in Equation 32? It is problematic to estimate the diminished pressure force on the inner surface of the ejection prior to complete dipolarization without assuming a model of the field structure in reconnection outflow, which is beyond the scope of this analysis.

Appendix D: Tension Force for Torus

We revisit the change in tension estimated in Equation 8 above to investigate the effect, if any, of the axial curvature that gives rise to the hoop force, since this could also affect the change in tension from $B_{\mathrm{P}}$. To get the total (sum of upward and downward) tension, we now use Equation 12 in Equation 5 and integrate over $[-\pi,\pi]$,

$$\begin{aligned} \Delta F_{\mathrm{tension}} =& \frac{1}{4\pi} \int \mathrm{d}V \, \hat{z} \cdot(\boldsymbol {B} \cdot \boldsymbol {\nabla } ) \boldsymbol {B} \end{aligned}$$

(59)

$$\begin{aligned} =& \frac{1}{4\pi} \int R \, \mathrm{d}\theta\, \mathrm{d}A \, B_{\mathrm{P}}(\theta) \frac{ \hat{z} }{R} \cdot\frac{\partial(B_{\mathrm{P}}(\theta) \hat{b})}{\partial \theta} \end{aligned}$$

(60)

$$\begin{aligned} =& \frac{\Delta\Phi}{4\pi} \int\, \mathrm{d}\theta\, \hat{z} \cdot\frac{ \partial( B_{\mathrm{P}}(\theta) \hat{b})}{\partial\theta} \end{aligned}$$

(61)

$$\begin{aligned} =& \frac{\Delta\Phi}{4\pi} \int_{-\pi}^{\pi} \, \mathrm{d}\theta \biggl( - \frac{\partial B_{\mathrm{P}}(\theta)}{\partial\theta} \sin\theta- B _{\mathrm{P}}(\theta) \cos\theta \biggr) \end{aligned}$$

(62)

$$\begin{aligned} =& \frac{- \Delta\Phi B_{\mathrm{mid}}}{4\pi} \int_{-\pi}^{\pi} \,\mathrm{d} \theta \biggl( \frac{r R \sin^{2} \theta}{(r + R \cos\theta)^{2}} + \frac{r \cos\theta}{r + R \cos\theta} \biggr) \end{aligned}$$

(63)

$$\begin{aligned} =& \frac{- \Delta\Phi B_{\mathrm{mid}}}{4\pi} \int_{-\pi}^{\pi} \,\mathrm{d} \theta \biggl( \frac{r R + r^{2} \cos\theta}{(r + R \cos\theta)^{2}} \biggr) \end{aligned}$$

(64)

$$\begin{aligned} =& \frac{- \Delta\Phi B_{\mathrm{mid}}}{4\pi} \int_{-\pi}^{\pi}\, \mathrm{d} \theta \biggl( \frac{(r/R) + (r/R)^{2} \cos\theta}{(r/R + \cos \theta)^{2}} \biggr) \end{aligned}$$

(65)

$$\begin{aligned} =& \frac{- \Delta\Phi B_{\mathrm{mid}} \, c}{4\pi} \int_{-\pi}^{\pi} \,\mathrm{d} \theta \biggl( \frac{1 + c \cos\theta}{(c + \cos\theta)^{2}} \biggr), \end{aligned}$$

(66)

where, as before, the unit vector of the poloidal field is given by $\hat{b} = \hat{\theta}= (\cos\theta\hat{x} - \sin\theta\hat{z})$, $\mathrm{d}V = \mathrm{d}A \, R \,\mathrm{d}\theta$, $\Delta\Phi= B_{\mathrm{P}} \, \Delta A$ is the flux that reconnects, and in the last line we have defined $c = r/R$.

From Dwight (1961) (p. 106), we first evaluate

$$\begin{aligned} \int_{-\pi}^{\pi}\, \mathrm{d}\theta\frac{1}{(c + \cos\theta)^{2}} =& \frac{\sin\theta}{(1 - c^{2})(c + \cos\theta)} \bigg\vert _{-\pi}^{\pi}- \frac{c}{1 - c^{2}} \int_{-\pi}^{\pi} \,\mathrm{d}\theta\frac{1}{(c + \cos\theta)} \end{aligned}$$

(67)

$$\begin{aligned} =& \frac{c}{c^{2} - 1} \int_{-\pi}^{\pi} \,\mathrm{d}\theta\frac{1}{(c + \cos\theta)}. \end{aligned}$$

(68)

Second, and also from Dwight (1961) (p. 106), we evaluate

$$\begin{aligned} \int_{-\pi}^{\pi} \,\mathrm{d}\theta \frac{c \cos\theta}{(c + \cos\theta)^{2}} =& \frac{c^{2} \sin\theta}{(c^{2} - 1)(c + \cos\theta)} \bigg\vert _{-\pi} ^{\pi}- \frac{c}{c^{2} - 1} \int_{-\pi}^{\pi} \,\mathrm{d}\theta\frac{1}{(c + \cos\theta)} \end{aligned}$$

(69)

$$\begin{aligned} =& - \frac{c}{c^{2} - 1} \int_{-\pi}^{\pi} \,\mathrm{d}\theta\frac{1}{(c + \cos\theta)} . \end{aligned}$$

(70)

Equations 68 and 70 are equal and opposite.

This cancellation is reasonable, given that our model poloidal field is essentially circular, so the curvature is uniform around the flux tube over which the force density is integrated. It is true that, due to the higher flux density on the inner section of the flux tube, the force density is higher there. But the force density is not integrated over equal volumes for the inner and outer segments; it is over different volumes threaded by equal amounts of flux.