A Minimum Energy Fit Method to Reconstruct Photospheric Velocity and Magnetic Diffusivity in Active Regions from Observed Magnetograms and Dopplergrams

Abstract

We introduce MEF-R, a generalization of the minimum energy fit (MEF; Longcope, Astrophys. J. 612, 1181, 2004) to a non-ideal (resistive) gas. The new technique requires both vector magnetograms and Doppler velocities as input fields. However, in the case of active regions observed only with the Michelson–Doppler Imager (MDI) onboard the Solar and Heliospheric Observatory (SOHO) such as AR 9077, we have only access to line-of-sight magnetograms. We reconstruct two-dimensional maps of the magnetic diffusivity η(x,y) together with velocity components v _x (x,y), v _y (x,y), and v _z (x,y) under the linear force-free magnetic field approximation. Computed maps for v _z (x,y) very well match the Doppler velocities v _r (x,y). We find the average value 〈η〉≈10⁸ m² s⁻¹ with a standard deviation of ≈ 10¹⁰ m² s⁻¹. Such high values of η(x,y) are to be expected at some places since our magnetic diffusivity is actually eddy-diffusivity. Inside AR 9077, the maps of η(x,y) do not resemble closely the maps from classical models of the magnetic diffusivity, but they are closer to η as a function of temperature than to η as a function of electric current density.

1 Introduction

Observations and numerical simulations show that in solar active regions, flares are often preceded by emerging sunspots (Ilonidis, Zhao, and Kosovichev 2011) under the form of vertical plasma motions (Bellot Rubio et al. 2001; Harra et al. 2012).

Various techniques have been proposed to reconstruct velocity vectors from any consecutive set of line-of-sight or vector magnetograms. The frozen-in-flux theorem (Alfvén 1942) is valid for a perfectly conducting fluid with no magnetic resistivity. Magnetic induction B is frozen-in to the plasma and passively follows plasma motions v. To this date and although it could have been theoretically possible, none of these techniques have been used for resistive plasmas. Local correlation tracking (LCT) would work best if the line-of-sight magnetic field B _ℓ is advected in a velocity field with a constant profile. However, such a field being not necessarily a solution of the magnetic induction equation, LCT alone has been shown to be inconsistent with the equation of magnetic induction (Schuck 2005). The method of inductive local correlation tracking (ILCT; Welsch et al. 2004; Schuck 2005) combines both. If vector magnetograms computed from the Stokes polarimetry are used, the minimum structure reconstruction (MSR; Georgoulis and LaBonte 2005) addresses the 180^∘ azimuth ambiguity (e.g. Metcalf et al. 2006) but does not work in the case of rapidly varying local magnetic fluxes such as an emergence or submergence. As far as the motions are restricted to horizontal directions, techniques using line-of-sight magnetograms are known to work, but to reconstruct vertical velocities vector magnetograms should be used (Schuck 2008). The differential affine velocity estimator (DAVE) for vector magnetograms (Schuck 2008) finds a two-dimensional affine profile for all three components of the photospheric velocity but does not need Doppler velocities. The minimum energy fit (MEF; Longcope 2004) with a reference background velocity v _r (which could possibly be taken from the Doppler velocity) is a self-consistent method that gives a unique vector velocity field solution to the ideal magnetic induction equation. Due to the stabilizing effect of strong magnetic fields, it is reasonable to have the total kinetic energy minimal in active regions except during flares or during the emergence of an active region. A poloidal–toroidal decomposition (PTD) of the magnetic field (Fisher et al. 2010) includes Doppler velocity observations. Doppler velocities have to be taken into account as a constraint to compute accurate electric fields and Poynting fluxes (Fisher, Welsch, and Abbet 2012b). Hybrid techniques are also proposed. A combination of MEF, LCT, and Doppler velocity is best to reconstruct v and this is shown by using anelastic MHD (ANMHD; Fan et al. 1999) test flows (Ravindra, Longcope, and Abbett 2008). FLCT and DAVE (Welsch et al. 2009) can be used to study photospheric flows and deduce energy fluxes to be compared with soft X-ray flux data. ILCT and MEF (Santos, Büchner, and Zhang 2008) have been used to compute emerging/submerging flow as well as horizontal motions.

To test any algorithm, analytical solutions are useful but are very difficult to find. Therefore, specific output data from numerical simulations of convection have been used instead. For instance ANMHD (Fan et al. 1999) was used to compute solar-like anelastic convection (Lantz and Fan 1999) but without the complexity of the photosphere. Most of the above techniques were compared (Welsch et al. 2007) and have shown a performance comparable to (but slightly lower overall than) MEF. It was found generally difficult to reconstruct v _z from v _r (Georgoulis and LaBonte 2005). A method like MEF (Longcope 2004) may compute v _z , if it has some similarities with v _r , starting from B _x,y,z (t) and B _x,y,z (t+dt) only if v _r is taken as a background vertical reference velocity.

To reconstruct a velocity field, MEF needs sequences of vector magnetograms. Such measurements are now made at regular time intervals and high resolution by ground-based observatories (e.g. the Vector Spectromagnetograph (VSM) from the Synoptic Optical Long-term Investigations of the Sun (SOLIS; Keller et al., 2001) or the Near InfraRed Imaging Spectropolarimeter (NIRIS; Cao et al. 2012) of the New Solar Telescope (NST) of the Big Bear Solar Observatory (BBSO) and by instruments like the Spectro-Polarimeter of the Solar Optical Telescope onboard Hinode (Kosugi et al. 2007) or the Helioseismic and Magnetic Imager (HMI; Schou et al. 2012) onboard the Solar Dynamics Observatory (SDO).

However, in this study of AR 9077, we used the line-of-sight magnetograms B _ℓ from the Michelson–Doppler Imager (MDI; Scherrer et al. 1995) onboard Solar and Heliospheric Observatory (SOHO). In this case, the only way B _x , B _y , and B _z can be reconstructed from B _ℓ alone is to use the force-free (FF) assumption.

The photosphere is a dynamic medium (DeRosa et al. 2009) and there is an interaction between the Lorentz force in the lower corona and the magnetic field in the photosphere and especially during flares (Fisher et al. 2012a). Nevertheless, except during the emergence of an active region or during a flare, the magnetic field of the photosphere has been approximated as force-free (Moon et al. 2002; Tiwari 2011) but this may be only true at 400 km above the photosphere (Metcalf et al. 1995) or inside sunspots where the magnetic field is the strongest (Tiwari 2011). In this study, we have used the linear force-free approximation (LFF; Nakagawa and Raadu 1972), with the twist α as a free parameter taken from the literature (e.g. Régnier and Priest 2007). Geometrical distortion due to sphericity of the solar surface is a problem if the active region under study is located too far from the center of the solar disk. But even if corrected (e.g. Welsch et al. 2009), part of the real value of B _z has been lost in the projection.

There are several mechanisms to explain why the reconstructed v _z is not v _r . Here we suppose that the magnetic field is not completely frozen-in to the plasma and that there must exist an eddy magnetic diffusivity inside the photosphere and the chromosphere that would be due to small scale fluctuations of unresolved current, temperature, or velocity. Indeed, theoretical magnetic diffusivities (Ohmic, Hall, and ambipolar) in the photosphere and chromosphere are in the range of η≈[10³,10⁶] m² s⁻¹ (e.g. Singh et al. 2011; Pandey and Wardle, 2012, 2013) or even higher η _O≈10⁸ m² s⁻¹ (Abramenko et al. 2011; Cameron, Vögler, and Schüssler 2011) but are pixel-size dependent (Chae, Litvinenko, and Sakurai 2008). Such high values are explained as turbulent or eddy magnetic diffusivity (e.g. Chae, Litvinenko, and Sakurai 2008) with a smallest resolved scale (the subgrid) as large as a solar granule (Simon and Weiss 1997). Higher values of the magnetic diffusivity would locally produce stronger Joule heating (Spangler 2009). Reconnection of the magnetic field lines may occur not only in the corona but also in the chromosphere (Heggland, De Pontieu, and Hansteen 2009). This can be modeled by a critical value of the electric current of J _c≈1.4×10⁻³ A m⁻² (Büchner, Nikutowski, and Otto 2004), above which the magnetic resistivity would sharply increase. In this case, η _eddy is due to small scale current instabilities (Lu 1995; Klimas et al. 2004; Uritsky and Klimas 2005).

The purpose of this study is to reconstruct (v _x , v _y , v _z ) from (B _x , B _y , B _z ) computed from B _ℓ observed with SOHO/MDI under the assumption of the force-free condition and using the resistive magnetic induction equation. Anomalous diffusivity η _eddy would be adjusted locally so that v _z be as close as possible to the observed Doppler velocity v _r while v _x and v _y be such that the total kinetic energy is minimal. In this sense, our method could be labeled as a “Doppler-diffusivity matching” (DDM) technique. We have applied the new MEF with resistivity (MEF-R method) to SOHO/MDI observations of AR 9077 on 14 July 2000 having produced the X5.7 GOES X-ray class “Bastille” Day flare. It has been extensively studied in the literature (see the Topical Issue, Solar Physics 204, 2001). A detailed study of horizontal motions has shown that AR 9077 was in a highly sheared state and that the initiation of the two-ribbon flare followed an episode of flux emergence (Liu and Zhang 2001; Somov 2007). The motion of the flare propagation together with the dynamics of this two-ribbon system is best seen at 171 Å from TRACE (Transition Region and Coronal Explorer) data (Aschwanden 2008).

The manuscript is organized as follows. In Section 2 we explain in detail the processing of the data. In Section 3, we show that MEF alone does not produce vertical velocities matching the observed Doppler velocities. In Section 4, we derive MEF-R, a generalization of MEF to resistive plasmas. We start from the resistive induction equation and use the force-free condition. In Section 5, we use MEF-R to study AR 9077 using SOHO/MDI magnetograms and Dopplergrams. We discuss vertical velocity versus Doppler velocity, horizontal velocity vector maps, and the meaning of the magnetic eddy diffusivity. In Section 6, we show that the time evolution of Doppler velocity, magnetic diffusivity, and Poynting energy flux can predict the flare. Finally, in the conclusion (Section 7), we discuss open questions and work under way.

2 Data Preprocessing: AR 9077

To test MEF-R, we processed active region AR 9077. It has produced the “Bastille Day” flare on 14 July 2000, an X5.7 GOES X-ray class flare that has been studied by several authors (e.g. Chertok and Grechnev 2005; Aschwanden 2008).

We used moderate resolution (≈ 1.98 arcsec per pixel) line-of-sight full-disk magnetograms B _ℓ (t;t+dt) and Dopplergrams v _r (t;t+dt) recorded with SOHO/MDI (Table 1). The difficulty and the need of a complex processing have been emphasized by numerous authors in the past. There are several processing steps to do. First, we extracted a square domain of area (386×386 Mm²) around the sunspot of maximal lifespan. Second, we removed the bad pixels (e.g. X-ray or proton hits on the CCD). Third, we applied a local smoothing over 3×3 points whenever necessary (bad pixels or missing data) (e.g. Fuhrmann et al. 2011). Spherical distortion and projection effects have not been considered because AR 9077 was at latitude 17^∘N and close enough to disk center at the times we consider. We choose to crudely approximate photospheric fields as force-free (e.g. Moon et al. 2002; Seehafer et al. 2007; Tiwari 2011). Thus, vector magnetograms can be reconstructed from the line-of-sight SOHO/MDI magnetograms B _ℓ , which we assumed to be equal to B _z . We computed vector magnetograms (B _x ,B _y ,B _z ) from B _z ≈B _ℓ using a spectral Fourier–Laguerre technique based on the linear force-free assumption (Nakagawa and Raadu 1972) in which $\alpha^{2}=( k_{x}^{2}+k_{y}^{2} - k_{z}^{2} )$ with k _x =2π/L _x , k _y =2π/L _y , and k _z =π/L _z . The value of α was chosen such that α=〈B⋅∇×B〉/〈B⋅B〉 (〈 〉 represents the spatial average). The required mean value of the local twist (e.g. Hao and Zhang 2011) is taken as constant over the entire active region. We set for the entire time sequence α≈−1.5×10⁻² Mm⁻¹, a realistic value (e.g. Sakurai and Hagino 2003; Régnier and Priest 2007). The components B _x (x,y) and B _y (x,y) of the horizontal magnetic field B _h are shown in Figure 1. The resulting vector magnetogram (B _x ,B _y ,B _z ) is a force-free and divergence-free field with $\nabla\cdot{ {\boldsymbol{B}}}/\langle(\frac{\partial B_{x}}{\partial x} )^{2} + (\frac{\partial B_{y}}{\partial y} )^{2} + (\frac{\partial B_{z}}{\partial z} )^{2} \rangle^{1/2} \leqslant10^{-7}$ as in Contopoulos, Kalapotharakos, and Georgoulis (2011). For all three components, the polarity inversion lines can be seen near the center of the map (Figure 1).

Figure 1

Vector magnetograms (a) B _x (x,y), (b) B _y (x,y), and (c) B _z (x,y)≡B _ℓ (x,y) of AR 9077 on 14 July 2000. The magnetograms (a) and (b) were reconstructed from the line-of-sight magnetograms (c) recorded by SOHO/MDI by using the linear force-free hypothesis (Nakagawa and Raadu 1972) with α≈−1.5×10⁻² Mm⁻¹ (Régnier and Priest 2007). B has been averaged between 08:00 and 09:36 UT and smoothed with a 3×3 pixels spatial filter. The grid size is 256×256 pixels. The area covered is about 500×500 arcsec². The color scales range from −0.2 T to 0.2 T.

Table 1 AR 9077 on 14 July 2000. Times (UT) are given at which we computed v from B _ℓ magnetograms recorded by SOHO/MDI and Imaging Vector Magnetograph at Mees Observatory at Haleakala (16:33 UT).

The Doppler velocities v _r are also from SOHO/MDI data archives and were extracted over the same area on the solar disk. Because MDI uses the same Ni i 6768 Å line, both Dopplergrams and magnetograms are observed at the same optical depth, very close to the standard 5000 Å defining the altitude of the photosphere (e.g. Steffen 2009). The motion of the observer, the limb shift, as well as the Sun’s rotation have been removed using ‘standard’ models (Snodgrass 1984; Snodgrass and Ulrich 1990). But we did not process the data as completely as in Schuck (2010). In particular, the p-mode oscillations have not been removed. The p-modes could produce velocities up to a few hundred meters per second (e.g. Hathaway et al. 2000). Furthermore, Dopplergrams were only available at 12:00 and 16:54 UT on 13 July 2000, 00:16, 06:11 and 10:30 UT on 14 July 2000 and 05:05 and 11:20 UT on 15 July 2000. A second-order time interpolation has been used to produce Dopplergrams at the same times as available magnetograms (see Table 1).

The resulting maps have a grid size of 256×256 pixels corresponding to an area of about 500×500 arcsec² or 386×386 Mm² on the solar disk.

3 MEF Technique for Ideal MHD Alone

To compute photospheric velocities, MEF (Longcope 2004) needs sets of vector magnetograms (B _x ,B _y ,B _z ) taken at two consecutive times (t;t+dt). In the case of AR 9077, we had no access to time sequences of vector magnetograms. Also, as explained below (Section 4.1), we did not have enough information to compute the vertical derivatives of B. Thus, although MEF would be valid for any magnetic field, we had to use the force-free approximation μ ₀ J=α B.

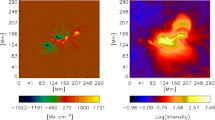
In this study, we have used the IDL version of MEF available at http://solar.physics.montana.edu/dana/ . To avoid divisions by zero during the computations using MEF, |B _z |⩾1 gauss (G) has been imposed locally as a minimum value except in the computations of 1/|B _z | where we impose |B _z |⩾40 G. This empirical value has been set above the noise (≈ 20 G) in our data. At the 11 times listed in Table 1, we computed velocities v and compared v _z (t) with the Doppler velocity v _r (t) observed with SOHO/MDI. We found that without any reference velocity field u=0, v _z (t) is very different from v _r (t) (not shown). Even when using v _r (t) as a background vertical velocity we find differences. As an example, using MEF and 1000 iterations, we computed the vertical velocity v _z between 08:00 and 09:36 UT, just before the flare. At this time, both Doppler and Zeeman shifts are still reliable. The vector magnetogram (B _x ,B _y ,B _z ) is shown as an average between 08:00 and 09:36 UT in Figure 1 and the corresponding Doppler velocity v _r is displayed in Figure 2(a). Although the minima are located at the right places, there are significant differences between v _r and MEF-computed v _z (Figure 2(b)). The differences are quantified by a scatter plot (Figure 2(c)). A quantitative global estimate of how close are two two-dimensional (2D) spatial distributions A(x,y) and B(x,y) is given by their correlation coefficient: C(A,B)=(Σ _x,y A⋅B)/(Σ _x,y A ²⋅Σ _x,y B ²)^1/2. We found that C(v _r ,v _z )≈0.906 for 1 G⩽|B _ℓ |⩽2500 G. If we separate a weak field contribution we obtain C(v _r ,v _z )≈0.909 for 1 G⩽|B _ℓ |⩽200 G. Likewise if we separate a strong-field contribution we obtain C(v _r ,v _z )≈0.805 for 500 G⩽|B _ℓ |⩽2500 G. The high values of correlation coefficients here are mostly due to the global minimization process of MEF and do not reflect local differences. As noted by Ravindra, Longcope, and Abbett (2008), Doppler velocity observations alone could conflict with the conservation of magnetic flux. We have made the hypothesis that these differences are due to the fact that the magnetic field is not simply frozen-in to the plasma and have generalized MEF to include a magnetic diffusivity (MEF-R). Due to the size of a pixel in our data (see below, 1 pixel ≈ 1500 km), one cannot expect η to be a collisional diffusivity but a turbulent or eddy diffusivity.

Figure 2

(a) Doppler velocity v _r (t) in AR 9077 recorded by SOHO/MDI on 14 July 2000. The Sun’s rotation has been removed. (b) v _z (t) as computed using MEF with v _r (t) as a background vertical velocity. The time interval is 08:00 – 09:36 UT and the grid size is 256×256 pixels in both panels. Panel (c) shows the scatter plot between v _z (t) and v _r (t).

4 MEF-R: A Generalization of the MEF Technique to Resistive Plasmas

In the following, we locate the photosphere at the origin of the vertical coordinate z=0 in Cartesian geometry. Each vector quantity observed or computed at the photospheric level has a vertical component, normal to the photospheric plane, subscripted with “z” and a horizontal component subscripted with “h”.

4.1 Resistive Induction Equation

The non-ideal or resistive induction equation is used here to describe the behavior of the photospheric magnetic field B and its time evolution

$$\begin{aligned} \frac{\partial {\boldsymbol{B}}}{\partial t} =& {\mathbf{\nabla}} \times \bigl[( {\boldsymbol{v}}\times {\boldsymbol{B}}) - \eta({ \mathbf{\nabla}} \times {\boldsymbol{B}}) \bigr] \\ =& {\mathbf{\nabla}} \times \bigl[( {\boldsymbol{v}}\times {\boldsymbol{B}}) - \eta\mu _{\mathrm{0}} {\boldsymbol{J}}\bigr] , \end{aligned}$$

(1)

where η=η(x,y;t) is the magnetic diffusivity and is a function of space and time,

$$ {\eta(x,y)} = \frac{1}{\mu_{\mathrm{0}} \sigma} , $$

(2)

σ being the conductivity. A consistent velocity flow can be derived, as in the case of non-resistive ideal MHD, by considering the vertical component of the non-ideal equation of magnetic induction (Equation (1))

$$\begin{aligned} \frac{\partial B_{z}}{\partial t} =& \bigl[{\mathbf{\nabla}} \times ( {\boldsymbol{v}}\times {\boldsymbol{B}}) \bigr]_{z} - ({\mathbf{\nabla}} \times\eta\mu_{\mathrm{0}} {\boldsymbol{J}})_{z} \\ =& {\mathbf{\nabla}_{h}} \cdot \bigl[(v_{z} {\boldsymbol{B}}_{h} - B_{z} {\boldsymbol{v}}_{h}) + \eta( \hat {\boldsymbol{z}} \times \mu_{\mathrm{0}} {\boldsymbol{J}}_{h}) \bigr] . \end{aligned}$$

(3)

Here we suppose that the discrepancies between v _z as computed by MEF and Doppler velocity v _r observed by SOHO/MDI are due to the fact that the magnetic field is not frozen-in to the plasma flow but there is also a magnetic diffusivity η(x,y). This may be only partially true since we did not have access to the vertical derivatives of the magnetic field outside of the FF assumption, but η(x,y) would not be a collisional magnetic diffusivity.

As noticed by Longcope (2004), it would be impossible to solve the resistive induction equation in a single plane. Indeed, the second term on the right-hand side of Equation (3) includes vertical spatial derivatives of first order for B _h . In order to approximate these derivatives, one must rely on data from at least two planes at different vertical heights at and above the photosphere, all at the same time t _j . Quantities such as J _x and J _y , or simply J _h , could be computed since we suppose that the magnetic field at the photospheric level is a force-free field.

4.2 Unknown Scalar Potentials

Helmholtz’s theorem allows for a differentiable vector function going to zero fast enough as r goes to infinity to be expressed as the sum of the gradient of a scalar function and the curl of a potential vector (e.g. Griffiths 2007). This approach was used by Longcope (2004) to rewrite Equation (3) in terms of two scalar potentials ϕ and ψ for an ideal MHD (η=0). Here we use Helmholtz’s theorem to decompose a vector function including a resistive term,

$$ {{\boldsymbol{F}}} = (v_{z} {\boldsymbol{B}}_{h} - B_{z} {\boldsymbol{v}}_{h}) + \eta( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}) . $$

(4)

The magnetic fields considered in this study are not bounded and could not be so, even locally, because they are force-free (Brownstein 1994). However, as mentioned above, Helmholtz’s theorem does not require a bounded domain to be valid. In the general case of α=α(x,y)=μ ₀ J _z /B _z , the differentiability of the vector function F is not always satisfied if η≠0 as its second term in Equation (4), $\eta( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h})$, cannot be differentiated where B _z is 0. The problem arises from the force-free approximation of B as the horizontal current density J _h depends on the inverse of B _z . As in the case of MEF (Section 3), we used a threshold so that |B _z |⩾40 G everywhere on the photospheric plane. Thus, with every condition satisfied, applying Helmholtz’s theorem to the vector function in Equation (3) yields

$$ {{\boldsymbol{F}}} = (v_{z} {\boldsymbol{B}}_{h} - B_{z} {\boldsymbol{v}}_{h}) + \eta( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}) = {\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\times\psi \ \hat {\boldsymbol{z}} } = {\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\psi\times \hat {\boldsymbol{z}} } . $$

(5)

The formalism introduced in Equation (5) leads to the same result for both resistive and ideal forms of the induction equation as we rewrite Equation (3) in terms of ϕ and ψ, i.e. a Poisson equation for ϕ,

$$\begin{aligned} \frac{\partial B_{z}}{\partial t} =& {\mathbf{\nabla}_{h}} \cdot ({\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\psi\times \hat {\boldsymbol{z}} }) \\ =& {\mathbf{\nabla}^2_{h} }\phi. \end{aligned}$$

(6)

Mathematically, ϕ has the form of the electrostatic potential arising from a charge distribution given by $\frac{\partial B_{z}}{\partial t}$ whereas ψ is a potential function generating the solenoidal part of the electric field (Longcope 2004). The same method can therefore be applied to the solution of Equation (6) for ϕ, i.e. reversing the Laplacian operator and using ϕ=0 as a boundary condition for all points that are not in the active region interior (Longcope 2004) or, in our study, at the border of the computational domain.

4.3 The Minimum Energy Fit

By rearranging the terms in Equation (5), the horizontal velocity v _h can be written as a function of ϕ, ψ, v _z , and η,

$$ {\boldsymbol{v}}_{h} = \frac{ [v_{z} {\boldsymbol{B}}_{h} - {\mathbf{\nabla}_{h} }\phi- {{\mathbf{\nabla}_{h} }\psi\times \hat {\boldsymbol{z}} } + \eta( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}) ]}{B_{z}} . $$

(7)

There are an infinite number of solutions for v _h as the formalism introduced in Equation (5) results in the resistive induction equation being satisfied regardless of the field ψ. As for ideal MHD, the minimization of a penalty function guarantees a unique solution for v _h . It is expected that inside an active region where the magnetic fields are strong the total kinetic energy would be reduced. Thus, we use the same energy-like functional W previously introduced for the MEF, the only difference being that it is also a function of a third field, η(x,y), as a result of Equation (7)

$$\begin{aligned} W \equiv W\{\psi,v_{z},\eta\} =& \int_{{M}}L \biggl\{ x,y, \psi,\frac{\partial\psi}{\partial x} ,\frac{\partial\psi }{\partial y} , v_{z}, \frac{\partial v_{z}}{\partial x} ,\frac{\partial v_{z}}{\partial y} , \eta,\frac{\partial\eta}{\partial x} , \frac{\partial\eta }{\partial y} \biggr\} \, \mathrm{d}x \, \mathrm{d}y \\ =& \frac{1}{2} \int_{{M}}{| {\boldsymbol{v}}_{h} - {\boldsymbol{u}}_{h}|^2 + |v_{z} - u_{z}|^2} \, \mathrm{d}x \, \mathrm{d}y \\ &{} + \lambda\int_{{M}} \biggl\vert \nabla_{h} \biggl(\eta\frac{|\mu_{\mathrm{0}} {\boldsymbol{J}}|}{B_{z}}\biggr)\biggr\vert ^2 \, \mathrm{d}x \, \mathrm{d}y , \end{aligned}$$

(8)

where M is a region of the photosphere and u _h and u _z are the components of the reference flow u that v tries to fit. For example, Doppler velocity could be used as a reference vertical velocity u _z . This possibly ill-posed problem is treated in MEF-R with a Tikhonov regularization (Tikhonov 1963) that maximizes correlation between neighboring points (x,y). Here λ is a Lagrange multiplier set to 0.4 px² in the case of the Spheromak (Section 4.5).

Minimization of the functional W in terms of ψ, v _z , and η is made using a set of three Euler–Lagrange equations involving the Lagrangian L,

$$\begin{aligned} {\frac{\partial L}{\partial v_{z}} }-{\frac{{\mathrm{d}} \frac {\partial L}{\partial{v_{z}}_{x}} }{{\mathrm{d}} x}}- {\frac{{\mathrm{d}} \frac{\partial L}{\partial{v_{z}}_{y}} }{{\mathrm{d}} y}} =& 0 , \end{aligned}$$

(9)

$$\begin{aligned} {\frac{\partial L}{\partial\psi} }-{\frac{{\mathrm{d}} \frac {\partial L}{\partial{\psi}_{x}} }{{\mathrm{d}} x}}- {\frac{{\mathrm{d}} \frac{\partial L}{\partial{\psi}_{y}} }{{\mathrm{d}} y}} =& 0 , \end{aligned}$$

(10)

$$\begin{aligned} {\frac{\partial L}{\partial\eta} }-{\frac{{\mathrm{d}} \frac {\partial L}{\partial{\eta}_{x}} }{{\mathrm{d}} x}}- {\frac{{\mathrm{d}} \frac{\partial L}{\partial{\eta}_{y}} }{{\mathrm{d}} y}} =& 0 , \end{aligned}$$

(11)

where we set ${v_{z}}_{x} \equiv{\frac{\partial v_{z}}{\partial x} }$, ${v_{z}}_{y} \equiv{\frac{\partial v_{z}}{\partial y} }$, ${\psi }_{x} \equiv{\frac{\partial\psi}{\partial x} }$, ${ \psi}_{y} \equiv{\frac{\partial\psi}{\partial y} }$, ${\eta }_{x} \equiv{\frac{\partial\eta}{\partial x} }$, ${ \eta}_{y} \equiv{\frac{\partial\eta}{\partial y} }$. Since ${\frac{\partial L}{\partial\psi} } = {\frac{\partial L}{\partial {v_{z}}_{x}} } = {\frac{\partial L}{\partial{v_{z}}_{y}} } = {\frac{\partial L}{\partial{\eta}_{x}} } = {\frac{\partial L}{\partial{\eta}_{y}} }= 0$, the above equations can be reduced to

$$\begin{aligned} {\frac{\partial L}{\partial v_{z}} } =& \frac{ {\boldsymbol{B}}_{h} \cdot ( {\boldsymbol{v}}_{h} - {\boldsymbol{u}}_{h})}{B_{z}} +(v_{z}-u_{z}) = 0 , \end{aligned}$$

(12)

$$\begin{aligned} -{\frac{{\mathrm{d}} \frac{\partial L}{\partial{\psi}_{x}} }{{\mathrm{d}} x}} -{\frac{{\mathrm{d}} \frac{\partial L}{\partial{\psi}_{y}} }{{\mathrm{d}} y}} =& {\mathbf{\nabla}_{h} }\cdot \biggl[ \frac{ \hat {\boldsymbol{z}} }{B_{z}} \times ( {\boldsymbol{v}}_{h}- {\boldsymbol{u}}_{h}) \biggr] = 0 , \end{aligned}$$

(13)

$$\begin{aligned} {\frac{\partial L}{\partial\eta} } =& \frac{( \hat {\boldsymbol{z}} \times\mu _{\mathrm{0}} {\boldsymbol{J}}_{h}) \cdot ( {\boldsymbol{v}}_{h} - {\boldsymbol{u}}_{h})}{B_{z}} = 0 . \end{aligned}$$

(14)

With the use of vector identities, one finds that ψ, v _z , and η must satisfy the following three coupled Euler–Lagrange equations:

$$\begin{aligned} v_{z} =& \frac{B_{z}^2 \ u_{z} + {\boldsymbol{B}}_{h} \cdot[{\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\psi \times \hat {\boldsymbol{z}} } + B_{z} {\boldsymbol{u}}_{h} - \eta( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h})]}{| {\boldsymbol{B}}|^2} , \end{aligned}$$

(15)

$$\begin{aligned} {\mathbf{\nabla}_{h}} \cdot \biggl(\ \frac{{\mathbf{\nabla}_{h} }\psi}{B_{z}^2} \biggr) =& { \mathbf{\nabla}_{h}} \cdot \biggl[\ \frac{ \hat {\boldsymbol{z}} \times (v_{z} {\boldsymbol{B}}_{h} - {\mathbf{\nabla}_{h} }\phi- B_{z} {\boldsymbol{u}}_{h} + \eta( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}) )}{B_{z}^2} \biggr] , \end{aligned}$$

(16)

$$\begin{aligned} \eta =& \frac{( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}) \cdot( {\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\psi\times \hat {\boldsymbol{z}} } + B_{z} {\boldsymbol{u}}_{h}-v_{z} {\boldsymbol{B}}_{h})}{|\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}|^2} . \end{aligned}$$

(17)

In the case of a resistive plasma, we obtain the same solutions as in the case of an ideal plasma, with the additional term η on the right-hand side. These equations stand for any magnetic field B; no restriction has been made on B. However, if the magnetic field B is a force-free field, it is parallel to the current density J so that $( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}) \cdot {\boldsymbol{B}}_{h} = 0$. In this case, the above Euler–Lagrange equations (Equations (15) and (17)) have a vanishing term and can be written as

$$\begin{aligned} v_{z} =& \frac{B_{z}^2 \ u_{z} + {\boldsymbol{B}}_{h} \cdot({\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\psi \times \hat {\boldsymbol{z}} } + B_{z} {\boldsymbol{u}}_{h}) }{| {\boldsymbol{B}}|^2} , \end{aligned}$$

(18)

$$\begin{aligned} {\mathbf{\nabla}_{h}} \cdot \biggl(\ \frac{{\mathbf{\nabla}_{h} }\psi}{B_{z}^2} \biggr) =& { \mathbf{\nabla}_{h}} \cdot \biggl[\ \frac{ \hat {\boldsymbol{z}} \times (v_{z} {\boldsymbol{B}}_{h} - {\mathbf{\nabla}_{h} }\phi- B_{z} {\boldsymbol{u}}_{h} + \eta( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}) )}{B_{z}^2} \biggr] , \end{aligned}$$

(19)

$$\begin{aligned} \eta =& \frac{( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}) \cdot( {\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\psi\times \hat {\boldsymbol{z}} } + B_{z} {\boldsymbol{u}}_{h})}{|\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}|^2} , \end{aligned}$$

(20)

where for numerical reasons, a lower limit of |μ ₀ J _h | must be imposed here. In 64-bit computing, we set it to 10⁻¹² N A⁻¹ m⁻².

To see the physical meaning of Equation (17) or (20), we can use Ohm’s Law,

$$ {\boldsymbol{E}}= -( {\boldsymbol{v}}\times {\boldsymbol{B}}) + \eta{\mu_{\mathrm{0}} {\boldsymbol{J}}} , $$

(21)

in which we can separate horizontal and vertical components using the Helmholtz decomposition (e.g. Equation (5)),

$$\begin{aligned} {\boldsymbol{E}}_{h} =& - \hat {\boldsymbol{z}} \times \bigl[(v_{z} {\boldsymbol{B}}_{h} - B_{z} {\boldsymbol{v}}_{h}) \bigr] + \eta \mu_{\mathrm{0}} {\boldsymbol{J}}_{h} \\ =& {\mathbf{\nabla}_{h} }\phi\times \hat {\boldsymbol{z}} - {\mathbf{\nabla}_{h} }\psi , \end{aligned}$$

(22)

$$\begin{aligned} E_{z} =& {\boldsymbol{v}}_{h} \cdot( \hat {\boldsymbol{z}} \times {\boldsymbol{B}}_{h}) + \eta{\mu _{\mathrm{0}} J_{z}} . \end{aligned}$$

(23)

Equation (14) together with vector identity A⋅(B×C)=B⋅(C×A)=C⋅(A×B) are combined with Equation (17). We then use Equation (22) to obtain

$$ \eta= \frac{\mu_{\mathrm{0}} {\boldsymbol{J}}_{h} \cdot {\boldsymbol{E}}_{h}}{|\mu _{\mathrm{0}} {\boldsymbol{J}}_{h}|^2} + \frac{(B_{z} {\boldsymbol{u}}_{h} - v_{z} {\boldsymbol{B}}_{h}) \cdot( \hat {\boldsymbol{z}} \times \mu_{\mathrm{0}} {\boldsymbol{J}}_{h})}{|\mu_{\mathrm{0}} {\boldsymbol{J}}_{h}|^2} . $$

(24)

Multiplying Equation (23) for the vertical component E _z by μ ₀ J _z and summing with Equation (24) gives

$$\begin{aligned} \eta =& \frac{\mu_{\mathrm{0}} {\boldsymbol{J}}\cdot {\boldsymbol{E}}}{|\mu_{\mathrm{0}} {\boldsymbol{J}}|^2} + \frac{\mu_{\mathrm{0}} {\boldsymbol{J}}\cdot( {\boldsymbol{v}}\times {\boldsymbol{B}})}{|\mu_{\mathrm {0}} {\boldsymbol{J}}|^2} \\ =& \frac{\mu_{\mathrm{0}} {\boldsymbol{J}}\cdot {\boldsymbol{E}}}{|\mu_{\mathrm{0}} {\boldsymbol{J}}|^2} - \frac{ {\boldsymbol{v}}\cdot(\mu_{\mathrm{0}} {\boldsymbol{J}}\times {\boldsymbol{B}})}{|\mu_{\mathrm {0}} {\boldsymbol{J}}|^2} . \end{aligned}$$

(25)

Equation (25) could have been found using the scalar product of the generalized Ohm’s law (Equation (21)) with μ ₀ J.

In the context of the eddy diffusivity model, the difference between the two terms in Equation (25) represents the transport of magnetic flux from processes other than the resolved v×B electric field. The above derivation is relevant to any magnetic field B. If, however, B is a force-free field, J×B=0 so that the last term of Equation (25) vanishes and we have

$$ \eta= \frac{\mu_{\mathrm{0}} {\boldsymbol{J}}\cdot {\boldsymbol{E}}}{|\mu_{\mathrm{0}} {\boldsymbol{J}}|^2} . $$

(26)

The physical meaning of this equation is the same as in the case of a non-force-free magnetic field without considering the work done by the magnetic force. Rewriting Equation (25) leads to

$$ { {\boldsymbol{J}}\cdot {\boldsymbol{E}}} = \frac{{\eta|\mu_{\mathrm{0}} {\boldsymbol{J}}|^2}}{\mu _{\mathrm{0}}} - {\boldsymbol{J}}\cdot ( {\boldsymbol{v}}\times {\boldsymbol{B}}) . $$

(27)

Using the generalized Ohm’s law (Equation (21)) and the magnetic flux conservation (Equation (1)), we obtain

$$\begin{aligned} \begin{aligned}[b] { {\boldsymbol{J}}\cdot {\boldsymbol{E}}} &= \frac{\eta{|\mu_{\mathrm{0}} {\boldsymbol{J}}|^{2}}}{\mu _{\mathrm{0}}} - {\boldsymbol{J}}\cdot( {\boldsymbol{v}}\times {\boldsymbol{B}}) \\ &= -\frac{ {\boldsymbol{B}}}{\mu_{\mathrm{0}}} \cdot{\frac{\partial {\boldsymbol{B}}}{\partial t} } - {\mathbf{\nabla}}\cdot{ {\boldsymbol{P}} } \\ &= -\frac{1}{2} {\frac{\partial B^{2}}{\partial t} } - {\mathbf{\nabla}}\cdot {{\boldsymbol{P}} } , \end{aligned} \end{aligned}$$

(28)

where ${\boldsymbol{P}} \equiv\frac{1}{\mu_{\mathrm{0}}} ( {\boldsymbol{E}}\times {\boldsymbol{B}})$ is the Poynting vector and Equation (28) is the differential form of the Poynting theorem (e.g. Griffiths 2007). As a consequence, we can express η as a function of the Poynting vector,

$$\begin{aligned} \eta =& \frac{\mu_{\mathrm{0}} {\boldsymbol{J}}\cdot {\boldsymbol{E}}}{|\mu_{\mathrm{0}} {\boldsymbol{J}}|^2} + \frac{\mu_{\mathrm{0}} {\boldsymbol{J}}\cdot( {\boldsymbol{v}}\times {\boldsymbol{B}})}{|\mu_{\mathrm {0}} {\boldsymbol{J}}|^2} \\ =& \frac{\mu_{\mathrm{0}}}{|\mu_{\mathrm{0}} {\boldsymbol{J}}|^2} \biggl[ -\frac{1}{2} \frac{\partial(\frac{| {\boldsymbol{B}}|^2}{\mu_{\mathrm{0}}})}{\partial t} - {\mathbf{\nabla}}\cdot {\boldsymbol{P}} \biggr] + \frac{\mu_{\mathrm{0}} {\boldsymbol{J}}\cdot( {\boldsymbol{v}}\times {\boldsymbol{B}})}{|\mu_{\mathrm {0}} {\boldsymbol{J}}|^2} . \end{aligned}$$

(29)

In the case of a force-free magnetic field, one obtains

$$\begin{aligned} \eta =& \frac{\mu_{\mathrm{0}} {\boldsymbol{J}}\cdot {\boldsymbol{E}}}{|\mu_{\mathrm{0}} {\boldsymbol{J}}|^2} \\ =& \frac{\mu_{\mathrm{0}}}{|\mu_{\mathrm{0}} {\boldsymbol{J}}|^2} \biggl[ -\frac{1}{2} \frac{\partial(\frac{| {\boldsymbol{B}}|^2}{\mu_{\mathrm{0}}})}{\partial t} - {\mathbf{\nabla}}\cdot {\boldsymbol{P}} \biggr] . \end{aligned}$$

(30)

4.4 Boundary Conditions for Magnetic Diffusivity η(x,y)

MEF takes boundary conditions in the form of a mask canceling values of ϕ(x,y) and v _z (x,y) at pixels on the border of the domain that includes the active region, ∂AR. In MEF-R, we use a Hann window over eight grid points on the sides of the computational domain for all quantities except for the magnetic diffusivity η(x,y). This produces an efficient mask, takes the whole area into consideration, and is compatible with the computation of vector magnetograms (Nakagawa and Raadu 1972). Equations (18) and (20) are minimization forms of W according to v _z and η. Solving Equation (20) for η is done in the same way as solving Equation (18) for v _z .

4.5 Testing MEF-R: The Spheromak

Spheromaks are plasmas with internal magnetic fields but strong internal electric currents. They resemble a bipolar active region with twisted flux (Longcope 2004). Due to finite magnetic diffusivity, they relax (Taylor 1974) toward a state of minimal magnetic energy while conserving global magnetic helicity (Bellan 2000). The consequence is that the magnetic field in the relaxed state is force-free (Bellan 2000). Since the Spheromak is a closed system, the relaxed magnetic field is a linear force-free field (Woltjer 1958). The relaxation process itself redistributes the current locally by reconnection processes (Garcia-Martinez 2012) and is equivalent to the effect of eddy magnetic diffusivity. The latter would vanish when the system has reached the relaxed state but there would be still remaining uniform resistivity.

To create an analytical test for MEF-R we proceeded as follows. We use the magnetic vector field (B _x ,B _y ,B _z )(x,y,z;t+dt/2) from the Spheromak (Bellan 2000) and an external velocity field (v _x ,v _y ,v _z )(x,y,z;t+dt/2) oriented in a single direction of space. We solved numerically the resistive magnetic induction equation (Equation (1)),

$$ \frac{\partial {\boldsymbol{B}}}{\partial t} = {\mathbf{\nabla}} \times \bigl[( {\boldsymbol{v}}\times {\boldsymbol{B}}) - \eta({\mathbf{\nabla}} \times {\boldsymbol{B}}) \bigr] , $$

using a second-order finite differences numerical discretization in space and a second-order leapfrog time-marching. This gives (B _x ,B _y ,B _z )(x,y,z;t,t+dt). Next, we used MEF-R with (B _x ,B _y ,B _z )(x,y,z;t,t+dt) and v _r =v _z (x,y,z;t+dt/2) to compute (v _x ,v _y ,v _z )(x,y,z;t+dt/2) and η(x,y;t+dt/2). We can then compare (v _x ,v _y ,v _z )(x,y,z;t+dt/2) (Figure 3(b)) and η(x,y;t+dt/2) (Figure 3(c)) with the original models.

Figure 3

Testing MEF-R using the Spheromak at given time t+dt/2 with a generating flow as a uniform velocity field v(t+dt/2)=4cos(35^∘)e _x +4sin(35^∘)e _y +4e _z . Here we show a cut in the plane z=−3 px. 2D vectors show the x- and y-components and the gray scale refers to the z-component. The Spheromak being closed, a circle is set to delimit the boundary. (a) The perpendicular components of the generating flow, (v _⊥x ,v _⊥y )(x,y) (vectors) and v _⊥z (x,y) (gray scale). (b) How MEF-R reconstructs the velocity field (v _x ,v _y )(x,y) (vectors) and v _z (x,y) (gray scale). (c) Magnetic diffusivity η _eddy(x,y) as reconstructed by MEF-R (gray scale). Field lines of $( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h})$ are superimposed. MEF-R distorts η _eddy along these lines (see Equation (17)).

As the test case Spheromak is purely analytical, we work in pixels (px) and dt units. The Spheromak has a radius a=20 px and its center is located at r _c(t)=(x _c(t),y _c(t),z _c(t))=(0,0,−3) px. The generating flow is given as v(t+dt/2)=4cos(35^∘)e _x +4sin(35^∘)e _y +4e _z with |v(t+dt/2)|≈5.6 px dt ⁻¹ (Figure 3(a)) and corresponds to a uniform translation of the Spheromak center along a constant direction (Longcope 2004). A uniform magnetic diffusivity has been set to η(x,y;t+dt/2)=10 px² dt ⁻¹. In Figure 3(a), we see only v _⊥x ,v _⊥y , and v _⊥z extracted from

$$v_{\perp} = {\boldsymbol{v}}- \bigl[( {\boldsymbol{v}}\cdot {\boldsymbol{B}})/ {\boldsymbol{B}}^2 \bigr] {\boldsymbol{B}}, $$

the component of v perpendicular to the magnetic field lines. The vertical velocity field of the Spheromak v _z (t+dt/2) (Figure 3(a)) is similar to the MEF-R inferred flow v _z (t+dt/2) (Figure 3(b)). The inferred horizontal components of v are somehow different, however (see vectors in Figures 3(a) and 3(b)). This is a consequence of the decay of kinetic energy W during the MEF-R iterative process. If we define the kinetic energy of the Spheromak numerically as

$$W = \Sigma_{x,y}{\bigl[v_{x}^2 + v_{y}^2 + (v_{z}-u_{z})^2 \bigr]} $$

and take the reference velocity u _h =0 and u _z =v _⊥z , we find the kinetic energy of the generating flow W ₀(t+dt/2)≈23540 px² dt ⁻² to be greater than the kinetic energy of the perpendicular component of the generating flow W _⊥(t+dt/2)≈15045 px² dt ⁻² as expected, the latter being itself greater than the kinetic energy of the inferred final state W _f(t+dt/2)≈976 px² dt ⁻²,

$${W}_{\mathrm{f}} < {W}_{\perp} < {W}_{0} \cdot $$

Our translation of the Spheromak is not a state of minimal kinetic energy and MEF-R, searching a flow of minimal kinetic energy, is not supposed to produce an inferred velocity matching exactly the initial flow.

Equation (14) predicts that in the absence of a horizontal reference flow u _h =0, the inferred horizontal velocity v _h should be perpendicular to $( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h})$. In other words, under the LFF assumption, MEF-R predicts that the minimal kinetic energy configuration of v will be such that v _h and B _h are parallel. However, neither the generating flow, the perpendicular component of the generating flow, nor the reference flow would have their horizontal component being parallel to B _h .

How MEF-R predicts the magnetic eddy diffusivity at time (t+dt/2) is shown in Figure 3(c). The mean value of the inferred magnetic diffusivity is almost unchanged with 〈η〉≈9 px² dt ⁻¹ although it is not uniform with a standard deviation of 12 px² dt ⁻¹. In Figure 3(c) we superimposed the field lines of $( \hat {\boldsymbol{z}} \times\mu_{\mathrm{0}} {\boldsymbol{J}}_{h})$ above the map of η(x,y;t+dt/2). We see that MEF-R distorts the magnetic diffusivity along these lines as can be seen from Equation (17).

4.6 Statistics of the Results

Finally, to have a global measure of the performance of MEF-R in the Spheromak test case, we computed the correlation coefficients between $v_{\perp{x,y,z}}^{\mathrm{s}}$ of the Spheromak and v _⊥x,y,z inferred from MEF-R. We found

$$\begin{aligned} C\bigl(v^{\mathrm{s}}_{\perp x},v_{\perp x}\bigr) \approx0.285, \qquad C\bigl(v^{\mathrm{s}}_{\perp y},v_{\perp y}\bigr) \approx0.137, \qquad C\bigl(v^{\mathrm{s}}_{\perp z},v_{\perp z}\bigr) \approx0.571. \end{aligned}$$

The mean 〈〉 and standard deviation σ[  ] of the difference between the Spheromak and inferred velocities are also computed. We found

$$\begin{aligned} & \bigl\langle v^{\mathrm{s}}_{\perp x} - v_{\perp x} \bigr\rangle \approx2.108~\mbox{px}\, \mathrm{d}t^{-1},\qquad \bigl\langle v^{\mathrm{s}}_{\perp y} - v_{\perp y} \bigr\rangle \approx 1.906~ \mbox{px}\, \mathrm{d}t^{-1}, \\ & \bigl\langle v^{\mathrm{s}}_{\perp z} - v_{\perp z} \bigr\rangle \approx1.529~\mbox{px}\, \mathrm{d}t^{-1}, \end{aligned}$$

and

$$\begin{aligned} &\sigma\bigl[ v^{\mathrm{s}}_{\perp x} - v_{\perp x}\bigr] \approx1.541~\mbox{px}\, \mathrm{d}t^{-1},\qquad \sigma\bigl[ v^{\mathrm{s}}_{\perp y} - v_{\perp y}\bigr] \approx1.412~\mbox{px}\, \mathrm{d}t^{-1}, \\ & \sigma\bigl[ v^{\mathrm{s}}_{\perp z} - v_{\perp z}\bigr] \approx1.735~\mbox{px}\, \mathrm{d}t^{-1}. \end{aligned}$$

The correlation and accuracy are higher for the vertical component of velocity as expected with MEF-R although the standard deviation is also slightly higher. A global measurement of the velocity differences in terms of vectors would give a lower value but with the same standard deviation,

$$\begin{aligned} \bigl\langle \bigl\vert \mathbf{v}^{\mathrm{s}}_{\perp}\bigr\vert - |\mathbf{v}_{\perp}| \bigr\rangle \approx3.471~\mbox{px}\, \mathrm{d}t^{-1},\qquad \sigma\bigl[ \bigl\vert \mathbf{v}^{\mathrm{s}}_{\perp} \bigr\vert - |\mathbf{v}_{\perp }|\bigr] \approx1.762~\mbox{px}\, \mathrm{d}t^{-1}. \end{aligned}$$

The distribution of the relative orientations between the two vector fields is given by $\langle\mathbf{v}^{\mathrm{s}}_{\perp} \cdot\mathbf{v}_{\perp} \rangle \approx3.392~\mbox{px}^{2}\, \mathrm{d}t^{-2}$ with standard deviation $\sigma[\mathbf{v}^{\mathrm{s}}_{\perp} \cdot\mathbf{v}_{\perp}] \approx6.201~\mbox{px}^{2}\,\mathrm{d}t^{-2}$. A better estimate is given by the average dot product of the normalized perpendicular velocities $\langle{{\mathbf{v}^{\mathrm{s}}_{\perp} \cdot\mathbf{v}_{\perp }} \over{|\mathbf{v}^{\mathrm{s}}_{\perp}| |\mathbf{v}_{\perp}|} } \rangle \approx0.959$ which follows the Cauchy–Schwarz inequality (Schrijver et al. 2006) and indicates that the two fields are mostly parallel. The results are not as good for the resistivity. The correlation coefficient, mean, and standard deviation of the difference between true and inferred values of the resistivity η are

$$\begin{aligned} C\bigl(\eta^{\mathrm{s}},\eta\bigr) \approx0.243,\qquad \bigl\langle \bigl\vert \eta^{\mathrm{s}}\bigr\vert - |\eta| \bigr\rangle \approx6.134~ \mbox{px}^2\,\mathrm{d}t^{-1},\qquad \sigma\bigl[ \bigl\vert \eta^{\mathrm{s}}\bigr\vert - |\eta|\bigr] \approx7.752~ \mbox{px}^2\,\mathrm{d}t^{-1}, \end{aligned}$$

with extremal values of the resistivity about 10 times greater (Figure 3(c)).

These results only reflect the fact that the external velocity and magnetic diffusivity we imposed for the relaxed Spheromak are rather arbitrary and not consistent with a state of minimal kinetic energy as previously defined. More statistics are computed (e.g. Schrijver et al. 2006) and a comparison with the case when we not only impose u _z but also u _x and u _y are given in Tables 2 and 3 (Appendix A).

Table 2 Various statistics to test the accuracy of MEF-R in the Spheromak case. The coefficient of correlation C, normalized error E _N, mean error E _M, ratio of “energies” ϵ, and Cauchy–Schwarz inequality (e.g. Schrijver et al. 2006) are shown here for each component of the velocity and for the resistivity. Only the perpendicular component of velocity is considered here. For comparison purposes, the case where all three components (u _x ,u _y ,u _z ) are taken as background velocities is shown in the right column.

Table 3 Various statistics to test the accuracy of MEF-R in the Spheromak case. Mean and standard deviation of (i) the angle distribution between “exact” Spheromak and MEF-R-based velocity vectors, (ii) the difference between scalar or vector fields corresponding to “exact” Spheromak and MEF-R-based fields, and (iii) the difference between magnetic diffusivities based on the “exact” Spheromak and MEF-R. Only the perpendicular components of velocity are considered here. For comparison purposes, the case where all three components (u _x ,u _y ,u _z ) are taken as background velocities is shown in the right column.

5 Data Processing Using MEF-R: AR 9077

In MEF, v _r can be used as a vertical background velocity. In MEF-R, we precisely adjust the magnetic diffusivity so that v _z is as close as possible to v _r . We want to compute both v(x,y) and η(x,y). Whenever we had to compute ${1 \over B_{z}}$, the vertical component B _z (x,y) was further thresholded, |B _z (x,y)|⩾40 G, to avoid dividing by zero or computer round-off values. This value is chosen to be above the noise (≈ 20 G in our data).

5.1 Testing MEF-R: Numerical Convergence

Numerical simulations of reconnection processes in the lower corona have been done with a variable magnetic diffusivity η(J) as an explicit function of current density J (e.g. Chen and Shibata 2000; Otto 2001) or η(v _ed) varying with electron velocity v _ed (Miyagoshi and Yokoyama 2004). However, to our knowledge no code simulating convection up to the photosphere and using the variable η(x,y) is currently available. This is left for future work. Nevertheless, we did check numerically that the solution was indeed a unique solution to the magnetic induction equation. In Figure 4(a) we display the scaled residuals of the vertical component of the magnetic induction equation (Equation (3)). Here we have rescaled the residuals by the standard deviation of the variable $\frac{\partial B_{z}}{\partial t}$. Scales range from −10.7 to 11.2 with a mean value at 0.00239 and standard deviation of 0.9296. The convergence process itself is shown in Figure 4(b). The kinetic energy scale here is in (px dt ⁻¹)² (see Table 4 in Appendix B). The convergence is nearly obtained at 400 iterations. After 1000 iterations there is no significant improvement in the convergence.

Figure 4

(a) Map of the scaled residuals of the vertical component of equation of conservation of magnetic flux (Equation (3)) corresponding to the time interval 08:00 – 09:36 UT of 14 July 2000 in AR 9077. Residuals have been rescaled by the standard deviation of the variable $\frac{\partial B_{z}}{\partial t}$. (b) Convergence curve of the MEF-R. Kinetic energy scale here is in (px dt ⁻¹)².

Table 4 Conversion factors from MKSA to MEF.

5.2 Vertical Velocity Versus Doppler Velocity

As expected, after 1000 iterations of MEF-R, we found that v _z (t) is very close to Doppler velocity v _r (t) (Figures 5(a) and 5(b)), in particular inside the active region. This is to be compared with Figure 2 where v _z (x,y) was computed using MEF for a non-resistive ideal gas. There are still differences, however, as can be seen on a scatter plot (Figure 5(c)) due to iterative noise amplification by MEF-R of uncorrected bad pixels on the two vector magnetograms we used. This can be quantified using the histograms of v _z (x,y;t) and v _r (x,y;t) plotted in Figure 5(d) and occurs mostly for the highest values of velocity |v _z (x,y;t)| although due to the minimization process v _z is slightly smaller than v _r . The correlation coefficients are C(v _r ,v _z )≈0.9937 for 1 G⩽|B _ℓ |⩽2500 G, with a weak field contribution C(v _r ,v _z )≈0.9939 for 1 G⩽|B _ℓ |⩽200 G, as good as its strong-field contribution C(v _r ,v _z )≈0.9909 for 500 G⩽|B _ℓ |⩽2500 G.

Figure 5

(a) Doppler velocity v _r (t) in AR 9077 recorded by SOHO/MDI on 14 July 2000. The Sun’s rotation has been removed. (b) v _z (t) as computed using MEF-R with magnetic diffusivity η(x,y;t) so that v _z (t)≈v _r (t). The time interval is 08:00 – 09:36 UT and the grid size is 256×256 pixels in both panels. Panel (c) shows the scatter plot between vertical velocity v _z (t) computed using MEF-R and Doppler velocity v _r (t). Panel (d) compares histograms of v _z (t) and v _r (t).

5.3 Horizontal Velocity

To compute v _h (x,y) we have used Equation (7). In Figure 6 we show the horizontal velocity vector field (v _x ,v _y ) computed with MEF-R using vector magnetograms and Doppler velocities between 08:00 and 09:36 UT. The use of a flat field constructed from |v _h (x,y)| as done for temperature T (Potts and Diver 2009) would produce a cleaner and smoother picture. In the active region where (B _x ,B _y ,B _z ) is strong the velocity is weaker, as expected given the stabilizing property of the magnetic field. Outside of the active region, the physics is more complex and, as noted by Longcope (2004), it is unlikely that we have computed the real velocity field.

Figure 6

Velocity vector field (v _x ,v _y ) in AR 9077, 14 July 2000 between times 08:00 and 09:36 UT, computed with MEF-R after 1000 iterations using vector magnetograms and Doppler velocities from SOHO/MDI. Scales range over [0:200] m s⁻¹. At strong-field locations spirals are rotating counterclockwise. The area is 500×500 arcsec².

An animation¹ depicting the evolution of the velocity fields shows that before the flare (e.g. 08:00 – 09:36 UT), there is extra vertical activity and little horizontal motions, with |v _z | being much larger than |v _h |. Quantitatively, the velocity vectors are mostly oriented vertically, with a maxima of ≈ 916 m s⁻¹, a mean value of ≈ 286 m s⁻¹ and a standard deviation of ≈ 121 m s⁻¹. The maximal horizontal velocity is ≈ 199 m s⁻¹, the mean is ≈ 18 m s⁻¹, and the standard deviation is ≈ 23 m s⁻¹.

It is the opposite at the time of the flare (10:30 – 11:12 UT). The motions are mostly horizontal and more chaotic, whereas vertical motions are more equally distributed and more coherent (not shown). During this lapse of time, the maximum value of the vertical velocity is ≈ 594 m s⁻¹, the mean value is ≈ 121 m s⁻¹, and the standard deviation is ≈ 81 m s⁻¹. The maximum value of the horizontal velocity is ≈ 628 m s⁻¹, the mean is ≈ 38 m s⁻¹, and the standard deviation is ≈ 56 m s⁻¹.

In this animation, at the time of the flare, chaotic flows occur everywhere in the active region and it is unclear whether it occurs mostly in the sunspots or around the polarity inversion lines. Note that the absorption line Ni i 6768 Å used to measure both Doppler and Zeeman shifts in SOHO/MDI could be perturbed by a strong flare and thus Doppler velocities and magnetic field values might not be accurate during a flare (e.g. Babin and Koval 2007).

5.4 Computation of the Magnetic Diffusivity

The values of eddy magnetic diffusivity η(x,y) are sparse but can equally be positive or negative (see below) with a mean value of ≈ 10⁸ m² s⁻¹ and standard deviation of ≈ 10¹⁰ m² s⁻¹ (Figure 7). These values can be much larger than the largest values computed from magnetograms by Chae, Litvinenko, and Sakurai (2008) using a generalization of the nonlinear affine velocity estimator of Chae and Sakurai (2008) and a pixel size of about 2 arcsec (1400 km). Negative extrema of η(x,y) may be partly due to noise in the data. Indeed, their amplitude could be reduced by using higher resolution data. In this case, they are unphysical. But some of the negative values of the diffusivity in Figure 8(a) are in strong magnetic field regions, where the relative error in field measurements is expected to be low. At these places, the action of negative eddy diffusivity would be to concentrate rather than disperse flux (e.g. Petrovay 1994). Such an explanation has been given in the case of a theoretical dynamo (Zheligovsky, Podvigina, and Frisch 2001).

Figure 7

Histogram of the magnetic diffusivity η(x,y) in AR 9077, 14 July 2000, 08:00 – 09:36 UT, compared with a Gaussian of the same variance. Exponential wings are the signature of intermittency. Log scale is used in the vertical axis. Mean value is ≈ 10⁸ m² s⁻¹ (vertical line). Standard deviation is σ≈10¹⁰ m² s⁻¹. |η(x,y)|⩾2×10¹⁰ m² s⁻¹ are due to noise.

Figure 8

(a) Eddy diffusivity η _eddy(x,y) in AR 9077, 14 July 2000, computed with MEF-R using our modeled vector magnetic field and Doppler velocities at 08:00 and 09:36 UT. (b) Map of the angles between the vectors J and E. (c) Magnetic diffusivity as a function of current density J=|J|, $\eta(J) = k (J^{2}-J_{\mathrm{c}}^{2})^{1/2} S(J-J_{\mathrm{c}})~\mbox{m}^{2}\,\mbox{s}^{-1}$ (Otto 2001). (d) Magnetic diffusivity as a function of temperature T, η(T)=c 10⁸ T ^−3/2 m² s⁻¹ (Spitzer 1962).

Locally, high values of turbulent diffusivity are considered greater than 10⁶ m² s⁻¹ for the photosphere (e.g. Abramenko et al. 2011) but values of 2.5×10⁸ m² s⁻¹ have been inferred (Simon and Weiss 1997) with a pixel of the size of a granule or larger. In fact, η(x,y) could be even higher in the lower corona (Wu et al. 2000) and the chromosphere (Miyagoshi and Yokoyama 2004; Heggland, De Pontieu, and Hansteen 2009).

The values of η _min and η _max are of the order of what we expect here for numerical-grid diffusivity dr ² dt ⁻¹≈3.9×10⁸ m² s⁻¹, although below these values the value of the magnetic diffusivity is likely distorted.

The normalized histogram or probability distribution function of the magnetic diffusivity η(x,y) between 08:00 and 09:36 UT is displayed on Figure 7 (solid line). It is different from a Gaussian distribution of the same variance (dashed line) but displays exponential wings characteristic of intermittency. The standard deviation is σ≈10¹⁰ m² s⁻¹. At the start of a flare, the temperature distribution is observed to be chaotic (e.g. Veronig et al. 2006). Since magnetic diffusivity depends on temperature (Spitzer 1962), it is expected that the variance of the magnetic diffusivity will also increase. This is what we see at 10:30 UT, the time of the flare, and at 12:48 UT, at the beginning of the thermalization phase (see below in Section 6).

The map of the magnetic diffusivity is shown in Figure 8(a). Spiral structures can be seen at the location of sunspots where there are strong unipolar magnetic fields. These spirals rotate counterclockwise in AR 9077 (Figure 8(a)). The direction of rotation of these spirals is related to the sign of the average twist α. In an active region in the southern hemisphere where α would be positive, we predict that these spiral features would rotate clockwise. The physical mechanism of the observed hemispheric distribution of active region helicity has been proposed to be due to the action of the Coriolis force on a rising Ω-shaped flux tube originating deep inside the convection layer below an active region (Sakurai and Hagino 2003).

For numerical reasons, |J _h |⩾10⁻³ A m⁻² must be used in the computation. This lower threshold value roughly equals the noise level in our data. Moreover, to better focus on the active region itself and to reduce discretization effects involving terms in 1/B _z (Longcope 2004) we have used a threshold value of |J _z |⩾10⁻² A m⁻² in the computation of Equation (20). Such values of |J _z | are observed at resolutions of 2.5 arcsec at the photosphere within sunspots (e.g. Krall et al. 1982; Deloach et al. 1984).

As can be seen in Equations (20) and (25), η _eddy is also a function of J and thus can be compared to η(|J|) (Otto 2001). The peaks of η(x,y) (Figure 8(a)) are located at the same places where photospheric currents are maximal (Figure 8(c)) and temperatures are minimal (Figure 11(b)) and where spiral centers are often located (Figures 6 and 8(a)). In fact, magnetic diffusivity in the photosphere and chromosphere can also be modeled as a function of temperature (Spitzer 1962; Kumar, Kumar, and Uddin 2011), η(T)=c 10⁸ T ^−3/2 (m² s⁻¹) where c≈5 is a constant (Figure 8(d)). Here we used the continuum intensity also measured by SOHO/MDI with the flat field corrected (Potts and Diver 2009) to derive T (Solanki, Walther, and Livingston 1993). We found that η(T) and η(|J|) are correlated with C(η(|J|),η(T))≈0.88 for 100 G⩽|B _ℓ |⩽2000 G and especially for the strongest magnetic fields 1000 G⩽|B _ℓ |⩽2000 G with C(η(|J|),η(T))≈0.98. But η _eddy does not well correlate with neither η(T) nor η(|J|). For 100 G⩽|B _ℓ |⩽2000 G, we computed C(η _eddy,η(|J|))≈0.41 and C(η _eddy,η(T))≈0.56. This is expected because the eddy diffusivity is not related to (molecular) resistivity but reflects the unresolved physics inside the subgrid.

To better understand the negative values of η _eddy, we have computed the corresponding map of angles between J and E (Figure 8(b)). A positive η occurs where angles are smaller than 90^∘ whereas negative η is for angles greater than 90^∘ and η=0 corresponds to 90^∘ between J and E. Here η _eddy, J, and E are eddy quantities representing macroscopic statistical effects, not actual processes.

5.5 The Meaning of η: Subgrid Eddy-Diffusivity

If magnetic diffusivity is small enough so that the velocity-dependent term is dominant in the generalized Ohm’s law, we have

$$\begin{aligned} {\boldsymbol{E}} =& -( {\boldsymbol{v}}\times {\boldsymbol{B}}) + \eta_{\mathrm{0}} \mu_{\mathrm{0}} {\boldsymbol{J}} \\ \approx& -( {\boldsymbol{v}}\times {\boldsymbol{B}}) , \end{aligned}$$

(31)

as in Longcope (2004). In such a case the MEF-R algorithm is able to compute v _z very close to v _r (Figure 5). But there are several places where the magnetic diffusivity takes negative values (Section 5.4). We have therefore to understand the physical meaning of η _eddy(x,y).

If the apparent diffusive effects of unresolved velocities are much greater than the advective transport of flux by velocities that can be resolved, then the electric field E can be modeled by resistivity only, namely

$$\begin{aligned} {\boldsymbol{E}} =& -( {\boldsymbol{v}}\times {\boldsymbol{B}}) + \eta_{\mathrm{eddy}} \mu_{\mathrm{0}} {\boldsymbol{J}} \\ \approx& \eta_{\mathrm{eddy}} \ \mu_{\mathrm{0}} {\boldsymbol{J}}. \end{aligned}$$

(32)

Making the scalar product of both sides of Equation (32) with J, we find an expression for η _eddy,

$$ {\boldsymbol{J}}\cdot {\boldsymbol{E}}\approx\mu_{\mathrm{0}} \eta_{\mathrm{eddy}} |{\boldsymbol{J}}|^2 . $$

(33)

However, since we consider only force-free magnetic fields, J and B are parallel and we have a strict equality instead of an approximation. We can now write η _eddy as

$$ \eta_{\mathrm{eddy}} = \frac{ {\boldsymbol{J}}\cdot {\boldsymbol{E}}}{\mu_{\mathrm{0}} |{\boldsymbol{J}}|^2} . $$

(34)

Equation (34) is equivalent to Equation (26) that we derived from Euler–Lagrange formalism for η within the force-free approximation and η is thus a magnetic turbulent diffusivity η≡η _eddy. The sign of η _eddy depends locally on the angle between the vectors J and E. If the magnetic field is not force-free, the solution is given by Equations (15), (16), and (17) whereas if the magnetic field is a force-free field it is given by Equations (18), (19), and (20). The relative orientation between J and E would be different in the two cases but the physical meaning of J⋅E⩽0 has to be understood as a statistical macroscopic effect.

To reconstruct an exact velocity field, one would need to involve the conservation of total energy and momentum (Fisher et al. 2010), i.e. to solve the full set of 3D MHD equations. However, in MEF-R we only use the vertical component of the magnetic induction equation. Using Equations (7) and (15) it can be shown that (v−u)⋅B=0, a result which the original MEF algorithm also yields. Splitting the velocity v into two components, one parallel to the magnetic field (v _∥) and one perpendicular to the magnetic field (v _⊥), it can be shown that

$$\begin{aligned} 0 =& ( {\boldsymbol{v}}- {\boldsymbol{u}}) \cdot {\boldsymbol{B}} \\ =& \bigl[( {\boldsymbol{v}}_{\perp}- {\boldsymbol{u}}_{\perp}) + ( {\boldsymbol{v}}_{\parallel}- {\boldsymbol{u}}_{\parallel })\bigr] \cdot {\boldsymbol{B}} \\ =& ( {\boldsymbol{v}}_{\parallel}- {\boldsymbol{u}}_{\parallel}) \cdot {\boldsymbol{B}}, \end{aligned}$$

(35)

which implies that if the reference flow u has a component parallel to the magnetic field B, then the inferred flow will be such that v _∥=u _∥. Therefore, unless the parallel component v _∥ is provided through a reference flow, both MEF and MEF-R can only provide the component of the velocity which is perpendicular to the magnetic field (v _⊥).

In this study, we have made the assumption that the observed Doppler velocity is entirely due to either ideal electric fields or to magnetic eddy diffusivity. Flux tubes are examples of loci where the plasma flows parallel to the magnetic field |(v×B)|≈0 and resistivity is negligible. This is only partially the case at the photospheric level. It is, however, mostly the case in sunspots where the field lines are almost vertical. There, parallel flows would most contribute to the Doppler shift. If the vector magnetic fields are correctly oriented, MEF should be able to reproduce v _z ≈v _r but only by using externally specified flow field (u _∥x ,u _∥y ). It is when and where the flow cannot be perpendicular that MEF cannot adjust v _z to v _r . And this could be the case because we made a further assumption by using force-free magnetic fields. If the vector magnetic field is incorrectly oriented, a DDM technique might be unable to match v _z with v _r unless it utilizes some eddy diffusivity to do so. In this case, it would be spurious eddy diffusivity.

A simple subgrid model of turbulent diffusivity in the case of isotropic turbulence has been proposed by Smagorinsky (1963) and later generalized to magnetic diffusivity (Theobald, Fox, and Sofia 1994). In this case, η _sg=C _e dr ²|J| is based on the hypothesis that the effect of subgrid current fluctuations is similar to eddy magnetic diffusivity (e.g. Lu 1995; Otto 2001; Klimas et al. 2004) that can be activated only if |J|⩾J _c (Figure 8(c)).

5.6 Spiral-like Structures and the Force-Free Assumption

The magnetic diffusivity η is characterized by the presence of various patterns including spiral-like structures (Figure 8(a)). As per Equation (14), with u _h =0, the minimization of the energy functional over the magnetic diffusivity η(x,y) results in v _h and $( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})$ being perpendicular, namely

$$ ( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h}) \cdot {\boldsymbol{v}}_{h} = 0 . $$

(36)

This implies that the resulting horizontal velocity v _h must be parallel to the horizontal current density J _h , as both vector quantities are non-zero. Since the horizontal magnetic field B _h is parallel to J _h under the force-free approximation, we conclude that v _h and B _h must also be parallel.

Mathematically, the expression of the magnetic diffusivity η under the force-free approximation given by Equation (20) can locally be interpreted as the scalar component of the projection of the Helmholtz decomposition vector $({\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\psi\times \hat {\boldsymbol{z}} })$ on the rotated density current vector $( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})$, normalized by |μ ₀ J _h |,

$$\begin{aligned} \eta =& \frac{({\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\psi\times \hat {\boldsymbol{z}} }) \cdot( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})}{|\mu_{0} {\boldsymbol{J}}_{h}|^2} \\ =& \frac{1}{|\mu_{0} {\boldsymbol{J}}_{h}|} \biggl[ ({\mathbf{\nabla}_{h} }\phi+ {{\mathbf{\nabla}_{h} }\psi\times \hat {\boldsymbol{z}} }) \cdot \frac{( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})}{ |\mu_{0} {\boldsymbol{J}}_{h}|} \biggr] . \end{aligned}$$

(37)

Here, $\frac{( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})}{|\mu_{0} {\boldsymbol{J}}_{h}|}$ is a unit vector.

For a non-zero magnetic diffusivity, we expect the resulting map to be reminiscent of the structure of $( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})$ (Figure 9(a)). The vectors of v _h , B _h , and J _h , as formulated within the LFF assumption, are found to be perpendicular to the streamlines of $( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})$ inside the photospheric plane. The streamlines of $( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})$ outline spiral-like structures on the map of the magnetic diffusivity (Figure 9(b)). This suggests that, as a result of Equation (37), spiral-like features seen in the maps of $( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})$ and consequently of η(x,y) might be artifacts of the LFF approximation used to reconstruct the magnetic field of AR 9077.

Figure 9

(a) Streamlines of rotated horizontal current density vector field $( \hat {\boldsymbol{z}} \times\mu_{0} {\boldsymbol{J}}_{h})$ together with vectors of inferred horizontal velocity v _h in AR9077, 14 July 2000, 08:00 – 09:36 UT, displayed over the map of magnetic eddy diffusivity η(x,y). (b) An enlargement of the area near the center of the domain.

6 Time Evolution: Catching the Flare

The time evolution of active region AR 9077 can be well traced using the time series of various physical quantities we can compute using MEF-R (Figure 10). Here 〈 . 〉 denotes an average over the entire area. Shortly before the flare (10:30 UT) there is a break in the motion of the plasma followed by a sharp upward motion just before and during the flare (Figure 10(a)). Observations as well as numerical simulations suggest the existence of such precursors in flaring active regions (Falchi and Mauas 2002; Alexander 2006; Ilonidis, Zhao, and Kosovichev 2011; Archontis and Hood 2012). Using semi-empirical models, Falchi and Mauas (2002) have shown that such motions of the chromosphere are needed to reproduce the time evolution of Si i 3905 Å and Ca ii K line profiles. E and J are oriented in the opposite directions only during the flare, i.e. during a large scale reconnection event (Figure 10(b)). Similar to the vertical velocity, the turbulent magnetic diffusivity η (Figure 10(b)) decays before the flare and strongly increases at the time of the flare. This is seen also in both models η(J) (Otto 2001) and η(T) (Spitzer 1962) (Figures 10(b) and 10(c)). Observations of active regions have shown that photospheric magnetic fields may change significantly during flares (Sudol and Harvey 2005) and thus must respond to coronal field restructuring (Wang and Liu 2010). The scale of those changes increases with the flare intensity. In X-class flares, abrupt field changes with amplitudes up to 450 G have been detected (Petrie and Sudol 2010).

Figure 10

(a) Doppler velocity 〈v _r 〉 observed with SOHO/MDI (red solid line with circles), the vertical velocity 〈v _z 〉 computed with MEF-R (blue dashed line with triangles), and X-ray flux recorded by GOES 8 in the 1.0 – 8.0 Å channel (green dashed line) in AR 9077, on 14 July 2000. (b) Mean eddy magnetic diffusivity 〈η〉 computed by MEF-R (solid line with circles, scale on the left axis) and the mean angle 〈E,J〉 (dashed line with triangles, scale on the right axis). (c) Models of the magnetic diffusivity function; 〈η(J)〉 (solid line with circles) and 〈η(T)〉 (dashed line with triangles). (d) Poynting flux 〈|P|〉 and its z-component 〈P _z 〉. The arrows indicate the time of the flare (10:30 UT) in all the panels.

The Poynting vector becomes almost vertical and directed upward during and just after the flare as can be seen when comparing the time evolution of 〈|P|〉 and P _z (Figure 10(d)). It has been seen in active regions that upward Poynting flux corresponds to flux emergence and not global plasma motion (Fan et al. 2011). Observations of Poynting flux across the photosphere in emerging active regions found similar values P _z ⩾10⁴ W m⁻² (e.g. Liu and Schuck 2012). Data-driven numerical simulations of the emergence of a flux tube have produced upward-directed vertical Poynting flux ≈ 10⁶ W m⁻² with a steep increase during emergence to ≈ 10⁷ W m⁻² on average over the area of the active region (Chen et al. 2014). Here, the vertical component of the Poynting flux P _z is slightly oriented upwards on average except at the time of the flare where it is strongly upwards (Figure 10(d)). The peaks of |P|, T, and η(J) are found at the same places where B _z is also maximal (not shown). If the photospheric resistivity is due to electric currents this would mean that at least part of the photospheric temperatures are due to Joule heating. But this is not the case with our supergranular turbulent magnetic diffusivity. Most of the energy flux radiated at the photospheric level is located in areas close to sunspots as displayed in a map of the modulus of the Poynting vector |P| (Figure 11(a)). At these places, the temperature is lower (Figure 11(b)).

Figure 11

(a) Modulus of the Poynting flux |P| at the photospheric level in AR 9077, 14 July 2000, 08:00 – 09:36 UT. (b) Temperature map from continuum intensity recorded by SOHO/MDI. Scales range over [4000:6000] (K).

7 Conclusions

When using the force-free field approximation, the MEF technique does not produce vertical velocity fields close to the observed Doppler velocities even given a reference background vertical velocity field. To address this point, we have supposed that, at least for a large scale (> 1.5 Mm), the photospheric magnetic field is not frozen-in to the plasma motions but that there must exist a magnetic eddy diffusivity term in the equation of magnetic flux conservation. We generalized the theory of MEF (Longcope 2004) to include a resistive term in Ohm’s Law.

Although our formulation is valid for any magnetic field B, we had to limit our algorithm to the particular case of force-free magnetic fields. There are two reasons for that. The first reason is that, in the case of AR 9077, we had only access to SOHO/MDI line-of-sight magnetograms that we identify with the vertical component of the magnetic field. The second reason is that MEF-R needs the vertical derivatives of the magnetic field components and here too the force-free hypothesis was a way of solving the problem.

But the force-freeness of the photosphere is now questionable (Liu, Zhao, and Schuck 2013) and DDM would overcompensate by creating a spurious eddy diffusivity. The reason is that parallel flows (|(v×B)|≈0) might contribute to the Doppler shift while being unrelated to either the diffusivity or the ideal electric field.

The algorithm could not be tested by comparison with other techniques because all of them, although they are able to process non-force-free vector magnetograms, are written for ideal MHD. Neither could we access local maps of observations of the magnetic diffusivity on the photosphere. But we used the analytical solution of the Spheromak (Bellan 2000) and verified that MEF-R partly reconstructs the input fields in the induction equation.

We focused on the particular active region AR 9077 on 14 July 2000 and used line-of-sight magnetograms together with Doppler velocities as recorded by SOHO/MDI. Although we removed the differential rotation of the Sun and the limb effect, there is still a slight distortion effect due to sphericity. However, the effect would be small because on 14 July 2000, AR 9077 was close to the center of the solar disk. We indeed found that MEF-R gives a very good match between the computed v _z and the observed v _r . However, we found that our computed magnetic diffusivity η(x,y) is in fact a turbulent diffusivity η _eddy(x,y) that could take negative values at some places. Nevertheless, on average over the whole area, most of the time we found positive and realistic values for η _eddy, in particular near the active region. The spatial distribution of η _eddy(x,y) is not well correlated with a model based on temperature η(T)(x,y), but the correlation is still better than with a model based on a critical current density η(|J|)(x,y). The correlation coefficients here are less than 0.41 and are valid for strong magnetic fields (100 G⩽|B _ℓ |⩽2000 G). Nevertheless, an interesting result is that η _eddy(x,y) maps display spiral structures near the loci of strongest unipolar magnetic field. However, such structures might be the result of the linear force-free assumption that was used to reconstruct the vector magnetograms of AR 9077.

If anomalous Doppler broadening observed in spectral lines of the photosphere is due to microturbulent velocities, we could then predict a 2D spatial correlation with the high values of our inferred eddy diffusivity. Such a correlation would validate our model. For this purpose, we are currently using high resolution SOLIS/VSM spectral datacubes.

A generalization of the method to non-force-free magnetic fields is straightforward and under way but the problem of the first order vertical derivatives still needs to be solved. The divergence-free condition on the magnetic field together with the Zeeman effect measured in spectropolarimetric observations of two lines Fe i 6301.5 and 6302.5 Å formed at different depths (Bommier et al. 2011) may be the key to this problem. In any case, at least to test the whole process, it is possible to use the 3D output of a radiative MHD simulation including a given model of the magnetic diffusivity (e.g. Abbett 2007; Abbett and Fisher 2012) for at least in the upper part of Sun’s convection zone including the photosphere and data driven by magnetograms and Doppler velocities (Vincent, Charbonneau, and Dubé 2012).

Appendices

Appendix A: Figures of Merit for the Spheromak Test

Statistical quantities are computed to test the accuracy of MEF-R in the Spheromak case. Only the perpendicular components of velocity are considered here. Given two 2D spatial scalar fields F(x,y) and f(x,y), we have computed the following quantities (e.g. Schrijver et al. 2006): the coefficient of correlation,

$$C = \bigl[\Sigma_{x,y}{ F^{\mathrm{s}}(x,y) \cdot f(x,y) }\bigr]\big/ \bigl[\Sigma _{x,y}{F^{\mathrm{s}}(x,y)^2} \Sigma_{x,y}{f(x,y)^2}\bigr]^{1/2} , $$

the normalized error,

$$E_{\mathrm{N}} = \Sigma_{x,y}{\bigl|f(x,y)-F^{\mathrm{s}}(x,y)\bigr|}\big/\Sigma _{x,y}{\bigl|F^{\mathrm{s}}(x,y)\bigr|} , $$

and the mean error,

$$E_{\mathrm{M}} = \frac{1}{N} \Sigma _{x,y} \bigl[{\bigl|f(x,y)-F^s(x,y)\bigr|\big/\bigl|F^s(x,y)\bigr|}\bigr] . $$

Here E _M and E _N are measures of differences between the two scalar fields. The ratio of “energies”,

$$\epsilon= \Sigma_{x,y}{f(x,y)^2}/\Sigma_{x,y}{F^s(x,y)^2} $$

is a measure of how well the model estimates the quadratic norm of the field. The “Cauchy–Schwarz inequality”,

$$C_{\mathrm{CS}} = \frac{1}{N} \Sigma_{x,y}{ \bigl[F^{\mathrm{s}}(x,y) \cdot f(x,y)\bigr]\big/\bigl[\bigl|F^{\mathrm{s}}(x,y)\bigr|\bigl|f(x,y)\bigr| \bigr] } $$

is a dimensionless measure of the relative orientation between the two vector fields. In the above formulas F ^s(x,y) is an “exact” analytical Spheromak scalar field and f(x,y) is the corresponding scalar field inferred from MEF. N is the number of grid points in (x,y).

The coefficient of correlation C, normalized error E _N, mean error E _M, and ratio of “energies” ϵ are shown in Table 2 for each component of the velocity and for the resistivity. In Table 3 we display the mean and standard deviation of the difference between scalar or vector velocity fields corresponding to the “exact” Spheromak and MEF-R-based fields. In both Tables 2 and 3 we have compared two cases. First (left column), we impose u _z only as a background velocity. Second (right column), we impose all three components (u _x ,u _y ,u _z ).

Appendix B: Conversion of Units

In MEF, time and space units are dt=t ₂−t ₁ and pixels (px). Conversion formulas to SI units are listed in Table 4. Here B is the magnetic induction, t is the time, v is the velocity, E is the electric field, P is the Poynting flux, μ ₀ is the magnetic permeability, I and J are the current and the current density, ϕ and ψ are electric potentials, η is the magnetic diffusivity, n is the number of gridpoints in each direction of 2D space, dt is the time between two consecutive magnetograms, L is the size of the area under study, and px stands for the size of a ‘pixel’.