Introduction

It is important to identify models that fit citation distributions well for several reasons. A good model can be used to identify anomalous sets of articles that are not fitted well by the model, suggesting indexing or classification errors, can help with the design of effective impact indicators and confidence intervals, and is important when performing regression analyses to identify factors that influence citations. A common problem when fitting statistical models to citation data is that the number of uncited articles (0 s) differs from that expected by the best fitting model, perhaps due to citation indexing policies selecting the wrong balance of high and low impact journals. This problem might be remedied by fitting a zero-inflated or a zero-deflated (i.e., a zero-modified) distribution that allows the predicted number of zeros to more closely approximate the number of zeros in a dataset.

A previous study fitted zero-inflated versions of the discretised log-normal and hooked power law distributions to citation count data from 23 Scopus categories, finding that zero-inflation occurred in nearly all cases (Thelwall 2016). The zero-inflation was hypothesised to be a consequence of “inherently unciteable articles”, such as magazine articles. Zero-counts due to unciteability are an example of “perfect” or “structural” zeros: data that are constrained to be zeros due to some feature of the data generating process. In contrast, other zeros are referred to as non-perfect or count zeros. In this context, a non-perfect zero would be a paper that is citeable but has not been cited. In essence, zero-inflated models seek to estimate the proportion of perfect zeros present in data and fit a count distribution to the remaining data.

A less well-studied phenomenon is zero-deflation, where data is well-fitted by a given count distribution, but there are less zeros present in the data than would be expected under the distribution. Zero-deflation may arise for citation counts from the Web of Science (WoS), Scopus or any other citation database with selective inclusion criteria because uncited articles may be less likely to be indexed. WoS and Scopus have poorer coverage of non-English journals than of English journals so the absence of non-English journals may contribute to zero-deflation. This may be particularly relevant for fields containing nation-specific agricultural, legal, culture, or politics research.

Whilst previous scientometric studies have fitted zero inflated distributions to citation count data, none have fitted zero-deflated or zero-modified distributions. This paper introduces zero-modified versions of the hooked power law and discretized log-normal distributions previously shown to fit citation data well (Thelwall 2016), and also zero-modified version of the discrete Weibull distribution. The discrete Weibull distribution is capable of modelling highly skewed count data with more zeros and thus is a good candidate model for citation counts (Brzezinski 2015). Discrete Weibull distributions may be fitted to data using the R-Package DWreg (Vinciotti 2016). The pure power law distribution is not considered because it usually requires low cited articles to be ignored for fitting and therefore is not a credible citation distribution. This paper also introduces an algorithm that fits both negative and positive zero-modification parameters and determines the standard errors of the zero-modification (and other) parameters, which in turn enables the calculation of confidence intervals for these parameters, and the performance of statistical tests on them. The algorithms are tested on a sample set of citation data from 23 fields to assess the extent to which the new distributions fit citation count data. The circumstances in which one of the models under consideration may be the best fit are also discussed.

Distributions

Hooked power law

The hooked power law is a generalised version of the power law model (Pennock et al. 2002). The hooked power law has probability mass function:

$$f\left( {x;B,\alpha } \right) = \left\{ {\begin{array}{ll} {A\left( {B + x} \right)^{ - \alpha } } &\quad {x = 0,1,2, \ldots } \\ 0 &\quad { {\text{otherwise}}} \\ \end{array} } \right.$$

where \(B\) and \(\alpha\) are model parameters, and \(A\) is a constant chosen so that \(\sum\nolimits_{x = 0}^{\infty } {f\left( {x;B,\alpha } \right) = 1}\).

Discretized log-normal

A (continuous) random variable is log-normally distributed if its logarithm is normally distributed. It has probability density function:

$$f\left( {x;\mu ,\sigma } \right) = \frac{1}{{x \sigma \sqrt {2\pi } }}{ \exp }\left( { - \frac{{\left( {\ln \left( x \right) - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right),\quad x > 0, \sigma > 0, \mu \in \left( { - \infty , + \infty } \right).$$
(1)

To discretise the distribution, (i.e., convert it into a form that models the situation where \(x\) is a positive integer), integrate \(f\left( {x;\mu ,\sigma } \right)\) over unit intervals about positive integer values of \(x\), and divide by \(K = \mathop \smallint \limits_{0.5}^{\infty } f\left( {x;\mu ,\sigma } \right){\text{d}}x\), where \(f\) is as at \(\left( 1 \right)\) above. Thus, the probability mass function of the discretised log-normal distribution is:

$$g\left( {x;\mu ,\sigma } \right) = \left\{ {\begin{array}{ll} {\frac{1}{K}\mathop \smallint \limits_{x - 0.5}^{x + 0.5} f\left( {x;\mu ,\sigma } \right){\text{d}}x } & {x = 1,2,3, \ldots } \\ 0 & {\text{otherwise}} \\ \end{array} } \right.$$

Discrete Weibull

The discrete Weibull distribution has probability mass function:

$$f\left( {x;q ,\beta } \right) = \left\{ {\begin{array}{ll} {q^{{x^{\beta } }} - q^{{\left( {x + 1} \right)^{\beta } }} } & {x = 0,1,2,3, \ldots } \\ 0 & {\text{otherwise}} \\ \end{array} } \right.$$

where \(0 < q < 1\) and \(\beta > 0\).

Zero-modified models

A zero-modified model (see, for example, Dietz and Böhning 2000) has the probability mass function:

$$f\left( {x;\omega,\varTheta } \right) = \left\{ {\begin{array}{ll} {\omega + \left( {1 - \omega } \right)f^{*} \left( {x;\varTheta } \right) } & {x = 0 } \\ {\left( {1 - \omega } \right)f^{*} \left( {x;\varTheta } \right)} & { x = 1,2,3, \ldots } \\ 0 & {\text{otherwise}} \\ \end{array} } \right.$$
(2)

where \(\varTheta\) is a set of parameters and \(f^{*} \left( {x;\varTheta } \right)\) is a probability mass function. For negative \(\omega\) the distribution is known as a zero-deflated distribution and for positive \(\omega ,\) it is known as a zero-inflated distribution. For \(\omega = 0\) the model reduces to the non-modified model, \(f^{ *}\), if \(\omega = 1\) the model is a “zero-model’’, i.e. one where all data are zero. Zero-inflated models are used to model data that has excess zeros (more zero counts than expected under the model \(f^{*}\)). For example, if 100 data points/observations follow a Poisson distribution with parameter 1, we would expect to observe about \(100 \times e^{ - 1} = 36.8\) zeros. Substantially more zeros would therefore indicate possible zero-inflation. Zeros may stem from two distinct processes, “Non-excess’’ zeros where zeros occur by chance, in the same manner as 1 s, 2 s,…; and another process by which some data are constrained to be zeros (perfect or structural zeros).

For a zero-deflated model, \(\omega < 0\), but may take values \(< - 1\). To see this, note that

$$\begin{array}{l} f\left( {0;\omega ,\varTheta } \right) \ge 0 \Leftrightarrow \omega + \left( {1 - \omega } \right)f^{*} \left( {0;\varTheta } \right) \ge 0 \hfill \\ \Rightarrow \omega \left( {1 - f^{*} \left( {0;\varTheta } \right)} \right) + f^{*} \left( {0;\varTheta } \right) \ge 0 \hfill \\ \Rightarrow \omega > \frac{{ - f^{*} \left( {0;\varTheta } \right)}}{{1 - f^{*} \left( {0;\varTheta } \right)}} \hfill \\ \end{array}$$
(3)

For example, if \(f^{*}\) is a Poisson distribution with parameter \(0.5\) then \(f^{*} \left( {0;0.5} \right) = { \exp }\left( { - 0.5} \right) = 0.6065\) and hence \(\omega\) is valid provided

$$\omega \ge - \frac{0.6065}{1 - 0.6065} = - 1.54$$

The interpretation of negative values of \(\omega\) is not as straightforward as those of positive values. The most straightforward interpretation is to regard \(1 - \omega\) as the proportionate increase in the expected number of observed positive values. For example, if \(\omega = - 1.5\), then we would expect to observe approximately \(1 - \left( { - 1.5} \right) = 2.5\) times more 1 s, 2 s, 3 s etc. in the data than we would in the non-modified model. Zero-deflation in data can be a consequence of some zero-counts not being included (e.g., Mendonca 1995).

Data and methods

The data analysed in this article consist of citation counts for journal articles published in 2012 from 23 Scopus categories, with up to 5000 journal articles for most of the categories. The citation counts were downloaded from Scopus in November 2017. If there were greater than 5000 articles in a category the most recent 5000 articles were selected. This provides a coherent collection of articles with 5–6 years of citations (see “Appendix 1”).

A previously published algorithm fits zero-inflated discrete log-normal and zero-inflated hooked power law models to covariate-free data (the zero-inflation parameter is estimated to two decimal places) (Thelwall 2016). This model is easily extended to zero-inflated versions of any count model but is unable to fit negative zero-modification parameters. In this article, we propose an algorithm that will enable the fitting of negative (and positive) values of \(\omega\), will estimate the value of \(\omega\) to many decimal places, and is much faster. R code to fit the models discussed in this paper is available online.Footnote 1

This algorithm is based upon maximization of the log-likelihood of the relevant zero-modified models via the optim command of R. The optim function offers different optimisation algorithms, including conjugate gradient, quasi-Newton, Nelder–Mead and simulated annealing. The default method is a derivative-free Nelder–Mead algorithm that does not require the computation of the gradient. It also is a method for solving high-dimensional linear optimisation problems with constraints that is non-sensitive and robust to discontinuities in the likelihood surface, and generally requires relatively few function evaluations to achieve convergence.

The above-mentioned algorithms have several advantages over techniques such as Newton–Raphson and Fisher Scoring. In particular, they optimise the log-likelihood function of the parameters simultaneously as opposed to individually. Consequently, the estimators obtained are better than those obtained by maximising the likelihood with respect to each parameter. Such techniques have been around a long time but have only become practical in recent years due to improved computing power.

An advantage of the optim command is its output. It includes the parameter estimates (including the estimate of the zero-modification parameter), the value of the likelihood of the model, and the Hessian matrix (Faraway 2005). The diagonal entries of the matrix inverse are proportional to the standard errors of the parameter estimates. The issue of whether there is zero inflation or deflation is dealt with by the sign of the estimate of the zero-modification parameter. The log-likelihood of the model is also outputted, which enables the calculation of corresponding Akaike Information Criterion (AIC) introduced by Akaike (1974), and thus enables the model fits to be compared. The model usually considered “best” is the one with the lowest AIC. The AIC is essentially an adjusted version of the log-likelihood, with the adjustment being to account for differing numbers of variables between models. The models corresponding to the discrete lognormal, hooked power law, and Weibull have to be fitted independently and the comparison carried out manually. The code supplied is easily modified for other distributions.

As is mentioned above, the standard errors of the parameter estimates can be computed from the Hessian matrix. This is especially useful for the calculation of confidence intervals for the zero-modification parameter (as well as any other parameters). For the computation of the confidence intervals related to the zero-modification parameter \(\omega\) the formula \(\hat{\omega } \pm {\mathcal{Z}}_{{1 - \frac{\alpha }{2}}} *Se\left( {\hat{\omega }} \right)\) is used where \(Se\) is the standard error of the maximum likelihood estimate of \(\omega\) and \({\mathcal{Z}}_{{1 - \frac{\alpha }{2}}}\) is the \(\left[\left( {1 - \frac{\alpha }{2}} \right) \times 100\right]\)-th percentile of a standard normal distribution. Thus, for \(\alpha = 0.05,{ \mathcal{Z}}_{{1 - \frac{\alpha }{2}}}\) = 1.96, values of \(\omega\) between the interval’s limits are compatible with the data.

Having the estimates of the standard deviations of the parameters also enables the performance of hypothesis tests related to the parameters. In particular it enables the test \(H_{0} :\omega = 0\) to determine whether there is statistical evidence of zero-modification in the data. Whilst American Statistical Association (Wasserstein and Lazar 2016) guidelines concerning the misuse of p-values and confidence intervals has led to debate about their use, the guidelines are primarily concerned with the misuse use of p-values and confidence intervals and do not advise their abandonment. Indeed, the guidelines state that “P-values can indicate how incompatible the data are with a specified statistical model’’.

Several tests exist to test for zero-modification, including likelihood ratio tests, score tests, and the Wilson–Einbeck test (Wilson and Einbeck 2019). Note that whilst the Vuong test for non-nested models has been used as a test of zero-inflation, this is erroneous (Wilson 2015). This paper uses the Wald test (Wasserman 2006) to test: \(H_{0} :\omega = 0\) against the alternative: \(H_{1} :\omega \ne 0\) with \(W = \frac{{\hat{\omega }}}{{Se\left( {\hat{\omega }} \right)}}\). We employ the Wald test as it directly tests the significance of the estimate of the zero-modification parameter without necessitating the fitting of the non-zero-modified model.

Finally, as it was mentioned for assessment of the fitted model, the AIC is used to show whether one model fits the data set better than another when the models in question contain differing numbers of parameters or predictor. Because there isn’t any information about the distribution of the AIC values, the non-parametric bootstrap method is used to compute confidence intervals for the AIC values of the mentioned models for all 23 categories, using the R package “Boot’’ (Canty and Ripley 2019). The bootstrap method (Efron 1979) is a resampling technique used to estimate statistics on a population by sampling a dataset with replacement. For example, in our case for one subject, a sample with size \(n\) from the data was drawn with replacement, and this was replicated B times. Each re-sampled sample of the data is considered as a bootstrap sample, so there are B bootstrap samples. For each bootstrap sample, the model is fitted, and AIC value is computed. There are B values of AIC and choosing the 2.5% and 97.5% percentiles gives a 95% percent confidence interval for AIC related to each zero-modified versions of the count distributions. This uses the R package “Boot’’.

Results

Proportions of uncited articles

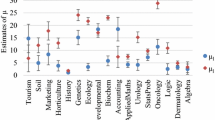
Uncited articles are far more common is some disciplines than in others (Fig. 1). Cultural Studies, Economics & Econometrics, Health Social Science, and Pharmaceutical Science have the greatest proportions of zero counts. In subjects such as Pharmaceutical Science large numbers of uncited articles might arise from publications which are not fully peer reviewed that might be regarded as magazines rather than journals being included in the database.

Fig. 1
figure 1

The proportions of uncited articles (zeros) in citation data from 23 Scopus categories. Circle areas are proportional to proportions of zeros

Full size image

Zero-modified discretised log-normal distribution

The zero-modification parameter estimates for the discretised log-normal distribution are all positive, the largest estimates being for Health Social Science and Economics and the smallest for Filtration & Separation and Global & Planetary Change (Fig. 2, see also “Appendix 2”). There is almost universal zero-inflation relative to the discretized log-normal distribution. The zero-inflation parameter estimates for 22 of the 23 subjects are significant at a level of significance of α = 0.05, with only Health Information Management returning a non-significant estimate: its confidence interval includes zero and its p value is also 0.07 which is larger than α = 0.05 (it is clear that the confidence intervals and the p-values related to the parameter estimates are compatible, i.e. 0 is outside of the confidence interval when p = 0.05, and inside otherwise).

Fig. 2
figure 2

Zero-modification parameters and 95% confidence intervals relative to a zero-modified discretised log-normal distribution for 23 Scopus categories

Full size image

Zero-modified hooked power law distribution

Relative to a hooked power law distribution both significant positive (13 subjects) and significant negative (6 subjects) estimates of the zero-modification parameter occur, as well as 4 non-significant estimates (Fig. 3, see also “Appendix 3”). There is both zero-inflation and zero-deflation, and possibly no zero-modification relative to the hooked power law distribution.

Fig. 3
figure 3

Zero-modification parameters and their confidence intervals relative to a zero-modified hooked power law distribution for 23 Scopus categories

Full size image

Zero-modified discretised Weibull distribution

Relative to a discrete Weibull distribution only one estimate of the zero-modification parameter is significantly positive, 15 being significantly negative and 7 non-significant (Fig. 4, see also “Appendix 4”). There is both zero-inflation and zero-deflation and possibly no zero-modification relative to the discretise Weibull distribution.

Fig. 4
figure 4

Zero-modification parameters and their confidence intervals relative to a zero-modified discrete Weibull distribution for 23 Scopus categories

Full size image

Assessment of the models based on AIC

None of the models under consideration fits best in all cases (Table 1), the zero-modified hooked power law being best (under the AIC criterion) in 13 cases, the zero-modified Weibull in 6 cases and the zero-modified discrete log-normal in 4 cases. Table 1 suggests the best of the models under consideration for a given subject area. For 21 out of the 23 categories the estimate of the zero-modification parameter for the model with the lowest AIC is in the interval (− 0.04, 0.08). Given the maturity of Scopus, it seems reasonable that there will be few categories for which more than 8% of articles are unciteable for the reason previously outlined, or for which more than approximately 4% of relevant articles with zero-citations are missing from the database. It is therefore reasonable to speculate that if the value of the fitted zero-modification parameter is substantially outside of (− 0.04,0.08) then there are doubts about the suitability of the model. The two exceptions to this for the models under consideration here are Health and Social Science and Cultural Studies. For the former, the best fitting model was the zero-modified hooked power law with a zero-modification parameter estimate of 0.16, and for the former the zero-modified Weibull with a zero-modification parameter of − 0.59.

Table 1 AIC values and the estimates of zero-modification parameter for zero-modified version of discretised log-normal, hooked power law and Weibull for 23 Scopus categories
Full size table

Further insights may be gained by examining the nature of the distributions. As is clear from its probability mass function, the hooked power law distribution is a decaying distribution, that is zeros have the greatest probability of being observed, followed by a 1, followed by a 2 etc., (hence a hooked power law distribution has a zero-mode), the probability of observing a zero being increased if zero-inflation is present. In contrast, a Weibull distribution may have a mode at a positive value. This requires a beta parameter > 1, which is not the case for all such estimates for the data being considered here. A discretised log-normal distribution does in general have a positive mode but may have a zero mode if the values of its two parameters are close. Of course, while zero-inflation may result in a zero-inflated discretised log-normal distribution having a mode at zero, a secondary mode will usually occur at a positive value. Two of the four subject areas for which the discrete log-normal is the best fitting model have an observed mode greater than zero; whilst the observed citation counts for Computer Science Applications have a zero mode, from “Appendix 2” the estimates of the parameters of the non-zero part of the model are 1.56 and 1.29, and hence the data are consistent with a zero-modified discrete log-normal distribution. The remaining subject area that is best fitted by a zero-modified discrete log-normal distribution is Virology, whilst here the observed mode is at zero, there is a secondary mode at 4.

For all other categories the observed citation counts follow a descending pattern and thus are candidates for being best fitted by a zero-modified hooked power law or a zero-modified Weibull, (for Neuropsychology & Physiological Psychology the number of observed 0 s and 1 s are 207 and 213 respectively, but for this subject area there is zero-deflation relative to a hooked power law distribution, and once this deflation has been taken into account the observed distribution decays). For the data considered, in four of the six subject areas for which the zero-modified Weibull is the best fitting distribution, the estimate of the zero-modification parameter is non-significant, the exceptions being Metals and Alloys, which is significant at a level of 0.05, but not at 0.02, and Cultural Studies. Whilst the estimated zero-modification parameter of − 0.594 relative to a zero-modified Weibull distribution is significant, as discussed above such a parameter estimate does not seem feasible. The same is true for the estimates of 0.117 and 0.161 relative to the hooked power law and discrete log-normal, indicating that this subject area should be further investigated.

Figures 5, 6, and 7 contain examples of the observed distribution of citation counts for subject areas best fitted by zero-modified versions of discrete log-normal, hooked power law, and Weibull distributions.

Fig. 5
figure 5

Example of observed data with non-zero-mode: global and planetary change (best fitted by the zero-modified discrete log-normal in blue). (Color figure online)

Full size image
Fig. 6
figure 6

Example of data with a zero-mode: computational mechanics (best fitted by the zero-modified hooked power law in blue). (Color figure online)

Full size image
Fig. 7
figure 7

Example of data with a zero-mode: energy engineering and power technology. Here the number of zeros is much greater than the number of any other count, but there is no evidence of zero inflation relative to a Weibull distribution (best fitted by the zero-modified Weibull in blue). (Color figure online)

Full size image

“Appendix 5” presents (bootstrapped) confidence intervals for the AIC values for the various subject areas under the three distributions considered. If confidence intervals for the AICs of two different models overlap, then there is not significant evidence that one model is better than the other. For any given subject area considered in this paper the confidence intervals of the AICs of all three distributions overlap, and thus it may not be claimed that the “best fitting distribution” fits significantly better than the remaining two. Whilst, say a zero-inflated hooked power law distribution might fit the observed data from a given category best, it is not possible to claim with certainty that this distribution will always be the best fitting model for that category.

Discussion

The principal purpose of this paper is to introduce the concept of zero modified models that admit both zero-deflation and inflation, rather than to discuss the implications of the fitted distributions and estimated parameters for the fields under analysis. Some results are included that are of interest in themselves, however. It is clear from the results that zero-modification is not an absolute concept but occurs relative to a given distribution. For example, the estimated value of the zero-modification parameter for Neuropsychology and Physiological Psychology is 0.044 relative to the discretised log-normal distribution, but − 0.040 relative to a hooked power law distribution, both estimates being significant. Thus, with the former distribution as the base-model there is statistical evidence of zero-inflation and hence “unciteable articles” within the field, but with the latter as the base distribution there is no such evidence of unciteable articles; instead there is evidence that some uncited articles may have been excluded. It is thus important to determine the best fitting base distribution to accurately determine the presence of zero-inflation or zero-deflation (or the absence of either), the presence of zero inflation/deflation relative to one model is insufficient to prove that there are perfect or omitted zeros. It is also important to consider the reality of a model, and not just rely on statistics. If for example an estimate of 0.50 for the zero-inflation parameter occurs, is it feasible that half of the articles in the field under consideration are unciteable?

The zero-modified hooked power law distribution is the best fitting model for 13 subject areas, the zero-modified Weibull best fitting for 6 subject areas, the other 4 being best fitted by the zero-modified discrete log-normal (Table 1). A zero-modified discrete log-normal tends to be the best fitting model when there is a positive mode or secondary mode, the zero-modified Weibull tends to be the best fitting model when there is no evidence of zero-modification relative to this distribution, and the zero-modified hooked power law when the observed citation counts follow a decaying distribution with evidence of zero-modification. These results are not clear-cut, however, and the incorporation of independent variables such as individual, institutional and international collaboration, journal and reference impacts, abstract readability, reference and keyword totals, paper, abstract and title lengths may lead to more precise conclusions. The results comparing distributions are limited to small samples of Scopus categories. Other years and categories may give differing results. The citation count distributions may also be affected by articles published in January having almost a year longer to be cited than articles published in December.

Conclusion

This article introduces zero-modified distributions for citation count data, focussing on zero-modified hooked power law, discrete log-normal and Weibull distributions. The new fitting method allows the estimation of both positive and negative zero-modification parameters, enabling the determination of confidence intervals for and statistical tests of parameter estimates. The results showed that each distribution fits citation count data better than the others for some Scopus categories, and so it seems unlikely that there is a single best distribution for citation count data. The results also show that both zero-inflation and zero-deflation occur for citation count data but changing a base model can alter one type to another. As a consequence of this, it is important to be wary of making definitive statements concerning zero-inflation or zero-deflation. The nature of the distribution of the observed citation counts is also an indicator of the most likely candidate of the mentioned distributions that has the best fit. For cases with the existence of a positive mode or secondary mode, a zero-modified discrete log-normal tends to have the best fit, but for the cases with no evidence of zero-modification relative to the distribution, the zero-modified Weibull is the candidate with the best fit. For the cases with a decaying distribution accompanied by evidence of zero-modification, the zero-modified hooked power law provides the best fit.

Overall, based on the previous research related to the modelling of citation count data, it seems that the non-zero-modified and more zero-modified versions of the mentioned distributions are more compatible with the initial characteristics of citation count data (mass point at zero, highly-right skewness, and heteroskedasticity). The incorporation of independent variables such as individual collaboration, journal internationality, and reference impacts may lead to more precise conclusions.