Abstract
Density functional theory (DFT) calculations and atomistic Monte Carlo simulations were performed on hexahydro-1,3,5-triphenyl-s-triazine (Inh1), hexahydro-1,3,5-p-tolyl-s-triazine (Inh2), hexahydro-1,3,5-p-methoxyphenyl-s-triazine (Inh3), hexahydro-1,3,5-p-aminophenyl-s-triazine (Inh4), hexahydro-1,3,5-p-nitrophenyl-s-triazine (Inh5) molecules in order to study their reactivity and adsorption behaviour towards steel corrosion. DFT results indicate that the active sites of the molecules were mainly located on the N atoms of the triazine ring and on the aromatic rings containing substituted polar groups. Monte Carlo simulations were applied to search for the most stable configuration for the adsorption of the inhibitor molecules on Fe(110) surface both in vacuum and in aqueous solution. The investigated molecules exhibited strong interactions with iron surface. In aqueous solution all the investigated molecules displaced water molecules and were strongly attracted to the Fe surface as evident in their large negative adsorption energies compared to that in vacuum. The DFT reactivity indicators as well as the adsorption strength from the outputs of Monte Carlo simulations of the studied molecules on Fe(110) surface in vacuum and in the presence of water follow the trend: Inh4 > Inh3 > Inh2 > Inh1 > Inh5. The theoretical data obtained are in good agreement with the experimental inhibition efficiency results earlier reported.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Corrosion is defined as the progressively destruction of especially metals by chemical reaction with various molecules in their environment. The control of this undesired process can be achieved with the use of various methods. One of the most effective alternatives for the protection of metallic surfaces against corrosion is to use the organic inhibitors containing nitrogen, oxygen, sulphur and aromatic ring in their molecular structure [1, 2].
Experimental methods are useful in understanding of inhibition mechanism but it should be stated that they are generally expensive, time-consuming and are deficient in studying inhibition mechanism at 3-dimensional atomic level. With the improvement of hardware and software, in recent times, density functional theory (DFT) and molecular simulation methods became fast and powerful tools to predict the corrosion inhibition efficiencies of complex molecules against corrosion of metal surfaces [3–12]. It is important to note that many corrosion publications contain quantum chemical calculations. Through such calculations, the corrosion inhibition efficiencies of molecules are associated with quantum chemical parameters such as the energies of the highest occupied molecular orbital (E HOMO) and the lowest unoccupied molecular orbital (E LUMO), HOMO–LUMO energy gap (∆E), chemical hardness (η), softness (σ), electronegativity (χ), proton affinity (PA), electrophilicity (ω) and nucleophilicity (ε). A recent comprehensive review by us on the use of DFT as a tool in the design of corrosion inhibitors is available in the literature and the references therein [13].
The aim of the present work is to evaluate the corrosion inhibition efficiencies of hexahydro-1,3,5-triphenyl-s-triazine (Inh1), hexahydro-1,3,5-p-tolyl-s-triazine (Inh2), hexahydro-1,3,5-p-methoxyphenyl-s-triazine (Inh3), hexahydro-1,3,5-p-aminophenyl-s-triazine (Inh4), and hexahydro-1,3,5-p-nitrophenyl-s-triazine (Inh5) molecules from information provided by DFT and Monte Carlo simulation results. The 2D molecular structures of the investigated compounds are given in Fig. 1.
Computational details
Quantum chemical calculations
Density functional theory methods have been extensively used to predict the chemical reactivity properties of molecules. In the present study, the input files of studied molecules were prepared with Gauss View 5.0.8 [14]. A full optimization was performed using the 6-311G++ (d,p) basis set for all molecules because this basis set is well known to provide accurate geometries and electronic properties for a wide range of organic compounds. Quantum chemical calculations regarding studied inhibitors were made using HF and DFT/B3LYP methods with SDD, 6-31G (d,p) and 6-31++G (d,p) basis set in the gas phase [15]. It is well known that electrochemical corrosion happens in the aqueous phase. Thus, the calculations stated above for molecules were repeated also for aqueous phase. In addition, to determine more accurately the proton affinities of inhibitor molecules, we performed all the calculations also for protonated inhibitor molecules.
Density functional theory has provided important facilities to scientist for the understanding of chemical reactivity of chemical species [16–18]. Within the framework of the DFT, chemical reactivity descriptors such as chemical hardness, chemical potential, and electronegativity are defined as derivate of electronic energy (E) with respect to number of electron (N) at a constant external potential υ(r). Chemical potential, chemical hardness and electronegativity are given as follows [19–21]:
Using the finite difference approximation, these reactivity descriptors can be calculated approximately via the following equations.
where I and A are first vertical ionization energy and electron affinity values of any chemical system, respectively.
Koopman’s theorem [22], provides an alternative molecular orbital theory method to calculate the ionization energies and electron affinities of molecules. According to this theorem, the negative of the highest occupied molecular orbital energy and the negative of the lowest unoccupied molecular orbital energy correspond to ionization energy and electron affinity, respectively (−E HOMO = IE and −E LUMO = EA). Consequently, chemical hardness and chemical potential can be expressed as:
The global softness (σ) is a measure of the polarization of electron cloud of chemical species and is the inverse of global hardness. Global softness is given as:
In 1999, Parr et al. [23], proposed a global electrophilicity index (ω) based on chemical hardness and electronegativity of chemical species. They introduced the global electrophilicity index via the following equation and stated that nucleophilicity (ε) is the inverse of the electrophilicity (ε = 1/ω).
Generally, corrosion inhibitors have high tendency towards protonation in acidic solution. Hence it is important to investigate the chemical properties of protonated forms of studied molecules. In this way, proton affinities (PA) of studied molecules can be readily determined. It is known that proton affinity values of chemical species provide remarkable clues about their electron donating ability. The proton affinities of inhibitors can be estimated via the following equation:
where E pro and E non-pro are the total energies of the protonated and the non-protonated inhibitors respectively, \(E_{{{\text{H}}_{2} {\text{O}}}}\) is the total energy of a water molecule and \(E_{{{\text{H}}_{3} {\text{O}}^{ + } }}\) is the total energy of the hydronium ion.
Monte Carlo simulations
The Monte Carlo (MC) simulation was adopted to compute the low configuration adsorption energy of the interactions of the five triazine derivatives on clean iron surface. For the whole simulation procedure, the universal force field (UFF) was used to optimize the structures of all components of the system of interest. For the gas phase study, the simulation was carried out with Fe(110) crystal with a slab of 5 Å in depth with periodic boundary conditions in order to simulate a representative part of an interface devoid of any arbitrary boundary effects. The Fe(110) plane was next enlarged to a (8 × 8) supercell to provide a large surface for the interaction of the inhibitors. After that, a vacuum slab with 30 Å thickness was built above the Fe(110) plane. In the simulation involving the aqueous phase, 30 molecules of water were added to the simulation box. The simulation box was also enlarged to (12 × 12) supercell with a vacuum slab of 50 Å thickness in order to accommodate the water molecules. The Monte Carlo simulation was carried out using Adsorption Locator module in Materials Studio 7.0 commercial software licensed from Accelrys Inc. USA.
Results and discussion
Quantum chemical study
The corrosion inhibition efficiencies of five triazines namely Hexahydro-1,3,5-triphenyl-s-triazine (Inh-1), Hexahydro-1,3,5-p-tolyl-s-triazine (Inh-2), Hexahydro-1,3,5-p-methoxyphenyl-s-triazine (Inh-3), Hexahydro-1,3,5-p-aminophenyl-s-triazine (Inh-4) and Hexahydro-1,3,5-p-nitrophenyl-s-triazine (Inh-5) is investigated in this work using quantum chemical calculations and Monte Carlo simulations approach. Recently, Shukla et al. [24], synthesized these triazines and they studied the corrosion inhibition performances of mentioned compounds against the corrosion of mild steel 1 N HCl solution using weight loss, polarization resistance, Tafel polarization and electrochemical Impedance spectroscopy techniques. In this study, the experimental corrosion inhibition efficiency ranking of these molecules was given as: Inh4 > Inh3 > Inh2 > Inh1 > Inh5.
Corrosion inhibition efficiencies of inhibitors can be compared through quantum chemical parameters such as chemical hardness, electronegativity, proton affinity, softness, electrophilicity, nucleophilicity, ∆E energy gap, E HOMO and E LUMO because these parameters provide the important information about electron donating or electron accepting abilities of the inhibitors. Calculated quantum chemical parameters for protonated and non-protonated forms of studied molecules in both gas phase and aqueous phase are presented in Table 1, 2, 3, and 4.
The energy of HOMO is associated with the electron donating ability of a molecule. High values of energy of HOMO state that the molecule is prone to donate electrons to appropriate acceptor molecules with low energy and empty molecular orbital. On the other hand, LUMO energy level is an indicator of electron accepting abilities of molecules. It is important to note that the molecules that have lower LUMO energy value have more electron accepting ability. From the light of information in Tables 1 and 2, considering HOMO and LUMO energies calculated by various methods and basis sets, one can write corrosion inhibition ranking of studied molecules as: Inh4 > Inh3 > Inh2 > Inh1 > Inh5.
Chemical hardness, softness and ∆E are quantum chemical parameters closely associated with each other. Chemical hardness is defined resistance towards electron cloud polarization or deformation of chemical species and it is one of concepts that have important application in topics such as complex stability, chemical reactivity, estimation of formed products in a reaction, solubility of molecules. This concept which is required to understand many aspects of chemical interactions was revealed by Pearson with a study of the generalized acid–base reaction of G. N. Lewis. Softness is the inverse of the chemical hardness and this parameter is a measure of polarizabilities. As is known, both softness and hardness are given based on HOMO and LUMO orbital energies as a result of Koopman’s theorem. Hard molecules which have high HOMO–LUMO energy gap cannot act as good corrosion inhibitor. However, soft molecules which have low HOMO–LUMO energy gap are good corrosion inhibitors because they can easily give to metals. According to our theoretical results, we can write the corrosion inhibition efficiency order as: Inh4 > Inh3 > Inh2 > Inh1 > Inh5. This is in good agreement with experimental observations.
The electronegativity values of inhibitors are important parameters in terms of electron transfer between the metal and inhibitor. According to Sanderson’s electronegativity equalization principle, electron transfer between metal and inhibitor continues until their electronegativity values become equal with each other. It is seen from the Eq. (10) that the electron transfer value between metal and inhibitor decreases as the electronegativity values of inhibitor increases.
where ∆N is electron transfer between metal and inhibitor. χ M and χ inh are electronegativity of metal and electronegativity of inhibitor, respectively. η M and η inh represent chemical hardness value of metal and chemical hardness value of inhibitor, respectively.
High electronegativity indicates low inhibition efficiency and considering this information and data in Tables 1 and 2, we can write the corrosion inhibition efficiency ranking of studied molecules as: Inh4 > Inh3 > Inh2 > Inh1 > Inh5.
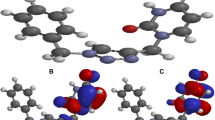
Molecular electrostatic potential (ESP) maps regarding studied molecules provide a visual method to understand the parts in which the electron density is higher than other parts in the molecule and to determine the reactive center of molecule. In the Fig. 2, ESP maps for mentioned molecules are indicated. The different values of the electrostatic potential have been shown with the help of different colors. In these maps, red color stands for the region of the most negative electrostatic potential, blue color stands for the region of the most positive electrostatic potential and green color stands for the region of the zero electrostatic potential. We made the protonation process taking into advantage from ESP maps and calculated the quantum chemical parameters and total energy values of molecules. The results obtained are presented in Tables 3 and 4. Then, we determined the proton affinity values of molecules considering (Eq. 9). According to Lewis acid–base definition, a Lewis base is defined as chemical species that donate electron pair. In this sense, corrosion inhibitors act as Lewis bases. The basicity of a molecule will increase with increasing of its proton affinity. Namely, proton affinity is a measure of the basicity. According to proton affinity values given in the Tables 1 and 2 for studied compounds, the inhibition efficiencies of mentioned compounds follow the order: Inh5 > Inh4 > Inh3 > Inh2 > Inh1. This implies that the computed proton affinity values are not in agreement with the inhibition efficiency ordering of the triazine derivatives obtained experimentally.
The electrophilicity index (ω) is an important parameter that indicates the tendency of the inhibitor molecule to accept the electrons. Nucleophilicity (ε) is physically the inverse of electrophilicity (1/ω). For this reason, it should be stated that a molecule that have large electrophilicity value is ineffective against corrosion while a molecule that have large nucleophilicity value is a good corrosion inhibitor. Thus, for studied molecules, we can write the inhibition efficiency ranking as: Inh4 > Inh3 > Inh2 > Inh1 > Inh5.
For the studied molecules, considering calculated quantum chemical parameters and the rankings given above, we propose that the inhibition efficiencies of these compounds follow the order: Inh4 > Inh3 > Inh2 > Inh1 > Inh5. This proposal is compatible with both experimental data and theoretical expectations. The electronegativity of functional groups are taken into consideration significantly to explain inductive effects of functional groups. As is known, –NO2 is an electron accepting functional group and an inhibitor containing this functional group is not effective against corrosion as other inhibitors. On the other hand, it is expected that an inhibitor containing a good electron donating group such as NH2 will be the best inhibitor compared to others.
Monte Carlo simulation results
We carried out Metropolis Monte Carlo (MC) simulation to sample possible low energy searches of the configuration space of the inhibitors on clean iron surface in vacuum and in aqueous solution as the temperature is gradually decreased. In MC simulation, the structures of the inhibitor components are minimized around the clean iron surface by undergoing random rotation and translation until they satisfy certain specified criteria. The configuration that results from one of these steps is accepted or rejected according to the selection rules of the Metropolis Monte Carlo method. More details on Monte Carlo simulations approaches to corrosion inhibition studies are documented by us and others [25–29].
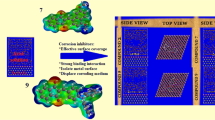
Typical energy profile made up of the total energy, average total energy, van der Waals energy, electrostatic energy and intramolecular energy for Inh-4 adsorption on Fe(110) in vacuum is depicted in Fig. 3. Also the most stable low energy configuration for the adsorption of (a) Inh-1, (b) Inh-2, (c) Inh-3, (d) Inh-4 and (e) Inh-5 on Fe(110) in vacuum obtained using the Monte Carlo simulation is also presented in Fig. 4. It is clear that the whole simulation process attends equilibrium as depicted in Fig. 3. From Fig. 4, it is seen that all the triazine derivatives investigated possess a number of lone-pair electrons containing N, O atoms as well as π-aromatic systems. This makes it possible for electrons to be donated to the unoccupied d-orbitals of iron to form a stable coordination bonding.
Table 5 presents the adsorption energies for Inh-1, Inh-2, Inh-3, Inh-4 and Inh-5 on Fe(110) in vacuum obtained using the Monte Carlo simulation. It is clear that the ranking of the adsorption of the triazine derivatives investigated on Fe(110) in vacuum follows the order: Inh-4 > Inh-3 > Inh-2 > Inh-1 > Inh-5. This ordering is the same as the experimentally obtained inhibition efficiency. Inh-4 is the best inhibitor due the electron donating effect of the substituted -NH2 groups on the aromatic rings attached to the triazine moiety. While Inh-5 is the least due to the electron withdrawing effect of the three -NO2 groups. It follows that the substitution of NH2 on the aromatic rings enhances the ability of the molecules to bind to the steel surface more than the presence of –CH3 and –OCH3 groups present in Inh-2 and Inh-3.
In order the mimic the real corrosive environment, it is imperative to consider the effect of water addition in the Monte Carlo simulation. Figure 5 shows a typical plot of energy distribution for Inh-4/H2O/Fe(110) system during energy optimization process (Inh-5:H2O = 1:30). The most stable low energy adsorption configurations of the inhibitors on Fe(110)/H2O system using Monte Carlo simulations are depicted in Fig. 6. As is seen from Fig. 6, all the inhibitors adsorbed at a parallel position on the Fe surface so as to maximize surface contact and enhance surface coverage. The values for the adsorption energies of the Monte Carlo simulations for both inhibitors and water are listed in Table 6. It is generally acknowledged that the primary mechanism of corrosion inhibitor interaction with steel is by adsorption. So the adsorption energy can provide us with a direct tool to rank inhibitor molecules. High negative adsorption energy indicates the system with the most stable and stronger adsorption [30–33]. It is quite clear from Table 6 that the adsorption energies of the inhibitors on iron surface in the presence of water follows the order Inh-4 > Inh-3 > Inh-2 > Inh-1 > Inh-5. This ordering also corroborates the result obtained in vacuum but with higher values of adsorption energies. Inh-4 is the best corrosion inhibitor and the same as the experimental determined inhibition efficiency for the inhibitors. In all cases, the adsorption energies of the inhibitors are far higher than that of water molecules as evident in Table 6. This indicates the possibility of gradual substitution of water molecules from the surface of iron surface resulting in the formation of a stable layer which can protect the iron from aqueous corrosion.
Conclusion
Density functional theory at B3LYP with different basis sets and Monte Carlo simulation were employed to evaluate the corrosion inhibition activity of some Schiff base derivatives at the molecular level. The neutral and protonated forms were considered in DFT calculations in gas and aqueous phases. The following conclusions could be drawn from this study:
-
1.
Excellent correlations have been obtained between calculated theoretical parameters of the investigated triazine compounds and their experimentally determined inhibition efficiencies.
-
2.
The DFT results rank the inhibition capabilities of the inhibitors in the following order: Inh4 > Inh3 > Inh2 > Inh1 > Inh5.
-
3.
All the values of the adsorption energies in both vacuum and in water are negative, which is an indication of spontaneous and strong adsorption process.
-
4.
In aqueous solution all the investigated molecules displaced water molecules and were strongly attracted to the Fe surface as evident in their large negative adsorption energies compared to that in vacuum.
-
5.
Monte Carlo simulations rank the inhibition capabilities of the inhibitors in the following order: Inh4 > Inh3 > Inh2 > Inh1 > Inh5, both in vacuum and in water.
-
6.
The theoretical results are in agreement with the experimentally determined inhibition efficiencies. These outcomes are important towards rational design of new triazine corrosion inhibitors.
References
R. Hasanov, M. Sadıkoğlu, S. Bilgic, Appl. Surf. Sci. 253, 3913 (2007)
M. Ozcan, R. Solmaz, G. Kardas, I. Dehri, Colloid Surf. A Physicochem. Eng. Asp. 325, 57 (2008)
K. Bhrara, H. Kim, G. Singh, Corros. Sci. 50, 2747 (2008)
E.E. Oguzie, Y. Li, S.G. Wang, F. Wang, RSC Adv. 1, 866 (2011)
M.A. Chidiebere, C.E. Ogukwe, K.L. Oguzie, C.N. Eneh, E.E. Oguzie, Ind. Eng. Chem. Res. 51, 668 (2012)
J. Cruz, L.M.R. Martinez-Aguilera, R. Salcedo, M. Castro, Reactivity properties of derivatives of 2-imidazoline: An ab initio DFT study. Int. J. Quantum Chem. 85, 546–556 (2001)
J. Zhang, G. Qiao, S. Hu, Y. Yan, Z. Ren, L. Yu, Corros. Sci. 56, 176 (2011)
G. Gece, S. Bilgic, Corros. Sci. 51, 1876 (2009)
T. Arslan, F. Kandemirli, E.E. Ebenso, I. Love, H. Alemu, Corros. Sci. 51, 35 (2009)
N. Kovacevic, A. Kokalj, J. Phys. Chem. C 115, 24189 (2011)
K.F. Khaled, Electrochim. Acta 53, 3484 (2008)
M.K. Awad, M.R. Mustafa, M.M. Abo Elnga, J. Mol. Struct. (THEOCHEM) 959, 66–74 (2010)
I.B. Obot, D.D. Macdonald, Z.M. Gasem, Corros. Sci. 99, 1 (2015)
R.D. Dennington, T.A. Keith, C.M. Millam, GaussView 5.0 (Gaussian Inc, Wallingford, 2009)
M.J. Frisch et al., Gaussian 09, Revision C.01 (Gaussian Inc, Wallingford, 2009)
R.G. Parr, W. Yang, Density Functional Theory of Atoms and Molecules (Oxford University Press, Oxford, 1989)
R.M. Dreizler, E.K.U. Gross, Density Functional Theory (Springer, Berlin, 1990)
P.K. Chattaraj, Chemical Reactivity Theory: A Density Functional View (Taylor & Francis/CRC Press, Boca Raton, 2009)
S. Kaya, C. Kaya, Comput. Theor. Chem. 1054, 42 (2015)
S. Kaya, C. Kaya, Mol. Phys. 113, 1311 (2015)
S. Kaya, C. Kaya, J. Phys. Theor. Chem. 11, 155 (2015)
T. Koopmans, Physica 1, 104 (1934)
R.G. Parr, L.V. Szentpaly, S. Liu, J. Am. Chem. Soc. 121, 1922 (1999)
S.K. Shukla, A.K. Singh, M.A. Quraishi, Int. J. Electrochem. Sci. 7, 3371 (2012)
J. Tan, L. Guo, T. Lv, S. Zhang, Int. J. Electrochem. Sci. 10, 823 (2015)
L. Guo, S. Zhu, S. Zhang, Q. He, W. Li, Corros. Sci. 87, 366 (2014)
I.B. Obot, S.A. Umoren, Z.M. Gasem, R. Suleiman, B. El Ali, J. Ind. Eng. Chem. 21, 1328 (2015)
A.M. Kumar, R.S. Babu, I.B. Obot, RSC Adv. 5, 19264–19272 (2015)
I.B. Obot, A. Madhankumar, S.A. Umoren, Z.M. Gasem, J. Adhes. Sci. Technol. 29, 2130 (2015)
Y. Sasikumar, A.S. Adekunle, L.O. Olasunkanmi, I. Bahadur, R. Baskar, M.M. Kabanda, I.B. Obot, E.E. Ebenso, J. Mol. Liq. 211, 105 (2015)
I.B. Obot, E.E. Ebenso, M.M. Kabanda, J. Environ. Chem. Eng. 1, 431 (2013)
I.B. Obot, N.O. Obi-Egbedi, E.E. Ebenso, A.S. Afolabi, Res. Chem. Intermed. 39, 1927 (2012)
S.A. Umoren, I.B. Obot, Z.M. Gasem, Ionics 21, 1171 (2015)
Acknowledgments
The authors would like to acknowledge the support and fruitful collaboration between the Center of Research Excellence in Corrosion (CORE-C), at King Fahd University of Petroleum and Minerals (KFUPM) Saudi Arabia and the Department of Chemistry, Faculty of Science, Cumhuriyet University, Turkey.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Obot, I.B., Kaya, S., Kaya, C. et al. Theoretical evaluation of triazine derivatives as steel corrosion inhibitors: DFT and Monte Carlo simulation approaches. Res Chem Intermed 42, 4963–4983 (2016). https://doi.org/10.1007/s11164-015-2339-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11164-015-2339-0