Non-linear volatility with normal inverse Gaussian innovations: ad-hoc analytic option pricing

Abstract

This paper proposes an approximate closed-form option-pricing model based on a non-linear GARCH process with Normal Inverse Gaussian (NIG) Lévy innovations. We develop the mathematical framework and demonstrate how to obtain a closed-form solution to the option price when the return dynamics are characterized by NIG innovations for volatility that follow a non-linear GARCH process. Using a sample of S&P 500 index options, we calibrate the proposed model alongside popular existing models. Overall, from a unified comparison of various analytic pricing approaches, we find that our model performs significantly better than existing models, both in-sample and out-of-sample.

1 Introduction

Well-known drawbacks of the seminal Black–Scholes (1973) option-pricing model are, first, it fails to account for skewness and heavy tails in the underlying asset and, second, volatility clustering over time. A number of approaches have been suggested to deal with these drawbacks. Notable among these are the jump-diffusion model (Merton 1976; Psychoyios et al. 2010), the stochastic volatility model (Hull and White 1987; Heston 1993; Bates 2003; He and Lin 2023), the GARCH option pricing models based on Engle (1982) and Bollerslev (1986) (e.g., Duan 1995; Heston and Nandi 2000; Barone-Adesi et al. 2008), and the Lévy approach (e.g., Geman et al. 2001; Geman 2002; Carr et al. 2002; Dingec and Hormann 2012; Muroi and Suda 2023).

The jump-diffusion approach considers discrete jumps as well as diffusion in stock prices, but the volatility is modeled as a second stochastic process under the stochastic volatility approach. The Lévy approach considers stock prices that follow a Lévy process. This approach has been further extended by Carr and Wu (2004) and Huang and Wu (2004) using time-changing Lévy processes to tackle the empirical features of observed option prices. Ornthanalai (2014) finds that models that do not price jump risk under Lévy processes cannot explain the divergence between the physical and risk-neutral probability measures, and that the model with infinite-activity jumps, rather than Brownian increments, is more relevant for option pricing.

This paper addresses the interface of the GARCH and Lévy bodies of literature and proposes an alternative—yet complementary—approach to those of Carr and Wu (2004) and Huang and Wu (2004). Our aim is to provide convincing yet fast-to-calculate treatment of option pricing under a special-case Lévy process—the Normal Inverse Gaussian (NIG). GARCH models have proven to be effective in capturing important characteristics of financial asset returns, such as volatility clustering, long-run variance reverting, and the leverage effect (e.g., Oh and Park 2023). Furthermore, it has been well-documented in the option pricing literature that GARCH option pricing models offer implementation advantages compared to continuous-time stochastic volatility models (e.g., Heston and Nandi 2000; Christofferson et al. 2012). The Normal Inverse Gaussian (NIG) Levy innovations can be represented as a mixture of normal densities, where the mixing distribution follows a generalized inverse Gaussian density. The literature has discussed NIG as a good candidate for modeling stock returns due to its ability to account for the skewness, kurtosis, and other deviations from normality exhibited by stock returns (e.g., Geman 2002). Moreover, the mixing process of NIG is not necessarily continuous, which adds to its flexibility and applicability in modeling real-world financial data.

We aim to achieve an analytical option pricing solution by replacing NIG innovations with approximately normal innovations. In prior work, Moolman (2008), Kim et al. (2008, 2010), and Ornthanalai (2014) embed a GARCH model within a Lévy process, while Badescu et al. (2015) propose a non-Gaussian GARCH option-pricing model. However, these studies rely on the Monte Carlo simulation to price options and, as such, do not benefit from an analytic approach. Another notable example in the same spirit is Mercuri (2008), who combines GARCH with tempered stable (TS) innovations and provides an analytical solution comparable to ours. However, the GARCH-TS volatility dynamics used by Mercuri (2008) are applicable only for innovations coming from a positive Lévy process.¹ We, on the other hand, introduce a mathematical framework with a nonlinear volatility dynamic approximated by replacing standard NIG innovations with standard normal innovations. We demonstrate how ad-hoc analytic solutions can be derived in the presence of both positive and negative Lévy innovations.

We focus on the pricing of European options, for which we first need to know the risk-neutral density at maturity. However, a problem with the standard GARCH setup is that we only know the risk-neutral distribution one step ahead. To overcome this difficulty, Heston and Nandi (2000) propose a GARCH-like model with normal innovations, for which they compute the characteristic function of the underlying asset using a recursive procedure and then employ the Fourier inversion approach of Heston (1993) to price options. Unfortunately, their model is not sufficiently flexible to explain the well-known option biases observed from the normality-based Black and Scholes model, particularly for short-term maturity options. Christoffersen (2006) conjectures that this limitation might be due to the fact that their single-period innovations are normal. Various attempts have subsequently been made to relax the normality assumption in the context of longer-horizon GARCH option pricing. For example, Badescu and Kulperger (2008) replace normality with a semi-parametric approach and then use Monte Carlo simulation to price the options. This, however, is time-consuming to implement and also inefficient as it uses only stock price information, not the information contained in option prices.

The present paper seeks to fill this gap by offering an approximate closed-form solution to price European options under a GARCH framework, where innovations follow a NIG Lévy process. This approximation technique is the key to offering a closed-form solution, and it has the potential to be applied to other Lévy innovations, especially those which are not subordinators.² Analytic pricing is practically useful as it makes option pricing much faster to compute in real time. The closed-form solution, combined with the Fractional Fourier Transform (FRFT) approach to pricing derivatives, allows us to estimate the parameters from a single calibration more efficiently and much faster. Options data from Chicago Board Options Exchange (CBOE) corresponding to a relatively calm market offers excellent empirical evidence in support of the model we propose. Our conjecture is that the explicit time-varying skewness and kurtosis modelled in our proposed approach explains the significant improvement over other option pricing models. Such a framework may also be useful for option pricing using other GARCH processes, in addition to other Lévy innovations.³

The remaining structure of this paper is as follows: Sect. 2 derives the closed-form GARCH option-pricing formula with NIG-Lévy innovations. Section 3 discusses data and implementation issues. Section 4 discusses the goodness-of-fit measures used in calibration and analysis, and Sects. 5 and 6 present calibration and empirical results. Section 7 concludes.

2 Closed-form Garch option pricing with Nig-Lévy innovations

Two important contributions in the GARCH-Lévy area are Christoffersen et al. (2010) and Christoffersen et al. (2012). The former work sets out the broad characterizations of Lévy dynamics but does not apply their model to options data or offer explicit derivations for the Lévy innovations that have been extensively used in the derivatives pricing literature. The latter tackles affine GARCH dynamics with Lévy innovations and demonstrates that closed-form pricing is not possible for innovations based on Lévy processes exhibiting both positive and negative jumps.

We develop a mathematical framework to derive approximate closed-form formulae similar to those of Heston and Nandi (2000). More specifically, we replace the conditional normal innovations with innovations derived from the Normal Inverse Gaussian (NIG) process, which is a form of the Lévy process.

Let us assume that the stock price follows the process,

$$S_{t} = S_{t - 1} e^{{X_{t} }} ,$$

(1)

where X_t follows a time-varying NIG Lévy process. The characteristic function of X_t is that of NIG (α, β, δt). In particular, the random variable X₁ is given by⁴

$$E\left( {e^{ - iuX} } \right) = \exp \left( { - \delta \left\{ {\sqrt {\alpha^{2} - \left( {\beta + iu} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right\}} \right)$$

(2)

where $u$ is the characteristic function index.

To price an option, however, we also need the conditional distribution of the underlying asset at a multi-period-ahead maturity, T′. We derive such a distribution following the recursive method developed by Heston and Nandi (2000). Their recursive procedure is based on the idea that the conditional MGF can be expressed as

$$E\left[ {e^{{u\log \left( {S_{T} } \right)}} |\Im_{t} } \right] = S_{t}^{u} \exp \left[ {A\left( {t,T,u} \right) + B\left( {t,T,u} \right)\sigma_{t + 1} } \right]$$

(3)

where $\sigma_{t}$ denotes the variance at time $t$, and $u$ represents the index defining the characteristic function. The goal is to solve for $A\left( {t,T,u} \right)$ and $B\left( {t,T,u} \right)$ for the NIG-Lévy innovations characterizing $\sigma_{t}$.⁵

We project Eq. (1) one period ahead to obtain

$$E\left[ {e^{{u\log \left( {S_{T} } \right)}} |\Im_{t + 1} } \right] = S_{t + 1}^{u} \exp \left[ {A\left( {t + 1,T,u} \right) + B\left( {t + 1,T,u} \right)\sigma_{t + 2} } \right]$$

(4)

We assume that the general form of the conditional MGF holds at time t + 1 and use the iterative property of conditional expectations (which is the central feature of the Heston and Nandi (2000) recursive approach) to obtain the corresponding expression for the conditional MGF at time t:

$$\begin{aligned} E\left[ {e^{{u\log \left( {S_{T} } \right)}} |\Im_{t} } \right] = & E\left[ {E\left[ {e^{{u\log \left( {S_{T} } \right)}} |\Im_{t + 1} } \right]|\Im_{t} } \right] \\ \mathop = \limits^{\left( 2 \right)} & E\left[ {S_{t + 1}^{u} \exp \left[ {A\left( {t + 1,T,u} \right) + B\left( {t + 1,T,u} \right)\sigma_{t + 2} } \right]|\Im_{t} } \right] \\ \end{aligned}$$

(5)

Using Eq. (1), we have $S_{t + 1}^{u} = S_{t}^{u} e^{{uX_{t + 1} }}$. Plugging this into Eq. (5), we get

$$\begin{aligned} E\left[ {e^{{u\log \left( {S_{T} } \right)}} |\Im_{t} } \right] = & E\left[ {S_{t}^{u} e^{{uX_{t + 1} }} \exp \left[ {A\left( {t + 1,T,u} \right) + B\left( {t + 1,T,u} \right)\sigma_{t + 2} } \right]|\Im_{t} } \right] \\ = & S_{t}^{u} E\left[ {e^{{uX_{t + 1} }} \exp \left[ {A\left( {t + 1,T,u} \right) + B\left( {t + 1,T,u} \right)\sigma_{t + 2} } \right]|\Im_{t} } \right] \\ \end{aligned}$$

(6)

Hence, no matter the number of steps between t and T, we can use Eqs. (4) and (5) recursively to derive the conditional moment generating function (MGF) at any maturity T, given the information available up to t. A comparison of (3) and (6) then allows us to derive the recursive relations for the coefficients $A\left( {t,T,u} \right)$ and $B\left( {t,T,u} \right)$.

2.1 NIG time-varing LÉVY innovations

We now derive the recursive coefficient relations for the NIG-Lévy innovations. Given that the stock price follows the dynamics (1), the log return process has a GARCH structure:

$$X_{t} = r + \lambda \sigma_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}$$

(7)

here $r$ denotes the risk-free rate, $\lambda$ is the price of risk for variance, $\sigma_{t}$, $z_{t} |\Im_{t - 1} \sim NIG\left( {\alpha ,\beta ,\delta \sigma_{t} } \right)$, and the variance process, $\sigma_{t}$,⁶ follows the GARCH (1, 1) specification

$$\sigma_{t} = \beta_{0} + \beta_{1} \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} + \alpha_{1} \sigma_{t - 1} ,$$

(8)

where the above scaling ensures unit variance for innovations.

Proposition 2.1.1

For the GARCH dynamics in (7) with $z_{t} |\Im_{t - 1} \sim NIG\left( {\alpha ,\beta ,\delta \sigma_{t} } \right)$, where $\sigma_{t}$ is the variance process defined in (8), the conditional skewness and conditional kurtosis can be obtained as in (37) and (38) in Appendix 1. (See Appendix 1 for the proof.)

Proposition 2.1.2

For the GARCH dynamics in (7) with $z_{t} |\Im_{t - 1} \sim NIG\left( {\alpha ,\beta ,\delta \sigma_{t} } \right)$, where $\sigma_{t}$ is the variance process defined in (8), the equivalent martingale relationships among the parameters are given by (43–45) and (48, 49). (See Appendix 2 for the proof.)

Now we use the above two Eqs. (7) and (8) to replace X_t+1 and $\sigma_{t + 2}$ in Eq. (6) to obtain the following GARCH NIG-Lévy dynamics:

$$\begin{gathered} E\left[ {e^{{u\log \left( {S_{T} } \right)}} |\Im_{t} } \right] \hfill \\ = S_{t}^{u} E\left[ {\left. {e^{{u\left( {r + \lambda \sigma_{t + 1} - \frac{{z_{t + 1} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)}} \exp \left[ \begin{gathered} A\left( {t + 1,T,u} \right) + \hfill \\ B\left( {t + 1,T,u} \right)\left( {\beta_{0} + \beta_{1} \frac{{z_{t + 1} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} + \alpha_{1} \sigma_{t + 1} } \right) \hfill \\ \end{gathered} \right]} \right|\Im_{t} } \right] \hfill \\ \end{gathered}$$

(9)

$$\begin{aligned} & = S_{t}^{u} E\left[ {\exp \left\{ \begin{gathered} ur + \lambda u\sigma_{t + 1} + A\left( {t + 1,T,u} \right) + \beta_{0} B\left( {t + 1,T,u} \right) \hfill \\ + \alpha_{1} \sigma_{t + 1} B\left( {t + 1,T,u} \right) + \frac{{\left[ {\beta_{1} B\left( {t + 1,T,u} \right) - u} \right]z_{t + 1} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}|\Im_{t} \hfill \\ \end{gathered} \right\}} \right] \\ & \mathop = \limits^{{}} S_{t}^{u} \exp \left\{ \begin{gathered} ur + \lambda u\sigma_{t + 1} + A\left( {t + 1,T,u} \right) + \beta_{0} B\left( {t + 1,T,u} \right) \hfill \\ + \alpha_{1} \sigma_{t + 1} B\left( {t + 1,T,u} \right) - \delta \sigma_{t + 1} \left[ {\sqrt {\alpha^{2} - \left( {\beta + \frac{{\left[ {\beta_{1} B\left( {t + 1,T,u} \right) - u} \right]}}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right] \hfill \\ \end{gathered} \right\} \\ & {\text{since }}\,\,\,\,z_{t + 1} |\Im_{t} \sim NIG\left( {\alpha ,\beta ,\delta \sigma_{t + 1} } \right) \\ & = S_{t}^{u} \exp \left\{ \begin{gathered} ur + A\left( {t + 1,T,u} \right) + \beta_{0} B\left( {t + 1,T,u} \right) \hfill \\ + \left\{ {\lambda u + \alpha_{1} B\left( {t + 1,T,u} \right) - \delta \left[ {\sqrt {\alpha^{2} - \left( {\beta + \frac{{\left[ {\beta_{1} B\left( {t + 1,T,u} \right) - u} \right]}}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right]} \right\}\sigma_{t + 1} \hfill \\ \end{gathered} \right\} \\ \end{aligned}$$

(10)

Comparing Eqs. (3) and (9), we then obtain the following recursive relations:

$$\begin{aligned} & A\left( {t,T,u} \right) = ur + A\left( {t + 1,T,u} \right) + \beta_{0} B\left( {t,T,u} \right) \\ & B\left( {t + 1,T,u} \right) = \lambda u + \alpha_{1} B\left( {t,T,u} \right) - \delta \left[ {\sqrt {\alpha^{2} - \left( {\beta + \frac{{\left[ {\beta_{1} B\left( {t,T,u} \right) - u} \right]}}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right] \\ \end{aligned}$$

(11)

Since $z_{t} |\Im_{t - 1} \sim NIG\left( {\alpha ,\beta ,\delta \sigma_{t} } \right)$ often assumes positive as well as negative values, we restrict ourselves to nonlinear dynamics of the Heston and Nandi (2000) type.

Let us assume the following nonlinear risk-neutral dynamics⁷:

$$\begin{aligned} \sigma_{t} = & \beta_{0} + \beta_{1} \left[ {\frac{{NIG\left( {\alpha ,\beta ,\delta \sigma_{t - 1} } \right)}}{{\sqrt {\alpha^{2} \sigma_{t - 1} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} - \gamma \sqrt {\sigma_{t - 1} } } \right]^{2} + \alpha_{1} \sigma_{t - 1} \\ = & \beta_{0} + \beta_{1} \left[ {\frac{{NIG\left( {\alpha ,\beta ,\delta \sigma_{t - 1} } \right) - \mu + \mu }}{{\sqrt {\alpha^{2} \sigma_{t - 1} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} - \gamma \sqrt {\sigma_{t - 1} } } \right]^{2} + \alpha_{1} \sigma_{t - 1} \\ = & \beta_{0} + \beta_{1} \left[ {stdNIG + \frac{\mu }{{\sqrt {\alpha^{2} \sigma_{t - 1} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} - \gamma \sqrt {\sigma_{t - 1} } } \right]^{2} + \alpha_{1} \sigma_{t - 1} \\ \end{aligned}$$

(12)

where μ is the expected value of a $NIG\left( {\alpha ,\beta ,\delta \sigma_{t - 1} } \right)$ random variable and is given by Eq. 31 in Appendix 1. Moreover, this modification of the volatility dynamics re-establishes the historical and risk-neutral relation of $\beta_{1}$ and introduces a new historical and risk-neutral relation for the new parameter $\gamma$, as described in Appendix 2. We can further simplify the above equation to obtain

$$\sigma_{t} = \beta_{0} + \beta_{1} \left[ {stdNIG + \left\{ {\frac{\beta \sqrt \delta }{{\alpha \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{1}{4}}} }} - \gamma } \right\}\sqrt {\sigma_{t - 1} } } \right]^{2} + \alpha_{1} \sigma_{t - 1}$$

(13)

A problem with this characterization of volatility, however, is that when $\sigma_{t}$ is plugged into Eq. (6), it does not yield explicit recursive relations for $A\left( {t,T,u} \right)$ and $B\left( {t,T,u} \right)$. Consequently, no closed-form European option valuation is possible without further approximation.⁸

Our proposed solution is to apply an approximation to the dynamics in (13) that yields to closed-form valuation techniques similar to those of Heston and Nandi (2000). In particular, when the dynamics (13) are characterized for NIG innovations, we propose an ad-hoc approximation that preserves the characterization of dynamics but replaces the standard NIG innovations with standard Normal innovations:

$$\sigma_{t} \approx \beta_{0} + \beta_{1} \left[ {stdNormal + \left\{ {\frac{\beta \sqrt \delta }{{\alpha \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{1}{4}}} }} - \gamma } \right\}\sqrt {\sigma_{t - 1} } } \right]^{2} + \alpha_{1} \sigma_{t - 1}$$

(14)

This ad-hoc approximation is motivated by Heston and Nandi (2000) closed-form pricing based on the following relation involving a standard Normal random variable,

$$E\left[ {\exp \left\{ {a\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} + b} \right)^{2} } \right\}} \right] = \exp \left\{ { - \frac{1}{2}\ln \left( {1 - 2a} \right) + \frac{{ab^{2} }}{1 - 2a}} \right\},$$

(15)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} \sim N\left( {0,1} \right)$.

We apply the volatility dynamics (14) (which are characterized by NIG innovation but approximated through the replacement of standard NIG variates with standard Normal variates) in the general recursive relation (6):

$$\begin{aligned} & E\left[ {e^{{u\log \left( {S_{T} } \right)}} |\Im_{t}^{1} } \right] \\ & \, = S_{t}^{u} E\left[ {e^{{u\left( {r + \lambda \sigma_{t + 1} - \frac{{z_{t + 1} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)}} \exp \left[ \begin{gathered} A\left( {t + 1,T,u} \right) + \hfill \\ B\left( {t + 1,T,u} \right)\left( {\beta_{0} + \beta_{1} \left[ {z + \left\{ {\frac{\beta \sqrt \delta }{{\alpha \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{1}{4}}} }} - \gamma } \right\}\sqrt {\sigma_{t + 1} } } \right]^{2} + \alpha_{1} \sigma_{t + 1} } \right) \hfill \\ \end{gathered} \right]|\Im_{t}^{1} } \right] \\ \end{aligned}$$

(16)

We then apply the relation (15, 16) to simplify further:

$$\begin{aligned} & E\left[ {e^{{u\log \left( {S_{T} } \right)}} |\Im_{t}^{1} } \right] \\ & \mathop = \limits^{{}} S_{t}^{u} \exp \left\{ {u\left( {r + \lambda \sigma_{t + 1} } \right) - \delta \sigma_{t + 1} \left[ {\sqrt {\alpha^{2} - \left( {\beta + \frac{{\left( { - u} \right)}}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right]} \right\} \\ & {\text{exp}}\left\{ \begin{gathered} A\left( {t + 1,T,u} \right) + B\left( {t + 1,T,u} \right)\beta_{0} - \frac{1}{2}\log \left[ {1 - 2B\left( {t + 1,T,u} \right)\beta_{1} } \right] \hfill \\ + B\left( {t + 1,T,u} \right)\beta_{1} \left( {\frac{\beta \sqrt \delta }{{\alpha \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{1}{4}}} }} - \gamma } \right)^{2} \sigma_{t + 1} \frac{1}{{1 - 2B\left( {t + 1,T,u} \right)\beta_{1} }} + \alpha_{1} B\left( {t + 1,T,u} \right)\sigma_{t + 1} \hfill \\ \end{gathered} \right\} \\ & {\text{since}}\,\,\,\,z_{t + 1} |\Im_{t - 1}^{1} \sim NIG\left( {\alpha ,\beta ,\delta \sigma_{t + 1} } \right) \\ & = S_{t}^{u} \exp \left\{ \begin{gathered} ur + A\left( {t + 1,T,u} \right) + \beta_{0} B\left( {t + 1,T,u} \right) - \frac{1}{2}\log \left[ {1 - 2B\left( {t + 1,T,u} \right)\beta_{1} } \right] \hfill \\ + \left[ \begin{gathered} \lambda u + \alpha_{1} B\left( {t + 1,T,u} \right) - \delta \left[ {\sqrt {\alpha^{2} - \left( {\beta + \frac{{\left( { - u} \right)}}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right] \hfill \\ + B\left( {t + 1,T,u} \right)\beta_{1} \left( {\frac{\beta \sqrt \delta }{{\alpha \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{1}{4}}} }} - \gamma } \right)^{2} \frac{1}{{1 - 2B\left( {t + 1,T,u} \right)\beta_{1} }} \hfill \\ \end{gathered} \right]\sigma_{t + 1} \hfill \\ \end{gathered} \right\} \\ \end{aligned}$$

(17)

A comparison of Eqs. (17) and (3) gives the following recursive relations:

$$\begin{aligned} & A\left( {t,T,u} \right) = ur + A\left( {t + 1,T,u} \right) + \beta_{0} B\left( {t + 1,T,u} \right) - \frac{1}{2}\log \left[ {1 - 2B\left( {t + 1,T,u} \right)\beta_{1} } \right] \\ & B\left( {t,T,u} \right) = \lambda u + \alpha_{1} B\left( {t + 1,T,u} \right) - \delta \left[ {\sqrt {\alpha^{2} - \left( {\beta + \frac{{\left( { - u} \right)}}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right] \\ & \quad + B\left( {t + 1,T,u} \right)\beta_{1} \left( {\frac{\beta \sqrt \delta }{{\alpha \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{1}{4}}} }} - \gamma } \right)^{2} \frac{1}{{1 - 2B\left( {t + 1,T,u} \right)\beta_{1} }} \\ \end{aligned}$$

(18)

2.2 Option pricing and calibration methodology

We obtain the option prices through Fourier Inversion as in Heston (1993) and Heston and Nandi (2000), where having recursive relations for ‘A’ and ‘B’ suffices to obtain analytic results for prices. However, we evaluate the integrals with FRFT, instead of FFT or other numerical integration. For the closed-form (up to numerical integration) GARCH model with NIG innovations, we denote the model call option price by $C^{cfgnig}$(where the subscript represents closed-form GARCH-NIG). This model has seven parameters to be estimated, $\left[ {\beta_{0} ,\beta_{1} ,\alpha_{1} ,\gamma ,\alpha ,\beta ,\delta } \right]$.⁹

Given the parameter constraints, we treat the calibration as a constrained optimization problem rather than a simple nonlinear least-squares one. The constraints arise from the GARCH structure as well as the usual NIG parameterization,$\beta_{0} \ge 0,\beta_{1} \ge 0,\alpha_{1} \ge 0$, $\alpha_{1} + \beta_{1} < 0$, $\alpha > 0$, and $\left| \beta \right| \le \alpha$, i.e., $- \alpha - \beta < 0,\delta > 0$. Thus, the calibration of the model comes from the solution to the following optimization problem¹⁰:

$$\begin{aligned} & Minimize\left[ {\sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {C_{i}^{market} - C_{i}^{cfgnig} \left[ {\beta_{0} ,\beta_{1} ,\alpha_{1} ,\gamma ,\alpha ,\beta ,\delta } \right]} \right)^{2} } } } \right] \\ & s.t. \, \,\,\,{\text{A}}\left[ {\beta_{0} ,\beta_{1} ,\alpha_{1} ,\gamma ,\alpha ,\beta ,\delta } \right]^{\prime } \le b, \\ \end{aligned}$$

(19)

where

$$A = \left( {\begin{array}{*{20}c} { - 1} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & { - 1} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & { - 1} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & { - 1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & { - 1} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & { - 1} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & { - 1} \\ \end{array} } \right)$$

and

$$b = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ \end{array} } \right].$$

We address twelve basic models in the Levy-jump literature and in the heteroskedastic GARCH option pricing literature: (1) BS: Black–Scholes (1973) model, (2) VG: Variance Gamma of Madan et al. (1998), (3) NIG: Normal Inverse Gaussian model of Schouten (2003), (4) JD-DE¹¹: Double exponential jump diffusion model of Kou (2002), (5) CGMY¹²: Carr et al. (2002) model, (6) Heston: Heston (1993) stochastic volatility model, (7) HN(R): restricted version of Heston and Nandi (2000) GARCH model, (8) HN(U): unrestricted version of Heston and Nandi (2000) GARCH model, (9) Scott: Scott (1997) model, (10) Bates: Bates (1996) model, (11) GARCH-IG: Christoffersen et al.’s (2006) model,¹³ and (12) GARCH-NIG: our proposed closed-form GARCH model with NIG innovations. Table 1 presents the characteristics functions for each of these models.

Table 1 Jump and SV models and their risk-neutral characteristic functions

3 Data and filtering

We use daily records of options written on the S&P 500 index traded on the Chicago Board Options Exchange (CBOE). We retrieve the S&P 500 index put and call option quotes from Thompson Reuter Tick history. For in-sample calibration, we use a sample period that runs from January 2012 through December 2013, and for out-of-sample assessment we employ data up until June 2014.¹⁴ We use data every Wednesday, as it is the day of the week least likely to be a holiday, and it is less likely to be impacted by day-of-the-week effects (Ornthanalai 2014).¹⁵

We then filter our data using the same rules applied by Heston and Nandi (2000):

• We do not consider any option of a particular moneyness or maturity more than once in our sample.¹⁶ This eliminates a large number of observations.

• We exclude deep out-of-the-money and deep in-the-money options because these are either infrequently traded and/or have low enough prices for the bid-ask spread to constitute a major portion of the price. To be precise, only records having an index-to-strike ratio between 0.9 and 1.1 are included in our sample.

• We only include options that have between six and 100 days to expiration. We eliminate very long-term options because they are not actively traded and are prone to mispricing. Conversely, we eliminate very short-term options because they have substantial time decay, which makes it difficult to reliably determine the volatility parameter.

After applying the filtering rules described above, we have 8404 options over the time window. Table 2 presents descriptive statistics for the option quotes based on moneyness and maturity. We define moneyness as S/K where S is the underlying index price at maturity t, and K is the strike price.

Table 2 S&P 500 Index Options data, 2012–2014

4 Goodness-of-fit

To assess in-sample goodness-of-fit, we use the Root Mean Square Measure, RMSE, which considers quadratic deviations between model and market prices:

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {C_{i}^{market} - C_{i}^{model} } \right)}^{2} } .$$

(20)

To assess out-of-sample goodness-of-fit, we use a naive measure known as the average absolute error (AAE), which considers linear deviations between model and market prices:

$$AAE = \sum\limits_{i = 1}^{N} {\frac{{\left| {C_{i}^{market} - C_{i}^{model} } \right|}}{N}} .$$

(21)

We also assess out-of-sample goodness-of-fit using Mean-Outside-Error (MOE), which is used to assess a model’s average tendency to over-price or underprice:

$$MOE = \sum\limits_{i = 1}^{N} {\frac{{\left[ {\left( {C_{i}^{model} - {\text{ask}}_{{\text{i}}} } \right){\rm I}_{{\left\{ {C_{i}^{model} - {\text{ask}}_{{\text{i}}} } \right\}}} + \left( {C_{i}^{model} - {\text{bid}}_{{\text{i}}} } \right){\rm I}_{{\left\{ {C_{i}^{model} - {\text{bid}}_{{\text{i}}} } \right\}}} } \right]}}{N}} .$$

(22)

When assessing out-of-sample performance, we restrict our reported results to models that explicitly incorporate stochastic volatility. We find that models that incorporate jumps provide an excellent fit over very short periods (e.g., 1 day or a couple of days’ observations), but such models perform much worse for long periods relative to models which consider explicit stochastic volatility dynamics. Consequently, we restrict our out-of-sample performance to seven models: Heston (1993) continuous-time stochastic volatility model, restricted and unrestricted versions of Heston and Nandi (2000) discrete-time GARCH volatility model with normal innovations (HN(R) and HN(U)), Scott (1997), Bates (1996), Christoffersen et al. (2006), and our GARCH-NIG model.

5 Calibration

We report calibrations using a cross-section of options recorded during a relatively calm time frame, 2012–2014.¹⁷ We then conduct a robustness study using option data in 2015 subject to market participants’ exposure to point-in-time (1 day) data with minimal market information content, instead of huge cross-sectional information content.

Our in-sample calibration uses option information over 2 years periods. Specifically, we calibrate the models using options traded from January 1, 2012, to December 31, 2013. We then use the first 6 month’s contracts in 2014 to assess the models’ out-of-sample performance. Table 3 reports the in-sample results for 2012–2013 calibrations, and Table 4 reports the out-of-sample results. The robustness analysis includes calibrating all models subject to the minimal information content of options on one single day, but in contrast to the results in Table 3, now in a highly volatile market. The robustness results are presented in Table 5.¹⁸

Table 3 Calibration with options traded over the period January 1, 2012–December 31, 2013

Table 4 Out-of-sample valuation errors for call options traded in the first half of 2014

Table 5 Robustness investigation with point-in-time S&P 500 index options

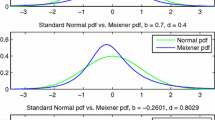
Before we present the results and empirical analysis of our model, we talk about an important facet which in this current version of the paper is rather discussed in a limited fashion.¹⁹ The effect of approximating the dynamics in Eq. (13) by the dynamics in Eq. (14) has been illustrated in Fig. 1 in Appendix 4. For this illustration, we purposefully used the parameters calibrated from option prices traded on an unusually highly volatile day, namely August 24th, 2015 (as in Table 5). As a consequence, the daily volatilities under both GARCH-NIG and approximate GARCH-NIG models are found to be higher than usual market volatilities. Moreover, what is primarily worth noting is that replacing stdNIG innovations in (13) with stdNormal innovations in (14) has very little effect on both volatility and return distribution. This primarily justifies that the ad-hoc approximation required for analytic valuation under this non-linear GARCH-NIG model does mostly retain the features of original distribution (without approximation), so it does justify obtaining closed-form option prices through such ad-hoc approximation. It goes without saying that such pricing and their sensitivities, due to approximation, should be investigated thoroughly through simulation-based option pricing under both approximate and exact dynamics in Eqs. (13) and (14); and we understand that such a simulation study is equally important as using the analytic pricing without simulation. However, such a simulation study must consider different categories of options (ATM/ITM/OTM as well as short, medium, and long-term options) separately as bias and approximation effects will be different for different categories; thus, it naturally justifies a whole new work. In this current paper, with this initial evidence that approximation has no big concern, as presented in Appendix 4, we solely focus on our model’s usefulness as an alternative analytic pricing model.²⁰

6 Results

We first present and analyze our main calibration results, both in-sample and out-of-sample, followed by a discussion on robustness studies of calibrations.

6.1 In-sample calibration

The parameter estimates for the twelve option pricing models discussed at the end of Sect. 2 are reported in Table 3. In implementing sophisticated alternatives to the benchmark BS model, we resort to the FRFT technique as in Chourdakis (2004) and Mozumder et al. (2015). FRFT is very fast compared to FFT and other numerical techniques of integration; however, with slightly less precision. In our calibration, due to the application of FRFT, we can consider all 5848 options over the period of January 1, 2012–December 31, 2013, as one vector. This approach is different from the approach considered in Bakshi et al. (1997), Heston and Nandi (2000), and other similar studies where calibrations are conducted week by week and take the average of the RMSEs and parameter values over the entire sample period as final estimates. Our approach requires some extra effort to implement Heston and Nandi (2000), Christoffersen et al. (2006), and our GARCH-NIG model as it becomes necessary to filter out the volatilities in the entire sample (e.g., for the full 2012–2013 period) simultaneously. This one-shot FRFT based calibration of all options together has some bearing on the models’ out-of-sample performance. When calibrating Scotts (1997), Bates (1996), and other models, we use the estimates proposed by the corresponding authors as initial guesses in optimization.

From the parameter estimates in Table 3, we find that BS-implied volatility is relatively low during our sample period, being at 7% per year. In the VG model, the σ and υ parameters are of acceptable order and sign, and the θ parameter is positive and significant, indicating the market’s upward trend over the sample period. Other models also have satisfactory parameter estimates and significance, with a few exceptions for some parameters of discrete-time HN, GARCH-IG, and GARCH-NIG models. The standard errors are obtained by numerically inverting the Jacobian of the RMSE loss functions.

The most surprising fact in Table 3 is the uncanny similarity between the performance of JD-DE and BS models. The RMSE of JD-DE is 2.3807 and is smaller than the BS RMSE, 2.3851. Here, it is worth remembering that though FRFT yields very quick pricing results, though it is in general less precise than FFT and other numerical integration techniques.²¹ The point whether in a highly volatile market JD-DE model’s performance would be better than the BS model is addressed in our robustness section. Similar results may apply to the performance of Heston’s (1993) stochastic volatility and BS model. Heston and Nandi (2000) do not characterize the skewness and kurtosis in a time-varying fashion in their GARCH-Normal model. This is one of the fundamental differences between Heston and Nandi (2000) and our GARCH-NIG model, and partly the Christoffersen et al. (2006) GARCH-IG model.²²

The outperformance of Bates (1996) and Scott (1997) model over Christoffersen et al. (2006) GARCH-IG model are due to the attributes of additional parameters and partly due to the stochastic interest rate feature of Scott’s (1997) model.²³ Comparing the performance between Heston (1993) and Heston and Nandi (2000), we find that they are close to each other, as the Heston (1993) model is the continuous-time limit of the discrete-time Heston and Nandi (2000) model.²⁴ Compared to Christoffersen et al. (2006) GARCH-IG model, our model’s further enhanced performance could be either be due either to the additional feature of the particular non-linear GARCH of the Heston and Nandi type²⁵ or to the time-evolving characterizations of both skewness and kurtosis in our model.²⁶

Outside these analyses, the Lévy models, VG, NIG, and CGMY, show modest improvements over the performance of the BS model; however, they are not significant enough to beat any stochastic or time-varying volatility model, which is consistent with the findings in the literature (see Mozumder et al. (2013)).

Overall, we find that the BS model provides the poorest fit with an RMSE of 2.38 (which, however, is much lower compared to what other studies report; perhaps partly due to our targeting of low volatility periods or perhaps because in not-so-turbulent periods BS is overall not a very apt model). Somewhat surprisingly, the second-poorest performing model turns out to be JD-DE with an RMSE of 2.38 (preferred over BS only after two digits of RMSE). Pure jump Lévy models come as the next poorest type of model, with VG, NIG, and CGMY model RMSEs as 2.35, 2.36, and 2.37, respectively. Heston and Nandi (2000) and Heston (1993) models have RMSEs of 2.36(R), 2.28(U), and 2.34, respectively, and seem correctly ordered, as discussed in Mozumder et al. (2013), Heston and Nandi (2000). Then comes Christoffersen (2006) GARCH with IG innovations. It is a nice feature to perform better than Heston and Nandi (2000) GARCH, which has normal innovations, and indeed so with an RMSE of 2.26. Bates (1996) continuous-time stochastic volatility with normal jumps and Scott (1997) continuous-time stochastic volatility with jumps and stochastic interest rates naturally perform better than any model we consider (except our proposed GARCH-NIG model) with RMSEs of 2.21 and 2.20, respectively. Finally, the best among our considered models is our proposed GARCH-NIG model with an RMSE of 1.70, and the distinct performance is due to the rich characterization that we have already discussed.²⁷

We could have considered options data from more recent period, however, the period of January 2012–December 2013 is exceptionally stable relative to other periods in the decade leading up to the inception of COVID. Almost all the studies in the literature care how differently a sophisticated model performs, improving on the performance of other models available at that moment; however, our empirical study focuses on how similarly most of the otherwise sophisticated models may perform in a calm market and how significant an improvement might be achieved by our GARCH-NIG model over the performance of most of models during a calm market.

6.2 Out-of-sample results

The out-of-sample analysis uses options for a 6-months window after the models are calibrated using 2 years of option data. The results, presented in Table 4, show that our proposed ad-hoc analytic GARCH-NIG model outperforms the other models based on the out-of-sample RMSE criterion in all moneyness-maturity groups. Similarly, by the other two measures, AAE and MOE, the GARCH-NIG model always outperforms the other models.

As in Table 4, the average goodness-of-fit results are achieved using BS, Heston, HN(R), HN(U), Scott, Bates, and GARCH-IG are of a similar order of magnitude amongst the different categories of maturity and moneyness. In some categories, particularly with short maturities, the single parameter BS model beat most of the otherwise sophisticated alternative models.²⁸ This finding might seem surprising at first glance but, looking into overall performance of sophisticated alternatives, this turns out not to be a big surprise. Our GARCH-NIG looks distinct due to its structural richness with non-linear GARCH and time-varying skewness (Eq. 37) and kurtosis (Eq. 38).²⁹

In sum, our proposed ad-hoc analytic GARCH-NIG model outperforms many existing models by a variety of criteria across different sample sizes and time periods. This strong performance would appear to be due to the unique features of our model that enable it to incorporate the observed empirical characteristics of the asymmetry of the risk-neutral distribution, volatility clustering, and fat tails through volatility-evolving conditional higher moments.

6.3 Discussion on robustness

Our in-sample analysis involves a deliberately chosen calm period in the last decade, namely option contracts on the S&P 500 index traded over January 2012–December 2013. In robustness analysis, we do the opposite. We pick a highly volatile day, 24th August 2015, to recalibrate and assess all twelve models (opposite to assessing a low volatility period in the main calibration). And we use minimal market information in options traded on a single day, a total of 78 option contracts (contrary to assessing the models with the information content of 2 years of traded options, 5848 contracts, in the main calibration).³⁰ Moreover, due to space constraints, the reported robustness results do not include those involve calibrating all models on different cross-sections of options data over other refined periods. For example, in unreported results, we consider option contracts traded over the first 6 months of 2015 for in-sample calibrations and the last 6 months of 2015 for out-of-sample validation of the models.³¹

We present the calibration results in Table 5, which shows that on a highly volatile day (likely to be caused by jump fluctuations of the underlying), JD-DE distinctly outperforms the BS model. The same is true for pure jump Lévy models, VG, NIG, and CGMY. The Heston (1993) model, though, which outperforms models without stochastic volatility (e.g., BS, JD-DE, VG, NIG, CGMY), now performs better than in the main calibration conducted purposefully in a low volatility regime in January 2012–December 2013. Nonetheless, and somewhat surprisingly, Heston (1993) model gets significantly beaten by its discrete-time counterparty, Heston and Nandi (2000) models, the restricted HN (R) and unrestricted HN (U) versions. This surprising result might be partly due to the fact that calibrations on a single day (using options traded on that particular day alone) do not differentiate much between time continuity and time discreteness of the models. The Scott (1997) model beating the Bates (1996) model and most of the other models by such big margins is also surprising. After all, between Scott’s and Bates’ models, the only difference is allowing the interest rate to be stochastic or not.³² Christoffersen (2006) GARCH-IG model beats Bates, Heston, and pure jump Lévy models VG, NIG, and CGMY by various margins is consistent with our main calibration. However, the inconsistencies with our main calibration are that it is now beaten by both HN (U) and HN (R).³³ However, there is no explanation in the literature why a model with a non-linear GARCH structure incorporating the flexibility of modelling both positive and negative shocks (no matter how poor the normal distribution is) cannot frequently outperform a model that models only positive shocks (no matter how rich the inverse Gaussian distribution is).³⁴

Finally, and most importantly, the robust out-performance of our GARCH-NIG model, both in the main calibration shown in Sects. 6.1 and 6.2, as well as all other calibrations with different 6-months windows, confirms that GARCH-NIG has obvious advantages over all other models no matter whether the sample exhibits high or low volatility, or is long (2 years) or short (1 day). The superior performance of GARCH-NIG model can be attributed to its adoption of the particular, non-linear type of GARCH dynamics in Heston and Nandi (2000), combined with NIG innovations that allow modelling of both positive and negative shocks, and enriched with both time-varying skewness and time-varying kurtosis. We close our discussion on robustness with the observation that, based on our calibration experiment in Sect. 6.1 and those discussed in this robustness section (both present and unpresented calibrations), most of the parameters in all of the models are found to fluctuate over time and across samples.

7 Conclusion

This paper addresses the interface of the GARCH and Lévy bodies of literature and proposes an alternative approach. Our aim is to provide a fast yet convincing treatment of option pricing under a special-case Lévy process—the Normal Inverse Gaussian (NIG). This approach provides a mathematical framework with nonlinear volatility dynamics approximated by replacing standard NIG innovations with standard normal innovations, and demonstrates how ad-hoc analytic solutions can be derived in the presence of both positive and negative Lévy innovations. Given that the GARCH-NIG model has more flexibility to describe the conditional evolution of skewness and the conditional evolution of kurtosis, we might expect it to accommodate cross-strike and cross-maturity features better than other models do. For example, skewness and kurtosis in the Heston and Nandi (2000) model are determined (and hence constrained) by GARCH structural parameters, whereas in the GARCH-NIG models, skewness and kurtosis are treated in a more flexible, time-varying fashion based on non-normal rather than normal innovations. Similarly, the continuous-time SVJ or SVJJ models are limited by their Markovian structure, whereas the GARCH-NIG model is not.

We use weekly S&P 500 index options from January 2012 through to December 2014 for in-sample calibration and data from January 2015 to June 2015 for out-of-sample assessment. When assessing out-of-sample performance, we restrict our reported results to models that explicitly incorporate stochastic volatility. We find that models that incorporate jumps provide excellent fits over very short periods (e.g., 1 day or a couple of days’ observations). But such models perform much worse for long periods relative to models that consider explicit stochastic volatility dynamics. Consequently, we restrict our out-of-sample performance assessment to seven competing models: Heston’s (1993) continuous-time stochastic volatility model, restricted and unrestricted versions of Heston and Nandi’s discrete-time GARCH volatility model with normal innovations (Heston and Nandi 2000), Scott’s (1997) model, Bates’ (1996) model, Christoffersen et al.’s (2006) model, and our novel GARCH-NIG model.

Our proposed ad hoc analytic GARCH-NIG model outperforms many existing models by a variety of criteria across different sample sizes and time periods. This is apparently due to the unique features of our model where we can incorporate evolving with conditional skewness (Eq. 37) and kurtosis (Eq. 38); so, we can incorporate the evolving structural richness of a non-linear GARCH structure. We are thus able to incorporate observed empirical characteristics of the asymmetry of the risk-neutral distribution, volatility clustering, and fat tails.

Two natural extensions lend themselves to further investigation. The first and most obvious is to undertake comparable analyses of other Lévy processes—the Variance-Gamma, CGMY, and so forth—and then to compare the performance of these different processes.³⁵ A second extension, first identified by Bates (2003), is to further investigate and model the extent to which cross-sectional option-pricing patterns could be made quantitatively consistent with the time-series patterns of the underlying asset price. Ideally, the risk-neutral characteristic functions, which are often used to reveal cross-sectional option-pricing patterns, could be used to reveal the time-series properties of the underlying asset as well, and so ensure consistency between the two. Currently, however, this remains a challenge. Part of the problem would appear to be that instantaneous option-price evolution in standard models is not fully captured by underlying asset price movements. Part of the problem might also relate to the fact that the heteroscedasticity of GARCH conflicts with the stationary Markov time-series properties of standard models. Since the GARCH-NIG is free of these limitations, we would speculate that the greater flexibility of the GARCH-NIG may hold the key to achieving this objective.

Appendices

Appendix A

1.1 Moments of NIG Lévy innovation

A NIG (α, β, δ) is infinitely divisible and the associated Lévy process has the distribution of increments over [s, t + s] characterized by a NIG (α, β, δt). Schouten (2003) shows that the first four moments of the X ~ NIG (α, β, δ) random variable are:

$$E\left[ X \right] = \frac{\delta \beta }{{\sqrt {\alpha^{2} - \beta^{2} } }}$$

(23)

$$V\left[ X \right] = \alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}}$$

(24)

$$Skew\left[ X \right] = 3\beta \alpha^{ - 1} \delta^{{ - \frac{1}{2}}} \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{1}{4}}}$$

(25)

$$Kurt\left[ X \right] = 3\left( {1 + \frac{{\alpha^{2} + 4\beta^{2} }}{{\delta \alpha^{2} \sqrt {\alpha^{2} - \beta^{2} } }}} \right)$$

(26)

With the moments of the NIG random variable as in (23–26), the first two conditional moments of the log-returns become:

$$\begin{aligned} E\left[ {X_{t} |\Im_{t - 1} } \right] = & E\left[ {r + \lambda \sigma_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}|\Im_{t - 1} } \right] \\ = & r + \lambda \sigma_{t} - \frac{{\frac{{\delta \sigma_{t} \beta }}{{\sqrt {\alpha^{2} - \beta^{2} } }}}}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} \\ = & r + \left( {\lambda - \frac{\beta \sqrt \delta }{{\alpha \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{1}{4}}} }}} \right)\sigma_{t} \\ \end{aligned}$$

(27)

$$\begin{aligned} V\left[ {X_{t} |\Im_{t - 1} } \right] = & V\left[ {r + \lambda \sigma_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}|\Im_{t - 1} } \right] \\ = & \frac{{\alpha^{2} \delta \sigma_{t} \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} }}{{\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} }} \\ = & \sigma \\ \end{aligned}$$

(28)

Thus the dynamics of X_t is a scaled and shifted version of $z_{t} |\Im_{t - 1} \sim NIG\left( {\alpha ,\beta ,\delta \sigma_{t} } \right)$. The conditional skewness and kurtosis are:

$$\begin{gathered} Skew\left[ {X_{t + 1} |\Im_{t - 1} } \right] = 3\beta \alpha^{ - 1} \left( {\delta \sigma_{t} } \right)^{{ - \frac{1}{2}}} \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{1}{4}}} \hfill \\ \, \hfill \\ \end{gathered}$$

(29)

$$\begin{gathered} Kurt\left[ {X_{t + 1} |\Im_{t - 1} } \right] = 3\left( {1 + \frac{{\alpha^{2} + 4\beta^{2} }}{{\delta \sigma_{t} \alpha^{2} \sqrt {\left( {\alpha^{2} - \beta^{2} } \right)} }}} \right) \hfill \\ \, \hfill \\ \end{gathered}$$

(30)

The existence of conditional skewness and conditional kurtosis ensures that smile-skew patterns can be modeled when log-return dynamics follow a GARCH with NIG-Lévy innovations.

Appendix B

2.1 GARCH with NIG Lévy innovation and equivalent martingale measure

We select an Equivalent Martingale Measure (EMM) that depends on finding a solution to the conditional Esscher equation (Gerber et al. 1994; Shiu et al. 2004)

$$\frac{{M_{{X_{t} |\Im_{t - 1} }} \left( {\hat{\theta }_{t} + 1} \right)}}{{M_{{X_{t} |\Im_{t - 1} }} \left( {\hat{\theta }_{t} } \right)}} = e^{{r_{t} }}$$

(31)

where $M_{{X_{t} |\Im_{t - 1} }} \left( s \right)$ is the conditional moment-generating function (MGF) defined as

$$M_{{X_{t} |\Im_{t - 1} }} \left( s \right) = E\left[ {e^{{sX_{t} }} |\Im_{t - 1} } \right]$$

(32)

In the case of GARCH dynamics with NIG-Lévy innovations (7), the conditional Esscher Eq. (31) becomes

$$\begin{aligned} & \frac{{E_{t - 1} \left[ {e^{{\left( {\hat{\theta }_{t} + 1} \right)\left( {r + \lambda \sigma_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)}} } \right]}}{{E_{t - 1} \left[ {e^{{\hat{\theta }_{t} \left( {r + \lambda \sigma_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)}} } \right]}} = e^{{r_{t} }} \\ & \Rightarrow \frac{{E_{t - 1} \left[ {e^{{ - \left( {\hat{\theta }_{t} + 1} \right)\left( {\frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)}} } \right]}}{{E_{t - 1} \left[ {e^{{ - \hat{\theta }_{t} \left( {\frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}} \right)}} } \right]}} = e^{{ - \lambda \sigma_{t} }} , \\ \end{aligned}$$

(33)

which simplifies to (34) using the constant, $c = \frac{ - 1}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}$:

$$\frac{{E_{t - 1} \left[ {e^{{\left( {\hat{\theta }_{t} + 1} \right)z_{t} c}} } \right]}}{{E_{t - 1} \left[ {e^{{\hat{\theta }_{t} z_{t} c}} } \right]}} = e^{{ - \lambda \sigma_{t} }}$$

(34)

Inserting Eq. (2) into (34) we obtain:

$$\begin{aligned} e^{{ - \lambda \sigma_{t} }} = & \frac{{\exp \left( { - \delta \left\{ {\sqrt {\alpha^{2} - \left( {\beta + \left( {\hat{\theta }_{t} + 1} \right)c} \right)^{2} } - \sqrt {\left( {\alpha^{2} - \beta^{2} } \right)} } \right\}} \right)}}{{\exp \left( { - \delta \left\{ {\sqrt {\alpha^{2} - \left( {\beta + \hat{\theta }_{t} c} \right)^{2} } - \sqrt {\left( {\alpha^{2} - \beta^{2} } \right)} } \right\}} \right)}} \\ = & \exp \left( { - \delta \left\{ {\sqrt {\alpha^{2} - \left( {\beta + \left( {\hat{\theta }_{t} + 1} \right)c} \right)^{2} } - \sqrt {\alpha^{2} - \left( {\beta + \hat{\theta }_{t} c} \right)^{2} } } \right\}} \right) \\ \end{aligned}$$

(35)

Given the parameters of the NIG-Lévy process, α, β, δ and the GARCH volatility process $\sigma_{t}$ in Eq. (8), the solution $\hat{\theta }_{t}$ of (35) can be used to describe the distribution of log-returns as

$$\tilde{M}_{{X_{s} |\Im_{s - 1} }} \left( l \right) = \frac{{M_{{X_{s} |\Im_{s - 1} }} \left( {l + \hat{\theta }_{t} } \right)}}{{M_{{X_{s} |\Im_{s - 1} }} \left( {\hat{\theta }_{t} } \right)}}$$

(36)

Given our assumed distribution for innovations and the fact that the GARCH one-period-ahead volatility is known, (36) becomes

$$\begin{aligned} \tilde{M}_{{X_{s} |\Im_{s - 1} }} \left( l \right) = & \frac{{E_{t - 1} \left[ {e^{{\left( {\hat{\theta }_{t} + l} \right)\left( {r + \lambda \sigma_{t} + z_{t} c} \right)}} } \right]}}{{E_{t - 1} \left[ {e^{{\hat{\theta }_{t} \left( {r + \lambda \sigma_{t} + z_{t} c} \right)}} } \right]}};z_{t} |\Im_{t - 1} \sim NIG\left( {\alpha ,\beta ,\delta \sigma_{t} } \right) \\ = & \frac{{e^{{l\left( {r + \lambda \sigma_{t} } \right)}} E_{t - 1} \left[ {e^{{\left( {\hat{\theta }_{t} + l} \right)cz_{t} }} } \right]}}{{E_{t - 1} \left[ {e^{{\hat{\theta }_{t} cz_{t} }} } \right]}} \\ \mathop = \limits^{ \, } & e^{{l\left( {r + \lambda \sigma_{t} } \right)}} \exp \left( { - \delta \left\{ {\sqrt {\alpha^{2} - \left( {\beta + \left( {\hat{\theta }_{t} + l} \right)c} \right)^{2} } - \sqrt {\alpha^{2} - \left( {\beta + \hat{\theta }_{t} c} \right)^{2} } } \right\}} \right) \\ = & e^{{l\left( {r + \lambda \sigma_{t} } \right)}} \exp \left( { - \delta \left\{ {\sqrt {\alpha^{2} - \left( {\beta + \hat{\theta }_{t} c + lc} \right)^{2} } - \sqrt {\alpha^{2} - \left( {\beta + \hat{\theta }_{t} c} \right)^{2} } } \right\}} \right) \\ \end{aligned}$$

(37)

Comparing Eqs. (2) and (37), we recognize that under-EMM innovations are NIG-distributed with a new characterization, $\beta^{\prime} = \beta + \hat{\theta }_{t} c$.

We also need to see what other parameters are influenced by this new characterization. We start with the dynamics of the volatility under the martingale measure:

$$\begin{aligned} \sigma^{\prime}_{t} = \tilde{V}\left[ {X_{t} |\Im_{t - 1} } \right] = & \tilde{V}\left[ {r + \lambda \sigma_{t} - \frac{{z_{t} }}{{2\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}|\Im_{t - 1} } \right] \\ = & \frac{{\alpha^{2} \delta \sigma_{t} \left( {\alpha^{2} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} }}{{\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} }} \\ = & \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \sigma_{t} \\ \end{aligned}$$

(38)

Thus, the market and real measures are related through the characterization $\beta^{\prime} = \beta + \hat{\theta }_{t} c$, and the market and real volatility processes are related through $\sigma^{\prime}_{t} = \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \sigma_{t} .$

We next identify the remaining parameters that require new characterization to keep the return dynamics equivalent. Under the real measure we have

$$\begin{aligned} & X_{t} = r + \lambda \sigma_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} \\ & \Rightarrow X_{t} = r + \lambda \left[ {\frac{{\alpha^{2} - \beta^{2} }}{{\alpha^{2} - \beta^{{\prime}{2}} }}} \right]^{{ - \frac{3}{2}}} \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \sigma_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} \\ & \Rightarrow X_{t} = r + \lambda \left[ {\frac{{\alpha^{2} - \beta^{2} }}{{\alpha^{2} - \beta^{{\prime}{2}} }}} \right]^{{ - \frac{3}{2}}} \sigma^{\prime}_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} \\ & \Rightarrow X_{t} = r + \lambda^{\prime}\sigma^{\prime}_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} \\ & {\text{where}}\,\,\,\, \, \lambda^{\prime} = \lambda \left[ {\frac{{\alpha^{2} - \beta^{2} }}{{\alpha^{2} - \beta^{{\prime}{2}} }}} \right]^{{ - \frac{3}{2}}} \\ \end{aligned}$$

(39)

hence we introduce $\alpha^{\prime},\beta^{\prime},\delta^{\prime}$, replacing $\alpha ,\beta ,\delta$ for the dynamics to be characterized by a martingale measure. We can achieve this from the following:

$$\begin{aligned} \alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} = & \alpha^{2} \delta \left[ {\frac{{\beta^{2} }}{{\beta^{{\prime}{2}} }}} \right]^{{ - \frac{3}{2}}} \left( {\frac{{\beta^{2} }}{{\beta^{{\prime}{2}} }}\alpha^{2} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} \\ = & \left( {\alpha^{2} \frac{{\beta^{2} }}{{\beta^{{\prime}{2}} }}} \right)\left( {\delta \frac{{\beta^{\prime}}}{\beta }} \right)\left( {\frac{{\beta^{2} }}{{\beta^{{\prime}{2}} }}\alpha^{2} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} \\ = & \alpha^{{\prime}{2}} \delta^{\prime}\left( {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} \\ \end{aligned}$$

(40)

$${\text{where}}\,\,\,\alpha^{\prime} = \alpha \frac{{\beta^{\prime}}}{\beta }\,\,\,\,\,{\text{and}}\,\,\,\,\,\delta^{\prime} = \delta \frac{{\beta^{\prime}}}{\beta }$$

We now have the equivalent dynamics for log-returns under the martingale measure

$$X_{t} = r + \lambda^{\prime}\sigma^{\prime}_{t} - \frac{{z_{t} }}{{\sqrt {\alpha^{{\prime}{2}} \delta^{\prime}\left( {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} } }}\,\,\,{\text{with}}\,\,\,\,z_{t} |\Im_{t - 1} \sim NIG\left( {\alpha^{\prime},\beta^{\prime},\delta^{\prime}\sigma^{\prime}_{t} } \right)$$

(41)

where the parameters of the equivalence-maintaining martingale dynamics are related to those of the market dynamics through

$$\sigma^{\prime}_{t} \, = \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \sigma_{t}$$

(42)

$$\beta^{\prime} = \beta + \hat{\theta }_{t} c$$

(43)

$$\alpha^{\prime} = \alpha \frac{{\beta^{\prime}}}{\beta } \,$$

(44)

$$\delta^{\prime} = \delta \frac{{\beta^{\prime}}}{\beta }$$

(45)

As a last step, we need to work out the corresponding changes in the GARCH parameters. The GARCH dynamics are

$$\begin{aligned} & \, \sigma_{t} = \beta_{0} + \beta_{1} \frac{{z_{t} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} + \alpha_{1} \sigma_{t - 1} \\ & \Rightarrow \sigma_{t} \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} = \beta_{0} \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} + \beta_{1} \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \frac{{z_{t + 1} }}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }} + \alpha_{1} \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \sigma_{t - 1} \\ \end{aligned}$$

(46)

Thus, the equivalent GARCH volatility dynamics under the martingale measure can be written as

$$\sigma^{\prime}_{t} = \beta^{\prime}_{0} + \beta^{\prime}_{1} \frac{{z_{t} }}{{\sqrt {\alpha^{{\prime}{2}} \delta^{\prime}\left( {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} } }} + \alpha_{1} \sigma^{\prime}_{t - 1} \,\,\,{\text{with }}\,\,\,z_{t} |\Im_{t - 1} \sim NIG\left( {\alpha^{\prime},\beta^{\prime},\delta^{\prime}\sigma^{\prime}_{t} } \right),$$

(47)

where

$$\beta^{\prime}_{0} = \beta_{0} \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}}$$

(48)

$$\beta^{\prime}_{1} = \beta_{1} \left[ {\frac{{\alpha^{2} - \beta^{{\prime}{2}} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}}$$

(49)

We now need the corresponding risk-neutral characterization to be used for option pricing. First, note that with the scaling factor $u = - \frac{1}{{\sqrt {\alpha^{2} \delta \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} } }}$ Eq. (7) becomes:

$$X_{t} = r + \lambda \sigma_{t} + uz_{t}$$

(50)

The MGF under the risk-neutral measure can then be obtained from the following expression for the NIG characteristic function:

$$\begin{aligned} E_{t}^{Q} \left( {e^{{uz_{t + 1} }} } \right) = E_{t}^{Q} \left( {e^{{i\left( { - iu} \right)z_{t + 1} }} } \right) = & \exp \left\{ { - \delta^{\prime}\sigma^{\prime}_{t + 1} \left\{ {\sqrt {\alpha^{{\prime}{2}} - \left( {\beta^{\prime} + i\left( {iu} \right)} \right)^{2} } - \sqrt {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } } \right\}} \right\} \\ = & \exp \left\{ { - \delta^{\prime}\sigma^{\prime}_{t + 1} \left\{ {\sqrt {\alpha^{{\prime}{2}} - \left( {\beta^{\prime} + u^{2} } \right)^{2} } - \sqrt {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } } \right\}} \right\} \\ \end{aligned}$$

(51)

Hence:

$$\begin{aligned} E_{t}^{Q} \left( {e^{{X_{t + 1} }} } \right) = & e^{{\left( {r + \lambda^{\prime}\sigma^{\prime}_{t + 1} } \right)}} \exp \left\{ { - \delta^{\prime}\sigma^{\prime}_{t + 1} \left\{ {\sqrt {\alpha^{{\prime}{2}} - \left( {\beta^{\prime} + u} \right)^{2} } - \sqrt {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } } \right\}} \right\} \\ = & e^{{\left( {r + \lambda^{\prime}\sigma^{\prime}_{t + 1} } \right)}} \exp \left\{ { - \delta^{\prime}\sigma^{\prime}_{t + 1} \left\{ {\sqrt {\alpha^{{\prime}{2}} - \left( {\beta^{\prime} - \frac{1}{{\sqrt {\alpha^{{\prime}{2}} \delta^{\prime}\left( {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} } }}} \right)}^{2} - \sqrt {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } } \right\}} \right\} \\ \end{aligned}$$

(52)

We want to choose $\lambda^{\prime}$ under Q in terms of other risk-neutral parameters such that

$$\begin{aligned} & E_{t}^{Q} \left( {e^{{X_{t + 1} }} } \right) = e^{{\left( {t + 1 - t} \right)r}} \\ & \Rightarrow e^{{\left( {r + \lambda^{\prime}\sigma^{\prime}_{t + 1} } \right)}} \exp \left\{ { - \delta^{\prime}\sigma^{\prime}_{t + 1} \left\{ {\sqrt {\alpha^{{\prime}{2}} - \left( {\beta^{\prime} - \frac{1}{{\sqrt {\alpha^{{\prime}{2}} \delta^{\prime}\left( {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} } }}} \right)^{2} } - \sqrt {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } } \right\}} \right\} = e^{r} \\ & = e^{r} \exp \left\{ {\sigma^{\prime}_{t + 1} \left( {\lambda^{\prime} - \delta^{\prime}\left\{ {\sqrt {\alpha^{{\prime}{2}} - \left( {\beta^{\prime} - \frac{1}{{\sqrt {\alpha^{{\prime}{2}} \delta^{\prime}\left( {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} } }}} \right)^{2} } - \sqrt {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } } \right\}} \right)} \right\} = e^{r} \\ \end{aligned}$$

(53)

Since $\sigma^{\prime}_{t + 1} \ne 0$,

$$\lambda^{\prime} = \delta^{\prime}\left\{ {\sqrt {\alpha^{{\prime}{2}} - \left( {\beta^{\prime} - \frac{1}{{\sqrt {\alpha^{{\prime}{2}} \delta^{\prime}\left( {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } \right)^{{ - \frac{3}{2}}} } }}} \right)^{2} } - \sqrt {\alpha^{{\prime}{2}} - \beta^{{\prime}{2}} } } \right\}$$

(54)

The above equation is the final characterization that we use in the MGF expression, which, in turn, is used in our pricing and calibration.

Appendix C

3.1 Relationship between parameters under the risk-neutral and historical risk measures

$$\sigma_{t} = \beta_{0} + \beta_{1} \left[ {\frac{{NIG(\alpha ,\,\beta ,\,\delta \sigma_{t - 1} )}}{{\sqrt {\alpha^{2} \sigma_{t - 1} \delta \left( {\alpha^{2} - \beta^{2} } \right)}^{{ - \frac{3}{2}}} }} - \gamma \sqrt {\sigma_{t - 1} } } \right]^{2} + \alpha_{1} \sigma_{t - 1}$$

As in Eq. (46) we multiply both sides of the above equation by $\left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}}$:

$$\begin{aligned} \sigma_{t} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} = & \,\beta_{0} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} + \beta_{1} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \left[ {\frac{{NIG(\alpha ,\beta ,\delta \sigma_{t - 1} )}}{{\sqrt {\alpha^{2} \sigma_{t - 1} } \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} }} - \gamma \sqrt {\sigma_{t - 1} } } \right]^{2} \\ & + \,\alpha_{1} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \sigma_{t - 1} \\ \end{aligned}$$

$$\begin{aligned} = & \,\beta_{0} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \\ & + \beta_{1} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \left[ {\frac{{NIG(\alpha ,\beta ,\delta \sigma_{t - 1} )}}{{\sqrt {\alpha^{2} \sigma_{t - 1} } \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} }}\frac{{\left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{4}}} }}{{\sqrt {\left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \sigma_{t - 1} } }} - \frac{\gamma }{{\left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{4}}} }}\sqrt {\left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \sigma_{t - 1} } } \right]^{2} \\ & + \,\alpha_{1} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \sigma_{t - 1} \\ \end{aligned}$$

Using Eq. (42):

$$\begin{aligned} \sigma_{t}^{\prime } = & \,\beta_{0} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \\ & + \beta_{1} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} \left[ {\frac{{NIG(\alpha^{\prime } ,\beta^{\prime } ,\delta^{\prime } \sigma^{\prime }_{t - 1} )}}{{\sqrt {\alpha^{2} \sigma_{t - 1} } \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \frac{3}{2}}} \sigma^{\prime }_{t - 1} }} - \frac{\gamma }{{\left\{ {\left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{4}}} } \right\}^{2} }}\sqrt {\sigma^{\prime }_{t - 1} } } \right]^{2} + \alpha_{1} \sigma^{ \prime }_{t - 1} \\ \end{aligned}$$

Using Eq.(40):

$$\sigma_{t}^{\prime } = \,\beta_{0} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} + \beta_{1} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{ - 3} \left[ {\frac{{NIG(\alpha^{\prime } ,\beta^{\prime } ,\delta^{\prime } \sigma^{\prime }_{t - 1} )}}{{\sqrt {\alpha^{\prime 2} \delta^{\prime } \left( {\alpha^{\prime 2} - \beta^{\prime 2} } \right)^{{ - \frac{3}{2}}} \sigma^{\prime }_{t - 1} } }} - \frac{\gamma }{{\left\{ {\left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{4}}} } \right\}^{2} }}\sqrt {\sigma^{\prime }_{t - 1} } } \right]^{2} + \alpha_{1} \sigma^{ \prime }_{t - 1}$$

This can be written as

$$\sigma_{t}^{\prime } = \,\beta^{\prime }_{0} + \beta^{\prime }_{1} \left[ {\frac{{NIG(\alpha^{\prime } ,\beta^{\prime } ,\delta^{\prime } \sigma^{\prime }_{t} )}}{{\sqrt {\alpha^{\prime 2} \delta^{\prime } \sigma^{\prime }_{t - 1} \left( {\alpha^{\prime 2} - \beta^{\prime 2} } \right)^{{ - \frac{3}{2}}} } }} - \gamma^{\prime } \sqrt {\sigma^{\prime }_{t - 1} } } \right]^{2} + \alpha_{1} \sigma^{\prime }_{t - 1}$$

where

$$\beta^{\prime }_{0} = \beta_{0} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{2}}} ,\,\,\,\beta_{1}^{\prime } = \beta_{1} \left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{ - 3} \,\,\,{\text{and}}\,\,\,\gamma^{\prime } = \frac{\gamma }{{\left\{ {\left[ {\frac{{\alpha^{2} - \beta^{\prime 2} }}{{\alpha^{2} - \beta^{2} }}} \right]^{{ - \frac{3}{4}}} } \right\}^{2} }}$$

Thus, by modifying the volatility dynamics (introducing nonlinearity) the relationships between some parameters under historical and risk-neutral measures also change—in particular, the GARCH parameter $\beta_{1}$ (historical) and $\beta_{1}^{\prime }$ (risk-neutral) are not related as shown in (B19) in the paper but as shown above. Moreover, the new parameter $\gamma$ (historical) in the modified volatility dynamics becomes $\gamma^{\prime }$ (risk-neutral), as shown above.

Appendix D

See Fig. 1.

Fig. 1

Effects of approximating GARCH-NIG, Eqs. (13), by (14). The approximation has apparently little effect on ultimate return distribution, but it allows us to obtain an analytic formula for pricing European options under GARCH-NIG dynamics with non-linear volatility. We use the parameters from Table 5 to conduct this simulation study. KS stands for kernel smooth