Risk-adjusted option-implied moments

Abstract

This paper provides a new way of converting risk-neutral moments into the corresponding physical moments, which are required for many applications. The main theoretical result is a new analytical representation of the expected payoffs of put and call options under the physical measure in terms of current option prices and a representative investor’s preferences. This representation is then used to derive analytical expressions for a variety of ex-ante physical return moments, showing explicitly how moment premiums depend on current option prices and preferences. As an empirical application of our theoretical results, we provide option-implied estimates of the representative stock market investor’s disappointment aversion using S&P 500 index option prices. We find that disappointment aversion has a procyclical pattern. It is high in times of high index levels and declines when the index falls. We confirm the view that investors with high risk aversion and disappointment aversion leave the stock market during times of turbulence and reenter it after a period of high returns.

1 Introduction

The use of option prices to gain information about the underlying asset’s return distribution is an important idea in finance. Certainly, the most prominent example is implied volatility, which goes back to Latané and Rendleman (1976). More recent developments have moved forward from simple Black–Scholes volatilities to model-free implied volatilities (Britten-Jones and Neuberger 2000; Jiang and Tian 2005) and higher-order implied moments (Bakshi et al. 2003; Neuberger 2012). Implied moments are used extensively in a variety of applications, such as forecasting [see the survey articles by Poon and Granger (2003), Christoffersen et al. (2012), and Giamouridis and Skiadopoulos (2012)], risk measurement (Buss and Vilkov 2012; Chang et al. 2012; Baule et al. 2016; Hollstein and Prokopczup 2016), portfolio selection (Aït-Sahalia and Brandt 2008; Kostakis et al. 2011; DeMiguel et al. 2013; Kempf et al. 2015; Schneider 2015), asset pricing (Conrad et al. 2013; An et al. 2014), and the study of financial market integration (Siriopoulos and Fassas 2013).

Option-implied moments have the drawback that they are formed under the risk-neutral probability measure, whereas many applications require moments under the physical (real-world, actual, subjective) probability measure. Ideally, one would exploit all information contained in current option prices and obtain a simple but economically sound method to adjust for risk, that is, to move from the risk-neutral moment to the corresponding physical moment. This paper provides such a method by showing explicitly how the risk adjustment depends on current option prices and risk preferences.

The main theoretical result of our paper states how the expected payoffs of call and put options under the physical measure depend on current option prices and the utility function of a representative investor. This result has many potential uses. One specific use is to express the underlying’s ex ante return moments under the physical measure, which we call risk-adjusted implied moments, in terms of observed option prices and preferences. The presented methodology is very general. It applies to implied moments as in Neuberger (2012), implied moments as in Bakshi et al. (2003), which refer to log returns, and to the corresponding moments of discrete returns. It can deal with both central and non-central moments and is not restricted to a specific utility function.

As an empirical application, we use the presented methodology to study the model of a representative investor with disappointment aversion, as introduced by Gul (1991). We show that disappointment aversion has a strong effect on the expected returns of out-of-the-money call options on the Standard & Poor’s (S&P) 500 index, but almost no effect on the returns of out-of-the money put options. A further analysis shows that the disappointment model leads to a negative ex ante variance risk premium and a positive skewness risk premium for reasonable preference parameters. Finally, we estimate the implied relative risk aversion and disappointment aversion of the representative stock market investor from cross-sections of S&P 500 index option prices. Our results show that disappointment aversion has a strong time variation and is economically significant in specific periods. We find a procyclical pattern: Disappointment is high in times of high index levels and declines when the index falls. Our findings confirm the view that investors with high risk aversion and high disappointment aversion leave the stock market during times of turbulence and reenter it after a period of high returns.

The major advantage of our approach is the availability of exact analytical expressions for risk-adjusted implied moments which facilitate the economic understanding and allow for numerically stable moment calculations. Our approach shares this advantage with model-free (risk-neutral) implied moments developed by Britten-Jones and Neuberger (2000), Bakshi et al. (2003), and Neuberger (2012), which are very popular in both research and practice.¹ An alternative approach to adjusted implied moments for risk is to transform the full risk-neutral density into a physical density under certain preference assumptions. Such an approach, as followed by Rubinstein (1994), Bliss and Panigirtzoglou (2004), and Kostakis et al. (2011),² adjusts all moments simultaneously. However, it does not provide analytical expressions for the resulting risk-adjusted moments.

Explicit theoretical results on the relation between risk-neutral and ex ante physical moments are rare. One major exception is a theorem by Bakshi et al. (2003) showing that risk-neutral skewness can be approximated by variance, skewness, and kurtosis under the physical probability measure and the preferences of a representative investor.³ Bakshi and Madan (2006) provide a similar approximation of the risk-neutral variance.⁴ In our approach, however, we reverse the direction and describe physical moments in terms of current option prices and preferences. Moreover, our results supply an exact characterization for all moments of the return distribution.

On the empirical side, our paper is related to studies on variance and skewness risk premiums. It is a stylized fact that the realized variance risk premium is (on average) negative for stock indexes (Coval and Shumway 2001; Bakshi and Kapadia 2003; Carr and Wu 2009). Kozhan et al. (2013) and Sasaki (2016) document a corresponding positive skewness risk premium. Our work contributes to this literature by investigating a representative investor model with disappointment aversion together with the market expectations contained in option prices. As our empirical results based on S&P 500 options show, the disappointment model leads to a negative average ex ante variance risk premium and a positive average ex ante skewness risk premium for reasonable preference parameters over the period from 1996 to 2011.

Finally, our paper is related to studies on implied estimators of preference parameters. Jackwerth (2000) and Bliss and Panigirtzoglou (2004) exploit information from option prices to imply the relative risk aversion of the representative stock market investor. We use preferences with disappointment aversion and simultaneously estimate implied risk aversion and disappointment aversion.

The remainder of the paper is organized as follows. Section 2 presents our main theoretical result, which links expected payoffs of call and put options to option prices and preferences. This result is applied in Sect. 3 to derive risk-adjusted implied moments. The following Sect. 4 presents our data set and explains how moments are computed. Section 5 provides illustrations of the effect of risk aversion and disappointment aversion on expected options payoffs and return moments. Section 6 presents our implied estimates of relative risk aversion and disappointment aversion. Section 7 concludes the paper.

2 Expected payoffs under the physical measure

Our analysis exploits the relation between physical and risk-neutral densities, as outlined, for example, by Aït-Sahalia and Lo (2000). Consider a risky market portfolio with current price $S_{t}$, traded on a frictionless, complete market, and a risk-free asset with constant interest rate r. A representative investor exists and assigns utility $U(S_{t+\tau })$ to the future payoff $S_{t+\tau }$, $\tau >0$, according to a utility function U. In such a setting, the relation between the physical density function, $p(S_{t+\tau })$, and the risk-neutral density function, $q(S_{t+\tau })$, is⁵

$$\begin{aligned} p(S_{t+\tau }) \; = \; \frac{q(S_{t+\tau })}{c \cdot U'(S_{t+\tau })}, \qquad \text {with } \quad c \;\equiv \; \int \frac{q(x)}{U'(x)}dx. \end{aligned}$$

(1)

Equation (1) shows how the physical density can be obtained from knowledge of the risk-neutral density and the utility function of the representative investor. Note, however, that $S_{t+\tau }$ refers to the whole market and not to any individual asset traded on the market.

Our goal is now to establish a similar link between expected payoffs of contingent claims under the physical measure, expected (discounted) options payoffs under the risk-neutral measure (i.e., option prices), and the utility function. Denote the expected discounted payoff of a call option (put option) with strike price K and time to maturity $\tau$ under the physical measure as

$$\begin{aligned} C^P(t,\tau ,K)&\equiv \; E^P \left[ e^{-r\tau } (S_{t+\tau } -K)^+ \right] , \end{aligned}$$

(2)

$$\begin{aligned} P^P(t,\tau ,K)&\equiv \; E^P \left[ e^{-r\tau } (K -S_{t+\tau })^+ \right] . \end{aligned}$$

(3)

The following proposition shows how $C^P(t,\tau ,K)$ and $P^P(t,\tau ,K)$ can be expressed in terms of current options prices and the utility function.⁶ The proof is provided in the Appendix.

Proposition 1

If the relation between physical and risk-neutral density is as in Eq. (1) and the utility function of the representative investor is twice continuously differentiable with $U'>0$ and $U''<0$, then

$$\begin{aligned} C^P(t,\tau ,K)= & {} \frac{C(t,\tau ,K)}{c \cdot U'(K)} \nonumber \\&+ \int \limits _{K}^{\infty } \frac{-U''(x)}{c \cdot U'(x)^2} \left\{ C(t,\tau ,x) + (x-K) D(t,\tau ,x) \right\} dx, \end{aligned}$$

(4)

$$\begin{aligned} P^P(t,\tau ,K)= & {} \frac{P(t,\tau ,K)}{c \cdot U'(K)} \nonumber \\&- \int \limits _{0}^{K} \frac{-U''(x)}{c \cdot U'(x)^2} \left\{ P(t,\tau ,x)+ (K-x)(e^{-r\tau }-D(t,\tau ,x)) \right\} dx,\qquad \end{aligned}$$

(5)

$$\begin{aligned} with \,\,\,\,c \; = \; \int \limits _{0}^{\infty } \frac{-U''(x)}{U'(x)^2} e^{r\tau }D(t,\tau ,x)dx + \frac{1}{U'(0)}, \end{aligned}$$

where $C(t,\tau ,K)$ and $P(t,\tau ,K)$ are the prices of call and put options, respectively, with strike price K and time to maturity $\tau$, and $D(t,\tau , K)$ denotes the price of a digital option that pays one dollar if $S_{t+\tau }$ is above the strike price K.

The result in Proposition 1 is remarkable for several reasons. First, the expected (discounted) payoffs of both call and put options under the physical measure are expressed in terms of current prices of calls, puts, and digital options, the risk-free interest rate, and the utility function only. Knowledge of the full risk-neutral density is not required, which avoids numerical problems (see Bliss and Panigirtzoglou (2002) for a discussion of these issues, particularly the need for the second derivatives of option prices with respect to the strike price). Instead, the expressions in Eqs. (4) and (5) can be obtained via stable numerical integration.

Second, the proposition shows a simple way to study the effects of risk aversion on the expected returns of call and put options. If the utility function is linear, i.e., there is no risk aversion, Eqs. (4) and (5) confirm that $C^P(t,\tau ,K) = C(t,\tau ,K)$ and $P^P(t,\tau ,K) = P(t,\tau ,K)$. With growing risk aversion, however, the integrals on the right-hand sides of Eqs. (4) and (5) gain importance. Since these integrals are always positive, it follows that risk aversion leads to $C^P(t,\tau ,K) > C(t,\tau ,K)$ and $P^P(t,\tau ,K) < P(t,\tau ,K)$, which is very intuitive. Because the payoff of a call option is positively related to the payoff of the underlying asset (the market), a higher risk aversion of the representative investor is associated with higher expected payoffs of calls. Since the current market prices of options are given, higher risk aversion is also associated with higher expected call returns. In contrast, for put options, payoffs are negatively related to the payoff of the underlying asset, and a higher risk aversion reduces the required expected returns. Finally, Proposition 1 can be used to express the expected payoffs of more general contingent claims in terms of option prices and the utility function of the representative investor, as stated in the following proposition.

Proposition 2

Let $H(S_{t+\tau })$ be a twice continuously differentiable function of the price $S_{t+\tau }$, which represents the payoff function of a contingent claim maturing at time $t+\tau$. Then the time t expected payoff $E^P\left[ H(S_{t+\tau })\right]$ of the contingent claim under the physical measure equals

$$\begin{aligned} E^P\left[ H(S_{t+\tau })\right]&= H(S_t) + H'(S_t)e^{r \tau }\left[ C^P(t,\tau ,S_t) - P^P(t,\tau ,S_t) \right] \nonumber \\&\quad + e^{r \tau }\int \limits _{S_t}^{\infty } H''(K)C^P(t,\tau ,K)dK \nonumber \\&\quad + e^{r \tau }\int \limits _{0}^{S_t} H''(K)P^P(t,\tau ,K)dK, \end{aligned}$$

(6)

with $C^P(t,\tau ,K)$ and $P^P(t,\tau ,K)$ from Proposition 1.

To prove Proposition 2, we exploit the spanning argument of Bakshi and Madan (2000) and Carr and Madan (2001). If H is a twice continuously differentiable function, then $H(S_{t+\tau })$ equals

$$\begin{aligned} H(S_{t+\tau })&= H(S_t) + (S_{t+\tau }-S_t)H'(S_t) \nonumber \\&\quad + \int \limits _{S_t}^{\infty } H''(K)(S_{t+\tau }-K)^+dK\nonumber \\&\quad + \int \limits _{0}^{S_t} H''(K)(K-S_{t+\tau })^+dK. \end{aligned}$$

(7)

Now we take expectations under the physical measure P on both sides of Eq. (7) and apply Fubini’s theorem to obtain

$$\begin{aligned} E^P\left[ H(S_{t+\tau })\right]&= H(S_t) + H'(S_t) E^P\left[ (S_{t+\tau }-S_t) \right] \nonumber \\&\quad + e^{r \tau }\int \limits _{S_t}^{\infty } H''(K)C^P(t,\tau ,K)dK \nonumber \\&\quad + e^{r \tau }\int \limits _{0}^{S_t} H''(K)P^P(t,\tau ,K)dK. \end{aligned}$$

(8)

Finally, note that $S_{t+\tau } - S_t = (S_{t+\tau }-S_t)^+ - (S_t-S_{t+\tau })^+$. Taking expectations yields $E^P\left[ S_{t+\tau } - S_t\right] = e^{r \tau }\left[ C^P(t,\tau ,S_t) - P^P(t,\tau ,S_t) \right]$. $\square$

Proposition 2 delivers the expected payoff of a contingent claim written on $S_{t+\tau }$ as a function of the current price $S_t$ of the underlying asset, current option prices, and the utility function of the representative investor. Since the same reasoning that led to Eq. (6) applies under the risk-neutral measure (Bakshi et al. 2003), we obtain the following ex ante risk premium of the contingent claim:

$$\begin{aligned} E^P\left[ H(S_{t+\tau })\right] - E^Q\left[ H(S_{t+\tau })\right] \;= & {} H'(S_t)e^{r \tau }\left[ (C^P(t,\tau ,S_t)-C(t,\tau ,S_t)) \right. \nonumber \\&\left. \quad - (P^P(t,\tau ,S_t)-P(t,\tau ,S_t)) \right] \nonumber \\&+\, e^{r \tau }\int \limits _{S_t}^{\infty } H''(K)(C^P(t,\tau ,K)-C(t,\tau ,K))dK \nonumber \\&+ \, e^{r \tau }\int \limits _{0}^{S_t} H''(K)(P^P(t,\tau ,K)-P(t,\tau ,K))dK.\nonumber \\ \end{aligned}$$

(9)

As Eq. (9) shows, there is an explicit formula for the risk premiums of general contingent claims which only requires current (time t) option prices and the preferences of the representative investor. Ex ante risk premiums have many potential applications, such as the performance measurement of portfolio strategies with options. In this paper, however, our goal is to study appropriate risk adjustments and risk premiums for moments of the return distribution.

Table 1 Physical moments as functions of option prices

3 Moments under the physical measure

Different moments of the return distribution result from different choices of the function $H(S_{t+\tau })$. Table 1 shows some important cases. The first column of the table presents the specific choice of the function $H(S_{t+\tau })$. For the calculation of risk-adjusted implied moments, we have to evaluate the function H (and its first and second derivatives) at certain points ($S_t$ and K), as can be seen from Eq. (6). The second column provides the corresponding values of $H(S_t)$, $H'(S_t)$, and $H''(K)$. Finally, the third column presents the resulting risk-adjusted implied moment according to Proposition 2. Such a moment is a model-free implied one in the sense that it exploits information from current options prices without reference to a specific option pricing model. It is model-dependent, however, because of its reliance on the utility function of the representative investor. Risk-adjusted implied moments are moments under the physical measure, a property they share with realized moments. In contrast to realized moments, however, which exploit ex post realized prices, they are ex ante moments. For simplicity, we call them ex ante physical moments or just physical moments.

Panel A of Table 1 considers the variance and skewness measures by Neuberger (2012), who suggests $2E(\frac{S_{t+\tau }}{S_t} - 1 - \ln \frac{S_{t+\tau }}{S_t})$ as a generalized variance and $6 E(2+\ln \frac{S_{t+\tau }}{S_t} -2\frac{S_{t+\tau }}{S_t} +\frac{S_{t+\tau }}{S_t} \ln \frac{S_{t+\tau }}{S_t})$ as an approximation of the third (non-central) moment of log returns. The motivation for these moment measures is their aggregation property. Aggregation guarantees that higher-frequency data can be used to obtain unbiased estimates of the physical moment over the return period.⁷ Panel B considers the higher non-central moments ($k \ge 2$) of log returns. The corresponding risk-neutral model-free implied moments were derived by Bakshi et al. (2003) and are widely applied. For some applications, however, such as portfolio optimization, we require moments of discrete returns instead of log returns. Therefore, Panel C considers discrete returns.⁸

To obtain central moments, we additionally need to express the expected return in terms of vanilla option prices and the utility function. Consider discrete returns first. Since $S_{t+\tau } - S_t = (S_{t+\tau }-S_t)^+ - (S_t-S_{t+\tau })^+$, the expected return equals

$$\begin{aligned} E^P\left[ \frac{S_{t+\tau } - S_t}{S_t}\right]&= E^P\left[ \frac{(S_{t+\tau }-S_t)^+}{S_t}\right] - E^P\left[ \frac{(S_t-S_{t+\tau })^+}{S_t}\right] \nonumber \\&= \frac{e^{r \tau }}{S_t}\left( C^P(t,\tau , S_t) - P^P(t, \tau , S_t)\right) . \end{aligned}$$

(10)

For log returns, apply the spanning argument of Bakshi and Madan (2000) and Carr and Madan (2001) again. With $H(S_{t+\tau }) = \log \frac{S_{t+\tau }}{S_t}$, we obtain $H(S_t) = 0, H'(S_t) = \frac{1}{S_t}$, and $H''(K) = -\frac{1}{K^2}$, leading to⁹

$$\begin{aligned} E^P\left[ \log \frac{S_{t+\tau }}{S_t}\right]&= \frac{e^{r \tau }}{S_t}\left( C^P(t, \tau , S_t) - P^P(t, \tau , S_t)\right) \nonumber \\&\quad - e^{r \tau } \int \limits _{S_t}^{\infty } \frac{1}{K^2} C^P(t, \tau , K)dK \nonumber \\&\quad - e^{r \tau } \int \limits _{0}^{S_t} \frac{1}{K^2} P^P(t, \tau , K)dK. \end{aligned}$$

(11)

The results in Table 1 are useful for different purposes. An immediate application is the prediction of moments, like the variance, for use in risk management or portfolio optimization. Information from current option prices has been shown to be very useful in this respect.¹⁰ However, predictions under the physical measure are ultimately needed. Our results show how to use option-implied information in combination with an assumption about risk preferences to arrive at the required predictions.

Another application concerns the understanding of risk premiums. Because the risk-neutral counterparts of $E^P\left[ H(S_{t+\tau }) \right]$ are readily available (one simply has to replace $C^P$ and $P^P$ by the corresponding call and put prices, respectively), the results in Table 1 allow us to express the ex ante risk premium contained in physical moments in terms of current prices (spot price and option prices) and risk aversion [see Eq. (9)]. A corresponding analysis is provided in Sect. 5. Finally, we can reverse the procedure and use the results in Table 1 to obtain implied estimates of the representative investor’s preferences. Such an empirical application is presented in Sect. 6.

4 Data and moment calculations

The options data set for our empirical analyses consists of European options written on the S&P 500 spot index traded on the Chicago Board Options Exchange (CBOE). The data source is OptionMetrics and the data period covers January 1996 to December 2011. We use the one-month put and call options which mature every month. The matching interest rates and spot prices of the underlying index are also provided by OptionMetrics.

The analyses concentrate on the variance measure $2E(\frac{S_{t+\tau }}{S_t} - 1 - \ln \frac{S_{t+\tau }}{S_t})$ and the skewness measure $6 E(2+\ln \frac{S_{t+\tau }}{S_t} -2\frac{S_{t+\tau }}{S_t} +\frac{S_{t+\tau }}{S_t} \ln \frac{S_{t+\tau }}{S_t})$ of Neuberger (2012). The major advantage of these measures is the availability of realized moments for both variance and skewness¹¹ in addition to the risk-neutral and physical moments.

The computation of risk-neutral and physical moments [according to Table 1 and Eqs. (4) and (5)] follows a standard procedure, as outlined, for example, by Chang et al. (2012). For every month in the data period, we select the first trading day after the expiration day of expiring options contracts at the CBOE. This choice guarantees the existence of options series with times to expiration close to our one-month time horizon. We take the implied Black–Scholes volatilities provided by OptionMetrics of all out-of-the money put and call options and fit a cubic spline to obtain a smooth volatility curve. Outside the available range of strike prices, the volatility curve is assumed to be flat. Then, we select 1,500 equally spaced strike prices on the interval $[1.001, 3\cdot S_t]$. For these 1,500 strike prices, the corresponding implied volatilities are converted back into call and put prices via the Black–Scholes formula. The same volatility curves are used to obtain prices for digital options¹² via the corresponding Black–Scholes type formula.¹³ With these option prices, we calculate the implied moments under the risk-neutral measure and, given a parameterization of the utility function, under the physical measure.

Realized moments are required for the estimation of implied preference parameters in Sect. 6. The computation of realized variance and skewness follows Kozhan et al. (2013). For the return period starting at time t and ending at time $t+\tau$, which is one month in our study, all daily returns within this period are used for the calculations. Let n be the number of days in the return period and $r_{i}$ be the log return of the index on day i. Then the realized variance $rv_{t,t+\tau }$ and the realized skewness $rs_{t,t+\tau }$ are

$$\begin{aligned} rv_{t,t+\tau }= & {} \sum \limits _{i=1}^{n}2(e^{r_{i}} -1 -r_{i}), \end{aligned}$$

(12)

$$\begin{aligned} rs_{t,t+\tau }= & {} \sum \limits _{i=1}^{n}3\delta v^E_{i,t+\tau }(e^{r_{i}} -1)+6(2-2e^{r_{i}} +r_{i}+r_{i}e^{r_{i}}), \end{aligned}$$

(13)

where $\delta v^{E}_{i,t+\tau }$ is the change from day $i-1$ to day i of another volatility measure, called the variance of the entropy contract, which is calculated from the cross section of option prices each day and refers to the period until $t+\tau$.¹⁴ Because skewness is usually reported as a standardized measure, we follow this practice and finally calculate $rskew_{t,t+\tau } = rs_{t,t+\tau }/(rv_{t,t+\tau })^{3/2}$.

5 The impact of investor preferences on expected option payoffs and moments

Propositions 1 and 2 provide a basis for quantifying the impact of investor preferences on expected options payoffs and ex ante physical moments of the underlying’s return distribution. The resulting effects are likely to depend on current market conditions. In our approach, these market conditions are captured by the cross section of current option prices. For an illustration, we consider the market conditions (observed option prices) on January 20, 2004, which is the midpoint of our data sample.

In addition to the state of the options market, we have to specify investor preferences. We consider a representative investor with disappointment aversion, as introduced by Gul (1991). The disappointment model is often implemented as a generalization of CRRA utility. It allows investors to weight losses more heavily than gains, as in prospect theory, and captures both risk aversion and disappointment aversion. The corresponding utility function with disappointment aversion is shown in Eq. (14).¹⁵

$$\begin{aligned} U(W) \; = \; {\left\{ \begin{array}{ll} \frac{W^{1-\gamma }-1}{1-\gamma } \\ \frac{W^{1-\gamma }-1}{1-\gamma } - \left( \frac{1}{A} - 1\right) \left[ \frac{F_{t,t+\tau }^{1-\gamma }-1}{1-\gamma } - \frac{W^{1-\gamma }-1}{1-\gamma } \right] \end{array}\right. } \quad \text {if} \quad \begin{matrix} W > F_{t,t+\tau }, \\ W \le F_{t,t+\tau }, \end{matrix} \end{aligned}$$

(14)

where W denotes terminal wealth. The utility function has two parameters: $\gamma$ is the coefficient of relative risk aversion and $A\le 1$ the coefficient of disappointment aversion. With $A=1$, we obtain CRRA utility. If A is smaller than one, the representative investor weights losses and gains differently and shows disappointment aversion. In addition, the forward price $F_{t,t+\tau }$ enters into the utility function. It serves as the reference point for the definition of losses.¹⁶

Fig. 1

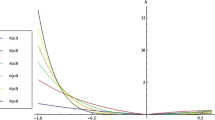
Effects of investor preferences on the expected payoffs of call and put options under the physical measure. a Part A: varying the coefficient of relative risk aversion b Part B: varying the coefficient of disappointment aversion. This figure shows the expected payoffs of at-the-money and out-of-the-money call and put options for different strike prices and different investor preferences. Values are based on the spot and derivatives prices for the S&P 500 index on January 20, 2004, and use the formulas from Eqs. (4) and (5). The forward price on that date was 1138.23. In both parts of the figure, the expected payoffs of calls are presented on the right-hand side (strike prices above forward price) and the expected payoffs of puts are given on the left-hand side (strike prices below forward price). Expected payoffs are calculated under the assumption of a representative investor with utility function according to Eq. (14). The solid line depicts the benchmark case of a risk-neutral representative investor (No Risk-Adjustment). In Part A, the dashed line refers to an investor with relative risk aversion of 2 and the dotted line refers to an investor with relative risk aversion of 4. In both cases, the parameter of disappointment aversion is 1. In Part B, the dashed line refers to an investor with disappointment parameter of 0.85 and the dotted line refers to an investor with disappointment parameter of 0.70. In both cases, the relative risk aversion parameter is 2. Note that for put options the dashed line and the dotted line are almost indistinguishable, i.e., the variation of the disappointment parameter has almost no effects on put payoffs

Figure 1 shows how the expected payoffs of options written on the S&P 500 index change with different degrees of relative risk aversion (Part A) and with different levels of disappointment aversion (Part B) under the market conditions on January 20, 2004.¹⁷ The horizontal axes depict different strike prices. Strike prices to the right of the forward price (1138.23) refer to call options and those to the left of the forward price refer to put options. For Part A, the coefficient of disappointment aversion A is set to one, that is, we study the effects of changing relative risk aversion in a CRRA setting. In Part B, the coefficient of relative risk aversion $\gamma$ is set to 2. In both parts, the solid lines show the benchmark case of a risk-neutral representative investor.

As expected, higher relative risk aversion (RRA) leads to higher expected payoffs for calls and lower expected payoffs for puts. The representative investor requires a higher return of call options and a lower return of put options with increasing risk aversion. However, the effects on calls and puts are not symmetric. Moving from risk neutrality to a relative risk aversion of 2 or 4 has a much stronger effect on puts than on calls. Even put options that are far out of the money react to changes in risk aversion, whereas the corresponding call options show almost no effect. The reason for such a different reaction is that current option prices can capture asymmetries in the return distribution. Therefore, Part A of Fig. 1 highlights the importance of conditioning on current market information when risk premiums and risk adjustments are studied. A particularly interesting case refers to a strike price equal to the forward price (1138.23). This is the only point in the graph where we show the effects for call and put options with the same strike. Because prices of calls and puts are identical for this strike price according to put-call parity, the expected payoffs in a risk-neutral world should also be identical, explaining the continuity of the solid line. With a risk averse representative investor, however, call payoffs are higher than put payoffs, explaining the discontinuity of the dashed and dotted lines.

Part B of the figure shows the effects of varying disappointment aversion on the expected payoffs of put and call options. Similar to the case of relative risk aversion, with increasing disappointment aversion the representative investor requires call options to have a higher return. However, the behavior for put options is distinctly different. The effects of disappointment aversion on the expected payoffs are negligible (the dotted line is almost indistinguishable from the dashed line). The observed difference to the risk-neutral case stems almost exclusively from the effect of a positive relative risk aversion. This finding of distinctly different effects of disappointment aversion on calls and puts is an interesting property of the disappointment model. The following rationale provides some intuition for this result: According to Eq. (14), greater disappointment leads to lower utility in all states below the forward price. For at-the-money or out-of-the-money call options, these states lead to a complete loss of the premium. Therefore, the greater the disappointment aversion, the higher the expected return (expected payoff) of the call options. For at-the-money or out-of- the-money put options, however, we have two effects. First, for very bad states far below the forward price, put options provide gains, which are all the more valuable the greater the disappointment aversion is. Second, for states below the forward price but close to it, put options lead to losses because of the put premium. Greater disappointment aversion makes these losses more harmful for the representative investor. As Part B of Fig. 1 shows, the two effects seem to offset each other almost completely for the price data on January 20, 2004.

A similar analysis can be carried out for the variance and skewness of index returns. Part A of Fig. 2 shows how the ex ante physical moments change with different levels of relative risk aversion, ranging from 1 to 12. The coefficient of disappointment aversion is set to 1 in all cases, that is, we study the case of CRRA utility. Again, the data refer to January 20, 2004. As a reference point, it is instructive to recall what would happen under a log-normal price distribution. In this case, relative risk aversion has no effect on either variance or skewness (Bakshi et al. 2003, p. 110). Part A of Fig. 2, however, shows a significant effect. Therefore, current option prices indicate a non-normal return distribution.

Fig. 2

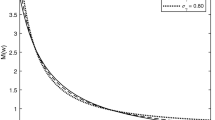
Effects of investor preferences on the physical variance and skewness. a Part A: varying the coefficient of relative risk aversion b Part B: varying the coefficient of disappointment aversion. This figure shows the ex ante return variance and skewness under the physical measure for different investor preferences. Values are based on spot and derivatives prices for the S&P 500 index on January 20, 2004, and use the formulas from Panel A of Table 1. The dotted lines show the variance multiplied by 100 and the solid lines show the skewness. In addition, there are vertical lines (dotted ones for the variance and solid ones for the skewness) that show the risk-neutral moments (No Risk-Adjustment) as reference points. The scale on the vertical axis on the left-hand side of the figure refers to variance and the scale on the right-hand side of the figure refers to skewness. The representative investor has a utility function according to Eq. (14). In Part A, the parameter of disappointment aversion is 1 and the coefficient of relative risk aversion varies from 1 (log utility) to 12. In Part B, the parameter of relative risk aversion is 2 and the coefficient of disappointment aversion varies from 1 to 0.5

Fig. 3

Implied variance and skewness risk premiums over time. a Part A: implied variance risk premiums. b Part B: implied skewness risk premiums. This figure shows the time series of the implied ex ante variance risk premiums (Part A) and skewness risk premiums (Part B) for the period January 1996– December 2011. The premiums are estimated under the assumption of a representative investor with utility function according to Eq. (14). The solid lines refer to the case of a relative risk aversion of 2 and no disappointment aversion (RRA = 2.0). The dotted lines provide the premiums under the assumption of a relative risk aversion of 2 and a disappointment aversion of $A=0.8$ (DA = 0.8)

When variance is examined, two effects are worth mentioning. First, because the risk-neutral variance ($\times$100) is 0.213 (shown as a vertical line in the figure), the ex ante physical variance is below the risk-neutral variance for all levels of risk aversion between 1 and 12, showing a negative variance risk premium. Second, the ex ante variance is not a monotonic function of risk aversion but has a minimum at a relative risk aversion of 5.40. The negative variance risk premium is well in line with a hedging argument put forward by Carr and Wu (2009). If investors dislike a larger variance, they are willing to pay a premium for an instrument that makes payments if the variance increases, like a variance swap, implying that the swap rate (risk-neutral variance) is above the ex-ante physical variance. A negative realized variance risk premium is also consistent with previous empirical research (Coval and Shumway 2001; Bakshi and Kapadia 2003; Carr and Wu 2009).

The ex ante skewness generally increases with $\gamma$, ranging from a negative value of −2.010 for a risk-neutral investor (shown as a vertical line in the figure) to a positive value of 1.716 for an investor with $\gamma =12$. Therefore, the representative investor model with CRRA utility implies a positive skewness risk premium on January 20, 2004. Moreover, ex ante skewness seems to be quite sensitive to the level of risk aversion. A positive skewness risk premium is also reasonable with respect to the above hedging argument. If investors dislike a lower skewness (distribution more skewed to the left), then they are willing to pay a premium for instruments that make positive payments if the skewness decreases. Therefore, the risk-neutral skewness should be below the ex-ante physical skewness. Empirical evidence on a positive realized skewness risk premium is provided by Kozhan et al. (2013) and Sasaki (2016).

Part B of Fig. 2 shows the corresponding analysis for different levels of disappointment aversion, ranging from 1 to 0.5. In all cases, the coefficient of relative risk aversion $\gamma$ is set to 2. Again, we added two vertical lines (No Risk-Adjustment) that refer to a risk-neutral representative investor as a reference point. We find that both, variance and skewness, increase in disappointment aversion. In contrast to the effects of relative risk aversion, an increasing disappointment aversion translates almost linearly into higher variances and skewnesses. If disappoint aversion increases by 0.1, variance ($\times$100) increases by about 0.013 and skewness by about 0.144.

The results in Fig. 2 refer only to a single date, but the main observations hold more generally for the data set as a whole, which is documented in Fig. 3 and Table 2.

Table 2 Descriptive statistics of the physical variance and skewness for different investor preferences

Figure 3 shows the time series of implied variance and skewness risk premiums. Part A refers to the variance and Part B to the skewness. As we can see, the variance risk premium obtained from the model is negative most of the time but can vary substantially. This observation stresses the importance of conditioning on the current market situation. As the comparison of the solid and dotted lines shows, disappointment aversion always leads to a higher variance risk premium. The skewness risk premium is always positive and also shows a strong time variation. Disappointment aversion generally leads to even higher skewness risk premiums.

Table 2 provides some descriptive statistics on implied variances and skewnesses for all 192 months in the sample and different combinations of preference parameters. Panel A refers to the variance and Panel B to the skewness. When looking at either the mean, the median, or the quartiles Q1 and Q3, we see that the variance first decreases with relative risk aversion and then increases. On average, the minimum is reached between 2 and 3, which is a reasonable estimate of the overall level of investor risk aversion. The variation of the disappointment parameter shows that variance increases with greater disappointment aversion. With reasonable values for both relative risk aversion and disappointment aversion, the disappointment model leads to a negative variance risk premium on average. In contrast to the variance, skewness generally increases with both $\gamma$ and A and the disappointment model leads to a positive skewness risk premium on average. For both variance and skewness, there is substantial variation over time for any fixed level of relative risk aversion and disappointment aversion. The standard deviation increases for variance and skewness with higher degrees of relative risk aversion. For an increasing level of disappointment, only the standard deviation of the variance increases, while the variation of the skewness declines.

6 Implied disappointment aversion

In this section, we further investigate the disappointment model. Preferences with disappointment aversion have received growing attention in finance. Applications of disappointment aversion include the classical problem of allocating funds between stocks and bonds (Ang et al. 2005), the study of economic benefits from giving investors access to options (Driessen and Maenhout 2007), and the analysis of market-timing strategies (Kostakis et al. 2011). Equilibrium models based on a representative investor with disappointment aversion have also been used to explain risk premiums in financial market. In this respect, the model by Babiak (2016) explains a negative variance risk premium while simultaneously matching the average market risk premium, market volatility and risk-free rate; and the model by Schreindorfer (2014) leads to a negative variance risk premium that also predicts returns over short time horizons.

Although the cited studies give important insights on the effects of disappointment aversion, to our knowledge this study is the first that provides estimates of the magnitude of disappointment aversion from market data.

Our analysis follows the general idea of Jackwerth (2000) and Bliss and Panigirtzoglou (2004) to imply preference parameters from option prices. To do so, we use the model of a representative investor with utility function according to Eq. (14) and implement an optimization procedure that simultaneously estimates the parameter of relative risk aversion $\gamma$ and the coefficient of disappointment aversion A by minimizing differences between ex ante physical moments and realized moments. Ex ante physical moments and realized moments are obtained for each month of our data period from January 1996 to December 2011 as outlined in Sect. 4. In particular, we obtain the implied estimates from

$$\begin{aligned} (\gamma , A)_t \; = \; \frac{1}{12} \sum \limits _{i = t-13}^{t-1} \underset{(\gamma , A)}{\text {argmin}} \left( \, \left| 1- \frac{pv^{(\gamma , A)}_{i,i+1}}{rv_{i,i+1}} \right| + \left| 1 - \frac{ps^{(\gamma , A)}_{i,i+1}}{rs_{i,i+1}} \right| \, \right) , \end{aligned}$$

(15)

Fig. 4

Implied relative risk aversion and disappointment aversion over time. a Part A: implied relative risk aversion. b Part B: implied disappointment aversion. This figure shows implied coefficients of relative risk aversion (Part A, solid line) and disappointment aversion (Part B, solid line) together with the level of the S&P 500 index (dashed line) for the period January 1997– January 2012. The implied preference parameters are estimated under the assumption of a representative investor with utility function according to Eq. (14). The parameter estimates are obtained from Eq. (15)

where $rv_{t,t+1}$ refers to the realized variance and $rs_{t,t+1}$ to the non-standardized realized skewness from time t to $t+1$. $pv^{(\gamma , A)}_{t,t+1}$ and $ps^{(\gamma , A)}_{t,t+1}$ are the respective ex ante physical moments resulting from the disappointment model with relative risk aversion $\gamma$ and disappointment aversion A. For the optimization, we perform a grid search for values of $\gamma$ between 1 and 15 with a step size of 0.25 and for values of A between 1 and 0.5 with a step size of 0.025.¹⁸ At each point in time, we select the pair $(\gamma , A)$ which simultaneously minimizes the relative absolute error between the realized and the risk-adjusted variances and skewnesses. To achieve stable estimates of $(\gamma , A)$ at time t, we take the average parameters from the minimization process over the past 12 months.

Our data covers the period from January 1996 to December 2011; hence, our optimization procedure yields estimates of implied disappointment aversion over the period from January 1997 to January 2012. Figure 4 shows the time series of the parameters $\gamma$ (Part A of the Figure) and A (Part B of the Figure) as well as the corresponding index level of the S&P 500. Panel A of Table 3 presents descriptive statistics for relative risk aversion ($\gamma$) and disappointment aversion (A). The descriptive statistics confirm that the magnitudes of the implied preference parameters are reasonable. The estimated coefficient of relative risk aversion is always in the range between 1 and 3.19, which is in line with values suggested in the literature (Mehra and Prescott 1985). With respect to disappointment aversion, Ang et al. (2005) show that a value of $A=0.6$ leads to non-participation in the stock market for the classical asset allocation problem to choose between stocks and bonds, suggesting that reasonable values for A fall in the range between 1 and 0.6. This is the case for our estimates which attain a minimum value of 0.84.

Figure 4 shows that both implied risk aversion and disappointment aversion vary over time. In relation to the level of the S&P 500 index, we find a procyclical pattern. In times of a rising stock market, risk aversion and disappointment aversion tend to be high (high $\gamma$ and low A). However, in falling markets they both decline with disappointment aversion being close to 1. These findings are consistent with the results of a study on forward-looking market risk premiums by Duan and Zhang (2014), who also find a relatively low relative risk aversion of the aggregate stock market investor at the peak of the financial crisis in late 2008 and early 2009.

Table 3 Implied estimates of disappointment aversion and relative risk aversion

As the representative agent that we use in the disappointment model represents the aggregate of all investors, our findings are consistent with the view that investors with high levels of risk aversion and disappointment aversion leave the stock market during turbulent times and reenter it after a period of high returns. For example, this pattern can be seen in the period from 2000 to 2008. After the dot-com bubble burst in 2000, disappointment aversion decreases considerably, indicating that investors with high level of disappointment aversion leave the market in this period. When the stock market shows a stable recovery after 2003, disappointment-averse investors seem to reenter the stock market, leading to higher aggregate disappointment aversion. However, when the financial crisis hits the market in 2008, both risk aversion and disappointment are very low again. The visual impression in Fig. 4 is also confirmed by a regression analysis. If we regress the implied preference parameters on the market returns of the previous year, we find highly significant coefficients, as given in Panel B of Table 3. When previous markets returns are high, both relative risk aversion and disappointment aversion tend to be at a high level as well.

Our results do not support an alternative view stating that risk aversion of the aggregate stock market investor is increasing if markets go down. In their analysis of the VIX, Bekaert et al. (2013) find a co-movement of risk aversion and stock market volatility, which could be interpreted as a support for this alternative view. Although volatility is often higher in down markets, market downturn and volatility are still distinct concepts.

7 Conclusions

This paper presents a new and exact characterization of the expected payoffs of call and put options under the physical probability measure in terms of current option prices and the preferences of a representative investor. The result allows us to exploit the full information contained in current prices in order to study the effects of risk preferences on the expected performance of options. This could help to define proper benchmarks for measuring the performance of trading strategies with options. It could also be useful for the design of structured products, because one can study a product’s required return for different groups of investors (with different risk preferences) in a current market situation.

An important application of our major theoretical result is the risk adjustment of option-implied moments. We show explicitly how the risk adjustment that transforms risk-neutral moments into physical moments can be performed. We use our theoretical results for an empirical study on disappointment aversion and show that disappointment aversion has a strong effect on the expected returns of out-of-the-money call options on the S&P 500 index but almost no effect on the returns of out-of-the money put options. Moreover, the disappointment model leads to a negative variance risk premium and a positive skewness risk premium on average for reasonable parameter values. We further provide option-implied estimates of the disappointment aversion of the representative stock market investor and show that disappointment aversion can be very strong in times of high index levels. Our findings confirm the view that investors with a high level of disappointment aversion leave the stock market during times of turbulence and reenter it after a period of high returns.

Several open issues could be explored in future research. One major task is to find specifications of the utility function that are best suited to improving volatility predictions. Another issue concerns the question of which model is best suited to explaining both variance and skewness risk premiums (and potentially premiums associated with even higher moments). A related question is the simultaneous explanation of risk premiums for different assets. This task would require an extension of the theory, however, as it is an open question how the risk adjustment for the whole market translates into a corresponding risk adjustment for individual assets.

Appendix

To prove Proposition 1, we use Eq. (1) and the following result from measure theory¹⁹:

Let $(\Omega ,\mathcal {A},\mu )$ be a finite measure space, f a non-negative, real-valued measurable function, and $\varphi :[0,\infty ) \rightarrow [0,\infty )$ a continuously differentiable and monotonically increasing function with $\varphi (0)=0$. Then,

$$\begin{aligned} \int \varphi \circ f \, d\mu \; = \; \int \limits _{0}^{\infty } \varphi '(x) \, \mu (f>x) \, dx. \end{aligned}$$

(16)

Since U is twice continuously differentiable, the function $\frac{1}{U'(x)}$, $x\in [0,\infty )$, has the following properties:

• (i) $\frac{1}{U'(x)}$ is continuously differentiable, since it is a composition of continuously differentiable functions;

• (ii) $\frac{1}{U'(x)}$ increases monotonically for all $x>0$, since $\left( \frac{1}{U'(x)}\right) '=\frac{-U''(x)}{U'(x)^2}>0$;

• (iii) for $x \rightarrow 0$, $\frac{1}{U'(x)}$ reaches its minimum and converges to a non-negative value. Therefore, $\frac{1}{U'(x)}$ is a non-negative function.

It follows that $\frac{1}{U'(x)}-\frac{1}{U'(0)}$ satisfies all conditions required for $\varphi$, where $\frac{1}{U'(0)}$ stands for $\lim \limits _{x \rightarrow 0} \,\, \frac{1}{U'(x)}$.

The discounted expected payoff of a call option under the physical measure equals

$$\begin{aligned} C^{P}(t,\tau ,K)&= E^P \left[ e^{-r\tau } (S_{t+\tau } -K)^+ \right] \\&= \int \limits _{0}^{\infty } e^{-r\tau } (S_{t+\tau }-K)^+ P(dS_{t+\tau }). \end{aligned}$$

Using the relation between physical and risk-neutral measures from Eq. (1) yields

$$\begin{aligned}&\frac{1}{c} \cdot \int \limits _{0}^{\infty } e^{-r\tau } (S_{t+\tau }-K)^+ \frac{1}{U'(S_{t+\tau })} Q(dS_{t+\tau }) \\&\quad = \frac{1}{c} \cdot \int \limits _{0}^{\infty } \left\{ \frac{1}{U'(S_{t+\tau })} - \frac{1}{U'(0)} + \frac{1}{U'(0)}\right\} \underbrace{e^{-r\tau } (S_{t+\tau }-K)^+ Q(dS_{t+\tau })}_{\equiv \mu _C(dS_{t+\tau })}, \end{aligned}$$

where $\mu _C$ defines a measure. We can now apply the above result from measure theory, which leads to

$$\begin{aligned} C^{P}(t,\tau ,K)&= \frac{1}{c} \cdot \int \limits _{0}^{\infty } \frac{-U''(x)}{U'(x)^2} \mu _{C}\{S_{t+\tau }>x\} dx + \frac{C(t,\tau ,K)}{c \cdot U'(0)} \\&= \frac{1}{c} \cdot \int \limits _{0}^{\infty } \frac{-U''(x)}{U'(x)^2} \left\{ \int \limits _{x}^{\infty } e^{-r\tau } (S_{t+\tau }-K)^+ Q(dS_{t+\tau })\right\} dx \\&\quad +\frac{C(t,\tau ,K)}{c \cdot U'(0)} . \end{aligned}$$

For $x<K$, the inner integral $\int \limits _{x}^{\infty } e^{-r\tau } (S_{t+\tau }-K)^+ Q(dS_{t+\tau })$ equals the value of a plain-vanilla call option with strike price K. For $x > K$, it follows that

$$\begin{aligned}&\int \limits _{x}^{\infty } e^{-r\tau } \underbrace{(S_{t+\tau }-K)^+}_{> 0} Q(dS_{t+\tau }) \\&\quad = \int \limits _{x}^{\infty } e^{-r\tau } (S_{t+\tau }-x) Q(dS_{t+\tau }) +\int \limits _{x}^{\infty } e^{-r\tau } (x-K) Q(dS_{t+\tau })\\&\quad = C(t,\tau ,x) + (x-K) e^{-r\tau } Q\{S_{t+\tau }>x\} \\&\quad = C(t,\tau ,x) + (x-K) D(t,\tau ,x), \end{aligned}$$

where $D(t,\tau ,x)$ denotes the price of a digital option that pays $1 if $S_{t+\tau }>x$.

Finally, we obtain the following expression:

$$\begin{aligned} C^P(t,\tau ,K)= & {} \frac{1}{c} \cdot \int \limits _{0}^{\infty } \frac{-U''(x)}{U'(x)^2} C(t,\tau ,K)1_{\{x < K \}} dx + \frac{C(t,\tau ,K)}{c \cdot U'(0)} \\&+ \frac{1}{c} \cdot \int \limits _{0}^{\infty } \frac{-U''(x)}{U'(x)^2} \left\{ C(t,\tau ,x) + (x-K) D(t,\tau ,x) \right\} 1_{\{x > K \}} dx \\= & {} \frac{1}{c} \cdot C(t,\tau ,K) \left\{ \frac{1}{U'(K)}-\frac{1}{U'(0)}\right\} + \frac{C(t,\tau ,K)}{c \cdot U'(0)} \\&+ \frac{1}{c} \cdot \int \limits _{K}^{\infty } \frac{-U''(x)}{U'(x)^2} \left\{ C(t,\tau ,x) + (x-K) D(t,\tau ,x) \right\} dx . \end{aligned}$$

The expression for the constant c can be derived similarly:

$$\begin{aligned} c = \int \limits _{0}^{\infty } \left\{ \frac{1}{U'(S_{t+\tau })} - \frac{1}{U'(0)} + \frac{1}{U'(0)}\right\} Q(dS_{t+\tau }). \end{aligned}$$

Applying the above result from measure theory to the measure Q yields

$$\begin{aligned} c&= \int \limits _{0}^{\infty } \frac{-U''(x)}{U'(x)^2} \Bigg \{ \int \limits _{x}^{\infty } Q(dS_{t+\tau }) \Bigg \} dx + \frac{1}{U'(0)}\\&= \int \limits _{0}^{\infty } \frac{-U''(x)}{U'(x)^2} e^{r\tau } D(t,\tau ,x) dx + \frac{1}{U'(0)}. \end{aligned}$$

The proof for the expected discounted payoff of a put option proceeds similarly. $\square$