Introduction

Sodium borohydride hydrolysis is an exothermic reaction and comes rather slowly. To speed up this process uses the catalysts to achieve the reaction rate required. In recent years, a large number of works have been published on the catalytic hydrolysis of NaBH4 [1,2,3,4,5,6] and on the description of this process using various kinetic models for dilute solutions [7,8,9,10,11,12]. At the same time, the mechanism of catalytic hydrolysis has not been thoroughly studied and remains an open field of research. Heterogeneous hydrolysis reactions occur on neutral particles adsorbed by the catalyst surface (molecules, metastable complexes). In a number of publications dealing the NaBH4 hydrolysis, the authors propose adsorption schemes involving \({\text{BH}}_{4}^{ - }\) and/or OH– ions [13,14,15,16,17,18,19,20]. Since ions of the same sign cannot be adsorbed on solid catalyst particles in significant amounts, the authors propose a mechanism of the process involving two active centers connected electrically. In our opinion, this scheme does not eliminate the question of the electrical neutrality of the catalyst surface, since each such pair is negatively charged. Ion adsorption processes are characteristic of electrochemical cells when current flows. It can be assumed that the schemes with ion adsorption came from the study of direct sodium borohydride fuel cell [21, 22], and in this case there should be no generation of hydrogen, because it is oxidized to water in the fuel cell.

A finely dispersed Co/TiO2 catalyst was studied. One of the remarkable characteristics of this catalyst is the stability of its properties upon repeated use [23]. It should be noted that, in terms of the efficiency/cost parameter, powdered cobalt catalysts are among the most effective [24,25,26,27,28,29,30]. There are two pathways to accelerate hydrolysis: increasing the temperature and increasing the amount of catalyst. When using a catalyst, it is expected that an increase in its amount would lead to the proportional acceleration of the process, and one of the aims of the present article was to test this claim. A series of isothermal experiments was carried out varying catalyst amounts in a wide range. The presented study was not specifically related to developing technology, and was focused on studying the kinetic features of catalytic hydrolysis of high-concentration NaBH4 solutions, typical for hydrogen generators.

Experimental

Sigma-Aldrich NaBH4 granular powder with a purity of 98% was used as the initial component. All chemical reagents used in the preparation of catalysts and hydrogen generation measurements were of analytical grade and did not require any purification. Titanium dioxide micron powder with a purity of 99.99%, a particle size of 325 mesh (M325), and a tetragonal crystal structure from Nanografi Nano Technology was used. Cobalt nanoparticles (Co NPs) were prepared by pouring a deionized aqueous solution of NaBH4 as a reducing agent into the solution of Co(OAc)2–PVP with vigorous stirring. The resulting black powder of Co NPs separated from the solution was thoroughly washed with deionized water, acetone, and hexane, dried in a vacuum at 60 °C, and stored in a box. In order to deposit Co NPs on TiO2 powder, 50 mg Co NPs have been suspended in 20 ml of hexane and sonicated for 3 min. 1.5 g of TiO2 (M325) has been suspended in 40 ml of hexane in another vessel and sonicated for 1 min. The suspensions have been mixed and stirred for 30 min, and sonicated for 3 min to obtain gray color Co/TiO2 which are magnetically separated and dried under vacuum at 60 °C for further catalytic applications.

Kinetic experiments were carried out in closed reactors with maximum tightness, as hydrogen generated from NaBH4 hydrolysis has a high fluidity. All units and parts of the experimental installation are made of stainless steel. Keller electronic sensor for operating pressure 50 bar is used to measure the pressure in the reactor. The temperature of the solution in the reactor is measured by a Pt100 platinum thermal resistor.

We used working solution with NaBH4 molality \(C_{{{\text{NaBH}}_{4} }}\) = 4.23 mol kg−1 prepared by adding 10 ml of distilled water to 1.6 g of NaBH4 during all experiments. The amount of catalyst was varied from 0.006

to 0.6 g. The error in determining the degree of decomposition is associated with the calculation of the water vapor pressure over the solution and uncontrolled hydrogen leaks through the seals. The last factor is cumulative and the total error can reach ~ 5% at the end of the process. The errors associated with NaBH4 and H2O weighing and pressure and temperature measurements are much smaller (< 0.3%). The NaBH4 solution was prepared directly inside the reactor using water cooled to ≈ 15 °C. Then the catalyst powder was added to the reaction solution, the reactor was sealed and placed in a thermostat providing the desired temperature. Solution temperature and pressure in the reactor was recorded during hydrolysis. Using these measurements, the following characteristics of the hydrolysis were calculated: the amount of generated hydrogen, decomposition degree \(\xi \left( {\text{t}} \right)\), and the rate of hydrogen generation. Developed technique of calculating \(\xi \left( t \right)\) using measured values of pressure and solution temperature was described in previous articles [23, 31] in details. To plot the temperature dependence of the kinetic coefficients, we used two series of isothermal experiments with catalyst amount \(m_{{{\text{cat}}}}\) = 0.01 and 0.05 g carried out at five temperatures from 20 °C and 60 °C.

Analysis of the experimental data

In a series of experiments with different catalyst amount varying up to 100 times, the issue of the role of homogeneous hydrolysis in the experiments performed is topical, especially in the case of small amounts of catalyst. In the general notation, taking into account homogeneous and heterogeneous hydrolysis processes, the equation for the rate of hydrogen generation in the isothermal mode is:

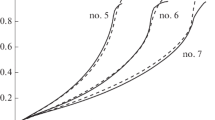
$$\frac{{dN_{{H_{2} }} }}{dt} = 4V_{{{\text{sol}}}} C_{{{\text{NaBH}}_{4} }}^{0} \frac{d\xi }{{dt}} = V_{{{\text{sol}}}} R_{\hom } + S_{{{\text{cat}}}} m_{{{\text{cat}}}} R_{{{\text{het}}}} ,$$
(1)

Here \(N_{{{\text{H}}_{2} }}\) is the number of moles of generated hydrogen, \(V_{{{\text{sol}}}}\) is solution volume, \(R_{{{\text{hom}}}}\) and \(R_{{{\text{het}}}}\) are hydrogen generation rates in homogeneous reactions per unit volume and in heterogeneous reactions per unit of catalyst surface, \(S_{{{\text{cat}}}}\) is the surface area of one gram of catalyst. Calculated degree of NaBH4 decomposition versus time is shown in Fig. 1.

Fig. 1
figure 1

Effect of the amount of catalyst on NaBH4 decomposition at 30 °C. \(C_{{{\text{NaBH}}_{4} }}\) = 4.23 mol kg.−1

Full size image

In the experiments with the catalyst, the decrease in the hydrolysis rate is observed only at the initial site. Then, the process proceeds with almost constant rate (curves 2 and 3 in Fig. 1a). With further increase in the amount of catalyst in the second phase of hydrolysis, even a slight increase in the rate of the process is observed (curves 4–7 in Fig. 1b).

The final stage with a drop in the hydrogen generation rate to zero is due to diffusion mode of the catalytic process. We noted an interesting feature, all processes start in a homogeneous mode, i.e. the second term in Eq. 1 does not come in operation instantly, but after some time. Naturally, the more catalyst, the earlier the catalytic process becomes the dominant one. The fact that there is a delay between timing of catalyst immersion in solution and the start of heterogeneous reactions demands more research and explanation.

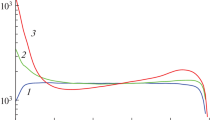
Hydrogen generation rate \({\text{Q}}_{{{\text{H}}_{2} }} = 4{\text{N}}_{{{\text{NaBH}}_{4} }}^{0} \frac{d\xi }{{dt}}\), which is obtained by differentiation and subsequent smoothing of the dependency \(\xi \left( t \right)\), is more feasible for analysis, rather than operating with \(\xi \left( t \right)\) only. Using pairs of time dependencies \(\xi \left( t \right)\) and \(Q_{{H_{2} }} (t)\) it is possible to construct a functional dependence \({\text{Q}}_{{{\text{H}}_{2} }} \left( \xi \right)\). Such consideration is convenient to analyze experiments of different durations (see Fig. 1), since the function \(\xi \left( t \right)\) changes monotonically from 0 to 1. The graphs \({\text{Q}}_{{{\text{H}}_{2} }} \left( \xi \right)\) (Fig. 2) describe six experiments with catalyst and solely homogeneous hydrolysis. The crosses on the curves of catalytic experiments comply with the excess of catalytic hydrolysis over homogeneous one by 10 times. In other words, the process can be considered predominantly heterogeneous to the right of cross marks. Heterogeneous reactions came into the diffusion mode with a rapid drop in the rate of hydrogen generation in the final stage of hydrolysis. Depending on the amount of catalyst, the transition occurred at \(\xi\) = 0.85 ÷ 0.9. From a kinetic point of view, the diffusion mode is not interesting at all, since it depends on convection and diffusion processes in a particular reactor.

Fig. 2
figure 2

Effect of the amount of catalyst on hydrogen generation at 30 °C. \(C_{{{\text{NaBH}}_{4} }}\) = 4.23 mol kg.−1

Full size image

When constructing graphs in Fig. 2, the velocity values are corrected according to the measured temperature of the solution, which is not equal to the temperature of the thermostat. This temperature difference \({\text{T}}_{{{\text{sol}}}} \left( \xi \right) - {\text{T}}_{{{\text{therm}}}} \left( \xi \right)\) is shown in Fig. 3 for all experiments.

Fig. 3
figure 3

Effect of the amount of catalyst on deviation of \(T_{{{\text{sol}}}}\) from \(T_{{{\text{therm}}}}\) versus NaBH4 decomposition degree in thermostat at 30 °C. \(C_{{{\text{NaBH}}_{4} }}\) = 4.23 mol kg.−1

Full size image

The power of generated heat is proportional to the rate of hydrogen generation. Accordingly, the greater temperature deviation, the higher the rate of hydrogen generation is. Increasing the temperature of the solution, in turn, accelerates the hydrolysis and heat release. Such a process can transfer to a mode of the thermal explosion type. And, consequently, the maximum temperature of the solution is moderated by water evaporation and the transition of hydrolysis to the diffusion mode. It is worth noting, that in the “explosion” mode, the temperature peak recorded by the thermocouple was always lower than actual value, both due to the inertia of the thermocouple and owing to the inhomogeneity of heat transfer in the reactor.

The rationale for this correction was to bring the rate of hydrogen generation measured at solution temperature, to the rate at thermostat temperature. We used the value of activation energy U = 7710 K for this catalyst in our study [23] to correct the value of hydrogen generation rate.

$$\tilde{Q}_{{H_{2} }}^{{}} \left( \xi \right) = Q_{{H_{2} }}^{{}} \left( \xi \right){\text{exp}}\left[ { - U\left( {\frac{1}{{T_{{{\text{therm}}}} \left( \xi \right)}} - \frac{1}{{T_{{{\text{sol}}}} \left( \xi \right)}}} \right)} \right]$$
(2)

Here \(\tilde{Q}_{{{\text{H}}_{2} }}^{{}}\) is the rate of hydrogen generation, corrected for the deviation of the solution temperature from the thermostat temperature, U is activation energy.

This approach is not rigorous, and the function \(\tilde{Q}_{{{\text{H}}_{2} }} \left( \xi \right)\) still describes the isothermal mode at 30 °C better than \({\text{Q}}_{{{\text{H}}_{2} }} \left( \xi \right)\). Figure 2 illustrates the transition from a solely homogeneous hydrolysis to an almost heterogeneous process. The experiments with \(m_{{{\text{cat}}}}\) = 0.1, 0.3, and 0.6 g were closest to the model of heterogeneous hydrolysis. The specific rate of catalytic hydrogen generation \(q_{{{\text{H}}_{2} }}^{{{\text{het}}}} \left( \xi \right)\) for these three experiments was assessed as

$$q_{{H_{2} }}^{{{\text{het}}}} \left( \xi \right) = \frac{{\tilde{Q}_{{H_{2} }}^{{{\text{het}} + \hom }} \left( \xi \right) - \tilde{Q}_{{H_{2} }}^{\hom } \left( \xi \right)}}{{m_{{{\text{cat}}}} }} = S_{{{\text{cat}}}} R_{{{\text{het}}}} \left( \xi \right)$$
(3)

Here \(\tilde{Q}_{{{\text{H}}_{2} }}^{{\text{het + hom}}}\) and \(\tilde{Q}_{{{\text{H}}_{2} }}^{{{\text{hom}}}}\) are the rate of hydrogen generation in experiments with a catalyst and in a homogeneous experiment, corrected for the deviation of the solution temperature from the thermostat temperature. Let’s note that the subtraction of hydrolysis rates is valid for functional dependence on \(\xi\) and impossible for the functions dependant on time. At the same time, such a subtraction operation is not rigorous, in the sense that this is an approximate approach, and it does not substitute the solution of Eq. 1 in the case of detailed modeling of homogeneous-heterogeneous hydrolysis, especially in the initial time interval.

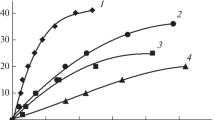
The dependencies \({\text{q}}_{{{\text{H}}_{2} }}^{{{\text{het}}}} \left( \xi \right)\) are presented within interval 0.18 < \(\xi\) < 0.8 in Fig. 4. The right boundary 0.8 was chosen to exclude both the diffusion mode and domains with insufficient temperature correction.

Fig. 4
figure 4

Specific rate of catalytic hydrogen generation versus NaBH4 decomposition degree in the experiments at 30 °C with different amount of catalyst: 1–0.1 g, 2–0.3 g, 3–0.6 g; 4–average specific rate of catalytic hydrolysis. \(C_{{{\text{NaBH}}_{4} }}\) = 4.23 mol kg.−1

Full size image

Observed fibration of the curves (Fig. 4) with a decrease in the specific generation rate and with an increase of catalyst amount, we tend to associate rather with physical factors than with chemical ones. In the experimental procedure used, the amount of the catalyst was controlled, but the instability in the properties of these catalyst samples, for example, due to the particle size distribution function, was not taken into account. There is also the problem of non-uniform distribution of catalyst particles over solution volume, with the possibility for some of the particles be on the bottom and walls of reactor. Part of the surface of such particles does not work. With an increase in the number of particles (amount of catalyst), the probability of such events increases as well as the probability of particles coagulation.

Having observed the fibration of the curves (Fig. 4) with a decrease in the specific generation rate and with an increase of catalyst amount, we tend to associate rather with physical factors than with chemical ones. In the experimental procedure used, the amount of the catalyst was controlled, but the instability in the properties of these catalyst samples, for example, due to the particle size distribution function, was not taken into account. There is also the problem of non-uniform distribution of catalyst particles over solution volume, with the possibility for some of the particles be on the bottom and walls of reactor. Part of the surface of such particles does not work. With an increase in the number of particles (amount of catalyst), the probability of such events increases as well as the probability of particles coagulation.

Another (chemical) hypothesis should elucidate the increase in the number of catalyst particles with a change in the component composition of the solution and, thus, with a change in hydrolysis rate. We have not yet been able to propose such a mechanism, and therefore, having averaged the data of 3 processes, we obtained curve 4 (Fig. 4).

Experimental verification of the physical hypothesis of the curves fibration in Fig. 4 is difficult and laborious, since it involves the control of the individual properties of each catalyst sample before its further use in the experiment. Throwing this questions open, we turned to a kinetic model that includes adsorption/desorption processes and heterogeneous reactions to explain the growth of hydrolysis rate with an increase in hydrolysis degree \(\xi\) (Fig. 4).

Basic provisions for the model of NaBH4 catalytic hydrolysis

Obeying the condition of neutrality of the adsorbed particles leads to the hypothesis that at the participation of ions an adsorption of certain complex consisting of two ions of different signs occurs. In aqueous NaBH4 solutions, H2O molecules and \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]\) complexes are neutral. We used the notation \({\text{H}}_{2} {\text{O}}^{{\text{S}}}\) and \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]^{{\text{s}}}\) for these particles in the adsorbed state. There are no other neutral particles in the solution at the beginning of hydrolysis. As the final ion \({\text{B}}\left( {{\text{OH}}} \right)_{4}^{ - }\) is formed, that leads to formation of boric acid molecules, which can also be adsorbed, but they cannot participate in reactions accompanied by hydrogen generations. Therefore, their adsorption was not considered. Thus, the probability of a reaction is higher in collisions with such particles, than in a collision of the same particles in solution. Theoretically, the following irreversible reactions comprising \({\text{H}}_{2} {\text{O}}^{{\text{S}}}\) and \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]^{{\text{s}}}\) can be written:

$${\text{H}}_{2} {\text{O}}^{S} + {\text{BH}}_{4}^{ - } \to {\text{H}}_{2} + {\text{BH}}_{3} {\text{OH}}^{ - }$$
(4)
$${\text{H}}_{2} {\text{O}}^{{\text{S}}} + \left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right] \to {\text{H}}_{2} + \left[ {{\text{BH}}_{3} {\text{OH}}^{ - } \cdot {\text{H}}^{ + } } \right]$$
(5)
$$\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]^{{\text{S}}} + {\text{OH}}^{ - } \to {\text{H}}_{2} + {\text{BH}}_{3} {\text{OH}}^{ - }$$
(6)
$$\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]^{{\text{S}}} + {\text{H}}_{2} {\text{O}} \to {\text{H}}_{2} + \left[ {{\text{BH}}_{3} {\text{OH}}^{ - } \cdot {\text{H}}^{ + } } \right]$$
(7)

In this reaction scheme, reactions 5 and 7 are analogues of the same channel of a homogeneous reaction that occurs when a water molecule collides with a complex. Reaction 4 is an analogue of another homogeneous hydrolysis channel at collision of water molecule with \({\text{BH}}_{4}^{ - }\) ion. In case of Eq. 4, there is no paired reaction similar to Eq. 7 due to the impossibility of \({\text{BH}}_{4}^{ - }\) adsorption. There are doubts regarding the feasibility of reaction 6, as in the homogeneous case, the collision of the complex with an ion OH– leads to the destruction of the complex

$$\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right] + {\text{OH}}^{ - } \to {\text{BH}}_{4}^{ - } + {\text{H}}_{2} {\text{O}}$$
(8)

It is this reaction that explains the slowdown of homogeneous hydrolysis with an increase in the concentration of OH– ions in the solution. It is very likely that at heterogeneous scenario the collision of these particles would result in the destruction of the complex, rather than the reaction 6 behavior. Further we used the abbreviations as \(\left[ {{\text{comp}}} \right] \equiv \left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]\) and \({\text{W}} \equiv {\text{H}}_{2} {\text{O}}\). To describe heterogeneous reactions, we introduced functions to characterize the degree of filling of the catalyst surface with various adsorbed particles. We embraced a model with three states of active centers: free \(\varepsilon_{{{\text{empt}}}}\), \(\varepsilon_{{\text{W}}}\) and \(\varepsilon_{{\left[ {{\text{comp}}} \right]}}\) in terms of occupation by water molecules and complexes accordingly:

$$\varepsilon_{{\text{W}}} + \varepsilon_{{\left[ {{\text{comp}}} \right]}} + \varepsilon_{{{\text{empt}}}} = 1$$
(9)

Adsorption of a particle can occur when it collides with a free adsorption site \(\varepsilon_{{{\text{empt}}}}\). Particle desorption occurs when a certain particle of the solution collides with an adsorbed particle. We formulated the equilibrium of these processes as:

$$\varepsilon_{{{\text{empt}}}} K_{{\text{W}}}^{{{\text{SD}}}} j_{{\text{W}}}^{{\text{S}}} = \varepsilon_{{\text{W}}} j_{{\text{W}}}^{{\text{D}}} ,\quad \quad \varepsilon_{{{\text{empt}}}} K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} j_{{\left[ {{\text{comp}}} \right]}}^{{\text{S}}} = \varepsilon_{{\left[ {{\text{comp}}} \right]}} j_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}}$$
(10)

The flux density \(j_{i}\) is proportional to the number of particles of type i in the volume of the solution, and then the ratio of fluxes is equal to the ratio of the number of particles. Solving Eqs. 9 and 10, we obtained an expression for \(\varepsilon_{{\text{W}}}\) and \(\varepsilon_{{\left[ {{\text{comp}}} \right]}}\):

$$\varepsilon_{{\text{W}}} = \frac{{K_{{\text{W}}}^{{{\text{SD}}}} \frac{{N_{{\text{W}}}^{{\text{S}}} }}{{N_{{\text{W}}}^{{\text{D}}} }}}}{{1 + K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} \frac{{N_{{\left[ {{\text{comp}}} \right]}} }}{{N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}} }} + K_{{\text{W}}}^{{{\text{SD}}}} \frac{{N_{{\text{W}}}^{{\text{S}}} }}{{N_{{\text{W}}}^{{\text{D}}} }}}}$$
(11)
$$\varepsilon_{{\left[ {{\text{comp}}} \right]}} = \frac{{K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} \frac{{N_{{\left[ {{\text{comp}}} \right]}} }}{{N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}} }}}}{{1 + K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} \frac{{N_{{\left[ {{\text{comp}}} \right]}} }}{{N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}} }} + K_{{\text{W}}}^{{{\text{SD}}}} \frac{{N_{{\text{W}}}^{{\text{S}}} }}{{N_{{\text{W}}}^{{\text{D}}} }}}}$$
(12)

Here \(N_{{\left[ {{\text{comp}}} \right]}}\) is the number of moles of the resulting complex, \(N_{{\text{W}}}^{{\text{S}}}\) the number of water moles involved in the adsorption process, \(N_{{\text{W}}}^{{\text{D}}}\) and \(N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}}\) are the number of particles that initiate the desorption of adsorbed water molecules and complexes, \(K_{{\text{W}}}^{{{\text{SD}}}}\) and \(K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}}\) are the equilibrium constant of adsorption/desorption of water and of the complex. Different particles colliding with an adsorbed particle are capable of causing desorption with different probabilities. The choice of the “leading” particle initiating desorption is sometimes a non-trivial task. First of all, it can be expected that such a particle will be the most numerous molecules, i.e. water molecules. Although, for example, a collision with an ion OH– may be more efficient in terms of desorption of an adsorbed complex. The flux density of particles i involved in reaction on unit surface of the catalyst is equal to the difference between the densities of the incident and reflected reagent fluxes, for example, while considering Eq. 4 an expression can be written:

$$J_{{\text{i}}} = j_{{\text{i}}}^{{{\text{fall}}}} - j_{{\text{i}}}^{{{\text{refl}}}}$$
(13)

Here \(j_{{{\text{BH}}_{4}^{ - } }}^{{{\text{fall}}}}\) and \(j_{{{\text{BH}}_{4}^{ - } }}^{{{\text{refl}}}}\) are the density of the incident and reflected reagent flow.

Two modes of a heterogeneous process are possible, i.e. kinetic and diffusion. These modes were investigated on the example of \({\text{BH}}_{4}^{ - }\) ion. In the kinetic mode, \(j_{{{\text{BH}}_{4}^{ - } }}^{{{\text{refl}}}}\) is slightly less \(j_{{{\text{BH}}_{4}^{ - } }}^{{{\text{fall}}}}\), and their difference is controlled by the properties of the catalyst and is dependent on temperature \(J_{{{\text{BH}}_{4}^{ - } }} \equiv R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} \left( T \right)\). Quantitatively this expression determines the rate of a heterogeneous reaction in the kinetic mode. Here, the superscript indicates the adsorbed particle onto which the flux of particles denoted by the subscript falls. In isothermal mode the rate constant of the heterogeneous reaction \(R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}}\) = const that means a zero order reaction. In the diffusion mode, the flux density of reacting particles per unit surface of the catalyst is practically equal to the density of the incident reagent flux \(J_{{{\text{BH}}_{4}^{ - } }}\)≈\(j_{{{\text{BH}}_{4}^{ - } }}^{{{\text{fall}}}}\), which is always less than \(R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}}\), and is controlled by convective and diffusion processes in the solution. A heterogeneous process that begins in the kinetic mode can end in the diffusion mode if the reagent concentration finally tends to zero due to process. The condition for the transition from the kinetic mode to the diffusion one can be written using the diffusion coefficient \(D_{{{\text{BH}}_{4}^{ - } }}\), the diffusion scale \(h_{{{\text{dif}}}}\) and the threshold reagent concentration \(\tilde{C}_{{{\text{BH}}_{4}^{ - } }}\):

$$R_{{{\text{BH}}_{{4}}^{ - } }}^{{\text{W}}} \approx D_{{{\text{BH}}_{4}^{ - } }} \frac{{\tilde{C}_{{{\text{BH}}_{4}^{ - } }} }}{{h_{{{\text{dif}}}} }},\quad \quad \tilde{C}_{{{\text{BH}}_{4}^{ - } }} \approx \frac{{R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} h_{{{\text{dif}}}} }}{{D_{{{\text{BH}}_{4}^{ - } }} }}$$
(14)

Using powder catalysts it is worth noting, that in diffusion mode, the rate of hydrogen generation decreases both due to a decrease in \({\text{BH}}_{4}^{ - }\) concentration and growth of \(h_{{{\text{dif}}}}\) scale.

Writing the rate of hydrogen generation comprising heterogeneous reactions in general form using fluxes, we did not yet specify their mode. Also, we accepted the widely used hypothesis that the slowest process is the hydrolysis of the main ion \({\text{BH}}_{4}^{ - }\), and the three subsequent reactions are “fast”, i.e. accompanied by formation of 4 H2 molecules. In this case, Eq. 1 can be rewritten in the heterogeneous approximation:

$$\frac{{dN_{{{\text{H}}_{2} }} }}{{m_{{{\text{cat}}}} dt}} = 4S_{{{\text{cat}}}} \left[ {\varepsilon_{{\text{W}}} \left( {J_{{{\text{BH}}_{4}^{ - } }} + J_{{\left[ {{\text{comp}}} \right]}} } \right) + \varepsilon_{{\left[ {{\text{comp}}} \right]}} \left( {J_{{{\text{OH}}^{ - } }} + J_{{\text{W}}} } \right)} \right]$$
(15)

Here \(J_{{\text{i}}}\) is the flux density of particles i reacted per unit surface of the catalyst. Comparing the behavior of the average specific rate of catalytic hydrolysis (Fig. 4, curve 4) and the functions on the right side of Eq. 15, we noted that only the function \(\varepsilon_{{\text{W}}} \left( \xi \right)\) can be of growing nature. The product \(\varepsilon_{{\text{W}}} \left( {J_{{{\text{BH}}_{4}^{ - } }} + J_{{\left[ {{\text{comp}}} \right]}} } \right)\) can be a growing function, when one of two reactions either (4) or (5) takes place in the kinetic mode. The concentration of the main ion \({\text{BH}}_{4}^{ - }\) is several orders of magnitude higher than the one of complexes \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]\). Consequently, it was logical to expect that it was reaction (4) that proceeds in the kinetic mode. Considering very simple behavior of curve 4 in Fig. 4, one can be assumed that the role of other hydrolysis channels for this catalyst is insignificant, and for the primary analysis, only term modeling heterogeneous hydrolysis was left in Eq. 15:

$$\frac{{dN_{{{\text{H}}_{2} }} }}{{m_{{{\text{cat}}}} dt}} = 4S_{{{\text{cat}}}} \varepsilon_{{\text{W}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}}$$
(16)

Thus, Eqs. 11, 12, and 16 provide a minimal version of the kinetic model of heterogeneous processes on the Co/TiO2 catalyst. In general it is worth noting that it may be necessary to extend the model of another catalyst adding other hydrolysis channels from the list of reactions in Eqs. 4–7. Since the parameters \(S_{{{\text{cat}}}}\) and \(R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}}\) are constants in Eq. 16, \(\varepsilon_{{\text{W}}} \left( \xi \right)\) must be growing function (see Fig. 4). There are two functional dependencies on \(\xi\), i.e. \(N_{{\text{W}}}^{{\text{S}}} /N_{{\text{W}}}^{{\text{D}}}\) and \(N_{{\left[ {{\text{comp}}} \right]}} /N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}}\) in Eq. 11. In the course of hydrolysis, \(N_{{\left[ {{\text{Comp}}} \right]}}\) decreases and tends to zero at \(\xi \to 1\), which means rising function \(\varepsilon_{{\text{W}}} \left( \xi \right)\). The ratio \(N_{{\text{W}}}^{{\text{S}}} /N_{{\text{W}}}^{{\text{D}}}\) is an increasing function of \(\xi\), if there is a decrease in the number of particles causing desorption \(N_{{\text{W}}}^{{\text{D}}}\) and/or growth of \(N_{{\text{W}}}^{{\text{S}}}\). We suggested two options for the behavior of \(K_{{\text{W}}}^{{{\text{SD}}}} \left( {N_{{\text{W}}}^{{\text{S}}} /N_{{\text{W}}}^{{\text{D}}} } \right)\) and \(K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} \left( {N_{{\left[ {{\text{comp}}} \right]}} /N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}} } \right)\) functions, which ensure an increase of \(\varepsilon_{{\text{W}}}\) with \(\xi\) growth.

I. The function \(K_{W}^{SD} \left( {N_{{\text{W}}}^{{\text{S}}} /N_{{\text{W}}}^{{\text{D}}} } \right)\) is almost constant and can be replaced by an average value. The function \(K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} \left( {N_{{\left[ {{\text{comp}}} \right]}} /N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}} } \right)\) decreases in proportion to the power of (\(1 - \xi\)). If to accept the last assumption, we can use an approximate description of changing \(N_{{\left[ {{\text{comp}}} \right]}}\) and its correct asymptotic behavior as \(\xi\) varies, instead of studying the kinetics of reactions controlling \(N_{{\left[ {{\text{comp}}} \right]}}\) change.

II. Since \(K_{{\left[ {{\text{Comp}}} \right]}}^{{{\text{SD}}}} \left( {N_{{\left[ {{\text{Comp}}} \right]}} /N_{{\left[ {{\text{Comp}}} \right]}}^{{\text{D}}} } \right) < < K_{{\text{W}}}^{{{\text{SD}}}} \left( {N_{{\text{W}}}^{{\text{S}}} /N_{{\text{W}}}^{{\text{D}}} } \right)\), the adsorption of complexes does not play a significant role and \(\varepsilon_{{\text{W}}}\) depends only on \(K_{{\text{W}}}^{{{\text{SD}}}} \left( {N_{{\text{W}}}^{{\text{S}}} /N_{{\text{W}}}^{{\text{D}}} } \right)\), which is substantially less than 1.

Under the hypothesis I, the increase in hydrogen generation was explained by the decrease to zero of \(K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} \left( {N_{{\left[ {{\text{comp}}} \right]}} /N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}} } \right)\), which caused an increase in \(\varepsilon_{{\text{W}}} \left( \xi \right)\). If we assume \(N_{{\text{W}}}^{{\text{S}}} /N_{{\text{W}}}^{{\text{D}}}\) = const and redefine the equilibrium constant \(\tilde{K}_{{\text{W}}}^{{{\text{SD}}}} = {\text{K}}_{{\text{W}}}^{{{\text{SD}}}} \left( {N_{{\text{W}}}^{{\text{S}}} /N_{{\text{W}}}^{{\text{D}}} } \right) = {\text{const}}\), then Eq. 16 can be rewritten as:

$$\frac{{dN_{{{\text{H}}_{2} }} }}{{m_{{{\text{cat}}}} dt}} = \frac{{4S_{{{\text{cat}}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} \tilde{K}_{{\text{W}}}^{{{\text{SD}}}} }}{{1 + \tilde{K}_{{\text{W}}}^{{{\text{SD}}}} + K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} \frac{{N_{{\left[ {{\text{comp}}} \right]}} }}{{N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}} }}}} = \frac{{4S_{{{\text{cat}}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} \frac{{\tilde{K}_{{\text{W}}}^{{{\text{SD}}}} }}{{1 + \tilde{K}_{{\text{W}}}^{{{\text{SD}}}} }}}}{{1 + \frac{{K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} }}{{1 + \tilde{K}_{{\text{W}}}^{{{\text{SD}}}} }}\frac{{N_{{\left[ {{\text{comp}}} \right]}} }}{{N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}} }}}} \approx \frac{{4G_{1} }}{{1 + G_{2} \left( {1 - \xi } \right)}}$$
(17)

There are two combined expressions \(G_{1} \equiv S_{{{\text{cat}}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} \frac{{\tilde{K}_{{\text{W}}}^{{{\text{SD}}}} }}{{1 + \tilde{K}_{{\text{W}}}^{{{\text{SD}}}} }}\), \(G_{2} \equiv \frac{{K_{{\left[ {{\text{comp}}} \right]}}^{{{\text{SD}}}} }}{{1 + \tilde{K}_{{\text{W}}}^{{{\text{SD}}}} }}A\) in Eq. 17. We approximated the decreasing function \(N_{{\left[ {{\text{comp}}} \right]}} /N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}}\) by the simplest expression \(A\left( {1 - \xi } \right)\). By tuning the parameters G1 and G2 we determined the best approximation G1 = 2.74, G2 = 2.06 for data (Fig. 4). Modeling results and experimental data (curve 4 in Fig. 4) are plotted in Fig. 5.

Fig. 5
figure 5

Average specific rate of catalytic hydrolysis versus NaBH4 decomposition degree, experiment–solid line and model tuning using (17)–dashed line. \(C_{{{\text{NaBH}}_{4} }}\) = 4.23 mol kg−1, 30 °C

Full size image

Thus, the hypothesis I allows describing of experimental data of isothermal experiments and determine the values of two kinetic complexes for the temperature used in the experiment G1(30 °C) \(\approx\) 2.74, G2(30 °C) \(\approx\) 2.06. It needs to perform a series of experiments at different temperatures to obtain their functional dependencies on temperature, and find Arrhenius approximation coefficients. The results of such experiments are presented in Section “Temperature dependences of kinetic coefficients”. But the problem is that we deal with combinations of kinetic characteristics, and the activation energy for G1(T) determined in this way can be only attributed to the rate of a heterogeneous reaction \(R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}}\) if \(\tilde{K}_{{\text{W}}}^{{{\text{SD}}}}\) >  > 1. Otherwise \(\tilde{K}_{{\text{W}}}^{{{\text{SD}}}}\) <  < 1, the activation energy characterizes the product \(R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} \tilde{K}_{{\text{W}}}^{{{\text{SD}}}}\). It is hardly necessary to interpret G2(T), since it is a formal approximation of the kinetic characteristics of the bulk reactions of the formation and destruction of complex \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]\).

The fact that the hypothesis I is capable of describing experiments does not mean that this hypothesis corresponds to reality, as functional dependency is very simple (Fig. 4, curve 4). Perhaps, the experiments can also be described by hypothesis II, in which the equation models hydrogen generation:

$$\frac{{dN_{{{\text{H}}_{2} }} }}{{m_{{{\text{cat}}}} dt}} \approx 4S_{{{\text{cat}}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} K_{{\text{W}}}^{{{\text{SD}}}} \frac{{N_{{\text{W}}}^{{\text{S}}} }}{{N_{{\text{W}}}^{{\text{D}}} }}$$
(18)

In this case, the function \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right)/N_{{\text{W}}}^{{\text{D}}} \left( \xi \right)\) must increase, and we must formulate assumptions concerning the behavior of \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right)\) and \(N_{{\text{W}}}^{{\text{D}}} \left( \xi \right)\) functions. For water molecules, three types are distinguished in electrolyte solutions. The molecules of first type are associated into hydration complexes of positive Na+ ions, the second ones are associated into hydration complexes of negative OH– ions, and the third ones are free. Let's denote these types of water molecules as \({\text{H}}_{2} {\text{O}}_{ + }\), \({\text{H}}_{2} {\text{O}}_{ - }\) and \({\text{H}}_{2} {\text{O}}_{F}\) correspondingly. It is clear that the properties of such molecules differ, that raises two questions: what type of water molecules are preferentially sorbed, and what type causes desorption. The dipole moments of \({\text{H}}_{2} {\text{O}}_{ + }\) and \({\text{H}}_{2} {\text{O}}_{ - }\) molecules are oriented differently, and the velocity of their thermal motion (the velocity of the complex) is lower than that of free molecule \({\text{H}}_{2} {\text{O}}_{F}\). One can assume that water molecules are adsorbed from hydration complexes, and desorption is initiated by free water molecules.

The number of free molecules \(N_{{{\text{H}}_{2} {\text{O}}_{F} }}\) in solution decreases due to hydrolysis (i.e. \(N_{{\text{W}}}^{{\text{D}}} \left( \xi \right)\) is decreasing function).

$$N_{{{\text{H}}_{2} {\text{O}}_{F} }} = N_{{{\text{H}}_{2} {\text{O}}}}^{0} - N_{{{\text{H}}_{2} {\text{O}}_{ + } }} - N_{{{\text{H}}_{2} {\text{O}}_{ - } }} - 4\xi N_{{{\text{NaBH}}_{4} }}^{0}$$
(19)

As amount of Na+ ions in the solution does not change during hydrolysis, \(N_{{{\text{H}}_{2} {\text{O}}_{ + } }}\) does not change as well. We cannot predict the change in the number of OH– ions; both \(N_{{{\text{H}}_{2} {\text{O}}_{ - } }}\) increase and decrease can be possible.

The coordination numbers of Na+ and OH.– ions are approximately the same, and we used the same number k:\(N_{{{\text{H}}_{2} {\text{O}}_{ + } }} = kN_{{{\text{Na}}^{ + } }}\), \(N_{{{\text{H}}_{2} {\text{O}}_{ - } }} = kN_{{{\text{OH}}^{ - } }}\). Further, three pathways of water molecules adsorption were proposed:\(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right) = N_{{{\text{H}}_{2} {\text{O}}_{ + } }} = kN_{{{\text{NaBH}}_{4} }}^{0}\), \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right) = N_{{{\text{H}}_{2} {\text{O}}_{ - } }} = kN_{{{\text{OH}}^{ - } }}\) and \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right) = N_{{{\text{H}}_{2} {\text{O}}_{ + } }} + N_{{{\text{H}}_{2} {\text{O}}_{ - } }} = kN_{{{\text{NaBH}}_{4} }}^{0} + kN_{{{\text{OH}}^{ - } }}\). Since \(N_{{{\text{Na}}^{ + } }} > > N_{{{\text{OH}}^{ - } }}\) in aqueous solutions of sodium borohydride, the first and third variants are almost identical and \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right) \approx {\text{const}}\). In this case, the growth of \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right)/N_{{\text{W}}}^{{\text{D}}} \left( \xi \right)\) is completely related to the decrease of \(N_{{\text{W}}}^{{\text{D}}} \left( \xi \right)\)

$$N_{{\text{W}}}^{{\text{D}}} \left( \xi \right) = N_{{{\text{H}}_{{2}} {\text{O}}_{F} }} \left( \xi \right) = N_{{{\text{H}}_{2} {\text{O}}}}^{0} - kN_{{{\text{NaBH}}_{4} }}^{0} - kN_{{{\text{OH}}^{ - } }} - 4\xi N_{{{\text{NaBH}}_{4} }}^{0} \approx N_{{{\text{H}}_{2} {\text{O}}}}^{0} - N_{{{\text{NaBH}}_{4} }}^{0} \left( {k + 4\xi } \right)$$
(20)

Remarkably, there are no unknown kinetic parameters in Eq. 20. The coordination number \(k\) is a function of ion concentration and solution temperature. All our experiments were carried out with solutions of identical concentration and, in this case, \(k\) may differ for experiments with different temperatures, but be nearly identical for experiments with the same temperature. This hypothesis was analyzed by approximating the dependence of the average specific rate of catalytic hydrolysis (curve 4 in Fig. 4) using (21) comprising parameters \(B_{1} \equiv S_{{{\text{cat}}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} K_{{\text{W}}}^{{{\text{SD}}}}\) and \(k\)

$$\frac{{dN_{{{\text{H}}_{2} }} }}{{m_{{{\text{cat}}}} dt}} \approx 4S_{{{\text{cat}}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} K_{{\text{W}}}^{{{\text{SD}}}} \frac{{N_{{\text{W}}}^{{\text{S}}} }}{{N_{{\text{W}}}^{{\text{D}}} }} = \frac{{4S_{{{\text{cat}}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} K_{{\text{W}}}^{{{\text{SD}}}} N_{{{\text{NaBH}}_{4} }}^{0} k}}{{N_{{{\text{H}}_{2} {\text{O}}}}^{0} - C_{{{\text{NaBH}}_{4} }}^{0} \left( {k + 4\xi } \right)}} = \frac{{4B_{1} k}}{{N_{{{\text{H}}_{2} {\text{O}}}}^{0} /N_{{{\text{NaBH}}_{4} }}^{0} - \left( {k + 4\xi } \right)}}$$
(21)

If \(N_{{{\text{OH}}^{ - } }} \left( \xi \right)\) is a growing function, we cannot analyze \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right) = kN_{{{\text{OH}}^{ - } }}\), as developed model doesn’t comprise kinetics of OH– ion change during hydrolysis.

Temperature dependences of kinetic coefficients

Using results of kinetic experiments we analyzed the possibilities of approximating the dependence (curve 4 in Fig. 4) employing Eqs. 17 and 21. The experiments were carried out at 30 °C and different amounts of catalyst. An analysis of these data proved that the specific rates of hydrogen generation weakly depend on the amount of catalyst, and this dependence can be explained by fluctuations in the properties of catalyst samples in different experiments. Therefore, several series experiments were carried out with \(m_{{{\text{cat}}}}\) = 0.01 and 0.05 g at 20, 30, 40, 50, and 60 °C (Fig. 6) to determine G1(T) and G2(T).

Fig. 6
figure 6

Effect of temperature and amount of catalyst on NaBH4 decomposition. 1 – homogeneous process, 2 – 0.01 g, 3 – 0.05 g of catalyst. = 4.23 mol.kg-1

Full size image

These data were processed in accordance with the methodology explained above, but their specific rates similar to those shown in Fig. 4 (curves 1–3) were not averaged; the values G1(T) and G2(T) were determined for each of the 10 experiments with the Co/TiO2 catalyst.

Table 1 provides these data, and Arrhenius approximation is presented in Fig. 7. The average relative error for determined parameters are calculated as \(rms = 100\sqrt {\frac{{\sum\limits_{i = 1}^{n} {\left( {\frac{{f_{{\text{i}}}^{{{\text{experimental}}}} }}{{f_{{\text{i}}}^{{{\text{model}}}} }} - 1} \right)^{2} } }}{n}}\). The value of n is varied from 35 to 39 in 10 considered experiments.

Table 1 Calculated values of G1 and G2 at different temperatures
Full size table
Fig. 7
figure 7

Approximation of a G1(T) and b G2(T) by the Arrhenius exponent. \(\bullet\)–\(m_{{{\text{cat}}}}\) = 0.01 g, \(\circ\)–\(m_{{{\text{cat}}}}\) = 0.05 g, \({\mathbf{ + }}\) is the value found from the averaged function of line 4 in Fig. 4

Full size image

The function \(G_{1} \left( T \right) \equiv S_{{{\text{cat}}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} \frac{{\tilde{K}_{{\text{W}}}^{{{\text{SD}}}} }}{{1 + \tilde{K}_{{\text{W}}}^{{{\text{SD}}}} }}\) is fairly well approximated by the Arrhenius exponent, but at the same time, data fibration is reliably observed. All points corresponding to \(m_{{{\text{cat}}}}\) = 0.01 g are above the points with \(m_{{{\text{cat}}}}\) = 0.05 g. The resulting value of the activation energy 7541 K can be considered as a characteristic of the heterogeneous reaction (4) \(R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}}\), and the stratification can be associated with \(\frac{{\tilde{K}_{{\text{W}}}^{{{\text{SD}}}} \left( {m_{{{\text{cat}}}} } \right)}}{{1 + \tilde{K}_{{\text{W}}}^{{{\text{SD}}}} \left( {m_{{{\text{cat}}}} } \right)}}\). If \(\tilde{K}_{{\text{W}}}^{{{\text{SD}}}}\) >  > 1, then the dependence on \(m_{{{\text{cat}}}}\) is weak. It is worth noting that the value obtained is close to 7710 K found in [23] using a simplified data processing procedure (without taking into account the acceleration of hydrolysis).

The function G2(T) is clearly more complex than the Arrhenius exponent. The observed data stratification and complex behavior is due to insufficient approximation accuracy \(N_{{\left[ {{\text{comp}}} \right]}} /N_{{\left[ {{\text{comp}}} \right]}}^{{\text{D}}} \approx A_{{\text{C}}} \left( {1 - \xi } \right)\). Although the “activation energy” of −900 K found for G2(T) is hardly worth analyzing, note that it is negative, i.e. corresponds to the physical trend for decreasing of the equilibrium constants of adsorption/desorption processes with temperature growth. Data processing using (21) similarly to that carried out above, is presented in Table 2 and in Fig. 8.

Table 2 Calculated values of B1 and k at different temperatures
Full size table
Fig. 8
figure 8

Approximation a of B1(T) by the Arrhenius exponent and b k(T). \(\bullet\)–\(m_{{{\text{cat}}}}\) = 0.01 g, \(\circ\)–\(m_{{{\text{cat}}}}\) = 0.05 g; \({\mathbf{ + }}\)–the value found from the averaged function of line 4 (Fig. 4)

Full size image

A fibration of data with a very regular shift is clearly observed in Fig. 8 for a series of experiments with \(m_{{{\text{cat}}}}\) = 0.01 and 0.05 g. As \(B_{1} \equiv S_{{{\text{cat}}}} R_{{{\text{BH}}_{4}^{ - } }}^{{\text{W}}} K_{{\text{W}}}^{{{\text{SD}}}}\) must depend on temperature only, i.e. stratification by \(m_{{{\text{cat}}}}\) means induced effect. The weakness of model based on hypothesis II was in the assumption \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right) = N_{{{\text{H}}_{2} {\text{O}}_{ + } }}\), which simplified the formulation and we could model without using \(N_{{{\text{H}}_{2} {\text{O}}_{ - } }}\). As a consequence, an increase in the hydrolysis rate is achieved by changing k, which may depend on solution concentration and temperature, but k is not a function of catalyst amount. Nevertheless, the values k turned out to be quite reasonable and show decreasing trend with temperature growth. Two other versions of model II: \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right) = N_{{{\text{H}}_{2} {\text{O}}_{ - } }}\) and \(N_{{\text{W}}}^{{\text{S}}} \left( \xi \right) = N_{{{\text{H}}_{2} {\text{O}}_{ + } }} + N_{{{\text{H}}_{2} {\text{O}}_{ - } }}\) can change the situation, but require modeling of homogeneous kinetics of OH– ions. Models I and II are antagonistic, i.e. this requires to make a choice in favor of one of them. Determined activation energy value of 7541 K for \(G_{1} \left( T \right)\) is much more closer to 7710 K found in [23] than to 8408 K for B1(T). Besides, \(\ln G_{1} \left( {1/T} \right)\) (Fig. 7a) demonstrates a minimal fibration of data. This may be considered as substantive argument for the rationality of hypothesis I, however, in our opinion, hypothesis II should not be rejected yet.

Discussion

In the study of catalytic hydrolysis, it is wise to minimize the influence of irreversible homogeneous reactions. Usually, the amount of catalyst is increased in order to assure the predominance of heterogeneous processes. In this case, the intensity of hydrolysis and, accordingly, the amount of heat released grows. This generates difficulties in realizing isothermal process. In other words, homogeneous hydrolysis cannot be neglected when using “small” amounts of catalyst. When experimenting with large amounts of catalyst it is necessary to take into account the non-uniformity of temperature in the solution; it is difficult to do, because hydrolysis accelerates due to temperature growth and, accordingly, the power of heat generation increases. Such processes can lead to the exponential growth in solution temperature, despite the fact that the reactor is in the thermostat.

This article demonstrates a technique developed to process data of experiments with a relatively small amount of catalyst. The proposed method makes it possible to correct the measured rate of H2 generation by amount of homogeneous generation. Thus, the area in which hydrolysis can be considered heterogeneous is extended. When processing the data, one has to resort to numerical differentiation of the \(\xi \left( t \right)\) function, smoothing of the derivative obtained and construction of \(Q_{{{\text{H}}_{2} }} \left( \xi \right)\) function (rate of H2 generation as a function of decomposition degree \(\xi \left( t \right)\)). The accuracy of this method of processing depends both on the properties of the measuring equipment and on the quality of the smoothing algorithms. An alternative variant of experimental technique with measuring H2 generation by mass flow meter (MFM) and not measuring \(\xi \left( t \right)\). In this case, instead of differentiating \(\xi \left( t \right)\), the function \(Q_{{{\text{H}}_{2} }} \left( t \right)\) is integrated, that does not reduce processing accuracy. The technique using MFM is preferred for kinetic experiments because it directly measures the rate of H2 generation, but its implementation is based on high-performance MFM.

The effect of an increase in the specific rate of hydrogen generation with increasing \(\xi\) was observed for the Co/TiO2 catalyst in our experiments as well as in some other works [11, 25, 32,33,34,35,36,37] with Co catalysts. Such an effect n experiments on the catalytic hydrolysis of NaBH4 appears quite rarely, and we have not seen any discussion of the reasons for such acceleration in the literature. We proposed two-component model of adsorption water molecules \({\text{H}}_{2} {\text{O}}^{{\text{S}}}\) and complexes \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]^{{\text{s}}}\) to analyze the kinetics of the catalytic process.

Two hypotheses were put forward to explain the observed acceleration of the process with \(\xi\) growth. The first hypothesis associates this acceleration with a growth of \({\text{H}}_{2} {\text{O}}^{{\text{S}}}\) amount due to \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]^{{\text{s}}}\) decrease. The second hypothesis assumed single-component adsorption of \({\text{H}}_{2} {\text{O}}^{{\text{S}}}\), and the acceleration of hydrolysis was associated with a change of fluxes of water molecules controlling adsorption and desorption. The foundation of this hypothesis is the ion hydration model, which divides water molecules into three types \({\text{H}}_{2} {\text{O}}_{ + }\), \({\text{H}}_{2} {\text{O}}_{ - }\) and \({\text{H}}_{2} {\text{O}}_{{\text{F}}}\). Two developed models were applied to obtain the increase of hydrolysis rate observed in experiments, and to calculate the activation energy of a heterogeneous reaction. Both models comprise two unknown parameters. These parameters were tuned individually to fit each experiment. As shown in calculations for all experiments, both models well approximated the segment of the kinetic curves with an increase in the hydrolysis rate (similarly to Fig. 5). However, the temperature dependences of the model parameters for two series of experiments \(m_{{{\text{cat}}}}\) = 0.01 and 0.05 g turned out to be shifted relative to each other. Discussing data fibration in six isothermal experiments in Section “Analysis of the experimental data” we assumed that this is due to varying the properties of catalyst samples. However, two series of 5 experiments with different temperatures showed a regular rather than random bias in the data. The reason of observed fact is unknown and requires further investigation.

Since information about homogeneous reactions that control the formation and destruction of complexes is not available in the literature, we simplified our models of catalytic hydrolysis. However, it turned out that such simplification does not allows making a choice in favor of one of the two alternative hypotheses to explain the growth of H2 generation rate in the second phase of hydrolysis. The development of a model of homogeneous formation and destruction processes is an urgent problem. The solution of this problem is relevant for the description of both homogeneous and catalytic hydrolysis.

The number of \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]\) complexes is strictly dependent affected by concentration of OH- ions. A natural way to vary the OH- concentration widely is to use aqueous alkaline solutions. An effective way to develop a model of complex formation and destruction would be to study homogeneous hydrolysis in aqueous alkaline solutions with varying NaOH concentration over a wide range.

Conclusion

Following a comparison of the data of a homogeneous experiment with the data of experiments with different amounts of catalyst, it was established that, in all cases, hydrolysis began in a homogeneous mode, i.e. heterogeneous reactions were triggered with a delay. This means that the initial section of the graph of hydrolysis rate cannot be processed according to the model of the catalytic process.

Two types of neutral particles \({\text{H}}_{2} {\text{O}}^{{\text{S}}}\) and \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]^{{\text{s}}}\) were considered in the proposed adsorption model. These particles were considered as initiators of irreversible heterogeneous hydrolysis reactions. The processing of experimental data showed that for the studied Co/TiO2 catalyst the main heterogeneous process is collision of \({\text{H}}_{2} {\text{O}}^{{\text{S}}}\) and \({\text{BH}}_{4}^{ - }\) ions from solution.

The effect of accelerating the rate of hydrolysis in the final phase on the Co/TiO2 catalyst is reliably observed. Developed model should be supplemented with homogeneous reactions controlling the formation and destruction of \(\left[ {{\text{BH}}_{4}^{ - } \cdot {\text{H}}^{ + } } \right]\) complexes.