Double function method for the confirmation of the reaction mechanism of LiCoPO₄ nanoparticle formation, reliable activation energy, and related thermodynamic functions

Abstract

In this study, dehydration I and II, polycondensation, and decarbonization processes of the thermal solid-state reaction between CoHPO₄⋅3H₂O and Li₂CO₃ were observed and the LiCoPO₄ nanoparticles were obtained. For the sample characterization, the TG/DTG/DTA, FTIR, and AAS/AES techniques were applied. Structures and morphologies were investigated by the XRD and SEM techniques, respectively. To calculate the variable activation energy ($E_{\alpha }$) value, various isoconversional equations were used. In addition, the iterative isoconversional equations were also used to obtain the more reliable $E_{\alpha }$ values of 64.04 ± 3.20, 78.54 ± 3.23, 100.41 ± 6.00, and 140.07 ± 5.02 kJ mol⁻¹ for the first (regions I and II), second, and final steps, respectively. The first (regions I and II) as well as the second and final steps were confirmed to be a single-step kinetic process with the unique kinetic parameters. The double function $y(\alpha )$ and $z(\alpha )$ method was used to confirm the reaction mechanisms and found to be $R_{2}$, $R_{3}$, $A_{3}$, and $P_{3}$ corresponding to contracting cylinder, contracting sphere, assumed random nucleation (and its subsequent growth), and nucleation processes, respectively. The studied processes lead to the formation of the final nanoparticle product LiCoPO₄. The four pre-exponential factors calculated using $E_{\alpha }$ and mechanism functions were found to be 1.01 (±0.016) × 10⁷, 7.80 (±0.009) × 10⁷, 4.52 (±0.010) × 10⁵, and 1.03 (±0.003) × 10⁶ s⁻¹, respectively. The related standard thermodynamic functions of the transition-state complexes were evaluated by using the calculated kinetic parameters.

Introduction

The basic requirements for the development of superior Li-ion batteries are energy density, safety, low cost, and environmental friendliness, which directly relate to the quality of the cathode performance. Cathode materials with olivine-structured LiXPO₄ (X = Fe, Co, Mn, and Ni) have been used as the substitution of the commercial LiCoO₂ cathode [1] because of their native stability and the advanced electrochemical characters. The Fe, Co, Mn, and Ni title phosphate compounds have become promising candidates owing to the strong P–O covalent bond of the ${\text{PO}}_{ 4}^{ 3- }$ unit and its stability [2]. LiCoPO₄ (LCP) shows higher electrochemical performance than LiFePO₄ (LFP). LCP has a theoretical capacity of 167 mAh g⁻¹ and a working potential of 4.8–4.9 V [3], which is very important for the development of Li-ion battery applications in mobile technologies. In addition, the lattice volume change during charge/discharge processes between the CoPO₄ and LCP compounds is ~2%, which is less than FePO₄/LFP and MnPO₄/LiMnPO₄ (LMP) couples of ~7 and ~9%, respectively [2, 4]. According to the above-mentioned properties, the LCP cathode material may be one of the most advanced among the LiXPO₄ materials. Cobalt phosphate hydrate nanosheets (CPHNs, CoHPO₄⋅3H₂O) were synthesized by a one-pot hydrothermal method [5]. CPHN is produced for constructing the supercapacitor electrodes. According to the nanostructures, the electrode shows a specific capacitance of 413 F g⁻¹ without obvious decay even after 3000 charge/discharge cycles [5]. In our previous works [6, 7], the LiXPO₄ (X = Mn, Mg, Mn_0.5Mg_0.5, and Co_0.5Mg_0.5) compounds were synthesized via the corresponding hydrate precursors (NH₄XPO₄⋅H₂O) and compared by two different Li sources of LiOH⋅H₂O and Li₂CO₃. It was found that Li₂CO₃ showed smaller particle size. The performance of LiXPO₄ that was used as a cathode electrode in Li batteries was greatly improved by reducing the particle sizes, intimate conducting phase coating, and metal supervalent doping [6, 7]. The nanosized particles were used for improving the performance of batteries because of their ability to reduce the diffusion length for electrons and Li ions as well as increasing the effective reaction areas of the charge/discharge processes in the battery cell [6, 7]. In addition, the LMP cathode material was successfully synthesized by the thermal solid-state reaction between MnHPO₄⋅3H₂O and Li₂CO₃ [8].

The benefits of kinetic analyses are the prediction of the process rates, material lifetimes, and the interpretation of experimentally determined kinetic parameters [9] (or kinetic triad [10]) including activation energy ($E$), which is calculated by each conversion $\alpha$ and denoted as $E_{\alpha }$(variable activation energy), pre-exponential factor or $A$, and the reaction mechanism functions $f(\alpha )$ and $g(\alpha )$. Both the functions $f(\alpha )$ and $g(\alpha )$ are applied as the mathematical expression to describe the thermal decomposition or formation processes. In addition, an important requirement to understand the chemical reaction process is that one should have the knowledge of the thermodynamic properties such as standard enthalpy $\Delta H^{0 \ne }$, standard entropy $\Delta S^{0 \ne }$, and standard Gibbs free energy $\Delta G^{0 \ne }$ of activation. The thermal analysis by the thermogravimetry/differential thermal gravimetry/differential thermal analysis (TG/DTG/DTA) method is widely used for the measurements of kinetic and thermodynamic properties by the thermal decomposition process of the studied system [9].

Therefore, the objective of this work was to synthesize the LCP compound with the nanoparticle sizes as well as to evaluate the reliable values of the kinetics, reaction mechanism, and thermodynamic functions of the LCP formation by the thermal solid-state reaction between the synthesized hydrate precursor, CoHPO₄·3H₂O, and Li₂CO₃ as a Li source. The studied samples were characterized by TG/DTG/DTA, Fourier transform infrared spectroscopy (FTIR), and atomic absorption spectrophotometry/atomic emission spectrophotometry (AAS/AES). The structures and morphologies were investigated by X-ray powder diffraction (XRD) and scanning electron microscopy (SEM), respectively. The more reliable activation energy $E_{\alpha }$ values were determined by various isoconversional methods such as the Ozawa–Flynn–Wall (OFW) [6], Tang [11], Starink [12], and Kissinger–Akahira–Sunose (KAS) [6] equations. The iterative OFW (iOFW) and iterative KAS (iKAS) [6, 13] equations, which are other types of the isoconversional methods, were selected to increase the accuracy of the $E_{\alpha }$ value. The more reliable $f(\alpha )$ value of the LCP formation was determined by comparing the experimental and model plot results from the double function check of $y(\alpha )$ and $z(\alpha )$ as established by Málek [9, 14, 15]. The value of $A$ was calculated using the obtained reliable $E_{\alpha }$ and $f(\alpha )$. The related thermodynamic functions of the transition-state complexes were estimated by using the reliable kinetic parameters. The kinetic parameters and thermodynamic functions of the LCP formation from the CoHPO₄⋅3H₂O precursor were evaluated and reported for the first time.

Experimental section

Preparation

The hydrated precursor, CoHPO₄⋅3H₂O, was prepared by a direct precipitation reaction according to the literature [8, 16]. In a typical synthesis, 25 mL of 0.2 M CoCl₂⋅6H₂O solution was added to 25 mL of 0.2 M H₃PO₄ solution with the mole ratio of cobalt to phosphate of 1:1. The pH of the reaction mixture was adjusted to 7 by the addition of 25 mL of 0.4 M NaOH solution. Then, the violet precipitates were obtained. The precipitates were filtered and washed with deionized (DI) water several times to remove ions from the incomplete reaction. Finally, the synthesized hydrate precipitates were dried and kept in a desiccator. Then, the title hydrate was converted to LCP by the thermal solid-state reaction with Li₂CO₃. The stoichiometric molar ratio of CoHPO₄⋅3H₂O to Li₂CO₃ of 2:1 was finely grounded by hand in an alumina mortar for 45–50 min. After 2 h of the calcination at 730 °C under a heating rate of 5 °C min⁻¹ in an alumina crucible without pressing the lid, the LCP compound was obtained and washed several times with DI water, dried at 110 °C for overnight, and kept in the desiccator for further investigations. The preparations of the synthesized hydrate precursor, CoHPO₄⋅3H₂O, and its thermal solid-state reaction product, LCP, were carried out according to the following equations:

Direct-precipitation reaction:

$${\text{CoCl}}_{ 2} \cdot 6 {\text{H}}_{ 2} {\text{O}}\left( {\text{aq}} \right) \, + {\text{ H}}_{ 3} {\text{PO}}_{ 4} \left( {\text{aq}} \right) \, + {\text{ 2NaOH}}\left( {\text{aq}} \right) \, \to {\text{ CoHPO}}_{ 4} \cdot 3 {\text{H}}_{ 2} {\text{O}}\left( {\text{s}} \right) \, + {\text{ 2NaCl}}\left( {\text{aq}} \right) \, + {\text{ 5H}}_{ 2} {\text{O}}\left( {\text{l}} \right)$$

(1)

Thermal solid-state reaction:

$$2 {\text{CoHPO}}_{ 4} \cdot 3 {\text{H}}_{ 2} {\text{O}}\left( {\text{s}} \right) \, + {\text{ Li}}_{ 2} {\text{CO}}_{ 3} \left( {\text{s}} \right) \, \to {\text{ 2LiCoPO}}_{ 4} \left( {\text{s}} \right) \, + {\text{ 7H}}_{ 2} {\text{O}}\left( {\text{g}} \right) \, + {\text{ CO}}_{ 2} \left( {\text{g}} \right)$$

(2)

Characterization

The water content in the synthesized crystalline hydrate CoHPO₄⋅3H₂O was determined by TG/DTG/DTA methods on Pyris Diamond (Perkin-Elmer), whereas the lithium content of its thermal solid-state reaction product, LCP, was determined by the AES method (Perkin-Elmer, Analyst 100). The cobalt contents of both hydrate and LCP were determined by the AAS method coupled with the AES instrument. The FTIR spectra were recorded in a wavenumber range of 4000–370 cm⁻¹ using the KBr pellet technique (Merck, spectroscopy grade) on a Perkin-Elmer spectrum GX FTIR/FT Raman spectrophotometer with 32 scans and a resolution of 4 cm⁻¹. The structures of the studied compounds were determined by using the XRD method on a D8 Advanced Powder Diffractometer (Bruker AXS, Karlsruhe, Germany) with Cu K_α radiation, λ = 0.15406 Å, and compared with the standard Powder Diffraction File (PDF) database of the International Center for Diffraction Data (ICDD). The 2θ angles were found to be between 5° and 70° with an increment of 0.02° and 1 s per step scan speed. The lattice parameters and lattice volumes were determined by a least-squares refinement of the XRD data with the aid of a computer program corrected for systematic experimental errors. The crystallite sizes (D) were calculated using the Scherrer equation:

$$D = \frac{k\lambda }{\beta \cos \theta }$$

(3)

Here λ is the wavelength of the X-ray radiation, k is a constant fixed as 0.89, θ is the diffraction angle, and β is the full width at half-maximum of the XRD peak intensity [17]. The morphologies of the samples were investigated by using the SEM technique (LEO SEM VP1450) after gold coating.

Isoconversional kinetic method

The isoconversional kinetic method or the model-free method has been studied at a constant heating rate or by using a nonisothermal method [13, 18–20]. The TG/DTG/DTA experiments of the mixture of the synthesized hydrate precursor, CoHPO₄⋅3H₂O, and Li₂CO₃ (Li source) were carried out at four different heating rates of 5, 10, 15, and 20 °C min⁻¹ over a temperature range of 50–900 °C in air atmosphere with an air flow rate of 100 mL min⁻¹. An accurate sample mass of 8.5 mg was filled into an alumina pan without pressing the lid. The TG/DTG/DTA curves were plotted by using α-Al₂O₃ as the reference material.

Theoretical Method

According to the isoconversional procedure [13, 18–20], the thermal decomposition kinetic investigation of the single crystalline compound is a solid-state reaction of the following type [21–23]:

$${\text{A}}\left( {\text{s}} \right) \, \to {\text{ B}}\left( {\text{s}} \right) \, + {\text{ C}}\left( {\text{g}} \right)$$

(4)

The solid-state reaction of two or more than two crystalline compounds can be described as the following type [6, 7]:

$$\sum {\text{A}}_{i} \left( {\text{s}} \right) \, \to \, \sum {\text{B}}_{j} \left( {\text{s}} \right) \, + \, \sum {\text{C}}_{k} \left( {\text{g}} \right)$$

(5)

Here i, j, and k are the chemical crystalline compound species. In addition, a novel theory for kinetic analysis of solid-state decompositions was formulated by L’vov [10, 24–26]. The alternative approach to analyzing decomposition kinetics [10, 24–26] is identified to be:

$${\text{A}}_{\text{a}} {\text{B}}_{\text{b}} \left( {{\text{s}}/{\text{l}}} \right) \, \leftrightarrow {\text{ aA}}\left( {\text{g}} \right) \, + {\text{ bB}}\left( {\text{g}} \right) \to {\text{aA}}\left( {\text{s}} \right) \, + {\text{ bB}}\left( {\text{g}} \right)$$

(6)

The isoconversional kinetic method is a model-free method (considering without a reaction kinetic model), which measures the absolute temperatures ($T$) corresponding to the fix value of the extent of conversion ($\alpha$) at different heating rates ($\beta$) ($\beta = \frac{dT}{dt}$ in K min⁻¹, where $t$ is time in min). The $\alpha$ values from thermogravimetric data were defined as the ratio of the actual mass loss to the total mass loss corresponding to the investigated process:

$$\alpha = \frac{{m_{0} - m_{t} }}{{m_{0} - m_{f} }}$$

(7)

Here $m_{t}$ is the mass of the sample at time $t$, $m_{0}$ and $m_{f}$ are the masses of the sample at the beginning and end of the mass loss, respectively, in the reaction result of the TG curve.

Considering the isoconversional kinetic theory, the thermal decomposition kinetic equation of the solid-state reaction [27–29] is assumed to be based on the following equation:

$$\frac{d\alpha }{dt} = Af(\alpha )\exp \left( {\frac{{ - E_{\alpha } }}{RT}} \right)$$

(8)

Equation 8 can be modified to be

$$\beta \frac{d\alpha }{dT} = Af(\alpha )\exp \left( {\frac{{ - E_{\alpha } }}{RT}} \right)$$

(9)

Consequently, Eq. 9 can be rearranged and integrated to be expressed as

$$g(\alpha ) = \int\limits_{0}^{\alpha } {\frac{d\alpha }{f(\alpha )}} = \frac{A}{\beta }\int\limits_{0}^{T} {\exp \left( {\frac{{ - E_{\alpha } }}{RT}} \right)dT}$$

(10)

Here $E_{\alpha }$ is the apparent activation energy, $A$ is the pre-exponential factor, $R$ is the gas constant (8.134 J mol⁻¹ K⁻¹), and $f(\alpha )$ is the reaction mechanism function or the conversion function in the differential form, which describes the physical meaning of the chemical reaction. $g(\alpha )$ on the left-hand side of Eq. 10 is the integral form of $f(\alpha )$. Various scientists suggested different methods for solving Eq. 10. Thus, the kinetics of solid-state reactions can be described by various equations depending on their reaction mechanisms. The solution of the integral in Eq. 10 depends on the explicit expression of the $f(\alpha )$ function.

Determination of the variable activation energy $E_{\alpha }$

The variable activation energy $E_{\alpha }$ is one of the fundamental quantities influencing each physical process. This quantity is the key value that is used to describe the kinetic behavior of the studied process because it represents either exact or apparent energetic barriers of the transition-state complexes. In the other word, the variable activation energy $E_{\alpha }$ value is usually calculated, $E_{\alpha }$ sometimes being interpreted to identify a rate controlling step, for example, the energy required to rupture a specific reactant bond [10]. The integral isoconversional method is used to calculate the variable $E_{\alpha }$ value. This method is developed from the isoconversional principle application of the integral in Eq. 10 that does not have a simple solution for a temperature program. However, a solution can also be obtained for a nonisothermal temperature program [9]:

$$g(\alpha ) = A\exp \left( {\frac{{ - E_{\alpha } }}{RT}} \right)t$$

(11)

Equation 12 can be obtained by certain simple rearrangement followed by the isoconversional principle application:

$$\ln t_{\alpha ,i} = \ln \left[ {\frac{g(\alpha )}{A}} \right] + \frac{{E_{\alpha } }}{{RT_{i} }}$$

(12)

Here $t_{\alpha ,i}$ is the time to obtain a given $\alpha$ at different $T_{i}$. This equation is used for an integral isoconversional method under isothermal conditions. The $E_{\alpha }$ value is determined from the slope of the plot between $\ln t_{\alpha ,i}$ and $\frac{1}{{T_{i} }}$ [9].

For the commonly used constant heating rate run or a nonisothermal program, Eq. 5 can be transformed into Eq. 10, which does not have a simple solution. Therefore, there are a number of integral isoconversional methods that differ in approximations of the temperature integral in Eq. 10. Many series of these approximations give rise to linear equations of the following general form [9]:

$$\ln \frac{\beta }{{T^{B} }} = Const - C\frac{{E_{\alpha } }}{RT}$$

(13)

Here B and C are the parameters determined by the type of the temperature integral approximation; for example, the Murray and White approximation [9], which is a very crude approximation that yields B = 0 and C = 1.0516 so that Eq. 13 takes the following form known as the OFW equation:OFW:

$$\ln \beta = \ln \frac{0.0048AE}{g(\alpha )R} - 1.0516\frac{{E_{\alpha } }}{RT}$$

(14)

A more accurate approximation by Tang gives B = 1.894661 and C = 1.0001450. Hence, Eq. 13 is referred to as the Tang equation:Tang:

$$\ln \frac{\beta }{{T^{1.894661} }} = \ln \frac{{AE_{\alpha } }}{g(\alpha )R} + 3.635041 + 1.894661\ln E_{\alpha } - 1.0001450\frac{{E_{\alpha } }}{RT}$$

(15)

When B = 1.92 [9] and C = 1.0008, the Starink approach is obtained. Hence, Eq. 13 is referred to as the Starink equation:

$$\ln \frac{\beta }{{T^{1.92} }} = Const - 1.0008\frac{{E_{\alpha } }}{RT}$$

(16)

The Murray and White approximation [9] sets B = 2 and C = 1 and leads to another popular equation that is called the KAS equation:

$$\ln \frac{\beta }{{T^{2} }} = \ln \frac{AR}{{g(\alpha )E_{\alpha } }} - \frac{{E_{\alpha } }}{RT}$$

(17)

In addition, the iterative isoconversional OFW (iOFW) and KAS (iKAS) equations were used to calculate the more reliable $E_{\alpha }$ values according to the following equations [6, 8]:iOFW:

$$\ln \frac{\beta }{H(x)} = \ln \frac{0.0048AE}{g(\alpha )R} - 1.0516\frac{{E_{\alpha } }}{RT}$$

(18)

iKAS:

$$\ln \frac{\beta }{{\pi (x)T^{2} }} = \ln \frac{AR}{g(\alpha )E} - \frac{{E_{\alpha } }}{RT}$$

(19)

In these equations, the following quantity is used:

$$H(x) = \frac{{\exp ( - x)\pi (x)/x^{2} }}{0.0048\exp ( - 1.0516x)}$$

(20)

Here $x = \frac{{E_{\alpha } }}{RT}$, whereas $\pi (x)$ is expressed by the eighth-order rational equation of the approximation formula of Pérez-Maqueda and Criado [30]:

$$\pi (x) = \frac{{x^{7} + 70x^{6} + 1886x^{5} + 24920x^{4} + 170136x^{3} + 577584x^{2} + 844560x + 357120}}{{x^{8} + 72x^{7} + 2024x^{6} + 28560x^{5} + 216720x^{4} + 880320x^{3} + 1794240x^{2} + 1572480x + 403200}}$$

(21)

The iterative procedure was performed using the following three steps: first, assume $H(x)$ or $\pi (x)$ = 1, respectively, for iOFW or iKAS to estimate the initial value or $E_{\alpha ,1}$. Isoconversional methods stop the calculation at this step. Second, use $E_{\alpha ,1}$ to calculate a new value or $E_{\alpha ,2}$ from the plot of $\ln \frac{\beta }{H(x)}$ versus $\frac{1}{T}$ (for iOFW) or $\ln \frac{\beta }{{\pi (x)T^{2} }}$ versus $\frac{1}{T}$ (for iKAS). Finally, repeat the second step, replacing $E_{\alpha ,1}$ by $E_{\alpha ,2}$. When $E_{\alpha ,i} - E_{\alpha ,i - 1}$ < 0.1 kJ mol⁻¹, the last $E_{\alpha ,i}$ value will be considered to be the variable $E_{\alpha }$ value of the studied reaction.

Reaction mechanisms

In order to determine the more reliable reaction mechanism of the studied system, the Málek method [9, 14, 15] was used to choose an appropriate reaction mechanism. According to the Málek method, Eq. 8 can be rearranged to obtain Eq. 22 for further determination of the $y(\alpha )$ function:

$$y(\alpha ) = \left( {\frac{d\alpha }{dt}} \right)_{\alpha } \exp \left( {\frac{{E_{\alpha } }}{{RT_{\alpha } }}} \right) = Af(\alpha )$$

(22)

Here $y(\alpha )$ values are directly determined from the experimental data by substituting the calculated $E_{\alpha }$ into Eq. 22. Then, for each value of $\alpha$, one needs to determine the experimental values of $\frac{d\alpha }{dt}$ or rewrite it as $\left( {\frac{d\alpha }{dt}} \right)_{\alpha }$ and the corresponding values of $T$ or rewrite it as $T_{\alpha }$. The resulting $y(\alpha )$ values are plotted as a function of $\alpha$ and compared with the master theoretical $y(\alpha )$ plots. From a series of experimental kinetic curves, $\left( {\frac{d\alpha }{dt}} \right)_{\alpha }$ versus $T_{\alpha }$ obtained at different $\beta$ values lead to a series of the experimental $y(\alpha )$ plots. The resulting numerical values of $y(\alpha )$ should not demonstrate any significant variation with $\beta$ giving rise to a single dependence of $y(\alpha )$ on $\alpha$. As can be seen from Eq. 22, the shape of the master theoretical $y(\alpha )$ plots is entirely determined by the shape of the $f(\alpha )$ functions that represent the reaction models in Table S1 (Supplementary Information) [31–33], where $A$ is a constant. However, as $A$ is yet unknown, the experimental and theoretical $y(\alpha )$ plots have to be normalized in a similar manner. For practical reasons, the $y(\alpha )$ plots are normalized by varying from 0 to 1.

In addition, the $z(\alpha )$ function was also used to determine a reaction mechanism. The temperature integral in Eq. 10 can be resolved as follows [9]:

$$g(\alpha ) = \frac{{AE_{\alpha } }}{\beta R}\exp ( - x)\frac{\pi (x)}{x}$$

(23)

Combining Eqs. 22 and 23 followed by some rearrangements allows one to introduce the $z(\alpha )$ function as:

$$z(\alpha ) = f(\alpha )g(\alpha ) = \left( {\frac{d\alpha }{dt}} \right)_{\alpha } T_{\alpha }^{2} \left[ {\frac{\pi (x)}{{\beta T_{\alpha } }}} \right]$$

(24)

The fact that the term $\left[ {\frac{\pi (x)}{{\beta T_{\alpha } }}} \right]$ in Eq. 24 has a negligible effect on the shape of the $z(\alpha )$ function has been established [9]. Thus, the shapes of $z(\alpha )$ can be determined for each value of $\alpha$ by multiplying the experimental values of $\left( {\frac{d\alpha }{dt}} \right)_{\alpha }$ and $T_{\alpha }^{2}$. The resulting experimental values of $z(\alpha )$ are plotted as a function of $\alpha$ and compared with the master theoretical $z(\alpha )$ plots. From a series of experimental kinetic curves measured at different $\beta$, one can obtain a series of the experimental $z(\alpha )$ plots that should, however, yield a single dependence of $z(\alpha )$ on $\alpha$, which is practically independent of $\beta$. The theoretical $z(\alpha )$ plots are obtained and normalized by varying from 0 to 1 by plotting the multiple product of $f(\alpha )g(\alpha )$ versus $\alpha$ in Table S1 (Supplementary Information) for different reaction models.

A suitable reaction mechanism is identified as the best match between the experimental and theoretical $y(\alpha )$ together with master experimental and theoretical $z(\alpha )$ plots. The comparison methods obtained by the $y(\alpha )$ and $z(\alpha )$ functions are effective techniques recommended by the Kinetics Committee of the International Confederation for Thermal Analysis and Calorimetry (ICTAC) [9].

Pre-exponential Factor A

Under the maximum reaction rate condition, the second derivative of the conversion factor or $\frac{{d^{2} \alpha }}{{dt^{2} }}$ of Eq. 8 is zero, i.e.,

$$\frac{{d^{2} \alpha }}{{dt^{2} }} = \left[ {\frac{{\beta E_{0} }}{{RT_{\hbox{max} }^{2} }} + Af^{\prime}(\alpha_{\hbox{max} } )\exp \left( {\frac{{ - E_{0} }}{{RT_{\hbox{max} } }}} \right)} \right]\left[ {\frac{d\alpha }{dt}} \right]_{\hbox{max} } = 0$$

(25)

Here $f^{\prime}(\alpha ) = \frac{df(\alpha )}{d\alpha }$ is the first derivative modified by $\frac{df(\alpha )}{dt} \cdot \frac{d\alpha }{d\alpha }$ and the subscript “max” in Eq. 25 denotes the values related to the maximum of the DTG curve obtained at a given heating rate. As a result of Eq. 25, the following equation can be written:

$$\frac{{\beta E_{0} }}{{RT_{\hbox{max} }^{2} }} + Af^{\prime}(\alpha_{\hbox{max} } )\exp \left( {\frac{{ - E_{0} }}{{RT_{\hbox{max} } }}} \right) = 0$$

(26)

After simple rearrangements of Eq. 26, $A$ can be expressed as shown by Eq. 27 [9]:

$$A = \frac{{ - \beta E_{0} }}{{RT_{\hbox{max} }^{2} f^{\prime}(\alpha_{\hbox{max} } )}}\exp \left( {\frac{{E_{0} }}{{RT_{\hbox{max} } }}} \right)$$

(27)

Results and discussion

Characterization

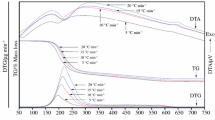
The TG/DTG/DTA curves of the thermal solid-state reaction between the synthesized hydrate precursor, CoHPO₄⋅3H₂O, and Li₂CO₃ at four different heating rates are shown in Fig. 1. The mass loss started at about 80 °C and ended up at about 730 °C for $\beta$ = 5 °C min⁻¹. The observed total mass loss in the TG curve is 39.93%, which is in good agreement with the theoretical value of 40.10%. The thermal solid-state reaction of the title system below 730 °C occurs in three steps. Mass losses in the first step (80–210 °C) and the second step (210–550 °C) were 23.19 and 4.72%, respectively, whereas for the final step (550–730 °C) the mass loss was calculated to be 12.02%, which agree very well with the theoretical values of 23.23, 4.74, and 12.03%, respectively, for the three steps. The first step corresponds to the elimination of water molecules or the dehydration process to form the CoHPO₄ compound. The dehydration process, in the first step, shows the main peak with a shoulder, which corresponds to the elimination of water molecules at different sites with different strengths of hydrogen bonding in the hydrate crystal structure. The sharp peak with the shoulder agrees with the literature [8, 16]. The second step corresponds to the elimination of water constituent of ${\text{HPO}}_{ 4}^{ 2- }$ anions (polycondensation) to give an amorphous phase of cobalt pyrophosphate (Co₂P₂O₇). Moreover, the exothermic peak (Fig. S1, Supplementary Information) in the DTA curve at about 620 °C for $\beta$ = 5 °C min⁻¹ can be described as the phase transition from an amorphous Co₂P₂O₇ to a monoclinic phase Co₂P₂O₇. The final step corresponds to the elimination of carbon dioxide molecule (decarbonization) to form the orthorhombic phase of lithium cobalt phosphate (LCP). The maximum yield of LCP was at around 730 °C for $\beta$ = 5 °C min⁻¹. When compared with the complete reaction temperature of the thermal solid-state reaction between MnHPO₄⋅3H₂O and an Li source of Li₂CO₃ obtained at 750 °C at the same heating rate to receive the LMP cathode electrode material [8], the complete reaction temperature of this work to generate the LCP cathode electrode material is 730 °C, which shows lower temperature than in the case of the MnHPO₄⋅3H₂O compound (750 °C) and hence saving both time and energy. According to the results in Fig. 1, the thermal solid-state reaction between the CoHPO₄⋅3H₂O precursor and Li₂CO₃ can be expressed as follows:

Fig. 1

Thermal solid state reaction processes between the synthesized precursor CoHPO₄⋅3H₂O and Li₂CO₃ demonstrated as TG (a) and DTG (b) curves in the temperature range of 50–850 °C at different four heating rates of 5, 10, 15 and 20 °C min⁻¹

First step (80–210 °C), dehydration:

$${\text{CoHPO}}_{ 4} \cdot 3 {\text{H}}_{ 2} {\text{O}}\left( {\text{s}} \right) \, \to {\text{ CoHPO}}_{ 4} \left( {\text{s}} \right) \, + {\text{ 3H}}_{ 2} {\text{O}}\left( {\text{g}} \right)$$

(28)

The second step (210–550 °C) is the elimination of water constituent (polycondensation):

$$2 {\text{CoHPO}}_{ 4} \left( {\text{s}} \right) \, \to {\text{ Co}}_{ 2} {\text{P}}_{ 2} {\text{O}}_{ 7} \left( {\text{s}} \right) \, + {\text{ H}}_{ 2} {\text{O}}\left( {\text{g}} \right)$$

(29)

The final step (550–730 °C) is decarbonization:

$${\text{Co}}_{ 2} {\text{P}}_{ 2} {\text{O}}_{ 7} \left( {\text{s}} \right) \, + {\text{ Li}}_{ 2} {\text{CO}}_{ 3} \left( {\text{s}} \right) \, \to {\text{ 2LiCoPO}}_{ 4} \left( {\text{s}} \right) \, + {\text{ CO}}_{ 2} \left( {\text{g}} \right)$$

(30)

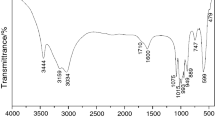
The FTIR spectra of the synthesized hydrate precursor, CoHPO₄⋅3H₂O, and its thermal solid-state reaction product LCP are shown in Fig. 2. The spectrum of CoHPO₄⋅3H₂O (Fig. 2a) illustrates broad bands with maxima around 3522 and 3280 cm⁻¹, which are assigned to the asymmetric ν₃(B₂) and symmetric ν₁(A₁) of O–H stretching vibrations, respectively. However, the doublet bands observed at 1711 and 1652 cm⁻¹ are assigned to two different ν₂(A₁) bending modes of the H₂O molecule at different sites and different hydrogen bond strengths of the synthesized crystalline hydrate. This result agrees with the TG/DTG/DTA results indicating that the water molecules were eliminated at two main temperatures. According to the FTIR spectrum of LCP in Fig. 2b, the strong bands with three maximum peaks at 1147, 1103, and 1076 cm⁻¹ are attributed to asymmetric stretching ν₃(F₂), whereas the single maximum peak at 977 cm⁻¹ is attributed to the symmetric stretching ν₁(A₁) mode of the ${\text{PO}}_{ 4}^{ 3- }$ unit. The other vibrational modes of the ${\text{PO}}_{ 4}^{ 3- }$ unit at 644, 587, and 546 cm⁻¹ are assigned to the resolved triply degenerate ν₄(F₂) stretching mode, whereas the resolved doubly degenerate ν₂(E) bending modes are obtained at 510 and 465 cm⁻¹. In addition, the single very weak band at 398 cm⁻¹ was described as the Mn–O stretching (ν_Mn–O). The FTIR spectrum of CoHPO₄⋅3H₂O is very similar to those of MnHPO₄⋅3H₂O [8], Mn_0.9Co_0.1HPO₄⋅3H₂O [16], and MgHPO₄⋅3H₂O [34]. In typical descriptions, the vibrational spectra of the ${\text{HPO}}_{ 4}^{ 2- }$ unit are observed in the regions of 3016–2620 cm⁻¹ with the observed maximum peaks at 2928 and 2560–2280 cm⁻¹ (two peaks at 2482 and 2406 cm⁻¹), which are assigned to the asymmetric stretching ν_OH(${\text{HPO}}_{ 4}^{ 2- }$) and symmetric stretching ν_OH(${\text{HPO}}_{ 4}^{ 2- }$), respectively. Furthermore, the vibrational spectra are obtained in the regions of 1300–1130 cm⁻¹ (two peaks at 1244 and 1172 cm⁻¹), 1130–940 cm⁻¹ (two peaks at 1065 and 1015 cm⁻¹), 940–840 cm⁻¹ (a peak at 899 cm⁻¹), 840–580 cm⁻¹ (a peak at 696 cm⁻¹), and 580–440 cm⁻¹ (a peak at 518 cm⁻¹), and these modes are assigned to ν(PO₃), δ(POH), ν(PO₂(OH)), γ(POH), and δ(PO₃), respectively [8, 16, 34]. The water bands at 3522, 3280 cm⁻¹ and 1711, 1652 cm⁻¹ disappeared after the calcination, which indicates the elimination of H₂O from the synthesized CoHPO₄⋅3H₂O compound to form an orthorhombic phase of the LCP compound.

Fig. 2

FTIR spectra by KBr technique operated at room temperature of the synthesized precursor CoHPO₄⋅3H₂O (a) and its thermal solid state reaction LCP (b) in the wavenumber range of 4000-370 cm⁻¹

The XRD patterns of the synthesized hydrate precursor CoHPO₄⋅3H₂O and its thermal solid-state reaction product LCP are presented in Fig. 3. The strong intensity and smooth baseline of diffraction patterns of both the precursor and the LCP product indicate their high crystallinity. According to Fig. 3a, all diffraction peaks are indexed as the orthorhombic phase of CoHPO₄⋅3H₂O with the space group Pmc2 ₁ ($C_{2v}^{2}$, No. 26) according to the PDF No. 39-0702 (CoHPO₄⋅3H₂O), a = 10.790, b = 8.358, and c = 25.910 Å. The calculated lattice parameters are a = 10.786, b = 8.355, and c = 25.908 Å with α = β = γ = 90°. The corresponding calculated lattice volume and crystallite size are 2334.75 Å³ and 52.6 nm, respectively. A diffraction pattern of the well-crystalline phase compound (Fig. 3b) observed after the thermal solid-state reaction of the precursor is indexed as the LCP compound when compared with PDF No. 32-0552, which is in the orthorhombic space group Pnma ($D_{2h}^{16}$, No. 62). The standard lattice parameters are a = 5.922, b = 10.200, and c = 4.701 Å. In this work, the calculated lattice parameters are a = 5.925, b = 10.195, and c = 4.698 Å with α = β = γ = 90°. The corresponding lattice volume and crystallite size are 283.92 Å³ and 40.2 nm, respectively.

Fig. 3

XRD patterns operated at room temperature with the hkl plane of the synthesized precursor CoHPO₄⋅3H₂O (a) compared with the standard PDF data # 39-0702 and its thermal solid state reaction product LCP (b) compared with the standard PDF data # 32-0552 in the 2θ range of 5–70°

In Fig. 4a, the SEM micrograph of the synthesized hydrate precursor CoHPO₄⋅3H₂O illustrates the plate-like crystals with a width of about 5–7 µm and a length of 7–11 µm together with the smaller irregular particles of about 1–3 µm. Fig. S2 (Supplementary Information) shows two phase morphologies. According to this figure, the micrograph was obtained from the mixture between the CoHPO₄⋅3H₂O precursor and Li₂CO₃ (Li source) before the beginning of the thermal solid-state reaction. The dominated plates are CoHPO₄⋅3H₂O, which are confirmed from Fig. 4a. On the other hand, the overhang or smaller particles are Li₂CO₃. The typical SEM micrograph of the LCP compounds is shown in Fig. 4b. According to this figure, the morphologies of the thermal solid-state reaction product LCP are different from those of the synthesized CoHPO₄⋅3H₂O precursor. The thermal conditions play an important role in the structural and morphological properties of the LCP phase. The final solid-state reaction product, LCP, shows the nanoparticle sizes of the seed-like particles. The nanosizes of the particles in Fig. 4b show the smaller sizes of about less than 10 nm together with the bigger seed particles in the range of about 10–300 nm. The effect of the Li source is attributed to the additional elimination of gas (decarbonization) that influences the reduction in the particle size [7]. The reduction of the particle size to the nanoscale is proven to improve the performance of the electrodes because the small particle size can shorten the diffusion length of electrons and Li ions as well as increase the effective reaction areas of the charge/discharge processes for the lithiation and delithiation processes, respectively [35, 36]. The LCP compound shows different morphologies from its precursor (CoHPO₄⋅3H₂O) due to the whole decomposition sequence of the following types: dehydration, polycondensation, and decarbonization processes.

Fig. 4

SEM micrographs after gold coating technique of the synthesized precursor CoHPO₄⋅3H₂O (a) showing the plate-like crystals and the thermal solid state reaction product LCP (b) showing the nanoparticle sizes of the seed-like particles

The mole numbers of the metals per chemical formula of the synthesized hydrate precursor and its final thermal solid-state reaction product were determined by the AAS and AES methods for Co and Li, respectively. The results show that the mole numbers of Co and Li metals are 0.98 and 0.96 mol per chemical formula of LCP, respectively. However, the mole number of water calculated from TG data was found to be 2.95 mol per chemical formula of CoHPO₄⋅3H₂O. These results together with the FTIR spectra and XRD patterns confirmed the formula for the synthesized hydrate precursor to be CoHPO₄⋅3H₂O and its thermal solid-state reaction product to be LCP.

Kinetics, mechanisms, and thermodynamics

Variable $E_{\alpha }$ values

The nonisothermal TG/DTG/DTA curves (Fig. 1) show three decomposition steps during the solid-state reaction processes between the synthesized CoHPO₄⋅3H₂O precursor and Li₂CO₃ (Li source) at four different heating rates $\beta$ of 5, 10, 15, and 20 °C min⁻¹. The peak temperature increases with an increase in $\beta$. This result is attributed to the fact that at the high heating rate there is not enough time for curing, and thus the TG/DTG/DTA curves will shift to a high temperature to compensate the reduced time [37]. The isoconversional OFW, Tang, Starink, and KAS equations were used to evaluate the variable $E_{\alpha }$ values. In addition, the isoconversional iOFW and iKAS equations were also used to evaluate the reliable $E_{\alpha }$ values. The variable $E_{\alpha }$ values of the three thermal decomposition steps during the solid-state reaction corresponding to different $\alpha$ (ranging from 0.10 to 0.90 with an increment of 0.02) are also obtained. The relation between variable $E_{\alpha }$ and $\alpha$ for $\alpha < 0.10$ and $\alpha > 0.90$ is not a major concern mechanically because these parameters can be significantly affected by the possible minor errors in the determination of the baseline [9]. Table S2 (Supplementary Information) shows the variable $E_{\alpha }$ values obtained by the six isoconversional equations (OFW, Tang, Starink, KAS, iOFW, and iKAS) including standard deviations (SD). The variable $E_{\alpha }$ values calculated by the isoconversional iOFW and iKAS methods provide the same values [6].

The $E_{\alpha } - \alpha$ relations in terms of the shape of curves for the first, second, and final steps calculated by the isoconversional iOFW and iKAS methods are shown in Fig. 5. If the $E_{\alpha }$ values are roughly constant over the entire conversion range of $\alpha$ and if no shoulders in the reaction rate curve or $\frac{d\alpha }{dt}$ are observed, the reaction process is dominated by a single-step reaction and can be adequately described by a single-step model [9, 38]. However, it is more common that the reaction parameters (such as $\frac{d\alpha }{dt}$, $E_{\alpha }$, and $A$) significantly vary with the conversion $\alpha$. If the reaction rate curve or $\frac{d\alpha }{dt}$ has multiple peaks and/or shoulders, the $E_{\alpha }$ and $A$ values at appropriate levels of conversion $\alpha$ can be used as an input to the multistep model-fitting computations [9, 21, 38, 39]. In addition, if the $E_{\alpha }$ values are independent of conversion $\alpha$, it can be considered as the single-step so that the changes of the maximum or minimum $E_{\alpha }$ values from the average one must be less than 10% [9].

Fig. 5

Independence of $E_{\alpha }$ on $\alpha$ with relative errors for three thermal solid state reaction processes (first step, dehydration; second step, polycondensation and final step, decarbonization) obtained from isoconversional iterative equations

The average calculated variable $E_{\alpha }$ values from isoconversional iterative equations for the first, second, and final thermal solid-state reaction processes were determined to be 68.28 ± 2.63, 100.41 ± 6.00, and 140.07 ± 5.02 kJ mol⁻¹ with the corresponding average correlation coefficient $r^{2}$ of 0.9926, 0.9895, and 0.9941, respectively, for the iKAS plots ($\ln \frac{\beta }{{h(x)T^{2} }}$ versus $\frac{1}{T}$). Furthermore, Table S2 (Supplementary Information) shows the calculated variable $E_{\alpha }$ values obtained from the six isoconversional equations (OFW, Tang, Starink, KAS, iOFW, and iKAS). The calculated variable $E_{\alpha }$ values (Fig. 5 and Table S2 in the Supplementary Information) for the studied system are found to increase in the following sequence: the first (dehydration process), second (polycondensation process), and final (decarbonization process) steps, respectively. The relation between $E_{\alpha }$ and $\alpha$ in the first step shows two regions from obvious discontinuous values: region I ($0.10 \le \alpha \le 0.66$) shows the invariable $E_{\alpha }$ values. In contrast, region II ($0.68 \le \alpha \le 0.90$) shows the jump or increase in the $E_{\alpha }$ values. However, the discontinuous range is $0.66 < \alpha < 0.68$, which represents the change in the reaction mechanism of the thermal solid-state reaction of the title system. These results agree with the TG/DTG/DTA spectra (multiple peaks or shoulder) and the FTIR spectrum consisting of two bending modes of H₂O instead of the single band. In addition, Table 1 shows the percentage of the relative $E_{\alpha ,\hbox{max} }$ and $E_{\alpha ,\hbox{min} }$ values obtained by the six isoconversional equations to be 17.13% in the first step (for both regions I and II), which is higher than 10%. Compared with the second and final steps, the relative errors are less than 10%. However, when the relative errors of each region (regions I and II) are considered in the first step, these values are found to be less than 10%. In addition, the SD values from Table S2 (Supplementary Information) show slight deviations. Therefore, regions I and II as well as the second and final processes can be considered as featuring single-step kinetics.

Table 1 Average $E_{\alpha }$, relative $E_{\alpha ,\hbox{max} }$ and relative $E_{\alpha ,\hbox{min} }$ values obtained from various isoconversional equations

Figs. 1, 2, and 5 as well as Tables S2 (Supplementary Information) and 1 show that the thermal solid-state reaction of the first step is a kinetically complex process and cannot be considered as a single-step reaction. However, each region (regions I and II) could be separately considered a single-step process because of the above explanation and can be described by a unique kinetic triplet. The average $E_{\alpha }$ values of regions I and II were calculated by the isoconversional iterative equations and found to be 64.04 ± 3.20 and 78.54 ± 3.23 kJ mol⁻¹, respectively. The relative errors between the maximum or the minimum $E_{\alpha }$ and the average $E_{\alpha }$ values of regions I and II of the first step as well as the second and final steps are shown in Fig. 5 (only iterative calculations) and Table 1. The calculated maximum relative errors are 9.05, 4.69, 7.27, and 5.65%, respectively, which are less than 10%. Therefore, regions I and II of the first step as well as the second and final steps were also considered to be a single-step reaction process and can be adequately described by a unique kinetic triplet ($E_{\alpha }$,$A$, and $f(\alpha )$ or $g(\alpha )$). According to the results from Figs. 1, 2, and 5 as well as Table S2 (Supplementary Information) and 1, the first thermal solid-state reaction process between the synthesized hydrate compound CoHPO₄⋅3H₂O and Li₂CO₃ is expressed as follows:

First step (80–210 °C):

Region I (single-step process), dehydration I:

$${\text{CoHPO}}_{ 4} \cdot 3 {\text{H}}_{ 2} {\text{O}}\left( {\text{s}} \right) \, \to {\text{ CoHPO}}_{ 4} \cdot y{\text{H}}_{ 2} {\text{O}}\left( {\text{s}} \right) \, + x{\text{H}}_{ 2} {\text{O}}\left( {\text{g}} \right)$$

(31)

Region II (single-step process), dehydration II:

$${\text{CoHPO}}_{ 4} \cdot y{\text{H}}_{ 2} {\text{O}}\left( {\text{s}} \right) \, \to {\text{ CoHPO}}_{ 4} \left( {\text{s}} \right) \, + y{\text{H}}_{ 2} {\text{O}}\left( {\text{g}} \right)$$

(32)

Here x + y is equal to 3 mol of water, whereas the second and final steps are shown in Eqs. 29 and 30, respectively.

Reaction mechanism

The reaction mechanism function is essential to identify the kinetic process. If the mechanism is unknown, the kinetic parameters are meaningless or incomplete. According to the experimental data and the variable $E_{\alpha }$ values obtained from the isoconversional iterative equations (Eqs. 18 and 19), the variation of $\frac{d\alpha }{dt}$ versus $\alpha$ values for the thermal solid-state reaction between the synthesized CoHPO₄⋅3H₂O and Li source (Li₂CO₃) can be determined. Fig. S3 (Supplementary Information) illustrates the variation of $\frac{d\alpha }{dt}$ versus $\alpha$ values at a heating rate of 5 °C min⁻¹. After that, the above-mentioned Málek equations (Eqs. 22 and 24) were also used to generate the experimental plots between the normalized $y(\alpha )$ or $z(\alpha )$ versus $\alpha$ for $\beta = 5$  °C min⁻¹. The resulting experimental plots show nonsignificant variation, as well as for the other three heating rates (10, 15, and 20 °C min⁻¹). Subsequently, the determination of the reaction mechanism functions for the three thermal solid-state reaction processes are established by comparing the experimental and reaction model plots. The reaction model plots are obtained from 35 of $f(\alpha )$ for the $y(\alpha )$ function and the multiple products of $f(\alpha )g(\alpha )$ for the $z(\alpha )$ function as shown in Table S1 (Supplementary Information). These plots represent the most probable mechanism functions and are shown in Fig. 6 (for the $y(\alpha )$ function) and Fig. 7 (for the $z(\alpha )$ function) by inserting the values of $\alpha$ from 0 to 1 with an increment of 0.02 for each selected reaction model.

Fig. 6

Experimental (different symbols) and model plots (solid line) obtained from $y(\alpha )$ function of three thermal solid state reaction processes (first step, dehydration; second step, polycondensation and final step, decarbonization) at a heating rate of 5 °C min⁻¹

Fig. 7

Experimental (different symbols) and model plots (solid line) obtained from $z(\alpha )$ function of three thermal solid state reaction processes (first step, dehydration; second step, polycondensation and final step, decarbonization) at a heating rate of 5 °C min⁻¹

According to the compared results, the most probable mechanism functions for the first (regions I and II), second, and final thermal solid-state reaction processes are determined and the best matching mechanism functions are $R_{2}$, $R_{3}$, $A_{3}$, and $P_{3}$. The results indicate that the sequence of the reaction processes are controlled by the decomposition processes such as contracting cylinder (cylindrical symmetry, $R_{2}$), contracting sphere (spherical symmetry, $R_{3}$), assumed random nucleation and its subsequent growth ($A_{3}$, Avrami–Erofeev model), and nucleation reactions ($P_{3}$). That means the first thermal solid-state reaction processes occurred as two consecutive reaction mechanisms. In the conversion range of $0.10 < \alpha < 0.66$, the conversion is controlled by contracting cylinder, and then it was changed to the contracting sphere in the conversion range of $0.68 < \alpha < 0.90$. However, the discontinuous conversion range of $0.66 < \alpha < 0.68$ indicates the change in the reaction mechanism (from $R_{2}$ to $R_{3}$) of the thermal solid-state reaction processes. Table 2 shows the reaction mechanism functions obtained from the thermal solid-state reaction between different synthesized hydrate precursors of MnHPO₄⋅3H₂O (from the previous work [8]) and CoHPO₄⋅3H₂O (from the present work), and an Li source of Li₂CO₃ for the LMP formation and the LCP formation, respectively. Both cases show that the reaction mechanisms for the dehydration are of type $R$ and the polycondensation is of type $A$, whereas the decarbonization is of type $P$. Hence, different functions may be attributed to the structural shape of both hydrate precursors. Generally, manganese forms the octahedral coordination shape with oxygen or Mn–O₆, whereas cobalt forms the tetrahedral coordination shape with oxygen or Co–O₄ resulting in different XRD patterns and space groups of both MnHPO₄⋅3H₂O (space group Pbca) and CoHPO₄⋅3H₂O (space group Pmc2 ₁ ) compounds. The overall reaction mechanisms of the studied thermal solid-state reaction processes can produce the nanoparticle sizes of the LCP cathode material which can increase the electrochemical performance of the Li-ion battery in the industrial applications.

Table 2 Reaction mechanisms obtained from LMP [8] and LCP (this work) formations

Pre-exponential factor A

After the selection of the reaction mechanism [9], Eq. 27 was used to calculate the pre-exponential factor $A$ of the thermal solid-state reaction processes of the studied system. All parameters were substituted into Eq. 27 at a heating rate of $\beta = 5$ °C min⁻¹, $E_{\alpha }$ = 64.04 ± 3.20 and 78.54 ± 3.23 kJ mol⁻¹, and the first derivative of the reaction differential functions $f^{\prime}(\alpha ) = \frac{ - 1}{{(1 - \alpha )^{1/2} }}$ ($R_{2}$) and $\frac{ - 2}{{(1 - \alpha )^{1/3} }}$ ($R_{3}$) for regions I and II, respectively, of the first thermal solid-state reaction process. However, the substituted values are $E_{\alpha }$ = 100.41 ± 6.00 and 140.07 ± 5.02 kJ mol⁻¹ and $f^{\prime}(\alpha ) = 3 + 3\ln (1 - \alpha ) - \frac{1}{{[ - \ln (1 - \alpha )]^{1/3} }}$ ($A_{3}$) and $\frac{2}{{\alpha^{1/3} }}$ ($P_{3}$), respectively, for the second and final thermal processes. The maximum temperature $T_{\hbox{max} }$ obtained from DTG peaks for the first (regions I and II), second, and final processes are 427.23, 461.23, 769.12, and 987.81 K. All above-mentioned parameters were substituted into Eq. 27 to calculate the corresponding pre-exponential factor $A$. The $A$ values for the first (regions I and II), second and final thermal solid-state reaction processes were found to be 1.01 (±0.016) × 10⁷, 7.80 (±0.009) × 10⁷, 4.52 (±0.010) × 10⁵, and 1.03 (±0.003) × 10⁶ s⁻¹.

Equation 8 is generalized according to each thermal solid-state reaction process as follows:

$$\frac{{d\alpha_{i} }}{dT} = \frac{{A_{i} }}{\beta }\exp \left( {\frac{{ - E_{i} }}{RT}} \right)f_{i} (\alpha )$$

(33)

All thermal solid-state reaction kinetic equations for the synthesized CoHPO₄⋅3H₂O precursor and Li₂CO₃ are as follows:First step (region I):

$$\frac{{d\alpha_{1} }}{dT} = \frac{{1.01 \times 10^{7} }}{\beta }\exp \left( {\frac{ - 64.04}{RT}} \right)2(1 - \alpha_{1} )^{1/2}$$

(34)

First step (region II):

$$\frac{{d\alpha_{2} }}{dT} = \frac{{7.80 \times 10^{7} }}{\beta }\exp \left( {\frac{ - 78.54}{RT}} \right)3(1 - \alpha_{2} )^{2/3}$$

(35)

Second step:

$$\frac{{d\alpha_{3} }}{dT} = \frac{{4.52 \times 10^{5} }}{\beta }\exp \left( {\frac{ - 100.41}{RT}} \right)3(1 - \alpha_{3} )[ - \ln (1 - \alpha_{3} )]^{2/3}$$

(36)

Final step:

$$\frac{{d\alpha_{4} }}{dT} = \frac{{1.03 \times 10^{5} }}{\beta }\exp \left( {\frac{ - 140.07}{RT}} \right)3\alpha_{4}^{2/3}$$

(37)

Here $\alpha_{1}$ and $\alpha_{2}$ are the extent of conversions in regions I and II, respectively, for the first reaction process, and $\alpha_{3}$ and $\alpha_{4}$ are the extent of conversions for the second and final reaction processes, respectively. The sum of the extent of conversions of $\alpha_{1}$ and $\alpha_{2}$ (or $\alpha_{1} + \alpha_{2}$) is equal to 1, whereas the conversion value of each $\alpha_{3}$ and $\alpha_{4}$ is 1.

Thermodynamic functions

According to the transition-state complex theory of Eyring [40], the standard entropy change of transition-state complex (standard entropy of activation, $\Delta S^{0 \ne }$) is related to the pre-exponential factor $A$(kinetic parameter) as follows:

$$\Delta S^{0 \ne } = R\ln \frac{Ah}{{e\chi k_{B} T}}$$

(38)

Here $e$ is the Neper number and equal to 2.7183, $\chi$ is the transition factor and equal to 1 for the monomolecular reaction, $k_{B}$ and $h$ are the Boltzmann constant (1.3806 × 10⁻²³ J K⁻¹) and the Planck constant (6.6261 × 10⁻³⁴ J s), respectively, $T$ (K) is the peak temperature from the DTG curve, which is the same as the previous calculation of the pre-exponential factor $A$ at $\beta = 5$  °C min⁻¹, and $R$ is the gas constant.

The standard enthalpy change (standard heat of activation, $\Delta H^{0 \ne }$) and the standard Gibbs free energy change of the transition-state complex ($\Delta G^{0 \ne }$) were calculated according to Eqs. 39 and 40 as follows. Standard enthalpy change:

$$\Delta H^{0 \ne } = E_{\alpha } - RT$$

(39)

Standard Gibbs free energy change:

$$\Delta G^{0 \ne } = \Delta H^{0 \ne } - T\Delta S^{0 \ne }$$

(40)

The calculated $\Delta S^{0 \ne }$ for the first (regions I and II), second, and final thermal solid-state reaction processes are −122.13 ± 34.45, −105.76 ± 56.24, −152.83 ± 50.83, and −148.04 ± 48.57 J K⁻¹ mol⁻¹, respectively. The corresponding values of $\Delta H^{0 \ne }$ are 60.49 ± 5.52, 74.71 ± 6.05, 94.02 ± 3.94, and 131.86 ± 31.93 kJ mol⁻¹, whereas the corresponding values of $\Delta G^{0 \ne }$ are 112.66 ± 14.48, 123.48 ± 25.33, 211.56 ± 38.70, and 278.09 ± 44.79 kJ mol⁻¹. The negative $\Delta S^{0 \ne }$ values of all thermal solid-state reaction processes show that the activated states are less disordered compared to the initial states, which may be interpreted as a “slow” stage [6]. The endothermic peaks in the DTA curves agree well with the positive sign of $\Delta H^{0 \ne }$. The positive $\Delta G^{0 \ne }$ values confirm that the thermal decomposition reactions are nonspontaneous processes.

Conclusions

The thermal solid-state reaction between CoHPO₄⋅3H₂O and Li₂CO₃ was observed to appear in three processes in the sequence of dehydration (separated into dehydration I and II), polycondensation, and decarbonization processes, respectively. The final product was confirmed to be the LCP nanoparticles. The kinetic study of the title reaction was carried out using the nonisothermal or constant heating rate runs of the isoconversional method. The reliable $E_{\alpha }$ values were calculated by various isoconversional equations followed by isoconversional iterative equations in order to increase the accuracy of the reliable $E_{\alpha }$ values. The independence of the $E_{\alpha }$ values on $\alpha$ for all reaction processes indicates that the first (regions I and II), second, and final steps are a single-step process and can be adequately described by a unique kinetic triplet. The reliable reaction mechanisms were obtained by the comparison between the experimental and model plots of the $y(\alpha )$ and $z(\alpha )$ functions. The reliable reaction mechanisms applied for regions I and II are contracting cylinder ($R_{2}$) and contracting sphere ($R_{3}$) models, respectively. On the other hand, the reaction mechanisms applied for the second and final steps are the assumed random nucleation and its subsequent growth (Avrami–Erofeev, $A_{3}$) and the nucleation ($P_{3}$) models. The related thermodynamic functions of the transition-state complexes were calculated by using the kinetic parameters and these are found to agree well with the thermal analysis data.