1 Introduction

Assessing and comparing student performance have been important and fascinating areas of educational research. Literature is abundant and covers diverse topics such as measuring differences in student performance due to differences in teacher performance (e.g., Ross 1992; Hill et al. 2005), study subjects (e.g., Gamoran and Hannigan 2000; Chen and Zitikis 2017), examination formats (e.g., Agarwal et al. 2008; Heijne-Penninga et al. 2008, 2010), and gender (e.g., Leedy et al. 2003; Nguyen et al. 2005; Putwain 2008; Wade et al. 2017).

Various methods for collecting relevant data have been employed, including observational studies and experiments, open- and closed-book examinations. Furthermore, various statistical techniques have been used, including linear and nonlinear regression, with the Pearson correlation coefficient naturally arising as a measure of relationship between variables (e.g., Krasne et al. 2006; Agarwal et al. 2008; Heijne-Penninga et al. 2008, 2010; Thorndike and Thorndike-Christ 2010).

In addition to research by professional educators, a considerable body of specialized statistical literature has utilized educational data to illustrate various methods and techniques, including distance-based and classical multivariate analyses (e.g., Groenen and Meulman 2004), Bayesian analysis (e.g., Efron 2012), orthogonal simple component anlaysis (e.g., Anaya-Izquierdo et al. 2011), and robust structural equation modelling with missing data and auxiliary variables (e.g., Yuan and Zhang 2012). Furthermore, Qoyyimi and Zitikis (2014), Qoyyimi and Zitikis (2015) have employed Gini-based arguments to assess the lack of relationship in multivariate educational data. Chen and Zitikis (2017) use an index of increase to quantify the amount of monotonicity in nonlinear relationships. Duzhin and Gustafsson (2018) suggest an automated procedure for analyzing educational data based on machine learning, with features such as decision making that accounts for students’ prior knowledge.

As is usually the case with methods that condense raw data into a few parameters, some information inevitably gets lost in the process. The loss is sometimes acceptable, but sometimes is not. An example of the latter case would be the use of the Pearson correlation coefficient, as it gives the same value irrespective of which of the two variables under consideration is explanatory or response. Later in this paper, we shall illuminate these issues using educational data, and will in turn put forward arguments in favour of an index of increase (Davydov and Zitikis 2017) as a measure for quantifying the presence of monotonicity in inherently non-monotonic scatterplots. The index has recently been employed by Chen and Zitikis (2017) to revisit a dataset of Thorndike and Thorndike-Christ (2010), with further theoretical insights worked out by Chen et al. (2018).

Our current research builds upon the work of Chen and Zitikis (2017), but unlike that work, we explore the rich data reported by Mardia et al. (1979, pp. 3–4). Due to the popularity of this textbook, the data have been frequently used by statisticians and others to illustrate various notions and techniques of Multivariate Analysis. Consequently, and naturally, the data are available in several computing packages, such as MVT (Osorio and Galea 2015). In the current paper we revisit the data with the aid of additional insights on the topic that have been acquired since the publication of Chen and Zitikis (2017).

We have organized the rest of this paper as follows. In Sect. 2, we describe the dataset of Mardia et al. (1979, pp. 3–4) and give its preliminary analysis. In Sect. 3, we fit certain functions to the data and give reasons why this exercise is of interest, and sometimes even necessary. In Sect. 4, we explain basic concepts and intuition behind the index of increase, which can take on several forms depending on the nature of available data (e.g., scatterplots, fitted functions, etc.). In Sect. 5, we use the index to illuminate directional relationships between several subjects. Section 6 finishes the paper with a summary of main contributions and concluding notes.

1.1 Notation

Throughout the paper we use the notation \({\mathrm {I}}\) when discussing the index of increase in generic terms. When the index is applied on scatterplots, we tend to use the notation \({\mathrm {I}}({\mathbf {x}},{\mathbf {y}})\) [definition (4)], where \({\mathbf {x}}\) and \({\mathbf {y}}\) are n-dimensional vectors of explanatory and response variables, respectively. When the explanatory data \({\mathbf {x}}=(x_1,\dots , x_n)\) do not have ties (i.e., \(x_i\ne x_j\), \(1\le i, j \le n\)), we emphasize this fact by using the notation \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})\) [definition (3)]. When the index is calculated from fitted to data functions, denoted by h, we use the notation \({\mathrm {I}}(h)\) for the corresponding index [definition (1)]. A numerical approximation for \({\mathrm {I}}(h)\) is denoted by \({\mathrm {I}}_k(h)\) [definition (2)], with the latter approaching \({\mathrm {I}}(h)\) when k gets larger. In the process of analysis, we sometimes find it useful to restrict explanatory variables to certain regions, say intervals [L, U], and then calculate the corresponding index values. In such instances, we denote the index by \({\mathrm {I}}({\mathbf {x}},{\mathbf {y}}\mid L,U)\) for scatterplots [definition (7)] and \({\mathrm {I}}(h\mid L,U)\) for fitted functions h.

Remark 1

The notation is revealing: our dataset is in the form of scatterplots, which we sometimes analyze as they are, but sometimes truncate to certain sub-scatterplots (e.g., with explanatory variables restricted to some intervals [L, U]), or to which we sometimes fit continuous functions and then analyze the functions. There are several reasons for such transformation, one of them being outliers, whose ability to distort statistical analyses and thus decision making should not be underestimated. We shall illustrate this point with an example (kindly provided by one of the reviewers of this paper) in Sect. 4.2, where we give a computational formula for the index of increase.

2 Data and an idea of measuring increase

The dataset of Mardia et al. (1979, pp. 3–4) consists of \(n = 88\) examination scores in five subjects: Algebra, Analysis, Mechanics, Vectors, and Statistics. The scores are out of 100 possible in each of the five subjects, with the scores in Mechanics and Vectors coming from closed-book examinations, and the scores in Algebra, Analysis, and Statistics coming from open-book examinations. In Fig. 1 we give a snapshot of the data based on commonly used scatterplots and least-squares regression lines. The response variables are noted in the rows and the explanatory ones in the columns. The corresponding values of the Pearson correlation coefficient r are inside of each of the twenty off-diagonal panels. For example, the panel with \(r=0.553\) in the top row is the scatterplot of Vectors vs Mechanics, whereas the panel with the same \(r=0.553\) one row below is the scatterplot of Mechanics vs Vectors. The slopes of the fitted lines are different because the variances of the explanatory and response variables are different. Each of the five diagonal panels has, obviously, \(r=1\)

Fig. 1
figure 1

Least-squares regression lines fitted to the data of Mardia et al. (1979, pp. 3–4) with the corresponding values of the Pearson correlation coefficient \(r=r({\mathbf {x}},{\mathbf {y}})\)

Full size image

.

Note that the reported r values are symmetric with respect to the two variables under consideration, although the study subjects clearly lack symmetry with respect to each other. Hence, the use of r in the current context is hardly suitable. The slope \(b=r s_y/s_x\) of the linear regression line is a better choice, where \(s_x\) and \(s_y\) denote the standard deviations of the explanatory and response variables, respectively. However, the scatterplots can hardly suggest linear patterns. Hence, neither r nor b seems to be particularly informative in the current context. Given our goal to understand and even predict how changes in the scores of one study subject are reflected in the scores of another subject, we therefore find it desirable to search for alternative ways for quantifying nonlinear relationships.

Note that although b is not perfect, it is nevertheless better than r, and this is in part due to asymmetry of b with respect to the explanatory and response variables. This feature is natural when quantifying dependence, as elucidated by Reimherr and Nicolae (2013, p. 119). If, however, symmetry is desirable for any reason, then it can be imposed by symmetrization, which can be achieved in many ways (see, e.g., Reimherr and Nicolae 2013, p. 120). We shall briefly come back to this topic at the end of Sect. 3, noting now that the measure that we are to employ for quantifying relationships between study subjects is asymmetric, which we find natural and appropriate.

Namely, to assess how much a pattern (scatterplot, function, etc.) is increasing, we measure its distance from the set of decreasing patterns. Hence, if the pattern is decreasing, the distance is 0. By normalizing the distance, we do not allow it to exceed 1. Not going into any more mathematical details at the moment (Davydov and Zitikis 2017), we obtain an index of increase, denoted by \({\mathrm {I}}\), with the following features:

  • it takes values only in the interval [0, 1],

  • vanishes when there are no segments of increase,

  • takes the maximal value 1 when there are no segments of decrease,

  • exceeds 0.5 when the pattern is more upward than downward,

  • is smaller than 0.5 when the pattern is more downward than upward.

To illustrate the features, in Fig. 2 we have depicted the dataset of Mardia et al. (1979, pp. 3–4) by connecting the consecutive data points using straight lines, which have enabled us to calculate the index of increase for each panel using a computational formula that we shall give and discuss later in this paper. Note, for example, that Algebra versus Vectors, Algebra versus Analysis, Algebra versus Statistics have the largest three values, thus implying that the corresponding patterns are most increasing among the twenty off-diagonal panels. We can interpret this by saying that students with higher scores in Algebra tend to have higher scores in Vectors (\({\mathrm {I}}=0.576\)), Analysis (\({\mathrm {I}}=0.575\)), and Statistics (\({\mathrm {I}}=0.578\)) than in any other study subject. This, we think, is due to Algebra being a fundamental subject for Vectors, Analysis, and Statistics. For strong arguments and evidence in favour of Algebra, we refer to Gamoran and Hannigan (2000).

Fig. 2
figure 2

Piece-wise linear fits to the data of Mardia et al. (1979, pp. 3–4) with the corresponding values of the index of increase \({\mathrm {I}}={\mathrm {I}}({\mathbf {x}},{\mathbf {y}})\)

Full size image

Vectors versus Algebra (\({\mathrm {I}}=0.527\)) and Statistics versus Algebra (\({\mathrm {I}}=0.546\)) have lower indices than the three ones mentioned in the previous paragraph, and so we are less confident that better performance in Vectors and Statistics would lead to higher scores in Algebra. Furthermore, Analysis versus Algebra (0.566) has just a slightly lower index than the three top ones. This, we think, is due to Analysis and Algebra being fundamental subjects, and thus students possibly viewing them as equally important, or equally challenging, and thus demanding similar study efforts.

Among the twenty panels, Statistics versus Mechanics has the lowest index (\({\mathrm {I}}=0.514\)), which is not far away from the boundary value 0.500 separating more increasing patterns from more decreasing ones.

Remark 2

In the above discussion, to illustrate the mathematical concept of the index of increase, we treated the dataset of Mardia et al. (1979, pp. 3–4) as a “population,” and not as a sample with variability. We shall do so quite often throughout the paper, but we shall also let the reader know our thoughts on the statistical side of the subject matter (see, e.g., Remark 5, and also the second half of concluding Sect. 6).

3 Functions, fitted curves, and interchangeability

The index of increase can be calculated not only from (discrete) scatterplots, such as those in Fig. 2, but also from continuous functions. The latter ones naturally, and sometimes inevitably, arise due to several reasons:

  • The phenomena under consideration might be modelled using continuous functions, which could, for example, arise as solutions to differential equations, as is frequently the case in mathematical biology, as well as in other areas dealing with dynamical modelling.

  • Continuous functions may arise due to fitting curves to scatterplots (e.g., Hastie et al. 2009; Murphy 2012, and references therein). Such fitting might also be done by the researcher already possessing raw data but wishing to smooth out noise from the data, mitigate the influence of potential outliers, or due to some other statistical considerations.

  • Fitted curves may be the only objects available to the researcher for analysis and decision making, due to reasons such as ethics and confidentiality. For example, research that involves the use of personal data, irrespective of whether the data are identifiable or de-identified, requires a research ethics board review at most institutions. Scatterplots would be among such datasets, but the fitted curves would hardly be such.

Irrespective of the origins of continuous functions, calculating their indices of increase is discussed in Sect. 4.1. In the next subsection, for comparative and illustrative purposes, we shall fit curves to the scatterplots of Fig. 2 and also provide the values of their indices of increase calculated using a method to be described later in this paper.

3.1 Fitted curves

To illustrate, we employ one of the most commonly used regression methods for fitting nonlinear relationships, which is locally estimated scatterplot smoothing, or LOESS for short. It is a non-parametric method that combines multiple regression models and k-nearest-neighbor-based meta-models. Jacoby (2000) describes the LOESS methodology in detail, including how to fit LOESS functions and perform goodness-of-fit tests, with particular attention on those cases when subject-matter knowledge suggests nonlinear relationships but little, if anything, is known about the actual underlying functional forms. This is precisely the situation we deal with in the current paper.

There have been many uses of LOESS in educational research, and from those studies we gain valuable insights relevant to the topic of the present paper. For example, Abramo et al. (2012) use LOESS regression to explore the influence of research group’s size on research productivity, with emphasis on the Italian higher-education system. Avendano et al. (2009) employ LOESS to explore the impact of educational level on changes in health outcomes among Europeans, with analyses performed separately for regions with different welfare state regimes.

Coming back to the dataset of Mardia et al. (1979, pp. 3–4) and using the R package \(\texttt {stats}\) (R Core Team 2017), we have implemented the \(\texttt {loess}\) function with its default parameter \({\texttt {span}} = 0.75\). The resulting curves are depicted in Fig. 3. We note in this regard that the parameter \(\texttt {span}\) controls smoothness: the larger the value, the smoother (i.e., less wiggly) is the fitted function. Some of the reported values of \({\mathrm {I}}\) in the panels of Fig. 3 are equal to 1, thus implying that the fitted functions are increasing everywhere on their domains of definition. Interestingly, some index values are equal to 1 even when the horizontal and vertical axes are interchanged, as is, for example, for Algebra versus Analysis and Analysis versus Algebra. We should not, however, hastily infer from these values that Algebra and Analysis are interchangeable subjects: first, the rates at which the two fitted functions increase are different, and second, the values of the two indices are influenced by the degree of smoothing, governed by the parameter \(\texttt {span}\). We shall illustrate the latter feature later in the paper, when we set \(\texttt {span} = 0.35\), in addition to the default value \(\texttt {span} = 0.75\).

Fig. 3
figure 3

LOESS fitted functions \(h=h_{0.75}\) to the data of Mardia et al. (1979, pp. 3–4) with the corresponding values of the index of increase \({\mathrm {I}}={\mathrm {I}}(h_{0.75})\)

Full size image

We conclude this subsection with Table 1, which summarizes our findings so far. Specifically, in the table we report the values of the Pearson correlation coefficient \(r=r({\mathbf {x}},{\mathbf {y}})\) (Fig. 1), and also those of \({\mathrm {I}}={\mathrm {I}}({\mathbf {x}},{\mathbf {y}})\) for the raw data (Fig. 2) and \({\mathrm {I}}={\mathrm {I}}(h)\) for the LOESS fits under the default parameter \(\texttt {span} = 0.75\) (Fig. 3).

Table 1 Summary statistics for all subjects
Full size table

3.2 Interchangeability of study subjects

In Table 1 we have also reported the values of the relative index \({\mathrm {RI}}\%:= {\mathrm {RI}}\times 100\%\) of interchangeability of \({\mathbf {x}}\) and \({\mathbf {y}}\), where

$$\begin{aligned} {\mathrm {RI}}:={\mathrm {RI}}({\mathbf {x}},{\mathbf {y}})={{\mathrm {I}}({\mathbf {x}},{\mathbf {y}}) \over {\mathrm {I}}({\mathbf {y}},{\mathbf {x}})} -1, \end{aligned}$$

and also the values of the absolute index of interchangeability \({\mathrm {AI}}\%:= {\mathrm {AI}}\times 100\%\) of \({\mathbf {x}}\) and \({\mathbf {y}}\), where

$$\begin{aligned} {\mathrm {AI}}:={\mathrm {AI}}({\mathbf {x}},{\mathbf {y}})=\big | {\mathrm {I}}({\mathbf {x}},{\mathbf {y}})-{\mathrm {I}}({\mathbf {y}}, {\mathbf {x}})\big | . \end{aligned}$$

We note that the indices \({\mathrm {RI}}\) and \({\mathrm {AI}}\), which are also mentioned in the concluding section of Chen and Zitikis (2017), are not specific to the index \({\mathrm {I}}\). Indeed, \({\mathrm {RI}}\) and \({\mathrm {AI}}\) can be calculated for any index of interest, including the Pearson correlation coefficient \(r=r({\mathbf {x}},{\mathbf {y}})\), but in the latter case, the values of \({\mathrm {RI}}\) and \({\mathrm {AI}}\) are always 0 due to the symmetry of r with respect to \({\mathbf {x}}\) and \({\mathbf {y}}\). The latter note highlights the unsuitability of r in the context of current research.

4 Index of increase

In the previous sections, we introduced the index of increase via its properties, and illustrated its performance with numerical results. The latter task required actionable formulas, adapted for the two scenarios of particular interest: scatterplots and functions. We next provide and discuss such formulas, starting with functions.

4.1 The index for functions

Let \(h: [L, U] \rightarrow {\mathbb {R}} \) be a real-valued function defined on an interval [L, U]. For example, h could be a LOESS function fitted to a scatterplot \(\{ (x_{i}, y_{i}),\,i=1,\dots , n \}\), with \(L=\min _i \{x_i\} \) and \(U=\max _i \{x_i\} \) being the smallest and largest x-values, respectively.

The index of increase of h is, by definition, the normalized distance between the function h and the set of all decreasing (precisely speaking, non-increasing) functions (Davydov and Zitikis 2017). Hence, the index is equal to 0 when the function h is decreasing, and is equal to 1 when it is increasing (precisely speaking, non-decreasing). When h is differentiable, the formula for this distance-based index is (Davydov and Zitikis 2017)

$$\begin{aligned} {\mathrm {I}}(h) = \frac{\int _{L}^{U} (h'(x))_{+}\,{\mathrm {d}}x}{\int _{L}^{U}|h'(x)|\,{\mathrm {d}}x}, \end{aligned}$$
(1)

where \(z_{+}\) denotes the positive part of any real number z, that is, \(z_{+}=z\) when \(z>0\) and \(z_{+}=0\) otherwise.

A practical way to calculate the index \({\mathrm {I}}(h)\) is via discretization. Namely, we first divide the interval [L, U] into many small subintervals \([d_{i-1}, d_{i}]\), \(2\le i \le k\), where \(d_{i} = L + \frac{i-1}{k-1}(U-L)\), \(1\le i \le k\). Then we calculate

$$\begin{aligned} {\mathrm {I}}_{k}(h) = \frac{\sum _{i=2}^{k}(h(d_{i})-h(d_{i-1}))_{+}}{\sum _{i=2}^{k}|h(d_{i})-h(d_{i-1})|}. \end{aligned}$$
(2)

It has been shown (Davydov and Zitikis 2017; Chen and Zitikis 2017) that when k grows indefinitely, \({\mathrm {I}}_{k}(h)\) converges to \( {\mathrm {I}}(h)\). Based on this fact, we can calculate \({\mathrm {I}}(h)\) at any desired precision by calculating \({\mathrm {I}}_{k}(h)\) for a sufficiently large k.

Remark 3

The parameter k, which is not to be confused with the scatterplot size n, is chosen by the researcher, and can be as large as computing time and power permit. For example, Chen and Zitikis (2017) show that for their chosen illustrative functions, setting \(k=20{,}000\) is sufficient to reach the true value of \({\mathrm {I}}(h)\) at the precision of six decimal digits.

4.2 The index for scatterplots

By their very nature, scatterplots are discrete, but even when we connect their points with straight lines, the resulting functions, though continuous, are not differentiable and thus formula (1) cannot be engaged. For this reason, Chen and Zitikis (2017) propose a modification, which resembles formula (2) of the numerical approximation \({\mathrm {I}}_{k}(h)\). To describe it, let \(\{ (x_{i}, y_{i}),\,i=1,\dots , n \}\) be the scatterplot under consideration. For the sake of simplicity, let all the \(x_i\)’s be different, the assumption that we shall remove in Sect. 4.3. Hence, we can, and thus do, uniquely order the \(x_i\)’s from the smallest to the largest, thus obtaining \(x_{1:n}< x_{2:n}< \cdots <x_{n:n}\) that are called order statistics (e.g., David and Nagaraja 2003).

For every \(x_{i:n}\), we find the corresponding point \((x_{j}, y_{j})\) in the scatterplot, with j determined by the equation \(x_j=x_{i:n}\). We denote the second coordinate of the point \((x_{j}, y_{j})\) by \(y_{[i:n]}\), which is usually called the \(i^{\mathrm {th}}\) concomitant (e.g., David and Nagaraja 2003). The index of increase is defined by the formula (Chen and Zitikis 2017)

$$\begin{aligned} {\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}}) = \frac{\sum _{i=2}^{n}(y_{[i:n]}-y_{[i-1:n]})_{+}}{\sum _{i=2}^{n}|y_{[i:n]}-y_{[i-1:n]}|}, \end{aligned}$$
(3)

with the superscript “0” reminding us that there are no ties among the x’s.

To easily interpret the index \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}}) \), we first note that the numerator in its definition (3) sums up all the upward movements \(y_{[i:n]}-y_{[i-1:n]}>0\), while the denominator sums up the absolute values of all the movements \(y_{[i:n]}-y_{[i-1:n]}\in {\mathbb {R}}\), upward and downward. Hence, the index of increase is the proportion of upward movements among all the movements. In particular, when \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})<0.5\), the proportion of downward movements is larger than that of upward movements, and so the pattern looks more decreasing than increasing. Analogously, when \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})>0.5\), the proportion of upward movements is larger than that of downward movements, and so the pattern looks more increasing than decreasing. When \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})\) is near 0.5, the proportions of upward and downward movements are similar, thus suggesting that the values of the first and the last concomitants (i.e., of \(y_{[1:n]}\) and \(y_{[n:n]}\)) must be similar. The following property establishes this observation rigorously.

Property 1

We have \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})=0.5\) if and only if \(y_{[1:n]}=y_{[n:n]}\).

This property follows from the equations \(z=z_{+}-z_{-}\) and \(|z|=z_{+}+z_{-}\), which imply the equivalence of \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})=0.5\) and \(\sum _{i=2}^{n}(y_{[i:n]}-y_{[i-1:n]})=0\), the latter being equivalent to \(y_{[1:n]}=y_{[n:n]}\).

Remark 4

Based on definition (3) and Property 1, we can now complete Remark 1 by providing an example (suggested by one of the reviewers of this paper) in order to show how much outliers can skew our analysis, as they usually do with any statistical analysis. Namely, suppose that the scatterplot consists of n points, with the left- and right-hand points having the same y-coordinates (i.e., \(y_{[1:n]}=y_{[n:n]}\)). However, all the points except the right-most point have strictly increasing y-coordinates. Hence, we can say that the scatterplot exhibits a strictly increasing pattern, with the right-most point being an outlier. By Property 1, we have \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})=0.5\), but if we remove the outlier (i.e., the right-most point) and calculate the index of increase for the just obtained sub-scatterplot, we get \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})=1\), because the sub-scatterplot exhibits an increasing pattern and thus the numerator and the denominator on the right-hand side of definition (3) coincide. Of course, from the strictly mathematical point of view, given the original scatterplot with no points removed, the index \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})\) does not lie by giving us the value 0.5, as the trend that arises from the scatterplot ends at the same height on the right-hand side as it started on the left-hand side, thus technically making the trend neither increasing nor decreasing. Yet, the statistician would likely remove the right-hand point, calculate the index value 1, and would disagree with the mathematician’s conclusion. Both would be right in their own ways.

Another notable property of \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})\) is translation and scale invariance, utilized by Chen and Zitikis (2017) in order to unify the scales of measurement of different scatterplots.

Property 2

For all real \(\alpha ,\beta \in {\mathbb {R}} \) and all positive \(\gamma ,\delta > 0\), we have

$$\begin{aligned} {\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}}) ={\mathrm {I}}\left( \gamma ({\mathbf {x}}-\alpha ), \delta ({\mathbf {y}}-\beta )\right) . \end{aligned}$$

This property is particularly useful when dealing with student performance on different subjects, when they are assessed using different score scales. Indeed, the property says that shifting and stretching (or shrinking) data do not affect the value of the index.

Remark 5

The parameter n, though arbitrary, is nevertheless fixed throughout this paper. The statistical tradition of letting n grow indefinitely is not appropriate in the context of the present research, since uncontrollably expanding class sizes do not facilitate insights that we aim to gain in the paper; more on this topic will be in concluding Sect. 6. Nevertheless, one may naturally wish to assess the estimator’s variability for a given fixed n, due to reasons such as testing one- or two-sample hypotheses. In such cases, we would suggest using the (exact) permutation test (e.g., Wasserman 2006, pp. 161–164).

4.3 Adjustments due to data ties

The index of increase \({\mathrm {I}}^0({\mathbf {x}},{\mathbf {y}})\) is defined under the assumption that all x’s are different, but quite often this assumption is violated. Hence, we suggest the following modification (cf. Chen and Zitikis 2017). Given any scatterplot \(\{ (x_{i}, y_{i}),\,i=1,\dots , n \}\), let \(x_{1}^{*}, x_{2}^{*}, \dots , x_{m}^{*}\) denote all the \(m(\le n)\) distinct values among \(x_{1}, x_{2}, \dots , x_{n}\). For each \(x_{i}^{*}\), let \({\mathscr {Y}}_i\) be the set all those y’s whose corresponding x’s are equal to \(x_{i}^{*}\). Each set \({\mathscr {Y}}_i\) has at least one element, and let \(y_{i}^{*}\) denote the median of the elements in \({\mathscr {Y}}_i\). This gives rise to the modified scatterplot \(\{ (x_{i}^{*}, y_{i}^{*}),\,i=1,\dots , m \}\) with distinct x’s, and thus with uniquely defined order statistics \(x_{1:m}^{*}< x_{2:m}^{*}< \cdots < x_{m:m}^{*}\) and their corresponding concomitants \(y_{[1:m]}^{*} , y_{[2:m]}^{*} , \dots , y_{[m:m]}^{*}\). Applying definition (3) on the just constructed modified scatterplot, we obtain the index of increase

$$\begin{aligned} {\mathrm {I}}({\mathbf {x}},{\mathbf {y}}) = {\sum _{i=2}^{m}(y_{[i:m]}^{*}-y_{[i-1:m]}^{*})_{+} \over \sum _{i=2}^{m}|y_{[i:m]}^{*}-y_{[i-1:m]}^{*}|} . \end{aligned}$$
(4)

The values of \({\mathrm {I}}\) that we earlier reported in Fig. 2 are actually those of the just defined index \({\mathrm {I}}({\mathbf {x}},{\mathbf {y}})\), because the data of Mardia et al. (1979, pp. 3–4) contain ties among x-coordinates.

Remark 6

Given \((x_{i}^{*}, {\mathscr {Y}}_i)\), instead of calculating the median of the values inside \({\mathscr {Y}}_i\), we may calculate their mean or some other summary statistic. The various possibilities available to the researcher depend on the data under consideration and/or the researcher’s point of view.

4.4 Scatterplots over a specific range

In our explorations so far, we have utilized all the scatterplot points. Hence, piecewise linear and LOESS fitted functions have been defined on the scatterplot-specific interval \([x_{1:n},x_{n:n}]\), where \(x_{1:n}=\min _i \{x_i\} \) and \(x_{n:n}=\max _i \{x_i\} \). There are, however, situations (as the one we shall encounter in the next section) when we wish to assess monotonicity only on a certain subinterval [L, U] of \([x_{1:n},x_{n:n}]\). This can be desirable due to a number of reasons, such as:

  • A few left- and right-hand points of the scatterplot might be outliers, and we shall encounter such a situation in the next section; see Remark 7 therein. Hence, removing the points might be warranted. This idea of truncation in order to improve the robustness of statistical analysis has long been employed by statisticians, and in various situations. For example, to robustify the classical sample mean as an estimator of the population mean, one typically uses trimmed or winsorized means (e.g., Serfling 1980; Jurečková et al. 2019).

  • One may wish to explore the scores of only a certain portion of the entire class, such as the middle 80% of students, with 10% of under- and 10% of over-performing students treated in special ways in order to make their learning experience more fulfilling.

  • When comparing several scatterplots, which we frequently do throughout this paper, it is advisable to make their ranges comparable, since comparing monotonicity of, for example, two scatterplots with one covering the entire interval [0, 100] and another only [60, 100] may not lead to meaningful conclusions.

Hence, since L and U may not be the minimal and maximal x’s of the scatterplot, we therefore need a modification of our previous considerations. This can be done by artificially, though quite naturally, augmenting the scatterplot with points \((L, y_{L}^{*})\) and \((U, y_{U}^{*})\) with specially constructed y-coordinates \(y_{L}^{*}\) and \(y_{U}^{*}\), as described next. Namely, let \(\{ (x_{i}, y_{i}),\,i=1,\dots , n \}\) be the scatterplot under consideration, and let [L, U] be a subinterval of \([x_{1:n},x_{n:n}]\) of particular interest to the researcher. We convert this scatterplot into the modified one \(\{ (x_{i}^{*}, y_{i}^{*}),\,i=1,\dots , m \}\) with \(m(\le n)\) distinct x-coordinates. Among the points of the modified scatterplot, we find \((x_{l:m}^{*}, y_{[l:m]}^{*})\) and \((x_{(l+1):m}^{*}, y_{[(l+1):m]}^{*})\) such that \(x_{l:m}^{*}\) is the closest x-coordinate to the left of (or equal to) L, and \(x_{(l+1):m}^{*}\) is the closest x-coordinate to the right of (or equal to) L. To L we attach

$$\begin{aligned} y_{L}^{*} = y_{[l:m]}^{*} + \frac{y_{[(l+1):m]}^{*} - y_{[l:m]}^{*}}{x_{(l+1):m}^{*}-x_{l:m}^{*}}(L - x_{l:m}^{*}) \end{aligned}$$
(5)

and arrive at the point \((L, y_{L}^{*})\), which we add to the modified scatterplot. Analogously we arrive at the point \((U, y_{U}^{*})\) with

$$\begin{aligned} y_{U}^{*} = y_{[(u-1):m]}^{*} + \frac{y_{[u:m]}^{*} - y_{[(u-1):m]}^{*}}{x_{u:m}^{*}-x_{(u-1):m}^{*}}(U - x_{(u-1):m}^{*}), \end{aligned}$$
(6)

where \((x_{(u-1):m}^{*}, y_{[(u-1):m]}^{*})\) and \((x_{u:m}^{*}, y_{[u:m]}^{*})\) are the two points in the modified scatterplot such that \(x_{(u-1):m}^{*}\) is the closest x-coordinate to the left of (or equal to) U, and \(x_{u:m}^{*}\) is the closest x-coordinate to the right of U. With

$$\begin{aligned} z_{[i:m]}^{*}= \left\{ \begin{array}{ll} y_{L}^{*} &{} \hbox { when } \quad i=l, \\ y_{[i:m]}^{*} &{} \hbox { when } \quad i=l+1,\dots , u-1, \\ y_{U}^{*} &{} \hbox { when } \quad i=u , \end{array} \right. \end{aligned}$$

we define the (conditional on [L, U]) index of increase

$$\begin{aligned} {\mathrm {I}}({\mathbf {x}},{\mathbf {y}}\mid L,U) = {\sum _{i=l+1}^{u}(z_{[i:m]}^{*}-z_{[i-1:m]}^{*})_{+} \over \sum _{i=l+1}^{u}|z_{[i:m]}^{*}-z_{[i-1:m]}^{*}|} . \end{aligned}$$
(7)

Our following explorations of the dataset of Mardia et al. (1979, pp. 3–4) rely on this index.

5 A revisit of Mardia et al. (1979, pp. 3–4)

Based on the dataset of Mardia et al. (1979, pp. 3–4) and using the just introduced conditional index of increase, we next explore relationships between the scores from closed-book examinations (Sect. 5.1), open-book examinations (Sect. 5.2), and also general performance based on the combined scores arising from closed- and open-book examinations (Sect. 5.3). When comparing any pair of scatterplots, we do so based on only those points whose x-coordinates are in the largest common interval [L, U].

Namely, let the two scatterplots be \(\{(x_{i}, y_{i}),\,i=1,\dots , n_1\}\) and \(\{(v_{i}, w_{i}),\,i=1,\dots , n_2\}\) with some \(n_1\) and \(n_2\); for every scatterplot of Mardia et al. (1979, pp. 3–4), we have \(n_1=n_2=n=88\). Using the median adjustment described in Sect. 4.3, the two scatterplots reduce to the modified scatterplots \(\{(x_{i}^{*}, y_{i}^{*}),\,i=1,\dots , m_1\}\) and \(\{(v_{i}^{*}, w_{i}^{*}),\,i=1,\dots , m_2\}\), respectively. The endpoints of their common interval [L, U] are calculated by the formulas

$$\begin{aligned} L={\mathrm {max}}\{x_{1:m_{1}}^{*}, v_{1:m_{2}}^{*}\} \quad {\text {and}} \quad U={\mathrm {min}}\{x_{m_{1}:m_{1}}^{*}, v_{m_{2}:m_{2}}^{*}\}. \end{aligned}$$
(8)

5.1 Closed-book examinations

Vectors and Mechanics are the only two subjects in the dataset of Mardia et al. (1979, pp. 3–4) that were assessed using closed-book examinations. To illuminate relationships between the scores in these subjects, in Fig. 4 we have depicted Mechanics versus Vectors as well as Vectors versus Mechanics over their common range \([L,U]=[9, 77]\), which we obtained using formula (8). For the LOESS fits, we have used the default \(\texttt {span} = 0.75\) and also \(\texttt {span} = 0.35\). The former smoothes out more fluctuations and thus reveals general patterns, which are fairly increasing, whereas \(\texttt {span} = 0.35\) maintains more minute details. Table 2 summarizes the results.

Fig. 4
figure 4

Piece-wise linear fits (a, b), and the LOESS fits (c, d) when the span is 0.75 (thicker) and 0.35 (thinner) with the index \({\mathrm {I}}={\mathrm {I}}(h_{0.35})\) in parentheses

Full size image
Table 2 Closed-book examination summaries
Full size table

The reported values of the index I suggest that Vectors versus Mechanics exhibits a more increasing pattern than Mechanics versus Vectors. This is also seen from the values of the relative index of interchangeability, RI%, which is positive for Vectors versus Mechanics (and thus negative for Mechanics versus Vectors) irrespective of the degree of smoothing. Hence, we conclude that students with higher scores in Vectors are more likely to get higher scores in Mechanics than the other way around, that is, when Mechanics precedes Vectors. This, we think, is due to the fact that Vectors is a fundamental subject for learning Mechanics; think of, e.g., the notion of force. To support this observation, we refer to the introductory sections of the classical textbook by Synge and Griffith (1949), who first recall basics of Vectors and only then teach Mechanics.

In view of the above, it becomes revealing why curriculum developers tend to include Mechanics modules into Mathematics classes. To illustrate the point, Kitchen et al. (1997) argue that in order to strengthen the appreciation of Mathematics, students should study Kinematics, Statics, and Dynamics, which make up parts of Mechanics and require knowledge of Vectors. Moreover, the authors argue that the use of illustrations based on Mechanics make Mathematics more relevant and thus more appreciated. Consequently, changes in Mathematics curricula have the potential of affecting Mechanics modules, which can in turn become particulary worrisome among those who teach first-year engineering students at universities (e.g., Lee et al. 2006, and references therein). The results reported in Table 2 are in good agreement with the aforementioned observations, and may therefore lend support to those in favour of encouraging students not to avoid “harder” study subjects.

We now take a look at the issue of interchangeability of Mechanics and Vectors with the aid of the absolute index of interchangeability, AI%. For the raw scatterplot, AI% is 2%, which is a relatively small number, likely due to the noise, but not to the pattern itself. We can smooth out the noise using a LOESS fit with a large \(\texttt {span}\) value. For example, the default value \(\texttt {span} = 0.75\) smoothes out a lot of variability and makes the two fits virtually increasing: the index I values are 0.972 and 0.979, quite close to the maximum 1. By setting \(\texttt {span} \) to 0.35, the absolute index of interchangeability surges to \(12.6\%\), which is large, and we would therefore hesitate to state that Mechanics and Vectors are interchangeable. Reiterating our earlier discussion based on RI%, and also recalling our note concerning Synge and Griffith (1949), and further arguments by Kitchen et al. (1997), we would tend to believe that viewing Vectors as an explanatory variable for Mechanics is more appropriate than the other way around.

5.2 Open-book examinations

Algebra, Analysis, and Statistics are the three subjects in the dataset of Mardia et al. (1979, pp. 3–4) that were assessed using open-book examinations. Hence, we have three pairs of scatterplots, whose summaries are in Table 3, with corresponding Figs. 5, 6 and 7 relegated to “Appendix”. Note the different intervals [L, U] for each of the three pairs, and we shall therefore restrain from comparing, for example, Algebra versus Analysis and Algebra versus Statistics. However, we shall compare and discuss, for example, Algebra versus Analysis with Analysis versus Algebra.

Table 3 Open-book examination summaries
Full size table

Algebra and Analysis provide fundamental concepts for other subjects, such as Statistics, with Algebra playing a particularly prominent role, as argued by, e.g., Gamoran and Hannigan (2000). Based on the data of Mardia et al. (1979, pp. 3–4), we reach this conclusion from the raw data (\(\hbox {RI}\%=7.156\)) as well as from the moderate \(\hbox {LOESS}_{0.35}\) fit (\(\hbox {RI}\%=18.623\)). The default \(\hbox {LOESS}_{0.75}\) fit (\(\hbox {RI}\%=-0.800\)) gives a slight preference to Analysis over Algebra.

Remark 7

A possible reason for this change of preference is likely due to an outlier: one student’s Algebra score deviates considerably from the overall pattern of scores. Obviously, the LOESS fit under the default value \(\texttt {span} = 0.75\) smoothes out the outlier, making \({\mathrm {I}}({\mathrm {Analysis}}, {\mathrm {Algebra}}) \) equal to 1, whereas \({\mathrm {I}}({\mathrm {Algebra}}, {\mathrm {Analysis}})\) takes the value 0.992.

The observed slight uncertainty when deciding which of the two study subjects—Algebra or Analysis—should be taught first does not seem to really matter in practice because, as far as we are aware of, Algebra and Analysis are considered fundamental subjects, focussing on different aspects of mathematics, and are thus often taught at the same time. Hence, neither of them can be easily substituted by another one: better performance in these two subjects leads to better performance in other subjects, such as Statistics, as seen from the RI values in Table 3. Note in this regard that irrespective of the degree of smoothing, the RI values for Statistics versus Analysis and Statistics versus Algebra are negative, and thus the empirical evidence provided by Mardia et al. (1979, pp. 3–4) suggests that Analysis and Algebra should be taught first and only then Statistics.

5.3 Closed-book versus open-book examinations

In the previous two sections, we discussed subjects within closed-book examinations and also within open-book examinations. In the current section, we look at the six combinations with one subject from closed-book examinations and another subject from open-book examinations. Table 4 summarizes our findings, with corresponding Figs. 8, 9, 10, 11, 12 and 13 relegated to “Appendix”. Note from Table 4 that the values of the index of increase differ from those in Table 1. The piecewise linear and LOESS fits also differ from the corresponding ones in Figs. 2 and 3, because the latter two figures are not based on unified ranges, whose notion was only introduced in Sect. 4.4.

Table 4 Comparison for cross category
Full size table

From the RI values in Table 4, we see that irrespective of the degree of smoothing, Analysis as a study subject should precede Mechanics, which in turn should precede Statistics. Furthermore, Analysis should precede Vectors. If we do not take into account the RI values based on raw data and concentrate only on the two LOESS fits, then we conclude that both Mechanics and Vectors should precede Algebra. As to Vectors and Statistics, the two LOESS fits give somewhat conflicting suggestions, thus implying that the two subjects may not be good at determining each other’s scores. This we find natural: given our teaching experience, these two subjects—on the introductory level—are hardly related to each other. We should add, however, that advanced statistics requires good knowledge of vectors, matrices, and related concepts, which can in turn be used as illuminating examples when teaching vectors and matrices.

6 Concluding notes

Measuring relationships and, consequently, monotonicity relationships between paired variables is an important and highly challenging problem, especially when relationships

  • are inherently non-linear,

  • cannot be described using closed-form formulas.

To tackle such problems, we have employed the index of increase, which is a relatively new technique that has emerged from the works of Davydov and Zitikis (2017), Chen and Zitikis (2017) and Chen et al. (2018). Since the use of computers is essential, we have thoroughly described the packages and algorithms that we have used in our computations and explorations.

By revisiting the popular dataset of Mardia et al. (1979, pp. 3–4), which is frequently used by university teachers to illustrate various classical concepts of multivariate analysis, we have enabled those familiar with the textbook and the dataset to see the need for, and benefits of, thinking outside the box. To facilitate the task, we have provided a comprehensive explanation of the index of increase, its calculation techniques under various scenarios, and interpretations. For example, we have found the following relationships between different study subjects with respect to the timing of exposure to students:

  • Vectors \(\prec \) Mechanics (Sect. 5.1)

  • Algebra \(\prec \) Statistics (Sect. 5.2)

  • Analysis \(\prec \) Statistics (Sect. 5.2)

  • Algebra 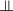Analysis (Sect. 5.2)

  • Analysis \(\prec \) Mechanics \(\prec \) Statistics (Sect. 5.3)

  • Analysis \(\prec \) Vectors (Sect. 5.3)

  • Mechanics \(\prec \) Algebra (Sect. 5.3)

  • Vectors \(\prec \) Algebra (Sect. 5.3)

  • Vectors 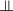Statistics (Sect. 5.3)

where \(S_1 \prec S_2\) means that prior familiarity with subject \(S_1\) is beneficial for learning subject \(S_2\), and S1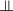S2 when the two subjects do not clearly exhibit \(S_1 \prec S_2\) or \(S_2 \prec S_1\), and can thus be taught in any order. (The sign 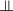is frequently used in Statistics and Probability to indicate independence, which in the current context connotes “timing independence.”)

Next, we make a few cautionary notes that we think are particularly important when dealing with problems such as those we have tackled in the present paper.

First, our interpretations and suggested decision-making are based on the data of Mardia et al. (1979, pp. 3–4), and should not be lightheartedly generalized or extended to other educational contexts. Nevertheless, as is the case with many statistical methods and techniques, they are insightful when used with care and in conjunction with subject-matter knowledge.

Second, not only the subject-matter knowledge that determines whether or not we are likely to be right (or wrong) when making decisions but also the knowledge of instructor’s personality and performance are crucial. For more details and references on this topic, and for associated consequences when teaching, e.g., Calculus and Algebra, we refer to Wade et al. (2017). The “conversation” by Taylor (2019) provides further enlightening thoughts and additional references.

Third, the classically trained statistical researcher would spontaneously ask what would happen if the sample size n (i.e., the class size in the current context) would grow indefinitely. Firstly, such situations cannot happen in the context of educational research, but if, for the sake of argument, this happens, then the answer would undoubtedly be “it would be a mess.” Interestingly, in contexts outside of educational research, such as insurance and finance (e.g., Gribkova and Zitikis 2018; Ren et al. 2019) and engineering (e.g., Gribkova and Zitikis 2019a, b), exploring the index of increase when the sample size n grows indefinitely is meaningful and even pivotal.

It is the latter studies from which we know that the above reply “it would be a mess” is indeed the correct answer, in the sense that if each observation is a non-deterministic outcome (as is the case with student marks), then when n grows to infinity, the index of increase inevitably converges to 0.5, meaning that the underlying scatterplot grows into a chaotic pattern, with no clear upward or downward trends. In a sense, this is natural and does manifest in large-size (say, more than 200 students) introductory statistics/calculus classes, whose main purpose, roughly speaking, is not to make subtle recommendations to students such as directing them to theoretical or computational statistics/calculus studies—this is usually done in upper-year and small class-size environments—but to simply make a general assessment of student suitability to achieve a comprehensive university-level education.

Finally, a few notes concerning future work are in order. First, we reiterate that our choice of the classical dataset of Mardia et al. (1979, pp. 3–4) has been deliberate: we have aimed at contrasting classical and new techniques in a highly accessible way. But this, in turn, raises an interesting research question. Namely, with the currently rapidly developing societal need for more computer proficiency and familiarity with topics such as machine learning and artificial intelligence, are the above reached conclusions based on an old dataset still relevant today? To have well-informed answers, and we think there is no single correct answer to this question, one would need to run observational and experimental studies, whose outcomes may depend on geographical regions, societal traditions, and so on. These are very interesting research problems, and much has already been done by educational researchers; the present paper offers them an additional tool of analysis.