Analysing necessity and sufficiency with Qualitative Comparative Analysis: how do results vary as case weights change?

Abstract

Ragin’s Qualitative Comparative Analysis (QCA) and related set theoretic methods are increasingly popular. This is a welcome development, since it encourages systematic configurational analyses of social phenomena. One downside of this growth in popularity is a tendency for more researchers to use the approach in a formulaic manner—something made possible, and more likely, by the availability of free software. We wish to see QCA employed, as Ragin intended, in a self-critical manner. For this to happen, researchers need to understand more of what is going on behind the results generated by the available software packages. One important aspect of set theoretic analyses of sufficiency and necessity is the effect that the distribution of cases in a dataset can have on results. We explore this issue in a number of ways. We begin by exploring how both deterministic and nondeterministic data-generating processes are reflected in the analyses of populations differing in only the weights of types of cases. We show how and why weights matter in causal analyses that focus on necessity and also, where models are not fully specified, sufficiency. We then draw on this discussion to show that a recent textbook discussion of hidden necessary conditions is weakened as a result of its neglect of weighting issues. Finally, having shown that case weights raise a number of difficulties for set theoretic analyses, we offer suggestions, drawing on two imagined population datasets concerning health outcomes, for mitigating their effect.

Ragin’s Qualitative Comparative Analysis (QCA) provides a way of undertaking case-based configurational analysis, focusing on the necessary and sufficient conditions for an outcome. QCA is increasingly used to undertake systematic set-theoretic analyses of small to medium sized datasets and, occasionally, to analyse large survey datasets. While regression approaches typically aim to estimate the net effects of variables on an outcome, while controlling for other variables, QCA typically focuses on the consequences of conjunctions of conditions (Ragin 1987, 2000, 2008). Whether QCA is a method for establishing causal or descriptive knowledge is currently a matter of debate. Baumgartner (2014), who has developed the related Boolean technique of coincidence analysis (CNA), argues that the Boolean analysis of regularities is the correct route to the establishment of causes as difference-makers. Others see QCA as a more descriptive approach. We have argued elsewhere (Cooper and Glaesser 2012) that QCA is best used with some additional method such as process-tracing when causal understanding is sought. Gerring (2012, pp. 356–358) makes similar points, discussing what Ragin and others have written on this topic.

An important question to ask of any method is how it functions when confronted with a thought experiment in which we postulate some assumed causal structure which should, ceteris paribus, generate a particular set of regular relationships between explanatory conditions and some outcome. Assuming a particular causal relation, and an associated data generating process, we would want the results delivered by any analytic method to reflect these, at least in those cases where we correctly enter all the conditions into our analysis. In practice, of course, social scientists often analyse data via less than perfectly specified models, and it is therefore also important to explore, as we will for the case of QCA, how a method copes, given a postulated assumed causal structure, when some explanatory conditions are omitted from the analytic model and/or some redundant ones are included.

We write then on the assumption that simulations using simple examples are often useful for assessing the extent to which methods can deliver findings that reflect validly some assumed underlying causal structure (Baumgartner 2014). They can also serve a useful purpose in increasing scholars’ understanding of the potential pitfalls associated with any analytic algorithm, especially those that arise when, as is typical, we have less than perfect knowledge of the factors causally relevant to an outcome.

Our particular concern in this paper is whether and how weighting, i.e., the distribution of types of cases with certain characteristics in the sample and/or the population under study, affects analytic results when QCA is employed. The importance of this issue has become clear to us while undertaking QCAs of various datasets (Cooper 2005; Glaesser and Cooper 2012) and when reflecting on arguments made in Schneider and Wagemann (2012) concerning the sources of “hidden necessary conditions” in Boolean analyses. We will discuss case weights in the context of crisp set QCA. We will not address fuzzy set QCA but the reader familiar with QCA will be able to see that parallel issues arise when fuzzy sets are employed. The arguments we make are of general relevance, and not specific to small, medium or large n QCA. There will be some specific situations, however, where the use, in minimising a truth table, of a frequency threshold would affect the ways in which weights affect an analysis.

To follow our arguments, any reader new to QCA will need a brief introduction to the indices used in crisp set QCA. The paper has the following structure:

• Section 1 introduces essential elements of crisp set QCA.

• Section 2 explores the problems that the relative proportions of cases can produce for QCA users with varying degrees of knowledge of the full set of causes of some outcome who research, in terms of quasi-sufficiency and quasi-necessity, a simple deterministic structure.

• Section 3 considers a non-deterministic structure.

• Section 4 discusses related problems in Schneider and Wagemann’s treatment of necessary conditions.

• Section 5, in the light of the problems pointed to in the earlier sections, considers possible ways QCA users might mitigate their consequences.

1 QCA (crisp set): bare bones of measures

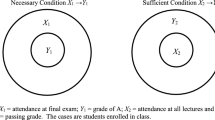
For strict sufficiency of a condition, or a conjunction of conditions, X for Y, we need, wherever X is present, to find Y also present. This requires the set of cases with the condition X to be a subset of the cases with the outcome Y (the left-hand side of Fig. 1). For strict necessity of a condition Z for Y, on the other hand, we need, given the outcome Y, always to find the condition Z present. This requires the set of cases with the outcome Y to be a subset of the set of cases with the condition Z (the left-hand side of Fig. 2). In practice, subset relations in the social world are frequently not as perfect as these. The more realistic right-hand sides of the two figures show such approximations to sufficiency (Fig. 1) and necessity (Fig. 2). Ragin (2008) uses, for crisp sets, a simple measure of the closeness of such relations to strict subsethood. Consider sufficiency. On the right-hand side of Fig. 1, he takes the proportion of cases in X that fall within the boundaries of Y as a measure of the consistency of these data with sufficiency. Such imperfect subset relations are usually described with the terms quasi-sufficient and, for necessity, quasi-necessary. In the case of Fig. 1, the right-hand side would give us a consistency of the order of 0.8, usually taken as large enough to support a claim of quasi-sufficiency.

Fig. 1

Strict and quasi-sufficiency of X for Y

Fig. 2

Strict and quasi-necessity of Z for Y

Alongside these measures of consistency, Ragin (2006, 2008) defines associated measures of coverage. These assess the empirical importance of a condition. In the case of sufficiency, coverage assesses the extent to which a condition X “covers” the outcome set, i.e., how many cases of the outcome are “explained” by the condition. It is mathematically equivalent to the measure of the consistency with necessity of X for Y, i.e., how much of Y is also X. In Fig. 1 the coverage of X is low (and, correspondingly, X is not necessary or quasi-necessary for Y). For a necessary condition Z, coverage assesses the extent to which it is also sufficient for the outcome. Z’s coverage is mathematically equivalent to the consistency with sufficiency of Z. In Fig. 2, the coverage of the necessary condition Z is low (and, correspondingly, Z is not sufficient or quasi-sufficient for Y).

Finally, it is important to note that it is usually configurations, or conjunctions of causes, that are the focus of analysis in QCA. These are represented by such expressions as $(\mathrm{P}^{*}\mathrm{Q}^{*}$ $\sim$R) $+$ $(\mathrm{M}^{*}\mathrm{N})$ where the * indicates set intersection (logical AND), the $\sim$ negates a set (“not R” in our example), and $+$ indicates set union (logical OR). A conjunction such as $\mathrm{P}^{*}\mathrm{Q}^{*}$ $\sim$R is allowed into the final solution if, say, at least 80 % of the cases in the set $\mathrm{P}^{*}\mathrm{Q}^{*}$ $\sim$R achieve the outcome under study. If it is also true that the configuration P*Q*R meets this 80 % threshold for quasi-sufficiency, then the terms $\mathrm{P}^{*}\mathrm{Q}^{*}$ $\sim$R and $\mathrm{P}^{*}\mathrm{Q}^{*}$R can be minimised to $\mathrm{P}^{*}\mathrm{Q}$ on the grounds that the absence or presence of R, given the chosen threshold, makes no relevant difference to the proportion of cases achieving the outcome.

2 A simple deterministic structure

We will explore the problems that may arise as a result of inadequate reflection on the analytic effects of case weights for those wishing to undertake causal analysis via QCA or similar techniques. We will initially work outwards from a postulated causal structure, showing how the distribution of cases in a dataset, given this structure, impacts on measures of consistency with sufficiency and necessity. It is important to hold in mind that we are assuming that this structure exists in the world but that the social scientist undertaking the analysis of its effects may have a far from perfect knowledge of it.

The first postulated structure links two factors, a condition T and an outcome O. Whenever T is present, and only when T is present, does O occur. We will also assume, however, that our imagined researchers may variously believe that T is the crucial cause of O, or that a factor S is the sole cause of the outcome, or that S and T together are important. For this reason, we set out four empirical relationships between the presence and absence of S, T and O that are compatible with the structure.¹ A plausible substantive interpretation of 1–4 might be that T represents having high cognitive ability, and S membership of the dominant ethnic group in a society where there are just two ethnic groups, while O is some career outcome.

$$\begin{aligned} \mathrm{S}^{*}\mathrm{T} => \mathrm{O} \end{aligned}$$

(Implication 1)

$$\begin{aligned} \mathrm{S}^{*}\sim \mathrm{T} =>\, \sim \!\mathrm{O} \end{aligned}$$

(Implication 2)

$$\begin{aligned} \sim \!\mathrm{S}^{*}\mathrm{T} => \mathrm{O} \end{aligned}$$

(Implication 3)

$$\begin{aligned} \sim \!\mathrm{S}^{*}\sim \!\mathrm{T} =>\,\sim \!\mathrm{O} \end{aligned}$$

(Implication 4)

Now, a researcher using QCA who correctly believes that T is the cause of O will find, on collecting data of adequate quality, that T is both sufficient and necessary for O, i.e., $\mathrm{T} <=> \mathrm{O}.$ We now, however, explore the case of a researcher who believes that both T and S matter for the outcome. Such a researcher will collect data on S, T and O in order to construct a truth table to explore the evidence for implications 1–4. Such a truth table will have the form shown in Table 1 where A–D stand for the number of cases in the four configurations.

Table 1 Truth table representing implications 1–4

Ignoring for the moment the numbers of cases in the rows, we could describe this table by ST $+\sim$ST $<=>$ O² (writing $\mathrm{S}^{*}\mathrm{T}$ as ST for convenience), or, after minimising the left-hand side, $\mathrm{T} <=> \mathrm{O}.$ T is both sufficient and necessary for O, as we want. What happens if we begin to vary the number of cases per row? Table 2 shows two possible distributions of A–D.

Table 2 Two sets of values for A–D

Whatever the values of A–D,³ ST and $\sim$ST will always be found to be sufficient for O. T will always be found to be necessary for O. The solution will remain $\mathrm{T} <=> \mathrm{O}.$ But now consider a researcher who believes that only S matters and therefore collects no data on T. The truth table will reduce to just two rows, one for S (with A + B cases) and one for $\sim$S (with C + D cases). The consistency with sufficiency of S is given by A/(A + B). For dataset 1 it is 0.8, and for dataset 2 it is 0.923. The consistency of S with necessity is given by A/(A + C). For dataset 1 it is 0.485; for dataset 2 0.906.

In the case of dataset 2 the result suggests that S is both quasi-sufficient and quasi-necessary for O. For dataset 1, on the other hand, there is good support for quasi-sufficiency but none for quasi-necessity. Remember the causal structure is fixed. Only the weights of cases have changed. Given that in much empirical research there is incomplete knowledge of the causal factors producing an outcome, this dependency of the solution on the weights of cases is clearly an important issue for users of QCA and related techniques. In this case, for dataset 2, the pattern of case weights has misled the analyst who believed S was the crucial cause.

Now, since we know, by our design of the thought experiment, the generative causal basis underlying 1–4, we know that S is not necessary, since implication 3, compatible with $\mathrm{T} <=> \mathrm{O},$ says $\sim$ST $=>$ O. A problem exists concerning the assessment of the necessity of S for the researcher who believes S is the cause of O. Note that we can imagine population proportions which raise the consistency of S with necessity much higher. If we give C in dataset 2 the value of 1, then we have a consistency of 48/(48 $+$ 1), i.e., 0.980. It is worth looking at the range of possible values for the consistency with necessity of S in our example (where $\mathrm{T} <=> \mathrm{O}$). If we fix A at 100 and let C vary in relation to it (from 1 to 100 for illustration)⁴ then it is easy to see that the consistency varies from a little over 0.99 to exactly 0.50. This is shown in Fig. 3.

Fig. 3

Quasi-necessity of S as the ratio of A to C varies

It is often argued that the necessity (or sufficiency coverage) of a factor should only be assessed where the factor has first been shown to be sufficient (Ragin 2008). However, given less than perfect knowledge of the causal factors operating on an outcome, the distribution of cases, as we have seen, also affects consistency with sufficiency. Again, consider the researcher who believes S is the crucial cause. Returning to datasets 1 and 2, we can see that the consistency with sufficiency of S is given by A/(A $+$ B). In dataset 1 it is 16/(16 $+$ 4), or 0.800. In dataset 2, it is 48/(48 $+$ 4), or 0.923. If we change the value of A to 2 in dataset 2, this consistency becomes 2/(2 $+$ 4), or just 0.333. If we fix A at 100 and, illustratively, let B vary from 1 to 100, then the consistency of S with sufficiency varies from 0.99 to 0.5, as did its consistency with necessity when varying C. Now, in this simple deterministic world, both B and C can be varied independently of A and of each other without affecting implications 1–4. We assume our generative causal structure remains intact under these changes. We can for example, having fixed A at 100, and leaving the irrelevant D at 5, reverse the values of B and C in two new datasets 3 and 4 (Table 3). When we do this, we switch the consistencies of S with sufficiency and necessity, as Table 3 records.

Table 3 Two more datasets

We have shown that, given a fixed causal structure, and a researcher with incomplete knowledge of which causes matter, a wide range of results for consistencies are possible, simply as a result of changes in the weights of types of cases in the dataset. This suggests that, for any researcher thinking causally rather than descriptively, QCA analyses that ignore the effects of case weights on consistency formulae may be problematic. To this point we have considered a deterministic structure but allowed its analysis in terms of quasi-sufficiency and quasi-necessity. In the next section we will assume that the causal structure is not fully deterministic.

3 A non-deterministic causal scenario

We continue by considering a simple non-deterministic structure in which there are two causal factors, S and T, and an outcome O. The assumption is again that there is a particular structure in the world, but that the researcher has imperfect knowledge of its features. The postulated structure is such that, for the four possible configurations of S and T and their negations, all else being equal, the proportions gaining the outcome O are those shown in Table 4.⁵ Here, differently from the earlier structure, we are assuming that both S and T are causes of O. We will also assume, however, that a researcher might suspect that S alone, or T alone, or both S and T may be causes of O.

Table 4 Consistencies with sufficiency for four configurations

For the sake of our illustration of the ways weights may affect various researchers’ findings we will consider three possible datasets, shown in Table 5.⁶ Table 6 sets out all indices of consistency with sufficiency and necessity that pass a threshold of 0.8, adding the coverage figures in brackets. For completeness, given that any researcher may or may not know correctly what the true causes of O are, we have included in the table all of S, T, their negations and conjunctions of these.

Table 5 Three invented populations

Table 6 Consistencies above 0.8 with sufficiency and necessity (coverage in brackets)

First, we can see from Table 6 that, considering quasi-sufficiency, the results from all three populations tell us that ST is quasi-sufficient for O at a very high level (0.99). Any researcher correctly believing that S and T are both causes here would have found this result to be unaffected by the different weighting of cases in the three datasets. The researcher believing just S to be the cause of O would have found S to be sufficient, using a threshold of 0.8, in datasets A and B but not C. If s/he had happened to use a stricter threshold of 0.9, then S would have been found to be sufficient in just dataset B. Weighting matters, unless we assume a researcher with full knowledge of the causes operating.

Measures of necessity are also affected by the case weights, of course. For a researcher who enters both S and T in their QCA model, and finds the solution for sufficiency of $\mathrm{ST} => \mathrm{O},$ the consistency with necessity of ST will vary across the three datasets from 0.510 in dataset A, through 0.822 in B, to 0.142 in C. Separate assessments of the necessity of the two factors are also weights-dependent. T only passes the 0.8 threshold in dataset B. S passes it in all three datasets to differing degrees.⁷

How important are these effects of weights? The answer partly hinges on the position one takes on the purpose of QCA and related techniques. Baumgartner (2014) argues that the purpose of Boolean techniques is to gain causal knowledge via the analysis of regularities, and that this requires, ideally, a solution of the form $\mathrm{C}_{1}+\mathrm{C}_{2}+\mathrm{C}_{3} <=> \mathrm{O},$ where the disjunction of conjuncts on the left-hand side is both sufficient and necessary for the outcome O. On this argument, if ST $<=> \mathrm{O}$ appears as the solution, with ST both sufficient and necessary for O, then this lends support to a causal claim. Using our threshold of 0.8, and when the researcher correctly believes both S and T matter, this solution would appear for population B, but not for A or C. The key point is perhaps that any causal conclusions based merely on an analysis of the regularities deriving from our postulated causal structure will vary with the weights characterising our dataset. If the researcher is assumed to know that S and T matter, the key problem in this particular scenario concerns the ways the assessment of necessity vary with case weights. Any researcher deciding on the necessity of a causal condition, or a combination of conditions, purely on the basis of the consistency with necessity taken from a particular population would seem to be effectively assuming that the distribution of cases in this particular population is, in some sense, privileged.⁸

There is another view of this issue. Someone arguing that the sufficiency of ST is the crucial matter to uncover might argue that the varying assessments of nearness to necessity—in their guise of coverage—merely give us useful descriptive information about the empirical importance of this pathway in the three datasets. Ragin has argued this position, arguing that the best uses of the truth table analysis in QCA are “more descriptive”, providing “a basis for causal interpretation at the individual case level”.⁹ Here the analysis of sufficiency is prioritised and any subsequent assessment of the necessity of individual factors appearing in solutions should depend not only on the numerical index of consistency with necessity but should also entail “a good measure of corroborating substantive evidence and theoretical argumentation”.¹⁰

Considering in this section a non-deterministic causal structure, we have shown again that case weights matter. In the case of necessity, even when we assumed, initially, that we knew that S and T are the important causal factors, and that we knew the causal consequences for the outcome of their various conjunctions, we found the assessment of necessity of some conditions and configurations varying across our three populations. We want now to show how these weighting problems considered so far are reflected in a recent discussion by Schneider and Wagemann of “hidden necessary conditions”. We have previously pointed out some problems with their textbook discussion of “hidden necessary conditions” (Cooper et al. 2014). We will revisit these, but then develop a more general perspective on one of the issues they raise, drawing on our discussion earlier in this paper.

4 Schneider and Wagemann on “hidden necessary conditions” and inconsistent truth table rows

So far, in thought experiments, we have considered the problems weights might cause given two causal structures, one deterministic, one not. We will now discuss an example from a prominent textbook on set theoretic methods (Schneider and Wagemann 2012) where the generative causal structure is, as is often the case in empirical science, unknown to the analyst. The focus in this section is on assessing quasi-necessity.

Having previously discussed “hidden necessary conditions” due to incoherent counterfactuals in the context of limited diversity¹¹ Schneider and Wagemann (2012) begin their second section on “hidden necessary conditions” by arguing that such incoherent assumptions about remainders are not the only reason for the disappearance of necessary conditions. They note that necessary conditions can disappear even from a conservative solution term (their preferred term for what Ragin terms a complex solution). This can arise, they say, when “inconsistent truth table rows are included in the logical minimisation that contain the absence of the necessary condition” (p. 225). By “inconsistent” rows, they refer to rows containing cases where some achieve the outcome and some do not. They illustrate this possibility with the hypothetical example reproduced here as Table 7.

Table 7 Schneider and Wagemann’s (2012) Table 9.2

Schneider and Wagemann’s argument proceeds as follows. Looking at row 7 of Table 7, it can be seen that, of these five cases that are AB$\sim$C, four have the outcome Y. This configuration is therefore quasi-sufficient for Y, with a consistency of 0.8. If we run a QCA on the truth table in Table 7 that allows row 7 to go forward (i.e., accepting a consistency of 0.8 as adequate for quasi-sufficiency) we obtain the following minimised solution:

$$\begin{aligned} \mathrm{A}\!\sim \!\mathrm{C}\,+\,\sim \!\mathrm{BC} => \mathrm{Y}. \end{aligned}$$

(1)

The first term, A$\sim$C, has a consistency with sufficiency of 0.93 and the second, $\sim$BC, of 1.0. As Schneider and Wagemann note, no single condition appears in both paths and one might be “tempted to conclude there is no necessary condition for Y” (p. 226). They note, however, that separate tests for necessary conditions show $\sim$B to be necessary for Y, with a very high consistency of 0.92.¹² They argue that, “based on the empirical evidence, we have good reasons to consider $\sim$B to be a relevant necessary condition for Y”. They argue (p. 226) that $\sim$B disappears because it is “minimized from the sufficiency solution by matching row 5 of Table 9.2 (A$\sim$B$\sim$C) with the inconsistent row 7 (AB$\sim$C) into the sufficient path A$\sim$C. $\ldots$ thus, the necessary condition disappears from the sufficiency solution because both the former and the latter are not fully consistent.”

Our earlier discussion of the effects of the relative numbers of cases suggests this is far from the whole story. To see why, consider a small change in the truth table, one that removes the problem of inconsistency. Assume, contrary to what we see in Table 7, that all five cases in row 7 achieve the outcome Y. What then happens when we undertake a QCA that parallels that reported by Schneider and Wagemann? On the basis of changing just one case from not having to having the outcome, we obtain the same algebraic solution as in Eq. 1 (though in this case both terms are strictly sufficient, i.e., have consistencies of 1). And, once again, $\sim$B is quasi-necessary for Y (with a consistency of 0.90 rather than 0.92). We have no inconsistent rows, but we still have the “problem”. Clearly, $\sim$B, when it is a quasi-necessary condition, can disappear from the solution even in the absence of the inconsistency in row 7.

The problem of this hidden necessary condition is not then due to the inconsistency of row 7 per se. What then is its cause? Our earlier discussion suggests that the relative number of cases per row may be a crucial factor: analysing deterministic datasets 1 and 2, we found that a researcher focusing attention on the single condition S would find the condition S quasi-necessary for dataset 2, but not for dataset 1, simply as a result of the differing distributions of case numbers in the configurations. A glance at Schneider and Wagemann’s truth table shows there are quite different numbers of cases in its various rows. It is therefore instructive to undertake another analysis. If we increase the number of cases in row seven to 40, but retain the proportion in this row achieving the outcome at 0.8, we obtain the same solution for sufficiency (with the first term having a consistency of 0.84 and the second of 1), but we now find that a test for the necessity of $\sim$B returns a consistency of only 0.58. $\sim$B is no longer a quasi-necessary condition. The “problem” of its being a hidden necessary condition disappears. The inconsistency of row 7 is not the fundamental problem. Even given this inconsistency, we can remove the problem of the disappearance of $\sim$B by reweighting so that it is no longer a necessary condition in the first place. This is what we found earlier when we kept the proportion of cases within the configurations obtaining the outcome the same in populations A–C (see Sect. 3), but varied the case numbers. Our varying of the numbers had a marked effect on whether or not certain conditions or configurations of conditions passed the threshold for quasi-necessity.

The fundamental problem is not due to inconsistencies per se (though these will certainly modify the way it appears) but to the weight of cases in the rows of truth tables, coupled with the manner in which the arithmetic of proportions works. Indeed, we can make the problem much worse by running the analysis with just one case in row 7—a case which has the outcome—and therefore with no inconsistency characterising this row. Doing this, we obtain the solution for sufficiency in Eq. 1 (with both terms having consistencies of 1) while the consistency with necessity of $\sim$B rises to an almost perfect 0.98, higher than the 0.92 that provided the basis for Schneider and Wagemann’s arguments.

Clearly, Schneider and Wagemann, in choosing their example, have brought an important issue to our attention. In our view, however, in concentrating on just the inconsistency, they have not treated it in a general enough fashion. We also need to consider weights. To explore the consequences of weighting for their example, we will now consider how several consistency and coverage measures vary as we change the weighting of the rows in their table. We will present two graphs that illustrate the general patterns we find as we vary the number of cases in row 7 while holding the other case numbers constant. The first graph (Fig. 4) maintains Schneider and Wagemann’s consistency of 0.8 for row 7. In the second (Fig. 5) we move away from their focus on inconsistency and raise the consistency of row 7 to a perfect 1.0.

Figure 4 shows how the consistency with necessity of $\sim$B falls away as we increase the number of cases in row 7. Schneider and Wagemann choose to have five cases in this row—a small number in relation to the rows including $\sim$B that achieved the outcome (respectively 20, 10 and 15). It is important to note that, given the particular distribution of cases in the other rows, the consistency with necessity of $\sim$B falls away much more quickly than does that of the consistency of the solution for sufficiency itself. Once we have 25 cases in row 7 we find that the consistency with necessity of $\sim$B is below 0.7 and the original problem of $\sim$B being a (hidden) necessary condition begins to disappear.

Fig. 4

Solution is A$\sim$C+$\sim$BC: effect of changing the number of cases in AB$\sim$C (in which configuration 80 % achieve the outcome)

Fig. 5

Solution is A$\sim$C+$\sim$BC: effect of changing the number of cases in AB$\sim$C (in which configuration 100 % achieve the outcome)

Figure 5, where the AB$\sim$C row now has 100 % consistency with sufficiency rather than 80 %, shows a perhaps more striking pattern than Fig. 4. Here, looking at the situation where there are just five cases in row 7 (i.e., reproducing Schneider and Wagemann’s case numbers), we have a consistency with necessity of $\sim$B of 0.90—very close to that of 0.92 in Schneider and Wagemann’s original “inconsistent row” example. If we drop the cases in row 7 to 4 then, even without any inconsistency, we are back to their result: a consistency with necessity of $\sim$B of 0.92 while $\sim$B still does not appear in all the terms in the solution for sufficiency. The overall solution, A$\sim$C$+\sim$BC, maintains a perfect consistency of 1.0 here as the number of cases in row 7 is varied. There is a sense in which the inconsistent case introduced by Schneider and Wagemann to make their argument concerning a hidden necessary condition is actually irrelevant. If we delete just this case from the dataset, the row AB$\sim$C (now with a consistency of exactly 1) goes forward into the solution A$\sim$C +$\sim$BC, and the consistency with necessity of $\sim$B remains at 0.92.¹³ Perhaps the most important general point to emphasise about Fig. 5 is that, given perfect sufficiency for all of the rows of Table 7, the necessity index for $\sim$B changes as we vary the weight of cases in AB$\sim$C. The coverage indices for the two minimised terms in the solution also vary (but always add to 1). It makes sense to see coverage here as indicating the relative empirical importance of the two pathways A$\sim$C and $\sim$BC as the weights change.

We have shown by first considering hypothetical examples in Sects. 2 and 3 and then discussing Schneider and Wagemann’s (2012) example that analytic work using QCA must pay more attention to the weights of cases in the rows of truth tables than has been, to now, usual. This is particularly important in the case of causally oriented analyses of necessity but, in addition, when we cannot be sure we have a full and correctly specified model of the causal structure we are exploring, the relative weights may also, as we have shown earlier, adversely affect analyses of sufficiency. Schneider and Wagemann (2012), addressing situations where the analysis of necessary conditions can go awry, have argued that the inconsistency in a row of a truth table is a crucial factor. We have argued, by generalising their example, that the crucial factor is actually not this inconsistency but the case weights characterising a truth table. Their problem of a hidden quasi-necessary condition both can arise in the absence of any such inconsistency and also fail to appear in the face of one.

Schneider and Wagemann, arguing that this problem is due to the inconsistent row, propose the “imperfect remedy” of increasing thresholds for consistency. They point out that had a stricter threshold for sufficiency of 1.0 been used to analyse Table 7, then the inconsistent row AB$\sim$C would not have been allowed into the minimisation process and the “necessary condition $\sim$B would not thus have been logically minimised away”. However, as they note, were the same threshold used for testing necessity, $\sim$B would no longer be a necessary condition. We have shown that this problem is a more difficult one than they suggest, having its roots not so much in inconsistent rows as in the distribution of cases across rows (even where there are no inconsistencies at all). For this reason, even in truth tables with no inconsistent rows, the problem needs to be at the forefront of a QCA-user’s mind. We therefore need more discussion of how to deal with this problem.

5 What to do about this problem?

We have considered the difficulties that can arise if the issue of case weights is not taken seriously. In the rest of the paper we will discuss what we might do to alleviate the problematic effects of varying weights across populations. We will focus, given the space available, on necessity, and consider it in the simplest context of having full knowledge of the causal structure.¹⁴ We start by considering the usefulness here of measures of empirical importance such as coverage and relevance. We then develop an alternative approach that we first suggested in Cooper et al. (2014).

5.1 Measures of trivialness and relevance: a way forward?

Can the work that has been done on measures of coverage, triviality and relevance (Goertz 2006; Ragin 2006; Schneider and Wagemann 2012) offer us a way to address the issues raised earlier? To explore this question, we will employ a thought experiment involving two populations sharing the same causal structure. Consider Table 8. This, we will assume for the moment, is the full data from a small population (Society D) on the relation between nourishment in pregnancy and the health of babies. We will also assume that there is an underlying causal relation between maternal nourishment and a baby’s health. In this population the majority of mothers (69.94 %) are adequately nourished (our X). Most babies (71.68 %) are healthy (our Y).

Table 8 Society D

Having an adequately nourished mother is close to being perfectly sufficient for the subsequent health of the baby. In addition, when the mother is not adequately nourished, over 90 % of babies are unhealthy. Maternal nourishment clearly matters. It is also clear that having an adequately nourished mother is a quasi-necessary condition for being a healthy baby (consistency of 0.968, coverage of 0.992). Adequate nourishment is both quasi-necessary and quasi-sufficient for a healthy baby. Now we consider how some of the measures of the trivialness and/or relevance of a necessary condition behave with these data.

Goertz (2006) argues that a necessary condition becomes more relevant as it becomes more sufficient. Adequate nourishment passes this test, and, correspondingly, Ragin’s (2006) coverage measure is high. Goertz also argues that the number of cases in the $\sim$X, $\sim$Y cell allows us to assess the trivialness of a necessary condition. Zero cases in this cell indicate trivialness. We have 1,200 cases here, far from zero. This is certainly large enough for us to be able to check, for example, that $\sim$X tends to imply $\sim$Y which we want to see when X tends to being necessary for Y.

Schneider and Wagemann (2012, pp. 233–237) argue that X and Y being nearly constants is another basis for a necessary condition being trivial. They offer a formula for assessing trivialness and relevance (on a single scale) that addresses this problem, claiming (p. 237) that this parameter: “... can be deemed a valid assessment of the relevance of a necessary condition. Low values indicate trivialness and high values relevance.”¹⁵ Applying the “Schneider-Wagemann formula¹⁶ for relevance”, where low scores on a 0–1 scale indicate trivialness, and high scores relevance, then we obtain for the necessary condition “adequate nourishment” a score of 0.981. Adequate nourishment is, on their measure, a relevant necessary condition. All seems well so far, with the various parameters lining up.

But now consider our focus—weighting. Consider Table 9, taken from a second society (Society E), where just the weight of cases in the $\sim$X row happens to be different. The consistency with quasi-sufficiency of X and $\sim$X for Y are unchanged. Consider the rows. Having an adequately nourished mother is again close to being perfectly sufficient for the subsequent health of the baby. Again, when the mother is not adequately nourished, over 90 % of babies are unhealthy. Having an adequately nourished mother is a necessary condition for being a healthy baby (consistency of almost 1, coverage of 0.992). Again, adequate nourishment is quasi-necessary and quasi-sufficient for a healthy baby.

Table 9 Society E

We don’t now have many cases in the $\sim$X$\sim$Y cell, but enough, we think, to check that $\sim$X tends to imply $\sim$Y.¹⁷ By this test, and coverage, the necessary condition X remains non-trivial and relevant. However, in Schneider and Wagemann’s terms, both X and Y are nearly constants—the cases in this cell dominate—and, if we turn to their trivialness/relevance formula, then we get for the quasi-necessary “adequate nourishment” a low score of 0.342. Adequate nourishment, on their measure, is a trivial necessary condition. We can see that their formula is sensitive to the weights of the X and $\sim$X rows, when nothing else, and certainly not the causal consequences of X and $\sim$X, is changed. Table 10 summarises several measures for the two societies.

Table 10 Various indices for societies D and E

There is a small difference in the necessity of X for Y, but on Ragin’s measure of importance (coverage, or the sufficiency of X for Y), the necessary condition is equally important in the two populations. The crucial difference is in the result from Schneider and Wagemann’s formula. What should we make of this? Can it help us, for example, advise a policy maker? Two possible views follow.

• (1) A counterfactual thought experiment can be undertaken in which we shift the cases from the $\sim$X row into the X row and then, assuming all else remains equal,¹⁸ allocate the health outcomes to these new cases of X that the original cases of X have. The point of this is to simulate what would happen if we were able, ceteris paribus, to remove maternal malnourishment from the population. Doing this for Table 8, we produce a reduction in the number of unhealthy babies from 1,225 to 36 (a 97.08 % reduction). For Table 9, the corresponding result is a 32.14 % reduction¹⁹, indicating a sense in which maternal nutrition is a less important factor in society E than D. This experiment suggests that the S-W formula can help us.

• (2) There is, however, an alternative view. The results of the thought experiment required us to have two populations to compare. It is easy to imagine a situation in which we only have an analysis of one population. If this had happened to be the population in Table 9—and this seems just as likely a scenario as that in Table 8—then the S-W formula would have reported that X is a trivial, not a relevant necessary condition. In spite of this, in this population, all else being equal, changing the nutritional status of the mothers in the $\sim$X row would produce a substantial reduction in the numbers of unhealthy babies. Twelve²⁰ of the 12 unhealthy babies in the $\sim$X row would become healthy. The overall number of unhealthy babies would see a 32.14 % reduction. In these senses, it isn’t a trivial condition.

Both populations are possible scenarios. In each the generative causal structure is the same (i.e., X and $\sim$X generate the same proportions of the two possible outcomes). Only the relative weights of X and $\sim$X cases differ. The reason, of course, that in our first thought experiment we saw a greater reduction in unhealthy babies was simply because, while the generative causal structure remained the same, proportionally more of these appeared in the $\sim$X row.²¹

What conclusion might we draw from this section? One possible lesson might be that it is often worth introducing some policy-oriented thought experiments into the discussion of such matters as trivialness and relevance. Much discussion of these matters rightly focuses on the relative sizes of the sets X and Y, and related matters, and attempts to develop generally applicable formulae. But we know from other summarising measures that it is important to bear in mind the details of any particular case. The arithmetic average, for example, is a useful measure, as long as the distribution being summarised isn’t bimodal, doesn’t have many outliers, etc. In the same way as the latter features can cause problems for the interpretation of an average, we think that the weights of the rows of truth tables can cause problems when interpreting the meaning and implications of measures used in QCA. We must be careful when employing formulaic approaches.

5.2 Another approach

With that advice in mind, we will indicate one way of thinking about the problem that can keep things clear in one’s mind when undertaking the analysis of truth tables. To illustrate this, we will return to Table 7. The suggested approach involves regarding each row as evidence for the sufficiency or otherwise of the configuration it represents, while ignoring at this stage finer details concerning the degree of consistency with sufficiency (or necessity).²² Assume, for the sake of argument, that the evidence for each configuration in Table 7 is considered good enough to treat it as warrant for the eight claims in Table 11.

Table 11 Eight statements concerning sufficiency (idealised version of Table 7)

Looking at the truth table in this way, we see that $\sim$B is not strictly a necessary condition for Y, since AB$\sim$C $=>$ Y. If we were to run a QCA on the temporary assumption that there is just one case per row, we would obtain a consistency with necessity for $\sim$B for Y of 0.75, reflecting the fact it appears in three of the four rows to the left of Table 11. It can readily be seen, however, that the higher the number of cases for the three lower rows to the left of Table 11 ($\sim$A$\sim$BC, A$\sim$BC, A$\sim$B$\sim$C) in relation to those for the row AB$\sim$C, the higher will be the reported consistency with necessity of $\sim$B for Y, and the more serious the problem of this quasi-necessary condition being hidden in the solution for sufficiency will appear to be. If we allocate three cases each to the three lower rows on the left-hand side, leaving the row AB$\sim$C with just one, then consistency with necessity for $\sim$B for Y is 0.90. If, however, we allocate 10 cases to AB$\sim$C, while leaving the lower three rows with just one case each, then the consistency with necessity for $\sim$B for Y falls to 0.23.

We can apply this same approach to the simple dataset from societies D and E. In both cases we can argue, let’s assume, that we have good enough evidence for the two (quasi-sufficiency) claims:

• (1) Adequately nourished mother =$>$ Healthy baby

• (2) NOT (Adequately nourished mother) =$>$ NOT (healthy baby)

The first of these is equivalent to the left-hand side of Table 11; the second to the right-hand side. If we were to pretend for a moment that these are both sufficient rather than (strong) quasi-sufficient claims, we could deduce from (2) the necessity of an “adequately nourished mother” for a healthy baby. This would enable us to say, having temporarily ignored the differing weights of X and $\sim$X, that, for both societies D and E, our X is sufficient and necessary for Y (or, more strictly, quasi- in both cases). From this one-case-per-row perspective, the weights of the cases in the rows of D and E make no difference to this conclusion. We know, however, that when these sufficiency relations are expressed in a particular simulated social setting characterised by some particular number of cases in the X and $\sim$X rows, the quasi-necessity of X is, in some sense, of a different sort in D to that in E, in so far as getting rid of malnourishment would remove a larger percentage of unhealthy babies in D than in E.

5.3 A dilemma and a suggested response

Where does this leave us? We have shown, by analysing several simulated datasets, that the weights of cases in the rows of a truth table will affect QCA results concerning the consistency with necessity and, in some situations, sufficiency of a factor.

Should we worry about the fact that assessments of necessity, for example, vary as the weights of cases in rows of truth tables vary? We suspect that the position a scholar will take here will reflect their philosophical position. Someone of an empiricist frame of mind might want to argue that the assessment of necessity should accurately reflect just the observed patterns of data in whatever society is being studied. If the observed world, with our assumed causal structure in Sect. 2 (resulting in implications 1–4), looks like our dataset 2, and if we only enter S into our model, then S is quasi-sufficient and quasi-necessary for O, but if the world looks like our dataset 1 then it is only quasi-sufficient.

On the other hand, a realist (e.g., Bhaskar 1975, 1979; Pawson 1989) might argue that if we have adequate evidence from the study of the four types of case in datasets 1 and 2 in Sect. 2 such that we can complete the one case per row table shown here as Table 12, and, better still, also have an understanding of plausible causal mechanisms that suggests T is causally relevant and S not, then, irrespective of the weights of cases²³ we can say that in both worlds observed via these datasets, T is sufficient and necessary for O, and S is not necessary for O. For the realist, we think, this would provide a single right answer.

Table 12 Four statements concerning sufficiency (from Sect. 2)

As we saw in the previous section, we could also, in a similar way, argue for a single correct answer in the analysis of the societies D and E. However, this single answer doesn’t capture the important “empirical” difference we saw between these societies when we carried out the thought experiment of removing malnourishment in mothers. We suggest the following resolution of this dilemma.

When analysing necessary conditions within a strictly causal perspective, it is informative to perform our one-case-per-row exercise. There seems to be a sense in which the answer this gives will be the right one, especially for a realist. If, in both societies D and E, there are causal processes that lead to (i) (nearly) all babies of malnourished mothers being unhealthy and (ii) (nearly) all babies of adequately nourished mothers being healthy, then it would seem right to privilege these two sufficiency claims (which parallel and actually arise from generative causal processes)—PLUS the implication of (i) that adequate maternal nourishment is also necessary for a baby’s health—over any formulaic results such as those deriving from the S-W relevance formula (which showed adequate nourishment to be a relevant necessary condition in one of these societies but not in the other).

On the other hand, the S-W formula did capture an important difference of relevance to policy makers in the two societies. Similarly, Ragin’s coverage measure for necessity also captures something crucial for policy makers about the empirical importance of nourishment in both societies (that it is not only necessary but also sufficient for a healthy outcome). We therefore also suggest a second stage in which the nature of necessary conditions that have passed the test of the one-case-per-row exercise are explored by means of the various approaches developed by Ragin, Goertz and Schneider and Wagemann but also by means of various thought experiments of the sort we have used here.²⁴ In addition, wherever possible, reference to plausible causal mechanisms is also likely to be helpful when judging what the necessity of a condition actually comprises.

Ideally, of course, any scholar employing a Boolean approach will aim to establish a disjunction of configurations jointly sufficient and necessary for an outcome (Baumgartner 2014). To achieve this s/he will need, as well as eliminating redundant factors, to avoid omitting key explanatory factors from analytic models. In the latter ideal scenario, the issues we have raised become less important, though the assessment of the necessity of individual conditions will still vary with weights. Knowledge of plausible generative mechanisms, whether derived from theory or from within-case studies, will be useful in approaching this goal. However, most scholars will not achieve this degree of perfect explanatory knowledge and therefore need, we believe, to take account of the issues we have discussed.

We have argued before (Cooper and Glaesser 2012; Cooper et al. 2014) that there is more complexity in QCA than sometimes first meets the eye. Case weights add another layer of complexity to those we have previously discussed. Our view, confirmed by the exercise we have undertaken here, is that QCA users should always try to see beneath and around any formulaic approaches in the set theoretic field. We hope our discussion here, and any further work it encourages, will support such an approach.