1 Introduction

Cavity optomechanics (COM), a crossover field of nanophysics and quantum optics, explores the interaction between optical mode and movable mechanical oscillator via radiation pressure [1,2,3,4]. The rapid development of COM has brought diverse potential applications such as ground state cooling of mechanical resonators [5,6,7,8,9], gravitational wave detectors [10], and precision measurement [11, 12]. COM provides an attractive platform for researching many interesting quantum and classical phenomena, e.g., storage of light pulses [13, 14], optical bistability [15,16,17] and optomechanically induced transparency (OMIT) [18,19,20,21].

Electromagnetically induced transparency (EIT) [22,23,24,25] is a quantum interference phenomenon appearing in three-level atoms. When the atomic medium is driven by strong control field, its resonance absorption peak is completely suppressed and a transparent window appears. EIT was first theoretically predicted by Harris et al. [22], and experimentally verified in strontium vapor by Boller et al. [23]. After these years of development, slow light [26], optical switch [27], enhanced nonlinearity [28] and multiple-EIT [29,30,31,32] have been explored. OMIT, a phenomenon analogous to EIT, arises from the destructive interference between the two different absorption channels of probe photons. OMIT has developed rapidly since it was demonstrated theoretically by Agarwal and Huang [18] and experimentally by Weis et al. [19]. Other typical examples of the control of output spectra can be observed in the optomechanical system (OMS) like optomechanically induced absorption (OMIAb) [33, 34], and optomechanically induced amplification (OMIAm) [35]. In recent years, the properties of cascaded OMIT [36], nonreciprocal OMIT [37,38,39,40], reversed OMIT [41, 42], vector OMIT [43], nonlinear OMIT [44,45,46], two-color OMIT [47], and PT-symmetric OMIT [48, 49] have been studied theoretically and experimentally.

In addition, the Laguerre-Gaussian (L-G) cavity or rovibrational cavity [50,51,52,53,54], whispering-gallery-mode microcavity [44, 55], parity-time (PT)-symmetric phase transitions structure [48, 49, 56,57,58], and OMS with two mechanical resonators [59,60,61] are important platforms to explore optical properties. Due to the strong compatibility of the OMS, the combination with nonlinear media has attracted the attention of researchers [46, 62,63,64]. The optical responses based on OMS with degenerate optical parametric amplifier (OPA) have been studied in recent years, for example, the micromechanical mirror in a hybrid system composed of degenerate OPA and Fabry-Pérot (FP) cavity can be cooled from room temperature 300 K to sub-Kelvin temperatures [65], the output power at the Stokes (anti-Stokes) frequency can be influenced strikingly by the OPA [66], and the long-lived slow light and a switch from superluminal to subluminal propagation are achieved by tuning the parameters of OPA [67]. On the other hand, mechanical pump has been used as a measure to regulate OMS by driving mechanical resonator (MR). Due to the external pump providing an additional approach to generate complicated quantum interference effects, many people are devoted to the study of systems with external pump. Xu and Li show that the large positive or negative group delay can be obtained by adjusting mechanical pump [68], the OMIT behavior of the probe field exhibits a phase-dependent effect leading to the switch from OMIT to OMIAb or OMIAm [69], and OMIT peaks can be amplified either symmetrically or asymmetrically by setting and selectively driving one of the two MRs [61].

Motivated by these previous works, we consider a L-G rovibrational cavity system including an OPA and a mechanical pump. We show that when the mechanical pump is manipulated, the transition from OMIT to OMIAb and OMIAm can be easily achieved. The group delay switching from slow light to fast light is tunable by the related parameters of OPA and the mechanical pump. In addition, the efficiency of OSSG is effectively enhanced under the action of OPA compared with Ref. [52] and can be flexibly adjusted by tuning the mechanical pump.

The organization of this paper is as follows. In Sect. 2, we present the theoretical description of the L-G cavity system and give the analytical expressions of the first-order sidebands and the second-order sidebands. In Sect. 3, by adopting experimentally available parameters, we discuss the effects of OPA and mechanical pump on the optical response properties and analyze the results deeply. Finally, the conclusion is given in Sect. 4.

2 Theoretical models and equations

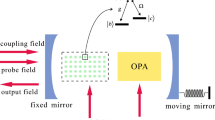
As shown in Fig. 1, the model that we consider consists of two spiral phase plates, which both act as cavity mirrors and form a L-G cavity with cavity mode of frequency \(\omega_{c}\). An OPA including nonlinear gain \(G_{A}\) is put into this cavity. \(\theta\) is the phase of the field driving the OPA. The partially transparent input mirror is fixed but does not affect the charge of the input field. The perfectly-reflect rotational mirror adds a topological charge of 2 l to the light beam on the reflection, which can vibrate along as well as rotate about the cavity axis. A mechanical pump with amplitude \(\varepsilon_{m}\), frequency \(\delta { = }\omega_{p} - \omega_{c}\), and relative phase \(\phi_{m}\) is incident on the RM. We assume that a strong driving field having a Gaussian profile and zero topological charge with frequency \(\omega_{d}\) and a weak probe field with frequency \(\omega_{p}\) are drving this system.

Fig. 1
figure 1

Schematic diagram of the L-G rovibrational-cavity optomechanical system consists of a rigidly fixed input mirror (IM) and a rotational one (RM) driven by a mechanical pump. The cavity mode is the L-G mode and is driven by a strong Gaussian beam with zero topological charge and a weak probe field. A degenerate OPA is bedded in the cavity. \(\phi_{0}\) is the equilibrium position of the rotational mirror, and the angle \(\phi\) indicates the angular displacement under the action of the torsion

Full size image

In a rotating frame at the frequency of the driving laser \(\omega_{d}\), the Hamiltonian is written as follows:

$$ \begin{aligned} H = & \,\,\,\hbar \Delta_{c} c^{\dag } c + \hbar \omega_{m} b^{{\mathbf{\dag }}} b + \left( {\frac{{L_{z}^{2} }}{2I} + \frac{1}{2}I\omega_{\phi }^{2} \phi^{2} } \right) \\ - & \,\,\,\hbar g_{\phi } c^{{\mathbf{\dag }}} c\phi - \hbar g_{z} c^{{\mathbf{\dag }}} c\left( {b^{{\mathbf{\dag }}} + b} \right) + i\hbar G_{A} \left( {e^{i\theta } c^{{{\mathbf{\dag }}2}} - H.c.} \right) + H_{d} , \\ \end{aligned} $$
(1)

where \(\Delta_{c} = \omega_{c} - \omega_{d}\) denotes the detuning of cavity mode from the driving field. \(c \, \left( {c^{\dag } } \right)\) is the annihilation (creation) operator for the cavity mode. \(b \, \left( {b^{\dag } } \right)\) describes the annihilation (creation) of RM. \(\phi\) and \(L_{z}\) are, respectively, the angular displacement and angular momentum of the RM, satisfying the relation \(\left[ {\phi ,L_{z} } \right] = i\hbar\). \(I = mr^{2} /2\) is the moment of inertia about the cavity axis passing through its center, where \(m\)\(\left( r \right)\) is the mass (radius) of the rotational mirror. \(\omega_{\phi }\) \(\left( {\omega_{z} } \right)\) expresses the angular rotation (linear vibration) frequency of the RM. \(g_{\phi } = cl/L\) \(\left( {g_{z} = \omega_{c} /L} \right)\) with \(L\) being the length of the cavity and \(c\) being the velocity of light is the optorotational (radiation pressure) coupling strength between the single photon and the RM. The last term \(H_{d}\) represents the interaction between the driving fields and the OMS

$$ H_{d} = i\hbar \left( {\varepsilon_{d} c^{\dag } + \varepsilon_{p} c^{\dag } e^{{ - i\delta t - i\phi_{pc} }} - \varepsilon_{m} b^{\dag } e^{{ - i\delta t - i\phi_{m} }} - H.c.} \right), $$
(2)

where \(\varepsilon_{d} { = }\sqrt {2\kappa P_{d} /\hbar \omega_{d} }\) \(\left( {\varepsilon_{p} { = }\sqrt {2\kappa P_{p} /\hbar \omega_{p} } } \right)\) is the amplitude of the driving (probe) field, and \(P_{d} \left( {P_{p} } \right)\) corresponds to their laser power. The parameter \(\phi_{pc}\) stands for the relative phase between the probe and driving field.

We are interested in the mean response of the system to the probe field, then the thermal noise and vacuum noise are safely neglected in the case of strong input fields. By using the factorization assumption \(\left\langle {AB} \right\rangle { = }\left\langle A \right\rangle \left\langle B \right\rangle\) [18], starting from the Heisenberg equations of motion and considering the dissipations of the cavity field and the RM, we can obtain the following Heisenberg-Langevin equations:

$$ \begin{gathered} \left\langle {\dot{c}} \right\rangle = - \left( {\kappa + i\Delta^{\prime}} \right)\left\langle c \right\rangle + 2G_{A} e^{i\theta } + \varepsilon_{d} + \varepsilon_{p} e^{{ - i\delta t - i\phi_{m} }} , \hfill \\ \left\langle {\dot{L}_{z} } \right\rangle = - I\omega_{\phi }^{2} \left\langle \phi \right\rangle + \hbar g_{\phi } \left\langle {c^{{\mathbf{\dag }}} } \right\rangle \left\langle c \right\rangle - \gamma_{\phi } \left\langle {L_{z} } \right\rangle , \hfill \\ \left\langle {\dot{\phi }} \right\rangle = \frac{{\left\langle {L_{z} } \right\rangle }}{I}, \hfill \\ \left\langle {\dot{b}} \right\rangle = - \left( {\gamma_{m} + i\omega_{m} } \right)\left\langle b \right\rangle + ig_{z} \left\langle {c^{\dag } } \right\rangle \left\langle c \right\rangle - \varepsilon_{m} e^{{ - i\delta t - i\phi_{m} }} , \hfill \\ \end{gathered} $$
(3)

where \(\Delta^{\prime} = \Delta_{c} - g_{z} \left( {b^{\dag } + b} \right) - g_{\phi } \phi\) is an effective detuning between the L-G cavity mode and the driving field. \(\gamma_{z}\) and \(\gamma_{\phi }\) denote the decay rates for vibrational and rotational modes of the RM, respectively. In the case of \(\left\{ {\varepsilon_{p} , \, \varepsilon_{m} } \right\} < < \varepsilon_{d}\), we express the dynamical variables as the sum of their steady-state values and small fluctuations, i.e., \(c = c_{s} + \delta c\) and \(b = b_{s} + \delta b\). The steady-state values of the dynamical variables are

$$ \begin{gathered} c_{s} = \frac{\Lambda + \kappa - i\Delta }{{\kappa^{2} + \Delta^{2} - \left| \Lambda \right|^{2} }}\varepsilon_{d} , \hfill \\ L_{zs} = 0, \hfill \\ \phi_{s} = \frac{{\hbar g_{\phi } \left| {c_{s} } \right|^{2} }}{{I\omega_{\phi }^{2} }}, \hfill \\ b_{s} = \frac{{ig_{z} \left| {c_{s} } \right|^{2} }}{{\gamma_{m} + i\omega_{m} }}, \hfill \\ \end{gathered} $$
(4)

here \(\Delta = \Delta_{c} - g_{z} \left( {b_{s}^{*} + b_{s} } \right) - g_{\phi } \phi_{s}\) and \(\Lambda = 2G_{A} e^{i\theta }\). To calculate the amplitudes of the first-order and second-order sidebands, we make ansatz with the perturbation terms as [19]:

$$ \begin{gathered} \delta c = C_{1}^{ - } e^{ - i\delta t} + C_{1}^{ + } e^{i\delta t} + C_{2}^{ - } e^{ - 2i\delta t} + C_{2}^{ + } e^{2i\delta t} , \hfill \\ \delta b = B_{1}^{ - } e^{ - i\delta t} + B_{1}^{ + } e^{i\delta t} + B_{2}^{ - } e^{ - 2i\delta t} + B_{2}^{ + } e^{2i\delta t} , \hfill \\ \delta L_{z} = L_{1}^{ - } e^{ - i\delta t} + L_{1}^{ + } e^{i\delta t} + L_{2}^{ - } e^{ - 2i\delta t} + L_{2}^{ + } e^{2i\delta t} , \hfill \\ \delta \phi = \Phi_{1}^{ - } e^{ - i\delta t} + \Phi_{1}^{ + } e^{i\delta t} + \Phi_{2}^{ - } e^{ - 2i\delta t} + \Phi_{2}^{ + } e^{2i\delta t} , \hfill \\ \end{gathered} $$
(5)

where the coefficients \(C_{1}^{ - } , \, C_{1}^{ + }\) are the coefficients of first upper and lower sidebands. Similarly, \(C_{2}^{ - } , \, C_{2}^{ + }\) are the coefficients of the second upper and lower sidebands, respectively.

The analytical method of describing the second-order sideband generation has been proposed in Ref. [70]. The results of the first-order and second-order upper sidebands are given by respectively:

$$ C_{1}^{ - } = \frac{{\lambda_{3} \left( \delta \right)\varepsilon_{p} e^{{ - i\phi_{pc} }} + ig_{z} \left( {\gamma_{z} - i\delta - i\omega_{z} } \right)\lambda_{1} \left( \delta \right)\lambda_{3} \left( \delta \right)\left[ {c_{s}^{*} \lambda_{2} \left( \delta \right)F_{1} \left( \delta \right) - c_{s} } \right]\varepsilon_{m} e^{{ - i\phi_{m} }} }}{{1 - \lambda_{3} \left( \delta \right)\lambda_{2} \left( \delta \right)F_{1} \left( \delta \right)F_{2} \left( \delta \right)}}, $$
(6)
$$ C_{2}^{ - } = \frac{{\lambda_{3} \left( {2\delta } \right)f_{1} + \lambda_{2} \left( {2\delta } \right)\lambda_{3} \left( {2\delta } \right)F_{1} \left( {2\delta } \right)f_{2} }}{{1 - \lambda_{2} \left( {2\delta } \right)\lambda_{3} \left( {2\delta } \right)F_{1} \left( {2\delta } \right)F_{2} \left( {2\delta } \right)}}, $$
(7)

where \(\alpha_{1} = 2ig_{z}^{2} \omega_{z}\), \(\alpha_{2} \left( \delta \right) = i\hbar g_{\phi }^{2}\), \(\alpha_{3} \left( \delta \right) = \alpha_{1} \lambda_{1} \left( \delta \right)\), \(\alpha_{4} \left( \delta \right) = \alpha_{2} \chi \left( \delta \right)\), \(\alpha_{5} \left( \delta \right) = \alpha_{3} \left( \delta \right) + \alpha_{4} \left( \delta \right)\), \(\chi \left( \delta \right) = \left[ {I\left( {\omega_{\phi }^{2} - \delta^{2} - i\gamma_{\phi } \delta } \right)} \right]^{ - 1}\), \(\lambda_{1} \left( \delta \right) = \left[ {\left( {\gamma_{z} - i\delta } \right)^{2} + \omega_{z}^{2} } \right]^{ - 1}\), \(\lambda_{2} \left( \delta \right){ = }\left[ {\left( {\kappa - i\Delta - i\delta } \right) + \alpha_{5} \left( \delta \right)\left| {c_{s} } \right|^{2} } \right]^{ - 1} ,\) \(F_{1} \left( \delta \right) = \alpha_{5} \left( \delta \right)c_{s}^{2} + \Lambda\), \(F_{2} \left( \delta \right) = - \alpha_{5} \left( \delta \right)c_{s}^{*2} + \Lambda^{*}\), \(f_{1} = \alpha_{5} \left( {2\delta } \right)c_{s} \left( {C_{1}^{ + } } \right)^{*} C_{1}^{ - } + \alpha_{5} \left( \delta \right)\left[ {c_{s}^{*} C_{1}^{ - } + c_{s} \left( {C_{1}^{ + } } \right)^{*} } \right]C_{1}^{ - } \; - ig_{z} \left( {\gamma_{z} - i\delta - i\omega_{z} } \right)\lambda_{1} \left( \delta \right)\varepsilon_{m} e^{{ - i\phi_{m} }} C_{1}^{ - } ,\) and\(f_{2} = - \alpha_{5} \left( {2\delta } \right)c_{s}^{*} C_{1}^{ - } \left( {C_{1}^{ + } } \right)^{*} - \alpha_{5} \left( \delta \right)\left[ {c_{s}^{*} C_{1}^{ - } + c_{s} \left( {C_{1}^{ + } } \right)^{*} } \right]\left( {C_{1}^{ + } } \right)^{*} + ig_{z} \left( {\gamma_{z} - i\delta - i\omega_{z} } \right)\lambda_{1} \left( \delta \right)\varepsilon_{m} e^{{ - i\phi_{m} }} \left( {C_{1}^{ + } } \right)^{*} .\)

The results of the first-order can be written as:

$$ C_{1}^{ - } = c_{1 - } \varepsilon_{p} e^{{ - i\phi_{pc} }} + c_{2 - } \varepsilon_{m} e^{{ - i\phi_{m} }} , $$
(8)

According to the input–output relation [71]: \(c_{out} \left( t \right) = c_{in} \left( t \right) - \kappa c\left( t \right)\) with \(c_{out} \left( t \right)\left( {c_{in} \left( t \right)} \right)\) being the output (input) field operator of the cavity, we obtain the output field from the system in the rotating frame, which is given by

$$ \left\langle {c_{out} \left( t \right)} \right\rangle = \left( {\varepsilon_{c} - \kappa c_{s} } \right) + \left( {\varepsilon_{p} e^{{ - i\phi_{pc} }} - \kappa C_{1}^{ - } } \right)e^{ - i\delta t} - \kappa C_{1}^{ + } e^{i\delta t} . $$
(9)

Hence the transmission spectrum of the probe field is described as \(t_{p} = \left( {\varepsilon_{p} e^{{ - i\phi_{pc} }} - \kappa C_{1}^{ - } } \right)/\left( {\varepsilon_{p} e^{{ - i\phi_{pc} }} } \right).\) This formula can be written in two parts:

$$ t_{p} = t_{1} + nt_{2} e^{{ - i\phi_{n} }} , $$
(10)

where \(t_{1} = 1 - \kappa c_{1 - }\) describes the probe transmission without the external mechanical pump, and \(t_{2} = - \kappa c_{2 - }\) corresponds to the contribution from the mechanical pump. As defined in Ref. [70], the efficiency of the second-order sideband reads

$$ \eta { = }\left| {\frac{{\kappa C_{2}^{ - } }}{{\varepsilon_{p} }}} \right| $$
(11)

3 Results and discussion

In this section, to study the dependence of the probe transmission spectrum on different parameters of the system, we calculate Eqs. (7) and (8) with parameters from Ref. [51, 54, 72]: \(L = 10{\text{ mm}}\), \(\kappa = 25\pi {\text{ KHz}}\), \(\lambda = 1064{\text{ nm}}\), \(P_{d} = 34 \, \mu {\text{W}}\), \(m = 2 \, \mu {\text{g}}\), \(r = 16 \, \mu {\text{m}}\), \(\gamma_{z} = \gamma_{\phi } = 0.25\pi {\text{ KHz}}\), \(\omega_{z} = 100\pi {\text{ KHz}}\), \(\omega_{\phi } = 145\pi {\text{ KHz}}\), and the topological charge \(l = 70\). We assume that \(\omega_{12} = \left( {\omega_{z} + \omega_{\phi } } \right)/2\).

We first investigate the effect of the external mechanical pump on the transmitted probe field in the absence of the OPA. Figure 2a shows the transmission coefficient \(\left| {t_{p} } \right|^{2}\) as a function of \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa\) for different parameters of the external mechanical pump. When \(n = 0\), i.e., the model in Fig. 1 is changed to a simple Laguerre-Gaussian rovibrational cavity. That is, two narrow peaks and three absorption dips emerge in probe transmission spectrum, indicating the input probe field could be simultaneously transparent, the so-called double-OMIT, and the locations of peaks are corresponding to \(\omega_{z}\) and \(\omega_{\phi }\). When \(n = 0.1\) and \(\phi_{n} = 0\) the left transmission peak corresponding to radiation pressure coupling is enhanced with \(\left| {t_{p} } \right|^{2} = 1.66\). In Fig. 2b, left transmission rate is amplified further by increasing the mechanical driving strength. This is because of the interference between the OMIT process and the phonon-photon parametric process [61, 73]. However, the right transmission peak corresponding to optorotational coupling has no change. This result indicates that the optorotational coupling is robust against the external mechanical pump in this situation. When the external mechanical pump is set to \(n = 0.1\) and \(\phi_{n} = \pi\), the left transmission peak is suppressed with \(\left| {t_{p} } \right|^{2} = 0.52\). With the increase of mechanical driving strength, there is a different feature. As shown in Fig. 2c, a highly asymmetric spectrum appears due to the competition between the two OMIT processes. According to what we discussed above, the transmission spectrum can be controlled by the amplitude and phase of the mechanical pump.

Fig. 2
figure 2

Transmission coefficient \(\left| {t_{p} } \right|^{2}\) as a function of \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa\) for different values of a amplitude ratio \(n\) and phase \(\phi_{n}\), b \(n\) with \(\phi_{n} = 0\), c \(n\) with \(\phi_{n} = \pi\)

Full size image

In Fig. 3, the OPA is placed in the cavity. As shown in Fig. 3a, the OMIT window obviously broadens under the action of OPA but there is no change in peaks value. Figures 3b and c show the probe transmission spectrum in the presence of mechanical pump and OPA. It is found that the transparent window caused by optorotational coupling always appears at \(\Delta_{p} = \omega_{ \, \phi }\). The position of the right transparent windows does not change with \(G_{A}\) and \(\theta\). Nevertheless, the left OMIT window is further away from \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa = 0\) due to the effect of OPA. The physical reason is that the presence of OPA will change the photon number in optomechanical cavity and the displacement of the mechanical resonator. We find that when the OPA is considered in the system, the left peak is enhanced for \(n = 0.1\) and \(\phi_{n} = 0\) in Fig. 3b compared with Fig. 3a. In contrast, by setting \(n = 0.1\) and \(\phi_{n} = \pi\), a shorter left peak appears in Fig. 3c compared with Fig. 3a, which is the same as the situation in Fig. 2a. Clearly, the influence of mechanical driving is not altered under the existence of OPA. On the other hand, the influence of OPA will change for different parameters of mechanical driving. For example, the left transmission rate is suppressed due to the OPA when \(\phi_{n} = 0\). But it is opposite for \(\phi_{n} = \pi\). When \(\theta\) changes from \(\theta = \pi\) to \(\theta = 0\), the left peak value is enhanced or suppressed further. This result provides more methods to control the transmission spectrum.

Fig. 3
figure 3

Transmission coefficient \(\left| {t_{p} } \right|^{2}\) as function of \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa\) for different values of OPA with a \(n = 0\) and \(\phi_{n} = 0\), b \(n = 0.1\) and \(\phi_{n} = 0\), c \(n = 0.1\) and \(\phi_{n} = \pi\). Other parameters are the same as those in Fig. 2

Full size image

By giving the contour plot in Fig. 4, we study the influence of the mechanical pump on the probe transmission spectrum with the existence of the OPA. The \(\left| {t_{p} } \right|^{2}\) versus \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa\) and mechanical driving strength of external pump with \(\phi_{n} = 0\) is plotted in Fig. 4a. The power of driving field \(P_{d}\) is set to \(46\mu {\text{W}}\) in order to obtain a standard transparent window with \(\left| {t_{p} } \right|^{2} = 1\). We just give the transmission rate in \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa = \left[ { - 2,0} \right]\) due to there is no change in the right transmission rate. It can be seen that the transmission rate increases monotonically by increasing \(n\). It becomes apparent that the \(\left| {t_{p} } \right|^{2}\) can become larger than 1 when \(n\) exceeds a critical value. Therefore, the phenomenon of OMIAm is easily achieved in this hybrid system. Furthermore, Fig. 4b gives the dependence of \(\left| {t_{p} } \right|^{2}\) versus \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa\) and relative phase \(\phi_{n} /\pi\) with \(n{ = }0.1\) nearby \(\Delta_{p} = \omega_{z}\). It is found that the transmission of the probe light changes periodically by varying the phase of the mechanical driving field. Figure 4c presents \(\left| {t_{p} } \right|^{2}\) versus amplitude ratio \(n\) and phase \(\phi_{n} /\pi\). With the increases of \(n\), the left peak value increases monotonically around \(\phi_{n} = 0.25\pi\). However, for \(\phi_{n} = 1.25\pi\), \(\left| {t_{p} } \right|^{2}\) is first reduced to 0 and then increased above 1 with enhancing \(n\), which means the left OMIT window becomes a perfect absorption dip at the resonant point, and then increases from zero to exceed 1 with enhancing n above 0.6. These results show that the transmission rate can easily be equal to and larger than 1. These features provide a scheme to realize the phenomena of perfect transparency and OMIAm in this hybrid system. The physical mechanism will be explained as follows.

Fig. 4
figure 4

Contour plot of transmission coefficient \(\left| {t_{p} } \right|^{2}\) as functions of a \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa\) and mechanical driving strength of external pump with \(\phi_{n} = 0\); b \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa\) and relative phase \(\phi_{n} /\pi\) with \(n{ = }0.1\); c amplitude ratio \(n\) and phase \(\phi_{n} /\pi\) of mechanical pump with \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa = 0.9\). Here \(G_{A} = \kappa\) and the other parameters are the same as those in Fig. 2 except for \(P_{d} = 46\mu {\text{W}}\)

Full size image

The above pump-dependent effect in the transmission spectrum is caused by quantum interference between OMIT process and the mechanical pump effect given by Eq. (7). The \(\left| {t_{1} } \right|^{2}\), \(\left| {nt_{2} } \right|^{2}\), and \(\left| {t_{p} } \right|^{2}\) as a function of amplitude ratio \(n\) is plotted in Fig. 5. Here, \(\left| {t_{1} } \right|^{2}\) is the transmission rate in the absence of the mechanical drive, hence it keeps constant about 1 by varying n. Under the action of mechanical pump, \(\left| {nt_{2} } \right|^{2}\) increases monotonically with \(n\). There is destructive interference between \(\left| {t_{1} } \right|^{2}\) and \(\left| {nt_{2} } \right|^{2}\) for \(\phi_{n} = 1.25\pi\). And the strongest destructive interference \(\left| {t_{p} } \right|^{2} = 0\) appears around \(n = 0.6\), as presented in Fig. 5a. In contrast, there exists constructive interference between \(\left| {t_{1} } \right|^{2}\) and \(\left| {nt_{2} } \right|^{2}\) for \(\phi_{n} = 0.25\pi\). Especially a perfect constructive interference \(\left| {t_{p} } \right|^{2} \simeq 4\left| {t_{1} } \right|^{2} \simeq 4\left| {nt_{2} } \right|^{2}\) is obtained around \(n = 0.6\), as shown in Fig. 5b.

Fig. 5
figure 5

Plots of \(\left| {t_{1} } \right|^{2}\), \(\left| {nt_{2} } \right|^{2}\), and \(\left| {t_{p} } \right|^{2}\) as functions of amplitude ratio \(n\) of external pump for a \(\phi_{n} = 1.25 \, \pi\) and b \(\phi_{n} = 0.25 \, \pi\) with \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa = 0.9\). Here \(G_{A} = \kappa\) and the other parameters are the same as those in Fig. 4

Full size image

In the following, the fast and slow light effects in the weak probe field are studied. The rapid phase dispersion of the probe field usually corresponds to a sharp decrease in the group velocity, and the optical response of the system to the weak probe field can be described by group delay. The group delay of transmitted light is defined as:

$$ \tau_{g} = \frac{{d\Phi_{t} \left( {\omega_{p} } \right)}}{{d\omega_{p} }} = \frac{{d\left[ {\arg \left( {t_{p} \left( {\omega_{p} } \right)} \right)} \right]}}{{d\omega_{p} }} $$
(12)

where \(\tau_{g}\) represent the group delay of the output field. If the group delay is greater than zero, the system will show a slow light phenomenon, and if the group delay is less than zero, it will be a fast light phenomenon.

In Fig. 6, the dependence of group delay \(\tau_{g}\) on amplitude and phase of mechanical pump at \(\Delta_{p} = \omega_{12}\) is displayed with the introduction of an OPA medium. It is found from Fig. 6a that \(\tau_{g}\) is always positive and almost keeps invariable with increasing of the amplitude ratio \(n\) at \(\phi_{n} = 1.25\pi\). However, for \(\phi_{n} = 0.25\pi\), \(\tau_{g}\) has a switch between slow light and fast light and reaches minimum in \(n = 0.47\). The reason is that there exists a perfect destructive interference with \(\phi_{n} = 0.25\pi\) and \(n = 0.47\), which is the opposite of \(\Delta_{p} = \omega_{z}\). Figure 6b plots \(\tau_{g}\) versus phase \(\phi_{n} /\pi\) for different values of \(n\). It can be seen that \(\tau_{g}\) changes periodically with the phase \(\phi_{n}\). The group delay is not a monotonous function of the phase \(\phi_{n}\) and a larger (smaller) maximum (minimum) is obtained with enhancing \(n\), which originates from the slope of the phase dispersion becoming steeper by enhancing \(n\). Therefore, tunable fast and slow light effect is achievable by tuning the amplitude and phase of the external pump in this hybrid optomechanical system.

Fig. 6
figure 6

Group delay \(\tau_{g}\) versus a amplitude ratio \(n\) with \(\phi_{n} = 1.25 \, \pi\) and \(\phi_{n} = 0.25 \, \pi\), and b phase \(\phi_{n} /\pi\) with \(n = 0.05\), 0.15, and 0.3. We set \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa = 0\), \(G_{A} = \kappa\) and \(\theta = 0\). The other parameters are the same as those in Fig. 4

Full size image

In Fig. 7, we show the influence of the nonlinear gain of OPA on the group delay \(\tau_{g}\) of the output probe field. Figure 7 plots \(\tau_{g}\) versus \(G_{A} /\kappa\) for different values of mechanical pump. When mechanical pump is not present, the group delay \(\tau_{g}\) keeps positive and first increases and then decreases, that is, there is a maximum. By enhancing amplitude \(n\) to 0.1 and switching phase \(\phi_{n}\) to \(0.25\pi\), \(\tau_{g}\) converts from positive to negative and has a minimum. Tuning \(\phi_{n}\) to \(1.25\pi\), \(\tau_{g}\) also keeps positive. Therefore, the conversion between fast and slow light effect can be realized by suitably tuning the \(G_{A}\) and external mechanical pump.

Fig. 7
figure 7

Group delay \(\tau_{g}\) as a function of \(G_{A} /\kappa\) for different values of amplitude ration \(n\) and phase \(\phi_{n}\) of mechanical pump. The other parameters are the same as those in Fig. 4

Full size image

Optical second-order sideband generation, which is one of the prominent nonlinear effects in OMS, is usually not apparent. This is because the OSSG is mainly from the upconverted first-order sideband. The second-order sideband is generally suppressed due to the enhanced anti-Stokes field. Here, the influence of the external mechanical pump and OPA on the OSSG will be described in this section. From Fig. 8a, the OSSG has two peaks that are attributed to the radiation pressure and optorotational couplings between the L-G cavity mode and the RM. Compared to the absence of the external mechanical pump, the generation of the second-order sideband can be enhanced or suppressed by controlling the \(n\) and \(\phi_{n}\), which is similar to the OMIT spectrum. In Fig. 8d, we show the efficiency of OSSG under the simultaneous action of mechanical driving and OPA. Compared to the case without OPA, a remarkable enhancement can be obtained. By tuning \(G_{A} { = }\kappa\), the two peaks of efficiency \(\eta\) are enhanced from 0.25 to 11.8% in \(\omega_{z}\) and from 0.8 to 35.2% in \(\omega_{\phi }\) for \(n = 0\). It is clear that the OPA is dominant in terms of enhancement \(\eta\). The physical interpretation of this phenomenon is as follows: the cavity traps the OPA, the anti-Stokes field is no longer resonantly enhanced, and the upconverted process of the first-order sideband is strengthened, thus leading to the enhancement of the efficiency. The nonlinearity of the physical medium of the system plays an important role in the generation of the second-order or high-order sidebands. This giant enhancement of second-order sidebands can be used in precision measurement of very weak signals, e.g., single-charge detections [74, 75].

Fig. 8
figure 8

Efficiency \(\eta_{s}\) of the OSSG as a function of the \(\left( {\Delta_{p} - \omega_{12} } \right)/\kappa\) with a \(G_{A} = 0\) for different values of mechanical pump \(n = 0\),\(n = 0.1, \, \phi_{n} = 0.25\pi\), \(n = 0.1, \, \phi_{n} = 1.25\pi\) and b Magnified OSSG peak near \(\Delta_{p} = \omega_{z}\), c Magnified OSSG peak near \(\Delta_{p} = \omega_{\phi }\); d \(G_{A} = \kappa\) for different values of mechanical pump \(n = 0\),\(n = 0.1, \, \phi_{n} = 0.25\pi\), \(n = 0.1, \, \phi_{n} = 1.25\pi\) and e Magnified OSSG peak near \(\Delta_{p} = \omega_{z}\), f Magnified OSSG peak near \(\Delta_{p} = \omega_{\phi }\)

Full size image

4 Conclusions

In summary, this paper provides an in-depth study of the optical response of a hybrid optomechanical system under a coherent-mechanical force driving. An OPA medium is considered in this L-G cavity. It can be easily realized that OMIT swiches to OMIAb or OMIAm due to the quantum interference effect between different routes. We have demonstrated that the gain of the OPA, the phase and amplitude of the external pump can be used to tune fast and slow light. Moreover, the enhancement effect of the OPA on the second-order sideband generation is discussed. The present results may provide a new way to control light propagation using the OPA and the external time-dependent mechanical pump, which is helpful to understand the optical response properties of the nonlinear optomechanical devices and will have potential applications for quantum information processing.