Controllable optical response properties in a hybrid optomechanical system

Abstract

In this paper, we study theoretically the optical response properties of the output field in a hybrid optomechanical system, in which a degenerate optical parametric amplifier (OPA) and a $\varLambda$-type three-level atomic ensemble are placed in a driven optical cavity with a moving end mirror. We show that due to the presence of the OPA and the atomic medium, our proposal has the ability to exhibit the optical tristability and multiple optomechanically induced transparency (OMIT)-like effects. Moreover, the combined effects of optical amplification and OMIT-like as well as the tunable switch from slow-to-fast light can be realized by tuning the gain coefficient of the OPA and the phase of the field driving the OPA. In addition, the role of the OPA on the higher-order sideband generation has also been investigated. We find that the presence of the OPA contributes to the enhancement of the second-order sideband generation. These results provide a new way to engineer the hybrid optomechanical devices for applications in optical communications and signal processing.

1 Introduction

A prototypical optomechanical system (OMS) [1] consists of quantum optical fields and mechanical resonators, which are coupled with each other via radiation pressure. The intrinsic nonlinear nature of the radiation pressure interaction can generate several remarkable quantum effects in OMSs, such as cooling mechanical mode into its ground state [2,3,4,5,6], generating optical bistability [7, 8] and quantum squeezing [9,10,11,12,13]. Another intriguing example closely relevant to the present work is optomechanically induced transparency (OMIT), which has been studied both in theory [14, 15] and in experiment [16,17,18,19,20]. OMIT is an analog of electromagnetically induced transparency (EIT) well known in atomic physics [21,22,23,24,25,26,27], i.e., arising from the quantum destructive interference between different absorption channels of probe photons (by the cavity or by the phonon mode). This emerging subject has led to many meaningful applications, including slow and fast light [28,29,30], the precision measurement of coupling rate [31] and quantum information processing [32, 33]. Moreover, OMIT provides a versatile platform to explore a variety of novel quantum optical effects, such as nonlinear OMIT [34, 35], nonreciprocal OMIT [36] and PT-symmetric OMIT [37,38,39].

Recently, due to the strong compatibility of the OMS, different kinds of hybrid systems combining the OMS with other typical physical setups, such as charged systems [40], cold atoms [41,42,43,44,45,46] and nonlinear medium [5, 13, 47,48,49,50], have been created for diverse purposes. Atom-assisted OMSs being among the most favorite hybrid OMSs have earned more attention. For example, via introducing a Jaynes–Cummings interaction between a two-level system and the mechanical resonator of cavity OMS, an optomechanical analog of two-color OMIT has been researched in detail [42]; the controllable OMIT has been realized in the system consisting of a generic OMS and an atomic ensemble [43]; the normal-mode splitting and optomechanically induced absorption, amplification and transparency also have been investigated in a double-cavity hybrid OMS with two atomic ensembles [46]. On the other hand, the degenerate OPA based on second-order nonlinearity in optical crystals was the earliest candidate to produce squeezed light. It has been shown that the degenerate OPA inside an OMS can enhance optomechanical coupling, the effective damping rate of the mirror [5] and normal-mode splitting [47]. The enhancement of the effective mechanical damping rate can be used to increase the width of the OMIT [49] and to tune the group velocity of a propagating probe pulse.

Inspired by those previous works, in this paper, we investigate the optical response properties of the output probe field in a hybrid OMS consisting of an OPA and a $\varLambda$-type three-level atomic medium inside a driven cavity with a moving end mirror. We show that (i) under proper parameters, our proposal has the capability of showing tristable behavior where the gain coefficient of the OPA acts as a switch in changing the bistability of the system to a tristable manner; (ii) the presence of the OPA and the atomic ensemble can contribute to the occurrence of multiple OMIT-like effects. In particular, the combined effects of the OMIT-like and the optical amplification as well as the tunable switch from slow-to-fast light can be easily realized by tuning the gain coefficient of the OPA $G_{A}$ and the phase of the field driving the OPA $\theta$. The physical reason behind the above phenomena is: when the OPA is included in the OMS, the photon number in optomechanical cavity and the displacement of the mechanical resonator can be changed by adjusting $G_{A}$ and $\theta$, which will in turn influence the optical response properties of the system. In addition, we have indicated that the presence of the OPA can enhance the second-order sideband generation. This opens up a promising new way to enhance the nonlinear OMIT.

For our current proposal, the most relevant implementations consist in (i) whispery-gallery-mode resonators (microtoroids and microdisks, for example), where light circulates around its edge via total internal reflection, pushing the whole structure, hence exciting some of its mechanical modes [51], and (ii) superconducting resonators coupled to a drum-shaped capacitor, which acts as a mechanical degree of freedom [52,53,54]. In the past few years, some experiments have demonstrated that crystalline whispering-gallery-mode resonators possessing second-order optical nonlinearity [55,56,57,58,59,60,61] and superconducting circuits [52,53,54, 62,63,64,65] can be used to realize the parametric down-conversion process. In addition, whispery-gallery-mode resonators and superconducting resonators are also a good platform for realization of cavity QED [62, 63, 65,66,67]. Based on these experiments and theories, we believe that our proposal can be implemented, even if no corresponding experiments have been reported.

The paper is organized as follows. In Sec.  2, we introduce the theoretical model of the hybrid system and solve its dynamical equation. In Sect. 3, we study the effect of the degenerate OPA and the atomic ensemble on the absorptive behavior of the output probe field. In Sect. 4, we show that the presence of OPA leads to the enhancement of the second-order sideband generation. In Sect. 5, we summarize our main results.

2 Model

Fig. 1

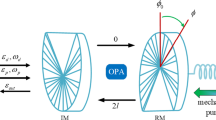
Schematic diagram of a typical optomechanical cavity with one movable end mirror; N identical $\varLambda$-type three-level atoms and a degenerate OPA are embedded in the cavity. The cavity is simultaneously driven by a strong coupling field and a weak probe field through the fixed cavity mirror. The $\varLambda$-type three-level atomic ensemble is driven by a strong control field. For the ith atom, the classical control field induces the atomic transition between $|a\rangle _{i}\leftrightarrow |c\rangle _{i}$ with Rabi frequency $\varOmega$. The cavity mode induces the atomic transition between $|a\rangle _{i}\leftrightarrow |b\rangle _{i}$ with coupling strength g. In addition, the nonlinear crystal OPA is pumped by an additional laser beam to produce parametric amplification

As shown schematically in Fig. 1, the model that we considered is a hybrid nonlinear OMS. A degenerate OPA and N identical $\varLambda$-type three-level atoms are placed in a Fabry–Perot cavity consisting of one fixed mirror and one movable mirror. In our configuration, the cavity mode with frequency $\omega _{0}$ is simultaneously driven by a strong coupling field with frequency (amplitude) $\omega _\mathrm{c}$ ($\varepsilon _\mathrm{c}$) and a weak probe field with frequency (amplitude) $\omega _\mathrm{p}$ ($\varepsilon _\mathrm{p}$), which then exert an optical radiation pressure on the movable cavity mirror. The states $|a\rangle _{i}$, $|c\rangle _{i}$ and $|b\rangle _{i}$ denote the excited, metastable and ground states of the ith atom, respectively. Specifically, for ith atom, the transition between $|a\rangle _{i}\leftrightarrow |b\rangle _{i}$ is induced by the cavity mode, which acts as a probe field. The transition between $|a\rangle _{i}\leftrightarrow |c\rangle _{i}$ is induced by a classical light of frequency $\nu$ with the Rabi frequency $\varOmega$, which serves as a strong coupling field. Moreover, the nonlinear crystal OPA is pumped by an additional laser beam with coupling coefficient $\lambda$ to produce parametric amplification. In general, the movable mirror is treated as a quantum mechanical harmonic oscillator with resonance frequency $\omega _{m}$, effective mass m and damping rate $\gamma _{m}$. With the above consideration, the total Hamiltonian for the hybrid system can be written as

$$\begin{aligned} \begin{aligned} H=&\left( \frac{p^{2}}{2m}+\frac{1}{2}m \omega _{m}^2 q^{2}\right) +\hbar \omega _{0}{a}^{\dag }{a}+\hbar \sum _{i=1}^{N}\left( \omega _{ab}\sigma _{aa}^{i}+\omega _{cb}\sigma _{cc}^{i}\right) \\&-\hbar G q {a}^{\dag }{a}+\hbar \sum _{i=1}^{N}\left( \varOmega e^{-i \nu t}\sigma _{ac}^{i}+g {a}\sigma _{ab}^{i}+\mathrm{H.c}\right) +i\hbar G_{A}(e^{i\theta } {a^{\dag }}^{2}-\mathrm {H.c})\\&+i\hbar \left( \varepsilon _\mathrm{c} {a}^{\dag }e^{-i\omega _\mathrm{c} t}+\varepsilon _\mathrm{p} {a}^{\dag }e^{-i\omega _\mathrm{p} t}-\mathrm {H.c}\right) , \end{aligned} \end{aligned}$$

(1)

where the first three terms are the free energies of the movable mirror, the cavity field and the three-level atomic medium, respectively. The position and momentum operators of the mechanical oscillator are denoted by q and p, respectively; a (${a}^{\dag }$) is the annihilation (creation) operator of the single-mode cavity; $\sigma _{\alpha \beta }^{i}=|\alpha \rangle _{i}\langle \beta |_{i}$ ($\alpha ,\beta =a,b,c$) is the projection ($\alpha =\beta$) or transition ($\alpha \ne \beta$) operator of the ith atom, and $\omega _{\alpha b}$ ($\alpha =a,c$) is the transition frequency between level $|\alpha \rangle$ and level $|b\rangle$. The fourth term describes the optomechanical interaction between the cavity field and the mechanical oscillator with single-photon coupling strength $G=\omega _{0}/L$ (L being the cavity length in mechanical equilibrium). The fifth term represents the light–atom interaction, where $g=-\mu \sqrt{\omega _{0}/2 V \varepsilon _{0}}$ describes the cavity–atom coupling with $\mu$ being the electric-dipole transition matrix element between two levels $|a\rangle _{i}$ and $|b\rangle _{i}$, V being the cavity volume and $\varepsilon _{0}$ being the vacuum permittivity. The sixth term corresponds to the coupling of the intracavity field with the OPA. $G_{A}$ is the nonlinear gain of the degenerate OPA, and $\theta$ is the phase of the field driving the OPA. The parameter $G_{A}$ is proportional to the pump amplitude $E_\mathrm{OPA}$, $G_{A}=\lambda E_\mathrm{OPA}$. The terms shown in the third line of Eq. (1) describe the interactions between the two driving fields and the cavity field, respectively. Here, $\varepsilon _\mathrm{c}=\sqrt{2\kappa p_\mathrm{c}/(\hbar \omega _\mathrm{c})}$ ($\varepsilon _\mathrm{p}=\sqrt{2\kappa p_\mathrm{p}/(\hbar \omega _\mathrm{p})}$) with $p_\mathrm{c}$ ($p_\mathrm{p}$) being the power of the coupling (probe) field and $\kappa$ being the cavity decay rate.

Then, we introduce the collective operators of the atomic medium to simplify the Hamiltonian, i.e., $B=\frac{1}{\sqrt{N}} \sum _{i=1}^{N}\sigma _{ba}^{i}$ and $C=\frac{1}{\sqrt{N}} \sum _{i=1}^{N}\sigma _{bc}^{i}$ [23, 24]. In the low-excitation limit with large N, the above operators behave as bosons and satisfy the standard commutation relations $[{B}, {B}^{\dag }]=1$ and $[{C}, {C}^{\dag }]=1$. Based on the collective operators, we obtain the new form of the Hamiltonian

$$\begin{aligned} \begin{aligned} H=&\left( \frac{p^{2}}{2m}+\frac{1}{2}m \omega _{m}^2 q^{2}\right) +\hbar \omega _{0}{a}^{\dag }{a}+\hbar \left( \omega _{ab}{B}^{\dag }{B}+\omega _{cb}{C}^{\dag }{C}\right) \\&-\hbar G q {a}^{\dag }{a}\!+\!\hbar \left( \varOmega e^{-i \nu t} {B}^{\dag } {C}+g \sqrt{N} {a} {B}^{\dag }\!+\!\mathrm{H.c}\right) \!+\!i\hbar G_{A}\left( e^{i\theta } {a^{\dag }}^{2}-\mathrm {H.c}\right) \\&+i\hbar \left( \varepsilon _\mathrm{c}{a}^{\dag }e^{-i\omega _\mathrm{c} t}+\varepsilon _\mathrm{p}{a}^{\dag }e^{-i\omega _\mathrm{p} t}-\mathrm {H.c}\right) .\qquad \end{aligned} \end{aligned}$$

(2)

By defining $a={\tilde{a}} e^{-i\omega _\mathrm{c} t}$, $B={\tilde{B}} e^{-i\omega _\mathrm{c} t}$, $C={\tilde{C}} e^{-i(\omega _\mathrm{c}-\nu )t}$ and taking the corresponding dissipation and fluctuation terms into consideration, the dynamics of the system governed by Eq. (2) satisfies the following nonlinear quantum Langevin equations

$$\begin{aligned} \begin{aligned} \dot{q}=&\frac{p}{m},\\ \dot{p}=&-m \omega _{m}^{2} q+\hbar G {\tilde{a}}^{\dag } {\tilde{a}}-\gamma _{m} p+\sqrt{2\gamma _{m}}\xi _\mathrm{in}{(t)},\\ \dot{{\tilde{a}}}=&-[\kappa +i(\omega _{0}-\omega _\mathrm{c})] {\tilde{a}}+i\hbar G {\tilde{a}}_{s}\langle q \rangle -i g \sqrt{N}{\tilde{B}}+\varLambda a^{\dag }\\&+\varepsilon _\mathrm{c}+\varepsilon _\mathrm{p}e^{-i\delta t}+\sqrt{2\kappa }{\tilde{a}}_\mathrm{in}{(t)},\\ \dot{{\tilde{B}}}=&-[\varGamma _{1}+i(\omega _{ab}-\omega _\mathrm{c})]{\tilde{B}}-i \chi {\tilde{a}}-i\varOmega {\tilde{C}}+\sqrt{2\varGamma _{1}}{\tilde{B}}_\mathrm{in}{(t)},\\ \dot{{\tilde{C}}}=&-[\varGamma _{2}+i(\omega _{cb}+\nu -\omega _\mathrm{c})] {\tilde{C}}-i\varOmega {\tilde{B}}+\sqrt{2\varGamma _{2}}{\tilde{C}}_\mathrm{in}{(t)}, \end{aligned} \end{aligned}$$

(3)

where $\chi =g\sqrt{N}$, $\varLambda =2G_{A}e^{i\theta }$ and $\delta =\omega _\mathrm{p}-\omega _\mathrm{c}$. Furthermore, $\varGamma _{1}$ ($\varGamma _{2}$) is the decay rate of the transition between $|a\rangle \leftrightarrow |b\rangle$ ($|a\rangle \leftrightarrow |c\rangle$), ${\tilde{a}}_\mathrm{in}{(t)}$ is the input vacuum noise associated with the cavity field, ${\tilde{B}}_\mathrm{in}{(t)}$ and ${\tilde{C}}_\mathrm{in}{(t)}$ are the input vacuum noises associated with the atomic medium and $\xi _\mathrm{in}{(t)}$ is the quantum Brownian noise.

Since we are interested in the mean response of the system to the probe field, the noise terms can be dropped because of the properties $\langle {\tilde{a}}_\mathrm{in}{(t)} \rangle$=$\langle {\tilde{B}}_\mathrm{in}{(t)} \rangle$=$\langle {\tilde{C}}_\mathrm{in}{(t)} \rangle$=$\langle \xi _\mathrm{in}{(t)}\rangle$=0 [14]. By setting all the time derivatives of Eq. (3) to zero, we can obtain the steady-state mean values of interest:

$$\begin{aligned} p_{s}= & {} 0,\quad q_{s}=\frac{\hbar G |{\tilde{a}}_{s}|^2}{m\omega _{m}^2}, \end{aligned}$$

(4)

$$\begin{aligned} {\tilde{a}}_{s}= & {} \frac{(\kappa -i\varDelta +L^{*})\varepsilon _\mathrm{c}+\varLambda \varepsilon _\mathrm{c}}{[(\kappa +i\varDelta +L)(\kappa -i\varDelta +L^{*})-|\varLambda |^2]}, \end{aligned}$$

(5)

where $L=\frac{\chi ^{2}[\varGamma _{2}+i\varDelta _{b}]}{[\varGamma _{1}+i\varDelta _{a}][\varGamma _{2}+i\varDelta _{b}]+\varOmega ^{2}}$, $\varDelta =\omega _{0}-\omega _\mathrm{c}-G q_{s}$, $\varDelta _{a}=\omega _{ab}-\omega _\mathrm{c}$ and $\varDelta _{b}=\omega _{cb}+\nu -\omega _\mathrm{c}$. It’s worth to indicate that $\varDelta _{a}$ and $\varDelta _{b}$ can be rewritten as $\varDelta _{a}=\omega _{m}-\varDelta _{ab}$ and $\varDelta _{b}=\omega _{m}+\varDelta _\mathrm{c}-\varDelta _{ab}$. Here $\varDelta _{ab}=\omega _{0}-\omega _{ab}$ and $\varDelta _\mathrm{c}=\nu -\omega _{ac}$. In the following, we fix $\varDelta _{b}=\omega _{m}$, which implies that the two-photon resonance $\varDelta _\mathrm{c}=\varDelta _{ab}$ for the atoms is always satisfied. As reported in Ref. [24], the EIT effect will appear, as long as the atomic medium is prepared in the two-photon resonance. Therefore, the $\varLambda$-type three-level atoms have no absorption and they do not consume photons. In addition, for simplification, we have set $o=\langle o\rangle$, where o is an any optical or mechanical operator.

Fig. 2

Effects of a the gain coefficient of OPA $G_{A}$ and b the phase of the field driving the OPA $\theta$ on the bistability of intracavity intensity for the hybrid optomechanical cavity. Here, $\theta =0.5\pi$ and $G_{A}=3\kappa$ are fixed in (a) and (b), respectively. Other relevant parameters are $\omega _{m}=2 \pi \times 947$ kHz, $m=145$ ng, $L=25$ mm, $\kappa =2 \pi \times 215$ kHz, $\gamma _{m}=2 \pi \times 141$ Hz, $G=\omega _{0}/L$, $\chi =0$, $\varOmega =40 \pi$ MHz, $\varGamma _{1}=62.8$ MHz, $\varGamma _{2}=62.8$ kHz, $\varDelta _{a}=\omega _{m}$ GHz and $\varDelta _{b}=\omega _{m}$

Fig. 3

Plot of $n_{a}$ versus $p_\mathrm{c}$. The red solid and the blue dash-dotted curves correspond to $\chi =0$ and $\chi =100$ MHz, respectively. Here, we fix $G_{A}=1.0\kappa$ and $\theta =0.5\pi$. Other relevant parameters are the same as those in Fig. 2

Due to the nonlinearity of Eq. (5), our system has the capability of showing multistability. Figure 2a depicts the response of the steady-state intracavity intensity ($n_{a}=|{\tilde{a}}_{s}|^2$) to the gain coefficient of the OPA. The considered parameters of the cavity optomechanics are similar to those in Ref. [14]: $\omega _{m}=2 \pi \times 947$ kHz, $m=145$ ng, $L=25$ mm, $\kappa =2 \pi \times 215$ kHz and $\gamma _{m}=2 \pi \times 141$ Hz. The parameters of atom are chosen from Ref. [24]: $\varOmega =40 \pi$ MHz, $\varGamma _{1}=62.8$ MHz, $\varGamma _{2}=62.8$ kHz and $\chi =100$ MHz. Besides, the atomic-cavity field detuning $\varDelta _{a}=-5$ GHz is considered here. From Fig. 2a, one can easily find that in the absence of the degenerate OPA and the atomic ensemble, due to the nonlinear nature of OMS, the system exhibits a bistable behavior. When we take the OPA into consideration, the domain of the bistability region can be enlarged with increasing $G_{A}$. This behavior occurs because the presence or absence of the OPA can change the mean photon number of the system, resulting in a different radiation pressure on the oscillating mirror. The result in Fig. 2b shows that changing $\theta$ can also influence the bistable behavior of the hybrid system. Moreover, the tristable behavior can be realized by choosing suitable $G_{A}$ and $\theta$ (see red solid curve in Fig. 3). Meanwhile, if the atomic medium is embedded in the cavity, the tristability region can be further increased (see blue dash-dotted curve in Fig. 3). By Comparing Figs. 2 and 3, we know that the switch between bistability and tristability can be realized by choosing proper values of $G_{A}$ and $\theta$.

Having discussed the mean field solutions, we now proceed to examine the fluctuation dynamics. We expand each operator as the sum of its steady-state value and a small fluctuation around it, i.e., $l = l_{s}+\delta l$, and inserting it into Eq. (3). After eliminating the steady-state values, the linearized quantum Langevin equations for the fluctuation operators take the form

$$\begin{aligned} \begin{aligned} \delta \dot{q}=&\frac{\delta p}{m},\\ \delta \dot{p}=&-m \omega _{m}^{2} \delta q+\hbar G \left( {\tilde{a}}_{s}^{\dag } {\delta {\tilde{a}}}+{\tilde{a}}_{s}\delta {\tilde{a}}^{\dag }+\delta {\tilde{a}}{\tilde{a}}^{\dag }\right) -\gamma _{m} \delta p,\\ \delta \dot{{\tilde{a}}}=&-(\kappa +i\varDelta _{0}) \delta {\tilde{a}}+i\hbar G({\tilde{a}}_{s}\delta q+\delta a\delta q)-i \chi {\delta {\tilde{B}}}+\varLambda \delta {\tilde{a}}^{\dag }+\varepsilon _\mathrm{p}e^{-i\delta t},\\ \delta \dot{{\tilde{B}}}=&-(\varGamma _{1}+i\varDelta _{a})\delta {\tilde{B}}-i \chi {\delta {\tilde{a}}}-i\varOmega {\delta {\tilde{C}}},\\ \delta \dot{{\tilde{C}}}=&-(\varGamma _{2}+i\varDelta _{b}){\delta {\tilde{C}}}-i\varOmega {\delta {\tilde{B}}},\\ \delta \dot{{\tilde{a}}}^{\dag }=&-(\kappa -i\varDelta _{0}){\delta {\tilde{a}}^{\dag }}-i\hbar G({\tilde{a}}_{s}^{\dag }\delta q+\delta {\tilde{a}}^{\dag }\delta q)+i \chi {\delta {\tilde{B}}^{\dag }}+\varLambda ^{*} \delta {\tilde{a}}+\varepsilon _\mathrm{p}^{*}e^{i\delta t},\\ \delta \dot{{\tilde{B}}}^{\dag }=&-(\varGamma _{1}-i\varDelta _{a})\delta {\tilde{B}}^{\dag }+i \chi {\delta {\tilde{a}}^{\dag }}+i\varOmega {\delta {\tilde{C}}^{\dag }},\\ \delta \dot{{\tilde{C}}}^{\dag }=&-(\varGamma _{2}-i\varDelta _{b}){\delta {\tilde{C}}^{\dag }}+i\varOmega {\delta {\tilde{B}}^{\dag }}. \end{aligned} \end{aligned}$$

(6)

The terms related to $\delta {\tilde{a}}\delta {\tilde{a}}^{\dag }$, $\delta a\delta q$ and $\delta {\tilde{a}}^{\dag }\delta q$ in Eq. (6) are attributed to the higher-order sideband generation.

To calculate the amplitudes of the first-order and second-order sidebands, we assume that the fluctuation terms $\delta {\tilde{a}}$ and $\delta q$ can be written as the following form:

$$\begin{aligned} \begin{aligned} \delta {\tilde{a}}=&A_{1}^{+}e^{-i\delta t}+A_{1}^{-}e^{i\delta t}+A_{2}^{+}e^{-2i\delta t}+A_{2}^{-}e^{2i\delta t},\\ \delta q=&q_{1}e^{-i\delta t}+q_{1}^{*}e^{i\delta t}+q_{2}e^{-2i\delta t}+q_{2}^{*}e^{2i\delta t}. \end{aligned} \end{aligned}$$

(7)

Here, we only focus on the fundamental OMIT and its second-order sideband process; the higher-order sidebands are ignored in Eq. (7). Substituting Eq. (7) into Eq. (6), and first neglecting the second-order parts in Eq. (7), leads to the linear response of the probe field:

$$\begin{aligned} {A}_{1}^{+} =&\frac{(R{(\delta )}\beta _{1}{(\delta )}+i\hbar G^{2} \vert {\tilde{a}}_{s} \vert ^{2}){\varepsilon _\mathrm{p}}}{R{(\delta )}\beta _{1}{(\delta )}\beta _{2}{(\delta )}+i\hbar G^{2} \vert {\tilde{a}}_{s} \vert ^{2}(\beta _{2}{(\delta )}-\beta _{1}{(\delta )})+i\hbar G^{2} {\tilde{a}}_{s}^2(\varLambda -\varLambda ^{*})-\varLambda ^2 R{(\delta )}}, \end{aligned}$$

(8)

$$\begin{aligned} q_{1} =&\frac{\hbar G(\beta _{1}{(\delta )}{\tilde{a}}_{s}^{\dag }+\varLambda ^{*}{\tilde{a}}_{s})}{R{(\delta )}\beta _{1}{(\delta )}\beta _{2}{(\delta )}+i\hbar G^{2} \vert {\tilde{a}}_{s} \vert ^{2}(\beta _{2}(\delta )-\beta _{1}(\delta ))+i\hbar G^{2} {\tilde{a}}_{s}^2(\varLambda -\varLambda ^{*})-\varLambda ^2 R{(\delta )}}, \end{aligned}$$

(9)

where

$$\begin{aligned} \begin{aligned} R{(\delta )}&=m(\omega _{m}^2-\delta ^2-i \delta \gamma _{m}),\\ \beta _{1}{(\delta )}&=\kappa -i(\varDelta +\delta )+M(\delta ),\\ \beta _{2}{(\delta )}&=\kappa +i(\varDelta -\delta )+L(\delta ),\\ M{(\delta )}&=\frac{\chi ^2 [\varGamma _{2}-i(\varDelta _{b}+\delta )]}{[\varGamma _{1}-i(\varDelta _{a}+\delta )][\varGamma _{2}-i(\varDelta _{b}+\delta )]+\varOmega ^{2}},\\ L{(\delta )}&=\frac{\chi ^2 [\varGamma _{2}+i(\varDelta _{b}-\delta )]}{[\varGamma _{1}+i(\varDelta _{a}-\delta )][\varGamma _{2}+i(\varDelta _{b}-\delta )]+\varOmega ^{2}}. \end{aligned} \end{aligned}$$

(10)

Combining Eqs. (6)–(9) gives the second-order sideband amplitude:

$$\begin{aligned} A_{2}^{+}= & {} \frac{\lambda _{1}q_{1}^{2}+\lambda _{2}A_{1}^{+}q_{1}}{R(2\delta )\beta _{1}(2\delta )\beta _{2}(2\delta )+i\hbar G^{2} \vert {\tilde{a}}_{s} \vert ^{2}(\beta _{2}(2\delta )-\beta _{1}(2\delta ))+i\hbar G^{2} |{\tilde{a}}_{s}|^2(\varLambda -\varLambda ^{*})-|\varLambda |^2 R(2\delta )},\nonumber \\ \end{aligned}$$

(11)

in which

$$\begin{aligned} \begin{aligned} \lambda _{1}=&-(\hbar G^2+\frac{\varLambda }{|{\tilde{a}}_{s}|^2}R(2\delta ))\alpha G{\tilde{a}}_{s}^{\dag },\\ \lambda _{2}=&-iG^2(\beta _{1}(2\delta )+\varLambda ^{*})\alpha +iG(R(2\delta )\beta _{1}(2\delta )+i\hbar G^{2} |{\tilde{a}}_{s}|^2),\\ \alpha =&-\frac{(\varLambda R(\delta )+\hbar G^2 |{\tilde{a}}_{s}|^2)}{i G(\beta _{1}(\delta )+\varLambda ^{*})}. \end{aligned} \end{aligned}$$

(12)

It’s obvious that $A_{2}^{+}$, being proportional to $|\varepsilon _\mathrm{p}|^2$, is indeed smaller than $A_{1}^{+}$ for a weak probe laser. We note that $A_{2}^{+}$ consists of two parts. The first part, being proportional to $q_{1}^2$, is a direct second-order sideband, and the other term is an upconverted first-order sideband.

The output probe field of this hybrid OMS can be obtained by using the input–output relation ${\tilde{a}}_\mathrm{out}(t)={\tilde{a}}_\mathrm{in}-\sqrt{\kappa }({\tilde{a}}_{s}+\delta {\tilde{a}})$ [68]. Note that only when the mechanical resonator oscillates at a low frequency (here $\omega _{m}=2\pi \times 947$ kHz) compared to the frequencies of the cavity mode and the driving fields, this input–output relation can be applied in this system. Once the moving mirror has an ultra-high frequency, the Casimir effect will appear [54, 69, 70], which will break this relation. As defined in Ref. [71], the transmission of the probe and the efficiency of the sideband read

$$\begin{aligned} t_\mathrm{p}=\frac{\kappa {A}_{1}^{+} }{\varepsilon _\mathrm{p}}-1, \quad \eta =\left| \frac{\kappa A_{2}^{+}}{\varepsilon _\mathrm{p}}\right| . \end{aligned}$$

(13)

By introducing $\varepsilon _{T}=t_\mathrm{p}+1$, we know that the real and imaginary parts of $\varepsilon _{T}$, respectively, represent the behaviors of absorption and dispersion. Without loss of generalities, we consider that the system is in the resolved sideband limit, i.e., $\omega _{m}\gg \kappa$ and $\varDelta \approx \omega _{m}$.

3 Multiple OMIT-like effects

Fig. 4

The probe absorption $\mathrm{Re}(\varepsilon _{T})$ as a function of $\delta /\omega _{m}$ with different atom–cavity coupling $\chi$. The green, red and blue correspond to $\chi =100$ MHz, $\chi =141$ MHz and $\chi =172$ MHz, respectively. Here, the degenerate OPA has been moved out from the optomechanical cavity, i.e., $G_{A}=0$. The power of the coupling power is $p_\mathrm{c}=2$ mW. Other parameters are the same as those in Fig. 2

In this section, we investigate the absorptive behavior of the output probe field and show that in the presence of the OPA and the atomic ensemble, the multiple transparency-like effects can be observed from the hybrid system. It is well known that a transparency window can be presented in a standard OMS, when such a system is driven by a strong control field and a weak probe field simultaneously. This naturally brings about the following questions: What will happen if the atomic medium and the degenerate OPA are placed in an OMS? How the atom–cavity coupling strength, the gain coefficient of the OPA and the phase of the field driving the OPA affect the behavior of OMIT? In order to answer the above issues and clarify their respective effects, we prefer to degrade this hybrid system into two simpler hybrid systems, that is to say, only one of the mediums is contained in the optomechanical cavity, either the atoms or the degenerate OPA. Firstly, We remove the degenerate OPA from the system and analyze the effect of the atoms on the output probe field. In this case, the corresponding $\varepsilon _{T}$ is simplified as

$$\begin{aligned} \varepsilon _{T}=\frac{\kappa }{\beta _{2}+\frac{E}{\frac{\gamma _{m}}{2}-i(\delta -\omega _{m})}}, \end{aligned}$$

(14)

in which $E=\frac{\hbar G^{2} \vert {\tilde{a}}_{s} \vert ^{2}}{2 m\omega _{m}}$. As shown in Fig. 4, there are two transparency windows. The transparency window located at resonant point ($\delta =\omega _{m}$) is indeed the OMIT, which is induced by the optomechanical interaction. The additional window located around $\delta =1.5\omega _{m}$ arises from the atom–cavity coupling. Hence, the larger the atom–cavity coupling strength, the wider the additional window. This double OMIT-like effects can still be observed from the optomechanical cavity with two-level atoms [46].

Fig. 5

Probe absorption $\mathrm{Re}(\varepsilon _{T})$ as a function of $\delta /\omega _{m}$ for a different $G_{A}$ and b different $\theta$. Here, the atom coupling strength $\chi =0$ and $p_\mathrm{c}=2$ mW. Further, $\theta =1.5\pi$ and $G_{A}=1.5\kappa$ have been fixed in (a) and (b), respectively. Other parameters are the same as those in Fig. 2

Then, we turn off the atom–cavity coupling, i.e., $\chi =0$, and turn to investigate the effect of the degenerate OPA on the properties of the output probe field. Under this condition, the expression of $\varepsilon _{T}$ becomes

$$\begin{aligned} \varepsilon _{T}=\frac{\kappa }{\kappa -i(\delta -\omega _{m})+\frac{(E+iW)}{\frac{\gamma _{m}}{2}-i(\delta -\omega _{m})}-\frac{\varLambda ^2}{\beta _{1}}}, \end{aligned}$$

(15)

where $W=\frac{\hbar G^{2} \vert {\tilde{a}}_{s} \vert ^{2}}{2\omega _{m}}$. From Fig. 5a, we find that except for the OMIT window, an additional window can also be observed in this case. This additional window is induced by the coupling between the degenerate OPA and the cavity field. As shown in Fig. 5a, with increase in the $G_{A}$, the width of OMIT window can be effectively widened. Figure 5b shows that the absorptive behavior of the output field can also be adjusted by tuning $\theta$. The interesting phenomenon is when $\theta$ changes from $\theta =0.5\pi$ or $\theta =1.5\pi$ to $\theta =0$, in $\delta <0$ region, the optical amplification substitutes the original OMIT-like phenomenon. (The negative absorption of the probe field means that the optical amplification effect appears.) However, in $\delta >0$ region, the feature of the transparency effect remains unchanged. Therefore, the combined effects of the optical amplification and the OMIT can be simultaneously observed from the output probe field (see green dot-dashed curve in Fig. 5b).

Now we explore the optical properties of the optomechanical cavity with atoms and the degenerate OPA. For this hybrid system, the corresponding $\varepsilon _{T}$ becomes

$$\begin{aligned} \varepsilon _{T}=\frac{\kappa }{\beta _{2}+\frac{(E+iW)}{\frac{\gamma _{m}}{2}-i(\delta -\omega _{m})}-\frac{\varLambda ^2}{\beta _{1}}}. \end{aligned}$$

(16)

From Fig. 6a, we find that the multiple transparency effects occur in such a hybrid OMS. Among the four dips, three of them can be recognized with the help of the above analysis. As we mentioned before, the dip located at $\delta =\omega _{m}$ is the OMIT window. The other two dips, which lie in the left- and right-hand sides of the OMIT window, originate from the OPA–cavity coupling and the atom–cavity coupling, respectively. As to the first dip (from left to right), it is the result of the indirect interplay between the degenerate OPA and the atomic medium. Once one of the two mediums is removed out of the optomechanical cavity, this dip will disappear. In particular, the width of the four dips can be adjusted by tuning the atom–cavity coupling, the gain coefficient of the OPA and the phase of the field driving the OPA. In addition, as shown in Fig. 6b, the combined effects of the double optical amplification and the double OMIT-like can be achieved by tuning $\theta$. Compared to the two simpler cases we discussed before (only one of the two mediums is contained in the optomechanical cavity), the present scheme can achieve more plentiful spectrum properties of the probe field. Here, we would like to point out that only the transparency window located at resonant point is genuine OMIT, which originates from destructive interference between different transition pathways. Once the strong control field is turned off, the OMIT effect will vanish. However, the other dips shown in Fig. 6 will still exist due to the fact that they arise from the Autler-Townes splitting [72]. Unlike EIT, the Autler-Townes splitting is a process involving strong-field-induced splitting of energy levels [73, 74].

Fig. 6

Probe absorption $\mathrm{Re}(\varepsilon _{T})$ as a function of $\delta /\omega _{m}$. Here, $p_\mathrm{c}=2$ mW. Other parameters are the same as those in Fig. 2

In our system, a slow-to-fast light switch can be easily achieved. In the region of OMIT, the abnormal dispersion $\phi _{t}=\mathrm{arg}(t_\mathrm{p})$ can induce the slowing or advancing of light. This feature can be characterized by the group delay of the probe field light

$$\begin{aligned} \tau _\mathrm{g}=\frac{\mathrm{d}\phi _{t}}{\mathrm{d}\delta }. \end{aligned}$$

(17)

A positive group delay with $\tau _\mathrm{g}>0$ corresponds to slow light propagation, and a negative group delay with $\tau _\mathrm{g}<0$ corresponds to fast light propagation. Figure 7 shows the group delay around the resonant point (i.e., $\delta \simeq \omega _{m}$) as a function of the pump power. We find that in the presence of OPA, the probe field experiences a slow-to-fast switch by adjusting $\theta$. The physical reason is that when the degenerate OPA is included, the quantum interference between the probe field and the generated anti-Stokes field depends strongly on $\theta$, which makes the optical response properties of the probe field become phase sensitive. Therefore, a tunable switch from slow-to-fast light can be achieved by adjusting the phase of the field driving the degenerate OPA.

Fig. 7

Group delay $\tau _\mathrm{g}$ as a function of the control power $p_\mathrm{c}$ with $\chi =100$ MHz. Other parameters are the same as those in Fig. 2

4 Second-order sideband in the hybrid OMS

Optical second-order sideband generation, which is one of the prominent nonlinear effects in OMS, has potential applications in precise sensing of charges [75] or weak forces [35], high-order squeezed frequency combs [76] and single-particle detection [77]. However, its efficiency is usually very small in the OMS. This is because the generation of the second-order sideband is mainly from the upconverted first-order sideband. If $\delta =\omega _{m}$ and $\varDelta =\omega _{m}$, the anti-Stokes field is resonantly enhanced, which leads to the suppression of the second-order sideband generation. Here, we show that the generation of the second-order sideband can be enhanced in the presence of OPA. From Fig. 8a, we find that due to the presence of the degenerate OPA, the spectrum of the second-order sideband becomes asymmetric. Moreover, compared to that in the absence of the OPA case, the efficiency of the second-order sideband generation is significantly enhanced with increasing of $G_{A}$. For example, the efficiency $\eta$ is about $6\%$ for $G_{A}=2.5\kappa$, which means that we have $\sim$ 2.6 times enhancement of $\eta$ by tuning $G_{A}$, indicating the advantage of using a hybrid nonlinear system. In addition, with the presence of the OPA, if the pump-cavity detuning $\varDelta$ and mechanical frequency $\omega _{m}$ are off resonance, the efficiency $\eta$ can be further enhanced. As shown in Fig. 8b, in which $G_{A} = 2.5\kappa$ and $\theta = 1.5\pi$ have been fixed, the efficiency $\eta$ can be enhanced to $8\%$ or $10\%$ for $\varDelta =0.6\omega _{m}$ or $\varDelta =1.6\omega _{m}$. This can be explained as follows: If we choose $\varDelta$ to be off resonant with the mechanical frequency $\omega _{m}$, the anti-Stokes field is no longer resonantly enhanced, and the upconverted process of the first-order sideband is strengthened, thus leading to the enhancement of the efficiency.

Fig. 8

Efficiency of the second-order sideband generation $\eta$ as a function of the detuning $\delta /\omega _{m}$ with different a gain coefficients of OPA $G_{A}$ and b pump-cavity detuning $\varDelta$. Here, the atomic detuning $\varDelta _{a}=\varDelta _{b}=\omega _{m}$, $P_\mathrm{c}=0.2$ mW and $\varepsilon _\mathrm{p}=0.05\varepsilon _\mathrm{c}$ are fixed. Other parameters are the same as those in Fig. 2

5 Conclusion

In conclusion, we have theoretically investigated the optical response properties of the output field in an optomechanical cavity, which contains a degenerate OPA and a $\varLambda$-type three-level atomic medium. We have shown that the presence of the OPA and the atomic ensemble can lead to the occurrence of the optical tristability and multiple OMIT-like phenomena. Specifically, the combined phenomena of double optical amplification and double OMIT-like effects as well as the tunable switch from slow to fast light can be realized by tuning the gain coefficient of the OPA and the phase of the field driving the OPA. Moreover, we have indicated that the degenerate OPA can be used to enhance the second-order sideband generation. These results are helpful to better understand the optical response properties of the nonlinear optomechanical devices, indicating that a wide range of optomechanical effects could be further steered with various optical nonlinearities.