1 Introduction

Protection of sensitive data is one of the main goals of cryptography, and to this end, secret sharing is one of the most important cryptographic primitives which has been widely studied. Secret sharing (SS) was introduced independently by Shamir [1] and Blakely [2]. A secret sharing scheme (SSS) consists of a secret to be shared among a set of participants with the stipulation that when some predetermined subsets of participants called qualified sets pool their information together, they can reconstruct their secret. Also, some specified subsets of participants called forbidden sets should not have any information about the secret.

Several real-life scenarios demand more flexible or general SSSs, and this necessity has given rise to the extensive study of several variants of SSSs. One such necessity is for a SSS to be able to share multiple secrets at one go. Such SSSs are called multi-secret sharing schemes(MSSS) [3,4,5,6,7]. SSSs are often model dependant. But generally what is done is that in a MSSS, several secrets are distributed among a group of participants by a dealer and depending on the model of reconstruction, several MSSSs have been proposed. In one such model, only authorized sets can reconstruct the all the secrets by combining their shares (or their pseudo shares), while other subsets cannot know any information about them. In another model, the stipulation is that as more and participants combine their shares, they can recover more number of secrets from the set of secrets which was originally shared. Such a variant is called a multi-threshold MSSS [8,9,10,11,12,13]. In another variant which is prevalent in the area of visual secret sharing, as more and more participants combine their shares, they get closer to a secret(this includes a predefined notion of closeness). This variant is named progressive secret sharing [14,15,16].

Related work With the advent of quantum computation, a natural extension of the above is to study quantum secret sharing (QSS) where the goal is to share and protect sensitive data in a quantum environment. QSS has been in extensively studied [17,18,19,20,21,22,23,24] The motivation to study QSS schemes(single secret) is twofold: (1) Semi-quantum: to share a classical secret in a quantum environment and (2) fully quantum: to share a quantum secret in a quantum environment. It has been pointed out by the authors in [20] that sharing a quantum state is more difficult than sharing classical information and hence fully quantum schemes are far lesser in number than semi-quantum ones. We have observed the same for quantum multi-secret sharing schemes(QMSSS) [25], and to the best of our knowledge, a QMSSS sharing quantum states has not been studied before. QMSSSs have found application in block-chains [26, 27] and in multiparty communication (secret sharing) [28,29,30,31]. We have also observed that in several MSSSs in the literature [13], the security is conditional and is based on the security of computationally hard problems like lattice-based problems. Construction of QSSSs using quantum walks has been studied recently in [32, 33]. The authors in [32] used quantum walks on a \(4\times d\) lattice folded into a torus and the Fourier coin to realize an entanglement-free QSS where the participants use a d-level state. In [33], the authors have utilized the additive properties of circular quantum walks to construct a threshold QSSS to share a single classical secret in a quantum environment. We have used product states in our constructions and the use of product states to construct entanglement-free QSS both in the both in the traditional and the multiparty case has been considered in [34, 35]. As we have noted before that sharing a quantum state in a quantum environment is a more challenging issue, we attempt to construct a more general fully quantum MSSS. Our construction works for general graphs and not only specialized graphs like the circle. Discrete-time quantum walks [36, 37] have also found application in other areas of quantum computation as in [38,39,40]. An excellent source containing several properties of discrete quantum walks is [41]. Quantum walks on graphs have been further studied in [42,43,44]. In visual SSSs, the secret is an image and the dealer splits the image into n shares (noise-like shadows). During reconstruction, the secret image can be reconstructed by k authorized shadows, while less than k shares reconstruct nothing of the original image. The advantage of visual secret sharing is that the secret image can be reconstructed by superimposing the k shares and with no cryptographic computation. In the progressive variant [14, 15, 45] of such schemes, the more the number of shadows are superimposed, the clearer (or closer to the original secret image) the reconstructed image is. In other words, the more the number of participants combine their shares, the closer they get to the secret. This involves a precise mathematical notion of closeness or clarity which varies among different papers in the literature. It is natural to study visual secret sharing in the quantum context [46, 47].

Quantum walks Quantum walks are quantum analogues of classical random walks. Just as classical randomized algorithms use random walks, quantum walks have proved to be beneficial to the design of quantum algorithms [48]. The evolution of a quantum walk in discrete time is specified by the product of two unitary operators: (1) a “coin flip” operator and (2) a conditional shift operator, which are applied repeatedly. So starting from an initial state, after a finite amount of time, there is a list of quantum states which are reachable from the initial state. This set of reachable states can be completely described by specifying the initial state, the coin flip operator and the shift operator(s).

Suppose we want to share a set of quantum secrets among participants. It is costly and poses implementation challenges to share each of the secrets to all the participants via quantum SSSs. However, if the set of secrets form a set of reachable states starting from an initial state, then it is enough to share the initial state, the coin flip operator and the conditional shift operators, and in one shot, we can share the whole set of quantum secrets among participants in a quantum environment. This is the idea that we explore and develop in this paper.

Another question that we address in this paper is the following: How to design the most general and practical quantum SSS? For a secret sharing scheme to be practical, it is desirable that the scheme can accommodate as many participants as possible (possibly infinite) without refreshing the system periodically or without communicating with the old participants from time to time. Such quantum schemes have been considered in [49, 50] and are called quantum evolving secret sharing schemes. Now if we use these schemes in conjunction with a multi-secret sharing scheme whose set of secrets is the set of the reachable states from a quantum walk, then we can have a truly general quantum secret sharing which can share arbitrarily many secrets among unbounded number of participants. This is possible because quantum walks can be performed on infinite lattices for as long as possible.

Our contributions Our main contributions are as follows:

  • First we construct an unconditional fully quantum MSSS—sharing a set of quantum states in a quantum environment utilizing a modification of the trap code [51, 52] to incorporate a incremental or multi-threshold properties.

  • Since the use of trap code causes a blow up in the dimension of the shares, in the following sections, we attempt to reduce the dimensions of the share states utilizing discrete-time quantum walks and remove the use of trap codes.

  • As applications, we construct multi-threshold variants of the quantum walk-based schemes which also do not use trap codes. We also show that our constructions can be used in the “progressive” setting where participants get closer to the secret as more and more participants combine their shares.

  • Our construction is entanglement-free which makes practical implementation easier and can be potentially applied on a larger number of participants as compared to schemes utilizing entanglement. While the results of this paper are theoretical and the paper has an algorithmic flavour, the flexibility and scalability of our constructions and the significant reduction in the dimension of the share states to make the constructed schemes within the reach of practical implementation should appeal to physicists and practitioners as well. To the best of the knowledge of the authors, the technique of modifying the trap code, application of our technique in the quantum progressive model and the use of discrete quantum walks in multi-threshold case have not been considered before.

Paper organization The paper is organized as follows. Section 2 describes the required tools and we give formal definitions of computational security of a QMSSS. In Sect. 3, we elaborate the construction of our QMSSS based on a modification of the trap code(see Sect. 3.1.1). In the next Sect. 4 we use quantum walks to construct variants of QMSSSs. The following Sect. 5 discusses generalizations to general access structures, outlines a model for a possible quantum progressive SSS and this followed by Sect. 6 where we discuss the security of our scheme against adversarial attacks. In Sect. 7, we compare our constructed scheme with the existing ones and study its advantages. In Sect. 8 we discuss some aspects and further applications of our scheme and we conclude the paper in Sect. 9.

2 Preliminaries

Definition 1

(Access structure) Let \({\mathcal {P}} = \{p_{1},\ldots ,p_{n}\}\) be a set of participants. A collection \(\Gamma \subseteq 2^{{\mathcal {P}}} \) is monotone if \(B \in \Gamma \) and \(B \subseteq C\) imply that \(C \in \Gamma \). An access structure over \({\mathcal {P}}\), \(\Gamma = (\Gamma _{YES}, \Gamma _{NO})\) is a pair of collections of sets \(\Gamma _{YES},\Gamma _{NO} \subseteq 2^{{\mathcal {P}}}\), such that \(\Gamma _{YES}\) and \(2^{{\mathcal {P}}} \backslash \Gamma _{NO}\) are monotone, and \(\Gamma _{YES} \cap \Gamma _{NO} = \phi \). Sets in \(\Gamma _{YES}\) are called qualified, and sets in \(\Gamma _{NO}\) are called forbidden sets.

Definition 2

(Threshold access structures) Let \(1 \le k \le n\). A k-out-of-n or (n, k) threshold access structure \(\Gamma \) over a set of participants \({\mathcal {P}} = \{p_{1},\ldots , p_{n}\}\) is the complete access structure accepting all subsets of size at least k, that is, \(\Gamma _{YES} = \{A \subseteq {\mathcal {P}}: |A| \ge k\}\) and \(\Gamma _{NO} = \{A \subseteq {\mathcal {P}}: |A| < k\}\).

Definition 3

(Multi-threshold access structures) A multi-threshold access structure consists of participants \({\mathcal {P}} = \{p_{1}, p_{2}, \ldots , p_{n}\}\) and independent \((t_{i}, n)\)-threshold access structures for \(i = 1, 2, \ldots , m\) satisfying \(t_{1}< t_{2}< \ldots < t_{m}.\)

Definition 4

(Secret sharing scheme (SSS) [1, 2]) For an access structure and S (\(|S |\ge 2\)) a domain of secrets, an SSS \({\mathcal {S}}\) consists of a pair of algorithms (SHARE; RECON) such that (i) SHARE is a probabilistic sharing algorithm for generating shares of participants and (ii) RECON is a deterministic reconstruction algorithm to recover the secret. SHARE and RECON satisfy the following conditions:

  1. 1.

    SHARE on input a secret \(s \in S\) outputs the shares \(\{\Pi _{1}^{(s)}, \ldots , \Pi _{n}^{(s)}\})\) of the participants.

  2. 2.

    Correctness For every secret \(s \in S\), every qualified subset in \(\Gamma _{YES}\) can reconstruct the secret. For \(s \in S\), and \(B \in \Gamma _{YES}\), it holds that

    $$\begin{aligned} Pr[RECON(\{\Pi _{i}^{(s)}\}_{i \in B}, B) = s] = 1, \end{aligned}$$

    where the probability is over the randomness of the sharing procedure.

  3. 3.

    Privacy For every unqualified subset \(B \notin \Gamma _{YES}\), and every two secrets \(s_{1}\) and \(s_{2}\) belonging to S, the distribution of the secret shares of parties in B generated with secret \(s_1\) and the distribution of the shares of parties in B generated with secret \(s_2\) are identical. Namely, the distributions \((\{\Pi _{i}^{(s_{1})}\}_{i \in B})\) and \((\{\Pi _{i}^{(s_{1})}\}_{i \in B})\) are identical.

Multi-secret sharing scheme (MSSS) A SSS where instead of a single secret, a set of secret is shared among participants. Let \(S = \{s_1,\ldots ,s_r\}\) be a set of secrets, where each \(s_i\) belonging to a set \(S_i\), is shared among participants in such a way that each subset of \({{\mathcal {P}}}\) can recover a certain subset of S, but has absolutely no information on the remaining secrets. We follow the definition of Blundo et al. [3] in the following. For each subset of participants \(A \subset {{\mathcal {P}}}\), we denote by \(S_A \subset S\) the set of secrets that can be recovered by the participants in A, referred to as the A-secret-set. For monotone access structures, for any \(A \subset B \subset {{\mathcal {P}}}\), it holds that \(S_A \subset S_B\).

Definition 5

(Multi-threshold multi-secret sharing scheme) Given n participants, thresholds, \(2 \le t_{1}< t_{2}< \ldots < t_{k} \le n\), and a set of secrets \({\mathcal {S}} = \{s_{1}, \ldots , s_{r}\}\), the following conditions are satisfied for a SSS to be multi-threshold and multi-SSS:

  1. 1.

    If the number of participants combining their shares is less than \(t_{1}\), no information about any secret in \({\mathcal {S}}\) can be obtained. For any subset \(A \subset {{\mathcal {P}}}\), participants have no information on any subset of secrets in \(S \setminus S_A\).

  2. 2.

    Any subset \(A \subset {{\mathcal {P}}}\) of participants can recover the A-secrets-set \(S_A\). More precisely, for an increasing chain of subsets of secrets \(S_{t_1} \subset S_{t_2} \subset \cdots \subset S_{t_k} =S\) indexed by the threshold values, a subset A of participants of size \(t_i \le |A |< t_{i+1}\) can recover the secrets of \(S_{t_i}\). If the number of participants combining their shares is greater or equal to \(t_{k}\), all secrets in \({\mathcal {S}}\) can be reconstructed.

Definition 6

(Pauli matrices) Single qubit Pauli matrices are

$$\begin{aligned}{} & {} I = \begin{bmatrix} 1 &{} 0\\ 0 &{} 1 \end{bmatrix}, X (= \sigma _{x}) = \begin{bmatrix} 0 &{} 1\\ 1 &{} 0 \end{bmatrix}, Z (= \sigma _{z}) = \begin{bmatrix} 1 &{} 0\\ 0 &{} -1 \end{bmatrix}\\{} & {} \text {and } Y = iXZ = \begin{bmatrix} 0 &{} -i\\ i &{} 0 \end{bmatrix}. \end{aligned}$$

An n-qubit Pauli matrix is given by the n-fold tensor product of single-qubit Paulis. The set of all n-qubit Pauli matrices is denoted by \({\mathbb {P}}_{n}\), where \(|{\mathbb {P}}_{n} |= 4^{n}.\)

Definition 7

(Quantum one-time pad [37]) n the Quantum one-time pad cryptosystem, we have

  • an n-qubit string \(\left| \xi \right\rangle = \left| \xi _{1}\right\rangle \ldots \left| \xi _{n}\right\rangle \),

  • shared key: two n-bit strings \(k, k'\).

  • To encode qubit by qubit: \(\left| \phi _{i}\right\rangle = \sigma _{x}^{k_{i}}\sigma _{z}^{k_{i}'}\left| \xi _{i}\right\rangle \).

  • To decode qubit by qubit: \(\left| \xi _{i}\right\rangle = \sigma _{z}^{k_{i}'}\sigma _{x}^{k_{i}}\left| \phi _{i}\right\rangle \).

Here, \(\left| x_{i}\right\rangle \), \(\left| \phi _{i}\right\rangle \) are qubits and \(\sigma _{x}\) and \(\sigma _{z}\) are Pauli matrices. When a quantum one-time pad is applied, to a party that does not know the key, the encoded text seems completely mixed (information theoretically) [53].

Definition 8

(Permutation map) A permutation map is a unitary operation that acts on n qubits and permutes the order of the qubits or equivalently permutes the indices of the qubits. A permutation \(\sigma \) on n qubits takes the i-th qubit to the \(\sigma (i)\)-th qubit.

Definition 9

(Trap code [51, 52]) In a trap code, we have

  1. 1.

    Encoding qubit by qubit

  • apply a [[n, 1, d]] quantum error-correcting code Enc which will correct up to t errors. (here \(d = 2t +1).\)

  • to the resulting, append n-qubit traps, first in the state \(\left| 0\right\rangle \left\langle 0\right| ^{\otimes n}\) (X-traps) and second in the state half \(\left| +\right\rangle \left\langle +\right| ^{\otimes n}\) ( Z-traps),

  • permute the resultant 3n qubits by a random permutation \(\sigma \), according to the key \(k_1\).

  • finally apply a Pauli encryption using the classical randomness in the key \(k_{2}\).

  • Mathematically, the encoding of a state \(\rho \) is denoted as

    $$\begin{aligned} P_{k_{2}} \sigma _{k_{1}}(Enc(\rho )\otimes \left| 0\right\rangle \left\langle 0\right| ^{\otimes n} \otimes \left| +\right\rangle \left\langle +\right| ^{\otimes n})\sigma _{k_{1}}^{\dagger }P_{k_{2}}, \end{aligned}$$

where corresponding to the two part secret key, \(k = (k_{1}, k_{2})\), \(\sigma _{k_{1}}\) is the \(k_{1}\)-th permutation, \(P_{k_{2}}\) is the \(k_{2}\)-th Pauli matrix.

  1. 2.

    Decoding

  • Apply the inverse Pauli according to key \(k_{2}\).

  • to the resulting apply the inverse permutation \(\sigma ^{-1}\) according to the key \(k_{1}.\)

  • measure X-traps in the computational basis and the Z-traps in the Hadamard basis. If they are not in their original state, it is rejected.

  • decode the quantum error-correcting code Enc.

It is required that the quantum error-correcting code used here is a Calderback-Shor-Steane (CSS) code and a self-dual code implemented by a Clifford circuit.

Definition 10

(Discrete-time quantum walk [41]) Quantum walk is the quantum version of classical random walks. The evolution of a quantum walk in discrete time is specified by the product of two unitary operators: (1) a “coin flip” operator and (2) a conditional shift operator, which are applied repeatedly. There are three existing models of quantum walks which we describe briefly as follows: (The notations and definitions are taken from [41])

  1. 1.

    Arc-reversal [42, 44] Consider an undirected graph \(G = (V,E)\) with \(|V |= n\) and \( |E |= m\). The state space is \({\mathbb {C}}^m\). Replace each edge of G with a pair of opposite arcs. The characteristic vectors \(e_{u,v}\) of the directed arcs (u, v) span \({\mathbb {C}}^{m}\). The coin flip map is given by the permutation matrix R that reverses each arc, i.e. \(Re_{u,v} = e_{v,u}.\) For any vertex u, let there be an order defined on its neighbours \(f_{u}: \{1,2, \ldots , \text {deg}(u)\} \longrightarrow \{v, v \text { is adjacent to } u \}.\) Denote by \(f_{u}(j)\) and \((u, f_{u}(j))\) the j-th neighbour and the j-th arc of u, respectively. Let \(C_{u}\) be a \(\text {deg}(u) \times \text {deg}(u)\) matrix which sends \((u, f_{u}(j))\) to a superposition of the all the outgoing arcs of u and satisfying \(C_{u}e_{j}= \sum _{k=1}^{\text {deg}(u)}(e_{k}^{T}C_{u}e_{j})e_{k}.\) The quantum coin is given by the block diagonal matrix \(C = [C_{1}, C_{2}, \ldots , C_{n}]\) with \(C_{i}\) forming the diagonal blocks. Hence, for each iteration, the transition matrix is given by \(U = RC\), combination of a quantum coin and an arc flip. Common choices for quantum coins are the Fourier coin \(F = (\frac{1}{\sqrt{d}}e^{2jk\pi i/d})_{jk}\) and the Grover coin \(G = \frac{2}{d}J - I.\)

  2. 2.

    Shunt-decomposition [43] In this case, the graphs are assumed to be d-regular. Hence, the state space \({\mathbb {C}}^{m}\) is isomorphic to \({\mathbb {C}}^{n} \otimes {\mathbb {C}}^{d}.\) The arc \((u, f_{u}(j)\)) can be represented by \(e_{u}\otimes e_{j}.\) The transition matrix is \(U = SC\), where C is a quantum coin as before and for each vertex, S maps its j-th arc to the jth arc of \(f_{u}(j).\) S is a \(0-1\) permutation matrix which is equivalent to the block diagonal matrix

    $$\begin{aligned} S= \begin{pmatrix} \begin{array}{llll} {P_{1}}&{}&{}&{}\\ &{}{P_{2}}&{}&{}\\ &{}&{}\ddots &{}\\ &{}&{}&{}{P_{d}}\\ \end{array} \end{pmatrix}, \end{aligned}$$

    where \(P_{j}\) maps a vertex to its j-th neighbour. U has the following decomposition:

    $$\begin{aligned} U = (P_{1} \otimes E_{11} + \ldots + P_{d} \otimes E_{dd})(E_{11}\otimes C_{1} + \ldots + E_{dd} \otimes C_{n}), \end{aligned}$$

    where \(E_{ij}\) is an elementary matrix with 1 in the ij-th entry and 0 elsewhere.

  3. 3.

    Two-reflections [38, 39] Let M be a Markov chain on G. let N denote the matrix obtained from M by taking the square root of its entries. Define

    $$\begin{aligned} Q_{1} = (e_{1} \otimes (Ne_{1}) \ldots e_{n} \otimes (Ne_{n})) \end{aligned}$$

and

$$\begin{aligned} Q_{2} = ((N^{T}e_{1})\otimes e_{1} \ldots (N^{T}e_{n})\otimes e_{n}). \end{aligned}$$

Since M is doubly stochastic, we have \(Q_{1}^{T}Q_{1} = Q_{2}^{T}Q_{2} = I.\) Finally, U is defined as

$$\begin{aligned} U = R_{1}R_{2} = (2Q_{1}Q_{1}^{T} - I)(2Q_{2}Q_{2}^{T} - I). \end{aligned}$$

Effectively, \(Q_{1}\) partitions the arcs according to their tails, and \(Q_{2}\) partitions the arcs according to their heads.

3 Technical details

Deviating from traditional SSSs for single secrets s, our aim is to share a subset of secrets \({\mathcal {S}}_{r}\subset {S}\) where the set of secrets is a finite set of quantum states \({\mathcal {S}} = \{\left| \phi _{1}\right\rangle , \left| \phi _{2}\right\rangle , \ldots , \left| \phi _{u}\right\rangle \}.\) We assume existence of quantum threshold SSS (both fully quantum [20] and semi-quantum [21] models) which we need for our constructions. In our constructed scheme, there is a minimum threshold \(t_{1}\). If the number of participants cross this threshold, they can reconstruct a certain minimum number of secret states but not the whole set of secrets. More number of participants are required to reconstruct more number of secret state. Finally, there is a maximum threshold and if the number of participants cross this threshold, they can reconstruct the full set of secrets. For concrete definition, we refer to Definition 5 suitably adjusted to the case of quantum secrets. For the ease of reference, we introduce the following terms.

Incremental thresholds \(1< t_{1}< t_{2}< \ldots< t_{k} < n,\) where n is the total number of participants and \(t_{i}\)’s are thresholds.

Fully qualified sets A set is fully qualified if the number of participants combining their shares p satisfies \(p \ge t_{k}.\)

Semi-qualified sets A set is semi-qualified if the number of participants combining their shares p satisfies \(t_{1} \le p < t_{k}.\)

Forbidden sets A set is forbidden if the number of participants combining their shares p satisfies \(p < t_{1}.\)

One may interpret the above conditions to be reminiscent of a ramp scheme. In a ramp SSS qualified sets can reconstruct the secret and forbidden sets have no information about the secret. There is a third class of subsets of participants called semi-qualified who have partial information about the secret. In the present context, we have chosen not to call our scheme a ramp scheme due to the fact that semi-qualified sets can completely recover a predetermined chosen subset of the set of secrets. We have not considered or have made no attempt to quantify the information context of a subset of secrets. However, in the case of progressive secret sharing (see Sect. 5.3), one may call our scheme a ramp scheme as there is a well-defined notion of closeness to the original secret and as more and more participants combine their shares, they get closer to the secret.

3.1 Main scheme

In this section, we put forward our constructions. In Sect. 3.1.1, we detail our modification to the trap code. Next (Sect. 3.1.2) based on this modification, we present the construction of a fully quantum QMSSS with multiple-thresholds where there is no relation between the secret quantum states. We describe in detail the correctness and privacy of our scheme in Sect. 3.2 and analyse the dimension of the shares states in Sect. 3.3.

3.1.1 Modification to the trap code

As we have mentioned before, our construction is based on a modification to the trap code. The modification is done as follows: Recall Definition 10 where mathematically the encoding of a state \(\rho \) is given by \(P_{k_{2}} \sigma _{k_{1}}(Enc(\rho )\otimes \left| 0\right\rangle \left\langle 0\right| ^{\otimes n} \otimes \left| +\right\rangle \left\langle +\right| ^{\otimes n})\sigma _{k_{1}}^{\dagger }P_{k_{2}}.\) By removing the Pauli operator, the state becomes \(\sigma _{k_{1}}(Enc(\rho )\otimes \left| 0\right\rangle \left\langle 0\right| ^{\otimes n} \otimes \left| +\right\rangle \left\langle +\right| ^{\otimes n})\sigma _{k_{1}}^{\dagger }.\) Consider the permutation \(\sigma \) without the index. Assume that \(\sigma \) has no fixed points, i.e. \(\sigma \) is a derangement and has the following form. Suppose \(\sigma : [n] \longrightarrow [n].\) Consider a partition of [n] as \([n] = n_{1} \cup n_{2} \cup \ldots \cup n_{r}.\) Let \(\sigma _{n_{i}}: [n] \longrightarrow [n]\) such that \(\sigma _{n_{i}}(j) = j\) for each \(j \in [n] \backslash n_{i}\) and \(\sigma _{n_{i}}(j) \ne j\) for each \(j \in n_{i}\), \(1 \le i \le r.\) Suppose

$$\begin{aligned} \sigma = \underset{1 \le i \le r}{\circ }\sigma _{n_{i}} = \sigma _{n_{1}}\circ \ldots \circ \sigma _{n_{r}}. \end{aligned}$$

In the original trap code, \(\sigma \) is chosen from all permutations of length n and the total number of choices is n!. In our case, we shall choose \(\sigma \) from all derangements of length \(|n_{i} |\), \(1 \le i \le r.\) It is well known that the total number of derangements of length \(|n_{i} |\) equals \(|n_{i} |\sum _{k=0}^{|n_{i} |}\frac{(-1)^{k}}{k!}.\) Hence, the total number choices for \(\sigma \) becomes

$$\begin{aligned} \prod _{i = 1}^{r}\left( |n_{i} |\sum _{k=0}^{|n_{i} |}\frac{(-1)^{k}}{k!}\right) . \end{aligned}$$

This choice does not affect privacy as the permutations are chosen uniformly at random. The advantage of such a decomposition is that one can share the indices of the smaller permutations in an incremental manner through a multi-threshold SSS. The effect is that as more and more participants combine their shares, more partitions of the permutation can be unpermuted and hence more number of secrets can be reconstructed. This is formalized in step 7 of procedure 1. It was noted in [51, 52] that the same permutation should be applied on all the input qubits. Note that, same permutations are used on each partition, and fresh keys for the quantum one-time pad (Pauli) are used, hence our modification does not hamper security.

Remark 1

This method of using a partitioned permutation is reminiscent of the two-level classical SSS of [54] where the share strings are partitioned into blocks and random permutations are applied on the smaller blocks. However, in our method, we partition the set of secrets instead of the shares. There is no attempt in [54] to reduce the share. In this paper, on the other hand, we are able to significantly reduce the dimension of the share states using quantum walks.

3.1.2 No relation between secret states

Let us suppose that we have an unknown set of quantum secrets \({\mathcal {S}} = \{\left| \phi _{1}\right\rangle , \left| \phi _{2}\right\rangle , \ldots , \left| \phi _{u}\right\rangle \}\). Based on a coin toss, an l-subset \({\mathcal {S}}_{r} =\{\left| \phi _{i_{1}}\right\rangle , \left| \phi _{i_{2}}\right\rangle , \ldots , \left| \phi _{i_{l}}\right\rangle \} \subseteq {\mathcal {S}}\) is chosen.

Basic components Consider an increasing chain of thresholds \(t_1<t_2<\cdots <t_r\). We shall assume that \(l \ge t_{r}\) otherwise by the pigeon hole principle, there must be thresholds \(t_{i}\) and \(t_{i+1}\) such that the number of secrets recovered by number of participants greater than \(t_{i}\) and \(t_{i+1}\) remain same and a threshold \(t_{i+1}\) becomes redundant. Let \((Sh_{Th}(n,k), Rec_{Th}(n,k))\) be a fully quantum perfect threshold SSS sharing a quantum state as in [20]. Let \((Share_{(t_i,n)},Rec_{(t_i,n)})\) be semi-quantum perfect threshold SSSs sharing classical secrets for all i as in [21].

figure a
figure b

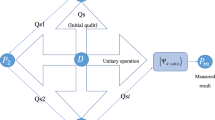
In Fig. 1, we give a schematic diagram of our construction.

Fig. 1
figure 1

Schematic diagram of QMSSS

Full size image

3.2 Correctness and privacy

The proof of correctness and security of the proposed scheme depend on the same properties of its basic building blocks. We first summarize/outline them and then move onto proving the correctness and security of our proposal.

Description of \((Sh_{Th}(n,k), Rec_{Th}(n,k))\) of [20]. Here, the secret is an unknown quantum state.

  1. 1.

    Distribution of shares via a polynomial computation: The dealer finds a suitable prime number d and sets a finite field \({\mathbb {Z}}_{d}\). Depending of the number of participants t who can recover the secret, the dealer randomly chooses \(t-1\) elements \(a_{i} \in {\mathbb {Z}}_d\) (\(i = 1,..., t-1\)). Next the dealer defines the polynomial \(f(x) = S + a_{1}x + \ldots + a_{t-1}x^{t-1}\), \(S \in {\mathbb {Z}}_{d}\). For n participants, the dealer evaluates the polynomial on n different elements of \({\mathbb {Z}}_{d}\) and sends the outputs privately to each participant.

  2. 2.

    Suppose the dealer generates an unknown sequence of states to be shared among the participants. Next comes the application of a phase shift operation \(R_{z}(\theta ) = \cos {\theta }\left| 0\right\rangle \left\langle 0\right| - \sin {\theta }\left| 0\right\rangle \left\langle 1\right| + \sin {\theta }\left| 1\right\rangle \left\langle 0\right| + \cos {\theta }\left| 1\right\rangle \left\langle 1\right| \) on every quantum state in the unknown sequence of quantum states generated by the dealer, where \(\theta = 2\pi - \frac{S}{N}\), N being the security coefficient.

  3. 3.

    Insertion of random decoy particles \(\left| 0\right\rangle , \left| 1\right\rangle , \left| +\right\rangle , \left| -\right\rangle \) for eavesdropping detection.

All the steps mentioned above are part of the secret sharing procedure in [20]. The corresponding secret recovery procedure consists of the application of the corresponding Lagrange’s interpolation and application of proper phase shift operations. The details are omitted.

Description of \((Share_{(n,k)}, Rec_{(n,k)})\) of [21]. Here, the secret is a classical secret \(S \in {\mathbb {Z}}_{d}.\) Next the dealer defines the polynomial \(f(x) = S + a_{1}x + \ldots + a_{t-1}x^{t-1}\), \(S \in {\mathbb {Z}}_{d}\) as before. For n participants, the dealer evaluates the polynomial on n different elements \(x_{i}\) of \({\mathbb {Z}}_{d}\) and satisfies each \(L_{i} = \prod _{1 \le j \le n, j\ne i}\frac{x_{j}}{x_{j} - x_{i}}\) is an integer and shares the outputs privately to each participant. During reconstruction, the dealer generates a two-qudit Bell state in the d-dimensional Hilbert space. The participants perform suitable unitary operations on this Bell state to reconstruct the secret. For more details, we refer the reader to [21].

Encoding of U See Sect. 4.4.3.

3.2.1 Description of procedures 1 and 2 and correctness of the scheme

Figure 1 gives a schematic diagram of our construction.

Procedure 1 SHARE1 Procedure 1 first chooses a subset \({\mathcal {S}}_{r}\) of the set of secrets \({\mathcal {S}}\). In step 2, this chosen subset is then partitioned into r partitions. For each partition, temporary composite states are created. This is done by taking the tensor product of the quantum states present in a partition. To the obtained state, the trap code operations are applied, i.e. a suitable quantum error-correcting code is applied, equal number of \(\left| 0\right\rangle \) and \(\left| +\right\rangle \) states are appended followed by a random permutation and the application of a random Pauli operator. Thus, from each partition, we obtain a composite state which looks completely mixed due to the application of the trap code. Finally, all the composite states from each of partitions are combined (tensored) to get the state \(\left| {\mathcal {S}}_{comp}\right\rangle .\) To this state, the underlying quantum threshold secret scheme is applied to get the shares of the participants. Additionally, the index \(k_{2}\) of the \(k_{2}\) Pauli operator is shared via an underlying semi-quantum threshold SSS. Similarly, the index of the random permutation for each of the partition has to be shared. This is again done by applying a semi-quantum threshold SSS.

Procedure 2 RECON1 Let us suppose that some k participants present their shares. If \(k \ge t_{0}\), then by applying the reconstruction procedure of the underlying quantum threshold SSS, the state \(\left| {\mathcal {S}}_{comp}\right\rangle \) is recovered. Similarly, by applying the reconstruction procedure of the underlying quantum threshold schemes, the index of the Pauli operator is recovered. Next, the greatest threshold \(t_{m}\) which is less than k is identified. From step 7, the indices of the respective permutations which were applied to the first m permutations are recovered. The random permutations are inverted, the trap states (\(\left| 0\right\rangle \) and \(\left| 1\right\rangle \) states are discarded), the QECC is decoded and hence, the secret quantum states which belong to the first m partitions are recovered.

Theorem 1

The constructed scheme is correct. Fully qualified sets can recover all the states in \({\mathcal {S}}_{r}\). If \(p_{1} < t_{m} \le p_{2}\), then the number of states recovered by \(p_{1}\) participants is strictly less than the number of states recovered by \(p_{2}\) participants.

Proof

A fully qualified set contains more than \(t_{r}\) number of participants. By the correctness of the underlying threshold schemes, the state \(\left| {\mathcal {S}}_{comp}\right\rangle \) can be recovered and also the index of the applied Pauli operator \(k_{2}\) can be identified to remove it from the recovered \(\left| {\mathcal {S}}_{comp}\right\rangle \) to get the state \(\left| {\mathcal {S}}_{comp2}\right\rangle .\) Since the number of participants satisfies all the thresholds, again by the correctness of the underlying threshold SSSs, all the indices of the permutations are recovered. The permutations are inverted, the applied error correcting code is decoded, and the original quantum states are obtained from the respective quantum lines. Note that, the number of partitions/states on which the applied permutation can be inverted depends on the number of thresholds the participants satisfy. Hence, suppose the maximum threshold satisfied is \(t_{m}\), then only the first m permutations can be unpermuted and finally recovered. Thus, we can conclude the second part of the theorem. \(\square \)

3.2.2 Privacy

Theorem 2

Forbidden sets cannot reconstruct any secret state. Any subset of participants which is not qualified cannot reconstruct the full set of secrets. The number of secret states reconstructed increases as the number of participants crosses the given thresholds.

Proof

Let us suppose that a forbidden set presents its shares. By the privacy of the underlying threshold SSSs, the recovered state is independent from \(\left| {\mathcal {S}}_{comp}\right\rangle \). Also, the recovered index of the permutations and the index of the Pauli operator are independent of the actual indices. Since these are independent events, one can conclude that the joint distributions for two different r-sets of quantum states \({\mathcal {S}}_{1}, {\mathcal {S}}_{2} \subseteq {\mathcal {S}}\), \((\{\Pi _{r}^{({\mathcal {S}}_{1})}\}_{r \le |{\mathcal {S}}|})\) and \((\{\Pi _{r}^{({\mathcal {S}}_{2})}\}_{r \le |{\mathcal {S}}|})\) are identical. Also, note that in contrast to trap codes where the probability is computed over all permutations of some length N(to be specified later), in our case, the probability is computed over all such permutations of length N which can be expressed as a product of r permutations(one for each partition). Clearly, if the maximum threshold satisfied is \(t_{m}\)(\(m < r\)), then the permutations corresponding to the partitions( \(> m\)) cannot be unpermuted. And hence not all states can be recovered. \(\square \)

3.3 Dimension of share states

We shall assume for ease of computation that the underlying quantum threshold SSS \((Sh_{Th}(n,k), Rec_{Th}(n,k))\) does not increase the dimension of the share state. We also note that applying a quantum one-time pad does not change the dimension of the state. In view of this, it is enough to compute the dimension of \(\left| {\mathcal {S}}_{comp}\right\rangle .\) Let the dimension of the states in \({\mathcal {S}}\) be bounded above by \(D_{{\mathcal {S}}}.\) Also, let the size of a partition be bounded above by \(P_{r}\). Let \(\mu \) be the factor by which the QECC increases the dimension of the state and suppose for each partition a maximum of M traps are applied. Hence, for each partition, the dimension of \(\left| {\mathcal {S}}_{comp1}^{w}\right\rangle \) is bounded above by \(K = D_{{\mathcal {S}}} \times P_{r} \times \mu \times M.\) Hence, the total dimension of \(\left| {\mathcal {S}}_{comp}\right\rangle \) is bounded above by \(O(K^{r}).\)

Furthermore, quantum states corresponding to the Pauli operators and the random permutations are also shared. Even for a small number of states and/or partitions the dimension of the shares corresponding to \(\left| {\mathcal {S}}_{comp}\right\rangle \) can become very large for practical applications. The blowup is also due to the QECC which increases dimension. This motivates us to consider techniques to significantly reduce the dimension of the share states which does not use trap codes. We describe the modifications in the following sections.

4 Modifications and variants

In this section, we attempt to reduce the dimension of the share states. The crucial assumption here is that there is a known relation between the secret quantum states. We show that this assumption helps to drastically reduce the dimension of the share states and also that the known relation between the secret states does not reveal any information about the states to the forbidden states. As a warm-up (Sect. 4.1), we present procedure 3 and 4, where the states are related by the powers of a single unitary operator. To model more general situations, we introduce our quantum walk-based constructions in Sect. 4.4.

4.1 Relation between quantum states described by a finite number of unitary operators

The main idea in this section is that to share a set of secrets with some known relations among the states, it is not necessary to share all the secret states. Again let us suppose that we have an unknown set of quantum secrets \({\mathcal {S}} = \{\left| \phi _{1}\right\rangle , \left| \phi _{2}\right\rangle , \ldots , \left| \phi _{u}\right\rangle \}\). In addition, let us suppose that \(\left| \phi _{i}\right\rangle = U^{i-1}(\left| \phi _{1}\right\rangle )\) for all \(i = 0,1, \ldots , n.\) In this case, it is enough to share \(\left| \phi _{1}\right\rangle \), the number of quantum states n and an encoding of the operator U. Hence, in Procedure 3, we essentially reduce the MSS problem to the case of sharing just three secrets, one quantum secret and two classical secrets in the quantum environment. However, situations need not be so simple and might demand complicated relations between known states. In view of this, we generalize the this method to more complicated scenarios using the concept of discrete-time quantum walks in Sect. 4.4.

figure c
figure d

4.2 Correctness and privacy

Theorem 3

The constructed scheme is correct, i.e. any k or more participants performing the reconstruction procedure by combining their shares can reconstruct all the secrets \(\left| \phi _{1}\right\rangle , \left| \phi _{2}\right\rangle , \left| \phi _{3}\right\rangle , \ldots , \left| \phi _{m}\right\rangle .\)

Proof

From Procedure 3 (i.e. SHARE2), we observe that the initial secret state \(\left| \phi _{1}\right\rangle \) is shared via an fully quantum (n, k) threshold SSS. The maximum power m to which U is raised and an encoding of U which are treated as classical secrets are shared using semi-quantum (n, k) threshold SSSs. Now from Procedure 4 (i.e. RECON2), we see that in order to reconstruct all the secrets, the respective reconstruction procedures are applied to recover \(\left| \phi _{1}\right\rangle \), m and U. Finally, the participants compute \(U(\left| \phi _{1}\right\rangle ), U^{2}(\left| \phi _{1}\right\rangle ), \ldots ,U^{m-1}(\left| \phi _{1}\right\rangle )\) to get the states \(\left| \phi _{2}\right\rangle , \left| \phi _{3}\right\rangle , \ldots , \left| \phi _{m}\right\rangle .\) \(\square \)

Theorem 4

(Privacy) Forbidden sets of participants (i.e. subsets with size less than or equal to \(k-1\)) cannot reconstruct any secret state.

Proof

To reconstruct all the secret states in the state, it is necessary to reconstruct \(\left| \phi _{1}\right\rangle \) and U. By the privacy of the underlying k-out-of-n quantum threshold SSSs, any forbidden set of participants (i.e. subsets containing \(\le k-1\) participants) cannot reconstruct either of \(\left| \phi _{1}\right\rangle \) or U. Hence, forbidden sets of participants cannot reconstruct any secret state. The reconstruction of m is not entirely necessary as the participants can start computing \(U^{i}(\left| \phi _{1}\right\rangle )\), and without the knowledge of m, the participants cannot claim with certainty that they have recovered all the quantum states. Hence, to exactly reconstruct all the secret quantum states, it is necessary to reconstruct all of \(\left| \phi _{1}\right\rangle \), m and U which a forbidden set of participants cannot. \(\square \)

4.3 Dimension of share states

Let \(D_{{\mathcal {S}}}\) be the dimension of \(\left| \phi _{1}\right\rangle \). Let us assume that application of the underlying quantum threshold SSS \((Sh_{Th}(n,k), Rec_{Th}(n,k))\) does not increase the dimension of the share state. Also, the semi-quantum threshold schemes share classical secret privately to the participants and utilize a d-dimensional state for secret reconstruction. In view of this, one can assume a constant times increase in the overall dimension of the share states. Assuming for ease of computation that the dimension of the share state due to sharing m is bounded above by \(D_{{\mathcal {S}}}\), the dimension of a share state is bounded above by \(O(D_{{\mathcal {S}}}^{2}).\) In comparison with the dimension obtained in Sect. 3.3, we have \(D_{{\mathcal {S}}}^{2} \ll K^{r}\) and this is a significant improvement.

4.4 Quantum multi-secret sharing schemes based on quantum walks

We can express a QMSSS in terms of a Discrete-Time Quantum Walk Model. We shall construct three SSSs based on the three types of discrete-time quantum walks we have defined in Sect. 2.

4.4.1 Arc reversal model

In this model, we have the following components:

  • A graph G where each edge is replaced by two directed edges(arcs) in the opposite direction. Let us suppose that X has n vertices and m arcs.

  • State space is \({\mathbb {C}}^{m}\) spanned by the characteristic vector of the arcs \(e_{u,v}\).

  • For each vertex u, there is a linear order \(f_{u}\) on its neighbours.

  • The transition matrix of an arc reversal quantum walk is given by \(U = RC\) where R is a permutation matrix that reverses an arc and C is a coin flip quantum operator. We may give the same quantum coin C to all the vertices or we can give different quantum coins to different vertices.

  • A QMSSS based on the Arc reversal model Let us suppose that we have a graph \(G = (V,E)\)(E consists of arcs), an arc reversal operator R and each vertex has two quantum coins \(C_{0}\) and \(C_{1}\). Hence, we have two phase transition matrices \(U_{0} = RC_{0}\) and \(U_{1} = RC_{1}.\) Let the characteristic vectors corresponding to the arcs be denoted by \(e_{u,v}\). Fix an \(N \in {\mathbb {N}}.\) The set of secrets is defined as

    $$\begin{aligned} {\mathcal {S}}_{N}= & {} \{A_{1}\circ A_{2}\circ \ldots \circ A_{i}(\left| \phi \right\rangle ), 1 \le i \le \log N, A_{i} = U_{0},U_{1}, \left| \phi \right\rangle \\ {}= & {} e_{u,v}, (u,v) \in E\}. \end{aligned}$$

    To choose a multi-secret, we do the following procedure. Let \(\left| \phi \right\rangle = e_{u,v}\) be a fixed initial state. For any \({\mathcal {X}} \le N\), let us consider the binary expansion of \({\mathcal {X}}\) denoted as \((x_{1}, x_{2}, \ldots , x_{\log {\mathcal {X}}})_{2}\). Hence, \(x_{k} =0,1(1\le k \le \log {\mathcal {X}}).\) Corresponding to \({\mathcal {X}}\), we can get a quantum multi-secret as follows: If \(x_{2} = 0\), then \(\left| \phi _{1}\right\rangle = U_{0}(\left| \phi \right\rangle )\), otherwise \(x_{2} = 1\) and \(\left| \phi _{1}\right\rangle = U_{1}(\left| \phi \right\rangle )\). Again if \(x_{3} = 0\), then \(\left| \phi _{2}\right\rangle = U_{0}(\left| \phi _{1}\right\rangle )\), otherwise \(x_{3} = 1\) and \(\left| \phi _{2}\right\rangle = U_{1}(\left| \phi _{1}\right\rangle )\) and this process is continued until we reach \(\log {\mathcal {X}}\). Formally, the multi-secret is

    $$\begin{aligned} {\mathcal {S}}_{{\mathcal {X}}} = \{A_{1}\circ A_{2}\circ \ldots \circ A_{i}(\left| \phi \right\rangle ), 1 < i \le \log {\mathcal {X}}, A_{1} = I, A_{i}= U_{x_{i}}\}. \end{aligned}$$

    Hence, in this process, it is necessary to share the initial state \(\phi \), a natural number \({\mathcal {X}}\). The remaining components like the graph G, and the unitary operators \(U_{1}\) and \(U_{2}\) may remain public or private depending on the model being used or depending on the maximum dimension of the share states that is allowable by the implementing devices. The procedure is formalized in the following algorithms.

figure e

Note \((Sh_{Th}(n,k), Rec_{Th}(n,k))\) is a fully quantum SSS to share the initial state in a quantum environment. This is the same scheme as described in Sect. 3.2. Again we omit the exact details and refer the reader to [20]. \((Share_{(n,k)}^{1}, Rec_{(n,k)}^{1})\) is a semi-quantum threshold SSS to share the classical secret \({\mathcal {X}}\). We have briefly described this scheme in Sect. 3.2 in the discussion of \((Share_{(n,k)}, Rec_{(n,k)})\) of [21]. Similarly, \((Share_{(n,k)}^{2}, Rec_{(n,k)}^{2})\) and \((Share_{(n,k)}^{3}, Rec_{(n,k)}^{3})\) are semi-quantum threshold schemes to share classical secrets in a quantum environment.

figure f

4.4.2 Shunt decomposition model

The shunt decomposition model can be utilized in a similar manner as in the arc reversal model. This model is useful when the underlying graph has a certain symmetry. In this model, the graph G is assumed to be d-regular. Both in the classical and quantum domain, special SSSs have been studied which can handle unbounded number of participants [49, 55]. We can similarly ask the following question: what if the number of secrets to be shared is unbounded? In this scenario, the shunt decomposition model becomes useful as this model has been applied to infinite paths and infinite grids. Here, also we have a coin operator C and a shift operator S and the transition matrix is given by \(U = SC.\) A QMSSS based on the shunt decomposition model can be easily constructed using procedures 5 and 6 by suitably modifying the quantum coin operators and the shift matrix S. Due to this similarity, we omit the exact details.

4.4.3 Two-reflections model

In this model, there is no quantum coin. The transition matrix is given by \(U = (2Q_{1}Q_{1}^{T} - I)(2Q_{2}Q_{2}^{T} - I)\) where \(Q_{1}\) and \(Q_{2}\) represent two partitions of the underlying graph G, one based on the head of the arcs and the other based on the tails of the arcs [41]. As has been noted in [41, 56], these partitions can come from different graph structures, e.g. orientable embeddings. The important observation is that to share the operator U, it is enough the share the doubly stochastic matrix M and the partition of the arcs as classical secrets to be protected in a quantum environment via the semi-quantum threshold SSS \((Share _{(n,k)}, Rec_{(n,k)}).\) One may use this U directly in Sect. 4.1.

4.5 Correctness and privacy

We first describe the share generation and reconstruction algorithms and then proceed to argue correctness and privacy of the scheme.

Procedure 5: In the SHARE3 algorithm, the secrets are the initial state \(\left| \phi _{1}\right\rangle \), the length of the random walk \({\mathcal {X}}\) and the transition operators \(U_{1}, U_{2}\). The state \(\left| \phi _{1}\right\rangle \) is shared by a fully quantum threshold SSS. To share X and the transitions operators \(U_{1}, U_{2}\) (or their proper encodings), we use semi-quantum threshold SS.

Procedure 6: The RECON3 procedure consists of recovering \(\left| \phi _{1}\right\rangle \), the length of the random walk \({\mathcal {X}}\) and the transition operators \(U_{1}, U_{2}\) by applying the respective reconstruction procedures of the underlying quantum threshold schemes. To reconstruct the remaining secrets, one considers the binary expansion of \({\mathcal {X}} = (x_{1}, x_{2}, \ldots , x_{\log {\mathcal {X}}})_{2}.\) If \(x_{2} = 0\), then \(\left| \phi _{2}\right\rangle = U_{0}\left| \phi _{1}\right\rangle \), otherwise \(\left| \phi _{2}\right\rangle = U_{1}\left| \phi _{1}\right\rangle .\) Again if \(x_{3} = 0\), then \(\left| \phi _{3}\right\rangle = U_{0}\left| \phi _{2}\right\rangle \), otherwise \(\left| \phi _{3}\right\rangle = U_{1}\left| \phi _{2}\right\rangle .\) This process is continued to finally recover all the states until \(\left| \phi _{\log {\mathcal {X}}}\right\rangle .\)

We now have the following theorem.

Theorem 5

The constructed scheme satisfies the correctness property, i.e. k participants combining their share can reconstruct all the secrets \(\left| \phi _{1}\right\rangle , \left| \phi _{2}\right\rangle , \left| \phi _{3}\right\rangle , \ldots , \left| \phi _{\log {\mathcal {X}}}\right\rangle .\) Also, the scheme satisfies privacy property, in particular, forbidden sets containing less than k of the participants cannot reconstruct any secret state.

Proof

The correctness property easily follows from the correctness of the underlying schemes viz. \((Sh_{Th}(n,k), Rec_{Th}(n,k))\), and \((Share_{(n,k)}^{1}, Rec_{(n,k)}^{1})\) and \((Share_{(n,k)}^{3}, Rec_{(n,k)}^{3})\). To reconstruct all the secret states in the state, it is necessary to reconstruct \(\left| \phi _{1}\right\rangle \), \({\mathcal {X}}\), \(U_{0}\) and \(U_{1}\). By the privacy of the underlying quantum threshold SSSs, any forbidden set of participants which contains less than k participants cannot reconstruct any of \(\left| \phi _{1}\right\rangle \), \({\mathcal {X}}\), \(U_{0}\) and \(U_{1}\). Moreover, the semi-quantum threshold schemes use a variant of Shamir’s polynomial-based secret sharing and, therefore, \(k-1\) or less number of shares statistically hides the secrets, viz. \(U_0\) and \(U_1\). Hence, forbidden sets of participants cannot reconstruct any secret state. The reconstruction of \({\mathcal {X}}\) is necessary as the bit pattern of \({\mathcal {X}}\) determines the further secret states \(\left| \phi _{2}\right\rangle , \ldots \left| \phi _{\log {\mathcal {X}}}\right\rangle \). Hence, to exactly reconstruct all the secret quantum states, it is necessary to reconstruct all of \(\left| \phi _{1}\right\rangle \), \({\mathcal {X}}\), \(U_{0}\) and \(U_{1}\) which a forbidden set of participants cannot. \(\square \)

4.6 On the dimension of share states and possibility of reduction

The analysis is similar as in Sect. 4.3. We have an exponential reduction from \(K^{r}\). However, the dimension of share states is more as compared to Sect. 4.3 due to more information to be shared among participants. Note that, depending on the model, one can even make \(U_{0}, U_{1}\) public and even then the forbidden states cannot reconstruct the set of secrets. Assuming for ease of computation that the dimensions of the states due to \(\left| \phi _{1}\right\rangle \), \({\mathcal {X}}\), \(U_{0}\) and \(U_{1}\) are bounded by \(D_{{\mathcal {S}}}\), then the over dimension of the share states becomes \(D_{{\mathcal {S}}}^{4}\). Depending on the model, one may make the operators \(U_{0}\) and \(U_{1}\) public and in that the dimension becomes \(D_{{\mathcal {S}}}^{2}.\) From the above discussion, we conclude that the steps 2 and 4 of procedure 5 are necessary.

For the practicality of implementation of quantum SSSs, the lesser the dimension of the share states, the easier it is to implement the scheme. To reduce the dimension, one can consider the possibility of making some of the steps of procedure 5 optional. Another instance where the dimension can be reduced is if we consider an interactive model. In this case, the dealer retains \({\mathcal {X}}\) and shares \(\left| \phi _{1}\right\rangle \), \(U_{0}\) and \(U_{1}\). The reconstruction procedure consists of \(\log {\mathcal {X}}\) rounds of interaction. In every round of interaction, the dealer tells the participants one bit in the binary expansion of \({\mathcal {X}}\). If the value is 0, participants apply \(U_{0}\) and if the value is 1, participants apply \(U_{1}\).

4.7 Generality of the construction

We have considered multi-SSSs where the quantum states are related to each other and this results in a major reduction in the dimension of the states. It may appear that it makes our construction restrictive in nature. We point out that by making a small modification, our construction can be applied to the case where there is no known relation between the secret states and still it is possible to reduce the dimension of the share states. Using the shunt decomposition model, we show that it is possible. Let the graph be chosen to be the complete graph \(K_{n}\). The coin operator S is equivalent to the block diagonal matrix

$$\begin{aligned} S= \begin{pmatrix} \begin{array}{llll} {P_{1}}&{}&{}&{}\\ &{}{P_{2}}&{}&{}\\ &{}&{}{\ddots }&{}\\ &{}&{}&{}{P_{d}}\\ \end{array} \end{pmatrix} \end{aligned}$$

The blocks are obtained from the linear orders defined for each vertices on the set of their neighbours. We randomize these orders and equivalently we choose random permutation matrices as the blocks in the matrix S. The final effect is that after one step of the random walk, the probability of going from one state to any of the other states is equal. Hence, we can treat this case as sharing multiple secret states which have no relation between them since the states are reached with equal probability.

5 Generalization and applications

5.1 General access structures

Our schemes use threshold quantum SSSs as basic building blocks, and as a result, they inherit the threshold property. We can think of our construction as a compiler which takes as input two QSSSs (one fully quantum, one semi-quantum) realizing the same threshold access structure and outputs an MSSS. A natural question is to ask whether we can generalize our methodology to construct MSSSs to realize general access structures. Intuitively, it seems that given any general access structure (with the monotonicity property), if we use a QSSS realizing the given general access structure as a basic building block, then our proposed compiler construction can be extended to MSSS for general access structures. Constructions for QSSSs realizing general access structures exist in the literature [57, 58].

However, the existing schemes have certain limitations which make them difficult to be used in our case. For example, the scheme of [58] shares a classical secret in a quantum environment and hence cannot be used in our case to share the initial quantum secret. Also, our goal in this paper is to make our construction entanglement-free which we have been able to achieve in our construction. In [58], secret keys are encoded in the entangled GHZ states. While using quantum SSSs for general access structures, one should be careful to avoid the consequences of the “no-cloning theorem” so that no two disjoint groups of participants can reconstruct the secret hence violating the “no-cloning theorem” [17]. To summarize, instead of using a threshold QSSS as the underlying scheme, one may use a quantum scheme realizing a general access structure provided it can share a quantum secret in a quantum environment, satisfies the no-cloning theorem and does not use entanglement (or uses minimal amount of entanglement). The scheme of [57] discusses the concept of quantum access structures where along with monotonicity, any two qualified sets must have a non-empty intersection. There the authors also discuss decomposition of quantum access structures, improved maximal quantum access structures and present QSSSs realizing these access structures. So these QSSSs can be used in our construction but again these QSSSs use entanglement to a large extent and hence impose practical problems.

To the best of our knowledge, such a QSSS which completely fits the above-mentioned constraints of our construction and realizes any general access structure is still not available in the literature. We note that our compiler construction can be extended to realize general access structures when a general fully quantum secret sharing comes into existence. In this paper, we focus on threshold access structures and leave general access structures as a future work.

Another practical situation may arise. Since we can think of our construction as a compiler, let us suppose that a fully quantum threshold SSS is available to share the initial quantum secret and a semi-quantum SSS realizing a general access structure is available to share the natural number \({\mathcal {X}}\). A natural question can be put forward: can the constructed compiler work when two different QSSSs realizing two different access structures are presented ? We can definitely use the scheme of [58] which works for a general access structure. However, it may happen that a qualified set of participants (for threshold) reconstruct the initial state but this set is not qualified in other SSS that is being used to share the natural number. Hence, the natural number is not recovered, and as the result, the remaining secret quantum states are not reconstructed. This defeats the purpose of the of paper as the goal is to reconstruct the full set of secret quantum states. So a clarification regarding which subsets of participants are qualified when two different access structures are used simultaneously is required. This restricts the usage of QSSSs which realize arbitrary general access structures. This however does not rule out the possibility of using any other access structure instead of threshold access structures.

In [59], the authors have introduced the notions of improvable access structures and realizable restrictions of access structures which we think can be used in a situation where a mix of threshold access structure and a different access structure is required. We have only considered threshold QSSSs for our purpose and do not explore this possibility of this mix in this current work. We leave this interesting avenue for a future work.

5.2 Modifications for the multi-threshold variant

The above MSSS based on the discrete quantum walk model can be generalized to handle multi-threshold scenario as in the Procedures 1 and 2. Instead of sharing \({\mathcal {X}}\) by a one-shot threshold scheme, one may split the binary expansion of \({\mathcal {X}}\) into partitions and share the partitions among the participants in a similar manner as we have done in the case of procedure 1. This simple modification makes our scheme a multi-threshold SSS.

5.3 Application in the progressive setting

Let us suppose that the set of secrets be of the form \(\left| \phi _{initial}\right\rangle = \left| \phi _{1}\right\rangle , \left| \phi _{2}\right\rangle , \ldots , \left| \phi _{n}\right\rangle = \left| \phi _{final}\right\rangle .\) Let us also suppose that there is predefined notion of distance d. Examples of such distances can be found in [60]. In the progressive setting, it is required that for \((1 \le i \le n-1\)),

$$\begin{aligned} d(\left| \phi _{i}\right\rangle , \left| \phi _{n}\right\rangle ) > d(\left| \phi _{i+1}\right\rangle , \left| \phi _{n}\right\rangle ). \end{aligned}$$

In this model, our constructions in procedures 1 and 2 can be directly applied to the effect that as more and more participants arrive, the reconstructed secret states get closer with respect to d to the final state \(\left| \phi _{n}\right\rangle .\) As we have noted in the sections following procedures 1 and 2 that existing relations between the states help in reducing the dimensions of the share states, if there exists some known relations between the states (which is usually the case in visual secret sharing), the dimension of the share states can also be reduced in this case. In addition, we can make the scheme progressive by considering the methods in Sect. 4.7.

6 Security against adversarial attacks

Since we have assumed the existence of the underlying threshold quantum schemes(fully quantum and semi-quantum) [20, 21], our constructed scheme inherits the security provided by those schemes for example the intercept and resend attack, entangle and measure attack, man-in-the-middle attack, Trojan horse attack. The scheme of [21] is also a verifiable SSS, and hence, the participants can judge whether the recovered secret is the original one and check whether some dishonest participants provide the fake shadows in the reconstruction. Also, the use of trap code provides \((2/3)^{d/2}\) security against Pauli attacks [51, 52], where d is the distance of the underlying quantum error-correcting code used.

7 Comparison with existing schemes

The main difference of our scheme with the existing ones is that our scheme is a fully quantum MSSS. This means that the secrets are quantum states as opposed to semi-quantum schemes which share classical data. The achieved privacy, security and the dimension of the shares are unconditional, meaning that the results do not depend on the security of computationally hard problems like the lattice-based problems [13]. Our scheme works for discrete-time quantum walks for general graphs, as opposed to the construction in [33] which uses quantum walk over the circle graph and also the construction in [32] where the quantum walk is on a lattice folded into a torus. We also note that the schemes of [32] and [33] are not multi-SSSs and also are semi-quantum schemes. Also note that using the shunt decomposition model, one can construct multi-SSSs with potentially unbounded number of secrets.

In [59], the authors demonstrate a way to improve quantum SSSs by encrypting a quantum state \(\left| S\right\rangle \) using a classical key K to obtain \(\left| {\tilde{S}}\right\rangle \) and sharing \(\left| {\tilde{S}}\right\rangle \) to only some selected participants and sharing the classical key K to some other participants via a classical SSS. For reconstruction, some participants recover K and the remaining participants using this key reconstruct \(\left| S\right\rangle \) from \(\left| {\tilde{S}}\right\rangle \). So one has to share less number of quantum states to the participants. This work was improved in [61] so that even more number of participants can carry classical shares. However, it was shown in [59] that this technique is not possible to be applied to various cases of quantum threshold schemes for example the 2-out-of-3 quantum threshold scheme. In this case, quantum states have to be shared to all three participants. The authors introduced the notion of an improvable QSSS which is a QSSS realizing an access structure \(\Gamma \) on a set of n participants and less than n quantum shares are sufficient to implement it. They proved that if a (n, k)-threshold scheme does not violate the no-cloning theorem, its minimal access structure is equal to the optimal one and is given by the expression \((k - \gamma ,n - \gamma )\) where \(\gamma = 2k - n - 1\). By this formula, the minimal restriction [59] of a (99, 100) QTSS is a (2, 3) QTSS and only three quantum shares are required to implement a hybrid quantum secret sharing scheme realizing a quantum (99, 100)-threshold scheme.

We can similarly use this technique in our scheme to reduce the number of quantum shares given to the participants and decrease implementation costs. We can reduce the dimension of the shares given to each of the participants who only receive the classical shares. But for the participants who receive the quantum shares, the dimension does not reduce any further than our method. We have essentially reduced an MSSS to a single-SSS utilizing quantum walks. The role of the secret key K in [59] is very much different from the role of \({\mathcal {X}}\). We do not use \({\mathcal {X}}\) to recover the initial state \(\left| \phi \right\rangle \) but rather to recover the remaining quantum secrets. The secret key K is comparable to the keys \(k_{1}\) and \(k_{2}\) corresponding to the permutation and the Pauli operator being used, respectively (See Definition 9). So for some of the participants receiving only these keys, the dimension of these participants can reduce to a some extent.

Also, this technique reduces the robustness of the construction. Since less number of quantum states are shared, the system is more susceptible to failure in case of errors arising from decoherence as compared to the case where all the participants have quantum shares.

8 Discussions

The main advantage of our construction is its generality. We are able to share multiple quantum secrets. Additionally, we have incorporated multi-threshold properties in the scheme, and our scheme is flexible enough to be used in a progressive model of secret sharing. All the schemes have been constructed keeping in mind the practical and implementation issues, and to this end, we have paid attention to the dimension of the share states in each of constructions. Table 1 compares the dimensions in each procedure and we see that assuming relations between the secret states is indeed advantageous. Our schemes inherit properties of the underlying threshold schemes [20, 21] both fully quantum and semi-quantum as they have been used without any modifications. This means that we get their security against adversarial attacks. Also, the scheme in [21] is a verifiable scheme, and hence, in our scheme also, we can verify if some participant presents wrong shares. The authors are unaware of any quantum scheme which assumes relation between secrets and suitably modifies the trap code. In the classical domain also while the technique of splitting the shares is quite prevalent [54], however, splitting the multiple secrets is not known to the authors.

Table 1 Comparison between dimensions
Full size table

9 Conclusion

We have given a compiler construction of an entanglement-free fully quantum multi-SSS which can accommodate a large number of participants into the system as opposed to entanglement-based methods. We have further showed that dimension of share states can be significantly reduced if we assume multiple secrets are related through quantum walk. In this paper, we have focussed on the threshold SSS and pointed out possible extensions to multi-threshold version of it. We leave open the interesting problems of extending the work to the case of multi-secret sharing in a mix of threshold and other access structures.