Quantum coherence dynamics of displaced squeezed thermal state in a non-Markovian environment

Abstract

The dynamical behavior of quantum coherence of a displaced squeezed thermal state in contact with an external bath is discussed in the present work. We use a Fano-Anderson type of Hamiltonian to model the environment and solve the quantum Langevin equation. From the solution of the quantum Langevin equation we obtain Green’s functions which are used to calculate the expectation value of the quadrature operators which are in turn used to construct the covariance matrix. We use a relative entropy based measure to calculate the quantum coherence of the mode. The single mode squeezed thermal state is studied in the Ohmic, sub-Ohmic and the super-Ohmic limits for different values of the mean photon number. In all these limits, we find that when the coupling between the system and the environment is weak, the coherence decays monotonically and exhibits a Markovian nature. When the system and the environment are strongly coupled, we observe that the evolution is initially Markovian and after some time it becomes non-Markovian. The non-Markovian effect is due to the environmental back action on the system. Finally, we also present the steady state dynamics of the coherence in the long time limit in both low and high temperature regime. We find that the qualitative behaviour of quantum coherence in the steady state remains the same in both the low and high temperature limits. But quantitative values differ because the coherence in the system is lower due to thermal decoherence.

1 Introduction

Quantum information has evolved from being a theoretical field to technological one in the last few decades [1]. Quantum systems are in general exposed to an external environment which can cause decoherence in the system [2]. In general, we model the environment as a many body quantum system which is also referred to as bath. When the quantum system is coupled to the bath, there is a dynamical change in the quantum properties of the system. Both the qualitative and quantitative nature of this dynamical change depends on the bath properties as well as on the coupling between the system and the environment. Qualitatively, there are two fundamental kinds of dynamics namely the Markovian and the non-Markovian dynamics [3, 4]. A knowledge of the dynamical change is important from the point of view of fabrication of quantum devices [5,6,7,8]. When the relaxation time of the bath is very short compared to the evolution time of the system, the quantumness of the system falls monotonically which is a Markovian decay [9,10,11]. For the non-Markovian dynamics, the bath relaxation time and the system evolution time are comparable to each other [4, 12]. Due to this we will observe a revival of quantumness due to environmental back action [13, 14]. Thus an open quantum system has a very rich and interesting structure which has formed the basis for several seminal works [15, 16].

Continuous variable systems can describe the interaction and propagation of electromagnetic waves and hence are a valuable resource in quantum information processing [17,18,19]. An electromagnetic field with quantized radiation modes can be denoted by bosonic modes. For n number of bosonic modes, the Hilbert space is $\otimes _{k=1}^{n} H_{k}$. The creation and annihilation operators of the kth bosonic field is given by $a^{\dag }_{k}$ and $a_{k}$ respectively. Alternatively, the continuous variable system can be described using the quadrature operators $\{x_{k}, p_{k} \}$ and for a n-mode system we have a 2n-dimensional vector which contains all the quadrature pairs. For a single mode continuous variable system, the quadrature operators are $\xi _{1} = x = (a + a^{\dag })$ and $\xi _{2} = p = -i (a - a^{\dag })$ and the 2D quadrature vector $\varvec{\xi } = \{ \xi _{1}, \xi _{2} \}$. It is well known that the quadrature operators satisfy the canonical commutation relation $[ \xi _{i}, \xi _{j} ] = 2i \Omega _{ij}$, with $\Omega _{ij}$ being the elements of the matrix

$$\begin{aligned} \varvec{\Omega } = \left( \begin{array}{cc} 0 &{}\quad 1\\ -\,1 &{}\quad 0\\ \end{array} \right) . \end{aligned}$$

(1)

A continuous variable quantum state which has representation in terms of Gaussian functions is referred to as a Gaussian state. Gaussian states are special class of continuous variable states which can be easily created and experimentally controlled using quantum optics procedure [18, 20]. Theoretically Gaussian states are easier to investigate and hence several discussions on continuous variable states are restricted to Gaussian states. In particular, a Gaussian state is completely characterized by the first and second moments of the quadrature field operators. For these operators we can construct a vector of the first moments $\overline{\varvec{\xi }} = ( \langle \xi _{1} \rangle , \langle \xi _{2} \rangle )$ and the covariance matrix $\varvec{V}$

$$\begin{aligned} V_{ij} = \langle \{ \Delta \xi _i, \Delta \xi _j \} \rangle = {\mathrm{Tr}} \left( \{ \Delta \xi _i, \Delta \xi _j \} \rho \right) . \end{aligned}$$

(2)

Here we consider $\{ \Delta \xi _i, \Delta \xi _j \} = (\Delta \xi _i \Delta \xi _j + \Delta \xi _j \Delta \xi _i )/2$, and the fluctuation operator is $\Delta \xi _{i} = \xi _{i} - \langle \xi _{i} \rangle$. In the present work we consider a single mode Gaussian state for which the matrix elements of the covariance matrix are

$$\begin{aligned} V_{ii}= & {} \langle \xi _i^2 \rangle - \langle \xi _i \rangle ^2, \end{aligned}$$

(3)

$$\begin{aligned} V_{ij}= & {} \frac{1}{2} \langle \xi _i \xi _j + \xi _j \xi _i \rangle - \langle \xi _i \rangle \langle \xi _j \rangle . \end{aligned}$$

(4)

Due to the positivity of the density matrix the covariance matrix has to satisfy the uncertainty relation $\varvec{V} + i \varvec{\Omega } \ge 0$.

Entanglement is one of the fundamental properties of a quantum system and has been studied in detail for finite dimensional and infinite dimensional systems. But entanglement is not the only unique property, rather it is one among an hierarchy of quantum properties. In the hierarchy, quantum coherence occupies the topmost level which nestles within it the other properties like nonlocality, steering, entanglement and discord [21]. This means that in a given quantum system, even when these properties are not present, quantum coherence might be present in the system. A scheme to estimate quantum coherence was introduced by Baumgratz et al. [22] from the perspective of quantum information theory. This led to an explosion of interest in the field of quantum coherence especially in defining new quantum coherence measures [23], resource theory of quantum coherence [24, 25] estimation of quantum coherence [26] and also in some applications [27,28,29]. Initially, most of these works were done on quantum systems with finite degrees of freedom. The quantum coherence of the finite dimensional system [22] is measured as the relative entropy distance between two matrices

$$\begin{aligned} {\mathcal {D}}(\rho ) = \min _{\sigma } S(\rho \Vert \sigma ) = \min _{\sigma } {\mathrm{Tr}} (\rho \log _{2} \rho - \rho \log _{2} \sigma ), \end{aligned}$$

(5)

where $\rho$ and $\sigma$ are the given quantum state and the incoherent state respectively. For a continuous variable system, the quantum coherence was initially investigated using a density matrix approach [30]. This method did not give a closed form expression for Gaussian states. Hence in Ref. [31], the authors made use of a covariance matrix method to quantify coherence in the system since the covariance matrix can completely characterize a Gaussian state. The coherence measure based on the covariance matrix is

$$\begin{aligned} C(\rho ) = \inf _{\delta } S(\rho \Vert \delta ). \end{aligned}$$

(6)

Here the minimization runs over all the incoherent Gaussian states. The closest incoherent state to a Gaussian state is the thermal state of the form

$$\begin{aligned} \rho _d = \sum _{n=0}^{\infty } \frac{\overline{\mu }^n}{(1+\overline{\mu })^{n+1}} \vert n \rangle \langle n \vert , \end{aligned}$$

(7)

with $\overline{\mu }={\mathrm{Tr}} [a^\dagger a \rho ]$ being the mean photon number associated with the Gaussian state. The entropy of a single mode Gaussian state is

$$\begin{aligned} S(\rho ) = \frac{\nu +1}{2} \log _{2} \frac{\nu +1}{2} - \frac{\nu -1}{2} \log _{2} \frac{\nu -1}{2}, \end{aligned}$$

(8)

where $\nu = \sqrt{{\mathrm{det}} {\varvec{V}}}$. Hence the relative entropy of coherence for the single mode Gaussian state is

$$\begin{aligned} C(\rho )= & {} S(\rho \Vert \rho _d) ={ \mathrm Tr} (\rho \log _2 \rho - \rho \log _2 \rho _d) \nonumber \\= & {} \frac{\nu -1}{2} \log _2 \frac{\nu -1}{2} - \frac{\nu +1}{2} \log _2 \frac{\nu +1}{2} \nonumber \\&+\, (\overline{\mu }+1) \log _2 (\overline{\mu }+1) - \overline{\mu } \log _2 \overline{\mu }. \end{aligned}$$

(9)

For our work, we use this relative entropy measure to estimate the coherence in the single mode quantum system [32]. Investigations on the open system dynamics of entanglement has been carried out on both qubit (finite dimensional) systems as well as on infinite dimensional (continuous variable) systems [33,34,35]. The entanglement dynamics presents unique features like sudden death [36] and revival of entanglement [37]. In the case of quantum coherence the dynamics has been investigated only for qubit systems [38,39,40]. In this work, we investigate the dynamics of a single mode Gaussian state which is a displaced squeezed thermal state. In Sect. 2, of the article we give a description of the system and the environment, and also the procedure to calculate the time evolved covariance matrix. We consider three different spectral densities in this manuscript and in Sect. 3, we compute the quantum coherence in the Ohmic environment. In Sects. 4 and 5 we describe the dynamical behavior of coherence in the sub-Ohmic and the super-Ohmic environments. A steady state analysis of the system is given in Sect. 6 and we give our conclusions in Sect. 7.

2 Formulation of the system-environment model and the dynamics

The quantum coherence dynamics of finite dimensional systems have been studied from both the theoretical [39, 40] and experimental [41] perspectives. An infinite dimensional case is considered in the present work where we consider the system to be a single bosonic mode of frequency $\omega _{0}$. The bath coupled to the system is a non-Markovian environment at a finite temperature. This non-Markovian environment is a structured bosonic reservoir [42] with a collection of infinite modes of varying frequencies. The system-environment combination can be described using the Fano-Anderson Hamiltonian [43, 44]

$$\begin{aligned} H = \hbar \omega _0 a^{\dagger }a + \hbar \sum _k \omega _k b_k^{\dagger }b_k + \hbar \sum _k \left( {\mathcal {V}}_k a^{\dagger } b_k + {\mathcal {V}}_k^{*} b_k^{\dagger }a \right) . \end{aligned}$$

(10)

Here, the factor ${\mathcal {V}}_{k}$ represents the coupling strength between the bath and the system and $a^{\dag }$ (a) is the creation (annihilation) operator where $\omega _{0}$ is the frequency of the system. For the kth mode of the bosonic reservoir with frequency $\omega _{k}$, $b^{\dag }_{k}$ ($b_{k}$) is the corresponding creation (annihilation) operator. This Hamiltonian is used in the study of several different models in the fields of atomic and condensed matter physics.

To solve the dynamics, we can use the Heisenberg equation of motion approach. The time evolved operators corresponding to the system and the environment are $a(t) = \hbox {e}^{\frac{i H t}{\hbar }} a \hbox {e}^{-\frac{i H t}{\hbar }}$ and $b_k(t) = \hbox {e}^{\frac{i H t}{\hbar }} b_k \hbox {e}^{-\frac{i H t}{\hbar }}$ and in the Heisenberg picture they satisfy

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t} a(t) = -\frac{i}{\hbar } \left[ a(t), H \right] = -i \omega _0 a(t) - i \sum _k {\mathcal {V}}_k b_k(t), \quad \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t} b_k(t) = - \frac{i}{\hbar } \left[ b_k(t), H \right] = -i \omega _k b_k(t) - i {\mathcal {V}}_k^{*} a(t). \quad \end{aligned}$$

(12)

To obtain the quantum Langevin equation [45] we solve Eq. (12) for $b_{k}$ and substitute the result in Eq. (11) which gives

$$\begin{aligned} {\dot{a}}(t) + i \omega _0 a(t) + \int _0^t \hbox {d}\tau g(t,\tau ) a(\tau ) = - i \sum _k {\mathcal {V}}_k b_k(0) \hbox {e}^{-i\omega _k t}. \end{aligned}$$

(13)

The non-Markovian memory effects between the system and the environment is characterized by the integral kernel $g(t,\tau ) = \sum _k |{\mathcal {V}}_k|^2 \hbox {e}^{-i\omega _k (t-\tau )}$. In the case of an environment with a continuous spectrum $g(t,\tau ) = \int _0^{\infty } \hbox {d}\omega J(\omega ) \hbox {e}^{-i\omega (t-\tau )}$ with $J(\omega )=\varrho (\omega ) |{\mathcal {V}}(\omega )|^2$ being the spectral density characterizing the non-Markovian memory of the environment. The factor $\varrho (\omega )$ is the density of states of the environment and $\omega$ is the continuously varying bath frequency. Since the quantum Langevin equation in Eq. (13) is linear, one can write $a(t) = u(t) a(0) + f(t)$. Here the time dependent coefficients u(t) and the noise operator f(t) satisfy the two integro-differential equations given below:

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} u(t)= & {} - i \omega _0 u(t) - \int _0^t \hbox {d}\tau g(t,\tau ) u(\tau ), \end{aligned}$$

(14)

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} f(t)= & {} -i \omega _0 f(t) - \int _0^t \hbox {d}\tau g(t,\tau ) f(\tau ) \nonumber \\&- i \sum _k {\mathcal {V}}_k b_k(0) \hbox {e}^{-i\omega _k t}. \end{aligned}$$

(15)

We can find u(t) by numerically solving Eq. (14) with the initial condition $u(0)=1$. To get f(t) we solve Eq. (15) subject to the initial condition $f(0)=0$ which gives

$$\begin{aligned} f(t) = - i \sum _k {\mathcal {V}}_k b_k(0) \int _0^t \hbox {d}\tau \hbox {e}^{-i\omega _k \tau } u(t,\tau ). \end{aligned}$$

(16)

where $u(t,\tau ) = u(t-\tau )$. The nonequilibrium thermal fluctuation is characterized by the correlation function given below

$$\begin{aligned} \langle f^{\dagger }(t) f(t)\rangle = v(t) = \! \! \int _{0}^{t} \! \! \! \hbox {d}\tau _1 \int _{0}^{t} \! \! \! \hbox {d}\tau _2 \; u(t, \tau _1) {{\widetilde{g}}}(\tau _1,\tau _2) u^{*}(t, \tau _2). \end{aligned}$$

(17)

Here we consider the initial state of the total system to be an uncorrelated product state i.e., $\rho _\mathrm{tot}(0)=\rho _S(0) \otimes \rho _E(0)$. For the environment with the Hamiltonian $H_E=\sum _k \hbar \omega _k b_k^{\dagger }b_k$, where $\beta = 1/k_\mathrm{B} T$ is the inverse temperature and $k_\mathrm{B}$ is the Boltzmann constant, the thermal state $\rho _E(0) = \exp (-\beta H_E)/{\mathrm{Tr}}[\exp (-\beta H_E)]$ is its initial environment state.

Here the time correlation function of the environment with continuous spectrum is

$$\begin{aligned} {{\widetilde{g}}}(\tau _1,\tau _2) = \int _0^{\infty } \hbox {d}\omega J(\omega ) {{\bar{n}}}(\omega ) \hbox {e}^{-i\omega (\tau _1-\tau _2)}. \end{aligned}$$

(18)

Here ${{\bar{n}}}(\omega )=1/(\hbox {e}^{\hbar \omega / k_\mathrm{B} T}-1)$ is the initial particle number distribution. The time dependent average values of the system are:

$$\begin{aligned}&\langle a(t) \rangle = u(t) \langle a(0) \rangle , ~~\langle a^{\dagger }(t) \rangle = u^{*}(t) \langle a^{\dagger }(0) \rangle , \end{aligned}$$

(19)

$$\begin{aligned}&\langle a(t) a(t) \rangle = (u(t))^{2} \langle a(0) a(0) \rangle , \end{aligned}$$

(20)

$$\begin{aligned}&\langle a^{\dagger }(t) a^{\dagger }(t)\rangle = (u^{*}(t))^{2} \langle a^{\dagger }(0) a^{\dagger }(0) \rangle , \end{aligned}$$

(21)

$$\begin{aligned}&\langle a^{\dagger }(t) a(t) \rangle = |u(t)|^{2} \langle a^{\dagger }(0) a(0) \rangle + v(t). \end{aligned}$$

(22)

Initially, the reservoir is in a thermal state and uncorrelated to the system so $\langle f(t)\rangle =\langle f^{\dagger }(t)\rangle =0$ and also $\langle f(t) f(t) \rangle =\langle f^{\dagger }(t) f^{\dagger }(t)\rangle =0$. The time evolved first and second moments of the quadrature operators viz $\langle \xi _1(t) \rangle$, $\langle \xi _2(t) \rangle$, $\langle \xi _1^2(t) \rangle$, $\langle \xi _2^2(t) \rangle$, $\langle \xi _1(t) \xi _2(t) \rangle$, and $\langle \xi _2(t) \xi _1(t) \rangle$ can be found from the time-dependent average values in Eqs. (19–22). From the moments of the quadrature operator one can express the time evolved covariance matrix as

$$\begin{aligned} V_{11}= & {} 1+ 2 v(t) + 2 |u(t)|^{2} \, {\mathrm{Cov}}(a^{\dagger }(0), a(0)) \nonumber \\&+\, (u(t))^{2} \, {\mathrm{Var}}(a(0)) + (u^{*}(t))^{2} \, \mathrm{Var}(a^{\dagger }(0)), \qquad \end{aligned}$$

(23)

$$\begin{aligned} V_{22}= & {} 1+ 2 v(t) + 2 |u(t)|^{2} \, {\mathrm{Cov}}(a^{\dagger }(0), a(0)) \nonumber \\&-\, (u(t))^{2} \, {\mathrm{Var}}(a(0)) - (u^{*}(t))^{2} \, \mathrm{Var}(a^{\dagger }(0)), \qquad \end{aligned}$$

(24)

$$\begin{aligned} V_{12}= & {} i (u^{*}(t))^{2} \; {\mathrm{Var}}(a^{\dag } (0)) - i ((u(t))^{2} \, {\mathrm{Var}}(a(0)). \end{aligned}$$

(25)

where ${\mathrm{Cov}}(a,b) = \langle a b \rangle - \langle a \rangle \langle b \rangle$ and ${\mathrm{Var}}(a) = {\mathrm{Cov}}(a,a)$. Due to the symmetry of the covariance matrix we also have $V_{12} = V_{21}$.

From the knowledge of the initial state and the environmental parameters, we can find the time evolved covariance matrix elements using the nonequilibrium Green’s functions u(t) and v(t). The spectral density $J(\omega )$ of the environment needs to be specified to calculate the Green’s functions. An Ohmic type spectral density,

$$\begin{aligned} J(\omega ) = \eta ~\omega \left( \frac{\omega }{\omega _\mathrm{c}} \right) ^{s-1} ~\hbox {e}^{-\omega /\omega _\mathrm{c}}, \end{aligned}$$

(26)

is considered in our work, since this can simulate a large class of thermal baths. In the above equation, $\omega _\mathrm{c}$ is the cut-off frequency of the environmental spectra and $\eta$ is the system-bath coupling strength. At the critical value of the coupling strength $\eta _\mathrm{c} = \omega _{0} /(\omega _\mathrm{c} \Gamma (s))$ a localized mode is generated and here $\Gamma (s)$ is the gamma function. The environment is classified as Ohmic for $s=1$ super-Ohmic for $s > 1$ and sub-Ohmic for $s<1$. The dynamics of coherence is measured for the displaced squeezed thermal state over a wide range of parameters. In the present work we consider the Hamiltonian which is bilinear in the creation and annihilation operators. Hence the Gaussian states preserve their form and remain Gaussian. Throughout our work we use a scaled temperature $T_\mathrm{s} = k_\mathrm{B} T/ \hbar \omega _{0}$, where $\omega _{0}$ is the frequency of the system.

In the present work we investigate the quantum coherence dynamics of a general Gaussian state of the form [46]

$$\begin{aligned} \rho = D(\alpha ) \ S(r) \ \rho _\mathrm{th} \ S^{\dag }(r) \ D^{\dag }(\alpha ), \end{aligned}$$

(27)

where $D(\alpha )$ and S(r) are the displacement and squeezing operators defined as:

$$\begin{aligned} D(\alpha )= & {} \exp (\alpha a^{\dag } - \alpha ^{*} a), \end{aligned}$$

(28)

$$\begin{aligned} S(r)= & {} \exp \left[ r (a^2 - a^{\dag 2})/2 \right] , \end{aligned}$$

(29)

with the thermal state $\rho _\mathrm{th}$ being:

$$\begin{aligned} \rho _\mathrm{th} = \sum _{n =0}^{\infty } \frac{\bar{n}^{n}}{(1+\bar{n})^{n+1}} |n \rangle \langle n |. \end{aligned}$$

(30)

The transient dynamics of a single mode Gaussian state with initial form as described in Eq. (27) is investigated for different values of the displacement parameter $\alpha$ and squeezing parameter r.

3 Quantum coherence evolution of displaced squeezed thermal state in a Ohmic environment

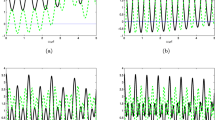
The transient dynamics of a single mode squeezed displaced thermal state in contact with a ohmic bath with spectral density $J(\omega ) = \eta \ \omega \exp (- \omega / \omega _\mathrm{c})$ is described in the present section. The mode is characterized by two parameters viz the displacement parameter ($\alpha$) and the squeezing parameter (r) and the dynamics are shown through the plots Figs. 1, 2, 3 and 4. From these plots we find that the amount of initial coherence is higher in systems with lower mean photon number.

Fig. 1

The time evolution of quantum coherence of a displaced squeezed thermal state in the low temperature limit $T_\mathrm{s} =1$, is shown above for a weakly coupled system ($\eta = 0.01 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use Ohmic spectral density ($s=1$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

Fig. 2

The time evolution of quantum coherence of a displaced squeezed thermal state in the high temperature limit $T_\mathrm{s} =20$, is shown above for a weakly coupled system ($\eta = 0.01 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use Ohmic spectral density ($s=1$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

Fig. 3

The time evolution of quantum coherence of a displaced squeezed thermal state in the low temperature limit $T_\mathrm{s} =1$, is shown above for a strongly coupled system ($\eta = 2.0 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use Ohmic spectral density ($s=1$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

Fig. 4

The time evolution of quantum coherence of a displaced squeezed thermal state in the high temperature limit $T_\mathrm{s} =20$, is shown above for a strongly coupled system ($\eta = 2.0 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use Ohmic spectral density ($s=1$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

In Figs. 1 and 2, the dynamics of quantum coherence of a weakly coupled system ($\eta = 0.01 \eta _\mathrm{c}$) is studied in the low temperature ($T_\mathrm{s}=1$) and high temperature ($T_\mathrm{s}=20$) limits respectively. The rate of fall of coherence decreases with increase in the displacement parameter and the squeezing parameter. Since there is no back flow of information, the quantum coherence decreases steadily with time. The initial coherence and the rate of fall also depends on the mean photon number $\bar{n}$. This is characteristic of the system that is weakly coupled to the environment. A comparison between the low and high temperature plots show that the coherence falls faster in the high temperature limit. This is because, apart from the loss of coherence due to the dissipative interaction with the environment, the system also suffers from decoherence due to the thermal effects.

The strongly coupled system ($\eta = 2.0 \eta _\mathrm{c}$) is studied through the plots in Figs. 3 and 4, corresponding to the low temperature ($T_\mathrm{s}=1$) and high temperature ($T_\mathrm{s}=20$) limits respectively. We find that the amount of coherence is higher at low temperature and the rate of fall of coherence is lesser for systems with higher value of displacement and squeezing parameter. The quantum coherence in the system initially falls faster and reaches a minimum value. Then it increases slightly and exhibits an oscillatory behavior. These oscillations indicate an information back flow which is a characteristic feature of a non-Markovian dynamics. Due to thermal decoherence in the high temperature limit, there is a faster fall of quantum coherence. Thus we find that the system dynamics is dependent on the strength of its coupling with the bath.

4 Quantum coherence dynamics of displaced squeezed thermal state in a sub-Ohmic environment

In the current section, we consider a sub-ohmic bath ($s<1$) and characterize the quantum coherence dynamics for the displaced squeezed thermal state. We take $s = 1/2$ and so the corresponding spectral distribution reads $J(\omega ) = \eta \sqrt{\omega \omega _\mathrm{c}} \exp (-\omega /\omega _\mathrm{c})$. The initial Gaussian state is characterized by two parameters viz the displacement parameter (‘$\alpha$’) and the squeezing parameter (‘r’). The transient dynamics of quantum coherence of this system under the variation of these parameters is shown through the plots in Figs. 5, 6, 7 and 8.

Fig. 5

The time evolution of quantum coherence of a displaced squeezed thermal state in the low temperature limit $T_\mathrm{s} =1$, is shown above for a weakly coupled system ($\eta = 0.01 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use sub-Ohmic spectral density ($s=1/2$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

Fig. 6

The time evolution of quantum coherence of a displaced squeezed thermal state in the high temperature limit $T_\mathrm{s} =20$, is shown above for a weakly coupled system ($\eta = 0.01 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use sub-Ohmic spectral density ($s=1/2$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

The coherence evolution in the weak coupling limit with $\eta = 0.01 \; \eta _\mathrm{c}$ is analyzed in Fig. 5 considering the low temperature ($T_\mathrm{s} =1$) limit and in Fig. 6 for the high temperature ($T_\mathrm{s} = 20$) limit. In both the high and low temperature limits we observe that the initial coherence is inversely proportional to the mean photon number $\bar{n}$. Since the coupling between the system and the environment is weak, the coherence decay exhibits a Markovian nature and the coherence falls steadily with time. When the displacement parameter and the squeezing parameter increases, the coherence decay rate increases. In the high temperature limit, the coherence falls faster as can be seen through the plots in Fig. 6. This is because thermal decoherence also contributes to the coherence degradation in addition to the decay due to the environmental effects.

Fig. 7

The time evolution of quantum coherence of a displaced squeezed thermal state in the low temperature limit $T_\mathrm{s} =1$, is shown above for a strongly coupled system ($\eta = 2.0 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use sub-Ohmic spectral density ($s=1/2$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

Fig. 8

The time evolution of quantum coherence of a displaced squeezed thermal state in the high temperature limit $T_\mathrm{s} =20$, is shown above for a strongly coupled system ($\eta = 2.0 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use sub-Ohmic spectral density ($s=1/2$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

Through the plots Figs. 7 and 8, we study the coherence dynamics in a system strongly coupled ($\eta = 2.0 \; \eta _\mathrm{c}$) to a sub-ohmic bath. The low temperature limit is described through the plots in Fig. 7 and the high temperature limit through Fig. 8. The amount of initial coherence is higher at lower temperature, with the coherence decay being faster for lower values of displacement and squeezing parameter. Here in the shorter time scales, the coherence falls faster and reaches a minimum value. Then it shows an oscillatory nature indicating a non-Markovian behavior for the strongly coupled system. This non-Markovian dynamics is indicative of information backflow in the system. Thus we find Markovian evolution for a weakly coupled system and a non-Markovian evolution for a strongly coupled system.

5 Non-Markovian dynamics of displaced squeezed thermal state in a super-Ohmic environment

The time dynamics of a single mode continuous variable state in contact with a super-Ohmic bath with $s > 1$ is studied in the present work. Towards this end, we consider a spectral density of the form $J(\omega ) =\eta (\omega / \omega _\mathrm{c})^{3} \exp (-\omega /\omega _\mathrm{c})$ in our investigations. The dynamical variation of coherence is studied by varying the displacement operator and the squeezing parameter. The results are displayed in the plots given through Figs. 9, 10, 11 and 12.

Fig. 9

The time evolution of quantum coherence of a displaced squeezed thermal state in the low temperature limit $T_\mathrm{s} =1$, is shown above for a weakly coupled system ($\eta = 0.01 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use super-Ohmic spectral density ($s=3$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

Fig. 10

The time evolution of quantum coherence of a displaced squeezed thermal state in the high temperature limit $T_\mathrm{s} =20$, is shown above for a weakly coupled system ($\eta = 0.01 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use super-Ohmic spectral density ($s=3$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

Fig. 11

The time evolution of quantum coherence of a displaced squeezed thermal state in the low temperature limit $T_\mathrm{s} =1$, is shown above for a strongly coupled system ($\eta = 2.0 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use super-Ohmic spectral density ($s=3$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

Fig. 12

The time evolution of quantum coherence of a displaced squeezed thermal state in the high temperature limit $T_\mathrm{s} =20$, is shown above for a strongly coupled system ($\eta = 2.0 \; \eta _\mathrm{c}$) for various values of the displacement parameter (‘$\alpha$’) and squeezing parameters (‘r’). The different lines correspond to the different values of $\bar{n}$ as follows: $\bar{n} = 0.1$ (blue), $\bar{n} = 1.0$ (red) and $\bar{n} = 10.0$ (black). We use super-Ohmic spectral density ($s=3$) with the cut-off frequency $\omega _\mathrm{c} = 5.0 \; \omega _{0}$ (Color figure online)

When the system is weakly coupled to the environment ($\eta = 0.01 \; \eta _\mathrm{c}$), it exhibits a Markovian decay. Hence we observe a characteristic behaviour where the quantum coherence decreases steadily. The coherence at time $t=0$ is dependent on the mean photon number with quantum coherence being inversely proportional to the mean photon number of the system. The coherence fall decreases with increase in the displacement parameter and the squeezing parameter. Again at higher temperatures, coherence falls faster due to the thermal decoherence effects. In contrast to the Ohmic and the sub-Ohmic case, the system does not exhibit a non-Markovian behavior in the strong coupling limit. Rather we observe a steady decay in the low temperature limit. In the high temperature limit, initially the coherence falls abruptly and then increases slightly and later saturates at a steady value. The final saturation value depends on the displacement and the squeezing parameter.

6 Steady state analysis

An important limit of an open quantum system is the long time limit, which can help us to understand steady state behaviour of the system. Towards this end we need the analytic solution of the integro-differential of u(t) which is given in Ref. [12] and reads as follows:

$$\begin{aligned} u(t) = {\mathcal {Z}} \hbox {e}^{-i \omega _b t}\!+\!\!\!\int _0^\infty \!\!\!\!\!\!\hbox {d}\omega \frac{J(\omega ) \hbox {e}^{-i\omega t}}{\left[ \omega - \omega _0 - \Delta (\omega ) \right] ^2 + \gamma ^2(\omega )}, \quad \end{aligned}$$

(31)

The first term arises due to the contribution of the localized mode in the Fano model. The second term is due to the continuous part of the spectra which causes dissipation. Since the localized mode produces dissipationless dynamics, the system can forever memorize some of its initial state information. Here

$$\begin{aligned} \Delta (\omega ) = {{{\mathcal {P}}}}\int _0^\infty \hbox {d}\omega ^{\prime } \frac{J(\omega ^{\prime })}{\omega -\omega ^{\prime }} \end{aligned}$$

(32)

is a principal value integral and $\gamma (\omega )= \pi J(\omega )$. They are the real and imaginary parts of the self-energy correction given by

$$\begin{aligned} \Sigma (\omega \pm i 0^{+})=\int _0^\infty \hbox {d}\omega ^{\prime } \frac{J(\omega ^{\prime })}{\omega -\omega ^{\prime } \pm i 0^{+}}=\Delta (\omega ) \mp i \gamma (\omega ). \end{aligned}$$

(33)

The conditions for the localized mode frequency is determined by the expression $\omega _{b} - \omega _{0} - \Delta (\omega _{b}) = 0$ and ${{\mathcal {Z}}}=\left[ 1 - \Sigma ^{\prime }(\omega _b) \right] ^{-1}$ is the amplitude of the localized mode. The steady state value of quantum coherence is determined by the steady state value of the Green’s functions given by

$$\begin{aligned} u(t_s)= & {} {{\mathcal {Z}}} \exp (-i \omega _b t_s) \end{aligned}$$

(34)

$$\begin{aligned} v(t_s)= & {} \int _{0}^{\infty } \hbox {d}\omega [{{\mathcal {D}}}_l(\omega ) + {{\mathcal {D}}}_\mathrm{c}(\omega ) ] {{\bar{n}}}(\omega ,T) \end{aligned}$$

(35)

where ${{\mathcal {D}}}_\mathrm{c}(\omega )=J(\omega )/[ \left( \omega - \omega _0 - \Delta (\omega ) \right) ^2 + \gamma ^{2}(\omega ) ]$ and ${{\mathcal {D}}}_l(\omega )=J(\omega ){{\mathcal {Z}}}^2/(\omega -\omega _b)^2$. Using these results we analyze the quantum coherence steady state values of the system in the strong coupling limit. We do not investigate the weak coupling limit since the coherence vanishes in the long time limit for this case.

Fig. 13

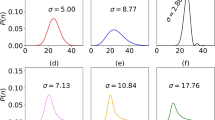
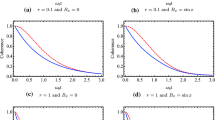
The steady state value of coherence in the long time limit $(t \rightarrow \infty )$ for a strongly coupled system $(\eta = 2.0 \eta _\mathrm{c})$ in contact with a Ohmic bath. Here the low temperature limit $(T_\mathrm{s} = 0.1)$ for mean photon number $\bar{n} = 0.1$ and $\bar{n} = 2.0$ is given through the plots in a, b respectively. The high temperature limit $(T_\mathrm{s} = 20.0)$ for mean photon number $\bar{n} = 0.1$ and $\bar{n} = 2.0$ is given through the plots in c, d respectively. The cut-off frequency used is $\omega = 5.0 \omega _{0}$

Fig. 14

In the long time limit $(t \rightarrow \infty )$ for a strongly coupled system $(\eta = 2.0 \eta _\mathrm{c})$ we investigate the steady state value of coherence in contact with a sub-Ohmic bath in this figure. The low temperature limit $(T_\mathrm{s} = 0.1)$ for mean photon number $\bar{n} = 0.1$ and $\bar{n} = 2.0$ is given through the plots a, b respectively. In plots c, d the high temperature limit $(T_\mathrm{s} = 20.0)$ for mean photon number $\bar{n} = 0.1$ and $\bar{n} = 2.0$ respectively. We use a cut-off frequency of $\omega = 5.0 \omega _{0}$

Ohmic case The steady state of quantum coherence for a Ohmic bath with spectral density $J(\omega ) = \eta \omega \exp (-\omega /\omega _\mathrm{c})$ is shown in Fig. 13, where we show the variation of coherence with the displacement parameter ($\alpha$) and the squeezing parameter (r). The plots Fig. 13a, b show the coherence change for the mean photon numbers of $\bar{n} = 0.1$ and $\bar{n} = 2.0$ in the low temperature limit of the environment. In the long time limit, when both the displacement parameter ($\alpha$) and the squeezing parameter (r) are zero, there is no coherence in the system. But if any one of them is finite, there is a finite amount of coherence. Also we find that the coherence varies faster with the decrease in the displacement parameter ($\alpha$) when compared to the squeezing parameter (r). From a comparison between the plots Fig. 13a, b we find that for low mean photon number $\bar{n} = 0.1$ the coherence decreases with increase in the squeezing parameter whereas for the high mean photon number $\bar{n} = 2.0$ the coherence increases with the squeezing parameter. From the results in Fig. 13c, d we find that the long time coherence exhibits the same qualitative behavior. But quantitatively, the amount of coherence is lower at high temperatures due to the thermal decoherence effects.

sub-Ohmic case The coherence variation with the displacement parameter ($\alpha$) and the squeezing parameter (r) in the long time limit is described for the sub-Ohmic bath with spectral density $J(\omega ) = \eta \sqrt{\omega \omega _\mathrm{c}} \exp (-\omega /\omega _\mathrm{c})$ through the plots in Fig. 14. The low temperature limit of the coherence variation is analyzed through the plots in Fig. 14a, b where we consider the mean photon number to be $\bar{n} = 0.1$ and $\bar{n} = 2.0$ respectively. Here we find that when both the displacement and squeezing parameters are zero the coherence vanishes since in this limit the state is an incoherent state. Comparatively the coherence falls faster with the displacement parameter when compared with the squeezing parameter. The high temperature regime is studied through the results in plots Fig. 14c, d for $\bar{n} = 0.1$ and $\bar{n} = 2.0$ respectively. The long time coherence in the high temperature limit exhibits the same qualitative behavior as the one in the low temperature limit.

super-Ohmic case The super-Ohmic case with spectral density $J(\omega ) =\eta (\omega / \omega _\mathrm{c})^{3} \exp (-\omega /\omega _\mathrm{c})$ is studied for the displacement parameter ($\alpha$) and squeezing parameter (r) in the long time limit and the results are shown through the plots in Fig. 15. For the mean photon numbers $\bar{n} = 0.1$ and $\bar{n} = 2.0$ the low temperature plots are shown through the figures in Fig. 15c, d respectively. As expected the coherence is zero when the state is incoherent, i.e., when both the displacement and the squeezing parameters are zero. On increasing the parameters the coherence increases and the rate of increase is higher for the displacement parameter than the squeezing parameter. The results in the low temperature limit maps similarly to the high temperature limit as well. This can be observed from the study of the results in the plots Fig. 15c, d respectively. The long time coherence in the high temperature limit exhibits the same qualitative behavior as the one in the low temperature limit. But quantitatively the coherence is lower for high temperature values than that of low temperature values. This is because the system exhibits a thermal decoherence at higher values of temperature.

Fig. 15

For a strongly coupled system, the steady state coherence in contact with a super-Ohmic bath is given through the figure. The low temperature limit $(T_\mathrm{s} = 0.1)$ for mean photon number $\bar{n} = 0.1$ and $\bar{n} = 2.0$ is given through the plots a, b respectively. The high temperature limit $(T_\mathrm{s} = 20.0)$ of the system for the mean photon number $\bar{n} = 0.1$ and $\bar{n} = 2.0$ is given in c, d repectively. Here the cut-off frequency used is s$\omega = 5.0 \omega _{0}$

7 Conclusion

The quantum coherence dynamics of a single mode squeezed displaced thermal state is analyzed in the present work. We adopt an open quantum system approach where we consider the environment to be a collection of infinite number of bosonic modes with varying frequencies. The coherence dynamics is studied in the finite temperature limit and considering different values for the system-bath coupling strength. The coherence is measured using the relative entropy measure where the distance to the closest thermal state is used. The number operator of the continuous variable state and the determinant of the covariance matrix completely characterizes the quantum coherence. The time evolved covariance matrix elements are obtained by solving the quantum Langevin equation for the bosonic mode operators. The two basic nonequilibrium Green’s functions namely u(t) and v(t) are determined by the time evolution of the field operators. The entire analysis is carried out under three different environmental spectral densities viz Ohmic, sub-Ohmic and super-Ohmic densities. In the weak interaction limit, when the bath and the system are weakly coupled with each other, the quantum coherence decreases monotonically with time. Meanwhile in the strong interaction limit, we observe that the coherence initially decreases but then it increases mildly and shows an oscillatory behavior. This oscillatory nature, signals the presence of non-Markovian behavior and is a characteristic feature of a strongly coupled system. From our analysis we find that the system with lower mean photon number has higher amount of initial coherence which falls faster. Apart from investigating the dynamics in a finite time interval, we also look at the coherence evolution in the long time ($t \rightarrow \infty$) limit. In this steady state limit, we show the dynamical variation of quantum coherence of the system when it is strongly coupled to the environment. We find that the qualitative behavior of the quantum coherence evolution in the steady state limit is same both in the low and high temperature limits. But quantitatively it is different because of thermal decoherence. Our investigations are important from the resource theory perspective in quantum information. It will help us to understand the dynamics, long time behavior and susceptibility of quantum coherence of different types of Gaussian states. These features are dependent on the different system-environment parameters and for a strong system-reservoir coupling we have calculated the steady state value of coherence that depends on the initial state. In the present work we have been able to characterize a mixed Gaussian state completely. A extension of the study of coherence dynamics to non-Gaussian will be the focus of our future works. Such investigations will require methods beyond the covariance matrix approach which works only for Gaussian systems.