Quantum state transfer by electromagnetic fields initialized in vacuum states in a system comprised of two consecutive cavities connected by an optical fiber in the presence of an external classical field

Abstract

The Hamiltonian of a system of two successive Jaynes-Cummings cells (JCCs) indirectly coupled through an optical fiber mode under the influence of an external classical field (ECF) is simplified. In the framework of unitary transformations of the atomic and bosonic delocalized operators, the simplification is carried out. Three dispersive regimes, namely, large optical fiber coupling strength (OFCS), large detuning, and comparable OFCS and detuning are considered. The analytical solutions of Schrödinger equation for the different Hamiltonians when the fields are initially in the vacuum states and initially the first and the second atoms are in the excited and the ground states, respectively, are presented. The exploitation of the atomic population inversion function (APIF) of a single atom to the track of the quantum state transfer (QST) between the distant atoms is considered. The temporal evolution of the APIF is investigated. Effects of the external classical fields couplings (ECFCs), and the OFCS on the APIF are analyzed. Analysis of the resulted features based on the difference between the ECFC and the localized and delocalized atomic frequencies is presented. The collapses-revivals phenomenon (CRP) is clearer in absence of the ECF. The behavior of both the APIF and the CRP follow those for the overlap of evanescent fields model while the rates of the QST in the two schemes are un equiv. The ECFs reformulate the initial quantum states and may augment the localized detuning. The ECFs either accelerate the transfer of the quantum state or delecerte it.

1 Introduction

Introducing the Jaynes–Cummings model (JCM) [1] was a key factor in understanding and realizing the interaction of matter and quantized electromagnetic field. JCM was designed for the study of the interaction of a two-level atom with a single mode quantized field. The JCM has received an enormous number of theoretical [1,2,3] and experimental [4, 5] studies. Such a studiousness attributes to its (i.e.,  JCM) mathematical solubility and its richness in displaying many phenomena, such as Rabi oscillation [6,7,8], collapses-revivals phenomenon [2, 3, 9,10,11,12,13,14,15,16,17,18,19,20], the capability of producing non-classical fields [15, 17, 18, 20,21,22,23,24,25].

In the main time many researchers have turned their attentions and devoted the efforts towards the extensions and the generalizations of the JCM. As the JCM is considered as a standard model in addition to the alternative models, introduced by Dick [26] and Tavis and Cummings [27] in order to study the dynamics of N identical two-level atoms resonantly interacting with a single mode of the electromagnetic field. For instance, it has been extended and generalized to include multi-photon, multi-mode processes [28,29,30,31,32,33,34,35,36,37,38,39,40], multi-level systems [34,35,36,37,38,39,40,41,42,43,44,45,46], and the intensity-dependent JCM [19, 34,35,36,37,38,39,40, 44, 47] from theoretical point of view.

It is well known that the collapses-revivals phenomenon is a quite generic phenomenon for the quantum systems. Also, it represents one of the most important phenomena reported for the JCM since it manifests the granular nature of the initial state of the field and a good evidence of discreteness of photons [2, 48]. Experimental realizations of JCM were observed in optical and radio frequency domains [49, 50]. Theoretically, the CRP has been extensively studied in the framework of various aspects of quantum optics [38, 51,52,53,54,55,56,57,58]. The collapses-revivals behaviors in the investigation of the APIF represents the reversibility of the quantum states [2, 3, 59]. It was shown that, within the JCM, the collapses and revivals periods of the APIF either result in purely periodic behavior [60, 61] or display an irregular character [59] according to the form of the interaction.

In some physical models, the situation is confined to trapping the atoms in a cavity. Thus, the studies in the framework of cavity quantum electrodynamics (CQED) have been devoted especially to the efforts of addressing the problems of quantum networks and quantum states transfer (QST) in order to enhancing the quantum information distribution. The quantum networks is a process by which the transportation of quantum information between distant quantum systems can be accomplished. The QST is a measurement for the exchanged energy among the atomic systems in the form of photons across large distances. The QST plays a central role in the quantum information field due to its potential applications in many topics of the quantum mechanics, quantum cryptography, quantum computer, quantum purification, etc [62,63,64,65,66,67,68,69,70,71,72,73,74].

Recently, the researchers have studied the problem of remote cavities (completely isolated), across the network; they may be interacting and communicated [75,76,77,78,79,80,81,82,83,84,85,86]. In fact, the remote cavities are considered as generalizations of the JCM. Coupled-cavity arrays schemes "as generalization to the remote cavities" have attracted and received much attention. Such attention is due to the easy handling of the individual sites and the presence of relatively long-lived atomic states suitable for the purpose of encoding a quantum information. Controlling the dynamics of the system in a better way becomes easier with such systems due to their providing of a number of degrees of freedom where photons can be hopping from cavity to another. These cavities may be coupled through the overlap of evanescent cavity fields [87,88,89,90] and through an optical fiber [94, 95]. Connecting the distant cavities through an optical fiber is considered a fundamental setup for quantum networks [94, 95].

The purpose of the present article is to study the features and the phenomena of the APIF due to the influences of the ECF and the OFCS in an extension to Ref [96] and to assure that the entanglement dynamics in this model differs significantly from that for the [97] in addition to reviewing the difference between the rates of the QST.

The structure of the article is as follows: In Sect. 2, we introduce the Hamiltonian of the considered system and proceed towards its interaction picture to obtain the effective Hamiltonian for three approximate dispersive regime. In Sect. 3, we solve the Schrödinger equation for all introduced Hamiltonians giving analytical expressions for the final wavefunction. In Sect. 4, we employ the analytical results formulated in Sect. 3 to investigate the properties of the APIF. We devote Sect. 5 to discuss the influences of the relevant parameters on the evolution of the APIF. Finally, in Sect. 6, we present our conclusion depending on the analytic and the numerical results.

Fig. 1

Scheme of two distant standard JCM indirectly connected by an optical fiber. The atoms are driven by on resonance an ECF. The ket $|e\rangle _{j}$ $\left( |g\rangle _{j}\right)$ represents the excited(lower) state of the atom

2 The Model

The considered model is a two coupled JCCs indirectly connected via an optical fiber. Each cavity contains a single two-level atom interact separately with a quantized electromagnetic field and driven by an ECF (see Fig. 1). The total Hamiltonian of the considered system can be cast as (we adopt $\hbar = 1$):

$$\begin{aligned} {\hat{H}}={\hat{H}}_{0}+{\hat{H}}_{int}. \end{aligned}$$

(1)

Generally, the Hamiltonian ${\hat{H}}$ can be written as follows:-

$$\begin{aligned} {\hat{H}}= & {} \overbrace{\sum \limits _{j=1}^{2}\left[ \omega _{j}{\hat{a}}^{+}_{j}{\hat{a}}_{j} +\frac{\Omega _{j}}{2}\sigma ^{z}_{j}+g_{j}({\hat{\sigma }}^{-}_{j}+{\hat{\sigma }}^{+}_{j})\right] +\omega _{f}{\hat{b}}^{+}{\hat{b}}}^{{\hat{H}}_{0}} \nonumber \\&+\overbrace{\nu \left[ b({\hat{a}}^{+}_{1}+{\hat{a}}^{+}_{2})+H.C.\right] +i\sum \limits _{j=1}^{2}\lambda _{j} ({\hat{a}}_{j}+{\hat{a}}^{+}_{j})({\hat{\sigma }}^{+}_{j}-{\hat{\sigma }}^{-}_{j})}^{{\hat{H}}_{int}}, \end{aligned}$$

(2)

The Hamiltonian ${\hat{H}}$, is a generalization of extensively studied earlier pictures [86, 98,99,100,101,102,103]. The parameters $\omega _{j}$, $\omega _{f}$, and $\Omega _{j}$ represent the frequencies of the quantized electromagnetic fields, the frequency of the fiber mode field and the frequencies of the atomic energies differences, respectively. Moreover, the parameters $\lambda _{j}$, $g_{j}$, and $\nu$ stand for the atom-field coupling in the cavity, the external classical field couplings (ECFCs), and the strength of the OFCS, respectively. The operators ${\hat{a}}^{+}_{j}$, and ${\hat{a}}_{j}$ are boson operators of the fields, they are controlled by the commutation relations $[{\hat{a}}_{j},{\hat{a}}^{+}_{k}]={\hat{I}}\delta _{jk}$: ${\hat{I}}$ denotes the unity operator while $\delta$ refers to the Kronecker delta. The boson operators ${\hat{b}}^{+}$, and ${\hat{b}}$ describe the fiber operators and behave as ${\hat{a}}^{+}_{j}$, and ${\hat{a}}_{j}$. The operators ${\hat{\sigma }}^{-}_{j}$, ${\hat{\sigma }}^{+}_{j}$, and $\sigma ^{z}_{j}$ are Pauli operators defined by $|g\rangle _{j}\langle e|$, $|e\rangle _{j}\langle g|$, and $|e\rangle _{j}\langle e|$-$|g\rangle _{j}\langle g|$, respectively.

2.1 Canonical transformations

The only motivation of the unitary canonical transformations is to obtain the wavefunction of the quantum systems. Treatment of the present quantum system is not an easy task because of the presence of the rotating and counter-rotating terms, driving terms, and cavity-cavity coupling term. The elimination of the ECFs couplings and optical fiber mode coupling strengths and the counter-rotating parts is an essential requirement for the simplification of the Hamiltonian of the considered model. The elimination will be carried out through two common transformations [86, 98,99,100,101,102,103]. We shall review these canonical transformations in what follows:

2.1.1 The first transformation

The driven parts can be removed via the usage of the following canonical transformation

$$\begin{aligned} \left( \begin{array}{c} \sigma ^{z}_{j}\\ \sigma ^{+}_{j}\\ \sigma ^{-}_{j} \end{array}\right)= & {} \left( \begin{array}{ccc} \cos (2\eta _{j}) &{} -\sin (2\eta _{j})&{} -\sin (2\eta _{j})\\ \frac{1}{2}\sin (2\eta _{j}) &{} \cos ^{2}(\eta _{j})&{} -\sin ^{2}(\eta _{j})\\ \frac{1}{2}\sin (2\eta _{j})&{} -\sin ^{2}(\eta _{j}) &{} \cos ^{2}(\eta _{j}) \end{array} \right) \left( \begin{array}{c} S^{z}_{j}\\ S^{+}_{j}\\ S^{-}_{j} \end{array}\right) . \end{aligned}$$

(3)

Which insures that ${\hat{\sigma }}^{+}_{j}-{\hat{\sigma }}^{-}_{j}=S^{+}_{j}-S^{-}_{j}.$ The parameters $\eta _{j}$ are chosen to be: $\eta _{j}=\frac{1}{2} \arccos (\frac{\Omega _{j}}{\sqrt{\Omega _{j}^{2}+4g_{j}^{2}}})=\frac{1}{2} \arccos (\frac{\Omega _{j}}{\varphi _{j}})$.

It is noted that the atomic frequency $\Omega _{j}$ is augmented to $\varphi _{j}={\sqrt{\Omega _{j}^{2}+4g_{j}^{2}}}$ which includes the classical field couplings $g_{j}$. Also, when the rotating wave approximation is considered, the Hamiltonian of Eq.(1) can be written as follows:-

$$\begin{aligned} {\hat{H}}= & {} \sum \limits _{j=1}^{2}[\omega _{j}{\hat{a}}^{+}_{j}{\hat{a}}_{j}+\frac{\varphi _{j}}{2}S^{z}_{j}+i\lambda _{j} ({\hat{a}}_{j}{\hat{S}}^{+}_{j}-{\hat{a}}^{+}_{j}{\hat{S}}^{-}_{j})]+\omega _{f}{\hat{b}}^{+}{\hat{b}} +\nu (b({\hat{a}}^{+}_{1}+{\hat{a}}^{+}_{2})+{\hat{b}}^{+}({\hat{a}}_{1}+{\hat{a}}_{2})).\nonumber \\ \end{aligned}$$

(4)

The atomic new operators ${\hat{S}}^{\pm }_{j}=|\pm \rangle _{j}\langle \mp |_{j}$, and ${\hat{S}}^{z}_{j}=|+\rangle _{j}\langle +|_{j} - |-\rangle _{j}\langle -|_{j}$, where, the relations between the localized and localized atomic eigenstates are governed by

$$\begin{aligned} |+\rangle _{j}= & {} \cos \zeta _{j}|e\rangle _{j}+\sin \zeta _{j}|g\rangle _{j},\nonumber \\ |-\rangle _{j}= & {} \cos \zeta _{j}|g\rangle _{j}-\sin \zeta _{j}|e\rangle _{j}. \end{aligned}$$

(5)

2.1.2 The second transformation

The elimination of the converter part is executed via the exploitation of the following unitary canonical transformations ${\hat{b}}=\frac{{\hat{C}}_{1}-{\hat{C}}_{2}}{\sqrt{2}}, and \;\; {\hat{a}}_{j}=\frac{1}{2}({\hat{C}}_{1}+{\hat{C}}_{2}-(-)^{j}\sqrt{2}{\hat{C}}_{0}).$ Then, Eq. (4) will be on the form

$$\begin{aligned} {\hat{H}}=\sum \limits _{\ell =0}^{2}\tilde{ \omega }_{\ell }{\hat{C}}_{\ell }^{+}{\hat{C}}_{\ell }+\sum \limits _{j=1}^{2}\left[ \frac{\varphi _{j}}{2}{\hat{S}}^{z}_{j}\right] +i\sum \limits _{j=1}^{2} \frac{\lambda _{j}}{2}[({\hat{C}}_{1}+{\hat{C}}_{2}-(-)^{j}\sqrt{2}{\hat{C}}_{0}){\hat{S}}^{+}_{j}-H.C.], \end{aligned}$$

(6)

For comprehensibility, we set $\omega _{j}=\omega _{0}=\omega _{f}$ ($j=1, 2$) which automatically leads to ${\tilde{\omega }}_{\ell }=\omega _{0}-(-)^{\ell }\sqrt{2} \nu (1-\delta _{0\ell }$).

2.2 Interaction picture

The interaction picture of the Hamiltonian depicted in Eq.(6) is controlled by ${\hat{H}}_{I}=e^{it{\hat{H}}_{0}} {\hat{H}}_{int}\, e^{-it{\hat{H}}_{0}}$, whereas

$$\begin{aligned} {\hat{H}}=\overbrace{\sum \limits _{\ell =0}^{2}\tilde{ \omega }_{\ell }{\hat{C}}_{\ell }^{+}{\hat{C}}_{\ell }+\sum \limits _{j=1}^{2}\left[ \frac{\varphi _{j}}{2}{\hat{S}}^{z}_{j}\right] }^{{\hat{H}}_{0}}+\overbrace{i\sum \limits _{j=1}^{2} \frac{\lambda _{j}}{2}[({\hat{C}}_{1}+{\hat{C}}_{2}-(-)^{j}\sqrt{2}{\hat{C}}_{0}){\hat{S}}^{+}_{j}-H.C.]}^{{\hat{H}}_{int}}. \end{aligned}$$

(7)

By using the Baker–Campbell–Hausdorff formula [104], we have

$$\begin{aligned} {\hat{H}}_{I}={\hat{H}}_{int}+(it)[{\hat{H}}_{0}, {\hat{H}}_{int}] +\frac{(it)^{2}}{2!}[{\hat{H}}_{0},[{\hat{H}}_{0}, {\hat{H}}_{int}]]+\frac{(it)^{3}}{3!}[{\hat{H}}_{0},[{\hat{H}}_{0},[{\hat{H}}_{0}, {\hat{H}}_{int}]]]+....., \end{aligned}$$

(8)

Due to some commutation relations, one can cast the interaction picture of the Hamiltonian ${\hat{H}}_{I}$ as follows:-

$$\begin{aligned} {\hat{H}}_{I}= & {} \sum \limits _{k=1}^{2} \frac{i\lambda _{k}}{2}[ \left( \sum \limits _{j=1}^{2} {\hat{C}}_{j} e^{-it({\tilde{\omega }}_{j}-\varphi _{k})}+\sqrt{2}{\hat{C}}_{0} e^{-it({\tilde{\omega }}_{0}-\varphi _{k})}\right) {\hat{S}}^{+}_{k}-H.C.] . \end{aligned}$$

(9)

2.3 The effective Hamiltonian

In this section we apply the method of Ref [105] to the current Hamiltonian in order to get the effective Hamiltonian in different dispersive regimes approximations. The effective Hamiltonian ${\hat{H}}_{eff}$ can be written through the following relation [105], ${\hat{H}}_{eff}=\overline{{\hat{H}}_{I}(t)}+\frac{1}{2}\left( \overline{[{\hat{H}}_{I}(t),\hat{ V}_{1}(t)]}-[\overline{{\hat{H}}_{I}(t)}, \overline{{\hat{V}}_{1}(t)}]\right) ,$ the skew-Hermitian operator ${\hat{V}}_{1}(t)$ in its simplest form, is written as follows:-

$$\begin{aligned} {\hat{V}}_{1}(t)= & {} \sum \limits _{k =1}^{2} \frac{i\lambda _{k}}{2}[(\sum \limits _{j=1}^{2}\frac{{\hat{C}}_{j}}{{\tilde{\omega }}_{j}-\varphi _{k}} e^{-it({\tilde{\omega }}_{j}-\varphi _{k})} +\sqrt{2}\frac{{\hat{C}}_{0}}{\omega _{0}-\varphi _{k}} e^{-it(\omega _{0}-\varphi _{k})}){\hat{S}}^{+}_{k}+H.C.] \nonumber \\ \end{aligned}$$

(10)

We are proceed to obtain the effective Hamiltonian in the language of the aforementioned limits i.e.,  $(\mathbf{i })$ large optical fiber mode coupling strength $(\mathbf{ii} )$ large detuning, and $(\mathbf{iii} )$ comparable optical fiber mode coupling strength and detuning. To make calculations more clearer and easier analytical computations, we again assume resonance of the atomic subsystems i.e.,  $\Omega _{j}=\Omega$ besides symmetric couplings case $i.e., \lambda _{j}=\lambda ,$ and $g_{j}=g$ $\Rightarrow$ $\varphi _{j}=\varphi$. Consequently, the detuning between the atomic modes ${\hat{S}}_{j}$, and ${\hat{C}}_{j}$ are $\Delta _{\iota }=\varphi -\omega _{\iota }$, $\iota =0,1,2$.

2.3.1 For large cavity-fiber coupling strength limit

This approximation is applicable when the condition $\sqrt{2}\nu>>\Delta _{0},\lambda$ is satisfied. Moreover, we assume that $\Delta _{0}$ ,  $\Delta _{1}$, and $\Delta _{2}$ > $\lambda$. These conditions ensure vanishing of the time average of both ${\hat{V}}_{1}(t)$ and ${\hat{H}}_{I}(t)$. The effective Hamiltonian is thus given by the formula $(\Im _{0}=\frac{\lambda ^{2}}{4} [ \sum \limits _{j=1}^{2}\frac{1}{\Delta _{j}}-\frac{2}{\Delta _{0}}])$

$$\begin{aligned} {\hat{H}}^{LC}_{eff}= & {} {\hat{H}}_{0}+\frac{\lambda ^{2}}{4} \left[ \sum \limits _{j=1}^{2}\frac{\hat{C_{j}}{\hat{C}}^{+}_{j}}{\Delta _{j}} +\frac{2{\hat{C}}_{0}{\hat{C}}^{+}_{0}}{\Delta _{0}}\right] \sum \limits _{j=1}^{2}|+\rangle _{j}\langle +|\nonumber \\&-\frac{\lambda ^{2}}{4}\left[ \sum \limits _{j=1}^{2}\frac{{\hat{C}}^{+}_{j}\hat{C_{j}}}{\Delta _{j}}+\frac{2 {\hat{C}}^{+}_{0} {\hat{C}}_{0}}{\Delta _{0}}\right] \sum \limits _{j=1}^{2}|-\rangle _{j}\langle -| +\Im _{0}\sum \limits _{<ij>}{\hat{S}}^{-}_{i}{\hat{S}}^{+}_{j}. \end{aligned}$$

(11)

2.3.2 For large detuning limit

In this limit, the atom is highly detuned from the photonic modes: $\Delta _{0}>> \sqrt{2}\nu , \lambda$. Also, both $\overline{{\hat{H}}_{I}(t)}$, and $\overline{{\hat{V}}_{1}(t)}$ vanish. The effective Hamiltonian takes the following form:

$$\begin{aligned} {\hat{H}}^{LD}_{eff}= & {} \frac{\lambda ^{2}}{8}\bigg [\!\left( \sqrt{2}{\hat{C}}_{2}{\hat{C}}^{+}_{0}\left( \frac{1}{\Delta _{0}}+\frac{1}{\Delta _{2}}\right) +H.C.\right) \nonumber \\&+\Bigl (\sqrt{2}{\hat{C}}_{0}{\hat{C}}^{+}_{1}\left( \frac{1}{\Delta _{0}}+\frac{1}{\Delta _{1}}\right) +H.C.\Bigr )\!\bigg ]\left( {\hat{S}}^{z}_{1}-{\hat{S}}^{z}_{2}\right) \nonumber \\&+\frac{\lambda ^{2}}{8}\bigg [\! \left( \hat{C_{1}}{\hat{C}}^{+}_{2} \left( \frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}\right) +H.C.\right) \!\bigg ]\left( {\hat{S}}^{z}_{1}+{\hat{S}}^{z}_{2}\right) + {\hat{H}}^{LC}_{eff}. \end{aligned}$$

(12)

2.3.3 For comparable OFCS and detuning limit

This approximation requires that the frequency of one of the two atoms is nearby equal to that for the corresponding delocalized photonic modes. Such requirement can be written mathematically as $\Delta _{1}\approx 0$. The effective Hamiltonian is reached and written as:

$$\begin{aligned} {\hat{H}}^{CSD}_{eff}= & {} {\hat{H}}_{0} +\frac{i\lambda }{2}\left[ {\hat{C}}_{1} ({\hat{S}}^{+}_{1}+{\hat{S}}^{+}_{2})-H.C.\right] + \frac{\lambda ^{2}}{4} \left[ \frac{{\hat{C}}_{2}{\hat{C}}^{+}_{2}}{\Delta _{2}}+\frac{2{\hat{C}}_{0}{\hat{C}}^{+}_{0}}{\Delta _{0}}\right] \sum \limits _{j=1}^{2}|+\rangle _{j}\langle +| \nonumber \\&-\frac{\lambda ^{2}}{4} \left[ \frac{{\hat{C}}^{+}_{2} {\hat{C}}_{2}}{\Delta _{2}}+\frac{2 {\hat{C}}^{+}_{0}\hat{ C}_{0}}{\Delta _{0}}\right] \sum \limits _{j=1}^{2}|-\rangle _{j}\langle -|+\frac{\lambda ^{2}}{4} \left[ \frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}}\right] \sum \limits _{<i,j>}{\hat{S}}^{-}_{i}{\hat{S}}^{+}_{j}. \end{aligned}$$

(13)

Now, we proceed to calculate the time-dependent wavefunction of the mentioned different Hamiltonians.

3 The wavefunction

We consider the two modes and the fiber mode to be initially prepared in the vacuum states, and the first atom is in its excited state while the second atom is in ground state. Eventually, according to the delocalized modes, the initial wavefunction becomes of the form

$$\begin{aligned} |\Psi _{AF}(0)\rangle = A_{1}(0)|++000\rangle +A_{2}(0)|+-000\rangle +A_{3}(0)|-+000\rangle +A_{4}(0)|--000\rangle . \end{aligned}$$

(14)

Based on the Hamiltonian (6) and the considered wavefunction (14) the time dependent wavefunction of the considered system can be formed as follows [$A_{j}(0)=\sin \eta \cos \eta \,\delta _{1j}+\cos ^{2} \eta \,\delta _{2j}-\sin ^{2} \eta \,\delta _{3j}-\sin \eta \cos \eta \,\delta _{4j}$]:

$$\begin{aligned} |\Psi _{AF}(t)\rangle= & {} \sum \limits _{j=1}^{19} A_{j}(t)|\psi _{j}\rangle . \end{aligned}$$

(15)

The wavefunction is assumed initially normalized and according to Schrödinger’s equation, it stays normalized as it evolves in time i.e.,  $\sum \limits _{j=1}^{19} |A_{j}(t)|^{2}=1$. Within the delocalized bosonic modes, it is formed as follows:

(16)

with

(17)

While the atomic density matrix for the two atoms, in the basis of $| + +>$, $| + ->$, $| - +>$, and $| - ->$, is

(18)

Then, the atomic density matrix for -atom, in the basis of $|+>_{1}$, and $|->_{1}$, is

(19)

Then, the atomic density matrix for -atom, in the basis of $|+>_{2}$, and $|->_{2}$, is

(20)

The three roots of the cubic equation $\tau ^{3}+X_{1}\tau ^{2}+X_{2}\tau +X_{3}=0$, can be cast as follows:-

$$\begin{aligned} \tau _{j}= & {} -\frac{X_{1}}{3}+\frac{2}{3}\left( \sqrt{X_{1}^{2}-3X_{2}}\right) \cos {(\theta _{j})},\qquad j=\mathbf{1,2, 3 }\nonumber \\ \theta _{j}= & {} \left( \frac{1}{3}\cos ^{-1}\left[ \frac{9X_{1}X_{2}-2X_{1}^{3}-27X_{3}}{2(X_{1}^{2}-3X_{2})^\frac{3}{2}}\right] +(j-1)\frac{2\pi }{3}\right) . \end{aligned}$$

(21)

3.1 For the full Hamiltonian

Because of the rather complicated calculations of the solution of the Schrödinger equations of the considered system, we only content with displaying analytical expressions for the coefficients of the wavefunction of the full Hamiltonian depicted in Eq.(6).

$$\begin{aligned}&\left( \begin{array}{c} A_{1}(t) \\ A_{2}(t) \\ A_{3}(t) \\ A_{4}(t) \\ A_{11}(t) \\ A_{12}(t) \\ A_{13}(t) \end{array}\right) =\left( \begin{array}{c} e^{-it\varphi }\sum \limits _{j=1}^{10} K_{j} e^{itn_{j}}\\ \frac{1}{2} \left( e^{it\frac{\Delta _{0}}{2}} \left[ c_{0} \cos \left( t\sqrt{\left( \frac{\Delta _{0}}{2}\right) ^{2}+\lambda ^{2}}\right) +d_{0} \sin \left( t\sqrt{\left( \frac{\Delta _{0}}{2}\right) ^{2}+\lambda ^{2}}\right) \right] +\sum \limits _{j=1}^{3}M^{[3]}_{j} e^{it\tau ^{[3]}_{j}}\right) \\ \frac{-1}{2} \left( e^{it\frac{\Delta _{0}}{2}} \left[ c_{0} \cos \left( t\sqrt{\left( \frac{\Delta _{0}}{2}\right) ^{2}+\lambda ^{2}}\right) +d_{0} \sin \left( t\sqrt{\left( \frac{\Delta _{0}}{2}\right) ^{2}+\lambda ^{2}}\right) \right] +\sum \limits _{j=1}^{3}M^{[3]}_{j} e^{it\tau ^{[3]}_{j}}\right) \\ A_{4}(0) e^{-it\varphi }\\ \sum \limits _{j=1}^{3} M^{[1]}_{j} e^{it(\tau ^{[1]}_{j}+\Delta _{1})}\\ \sum \limits _{j=1}^{3} M^{[2]}_{j} e^{it(\tau ^{[2]}_{j}+\Delta _{2})}\\ e^{it\frac{\Delta _{0}}{2}} \left( \kappa _{0} \cos \left( t\sqrt{\left( \frac{\Delta _{0}}{2}\right) ^{2}+\lambda ^{2}}\right) +\kappa _{1} \sin \left( t\sqrt{\left( \frac{\Delta _{0}}{2}\right) ^{2}+\lambda ^{2}}\right) \right) \end{array}\right) ,\nonumber \\ \end{aligned}$$

(22)

with $[\kappa _{0}, \kappa _{1}, c_{0},\,\, d_{0}]\!=\![0,\, \frac{-\frac{\lambda }{2} (A_{2}(0)-A_{3}(0))}{\sqrt{\left( \frac{\Delta _{0}}{2}\right) ^{2}+\lambda ^{2}}}, A_{2}(0)-A_{3}(0), \frac{-i\frac{\Delta _{0}}{2} (A_{2}(0)-A_{3}(0))}{\sqrt{\left( \frac{\Delta _{0}}{2}\right) ^{2}+\lambda ^{2}}}].$ Moreover, the $X_{1}$, $X_{2}$, and $X_{3}$ for the coefficients $A_{j}(t)$ ( $j=2, 3, 11, 12$) are as follows:-

Furthermore, the coefficients $M^{[j]}_{1}$, $M^{[j]}_{2}$, and $M^{[j]}_{3}$, in the language of the matrices, can be read as follows:-

Fig. 2

The time evolution of the $1^{st}$-atom, $W_{1}(t)$, for the Hamiltonian Eq.(1) subject to the state Eq.(14) while the system parameters values are $\omega _{0}=10\lambda$, $\eta =0$ and in (a) $\upsilon _{0}=0\lambda$, (b) $\upsilon _{0}=20\lambda$, and (c) $\upsilon _{0}=25\lambda$, with the blue curve $\vartheta _{0}=5$, the green curve $\vartheta _{0}=10$, and the red curve $\vartheta _{0}=15$ where in (1) $\Delta _{0}=\upsilon _{0}$, and $\nu =\frac{\vartheta _{0}}{\sqrt{2}}$, and in (2) $\nu =\frac{\upsilon _{0}}{\sqrt{2}}$, and $\Delta _{0}=\vartheta _{0}$

$$\begin{aligned} \left( \begin{array}{c}M^{[j]}_{1} \\ M^{[j]}_{2}\\ M^{[j]}_{3} \end{array}\right) = \left( \begin{array}{ccc} 1 &{} 1 &{} 1\\ \mathrm {\tau ^{[j]}_{1}}\, \mathrm {i} &{} \mathrm {\tau ^{[j]}_{2}}\, \mathrm {i} &{} \mathrm {\tau ^{[j]}_{3}}\, \mathrm {i}\\ - {\mathrm {\tau ^{[j]}_{1}}} &{} - {\mathrm {\tau ^{[j]}_{2}}} &{} - {\mathrm {\tau ^{[j]}_{3}}}\end{array}\right) ^{-1} \left( \begin{array}{c} \Re _{0} \\ \Re _{1}\\ \Re _{2} \end{array}\right) . \end{aligned}$$

(24)

Also, the parameters $\Re _{0}$, $\Re _{1}$, and $\Re _{2}$, for different j can be arranged as follows:-

More, the parameters $n_{j}$ are the eigenvalues of the degree algebraic equation which is formed as follows:-

$$\begin{aligned} \sum \limits _{\iota =0}^{10} n^{10-\iota } X_{\iota }=0. \end{aligned}$$

(26)

This algebraic equation is the characteristic of the ODE of ${\tilde{B}}_{1}(t)$ which is formulated as follows:-

$$\begin{aligned}&\left[ \aleph _{11} (\frac{d}{dt}-2i\Delta _{1})\aleph _{0} \left( \frac{d}{dt}\right) -\aleph _{1} (\frac{d}{dt}-2i\Delta _{1})\aleph _{00} \left( \frac{d}{dt}\right) \right] {\tilde{B}}_{1}(t)=0. \end{aligned}$$

(27)

The differentiable operators $\aleph _{00}$, and $\aleph _{11}$ are not shown here. The parameters $K_{j}$ can be determined in an easily manner was previously used in [106]. The analytical expressions of the remainder coefficients can easily be derived. In what follows we consider the cases of the different regimes.

3.2 For large OFCS and large detuning

For the Hamiltonians in Eqs.(11, 12), the nonzero coefficients of the final wavefunction are written as follows:-

$$\begin{aligned} \left( \begin{array}{c} A_{1}(t) \\ A_{2}(t)\\ A_{3}(t)\\ A_{4}(t) \end{array}\right) =\left( \begin{array}{c} A_{1}(0) \exp \left( -it(\varphi +\frac{\lambda ^{2}}{2} (\frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}+\frac{2}{\Delta _{0}}))\right) \\ e^{-it\frac{\lambda ^{2}}{4}\left( \frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}+\frac{2}{\Delta _{0}}\right) } \left[ A_{2}(0)\cos \left( \frac{t\lambda ^{2}}{4}\left( \frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}}\right) \right) -iA_{3}(0) \sin \left( \frac{t\lambda ^{2}}{4}\left( \frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}}\right) \right) \right] \\ e^{-it\frac{\lambda ^{2}}{4}\left( \frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}+\frac{2}{\Delta _{0}}\right) } \left[ A_{3}(0)\cos \left( \frac{t\lambda ^{2}}{4}\left( \frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}}\right) \right) -iA_{2}(0) \sin \left( \frac{t\lambda ^{2}}{4}\left( \frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}}\right) \right) \right] \\ A_{4}(0) \exp \left( it\varphi \right) \end{array}\right) .\nonumber \\ \end{aligned}$$

(28)

3.3 For comparable OFCS and detuning

For the Hamiltonian in Eq.(13), the nonzero coefficients of the final wavefunction can be written as follows:-

$$\begin{aligned} \left( \begin{array}{c} A_{1}(t)\\ A_{2}(t) \\ A_{3}(t)\\ A_{5}(t)\\ A_{8}(t)\\ A_{11}(t)\\ A_{17}(t)\\ \end{array}\right) =\left( \begin{array}{c} \sum \limits _{j=1}^{3} K_{j}\exp \left( it\left( k_{j}-\varphi -\frac{\lambda ^{2}}{2}(\frac{1}{\Delta _{2}}+\frac{2}{\Delta _{0}})\right) \right) \\ \frac{1}{4}e^{-it\frac{\lambda ^{2}}{2}(\frac{1}{\Delta _{2}}+\frac{2}{\Delta _{0}})}\left( +D_{23}(0)e^{it\frac{\lambda ^{2}}{4}(\frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}})}+e^{0.5it(\Delta _{1}+\frac{\lambda ^{2}}{\Delta _{0}})}\left[ e_{1}\cos (t\Xi )+e_{2}\sin (t\Xi )\right] \right) \\ \frac{1}{4}e^{-it\frac{\lambda ^{2}}{2}(\frac{1}{\Delta _{2}}+\frac{2}{\Delta _{0}})}\left( -D_{23}(0)e^{it\frac{\lambda ^{2}}{4}(\frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}})}+e^{0.5it(\Delta _{1}+\frac{\lambda ^{2}}{\Delta _{0}})}\left[ e_{1}\cos (t\Xi )+e_{2}\sin (t\Xi )\right] \right) \\ \frac{1}{2}\sum \limits _{j=1}^{3} M_{j}\exp \left( it\left( m_{j}-\omega _{2}-\frac{\lambda ^{2}}{4}(\frac{1}{\Delta _{2}}+\frac{2}{\Delta _{0}})\right) \right) \\ \frac{1}{2}\sum \limits _{j=1}^{3} M_{j}\exp \left( it\left( m_{j}-\omega _{2}-\frac{\lambda ^{2}}{4}(\frac{1}{\Delta _{2}}+\frac{2}{\Delta _{0}})\right) \right) \\ e^{0.5it(\Delta _{1}-\frac{\lambda ^{2}}{2\Delta _{2}})}\biggl [e_{11}\cos (t\Xi )+e_{22}\sin (t\Xi )\biggr ]\\ \sum \limits _{j=1}^{3} L_{j}\exp \biggl (it\biggl (l_{j}-2\omega _{2}+\varphi \biggr )\biggr ) \end{array}\right) , \nonumber \\ \end{aligned}$$

(29)

Fig. 3

The time evolution of the APIF of the $1^{st}$-atom, $W_{1}(t)$, for the Hamiltonian Eq.(1) subject to the state Eq.(14) while the system parameters values are $\omega _{0}=10\lambda$, $\eta =0$ and in (a) $\Delta _{0}=5\lambda$, (b) $\Delta _{0}=10\lambda$, and (c) $\Delta _{0}=15\lambda$, while in (1) $\Delta _{1}=0$, (2) $\Delta _{1}=-0.1 \lambda$, and (3) $\Delta _{1}=0.1\lambda$

Based on the imposed constraints in the current work, one via minor algebra operations, one can conclude that $[\Re _{23}=A_{2}(0)+A_{3}(0)],$ $\biggl [e_{1}, e_{2}, e_{11}, e_{22}, \Xi \biggr ]=\left[ \Re _{23}, -0.5i\Xi ^{-1}(\Delta _{1}+\frac{\lambda ^{2}}{2\Delta _{2}})\Re _{23}, 0, -0.5\lambda \Xi ^{-1}\Re _{23}, 0.5\sqrt{\Delta ^{2}_{1}+\frac{\lambda ^{4}}{4\Delta ^{2}_{2}}+\frac{\Delta _{1}\lambda ^{2}}{\Delta _{2}}+2\lambda ^{2}}\right] \!.$ Moreover, the parameters $k_{j}$, $l_{j}$, and $m_{j}$ all are copy of $\tau _{j}$ shown in (21). Moreover, the $X_{1}$, $X_{2}$, and $X_{3}$ for the coefficients $A_{j}(t)$ ($j=1, 17, 5, 8$) are as follows [$s= \Delta _{1}+\frac{\lambda ^{2}}{4}(\frac{1}{\Delta _{2}}+\frac{2}{\Delta _{0}})$]:-

The coefficients ${\mathcal {V}}_{j}$ $\equiv$ $K_{j}$, $M_{j}$, and $L_{j}$ are controlled by (${\mathfrak {v}}_{j}\equiv$ $k_{j}$, $l_{j}$, and $m_{j}$):-

$$\begin{aligned} \left( \begin{array}{c} {\mathcal {V}}_{1} \\ {\mathcal {V}}_{2} \\ {\mathcal {V}}_{3} \end{array}\right) =\left( \begin{array}{ccc} 1 &{} 1 &{} 1\\ {\mathfrak {v}}_{1}\, \mathrm {i} &{} {\mathfrak {v}}_{2}\, \mathrm {i} &{} {\mathfrak {v}}_{3}\, \mathrm {i}\\ - {\mathfrak {v}}^2_{1} &{} - {\mathfrak {v}}^2 _{2} &{} - {\mathfrak {v}}^2 _{3}\end{array}\right) ^{-1} \left( \begin{array}{c} \Re _{00}\\ \Re _{11}\\ \Re _{22} \end{array}\right) . \end{aligned}$$

(31)

Fig. 4

The time evolution of the APIF of the $1^{st}$-atom, $W_{1}(t)$, for the Hamiltonian Eq.(1) subject to the state Eq.(14) while the system parameters values are $\omega _{0}=\Omega =100\lambda$, and in (a) $\eta =\frac{0.900\pi }{9}$, (b) $\eta =\frac{1.000\pi }{9}$, and (c) $\eta =\frac{1.250\pi }{9}$, while in (1) $\sqrt{2}\nu =5\lambda$, (2) $\sqrt{2}\nu =10\lambda$, and in (3) $\sqrt{2}\nu =15\lambda$

Due to the enumerated relations-above, one is in a position to discuss many quantum aspects. But here we content to review the CRP in to the atomic inversion of a single atom.

4 Collapses-revivals phenomenon (CRP)

The CRP represents one of the most important nonclassical phenomena in the field of quantum optics. The observation of this phenomenon occurred during the course of interaction between the field and the atom within a cavity. This phenomenon is a pure quantum mechanical effect and having its origin in the granular structure of the photon- number distribution of the initial field [107]. The CRP has been seen in nonlinear optics for the single-mode mean-photon number of the Kerr nonlinear coupler [108] when the modes are initially prepared in coherent light, however, in this case the origin of the occurrence of such a phenomenon is in the presence of nonlinearity in the system (third-order nonlinearity specified by the cubic susceptibility). Also, the atomic density operator elements for a one atom in the old basis have the forms

$$\begin{aligned} \rho ^{[i]}_{ee}= & {} {\rho ^{[i]}_{++}}\cos ^{2} \eta - ({\rho ^{[i]}_{+-}}+{\rho ^{[i]}_{-+}}) \sin \eta \cos \eta -{\rho ^{[i]}_{--}}\, \sin ^{2} \eta ,\nonumber \\ \rho ^{[i]}_{eg}= & {} {\rho ^{[i]}_{+-}}\cos ^{2} \eta + ({\rho ^{[i]}_{++}}-{\rho ^{[i]}_{--}}) \sin \eta \cos \eta -{\rho ^{[i]}_{-+}}\, \sin ^{2} \eta ,\nonumber \\ \rho ^{[i]}_{ge}= & {} {\rho ^{[i]}_{-+}}\cos ^{2} \eta + ({\rho ^{[i]}_{++}}-{\rho ^{[i]}_{--}}) \sin \eta \cos \eta -{\rho ^{[i]}_{+-}}\, \sin ^{2} \eta ,\nonumber \\ \rho ^{[i]}_{gg}= & {} {\rho ^{[i]}_{++}}\sin ^{2} \eta + ({\rho ^{[i]}_{+-}}+{\rho ^{[i]}_{-+}}) \sin \eta \cos \eta -{\rho ^{[i]}_{--}}\, \cos ^{2} \eta . \end{aligned}$$

(33)

The APIF, W(t), which represents the difference between the population of the excited and the ground states. Approval of the APIF for the study of the QST is attributed to the easiness of the determination of both the places of the perfect QST (PQST) and the places of the synchronization of the two atoms (STAs): for specific times, the PQST is possible when $\sum _{i=1}^{2} W_{i}(t_{s})=0$ while the STAs is possible if $\sum _{i=1}^{2} (-)^{i+1} W_{i}(t_{v})=0$ ($W_{1}(t)$ is for the $1^{st}$ atom while $W_{2}(t)$ is for the $2^{nd}$ atom). The APIF can be formulated as follows:-

$$\begin{aligned} W_{i}(t)=\cos (2\eta )(\rho ^{[i]}_{++}-\rho ^{[i]}_{--})-\sin (2\eta )(\rho ^{[i]}_{+-}+\rho ^{[i]}_{-+}). \end{aligned}$$

(34)

5 Numerical results and discussion

In the present section, our interest focuses on the investigation of the APIF in accordance with different dispersive regimes. We give comments on the resulted features due to the variation of the inputs of both the atomic and photonic subsystems. We investigate the behavior of the APIF function on the basis of three categories. The first case is that where the OFCS is much larger than the detuning parameter, is expressed as $\sqrt{2}\nu$ $>>$ $\Delta _{0}$, while the opposite is for the second case, is expressed as $\Delta _{0}$ $>>$ $\sqrt{2}\nu$. The third case is that the OFCS is comparable to the augmented detuning, is expressed as $\sqrt{2}\nu$ $\approx$ $\Delta _{0}$. The investigation of the current model is limited to the case of starting the -atom initially from its excited state while the -atom starts initially from its ground state. We numerically exhibit the cases of the appearance of the CRP whether the action of the ECFs is (through the augmented frequency) considered or not. Furthermore, we confine ourselves to handle the problem only with positive parameters.

Fig. 5

Zoomed view of plots in Fig. 4

5.1 Absence of the ECF

Now, we discuss the time evolution of the APIF due to changes in both the detuning and the strength of the optical fiber coupling in the numerical computations during the absence of the ECF is considered. The strategy is to enable one of the two controlling parameters (namely, the strength of the optical fiber coupling, and the localized detuning) to exceed the other.

5.1.1 Large OFCS and large detuning

Visualization of the role played by the addition of large value of the strength of the optical fiber coupling requires realizing the behavior of the APIF for two remote cavities i.e.,  no an optical fiber mode and no a photon hopping. The figures and the numerical computations show that increasing the value of the localized detuning while the bosonic modes are uncorrelated shifts the minima of the atomic population inversion function upward and gives rise to more compressed Rabi-frequency (see frame(2a) in Fig. 2). This is an evidence that the rate of the quantum-information transfer between the atomic subsystems declines as a result of the increase of the value of the localized detuning. Generally speaking, the figures and the numerical computations indicate that the increase of the strength of the optical fiber coupling leads the APIF to exhibit periodic and regular oscillations of low frequency compared with those for the absence case and makes the APIF to reach almost its minimum extreme value in a periodic and a regular manner (compare frame(1a) with frame(a) in Fig. 2). The detuning parameter is of zero value (i.e.,  $\Delta _{0}=0$), the contribution of the continuity of the increase of the strength of the optical fiber coupling adds nothing to the behavior of the APIF as long as the values of the OFCS overtake that for the atom-field coupling (see frame(1a) in Fig. 2). It is observed that the numerical computations showcase that the first atom spends longer time in its ground state compared with its excited state when both the detuning and the strength of the cavity-fiber coupling are not taken into account (see maxima and minima in frame(1a) in Fig. 2). The previous remark is a great motivation for addressing the case of having nonzero detuning. The pursuit to the controlling factor in the change of the rate of the quantum information transfer is principle reason behind this choice. The figures show that the reduction of the quantum-information transfer between the atomic subsystems is an inevitable result of the growth of the detuning in the numerical computations regardless of the absence and the presence of the optical fiber coupling although the associated features to its growing in the numerical computations are completely different with the two investigations (compare frame(1a) with frames(1b, 1c) in Fig. 2) and (compare among the different colored curves in frame(2) in Fig. 2). In detail, the factor $(\frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}})$ controls the frequency of the APIF (see Fig. 2). Thus, one can manifest that the overlap between the values of both the detuning and the optical fiber coupling does not accord the same information (compare frame(1) with frame(2) in Fig. 2). All these results are in a complete conformity with those introduced in [96].

Fig. 6

The time evolution of the APIF of the $1^{st}$-atom, $W_{1}(t)$, for the Hamiltonian Eq.(1) subject to the state Eq.(14) while the system parameters values are $\omega _{0}=\Omega =100\lambda$, and in (a) $\eta =\frac{1.350\pi }{9}$, (b) $\eta =\frac{1.400\pi }{9}$, and (c) $\eta =\frac{1.450\pi }{9}$, while in (1) $\sqrt{2}\nu =5\lambda$, (2) $\sqrt{2}\nu =10\lambda$, and in (3) $\sqrt{2}\nu =15\lambda$

5.1.2 Comparable OFCS and detuning

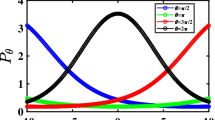
Now, we draw the attention to the discussion of the behavior of the time evolution of the APIF when the difference between the localized detuning and the strength of the optical fiber coupling its magnitude is either zero (i.e.,  the on resonance APIF, is depicted in frame(1) in Fig. 3) or infinitesimal value (i.e.,  the near resonance APIF, is depicted in frames(2, 3) in Fig. 3). Their equal values (i.e.,  $\Delta _{0}$, and $\sqrt{2}\nu$) are on the increase, interesting features are observed successively (i) modulating the amplitude until show what the so-called ring modulation (see frame(1) in Fig. 3), (ii) elongating the revivals periods (compare frame(1a) with frames(1b, 1c) in Fig. 3). When the detuning and the strength are of near resonance (say, $\Delta _{0}$ $\approx$ $\sqrt{2} \nu$ with negative $\Delta _{1}$), the resulted features are completely consistent with those for the on resonant case, except for nonequivalent quantum-information transfer between the atomic subsystems (compare frame(1) with frame(2) in Fig. 3). On the other hand, when $\Delta _{0}$ $\approx$ $\sqrt{2} \nu$ with positive $\Delta _{1}$, the CRP is absent while the atomic population inversion function exhibits quasi-periodic oscillations (compare frame(1) with frame(3) in Fig. 3). The assertion nonexhibiting the APIF a CRP with positive near resonance $\Delta _{1}$, is not even remotely true, but it (i.e.,  the CRP) can be appeared with much larger values of the detuning compared with those in on resonance and negative near resonance cases (plots are not considered here). Again, one can assert that the behavior of the APIF and the rate of the quantum-information transfer between the atomic subsystems may be controlled by the difference of the detuning and the strength of the optical fiber coupling (see Fig. 3). In other words, when the localized detuning and the strength of the optical fiber mode are approximately equal, the quantum-information transfer and the associated features are completely dependent on the change of $\Delta _{1}$. These three scenarios are in complete conformity with those appeared when the coupling between the cavities was by the overlap of evanescent cavity fields [98, 103].

Fig. 7

The time evolution of the APIF of the $1^{st}$-atom, $W_{1}(t)$, for the Hamiltonian Eq.(1) subject to the state Eq.(14) while the system parameters values are $\omega _{0}=\Omega =100\lambda$, and in (a) $\eta =\frac{1.520\pi }{9}$, (b) $\eta =\frac{1.545\pi }{9}$, and (c) $\eta =\frac{1.570\pi }{9}$, while in (1) $\sqrt{2}\nu =5\lambda$, (2) $\sqrt{2}\nu =10\lambda$, and in (3) $\sqrt{2}\nu =15\lambda$

5.2 Presence of the ECF

In this subsection, we are moving on towards addressing the effects of the ECFs on the time evolution of the APIF with giving essential differences between the current evolutions and their counterparts for the absence of the external classical fields was considered before. More clarification and fruitful investigation can be made through a harmonization among the controlling and relevant parameters. The investigation will be limited to the previously cited three investigated cases but with specific differences, given the augmentation of the localized due due to including the actions of the external classical fields.

5.2.1 Large OFCS and large detuning

• Large Delocalized Detuning First of all, it is foreknown from the analytical results that the parameter $\eta$ maps the relation between the atomic frequency and the coupling of the ECFs. Also, for a comprehensive investigation, we address two interesting categories, the first is exceeding the localized atomic frequencies to the couplings of the ECFs while the opposite is valid for the second category. When $\eta$ $<<$ $\frac{1}{2} \arctan \frac{4}{3}$, the figures and the numerical computations show that the increase of the ECFC not only leads the APIF to exhibit rapid and small oscillations "superpositions of fast and slow oscillations", but also, tends to the low frequency APIF and shift the minima of the APIF upward (compare frames(1a, 2a, 3a) with frames(1b-1c, 2b-2c, 3b-3c) respectively in Fig. 4). It is noticed that the action of the of the increase in the optical fiber coupling is immutable, its increase leads to shortening the revivals time (compare frame(1) with frames(2, 3) in Fig. 4). One can emphasize that the increase of the ECF coupling hinders the atom to populate its ground state (see Fig. 4). The aforementioned result is a direct indication that the increase of the coupling of the ECFs hinders the effectiveness of the strength of the optical fiber coupling (compare Figs. 3 and  4 with Fig. 4. Finally, growth of the ECFC due to the variation of $\eta$ with $\eta$ $<<$ $\frac{1}{2} \arctan \frac{4}{3}$ reduces in the quantum-information transfer rate between the atomic subsystems. Before proceeding to further investigations, we should clarify what in Fig. 4, they are the oscillations of the envelope of the revivals which carry fast oscillations (see Fig. 5). Moreover, we intend to deal with another two intervals, $\frac{1}{2}\arctan \frac{4}{3}$ < < $\eta$ < < $\frac{\pi }{3}$, exhibited in Fig. 6, and $\frac{\pi }{3}<<\eta<<\frac{1}{2}\arctan {2}$, depicted in Fig. 7. One can easily observe that the action of the ECF coupling is somewhat similar to its counterpart when the values $\eta>>\frac{1}{2}\arctan 2$ were considered (compare Fig. 4 with Figs. 6 and 7). The action of the increment of the ECF coupling not only it has the ability to lower the frequency of the APIF, but also, continuity of its increment leads to bringing the minima of the APIF upward (compare frames(1a, 2a, 3a) with frames(1b-1c, 2b-2c, 3b-3c) respectively in Figs. 4, 6 and 7). Being the atom is much far from its ground state is one of what differentiates the second interval from its predecessor (compare Fig. 4 with Figs. 6 and 7). Furthermore, beginning with $\eta>>\frac{1}{2}\arctan 2$, the time evolution of the APIF shows the expected phenomenon, namely; the CRP. Moreover, increasing the ECF coupling delays the appearance of the revivals periods and brings the minima of the APIF downward i.e.,  increasing the coupling of the ECF is considered as an accelerator to the atom to reach its ground state (see Fig. 8). On the other hand, the sustained growth to the strength of the optical fiber coupling leads to shortening the revivals times (compare frame(1) with frames(2, 3) in Fig. 8). This observation is not for a specific interval but for all considered intervals (compare frame(1) with frames(2, 3) in Figs. 4, 6, 7 and  8). Finally, it is obvious from the figures and the numerical computations that the rate of the elongation of the revivals times occurs as a result of the increase of the coupling of the ECFs and it is independent of the growth of the OFCS (compare frames(1a, 2a, 3a) with frames(1b-1c, 2b-2c, 3b-3c) respectively in Figs. 4, 6, 7 and  8). On the other hand, the rate of the shrinkage of the revivals times occurs as a result of the growth of the OFCS and it is independent of the ECFs coupling (compare frame(1) with frames(2, 3) in Figs. 4, 6, 7 and  8).

Fig. 8

The time evolution of the APIF of the $1^{st}$-atom, $W_{1}(t)$, for the Hamiltonian Eq.(1) subject to the state Eq.(14) while the system parameters values are $\omega _{0}=\Omega =10\lambda$, and in (a) $\eta =\frac{1.800\pi }{9}$, (b) $\eta =\frac{2.000\pi }{9}$, and (c) $\eta =\frac{2.200\pi }{9}$, while in (1) $\sqrt{2}\nu =5\lambda$, (2) $\sqrt{2}\nu =10\lambda$, and in (3) $\sqrt{2}\nu =15\lambda$

Fig. 9

The time evolution of the APIF of the $1^{st}$-atom, $W_{1}(t)$, for the Hamiltonian Eq.(1) subject to the state Eq.(14) while the system parameters values are $\omega _{0}=\Omega =10\lambda$, and in (a) $\eta =\frac{1.800\pi }{9}$, (b) $\eta =\frac{2.000\pi }{9}$, and (c) $\eta =\frac{2.200\pi }{9}$, while in (1) $\sqrt{2}\nu =250\lambda$, (2) $\sqrt{2}\nu =500\lambda$, and (3) $\sqrt{2}\nu =1000\lambda$

• Large OFCS Generally speaking, when OFCS takes values far beyond its competitor (i.e.,  the delocalized detuning), the features occur as a result of the growth of the ECFs in perfect match to those in the previous case (see Fig. 9). On the other hand, the role played by the continuity of the increase of the strength of the optical fiber coupling results in elongating the revivals periods. In fact, as in the case of the absence of the ECF, the strength of the optical fiber coupling adds no contribution when its value is much larger than that for the detuning (compare frame(1) with frames(2, 3) in Fig. 9).

5.2.2 Comparable OFCS and detuning

To go a step further, we pay some attention to investigate the considered scheme when the values of both the OFCS and augmented detuning are close to each others. Thus, this investigation must be compatible with the previously cited two hypotheses. The intelligibility of the present scenario may interrogate to stabilize the localized atomic frequency (say, $\Omega =10\lambda$). Previously, we have mentioned that the argument $\eta$ maps the relation between the augmented detuning and the atomic frequency. Based on the restrictions imposed in the current subsubsection, the strength of the optical fiber coupling becomes one of the relevant and controlling parameters. Considering a small value of the rotation angle $\eta$ leads the APIF to show a chaotic behavior and the atom to become nearer to its ground state than its excited state. Increasing $\eta$ not only gives rise to a shift upward of the mean of the APIF, but also causes an amplitude modulation. Such an amplitude modulation continues until the APIF exhibits the CRP. These collapses and revivals periods are greatly affected by the direct increase in the value of the argument ($\eta$) The revivals periods are prolonged as a result of the continuity of the increase of the rotation angle $\eta$. Finally, one can observe from the figures and the numerical computations that the atom does not have the ability to reach its destinations (compare frames(1a, 2a, 3a) with frames(1b-1c, 2b-2c, 3b-3c) respectively in Fig. 10). Ultimately, clearer collapses periods do not exist here. This may be attributed to having the vacuum states as initial states of the fields and no photons distributions are involved.

Fig. 10

The time evolution of the APIF of the $1^{st}$-atom, $W_{1}(t)$, for the Hamiltonian Eq.(1) subject to the state Eq.(14) while the system parameters values are $\omega _{0}=\Omega =10\lambda$, and $\sqrt{2}\nu =\Delta _{0}$, while in (1), (a) $\eta =\frac{0.900\pi }{9}$, (b) $\eta =\frac{1.000\pi }{9}$, and (c) $\eta =\frac{1.250\pi }{9}$, in (2), (a) $\eta =\frac{1.350\pi }{9}$, (b) $\eta =\frac{1.400\pi }{9}$, and (c) $\eta =\frac{1.450\pi }{9}$ and in (3), (a) $\eta =\frac{1.520\pi }{9}$, (b) $\eta =\frac{1.545\pi }{9}$, and (c) $\eta =\frac{1.570\pi }{9}$

5.3 The second atom information

As we have mentioned before, the purpose of the current work is to track the behavior of the QST and to indicate the essential difference between the rates of the transfer in the two schemes: The current scheme and the scheme in [97]. First, we intend to introduce some differences between the time evolutions of the APIFs, $W_{1}(t)$, and $W_{2}(t)$ in the numerical computations point of view. Second, through corresponding inputs in the two schemes and the effective Hamiltonians, we review and state which of the two schemes is of higher transfer rate?. It is preferable to address the numerical computations in the framework of the large OFCS limit seeing its intelligibility. The addressability will not only for the absence of the action of the ECFCs but also will be for the case of its presence. Based on the numerical computations and Figs. 2,  3 and Figs. 11,  12) one can approve what we have mentioned before: Perfect atomic states transfer is possible when $\sum _{i=1}^{2}W_{i}(t)=0$, while synchronization of the two atoms is also possible when $\sum _{i=1}^{2} (-)^{i+1} W_{i}(t)=0$. No need to call the corresponding figure of the other scheme to give an essential difference, enough to state that the rate of the energy transfer with the current scheme is higher compared with that for the other scheme. Moreover, it is observable when no action for the ECFCs, there is no a transfer for the energy between the atomic subsystems as long as there no a transmission line (compare frame(2a) in Fig. 2 with frame(2a) in Fig. 11). It is worth noting, when no a photons can be transfer from a cavity to another while the action of the ECFCs is considered, there is a possibility for the energy transferred between the atomic subsystems (plots are not shown here).

Fig. 11

The time evolution of the APIF of the $2^{nd}$-atom, $W_{2}(t)$, for the Hamiltonian Eq.(1) with the same parameters of the system which are exploited in the numerical computations for the Fig.(2)

6 Conclusion

In the aforementioned, we have investigated the CRP in the context of the APIF due to the influences of the atomic frequencies, localized and delocalized detuning, the couplings of the ECFs, and the OFCS. The investigation has been carried out based on the condition that the atom-field coupling is small comparable with the other parameters. The investigation has been analytically and numerically presented in the context of three dispersive regimes approximations as stated in the text. The general conclusions reached and illustrated by numerical results show that:

• The APIF is of a sinusoidal behavior as long as the action of the ECF is not considered while both the detuning and the OFCS have big differences in this case low increasing of the OFCS causes swinging the atom between its upper and lower states through the time evolution of the APIF".

• Prolongation and shrinkage of the revivals periods are controlled by the difference between both the detuning and the OFCS or rather controlled by the factor $(\frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}})$. Compressing and broadening the frequencies of the fluctuations of the APIF are also dependent on this difference or rather controlled by the same factor $(\frac{1}{\Delta _{1}}+\frac{1}{\Delta _{2}}-\frac{2}{\Delta _{0}})$.

• The actions of the ECFs are not considered, the APIF exhibits a CRP provided the detuning and the OFCS are having nonzero values but either on resonance or near resonance.

• The actions of the couplings of the ECFs are of wider range. This is attributed to the fact that they are not only confined to the inclusion of the augmented detuning but also extend to the determination of their place values to those of atomic frequencies.

• In consideration of the above-mentioned case, the minima of the APIF go downward as a result of the continuous increase of the couplings the external fields and their exceeding to a specific value of the localized atomic frequency.

• In contrast, the minima of the APIF go upward as a result of the continuous increase of the couplings ECFs: monotonically, (i) exceeding the delocalized detuning to the localized atomic frequency (ii) exceeding the localized atomic frequency to both the delocalized detuning and the ECF coupling respectively (iii) exceeding the localized atomic frequency to both the ECF coupling and the delocalized detuning.

• The APIF exhibits the CRP when the couplings of the ECFs exceed the localized atomic frequency whether the OFCS exceeds the augmented detuning or not.

• When the augmented detuning is on resonance or near resonance to the OFCS, incomplete CRP rises compared with its counterparts whether in the presence of the ECFs or not.

• The dispersive regimes are ones of the controlling factors for the rate of the energy transfer between the atomic subsystems: Each one of them is associated to a specific rate; no one of them is commensurate to the other.

Fig. 12

The time evolution of the APIF of the $2^{nd}$-atom, $W_{2}(t)$, for the Hamiltonian Eq.(1) with the same parameters of the system which are exploited in the numerical computations for Fig. 3