Entanglement and separability of graph Laplacian quantum states

Abstract

In this article, we study the entanglement properties of multi-qubit quantum states using a graph-theoretic approach. For this, we define entanglement and separability for m-qubit quantum states associated with a weighted graph on $2^m$ vertices. We further explore the properties of a block graph and a star graph to demonstrate criteria for entanglement and separability of these graphs.

1 Introduction

Quantum information and computation has emerged as an interdisciplinary research platform offering several potential applications in diverse academic domains. The efficient advantages offered by quantum resources are due to entanglement and nonlocal correlations existing between qubits as identified by entanglement measures, Bell-type inequalities and quantum discord. Recent trends in quantum information and computation have shown that applications of entanglement and nonlocality are being recognized in computing, security, machine learning, deep learning, biology, computational chemistry, finance and image processing. With the ever-growing applications of entanglement, there is also a need to classify and quantify entanglement and correlations in multiqubit networks. For example, the entanglement versus separability problem for two-qubit pure and mixed states are well established but the classification and quantification of entanglement in multi-particle systems [2, 18, 31, 34, 35] are increasingly complicated and hence require a much better physical interpretation and understanding. For a three-qubit pure state, several effective criteria have been defined, e.g., the entanglement criterion for states belonging to classes of three qubit pure states has been achieved by a complete stochastic local operations and classical communication (SLOCC) characterization [7, 9, 21]. Considering a multiuser network, classifying entanglement in multi-qubit systems is an important problem and has a special attribute in quantum theory [12, 17, 18]. However, with the increase in number of qubits the complexity increases enormously and proposing a general description to address entanglement versus separability becomes very challenging even for multi-qubit pure states. Clearly, the analysis of multi-qubit mixed states is even more intricate and demanding.

The graph-theoretic approaches are quite handy to solve numerous research problems [32, 33]. In one of its efficient approaches, the graph-theoretical approach has shown its outstanding potential toward quantum physics [13, 18] and information theory [3, 6, 8]. For this, the pictorial representation and physical interpretation of quantum states are provided by graphs [1, 5, 15]. The theory has been further used to model unitary operations and to interpret entanglement or separability properties of quantum states [4, 5, 10, 11, 15]. One of the important ways to define quantum states and their properties is to use the concept of density operators which can be further characterized by normalized Laplacian matrices for graphs [14, 26]. Likewise, we can relate any graph, to a particular quantum state by using its density operator. In particular, quantum states of simple and weighted graphs have been introduced in [5] and [15], respectively, where density operators are normalized combinatorial Laplacians having a unit trace. Moreover, a density operator—acting on a Hilbert space ${\mathbb {R}}^{n \times n}$ or ${\mathbb {C}}^{n \times n}$ with respect to the weights of edges of a graph—carries a block structure which can be associated with subsystems. In addition, an m-partite density operator acts on a Hilbert space ${\mathbb {R}}^{q_1} \otimes {\mathbb {R}}^{q_2} \otimes \ldots \otimes {\mathbb {R}}^{q_m}$ or ${\mathbb {C}}^{q_1} \otimes {\mathbb {C}}^{q_2} \otimes \ldots \otimes {\mathbb {C}}^{q_m}$, where $\otimes$ represents a tensor product [15, 16].

In this article, we readdress entanglement versus separability problem using the graph-theoretic approach for multi-qubit systems. For this, we explore graph-theoretical interpretations of entanglement and separability for n-qubit states associated with weighted, block and star graphs. We start our discussion with demonstrating a condition for the Laplacian of a weighted graph to be positive semi-definite and then use this condition to introduce the notion of a density operator for a multi-qubit graph/state. We further propose conditions for a density operator of a weighted graph to represent a pure or a mixed state. In addition, we also analyze entanglement and separability of states associated with weighted graphs to demonstrate many interesting conditions to characterize entanglement properties of weighted graphs. We further study entanglement properties of block graphs and star graphs. Our analysis shows that the state associated with a weighted graph (G, a) is entangled if at least one of the blocks of graph is associated with an entangled state. Moreover, if every vertex of a n-qubit graph G has degree $k \ge 2$ such that G has no cut-vertex, then the graph G is associated with a separable state. Interestingly, our results demonstrate that if r vertices are deleted from a star graph on $2^m$ vertices then the resulting graph on $2^s$ vertices is associated with an entangled quantum state such that $0 \le r \le 2(2^{(m-1)}-1)$. We further analyze the degree of entanglement in a star graph $G'$ obtained by adding adjacent edges to the original graph G, and show that the resultant graph $G'$ will have at least one block which is associated with an entangled state such that the entanglement measure of blocks of $G'$ would not exceed the entangled measure of blocks of G.

The article is organized as follows: In Sect. 2, we briefly discuss the properties of weighted graphs, the associated Laplacian operators and partial transpose of weighted graphs. In Sect. 3, we propose a condition for the Laplacian of a weighted graph (G, a) on $n = 2^{m}$ vertices to be positive semi-definite and address entanglement and separability issues in multi-qubit weighted graphs. Section 4 is dedicated toward characterizing entanglement properties of weighted, block and start graphs. In this section, we demonstrate several effective criteria to study the separability of n-qubit entangled states. Finally, in Sect. 5, we conclude the article.

2 Preliminaries

In this section, we first provide a brief review of weighted graphs and important terminologies such as adjacency matrix, degree matrix and Laplacian matrix which we will be using in the upcoming sections of the article to represent quantum states associated with a given weighted graph.

2.1 Weighted graphs

A graph G on n vertices is a pair (V(G), E(G)) , where $V(G)=\{v_1, v_2, \ldots , v_n\}$ is the set of vertices, and $E(G)\subseteq V(G) \times V(G)$ is the set of edges. Similarly, a weighted graph (G, a) is a graph together with a weight function $a:E(G) \rightarrow {{{\mathbb {F}}}}$ defined as follows: let $v_i, v_j \in V(G)$, and $(v_i, v_j) \in E(G)$, then $a(v_i,v_j)$ is weight from $v_i$ to $v_j$, $1\le i,j \le n$. If two distinct vertices $v_i$ and $v_j$ are connected with an edge, then we denote it by $v_i \sim v_j$. Clearly, $v_i=v_j$; $(v_i, v_i)$ $\in$ E(G), is a self-loop at vertex $v_i$ having the weight $a(v_{i},v_{i})$. In the special case when all nonzero weights in (G, a) are equal to 1, and there are no self-loops, it is called a simple graph. Further, if (G, a) is a weighted graph on n vertices then the adjacency matrix of (G, a), denoted by A(G), is a $n \times n$ matrix with (i, j)-th entry equals $a_{ij}=a({v_i, v_j})$ if $v_i \sim v_j$, otherwise 0.

2.1.1 Laplacian matrix of a weighted graph on ${{\mathbb {R}}}$

A weighted graph (G, a) is a graph together with a weight function $a:E(G) \rightarrow {{{\mathbb {R}}}}$ defined as follows,

• 1. $a({v_i, v_j}) \ne 0$ if ${v_i, v_j} \in E(G)$ and 0 otherwise.

• 2. $a({v_i, v_j}) = a({v_j, v_i})$

We can now proceed to define the Laplacian matrix of a weighted graph G as [15, 20]

$$\begin{aligned} L{(G)} = {D(G) - A(G) + {D_0}(G)}, \end{aligned}$$

(1)

where ${D_0}(G)$ is a diagonal matrix with i-th diagonal entry equals to $a(v_{i},v_{i})$ and D(G) is the degree matrix of (G, a). The degree matrix is a diagonal matrix with the i-th diagonal entry equals to the sum of all entries of i-th row (or column) of A(G), i.e., $\sum _{j=1}^{n} {a_{ij}}$. For a simple graph, the degree matrix D(G) of a vertex $v_i \in V(G)$ is defined as the number of edges in E(G) incident on $v_i$.

2.1.2 Laplacian matrix of a weighted graph on ${{\mathbb {C}}}$

One can further define a weighted graph (G, a) with a weight function $a:E(G) \rightarrow {{{\mathbb {C}}}}$ as,

• 1. $a({v_i, v_j}) \ne 0$ if ${v_i, v_j} \in E(G)$ and 0 otherwise.

• 2. $a({v_i, v_j}) = \bar{a({v_j, v_i})}$

The generalized Laplacian of a graph (G, a), which includes loops, is $L(G) =D(G) + A(G) - D_0(G)$ [15] where the degree matrix with i-th diagonal entry of vertex $v_i$ is given by [15]

$$\begin{aligned} d_{v_iv_i} = \sum _{v_i \in V(G), v_i \ne v_j} ||a({v_i, v_j}) || + a({v_i, v_i}). \end{aligned}$$

In general, L(G) is not positive semi-definite, however, for a simple graph it is positive semi-definite. For simple graphs, ${D_0}(G)=0$ and $L(G) = D_1(G) +D_2(G) - A_1(G)- A_2(G)$, where $D_1(G)$ and $D_2(G)$ are diagonal matrices, and diagonal entries are row sum of $A_1(G)$ and $A_2(G)$, respectively. Therefore, the Laplacian of a simple graph can be re-expressed as sum of Laplacian matrices of simple graphs. We utilize this property to analyze separability and entanglement problems in star graphs. In order to facilitate the discussion of our results, we also briefly discuss the decomposition of a Laplacian matrix for simple graphs in the Appendix.

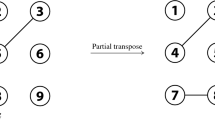
2.2 Conjugate partial transpose of a weighted graph

Let (G, a) be a graph on $n=pq$ vertices and vertex set $V(G)= \{v_{ij} | i=1,2,\ldots p \text { and } j=1,2,\ldots q \}$. Using (G, a), if one draws edges of the form $(v_{il},v_{kj})$, in place of all edges of the form $(v_{ij},v_{kl})$ where the weight is $\bar{a(v_{ij},v_{kl})}$, for all $j \ne l$ then the resulting graph $(G',a')$ is called as the conjugate partial transpose of the original graph (G, a) [11, 15, 19]. For example,

It is important to note that for a graph (G, a), the conjugate partial transpose of the Laplacian matrix L(G) may or may not be equal to the Laplacian matrix of the conjugate partial transpose of (G, a). For example,

Example 1

Consider the following graph $G_1$.

Clearly, the Laplacian matrix of $G_1$ is

$$\begin{aligned} L(G_1) =\begin{bmatrix} 2 &{} i &{} 0 &{} i\\ -i &{} 2 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} 0\\ -i &{} 1 &{} 0 &{} 2 \end{bmatrix}, \end{aligned}$$

and the conjugate partial transpose of $L(G_1)$ is

$$\begin{aligned} {\bar{L(G_1)}}^{PT} =\begin{bmatrix} 2 &{} i &{} 0 &{} 0\\ -i &{} 2 &{} -i &{} 1\\ 0 &{} i &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 2 \end{bmatrix}. \end{aligned}$$

Whereas, the conjugate partial transpose of the graph $G_1$, i.e., ${G_1}'$ is

and the Laplacian matrix of ${G_1}'$ is

$$\begin{aligned} L({G_1}') =\begin{bmatrix} 1 &{} -i &{} 0 &{} 0\\ i &{} 3 &{}-i &{} 1\\ 0 &{} i &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$

Therefore, $L({G_1}') \ne \bar{L(G_1)}^{PT}$.

Example 2

Consider the following graph $G_2$.

The Laplacian matrix of $G_2$ is

$$\begin{aligned} L(G_2) = \begin{bmatrix} 3 &{} -1 &{} -1 &{} -1\\ -1 &{} 3 &{} -1 &{} -1\\ -1 &{} -1 &{} 3 &{} -1\\ -1 &{} -1 &{} -1 &{} 3 \end{bmatrix}, \end{aligned}$$

and the partial transpose of $L(G_2)$ is

$$\begin{aligned} {L(G_2)}^{PT} = \begin{bmatrix} 3 &{} -1 &{} -1 &{} -1\\ -1 &{} 3 &{} -1 &{} -1\\ -1 &{} -1 &{} 3 &{} -1\\ -1 &{} -1 &{} -1 &{} 3 \end{bmatrix}. \end{aligned}$$

Similarly, the partial transpose of the graph $G_2$ is

and the Laplacian matrix of ${G_2}'$ is

$$\begin{aligned} L({G_2}') =\begin{bmatrix} 3 &{} -1 &{} -1 &{} -1\\ -1 &{} 3 &{} -1 &{} -1\\ -1 &{} -1 &{} 3 &{} -1\\ -1 &{} -1 &{} -1 &{} 3 \end{bmatrix} \end{aligned}$$

Here, $L({G_2}') = {L(G_2) }^{PT}$.

3 Density operator of a graph

In general, the state of a quantum system may not be in a pure state. Due to the inherent statistical nature of quantum theory, the description of a quantum state using density operator formalism provides a much better physical interpretation of the system under study. The density operator formalism is also considered as an alternate representation for pure states, and finds its applications in quantum error correction, quantum noise, quantum communication and measures of quantum entanglement [25, 34]. For studying several interesting properties of entanglement and nonlocality, the concepts of density operator, reduced density operator and partial transpose are widely utilized [1, 5, 11, 15, 19] . Here, we propose a graph-theoretic study using a density operator mechanism to understand entanglement and separability in multiqubit pure states.

For this, we first define the density operator $\rho _G$ of a graph (G, a) considering the case where the Laplacian of the graph is a positive semi-definite matrix and is given by the following expression

$$\begin{aligned} \rho _G = \frac{1}{Tr(L(G))} L(G) \end{aligned}$$

We now proceed to demonstrate a necessary and sufficient condition for the Laplacian matrix of a graph to be positive semi-definite. For a graph G associated with an m-qubit state, vertices are column basis on ${\mathbb {R}}^{q_1} \otimes {\mathbb {R}}^{q_2} \otimes \ldots \otimes {\mathbb {R}}^{q_m}$ or ${\mathbb {C}}^{q_1} \otimes {\mathbb {C}}^{q_2} \otimes \ldots \otimes {\mathbb {C}}^{q_m}$.

Theorem 3.1

Let (G, a) be a weighted graph on n vertices. If the Laplacian matrix $L(G)=[l_{ij}]_{n\times n}$ is positive semi-definite then $l_{ii}\ge 0$ and $det\begin{bmatrix} l_{ii} &{} l_{ij} \\ l_{ji} &{} l_{jj} \end{bmatrix}\ge 0$ for all i, j.

Proof

L(G) is positive semi-definite if $x^*L(G)x \ge 0$ for any vector $x=[x_1, x_2,\ldots , x_n]^T \in {{{\mathbb {C}}}}^n$, where $x^* = [\bar{x_1}, \bar{x_2},\ldots , \bar{x_n}]$ is conjugate transpose of x, i.e.,

$$\begin{aligned} \begin{bmatrix} \bar{x_1}&\bar{x_2}&\ldots&\bar{x_n} \end{bmatrix}\begin{bmatrix} l_{11} &{} l_{12} &{} \ldots &{} l_{1n}\\ l_{21} &{} l_{22} &{} \ldots &{} l_{2n}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ l_{n1} &{} l_{n2} &{} \ldots &{} l_{nn} \end{bmatrix}\begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \ge 0, \end{aligned}$$

or

$$\begin{aligned} \bar{x_1}(l_{11}x_1+l_{12}x_2+\cdots + l_{1n}x_n)+\cdots +\bar{x_n}(l_{n1}x_1+l_{n2}x_2+\cdots + l_{nn}x_n)\ge 0, \end{aligned}$$

or

$$\begin{aligned}&\bar{x_1}(l_{11}x_1+l_{12}x_2+\cdots + l_{1n}x_n)+\cdots +\bar{x_n}(l_{n1}x_1+l_{n2}x_2+\cdots \\&\quad + l_{nn}x_n)+ (n-2)(l_{11}\bar{x_1}x_1 +l_{22}\bar{x_2}x_2 + \cdots + l_{nn}\bar{x_n}x_n)\\&\quad -(n-2)(l_{11}\bar{x_1}x_1 +l_{22}\bar{x_2}x_2 + \cdots + l_{nn}\bar{x_n}x_n)\ge 0, \end{aligned}$$

or

$$\begin{aligned}&\{\bar{x_1}(l_{11}x_1+l_{12}x_2)+\bar{x_2}(l_{21}x_1+l_{22}x_2)\} +\cdots +\{\bar{x_{n-1}}(l_{n-1n-1}x_{n-1}\\&\qquad +l_{n-1n}x_{n})+\bar{x_n}(l_{nn-1}x_{n-1}+l_{nn}x_n)\}\\&\quad \ge (n-2)(l_{11}\bar{x_1}x_1 +l_{22}\bar{x_2}x_2 + \cdots + l_{nn}\bar{x_n}x_n), \end{aligned}$$

which implies

$$\begin{aligned} \begin{bmatrix} \bar{x_1}&\bar{x_2} \end{bmatrix}\begin{bmatrix} l_{11} &{} l_{12}\\ l_{21} &{} l_{22} \end{bmatrix}\begin{bmatrix}x_1 \\ x_2 \end{bmatrix} + \cdots + \begin{bmatrix} \bar{x_{n-1}}&\bar{x_n} \end{bmatrix}\begin{bmatrix} l_{n-1 n-1} &{} l_{n-1n}\\ l_{nn-1} &{} l_{nn} \end{bmatrix}\begin{bmatrix}x_{n-1} \\ x_n \end{bmatrix} \ge 0 . \end{aligned}$$

Thus, we have

$$\begin{aligned} \begin{bmatrix} \bar{x_{i}}&\bar{x_{j}} \end{bmatrix}\begin{bmatrix} l_{ii} &{} l_{ij}\\ l_{ji} &{} l_{jj} \end{bmatrix} \begin{bmatrix} {x_{i}} \\ {x_{j}} \end{bmatrix}\ge 0 \text { for all i<j}. \end{aligned}$$

Therefore, $l_{ii}\ge 0$ and $det \Bigg ( \begin{bmatrix} l_{ii} &{} l_{ij} \\ l_{ji} &{} l_{jj} \end{bmatrix} \Bigg ) \ge 0$ for all i, j. $\square$

Theorem 3.2

Let (G, a) be a weighted graph on $n =2^m$ vertices associated with an m-qubit state, and $\rho _G = [\rho _{ij}]_{n\times n}$ be its density operator. If (G, a) represents a pure state, then $\sum _{i=1}^{{n-1} }\sum _{j>i}^{n} \rho _{ii}\rho _{jj} = \sum _{i<j} {||\rho _{ij} || }^2$.

Proof

If $\rho _{G }$ is a pure state, then ${\mathrm{Tr}}({\rho _{G }}^2) = 1$, i.e.,

$$\begin{aligned} {\rho _{11}}^2 +{\rho _{22}}^2+\cdots +{\rho _{nn}}^2+ 2({||\rho _{12} ||}^2 +\cdots +{||\rho _{1n} ||}^2+\cdots +{||\rho _{n-1n} ||}^2)=1, \end{aligned}$$

which implies that,

$$\begin{aligned}&\rho _{11}\rho _{22}+ \cdots + \rho _{11}\rho _{nn}+\cdots + \rho _{n-1n-1}\rho _{nn}\\&\quad ={||\rho _{12} ||}^2 +\cdots +{||\rho _{1n} ||}^2+\cdots +{||\rho _{n-1n} ||}^2. \end{aligned}$$

Hence,

$$\begin{aligned} \sum _{i=1}^{n-1} \sum _{i<j}^{n} \rho _{ii}\rho _{jj} = \sum _{i<j} {||\rho _{ij} ||} ^2. \end{aligned}$$

$\square$

Example 3

The following graph is associated with a pure state as ${\mathrm{Tr}}({\rho _G}^2)=1$, and $\rho _{11}(\rho _{22}+\rho _{33}+\rho _{44})+\rho _{22}(\rho _{33}+\rho _{44})+\rho _{33}\rho _{44}= {||\rho _{12} ||}^2+{||\rho _{13} ||}^2+{||\rho _{14} ||}^2+{||\rho _{23} ||}^2+{||\rho _{24} ||}^2+{||\rho _{34} ||}^2=6.$

If (G, a) represents a mixed state, then ${\mathrm{Tr}}({\rho _G}^2 ) < 1$, so the following result holds,

Corollary 3.3

Let (G, a) be a weighted graph on $n=2^m$ vertices associated with an m-qubit state, and $\rho _G = [\rho _{ij}]_{n\times n}$ be its density operator. If (G, a) represents a mixed state, then $\sum _{i<j} {||\rho _{ij} ||} ^2 < \sum _{i=1}^{n-1} \sum _{j>i}^{n} \rho _{ii}\rho _{jj}$.

Example 4

The following graph is associated with a mixed state as ${\mathrm{Tr}}({\rho _G}^2)<1$, and $\rho _{11}(\rho _{22}+\rho _{33}+\rho _{44})+\rho _{22}(\rho _{33}+\rho _{44})+\rho _{33}\rho _{44}> {||\rho _{12} ||}^2+{||\rho _{13} ||}^2+{||\rho _{14} ||}^2+{||\rho _{23} ||}^2+{||\rho _{24} ||}^2+{||\rho _{34} ||}^2.$

Theorem 3.4

Let (G, a) be a weighted graph on $n=2^{p+q}$ vertices, where q is prime and the associated density operator $\rho _G$ is a block matrix of order $2^{q}$ consisting of blocks of order $2^p$. Then, $a(v_{ij},v_{kl})=\bar{a(v_{il},v_{kj})}$ and $a(v_{ij},v_{kl}) \in {{\mathbb {R}}}$ for $j=l$ if and only if $\bar{\rho _G}^{PT}=\rho _G= \rho _{G'}$ where $\rho _{G'}$ is a density operator of conjugate partial transpose of the graph (G, a).

Proof

Let $a(v_{ij},v_{kl})$ is a weight from vertex $v_{ij}$ to $v_{kl}$.

Moreover, we have

$$\begin{aligned} \rho _G =\frac{1}{Tr(L(G))}L(G)= \frac{1}{Tr(L(G))}\begin{bmatrix} l_{11} &{} l_{12} &{} . &{} . &{} . &{} l_{12^n}\\ l_{21} &{} l_{22} &{} . &{} . &{} . &{} l_{22^n}\\ . &{} . &{}. &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ l_{2^n1} &{} l_{2^n2} &{}. &{} . &{} . &{} l_{2^n2^n} \end{bmatrix}, \end{aligned}$$

where,

$$\begin{aligned} L(G)=\left[ \begin{array}{ccccc} \begin{bmatrix} l_{11} &{} .&{} .&{} .&{} a(v_{11},v_{12^p})\\ a(v_{12},v_{11}) &{}.&{} .&{} .&{} a(v_{12},v_{12^p})\\ . &{} .&{}.&{} .&{} .&{} .\\ . &{} .&{} .&{} .&{} .\\ a(v_{12^p},v_{11}) &{}.&{} .&{} .&{} l_{2^p2^p} \end{bmatrix} &{}.&{}.&{}.&{} \begin{bmatrix} a(v_{11},v_{2^q1}) &{} .&{} .&{} .&{} a(v_{11},v_{2^q2^p}) \\ a(v_{12},v_{2^q1} ) &{}.&{} .&{} .&{} a(v_{12},v_{2^q2^p})\\ . &{} .&{} .&{} .&{} .\\ . &{} .&{} .&{} .&{} .\\ a(v_{12^p},v_{2^q1}) &{} .&{} .&{} .&{} a(v_{12^p},v_{2^q2^p}) \end{bmatrix}\\ . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} .\\ \begin{bmatrix} a(v_{2^q1},v_{11}) &{}.&{} .&{} .&{} a(v_{2^q1},v_{12^p}) \\ a(v_{2^q2},v_{11}) &{}.&{} .&{} .&{} a(v_{2^q2},v_{12^p})\\ . &{} .&{} .&{} .&{} .\\ . &{} .&{} .&{} .&{} .\\ a(v_{2^q2^p},v_{11}) &{} .&{} .&{} .&{} a(v_{2^q2^p},v_{12^p}) \end{bmatrix} &{} .&{} . &{} . &{} \begin{bmatrix}l_{rr} &{} .&{} .&{} .&{} a(v_{2^q1},v_{2^q2^p}) \\ a(v_{2^q2},v_{11}) &{} .&{} .&{} .&{} a(v_{2^q2},v_{2^q2^p})\\ . &{} .&{} .&{} .&{} .\\ . &{} .&{} .&{} .&{} .\\ a(v_{2^q2^p},v_{2^q1}) &{} .&{} .&{} .&{} l_{2^n2^n} \end{bmatrix} \end{array}\right] , \end{aligned}$$

and $r= (2^q-1)2^p+1$. If $a(v_{ij},v_{ kl}) = \bar{a(v_{il},v_{kj}})$ and $a(v_{ij},v_{kl}) \in {{\mathbb {R}}}$ for $j=l$ then $\bar{{L_{ij}}}^T=L_{ij}= L(G')_{ij}$ for all i and j, where $L_{ij}$ is ${ij}^{th}$ block of L(G), and $L(G')$ is the Laplacian matrix of conjugate partial transpose of (G, a). Therefore, $\rho _{G'}= \rho _G= \bar{{\rho _G}}^{PT}$. The reverse implication is also true. $\square$

4 Entanglement and separability of Weighted graphs

In this section, we discuss the separability and entanglement of weighted graphs on $n=2^m$ vertices, associated with m-qubit states. We further demonstrate the separability and entanglement of quantum states corresponding to block graphs and star graphs.

It is evident that the density operator $\rho _G$ of a graph (G, a) on $n=pq$ vertices is separable if it can be written as a convex combination of the tensor product of density operators $\rho _{1}^{i}$ of order p and $\rho _{2}^{i}$ of order q, such that [18, 30],

$$\begin{aligned} \rho _G = \sum _{i} p_i \rho _{1}^{i}\otimes \rho _{2}^{i}, \end{aligned}$$

(2)

where $0 \le p_i \le 1$ and $\sum _{i} p_i=1$. Moreover, in order to evaluate the degree of entanglement in a two-qubit state, concurrence is considered as one of the standard measures. For example, concurrence of a two-qubit state $\rho _G$ is defined as $C(\rho _G)= max(0,\sqrt{\mu _1}-\sqrt{\mu _2}-\sqrt{\mu _3}-\sqrt{\mu _4})$ [35]. Here $\mu _1 \ge \mu _2 \ge \mu _3 \ge \mu _4$ are eigenvalues of the matrix $\rho _G \tilde{\rho _G}$; $\tilde{\rho _G}= P {\rho _G}^* P$ where asterisk represents complex conjugation and

$$\begin{aligned} P= \sigma _{y} \otimes \sigma _{y}=\begin{bmatrix} 0&{}0&{}0&{}-1\\ 0&{}0&{}1&{}0\\ 0&{}1&{}0&{}0\\ -1&{}0&{}0&{}0 \end{bmatrix}. \end{aligned}$$

The value of concurrence $C(\rho _G)$ lies in [0, 1], i.e., if $C(\rho _G) =0$, then the density operator $\rho _G$ represents a separable state otherwise it is considered as entangled; and if $C(\rho _G) =1$ then $\rho _G$ represents a maximally entangled state.

Theorem 4.1

Let (G, a) be a weighted graph on 4 vertices. Suppose the Laplacian L(G) is positive semi-definite having eigenvalues $\lambda _1 \ge \lambda _2 \ge \lambda _3 \ge \lambda _4$. If $\lambda _1 \le \lambda _2+\lambda _3,$ then (G, a) is associated with a two-qubit separable state.

Proof

As the Laplacian L(G) is positive semi-definite the density operator $\rho _G = \frac{1}{{\mathrm{Tr}}(L(G))}L(G)$ is also positive semi-definite. By the definition of $\tilde{\rho _G}$, we have, ${\mathrm{Tr}}(\rho _G)={\mathrm{Tr}}(\tilde{\rho _G})=1$ and $\tilde{\rho _G}$ is positive semi-definite. If $\rho _G$ and $\tilde{\rho _G}$ are two positive semi-definite matrices, then the following are equivalent [22, 29, 36]:

• 1. $\rho _G \tilde{\rho _G}$ is normal, that is, $[\rho _G \tilde{\rho _G}, (\rho _G \tilde{\rho _G})^*]= \rho _G \tilde{\rho _G}(\rho _G \tilde{\rho _G})^*- (\rho _G \tilde{\rho _G})^*\rho _G \tilde{\rho _G}=0.$

• 2. $\rho _G \tilde{\rho _G}$ is positive semi-definite.

The eigenvalues of $\rho _G$ are $\frac{\lambda _1}{\sum \lambda _i} \ge \frac{\lambda _2}{\sum \lambda _i}\ge \frac{\lambda _3}{\sum \lambda _i} \ge \frac{\lambda _4}{\sum \lambda _i}$. Let $\nu _1 \ge \nu _2 \ge \nu _3 \ge \nu _4$ be the eigenvalues of $\tilde{\rho _G}$ and $\mu _1 \ge \mu _2 \ge \mu _3 \ge \mu _4$ be the eigenvalues of matrix $\rho _G \tilde{\rho _G}$. Therefore, $\mu _1 \le \frac{\lambda _1}{\sum \lambda _i} \nu _1 \le \frac{(\lambda _2+\lambda _3 +\lambda _4)}{\sum \lambda _i} \nu _1 \le \mu _2+\mu _3+\mu _4$ [29, 37] which implies the concurrence for $\rho _G$ is equal to 0 as $C(\rho _G)= max(0,\sqrt{\mu _1}-\sqrt{\mu _2}-\sqrt{\mu _3}-\sqrt{\mu _4})$. Hence, (G, a) is associated with a separable state. $\square$

Theorem 4.2

Let (G, a) be a weighted graph on $n=2^m (m=p+q)$ vertices associated with an m-qubit state. Let $(n-2)$ vertices are isolated and there is one edge that lies between the remaining two vertices (loops can also be also considered on them). Suppose, $V(G)=\{ v_{ij}\}$ is the set of vertices, where $i=1,2,\ldots ,2^q$, and $j=1,2,\ldots ,2^p$. The graph (G, a) is entangled if and only if the edge lies between $v_{ij}$ and $v_{2^q-(i-1)~2^p-(j-1) }$ for any j.

Proof

Let (G, a) be a weighted graph on $n=2^m (m=p+q)$ vertices associated with an m-qubit state where $(n-2)$ vertices are isolated. If $V(G)=\{ v_{ij}\}$ is the set of vertices, where $i=1,2,\ldots ,2^q$, and $j=1,2,\ldots ,2^p$ then for a two-qubit state, there are four vertices $|{00}\rangle$, $|{01}\rangle$, $|{10}\rangle$, and $|{11}\rangle$. Therefore, a two-qubit quantum state associated with a weighted graph on 4 vertices is entangled if the edge lies between vertices $v_{ij}$ and $v_{2-(i-1) ~ 2-(j-1)}$, where $i=1,2$ and $j=1,2$.

Similarly, for a three-qubit state, there are eight vertices $( |{000}\rangle , |{001}\rangle , |{010}\rangle , |{011}\rangle , |{100}\rangle , |{101}\rangle , |{110}\rangle , |{111}\rangle )$. Therefore, a quantum state associated with a weighted graph on 8 vertices is entangled if the edge lies between $v_{ij}$ and $v_{2-(i-1)~ 4-(j-1)}$, where $i=1,2$ and $j=1,2,3,4$. Likewise for an m-qubit state, there are $2^m$ vertices $|{ \underbrace{000 \ldots 0}_{m}}\rangle , |{\underbrace{000\ldots 0}_{m-1}1}\rangle ,\ldots , |{0\underbrace{111\ldots 1}_{m-1}}\rangle$, $|{1\underbrace{000\ldots 0}_{m-1}}\rangle , \ldots , |{\underbrace{111 \ldots 1}_{m-1}0}\rangle$, and $|{\underbrace{111 \ldots 1}_{m}}\rangle$ and hence a quantum state associated with a weighted graph on $2^m$ vertices is entangled if edge lies between $v_{ij}$ and $v_{2^q-(i-1)~ 2^p-(j-1)}$, where $i=1,2, \ldots , 2^q$ and $j=1,2, \ldots , 2^p$. $\square$

Theorem 4.3

Let (G, a) be a weighted graph on $n=2^m$ vertices associated with an m-qubit state. If $det(\rho ^1_G) = 0$ then the state associated with (G, a) is separable, where $\rho ^1_G$ is a reduced density operator associated with the first qubit.

Proof

Let $\rho _G =[\rho _{ij}]_{n \times n}$ be a density operator which can be represented as a $2 \times 2$ block matrix, i.e.

$$\begin{aligned} \rho _G = \begin{bmatrix} A &{} B\\ {B^*} &{} C \end{bmatrix}, \end{aligned}$$

(3)

therefore,

$$\begin{aligned} \rho ^1_G=\begin{bmatrix} Tr(A) &{} Tr(B)\\ Tr({B^*}) &{} Tr(C) \end{bmatrix}. \end{aligned}$$

(4)

Since $det(\rho ^1_G) = 0$,

$$\begin{aligned}&(\rho _{11}+\cdots +\rho _{\frac{n}{2}\frac{n}{2}})(\rho _{{\frac{n}{2}+1}{\frac{n}{2}+1}}+\cdots +\rho _{nn})\nonumber \\&\quad -{||(\rho _{1{\frac{n}{2}+1}}+\rho _{2{\frac{n}{2}+2}}+\cdots +\rho _{\frac{n}{2}n}) ||}^2 = 0, \end{aligned}$$

(5)

or

$$\begin{aligned}&(\rho _{11}+\cdots +\rho _{\frac{n}{2}\frac{n}{2}})(\rho _{{\frac{n}{2}+1}{\frac{n}{2}+1}}+\cdots +\rho _{nn})\nonumber \\&\quad ={||(\rho _{1{\frac{n}{2}+1}}+\rho _{2{\frac{n}{2}+2}}+\cdots +\rho _{\frac{n}{2}{n}}) ||}^2. \end{aligned}$$

(6)

From equation (6), if ${||\rho _{1{\frac{n}{2}+1}}+\rho _{2{\frac{n}{2}+2}}+\cdots +\rho _{\frac{n}{2}{n}} ||}^2=0$ then either $(\rho _{11}+ \cdots +\rho _{\frac{n}{2}\frac{n}{2}})=0$ or $(\rho _{{\frac{n}{2}+1}{\frac{n}{2}+1}}+\cdots +\rho _{nn}) = 0$. Therefore, either $\rho _G = \begin{bmatrix} A &{} 0\\ 0 &{} 0 \end{bmatrix}$ or $\rho _G = \begin{bmatrix} 0 &{} 0\\ 0 &{} C \end{bmatrix}$ which suggests that $\rho _{G}$ is separable. On the other hand, if ${||\rho _{1{\frac{n}{2}+1}}+\rho _{2{\frac{n}{2}+2}}+\cdots +\rho _{\frac{n}{2}{n}} ||}^2 \ne 0$, then $\rho _G = \frac{1}{2A} \begin{bmatrix} 1 &{} 1\\ 1 &{} 1 \end{bmatrix} \otimes A$ or $\rho _G =\frac{1}{2A} \begin{bmatrix} 1 &{} i\\ -i &{} 1 \end{bmatrix} \otimes A$, hence, $\rho _G$ is separable. $\square$

Theorem 4.4

Let (G, a) be a weighted graph on $n=2^m$ vertices associated to an m-qubit state with at least two edges and the density operator $\rho _G$ be a block matrix. If $A_{bc} = {A_{cb}}^*$, where $A_{bc}$ is ${bc}^{th}$ block of the density operator $\rho _G$ then one cannot identify whether the underlying state is an entangled or a separable state. If $A_{bc} = i^r B_{bc} +i^s C_{bc} + i^t D_{bc}$ for $b <c$, $r=1$ or 4, $s=2$ or 3, $t=1$ or 2 or 3 or 4, where $B_{bc}$ and $C_{bc}$ are positive semi-definite matrices and $D_{bc}$ is a positive semi-definite diagonal matrix such that

$$\begin{aligned} E_{bb}=A_{bb}-\sum _{c \ne b} (B_{bc}+C_{bc}+D_{bc}) \ge 0, \end{aligned}$$

then the graph G is associated with a separable state.

Proof

Let (G, a) be a weighted graph on $2^n$ $(n=p+q)$ vertices associated with an n-qubit state where the associated density operator $\rho _G$ is a $2^{p} \times 2^{p}$ block matrix such that

$$\begin{aligned} \rho _G= \frac{1}{Tr(L(G))} \begin{bmatrix} A_{11} &{} A_{12}&{} \ldots &{} A_{12^p}\\ A_{21} &{} A_{22}&{} \ldots &{} A_{22^p}\\ \vdots &{} \vdots &{} \vdots &{}\vdots \\ A_{2^p1} &{} A_{2^p2}&{} \ldots &{} A_{2^p2^p} \end{bmatrix} \end{aligned}$$

Here, $A_{bc} = {A_{cb}}^*$, so for $b < c$, $A_{bc}$ can be decomposed as $A_{bc} = i^r B_{bc} +i^s C_{bc} + i^t D_{bc}$ where $r=1$ or 4, $s=2$ or 3, $t=1$ or 2 or 3 or 4. Further, $B_{bc}$ and $C_{bc}$ are positive semi-definite matrices and $D_{bc}$ is a positive semi-definite diagonal matrix. Therefore, if $A_{bc} = {A_{cb}}^*$ then $A_{cb} = (-i)^r B_{bc} + (-i)^s C_{bc} + (-i)^t D_{bc}$. Hence, one can evaluate that $\rho _G$ can be written as convex combination of tensor products if $E_{bb}=A_{bb}-\sum \limits _{c \ne b} (B_{bc}+C_{bc}+D_{bc}) \ge 0$. $\square$

Corollary 4.5

Let $\rho _G= \frac{1}{Tr(L(G))}\begin{bmatrix} A_{11} &{} A_{12}&{} \ldots &{} A_{12^p}\\ A_{21} &{} A_{22}&{} \ldots &{} A_{22^p}\\ \vdots &{} \vdots &{} \vdots &{}\vdots \\ A_{2^p1} &{} A_{2^p2}&{} \ldots &{} A_{2^p2^p} \end{bmatrix}$ be the density operator of a weighted graph (G, a) on $2^{n=p+q}$ vertices where $A_{ij}$ are Hermitian matrices of order $2^q$. If $A_{ij} = B_{ij} - C_{ij} + (-1)^m D_{ij}$ for $i \ne j$ where $B_{ij}$ and $C_{ij}$ are positive semi-definite matrices and $D_{ij}$ is a positive semi-definite diagonal matrix such that

$$\begin{aligned} A_{ii}-\sum _{j \ne i} A_{ij} \ge 0, \text { for all }i \end{aligned}$$

then the graph G is associated with a separable state where $Tr(L(G))= \sum _{i} Tr(E_{ii})+ 2\sum _{i}\sum _{j>i} Tr(B_{ij}) + Tr(C_{ij}) + Tr(D_{ij})$ and $E_{ii}=A_{ii}-\sum \limits _{j \ne i} ( B_{ij}+C_{ij}+D_{ij} )$.

Corollary 4.6

Let G be a weighted graph on $n=2^m$ ($m \ne 0$) vertices associated to an m-qubit state and $\rho _G$ be the density operator with $\rho _G = {\bar{\rho _G}}^{PT}$. If all off diagonal blocks are either positive or negative semi-definite and $A_{ii} \ge \sum \limits _{j \ne i} A_{ij}$, then the state is associate to a separable state.

Theorem 4.7

Let (G, a) be a weighted graph on $n=2^m$ vertices associated to an m-qubit state with at least two edges and the density operator $\rho _G$ be a block matrix. The state associated with the graph G is entangled if and only if $A_{ij} \ne {A_{ji}}^*$, where $A_{ij}$ is ${ij}^{th}$ block of $\rho _G$; and $A_{{ij}'} \ne {A_{{ji}'} }^*$ where $A_{{ij}'}$ is ${ij}^{th}$ block of $\rho _{G'}$ where $\rho _{G'}$ is a density operator obtained after interchanging columns $C_i$ with $C_j$, and corresponding rows $R_i$ with $R_j$ in $\rho _G$.

Proof

Let (G, a) be a weighted graph on $n=2^m$ vertices associated to an m-qubit state with at least two edges. The density operator $\rho _G = \frac{1}{Tr(L(G))}\begin{bmatrix} A_{11} &{} A_{12}&{} \ldots &{} A_{12^p}\\ A_{21} &{} A_{22}&{} \ldots &{} A_{22^p}\\ \vdots &{} \vdots &{} \vdots &{}\vdots \\ A_{2^p1} &{} A_{2^p2}&{} \ldots &{} A_{2^p2^p} \end{bmatrix}$ be a block matrix. Let us further assume that $A_{ij} \ne {A_{ji}}^*$, where $A_{ij}$ is ${ij}^{th}$ block of density operator $\rho _G$, and $A_{{ij}'} \ne {A_{{ji}'} }^*$ where $A_{{ij}'}$ is ${ij}^{th}$ block of $\rho _{G'}$.

Clearly, if the density operator $\rho _G$ of a graph (G, a) on $n=2^m$ vertices is separable then it can be written as a convex combination of the tensor product of density operators $\rho _{1}^{i}$ and $\rho _{2}^{i}$, such that [18]

$$\begin{aligned} \rho _G = \sum _{i} p_i \rho _{1}^{i}\otimes \rho _{2}^{i}, \end{aligned}$$

The separable representation clearly implies that $A_{ij} = {A_{ji}}^*$, which contradicts our assumption. Therefore, graph G associated to the quantum state cannot be written as a convex sum of tensor products of individual subsystems. Hence, the graph G associated to the quantum state is not separable if $A_{ij} \ne {A_{ji}}^*$ and $A_{{ij}'} \ne {A_{{ji}'} }^*$. $\square$

Example 5

Consider the graph $G_1$ associated with an entangled state, and represented as

The density operator for the graph $G_1$ is

$$\begin{aligned} \rho _{G_1}= \frac{1}{6}\left[ \begin{array}{rrrr} 1 &{} -1 &{} 0 &{} 0\\ -1 &{} 3 &{}-1 &{} -1\\ 0 &{} -1 &{} 1 &{} 0\\ 0 &{} -1 &{} 0 &{} 1 \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} {\rho _{G_1}}^{PT}= \frac{1}{6}\left[ \begin{array}{rrrr} 1 &{} -1 &{} 0 &{} -1\\ -1 &{} 3 &{} 0 &{} -1\\ 0 &{} 0 &{} 1 &{} 0\\ -1 &{} -1 &{} 0 &{} 1 \end{array}\right] . \end{aligned}$$

Here, $\rho _{G_1} \ne {{\rho _{G_1}}}^{PT}$ and blocks of $\rho _{G_1}$ are not symmetric matrix after interchanging columns and corresponding rows. Hence, the state associated with $G_1$ is entangled.

Example 6

Rigolin et al. [27, 28] have introduced maximally entangled four qubit states, but following our Theorems (4.4) and (4.7), one can easily show that the states are separable with an absence of genuine four-qubit entanglement. The graph $G_2$ depicted below serves as an example of the above theorem.

A brief description of Example 6 above is presented in the Appendix.

Example 7

The graph $G_3$ depicted below also serves as an example of the above Theorem 4.7.

Clearly, the state associated with the graph $G_{3}$ is entangled as also briefly demonstrated in the Appendix.

Example 8

As another illustration of the theorem, we consider the graph $G_{4}$ where the isolated vertices are not considered.

Similar to the previous example, in this case also the state associated with $G_{4}$ is an entangled state.

Example 9

Let us consider the state [23] $|{W}\rangle = \frac{1}{\sqrt{3}} (|{011}\rangle + e^{i\frac{4\pi }{3}}|{101}\rangle + e^{i\frac{2\pi }{3}}|{110}\rangle )$. Therefore, the density operator corresponding to the state $|{W}\rangle$ can be represented as

$$\begin{aligned} \rho = \frac{1}{{3}}\begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} e^{-{i\frac{4\pi }{3}}} &{} e^{-{i\frac{2\pi }{3}}} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}e^{{i\frac{4\pi }{3}}}&{} 0 &{} 1 &{} e^{{i\frac{2\pi }{3}}} &{} 0 \\ 0 &{} 0 &{} 0 &{} e^{{i\frac{2\pi }{3}}} &{} 0 &{} e^{-{i\frac{2\pi }{3}}} &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{bmatrix} \end{aligned}$$

Considering $\rho$ to be a block matrix, one can clearly show that all blocks are not Hermitian. Hence, using Theorem 4.7, the given state is an entangled state.

Example 10

We now consider another state represented in [23] as $|{z}\rangle = \frac{1}{2} (|{001}\rangle + |{010}\rangle + |{100}\rangle + e^{2i\phi }|{111}\rangle )$. Using the above state, one can express the density operator as

$$\begin{aligned} \rho = \frac{1}{{4}}\begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} e^{-{2i\phi } }\\ 0 &{} 1 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} e^{-{2i\phi } }\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} e^{-{2i\phi } }\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{{2i\phi } } &{} e^{{2i\phi } } &{} 0 &{} e^{{2i\phi } } &{} 0 &{} 0 &{} 1\\ \end{bmatrix} \end{aligned}$$

Similar to the previous example, if we consider $\rho$ to be a $2 \times 2$ block matrix, then the blocks are not Hermitian. Therefore, using Theorem 4.7, the given state is an entangled state.

Example 11

Here, we further extend our discussion by considering the state $\rho (T)$ from [38], represented as $\rho (T) = \frac{1}{Z}$ $\begin{bmatrix} e^{\frac{-\beta J}{2}}&{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{1}{2}e^{\frac{\beta (J-\delta )}{2}}(1+e^{\beta \delta }) &{} \frac{1}{2}e^{i\theta } e^{\frac{\beta (J-\delta )}{2}}(1-e^{\beta \delta }) &{}0\\ 0 &{}\frac{1}{2}e^{-i\theta } e^{\frac{\beta (J-\delta )}{2}}(1-e^{\beta \delta }) &{} \frac{1}{2}e^{\frac{\beta (J-\delta )}{2}}(1+e^{\beta \delta })&{}0\\ 0 &{} 0&{} 0 &{} e^{\frac{-\beta J}{2}} \end{bmatrix}$

where $Z=2e^{-{\frac{\beta J}{2}}}[1+e^{\beta J}cosh{\frac{\beta \delta }{2}}]$, $\beta = \frac{1}{kT}$, and $\delta =2J\sqrt{1+D^2}$.

In this case also, if we consider $\rho$ to be a $2 \times 2$ block matrix then the resultant blocks are not Hermitian. Clearly, the density operator cannot be written as a convex sum of tensor products of density operators. Using Theorem 4.7, if $e^{\frac{\beta (J-\delta )}{2}}(1-e^{\beta \delta }) \ne 0$ then the state is entangled. Alternately, as discussed above, for separability we must have $e^{\frac{\beta (J-\delta )}{2}}(1-e^{\beta \delta }) =0$ which is possible only if $J=0$. Theorem 4.4 further leads us to $E_{bb}=A_{bb}- A_{bc} \ge 0$ confirming that the state is a separable state if $e^{\frac{\beta (J-\delta )}{2}}(1-e^{\beta \delta }) =0$.

Similarly, using Theorem 4.1, for $J=0$ the density operator $\rho (T)$ can be re-expressed as $\rho (T)= \frac{1}{4} \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}$. Here $\lambda _1 =$ $\lambda _2=$ $\lambda _3=$ $\lambda _4$ where $\lambda _{i}$ are eigen values and $\lambda _1<\lambda _2+\lambda _3$, therefore, using Theorem 4.1, the state is a separable state for $J=0$.

Corollary 4.8

Let G be a simple graph on $2^n$ vertices with at least two edges associated with an n-qubit state and $\rho _G$ be the density operator. If $\rho _G \ne {\rho _G}^{PT}$ then G is associated with an entangled state.

Corollary 4.9

Let G be a simple graph on $2^n$ vertices associated with an n-qubit state. If the Laplacian matrix of G is expressed as $L(G)=\left[ \begin{array}{c|c} L_1 &{} 0 \\ \hline 0&{} L_2 \end{array} \right] + \left[ \begin{array}{c|c} D &{} B\\ \hline B&{} D \end{array} \right]$ , where D is a diagonal matrix whose elements are row sum of $-B$, then the graph G is associated with a separable state and $L_1$ and $L_2$ are Laplacian matrices of subgraph of G.

4.1 Entanglement and separability of Block graphs

We now proceed to discuss entanglement and separability in another important class of graphs, i.e., block graphs. For a connected graph G, a vertex $v \in V(G)$ is called a cut-vertex if $G-v$ is not connected. A maximal connected subgraph of G is called a block if it has no cut-vertex. A graph G is known as a block graph if every block of G is a complete graph. For example,

Theorem 4.10

Let (G, a) be a weighted block graph on $2^n$ vertices with k blocks, associated with an n-qubit state. The state associated with the weighted graph (G, a) is entangled if at least one of the blocks of graph is associated with an entangled state.

Proof

Let (G, a) be a weighted block graph having $2^n$ vertices with k blocks. The Laplacian matrix of the graph (G, a) can be written as $L(G)=L_{G_1}+L_{G_2}+ \dots +L_{G_k}$. Therefore, the density operator of the graph (G, a) is, $\rho _G=\frac{1}{Tr(L_{G_1}+L_{G_2}+ \dots +L_{G_k})} [L_{G_1}+L_{G_2}+ \dots +L_{G_k}]$. The density operator $\rho _G$ can be re-expressed as

$$\begin{aligned} \begin{aligned} \rho _G&=\frac{Tr(L_{G_1})}{Tr(L_{G_1}+L_{G_2}+ \dots +L_{G_k})} \Big \{ \frac{1}{Tr(L_{G_1})} [L_{G_1}] \Big \}\\&\quad + \frac{Tr(L_{G_2})}{Tr(L_{G_1}+L_{G_2}+ \dots +L_{G_k})} \Big \{ \frac{1}{Tr(L_{G_2})} [L_{G_2}] \Big \} \\&\quad + \dots +\frac{Tr(L_{G_k})}{Tr(L_{G_1}+L_{G_2}+ \dots +L_{G_k})} \Big \{ \frac{1}{Tr(L_{G_k})} [L_k] \Big \}. \end{aligned} \end{aligned}$$

Assuming the ${r}^{th}$ block of the graph (G, a) to be associated with an entangled state suggests that $A_{{G_r}_{ij}} \ne {(A_{{G_r}_{ji}})}^*$ where $A_{{G_r}_{ij}}$ is ${ij}^{th}$ block of $\rho _{G_r}$ which is a density operator associated with the ${r}^{th}$ block of the graph (G, a). Similarly, $A_{{G_r'}_{ij}} \ne {(A_{{G_r'}_{ij}})} ^*$ where $A_{{G_r'}_{ij}}$ is ${ij}^{th}$ block of $\rho _{G_r'}$ such that $\rho _{G_r'}$ is a density operator after interchanging columns $C_i$ with $C_j$, and corresponding rows $R_i$ with $R_j$ in $\rho _{G_r}$. Clearly, $A_{ij} \ne {(A_{ji})}^*$ and $A_{{ij}'} \ne {(A_{{ji}'})}^*$, where $A_{ij}$ is ${ij}^{th}$ block of $\rho _G$ and $A_{{ij}'}$ is ${ij}^{th}$ block of $\rho _{G'}$ where $\rho _{G'}$ represents a density operator after interchanging columns $C_i$ with $C_j$, and corresponding rows $R_i$ with $R_j$ in $\rho _G$. Therefore, using Theorem (4.7), the weighted block graph is associated with an entangled state. $\square$

Theorem 4.11

Let (G, a) be a weighted block graph on $2^{n}$ vertices associated with a $(n=p+q)$ qubit state. The state associated with the weighted graph (G, a) is separable if vertex sets of blocks are $\{v_{11},v_{12},\dots ,v_{12^q}\}$, $\{v_{21},v_{22},\dots ,v_{22^q}\}$, $\dots$,$\{v_{2^p1},v_{2^p2},\dots ,v_{2^p2^q}\}$, and $\{v_{ij},v_{kl} \}$ for $i \ne k$ where $k \ne 2^p-(i-1)$ and $l \ne 2^q-(j-1)$.

Proof

Let (G, a) be a weighted block graph on $2^{n}$ vertices associated with a $(n=p+q)$ qubit state. For the vertex sets of blocks , i.e., $\{v_{11},v_{12},\dots ,v_{12^q}\}$, $\{v_{21},v_{22},\dots ,v_{22^q}\}$,$\dots$,$\{v_{2^p1},v_{2^p2},\dots ,v_{2^p2^q}\}$, and $\{v_{ij},v_{kl} \}$ for $i \ne k$ where $k \ne 2^p-(i-1)$ and $l \ne 2^q-(j-1)$, the density operator can be expressed as $\rho _G= \frac{Tr(A)}{Tr(L(G))} \Big \{ \frac{1}{Tr(A)} [A] \Big \}+\frac{Tr(B)}{Tr(L(G))} \Big \{ \frac{1}{Tr(B)} [B]\Big \}$ where A is a diagonal block matrix which can therefore be expressed as a tensor product. Clearly B can also be expressed as a tensor product by Theorem (4.2), hence the proof. $\square$

Corollary 4.12

Let G be a simple graph on $2^n$ vertices associated with an n-qubit state. If every vertex of G has degree $k \ge 2$ and G has no cut-vertex, then the graph G is associated with a separable state

Proof

Let G be a simple graph on $2^n$ vertices associated with an n-qubit state. If every vertex of G has degree $k \ge 2$ and G has no cut-vertex, then the graph G is connected and $L(G)=\begin{bmatrix} L_1&{}0\\ 0&{}L_1 \end{bmatrix}+ \begin{bmatrix} D_1&{}B_1\\ {B_1} &{}D_1 \end{bmatrix}$,

where $L_1$ is the Laplacian of a subgraph of the simple graph G . $D_1$ is a diagonal matrix with the i-th diagonal entry equals to sum of absolute value of i-th row (or column) of $B_1$. Hence the proof. $\square$

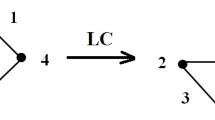
4.2 Entanglement and separability of Star graphs ($S_n$)

We further discuss the properties of star graphs where a star graph ($S_n$) is a complete bipartite graph on $n+1$ vertices or n edges, e.g.,

Theorem 4.13

Let G be a star graph on $2^m$ vertices associated with an m-qubit state. If r vertices are deleted from G then the resulting graph on $2^s$ vertices is associated with an entangled quantum state and $0 \le r \le 2(2^{(m-1)}-1)$.

Proof

Let G be a star graph such that $|{V(G)}|= 2^m$ ($m \ge 2$) and $|{E(G)}|= 2^m-1$. Since a star graph has cut vertices, it will have blocks that are equal in numbers to the number of edges. By Theorem (4.2) at least one of the blocks of the star graph is associated with an entangled state because of the block containing an edge between $v_{ij}$ and $v_{2^q-(i-1)~ 2^p-(j-1)}$, where $i=1,2, \ldots , 2^q$ and $j=1,2, \ldots , 2^p$. Therefore, following Theorem (4.10), the state associated with star graph is an entangled state. If r vertices are deleted from G then the resulting graph $G'$on $2^s$ vertices will also be a star graph. Since every star graph on $2^m$ vertices is entangled, $G'$ is also associated with an entangled state. Clearly, $r = 2^m - 2^s = 2^s(2^{(m-s)} -1)$, where $s=1,2,\ldots ,m$ which shows that $0 \le r \le 2(2^{(m-1)} - 1)$. $\square$

Theorem 4.14

Let G be a star graph on $2^m$ vertices. Adding adjacent edges to the graph G results in $G'$ with blocks having either one edge or three edges. The resultant graph $G'$ will have at least one block which is associated with an entangled state and entanglement measure of blocks of $G'$ would not exceed the entangled measure of blocks of G.

Proof

Let G be a star graph on $2^m$ vertices and $G'$ be the resultant graph after adding r adjacent edges to the graph G, where $1 \le r \le \frac{|{E(G)}|-1}{2}$.

The graph $G'$ contains cut vertices and a minimum of $\frac{|{E(G)}|+1}{2}$ blocks. Since one block ${G_k}'$ of the graph $G'$ contains the edge between vertices $v_{ij}$ and $v_{2^q-(i-1)~ 2^p-(j-1)}$, where $i=1,2, \ldots , 2^q$ and $j=1,2, \ldots , 2^p$, thus by Theorem (4.2) and (4.7), ${G_k}'$ is associated with an entangled state. Further, we know that the degree of entanglement of a simple graph is equal to $\frac{1}{|{E(G)}|}$ for an entangled state and 0 for a separable state [20]; therefore, the degree of entanglement for all blocks of $G'$ can either be 0, or 1 or $\frac{1}{3}$, where the degree of entanglement for all blocks of G is either 0 or 1. Hence proved. $\square$

5 Conclusion

In this article, we demonstrated effective entanglement and separability conditions for weighted, block and star graphs associated with n-qubit states. Our analysis led us to describe entanglement properties of multi-qubit states utilizing characteristics of graphs and density operators. The study presented here is important from the perspective that characterization of weighted, block and star graphs in terms of entanglement and separability is relatively unexplored in comparison with simple graphs. We believe that the results obtained in this article will allow one to address entanglement and separability problem for these classes of graphs in an effective manner.

Appendix

1.1 A brief explanation of Examples (6) and (7)

• 1. Explanation of the example (6)

The density operator for the graph $G_2$ can be represented as

$$\begin{aligned} \rho _{G_2}= \frac{1}{4} \left[ \begin{array}{rrrrrrrrrrrrrrrr} 1&{} 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}-1&{}0&{}0&{}0&{}0&{}-1\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{} 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}-1&{}0&{}0&{}0&{}0&{}-1\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ -1&{} 0&{}0&{}0&{}0&{}-1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ -1&{} 0&{}0&{}0&{}0&{}-1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1 \end{array}\right] \end{aligned}$$

Using $\rho _{G_2}$ , one can verify that $\rho _{G_2} \ne {{\rho _{G_2}}}^{PT}$. Therefore, interchanging columns $C_9$ with $C_{11}$, and $C_{14}$ with $C_{16}$ and corresponding rows $R_9$ with $R_{11}$ and $R_{14}$ with $R_{16}$, we have

$$\begin{aligned}\rho _{G_2} \cong {\rho _{G_2}}'= \frac{1}{4} \left[ \begin{array}{rrrrrrrrrrrrrrrr} 1&{} 0&{}0&{}0&{}0&{}1&{}0&{}0&{}-1&{}0&{}0&{}0&{}0&{}-1&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{} 0&{}0&{}0&{}0&{}1&{}0&{}0&{}-1&{}0&{}0&{}0&{}0&{}-1&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ -1&{} 0&{}0&{}0&{}0&{}-1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ -1&{}0&{}0&{}0&{}0&{}-1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}\right] . \end{aligned}$$

Here, we can see that blocks are symmetric, satisfying the Theorem 4.4. Hence, the state associated with the graph $G_2$ is separable.

• 2. Explanation of the example (7)

Similar to the previous case, the density operator for the graph $G_3$ is expressed as

$$\begin{aligned} \rho _{G_3}= \frac{1}{4} \left[ \begin{array}{rrrrrrrrrrrrrrrr} 1&{} 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}-1\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{} 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}-1\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{} 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}-1\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ -1&{} 0&{}0&{}0&{}0&{}-1&{}0&{}0&{}0&{}0&{}-1&{}0&{}0&{}0&{}0&{}1 \end{array}\right] , \end{aligned}$$

In this case, we can see that we cannot get the symmetric blocks by interchanging the columns and corresponding rows. Therefore, the state associated with the graph $G_3$ is entangled.

1.2 Decomposition of the Laplacian matrix of a simple graph G

Every Laplacian matrix can be decomposed as a sum of Laplacian matrices of subgraphs ($G_1$, $G_2$, and $G_3$) of a graph G [24].

We have

$$\begin{aligned} L= \begin{bmatrix} \sum _{j=1}^{n} a_{1j}&{} -a_{12}&{} \ldots &{} -a_{1n}\\ -a_{21}&{} \sum _{j=1}^{n}a_{2j}&{} \ldots &{} -a_{2n}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ -a_{n1}&{} -a_{n2}&{} \ldots &{}\sum _{j=1}^{n} a_{nj} \end{bmatrix}. \end{aligned}$$

It is easy to see that L(G) can be rewritten as

$$\begin{aligned} L= & {} \begin{bmatrix} \sum _{j=1}^{\frac{n}{2}} a_{1j} &{}-a_{12} &{} \ldots -a_{1\frac{n}{2}}&{} 0&{} 0&{} \ldots &{} 0\\ -a_{21} &{}\sum _{j=1}^{\frac{n}{2}} a_{2j} &{} \ldots -a_{2\frac{n}{2}}&{} 0&{} 0 &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ -a_{\frac{n}{2}1} &{} -a_{\frac{n}{2}2} &{} \ldots \sum _{j=1}^{\frac{n}{2}} a_{\frac{n}{2}j} &{} 0 &{} 0 &{} \ldots &{} 0\\ 0 &{} 0&{} \ldots &{} 0 &{} 0 &{} \ldots &{} 0\\ 0 &{} 0 &{} \ldots &{} 0 &{} 0 &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} 0 &{} 0 &{} \ldots &{} 0 \end{bmatrix} \\&+\begin{bmatrix} 0 &{} 0 &{} \ldots 0 &{} 0&{} 0&{} \ldots &{} 0\\ 0 &{} 0 &{} \ldots 0 &{} 0&{} 0 &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \ldots 0 &{} 0 &{} \ldots &{} 0\\ 0 &{} 0&{} \ldots &{}0&{} \sum _{ j=\frac{n}{2}+1 }^{n} a_{ \frac{n}{2}+1 j } &{} -a_{ \frac{n}{2}+1 \frac{n}{2}+2 } &{} \ldots &{} -a_{ \frac{n}{2}+1 n}\\ 0 &{} 0 &{} \ldots &{}0 &{} -a_{\frac{n}{2}+2 \frac{n}{2}+1} &{} \sum _{j=\frac{n}{2}+1}^{n} a_{\frac{n}{2}+2 j} &{} \ldots &{} -a_{\frac{n}{2}+2 n}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} 0 &{} -a_{n \frac{n}{2}+1} &{} -a_{n \frac{n}{2}+2} &{} \ldots &{}0 &{} \sum _{j=\frac{n}{2}+1}^{n} a_{n j} \end{bmatrix} \\&+ \begin{bmatrix} \sum _{j=\frac{n}{2}+1}^{n} a_{1j}&{} \ldots &{} 0&{}-a_{1 \frac{n}{2}+1 } &{} \ldots &{} -a_{1n}\\ \vdots &{} \vdots &{}\vdots &{} \vdots &{} \vdots &{} \vdots \\ 0&{} \ldots &{} \sum _{j=\frac{n}{2}+1}^{n} a_{\frac{n}{2}j}&{} -a_{ \frac{n}{2} \frac{n}{2}+1 } &{} \ldots &{} -a_{ \frac{n}{2}n}\\ -a_{\frac{n}{2}+1 1} &{} \ldots &{} -a_{ \frac{n}{2}+1 \frac{n}{2}} &{} \sum _{j=1}^{\frac{n}{2}} a_{\frac{n}{2}+1 j} &{} \ldots &{} 0\\ \vdots &{} \vdots &{}\vdots &{} \vdots &{} \vdots &{} \vdots \\ -a_{n1} &{} \ldots &{} -a_{n \frac{n}{2}} &{} 0 &{} \ldots &{} \sum _{j=1}^{\frac{n}{2}} a_{n j}\\ \end{bmatrix}. \end{aligned}$$

To summarize, $L(G)=\begin{bmatrix} L_1&{}0\\ 0&{}0 \end{bmatrix}+ \begin{bmatrix} 0&{}0\\ 0&{}L_2 \end{bmatrix} + \begin{bmatrix} D_1&{}B_1\\ {B_2} &{}D_2 \end{bmatrix}$,

where $L_1$ and $L_2$ are also Laplacian of simple graphs and $D_1$ and $D_2$ are diagonal matrices with the i-th diagonal entry equals to the sum of absolute value of i-th row sum of $B_1$ and $B_2$.