1 Introduction

The quantifiers emerged from quantum information theory have been focused for the characterization of the quantum phase transition (QPT), e.g., quantum correlations [1,2,3,4,5,6,7,8,9,10] and the trace distance [11,12,13,14,15]. These measures are known to be useful to detect the QPT without any prior knowledge of the order parameters. QPT of many-body correlated systems has gained a considerable attention in the recent past and has become one of the interesting topics in the field of condensed-matter physics [16]. A QPT is a change in the behavior of the ground state that is caused at absolute zero temperature where only quantum fluctuations are relevant. Due to a change in an external parameter or a coupling constant, quantum fluctuations induce the QPT [16, 17]. At critical point, the existence of the QPT strongly influences the behavior of many-body systems and has a relation with the divergence of the correlation length and the gap vanishing in the excitation spectrum. The behavior of a many-body system is governed by non-analytic changes in the ground state of the system near the quantum critical points.

The quantification of entanglement may help in finding and characterizing QPT, since it may inherit the non-analytic behavior of the ground state energy [1,2,3,4,5]. Entanglement exhibits the nature of nonlocal correlations in quantum systems and can be considered as a beneficial characteristic of quantum information and a more precise resource of communication in quantum systems [18,19,20]. Quantum computations, quantum cryptography, superdense coding and teleportation of an unknown quantum state are some prominent applications of the quantum entanglement [20]. Most of the work that has been done on the measurement of entanglement is focused on the bipartite entanglement that can be estimated by using many quantifiers, e.g., concurrence [21, 22], von Neumann entropy [23], entanglement of formation [24] and negativity [25]. Bipartite entanglement only gives a partial characterization of a many-body quantum system [26]. The entanglement distribution may be complex in a many-body quantum system, because of more degrees of freedom, than in a two-body quantum system. A common example of an N-partite entangled state to realize some quantum information tasks is an N-qubit Greenberger–Horne–Zeilinger (GHZ) state [19],

$$\begin{aligned} |GHZ \rangle = \frac{1}{\sqrt{2}} \Big (|0 0 \cdots 0 \rangle + | 1 1 \cdots 1 \rangle \Big ). \end{aligned}$$
(1)

The reduced density matrix of the N-partite GHZ state is not an entangled state.

$$\begin{aligned} \rho _{AB}^{GHZ} = \frac{1}{2} \Big ( |0 0 \rangle \langle 0 0| + |1 1 \rangle \langle 1 1 |\Big ). \end{aligned}$$
(2)

Therefore, the bipartite entanglement cannot reveal the characteristics of a many-body quantum system and hence it is important to search for a suitable quantifier of the entanglement that can measure the multipartite entanglement [26], even though the use of entanglement in the study of QPT is complex in many particle systems [4, 5]. Residual entanglement, based on the monogamy inequality, is the most widely used measure of the entanglement between all bi-partitions and is different from the bipartite entanglement [26,27,28,29,30]. Monogamy of entanglement is an important property and it measures the relation of entanglement between different parties for a many-body quantum system [27,28,29,30]. For any arbitrary N-qubit state, a general monogamy inequality is obeyed by the squared entanglement of formation \(E_f^2\) and it indicates that unlike the classical correlations the quantum entanglement cannot be shared freely among three or more parties. Therefore, in a many-body quantum system, the monogamy property can be useful in characterization of the entanglement structure. The multipartite entanglement indicator (MEI) based on the monogamy inequality can effectively quantify the multipartite entanglement by estimating the residual entanglement [31].

Trace distance has been investigated for many one-dimensional spin chains and can also be verified experimentally by quantum state tomography and has been utilized for the study of QPT in a coupled cavity lattice at a finite temperature [14, 15]. It is a metric on the space of the density matrices and is a commonly used quantifier to measure how two states are distinguishable from each other [11]. It is invariant under unitary operations, monotonous under local operations, strongly convex, sub-additive and contractive [12, 13]. Trace distance is different from the fidelity. In the fidelity approach [32, 33], two ground states are compared whose Hamiltonian parameters are slightly varied, whereas a state is compared with its factorized state in trace distance approach.

There are several analytical and numerical approximation methods being used to study the QPT in many-body physics [16, 17]. More specifically the traditional mean field theory, that fails to recognize the quantum fluctuations in spin systems. This problem is overcome by considering the magnetic systems like Heisenberg spin models by using the idea of the renormalization, introduced by Wilson in quantum field theory (QFT). Afterward, based on renormalization, different methods have been introduced to study QPT in many-body systems, such as the quantum renormalization group (QRG) method [34], Monte Carlo renormalization group (MCRG) method [35] and the density matrix renormalization group (DMRG) method [36]. In the framework of DMRG, the trace distance has been studied for the detection of QPT [15]. MCRG and DMRG usually provide more accurate quantitative results as compared to QRG but the calculation of the critical exponents from the scaling behaviors often need high precision that may be computationally expensive for these numerical methods. QRG is an exquisite analytical method for the study of the QPT and the scaling behaviors at absolute zero temperature. QRG has been used to investigate the quantum information properties of critical systems recently and is found to be an efficient and powerful tool to study the QPT in various systems [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. In QRG, we applied Kadanoff’s block approach [52] to reduce the degrees of freedom that is well suited to perform analytical calculations in the lattice models and provide excellent results in higher dimensions [45,46,47,48].

Spin-\(\frac{1}{2}\) XXZ model is one of the simplest models for the one-dimensional anisotropic anti-ferromagnet [53]. In many-body systems, the computation of the renormalized parameters and the critical exponents is a challenging task for the two-dimensional Heisenberg XY model [45, 47], whereas much simpler computations are required for the two-dimensional XXZ model. XXZ model has a better description of the QPT as compared to other spin models. A two-dimensional XXZ model can be used to model the magnetic crystals (e.g., \(\text {K}_{2}\text {CuF}_{4}\), \(\text {ZnPSe}_{3}\) and \(\text {FePS}_{3}\)) [54,55,56], high temperature superconductors (e.g., \(\text {La}_{2}\text {CuO}_{4}\)) [57, 58], magnetic mono-layers (e.g., \(\text {CrI}_{3}\)) [59], super fluid films and lipid layers [60]. Despite the importance of the two-dimensional XXZ model, it has not been studied yet in the framework of QRG [61,62,63].

The paper is arranged as follows; in Sect. 2, we applied the QRG method to the two-dimensional Heisenberg XXZ model to find the renormalized coupling strength and the anisotropy. Sect. 3 explores the dependence of the multipartite entanglement and the trace distance on the anisotropy parameter. In Sect. 4, the renormalization, scaling and the non-analyticity of the derivative of the two quantifiers are studied. Sect. 5 is devoted for the conclusion made on the results obtained.

2 Implementation of QRG

We consider a two-dimensional anisotropic XXZ spin-\(\frac{1}{2}\) lattice of N sites. The Hamiltonian for this system can be written as,

$$\begin{aligned} H(J,\Delta )= & {} \frac{J}{4} \sum _{i=1}^{N} \sum _{j=1}^{N} \big [ (\sigma _{i,j}^x \sigma _{i+1,j}^x + \sigma _{i,j}^x \sigma _{i,j+1}^x ) + (\sigma _{i,j}^y \sigma _{i+1,j}^y + \sigma _{i,j}^y \sigma _{i,j+1}^y ) \nonumber \\&+ \Delta (\sigma _{i,j}^z \sigma _{i+1 ,j}^z + \sigma _{i,j}^z \sigma _{i,j+1}^z )\big ], \end{aligned}$$
(3)

where \(\Delta \) and J represent the anisotropy parameter and the coupling strength between the neighboring sites, respectively. \(\sigma ^{x}, \text { } \sigma ^{y} \text { and } \sigma ^{z}\) are the usual Pauli matrices. The Hamiltonian consists of three terms, the fixed quantum fluctuations in the system are given by the first two terms while an anisotropy parameter \(\Delta \) is introduced in the third term.

We apply Kadanoff’s QRG technique and divide the whole lattice in blocks, as shown in Fig. (1). For each QRG iteration, it is required a minimum number of five sites in a block to produce a self-similar Hamiltonian. We choose site-3, i.e., site-(2, 2) as the central site of each block. The Kadanoff’s procedure requires the decomposition of the total Hamiltonian H into two parts, the intra-block Hamiltonian \(H^B\) and the inter-block Hamiltonian \(H^{BB}\),

$$\begin{aligned} H = H^B + H^{BB} \end{aligned}$$
(4)
Fig. 1
figure 1

Upper panel: two-dimensional spin lattice is divided into blocks each containing five spins interacting with coupling strength J. Lower panel: the effective lattice is depicted by big blocks interacting with renormalized coupling strength \(J^{\prime }\) after QRG evolution

Full size image

The block Hamiltonian \(h_{k}^B\) for an arbitrary k-th block is,

$$\begin{aligned} h_{k}^B= & {} \frac{J}{4} \big [ (\sigma _{(2,2),k}^x \sigma _{(2,1),k}^x + \sigma _{(2,2),k}^x \sigma _{(2,3),k}^x + \sigma _{(2,2),k}^x \sigma _{(1,2),k}^x + \sigma _{(2,2),k}^x \sigma _{(3,2),k}^x ) \nonumber \\&\quad + (\sigma _{(2,2),k}^y \sigma _{(2,1),k}^y + \sigma _{(2,2),k}^y \sigma _{(2,3),k}^y + \sigma _{(2,2),k}^y \sigma _{(1,2),k}^y + \sigma _{(2,2),k}^y \sigma _{(3,2),k}^y ) \nonumber \\&\quad + \Delta (\sigma _{(2,2),k}^z \sigma _{(2,1),k}^z + \sigma _{(2,2),k}^z \sigma _{(2,3),k}^z + \sigma _{(2,2),k}^z \sigma _{(1,2),k}^z + \sigma _{(2,2),k}^z \sigma _{(3,2),k}^z ) \big ], \end{aligned}$$
(5)

and the interaction between k-th and (\(k+1\))-th block is represented by an inter-block Hamiltonian \(h_{k,k+1}^{BB}\) and can be written as,

$$\begin{aligned} h_{k,k+1}^{BB}= & {} \frac{J}{4} \big [ (\sigma _{(2,3),k}^x \sigma _{(2,4),k+1}^x + \sigma _{(2,3),k}^x \sigma _{(1,3),k+1}^x + \sigma _{(2,3),k}^x \sigma _{(3,3),k+1}^x + \sigma _{(3,2),k}^x \sigma _{(3,1),k+1}^x \nonumber \\&\; +\sigma _{(3,2),k}^x \sigma _{(3,3),k+1}^x + \sigma _{(2,1),k}^x \sigma _{(3,1),k+1}^x ) + (\sigma _{(2,3),k}^y \sigma _{(2,4),k+1}^y + \sigma _{(2,3),k}^y \sigma _{(1,3),k+1}^y \nonumber \\&\; + \sigma _{(2,3),k}^y \sigma _{(3,3),k+1}^y + \sigma _{(3,2),k}^y \sigma _{(3,1),k+1}^y + \sigma _{(3,2),k}^y \sigma _{(3,3),k+1}^y + \sigma _{(2,1),k}^y \sigma _{(3,1),k+1}^y ) \nonumber \\&\; + \Delta (\sigma _{(2,3),k}^z \sigma _{(2,4),k+1}^z + \sigma _{(2,3),k}^z \sigma _{(1,3),k+1}^z + \sigma _{(2,3),k}^z \sigma _{(3,3),k+1}^z + \sigma _{(3,2),k}^z \sigma _{(3,1),k+1}^z \nonumber \\&\; + \sigma _{(3,2),k}^z \sigma _{(3,3),k+1}^z + \sigma _{(2,1),k}^z \sigma _{(3,1),k+1}^z ) \big ]. \end{aligned}$$
(6)

The block Hamiltonian (\(H^{B}\)) and inter-block Hamiltonian (\(H^{BB}\)) for the whole lattice are,

$$\begin{aligned} H^{B} = \sum _{k=1}^{N/5} h_{k}^{B} \qquad \text {and} \qquad H^{BB} = \sum _{k=1}^{N/5} h_{k,k+1}^{BB}. \end{aligned}$$

Diagonalization of \(H^B\) gives two possible lowest energy levels, i.e., \(\epsilon _{0}^{1} = -\frac{J}{4} (\Delta + \sqrt{9 \Delta ^2+16} )\) and \(\epsilon _{0}^{2} = -\frac{J}{4} (\Delta + \sqrt{\Delta ^2+24} )\). The degenerate eigenvectors corresponding to the eigenenergy \(\epsilon _{0}^{1}\) are,

$$\begin{aligned} | \psi _{0}^{1} \rangle= & {} \frac{1}{\sqrt{p^2 + 4}} \nonumber \\&\quad \big [p (|\downarrow \downarrow \uparrow \downarrow \downarrow \rangle ) + (|\downarrow \downarrow \downarrow \downarrow \uparrow \rangle + |\downarrow \downarrow \downarrow \uparrow \downarrow \rangle + |\downarrow \uparrow \downarrow \downarrow \downarrow \rangle + |\uparrow \downarrow \downarrow \downarrow \downarrow \rangle ) \big ] \nonumber \\ | \psi _{0}^{2} \rangle= & {} \frac{1}{\sqrt{p^2 + 4}} \nonumber \\&\quad \big [ p (|\uparrow \uparrow \downarrow \uparrow \uparrow \rangle ) + (|\downarrow \uparrow \uparrow \uparrow \uparrow \rangle + |\uparrow \downarrow \uparrow \uparrow \uparrow \rangle + |\uparrow \uparrow \uparrow \downarrow \uparrow \rangle + |\uparrow \uparrow \uparrow \uparrow \downarrow \rangle ) \big ], \end{aligned}$$
(7)

and the degenerate eigenvectors corresponding to the eigenenergy \(\epsilon _{0}^{2}\) are,

$$\begin{aligned} |\phi _{0}^{1} \rangle= & {} \frac{1}{\sqrt{2(2 q^2 + 3)}} \nonumber \\&\quad \big [q (|\downarrow \downarrow \uparrow \downarrow \uparrow \rangle + |\downarrow \downarrow \uparrow \uparrow \downarrow \rangle + |\downarrow \uparrow \uparrow \downarrow \downarrow \rangle + |\uparrow \downarrow \uparrow \downarrow \downarrow \rangle ) + (|\downarrow \downarrow \downarrow \uparrow \uparrow \rangle \nonumber \\&\qquad \qquad \qquad + |\downarrow \uparrow \downarrow \downarrow \uparrow \rangle + |\downarrow \uparrow \downarrow \uparrow \downarrow \rangle + |\uparrow \downarrow \downarrow \downarrow \uparrow \rangle + |\uparrow \downarrow \downarrow \uparrow \downarrow \rangle + |\uparrow \uparrow \downarrow \downarrow \downarrow \rangle ) \big ] \nonumber \\ |\phi _{0}^{2} \rangle= & {} \frac{1}{\sqrt{2(2 q^2 + 3)}} \nonumber \\&\big [ q (|\downarrow \uparrow \downarrow \uparrow \uparrow \rangle + |\uparrow \downarrow \downarrow \uparrow \uparrow \rangle + |\uparrow \uparrow \downarrow \downarrow \uparrow \rangle + |\uparrow \uparrow \downarrow \uparrow \downarrow \rangle ) + (|\downarrow \downarrow \uparrow \uparrow \uparrow \rangle \nonumber \\&\qquad \qquad \qquad + |\downarrow \uparrow \uparrow \downarrow \uparrow \rangle + |\downarrow \uparrow \uparrow \uparrow \downarrow \rangle + |\uparrow \downarrow \uparrow \downarrow \uparrow \rangle + |\uparrow \downarrow \uparrow \uparrow \downarrow \rangle + |\uparrow \uparrow \uparrow \downarrow \downarrow \rangle ) \big ], \end{aligned}$$
(8)

where \(p = -\frac{1}{2} \left( 3 \Delta + \sqrt{9 \Delta ^2 + 16} \right) \), \(q = -\frac{1}{4} \left( \Delta + \sqrt{\Delta ^2 + 24} \right) \), \(|\uparrow \rangle \) and \(|\downarrow \rangle \) are the eigenstates of \(\sigma ^z\).

In Fig. (2), we plot the two lowest eigenenergies (\(\epsilon _{0}^{1}\) and \(\epsilon _{0}^{2}\)). A level crossing is seen at \(\Delta =1\). \(\epsilon _{0}^{1} = -\frac{J}{4} (\Delta + \sqrt{9 \Delta ^2+16} )\) is the lowest energy for \(\Delta > 1\), whereas \(\epsilon _{0}^{2} = -\frac{J}{4} (\Delta + \sqrt{\Delta ^2+24} )\) attains the lowest energy value for \(\Delta < 1\). The degenerate eigenvectors \(|\psi _{0}^{1,2} \rangle \) and \(|\phi _{0}^{1,2} \rangle \) are associated with the eigenenergies \(\epsilon _{0}^{1}\) and \(\epsilon _{0}^{2}\), respectively. The most suitable way is to solve the model separately for different regions, i.e., for \(\Delta > 1\) and \(\Delta < 1\). Here, we cannot follow this scheme because the projection operator constructed by the state vectors \(|\psi _{0}^{1,2} \rangle \) does not reproduce a self-similar Hamiltonian. If we choose the state vectors \(|\phi _{0}^{1,2} \rangle \), the projection operator constructed by these state vectors successfully reproduce the self-similar Hamiltonian but the critical value comes out to be \(\Delta = 5\) that is far beyond the critical value (\(\Delta _c \sim 1\)) calculated in previous literature for two-dimensional XXZ square lattice [64, 65] due to the reason that \(|\phi _{0}^{1,2} \rangle \) are not the degenerate ground states for \(\Delta > 1\). To resolve the problem we have to find some normalized combinations of the state-vectors \(|\psi _{0}^{1,2}\rangle \) and \(|\phi _{0}^{1,2}\rangle \), that should be able to capture the true critical value \(\Delta \sim 1\). We define these combinations as, \(|\chi _{0}^{1}\rangle = \frac{1}{\sqrt{2}} (|\psi _{0}^{1}\rangle - |\phi _{0}^{1}\rangle ) \) and \( |\chi _{0}^{2}\rangle = \frac{1}{\sqrt{2}} (|\psi _{0}^{2}\rangle + |\phi _{0}^{2}\rangle ) \).

Fig. 2
figure 2

Plot shows a comparison of the eigenenergies against anisotropy \(\Delta \) with \(J = 1\)

Full size image

We build the projection operator, \( P_{0}^{k} = |\Uparrow \rangle ^{k} \langle \chi _{0}^{1} | + |\Downarrow \rangle ^{k} \langle \chi _{0}^{2} |\), that projects onto the lowest energy subspace to obtain the required eigenstates. The new bases in the effective Hilbert space are \(|\Uparrow \rangle \) and \(|\Downarrow \rangle \). The projection operator P in factorized form is,

$$\begin{aligned} P=\prod _{k=1}^{N/5} P_{0}^{k}. \end{aligned}$$
(9)

The renormalized Hamiltonian is [37,38,39],

$$\begin{aligned} H \rightarrow H^{eff}= & {} P^{\dagger } H P \nonumber \\= & {} P^{\dagger } H^B P + P^{\dagger } H^{BB} P \nonumber \\= & {} H_{0}^{eff} + H_{1}^{eff}, \end{aligned}$$
(10)

where

$$\begin{aligned} H_{0}^{eff}= & {} P^{\dag } H^{B} P \nonumber \\ H_{1}^{eff}= & {} P^{\dag } H^{BB} P. \end{aligned}$$
(11)

The renormalized Pauli matrices \(\sigma ^{\prime a}\) are,

$$\begin{aligned} P_{0}^{I} \sigma _{i,I}^{a} P_{0}^{I} = \alpha _{i}^{a} \sigma _{I}^{\prime a}, \end{aligned}$$
(12)

with

$$\begin{aligned} \alpha _{1245}^{x} = \alpha _{1245}^{y} = -\frac{3 q}{2(2 q^2+3)} \quad&\text {and}&\quad \alpha _{3}^{x} = \alpha _{3}^{y} = -\frac{3}{2(2 q^2+3)} \nonumber \\ \alpha _{1245}^{z} = -\frac{(p^2 (q^2+3) +6)}{2(p^2+4)(2q^2+3)} \quad&\text {and}&\quad \alpha _{3}^{z} = \frac{3 p^2 - 8 q^2}{(p^2+4)(2q^2+3)}, \end{aligned}$$
(13)

where the indices 1, 2, 3, 4 and 5 indicate the sites in a single block as shown in Fig. (1). The effective Hamiltonian of the renormalized two-dimensional XXZ spin lattice is again a two-dimensional XXZ spin lattice with the renormalized parameters, i.e., the renormalized coupling strength \(J^{\prime }\) and renormalized anisotropy \(\Delta ^{\prime }\),

$$\begin{aligned} H^{eff}= & {} \frac{J^{\prime }}{4} \sum _{i=1}^{N/2} \sum _{j=1}^{N/2} \big [ (\sigma _{i,j}^x \sigma _{i+1 ,j}^x + \sigma _{i,j}^x \sigma _{i,j+1}^x ) + (\sigma _{i,j}^y \sigma _{i+1 ,j}^y + \sigma _{i,j}^y \sigma _{i,j+1}^y ) \nonumber \\&\qquad \qquad + \Delta ^{\prime } (\sigma _{i,j}^z \sigma _{i+1 ,j}^z + \sigma _{i,j}^z \sigma _{i,j+1}^z )\big ], \end{aligned}$$
(14)

where the renormalized parameters are

$$\begin{aligned} J^{\prime }= & {} J\Big (\frac{3q}{2(2 q^2+3)} \Big )^2 \nonumber \\ \Delta ^{\prime }= & {} \Delta \Big (\frac{(p^2 (q^2+3)+6)}{3q(p^2+4)} \Big )^2. \end{aligned}$$
(15)

To find the fixed points of the QRG equations, we put \(\Delta ^{\prime } = \Delta \) and compute the values of \(\Delta \), i.e., \(\Delta = 0, \; 1 \; \text {and} \; \Delta \rightarrow \infty \). \(\Delta = 0 \; \text {and} \; \Delta \rightarrow \infty \) represent the stable fixed points whereas \(\Delta = 1\) is the unstable fixed point that also represents the critical point \(\Delta _{c}\). For \(\Delta > 1\), the coupling strength parameter tends to be infinite which shows that the model goes down to the Ising model universality class, whereas for \(0 \le \Delta < 1\), the model approaches the stable fixed point \(\Delta = 0\). We may classify two different phases and the transition between the two phases can be achieved by the QRG technique.

3 Entanglement in two-dimensional XXZ spin lattice

3.1 Multipartite entanglement

In many-body quantum systems, more than two parties cannot freely share the entanglement because of the monogamy property of the entanglement. For an N-qubit system \(H_{X_1}\otimes H_{X_2} \cdots \otimes H_{X_N}\), an entanglement measure satisfies the monogamous relation if the entanglement of the particles \(X_1, X_2, X_3, \cdots , X_N \) satisfies the inequality,

$$\begin{aligned} E_{X_1|X_2, X_3,...,X_N} \ge E_{X_1 X_2} + E_{X_1 X_3} +.....+ E_{X_1 X_N}, \end{aligned}$$
(16)

where \(E_{X_1 X_j}\) with \( j=2,3, \cdots ,N \;\text {and}\; j \ne 1 \), is the entanglement quantification in two qubit system and \(E_{X_1|X_2, X_3, \cdots , X_N}\) is the entanglement quantification in the partition \(X_1 | X_2, X_3, \cdots , X_N \).

According to the Schmidt decomposition for an N-qubit pure state \(|\psi \rangle _{X_1 | X_2,...,X_N}\) [66], the subsystem \(X_2, \cdots , X_N \) is equal to a logic qubit \(X_{2, \cdots ,N}\) or \(X_R\). It means that by utilizing the equation for a two qubit state \(\rho _{XY}\) the bipartite entanglement of formation \(E_{XY}\) can be computed as a function of concurrence \(C_{XY}\) [22].

$$\begin{aligned} E_{XY} = h\Big (\frac{1 + \sqrt{1 - C^{2}_{XY}}}{2}\Big ), \end{aligned}$$
(17)

where \(h(x) = -x\log _{2}(x) - (1-x)\log _{2}(1-x)\) is the Shannon binary entropy and the concurrence \(C_{XY}\) is [22],

$$\begin{aligned} C_{XY} = \max \{0, \sqrt{\lambda _1} - \sqrt{\lambda _2} - \sqrt{\lambda _3} - \sqrt{\lambda _4} \}, \end{aligned}$$
(18)

\(\lambda _{i} (i=1,2,3,4)\) are the nonnegative eigenvalues of the matrix \(\rho _{XY} (\sigma _y \otimes \sigma _y)\rho ^{*}_{XY} (\sigma _y \otimes \sigma _y)\) in descending order. The multipartite entanglement of formation \(E_{X_1|X_2, X_3, \cdots , X_N}\) can be computed for both pure and mixed states. For a pure state,

$$\begin{aligned} E_{X_1|X_2, X_3, \cdots , X_N} = S (\rho _{X_1}) = \sum _{k} \lambda _{k} \; \log _{2} (\lambda _{k}), \end{aligned}$$
(19)

where \( S (\rho _{X_1}) \) is the von Neumann entropy with \(\lambda _{k}\) are the eigenvalues of \(\rho _{X_1}\). For a mixed state, it can be computed by Koashi–Winter formula [67], by a purified state \(|\psi \rangle _{X_1 | X_2, \cdots ,X_N}\) with \(\rho _{X_1 | X_2, \cdots ,X_N} = Tr_{R} (|\psi \rangle \langle \psi |) = tr_{R}(\rho _{X_2, X_3, \cdots ,X_N})\),

$$\begin{aligned} E_{X_1|X_2, X_3, \cdots , X_N} = D(X_1 |X_R) + S(X_1 |X_R), \end{aligned}$$
(20)

where \(S(X_1 |X_R) = S(X_1 X_R) - S(X_R) \) is the quantum conditional entropy and \(D(X_1 | X_R)\) is the quantum discord [68,69,70,71,72],

$$\begin{aligned}&D(X_1 | X_R) = \min _{M_k} \sum _{k} p_k S(X_1 | X^R_k) - S(X_1 |X_R)\nonumber \\&\quad = \min _{M_k} \sum _{k} p_k S(\rho _{{(X_1)}_k}) - S(X_1 |X_R), \end{aligned}$$
(21)

where \(\{M_k\}\) is a complete set of projection operators performed locally on the subsystem \(X_R\) and the minimum running over all possible positive operator-valued measures.

We have already discussed that for an arbitrary N-qubit mixed state the monogamy inequality is obeyed by the squared entanglement of formation \(E_f^2\). The proposed MEI \(\tau \) for the quantification of the multipartite entanglement can be written as,

$$\begin{aligned} \tau _{X_1|X_2, X_3, \cdots ,X_N} = E^2_{X_1 |X_2, \cdots ,X_N} - \sum _{j\ne 1} E^2_{X_1 |X_j}. \end{aligned}$$
(22)

To calculate \(\tau \) for the two-dimensional XXZ spin lattice, the density matrix \(\rho \) is computed by considering one of the degenerate ground states \(|\psi _{0}^{1}\rangle \),

$$\begin{aligned} \rho = |\psi _{0}^{1} \rangle \langle \psi _{0}^{1}|. \end{aligned}$$
(23)

It has been mentioned earlier that in our five site model the middle site is the site-3. When we trace out four subsystems, we get the density operators of the individual subsystems, which are \(\rho _{1} = \rho _{2} = \rho _{4} = \rho _{5} \ne \rho _{3}\), where \(\rho _{1} = Tr_{2345} (\rho )\). If three subsystems are traced out, the reduced density operators of the neighboring sites are, \(\rho _{12} = \rho _{14} = \rho _{15} \ne \rho _{13} \) and \(\rho _{13} = \rho _{23} = \rho _{34} = \rho _{35}\). Following this, we can find the pairwise entanglement of formation, \(E_{12} = E_{14} = E_{15} \ne E_{13}\) and \(E_{13} = E_{23} = E_{34} = E_{35}\) [73]. The reduced density matrices \(\rho _{12}\) and \(\rho _{13}\) can be computed from the density matrix \(\rho \) by using the definition of partial trace,

$$\begin{aligned} \rho _{12} = \frac{1}{\left( p^2 + 4\right) } \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} \left( p^2 + 2\right) \\ \end{array} \right) , \quad \rho _{13} = \frac{1}{\left( p^2 + 4\right) } \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} p &{} 0 \\ 0 &{} p &{} p^2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 3 \\ \end{array} \right) . \end{aligned}$$
(24)
Fig. 3
figure 3

Variation of the MEIs \(\tau _3\) (symmetric) and \(\tau _1\) (non-symmetric) versus anisotropy \(\Delta \)

Full size image

The symmetric and non-symmetric MEIs can be computed by using Eq. (22) and in our five-partite case,

$$\begin{aligned} \tau _{3 | 1245} = E^{2}_{3 | 1245} - \big ( E^{2}_{13} + E^{2}_{23} + E^{2}_{34} + E^{2}_{35} \big ). \end{aligned}$$
(25)

In a similar way, we can compute the MEI for the non-symmetric case,

$$\begin{aligned} \tau _{1 | 2345} =E^{2}_{1 | 2345} - \big ( E^{2}_{12} + E^{2}_{13} + E^{2}_{14} + E^{2}_{15} \big ). \end{aligned}$$
(26)

For the convenience, we denote the indicators as \(\tau _{3}\) and \(\tau _{1}\) for the symmetric and non-symmetric case, respectively. The multipartite entanglement can be distinguished by using the definition of MEIs, \(\tau _{3}\) and \(\tau _{1}\). To find the analytical forms of \(\tau _{3}\) and \(\tau _{1}\), we have to solve Eqs. (17)–(19) and then use in Eqs. (25)–(26). To avoid complexity, we list only the symmetric MEI, \(\tau _3\). It is clear that \(\tau _{3}\) and \(\tau _{1}\) are the functions of the anisotropy \(\Delta \) only. In Fig. (3), the variation of the MEIs \(\tau _{3}\) and \(\tau _{1}\) with the anisotropy parameter \(\Delta \) is shown. We note that the value of \(\tau _3\) is effectively greater than \(\tau _1\) for \(\Delta < 5\), since site-3 is directly correlated with the other four sites, whereas site-1 is not directly correlated with the other sites except site-3. Both \(\tau _{3}\) and \(\tau _{1}\) decrease with an increase in anisotropy parameter \(\Delta \) and have almost similar behavior. Therefore, we only consider the symmetric MEI \(\tau _{3}\) for detailed analysis. For instance, we discuss shortly the ratios of the MEIs with the pairwise entanglement to highlight the importance of the monogamy property in a many-body quantum system. It can be seen in Fig. (4) that the ratios \(\frac{\tau _{3}}{E_{13}}\), \(\frac{\tau _{3}}{E_{34}}\) and \(\frac{\tau _{3}}{E_{3|1245}}\) decrease with an increase in anisotropy \(\Delta \) as in the case of \(\tau _3\). \(\frac{\tau _{3}}{E_{13}}\) and \(\frac{\tau _{3}}{E_{34}}\) are same for any value of anisotropy \(\Delta \), since the pairwise entanglement \(E_{13}\) and \(E_{34}\) are equal because of symmetry. For non-symmetric case, the plots of the ratios \(\frac{\tau _{1}}{E_{12}}\), \(\frac{\tau _{1}}{E_{13}}\) and \(\frac{\tau _{1}}{E_{1|2345}}\) are shown in Fig. (5). We would like to point out that the effect of the anisotropy \(\Delta \) on these ratios are similar to the symmetric ones. Moreover, the ratio \(\frac{\tau _{1}}{E_{12}}\) remains stronger than the ratio \(\frac{\tau _{1}}{E_{13}}\) for a wide range of anisotropy. This difference is because of the pairwise entanglement \(E_{13}\) is stronger than \(E_{12}\), as site-1 and site-2 are not directly correlated. Furthermore, at \(\Delta = 0\) the value of \(\tau _3\) is approximately four times greater than \(\tau _1\) while the ratio \(\frac{\tau _{3}}{E_{3|1245}}\) is twice of the value of \(\frac{\tau _{1}}{E_{1|2345}}\) and hence strengthens the fact that the entanglement distribution in a many-body quantum system is more complex than in a two-body system. The analytical form of the MEI \(\tau _3\) is,

$$\begin{aligned} \tau _{3}= & {} -\frac{1}{4 (\ln {2})^2} \Big [\left( 2+\sqrt{s^2+3}\right) \nonumber \\&\quad \ln \left( \frac{1}{4} \left( 2+\sqrt{s^2+3}\right) \right) +\left( 2-\sqrt{s^2+3}\right) \ln \left( \frac{1}{4} \left( 2-\sqrt{s^2+3}\right) \right) \Big ]^2 \nonumber \\&\qquad +\frac{1}{4 (\ln {2})^2} \Big [ (1-s) \ln \left( \frac{1-s}{2}\right) +(1+s) \ln \left( \frac{1+s}{2}\right) \Big ]^2 , \end{aligned}$$
(27)

where \(s = \frac{p^2 - 4}{p^2 + 4}\). Since \(p = -\frac{1}{2} \left( \sqrt{9 \Delta ^2 + 16} + 3 \Delta \right) \); consequently, the MEI \(\tau _3\) is a function of anisotropy \(\Delta \) only.

Fig. 4
figure 4

The ratios of the symmetric MEI to the entanglement of formation are plotted against anisotropy \(\Delta \), a \(\frac{\tau _{3}}{E_{13}}\) and \(\frac{\tau _{3}}{E_{34}}\) and b \(\frac{\tau _{3}}{E_{3|1245}}\)

Full size image
Fig. 5
figure 5

The ratios of the non-symmetric MEI to the entanglement of formation are plotted against anisotropy \(\Delta \), a \(\frac{\tau _{1}}{E_{12}}\) and \(\frac{\tau _{1}}{E_{13}}\) and b \(\frac{\tau _{1}}{E_{1|2345}}\)

Full size image

3.2 Trace distance

Along with the QRG method, we apply the trace distance measure (TD) for the investigation of QPT of the two-dimensional XXZ spin lattice. The numerical value of trace distance varies from 0 to 1. \(TD \text { }=\text { } 0\) if and only if the two states are identical and \(TD \text { }=\text { } 1\) if the two states are maximally non-identical. Trace distance has been verified as a successful quantifier to capture the QPT for one-dimensional XXZ and XY spin chains [48, 49]. If the positive operators \(\rho _X\) and \(\rho _Y\) represent two quantum states, then the TD is defined as half the trace norm of \(\rho _X - \rho _Y\),

$$\begin{aligned} TD(\rho _X, \rho _Y) = \frac{1}{2} \Vert \rho _{X} - \rho _{Y} \Vert . \end{aligned}$$
(28)

The trace norm of the operator \(\rho _{X} - \rho _{Y}\) is, \(\Vert \rho _{X} - \rho _{Y}\Vert = Tr |\rho _{X} - \rho _{Y}| = Tr \sqrt{(\rho _{X} - \rho _{Y})^{\dagger } (\rho _{X} - \rho _{Y})}\). TD can also be calculated using the eigenvalues \(\lambda _j\) of the operator \(\rho _{X} - \rho _{Y}\) by using the following relation,

$$\begin{aligned} TD(\rho _X, \rho _Y) = \frac{1}{2} \sum _j |\lambda _{j}| = \frac{1}{2} \sum _j \sqrt{\lambda ^{*}_{j} \lambda _{j}}. \end{aligned}$$
(29)

In our model, there are five sites per block so we calculate the TD between the state \(\rho = |\psi _{0}^{1} \rangle \langle \psi _{0}^{1}| \) and its marginal state \(\rho _{1234} \otimes \rho _{5}\), where \(\rho _{1234} = Tr_{5} (\rho )\) and \(\rho _{5} = Tr_{1234} (\rho )\). Thus,

$$\begin{aligned} TD = \frac{1}{2} \Vert \rho _{12345} - \rho _{1234} \otimes \rho _{5} \Vert . \end{aligned}$$
(30)

We find the analytical form of the trace distance TD and further utilize it to find the criticality of the model.

$$\begin{aligned} TD = \frac{1}{2} \Big [\Big | \frac{p^2+3}{\left( p^2+4\right) ^2} \Big | + \Big | \frac{p^2+5}{\left( p^2+4\right) ^2} \Big | + \frac{2}{| p^2+4 | ^2} \Big ], \end{aligned}$$
(31)

where \(p = -\frac{1}{2} \left( \sqrt{9 \Delta ^2 + 16} + 3 \Delta \right) \). Hence, the trace distance TD is a function of anisotropy \(\Delta \) only. In Fig. (6), the TD is plotted against the anisotropy \(\Delta \). The plot is similar to that of the MEI \(\tau _3\), a decrease in the entanglement quantifier with an increase in anisotropy \(\Delta \).

Fig. 6
figure 6

Variation of the trace distance (TD) between the neighboring sites, e.g., (site-1 and -5) versus anisotropy \(\Delta \)

Full size image

4 Criticality in two-dimensional XXZ spin lattice

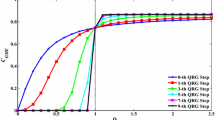
The plots of the MEI, \(\tau _{3}\) as a function of the anisotropy parameter \(\Delta \) for different numbers of QRG iterations are shown in Fig. (7). After enough QRG iterations, it can be seen that the plots of \(\tau _{3}\) cross each other at the critical point \(\Delta _c = 1\) and there are two non-identical saturated values of \(\tau _{3}\). \(\tau _{3} \rightarrow 0 \), in the Ising limit and \( \Delta > 1 \), can be due to the lack of the quantum correlations. \(\tau _{3} \approx 0.5 \) for \( 0 \le \Delta < 1 \), and that may be due to the transverse interactions and any long range order may be destroyed. These two, unlike saturated values of \(\tau _{3}\) represent two separate phases, the Néel phase (\(\Delta > 1 \)) and the spin-fluid phase (\( 0 \le \Delta < 1 \)). The divergence between the two phases is more clear for the large-sized systems as in the case of one-dimensional XXZ spin chain [9].

A non-analytic behavior at a critical point in some physical quantity is an attribute of QPT. Quantum critical point is characterized by scale invariance and universality, dictated by the symmetry. The existence of the quantum critical point has large influence on the physics near the critical value \(\Delta _c\) at absolute zero, where a system undergoes a QPT between two distinct stable phases [74]. A QPT approach mainly focuses on the identification of an order parameter that quantifies the symmetry breaking [48]. Furthermore, at critical point, the correlation length is divergent and hence leads to a scaling behavior [19]. It has been verified that the entanglement for an Ising transverse field and for XX model in a transverse field shows a scaling behavior in the vicinity of the critical point [2]. For the two-dimensional XXZ model, the entanglement between a block and the rest of the system shows an extreme at the critical point. It has been discussed that for the two-dimensional XXZ model, a large system (\(N = 5^{n+1} \)) can be described effectively by five sites per block with the renormalized coupling parameters of the n-th QRG iteration. Thus, the entanglement between the two parties of the system each containing \(\frac{N}{5}\) effective sites can be represented by the entanglement between the two renormalized sites.

Fig. 7
figure 7

Evolution of MEI \(\tau _{3}\) versus anisotropy \(\Delta \) for different numbers of QRG iterations

Full size image
Fig. 8
figure 8

The divergence of first derivative of MEI \(\tau _{3}\) with increasing number of QRG iterations is plotted in the range \(0 \le \Delta \le 3\)

Full size image
Fig. 9
figure 9

a A straight line shows the scaling behavior of \(\Delta _m\) in terms of system size N, where \(\Delta _m\) is the position of the minimum in Fig. (8). b A linear plot of \(\ln \big |\frac{d\; \tau _{3} }{d\Delta } \big |_{\Delta _{m}}\) against \(\ln N \), shows a scaling behavior

Full size image

For increasing QRG iterations, we plot \(\frac{d \tau _{3}}{d\Delta }\) versus \(\Delta \) in Fig. (8), that shows the non-analytic behavior near the critical point as the thermodynamic limit is achieved. The non-analyticity is because of the discontinuous change of \(\tau _{3}\) at \(\Delta _{c} = 1\), in the thermodynamic limit. In Fig. (9), we estimate the critical exponent \(\mu _1 \simeq 0.15\) by plotting the \(\log \) of the equation \(\Delta _{m} = \Delta _{c} + N^{-\mu _1} \), where \(\Delta _{m}\) is the value of anisotropy where \(\frac{d \tau _{3}}{d\Delta }\) is minimum. Near the critical point, the behavior of the correlation length \(\xi \) refers to the scaling of the position of \(\Delta _{m}\). The correlation length covers the system size, i.e., \(\xi \sim N \), as the thermodynamic limit is reached. On comparison with \(\xi \sim (\Delta _{m} - \Delta _{c})^{-\nu } \), we can compute the expression \(\Delta _{m} = \Delta _{c} + N^{1/\nu } \), the scaling form of \(\Delta _{m}\), that implies that the critical exponent \(\mu _{1}\) and the correlation length exponent \(\nu \) are inverse of each other, \(\mu _{1} = \nu ^{-1}\) [19]. Furthermore, the scaling behavior of \(\big |\frac{d \tau _{3}}{d\Delta } \big |_{\Delta _{m}}\) versus N can be extrapolated. Figure (9) shows a linear graph between \(\ln \big |\frac{d \tau _{3}}{d\Delta } \big |_{\Delta _{m}} \) and \(\ln N \). From it we can easily deduce that \(\big |\frac{d \tau _{12}}{d\Delta } \big |_{\Delta _{m}} \sim N^{\mu _{2}}\), where the critical exponent \(\mu _{2} \simeq 0.13 \). Near the critical point, the correlation length exponent \(\nu \) predicts the behavior of the correlation length \(\xi \) near the critical point \(\Delta _{c}\), by following the relation \(\xi \sim (\Delta -\Delta _{c})^{-\nu }\). After first QRG iteration, the correlation length scales as \(\xi \rightarrow \xi ^{(1)} = \xi /n_{B} \), where \(n_{B} = 5\) is the number of sites in each individual block. The n-th QRG iteration for the correlation length can be predicted as, \(\xi ^{(n)} \sim (\Delta _{n} -\Delta _{c})^{-\nu } = \xi /n_{B}^{n}\). The above mentioned expressions are useful to relate \(\big |\frac{d\Delta _{n}}{d\Delta } \big |_{\Delta _{c}}\) and the correlation length exponent \(\nu \) by an equation, \(\big |\frac{d\Delta _{n}}{d\Delta } \big |_{\Delta _{c}} = N^{1/\nu }\). Therefore, by comparison the correlation length exponent \(\nu \) and the critical exponent \(\mu _{2}\) can be related to each other, \(\mu _{2} = \nu ^{-1}\), similar to that in case of the bipartite entanglement [8]. These results endorse that the implementation of the QRG on the multipartite entanglement genuinely captures the criticality (at \(\Delta = 1\)) of the two-dimensional XXZ model.

Moreover, we would like to indicate that instead of bipartite entanglement, multipartite entanglement might be a more suitable indicator for studying QPT in the spin lattice systems. To capture many-body characters in a spin lattice system the ability of the bipartite entanglement is limited. Although the bipartite entanglement has been proven a good indicator that successfully captures the quantum critical points but it may fail to characterize the true quantum critical points [75, 76]. We computed the multipartite entanglement to explore the characters of many-body systems and found it a better indicator as compared to the bipartite entanglement because we may lose some important information about the many-body system. It means that the multipartite entanglement provides a better view and a deeper physical insight into the characteristics of a many-body system and may be more advantageous than the bipartite entanglement to reveal the QPT of spin chain systems [77,78,79].

Fig. 10
figure 10

Evolution of the trace distance TD versus anisotropy \(\Delta \) for few QRG iterations

Full size image
Fig. 11
figure 11

The divergence of first derivative of trace distance TD for few QRG iterations is plotted in the range \(0 \le \Delta \le 3\)

Full size image
Fig. 12
figure 12

a The scaling behavior of \(\Delta _m\) in terms of system size N is represented by a straight line, where \(\Delta _m\) is the position of the minimum of \(\frac{d\; TD }{d\Delta }\) in Fig. (11). b A linear plot of \(\ln \big |\frac{d\; TD }{d\Delta } \big |_{\Delta _{m}}\) against \(\ln N \) shows a scaling behavior

Full size image

The trace distance TD is also capable to capture the QPT point. In Fig. (10), it can be seen that TD attains different saturated values for the regions \(0 \le \Delta < 1\) and \(\Delta > 1\). Here, \(\Delta =1\) represents the QPT point as mentioned earlier in the case of \(\tau _{3}\). To observe the criticality in the model, the first derivative of the trace distance, \(\big |\frac{d\; TD}{d\Delta } \big |\) is analyzed. Figure (11) shows a singular behavior of \( \big |\frac{d\; TD}{d\Delta } \big |\) at the critical point with increasing QRG iterations. The scaling behavior of both \(\Delta _{m}\) and \(\big |\frac{d\; TD}{d\Delta } \big |\) is plotted in Fig. (12). \(\Delta _m\) are the values where the first derivative of the trace distance TD is minimum. It represents that \(\Delta _{m}\) scales as \(\Delta _{m} = \Delta _{c} + N^{-\mu _{3}}\), where \(\mu _{3} \simeq 0.15 \). Furthermore, the scaling of the derivatives of TD and \(\tau _{3}\) resemble with each other, and \(\big |\frac{d\; TD}{d\Delta } \big |_{\Delta _{m}} \sim N^{\mu _4}\), where \(\mu _{4} \simeq 0.13 \), for a large-sized system. The two critical exponents (\(\mu _{3}\; \text {and} \; \mu _{4} \)) obtained by the trace distance TD are in agreement with the ones computed by the MEI \(\tau _3\). Near the critical point, these critical exponents are related to the correlation length exponent \(\nu \). It indicates that in the limit of large scale behavior both the entanglement measures, the MEI \(\tau _{3}\) and the trace distance TD, scales in the same manner and both are capable to depict the ground state characteristics and show distinctive behavior at the critical point. Apart from this, the alike characteristics govern to estimate the consistent critical exponents for the MEI (\(\mu _{1} \approx \mu _{2} \)) and for the trace distance (\(\mu _{3} \approx \mu _{4} \)) that presents the universality of the QPT and shows that the chosen physical quantity does not affect the existence of the QPT.

5 Conclusion

We computed the two entanglement quantifiers, MEI (\(\tau \)) and the trace distance (TD) for the two-dimensional Heisenberg XXZ model. We explored the dependence of the MEI and trace distance on anisotropy parameter \(\Delta \). We found that the multipartite entanglement is a better indicator as compared to the bipartite entanglement and provides more physical insight of a many-body quantum system. The QRG method is implemented to the two-dimensional XXZ model to produce the self-similar Hamiltonian and the renormalized coupling parameters are obtained. Both quantifiers are equally capable to capture the QPT at the critical point \(\Delta _c =1\). Besides the similar behavior of both the quantifiers, the critical exponents too are consistent. At critical point, the non-analytic behavior of the first derivative of the quantifiers represents that the model obeys the scaling behavior in the thermodynamic limit.